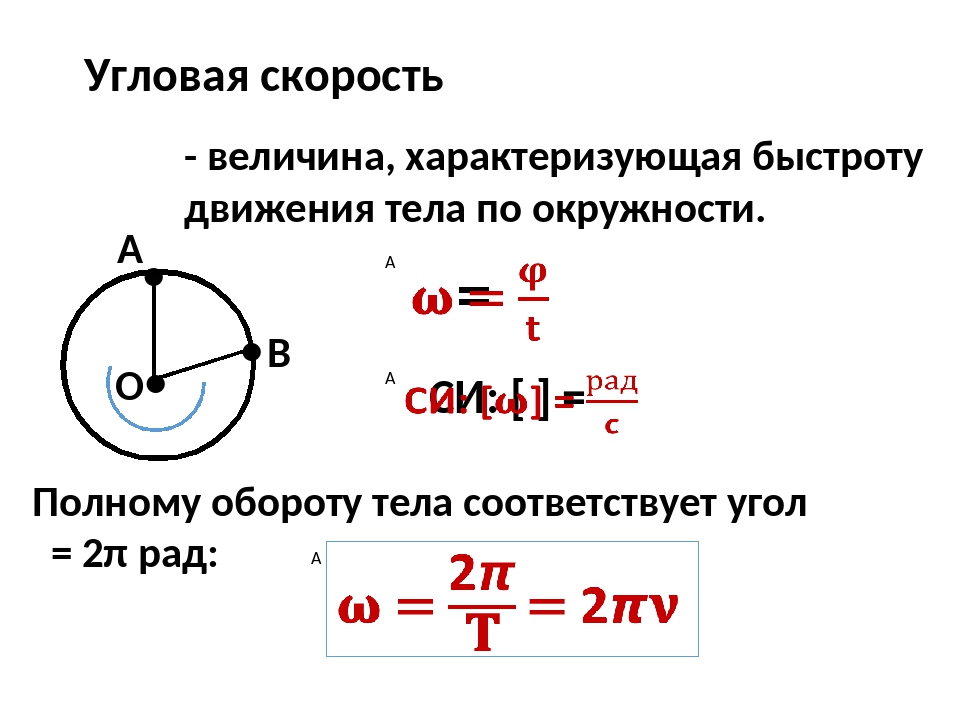
Линейная скорость вращения: Движение точки по окружности. Твердое тело
Линейная скорость: формула нахождения
С точки зрения физики абсолютного покоя не существует. Каждое тело и частицы, которые его составляют, находятся в постоянном движении друг относительно друга. Важной кинематической величиной, характеризующей движение, является скорость. В данной статье приведем формулы линейной скорости для различных типов перемещения тел в пространстве.
Что такое линейная скорость?
Речь идет о физической величине, которая показывает, какое расстояние в пространстве проходит тело за единицу времени. Как правило, скорость обозначают буквой v¯, где символ черты говорит о том, что она является векторной величиной. Измеряется скорость в метрах в секунду (м/с), километрах в час (км/ч), милях в час (мил/ч) и других единицах, предполагающих отношение расстояния ко времени.
Вектор скорости v¯ показывает направление реального перемещения тела. Этим он отличается от вектора ускорения, который направлен в сторону действующей силы, но не в сторону движения тела, хотя они могут совпадать.
Мгновенная и средняя скорости
Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
v¯ = dl¯/dt.
Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
v¯ = Δl¯/Δt, где Δt>>dt.
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Равномерное движение по прямой линии
Это идеализированный тип движения, который предполагает, что тело в течение некоторого промежутка времени движется вдоль прямой в пространстве. При этом скорость тела не меняется. Обозначая пройденный путь символом l, получаем формулу:
l = v*t.
Здесь v = const.
Этот тип движения рассматривался еще философами Античной Греции. Они полагали, что для движения тел необходимо прикладывать некоторую силу, поэтому естественным состоянием всех окружающих объектов является покой. Только с приходом эпохи Возрождения благодаря работам Галилея и Ньютона было показано, что если на тело не воздействуют внешние силы, то равномерность и прямолинейность его движения не нарушается.
Скорость при движении по прямой с ускорением
Когда появляется внешняя сила, то ее действие на тело приводит к изменению скорости тела. В динамике эта ситуация описывается вторым законом Ньютона:
В динамике эта ситуация описывается вторым законом Ньютона:
F¯ = m*a¯.
Если действие силы F¯ происходит на покоящееся изначально тело массой m, то формула нахождения линейной скорости в любой момент времени t примет вид:
v¯ = a¯*t.
В данном случае обе векторные величины направлены в одну и ту же сторону. Эта формула может применяться для описания разгона какого-либо транспортного средства.
Теперь предположим, что автомобиль двигался с некоторой скоростью v0¯, а затем начал останавливаться. В этой случае соответствующее кинематическое уравнение примет вид:
v¯ = v0¯ + a¯*t.
Поскольку модуль скорости |v¯| авто будет уменьшаться со временем, в скалярной форме это равенство запишется так:
v = v0 — a*t.
В данном случае вектора скорости и ускорения направлены в противоположных направлениях.
Все формулы линейной скорости, приведенные в этом пункте, описывают прямолинейное движение с постоянным ускорением.
Вращение тел
Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
M = I*α.
Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
ω = θ/t.
Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
ω = α*t.
Для измерения всех угловых величин используются радианы.
Формула линейной скорости вращения
Выше отмечалось, что вращение удобно описывать в угловых характеристиках. Тем не менее в некоторых случаях важно знать, чему равна линейная скорость по окружности. Формула для этого случая приведена ниже:
Тем не менее в некоторых случаях важно знать, чему равна линейная скорость по окружности. Формула для этого случая приведена ниже:
v = ω*r.
Здесь r — радиус окружности, равный расстоянию от любой точки траектории тела до оси вращения. Связывающую линейную и угловую скорость формулу получить несложно самостоятельно. Для этого достаточно рассмотреть, какое расстояние по окружности преодолеет тело за известное время t.
Приведенное выражение можно использовать для вычисления линейных скоростей космических тел, например, нашей Земли, вращающейся вокруг Солнца.
Линейная скорость и центростремительное ускорение
Скорость является величиной векторной. Это означает, что тело получает ускорение не только при изменении модуля величины v, но и при изменении ее направления. Последняя ситуация реализуется во время вращения. Вектор мгновенной скорости тела всегда направлен по касательной к окружности. Если за равные промежутки времени тело описывает равные углы относительно центра вращения, то такое движение является равномерным с точки зрения модуля скорости.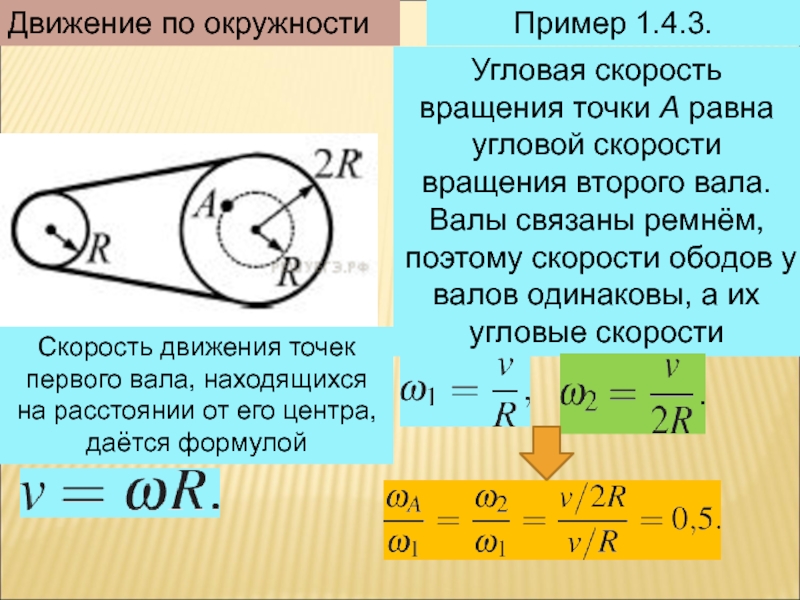
Отклонение от прямолинейного движения во время вращения происходит за счет действия центростремительной силы, вызывающей центростремительное ускорение. Оно направлено всегда перпендикулярно скорости, поэтому изменить ее модуль не может. Ускорение центростремительное ac можно вычислить по формуле:
ac = v2/r.
Абсолютная величина ускорения ac показывает, насколько велики центробежные силы, связанные с инерцией вращающегося тела. Практическим примером является занос автомобиля во время крутого поворота. Заметим, что с уменьшением радиуса ac растет медленнее, чем с увеличением линейной скорости.
Задача на определения линейной скорости нашей планеты
Каждый человек понимает, что если автомобиль движется со скоростью 100 км/ч, то эта цифра является достаточно большой в сравнении со скоростями, с которыми люди сталкиваются в повседневной жизни. Любопытно сравнить указанную цифру со скоростью вращения Земли по своей орбите.
Для оценки этой скорости возьмем следующие данные:
- радиус орбиты — 150 млн км;
- период одного оборота — 365 земных дней.
Для определения требуемой величины воспользуемся формулой линейной и угловой скорости:
v = ω*r.
Значение ω через период T определяется так:
ω = 2*pi/T.
Тогда для v приходим к равенству:
v = 2*pi*r/T.
Подставляя данные из условия задачи, получим линейную скорость 107,5 тысяч км/ч! Эта цифра означает, что наша Земля перемещается в космическом пространстве в 1000 раз быстрее, чем автомобиль движется по дороге. Мы не чувствуем этой гигантскую скорости, поскольку силы гравитации Земли увлекают за собой атмосферу так, что она находится в покое относительно поверхности планеты.
Глава 7. Движемся по орбитам – FIZI4KA
В этой главе. . .
- Постигаем равномерное вращательное движение
- Изучаем угловое ускорение
- Испытываем влияние центростремительной силы
- Учитываем перемещение, скорость и ускорение
- Движемся по орбите под действием законов Ньютона и силы гравитационного притяжения
- Поддерживаем вращение в вертикальной плоскости
Вращательное движение выполняют искусственные спутники вокруг планет, гоночные автомобили по трекам и даже пчелы вокруг ульев. В предыдущих разделах рассматривались такие характеристики прямолинейного движения, как перемещение, скорость и ускорение. В этой главе мы снова рассмотрим их, но теперь уже для вращательного движения.
В предыдущих разделах рассматривались такие характеристики прямолинейного движения, как перемещение, скорость и ускорение. В этой главе мы снова рассмотрим их, но теперь уже для вращательного движения.
Для перечисленных выше характеристик прямолинейного движения есть аналоги, характеризующие вращательное движение, а именно: угловое перемещение, угловая скорость и угловое ускорение. Как видно из их названия, роль перемещения во вращательном движении играет
Держим курс: равномерное вращательное движение
Если объект движется с постоянной по величине скоростью по окружности, то такое движение называется равномерным вращательным движением. Примерами такого движения являются движение гоночного автомобиля по круглому треку и стрелки на циферблате часов. На рис. 7.1 показан мяч для игры в гольф, привязанный нитью к шесту и совершающий движение по окружности. Мяч совершает движение с одинаковой по величине скоростью, но с изменяющимся направлением. Потому такое движение мяча называется равномерным вращательным движением.
Примерами такого движения являются движение гоночного автомобиля по круглому треку и стрелки на циферблате часов. На рис. 7.1 показан мяч для игры в гольф, привязанный нитью к шесту и совершающий движение по окружности. Мяч совершает движение с одинаковой по величине скоростью, но с изменяющимся направлением. Потому такое движение мяча называется равномерным вращательным движением.
Время, которое требуется мячику (или какому-либо другому объекту), чтобы полностью обогнуть окружность, называется периодом и обозначается символом \( T \). Период и линейную скорость можно легко связать, если известно пройденное расстояние, т.е. длина окружности \( 2\pi r \), а точнее ее радиус \( r \). Итак, линейная скорость мячика \( v \) равна:
а период вращения \( T \) равен:
Допустим, что длина нити равна 1 м, а период вращения равен 0,5 с. Чему в таком случае будет равна линейная скорость мячика? Подставим численные значения в одно из предыдущих соотношений и получим:
Итак, мячик вращается с линейной скоростью 13 м/с!
Меняем направление: центростремительное ускорение
При вращательном движении по окружности линейная скорость мячика постоянно меняет направление, как показано на рис.
Это правило справедливо для всех объектов: вектор линейной скорости объекта, равномерно вращающегося по окружности, всегда перпендикулярен радиусу окружности.
Если в показанных на рис. 7.2 положениях нить, удерживающая мяч, оборвется, то куда полетит мяч? Если в этот момент вектор линейной скорости направлен влево, то мяч полетит влево, а если этот вектор направлен вправо, то мяч полетит вправо, и т.д. Этот, казалось бы, простой и интуитивно понятный момент часто вызывает трудности у тех, кто впервые постигает физику.
Всегда следует помнить, что вектор линейной скорости объекта, выполняющего равномерное вращательное движение, всегда направлен под прямым углом к радиусу вращения в текущей точке траектории.
(В общем случае неравномерного криволинейного движения эта компонента вектора скорости, перпендикулярная радиусу вращения и касательная к траектории движения, называется тангенциальной компонентой, а перпендикулярная ей компонента — нормальной компонентой. — Примеч. ред.)
Управляем скоростью с помощью центростремительного ускорения
Особенностью равномерного вращательного движения является постоянство величины линейной скорости. Это значит, что вектор ускорения не имеет компоненты, параллельной вектору линейной скорости, поскольку в противном случае величина линейной скорости менялась бы. Однако при равномерном вращательном движении меняется только направление линейной скорости. Такое изменение линейной скорости поддерживается центростремительным ускорением, направленным к центру окружности вращения и перпендикулярно вектору линейной скорости.
В примерах на рис. 7.1 и 7.2 на мяч со стороны нити действует сила натяжения нити, которая поддерживает его движение по окружности. Именно эта сила сообщает мячу центростремительное ускорение \( a_ц \), вектор которого показан на рис. 7.1. (Попробуйте раскрутить мяч с помощью привязанной к нему нити, и вы сразу же почувствуете действие этой силы со стороны нити.)
Именно эта сила сообщает мячу центростремительное ускорение \( a_ц \), вектор которого показан на рис. 7.1. (Попробуйте раскрутить мяч с помощью привязанной к нему нити, и вы сразу же почувствуете действие этой силы со стороны нити.)
Часто возникает вопрос: если вектор ускорения мяча направлен к центру окружности, то почему мяч не движется к центру? Дело в том, что при равномерном вращательном движении это ускорение меняет только направление, а не величину линейной скорости.
Определяем величину центростремительного ускорения
Нам уже известно направление вектора центростремительного ускорения, а чему же равна его величина? Итак, величина центростремительного ускорения объекта, равномерно движущегося с линейной скоростью \( v \) по окружности с радиусом \( r \), равна:
Как видите, величина центростремительного ускорения обратно пропорциональна радиусу окружности \( r \) и прямо пропорциональна квадрату скорости \( v \). Поэтому не удивительно, что автомобиль на более крутых поворотах испытывает более сильное центростремительное ускорение.
Стремимся к центру: центростремительная сила
На крутых поворотах действие центростремительного ускорения обеспечивается трением шин по дороге. Какую силу нужно приложить, чтобы удержать движущийся со скоростью \( v \) автомобиль на повороте с радиусом кривизны \( r \)?
Допустим, что в примере на рис. 7.1 легкий мяч заменили на тяжелое пушечное ядро. Теперь, чтобы поддерживать движение ядра по окружности с тем же радиусом и периодом вращения, потребуется гораздо большая сила.
Дело в том, что сила \( F=ma \) равна произведению ускорения \( a \) и массы \( m \), а значит, увеличение массы объекта (замена мяча на ядро) неизбежно приводит к необходимости увеличения силы для обеспечения прежнего ускорения.
Центростремительная сила \( F_ц \), необходимая для равномерного вращения по окружности с радиусом \( r \) объекта массой \( m \) с постоянной скоростью \( v \), равна:
С помощью этого уравнения можно легко определить силу, необходимую для равномерного вращения объекта по окружности с известной массой, скоростью и радиусом окружности.
Обратите внимание, что если объект движется по той же окружности, но с разной скоростью, то он будет испытывать разную центростремительную силу.
В примерах на рис. 7.1 и 7.2 мяч движется со скоростью \( v \) = 13 м/с и удерживается нитью длиной 1,0 м, т.е. в данном случае радиус окружности \( r \) = 1 м. Какая сила потребуется, чтобы поддерживать такое же движение для пушечного ядра с массой 10 кг? Подставляя численные значения в уже известную нам формулу, получим:
Приличная сила! Остается только надеяться, что ваши руки достаточно сильны, чтобы удержать ядро.
Является ли центростремительная сила реальной силой?
Центростремительная сила не является каким-то особым типом взаимодействия. Она имеет отношение только к объекту, движущемуся по криволинейной траектории, и необходима для удержания объекта на данной траектории. Поэтому ее часто называют центростремительно-необходимой силой.
Довольно часто новички считают центростремительную силу каким-то новым фундаментальным типом взаимодействия. И это понятно, поскольку известные нам силы (например, сила гравитации и сила трения) имеют вполне определенный источник, который не зависит от траектории движения. Но это совсем не так для центростремительной силы. Центростремительная сила возникает из
необходимости удержания объекта на криволинейной траектории. Сумма всех остальных сил, действующих на объект, который движется по криволинейной траектории, должна быть равна центростремительной силе. (Если объект движется по прямолинейной траектории, а затем ему нужно изменить направление движения, то для этого придется приложить силу, равную центростремительной силе. — Примеч. ред.)
Вписываемся в повороты: учитываем радиус и наклон
Если вам приходилось ехать на автомобиле или велосипеде или даже бежать трусцой, то наверняка вы заметили, что в крутой поворот проще вписаться, если поверхность дороги немного наклонена внутрь поворота.
Представьте, что автомобилю с массой 1000 кг нужно вписаться в поворот с радиусом Юм, а коэффициент трения покоя (подробнее о нем см. главу6) равен 0,8. (Здесь используется коэффициент трения покоя, поскольку предполагается, что шины по поверхности дороги.) Какую максимальную скорость может развить этот автомобиль без риска не вписаться в поворот. Итак, сила трения покоя шин о поверхность дороги \( F_{трение\,покоя} \) должна обеспечивать центростремительную силу:
где \( m \) — это масса автомобиля, \( v \) — его скорость, \( r \) — радиус, \( \mu_п \) — коэффициент трения покоя, a \( g \) = 9,8 м/с Отсюда легко находим скорость:
Отсюда легко находим скорость:
(Обратите внимание, что максимальная безопасная скорость прохождения поворота не зависит от массы автомобиля. — Примеч. ред.)
Это выражение выглядит очень просто, а после подстановки в него численных значений получим:
Итак, максимальная скорость безопасного проезда при таком повороте равна 8,9 м/с. Пересчитаем в единицы “км/ч”, в которых скорость указана на спидометре, и сравним. Получается, что 8,9 м/с = 32 км/ч, а на спидометре всего 29 км/ч. Прекрасно, но далеко не все водители умеют так быстро рассчитывать безопасную скорость прохождения поворотов. Поэтому конструкторы дорог часто строят повороты с наклоном внутрь, чтобы обеспечить центростремительное ускорение не только за счет силы трения, но и за счет горизонтальной компоненты силы гравитации.
На рис. 7.3 показан пример поворота дороги с некоторым наклоном под углом \( \theta \) к горизонтали. Предположим, что конструкторы решили полностью обеспечить центростремительное ускорение только за счет горизонтальной компоненты силы гравитации (т. е. без учета силы трения) \( F_н\sin\theta \), где \( F_н \) — это нормальная сила (подробнее о ней см. в главе 6). Тогда:
е. без учета силы трения) \( F_н\sin\theta \), где \( F_н \) — это нормальная сила (подробнее о ней см. в главе 6). Тогда:
В вертикальном направлении на автомобиль действует сила гравитации \( mg \), которая уравновешивается вертикальной компонентой нормальной силы \( F_н\cos\theta \):
или, иначе выражая это соотношение, получим:
Подставляя это выражение в прежнее соотношение между центростремительной силой и нормальной силой, получим:
Поскольку \( \sin\theta/\!\cos\theta=tg\,\theta \) в то
Отсюда легко получаем, что угол наклона поворота дороги \( \theta \) равен:
Именно это уравнение используют инженеры при проектировании дорог. Обратите внимание, что масса автомобиля не влияет на величину угла, при котором центростремительная сила полностью обеспечивается только горизонтальной компонентой нормальной силы. Попробуем теперь определить величину угла наклона поворота с радиусом 200 м для автомобиля, движущегося со скоростью 100 км/ч или 27,8 м/с:
Для обеспечения безопасного движения автомобиля со скоростью 100 км/ч в повороте с радиусом 200 м без учета силы трения, инженеры должны создать наклон около 22°. Отлично, из вас может получиться неплохой инженер-конструктор автомагистралей!
Отлично, из вас может получиться неплохой инженер-конструктор автомагистралей!
Вращательное движение: перемещение, скорость и ускорение
Если вы привыкли решать задачи о прямолинейном движении типа “некто движется из пункта А в пункт Б”, то задачи о вращательном движении можно формулировать аналогично, но для этого нужно приобрести некоторый опыт. На рис. 7.1 мяч движется криволинейно по окружности, а не прямолинейно по линии. Это движение можно было бы описать как комбинацию прямолинейных движений с координатами X и Y. Однако гораздо удобнее характеризовать его иначе, а именно как вращательное движение с одной координатой \( \theta \). В данном примере вращательного движения перемещение можно характеризовать углом \( \theta \) так же, как в прямолинейном движении перемещение характеризуется расстоянием \( s \). (Более подробно перемещение при прямолинейном движении описывается в главе 3.)
Стандартной единицей измерения перемещения при вращательном движении является радиан (рад), а не градус. Полная окружность охватывает угол величиной \( 2\pi \) радиан, что равно 360°. Соответственно, половина окружности охватывает угол величиной \( \pi \) радиан, а четверть окружности — \( \pi/2 \).
Полная окружность охватывает угол величиной \( 2\pi \) радиан, что равно 360°. Соответственно, половина окружности охватывает угол величиной \( \pi \) радиан, а четверть окружности — \( \pi/2 \).
Как преобразуются величины углов из градусов в радианы и обратно? Достаточно определить, сколько радиан приходится на один градус, т.е. вычислить отношение \( 2\pi \)/360°. Например, величина угла 45° в радианах равна:
Аналогично, для преобразования величины угла из радианов в градусы следует определить, сколько градусов приходится на один радиан, т.е. вычислить отношение 360°/\( 2\pi \). Например, величина угла \( \pi/2 \) в градусах равна:
Формулировка вращательного движения в терминах прямолинейного движения очень удобна. Напомним основные формулы прямолинейного движения, которые подробно описываются в главе 3:
Теперь для вывода аналогичных основных формул вращательного движения достаточно в формулах прямолинейного движения вместо расстояния \( s \), которое характеризует прямолинейное перемещение, подставить угол \( \theta \), который характеризует угловое перемещение. А как определяется угловая скорость? Очень просто. Угловая скорость \( \omega \) определяется аналогично, как изменение угла за единицу времени, и равна количеству радианов, пройденных за секунду:
А как определяется угловая скорость? Очень просто. Угловая скорость \( \omega \) определяется аналогично, как изменение угла за единицу времени, и равна количеству радианов, пройденных за секунду:
Обратите внимание, как похоже это выражение для угловой скорости на выражение для линейной скорости:
Давайте теперь вычислим угловую скорость мяча на рис. 7.1. Он совершает полный круг, охватывающий \( 2\pi \) радиан, за 1/2 с, а значит, его угловая скорость равна:
(Величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине ее радиуса. Поэтому радиан — это безразмерная величина, и ее обозначение (рад) часто опускается. Соответственно, угловую скорость принято указывать “в обратных секундах” как с-1, т.е. без указания единицы измерения углов. — Примеч. ред.)
Угловое ускорение \( \alpha \) определяется аналогично линейному ускорению:
Оно определяется как изменение угловой скорости за единицу времени и измеряется в радианах на секунду в квадрате. {-1} \), то чему равно угловое ускорение? Подставим эти численные значения в предыдущую формулу и получим:
{-1} \), то чему равно угловое ускорение? Подставим эти численные значения в предыдущую формулу и получим:
Итак, для описания вращательного движения у нас есть следующие аналоги: для линейного перемещения \( s \) — угловое перемещение \( \theta \), для линейной скорости \( v \) — угловая скорость \( \omega \) и для линейного ускорения \( a \) — угловое ускорение \( \alpha \).
На основании этой аналогии можно легко вывести основные формулы вращательного движения (подобно основным формулам прямолинейного движения, которые подробно описываются в главе 3):
Более подробно эти выражения рассматриваются далее в главе 10 при описании момента импульса и момента силы.
Бросаем яблоко: закон всемирного тяготения Ньютона
Чтобы проводить опыты с вращательным движением, необязательно привязывать мячики к нитям и вращать их вокруг себя. Например, Луне совсем не нужны никакие нити, чтобы вращаться вокруг Земли. А дело в том, что необходимую центростремительную силу, вместо силы натяжения нити, обеспечивает сила гравитационного притяжения.
Один из важнейших законов физики, а именно закон всемирного тяготения, вывел еще сэр Исаак Ньютон. Согласно этому закону любые два тела притягиваются друг к другу с некоторой силой. Величина этой силы притяжения между телами с массами \( m_1 \) и \( m_2 \), которые находятся на расстоянии \( r \) друг от друга, равна:
где \( G \) — это константа, равная 6,67·10-11 Н·м2/кг2.
Благодаря этому уравнению можно легко вычислить силу гравитационного притяжения между двумя телами. Например, какова сила гравитационного притяжения между Землей и Солнцем? Солнце имеет массу около 1,99·1030 кг, Земля — 5,97·1024 кг, а расстояние между ними равно 1,50·1011 м. Подставляя эти числа в закон всемирного тяготения Ньютона, получим:
Историческая яблоня
Как известно, яблоко упало на голову Исаака Ньютона, и он открыл закон всемирного тяготения. Неужели это так и было? Правда ли, что какое-то падающее яблоко натолкнуло его на верную мысль или, по крайней мере, привлекло внимание Ньютона к данной теме? Согласно последним историческим исследованиям, весьма маловероятно, что именно падение яблока на голову великого ученого вдохновило его.
2 \) для силы гравитационного притяжения справедливо независимо от расстояния между двумя массивными телами. В обыденных ситуациях часто приходится иметь дело с небольшими (по сравнению с размерами Земли) объектами на поверхности Земли, т.е. на фиксированном расстоянии между центром Земли и центром небольшого объекта. Силу гравитационного притяжения (или силу тяжести), действующую на небольшой объект, часто называют весом. Вес \( F_g \) равен произведению массы \( m \) на ускорение свободного падения \( g \), т.е. \( F_g = mg \). Массу измеряют в граммах, килограммах, центнерах, каратах и т.д., а вес — в динах, ньютонах и даже фунт-силах.
Попробуем вычислить ускорение свободного падения на поверхности Земли, пользуясь законом всемирного тяготения. Формула веса тела с массой \( m_1 \) нам известна:
Она создается силой гравитационного притяжения между этим телом и Землей и равна этой силе:
Здесь \( r \) — это радиус Земли, равный 6,38·106 м, а \( m_2 \) — ее масса, равная 5,97·1024 кг.
Сокращая массу тела \( m_1 \) в обеих половинах предыдущего равенства, получим:
Подставляя численные значения, получим:
Так, благодаря закону всемирного тяготения Ньютона мы смогли вычислить значение ускорения свободного падения, уже известное нам из прежних глав. Как видите, для этого нам потребовались значения константы всемирного тяготения \( G \), радиуса Земли \( r \) и ее массы \( m_2 \). (Конечно, значение ускорения свободного падения \( g \) можно определить экспериментально, измеряя время падения предмета с известной высоты. Но, согласитесь, гораздо интересней использовать последнюю формулу, для применения которой потребуется экспериментально измерить… радиус и массу Земли. Шутка!)
Исследуем орбитальное движение с помощью закона всемирного тяготения
Небесные тела в космическом пространстве из-за силы гравитационного притяжения вращаются друг относительно друга: спутники — вокруг своих планет (как Луна — вокруг Земли), планеты — вокруг звезд (как Земля — вокруг Солнца в Солнечной системе), а звезды — вокруг центра Галактики (как Солнце — вокруг центра нашей галактики, т.
е. Млечного пути), а Галактика — вокруг местной группы галактик (как Млечный путь — вокруг нашей Местной группы галактик). Во всех этих случаях тела удерживаются центростремительной силой, которую обеспечивает сила гравитации. Как показано ниже, такая центростремительная сила несколько отличается от той, которая известна нам по прежнему примеру с вращающимся на нитке мячом для игры в гольф. В следующих разделах рассматриваются широко известные законы вращения тел под действием силы гравитационного притяжения, так называемые законы Кеплера, т.е. соотношения между параметрами вращательного движения: периодами вращения, радиусами и площадями орбит вращения.
Вычисляем скорость спутника
Чему равна скорость спутника, вращающегося вокруг планеты по орбите с постоянным радиусом? Ее можно легко определить, приравнивая центростремительную силу:
и силу гравитации:
В итоге получаем:
После простых алгебраических операций получим следующее выражение для скорости вращения:
Это уравнение определяет скорость вращения спутника по постоянной орбите независимо от его происхождения, будь-то искусственный спутник Земли, как рукотворный космический корабль на постоянной орбите, или естественный спутник Земли, как Луна.
Подсчитаем скорость вращения искусственного спутника Земли, вращающегося вокруг Земли. Для этого нужно в предыдущую формулу подставить массу Земли и расстояние от космического орбитального спутника до центра Земли.
Рукотворные спутники Земли обычно вращаются на высоте около 640 км, а радиус Земли, как известно, равен 6,38·106 м. Можно считать, что искусственные спутники вращаются на круговой орбите с радиусом около 7,02·106 м. Подставляя это и другие известные нам численные значения в предыдущую формулу, получим:
В этом месте нужно сделать несколько важных замечаний.
Значение 7,02·106 м в знаменателе обозначает расстояние от спутника до центра Земли, а не расстояние от спутника до поверхности Земли, равное 640 км. Помните, что в законе всемирного тяготения под расстоянием между телами подразумевается расстояние между их центрами масс, а не между их поверхностями.
В данном примере предполагается, что космический корабль находится достаточно высоко и не испытывает влияние атмосферы, например силу трения от соприкосновения с ней.
На самом деле это не так. Даже на такой большой высоте как 640 км, космический корабль теряет скорость, вследствие трения в разреженных слоях атмосферы. В результате его скорость уменьшается, а сам корабль постепенно снижается. (Более подробно об этом рассказывается ниже.)
Движение искусственного спутника вокруг Земли можно рассматривать как “вечное” падение. От фактического падения его “удерживает” только то, что вектор скорости всегда направлен перпендикулярно радиусу окружности вращения. Действительно, именно из-за такого “вечного” падения космонавты испытывают чувство невесомости. Дело в том, что космонавты и их космический корабль “вечно” падают по касательной к орбите вращения вокруг Земли, но при этом нисколько не приближаются к Земле.
В практических целях часто важнее знать период обращения искусственного спутника, а не его скорость. Это нужно, например, в ситуации, когда требуется определить момент выхода на связь с космическим кораблем.
Вычисляем период обращения спутника
Периодом обращения спутника называется время, которое необходимо ему, чтобы совершить полный цикл вращательного движения по орбите.
Если нам известна орбитальная скорость движения \( v \) спутника по окружности с радиусом \( r \) (см. предыдущий раздел), то можно легко и просто вычислить период обращения \( T \). За период обращения спутник преодолевает расстояние, равное длине окружности \( 2\pi r \). Это значит, что орбитальная скорость \( v \) спутника равна \( 2\pi r/T \). Приравнивая это соотношение и полученное ранее выражение для орбитальной скорости
где \( m \) — масса Земли, получим:
Отсюда легко получить следующее выражение для периода обращения спутника:
Линейные скорости и ускорение. Связь между линейными и угловыми кинематическими величинами. Аналогия формул, описывающих поступательное и вращательное движение твердого тела
Линейная скорость точки, движущейся равномерно по окружности, равна угловой скорости, умноженной на радиус окружности. линейная скорость равна произведению угловой скорости на радиус тела; период равен удвоенному числу ПИ деленному на угловую скорость; период равен единице деленной на частоту;.
Линейное ускорение — изменение скорости тела по модулю. В отличае от углового ускорения — изменения скорости по направлению. Для того чтобы связать линейную скорость v произвольной точки А твердого тела с угловой скоростью ω вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на dt. Учитывая, что dr/dt=v и dφ/dt=ω, получим
v=[ω,r] (1.10)
т.е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки. Поступательное и вращательное движение твердого тела Поступательным движением твердого тела называется такое движение, при котором любая прямая, связанная с телом, перемещается в пространстве, оставаясь параллельной самой себе. Другими словами, при поступательном движении отсутствуют какие- либо повороты тела. При вращательном движении все точки тела, лежащие на некоторой прямой, остаются неподвижными во все время движения. Указанная прямая называется осью вращения. Точки тела, не лежащие на оси вращения, движутся в плоскостях, перпендикулярных оси вращения, по окружностям с центром на оси.
Поступательное движение. Понятие материальной точки. Траектория, путь, перемещение, закон движения. Средняя и истинная (мгновенная) скорость. Криволинейное движение. Нормальное и тангенциальное ускорения
Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему первоначальному положению. Материальная точка – физическая модель объекта Модель – абстрактная система, являющаяся упрощенной копией реальной системы. Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи. Положение материальной точки характеризуется тремя координатами (x,y,z) или радиус-вектором единичные вектора (орты). Принцип независимости движения Число независимых координат, полностью определяющих положение точки в пространстве, называется число степеней свободы. — радиус вектор. Траектория – кривая, которую описывает радиус вектор материальной точки при её движении. В зависимости от формы траектории движение разделяется на — прямолинейное, — криволинейное. Расстояние, отсчитанное вдоль траектории, (длина участка траектории) называется длиной пути S. — скалярная функция. Направленный отрезок прямой (вектор), соединяющий начальную и конечную точки траектории называется вектором перемещения (перемещением). Скорость движения материальной точки. Понятие о кривизне Материальная точка движется по криволинейной траектории. За время Δt 1 точка проходит путь S 1 и получает приращение Δr 1, За время Δt 2 – Δr 2. Для характеристики движения материальной точки вводится понятие скорости – векторная величина. Вектор средней скорости – отношение перемещения к промежутку времени Вектор средней скорости характеризует изменение положения радиус-вектора. Средняя скорость неравномерного движения – средняя скорость такого равномерного движения, при котором материальная точка за то же время проходит тот же путь. Если стремится к предельному значению. Мгновенная скорость материальной точки – векторная величина, равная первой производной радиус-вектора движущейся точки по времени.
, следовательно, модуль мгновенной скорости равен первой производной пути по времени: Мгновенная скорость – проекции вектора скорости на оси координат. Криволинейное движение Δφ — угол между касательными в точках, отстоящих друг от друга на расстоянии ΔS. Кривизна траектории характеризует скорость поворота касательной при движении или степень искривленности кривой. Радиус кривизны траектории в данной точке есть величина обратная кривизне Радиус кривизны траектории в данной точке есть радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой. Нормальное и тангенциальное ускорение нормальное ускорение характеризует изменение скорости по направлению. Вектор направлен в данной точке перпендикулярно скорости к центру кривизны траектории (центростремительное ускорение). тангенциальное ускорение характеризует изменение скорости по величине и направлено вдоль скорости (или в обратную сторону). Любое криволинейное движение можно представить как суперпозицию поступательного и вращательного движений
PPT — Вращение PowerPoint Presentation, скачать бесплатно
y x Rotation • Представьте, что вы смотрите на вращающееся велосипедное колесо: • Как бы вы описали положение точки (например, отражателя) на этом колесе с течением времени? • Вы можете отслеживать координаты (x, y) этой точки: (x, y)
y x Угловое положение q • Вместо этого удобнее описывать угол q, который образует точка отражателя с осью x в фиксированной системе координат: • Определение положительного направления вращения определяет знак (+ или -) координаты q: • Мы используем радианы (рад) в качестве единицы измерения угла q (углового положения) + qнегатив + yy qположительного qqxxq = 1 рад, когда он образует длину дуги s = r
Угловая скорость • Таким образом, q (в радианах) = s / r или s = rq • Для преобразования между радианами и градусами используйте коэффициент преобразования, например: 180 ° = p радиан • В определить количество радианов в 32 °: (x рад) (180 °) = (p rad) (32 °) x = 0.
5585 рад • Вращательное движение можно описать по аналогии с линейным движением: • Таким образом, мы можем определить волну средней угловой скорости следующим образом: В момент времени t = t1: В момент времени t = t2: q1 q2 xx (зависит от углового смещения q2 — q1)
Угловая скорость • Мы также можем определить мгновенную угловую скорость аналогично линейному случаю: • Единицы угловой скорости — радиан / сек • 1 об / с = 2p рад / с, поэтому 1 об / мин = 1 об / мин = 2p / 60 рад / с • Направление w определяется Правилом правой руки: • Согните пальцы правой руки в направлении вращения • Большой палец указывает в направлении w • Таким образом указывает на ось вращения, параллельную оси вращения (не в направлении вращения) • Примечание что все точки на вращающемся объекте движутся по кругу с центром вокруг оси вращения
Угловое ускорение • Средняя скорость изменения во времени называется средним угловым ускорением aave: • Угловое ускорение в определенный момент времени равно Instantaneo us угловое ускорениеa: • Когда ось вращения фиксирована, она располагается вдоль этой оси (аналогично), но может указывать в том же или противоположном направлении, что и w (т.
е.е. параллельно или антипараллельно w)
Качественные отношения между вандой • Качественное поведение вандак можно резюмировать в следующей таблице: • Это были те же отношения между линейной скоростью и ускорением в главе 2! (более быстрое вращение в направлении + направление) Тот же знак (более быстрое вращение в направлении — направление) (более медленное вращение в направлении — направление) Противоположный знак (более медленное вращение в направлении + направление)
Постоянное угловое ускорение w Постоянное угловое ускорение означает постоянную скорость увеличения forw • Для особого случая постоянного углового ускорения thenwvs.График t становится прямой линией: • По аналогии с движением с постоянным линейным ускорением: • Обратите внимание на сходство между линейными (x, v, a) и угловыми (q, w, a) величинами и отношениями t
v rqx Ось вращения, связывающая линейную и угловую кинематику • Снова рассмотрим отражатель на вращающемся колесе велосипеда: • Угол q (в радианах) и длина дуги, заданная q, связаны соотношением s = rq • Таким образом, линейное смещение Ds и угловое смещение Dq связаны следующим образом: разматывания струны с колеса) • Называется условием «противоскольжения».
• Аналогичное соотношение сохраняется между линейной (или тангенциальной) скоростью v и угловой скоростью w: • Чем дальше точка от оси вращения, тем больше ее линейная скорость для заданное значение w
Связь линейной и угловой кинематики • Это соотношение верно для каждой точки твердого тела • Жесткое тело = объект, имеющий идеальную конечная и неизменная форма и размер • Таким образом, все точки имеют одинаковую угловую скоростьw • Сделав еще один шаг вперед, мы видим другую аналогичную взаимосвязь между тангенциальным ускорением и угловым ускорением: • В общем, тангенциальное ускорение изменяет линейную скорость точки на вращающийся объект (т.е. величина скорости)
Пример Задача № 7.12 Диск диаметром 45,0 см вращается с постоянным угловым ускорением 2,50 рад / с2. Он начинается в состоянии покоя при t = 0, и линия, проведенная от центра диска к точке P на ободе диска, составляет в это время угол 57,3 ° с положительной осью x.
При t = 2,30 с найдите (a) угловую скорость колеса, (b) линейную скорость и тангенциальное ускорение P, и (c) положение P (в градусах относительно положительной оси x ).• Решение (подробности приведены в классе): • 5,75 рад / с • 1,29 м / с, 0,562 м / с2 • 76,2 ° против часовой стрелки от оси + x
CQ1: Интерактивный концептуальный пример: На какой анимации показано правильный путь мяча после обрыва струны? • Анимация A • Анимация B • Анимация C • Анимация D • Анимация E PHYSLET Упражнение 7.1.2, Prentice Hall (2001)
Равномерное круговое движение • Круговое движение шайбы на горизонтальном столе без трения с постоянной скоростью: Вид сверху: по касательной к окружности в каждой точке. Изменение направления означает ускорение, направленное к центру окружности R
Величина = arad = v2 / R («центростремительное» ускорение ) Равномерное круговое движение R Или, поскольку v = Rw: arad = R2w2 / R = Rw2 • Источник arad: центростремительная сила • Из 2-го закона Ньютона: F = Fnet = marad = mv2 / R
Круговое движение в вертикальной плоскости мг • Рассмотрим круговое движение объекта, повернутого в вертикальном круге путь: • Вверху: Fc = Fnet = –mg — T • Внизу: Fc = Fnet = T — мг TT мг
Fp Fp (вверху) (внизу) мг мг Анализ качающейся емкости Вода Вверху: + y Внизу: vt vb Диаграммы свободного тела воды: Сила, действующая на воду ведром наверху: SFy = may = m (–vt2 / r) — Fp — mg = m (–vt2 / r) Fp = m (vt2 / r) — мг
Анализ качающегося ведра с водой Минимальное значение vt для воды, остающейся в ведре: Минимум f Ведро orce может воздействовать на воду равно нулю, поэтому установите Fp = 0 (arad = –g) и найдите минимальную скорость vt, min: 0 — mg = m (–vt, min2 / r) vt, min2 = rg vt, min = (rg) 1/2 Сила, действующая на воду ведром на дне: SFy = may = m (vb2 / r) Fp — mg = m (vb2 / r) Fp = m (vb2 / r) + mg * Помните что центростремительная сила не является особой внешней силой, действующей на тело — это просто название чистой внешней силы, направленной к центру кругового движения
1 2 H — 2R y y2 = 2R H y1 = 0 Дизайн американских горок типа «петля-петля» Предположим, мы хотим разработать следующие американские горки «петля-петля»: R Какова минимальная высота H, необходимая для того, чтобы автомобиль американских горок оставался на трассе в верхней части петли.
? (Автомобиль падает только под действием силы тяжести.) • Сохранение механической энергии: ½ mv12 + mgy1 = ½ mv22 + mgy2 • Предположим, что американские горки начинаются с покоя на вершине холма. Тогда мы имеем: mgH = ½ mv22 + mg (2R) • v22 = 2mg (H — 2R) / m = 2g (H — 2R)
Конструкция американских горок «петля — петля» • Для автомобиля чтобы безопасно пройти через петлю: acar = arad g (вспомните воду в ведре) • arad = v22 / Rg • 2g (H — 2R) / R g • H R / 2 + 2R = 5R / 2 • H 5R / 2 Так, например, если R = 22 см, то H должно быть не менее 55 см.
Пример задачи № 7.75 В популярном аттракционе в парке аттракционов вращающийся цилиндр радиусом 3,00 м приводится во вращение с угловой скоростью 5,00 рад / с (см. Рисунок справа). Затем пол падает, оставляя всадников подвешенными к стене в вертикальном положении. Какой минимальный коэффициент трения между одеждой всадника и стеной необходим, чтобы всадник не поскользнулся? Решение (подробности приведены в классе): ms = 0,131
Пример проблемы №7.
31 Ребенок весом 40,0 кг катается на колесе обозрения, которое вращается четыре раза в минуту и имеет диаметр 18,0 м. а) Что такое центростремительное ускорение ребенка? б) Какую силу (величину и направление) кресло оказывает на ребенка в самой нижней точке езды? (c) Какую силу кресло оказывает на ребенка в самой высокой точке езды? (d) Какую силу оказывает сиденье на ребенка, когда ребенок находится на полпути между верхом и низом? 9,0 м (Исходный рисунок из University Physics, Young and Freedman, 11th Ed., Pearson Addison Wesley) Решение (подробности приведены для класса): (a) 1,58 м / с2 (b) 455 N вверх (c) 329 N вверх (d) 397 N направлено внутрь под 80,8 ° над горизонтом
CQ2: Интерактивный пример задачи: безопасность гоночного автомобиля Какова максимальная линейная скорость автомобиля до того, как он начнет заносить с трассы? • 20 м / с • 30 м / с • 50 м / с • 100 м / с • 400 м / с (ActivPhysics Online Problem # 4.5, Pearson / Addison Wesley)
Gravitation • Мы уже знакомы с концепция гравитационного притяжения из концепции веса (сила гравитационного притяжения, проявляемая Землей): • Ньютон обобщил эту силу на силу, действующую между любыми двумя телами в своем Законе гравитации (1687 г.
): • По словам Ньютона: таким образом, я сравнил необходимую силу с удерживали Луну в ее орбите с помощью силы тяжести на поверхности Земли, и нашли их почти ответ.• Величина силы тяжести: • G = константа = 6,67 10–11 Нм2 / кг2 • Очень малое значение гравитация — слабая (самая слабая!) Сила • Гравитация очень важна для больших масс, однако W = mg
m1 Fg Гравитация r Demo Fg m2 • Направление гравитационной силы: • Вдоль линии, соединяющей 2 частицы (сила притяжения) • m1 оказывает силу равной величины, противоположное направление asm2 проявляет наm1 (3-й закон Ньютона) интегральное исчисление), что: • Верно для точек вне распределения материи • Внутри сферы все обстоит иначе — для твердой сферы с однородной плотностью Fg пропорционально tor m1 m2 Fg Fg Fg Fg m1 m2 = rr (точечные массы сосредоточены в центрах ) (сферически-симметричные массы)
Гравитация | Fg | R • График | Fg | vs.r для твердой сферы с однородной плотностью: • Когда одна из масс — Земля (имеющая массу mE): Fg = GmEm / r2, где r = dist.
от центра к центру Земли • На поверхности Земли: Fg = GmEm / RE2 (RE = радиус Земли) • Это просто вес массы m на поверхности: W = Fg = GmEm / RE2 (опять же, измеряется на поверхности Земли) ~ 1 / r2 ~ rr
Вес • Но мы также определили вес как W = мг, поэтому очевидно: g = GmE / RE2 = (6,67 10–11 Нм2 / кг2) (5,97 1024 кг) / (6,38 106 м) 2 = 9.8 м / с2 (в соответствии со значением, которое мы использовали до сих пор) • Теперь мы можем видеть, как и вес, и гравитационное ускорение уменьшаются с расстоянием от Земли: • W = GmEm / r2 • a = Fg / m = GmE / r2 • Так почему же космонавт космического корабля, вращающегося вокруг Земли, испытывает чувство невесомости?
CQ3: Если M — масса Земли, m — масса Луны , а d — расстояние между их центрами, что из следующего дает мгновенную скорость Луны, вращающейся вокруг Земли. ? (Универсальная гравитационная постоянная дана Г.)
CQ4: Если радиус орбиты спутника, вращающегося вокруг Земли , уменьшается в 2 раза, гравитационная сила на Земле: • уменьшится в 2 раза • останется прежней.
• увеличение в 2 раза • увеличение в 4 раза.
Пример задачи №7.41 • Спутник движется по круговой орбите вокруг Земли со скоростью 5000 м / с. Определите • высоту спутника над поверхностью Земли и • период орбиты спутника.Решение (подробности приведены в классе): (a) 9,57 106 м (b) 5,57 h
6,1 Угол вращения и угловая скорость — Физика
6,1 Угол вращения и угловая скорость — Физика | OpenStaxSkip к ContentPhysics 6.1 Угол поворота и угловая скорость
- Предисловие
- Введение
- 1.1 Физика: определения и приложения
- 1.2 Научные методы
- 1.3 Язык физики: физические величины и единицы
- Ключевые термины
- Сводка по разделу
- Ключевые уравнения
- Элементы концепции
- Элементы критического мышления
- Проблемы
- Задача производительности
- Множественный выбор
- Короткий ответ
- 201
- 201 Расширенный ответ
- 201
- 201 Расширенный ответ One Dimension
- Введение
- 2.
1 Относительное движение, расстояние и смещение
- 2.2 Скорость и скорость
- 2.3 Графики зависимости положения от времени
- 2.4 Графики зависимости скорости от времени
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Задача производительности
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 3.1 Ускорение
- 3.2 Представление ускорения с помощью уравнений и графиков
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Задача производительности
- Краткий ответ
- Расширенный ответ
- 4 Силы и законы движения Ньютона
- Введение
- 4.
1 Сила
- 4,2 Первый закон движения Ньютона: инерция
- 4,3 Второй закон движения Ньютона
- 4,4 Третий закон движения Ньютона
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
- Концептуальные элементы
- Критические концепции Элементы
- Проблемы
- Задача производительности
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- 5 Движение в двух измерениях
- Введение
- 5.1 Сложение и вычитание векторов: графические методы
- 5.2 Сложение и вычитание векторов: аналитические методы
- 5.3 Движение снаряда
- 5.4 Наклонные плоскости
- 5.5 Простое гармоническое движение
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Задача производительности
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- 6 Круговое и вращательное движение
- 61 Угол поворота и угловая скорость
- 6.
2 Равномерное круговое движение
- 6.3 Вращательное движение
- Ключевые термины
- Сводка раздела
- Ключевые уравнения
- Элементы концепции
- Элементы критического мышления
- Проблемы с производительностью
- Проблемы с производительностью
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- 7 Закон тяготения Ньютона
- Введение
- 7.1 Законы движения планет Кеплера
- 7.2 Закон всемирного тяготения Ньютона и общая теория относительности Эйнштейна
- Ключевые термины
- Резюме раздела
- Ключевые уравнения
- Концептуальные элементы
- Элементы критического мышления
- Задачи для выполнения задач
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 8.
1 Линейный импульс, сила и импульс
- 8.2 Сохранение импульса
- 8.3 Упругие и неупругие столкновения
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
- Концептуальные элементы
- Критически важные задачи для мышления
- Проблемы производительности
Задача
- Множественный выбор
- Короткий ответ
- Расширенный ответ
9 Работа, энергия и простые машины
- Введение
- 9.1 Работа, мощность и работа-энергия, теорема
- 9.2 Механическая энергия и сохранение энергии
- 9.3 Простые машины
- Ключевые термины
- Резюме раздела
- Ключевые уравнения
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Performance Task
- Множественный выбор
- Короткий ответ
- Расширенный ответ
- Введение
- 10.
1 Постулаты специальной теории относительности
- 10.2 Последствия специальной теории относительности
- Ключевые термины
- Краткое содержание раздела
- Ключевые уравнения
- Концептуальные элементы
- Элементы критического мышления
- Проблемы
- Выбор задачи производительности
- Краткий ответ
- Расширенный ответ
11 Тепловая энергия, тепло и работа
- Введение
- 11.1 Температура и тепловая энергия
- 11.2 Тепло, удельная теплоемкость и теплопередача
- 11.3 Фазовое изменение и скрытая теплота
- Ключевые термины
- Краткое содержание раздела
Переходы CSS
Переходы CSS
CSS-переходов позволяет плавно изменять значения свойств в течение заданного времени.
Наведите указатель мыши на элемент ниже, чтобы увидеть эффект перехода CSS:
В этой главе вы узнаете о следующих свойствах:
переходзадержка переходапродолжительность переходапереходная собственностьфункция времени переходаБраузер Поддержка переходов
Числа в таблице указывают первую версию браузера, полностью поддерживающую свойство.
Имущество переход 26,0 10,0 16,0 6,1 12,1 задержка перехода 26,0 10,0 16,0 6,1 12.1 продолжительность перехода 26,0 10,0 16,0 6,1 12,1 переходная собственность 26,0 10,0 16,0 6,1 12,1 функция времени перехода 26,0 10.0 16,0 6,1 12,1 Как использовать переходы CSS?
Для создания эффекта перехода необходимо указать две вещи:
- свойство CSS, которое вы хотите добавить к
.- длительность эффекта
Примечание: Если часть длительности не указана, переход не будет иметь никакого эффекта, поскольку значение по умолчанию — 0.
В следующем примере показан красный элемент
размером 100 пикселей на 100 пикселей.элемент также указал эффект перехода для свойства ширины с продолжительностью 2 секунды:Пример
div {
ширина: 100 пикселей;
высота: 100 пикселей;
фон: красный;
переход: ширина 2с;
}Эффект перехода начнется, когда указанное свойство CSS (ширина) изменит значение.
Теперь давайте укажем новое значение для свойства width, когда пользователь наводит курсор на элемент
:Обратите внимание, что когда курсор выходит за пределы элемента, он постепенно возвращается к своему исходному стилю.
Изменить несколько значений свойств
В следующем примере добавляется эффект перехода для свойства width и height с длительностью 2 секунды для ширины и 4 секунды для высоты:
Укажите кривую скорости перехода
Свойство
функции времени переходаопределяет кривую скорости эффекта перехода.Свойство временной функции перехода может иметь следующие значения:
легкость— задает эффект перехода с медленным началом, затем быстрым, затем медленным завершением (по умолчанию)linear— задает эффект перехода с одинаковой скоростью от начала до концаeasy-in— задает эффект перехода с медленным стартомeasy-out— задает эффект перехода с медленным концомeasy-in-out— задает эффект перехода с медленным началом и концомcubic-bezier (n, n, n, n)— позволяет вам определять свои собственные значения в кубической функции БезьеВ следующем примере показаны некоторые из различных кривых скорости, которые можно использовать:
Пример
# div1 {функция-времени-перехода: линейная;}
Попробуй сам »
# div2 {функция-времени-перехода: легкость;}
# div3 {функция-времени-перехода: easy-in;}
# div4 {функция-тайминг-перехода: easy-out;}
# div5 {функция-перехода: легкость входа-выхода;}Задержать переходный эффект
Свойство
transition-delayопределяет задержку (в секундах) для эффекта перехода.В следующем примере задержка перед запуском составляет 1 секунду:
Переход + преобразование
В следующем примере к преобразованию добавляется эффект перехода:
Дополнительные примеры переходов
Свойства перехода CSS можно указать одно за другим, например:
Пример
div {
Попробуй сам »
свойство перехода: ширина;
продолжительность перехода: 2 с;
временная функция перехода: линейная;
задержка перехода: 1 с;
}или с помощью сокращенного свойства
переход:Проверьте себя упражнениями!
Свойства перехода CSS
В следующей таблице перечислены все свойства перехода CSS:
Имущество Описание переход Сокращенное свойство для установки четырех свойств перехода в одно свойство задержка перехода Задает задержку (в секундах) для эффекта перехода продолжительность перехода Указывает, сколько секунд или миллисекунд требуется эффекту перехода для завершения переходная собственность Задает имя свойства CSS, для которого применяется эффект перехода.

 (В общем случае неравномерного криволинейного движения эта компонента вектора скорости, перпендикулярная радиусу вращения и касательная к траектории движения, называется тангенциальной компонентой, а перпендикулярная ей компонента — нормальной компонентой. — Примеч. ред.)
(В общем случае неравномерного криволинейного движения эта компонента вектора скорости, перпендикулярная радиусу вращения и касательная к траектории движения, называется тангенциальной компонентой, а перпендикулярная ей компонента — нормальной компонентой. — Примеч. ред.) Довольно часто новички считают центростремительную силу каким-то новым фундаментальным типом взаимодействия. И это понятно, поскольку известные нам силы (например, сила гравитации и сила трения) имеют вполне определенный источник, который не зависит от траектории движения. Но это совсем не так для центростремительной силы. Центростремительная сила возникает из
Довольно часто новички считают центростремительную силу каким-то новым фундаментальным типом взаимодействия. И это понятно, поскольку известные нам силы (например, сила гравитации и сила трения) имеют вполне определенный источник, который не зависит от траектории движения. Но это совсем не так для центростремительной силы. Центростремительная сила возникает из  2 \) для силы гравитационного притяжения справедливо независимо от расстояния между двумя массивными телами. В обыденных ситуациях часто приходится иметь дело с небольшими (по сравнению с размерами Земли) объектами на поверхности Земли, т.е. на фиксированном расстоянии между центром Земли и центром небольшого объекта. Силу гравитационного притяжения (или силу тяжести), действующую на небольшой объект, часто называют весом. Вес \( F_g \) равен произведению массы \( m \) на ускорение свободного падения \( g \), т.е. \( F_g = mg \). Массу измеряют в граммах, килограммах, центнерах, каратах и т.д., а вес — в динах, ньютонах и даже фунт-силах.
2 \) для силы гравитационного притяжения справедливо независимо от расстояния между двумя массивными телами. В обыденных ситуациях часто приходится иметь дело с небольшими (по сравнению с размерами Земли) объектами на поверхности Земли, т.е. на фиксированном расстоянии между центром Земли и центром небольшого объекта. Силу гравитационного притяжения (или силу тяжести), действующую на небольшой объект, часто называют весом. Вес \( F_g \) равен произведению массы \( m \) на ускорение свободного падения \( g \), т.е. \( F_g = mg \). Массу измеряют в граммах, килограммах, центнерах, каратах и т.д., а вес — в динах, ньютонах и даже фунт-силах.
 е. Млечного пути), а Галактика — вокруг местной группы галактик (как Млечный путь — вокруг нашей Местной группы галактик). Во всех этих случаях тела удерживаются центростремительной силой, которую обеспечивает сила гравитации. Как показано ниже, такая центростремительная сила несколько отличается от той, которая известна нам по прежнему примеру с вращающимся на нитке мячом для игры в гольф. В следующих разделах рассматриваются широко известные законы вращения тел под действием силы гравитационного притяжения, так называемые законы Кеплера, т.е. соотношения между параметрами вращательного движения: периодами вращения, радиусами и площадями орбит вращения.
е. Млечного пути), а Галактика — вокруг местной группы галактик (как Млечный путь — вокруг нашей Местной группы галактик). Во всех этих случаях тела удерживаются центростремительной силой, которую обеспечивает сила гравитации. Как показано ниже, такая центростремительная сила несколько отличается от той, которая известна нам по прежнему примеру с вращающимся на нитке мячом для игры в гольф. В следующих разделах рассматриваются широко известные законы вращения тел под действием силы гравитационного притяжения, так называемые законы Кеплера, т.е. соотношения между параметрами вращательного движения: периодами вращения, радиусами и площадями орбит вращения.
 На самом деле это не так. Даже на такой большой высоте как 640 км, космический корабль теряет скорость, вследствие трения в разреженных слоях атмосферы. В результате его скорость уменьшается, а сам корабль постепенно снижается. (Более подробно об этом рассказывается ниже.)
На самом деле это не так. Даже на такой большой высоте как 640 км, космический корабль теряет скорость, вследствие трения в разреженных слоях атмосферы. В результате его скорость уменьшается, а сам корабль постепенно снижается. (Более подробно об этом рассказывается ниже.) Если нам известна орбитальная скорость движения \( v \) спутника по окружности с радиусом \( r \) (см. предыдущий раздел), то можно легко и просто вычислить период обращения \( T \). За период обращения спутник преодолевает расстояние, равное длине окружности \( 2\pi r \). Это значит, что орбитальная скорость \( v \) спутника равна \( 2\pi r/T \). Приравнивая это соотношение и полученное ранее выражение для орбитальной скорости
Если нам известна орбитальная скорость движения \( v \) спутника по окружности с радиусом \( r \) (см. предыдущий раздел), то можно легко и просто вычислить период обращения \( T \). За период обращения спутник преодолевает расстояние, равное длине окружности \( 2\pi r \). Это значит, что орбитальная скорость \( v \) спутника равна \( 2\pi r/T \). Приравнивая это соотношение и полученное ранее выражение для орбитальной скорости Линейное ускорение — изменение скорости тела по модулю. В отличае от углового ускорения — изменения скорости по направлению. Для того чтобы связать линейную скорость v произвольной точки А твердого тела с угловой скоростью ω вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на dt. Учитывая, что dr/dt=v и dφ/dt=ω, получим
Линейное ускорение — изменение скорости тела по модулю. В отличае от углового ускорения — изменения скорости по направлению. Для того чтобы связать линейную скорость v произвольной точки А твердого тела с угловой скоростью ω вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на dt. Учитывая, что dr/dt=v и dφ/dt=ω, получим
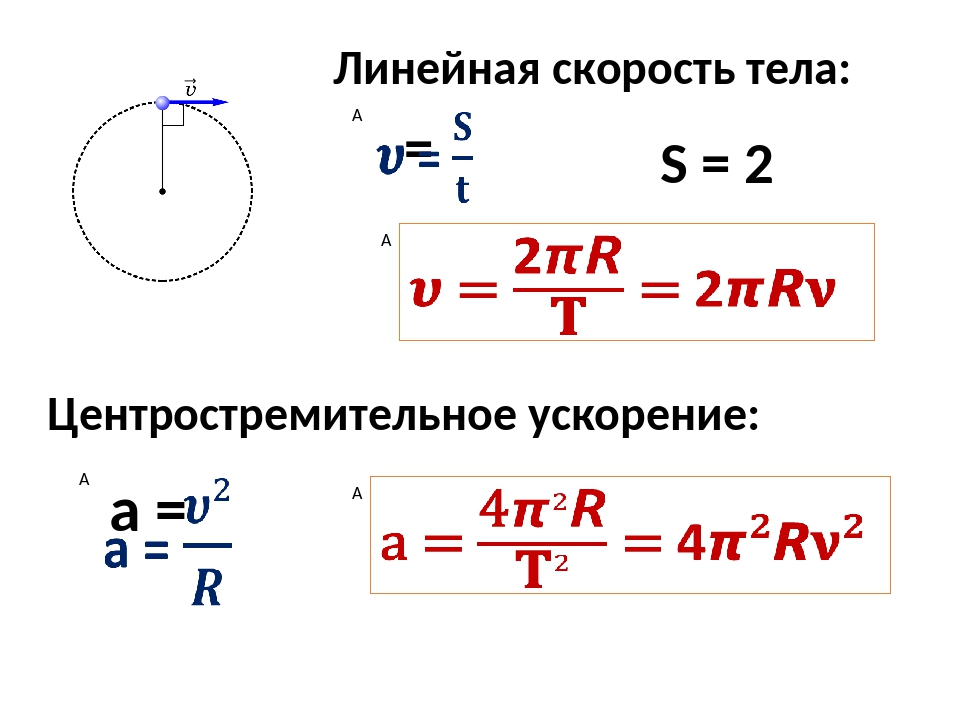 В зависимости от формы траектории движение разделяется на — прямолинейное, — криволинейное. Расстояние, отсчитанное вдоль траектории, (длина участка траектории) называется длиной пути S. — скалярная функция. Направленный отрезок прямой (вектор), соединяющий начальную и конечную точки траектории называется вектором перемещения (перемещением). Скорость движения материальной точки. Понятие о кривизне Материальная точка движется по криволинейной траектории. За время Δt 1 точка проходит путь S 1 и получает приращение Δr 1, За время Δt 2 – Δr 2. Для характеристики движения материальной точки вводится понятие скорости – векторная величина. Вектор средней скорости – отношение перемещения к промежутку времени Вектор средней скорости характеризует изменение положения радиус-вектора. Средняя скорость неравномерного движения – средняя скорость такого равномерного движения, при котором материальная точка за то же время проходит тот же путь. Если стремится к предельному значению. Мгновенная скорость материальной точки – векторная величина, равная первой производной радиус-вектора движущейся точки по времени.
В зависимости от формы траектории движение разделяется на — прямолинейное, — криволинейное. Расстояние, отсчитанное вдоль траектории, (длина участка траектории) называется длиной пути S. — скалярная функция. Направленный отрезок прямой (вектор), соединяющий начальную и конечную точки траектории называется вектором перемещения (перемещением). Скорость движения материальной точки. Понятие о кривизне Материальная точка движется по криволинейной траектории. За время Δt 1 точка проходит путь S 1 и получает приращение Δr 1, За время Δt 2 – Δr 2. Для характеристики движения материальной точки вводится понятие скорости – векторная величина. Вектор средней скорости – отношение перемещения к промежутку времени Вектор средней скорости характеризует изменение положения радиус-вектора. Средняя скорость неравномерного движения – средняя скорость такого равномерного движения, при котором материальная точка за то же время проходит тот же путь. Если стремится к предельному значению. Мгновенная скорость материальной точки – векторная величина, равная первой производной радиус-вектора движущейся точки по времени. , следовательно, модуль мгновенной скорости равен первой производной пути по времени: Мгновенная скорость – проекции вектора скорости на оси координат. Криволинейное движение Δφ — угол между касательными в точках, отстоящих друг от друга на расстоянии ΔS. Кривизна траектории характеризует скорость поворота касательной при движении или степень искривленности кривой. Радиус кривизны траектории в данной точке есть величина обратная кривизне Радиус кривизны траектории в данной точке есть радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой. Нормальное и тангенциальное ускорение нормальное ускорение характеризует изменение скорости по направлению. Вектор направлен в данной точке перпендикулярно скорости к центру кривизны траектории (центростремительное ускорение). тангенциальное ускорение характеризует изменение скорости по величине и направлено вдоль скорости (или в обратную сторону). Любое криволинейное движение можно представить как суперпозицию поступательного и вращательного движений
, следовательно, модуль мгновенной скорости равен первой производной пути по времени: Мгновенная скорость – проекции вектора скорости на оси координат. Криволинейное движение Δφ — угол между касательными в точках, отстоящих друг от друга на расстоянии ΔS. Кривизна траектории характеризует скорость поворота касательной при движении или степень искривленности кривой. Радиус кривизны траектории в данной точке есть величина обратная кривизне Радиус кривизны траектории в данной точке есть радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой. Нормальное и тангенциальное ускорение нормальное ускорение характеризует изменение скорости по направлению. Вектор направлен в данной точке перпендикулярно скорости к центру кривизны траектории (центростремительное ускорение). тангенциальное ускорение характеризует изменение скорости по величине и направлено вдоль скорости (или в обратную сторону). Любое криволинейное движение можно представить как суперпозицию поступательного и вращательного движений
 5585 рад • Вращательное движение можно описать по аналогии с линейным движением: • Таким образом, мы можем определить волну средней угловой скорости следующим образом: В момент времени t = t1: В момент времени t = t2: q1 q2 xx (зависит от углового смещения q2 — q1)
5585 рад • Вращательное движение можно описать по аналогии с линейным движением: • Таким образом, мы можем определить волну средней угловой скорости следующим образом: В момент времени t = t1: В момент времени t = t2: q1 q2 xx (зависит от углового смещения q2 — q1) е.е. параллельно или антипараллельно w)
е.е. параллельно или антипараллельно w) • Аналогичное соотношение сохраняется между линейной (или тангенциальной) скоростью v и угловой скоростью w: • Чем дальше точка от оси вращения, тем больше ее линейная скорость для заданное значение w
• Аналогичное соотношение сохраняется между линейной (или тангенциальной) скоростью v и угловой скоростью w: • Чем дальше точка от оси вращения, тем больше ее линейная скорость для заданное значение w При t = 2,30 с найдите (a) угловую скорость колеса, (b) линейную скорость и тангенциальное ускорение P, и (c) положение P (в градусах относительно положительной оси x ).• Решение (подробности приведены в классе): • 5,75 рад / с • 1,29 м / с, 0,562 м / с2 • 76,2 ° против часовой стрелки от оси + x
При t = 2,30 с найдите (a) угловую скорость колеса, (b) линейную скорость и тангенциальное ускорение P, и (c) положение P (в градусах относительно положительной оси x ).• Решение (подробности приведены в классе): • 5,75 рад / с • 1,29 м / с, 0,562 м / с2 • 76,2 ° против часовой стрелки от оси + x ? (Автомобиль падает только под действием силы тяжести.) • Сохранение механической энергии: ½ mv12 + mgy1 = ½ mv22 + mgy2 • Предположим, что американские горки начинаются с покоя на вершине холма. Тогда мы имеем: mgH = ½ mv22 + mg (2R) • v22 = 2mg (H — 2R) / m = 2g (H — 2R)
? (Автомобиль падает только под действием силы тяжести.) • Сохранение механической энергии: ½ mv12 + mgy1 = ½ mv22 + mgy2 • Предположим, что американские горки начинаются с покоя на вершине холма. Тогда мы имеем: mgH = ½ mv22 + mg (2R) • v22 = 2mg (H — 2R) / m = 2g (H — 2R) 31 Ребенок весом 40,0 кг катается на колесе обозрения, которое вращается четыре раза в минуту и имеет диаметр 18,0 м. а) Что такое центростремительное ускорение ребенка? б) Какую силу (величину и направление) кресло оказывает на ребенка в самой нижней точке езды? (c) Какую силу кресло оказывает на ребенка в самой высокой точке езды? (d) Какую силу оказывает сиденье на ребенка, когда ребенок находится на полпути между верхом и низом? 9,0 м (Исходный рисунок из University Physics, Young and Freedman, 11th Ed., Pearson Addison Wesley) Решение (подробности приведены для класса): (a) 1,58 м / с2 (b) 455 N вверх (c) 329 N вверх (d) 397 N направлено внутрь под 80,8 ° над горизонтом
31 Ребенок весом 40,0 кг катается на колесе обозрения, которое вращается четыре раза в минуту и имеет диаметр 18,0 м. а) Что такое центростремительное ускорение ребенка? б) Какую силу (величину и направление) кресло оказывает на ребенка в самой нижней точке езды? (c) Какую силу кресло оказывает на ребенка в самой высокой точке езды? (d) Какую силу оказывает сиденье на ребенка, когда ребенок находится на полпути между верхом и низом? 9,0 м (Исходный рисунок из University Physics, Young and Freedman, 11th Ed., Pearson Addison Wesley) Решение (подробности приведены для класса): (a) 1,58 м / с2 (b) 455 N вверх (c) 329 N вверх (d) 397 N направлено внутрь под 80,8 ° над горизонтом ): • По словам Ньютона: таким образом, я сравнил необходимую силу с удерживали Луну в ее орбите с помощью силы тяжести на поверхности Земли, и нашли их почти ответ.• Величина силы тяжести: • G = константа = 6,67 10–11 Нм2 / кг2 • Очень малое значение гравитация — слабая (самая слабая!) Сила • Гравитация очень важна для больших масс, однако W = mg
): • По словам Ньютона: таким образом, я сравнил необходимую силу с удерживали Луну в ее орбите с помощью силы тяжести на поверхности Земли, и нашли их почти ответ.• Величина силы тяжести: • G = константа = 6,67 10–11 Нм2 / кг2 • Очень малое значение гравитация — слабая (самая слабая!) Сила • Гравитация очень важна для больших масс, однако W = mg от центра к центру Земли • На поверхности Земли: Fg = GmEm / RE2 (RE = радиус Земли) • Это просто вес массы m на поверхности: W = Fg = GmEm / RE2 (опять же, измеряется на поверхности Земли) ~ 1 / r2 ~ rr
от центра к центру Земли • На поверхности Земли: Fg = GmEm / RE2 (RE = радиус Земли) • Это просто вес массы m на поверхности: W = Fg = GmEm / RE2 (опять же, измеряется на поверхности Земли) ~ 1 / r2 ~ rr • увеличение в 2 раза • увеличение в 4 раза.
• увеличение в 2 раза • увеличение в 4 раза. 1 Относительное движение, расстояние и смещение
1 Относительное движение, расстояние и смещение 1 Сила
1 Сила 2 Равномерное круговое движение
2 Равномерное круговое движение 1 Линейный импульс, сила и импульс
1 Линейный импульс, сила и импульс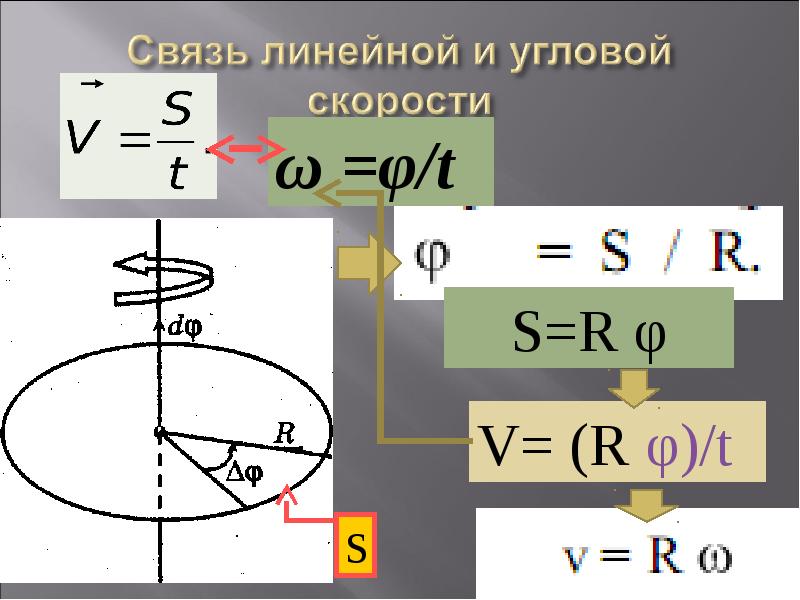 1 Постулаты специальной теории относительности
1 Постулаты специальной теории относительности