Пдд четные и нечетные дни: Знаки 3.29 и 3.30 описание и пояснение

Содержание

ОНФ опубликовал видеоролик о правилах стоянки и остановки автомобилей по четным и нечетным числам

На страницах проекта «Дорожная инспекция ОНФ/Карта убитых дорог» в социальных сетях и YouTube опубликован второй обучающий ролик для автомобилистов. В видеоуроке общественники рассказывают о правилах стоянки и остановки в зоне действия знаков 3.29 «Стоянка запрещена по нечетным числам месяца» и 3.30 «Стоянка запрещена по четным числам месяца», а также о штрафах за нарушения. Видеоролик эксперты дорожного проекта Народного фронта создали на основе промежуточных результатов теста на знание ПДД, запущенного в мобильном приложении «Убитые дороги» в июле 2019 г.

Тест в мобильном приложении прошли более 400 пользователей. Они ответили на 20 вопросов, составленных на основе самых распространенных нарушений. Вопросы описывают типичные ситуации на дорогах, которые могут вызвать сложности у водителей. Тест носит обучающий характер – в случае неправильного ответа появляются подсказки со ссылкой на соответствующий пункт ПДД.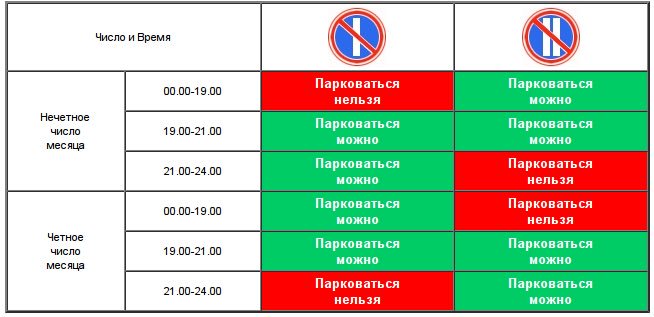

Больше всего ошибок пользователи допустили, отвечая на вопрос об остановке транспортного средства на перекрестке. Так, 76% респондентов не знают, где надо останавливаться: перед пешеходным переходом, светофором или пересечением проезжих частей. Трудности вызвал и вопрос о круговом движении – на него неправильно ответили около 51% автомобилистов. Эти темы эксперты проекта «Дорожная инспекция ОНФ/Карта убитых дорог» разобрали в первом обучающем ролике.

На вопрос о том, в каких случаях водитель должен быть в куртке, жилете или накидке со светоотражателями, неверный ответ дали 63% автомобилистов, а о траектории движения возле знака 6.3.1 «Место для разворота» – почти 59%. Меньше всего неправильных ответов пользователи дали, отвечая на вопросы о случаях для совершения вынужденной остановки (5%) и об обязанности пристегиваться ремнями безопасности (менее 2%).

«Участники Дорожной инспекции ОНФ в этом году проехали более 60 тысяч километров. Рейды показали, что автомобилисты в разных уголках страны допускают одни и те же ошибки: при стоянке, остановке, проезде перекрестков, движении по круговым перекресткам, – отметил

координатор проекта «Дорожная инспекция ОНФ/Карта убитых дорог», депутат Госдумы Александр Васильев.

– Проезд перекрестков, который вызывает много сложностей (40–45% неправильных ответов в зависимости от вопроса), мы разберем в следующем видеоуроке. Сегодня мы решили рассказать подробнее о правилах остановки и стоянки автомобилей – в вопросе о парковке по четным/нечетным дням допустили ошибку 22% респондентов. Также не все автомобилисты знают, что означают знаки 8.6.1-8.6.9 «Способ постановки транспортного средства на стоянку».

Чтобы пройти тест, нужно скачать приложение «Убитые дороги» в App Store или Google Play или обновить приложение, если оно уже установлено. Раздел «Тесты» расположен в меню слева. В нем будут размещаться другие тесты и опросы на знание ПДД и культуры вождения. Пройти тест можно только один раз.

Четный номер машины — катаешься по четным дням. К чему в Индии привела эта идея

Для разгрузки трафика на улицах городов Индии была введена оригинальная мера: в четные дни месяца по дорогам могут ездить машины с четными номерами, в нечетные дни, соответственно, с нечетными номерами.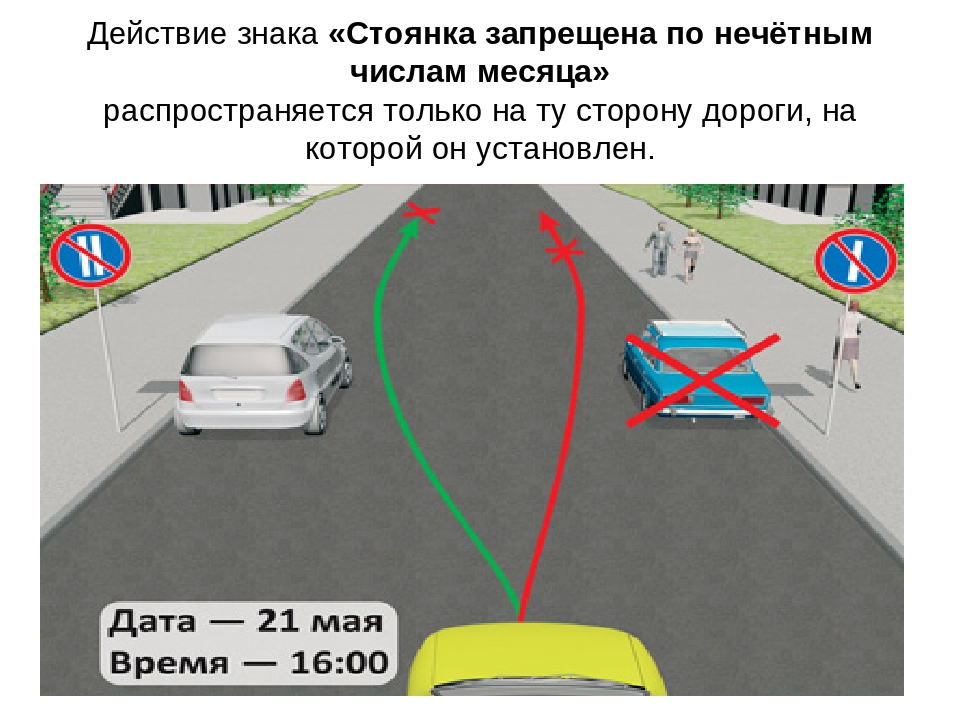

Может показаться, что правила ПДД универсальны для всех стран. На первый взгляд везде все одинаковое: и светофоры, и зебры-переходы, и дорожные знаки. Но на самом деле в каждом государстве есть свои нюансы дорожного движения. Например, в Японии действует правостороннее движение и почти нет пробок благодаря продуманной системе дорог. В России, наоборот, движение левостороннее, а автомобильные пробки в час пик — это почти символ столицы Москвы. В Китае и Гонконге вообще как будто никаких правил нет: и автомобилисты, и пешеходы передвигаются по улицам хаотично.

В Индии, которая является одной из самых густонаселенных стран мира, проблема пробок тоже стоит очень остро. Особенно хорошо это ощущается в крупных городах, таких как Дели. И его власти придумали весьма незаурядное решение проблемы.

Чет-нечет в условиях уличного движения

Несмотря на то, что в Индии большой процент населения относится к категории бедных, машин на дорогах ее городов очень много. Так что и поддерживать порядок на них тяжело. И никакие правила ДД тут не помогают. Поэтому требовалось найти какое-то оригинальное решение проблемы, как сократить количество транспорта на улицах, чтобы избавиться от пробок.

Власти одного из самых густонаселенных индийских мегаполисов Дели ввели новую схему движения: по четным дням на дороги смогут выезжать только машины, у которых номер заканчивается на четную цифру, и наоборот. Теоретически такая мера позволяет снизить количество автомобилей на дорогах в два раза. Автомобилистам пришлось бы пользоваться личным транспортом через день, а в остальное время кататься на муниципальном.

Также данная мера должна была решить и еще одну проблему — снизить количество выхлопных газов, поступающих в атмосферу. Ведь, как известно, экологическая обстановка в крупных городах Индии весьма неблагополучная. В стране из-за загрязненного воздуха умерли 1,2 млн человек.

Благие намерения привели к противоположному эффекту

Сразу после введения оригинальной меры несколько дней схема чет-нечет на дорогах работала отлично. Количество единиц личного автотранспорта действительно значительно уменьшилось. Но потом все стало даже хуже, чем было изначально: индийцы, лишенные колес, стали покупать в семьи по второй, третьей и даже четвертой машине. В итоге и концентрация выхлопных газов в атмосфере увеличилась на 25%. Пробки тоже стали собираться, как и раньше.

Проблема усугубляется тем, что индийцы в основном покупают дешевые подержанные автомобили, которые, естественно, не соответствуют никаким экологическим стандартам. В общем, благие намерения властей оказались в итоге малоэффективными. Тем не менее, в Индии периодически продолжают использовать схему попеременного движения машин с четными и нечетными номерами, рассчитывая со временем пробудить в гражданах сознательность.

Цифры из ПДД — Энциклопедия журнала «За рулем»

Под «знаком I» и «знаком «II» подразумеваются знаки 3.29 и 3.30

Расстояние, протяженность, размер
15 метров в населенных пунктах 30 метров вне населенных пунктов.	Минимальное расстояние от автомобиля до знака аварийной остановки.
50-100 метров в населенных пунктах 150-300 метров вне населенных пунктов.	Минимальное расстояние от предупреждающего знака до опасного участка.
100 метров видимость дороги хотя бы в одном направлении.	Минимальное расстояние, при котором запрещен разворот, задний ход, остановка на проезжей части.
Менее 300 метров.	Недостаточная видимость (дождь, туман и т.д.).
100 метров перед ж/д переездом или на нем.	Запрещен обгон.
50 метров перед ж/д переездом или после него.	Запрещена стоянка.
5 метров перед пешеходным переходом или на нем.	Запрещена остановка.
15 метров перед или после остановки МТС.	Запрещена остановка. Остановка разрешена для посадки и высадки пассажиров, если это не создает помех для МТС.
Менее 3 метров от сплошной линии разметки до борта автомобиля.	Запрещена остановка.
5 метров от шлагбаума. 10 метров до ближайшего рельса.	Минимальное расстояние для остановки перед ж/д переездом — если нет стоп-линии, знака STOP или светофора.
150 метров до встречного автомобиля.	Переключить «дальний» на «ближний».
Не более 4 метров.	Длина жесткой сцепки для буксира.
4 — 6 метров.	Длина гибкой сцепки для буксира.
1 метр спереди или сзади. 0.4 метра сбоку.	Максимальный размер, на который может выступать груз. Груз, выступающий больше указанного, должен быть обозначен знаком «крупногабаритный груз»
2 метра сзади. Более 2.5 по ширине.	Движение с таким грузом только по специальным правилам.
0.8 мм	Максимально допустимая остаточная глубина протектора для мотоциклов (категория L).
1.6 мм	Максимально допустимая остаточная глубина протектора для легковых автомобилей (категория М1).
Масса
Менее 3.5 тонны 750 кг До 8 человек	Дается право управлением автомобиля с «правами» категории В
Грузовики с РММ более 2.5 тонн	На любых дорогах с количеством полос больше двух занимать крайнюю левую полосу разрешается только для поворота налево и разворота.
Грузовики с РММ более 3.5 тонн	Запрещается движение далее 2-й полосы на магистралях.
Время
Менее 5 минут	Остановка.
Более 5 минут	Стоянка.
0:00 — 19 час	Запрещена стоянка для знака «I» по нечетным дням и знака «II» по четным
19:00 — 21:00 час	Разрешена стоянка для знаков «I» и «II» в любой день
21:00 — 24:00 час	Запрещена стоянка для знака «II» по нечетным дням и знака «I» по четным
Возраст
До 12 лет.	Перевозить на переднем сидении разрешается только в детском кресле. Запрещается перевозить на заднем сидении мотоцикла.
До 16 лет.	С этого возраста можно обучать вождению на автомобиле.
Скорость
Менее 40 км/ч по техническим параметрам или по состоянию.	Движение только по крайней правой полосе, кроме обгона, объезда, поворота налево или разворота.
Люфт
10 градусов.	Максимально допустимый люфт в рулевом управлении.
Уклон
До 23%.	Ручной тормоз должен обеспечить неподвижность автомобиля в снаряженном состоянии.
До 16%.	Ручной тормоз должен обеспечить неподвижность автомобиля с полной нагрузкой.

соотношение чисел в дате рождения определяет жизненный путь. Вычислите свою «комбинацию»

Считается, что судьба человека заложена в дате его рождения. Существуют три цифры, которые многое могут рассказать о том, что ждет человека в будущем, а также о его характере. Цифры эти подразделяются на четные и нечетные. Но, впрочем, давайте о всем по порядку.

Дата рождения

Вы родились в нечетный день, месяц и год? Ох, какая же интересная жизнь ждет вас, если верить нумерологии. Каждое соотношение чисел, их комбинация имеют определенное значение для будущего.

Рассчитываем свою комбинацию

Вначале давайте рассчитаем цифры даты рождения. К примеру, человек родился 24.04.1989 года:

Мы складываем цифры дня рождения: 2+4=6.
Затем, месяца рождения: 0+4=4
И наконец года рождения: 1+9+8+9=27. 2+7=9.

Итак, комбинация следующая: 6.4.9. А значит, четная-четная-нечетная.

Комбинации с первой по четвертую

Всего комбинаций восемь. Начнем с первой половины:

Комбинация №1. Нечетная-нечетная-нечетная.

Люди, рожденные под такими цифрами, очень чувствительны и уязвимы на эмоциональном уровне. Им сложно удерживать эмоциональное равновесие, груз собственных чувств нередко мешает продвинуться к цели.

Вместе с этим люди комбинации №1 очень открытые и душевные. Они прекрасно знают, что такое сочувствие, умеют помочь и наставить на путь истинный своего ближнего.

Эти люди — мечтатели. Рутинная работа и практичность — не их конек.

Комбинация №2. Нечетная-нечетная-четная.

Молчи, скрывайся и таи… Молчание — золото для людей с данной комбинацией. Если такие индивиды начинают говорить, то становятся очень уязвимыми. И сразу же найдутся те, кто захочет столкнуть человека с правильного пути, занять его место на карьерной лестнице или просто навредить.

Молчание — залог успеха для данной комбинации. А еще, люди этого типа чрезвычайно эмоциональные. Нередко именно эмоции управляют ими.

Художественное творчество — вот, что способствует реализации данной комбинации.

Комбинация №3. Нечетная-четная-нечетная

Это люди, у которых есть все качества для хорошей жизни. Они решительны, целеустремленны и всегда добиваются задуманного. Из людей с такой комбинацией чисел, как правило, получаются отменные руководители, архитекторы, изобретатели.

Комбинация №4. Четная-нечетная-нечетная

О, самооценке таких личностей можно только позавидовать. Они считают себя одаренными во всех отраслях, и действительно нет той сферы деятельности, в которой эти люди не попробовали бы себя.

Кроме того, люди с данной комбинацией склонны к различным мистическим учениям. Но большинство из них, несмотря на это, являются рациональными людьми и понимают, что мистика — мистикой, а материальные ценности еще никто не отменял.

Комбинации с пятой по восьмую

Про первые четыре все узнали. Осталось выяснить, что скрывается под комбинациями №№5-8.

Комбинация №5. Нечетная-четная-четная.

Люди, чья дата рождения связана с данной комбинацией, отличаются необычайной сдержанностью. Кажется, что у них никогда не бывает плохого настроения, терпению позавидовать можно, а родились они с улыбкой на лице. На самом деле, чтобы вызвать гневную реакцию у таких людей, необходимо хорошенько постараться.

Личности, рожденные под комбинацией №5 — настоящие «технари». Математика, химия, физика — это их конек. Из подобных личностей выходят отменные экономисты, бухгалтеры, биологи и т. д.

Что касается дружбы, в силу своей замкнутости таким людям сложно завязывать новые знакомства.

Комбинация №6. Четная-нечетная-четная.

Внешне люди, рожденные под комбинацией №6, кажутся холодными и неприступными. Эта холодность помогает им реагировать в самых сложных ситуациях быстро и грамотно. А в общении с близкими, друзьями и коллегами — лучше человека не сыскать.

На работе людей с такой комбинацией высоко ценят. Они организованны, всегда имеют варианты разрешения той или иной проблемы, умеют убеждать окружающих тонко и красиво.

Комбинация №7. Четная-четная-нечетная.

Призвание этих людей — помощь ближнему. Они полностью реализовывают себя, становясь врачами, психиатрами или психологами. У людей с комбинацией №7 нет различия между давними друзьями и шапочными знакомыми. Если кому-то из оных потребуется помощь, «семерки» всегда окажут ее.

У таких людей очень широкий кругозор, а также многие имеют хорошее образование, что помогает им добиться успехов в жизни.

Комбинация №8. Четная-четная-четная.

Эти люди приземленные, их совершенно не интересует творчество. Обычно успехов достигают в профессиях, связанных с точностью. Из «восьмерок» получаются отличные инженеры, учителя химии, физики или математики.

Друзья знают, что людей с данной комбинацией лучше не вытаскивать из собственного мира. Они с удовольствием проведут время дома, на собственной даче или на прогулке в лесу, чем пойдут в кафе, на дискотеку и в иные места для развлечений.

Как правило, «восьмерки» неудачливы в браке. А многие вообще предпочитают одинокую жизнь семейным радостям.

Заключение

Вот такая складывается картина, если верить нумерологии. Кто знает, быть может цифры имеют влияние на нашу жизнь, откладывают определенный отпечаток на судьбу.

Нашли нарушение? Пожаловаться на содержание

Четные и нечетные функции

Это особые типы функций

Четные функции

Функция «даже», когда:

f (x) = f (−x) для всех x

Другими словами, существует симметрия относительно оси Y (как отражение):

Это кривая f (x) = x ² +1

Их назвали «четными» функциями, потому что функции x ², x ⁴, x ⁶, x ⁸ и т. Д. Ведут себя так же, но есть и другие функции, которые ведут себя так же, например, cos (х):

Косинусная функция: f (x) = cos (x)
Это четная функция

Но четный показатель не всегда дает четную функцию, например (x + 1) ² — это , а не — четная функция.

Нечетные функции

Функция считается «нечетной», если:

−f (x) = f (−x) для всех x

Обратите внимание на минус перед f (x): −f (x) .

И получаем симметрию начала координат:

Это кривая f (x) = x ³ −x

Их назвали «нечетными», потому что функции x, x ³, x ⁵, x ⁷ и т. Д. Ведут себя так же, но есть и другие функции, которые ведут себя так же, например sin (x ) :

Функция синуса: f (x) = sin (x)
Это нечетная функция

Но нечетная экспонента не всегда дает нечетную функцию, например x ³ +1 — это , а не — нечетная функция.

Ни нечетное, ни четное

Пусть вас не вводят в заблуждение имена «нечетный» и «четный» … это всего лишь имен … и функция не обязательно должна быть четной или нечетной.

На самом деле большинство функций не являются ни нечетными, ни четными. Например, просто добавив 1 к приведенной выше кривой, получим:

Это кривая f (x) = x ³ −x +1

Это не нечетная функция , и это не четная функция .
Нечетно и нечетно

Четное или нечетное?

Пример: является ли f (x) = x / (x ² −1) четным или нечетным или ни одним?

Давайте посмотрим, что произойдет, если мы подставим −x :

f (−x) = (−x) / ((- x) ² −1)

= −x / (x ² −1)

= −f (х)

Итак, f (−x) = −f (x), что делает его нечетной функцией

Четное и нечетное

Единственная функция, которая является четной и нечетной , это f (x) = 0

Особые свойства

Добавляем:

Сумма двух четных функций четна
Сумма двух нечетных функций нечетная
Сумма четной и нечетной функции не является ни четной, ни нечетной (если одна функция не равна нулю).

Умножение:

Произведение двух четных функций является четной функцией.
Произведение двух нечетных функций является четной функцией.
Произведение четной функции и нечетной функции является нечетной функцией.

Четных и нечетных функций | Purplemath

Purplemath

Вас могут попросить «алгебраически» определить, является ли функция четной или нечетной.Для этого вы берете функцию и подключаете — x к x , а затем упрощаете. Если в итоге вы получите ту же функцию, с которой начали (то есть, если f (- x ) = f ( x ), поэтому все знаки совпадают), тогда функция даже. Если вы закончите с полной противоположностью того, с чего начали (то есть, если f (- x ) = — f ( x ), поэтому все знаки поменяны местами), тогда функция странно.

Во всех остальных случаях функция не является ни четной, ни нечетной.

Давайте посмотрим, как это выглядит в действии:

MathHelp.com

Определите алгебраически, является ли f ( x ) = –3 x ² + 4 четным, нечетным или ни одним из них.

Если я построю график, я увижу, что это «симметрично относительно оси y «; Другими словами, все, что делает график на одной стороне оси y , отображается на другой стороне:

Это зеркальное отображение оси y является отличительной чертой четных функций.

Также отмечу, что показатели степени у всех членов четные — показатель степени постоянного члена равен нулю: 4 x ⁰ = 4 × 1 = 4.Это полезные подсказки, которые убедительно подсказывают мне, что у меня здесь четная функция.

Но вопрос просит меня дать определение алгебраически , что означает, что мне нужно выполнить алгебру.

Итак, я вставлю — x в x и упрощу:

f (- x ) = –3 (- x ) ² + 4

= –3 ( x ²) + 4

= –3 x ² + 4

Я вижу, сравнивая исходную функцию с моим окончательным результатом выше, что у меня есть совпадение, что означает, что:

Определите алгебраически, является ли f ( x ) = 2 x ³-4 x четным, нечетным или ни одним из них.

Если я построю график, я увижу, что он «симметричен относительно начала координат»; то есть, если я начну с точки на графике с одной стороны оси y и проведу линию от этой точки через начало координат и продолжу такую же длину с другой стороны оси y , Я перейду к другой точке графика.

Вы также можете думать об этом как о половине графика на одной стороне оси y — это перевернутая версия половины графика на другой стороне оси y .Эта симметрия — отличительный признак нечетных функций.

Отметим также, что все показатели в правиле функции нечетные, поскольку второй член можно записать как 4 x = 4 x ¹. Это полезная подсказка. Я ожидал, что эта функция будет странной.

Вопрос просит меня произвести определение алгебраически, поэтому я вставлю x вместо x и упрощу:

f (- x ) = 2 (- x ) ³ — 4 (- x )

= 2 (- x ³) + 4 x

= –2 x ³ + 4 x

Чтобы данная функция была нечетной, мне нужно, чтобы в приведенном выше результате были все знаки, противоположные исходной функции.Так что напишу исходную функцию, а потом переключу все знаки:

исходный: f ( x ) = 2 ( x ) ³ — 4 ( x )

коммутируемый: — f ( x ) = — 2 x ³ + 4 x

Сравнивая это с тем, что у меня есть, я вижу, что они совпадают.Когда я подключил — x к x , все знаки поменялись местами. Это означает, что, как я и ожидал:

Определите алгебраически, является ли f ( x ) = 2 x ³-3 x ²-4 x + 4 четным, нечетным или ни одним из них.

Эта функция является суммой двух предыдущих функций.Но, хотя сумма нечетного и четного числа является нечетным числом, я не могу сделать то же самое о сумме нечетной и четной функции.

Обратите внимание, что график этой функции не имеет симметрии ни одного из предыдущих:

… и все его показатели не являются четными или нечетными.

Основываясь на показателях, а также на графике, я ожидал бы, что эта функция будет ни четным, ни , ни нечетным.Тем не менее, чтобы быть уверенным (и чтобы получить полную оценку моего ответа), мне нужно будет заняться алгеброй.

Я подключу — x для x и упрощу:

f (- x ) = 2 (- x ) ³-3 (- x ) ²-4 (- x ) + 4

= 2 (- x ³) — 3 ( x ²) + 4 x + 4

= –2 x ³ — 3 x ² + 4 x + 4

Путем быстрого сравнения я вижу, что это не соответствует тому, с чего я начал, поэтому эта функция не является четной.А что насчет странного?

Для проверки я запишу прямо противоположное тому, с чего я начал, — это исходная функция, но со всеми измененными знаками:

— f ( x ) = — 2 x ³ + 3 x ² + 4 x — 4

Это тоже не соответствует тому, что я придумал.Так что исходная функция тоже не странная. Затем, как я и ожидал:

f ( x ) не является ни четным, ни нечетным.

Как видите, сумма или разность четной и нечетной функции равна , а не нечетной функции. Фактически вы обнаружите, что сумма или разность двух четных функций — это еще одна четная функция, а сумма или разность двух нечетных функций — еще одна нечетная функция.

Существует (ровно) одна четная и нечетная функция; это нулевая функция, f ( x ) = 0.

Другими словами, «четный» и «нечетный» в контексте функций означают нечто совершенно иное, чем то, как эти термины используются с целыми числами. Не пытайтесь смешивать два набора определений; это только запутает вас.

Не думайте, что концепция четных и нечетных функций ограничивается полиномами только потому, что до сих пор во всех примерах использовались полиномиальные функции.Это не. Тригонометрия полна четных и нечетных функций, и другие типы функций также могут быть рассмотрены.

Определите, является ли g ( x ) = 3 / ( x ² + 2) четным, нечетным или ни одним из них.

Это рациональная функция. Процесс проверки четности, нечетности или ни того, ни другого не отличается от обычного.Начну с подключения — x для x :

г (- x ) = 3 / [(- x ) ² + 2]

= 3 / [( x ²) + 2]

= 3 / ( х ² + 2)

По сравнению с этим я вижу, что это то же самое, с чего я начал.Итак:

Вы можете найти полезным, отвечая на этот вопрос «четного или нечетного», явно записать — f ( x ), а затем сравнить это с тем, что вы получите для f (- x ). Это может помочь вам с уверенностью определить правильный ответ.

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в определении того, является ли функция четной, нечетной или ни одной из них.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку «бумажный самолетик», чтобы сравнить свой ответ с ответом Матвея.

(Щелкнув по «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)

URL: https://www.purplemath.com/modules/fcnnot3.htm

Калькулятор четных, нечетных или нулевых функций

Поиск инструмента

Четная или нечетная функция

Инструмент для проверки четности функции (четной или нечетной функции): он определяет способность функции (ее кривой) проверять симметричные отношения.

Результаты

Четная или нечетная функция — dCode

Тег (и): Функции

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор четных и нечетных функций

Инструмент для проверки четности функции (четной или нечетной функции): он определяет способность функции (ее кривой) проверять симметричные отношения.2 = f (x) $, поэтому функция квадрата $ f (x) $ четна.

Графически это означает, что противоположные абсциссы имеют одинаковые ординаты, это означает, что ось ординат является осью симметрии кривой, представляющей f.

Доказав это равенство для одного значения типа $ f (1) = f (-1) $, нельзя сделать вывод о наличии четности, а только сказать, что 1 и -1 имеют одно и то же изображение функцией $ f $.

Как проверить, нечетная ли функция?

Определение: Функция является нечетной, если равенство $$ f (x) = -f (-x) $$ верно для всех x из области определения.3 = f (x) $, поэтому кубическая функция $ f (x) $ нечетная.

Графически , это означает, что противоположные оси абсцисс имеют противоположные ординаты, это означает, что начало координат (центральная точка) (0,0) является центром симметрии кривой, представляющей $ f $.

NB: если нечетная функция определена в 0, то кривая проходит в начале координат: $ f (0) = 0 $

Доказав равенство для одного значения, такого как $ f (2) = -f (-2) $, мы не можем сделать вывод о несоответствии, а только сказать, что 2 и -2 имеют противоположные изображения функцией $ f $.

Как проверить, не является ли функция четной или нечетной?

Функция не является ни нечетной, ни четной, если ни одно из двух вышеупомянутых равенств не выполняется, то есть: $$ f (x) \ neq f (-x) $$ и $$ f (x) \ neq -f ( -x) $$

Пример: Определите четность $ f (x) = x / (x + 1) $, первое вычисление: $ f (-x) = -x / (- x + 1) = x / (x- 1) \ neq f (x) $ и второе вычисление: $ -f (-x) = — (- x / (- x + 1)) = -x / (x-1) = x / (- x + 1 ) \ neq f (x) $, следовательно, функция $ f $ не является ни четной, ни нечетной.

Какова четность тригонометрических функций (cos, sin, tan)?

В тригонометрии функции часто симметричны:

Функция косинуса $ \ cos (x) $ четная.

Синус-функция $ \ sin (x) $ нечетная.

Касательная функция $ \ tan (x) $ нечетная.

Почему функции называются четными или нечетными?

Развития сходящихся степенных рядов или многочленов четных (соответственно нечетных) функций имеют четные степени (соответственно нечетные).

Есть ли функция одновременно и четная, и нечетная?

Да, функция $ f (x) = 0 $ (функция постоянного нуля) является как четной, так и нечетной, потому что она соблюдает 2 равенства: $ f (x) = f (-x) = 0 $ и $ f (x) = -f (-x) = 0 $

Задайте новый вопрос

Исходный код

dCode сохраняет право собственности на исходный код онлайн-инструмента «Функция четности или нечетности». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) доступ к данным, скриптам или API не будет бесплатным, то же самое для загрузки четных или нечетных функций для автономного использования на ПК, планшете, iPhone или Android!

Нужна помощь?

Пожалуйста, заходите в наше сообщество Discord, чтобы получить помощь!

Вопросы / Комментарии

Сводка

Инструменты аналогичные

Поддержка

Форум / Справка

Ключевые слова

четный, нечетный, функция, четность, симметрия, тригонометрический, косинус, синус

Ссылки

Источник: https: // www.