Единица измерения угловой частоты: Единица измерения частоты, теория и онлайн калькуляторы

Конвертер угловой скорости и частоты вращения • Механика • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева

Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту

Общие сведения

Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.

Угловая скорость в спорте

Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.

При первобытнообщинном строе главными охотниками были мужчины

Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости

У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.

В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.

Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают.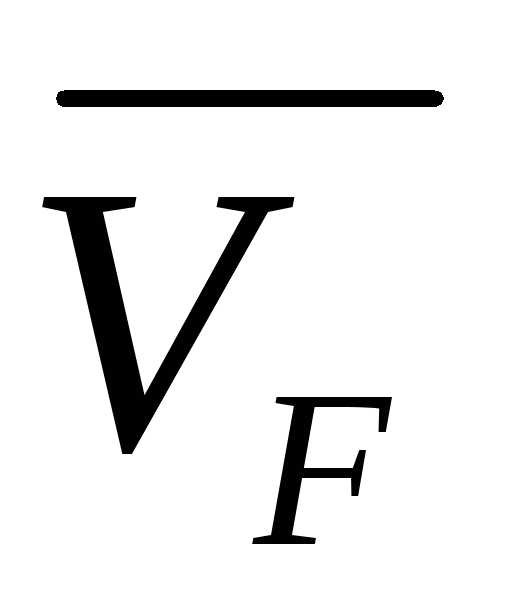 Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.

Угловая скорость и хранение данных на оптических носителях

Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4&nbsp200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15&nbsp000 оборотов в минуту на высокоэффективных серверах

Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим

частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной. Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.

Угловая скорость в космосе

Геостационарная орбита

На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники.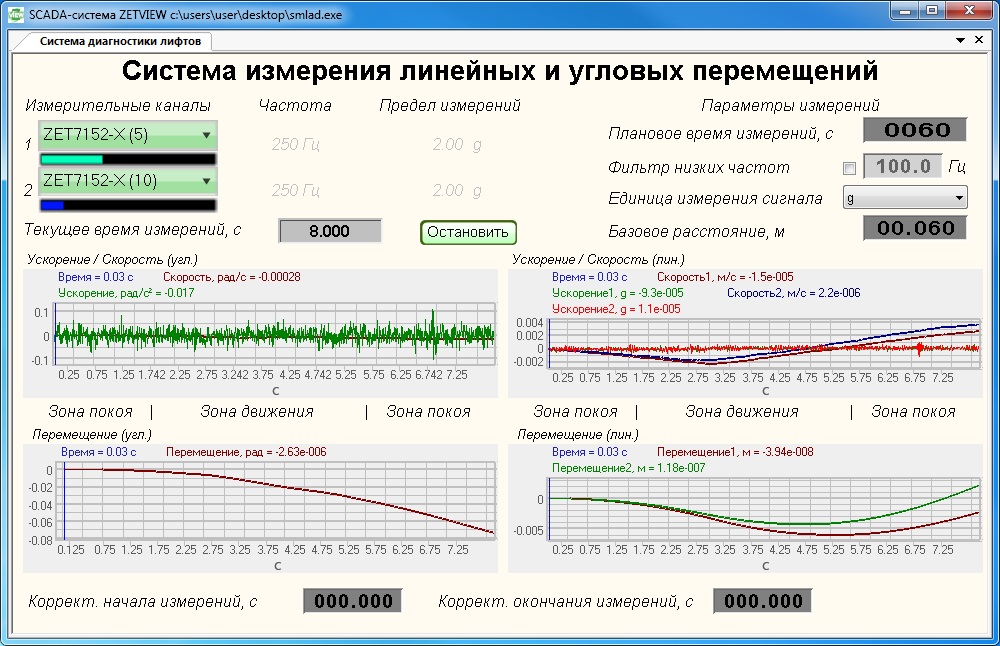 Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.

На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.

Спутниковые антенны

Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.

Литература

Автор статьи: Kateryna Yuri

Unit Converter articles were edited and illustrated by Анатолий Золотков

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.

Период и частота

Физика > Период и частота

 

Как найти период и частоту – определение и формула. Читайте, что такое угловая частота, цикл, частоты синусоидальных волн, единицы измерения, уравнения.

Период – продолжительность цикла повторяющегося события, а частота – количество циклов за временной промежуток.

Задача обучения

• Преобразование между частотой и периодом.

Основные пункты

• Регулярно повторяющееся движение – периодическое. Одно полное повторение – цикл.
• Продолжительность цикла – период.
• Частота отображает число циклов, осуществленное за определенный временной промежуток. Это обратная величина периода и определяется формулой f = 1/T.
• Некоторые перемещения лучше всего характеризовать угловой частотой (ω). Она относится к угловому смещению за временной промежуток. Вычисляется по формуле: ω = 2πf.

Термины

• Угловая частота – угловое смещение за временной промежуток.
• Период – длительность одного цикла в повторяющемся событии.
• Частота – соотношение количества раз (n) периодического явления за временную единицу (t): f = n/t.

Пример

Когда-то существовал викторианский трюк. Человеку нужно было вслушаться в звук мухи, воспроизвести музыкальную ноту на пианино и сказать, сколько раз летучая мышь ударила крыльями за секунду. Если это 200 раз в секунду, то частота движения – f = 200/1 с = 200 Гц. Период составляет 1/200-ю секунду: T = 1/f = (1/200) с = 0.005 с.

Период и частота

Эти термины используют для выражения повторного движения. Период – время, которое тратится на одно повторение. Один полноценный проход – цикл. Частота – количество циклов за конкретный временной промежуток (f).

Синусоидальные волны разных частот. Нижние обладают более высокими частотами, а горизонтальная ось отображает время.

Понятия выражаются в формуле: F = 1/T.

Допустим, частота сердца новорожденного составляет 120 раз в минуту, а период – половина секунды. Если вы отточите интуицию на ожидание сопряженности больших частот с короткими периодами (и наоборот), то избежите ошибок.

Единицы

Чаще всего частота рассчитывается в герцах (Гц). 1 Гц указывает на то, что событие происходит раз в секунду. Традиционная единица, применимая во вращающихся механических приборах, – обороты в минуту (об/мин). Единица периода – секунда.

Угловая частота

Частота периодического движения лучше всего передается через угловую частоту – ω. Она относится к угловому смещению на единицу времени или скорости перемены состояния синусоидальной формы волны. В виде формулы:

Колеса совершают вращение с частотой f циклов в секунду, что можно описать как ω радиан в секунду. Механическая связь позволяет линейным колебаниям поршней парового двигателя руководить колесами

у (t) = sin(θ(т)) = sin(ωt) = sin(2πft)

ω = 2πf

Угловая частота часто отображается в радианах на секунду.

---

Частота — Единицы измерения — Энциклопедия по машиностроению XXL

Целесообразно записать эти уравнения в безразмерном виде, введя следующие единицы измерения всех фигурирующих в них величин для длины, частоты, скорости, давления и температуры это будут соответственно h, v/li , v/h, pv /h и Ahv/x- Ниже в этом параграфе (а также в задачах к нему) все буквы обозначают соответствующие безразмерные величины. Уравнения принимают вид  [c.312]

В отличие от частоты релаксации резонансная частота очень стабильна и слабо зависит от температуры и других факторов. Поэтому спектральные линии служат эталонами единиц измерения.  [c.111]

Объектами государственной стандартизации являются общетехнические и организационно-методические правила и нормы (например, ряды номинальных частот и. напряжений электрического тока, допуски и посадки, резьбы, предпочтительные числа, нормы точности зубчатых передач и др.) научно-технические термины и обозначения единицы измерений и эталоны единиц измерений системы нормативно-технической, конструкторской, технологической, эксплуатационной и ремонтной документации, документации в области организации и управления производством и др.  

[c.47]

МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ ОТНОШЕНИЯ E l I]j ДЛЯ ТРЕХФАЗНЫХ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧ С ДВУМЯ СИСТЕМАМИ ПРИ ЧАСТОТЕ 50 Гц (ЕДИНИЦА ИЗМЕРЕНИЯ B-kA -km ) ПРИ ТРЕХ РАБОЧИХ НАПРЯЖЕНИЯХ (110-380 кВ)  [c.437]

Также возросли масштабы и объем работ в области метрологии и измерительной техники. За последнее время утвержден ряд новых государственных эталонов единиц измерений длины, массы, времени и частоты, ионизирующих излучений, силы тока, света и магнитного потока. Эти эталоны составляют уникальный комплекс измерительных средств, которые с наивысшей возможной точностью воспроизводят величины соответствуюш,их единиц измерений.  

[c.14]

Здесь X и о — параметры эмпирического распределения, полученные из результатов обработки (в единицах измерения) дг —середины интервалов по таблице эмпирического распределения в тех же единицах h — ширина интервала в тех же единицах я,-—частота (число наблюдений в интервале номер г) п — общее число наблюдений Л и S — масштабы графика в мм Xj j и уд,. —координаты точек полигона распределения в масштабе графика (точнее, Уд,- —высоты прямоугольников гистограммы).  [c.307]

Чтобы иметь возможность количественного сопоставления громкостей звуков различных частот, введено понятие об уровне громкости, единицей измерения которого является фон. По определению, уровень громкости в фонах численно  [c.350]

Источником звука является колеблющееся тело, например сгущение и разрежение воздуха, вызываемое взрывом или ударом молота о наковальню, колебание струны при прикасании к ней и т. д. Эти колебания образуют звуковую волну, действующую на слуховой орган человека они измеряются герцами. Герц — это единица измерения частоты колебаний, которая соответствует од-  

[c.126]

Э. единицы времени воспроизводят одновременно и единицу частоты—герц, их и наз. Э. времени и частоты. Поскольку единица длины—метр—воспроизводятся через секунду и скорость света, появилась тенденция к созданию единых исходных Э. времени, частоты и длины Э. времени и частоты—сложные комплексы, содержащие системы формирования единиц времени и частоты и шкал времени, системы измерения частот стабилизированных лазеров, служащих для воспроизведения размера метра, системы внеш. сличений национальных Э. между собой. На рис. 1 приведена структурная схема Э. времени и частоты России, являющегося частью единого Э. времени, частоты и длины.  [c.640]

При вычислении коэффициента быстроходности параметры в формулу (16.16) подставляют в следующих единицах измерения частота вращения рабочего колеса п — об/мин подача насоса Q — mV напор насоса Я — м.  [c.233]

Как правило, в селективных усилителях предусмотрен широкополосный режим работы Низкочастотные измерительные усилители применяют для усиления и измерения переменных напряжений в полосе частот от единиц герц до 200 кГц. Усилители этого класса могут иметь встроенные фильтры, позволяющие проводить измерение при строго заданном ходе частотных характеристик (кривые А, В, С, D) [Г2]  [c.240]

Единицы измерения % позволяют сопоставлять самые разные методы термометрии. Чувствительность 8 имеет вид функции, осциллирующей при изменении температуры с удвоенной частотой по сравнению с колебаниями интенсивности света.  

[c.159]

В молекулярной спектроскопии термин частота колебаний может относиться и к колебанию молекул (буквенное обозначение со, а единица измерения см ). Также встречается термин частота перехода атома пли молекулы с одного энергетического уровня иа другой (буквенное обозначение у). В этом случае речь идет не о числе переходов, а о энергии перехода, измеряемой в единицах частоты электромагнитных колебаний у  [c.12]

Наименование Тип Единица измерения Шкалы Частота, кГц Класс точно- сти Габариты, мм  [c.117]

Герц — единица измерения частоты колебаний, соответствующая одному периоду (циклу) в секунду.  [c.194]

Неотложной задачей является распространение точных измерений на области очень малых и больших значений измеряемых величин (малых и больших масс, глубокого вакуума и сверхвысоких давлений, сверхнизких и сверхвысоких температур, сверхвысоких частот и др.). Необходимость передачи размера единиц измерений приборам, измеряющим исчезающе малые или сверхбольшие значения величин, часто не позволяет ограничиваться одним эталоном ч требует создания нескольких независимых специальных эталонов для одной и той же величины.

 [c.14]

В отличие от частоты релаксации резонансная частота очень стабильна и слабо зависит от температуры и других факторов. Поэтому спектральные линии служат эталонами единиц измерения. С понижением температуры обычно лишь уменьшается затухание Г и максимум е» (со) становится более острым.  [c.139]

Очевидно, что единица измерения а, с , и, следовательно, параметр а представляет собой угловую скорость (иногда параметр о называют угловой частотой). Полный цикл колебания определяется углом 0= 2л. Время, в течение которого осуществляется этот цикл, представляет собой период колебаний. Таким образом, при 0= —2л время и, следовательно, 2л=ат, и поэтому параметр 0=2я/т.  [c.306]

В табл. 26 приведены данные о сроках службы, необходимой частоте регулировок, длительности замен и регулировок и относительных баллах ненадежности, учитывающих все эти факторы для перечисленных главных элементов гидросистем. За единицу измерения взята ненадежность насоса.  [c.57]

Здесь YJ — амплитуда колебаний массы Мр начальная фаза и ш — круговая частота свободных колебаний (число колебаний в 2я секунд). На рис. 13.9 показаны Т — период колебаний (наименьший интервал времени, через который повторяется любое значение колеблющейся величины),/= 1/Г — частота колебаний (число колебаний в 1 с). Единица Измерения частоты колебаний — Герц (Гц -  [c.352]

Частота — Единицы измерения и меры 5, 14 Чеканка 302, 991  [c.1141]

По проекту ГОСТа на единицы измерения физических величин угловую скорость в об1мин называют частотой вращения.  [c.107]

МЙКРО… (от греч. mikros — малый) — приставка к наименованию единицы измерения для образования наименования дольной единицы, составляю1цей одну миллионную долю от исходной единицы. Обозначается мк, U. Напр., 1 МКС (микросекунда) = 10″ с. МИКРОВОЛНОВАЯ СПЕКТРОСКОПИЯ — область радиоспектроскопии, в к-рой спектры атомов и молекул в газовой фазе исследуют в диапазоне от дециметровых до субмиллиметровых длин волн (10 — IQi Гц). Объектами М. с. являются вращательные и НЧ колебательные спектры молекул, молекулярных ионов, комплексов и радикалов, тонкая и сверхтонкая структура молекулярных спектров, спектры тонкой и сверхтонкой структуры атомов и ионов, электронные спектры возбуждённых атомов (см. Молекулярные спектры. Атомные спектры). В микроволновых спектрометрах используют монохроматические, перестраиваемые по частоте источники излучения — генераторы СВЧ  [c.133]

Си7(Мп1ь (в произвольных единицах), измеренная в переменном поле с частотой 200 Гц и среднеквадратичным значением напряжённости 2,3 Э, для состаренного при длительном низкотемпературном отжиге (Л), закалённого (.Q) и пластически деформированного (СТУ) образцов [б].  [c.154]

ФОН (от греч. phona — звук) — внесистемная единица измерения уровня громкости звука равна уровню громкости звука, для к-рого уровень звукового давления равногромкого с ним звука чистого тона с частотой 1000 Гц равен  [c.335]

В метрологии за основную принята система СИ. Ф. ф. к. в ней применяются для установления соотношений между единицами физ. величин с целью их воспроизведения. При этом возникает единая система взаимосвязанных эталонов осн. единиц. Такая система эталонов базируется в осн. на квантовых явлениях (квантовая метрология), ее осн. элемент—эталон времени-частоты. Повышение точности измерения с привело к тому, что оказалось выгоднее фиксировать значение константы с и принять (1983) новое определение единицы длины метра как расстояния, проходимого в вакууме плоской эл. Гк1агн. волной за (1/с) долю секунды. Т, о., эталон длины стал связан с эталоном времени-частоты, в результате чего точность воспроизведения единиць[ длины существенно повысилась.  [c.382]

Неправильно было бы делать вывод о том, что если ощущение определенных колебаний есть свойство человеческого организма, то эти колебания существуют только в ощущениях человека. Просто человеческий организм является прибором, могущим проводить замеры и имеющим определенную полосу пропускания . Что же касается того обстоятельства, что единицы измерения определяются свойствами применяемых при замерах приборов, то с этим приходится встречаться во всех областях техники и во многих областях науки. Человеческое ухо способно воспринимать колебания с частотами от 10 до 16 ООО—20 ОООгг , если эти колебания достаточны для создания определенного звукового давления. Такие колебания и называются звуковыми.  [c.320]

Шкала уровня громкости звука в фонах, которая при частоте в 1000 гц совпадает со шкалой уровня громкости звука в децибелах, является в последнем случае шкалой субъективных единиц измерения и, к сожалению, нелинейной шкалой из-за того, что закон Вебера — Фехнера о чувствительности человеческого уха очень грубо оценивает его свойства. Для получения линейной шкалы измерения уровня громкости звука введена субъективная  [c.330]

Единицей измерения уровня (силы) шума принят децибел (дб), а частота шума (вибрации) измеряется в герцах (Гц). Уровень шума в производстве измеряют шумо-мерами типа Ш-ЗМ, АШ-2М, ИНШ-2. Предельно допустимые значения производственного шума с учетом его частоты приведены в табл. 4.  [c.453]

При расчетах с учетом случайных нагрузок необходим график нагрузка—-частота пра1вило накопления повреждений наиболее просто применяется после сведения зависимости нагрузка— прогиб к ряду шагов (рис. 15.8). Если начертить кривую частоты нагрузки на одном листе с кривой а — lgЛf, тогда видно, во сколько р,аз один сложный цикл переменного нагружения больше любой дадной величины нагрузки, приходящейся на милю, за единицу времени или за какую-нибудь другую единицу измерения. Таким образом, мы получим вид циклов, обозначенных п. На рис. 15.8 число циклов нагрузки за милю между пределами нагрузки, изображенной отрезками ОА и ОВ, есть (это значит, что п =ВВ —А А циклов) повреждения, соответствующие этой группе нагрузок, определяются приблизительно Ав- Учитывая все интервалы нагружения,  [c. 407]

В международных рекомендациях величина, измеряемая в оборотах ь секунду (об[сек), именуется частотой вращения. Предполагается обсудить целесообразность введения этого иаименоваиия в стандарты СССР при согласовании проекта единого стандарта на единицы измерений. Очевидно, 1 об/сек = 2 рад сек.  [c.60]

В соответствии с определением, данным в главе 3, в этом параграфе за чувствительность мы будем принимать среднюю плотность экспозиции (плотность энергии) записывающего света, при которой записываемая синусоидальная решетка имеет дифракционную эффективность 1%. Единицей измерения чувствительности в этом случае будет Дж/см . Для экспериментального определения S на ПВМС записывается синусоидальная решетка с заданной пространственной частотой V. От величины v зависит амплитуда модуляции считывающего света. Поэтому для достижения однозначности вместе с чувствительностью должна указываться пространственная частота, при которой производились измерения. Как правило, в литературе приводятся чувствительности ПВМС для пространственных частот, соответствующих максимуму передаточной характеристики, где величина является минимальной.  [c.154]

За единицу интенсивности звука условно принят 1 б (белл) — наименьшая сила звукового давления, воспринимаемая ухом здорового человека. На практике обычно пользуются единицей, в 10 раз меньшей, — децибеллом 1 дб = 0,1 б). В качестве единицы измерения частоты звуковых колебаний принят герц — частота, соответствующая одному колебанию в секунду. Слуховой аппарат человека воспринимает звуковые колебания в пределах от 20 до 20 ООО Гц. Звуковые колебания частотой ниже 20 Гц называются инфразвуком, а выше 20 000 Гц—ультразвуком. Эти области звуковых колебаний человеком не воспринимаются, однако ультразвуковые колебания неблагоприятно действуют на организм человека. Они могут вызывать преждевременное утомление, слабость, сонливость, неприятное ощущение в ушах, головные боли. При длительном воздействии ультразвука нарушаются функции периферической нервной системы, вестибулярного аппарата, изменяется артериальное давление.  [c.123]

Единицы измерения Предельно допустимые уровни виброскорости (в 56) относительно 510- см/сек и соотоетствующие им абсолютные величины в см сек для октавных полос со среднегеометрическими и граничными частотами в гц  [c.266]

Интенсивность механических воздействий на РЭА зависит от объекта, на котором она устанавливается, и характеризуется частотой колебаний возмущающей силы, амплитудой или перемещением и мгновенной скоростью. Основные парамегры механических воздействий и их единицы измерения следующие  [c.736]

Ной — внесистемная единица измерения уровня шума. Предложена амер. ученым Крайтером. Он учел индивидуальность восприятия различными людьми звука данной частоты и громкости и усреднил эти данные. За один ной принята шумность равномерного шума в полосе частот 910—1090 Гц при уровен звукового давления 40 дБ. В наст, время система Крайтера принята в ряде западных стран. Нои сходны с сонами рост шумности вдвое соответствует росту уровня воспринимаемого шума на 10 РНдБ, т. е. 2 Ной = 50 PN дБ, 4 ной = 60 PN дБ и т. д. Перевод уровня шума, выраженного в НОЯХ, в децибелы осуществляется с помощью пересчетных таблиц.  [c.304]

В период с 1927 по 1934 г. Комитетом по стандартизации при Совете Труда и Обороны были утверждены первые стандарты на метрические меры, на механические, электрические, магнитные, тепловые, световые, акустические единицы, единицы рентгеновского излучения, радиоактивности, давления, частоты и времени. Международную температурнл ю шкалу и др. Основным недостатком утвержденных И стандартов на единицы измерения было то, что одни стандарты основывались на системе МТС (метр — тонна — секунда), а другие — на системе СГС  [c.13]

Неоднократно обращается внимание на возможные источники ошибок и недостатки приборов, а также на ограничения, налагаемые материалами и зависящие от экспериментатора. Следуя рекомендациям Комитета королевского общества, в тексте отдается предпочтение волновым числам, а не длинам золн. Аргументация принятия частот в шкале волновых чисел в качестве основных единиц измерения была кратко рассмотрена Джонсо м и Сандорфи [4]. Однако, поскольку многие результаты публи-  [c.11]

За единицу измерения положения полос быпо принято волновое число (V), которое выражается в обратных сантиметрах (см ) и называется обычно частотой, хотя на самом деле единица частоты (у) имеет размерность обратной секунды (сек. ). Для указания положения полосы используется также длина волны (X), измеряемая в микронах ( л). Соотнощение этих единиц определяется выражениями  [c.14]

Угловая скорость и частота вращения имеют одинаковую >азмерность (Т ), но разные единицы измерения угловая ско-юсть [со] = 1 рад/с, частота вращения [и] = 1 с , угловая частота ш]= 1 с следовательно, по единице физической величины иногда нельзя судить о самой величине.  [c.22]

---

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени

:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону

.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла,  — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени

.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой

:

где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице

.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где  — радиус-вектор точки (из начала координат),  — скорость этой точки.  — векторное произведение,  — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .

.

.

.

• Лурье А. И. Аналитическая механика\\ А. И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136

В каких единицах измеряется угловая скорость

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где — радиус-вектор точки (из начала координат), — скорость этой точки. — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .

Связь с конечным поворотом в пространстве

• Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве. Тогда угловая скорость, соответствующая этому повороту, равна

.

.

• Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .

.

См. также

Литература

• Лурье А. И. Аналитическая механика\ А. И. Лурье. – М.: ГИФМЛ, 1961. – С. 100-136

Wikimedia Foundation . 2010 .

Смотреть что такое «Угловая скорость» в других словарях:

УГЛОВАЯ СКОРОСТЬ — векторная величина, характеризующая быстроту вращения твёрдого тела. При равномерном вращении тела вокруг неподвижной оси численно его У. с. w=Dj/Dt, где Dj приращение угла поворота j за промежуток времени Dt, а в общем случае w=dj/dt. Вектор У.… … Физическая энциклопедия

УГЛОВАЯ СКОРОСТЬ — УГЛОВАЯ СКОРОСТЬ, скорость изменения угловой позиции предмета относительно фиксированной точки. Средняя величина угловой скорости w предмета, движущегося от угла q1 до угла q2 за время t выражается как (q2 q1)w)/t. Мгновенной угловой скоростью… … Научно-технический энциклопедический словарь

УГЛОВАЯ СКОРОСТЬ — УГЛОВАЯ СКОРОСТЬ, величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости w=Dj/Dt, где Dj приращение угла поворота за промежуток времени Dt … Современная энциклопедия

УГЛОВАЯ СКОРОСТЬ — векторная величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости , где приращение угла поворота за промежуток времени ?t … Большой Энциклопедический словарь

угловая скорость — Кинематическая мера вращательного движения тела, выражаемая вектором, равным по модулю отношению элементарного угла поворота тела к элементарному промежутку времени, за который совершается этот поворот, и направленным вдоль мгновенной оси… … Справочник технического переводчика

угловая скорость — векторная величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости ω = Δφ/Δt, где Δφ приращение угла поворота за промежуток времени Δt. * * * УГЛОВАЯ … Энциклопедический словарь

угловая скорость — kampinis greitis statusas T sritis automatika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus. угловая скорость, f pranc. vitesse angulaire, f … Automatikos terminų žodynas

угловая скорость — kampinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis, lygus kūno pasisukimo kampo pirmajai išvestinei pagal laiką: ω = dφ/dt; čia dφ – pasisukimo kampo pokytis, dt – laiko tarpas. Kai kūnas sukasi tolygiai … Penkiakalbis aiškinamasis metrologijos terminų žodynas

угловая скорость — kampinis greitis statusas T sritis fizika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus. угловая скорость, f pranc. vitesse angulaire, f … Fizikos terminų žodynas

Угловая скорость — величина, характеризующая быстроту вращения твёрдого тела. При равномерном вращении тела вокруг неподвижной оси численно его У. с. ω =Δφ/ Δt, где Δφ приращение угла поворота φ за промежуток времени Δt. В общем случае У. с. численно равна… … Большая советская энциклопедия

Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.

При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.

Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.

Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:

Угловая скорость выражается в радианах в секунду (рад/с).

При равномерном вращении, когда известна угловая скорость в начальный момент времени t _{= 0}, можно определить угол поворота тела за время t и тем самым положение точек тела:

За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:

Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:

А связь между линейной и угловой скоростями определяется соотношением:

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.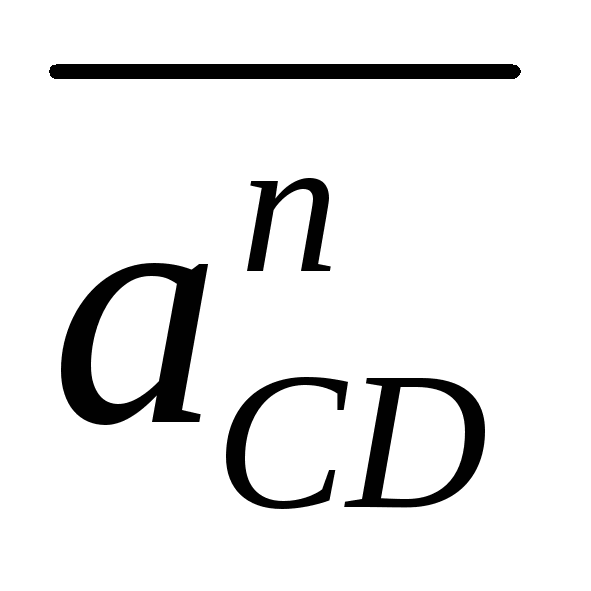

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Угловая частота — EtoneWiki

В физике угловая частота.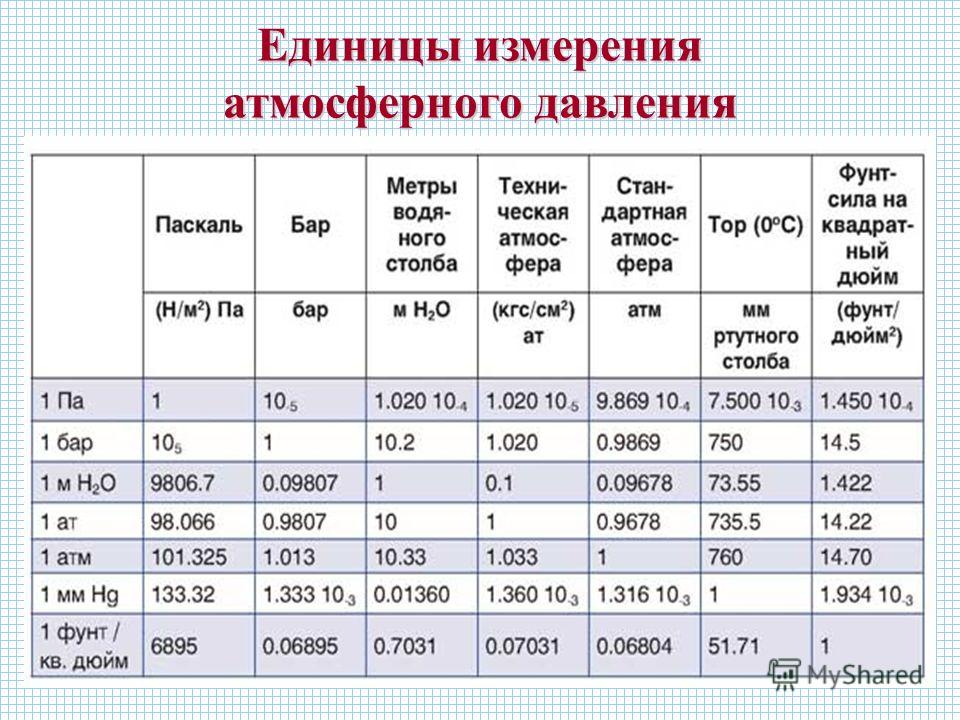 ω. (также называется угловой скоростью , радиальной частотой и радианной частотой) — это мера скорости вращения. Высокая угловая частота означает, что что-то вращается очень быстро. Угловая частота — это величина вектора угловой скорости , которая также известна как вектор угловой частоты [math] \ vec {\ omega} [/ math].

Он полезен во многих областях математики и естествознания, поскольку позволяет понять многие свойства физических объектов в нашем мире.{-1} [/ math]), так как с ним легче работать. Таким образом, угловая частота определяется выражением

 [математика] \ omega = \ frac {2 \ pi} {T} = 2 \ pi f [/ математика]
 

где [math] T [/ math] — это время (период) одного вращения (вращения), а [math] f [/ math] — это частота.

Если колесо поворачивается на угол [math] \ theta [/ math] за время [math] t [/ math], то угловая частота в любой момент определяется выражением,

 [математика] \ omega = \ frac {d \ theta} {dt} [/ math]
 

Если скорость вращения постоянна, это становится,

 [математика] \ omega = \ frac {\ theta} {t} [/ математика]
 

и так похоже на скорость.

Для объектов, движущихся по кругу, угловая частота также может быть задана как (в радианах),

 [математика] \ omega = \ frac {v} {r} [/ математика]
 

где [math] v [/ math] — это скорость, а [math] r [/ math] — это расстояние от середины круга.

Примеры

Угловая частота важна для определения того, может ли объект оставаться над землей против силы тяжести или же волчок может стоять. Это также важно для создания частоты подачи электроэнергии в сеть и уменьшения нагрева из-за трения в двигателях.3} [/ math]

, что ведет к одному из законов Иоганна Кеплера.

Сетевое питание

Генераторы на электростанциях вращаются с определенной частотой. Скорость, с которой они вращаются, дает нам частоту, с которой работают наши источники электроэнергии. Их можно замедлить с помощью больших тормозов или больших тяжелых колес, которые не позволяют генераторам вращаться слишком быстро.

Квартир

Примеры измерения угловой частоты:

Имя	Символ	Определение
Радиан в секунду	[математика] \ omega [/ математика]
Оборотов в минуту	[математика] об / мин [/ математика]	[математика] \ frac {60 \ omega} {2 \ pi} [/ математика]
Частота в секунду	[математика] f [/ математика]	[математика] \ frac {\ omega} {2 \ pi} [/ математика]
градусов в секунду	[математика] d [/ математика]	[математика] \ frac {180 \ omega} {\ pi} [/ математика]

Связанные страницы

Шаблон: Physics-stub

Механика

Ньютона — Почему $ \ sqrt {\ frac km} $ представляет угловую скорость, а не частоту?

«Угловая скорость» может использоваться взаимозаменяемо с «угловой частотой», но вы хотите четко различать их и «циклическую частоту», которую обычно называют просто «частотой».

Угловые величины измеряются в радианах в секунду, а циклическая частота равна «циклам в секунду» или герцам (Гц).

---

«Угол» здесь не очевиден с первого взгляда. Сначала есть два эквивалентных способа понять это:

• Просто примите математику в качестве ориентира $ \ omega $ появляется в аргументе синусов и косинусов, когда вы записываете временную эволюцию положения, скорости и т. Д., Поэтому $ \ omega t $ представляет угол и должен имеют угловые единицы.

• «Контрольный круг» Чтобы объяснить SHO в классе, где у учащихся нет исчисления, мы рассматриваем объект в равномерном круговом движении, а затем проецируем это движение в одномерном. ¹ В этом виде есть реальная угловая скорость вокруг реальной окружности, но мы просто используем ее, чтобы показать, что SHO эквивалентно поведению равномерного кругового движения вдоль единственной оси.

Вы можете возразить, что ни то, ни другое не очень удовлетворительно — одно чисто абстрактное, а другое относится к учебному / расчетному пособию, а не к объективной реальности — и, на мой взгляд, вы были бы правы.{-1} $. Но ты будешь ненавидеть себя утром.

---

¹ Я использую объект на вращающемся столе и прожектор, чтобы продемонстрировать эту конструкцию: тень объекта выполняет 1D SHO на стене. Я видел демонстрацию , в которой он был соединен с маятником, который можно было установить качающимся рядом со стеной, чтобы вы могли видеть, что качели и скольжение тени действительно соответствуют , но у меня никогда не было такого приспособления для мои собственные классы.

² Фазовое пространство — это абстрактное пространство (положение, импульс).Чтобы получить круговой путь для SHO, вы должны использовать подходящие масштабированные координаты, но они также являются теми, которые делают энергию системы пропорциональной квадрату вектора в этом пространстве и связаны с конструкцией, которую мы используем, чтобы получить операторы лестницы для ШО в квантовой механике и так далее. Все это очень элегантно, но вы не слишком внимательны, чтобы следить за деталями, когда люди впервые говорят вам, что $ \ sqrt {k / m} $ — это «угловая скорость».

Собственная угловая частота

— обзор

1.

Время нарастания

Время нарастания t _r — это время, необходимое для того, чтобы ответ x поднялся с 0 до установившегося значения y _SS . Это время, за которое колебательный отклик завершается четверть цикла, то есть ½π. Таким образом:

ω t _r = ½π

Таким образом, мы можем уменьшить время нарастания за счет увеличения собственной демпфированной частоты, это значение определяется незатухающей собственной угловой частотой и коэффициентом демпфирования, т.е.е.

ω = ωn (1 − ζ2)

и так:

Время нарастания иногда указывается как время, необходимое для увеличения отклика с 10% до 90% от установившегося значения.

2.

Пиковое время

Пиковое время t _p — это время, необходимое для увеличения отклика от 0 до первого пикового значения. Это время, за которое колебательный ответ завершает один полупериод, то есть π. Таким образом:

ω t _p = π

и, таким образом, используя:

ω = ωn (1 − ζ2)

, мы можем написать:

Когда ζ равно 1, время пика становится бесконечным; это указывает на то, что при критическом затухании установившееся значение никогда не достигается, а только приближается асимптотически.

3.

Перерегулирование

Перерегулирование — это максимальная величина, на которую отклик превышает установившееся значение и, таким образом, является амплитудой первого пика. Перерегулирование часто записывается как процент от установившегося значения.

Установившееся значение — это когда t стремится к бесконечности и, следовательно, y _SS = k . Так как y = 0, когда t = 0, тогда, поскольку e ⁰ = 1, тогда используя:

y = k [1 − e − ζωnt1 − ζ2 (Psin⁡ωt + Qcos⁡ωt)]

имеем:

0 = k [1−11 − ζ2 (0 + Q)]

и поэтому

Q = (1 − ζ2).

Перерегулирование происходит при ω t = π и, таким образом:

y = k [1 − e − ζωnt1 − ζ2 (Psin⁡ωt + Qcos⁡ωt)]

становится:

y = yss [1− e − ζωnπ / ω1 − ζ2 (0 − Q)]

Превышение — это разница между выходным сигналом в тот момент и установившимся значением. Следовательно:

перерегулирование = ySSe − ζωnπ / ω1 − ζ2Q = ySSe − ζωnπ / ω

Поскольку ω = ωn (1 − ζ2), мы можем записать:

перерегулирование = ySSexp⁡ (−ζωnπωn1 − ζ2) = ySSexp⁡ (−ζπ1 − ζ2)

Выражается в процентах от y _SS :

процентное превышение = exp⁡ (−ζπ1 − ζ2) × 100ɛ

Обратите внимание, что выброс не зависит от собственной частоты системы, но только по коэффициенту демпфирования. Когда коэффициент демпфирования приближается к 1, процент превышения приближается к нулю. В таблице 10.2 приведены значения процентного превышения для конкретных коэффициентов демпфирования.

Таблица 10.2. Процент превышения пика

.3

Коэффициент демпфирования	Превышение процентного отношения
0,2	52,7
0,3	37,2
0,4	25,4
0,5
0,6	9,5
0,7	4,6
0,8	1,5
0,9	0,2

4.

Коэффициент погружения

Индикация того, насколько быстро затухают колебания, обеспечивается коэффициентом оседания или декрементом . Это амплитуда второго выброса, деленная на амплитуду первого выброса.Первый выброс происходит, когда ω t = π, и поэтому:

первый выброс = ySSexp⁡ (−ζπ1 − ζ2)

Второй выброс происходит, когда ω t = 3π, и поэтому:

второй выброс = ySSexp⁡ (−3ζπ1 − ζ2)

Таким образом, коэффициент проседания определяется как:

Коэффициент проседания = второе превышение первого выброса = exp⁡ (−2ζπ1 − ζ2)

5.

Время установления

время установления t _с используется как мера времени, необходимого для затухания колебаний.Это время, необходимое для того, чтобы отклик оставался в пределах определенного процента от установившегося значения (см. Таблицу 10.2). Таким образом, за время установления 2% амплитуда колебаний должна упасть менее 2% от y _SS . Имеем:

y = k [1 − e − ζωnt1 − ζ2 (Psin⁡ωt + Qcos⁡ωt)]

с y _ss = k, ω = ωn (1 − ζ2) и, как было получено ранее в п.3, Q = (1 − ζ2). Амплитуда колебаний составляет ( y — y _SS ), когда y является максимальным значением. Максимальные значения возникают, когда ω t кратно π, и, таким образом, мы имеем cos ω t = 1 и sin ω t = 0. Для 2% времени установления время установления t _с это когда максимальная амплитуда составляет 2% от y ss, то есть 0,02 y _SS . Таким образом:

0,02yss = ysse − ζωnts

Логарифм дает 0,02 = -ζω _n t _s и, поскольку ln 0,02 = −3,9 или приблизительно 4, тогда:

время установления, если указанный процент составляет 2%.Если указанный процент равен 5%, уравнение принимает вид

6.

Количество колебаний до времени установления

Время, необходимое для завершения одного цикла, то есть периодическое время, составляет 1/ f , где f — частота, и поскольку ω = 2π f , то время для завершения одного цикла составляет 2π / f . При времени установления t _с количество возникающих колебаний составляет:

количество колебаний = время установления периодическое время

и, таким образом, для времени установления, определенного для 2% от установившегося значения:

число колебаний = 4 / ζωn2π / ω

Поскольку ω = ωn (1 − ζ2), то:

количество колебаний = 2ωn1 − ζ2πζωn = 2π1ζ2−1

Гц в радианы в секунду Преобразование (Гц в рад / с) )

Введите ниже частоту в герцах, чтобы преобразовать значение в радианы в секунду.

Как преобразовать герцы в радианы в секунду

Чтобы преобразовать измерение в герцах в радианы в секунду, умножьте частоту на коэффициент преобразования.

Поскольку один герц равен 6,283185 радиан в секунду, вы можете использовать эту простую формулу для преобразования:

радиан в секунду = герц × 6,283185

Частота в радианах в секунду равна герцам, умноженным на 6. 283185.

Например, вот как преобразовать 5 герц в радианы в секунду, используя формулу выше.

5 Гц = (5 × 6,283185) = 31,415927 рад / с

Следующая формула также может использоваться для преобразования угловой частоты в радианах в секунду в частоту в герцах:

ω = 2πƒ

Другими словами, угловая частота ω в радианах в секунду равна двукратному значению числа пи, умноженному на частоту ƒ в герцах.

Герцы и радианы в секунду — это единицы измерения частоты. Продолжайте читать, чтобы узнать больше о каждой единице измерения.

Герц формально определяется как частота, равная одному циклу в секунду. ^[1]

Герц — это производная единица СИ для частоты в метрической системе. Герц может быть сокращен как Гц ; например, 1 герц можно записать как 1 Гц.

Частоту в герцах можно выразить по формуле: Гц = CyclesTime _с

Радианы в секунду — это мера угловой частоты или скорости вращения, равная изменению ориентации или угла объекта в радианах в секунду.

Радианы в секунду можно обозначить как рад / с ; например, 1 радиан в секунду можно записать как 1 рад / с.

В формальных выражениях косая черта или солидус (/) используется для разделения единиц, используемых для обозначения деления в выражении. ^[2]

преобразование частоты в угловую частоту

7 марта 2007 г., 11:28:24, rijackson писал:
> Вот и снова. На эту тему было
> очень длинных веток>
>.
>
> Первая проблема заключается в том, что
> иногда очень полезно, чтобы
> рассматривал углы и телесные углы
> как измеренные, в других случаях
> это не так. Mathcad
> не соответствует тому, что он делает в
> в этом отношении. В MC11 углы
> безразмерны, а твердые
> имеют размеры. В
> MC12 и MC13 оба безразмерны. Поскольку рад равен
> безразмерным, он просто
> представлен как 1. «градус» равен
> конечно, также чисто числовой:
> число градусов в
> радианах. Итак, если вы поместите rad в
> заполнитель единиц, это
> будет рассматриваться как значение 1, а
> без измерения.
>
> Вторая проблема в том, что
> не существует внутренней
> связи между углом и
> частотой (Том не согласен, но
> я придерживаюсь своего
> одного оружия). Частота — это
> событий в секунду. Эти
> события могут быть чем угодно. Это
> может быть числом>
> оборотов в секунду, или
> числом> градусов в секунду,
>, или оно может иметь абсолютно не
> никакого отношения к углу, например,
> количество фотонов на
> во-вторых, частота тапа
> капает, или частота
> с которой эта тема кажется
> поднимается (высокая!).Если вы
> имеете дело с чем-то вроде
> механического движения, тогда вы делаете
> одно событие равным одному полному
> вращению, т.е. 2 * пи радиана — это
> очень удобно, и, следовательно,
> очень часто. Я думаю, что это очень
> скорее инженеры-механики
> взгляд на вещи
> хотя.
>
> Кстати, как вы думаете, почему
> градусов и радиан>
> обрабатываются по-разному? коэффициент масштабирования
> между двумя
> верен в ваших результатах.
> Кроме того, чего вы ожидаете,
> что вы пытаетесь выразить длиной
> в углах? Я
> знаю, что вы ожидаете от
> частот, но я не знаю,
> чего вы ожидаете от
> с длинами.
>
> Ричард

> Если вы,
> имеете дело с чем-то вроде
> механического движения, то делаете
> одно событие, равное одному полному
> вращению, т.е. 2 * пи радиана — это
> очень удобно, и, следовательно,
> очень распространен. В 2 раза больше массы] даст вам силу.

Fred Kohlhepp
[email protected]

Wikizero — Угловая частота

Угловая частота ω (в радианах в секунду), больше частоты ν (циклов в секунду, также называемых Гц) на коэффициент 2 π . На этом рисунке для обозначения частоты используется символ ν , а не f . Сфера, вращающаяся вокруг оси. Точки дальше от оси перемещаются быстрее, удовлетворяя ω = v / r .

В физике угловая частота ω (также обозначается терминами угловая скорость , радиальная частота , круговая частота , орбитальная частота , радианная частота и пульсация ) — скалярная мера скорости вращения. Он относится к угловому смещению в единицу времени (например, при вращении) или к скорости изменения фазы синусоидальной формы волны (например, в колебаниях и волнах), или к скорости изменения аргумента синусоидального сигнала. функция.Угловая частота (или угловая скорость) — это величина угловой скорости векторной величины. ^[1]

Один оборот равен 2π радиан, следовательно, ^{[1] [2]}

ω = 2πT = 2πf, {\ displaystyle \ omega = {{2 \ pi} \ over T } = {2 \ pi f},}

где:

ω — угловая частота или угловая скорость (измеряется в радианах в секунду),

T — период (измеряется в секундах),

f — обычная частота (измеряется в герцах) (иногда обозначается как ν ).

В единицах СИ угловая частота обычно выражается в радианах в секунду, даже если она не выражает величину вращения. С точки зрения размерного анализа, единица Герц (Гц) также верна, но на практике она используется только для обычной частоты f и почти никогда для ω . Это соглашение используется, чтобы помочь избежать путаницы ^[3] , которая возникает при работе с частотой или постоянной Планка, потому что единицы измерения угла (цикл или радиан) опущены в СИ. ^{[4] [5] [6] [7] [8]}

При цифровой обработке сигналов угловая частота может быть нормализована частотой дискретизации, давая нормированную частоту.

Примеры [править]

Круговое движение [править]

Во вращающемся или движущемся по орбите объекте существует связь между расстоянием от оси, r {\ displaystyle r}, тангенциальной скоростью, v {\ displaystyle v}, и угловая частота вращения. В течение одного периода, T {\ displaystyle T}, тело, совершая круговое движение, проходит расстояние vT {\ displaystyle vT}.Это расстояние также равно длине окружности пути, проложенного телом, 2πr {\ displaystyle 2 \ pi r}. Уравнивая эти две величины и вспоминая связь между периодом и угловой частотой, получаем: ω = v / r. {\ Displaystyle \ omega = v / r.}

Колебания пружины [править]

Объект, прикрепленный к пружина может колебаться. Если предположить, что пружина идеальная и безмассовая без демпфирования, тогда движение будет простым и гармоничным с угловой частотой, заданной как ^[9]

ω = км, {\ displaystyle \ omega = {\ sqrt {\ frac {k} {m}}},}

, где

k — жесткость пружины,

м — масса объекта.{2} x.}

LC-контуры [править]

Резонансная угловая частота в последовательном LC-контуре равна квадратному корню из обратной величины произведения емкости ( C , измеренной в фарадах) и индуктивности схема ( L , с единицей СИ Генри): ^[10]

ω = 1LC. {\ displaystyle \ omega = {\ sqrt {\ frac {1} {LC}}}.}

Добавление последовательного сопротивления (например, из-за сопротивления провода в катушке) не изменяет резонансную частоту последовательного LC-контура. Нахви, Махмуд; Эдминистер, Джозеф (2003). Очерк теории и проблем электрических цепей Шаума . Компании Макгроу-Хилл (McGraw-Hill Professional). С. 214, 216.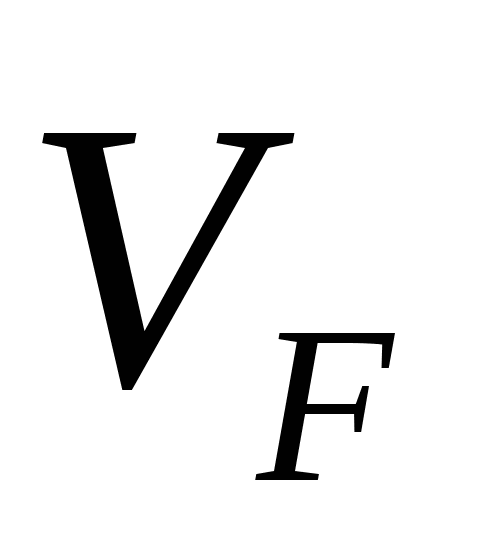 ISBN 0-07-139307-2 . (LC1)

Ссылки по теме:

Внешние ссылки [править]

Определение угловой частоты в физике.

Примеры угловой частоты в следующих разделах:

• Период и частота

  • Обратите внимание, что период и частота являются обратными друг другу.
  • Часто периодическое движение лучше всего выражается в терминах угловых частоты , представленных греческой буквой ω (омега).
  • Угловой частота относится к угловому смещению в единицу времени (например, при вращении) или скорости изменения фазы синусоидальной формы волны (например, в колебаниях и волнах), или скорости изменения аргумента синусоидальной функции.
  • Угловая частота часто выражается в радианах в секунду (напомним, что в круге 2π радиана).
  • Синусоидальные волны различных частот ; нижние волны имеют более высокие частоты , чем те, что выше.

• Фазоры

  • Фазоры используются для анализа электрических систем в синусоидальном установившемся состоянии и с однородной угловой частотой .
  • В физике фазовый вектор или фазор — это представление синусоидальной функции, амплитуда (A), частота (ω) и фаза (θ) не зависят от времени, как показано на схеме.
  • , показанный на рисунке ниже, представляет собой косинусоидальный сигнал с амплитудой A, частотой , и фазой θ.
  • Амплитуда A характеризует размах амплитуды 2A от пика до пика, угловая частота частота ω характеризует период T = 2π / ω между переходами от отрицательного к положительному нулю (или положительным пикам или отрицательным пикам) и фаза θ характеризует время τ = −θ / ω, когда сигнал достигает своего первого пика.
  • В синусоидальном установившемся состоянии каждое напряжение и ток (или сила и скорость) в системе синусоидальны с угловой частотой ω.

• Управляемые колебания и резонанс

  • \ omega $ — частота возбуждения для синусоидального приводного механизма.
  • F_0 $, управляющая частота $ \!
  • \ omega $, незатухающий угловой частота $ \!
  • Для определенной частоты возбуждения называется резонансной, или резонансной частотой $ \!
  • Установившееся изменение амплитуды с частотой и затухание управляемого простого гармонического генератора.

• Угловое ускорение, Alpha

  • Угловое ускорение — это скорость изменения угловой скорости , математически выраженная как $ \ alpha = \ Delta \ omega / \ Delta t $.
  • Угловое ускорение — это скорость изменения угловой скорости .
  • Угловое ускорение определяется как скорость изменения угловой скорости .
  • В форме уравнения угловое ускорение выражается следующим образом:
  • Единицами измерения углового ускорения являются (рад / с) / с или рад / с2.

• Волновая природа материи вызывает квантование

  • Если струна была свободна и ни к чему не прикреплена, мы знаем, что она могла бы колебаться на любой управляемой частоте .
  • Как только струна становится «связанной системой» с определенными граничными ограничениями, она допускает волны только с дискретным набором частот .
  • Угловой момент равен $ L = m_e v r $, поэтому мы получаем квантование углового момента :

• Постоянное угловое ускорение

  • Постоянное угловое ускорение описывает отношения между угловой скоростью , углом поворота и временем.
  • Просто используя нашу интуицию, мы можем начать видеть взаимосвязь таких величин вращения, как θ (угол поворота), ω (угловая скорость , скорость) и α (угловая скорость , ускорение).
  • Аналогичным образом кинематика вращательного движения описывает отношения между углом поворота, угловой скоростью , скоростью, угловым ускорением , и временем.
  • Как и в линейной кинематике, где мы предположили, что a является постоянным, здесь мы предполагаем, что угловое ускорение α является постоянным, и можем использовать соотношение: $ a = r \ alpha $, где r — радиус кривой.Точно так же у нас есть следующие отношения между линейными и угловыми значениями : $ v = r \ omega \\ x = r \ theta $
  • Свяжите угол поворота, угловую скорость , и угловое ускорение , с их эквивалентами в линейной кинематике

• Вращательные столкновения

  • В замкнутой системе угловой момент сохраняется так же, как и линейный импульс.
  • Для объектов с вращательной составляющей существует угловой момент .
  • Угловой момент математически определяется как L = Iω или L = rxp.
  • Объект, который имеет большую угловую скорость ω (), такой как центрифуга, также имеет довольно большой угловой момент .
  • После столкновения стрела прилипает к цилиндру качения, и система имеет чистый угловой момент , равный исходному угловому моменту стрелки до столкновения.

• Сохранение углового момента

  • Закон сохранения углового момента гласит, что, когда на объект не действует внешний крутящий момент, никакого изменения углового момента не произойдет.
  • Сохраняющаяся величина, которую мы исследуем, называется угловым моментом .
  • Обозначение для углового момента — буква L.
  • Если изменение углового момента ΔL равно нулю, то угловой момент постоянен; следовательно,
  • (I: инерция вращения, $ \ omega $: угловая скорость )

• Эффект Зеемана и ядерный спин

  • Эффект Зеемана — это расщепление атомных уровней на основе значения полного углового момента в направлении магнитного поля $ m_J $.