Формула окружной скорости: Движение по окружности
Окружная скорость — это… Что такое Окружная скорость?
- Окружная скорость
3.112 Окружная скорость — линейная окружная скорость шлифовального круга при работе.
Смотри также родственные термины:
3.5 окружная скорость v, м/с, и частота вращения n, мин-1 (rotational and peripheral speed):
Окружную скорость шлифовального круга вычисляют по формуле
где D — наружный диаметр шлифовального круга, мм;
частоту вращения шлифовального круга вычисляют по формуле
Определения термина из разных документов: окружная скорость v, м/с, и частота вращения n, мин-1
32. Окружная скорость концов лопастей несущего винта
ωнR
Средняя окружная скорость концевой точки лопасти несущего винта при вращении при βл = ξл = 0.

Примечание. Среднюю окружную скорость рулевого винта обозначают ωpRр.в
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
- окружающий шум
- окружная скорость v, м/с, и частота вращения n, мин-1
Смотреть что такое «Окружная скорость» в других словарях:
окружная скорость — Параллельные тексты EN RU It is suitable for high peripheral speeds (70m/s, no restriction as compared to a steel impeller) and can withstand high centrifugal forces. [Ziehl Abegg] Оно [такое рабочее колесо] позволяет развивать высокую окружную… … Справочник технического переводчика
окружная скорость — apskritiminis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Apskritimine orbita judančio taško greitis. atitikmenys: angl.
circular velocity; circumferential speed; peripheral speed vok. Kreisbahngeschwindigkeit, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
окружная скорость — apskritiminis greitis statusas T sritis fizika atitikmenys: angl. circular velocity; circumferential speed; peripheral speed vok. Kreisbahngeschwindigkeit, f; Umfangsgeschwindigkeit, f rus. круговая скорость, f; окружная скорость, f pranc.… … Fizikos terminų žodynas
окружная скорость — apskritiminis greitis statusas T sritis automatika atitikmenys: angl. circular velocity; circumferential speed; peripheral speed vok. Umfangsgeschwindigkeit, f rus. окружная скорость, f pranc. vitesse circulaire, f; vitesse périphérique, f … Automatikos terminų žodynas
окружная скорость зубчатого колеса — (ν) окружная скорость Скорость выбранной точки зубчатого колеса во вращательном движении вокруг его оси. Примечания 1. При отсутствии дополнительных указаний имеется в виду движение относительно неподвижного звена.

окружная скорость (на периферии долота) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN peripheral velocity … Справочник технического переводчика
окружная скорость бурового долота — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN circumferential drilling bit speedperipheral drilling bit speed … Справочник технического переводчика
окружная скорость конца лопасти
— (напр. вентилятора, ветроэнергетической установки) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN tip speed … Справочник технического переводчикаокружная скорость конца лопатки (турбины) — — [А.С.Гольдберг. Англо русский энергетический словарь.
 2006 г.] Тематики энергетика в целом EN tip speed … Справочник технического переводчика
2006 г.] Тематики энергетика в целом EN tip speed … Справочник технического переводчикаокружная скорость коронки — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN linear travel … Справочник технического переводчика
Круговое движение — это… Что такое Круговое движение?
- О разновидности перекрёстков: см. Круговой перекрёсток.
В физике кругово́е движе́ние — это вращение по кругу, т. е. это круговой путь по круговой орбите. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.
Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.
Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.
Формулы для равномерного кругового движения
Рис. 1: Взаимосвязи векторов равномерного кругового движения; вектор Ω, представляющий вращение, перпендикулярен к плоскости орбиты.Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть T, то угловая скорость вращения ω будет равна:
Если период вращения есть T, то угловая скорость вращения ω будет равна:
Скорость движения объекта равна
Угол поворота θ за время t равен:
Ускорение, вызванное изменением направления скорости, можно найти, если заметить, что скорость совершает полное изменение направления за то же самое время T, за которое объект делает один оборот. Тогда вектор скорости проходит путь длиной 2π
и направлено радиально к центру.
Взаимосвязи векторов показаны на рис. 1. Ось вращения изображена вектором Ω, перпендикулярно плоскости орбиты и имеет величину ω = dθ / dt. Направление вектора Ω выбрано в соответствии с правилом правой руки. По этому соглашению скорость это векторное произведение вида:
и есть вектор, перпендикулярный как Ω так и r ( t ), направленный по касательной к орбите и имеющий величину ω R. Аналогично, ускорение определяется как:
Аналогично, ускорение определяется как:
Оно представляет собой вектор, перпендикулярный как Ω так и v ( t ), имеющий величину ω |v| = ω2R и направление строго противоположно к r ( t ).
Постоянная скорость
В простейшем случае скорость, масса и радиус являются постоянными.
Рассмотрим тело массой один килограмм, движущееся по кругу радиуса один метр с угловой скоростью один радиан в секунду.
Теперь рассмотрим тело массы m, движущееся по кругу радиуса r с угловой скоростью ω.
- Скорость: v = r·ω.
- Радиальное ускорение: a = r·ω 2 = r −1·v 2.
- Центростремительная сила: F = m·a = r·m·ω 2 = r−1·m·v 2.
- Импульс тела: p = m·v = r·m·ω.
- Момент инерции: I = r 2·m.

- Момент импульса: L = r·m·v = r 2·m·ω = I·ω.
- Кинетическая энергия: E = 2−1·m·v 2 = 2−1
- Длина окружности орбиты: 2·π·r.
- Период движения: T = 2·π·ω −1.
- Частота: f = T −1 . (Вместо буквы f частота часто обозначается греческой буквой ν, которая, однако, часто неотличима от буквы v, используемой здесь для обозначения скорости).
- Квантовое число: J = 2·π·L h−1
Переменная скорость
В круговом движении полную силу, приложенную к объекту, можно разложить на две составляющие: центростремительную, удерживающую тело на круговой орбите (т. е. меняющую направление вектора скорости), и тангенциальную, направленную по касательной к окружности и вызывающую изменение длины вектора скорости (т.
Для примера, когда камень привязан к концу верёвки, он подвергается воздействию силы, мы можем разложить силу на радиальную и боковую составляющие. Радиальная направлена к центру (вовнутрь) окружности и вызвана тем, что веревка сопротивляется удлинению. А боковая составляющая определяет — будет вращение камня ускоряться или замедляться.
Описание кругового движения в полярных координатах
Траектория кругового движения тела может быть описана в полярной системе координат значениями фиксированного расстояние R от центра орбиты, являющейся точкой отсчёта, и угла ориентации θ (t) от некоторого фиксированного направления (рис. 2). Вектор перемещения является радиальным вектором от полюса до текущего положения:
где — единичный вектор, параллельный радиусу в момент t и направленный от полюса. Удобно также ввести единичный векторортогональный к , который назовём .
Скорость является производной перемещения по времени:
Поскольку радиус окружности является константой, радиальная составляющая скорости равна нулю. Единичный вектор имеет инвариантное по времени значение, так что при изменении времени его конец всегда лежит на окружности единичного радиуса, а угол θ такой же, как у . Если произошло малое приращение угла dθ за время dt, тогда описывает дугу единичной окружности со значением dθ (см. единичную окружность слева на рис. 2). Следовательно:
где направление изменения должно быть перпендикулярно к (или, другими словами, вдоль ), поскольку любое изменение d в направлении будет изменять величину . Знак положительный, потому что увеличение dθ влияет на объект и передвигается в направлении . Следовательно, скорость становится:
Ускорение тела также можно разложить на радиальную и тангенциальную составляющие. Ускорение есть производная скорости по времени:
Ускорение есть производная скорости по времени:
Производная по времени от находится таким же путём, как и для . Опять же, есть единичный вектор, и его конец расположен на единичной окружности, а угол равен π/2 + θ. Следовательно, приращение угла dθ вектора перемещает по дуге на величину dθ, и поскольку перпендикулярен к , мы имеем:
где отрицательный знак необходим, чтобы сохранить перпендикулярным к . (Иначе угол между и будет уменьшаться с увеличением dθ, см. единичную окружность слева на рис. 2). Следовательно, ускорение равно:
Центростремительное ускорение — это радиальная составляющая, направленная по радиусу вовнутрь:
тогда как тангенциальная составляющая изменяет значение скорости:
Описание кругового движения в комплексных числах
Круговое движение можно описать с использованием комплексных чисел.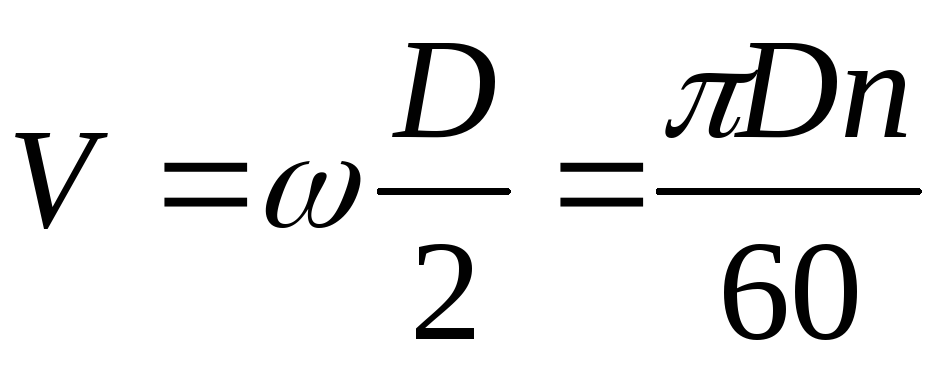 Пусть — ось вещественных чисел, а — ось мнимых чисел. Тогда положение тела может быть задано в виде комплексного «вектора» :
Пусть — ось вещественных чисел, а — ось мнимых чисел. Тогда положение тела может быть задано в виде комплексного «вектора» :
где есть мнимая единица, и
есть угол комплексного вектора по отношению к вещественной оси как функция времени t. Поскольку радиус есть константа:
где точка означает дифференциал по времени. В этих обозначениях скорость имеет вид :
а ускорение:
Первое слагаемое направлено против вектора перемещения, а второе — перпендикулярно ему, как и в предыдущих результатах.
Ссылки
См. также
что это⚠️, в чем измеряется, формула для расчета
Что такое угловая скорость
Угловая скорость (обозначается как \(\omega\)) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.
Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.
Единица измерения
В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)
Формула угловой скорости
Вектор угловой скорости определяется отношением угла поворота \((\varphi)\) к интервалу времени \((\mathcal t)\), за которое произошел поворот:
\(\omega=\frac{\triangle\varphi}{\triangle\mathcal t}\)
Зависимость угловой скорости от времени
Зависимость \(\varphi \) от \(\mathcal t\) наглядно показана на графике:
Угол, на который повернулось тело, характеризуется площадью под кривой.
Угловая скорость вращения, формула
Через частоту
\(\omega=2\pi\mathcal n\)
\(\mathcal n\) — частота вращения \((1/с)\)
\(\pi\) — число Пи (\(\approx 3,14\))
\(\mathcal n=\frac1T\)
\(T \)— период вращения (время, за которое тело совершает один оборот)
Через радиус
\(\omega=\frac vR\)
\(v\) — линейная скорость(м/с)
\(R\) — радиус окружности (м)
Как определить направление угловой скорости
Направление скорости в физике можно определять двумя способами:
- Правило буравчика.
 Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость. - Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.
Связь линейной и угловой скорости
Линейная скорость \((v)\) тела, расположенного на расстоянии \(R\) от оси вращения, прямо пропорциональна угловой скорости.
\(v=R\omega\)
\(R\) — радиус окружности (м)
Чему равна мгновенная угловая скорость
Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при \(\triangle\mathcal t\rightarrow0\) :
\(\omega=\lim_{\triangle\rightarrow0}\frac{\triangle\varphi}{\triangle\mathcal t}\)
Измеряется в рад/с
формула через радиус и ускорение, угловую скорость
Угловое ускорение – что это?
Угловое ускорение \(\varepsilon\) – физическая величина, характеризующая изменение угловой скорости при движении тела.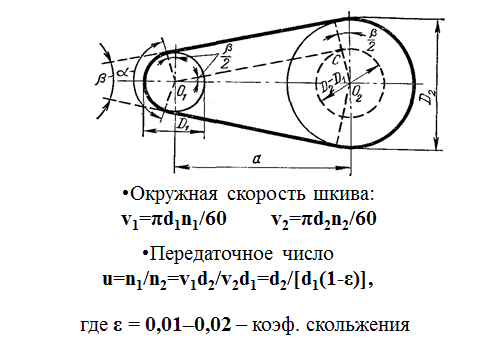 {-2}\)
{-2}\)
Угловая скорость
Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.
Угловая скорость \(\omega\) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.
При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).
Вектор угловой скорости направлен вдоль оси вращения.
Основные формулы для вычисления угловой скорости
Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):
- \(\omega=\frac nt\), где \(n\) – количество оборотов за единицу времени \(t\).
- \(\omega=\frac\varphi t\), где \(\varphi\) – угол поворота, \(t\) – время, за которое он совершен.
 2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)
2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)Угловое ускорение маховика
\(\varepsilon=\frac\omega t=\frac{2\pi n}t\), где \(n\) – количество оборотов за единицу времени \(t\).
Среднее угловое ускорение
Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.
\(\left\langle\varepsilon\right\rangle=\frac{\triangle\omega}{\triangle t}\)
Тангенциальное ускорение
Тангенциальным (касательным) ускорением \(a_\tau\) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.
\(a_\tau=\varepsilon r\), где \(\varepsilon\) – угловое ускорение, \(r\) – радиус кривизны траектории в заданной точке.
Мгновенное угловое ускорение
Мгновенное угловое ускорение \(\alpha\) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.
 2}\)
2}\)Движение по окружности, теория и онлайн калькуляторы
Значимым частным случаем перемещения материальной точки по заданной траектории служит движение по окружности. Местоположение точки на окружности можно задавать не при помощи расстояния от некоторой начальной точки (допустим A), а с помощью угла $\varphi $, который образуют радиусы, которые провели из центра окружности (O) к рассматриваемой частице (точка M) и из О в точку начала отсчета (A) (рис.1).
Скорость при движении по окружности
При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($\omega $), которая характеризует быстроту изменения угла $\varphi $:
\[\omega =\frac{d\varphi }{dt}\left(1\right).\]Определим, какова связь между линейной и угловой скоростями. Длину дуги АМ ($s$) (рис.1) можно найти как:
\[s=R\varphi \left(2\right),\]тогда изменение длины дуги за время$\ \Delta t$ равно$\ \Delta s$:
\[\Delta s=R\Delta \varphi \ \left(3\right). \]
\]Найдем отношение $\frac{\Delta s}{\Delta t}$, разделив обе части выражения (3) на $\Delta t$:
\[\frac{\Delta s}{\Delta t}=R\frac{\Delta \varphi }{\Delta t}\ \left(4\right).\]Перейдем к пределу в правой и левой частях равенства (4) при $\Delta t\to 0$, получим:
\[{\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}\ }=R{\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \varphi }{\Delta t}\ }\to v=R\omega \left(5\right).\]Ускорение материальной точки при движении по окружности
При движении по окружности (как при любом неравномерном криволинейном движении) ускорение можно разложить на две составляющие: тангенциальное ускорение (${\overline{a}}_{\tau }$), которое направлено по касательной к траектории движения точки и характеризующее быстроту изменения модуля скорости $v$ и центростремительной ускорение (${\overline{a}}_n$), направленное к центру кривизны траектории, определяющее быстроту изменения направления скорости.
Величина нормальной (центростремительной) компоненты ускорения вычисляется при помощи формулы:
\[a_n=\frac{v^2}{R}={\omega }^2R\ \left(6\right). \]
\]При равномерном перемещении по окружности величина центростремительного ускорения постоянна ($a_n=const).\ $Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Тангенциальное ускорение при движении по окружности вычисляют, как и при любом криволинейном движении:
\[{\overline{a}}_{\tau }=\frac{d\overline{v}}{dt}\left(7\right).\]Период и частота — характеристики равномерного движения по окружности
Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения ($T$), который определяют как время совершения материальной точкой полного оборота. Используют и частоту ($\nu$) обращения, которую опр
Движение по окружности и его основные характеристики
Наряду с движением вдоль прямой в школьной физике рассматривают движение по окружности. Для него, по аналогии с прямолинейным движением, вводятся понятия пройденного пути, скорости движения и ускорения.

В физике выделяют несколько видов движения тел. Движение по окружности – это один из случаев движения вдоль кривой линии — криволинейного движения.
Сравним понятия пройденного пути, скорости и ускорения для прямолинейного движения и движения по окружности.
Угловой путь
Для начала, вспомним, что линейное перемещение – это разница между конечным и начальным положением точки на оси (рис. 1).
\[ S = x – x_{0} \]
Рис. 1. Линейное перемещение равно разности между конечным и начальным положениями точки на оси
Рассмотрим теперь колесо (рис. 2). На горизонтальной линии, проходящей через диаметр колеса, справа отметим красную точку, от которой мы начнем отсчитывать углы. Условимся считать, что возле этой точки находится нулевой угол.
Рис. 2. Точка из положения 1 сместилась в положение 2, пройдя угловой путь
На ободе колеса выберем точку, например — ниппель. Сначала ниппель находился в точке 1. Точка 1 сдвинута на угол \(\gamma_{1}\) относительно начала отсчета.

Будем вращать колесо в направлении, обозначенном синей стрелкой. Повернем колесо на некоторый угол, так, чтобы к концу движения ниппель переместился в точку, обозначенную цифрой 2 на рисунке. Эта точка смещена на угол \(\gamma_{2}\) по отношению к началу отсчета.
По аналогии с поступательным движением, угловой путь, который прошел ниппель — это разница (разность) угловых положений точек 1 и 2.
\[\large \boxed{ \varphi = \gamma_{2} — \gamma_{1} }\]
\(\varphi \left( \text{рад}\right)\) – угловой путь измеряется в радианах.
Угловой путь – это угол, на который повернулся ниппель, по отношению к его начальному положению.
Угловая скорость — куда она направлена
Если тело двигалось равномерно (с неизменной скоростью), то линейную скорость можно определить по формуле
\[v = \frac{S}{t} \]
\(v \left( \frac{\text{м}}{c} \right)\) — линейная скорость – это путь, деленный на время, поэтому она имеет размерность метров деленных на секунду.

Аналогично линейному случаю, если угловой путь поделить на время движения, получим угловую скорость.
\[ \large \boxed{ \omega = \frac{\varphi}{t} } \]
\(\omega \left( \frac{\text{рад}}{c} \right)\) – угловая скорость – это угловой путь, деленный на время, поэтому она имеет размерность радиан деленных на секунду.
Угловая скорость \( \omega \), так же, как и линейная скорость, является вектором. Но в отличии от линейной скорости его направление можно определить по правилу буравчика (правого винта).
Примечание: Направление вектора угловой скорости \( \vec{\omega} \) можно определить по правилу буравчика (правого винта)!
На рисунке 3 окружность располагается в горизонтальной плоскости, а вектор \( \vec{\omega }\) направлен вдоль вертикальной оси вращения. Направление вращения указано синей стрелкой.
Рис. 3. Линейная и угловая скорости точки, вращающейся по окружности. Угловая скорость направлена по правилу правого винта вдоль оси вращения
При движении по окружности вектор линейной скорости \(\vec{v}\) изменяет свое направление.
 Но в каждой точке окружности вектор \(\vec{v}\) направлен по касательной к окружности, т. е. перпендикулярно радиусу.
Но в каждой точке окружности вектор \(\vec{v}\) направлен по касательной к окружности, т. е. перпендикулярно радиусу.Примечание: Касательная и радиус перпендикулярны, это известно из геометрии.
Если точка начнет вращаться в противоположную сторону, то векторы линейной и угловой скорости развернутся противоположно направлениям, указанным на рисунке 3.
Связь между линейной и угловой скоростью
Угловая и линейная скорость связаны математически. Линейная скорость – это векторное произведение вектора угловой скорости и вектора радиуса окружности.
Примечание: Радиус окружности – это вектор, он направлен от центра окружности к ее внешней границе.
Векторный вид:
\[\large \boxed{ \left[\vec{\omega}, \vec{R} \right] = \vec{v} }\]
Скалярный вид записи связи скоростей:
\[ \large \boxed{ \omega \cdot R = v }\]
\(\omega \left( \frac{\text{рад}}{c} \right)\) – угловая скорость;
\(v \left( \frac{\text{м}}{c} \right)\) — линейная скорость;
\(R \left( \text{м}\right)\) – радиус окружности.
 {-1} \]
{-1} \]Частота и период связаны обратной пропорциональностью:
\[ \large \boxed{ T = \frac{1}{\nu} } \]
Количество оборотов
Двигаясь по окружности достаточное время, тело может пройти не один оборот. Зная угловой путь \(\varphi \) мы можем вычислить количество N оборотов.
\[\large \boxed{ \varphi = 2 \pi \cdot N }\]
\( N \) – количество оборотов, скаляр. Обороты считают поштучно.
Связь между угловой скоростью и частотой
Разделим обе части уравнения на время t, в течение которого тело вращалось
\[ \frac{\varphi }{t} = 2 \pi \cdot \frac{N}{t} \]
Левая часть уравнения – это угловая скорость.
\[ \large \boxed{ \frac{\varphi }{t} = \omega }\]
А дробь в правой части – это частота
\[ \large \boxed{ \frac{N}{t} = \nu }\]
Таким образом, мы получили связь между угловой скоростью и частотой
\[ \large \boxed{ \left|\vec{\omega} \right|= 2 \pi \cdot \nu } \]
Примечание: Решая задачи на равноускоренное движение по окружности, удобно переходить от частоты к угловой скорости.
Калькулятор скоростей и подачи Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой.
Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой.| Формула
Как пользоваться калькулятором скоростей и подач?
Калькулятор скорости и подачи имеет два режима работы: режим предварительной настройки и ручной режим.
В предустановленном режиме вы можете выбрать операцию, материал инструмента, размер и количество зубьев, а также материал заготовки. Калькулятор содержит диапазон рекомендуемых скоростей резания для различных материалов , что позволяет рассчитать скорости вращения. Он также имеет соответствующие данные загрузки чипа для расчета скоростей подачи.
В ручном режиме вы можете установить скорость резки (обычно футов в минуту, — SFM), и он будет выводить скорость вращения в оборотах в минуту (об / мин), тем самым конвертируя SFM в об / мин. Вы также можете установить пользовательских нагрузок стружки для расчета скорости подачи.
 Давайте теперь подробно рассмотрим каждый режим.
Давайте теперь подробно рассмотрим каждый режим.Предустановленный режим
Если калькулятор находится в предустановленном режиме по умолчанию , выполните следующие действия, чтобы получить результат скорости и подачи:
- Выберите тип станка , операция , которую вы хотите выполнить.
- Выберите инструмент , материал инструмента : быстрорежущая сталь (обычно используется для сверл) или инструмент на твердосплавной основе.
- Выберите материал заготовки .
- Введите диаметр вращающегося элемента. Для всех операций, кроме токарной, это будет инструмент диаметром . Поскольку при токарной операции заготовка вращается, в этом случае следует использовать заготовку диаметром .
Затем вы увидите результаты для диапазона скоростей, который вы должны использовать.Для наилучшего результата начинайте с минимальной скорости и постепенно увеличивайте ее до среднего значения.
 Если вам нужна быстрая, но черновая обработка , продолжайте движение до максимальной скорости.
Если вам нужна быстрая, но черновая обработка , продолжайте движение до максимальной скорости.Затем введите , количество зубьев , которое должен использовать инструмент, чтобы получить диапазон используемых скоростей подачи. Показанные скорости подачи относятся к средней скорости вращения. Чтобы рассчитать скорость подачи при различных скоростях , введите число оборотов в минуту в поле настраиваемой скорости вращения . Как и в случае со скоростью вращения, чем ниже скорость подачи, тем плавнее, чем , тем окончание операции будет.
Ручной режим
При установке режима калькулятора на ручной режим , вам необходимо ввести минимальную и максимальную поверхностную скорость и загрузок стружки . Эти данные могут содержаться в спецификации используемого вами инструмента. Вот что вам следует сделать:
- Введите диаметр инструмента / заготовки , как в предустановленном режиме.

- Введите минимальную и максимальную скорость поверхности (или резания) , обычно выражаемую в единицах поверхностных футов в минуту.После этого вы сразу получите минимальную и максимальную скорость вращения.
- Введите число зубьев вашего инструмента.
- Введите минимум и максимальную нагрузку на стружку для вашего инструмента, операции и материала заготовки.
- Затем вы увидите минимальную и максимальную скорость подачи при средней скорости вращения.
- Как и в предустановленном режиме, вы можете затем ввести пользовательскую скорость вращения , для которой вы хотите рассчитать минимальную и максимальную скорости подачи .
Стивен Вудинг
Формула орбитальной скорости
В гравитационно связанных системах орбитальная скорость тела или астрономического объекта — это скорость, с которой оно вращается вокруг барицентра или, если объект намного менее массивен, чем самое большое тело в мире.
 система, ее относительная скорость по отношению к большему телу. Скорость в последнем случае может быть относительно поверхности самого большого тела или относительно его центра масс.
система, ее относительная скорость по отношению к большему телу. Скорость в последнем случае может быть относительно поверхности самого большого тела или относительно его центра масс.Этот термин может использоваться для обозначения средней орбитальной скорости, средней скорости на всей орбите или его мгновенной скорости в данной точке его орбиты.Максимальная орбитальная скорость (мгновенная) приходится на перицентр, а минимальная скорость для объектов на замкнутых орбитах — в апогее. В идеальных системах из двух тел объекты на открытых орбитах продолжают вечно замедляться по мере увеличения расстояния до центра тяжести.
орбитальная скорость = квадратный корень (гравитационная постоянная * масса притягивающего тела / радиус орбиты)
Уравнение:
,
У нас:
орбитальная скорость.
G = гравитационная постоянная.
M = масса притягивающего тела.
r = радиус орбиты.
Орбитальная скорость Вопросы:
1) Какая скорость вращения Земли по орбите?
Ответ: Сначала мы ищем значения по умолчанию для Земли, такие как масса и ее приблизительный радиус.

М = 5,98 * 10 24 кг.
G = 6,67 * 10 -11 Нм 2 / кг 2 .
г = 6370км.
= = 7 913,05 м / с.
v orb = 7913,05 м / с.
2) Международная космическая станция описывает круговую орбиту вокруг Земли на высоте около 400 км над ней. Применяя закон всемирного тяготения и второй закон Ньютона к центростремительному ускорению, он вычисляет орбитальную скорость космической станции в км / ч.
Ответ: Радиус Земли составляет 6371 км, поэтому расстояние, на котором расположена космическая станция от центра Земли, будет 6771 км (прибавляя высоту 400 км).
М = 5,98 * 10 24 кг.
G = 6,67 * 10 -11 Нм 2 / кг 2 .
r = 6771км.
= = 7675,15 м / с.
7675,15 м / с.
Как найти среднюю скорость (формула и примеры)
Определение средней скорости
Средняя скорость объединяет две идеи в двух словах: средняя, что означает среднее значение, полученное из множества отдельных точек данных, и скорость, которая представляет собой изменение позиции.

Вы можете рассчитать среднюю скорость для любого типа движения, если можете рассчитать время движения и измерить расстояние.
Содержание
- Определение средней скорости
- Формула средней скорости
- Как рассчитать среднюю скорость
- Проблемы со средней скоростью
Формула средней скорости
Средняя скорость — это общее расстояние, пройденное до рассматриваемого объекта, деленное на общее время, затраченное на прохождение этого расстояния, то есть общий период времени. Формула средней скорости:
Средняя скорость (с) = общее пройденное расстояние
Средняя скорость отличается от мгновенной скорости.
Мгновенная скорость
Средняя скорость учитывает все событие, например, автомобиль, разгоняющийся после остановки, ускоряющийся, едущий некоторое время, затем замедляющийся на желтый свет и, наконец, останавливающийся.
Автомобиль движется с разной скоростью.
 В любой момент автомобиль не движется со скоростью 55 миль в час (миль в час). Это может быть 0 миль в час, затем 7 миль в час в другой момент, затем 53 миль в час, затем 61 миль в час и, наконец, 3 мили в час, прежде чем вернуться к 0 миль в час.
В любой момент автомобиль не движется со скоростью 55 миль в час (миль в час). Это может быть 0 миль в час, затем 7 миль в час в другой момент, затем 53 миль в час, затем 61 миль в час и, наконец, 3 мили в час, прежде чем вернуться к 0 миль в час.Чтобы упростить измерения и добиться прогресса в решении физической или математической задачи, вы берете среднюю скорость всех дискретных событий, говоря, что машина проехала 5.5 миль за 6 минут:
с = 5,5 миль 6 мин. = 55 миль / ч
Все остальные измерения в определенные моменты путешествия — это мгновенных скоростей . В большинстве случаев вы делаете , а не , вам нужно знать формулу для мгновенной скорости, v , находя предел по мере того, как изменение во времени («мгновение») приближается к 0:
v = lim △ t → 0 △ x △ t
Мгновенные скорости колеблются во время события. Найти среднюю скорость намного проще — и обычно гораздо полезнее — чем вычислить мгновенную скорость.

Скалярные и векторные величины
Скорость — это скалярная величина . У него нет направления. У него есть только размер, то есть величина или масштаб. Скалярные величины могут изменяться от 0 (нет скорости) до бесконечно высокой.
Векторная величина имеет размер и направление, как в случае с движением самолета в небе. Скорость — это векторная величина.
Скорость, будучи скалярной величиной, никогда не может быть меньше нуля. Средняя и мгновенная скорости всегда являются скалярными величинами, что означает, что вы всегда можете измерить их числом.Расстояние и время также являются скалярными величинами и могут быть измерены числами.
Как рассчитать среднюю скорость
Чтобы вычислить среднюю скорость объекта, вы должны знать общее расстояние, которое проходит объект, и общее время, затраченное на его полное путешествие.
Треугольник расстояние / скорость / время удобен для вычисления этой и двух других скалярных величин (расстояния и времени):
Три части треугольника математически расположены в правильных положениях:
- Чтобы получить среднюю скорость, с, разделите общее расстояние на затраченное время: Dt
- Чтобы получить истекшее время t, разделите общее расстояние на скорость: Ds
- Чтобы получить расстояние D, умножьте скорость на количество времени: s × t
Допустим, вы хотите найти среднюю скорость тихоокеанской афалины.
 Вам говорят, что он может преодолеть расстояние 89,7 километра за 3 часа.
Вам говорят, что он может преодолеть расстояние 89,7 километра за 3 часа.Вставьте эти два заданных числа в треугольник в их двух углах, чтобы получить:
с = 89,7
Формула линейной скорости Физика | Решенные и практические вопросы
×
Извините !, эта страница сейчас недоступна для добавления в закладки.
Формулы линейной скорости Физика
Линейная скорость определяется как скорость изменения пройденного расстояния или расстояния за единицу времени.

Если dx — это изменение расстояния, а dt — изменение скорости, то линейная скорость определяется по формуле:
СМОТРЕТЬ БОЛЬШЕ
\ [Speed (s) = \ frac {dx} {dt} \]
Единица измерения линейной скорости в системе СИ — м / с.
Соотношение между линейной скоростью (x) и угловой скоростью (ω) в случае кругового движения определяется выражением:
Скорость (с) = rω
Где r = радиус круговой траектории
Пример:
Рассчитать линейную скорость тела, движущегося со скоростью 30 об / мин по круговой траектории радиусом 7 м?
Ответ:
Дано — Угловая скорость (ω) = 30 об / мин = π рад / с
= 5,237рад / с
Радиус r = 2 м
Линейная скорость определяется как
\ [v = r \ omega \]
\ [= 7 м \ times \ frac {22} {7} рад / с \]
\ [= 22 м / с \]
Вопрос:
Если объект покрывает расстояние 4 м за 2 секунды по круговой траектории радиусом 2 м, найти угловую скорость объекта.





 2006 г.] Тематики энергетика в целом EN tip speed … Справочник технического переводчика
2006 г.] Тематики энергетика в целом EN tip speed … Справочник технического переводчика
 Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.  2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)
2\varphi}{dt}=\overset.\omega=\overset{..}\varphi\)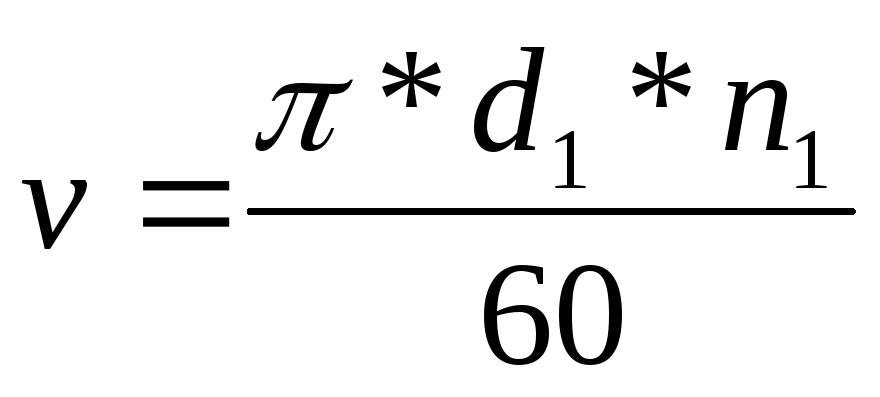 2}\)
2}\)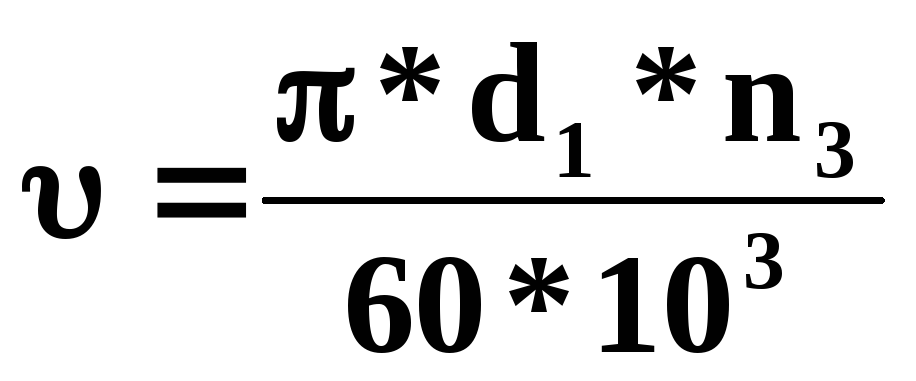 \]
\] \]
\]
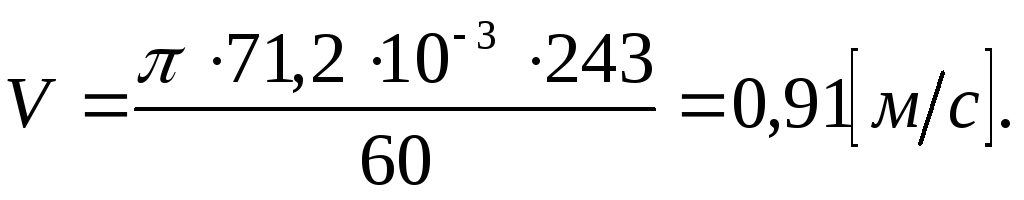

 Но в каждой точке окружности вектор \(\vec{v}\) направлен по касательной к окружности, т. е. перпендикулярно радиусу.
Но в каждой точке окружности вектор \(\vec{v}\) направлен по касательной к окружности, т. е. перпендикулярно радиусу. {-1} \]
{-1} \] Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой.
Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой. Давайте теперь подробно рассмотрим каждый режим.
Давайте теперь подробно рассмотрим каждый режим. Если вам нужна быстрая, но черновая обработка , продолжайте движение до максимальной скорости.
Если вам нужна быстрая, но черновая обработка , продолжайте движение до максимальной скорости.
 система, ее относительная скорость по отношению к большему телу. Скорость в последнем случае может быть относительно поверхности самого большого тела или относительно его центра масс.
система, ее относительная скорость по отношению к большему телу. Скорость в последнем случае может быть относительно поверхности самого большого тела или относительно его центра масс.

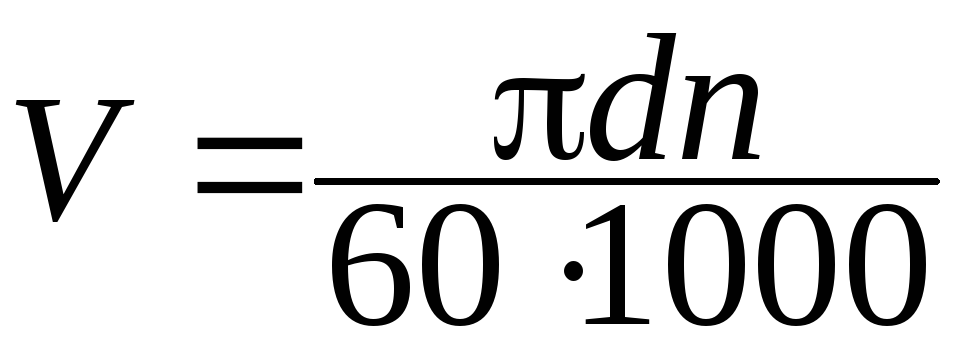 В любой момент автомобиль не движется со скоростью 55 миль в час (миль в час). Это может быть 0 миль в час, затем 7 миль в час в другой момент, затем 53 миль в час, затем 61 миль в час и, наконец, 3 мили в час, прежде чем вернуться к 0 миль в час.
В любой момент автомобиль не движется со скоростью 55 миль в час (миль в час). Это может быть 0 миль в час, затем 7 миль в час в другой момент, затем 53 миль в час, затем 61 миль в час и, наконец, 3 мили в час, прежде чем вернуться к 0 миль в час.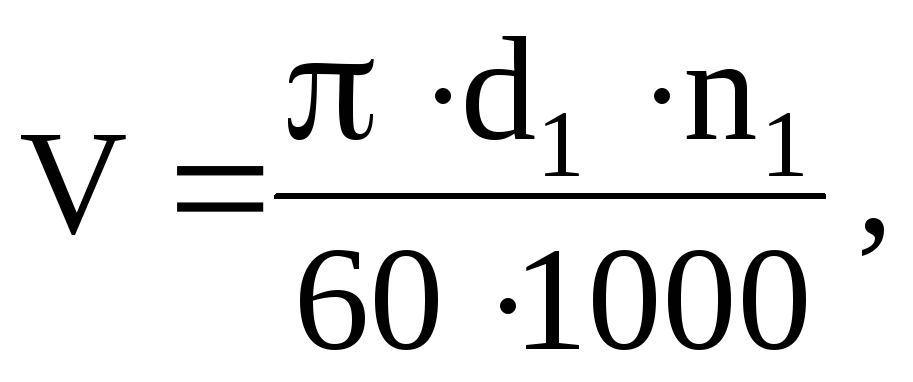
 Вам говорят, что он может преодолеть расстояние 89,7 километра за 3 часа.
Вам говорят, что он может преодолеть расстояние 89,7 километра за 3 часа.
