Формула полезной работы: Формула полезной работы в физике для КПД
Коэффициент полезного действия механизма. 7 класс
Коэффициент полезного действия механизма. 7 класс
- Подробности
- Просмотров: 156
При перемещении тела с помощью простых механизмов (рычагов, блоков, наклонной плоскости) приложенной силе приходится преодолевать не только вес самого груза.
Например:
Надо поднять груз с помощью подвижного блока на высоту.
Для поднятия груза человек прикладывает к веревке силу (F тяги).
Какую работу он при этом совершает?
Надо поднять непосредственно груз весом Р.
Кроме груза надо поднять еще веревку и блок весом Р бл.
Надо преодолеть трение о воздух и в осях блока, мешающее подьему.
1. Какую работу называют полной?
Полная ( или иначе затраченная) работа — это работа, совершенная приложенной силой, и равная работе по подъему груза и преодолению какого-либо сопротивления подъему.
1. Какую работу называют полезной?
Полезная работа — это работа приложенной силы, совершенная для подъема непосредственно груза.
Полезную работу обычно обозначают — Ап.
Совершаемая с помощью механизма полная работа всегда больше полезной работы.
Часть затрачиваемой работы расходуется на преодоление трения в оси механизма и сопротивления воздуха, а также на движение самого механизма.
3. Что такое коэффициент полезного действия механизма?
Отношение полезной работы к полной работе называется коэффициентом полезного действия.
Сокращенно коэффициент полезного действия обозначается КПД.
КПД обычно выражают числом или в процентах и обозначают греческой буквой, которая читается как «эта».
4. Может ли КПД быть больше единицы?
Полезная работа всегда меньше затраченной работы.
Поэтому КПД любого механизма всегда меньше 100% ( или меньше 1).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их вес.
4. Пример решения задачи на расчет КПД.
Задача.
На коротком плече рычага подвешен груз массой 100 кг.
Для его подъема к длинному плечу приложили силу 250 Н.
Груз подняли на высоту h1 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м.
Найти КПД рычага.
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
Формула работы через скорость
Скорость физического тела при воздействии на него силы меняется по модулю, т.е. увеличивается или уменьшается.
Определение 1
Работу можно рассматривать как изменение кинетической энергии движущегося тела в результате действия вызвавшей это изменение силы.
В простейшем случае, когда направления движения тела и приложенной к ней силы совпадают, работа прямопропорциональна интенсивности силы и расстоянию, пройденному телом под воздействием этой силы:
$A = F \cdot s = m \cdot v \cdot s$,
где:
- $F$ — сила,
- $s$ — расстояние,
- $m$ — масса,
- $v$ — скорость.
В Международной системе СИ работа измеряется в джоулях. Один джоуль равен работе по перемещению тела силой в 1 ньютон на расстояние в 1 метр. Выразив силу через массу и скорость, получим:
$Дж = кг \cdot \frac{м}{с^2} \cdot м = \frac{кг \cdot м^2}{с^2}$
На практике направления векторов движения тела и совершающей работу силы могут не совпадать. В таких случаях элементарную (выполненную на бесконечно малом, неотличимом от прямой участке траектории) работу удобно выражать как скалярное произведение векторов силы и элементарного перемещения точки по траектории. В пространственной системе координат это можно записать как
Готовые работы на аналогичную тему
$\delta A = F_x \cdot dx + F_y \cdot dy + Fz \cdot dz$
, где $F_x, F_y, F_z$ — проекции силы на координатные оси, $dx, dy, dz$ — соответствующие изменения вектора траектории.
Угол между векторами силы и перемещения показывает ускоряющим или замедляющим является воздействие. Если угол острый — работа положительна, при тупом угле она, соответственно, отрицательна.
Представив расстояние как произведение скорости на время, можно найти соотношение между элементарной работой и импульсом:
$\delta A = \bar{F} \cdot \bar{v} \cdot dt = \bar{v} \cdot dp $
, где $v$ — скорость, $dt$ — промежуток времени, за который совершается работа, $dp$ — изменение импульса тела за этот промежуток.
Если на физическое тело действуют сразу несколько сил, то следует провести векторное суммирование элементарных работ всех сил. При этом векторная сумма сил, действующих внутри тела, принимается равной нулю.
Работа для вращающегося тела определяется по формуле:
$\delta A = \bar{M} \cdot \bar{\omega} \cdot dt = \bar{M} \cdot d\bar{\phi}$
, где $\bar{M}$ — совокупный вращающий момент действующих на тело сил, $\bar{\omega}$ — мгновенная угловая скорость, $d\bar{\phi}$ — элементарный вектор поворота.
Любая машина или механизм, которые созданы человеком, призваны выполнять некоторую полезную работу. Для ее совершения следует затратить энергию. Вопрос соотношения затраченной и полезной работы рассмотрим на примере определения КПД рычага.
О рычаге
Рычагом называют любой простой механизм, который служит для преобразования силы по величине и направлению. Он состоит из балки и опоры, в общем случае имеет два плеча. На каждое из плеч оказывает действие сила. Обе силы стремятся повернуть плечи в противоположных направлениях. Поэтому одна из них всегда совершает работу против другой.
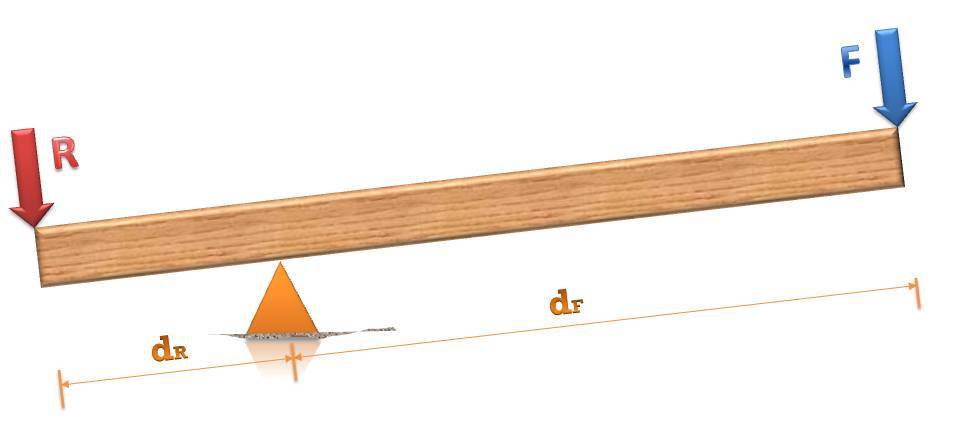
Рычаг позволяет выиграть в пути или в силе, при этом будет наблюдаться проигрыш в силе или в пути соответственно. Главная формула рычага, которая описывает равновесие его плеч, указана ниже:
F/R = dR/dF.
Здесь сила F совершает работу против веса груза R, действуя на плечо длиной dF. Груз находится на плече длиной dR. Формула отражает обратную пропорциональность между отношениями сил и плеч.
Следующий момент. Когда плечи начинают перемещаться, то одно из них поднимается на высоту h1, другое же опускается на высоту h2. Поскольку угол поворота плеч будет одинаковый, то, в отсутствие других сил, формулу выше можно переписать так:
F/R = h1/h2.
Дальше эта формула будет использоваться для определения КПД рычага.
КПД простого механизма

Напомним, что работой в физике называется величина, равная произведению силы на путь, в течение которого она действовала:
A = F * l.
КПД любого механизма характеризует эффективность его работы. Вычислить его можно по такой формуле:
КПД = Ап/Аз * 100%.
Где Ап — полезная работа, выполненная механизмом, Аз — работа, которую пришлось затратить.
Человечество на протяжении всей истории пытается создать механизмы, в которых бы Аз = Ап, но достичь этого равенства еще никому не удавалось. Затраченная работа всегда больше значения Ап.
Используя формулу для рычага, полученную в предыдущем пункте, можно записать формулу определения КПД рычага:
Ап = R * h1; Аз = F * h2;
КПД = Ап/Аз * 100% = R * h1/(F * h2) * 100%.
Если учесть соответствующее выражение для рычага, то может показаться, что КПД для него будет равен 100 %. Тем не менее это не так, поскольку постоянно существует трение в оси вращения и трение о воздух. В результате этих процессов затраченная работа частично расходуется на нагрев окружающей среды и деталей рычага, поэтому КПД механизма оказывается всегда меньше 100 %.
Задача на определение КПД
Предположим, что прилагаемая к рычагу сила F = 18 Н привела к подъему груза массой 3 кг на высоту 0,3 метра. Учитывая, что плечо приложения силы F опустилось при этом на 0,6 метра, вычислите КПД рычага.
Вычисляем полезную и затраченную работы:
Ап = R * h1 = m * g * h1 = 3 * 9,81 * 0,3 = 8,829 Дж;
Аз = F * h2 = 18 * 0,6 = 10,8 Дж.
Как видно, Аз > Ап. КПД рычага равен:
КПД = Ап/Аз * 100% = 8,829/10,8 * 100% = 81,75 %.
Увеличить это значение КПД можно, если применить смазку в оси вращения рычага.
Полезная работа формула физика
Совет 1: Как найти коэффициент полезного действия
Коэффициент полезного действия показывает отношение полезной работы, которая выполняется механизмом или устройством, к затраченной. Часто за затраченную работу принимают количество энергии, которое потребляет устройство для того, чтобы выполнить работу.
Вам понадобится
- — автомобиль;
- — термометр;
- — калькулятор.
Инструкция
- Для того чтобы рассчитать коэффициент полезного действия (КПД) поделите полезную работу Ап на работу затраченную Аз, а результат умножьте на 100% (КПД=Ап/Аз∙100%). Результат получите в процентах.
- При расчете КПД теплового двигателя, полезной работой считайте механическую работу, выполненную механизмом. За затраченную работу берите количество теплоты, выделяемое сгоревшим топливом, которое является источником энергии для двигателя.
- Пример. Средняя сила тяги двигателя автомобиля составляет 882 Н. На 100 км пути он потребляет 7 кг бензина. Определите КПД его двигателя. Сначала найдите полезную работу. Она равна произведению силы F на расстояние S, преодолеваемое телом под ее воздействием Ап=F∙S. Определите количество теплоты, которое выделится при сжигании 7 кг бензина, это и будет затраченная работа Аз=Q=q∙m, где q – удельная теплота сгорания топлива, для бензина она равна 42∙10^6 Дж/кг, а m – масса этого топлива. КПД двигателя будет равен КПД=(F∙S)/(q∙m)∙100%= (882∙100000)/( 42∙10^6∙7)∙100%=30%.
- В общем случае чтобы найти КПД, любой тепловой машины (двигателя внутреннего сгорания, парового двигателя, турбины и т.д.), где работа выполняется газом, имеет коэффициент полезного действия равный разности теплоты отданной нагревателем Q1 и полученной холодильником Q2, найдите разность теплоты нагревателя и холодильника, и поделите на теплоту нагревателя КПД= (Q1-Q2)/Q1. Здесь КПД измеряется в дольных единицах от 0 до 1, чтобы перевести результат в проценты, умножьте его на 100.
- Чтобы получить КПД идеальной тепловой машины (машины Карно), найдите отношение разности температур нагревателя Т1 и холодильника Т2 к температуре нагревателя КПД=(Т1-Т2)/Т1. Это предельно возможный КПД для конкретного типа тепловой машины с заданными температурами нагревателя и холодильника.
- Для электродвигателя найдите затраченную работу как произведение мощности на время ее выполнения. Например, если электродвигатель крана мощностью 3,2 кВт поднимает груз массой 800 кг на высоту 3,6 м за 10 с, то его КПД равен отношению полезной работы Ап=m∙g∙h, где m – масса груза, g≈10 м/с² ускорение свободного падения, h – высота на которую подняли груз, и затраченной работы Аз=Р∙t, где Р – мощность двигателя, t – время его работы. Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.
KakProsto.ru>
Какая формула у полезной работы?
Sandra
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу Аз и полезную работу Ап . Если, например, наша цель-поднять груз массой m на высоту Н, то полезная работа — это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:
Ап =FH= mgH
Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Что такое работа в физике определение формула. нн
Помогите расшифровать формулу по физике
КПД тепловых двигателей.физика (формулы,определения,примеры) напишите! физика (формулы,определения,примеры) напишите!
Похожие статьи
Формула работы
Работа — это результат, когда сила воздействует на объект и перемещает его на некоторое расстояние. Иногда направление движения объекта не совпадает с направлением силы. В этом случае только компонент силы, действующий в направлении движения, заставляет работать. По этой причине в формулу работы входит косинус угла между силой и расстоянием. Если сила и движение в одном направлении, то угол равен 0 радиан, (или 0 °).Косинус нуля: cos0 = 1. Единицами работы являются джоули (Дж), где 1 Дж = 1 Н ∙ м = 1 кг 9 м 2 / с 2 .
работа = сила х расстояние × косинус (угол между силой и направлениями движения)
W = Fd cosθ
W = работа (шт. J)
k = сила (ед. N)
d = расстояние ( м )
θ = угол между направлением силы и направлением движения
Формула работы Вопросы:
1) Трактор вытащил вагон, полный сена, на расстояние 1000 м .Сила, приложенная к фургону для перемещения на это расстояние, составляла 12 000 Н. Сила действовала в том же направлении, что и движение. Узнайте, сколько работы было проделано трактором, чтобы вытащить вагон.
Ответ: Сила и движение были в одном направлении, поэтому угол между ними равен 0 °. Работу можно найти по формуле:
W = Fd cosθ
W = Fd cos0
W = Fd (1)
W = (12 000 N) (1000 м )
W = 12 000 000 N 000 м
W = 12 000 000 J
Работа, проделанная трактором для перемещения вагона на заданное расстояние, составила 12 000 000 Дж, что также можно указать в мегаджоулях: 12.0 М J.
2) Мужчина толкает газонокосилку через свой двор. Сила, которую он прикладывает к рукоятке газонокосилки, наклонена вниз, на 60,0 ° от горизонтальной плоскости. Эта сила имеет величину 900 Н. Если он толкает газонокосилку 30,0 м , сколько работы было проделано для перемещения газонокосилки?
Ответ: Сила под углом 60,0 ° относительно движения. Работу можно найти по формуле:
W = Fd cosθ
W = Fd cos60 °
W = Fd (0.5)W = (900 Н) (30.0 м ) (0.5)
W = 13 500 Нм
W = 13 500 J
Работа, проделанная при перемещении газонокосилки на заданное расстояние, составила 13 500 Дж.
формула работы и примеры
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agaris Agard Agard Agard Agard Agard 2000 12000000- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Учебный курс по бизнес-классу 11000
- Учебная программа по экономическому классу
- Учебная программа по 12 классу
- Учебная программа по 12 классам
- Учебная записка по 12-му классу
- Решения TS Grewal Класс 12 Бухгалтерский учет
- Решения TS Grewal Класс 11 Бухгалтерский учет
- ML Решения Aggarwal Class 10 Maths
- ML Решения Aggarwal Class 9 Математика
- ML Решения Aggarwal Class 8 Maths
- ML Решения Aggarwal Class 7 Maths
Объяснение квадратичной формулы | Purplemath
Purplemath
Часто самый простой способ решить « топор 2 + bx + c = 0» для значения x состоит в том, чтобы разложить квадратичные числа, установить каждый коэффициент равным нулю, а затем решить каждый фактор. Но иногда квадратик слишком запутанный, или он вообще не учитывается, или вы просто не чувствуете, как факторинг.Хотя факторинг не всегда может быть успешным, Квадратичная формула всегда может найти решение.
Квадратичная формула использует « a «, « b » и « c » из « ax 2 + bx + c «, где « a «, » b «и» c «- просто числа; они являются «числовыми коэффициентами» квадратного уравнения, которое они дали вам решить.
MathHelp.ком
Квадратичная формула получена из процесса заполнения квадрата и формально имеет вид:
Квадратичная формула: для ax 2 + bx + c = 0, значения x , которые являются решениями уравнения, определяются как:
Чтобы квадратичная формула работала, ваше уравнение должно быть расположено в форме «(квадратичная) = 0».Кроме того, «2 a » в знаменателе Формулы находится ниже всего, что находится выше, а не только в виде квадратного корня. И там внизу «2 a », а не просто «2». Убедитесь, что вы стараетесь не бросать квадратный корень или «плюс / минус» в середине ваших расчетов, или я могу гарантировать, что вы забудете «вставить их обратно» в свой тест, и вы испортите себя вверх. Помните, что « b 2 » означает «квадрат ВСЕГО b , включая его знак», поэтому не оставляйте b 2 отрицательным, даже если b отрицательный, потому что квадрат негатива — это позитив.
Другими словами, не будьте неряшливыми и не пытайтесь использовать ярлыки, потому что это только навредит вам в долгосрочной перспективе. Поверь мне в этом!
Вот несколько примеров того, как работает квадратичная формула:
Это квадратичное значение имеет множитель:
x 2 + 3 x — 4 = ( x + 4) ( x — 1) = 0
..так я уже знаю, что решения x = –4 и x = 1. Как мое решение будет выглядеть в квадратичной формуле? Используя a = 1, b = 3 и c = –4, мое решение выглядит следующим образом:
Тогда, как и ожидалось, решение будет x = –4, x = 1.
Предположим, у вас есть топор 2 + bx + c = y , и вам говорят подключить ноль на y . Соответствующие значения x — это x -цепки графа. Таким образом, решение ax 2 + bx + c = 0 для x означает, среди прочего, что вы пытаетесь найти x -перехватов.Поскольку было два решения для x 2 + 3 x — 4 = 0, на графе должно быть два x -цепок. Графиком получим кривую ниже:
Как видите, точки пересечения x (красные точки выше) соответствуют решениям, пересекая ось x в точке x = –4 и x = 1.Это показывает связь между построением графика и решением: когда вы решаете «(квадратичное) = 0», вы находите x -цепки графа. Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать Квадратичную формулу (при необходимости) для решения квадратичного, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые x -цепки имеют те же десятичные значения, что и делать решения, предоставляемые квадратичной формулой.
Обратите внимание, однако, что отображение графика калькулятором, вероятно, будет иметь некоторую ошибку округления, связанную с пикселями, поэтому вы должны проверить, чтобы вычисленные и графические значения были достаточно близки; не ожидайте точного совпадения.
Решить 2 x 2 — 4 x — 3 = 0. При необходимости округлите свой ответ до двух десятичных знаков.
Нет факторов (2) (- 3) = –6, которые складываются в –4, поэтому я знаю, что этот квадратик не может быть учтен. Я буду применять Квадратичную формулу. В этом случае a = 2, b = –4 и c = –3:
Тогда ответ: x = –0.58, x = 2,58, округлено до двух знаков после запятой.
Предупреждение: «решение» или «корни» или «нули» квадратика обычно должны быть в «точной» форме ответа. В приведенном выше примере точная форма имеет форму с квадратными корнями из десяти. Вам понадобится калькуляционная аппроксимация, чтобы отобразить X-перехваты или упростить окончательный ответ в словесной задаче. Но если у вас нет веских оснований полагать, что ответ должен быть округленным, всегда указывайте точную форму.
Сравните решения 2 x 2 — 4 x — 3 = 0 с x -точками графика:
Как и в предыдущем примере, перехватчики x совпадают с нулями в квадратичной формуле. Это всегда правда. «Решения» уравнения также являются x -интекстами соответствующего графа.
URL: https: // www.purplemath.com/modules/quadform.htm
,Формула завершения работы в процессе — AccountingTools
Работа в процессе (WIP) — это инвентарь, который был частично завершен, но который требует дополнительной обработки, прежде чем он может быть классифицирован как запас готовой продукции. Объем завершающейся работы в процессе должен быть получен как часть процесса закрытия периода, а также полезен для отслеживания объема производственной деятельности. Расчет конечной незавершенной работы:
Начальный WIP + Затраты на производство — Стоимость произведенных товаров
= Окончание незавершенного производства
Например, в ABC International начальный WIP составляет 5000 долларов США, в течение месяца производственные затраты составляют 29 000 долларов США, и записывает 30 000 долларов США на стоимость товаров, произведенных в течение месяца.Его конечная незавершенная работа:
5000 долл. США. Начальный WIP + 29 000 долл. США. Производственные затраты — 30 000 долл. США на стоимость произведенного товара.
= 4000 долл. США. Окончание WIP
. порча и неправильное ведение записей могут привести к значительному расхождению между результатами формулы и стоимостью фактического незавершенного производства. В большинстве случаев эти дополнительные проблемы уменьшат объем завершающейся работы в процессе за счет начисления дополнительных расходов в текущий период.
Следовательно, некоторые компании используют два альтернативных метода для достижения окончательного незавершенного производства, а именно:
Запись № WIP . Производственный процесс может быть настолько быстрым или оптимизированным, что компания может завершить все производство к концу периода измерения, что приведет к отсутствию WIP. В качестве альтернативы, количество WIP может быть настолько незначительным (как это имеет место в некоторых средах точно в срок), что нет необходимости измерять его.
Провести подсчет .Вместо того, чтобы использовать формулу, проведите подсчет незавершенного производства и назначьте стандартные затраты в зависимости от стадии завершения. Этот подход довольно трудоемкий, и поэтому не рекомендуется.
Связанные курсы
Учет запасов
Как проводить аудит запасов
