Формула скорости движения по окружности: 1.6. Движение по окружности
Движение по окружности – формулы, графики, уравнения
4.6
Средняя оценка: 4.6
Всего получено оценок: 310.
4.6
Средняя оценка: 4.6
Всего получено оценок: 310.
Движение – это форма существования материи. Одним из видов движения является движение по окружности. Рассмотрим эту тему подробнее.
Равномерное движение по окружности
Равномерное движение по окружности – это движение, при котором траектория материальной точки представляет собой окружность, при этом длина пройденного пути за единицу времени постоянна.
Рис. 1. Примеры движения по окружности.Мгновенная скорость
Поскольку при равномерном движении по окружности длина пройденного за одно и то же время пути одинакова, то можно заключить, что мгновенная скорость на бесконечно малом участке при таком движении постоянна. Следовательно, можно составить уравнение, приравняв общую длину пути к произведению неизвестной скорости на время прохождения пути, откуда получить мгновенную скорость точки.
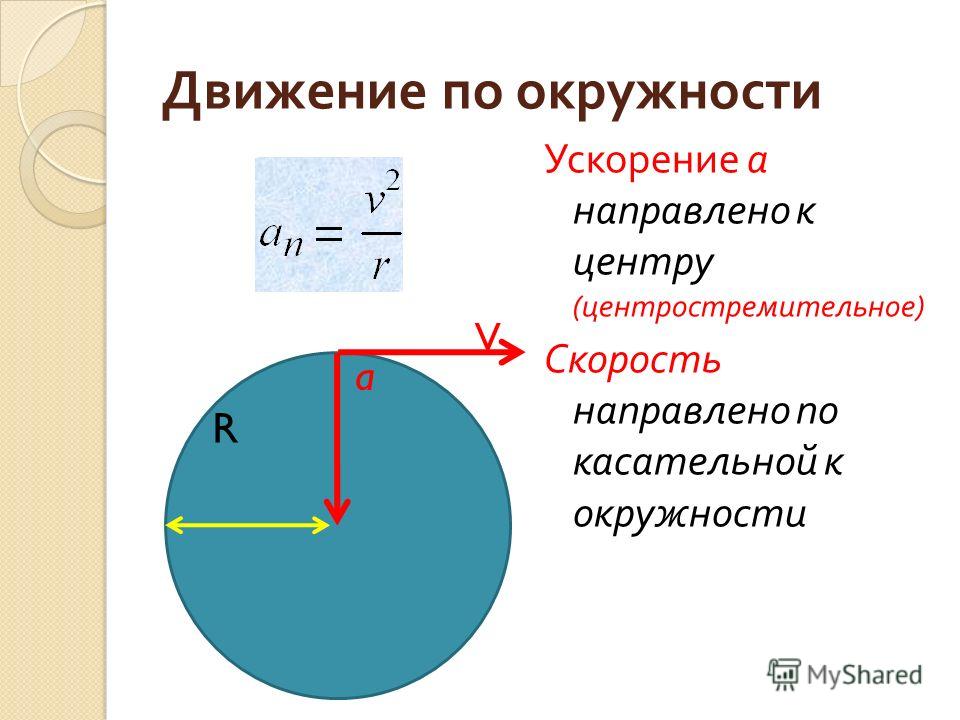
Длина окружности равна $2\pi R$. Если время прохождения одного оборота (период) равно $T$, то модуль мгновенной скорости находится по формуле:
$$v={2\pi R\over T}$$
Для определения направления мгновенной скорости принимается, что за короткое время движение материальной точки можно считать прямолинейным. В этом случае движение точки пройдет по хорде. При уменьшении рассматриваемого отрезка времени хорда будет неограниченно приближаться к касательной, в пределе сливаясь с ней.
Мгновенная скорость при движении по окружности направлена по касательной к этой окружности.
Центростремительное ускорение
Скорость – векторная величина, и хотя модуль мгновенной скорости постоянен, направление этого вектора непрерывно изменяется по мере прохождения круговой траектории. А согласно теории, любое изменение вектора скорости означает, что движение происходит с ускорением. Следовательно, равномерное движение по окружности – это движение с ускорением. Но, в случае движения по окружности это ускорение изменяет не модуль скорости, а его направление.
Как правило, источник центростремительного ускорения легко определяется. Например, для движения планет вокруг Солнца – это притяжение Солнца. Для точек вращающихся предметов – это молекулярные силы, удерживающие части предмета вместе. Для заворачивающего автомобиля – это сила сцепления колес с грунтом. Используя формулы движения по окружности – это ускорение всегда можно найти.
Если источник центростремительного ускорения исчезнет – тела начинают двигаться равномерно и прямолинейно в направлении имеющейся мгновенной скорости. Так происходит, например, с брызгами воды, когда колесо проезжает лужу, так происходит с раскрученным на шнуре предметом при обрыве шнура. Это доказывает, что мгновенная скорость направлена по касательной к окружности. Данное явление использовали древние метательные орудия – праща и требушет.
Что мы узнали
Равномерное движение по окружности – это такое движение материальной точки, при котором ее траектория представляет собой окружность. Перемещение по этой окружности происходит с постоянной частотой под действием центростремительного ускорения. Мгновенная скорость точки всегда направлена по касательной к окружности.
Перемещение по этой окружности происходит с постоянной частотой под действием центростремительного ускорения. Мгновенная скорость точки всегда направлена по касательной к окружности.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 310.
А какая ваша оценка?
Движение по окружности | fizmatuski.narod.ru
Движение по окружности
Движение по окружности – частный случай криволинейного движения.
При движении по окружности движение может быть:
- С постоянной по величине скоростью V=const
- С одинаково изменяющейся по величине скоростью Δ V= const
- С неодинаково изменяющейся по величине скоростью, ΔV разное, изменяется не одинаково.
!!! Но при этом во всех 3-х случаях V изменяется по направлению (всегда). Движение по окружности – это периодически повторяющееся движение.
Основными характеристиками такого движения являются:
— период – это время 1 полного оборота (t – все время, N – число оборотов за время t)— частота – число оборотов за 1с. (Гц)
l = 2πR – путь за 1 поворот (длина окружности) (м)
L = 2πRN – путь за N оборотов (м).
1.Рассмотрим движение с постоянной по величине скоростью. По определению, скорость это путь, пройденнфй телом за единицу времени:
— это путевая скорость движения тела по окружности. Зная значения величин, входящих в эту формулу, получим формулы скорости, которые выражают зависимость от основных характеристик движения по окружности:
ω = 2πn – циклическая частота или угловая скорость (число оборотов за 2π секунды), измеряется в (Гц = рад/с).
(Гц)
Аналогия: тело со V тело проходит путь L, со скоростью ω проходит угловой путь φ (поворачивается на угол).
Угловое расстояние: φ = ωt или φ = 2πN
— ускорение, которое показываем изменение направления скорости ( но не величины) т.к. всегда перпендикулярна и направлена к центру окружности, то это ускорение называется центростремительным:
— формула, определяющая центростремительное ускорение. Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения:
— формулы для вычисления центростремительного ускорения через основные характеристики.
Рассмотрим частные случаи движения тел по окружности:
1. Движение по одному кругу, но по окружностям разного радиуса:
Если т.А и т.В двигаются синхронно то они вместе совершают 1 оборот, значит Т1 = Т2 (периоды их оборотов одинаковы), а из этого следует
=> n1 = n2 => ω1 = ω2,Зная связь между линейной и угловой скоростями, между ускорением и угловой скоростью, получим выражения:
2.Рассмотрим случай, когда два тела совершают круговые движения, но связаны ременной или зубчатой передачей
ременная связь или зубчатая связь
В этом случае скорости движения двух тел равны (нет провисания ремня ): V1 = V2
Зная формулы, связывающие линейную скорость с периодом вращения и с ускорением, получим:
2. Более сложный случай, когда скорость изменяется по величине.
— это средняя путевая скорость движения тела по окружности, где её изменение по величине характеризуется тангенциальным ускорением: ат , изменение скорости по направлению характеризуется центростремительным ускорением а ц , которое в каждой точке разное, так как разной будет скорость движения по величине: . Эти два ускорения взаимно перпендикулярны т.к. ац направлено к центру окружности, а ат — по касательной ( если разгон, то по направлению скорости, если торможение, то в противоположную сторону).
Так как тангенциальное ускорение не изменяется, а центростремительное изменяется, то будет изменяться и общее ускорение
Изменение скорости приведёт к изменению связанных с ним характеристик: периода, частоты и угловой скорости вращения.
Вернуться к конспектам урока
Формула круговой скорости — GeeksforGeeks
При изменении скорости меняется и ускорение, но не в том же направлении. В результате объект, движущийся по круговой траектории, всегда должен иметь ускорение, перпендикулярное скорости. Круговое движение может быть как равномерным, так и неравномерным. Формула равномерного кругового движения будет обсуждаться с примерами в этом разделе. Осваиваем эту тему!
Осваиваем эту тему!
Что такое окружная скорость?
Круговая скорость определяется как скорость, которой обладает объект при равномерном круговом движении. Равномерное круговое движение — это двумерное движение, при котором объект движется по кругу с постоянной скоростью, а скорость изменяется в каждом месте из-за изменения направления вектора скорости.
Круговая скорость прямо пропорциональна радиусу кругового пути, но обратно пропорциональна времени, которое проходит объект.
- Обозначается символом v c .
- Единицей измерения является м/с.
- И размерная формула дается как [M 0 L 1 T -1 ].
Формула круговой скорости
Примеры задачМатематически она определяется как длина окружности кругового пути, деленная на затраченное время.
v c = 2πr/T
где,
- v c — круговая скорость,
- r — радиус кругового пути,
- T — затраченное время.
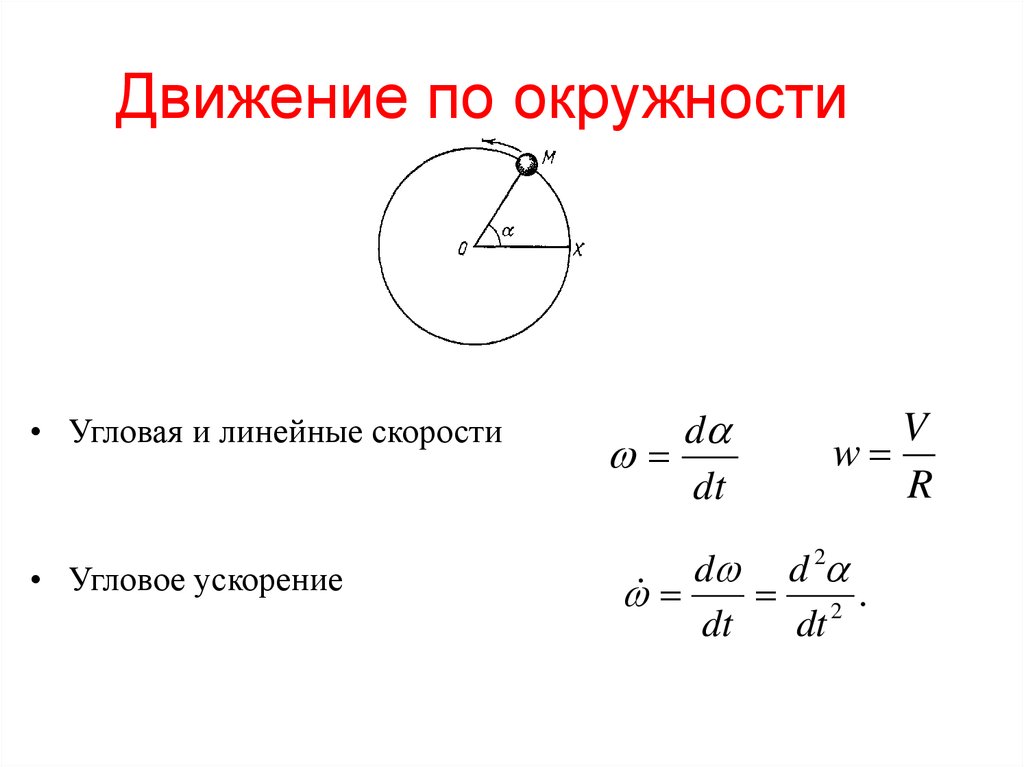
Однако круговую скорость также можно рассчитать, если задана угловая скорость ω, и она рассчитывается как
v c = ω r
, r – радиус кругового пути
Задача 1. Вычислить круговую скорость объекта, совершающего круговое движение, если радиус равен 3 м за время 4 с.
Решение:
Мы имеем,
R = 3
T = 4
Используем формулу, которую мы имеем,
В C = 2πr/T
= (2 × 3,14 × 3. )/4
= 18,84/4
= 4,71 м/с
Задача 2. Вычислить круговую скорость объекта, совершающего круговое движение, если радиус равен 5 м за время 2 с.
Решение:
У нас есть,
R = 5
T = 2
Используя формулу, которую мы имеем,
V C = 2πr/T
= (2 × 3,14 × 5)/2
= 31,4/2
= 15,7 м/с
Задача 3. Вычислить круговую скорость объекта, совершающего круговое движение, если радиус равен 4 м за время 7 с.
Вычислить круговую скорость объекта, совершающего круговое движение, если радиус равен 4 м за время 7 с.
Решение:
Имеем,
r = 4
T = 7
Используя формулу имеем,
V C = 2πr/T
= (2 × 3,14 × 4)/7
= 25,12/7
= 3,58 м/с
Проблема 4: Рассчитайте радиус, если циркулярный скорость тела, совершающего круговое движение, равна 5 м/с за время 3 с.
Решение:
Мы имеем
V C = 5
T = 3
Используем формулу, которую мы имеем,
V C = 2πr/T
=> R = R = R = R = R = R = R = R = R = R = R = R = R = R = R = R C = 2πr/T
=> R = R C = 2πr/T
=> r = v c T/2π= (5 × 3)/(2 × 3,14)
= 15/6,28
= 2,38 м
Задача 5. Вычислить круговую скорость объекта, если совершает круговое движение со скоростью 8 м/с за время 2 с.
Вычислить круговую скорость объекта, если совершает круговое движение со скоростью 8 м/с за время 2 с.
Решение:
Мы имеем,
V C = 8
T = 2
Используем формулу, которую мы имеем,
V C = 2πr/T
=> R = R = R = R = R = R = R = R = R = R = R = R = R = R = R C = 2πr/T
=> r = в с T/2π= (8 × 2)/(2 × 3,14)
= 16/6,28
= 2,54 м
скорость 7 м/с на радиусе 5 м.
Решение:
Мы имеем,
VC = 7
R = 5
Используем формулу, которую мы имеем,
В C = 2πr/T
=> T = 2πr/V. с
= (2 × 3,14 × 5)/7
= 31,4/7
= 4,48 с
Задача 7. Вычислить время, если круговая скорость объекта, совершающего круговое движение, равна 12 м/с для радиуса 8 м.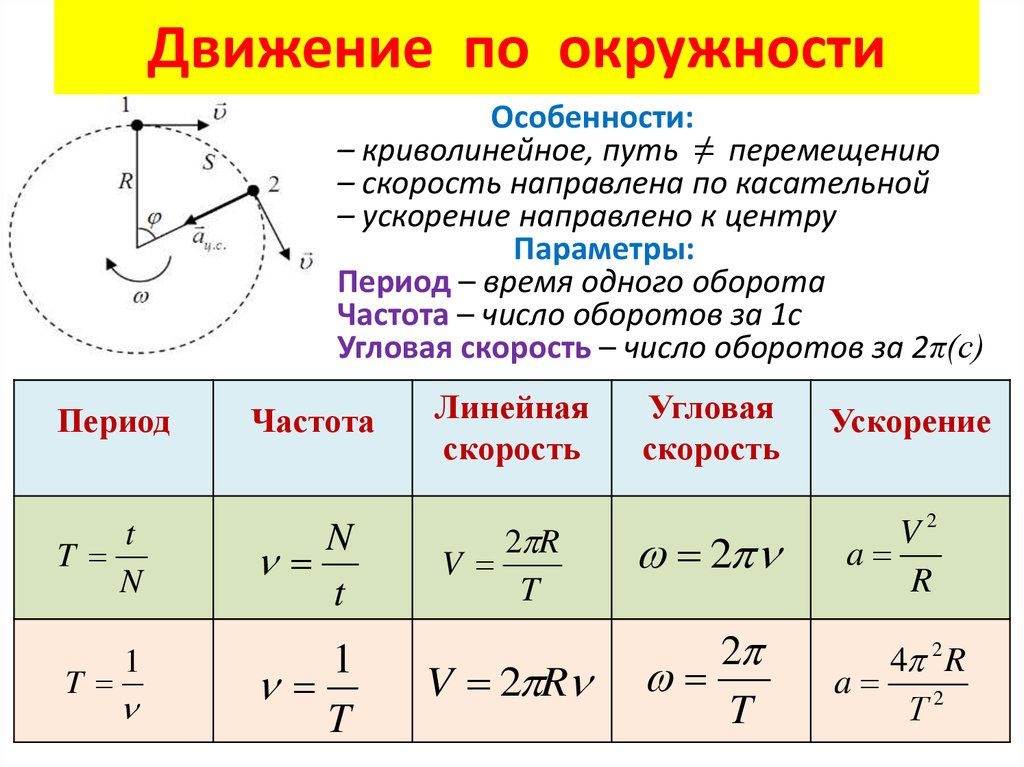
Решение:
Мы имеем,
V C = 12
R = 8
Используем формулу, которую мы имеем,
V C = 2πr/T
=> T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T = T. 2πr/v c
= (2 × 3,14 × 8)/12
= 50,24/12
= 4,18 с
Равномерное круговое движение
Равномерное круговое движение Объект, движущийся по окружности радиусом r
с постоянной скоростью v ускоряется.
направление вектора его скорости все время меняется, но величина
вектор скорости остается постоянным. Вектор ускорения не может иметь
компонента в направлении вектора скорости, так как такая компонента
вызвать изменение скорости. Поэтому вектор ускорения должен быть
перпендикулярно вектору скорости в любой точке окружности. Этот
ускорение называется радиальным ускорением
или центростремительное ускорение, и оно указывает
к центру круга. Величина центростремительной
вектор ускорения равен с = v 2 /r.
Этот
ускорение называется радиальным ускорением
или центростремительное ускорение, и оно указывает
к центру круга. Величина центростремительной
вектор ускорения равен с = v 2 /r.
Какова сила при различных обстоятельствах?
Исследуя этот вопрос, решим несколько задач.
Проблема:
Груз массой 3 кг, прикрепленный к легкой нити, вращается по горизонтальной поверхности без трения. стол. Радиус окружности равен 0,8 м, а струна может выдержать массу 25 кг до разрыва. Какой диапазон скоростей может иметь масса перед струной перерывы?
Решение:
- Обоснование:
Масса, прикрепленная к нити, вращается по горизонтали, стол без трения.
Предположим, что масса вращается с постоянной скоростью. это ускорение. Направление ускорения в сторону центр круга, а его величина v 2 /r. В струне есть напряжение. Нить натягивает массу с силой F, направленной к центру окружности. Этот
сила F отвечает за центростремительное ускорение,
F = мв 2 /р.
Этот
сила F отвечает за центростремительное ускорение,
F = мв 2 /р.
Струна может выдержать до разрыва массу 25 кг, т.е. может позволить массе до 25 кг висеть на веревке рядом с поверхность земли. Максимальное натяжение струны поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н. - Детали расчета:
v max 2 = F макс. об/мин = (250 Н)(0,8 м)/(3кг). v max = 8,1 м/с.
Проблема:
Монета, помещенная на расстоянии 30 см от центра вращающегося горизонтального поворотного стола
когда его скорость 50 см/с.
а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижна?
относительно поворотного стола?
б) Каков коэффициент статического трения между монетой и поворотным столом?
Решение:
- Обоснование:
Когда монета покоится относительно вращающегося поворотного стола, сила статическое трение между монетой и поворотным столом обеспечивает центростремительное ускорение.
Сила трения покоя имеет максимальное значение f с = μ с Н = мк с мг.
Настройка μ с мг = mv 2 /r, мы можем решить для μ s . - Детали расчета:
(а) Сила трения покоя между монетой и поворотным столом обеспечивает центростремительное ускорение.
(b) Величина максимального сила трения покоя равна f с = μ с Н. Это максимальная сила трения покоя равна mv 2 /r при v = 0,5 м/с. Имеем µ с N = µ с mg = mv 2 /r,
или μ с = v 2 /(rg) = (0,5 м/с) 2 /(0,3 м 9,8 м/с 2 ) = 0,085.
Проблема:
Рассмотрим конический маятник с грузом массой 80 кг на 10-метровом проводе, образующем угол.
θ = 5 o с вертикалью. Определить
(а) горизонтальная и вертикальная составляющая силы, действующей со стороны проволоки на
маятник и
(b) центростремительное ускорение боба.
Решение:
- Обоснование:
Диаграмма свободного тела боба показана справа.
Боб не меняет своего вертикального положения, y = константа, v y = a y = 0. Вертикальный компонент T должен иметь величина мг.
Горизонтальная составляющая Т обеспечивает центростремительное (радиальное) ускорение а р . - Детали расчета:
(a) Вертикальный компонент T должен иметь величина мг.
Tcos(5 o ) = мг, T = (80 кг 9,8 м/с 2 )/cos(5 или ) = 787 N
Величина горизонтальной составляющей T равна Tsin(5 o ) = 68,6 Н. Горизонтальная составляющая силы направлена к центру круг.(b) Tsin(5 o ) = ma r , a r = (68,6 Н)/(80 кг) = 0,857 м/с 2 .
Скорость боба находится из a r = v 2 /r, v = (a r r) ½ .
Так как r = (10 м)*sin(5 o ), имеем v = 0,86 м/с.
Проблема:
Автомобиль массой 1800 кг преодолевает неровность на дороге, идущей по дуге окружности.
радиусом 42 м.
а) С какой силой дорога действует на автомобиль при прохождении автомобиля?
наивысшая точка горки, если автомобиль движется со скоростью 16 м/с?
б) С какой максимальной скоростью может двигаться автомобиль, проезжая через этот горб?
потеря связи с дорогой?
Решение:
- Обоснование:
Показана схема свободного кузова автомобиля.Единственными силами, действующими на автомобиль, движущийся с постоянной скоростью, являются сила тяжести и нормальная сила, действующая на дорогу. Если эти силы равны по величине, автомобиль не разгоняется. Если автомобиль движется по дуга окружности, то она ускоряется. Ускорение равно r = v 2 /р. Следовательно, гравитационная сила должна иметь большую величины, чем нормальная сила.

- Детали расчета:
Нам нужно
мг — n = mv 2 /r, или n = m(g — v 2 /r).
n = (1800 кг)(9,8 м/с 2 — (16 м/с) 2 /(42 m)) = 6669 N(b) Автомобиль теряет контакт с дорогой, когда n становится равным нулю. Затем дорога больше не поддерживает машину. Это происходит, когда g — v 2 /r = 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3 РС.
Модуль 5: Вопрос 1
Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете поворот, который идеально накрен для скорости вашего автомобиля? Как направлена сила, приложенная на вас возле автокресла?
Обсудите это со своими однокурсниками на дискуссионном форуме!
Гравитация
Массивные объекты обладают инерцией. Требуется сила, чтобы изменить их состояние
движение. Все массивные объекты взаимодействуют через сила гравитации . Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
Частица массой m 1 действует с силой
F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
F 12 = (-G м 1 м 2 /r 12 2 )
( р 12 / р 12 ).
Здесь r 12 — расстояние между частицами 1
и 2, и ( r 12 /r 12 ) является
Единичный вектор , указывающий от частицы 1 к частице
2.
G — гравитационная постоянная, G = 6,67*10 -11 Нм 2 /кг 2 .
Сила F 21 , действующая на частицу массой m 2 действует на частицу массой m 1 , равно — F 12 , по третьему закону Ньютона. Сила тяжести всегда привлекательный.
Точка в объекте, от которой расстояние r 12 равно
измеряется его центр масс. Масса m 1 притягивает массу m 2 ,
и масса m 2 тянет за собой массу m 1 . Центр
масса каждого тела притягивается к центру масс другого
объект.
Центр
масса каждого тела притягивается к центру масс другого
объект.
Взвешивание земли
Радиус Земли R = 6368 км. Если вы подниметесь на гору высотой 1000 м,
ваше расстояние от центра земли изменится на (1/6368) * 100 % = 0,016 %
а величина гравитационной силы, действующей на вас, изменится на (1/6368) 2 *100
% = 2,4*10 -6 %. Для всех объектов вблизи поверхности земли
расстояние от центра почти постоянно, а величина
Поэтому вектор гравитационной силы приблизительно постоянен. За малым
расстояния, когда кривизной земной поверхности можно пренебречь,
направление вектора гравитационной силы также почти постоянно. Это указывает
прямо вниз к центру земли.
Сила тяжести, действующая на тело массой m на поверхности земли, равна
величина F = мг. Используя закон всемирного тяготения Ньютона, мы пишем GMm/R 2 =
мг, где М — масса Земли. Таким образом, мы имеем M = gR 2 /G.
Используя R = 6,4*10 6 м, находим M = (9,8 м/с 2 )(6,4*10 6 м) 2 /(6,67*10 -11 Н·м 2 /кг 2 ) =
6*10 24 кг.
Орбитальный
Гравитационное притяжение между объектом и землей притягивает объект к центру земли. Когда объект вращается вокруг Земли, направление силы тяжести на объекте постоянно меняется. радиус Земли настолько велик, что Земля кажется в некоторых местах плоской наблюдатель, стоящий на поверхности. Когда проблема касается только расстояний, которые намного меньше радиуса Земли, мы часто пренебрегаем кривизной земной поверхности и предположим, что сила гравитации направлена в одну и ту же направление вниз везде.
Ссылка: Спутник как снаряд
Предположим, что вблизи поверхности земли в
x-направление, как показано на рисунке выше. Первоначально он ускоряется только в
Y-направление. Но по мере движения объекта направление ускорения
изменения. Если начальная скорость объектов достаточно высока, мы должны принять
изменение направления силы учитывать при расчете объектов
траектория. Объект на круговой орбите вокруг Земли находится
постоянно падает к центру земли. Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Сила тяжести всегда направлена к центру объекта. круговой орбите и отвечает за центростремительное ускорение объект.
F = mv 2 /r
Для объекта вблизи поверхности земли F = mg и r = 6,4*10 6 м. Скорость орбитального объекта находится из mg = mv 2 /r, v 2 = gr = (9,8 м/с 2 )(6,4*10 6 м). У нас v = 7919 м/с, или примерно 8000 м/с. Требуется объект t = 2πr/v = (6,28*6,4*10 6 м)/(7919 м/с) = 5075 с = 84 мин, чтобы совершить полный оборот по орбите.
Если тот же объект двигался по круговой орбите с большим радиусом, сила
силы тяжести на объекте будет меньше. Поскольку мы удваиваем расстояние от
центра земли сила тяжести уменьшается в 1/4 раза.
центростремительное ускорение v 2 /r уменьшается в 1/4 раза. Этот
означает, что v 2 должен уменьшиться в ½ раза. Имеем v = 5600 м/с
а для совершения оборота по орбите требуется 14355 с = 240 мин.
Этот
означает, что v 2 должен уменьшиться в ½ раза. Имеем v = 5600 м/с
а для совершения оборота по орбите требуется 14355 с = 240 мин.
Объектов на геосинхронных орбитах совершить полный оборот за 24 часа или 86400 с. Следовательно, их скорость равна v = 2πr/(86400 с). Запись GMm/r 2 = mv 2 /r = m(2πr/(86400 с)) 2 /r, или r 3 = GM(86400s) 2 /(4π). мы можем решить это уравнение для радиуса геосинхронной орбиты. При М = 6*10 24 кг имеем r=42260 км. Геосинхронный спутник вращается вокруг 42260 км — 6400 км = 35860 км над поверхностью земли. Радиус его орбиты в 6,6 раза больше радиуса Земли.
Луна делает один оборот вокруг Земли за 27,3 дня. Мы можем найти расстояние до Луну таким же образом мы нашли расстояние до геосинхронного спутника. Расстояние от Земли до Луны 384400 км.
Проблема:
Когда падающий метеор находится на расстоянии над земной поверхностью в 3 раза больше Радиус Земли, каково ускорение ее свободного падения под действием силы тяжести приложенная к нему сила?
Решение:
- Обоснование:
Сила, действующая на метеор, равна F = ma = GMm/r 2 .



 Рассмотрим случай, когда два тела совершают круговые движения, но связаны ременной или зубчатой передачей
Рассмотрим случай, когда два тела совершают круговые движения, но связаны ременной или зубчатой передачей к. ац направлено к центру окружности, а ат — по касательной ( если разгон, то по направлению скорости, если торможение, то в противоположную сторону).
к. ац направлено к центру окружности, а ат — по касательной ( если разгон, то по направлению скорости, если торможение, то в противоположную сторону).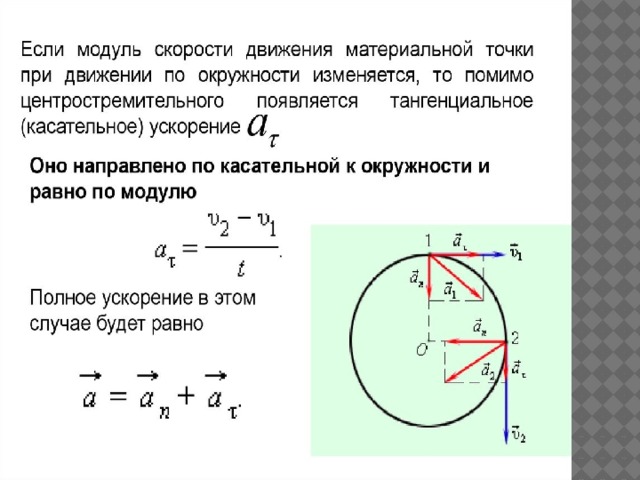
 Этот
сила F отвечает за центростремительное ускорение,
F = мв 2 /р.
Этот
сила F отвечает за центростремительное ускорение,
F = мв 2 /р.