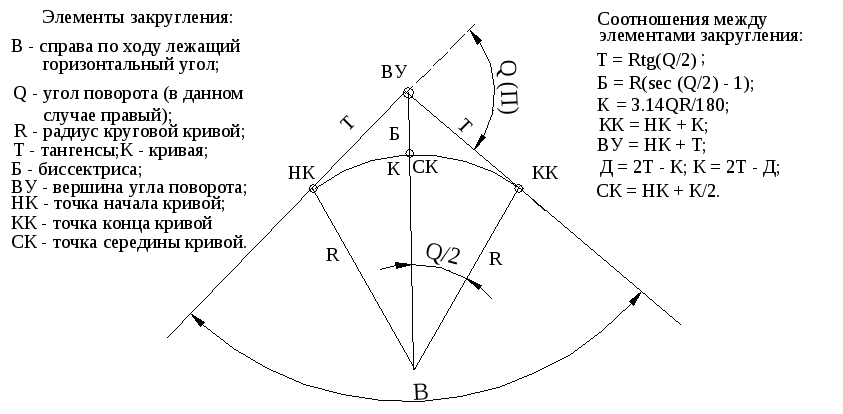
Как найти угол поворота формула: Угловое перемещение (угол поворота)
Угловое ускорение блока формула
Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.
Основные понятия
Угловое ускорение – величина, характеризующая изменение скорости с течением времени.
Пусть рассматриваемый промежуток времени это: Δ t = t 1 — t , а изменение угловой скорости составит Δ ω = ω 1 — ω , тогда числовое значение среднего углового ускорения за тот же интервал времени: » open=» ε = ∆ ω ∆ t = ε . Перейдем к пределу, когда Δ t > 0 , тогда формула углового ускорения будет иметь вид: ε = l i m ∆ t → 0 ∆ ω ∆ t = d ω d t = d 2 φ d t = ω ˙ = φ ¨ .
Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.
Размерность углового ускорения 1 T 2 (т.е. 1 в р е м я 2 ). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается р а д / с 2 или иначе: 1 с 2 ( с — 2 ) .
Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.
Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.
В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.
Рисунок 1 . Вектор углового ускорения
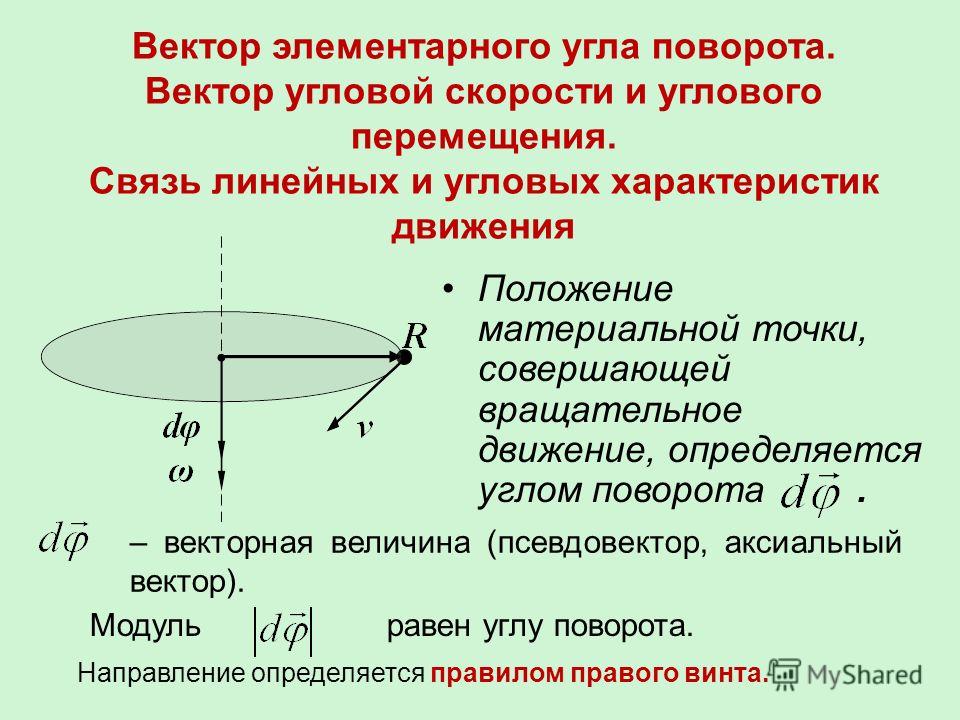
Если мы представим угловое ускорение как вектор ε → = d ω → d t , имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε → и ω → совпадут по направлениям (левая часть
рисунка 1 ) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка 1 ).
Закон равнопеременного вращения
Равнопеременное вращение
– вращение, при котором угловое ускорение во все время движения является постоянным ( ε = c o n s t ) .Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t 0 угол вращения равен ϕ = ϕ 0 ; угловая скорость — ω = ω 0 (т.е. ω 0 является начальной угловой скоростью).
Пусть в начальный момент времени t 0 угол вращения равен ϕ = ϕ 0 ; угловая скорость — ω = ω 0 (т.е. ω 0 является начальной угловой скоростью).
Выражение ε = d ω d t = ω ˙ = φ ¨ дает нам возможность сделать запись: d ω = ε d t . Проинтегрируем левую часть крайней записи в пределах от ω 0 до ω , а правую – в пределах от 0 до t , тогда:
ω = ω 0 + ε t , d φ = ω 0 d t + ε t d t .
Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:
Закон равнопеременного вращения: φ = φ 0 + ω t + ε t 2 2 .
Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.
Вращение является равнозамедленным, когда ω и ε противоположны по знаку.
Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R , тогда: α r = ε R . Нормальное ускорение имеет также связь с угловым: a n = ω 2 R . Учтем это выражение и для полного ускорения получим: a = a r 2 + a n 2 = R ε 2 + ω 4 Для равнопеременного движения: ω = ε t ; a n = ω 2 R = ε 2 t 2 R и a = R ε 2 + ε 4 t 4 = R ε 1 + ε 2 t 4 .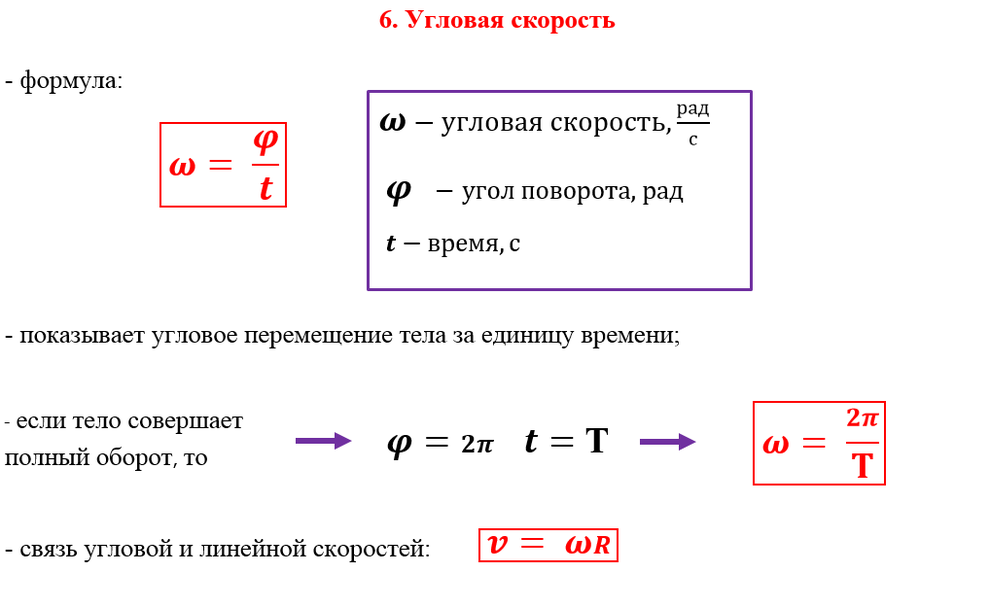
Практические примеры
На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.
Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки 2 . 1 . и 2 . 3 . показывают направление псевдовектора вверх, а рисунки 2 . 2 . и 2 . 4 . – вниз.
Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки 2 . 1 . и 2 . 4 . ). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2 . 2 . и 2 . 3 . ). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом R . При этом выражение ϕ = α t 3 отражает зависимость угла поворота от времени. Необходимо найти полное ускорение заданной точки как функцию времени.
Необходимо найти полное ускорение заданной точки как функцию времени.
Запишем выражения для угловой скорости и углового ускорения заданной точки:
ω = d φ d t = 3 α t 2 ; ε = 6 α t .
Полное ускорение запишем как:
a = a r 2 + a n 2 = R ε 2 + ω 4 = R 36 a 2 t 2 + 81 a 4 t 8 = 3 a t R 4 + 9 a 2 t 6 .
Угловое ускорение
.
Угловое ускорение характеризует силу изменения модуля и направления угловой скорости при движении твердого тела.
Ускорение точки твердого тела при свободном движении.
К понятию углового ускорения можно прийти, изучая определение ускорения точки твердого тела, находящегося в свободном движении. Определение скорости точки тела В (по формуле Эйлера) в свободном движении:
.
где — скорость точки тела А, которая была принята как полюс; — псевдовектор угловой скорости тела; — вектор, который был выпущен из полюса в точку – его скорость определяем. Продифференцировав это выражение по времени данное выражение, получаем:
Продифференцировав это выражение по времени данное выражение, получаем:
.
где — является ускорением полюса А; — псевдовектором углового ускорения.
Составляющая ускорения точки В, которая определяется через угловое ускорение называется вращательным ускорением точки В около полюса А.
.
Последнее слагаемое в полученной формуле, которое зависит от угловой скорости, называется осестремительным ускорением точки В вокруг полюса А.
.
Угловое ускорение при вращении тела вокруг неподвижной оси.
Когда происходит вращение тела около неподвижной оси, которая проходит через недвижимые точки тела О1 и О2, производные орта оси вращения = 0:
.
Отсюда вектор углового ускорения вычисляется тривиально через вторую производную угла поворота
или .
где — это алгебраическая величина углового ускорения.
Здесь
,
значит, вектор углового ускорения и вектор угловой скорости имеют одинаковое направление и тело имеет ускоренное вращение. Иначе, при , векторы угловой скорости и углового ускорения имеют противоположные направления, а, значит, тело вращается замедленно.
В теормехе обычно вводится понятие угловой скорости и углового ускорения, когда рассматривается вращение тела вокруг не двигающейся оси. При чем, для решения задачи используют зависимость от времени угла поворота тела
Отсюда закон движения точки тела можно выразить натурально, как длина дуги окружности, которую прошла точка, совершая поворот тела от определенного исходного положения φ = φ (t)
где R является расстоянием от точки до оси вращения.
Продифференцировав вышеуказанное выражение по времени, найдем алгебраическую скорость точки:
.
где является алгебраической величиной скорости угловой.
Через геометрическую сумму тангенциального и нормального ускорения можно выразить ускорение точки тела при вращении:
.
При этом тангенциальное ускорение выходит в виде производной от алгебраической скорости точки:
.
где является алгебраической величиной углового ускорения. А при помощи ниже приведенной формулы определим нормальное ускорение точки тела:
.
В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.
За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.
Угловое перемещение
Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:
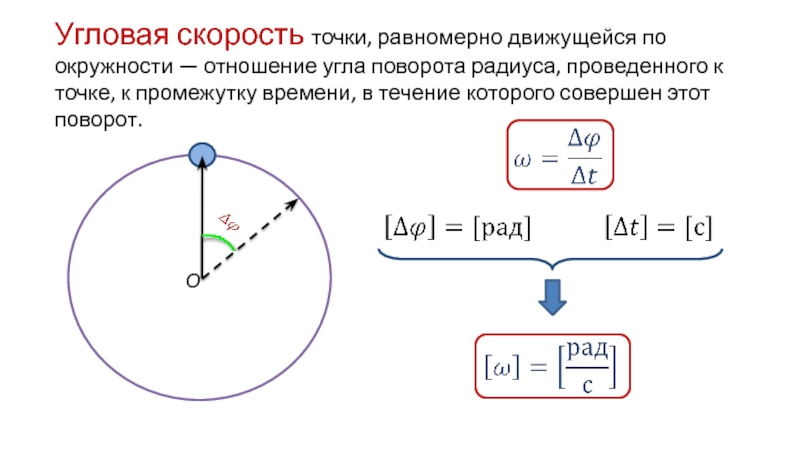
Угловая скорость и угловое ускорение
Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.
Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.
Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.
Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с 2 .
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.
Равномерное вращательное движение
Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями:
Равноускоренное вращательное движение
Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω+ εt, φ = φ + ωt + εt 2 /2.
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑц = v 2 /R = (ωR) 2 /R = ω 2 R.
Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑt = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.
Момент сил
Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.
Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M1 + M2 + …+ Mn.
Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R 2 mβ, β= M/mR 2 = M/I, где I = mR 2 — момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.
Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.
Примеры решения задач
Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.
Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω — εt.
Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω/t = 2πn/t.
Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).
Угол поворота ротора центрифуги за время t будет: φ(t)= φ + ωt + εt 2 /2. Учитывая выражение для углового ускорения и то, что φ = 0, находим: φ(t)= ωt/2 = πnt.
Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).
Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.
Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.
Найдем тормозной момент сил, действующий на диск: M = RF.
Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.
Найдем время, за которое диск остановится: t = ω/ε, где ω — начальная угловая скорость диска, которая равна 2πv.
Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).
Ответ: время остановки равно 2,5 с.
Тригонометрические функции произвольного угла с примерами решения
Содержание:
Тригонометрические функции произвольного углаУгол поворотаДо недавнего времени говоря об угле мы имели в виду угол, полученный между двумя неподвижными сторонами. Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
Начальное положение луча соответствует одной стороне угла, конечное положение — другой стороне. При вращении луча на координатной плоскости относительно начала координат в направлении по часовой стрелке или против часовой стрелки, можно получить различные углы.
Начальная сторона угла поворота совпадает с положительным направлением оси абсцисс. Сторону, полученную при вращении относительно начала координат (вершины угла), назовём конечной стороной. Принято считать, что если поворот происходит в направлении против часовой стрелки, то угол имеет положительное значение, при повороте в направлении по часовой стрелке, угол имеет отрицательное значение,
положительный угол отрицательный угол
Координатные оси разбивают координатную плоскость на 4 четверти. Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
Конечная сторона угла может совершить один или несколько оборотов относительно начала координат. Один полный оборот соответствует углу 360°. Существует бесконечное число углов поворота, у которых начальная и конечная стороны совпадают. Например, конечные стороны углов 30°и 390° совпадают. В общем, для углов поворота и (здесь произвольное целое число) конечные стороны совпадают.
Пример 1. Нарисуйте угол заданной величины. Определите какой четверти принадлежит конечная сторона угла.
Пример 2. На координатной плоскости покажите и запишите градусные меры двух положительных и одного отрицательного угла поворота, конечные стороны которых совпадают с конечной стороной угла 60°.
Радианное измерение угловУгол в один радиан-это центральный угол, у которого длина дуги равна радиусу. Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: . Величина угла, выраженная в радианах не зависит от длины радиуса (объясните, воспользуясь подобием фигур на рисунке).
Пример 1. Сколько радиан составляет центральный угол, длина дуги которого равна 12 см, если радиус окружности равен 4 см?
Решение: 1 радиан соответствует длине дуги 4 см. Дуге длиной 12 см будет соответствовать угол 12 : 4 = 3 радиан. Длина окружности . Если центральный угол, соответствующий дуге окружности радиуса равен 1 радиану, то дуге, равной; соответствует центральный угол . Ниже показаны радианные меры углов поворота.
Длина окружности . Если центральный угол, соответствующий дуге окружности радиуса равен 1 радиану, то дуге, равной; соответствует центральный угол . Ниже показаны радианные меры углов поворота.
Радианная мера одного целого оборота равна , градусная мера 360°. То есть, радиан = 360°. Отсюда можно установить следующую связь между радианной и градусной мерой. Преобразование радиан в градусы:
Преобразование градусов в радианы:
Таким образом, рад = 180°. Обозначение «рад’ часто опускают. Вместо рад = 180° обычно пишут = 180°. Отсюда получаем, что
Используя соответствующие радианные и градусные меры углов, расположенных в первой четверти, можно найти увеличенные в разы значения других углов. Например, если 30° = , тогда 150° =
Пример 2. Выразите углы, заданные в градусах радианами, а углы, заданные радианами в градусах, а) 60° ; б)
Решение.
а)60° = радиан — радиан 1,047 радиан
б) радиан
Пример 3. Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
Решение: Конечная сторона угла 45°совпадает с углами 405° и 315°, а также существует бесконечно много углов, конечные стороны которых совпадают с конечной стороной угла 45°: ;
,
или,
.
В радианах это можно записать как
и т.д. Все углы, конечные стороны которых совпадают с углом в общем виде записываются так:
Пример, а)
Все углы поворота, конечные стороны которых совпадают с углом
можно найти но формуле .
Как видно, в заданном интервале, расположен всего один угол 425°. Пример. д) Все углы поворота, конечные стороны которых, совпадают с этим углом можно найти по формуле .
Интервалу принадлежат углы
Длина дугиЗапишем формулу нахождения длины дуги, соответствующей центральному углу окружности радиуса . Используя радианную меру длину окружности можно найти ещё проще. По определению радиана, если , тогда длина дуги равна произведению радиуса и радианной меры угла: Длина дуги окружности находится с радиусом в прямо пропорциональной зависимости.
По определению радиана, если , тогда длина дуги равна произведению радиуса и радианной меры угла: Длина дуги окружности находится с радиусом в прямо пропорциональной зависимости.
Центральному углу соответствует сектор площадь которого равна . Учитывая что радиальная мера центрального угла равна и обозначив её через , запишем формулу нахождения площади сектора . Пример 1. Длина секундной стрелки часов равна 12 см. Определите длину дуги, которую описывает конец секундной стрелки за 15 секунд.
Решение. Секундная стрелка за 60 минут совершают один полный оборот. Это соответствует радианам. 15 секунд соответствуют части полного оборота: радиан. То есть, минутная стрелка за 15 секунд чертит дугу, соответствующую центральному углу . Длина этой дуги:
Пример 2. Найдите площадь и периметр закрашенного сектора на рисунке, если радиус круга равен 8 см. Закрашенной части круга соответствует центральный угол:
Площадь сектора равна:
(см2).
Периметр сектора равен сумме длин двух радиусов и длины дуги: (см)
Линейная скорость и угловая скоростьСкорость при движении по окружности, например, скорость движения произвольной точки Р колеса, которое вращается вокруг точки О, может быть вычислена двумя способами.
В первом случае, её можно найти используя расстояние и время. Эта скорость называется линейной скоростью. Во втором случае — используя угол поворота (центральный угол). Эта скорость называется угловой скоростью.
Если тело движется но окружности, то линейная скорость равна отношению пройденного пути (длины дуги окружности) к промежутку времени.
Если тело движется по окружности, то угловая скорость равна отношению угла поворота к промежутку времени.
Здесь (в радианах) — угол вращения за промежуток времени . Между линейной и угловой скоростью существует следующая связь:
линейная скорость = угловая скорость
Пример 3. Карусель совершает за минуту 8 полных оборотов.
Карусель совершает за минуту 8 полных оборотов.
а)Чему равна угловая скорость карусели за минуту(в радианах)?
б)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 3 м от центра окружности?
в)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 2 м от центра окружности?
Решение:
а) Один целый оборот при вращении соответствует центральному углу . За 8 оборотов этот угол равен . Угловая скорость за минуту равна радиан/мин.
б)Если лошадь находится на расстоянии 3 м от центра, то она движется по окружности радиуса 3 м.
Линейная скорость:м/мин
в)Если лошадь находится на расстоянии 2 м от центра, то она движется по окружности радиуса 2 м.
Линейная скорость:м/мин
Тригонометрические функцииТригонометрические отношении для угла зависят только от значения угла.
Пусть конечная сторона угла а при повороте пересекается с окружностью радиусом г, центр которой находится в начале координат, в точке Р(х; у).
Отношение ординаты точки Р к длине радиуса называется синусом угла :
Отношение абсциссы точки Р к длине радиуса называется косинусом угла :
Отношение ординаты точки Р к абсциссе называется тангенсом угла :
(здесь , то есть точка Р не расположена на оси ординат)
Отношение абсциссы точки Р к ординате называется котангенсом угла : (здесь , то есть точка Р не расположена на оси абсцисс)
Косинусом угла называется обратное значение для синуса:
(здесь )
Секансом угла называется обратное значение для косинуса:
(здесь )
Пример 1. Точка А (- 3; 4) расположена на конечной стороне угла поворота .
а) Изобразите решение примера.
б) Определите значения тригонометрических отношений для угла поворота .
Решение:
а)
б)
Координаты точки на окружности
Если заданная точка Р окружности находится на конечной стороне угла поворота , то она имеет координаты .
Пример 2. По данным рисунка найдите координаты точки Р.
Точка Р находится во II четверти и косинус отрицательный.
Для некоторых углов, конечная сторона расположена на одной из координатной оси. В этом случае, градусная мера угла поворота равна: или радиан, или радиан, или радиан, или радиан.
В этом случае координаты х или у равны или нулю, или абсолютному значению длины радиуса.
Пример 3. Найдём значения тригонометрических отношений для:
а) а = 90° ; б) а = 180°; в) а = 270° .
При всех допустимых значениях, каждому значению , соответствует единственное значение . Поэтому тригонометрические отношения являются функциями угла и называются тригонометрическими функциями.
Так как , то знак косинуса совпадает со знаком х.
Так как , то знак синуса совпадает со знаком у.
Тригонометрические функции произвольного угла. Нахождение значений тригонометрических функций произвольного угла при помощи острого угла
Нахождение значений тригонометрических функций произвольного угла при помощи острого углаЧтобы вычислить тригонометрические отношения для углов больше 90°, удобно использовать тригонометрические отношения острого угла.
Для любого угла поворота существует образованный конечной стороной и прямой, содержащий ось абсцисс.
Используя соответствующие острые углы можно определить тригонометрические отношения для любого произвольного угла. Эти значения можно вычислить точно для углов 30°, 45°, 60°, а для остальных острых углов — при помощи калькулятора.
Пример 1. Для следующих углов, определите острые углы:
а) б)
Решение:
а) конечная сторона угла 300° расположена в IV четверти. Соответствующий острый угол равен: 360°- 300° = 60°
б) конечная сторона угла расположена в III четверти. Соответствующий
острый угол равен:
Пример 2. Найдём значение основных тригонометрических функций для угла . Шаги решения:
Шаги решения:
1.Найдём наименьший положительный угол, конечная сторона которого совпадает с заданным углом и дополняет его до 360°: -135° + 360° = 225°
2.Для угла 225° найдём соответствующий острый угол 225° — 180° = 45°.
3.Определим какой четверти принадлежит угол -135° — угол III четверти.
4.Найдём значение тригонометрических функций для угла 45° и учтём знак этих функций в III четверти. Получим:
Тригонометрические функции для произвольного угла можно определить следующим образом:
•определяем соответствующий острый угол;
•находим значение тригонометрических функций для этого угла;
•определяем знак значения тригонометрических функций в зависимости от четверти.
Так как конечные стороны углов и совпадают, то значения тригонометрических функций этих углов одинаковы. Если угол изменяется на целое число оборотов, то значение тригонометрических функций не меняется.
Заметим, что если угол меняется на пол оборота, то значения тангенса и котангенса не изменяются.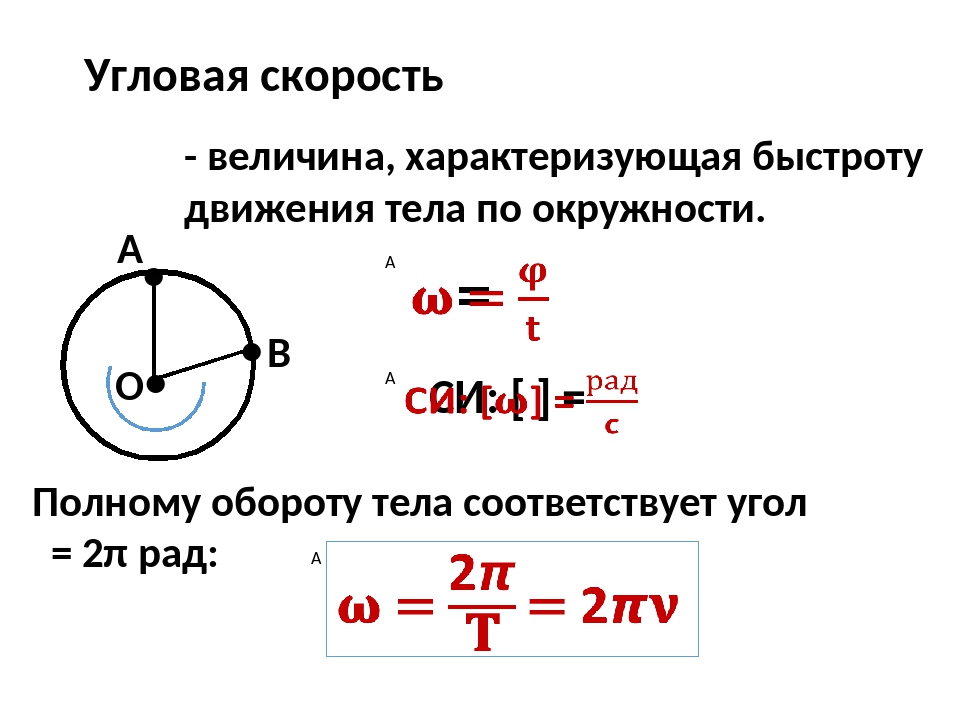
На самом деле, если углу поворота соответствует точка , а углу поворота (или ) соответствует точка , то :
В общем случае выполняются равенство:
Пример 3. Найдём допустимые значения , если . Так как в I и во II четвертях синус положителен.
, значит если , то
Абсцисса этой точки
Тогда или
Единичная окружность и тригонометрические функцииЗначения тригонометрических функций зависят только от значения угла и не зависят от радиуса окружности. Поэтому, не нарушая общности, можно принять . Окружность, центр которой находится в начале координат, с радиусом равным единице, называется единичной окружностью. Координаты точки, принадлежащей окружности удовлетворяют уравнению .
Если точка является точкой пересечения единичной окружности и конечной стороны угла поворота , то между ней и тригонометрическими функциями существует следующая связь: Таким образом, координаты точки принадлежащей единичной окружности, можно записать как: .
Также по заданным координатам можно найти следующие тригонометрические функции: . Зная, что при определённом повороте на единичной окружности, можно найти соответствующие координаты точки.
Для этого надо выполнить следующие шаги:
1) На единичной окружности отметим точки, соотвегствующие углу поворота , найдём координаты этих точек по формуле: .
2)Для некоторой точки, принадлежащей единичной окружности, например ,определите координаты симметричной точки. Как видно но рисунку, существует 3 точки, симметричные точке А, которые расположены во II, III и IV четвертях.
Точка В симметрична точке А относительно оси у, точка С — относительно начала координат, а точка D — относительно оси х. Абсолютные значения координат этих точек равны и отличаются только знаком.
3)Таким образом, можно определить координаты новых точек, зная координаты точки, принадлежащей I четверти. Т.е. получаем единичную окружность, на которой отмечены углы поворота и координаты точек.
Так как координаты точек на единичной окружности удовлетворяют условиям , то Наибольшее значение и равно 1, а наименьшее значение равно -1.
Пример 1. Для угла поворота вычислите значения основных тригонометрических функций.
Решение: Конечная сторона угла поворота расположена в III четверти. Этому углу соответствует острый угол . Точка пересечения конечной стороны угла с единичной окружностью симметрична точке относительно начала координат и соответствует точке .
Тогда ,
Пример 2. Точка А, с абсциссой расположена в III четверти и пересекается с единичной окружностью на стороне угла .
а)Найдём ординату точки А.
б)Изобразим рисунок, соответствующий условию и для угла найдём значения шести тригонометрических функций.
Решение:
а), . Так как точка расположена в III четверти .
Так как точка расположена в III четверти .
б),,,,
,.
Пример 3. Найдём наибольшее и наименьшее значение выражения .
Решение:
Таким образом, для выражения a НМЗ равно 1, а НБЗ равно 5.
Формулы приведенияЕсли объект находится в I четверти, то симметричный ему относительно оси у объект находится во II четверти. Симметричный последнему относительно оси х, объект находится в III четверти, и он совпадает с объектом, симметричным начальному объекту из I относительно начала координат. Обратите внимание, что отображение относительно оси у и отображение, относительно оси х, совпадают с поворотом на 180°.
При отображении относительно оси х, точка расположенная на конечной стороне угла изменяет координаты, как показано на рисунке.
То есть, при этом знак меняет только координата у. Таким образом, так как косинус зависит от х он не меняется, зато меняется знак синуса. Отсюда, для углов можно записать следующие зависимости между тригонометрическими функциями.
Отсюда, для углов можно записать следующие зависимости между тригонометрическими функциями.
То есть, синус, тангенс и котангенс нечётные функции, косинус-чётная.
Пример 1:
Конечные стороны углов поворота и 360° — симметричны относительно оси х. То есть .
Отсюда получаем:
Запишем для углов и 90° — прямоугольного треугольника с острым углом тригонометрические отношения:
При попарном сравнении равенств можно увидеть следующую связь-между значениями тригонометрических функций углов и 90° — .
Повернём конечную сторону угла поворота ещё на 90°. При этом точка Р(х; у), расположенная на стороне преобразуется в точку . По определению тригонометрических функций:
Запишем эти формулы в следующем виде:
Как видно но рисунку отображения относительно оси у и оси х эквивалентны повороту на 180°. Изменение координат, можно записать следующим образом:
Как видно по рисунку, при повороте угла а на 180° конечная сторона расположена в противоположных четвертях, но на одной прямой.
Пример 2.
Для получения аналогичных формул тригонометрических функций угла поворота достаточно записать и применить последовательность соответствующих формул.
Например:
Теперь запишем соответствующие формулы для угла поворота . Например:
При помощи полученных формул можно найти значения тригонометрических функций произвольного угла, зная значения для соответствующего острого угла. Эти формулы называются формулами приведения. Для формул приведений можно легко увидеть следующую закономерность
1)Если аргумент имеет вид или , то функция преобразуется в «сопряжённую» функцию (то есть синус в косинус или наоборот, а тангенс в котангенс или наоборот) угла .
2)Если аргумент имеет вид 180° ± или 360° ± , то функция преобразуется в одноимённую функцию угла .
В каждом из обоих случаев, знак полученной в результате преобразования функции имеет одинаковое значение со знаком острого угла в соответствующей четверти.
Для острого угла прямоугольного треугольника покажите, что , выполнив следующие шаги:
1)Запишите теорему Пифагора:
2)Каждую из сторон равенства разделите на с2:
3)Примените свойство степени:
4) Примите во внимание, что:
Связь между тригонометрическими функциями одного и того же углаТождество можно доказать и при помощи координат точки, принадлежащей единичной окружности.
По координатам точки на единичной окружности и по определениям тригонометрических функций имеем:
Для всех значений , при которых
Для всех значений , при которых
Из данных равенств имеем,что если для угла одновременно выполняются условия и , то справедливо тождество
Разделив обе чаете равенства поочередно на и на будем иметь:
Полученные выше равенства являются тождествами. Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать:
На основании основных тригонометрических можно написать:
При помощи основных тригонометрических тождеств можно упрощать тригонометрические выражения и вычислять модуль значения всех остальных функций, зная значение одной из них.
Пример 1. Используя основные тригонометрические тождества, докажите,что:
Доказательство:
Пример 2. Зная, что и угол принадлежит III четверти, найдите
остальные тригонометрические функции.
Из формул получаем:
Так как угол принадлежит III четверти, то
Тогда:
Формулы сложенияПрактическая работа .
1)Покажем по шагам, равенство выражения
a)Для значений и, вычислим значения выражения в левой части.
б)Для значений и, вычислим значения выражения в правой части.
2)Как можно вычислить значение тригонометрических функций для угла 15°, используя разность значений углов 45° и 30°(15° = 45° — 30°)?
Тригонометрические функции суммы и разности двух углов. Сначала докажем тождество
Сначала докажем тождество
На рисунке
а)для угла координаты точки Р1, взятой на единичной окружности равны , а для угла координаты точки Р2 равны . Разместим углы — , как показано на рисунке б).
Тогда, для угла координаты точки Рз будут . Из того, что (по признаку СУС ) следует, что .
Доказательство тождества
учитывая, что
справедливость тождества доказана.
Доказательство тождества
no формулам приведения группируя
no формуле косинуса разности с учётом формул приведения.
Доказательство тождества :
Пример 1. Найдём значение выражения если
Решение.
Пример 2.
Найдём значение выражения если
.
Решение.
Известно что . Если углу соответствует острый угол , то . Так как противолежащий катет равен 3, а гипотенуза 5, тогда прилежащий катет равен и учитывая, что угол III четверти, получим:.
Так как противолежащий катет равен 3, а гипотенуза 5, тогда прилежащий катет равен и учитывая, что угол III четверти, получим:.
Аналогично, если зная, что , получаем,
что .
Можно записать формулы сложения для тангенса и котангенса:
no определению no формулам сложения
Аналогичным образом можно показать, что :
Следствия из формул сложенияПрактическая работа.
Преобразуйте сумму в произведение, выполнив следующие шаги:
1)
решив систему уравнений найдите такие углы, чтобы их сумма была равна 70°, а разность
2)Запишите следующее 70° = 40° + 30°, 10° = 40° — 30° и упростите
Преобразование суммы(разности) в произведениеФормулы преобразования произведенияСправедливость данных тождеств можно показать при помощи формул сложения:
почленно складываем почленно складываем
Следующее тождество можно доказать аналогичным образом.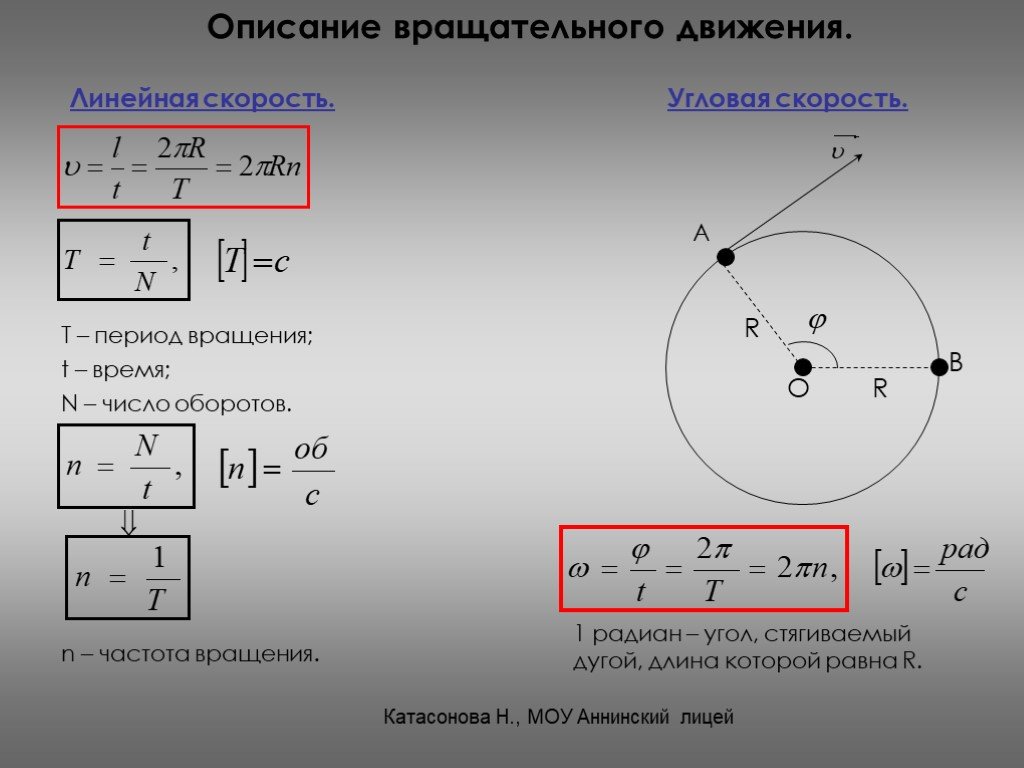
Формулы сложения позволяют выразить через тригонометрические функции угла .
Таким образом, получаем тождества, которые называются формулами двойного аргумента:
Формулы половинного аргументаИмеем, что
Отсюда: Заменяем в данной формуле на получаем:
Для половинных аргументов справедливы тождества. Знак в правой части в данном равенстве зависит от того, в какой четверги находится угол .
Пример 1. Упростим выражение .
Решение.
Пример 2. He используя калькулятор, вычислим значения и , зная, что угол принадлежит IV четверти и
Решение.
Пример 3. Найдём значений .
Решение:
Используем формулу половинного аргумента
угол I четверти и в этой четверти косинус положителен.
Пример 1. Раскроем скобки и упростим выражение.
Пример 2. Разложим на множители и упростим выражение.
Пример 3. Упростим рациональное выражение, содержащее тригонометрические функции.
Пример 4. Освободим знаменатель от радикала
Здесь .
Определить угол поворота и прогиб сечения В консольной балки
Пример задачи 5.15
Определить угол поворота и прогиб сечения В консольной балки (в долях от жесткости сечения ), рис. 5.28.
Решение
Эпюра изгибающих моментов от заданной нагрузки (грузовая эпюра ) показана на рис. 5.28, а.
Для определения прогиба в сечении В к свободной от заданной нагрузки балке (вспомогательное состояние) в названном сечении прикладывается вспомогательная единичная сосредоточенная сила (F = 1) и строится эпюра изгибающих моментов — единичная эпюра (рис. 5.28, б). Единичная сила направляется произвольно, т. е. в положительном или отрицательном направлении оси У.
5.28, б). Единичная сила направляется произвольно, т. е. в положительном или отрицательном направлении оси У.
Аналогичная операция производится для определения угла поворота сечения. Только в качестве вспомогательной единичной силы выступает единичный вспомогательный момент (М = 1), направляемый произвольно относительно оси X. Эпюра от единичного момента показана на рис. 5.28, в.
На рис. 5.28, б и в схема балки и единичные эпюры совмещены. Заметим, что балка имеет один расчетный участок как для ,
так для и что единичные эпюры прямолинейны и имеют вид треугольника или прямоугольника, а грузовая — криволинейна и имеет сложное очертание.
Для определения перемещений по способу Верещагина используются эпюры изгибающих моментов (грузовые и единичные). От одних из них берутся площади эпюр (), из других — ординаты (у) под центром тяжести первых. Поскольку грузовая эпюра имеет криволинейное очертание, площадь должна браться с этой эпюры.
Поскольку грузовая эпюра имеет криволинейное очертание, площадь должна браться с этой эпюры.
Для проведения расчета эпюра сложного очертания делится на простые фигуры: прямоугольник (от момента М) площадью
и параболический треугольник (от нагрузки q) площадью
На выделенных простых фигурах отмечаются их центры тяжести (см. табл. 5.1).
На единичных эпюрах отмечаются ординаты у, лежащие под центром тяжести составляющих частей грузовой эпюры . В данном примере ордината определяется как
Для определения углов поворота сечений ординаты берутся из единичной эпюры :
Прогиб в сечении В по формуле (5.12):
Все слагаемые в выражении прогибов положительны, так как площади и ординаты у лежат по одну сторону от оси эпюры. Положительные значения означают, что прогиб происходит в направлении единичной силы, т. е. вниз.
е. вниз.
Угол поворота сечения В
В полученном выражении слагаемые отрицательны, так как площади и ординаты у лежат по разную сторону от оси эпюры. Отрицательное значение означает, что поворот сечения происходит в направлении, противоположном направлению единичного момента, т. е. по ходу часовой стрелки (рис. 5.28, г).
Эпюра прогибов показана на рис. 5.28, г.
Таким образом, перемещения на свободном конце балки (в долях от жесткости сечения) (по ходу часовой стрелки), (вниз).
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
Новые координаты по вращению осей Калькулятор
- Назначение
- сила вращения
- Комментарий/Запрос
7 Вращение угол назад.
 Перечисленные уравнения X, Y предназначены для вращения по часовой стрелке, но калькулятор говорит вам определить против часовой стрелки как положительное. Вектор (1,0), повернутый на +90 градусов против часовой стрелки, равен (0,1). Этот калькулятор покажет вам (0,-1) при повороте на +90 градусов и (0,1) при повороте на -90 градусов.
Перечисленные уравнения X, Y предназначены для вращения по часовой стрелке, но калькулятор говорит вам определить против часовой стрелки как положительное. Вектор (1,0), повернутый на +90 градусов против часовой стрелки, равен (0,1). Этот калькулятор покажет вам (0,-1) при повороте на +90 градусов и (0,1) при повороте на -90 градусов.
Вы должны использовать положительные углы или по часовой стрелке или отрицательные углы против часовой стрелки для правильного ответа (противоположное тому, что он говорит делать).
[1] 2021/11/19 04:51 30-летний уровень / Инженер / Немного /
- /04 07:52 20-летний уровень / Средняя школа/ Университет/ Аспирант / Полезное /
- Цель использования
- Помощь в выполнении домашних заданий.
[2] 2021/11/08 20:50 20-летний уровень / Высшая школа/ Университет/ Аспирант / Полезный /
- Цель использования
- Вращение точек карты.
[4] 2021/10/08 02:55 Младше 20 лет / Старшая школа/ Университет/ Аспирант / Полезно /
- Цель использования
- Это очень полезно, особенно при попытке выяснить степени координат.

[5] 2021/06/17 05:24 Младше 20 лет / Начальная школа/ Учащийся средней школы / Полезно /
- Цель использования
- Отличный помощник и простой в использовании. Помогли мне получить легкую пятерку по математике.
[6] 2021/04/30 23:07 Младше 20 лет / Начальная школа / Учащийся средней школы / Очень /
- Цель использования
- Задание IXL
- Комментарий/Запрос
- по умолчанию против часовой стрелки.чтобы сделать это по часовой стрелке, добавьте «-» к градусам.
[7] 2021/04/23 14:43 Младше 20 лет / Начальная школа/ Учащийся средней школы / Очень /
- Цель использования
- Я использую это, чтобы помочь мне быстрее понять геометрию. Хотя я бы рекомендовал вращение фигур на координатной плоскости.
[8] 2021/03/29 01:23 Младше 20 лет / Начальная школа / Учащийся средней школы / Полезно /
- Цель использования
- домашнее задание
- Комментарий/Запрос
- пожалуйста, добавьте параметр против часовой стрелки
[9] 2021/03/26 05:17 Младше 20 лет / Начальная школа/ Учащийся средней школы / Полезно /
- Цель использования
- очень хорошо, помогло значительно поднять мою оценку во время раздел геометрии моего восьмого класса.

[10] 2021/03/10 02:26 — / Начальная школа/ Ученик младших классов средней школы / Очень /
CS184: Вычисление вращения в 3D
CS184: Вычисление вращения в 3D Заметки Лоры Даунс и Алекса БергаИспользование формулы Родригеса для вычисления оборотов
Предположим, мы поворачиваем точку p в пространстве на угол, b (позже также названный тета ) вокруг оси, проходящей через начало координат представлен единичным вектором a .
Сначала мы создаем матрицу A , которая представляет собой линейное преобразование, которое вычисляет векторное произведение вектора на с любым другим вектор, v .
| а х v = |
| = |
|

 Перечисленные уравнения X, Y предназначены для вращения по часовой стрелке, но калькулятор говорит вам определить против часовой стрелки как положительное. Вектор (1,0), повернутый на +90 градусов против часовой стрелки, равен (0,1). Этот калькулятор покажет вам (0,-1) при повороте на +90 градусов и (0,1) при повороте на -90 градусов.
Перечисленные уравнения X, Y предназначены для вращения по часовой стрелке, но калькулятор говорит вам определить против часовой стрелки как положительное. Вектор (1,0), повернутый на +90 градусов против часовой стрелки, равен (0,1). Этот калькулятор покажет вам (0,-1) при повороте на +90 градусов и (0,1) при повороте на -90 градусов.

 Компонент p параллельно , p par a , не изменится при преобразовании.
Компонент p перпендикулярно a , p per a будет вращаться вокруг оси в плоскости, перпендикулярной оси так же, как в 2D
Векторы p per a и p biper ar
правильной длины и ориентации, чтобы действовать как векторы x и y в этом двумерном вращении.
Компонент p параллельно , p par a , не изменится при преобразовании.
Компонент p перпендикулярно a , p per a будет вращаться вокруг оси в плоскости, перпендикулярной оси так же, как в 2D
Векторы p per a и p biper ar
правильной длины и ориентации, чтобы действовать как векторы x и y в этом двумерном вращении. 2 в
соответствующие места, мы получаем
2 в
соответствующие места, мы получаем
 Давайте узнаем о ротациях!
Давайте узнаем о ротациях! Вот фигура, повернутая на 90° по часовой стрелке и против часовой стрелки вокруг центральной точки.
Вот фигура, повернутая на 90° по часовой стрелке и против часовой стрелки вокруг центральной точки.
 Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C’:
Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C’: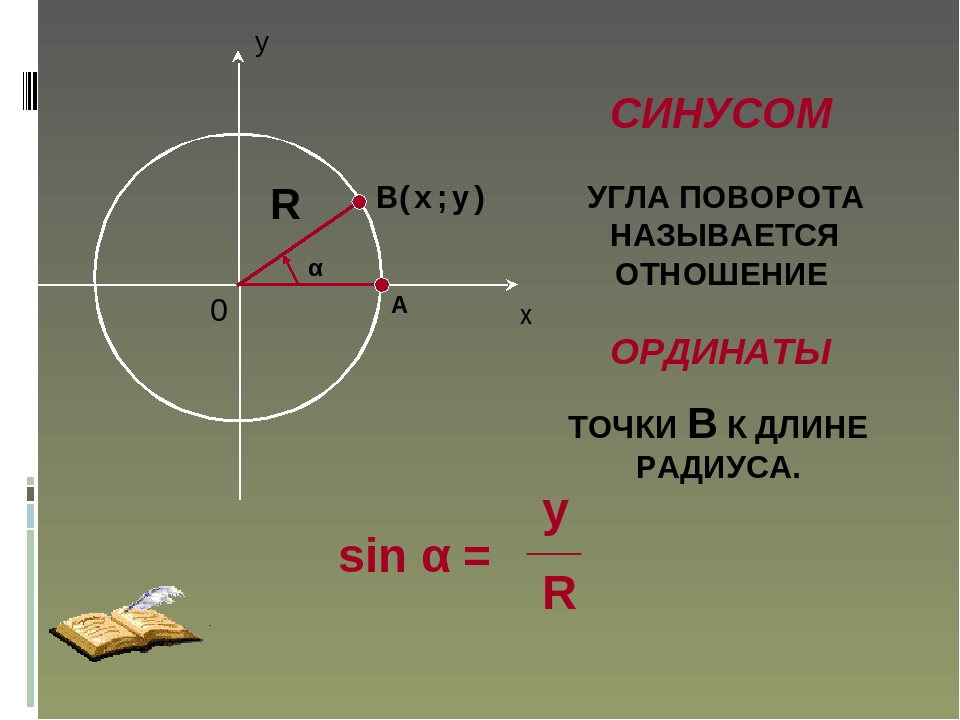 Воздушный змей KLMN показан на координатной сетке. Воздушный змей был повернут вокруг исходной точки, чтобы создать воздушный змей K’L’M’N’.Можете ли вы определить, какое вращение воздушного змея KLMN создало воздушный змей K’L’M’N’?
Воздушный змей KLMN показан на координатной сетке. Воздушный змей был повернут вокруг исходной точки, чтобы создать воздушный змей K’L’M’N’.Можете ли вы определить, какое вращение воздушного змея KLMN создало воздушный змей K’L’M’N’?
 Мы собираемся использовать (x,y) в (y,-x). Теперь применим правило к координатам вершин PQRS.
Мы собираемся использовать (x,y) в (y,-x). Теперь применим правило к координатам вершин PQRS. То, как мы разрезаем конус, будет определять тип конического сечения, образованного на пересечении. Круг образуется путем разрезания конуса плоскостью, перпендикулярной оси симметрии конуса. Эллипс образуется путем разрезания одного конуса наклонной плоскостью, не перпендикулярной оси симметрии.Парабола образуется путем разрезания плоскостью верхней или нижней части двойного конуса, тогда как гипербола образуется, когда плоскость пересекает верхнюю и нижнюю часть конуса. См. (Рисунок).
То, как мы разрезаем конус, будет определять тип конического сечения, образованного на пересечении. Круг образуется путем разрезания конуса плоскостью, перпендикулярной оси симметрии конуса. Эллипс образуется путем разрезания одного конуса наклонной плоскостью, не перпендикулярной оси симметрии.Парабола образуется путем разрезания плоскостью верхней или нижней части двойного конуса, тогда как гипербола образуется, когда плоскость пересекает верхнюю и нижнюю часть конуса. См. (Рисунок). В этом разделе мы сосредоточимся на общем уравнении формы, которое можно использовать для любой коники. Общая форма устанавливается равной нулю, а члены и коэффициенты даны в определенном порядке, как показано ниже.
В этом разделе мы сосредоточимся на общем уравнении формы, которое можно использовать для любой коники. Общая форма устанавливается равной нулю, а члены и коэффициенты даны в определенном порядке, как показано ниже.


 Введите исходные координаты и полный поворот, чтобы рассчитать новые координаты. (только вращение по часовой стрелке)
Введите исходные координаты и полный поворот, чтобы рассчитать новые координаты. (только вращение по часовой стрелке)
 Они могут и часто намного сложнее, чем вращение точек вокруг оси.
Они могут и часто намного сложнее, чем вращение точек вокруг оси.
 Умножение обеих сторон на 360° дает
Умножение обеих сторон на 360° дает Скаляры $\omega$ и $\alpha$ — это скаляры
угловая скорость и угловое ускорение твердого тела
тело (положительное против часовой стрелки).
Скаляры $\omega$ и $\alpha$ — это скаляры
угловая скорость и угловое ускорение твердого тела
тело (положительное против часовой стрелки).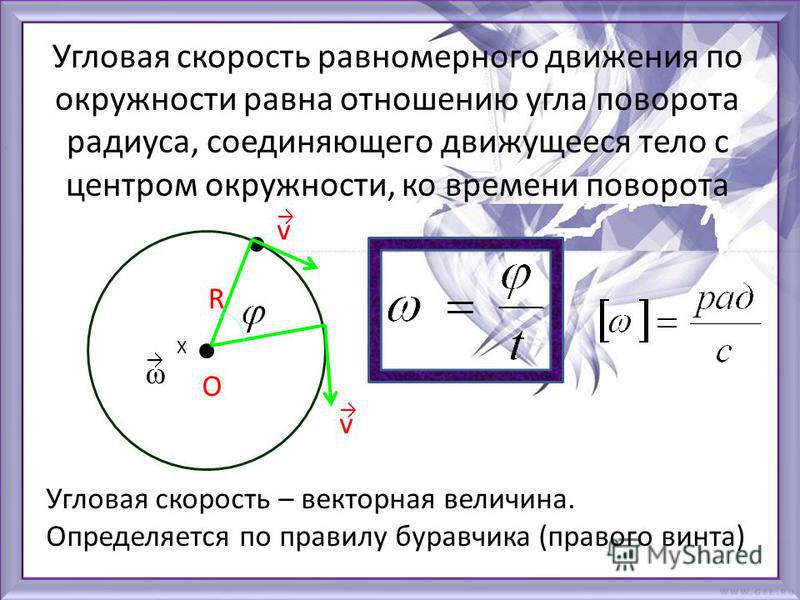
 2\,\vec{r}_{PM}$, как при выводе #rkg-e2.
2\,\vec{r}_{PM}$, как при выводе #rkg-e2.