Какой буквой обозначается угловая скорость: 404 — Страница не найдена
Угловая скорость как вектор. Выражения линейной скорости и касательного и нормального ускорений в виде векторных произведений
из «Курс теоретической механики »
Если твердое тело движется так, что две какие-нибудь его точки остаются неподвижными, то такое движение называется вращательным. Неподвижная прямая, проходящая через две неподвижные точки тела, называется осью вращения тела. Каждая точка тела, не лежащая на оси вращения, описывает при таком движении окружность, плоскость которой перпендикулярна к оси вращения и центр которой лежит на этой оси. [c.277]Производная от угла ф по времени называется угловой скоростью тела и обозначается буквой ш следовательно. [c.278]
Производная от угловой скорости по времени называется угловым ускорением тела и обозначается буквой е следовательно. [c.278]
Если тело вращается в направлении возрастания угла ф, т.
Таким образом, знак угловой скорости определяет направление положительное или отрицательное) вращения тела вокруг данной оси. [c.279]
Допустим, что ю 0 тогда, если е О, то угловая скорость возрастает, т. е. вращение тела является уско.ренным если же е О, то угловая скорость убывает — тело вращается замедленно. [c.279]
Предположим теперь, что 0 в этом случае при е О абсолютная величина угловой скорости убывает — тело вращается замедленно если же е О, то абсолютная величина угловой скорости возрастает — тело вращается ускоренно. [c.279]
Отсюда приходим к следующему заключению если ш и е имеют одинаковые знаки, то тело вращается ускоренно-, если ю и е имеют разные знаки, то вращение тела является замедленньш.
 [c.279]
[c.279]
Прп приблизительном подсчете угловой скорости можно принять л 3 тогда (о 0,1 и, т. е. угловая скорость тела равна приблизительно 0,1 числа оборотов в минуту. [c.280]
Если угловое ускорение тела постоянно, т. е. г = onst, то такое вращение тела называется равномерно переменным. [c.280]
Эти формулы, выражающие угловую скорость и угол поворота тела в зависимости от времени при равномерно переменном вращении, вполне аналогичны формулам для скорости и пройденного пути при равномерно переменном движении точки. Пусть (йо 0 тогда при 8 0 тело будет вращаться равномерно ускоренно если же 8 О, то будем иметь равномерно замедленное вращение тела. [c.281]
Перейдем теперь к определению скоростей и ускорений точек вращающегося твердого тела. Рассмотрим движение какой-нибудь точки М тела. Радиус окружности, которую описывает точка М, равный расстоянию этой точйи от оси вращения тела, обозначим через Л (рис.

Предположим, что тело вращается в положительном направлении, т. е. в направлении возрастания угла ф. [c.281]
Линейная скорость V направлена по касательной к окружности, которую описывает точка М, и, следовательно, перпендикулярна к плоскости, проходящей через эту точку и ось вращения тела (рис. 196 и 197). Итак, модуль линейной скорости точки вращающегося твердого тела равен произведению абсолютного (значения угловой скорости тела на расстояние этой точки от оси вращения. [c.282]
Что касается направления нормального ускорения , то оно направлено всегда по радиусу окружности, описываемой точкой М, к центру этой окружности. Поэтому это ускорение называется также центростремительным ускорением. [c.283]
Как нетрудно видеть из рис. 198 и 199, в случае ускоренного вращения острый угол а = агс1 нужно откладывать от радиуса МО в направлении, противоположном направлению вращения тела (по часовой стрелке на рис.
 198), а в случае замедленного вращения этот угол нужно откладывать от радиуса МО в нанрав-лении, совпадающем с направлением вращения тела (против часовой стрелки на рис, 199).
[c.283]
198), а в случае замедленного вращения этот угол нужно откладывать от радиуса МО в нанрав-лении, совпадающем с направлением вращения тела (против часовой стрелки на рис, 199).
[c.283]
Следовательно, при равномерном вращении тела ускорение w совпадает с нормальным (центростремительным) ускорением. [c.284]
Пример 78. Колесо с диаметром, равным d, вращается равномерно и делает п оборотов в минуту. Найти скорость и ускорение точек, лежащих на окружности колеса. [c.284]
Ускорение из совпадает с нормальным ускорением. [c.286]
Вернуться к основной статье
Простейшие движения твердого тела.

Простейшие движения твердого тела
Поступательное движение
Различают два вида простейшего движения твердого тела: поступательное движение и вращение вокруг неподвижной оси.
Движение тела, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению, называется поступательным.
Так, например, поршень двигателя относительно других деталей и узлов (гильзы, блока, головки цилиндров и т. п.) совершает поступательное движение.
Закономерности перемещения всех точек тела при поступательном движении можно описать движением любой из его точек. Этот вывод опирается на утверждения теоремы о поступательном движении твердого тела.
Теорема: при поступательном движении все точки твердого тела имеют одинаковые траектории, скорости и ускорения.
Пусть за время Δt тело, двигаясь поступательно, переместилось из положения АВ в положение А1В1, причем произвольная точка А прошла путь ΔsА, а другая произвольная точка В прошла путь ΔsВ по некоторым траекториям (дугам) АА1 и ВВ1 (см. рис. 1).
рис. 1).
Требуется доказать, что траектории, скорости и ускорения точек А и В при поступательном перемещении были одинаковы.
Соединим точки А и А1, В и В1 хордами. Так как АВ = А1В1
Возьмем промежуточное положение прямой А2В2 и соединим концы этого отрезка с точками А и А1, В и В1, как показано на рисунке.
Аналогично предыдущему можно доказать, что вписанные ломаные линии АА2А1 и ВВ2В1 имеют попарно равные и параллельные стороны.
Если бесконечное число раз удваивать число сторон этих ломаных линий, то в пределе они дадут дуги ΔsА и ΔsВ. Но так как эти ломаные линии всегда одинаковы, то они одинаковы и в пределе, следовательно, траектории произвольных точек А и В будут одинаковы.
Но так как эти ломаные линии всегда одинаковы, то они одинаковы и в пределе, следовательно, траектории произвольных точек А и В будут одинаковы.
Докажем теперь, что скорости и ускорения произвольных точек А и В, а, следовательно, и всех других точек тела в каждый данный момент времени будут равны.
Так как векторы перемещений точек А и В равны между собой (АА1 = ВВ1), то, разделив обе части этого векторного равенства на Δt и перейдя к пределу при Δt стремящемся к нулю, получим:
lim АА1/Δt = lim ВВ1/Δt при Δt→0.
Поскольку эти пределы являются векторами скоростей точек, следовательно vА = vВ.
Перенесем векторы скоростей vА1 и vВ1 в точки А и В и найдем векторы приращения скоростей ΔvА и ΔvВ. Рассмотрим треугольники АМN и ВМ1
 Эти треугольники конгруэнтны (равны), и их равные стороны попарно параллельны, следовательно, ΔvА = ΔvВ.
Эти треугольники конгруэнтны (равны), и их равные стороны попарно параллельны, следовательно, ΔvА = ΔvВ.Разделим обе части этого векторного равенства на Δt и перейдя к пределу при Δt стремящемся к нулю, получим:
lim ΔvА /Δt = lim ΔvВ /Δt при Δt→0 или аА = аВ.
Теорема доказана.
Таким образом, поступательное движение твердого тела вполне определяется движением одной из его точек и, следовательно, все формулы кинематики точки применимы для тела, движущегося поступательно.
***
Вращение вокруг неподвижной оси
Движение, при котором по крайней мере две точки твердого тела или неизменяемой системы остаются неподвижными, называется вращательным; прямая линия, соединяющая эти две точки, называется осью вращения.
В определении вращательного движения говорится о неизменяемой системе, потому что ось вращения может лежать и вне тела.
Вращательное движение в технике встречается очень часто. Во многих машинах имеются звенья, совершающие вращательное движение, например, валы, шкивы, зубчатые колеса, ступицы и т. п.
Следует отметить, что понятие вращательного движения может относиться лишь к телу, но не к отдельной точке, и, например, движение точки по окружности является не вращательным, а криволинейным движением.
Рассмотрим диск, вращающийся вокруг оси, перпендикулярной плоскости чертежа (см. рис. 2). Точка О – след этой оси.
Очевидно, что траектории точек вращающегося тела есть окружности различных радиусов, расположенные в плоскостях, перпендикулярных оси вращения, с центрами, лежащими на этой оси.
Пусть за время Δt диск повернулся на угол φ. При этом точка А прошла путь s
Так как точки, находящиеся на различном расстоянии от оси вращения, за один и тот же промежуток времени проходят разные пути, то, следовательно, они имеют разные скорости и ускорения. Отсюда следует, что линейное перемещение (путь), линейные скорость и ускорение точек не могут характеризовать вращательное движение тела в целом.
Отсюда следует, что линейное перемещение (путь), линейные скорость и ускорение точек не могут характеризовать вращательное движение тела в целом.
Вращательное движение тела можно характеризовать углом φ, на который повернулось тело за данный промежуток времени. Этот угол называется угловым перемещением тела.
Угловое перемещение тела выражается в радианах (рад) или оборотах (об); в последнем случае угловое перемещение обозначают N. Для установлении зависимости между этими величинами составим пропорцию:
1 об = 2π рад, N об = φ рад, откуда φ = 2πN рад,
где N – число оборотов тела.
Угловое перемещение есть функция времени, следовательно, закон вращательного движения в общем виде можно записать так: φ = f(t).
Из рис. 2 видно, что путь любой точки вращающегося тела может быть определен из уравнения:
s = rφ, где r – расстояние от точки до оси вращения.
Скорость любой точки тела определяется так:
v = ds/dt = d(rφ)/dt = r(dφ/dt)
(r вынесли за знак производной, так как для данной точки твердого тела эта величина постоянна).
Выражение dφ/dt называется угловой скоростью и обозначается ω.
Угловая скорость есть кинематическая мера движения вращающегося тела, характеризующая быстроту его углового перемещения: ω = dφ/dt.
Угловая скорость равна первой производной углового перемещения по времени. Единица угловой скорости – радиан в секунду (рад/с).
Формула для определения скорости любой точки вращающегося тела имеет следующий вид:
v = ωr.
Скорость точки в каждый момент времени прямо пропорциональна ее расстоянию от оси вращения, следовательно, график скоростей точек, например, диаметра В1В2, будет представлять собой два треугольника. Очевидно, что вектор скорости точки вращающегося тела направлен перпендикулярно радиусу, соединяющему эту точку с осью вращения.
Если точка лежит на поверхности вращающегося тела, то ее скорость называют окружной.
В технике часто скорость вращения выражают в оборотах в минуту, обозначают буквой n и называют частотой вращения. Зависимость между угловой скоростью и частотой вращения выглядит так:
Зависимость между угловой скоростью и частотой вращения выглядит так:
ω = πn/30 рад/с, где n = частота вращения тела (об/мин).
***
Различные случаи вращательного движения
Равномерное вращательное движение
Если тело вращается вокруг неподвижной оси с постоянной угловой скоростью, то движение называется равномерным.
При этом:
ω = const; φ = ωt.
Касательное, нормальное и полное ускорения любой точки равномерно вращающегося тела определяют так:
аτ = 0; ап = ω2r; а = ап = ω2r.
***
Неравномерное вращательное движение
Если угловая скорость вращающегося тела с течением времени меняется, то движение называется неравномерным.
В самом общем виде формулы неравномерного вращательного движения выглядят так:
φ = f(t); ω= Δφ/Δt.
Касательное движение любой точки неравномерно вращающегося тела определяют следующим образом:
aτ = dv/dt = d(ωr)/dt = r(dω/dt).
Выражение dω/dt обозначают α (альфа) и называют угловым ускорением.
Угловое ускорение есть кинематическая мера изменения угловой скорости вращающегося тела:
α = dω/t = d2φ/dt2.
Угловое ускорение равно первой производной угловой скорости или второй производной углового перемещения по времени. Единица углового ускорения – радиан на секунду в квадрате (рад/с2).
Формулу для определения касательного ускорения любой точки неравномерно вращающегося тела можно записать в таком виде: аτ = αr.
Нормальное ускорение определяется по такой же формуле, как и в случае равномерного вращения:
ап = ω2r.
Полное ускорение:
а = √[(аτ2) + (ап2)] = √[(αr)2 + (ω2r)2], откуда а = r √(α2 + ω4).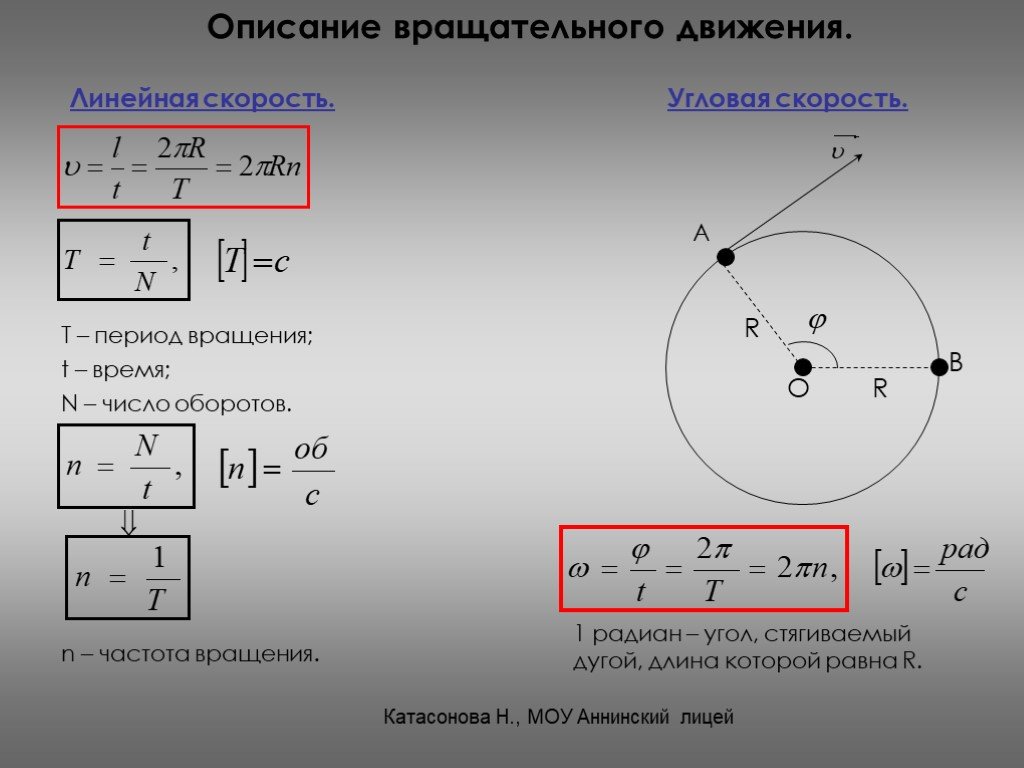
Направляющий тангенс полного ускорения можно определить так:
tg(а, ап) = аτ/ап = αr/(ω2r), откуда tg(a,aп) = α/ω2.
Если направление углового ускорения совпадает с направлением вращения, то вращательное движение является ускоренным, и наоборот.
***
Равнопеременное вращательное движение
Если тело вращается вокруг неподвижной оси с постоянным угловым ускорением, то движение называют равнопеременным.
Формулы для этого вида вращательного движения могут быть выведены при помощи интегрального исчисления.
Итак, если твердое тело вращается вокруг неподвижной оси равнопеременно, то:
α = dω/dt = const, откуда dω = αdt.
Интегрируя это равенство по t, получим:
∫dω = ∫αdt, где ω изменяется от 0 (начальная угловая скорость) до ω, t изменяется от 0 до t.
Получим окончательную формулу угловой скорости в следующем виде:
ω = ω0 + αt.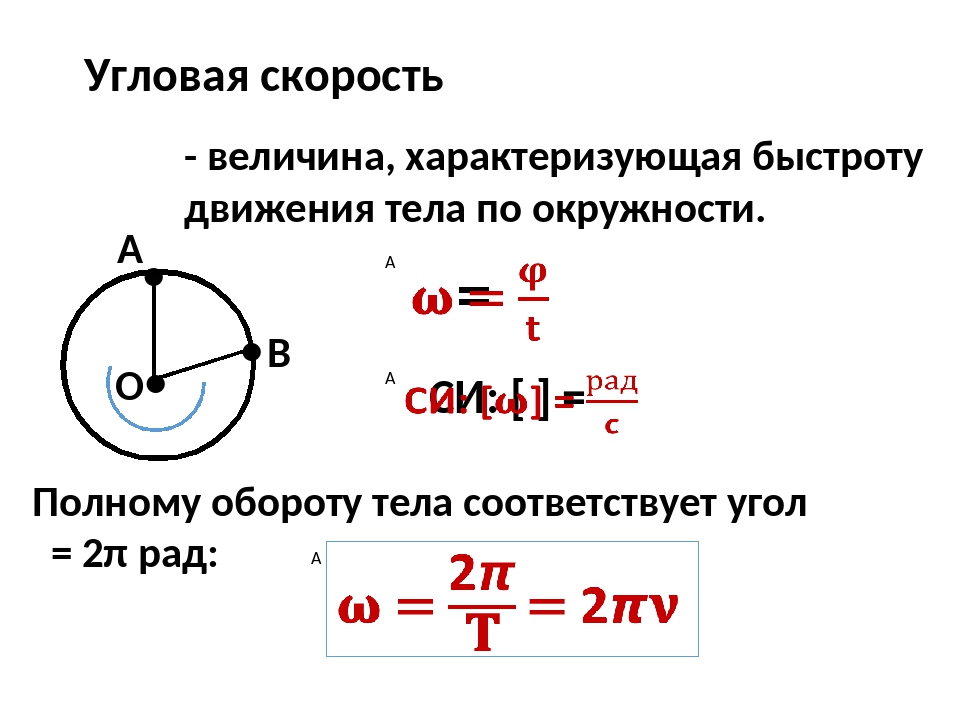
Далее выведем формулу углового перемещения. Так как при любом вращательном движении
dφ/dt = ω, то dφ = dω/dt,
то, интегрируя это равенство по t, получим:
∫dφ = ∫dω/dt = ∫( ω0 + αt)dt = ∫ω0dt + ∫αtdt; φ – φ0 = ω0t + αt2/2,
где φ0 – начальное угловое перемещение.
Очевидно, что в случае φ0 = 0, формула примет вид: φ = ω0t + αt2/2.
Итак, формулы для равнопеременного вращательного движения твердого тела записываются следующим образом:
α = const; ω = ω0 + αt; φ = ω0t + αt2/2.
Из этих формул можно получить формулы углового перемещения в другом виде:
φ = (ω2 – ω02)/(2α) или φ = (ω0 + ω)t/2.
***
Сложное движение точки и твердого тела
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Движение тела по окружности — конспект
В природе и технике очень часто встречается криволинейное движение. Он сложнее прямолинейный, так как существует множество криволинейных траекторий; это движение всегда ускоренный, даже когда модуль скорости не меняется.
Он сложнее прямолинейный, так как существует множество криволинейных траекторий; это движение всегда ускоренный, даже когда модуль скорости не меняется.
Но движение по любой криволинейной траектории можно приблизительно представить как движение по дугам круга.
При движении тела по окружности направление вектора скорости меняется от точки к точке. Поэтому когда говорят о скорости такого движения, подразумевают мгновенную скорость. Вектор скорости направлен по касательной к окружности, а вектор перемещения — по хордах.
Равномерное движение по окружности — это движение, во время которого модуль скорости движения не изменяется, изменяется только ее направление. Ускорение такого движения всегда направлено к центру окружности и называется центростремительным. Для того чтобы найти ускорение тела, которое движется по кругу, необходимо квадрат скорости разделить на радиус окружности.
Помимо ускорения, движение тела по кругу характеризуют следующие величины:
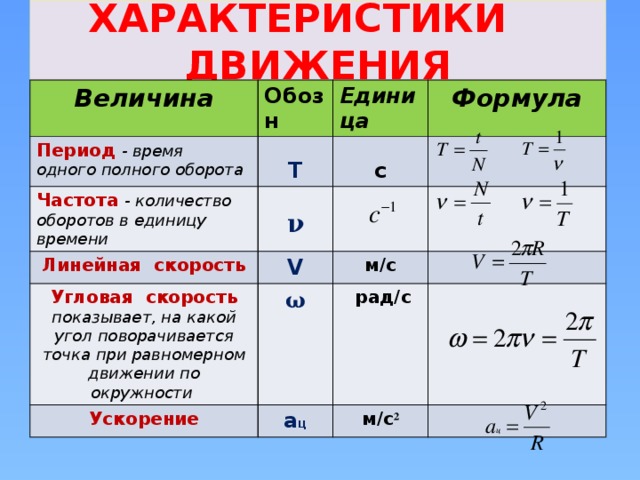
Период вращения тела — это время, за которое тело совершает один полный оборот. Период вращения обозначается буквой Т и измеряется в секундах.
Период вращения обозначается буквой Т и измеряется в секундах.
Частота вращения тела — это число оборотов в единицу времени. Частота вращения обозначается буквой ? и измеряется в герцах. Для того чтобы найти частоту, надо единицу разделить на период.
Линейная скорость — отношение перемещения тела до времени. Для того чтобы найти линейную скорость тела по окружности, необходимо длину окружности разделить на период (длина окружности равна 2? умножить на радиус).
Угловая скорость — физическая величина, равная отношению угла поворота радиуса окружности, по которой движется тело, до времени движения. Угловая скорость обозначается буквой ? и измеряется в радианах, разделенных на секунду. Найти угловую скорость можно, разделив 2? на период. Угловая скорость и линейная между собой. Для того чтобы найти линейную скорость, необходимо угловую скорость умножить на радиус окружности.
Вращательное движение | Облепиха
Какое бы тело мы ни взяли, оно, вообще говоря, может совершать только два простых движения. Прежде всего, оно может двигаться поступательно. При таком движении все точки тела перемещаются одинаково, то есть описывают одни и те же траектории.
Прежде всего, оно может двигаться поступательно. При таком движении все точки тела перемещаются одинаково, то есть описывают одни и те же траектории.
У поступательного движения есть хорошая отличительная черта: если тело движется таким образом, прямая, проведенная через две любые его точки, все время остается параллельной самой себе.
Если вы занимаетесь пенспиннингом, вам должен быть хорошо известен второй вид простейшего движения – вращательное. При таком движении все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Давайте подробнее поговорим об этом движении, взяв в качестве примера известную спортивную дисциплину – метание молота. Думаю, вы знаете в чем суть этого спорта: люди вращаются вокруг своей оси и стремятся как можно дальше бросить металлический шар, соединенный стальной проволокой с рукояткой. Во время броска атлет не только вращается, но и постепенно смещается к краю ограничительного круга, внутри которого он находится. Но мы будем предполагать, что он все время остается на месте и совершает только вращательное движение. В таком случае траектория молота (до броска) будет такой:
Но мы будем предполагать, что он все время остается на месте и совершает только вращательное движение. В таком случае траектория молота (до броска) будет такой:
На картинке схематично изображен вид сверху. Теперь перейдем к рассмотрению новых физических величин, которые вводятся для изучения подобного рода движений.
Первая характеристика, с которой мы познакомимся, называется угловым перемещением. Эта величина показывает угол поворота тела вокруг оси вращения. Измеряется в радианах (рад). Обозначается обычно через греческую букву “фи”: \varDelta{\vec{\varphi}}. Стрелочка наверху подчеркивает, что это вектор.
«Угловое перемещение – вектор? И куда же он направлен?» – спросите вы.
Сразу скажу, что это немного необычный вектор. Вектор углового перемещения направлен вдоль оси вращения, то есть перпендикулярен плоскости движения. При этом его конкретное расположение (вверх или вниз) зависит от направления, в котором будет происходить вращение: если объект вращается против часовой стрелки, вектор углового перемещения будет сонаправлен с осью z; если объект вращается по часовой стрелке, вектор углового перемещения будет направлен в другую сторону.
В общем, получается так: знак углового перемещения зависит от направления вращения. Если объект вращается против часовой стрелки, угловое перемещение считается положительным, если по часовой – отрицательным.
Надеюсь, что с направлением углового перемещения мы разобрались. Но как найти его числовое значение? Все просто. Угловое перемещение – это разница между углами, которые обозначали положение тела в начальный и конечный момент времени:
\boxed{\varDelta{\vec{\varphi}}=\varphi_2-\varphi_1}
Вы, наверное, уже сами заметили аналогию между угловым перемещением и тем перемещением, о котором мы говорили раньше. Молот движется по кругу, а мог бы двигаться по прямой. В таком случае мы бы искали разницу координат, а не углов.
А есть ли аналог «обычной» скорости для движения по кругу? Да. Это так называемая угловая скорость. Она также является векторной величиной и обозначается греческой буквой “омега”: \vec{\omega}. Угловая скорость характеризует быстроту вращения тела, она равна изменению углового перемещения ко времени, за которое это изменение произошло:
\boxed{\vec{\omega}=\dfrac{\varDelta{\vec{\varphi}}}{\varDelta{t}}}
Стоит также сказать, что измеряется она в рад/с. 2 и показывает, насколько быстро меняется угловая скорость: ⠀
2 и показывает, насколько быстро меняется угловая скорость: ⠀
\boxed{\vec{\varepsilon}=\dfrac{\varDelta{\vec{\omega}}}{\varDelta{t}}}
На что указывает знак углового ускорения? Он показывает, прибавляем мы некоторое число к нашей угловой скорости или, наоборот, отнимаем. Все аналогично случаю с обыкновенным ускорением.
Кратко повторим все наиболее важное.
Для описания вращательного движения вводятся новые величины, делающие его анализ более удобным: угловое перемещение, угловая скорость и угловое ускорение.
Угловое перемещение является векторной величиной и показывает, на какой угол повернулось тело. Если движение происходит по часовой стрелке, угловое перемещение принято считать отрицательным, если против – положительным.
Угловая скорость и угловое ускорение также являются векторными величинами. Угловая скорость характеризует быстроту вращения тела, а вот угловое ускорение помогает понять, как меняется сама угловая скорость.
Формулы по физике криволинейное движение.
 Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение
Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение6. Криволинейное движение. Угловое перемещение, угловые скорость и ускорение тела. Путь и перемещение при криволинейном движении тела.
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.
Криволинейное движение материальной точки считается равномерным движением, если модульскорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
Рис.
1.19. Траектория и вектор перемещения при
криволинейном движении.
При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), аl – длина траектории . Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
Рис. 1.20. Мгновенная скорость при криволинейном движении.
Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение :
или
Где v τ , v 0 – величины скоростей в момент времени t 0 + Δt и t 0 соответственно.
Тангенциальное
ускорение в
данной точке траектории по направлению
совпадает с направлением скорости
движения тела или противоположно ему.
Нормальное ускорение — это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.
Полное ускорение при равнопеременном криволинейном движении тела равно:
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).
Рис. 1.21. Движение тела при криволинейном движении.
Криволинейное движение
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Криволинейное
движение – это всегда движение с
ускорением, даже если по модулю скорость
постоянна. Криволинейное движение с
постоянным ускорением всегда происходит
в той плоскости, в которой находятся
векторы ускорения и начальные скорости
точки. В случае криволинейного движения
с постоянным ускорением в
плоскости xOy проекции v x и v y ее
скорости на оси Ox и Oy и
координаты x и y точки
в любой момент времениt определяется
по формулам
В случае криволинейного движения
с постоянным ускорением в
плоскости xOy проекции v x и v y ее
скорости на оси Ox и Oy и
координаты x и y точки
в любой момент времениt определяется
по формулам
Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением где r – радиус окружности.
Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.
При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих:
Нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:
v
– мгновенное
значение скорости, r –
радиус кривизна траектории в данной
точке.
Тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.
Полное ускорение, с которым движется материальная точка, равно:
Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.
Период обращения — это время, за которое тело совершается один оборот.
Обозначается период буквой Т (с) и определяется по формуле:
где t — время обращения, п — число оборотов, совершенных за это время.
Частота обращения — это величина, численно равная числу оборотов, совершенных за единицу времени.
Обозначается частота греческой буквой (ню) и находится по формуле:
Измеряется частота в 1/с.
Период и частота — величины взаимно обратные:
Если тело, двигаясь по окружности со скоростью v, делает один оборот, то пройденный этим телом путь можно найти, умножив скорость v на время одного оборота:
l
= vT. С
другой стороны, этот путь равен длине
окружности 2πr .
Поэтому
С
другой стороны, этот путь равен длине
окружности 2πr .
Поэтому
vT = 2πr,
где w (с -1) — угловая скорость.
При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения.
Угловая скорость (w ) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:
.
Связь между линейной и угловой скоростями:
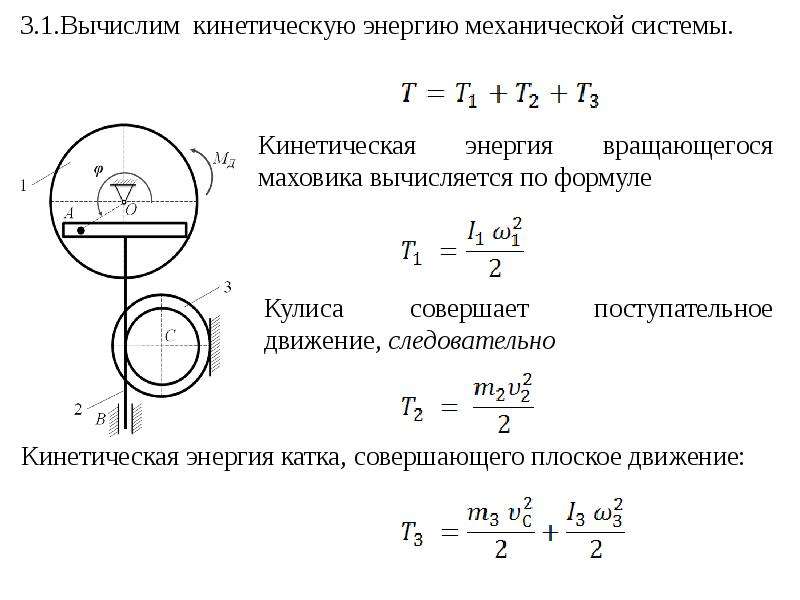
Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе.
В зависимости от формы траектории движение можно подразделять на прямолинейное и криволинейное. Чаще всего можно столкнуться с криволинейными движениями, когда траектория представлена в виде кривой. Примером такого вида движения является путь тела, брошенного под углом к горизонту, движение Земли вокруг Солнца, планет и так далее.
Примером такого вида движения является путь тела, брошенного под углом к горизонту, движение Земли вокруг Солнца, планет и так далее.
Рисунок 1 . Траектория и перемещение при криволинейном движении
Определение 1Криволинейным движением называют движение, траектория которого представляет собой кривую линию. Если тело движется по криволинейной траектории, то вектор перемещения s → направлен по хорде, как показано на рисунке 1 , а l является длиной траектории. Направление мгновенной скорости движения тела идет по касательной в той же точке траектории, где в данный момент располагается движущийся объект, как показано на рисунке 2 .
Рисунок 2 . Мгновенная скорость при криволинейном движении
Определение 2
Криволинейное движение материальной точки называют равномерным тогда, когда модуль скорости постоянный (движение по окружности), и равноускоренным при изменяющемся направлении и модуле скорости (движение брошенного тела).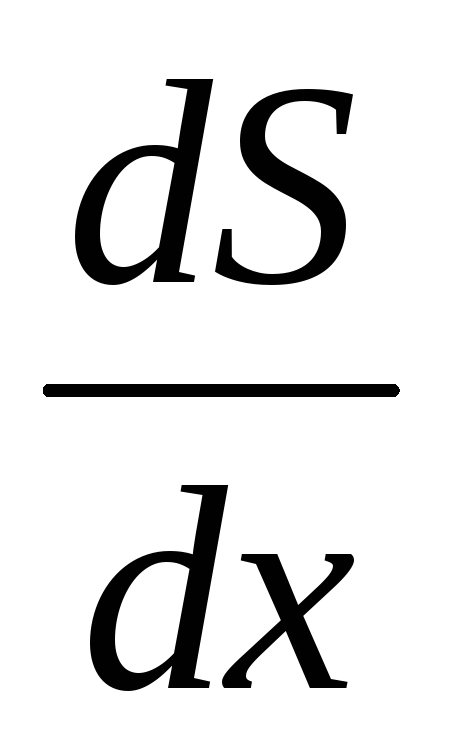
Криволинейное движение всегда ускоренное. Это объясняется тем, что даже при неизмененном модуле скорости, а измененном направлении, всегда присутствует ускорение.
Для того чтобы исследовать криволинейное движение материальной точки, применяют два метода.
Путь разбивается на отдельные участки, на каждом из которых его можно считать прямолинейным, как показано на рисунке 3 .
Рисунок 3 . Разбиение криволинейного движения на поступательные
Теперь для каждого участка можно применять закон прямолинейного движения. Такой принцип допускается.
Самым удобным методом решения считается представление пути в качестве совокупности нескольких движений по дугам окружностей, как показано на рисунке 4 . Количество разбиений будет намного меньше, чем в предыдущем методе, кроме того, движение по окружности уже является криволинейным.
Рисунок 4 . Разбиение криволинейного движения на движения по дугам окружностей
Замечание 1
Для записи криволинейного движения необходимо уметь описывать движение по окружности, произвольное движение представлять в виде совокупностей движений по дугам этих окружностей.
Исследование криволинейного движения включает в себя составление кинематического уравнения, которое описывает это движение и позволяет по имеющимся начальным условиям определить все характеристики движения.
Пример 1
Дана материальная точка, движущаяся по кривой, как показано на рисунке 4 . Центры окружностей O 1 , O 2 , O 3 располагаются на одной прямой. Необходимо найти перемещение
s → и длину пути l во время движения из точки А в В.
Решение
По условию имеем, что центры окружности принадлежат одной прямой, отсюда:
s → = R 1 + 2 R 2 + R 3 .
Так как траектория движения – это сумма полуокружностей, то:
l ~ A B = π R 1 + R 2 + R 3 .
Ответ: s → = R 1 + 2 R 2 + R 3 , l ~ A B = π R 1 + R 2 + R 3 .
Пример 2
Дана зависимость пройденного телом пути от времени, представленная уравнением s (t) = A + B t + C t 2 + D t 3 (C = 0 , 1 м / с 2 , D = 0 , 003 м / с 3) . Вычислить, через какой промежуток времени после начала движения ускорение тела будет равно 2 м / с 2
Решение
Ответ: t = 60 с.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Эта тема будет посвящена более сложному виду движения – КРИВОЛИНЕЙНОМУ . Как несложно догадаться, криволинейным называется движение, траектория которого представляет собой кривую линию . И, поскольку это движение сложнее прямолинейного, то для его описания уже не хватает тех физических величин, которые были перечислены в предыдущей главе.
Для математического описания криволинейного движения имеются 2 группы величин: линейные и угловые.
ЛИНЕЙНЫЕ ВЕЛИЧИНЫ.
1. Перемещение . В разделе 1.1 мы не стали уточнять различие между понятием
Рис.1.3 пути (расстояния) и понятием перемещения,
поскольку в прямолинейном движении эти
различия не играют принципиальной роли, да и
Обозначаются эти величины одной и той же бук-
вой S . Но, имея дело с криволинейным движением,
этот вопрос нужно прояснить. Итак, что такое путь
Итак, что такое путь
(или расстояние)? – Это длина траектории
движения. То есть, если Вы отследите траекторию
движения тела и измерите ее (в метрах, километрах и т.д.), вы получите величину, которая называется путем (или расстоянием) S (см. рис.1.3). Таким образом, путь – это скалярная величина, которая характеризуется только числом.
Рис.1.4 А перемещение — это кратчайшее расстояние между
точкой начала пути и точкой конца пути. И, поскольку
перемещение имеет строгую направленность из начала
Пути в его конец, то оно является величиной векторной
и характеризуется не только численным значением, но и
направлением (рис.1.3). Нетрудно догадаться, что, если
тело совершает движение по замкнутой траектории, то к
моменту его возвращения в начальное положение перемещение будет равно нулю (см. рис.1.4).
2 . Линейная скорость . В разделе 1.1 мы давали определение этой величины, и оно остается в силе, хотя тогда мы не уточняли, что эта скорость линейная. Как же направлен вектор линейной скорости? Обратимся к рис.1.5. Здесь изображен фрагмент
Как же направлен вектор линейной скорости? Обратимся к рис.1.5. Здесь изображен фрагмент
криволинейной траектории тела. Любая кривая линия представляет собой соединение между собой дуг разных окружностей. На рис.1.5 изображены только две из них: окружность (О 1 , r 1) и окружность (О 2 , r 2). На момент прохождения тела по дуге данной окружности ее центр становится временным центром поворота с радиусом, равным радиусу этой окружности.
Вектор, проведенный из центра поворота в точку, где в данный момент находится тело, называется радиусом-вектором. На рис.1.5 радиусы-векторы представлены векторами и . Также на этом рисунке изображены и вектора линейной скорости: вектор линейной скорости всегда направлен по касательной к траектории в сторону движения. Следовательно, угол между вектором и радиусом-вектором, проведенным в данную точку траектории, всегда равен 90°. Если тело движется с постоянной линейной скоростью, то модуль вектора изменяться не будет, тогда как его направление все время меняется в зависимости от формы траектории. В случае, изображенном на рис.1.5, движение осуществляется с переменной линейной скоростью, поэтому у вектора изменяется модуль. Но, поскольку при криволинейном движении направление вектора изменяется всегда, то отсюда следует очень важный вывод:
В случае, изображенном на рис.1.5, движение осуществляется с переменной линейной скоростью, поэтому у вектора изменяется модуль. Но, поскольку при криволинейном движении направление вектора изменяется всегда, то отсюда следует очень важный вывод:
при криволинейном движении всегда есть ускорение ! (Даже если движение осуществляется с постоянной линейной скоростью.) Причем, ускорение, о котором идет речь в данном случае, в дальнейшем мы будем называть линейным ускорением.
3 . Линейное ускорение . Напомню, что ускорение возникает тогда, когда изменяется скорость. Соответственно, линейное ускорение появляется в случае изменения линейной скорости. А линейная скорость при криволинейном движении может изменяться кок по модулю, так и по направлению. Таким образом, полное линейное ускорение раскладывается на две составляющие, одна из которых влияет на направление вектора , а вторая на его модуль. Рассмотрим эти ускорения (рис. 1.6). На этом рисунке
рис. 1.6
1.6
О
изображено тело, движущееся по круговой траектории с центром поворота в точке О.
Ускорение, которое изменяет направление вектора , называется нормальным и обозначается . Нормальным оно называется потому, что направлено перпендикулярно (нормально) к касательной, т.е. вдоль радиуса к центру поворота . Его еще называют центростремительным ускорением.
Ускорение, которое изменяет модуль вектора , называется тангенциальным и обозначается . Оно лежит на касательной и может быть направлено как в сторону направления вектора , так и противоположно ему :
Если линейная скорость увеличивается, то > 0 и их вектора сонаправлены;
Если линейная скорость уменьшается, то
направлены.
Таким образом, эти два ускорения всегда образуют между собой прямой угол (90º) и являются составляющими полного линейного ускорения , т.е.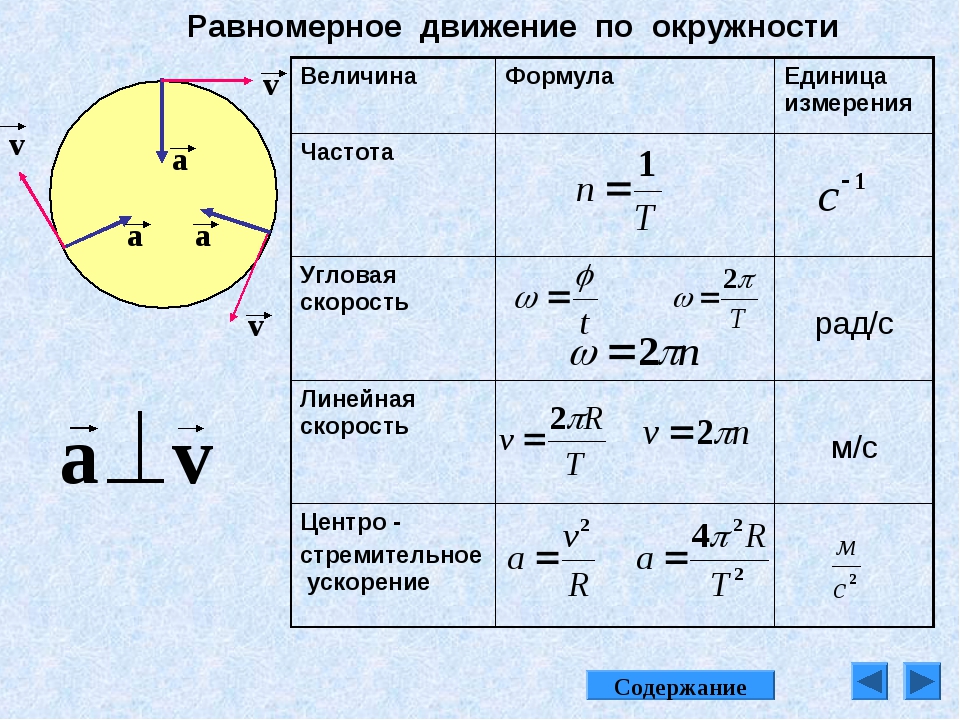 полное линейное ускорение есть векторная сумма нормального и тангенциального ускорения:
полное линейное ускорение есть векторная сумма нормального и тангенциального ускорения:
Замечу, что в данном случае речь идет именно о векторной сумме, но ни в коем случае не о скалярной. Чтобы найти численное значение , зная и , необходимо воспользоваться теоремой Пифагора (квадрат гипотенузы треугольника численно равен сумме квадратов катетов этого треугольника):
(1.8).
Отсюда следует:
(1.9).
По каким формулам рассчитывать и рассмотрим чуть позже.
УГЛОВЫЕ ВЕЛИЧИНЫ.
1 . Угол поворота φ . При криволинейном движении тело не только проходит какой-то путь и совершает какое-то перемещение, но и поворачивается на определенный угол (см. рис. 1.7(а)). Поэтому для описания такого движения вводится величина, которая называется углом поворота, обозначается греческой буквой φ (читается «фи»). В системе СИ угол поворота измеряется в радианах (обозначается «рад»). Напомню, что один полный оборот равен 2π радианам, а число π есть константа: π ≈ 3,14. на рис. 1.7(а) изображена траектория движения тела по окружности радиуса r с цетром в точке О. Сам угол поворота – это угол между радиус-векторами тела в некоторые моменты времени.
на рис. 1.7(а) изображена траектория движения тела по окружности радиуса r с цетром в точке О. Сам угол поворота – это угол между радиус-векторами тела в некоторые моменты времени.
2 . Угловая скорость ω – это величина, показывающая, как изменяется угол поворота за единицу времени. (ω – греческая буква, читается «омега».) На рис. 1.7(б) изображено положение материальной точки, движущейся по круговой траектории с центром в точке О, через промежутки времени Δt . Если углы, на которые поворачивается тело в течение этих промежутков, одинаковы, то угловая скорость постоянна, и это движение можно считать равномерным. А если углы поворота разные – то движение неравномерное. И, поскольку угловая скорость показывает, на сколько радиан
повернулось тело за одну секунду, то ее единица измерения – радиан в секунду
(обозначается «рад/с »).
рис. 1.7
а).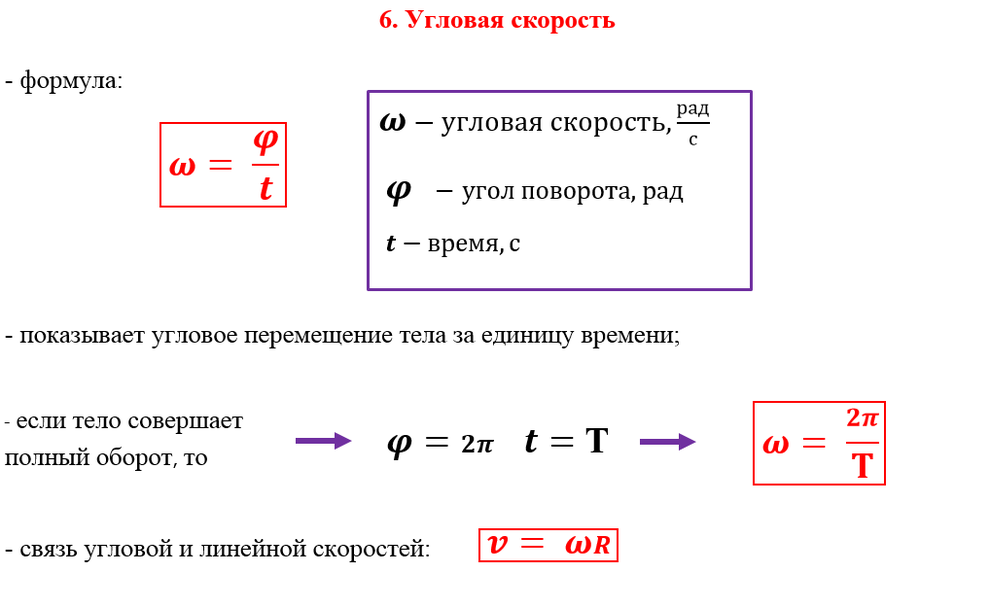 б). Δt
б). Δt
Δt
Δt
О φ О Δt
3 . Угловое ускорение ε – это величина, показывающая, как изменяется за единицу времени. И, поскольку угловое ускорение ε появляется тогда, когда изменяется, угловая скорость ω , то можно сделать вывод, что угловое ускорение имеет место только в случае неравномерного криволинейного движения. Единица измерения углового ускорения – «рад/с 2 » (радиан за секунду в квадрате).
Таким образом, таблицу 1.1 можно дополнить еще тремя величинами:
Табл.1.2
| № | физическая величина | определение величины | обозначение величины | единица измерения |
| 1. | путь | это расстояние, которое преодолевает тело в процессе своего движения | S | м (метр) |
2. | скорость | это расстояние, которое проходит тело за единицу времени (например, за 1 секунду) | υ | м/с (метр в секунду) |
| 3. | ускорение | это величина, на которую изменяется скорость тела за единицу времени | a | м/с 2 (метр за секунду в квадрате) |
| 4. | время | t | с (секунда) | |
| 5. | угол поворота | это угол, на который поворачивается тело в процессе криволинейного движения | φ | рад (радиан) |
| 6. | угловая скорость | это угол, на который поворачивается тело за единицу времени (например, за 1 сек.) | ω | рад/с (радиан в секунду) |
| 7. | угловое ускорение | это величина, на которую изменяется угловая скорость за единицу времени | ε | рад/с 2 (радиан за секунду в квадрате) |
Теперь можно перейти непосредственно к рассмотрению всех видов криволинейного движения, а их всего лишь три.
Кинематика изучает движение без выявления причин, вызывающих это движение. Кинематика является разделом механики. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени.
Основные кинематические величины:
— Перемещение() – вектор, соединяющий начальную и конечную точки.
r – радиус-вектор, определяет положение МТ в пространстве.
— Скорость – отношение пути ко времени.
— Путь – множество точек через которое прошло тело.
— Ускорение – скорость изменения скорости, то есть первая производная от скорости.
2.Ускорение при криволинейном движении: нормальное и тангенциальное ускорение. Плоское вращение. Угловая скорость, ускорение.
Криволинейное движение – это движение, траектория которого представляет собой кривую линию. Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д.
Криволинейное
движение –
это всегда ускоренное движение.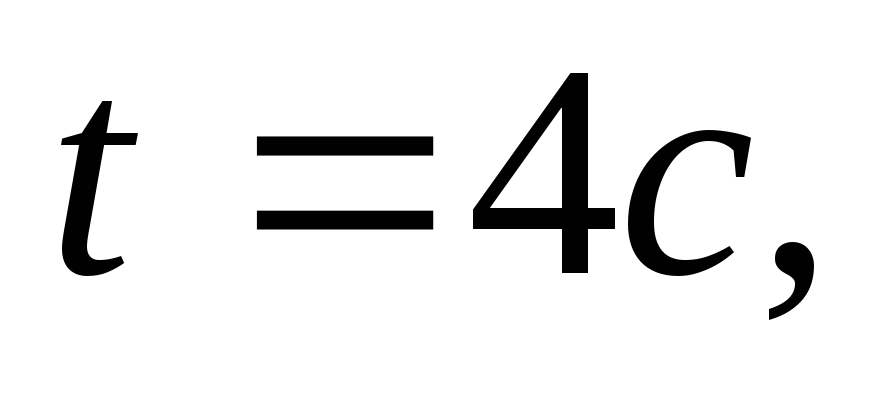 То
есть ускорение при криволинейном
движении присутствует всегда, даже
если модуль скорости не изменяется, а
изменяется только направление скорости.
То
есть ускорение при криволинейном
движении присутствует всегда, даже
если модуль скорости не изменяется, а
изменяется только направление скорости.
Изменение величины скорости за единицу времени – это тангенциальное ускорение :
Где 𝛖 τ , 𝛖 0 – величины скоростей в момент времени t 0 + Δt и t 0 соответственно. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение — это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Полное ускорение при равнопеременном криволинейном движении тела равно:
—угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ — рад/с.
Плоское
вращение – это вращение
всех векторов скоростей точек тела в
одной плоскости.
3.Связь между векторами скорости и угловой скорости материальной точки. Нормальное, тангенциальное и полное ускорение.
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Нормальное (центростремительное) ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное
ускорение при криволинейном движении складывается
из тангенциального и нормального
ускорений по правилу сложения векторов
и определяется формулой.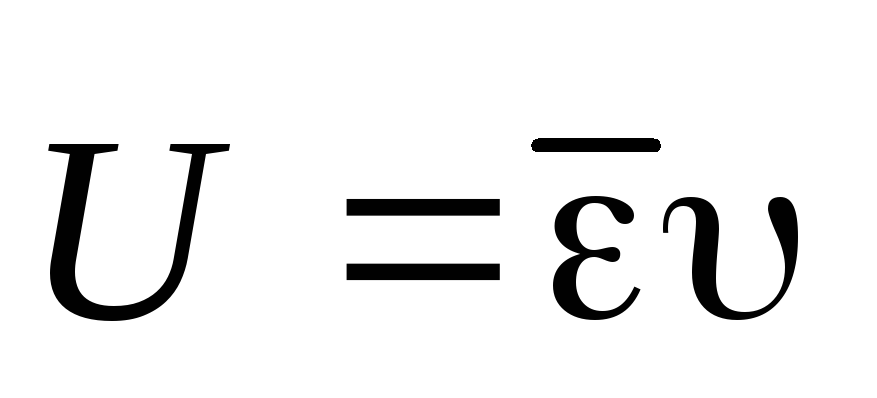
Криволинейные движения — движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Криволинейное движение — это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vxи vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам
Ни одно тело не движется все время с постоянной скоростью. Начиная движение, автомобиль движется быстрее и быстрее. Некоторое время он может двигаться равномерно, но потом он тормозит и останавливается. При этом автомобиль проходит разные расстояния за один и то же время.
Движение, при котором тело за равные промежутки времени проходит неодинаковые отрезки пути, называется неравномерным. При таком движении величина скорости не остается неизменной. В таком случае можно говорить лишь о средней скорости.
При таком движении величина скорости не остается неизменной. В таком случае можно говорить лишь о средней скорости.
Средняя скорость показывает, чему равно перемещение, которое тело проходит за единицу времени. Она равна отношению перемещения тела до времени движения. Средняя скорость, как и скорость тела при равномерном движении, измеряется в метрах, разделенных на секунду. Для того, чтобы характеризовать движение точнее, в физике применяют мгновенную скорость.
Скорость тела в данный момент времени или в данной точке траектории называется мгновенной скоростью. Мгновенная скорость является векторной величиной и направлена так же, как вектор перемещения. Измерить мгновенную скорость можно с помощью спидометра. В Системе Интернациональной мгновенная скорость измеряется в метрах, разделенных на секунду.
точка движение скорость неравномерный
В природе и технике очень часто встречается криволинейное движение. Оно сложнее прямолинейного, так как существует множество криволинейных траекторий; это движение всегда ускоренное, даже когда модуль скорости не меняется.
Но движение по любой криволинейной траектории можно приблизительно представить как движение по дугам круга.
При движении тела по окружности направление вектора скорости меняется от точки к точке. Поэтому когда говорят о скорости такого движения, подразумевают мгновенную скорость. Вектор скорости направлен по касательной к окружности, а вектор перемещения — по хордам.
Равномерное движение по окружности — это движение, во время которого модуль скорости движения не изменяется, изменяется только ее направление. Ускорение такого движения всегда направлено к центру окружности и называется центростремительным. Для того чтобы найти ускорение тела, которое движется по кругу, необходимо квадрат скорости разделить на радиус окружности.
Помимо ускорения, движение тела по кругу характеризуют следующие величины:
Период вращения тела — это время, за которое тело совершает один полный оборот. Период вращения обозначается буквой Т и измеряется в секундах.
Частота вращения тела — это число оборотов в единицу времени.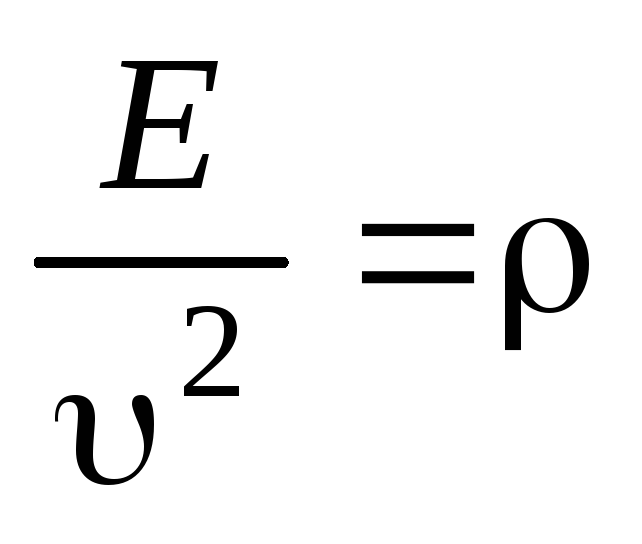 Частота вращения обозначается буквой? и измеряется в герцах. Для того чтобы найти частоту, надо единицу разделить на период.
Частота вращения обозначается буквой? и измеряется в герцах. Для того чтобы найти частоту, надо единицу разделить на период.
Линейная скорость — отношение перемещения тела до времени. Для того чтобы найти линейную скорость тела по окружности, необходимо длину окружности разделить на период (длина окружности равна 2? умножить на радиус).
Угловая скорость — физическая величина, равная отношению угла поворота радиуса окружности, по которой движется тело, до времени движения. Угловая скорость обозначается буквой? и измеряется в радианах, разделенных на секунду. Найти угловую скорость можно, разделив 2? на период. Угловая скорость и линейная между собой. Для того чтобы найти линейную скорость, необходимо угловую скорость умножить на радиус окружности.
Рисунок 6. Движение по окружности, формулы.
Исследовательская работа «Определение линейной и угловой скоростей точки, равномерно движущейся по окружности»
МОУ СОШ №2
Определение линейной и угловой скоростей точки, равномерно движущейся по окружности.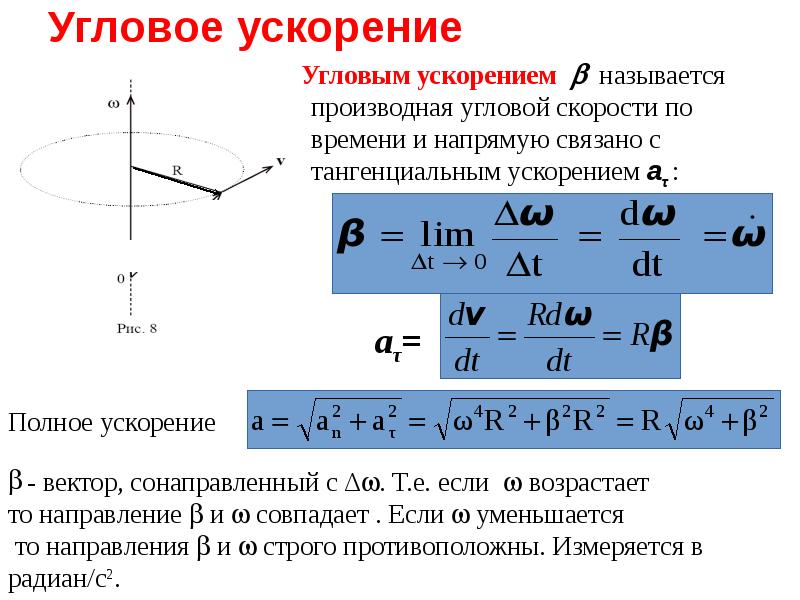
Исследовательская работа
по физике
Выполнил:
Ученик 10 «А» класса
МОУ СОШ №2
Костылев Сергей Анатольевич
Научный руководитель:
Мухина Г.В.
Объект исследования:
Вращающийся диск.
Предмет исследования:
Определение линейной и угловой скорости вращения диска.
Цель работы:
Проверить на практике правильность формулы зависимости линейной скорости от угловой для вращающегося диска V=ω*R
Задача:
Установить зависимость линейной скорости от угловой и радиуса вращения диска: определить линейную и угловую скорости диска.
Гипотеза:
Возможно, что линейная скорость вращения точек зависит от радиуса окружности, по которой двигаются точки диска; линейная и угловая скорости взаимосвязаны ( с увеличением угловой скорости линейная возрастает).
Введение:
При движении по криволинейной траектории, в том числе по окружности, скорость тела может изменяться как по модулю, так и по направлению. Возможно движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным. Такое движение называется равномерным движением по окружности.
Угловое перемещение измеряют в радианах (рад).
Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу.
Движение точки по окружности повторяется через определённые промежутки времени, равные периоду обращения.
Периодом обращения называется время, в течение которого тело совершает один полный оборот. Период обозначается буквой T и измеряют в секундах.
Период обозначается буквой T и измеряют в секундах.
Если за время t тело совершило N оборотов, то период обращения Т равен: Т = t / N
Частотой обращения называют число оборотов тела за одну секунду. ν = N / t
За единицу частоты принят 1 оборот в секунду. Эта единица называется герцем (Гц). 1 герц – это такая частота, при которой тело совершает один оборот за одну секунду. Частота и период обращения связаны следующим образом:
ν = 1 / T ; T = 1 / ν .
Движение тела по окружности характеризуется угловой скоростью. Угловая скорость – физическая величина, равная отношению углового перемещения к промежутку времени, за которое это перемещение произошло. Угловая скорость обозначается буквой ω (омега).
ω = φ / t .
За единицу угловой скорости принимают радиан в секунду
(рад/с).
За время, равное периоду обращения Т, тело совершает полный оборот, т. е. его угловое перемещение равно 2π. Поэтому угловая скорость при равномерном движении тела по окружности: ω = 2π / Т ; или ω = 2πν .
е. его угловое перемещение равно 2π. Поэтому угловая скорость при равномерном движении тела по окружности: ω = 2π / Т ; или ω = 2πν .
.
Выше рассматривалась такая характеристика криволинейного движения, как мгновенная скорость. Линейная скорость тела, равномерно движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории. Линейная скорость обозначается буквой υ.Так как модуль линейной скорости постоянен, то его можно определить по формуле: υ = S / t.
За время, равное периоду обращения, тело проходит путь, равный длине окружности, т.е. S = 2πR, поэтому
υ = 2πR / T.
Записанные равенства позволяют найти соотношение между угловой и линейной скоростями:
υ / ω = (2πR*T) / (T*2π) = R ; таким образом,
υ = ω *R и ω = υ / R.
Практическая часть:
Оборудование:
1)проигрыватель, 2)устройство для записи колебаний маятника, 3)секундомер, 4)транспортир, 5)лист белой бумаги (формат А-4), 6)ножницы, 7)нить, 8)набор иголок.
Ход работы
Определим угловую скорость вращения диска:
ω= φ/ t , где φ — угол поворота
t — время поворота
Угол поворота диска определим с помощью транспортира, время- с помощью записи колебаний маятника.
1)Определим период колебаний маятника по формуле:
T = t / N , где t – время наблюдения
N – число колебаний
Частота колебаний маятника: ν = 1 / Т
2)Включим проигрыватель, расположив над его диском
устройство для записи колебаний маятника,
предварительно прикрепив к диску лист белой бумаги.
На бумаге получим след от неподвижного маятника.
Он будет представлять окружность.
3)Приведём в движение маятник, отклонив его на угол
~ 5 . На листе получим запись колебаний маятника.
Используя её, определим одно полное колебание и
угол, на который повернётся диск за 1 полное
колебание маятника.
A 4) С помощью транспортира
определим угол поворота
диска φ= AOB .Время
φ
поворота диска равнопериоду колебания маятника:
B t = T
5) Вычислим угловую скорость
диска по формуле:
ω = φ / t = φ / T
6) Для определения линейной скорости диска
воспользуемся формулой: υ = S / t, где
S – длина дуги АВ ; t – время поворота диска
т.к. t = T, оно уже определено.
Длину дуги найдем с помощью нитки. Воткнём иголки
Воткнём иголки
в бумагу по всей длине дуги и с помощью нитки
найдём путь, пройденный диском от точки А до точки В.
Рассчитаем линейную скорость.
7) Проведём опыт 5 раз для нахождения среднего
значения Ѕ и Т.
Вычисления:
t
T =
N
0,99 с
T1 = =0,099 с
10 с
1 с
T2 = = 0,1 с
10 с
1,02 с
T3 = = 0,102 с
10 с
0,99 с
T4 = =0,099 с
10 с
0,99 с
T5 = = 0,099 с
10 с
T1 +T2 +T3 +T4 +T5 с 0,499
Tср. = = =0,099 с
5 5
φ1 рад
ω1 = ω1 = 3,5
T1 с
φ2 рад
ω2 = ω2 = 3,5
T2 с
φ3 рад
ω3 = ω3 = 3,4
T3 с
φ4 рад
ω4 = ω4 =3,5
T4 с
φ5 рад
ω5 = ω5 = 3,5
T5 с
ω1 + ω2 + ω3 + ω4 + ω5
ωср =
5
рад
ωср =3,48
с
S1 + S2 + S3 + S4 +S5 1,13 м
Sср = Sср = = 0,226 м
5 5
Sср м
Sср = 0,226 м vср = =2,28
Tср с
Проверим соотношение: v = ω R
Измерим радиус окружности R.
Определим ω R
И сравним с полученным экспериментально значением линейной скорости.
R =
ωср R =
vср =
Выясним зависимость линейной скорости от радиуса вращения точки. Меняя радиус вращения, определим значение линейной скорости движения точек. Результаты исследования представим в виде графика зависимости линейной скорости от радиуса окружности, по которой движутся точки диска.
Из графика следует, что скорость вращения точек диска пропорциональных радиусу окружности, что соответствует формуле v = ω R
Выводы:
Используя устройство для записи колебаний маятника, можно найти линейную и угловую скорости вращения диска проигрывателя.
vср = 2,28 м/с
ωср = 3,48 рад/с
Линейная и угловая скорости связаны соотношением:
v = ω R
Линейная скорость вращения точек диска зависит от радиуса окружности: чем больше радиус окружности, тем больше линейная скорость.

Используемая литература:
1) Большой справочник Физика. Дрофа, М.: 2008 год.
2) Большая школьная энциклопедия. Том 1. ОЛМА, М.: 2007 Г.
3) «Физика в школе» № 4, 1991 год, стр. 53.
Результаты запишем в таблицу:
опыта
Число
Колебаний
N
Время
Наблюдения
t , с
Период
Т,с
Тср
с
Угол поворота
φ, рад
φср,
рад
Длина дуги,
Ѕ,м
Ѕср,
м
Угловая скорость,
ω,рад\с
ωср
рад\с
υ
м\с
υср
м\с
1
10
0,99
0,099
0,099
3,5
3,5
0,215
0,226
3,5
3,48
2,17
2,28
2
10
1
0,1
3,5
0,23
3,5
2,3
3
10
1,02
0,2
3,5
0,22
3,4
2,15
4
10
0,99
0,099
3,5
0,22
3,5
2,22
5
10
0,99
0,099
3,5
0,245
3,5
2,47
Обороты и угловая скорость
Предположим, что \(\vec{a}\) не параллелен
\(\шляпа{б}\).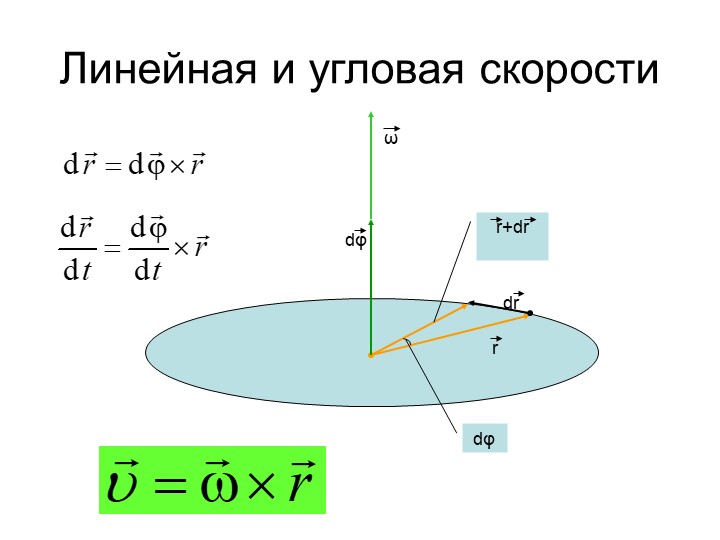 Тогда пусть \(\vec{v} = \hat{b} \times
\vec{a}\) и \(\vec{u} = \vec{v}
\times \vec{b}\), поэтому \(\hat{u}, \hat{v}, \hat{b}\)
является правым ортонормированным базисом. Брать
\(\phi\) угол между \(\vec{a}\) и
\(\шляпа{б}\). Затем мы делаем поворот на \(\theta\) в
плоскость \(\шляпа{u}\)-\(\шляпа{v}\):
Тогда пусть \(\vec{v} = \hat{b} \times
\vec{a}\) и \(\vec{u} = \vec{v}
\times \vec{b}\), поэтому \(\hat{u}, \hat{v}, \hat{b}\)
является правым ортонормированным базисом. Брать
\(\phi\) угол между \(\vec{a}\) и
\(\шляпа{б}\). Затем мы делаем поворот на \(\theta\) в
плоскость \(\шляпа{u}\)-\(\шляпа{v}\):
\[\begin{выровнено} \vec{a} &= a \sin\phi \,\шляпа{и} + а\cos\phi\,\шляпа{b} \\ \operatorname{Rot}(\vec{a};\theta,\hat{b}) &= a \cos\theta\sin\phi\,\hat{u} + a\sin\theta\sin\phi \,\шляпа{v} + \cos\phi\,\шляпа{b}.\конец{выровнено}\]
Теперь мы хотим преобразовать из
\(\шляпа{u},\шляпа{v},\шляпа{b}\) для записи повернутого
результат в терминах \(\vec{a}, (\hat{b} \times
\vec{a}), \шляпа{b}\). Для этого нам нужно работать
что такое \(\шляпа{u},\шляпа{v},\шляпа{b}\) с точки зрения
эти другие векторы.
\[\begin{align} \шляпа{v} &= \frac{\шляпа{b} \times \vec{a}}{\|\шляпа{b} \times \vec{a}\|} = \frac{\hat{b} \times \vec{a}}{a \sin\phi} \\ \шляпа{u} &= \frac{\vec{v} \times \шляпа{b}}{\|\vec{v} \times \vec{b}\|} = \ frac {\ vec {v} \ times \ hat {b}} {a \ sin \ phi} = \frac{(\шляпа{b} \times \vec{a}) \times \шляпа{b}}{a \sin\phi} = \frac{\hat{b} \times (\vec{a} \times \шляпа{b})}{а \sin\phi} \\ &= \frac{\vec{a} — (\шляпа{b} \cdot \vec{a}) \hat{b}}{a \sin\phi} = \frac{1}{a \sin\phi} \vec{a} — \frac{\hat{b} \cdot \vec{a}}{a \sin\phi} \hat{b}.\конец{выровнено}\]
Подставляя их в повернутое векторное выражение выше дает
\[\ начало {выровнено}
\operatorname{Rot}(\vec{a};\theta,\hat{b}) &= a
\cos\theta \sin\phi \, \left( \frac{1}{a \sin\phi}
\vec{a} — \frac{\hat{b} \cdot \vec{a}}{a
\sin\phi} \шляпа{b} \право) \\
& \qquad + a \sin\theta \sin\phi \, \left(
\ frac{\ hat {b} \ times \ vec {a}} {a \ sin \ phi} \ right)
+ a \cos\phi\,\hat{b} \\ &= \cos\theta
\,\vec{a} — \cos\theta \,(\hat{b} \cdot
\vec{a}) \,\шляпа{b} + \sin\theta \,(\шляпа{b} \times
\vec{a}) + a\cos\theta \,\hat{b} \\ &=
\cos\theta \,\vec{a} + (1 — \cos\theta) (\hat{b}
\cdot \vec{a}) \,\шляпа{b} + \sin\theta \,(\шляпа{b}
\times \vec{a}). \конец{выровнено}\]
\конец{выровнено}\]
греческих букв и символов: наиболее распространенное использование всех греческих букв
Если инженеры хоть немного знакомы с одним языком (хотя бы косвенно), то это греческий язык. Почему? Потому что греческие буквы — ежедневная часть жизни инженера, а инженеры привыкли каждый день бросаться своими именами. Инженеры, а также математики и ученые в ряде областей используют греческие буквы в качестве альтернативы числам или для описания характеристик объекта.
Итак, давайте рассмотрим все 24 греческие буквы и их значение в мире науки, математики и техники.
Источник: amzdeco Просто предупреждаю: если вы работаете в инженерной отрасли, не связанной со строительством или строительством, у вас могут быть другие применения для этих букв. Пожалуйста, не стесняйтесь сообщить нам, для чего вы используете эти буквы в разделе комментариев. Более того, строчные и прописные символы могут иметь разное значение при использовании в техническом контексте.
Вы можете рассматривать это как мини-справочник по использованию некоторых греческих букв.Без дальнейших задержек, вот греческие буквы на гиковском диалекте.
Альфа (α)Во-первых, альфа в нижнем регистре часто используется для обозначения альфа-частиц в физике. Он имеет множество других применений в науке и технике, в том числе для представления коэффициента поглощения, углов, углового ускорения, постоянной затухания, коэффициента усиления тока с общей базой, параметра отклонения состояния, температурного коэффициента сопротивления, коэффициента теплового расширения и температуропроводности.
Бета (β) В физике строчная буква Бета используется для обозначения бета-частиц или бета-лучей, которые представляют собой высокоэнергетические и высокоскоростные электроны. Он также используется для представления углов, коэффициента усиления тока с общим эмиттером, плотности потока, фазовой постоянной и постоянной длины волны.
Как вы уже догадались, еще одна радиационная буква — Гамма-излучение. Это одно из наиболее распространенных применений этой строчной буквы, в то время как прописная буква используется для аннотации граничного предела при выполнении двумерного анализа методом конечных элементов.Он также представляет электрическую проводимость и параметр Грюнайзена.
Дельта (Δ)Используемая во многих областях техники и физики, заглавная буква Дельта обычно обозначает разницу между любыми типами измерений. Например, если вы хотите узнать разницу между длиной 1 и длиной 2, запишите ее как ΔL. Интересно в этой греческой букве то, что строчные буквы могут обозначать две разные математические функции — функции Дирака и Кронекера.Он также используется для углов, коэффициента демпфирования (постоянная затухания), декремента, приращения и коэффициента вторичного излучения.
Эпсилон (ε) Возможно, здесь я необъективен, потому что я работаю в области строительства, но я часто использую строчную букву Эпсилон для обозначения деформации материала. В соответствии с заглавной дельтой деформация основного материала рассчитывается по следующей формуле.
В соответствии с заглавной дельтой деформация основного материала рассчитывается по следующей формуле.
ε = ΔL/L
Может также представлять емкость, диэлектрический ток, напряженность электрического поля, энергию электронов, излучательную способность, диэлектрическую проницаемость и константу 2.7128 или основание натуральных логарифмов.
Zeta (ζ)В инженерной динамике Zeta представляет коэффициент демпфирования колебательной системы. Его также можно использовать в других математических и физических приложениях для обозначения коэффициентов, координат и импеданса.
Eta (η)Строчная буква Eta имеет множество применений в физике и астрономии, например для представления конформного времени в космологии, химического потенциала, диэлектрической восприимчивости, эффективности, гистерезиса, собственного импеданса среды и собственного коэффициента зазора.
Тета (θ) Я полагаю, что каждый, кто читает это, знаком с этой греческой буквой, так как она обычно используется в тригонометрии. Он используется для представления угла поворота, углов, углового фазового смещения, сопротивления, теплового сопротивления и угла прохождения.
Он используется для представления угла поворота, углов, углового фазового смещения, сопротивления, теплового сопротивления и угла прохождения.
Если вам нравятся матрицы, вы должны знать, что йота в верхнем регистре используется в качестве единичной матрицы. Однако я обнаружил, что строчные буквы редко используются в инженерии, или, может быть, я просто никогда раньше не использовал уравнение со строчными буквами йота.Дайте нам знать, если у вас есть.
Каппа (κ)Постоянная гравитации Эйнштейна обозначается строчной Каппа, а в космологии кривизна Вселенной обозначается маленькой Каппа. Он также обозначает коэффициент связи и восприимчивость.
Лямбда (λ) Еще одна буква, с которой вы, вероятно, знакомы. Лямбда часто используется как символ длины волны как в науке, так и в технике. Но мое любимое использование лямбды в нижнем регистре — это ее обозначение собственного значения в линейной алгебре. Проблема собственных значений — это такой простой, но мощный расчет, который вы можете выполнять в задачах о вибрации. Он также используется в качестве линейной плотности заряда, постоянства и светочувствительности.
Проблема собственных значений — это такой простой, но мощный расчет, который вы можете выполнять в задачах о вибрации. Он также используется в качестве линейной плотности заряда, постоянства и светочувствительности.
Теперь Mu может означать множество вещей в физике и технике. Обычно Mu используется как префикс «микро» с точки зрения измерения. Итак, если вы хотите сказать микрометр, вы должны написать это как мкм. Он также используется для обозначения коэффициента усиления, магнитной проницаемости, микрона, подвижности и проницаемости.
Nu (ν)В мире строительства и машиностроения Nu определяет коэффициент Пуассона, который представляет собой отношение того, насколько материал уменьшается в ширину и увеличивается в длину при растяжении.
Xi (ξ) Еще одна греческая буква, являющаяся героем инженерной динамики — строчная Xi. Вместо того, чтобы записывать полный коэффициент демпфирования, его можно упростить, используя эту строчную букву. Это помогает, когда у вас действительно длинное уравнение.Он также используется для обозначения выходного коэффициента.
Это помогает, когда у вас действительно длинное уравнение.Он также используется для обозначения выходного коэффициента.
Эта греческая буква имеет более астрономическое значение, так как она обозначает пятнадцатую звезду в группе созвездий.
Пи (π)Возможно, это самая знаковая и известная греческая буква, она обозначает число Пи или 3,14159… и так далее. Пи обычно используется в геометрии, так как это отношение длины окружности к диаметру. Независимо от размера круга, отношение длины окружности к диаметру всегда равно Пи.
Rho (ρ)Это очень сбивало меня с толку, когда я учился в старшей школе. В основном это похоже на строчную букву P, но пишется по-разному. Он используется для обозначения плотности, а также коэффициента отражения, коэффициента отражения, удельного сопротивления и поверхностной плотности заряда.
Сигма (σ) Если и существует одна греческая буква, которая могла бы описать жизнь инженера, то это была бы строчная сигма, обозначающая ударение в большинстве инженерных отраслей. Напряжение подшипника, термическое напряжение, упругое напряжение, напряжение фон Мизеса и любые другие типы напряжения, о которых могут думать инженеры, обычно обозначаются как сигма. Однако сигма в верхнем регистре наиболее популярна для обозначения «суммы» любых значений.
Напряжение подшипника, термическое напряжение, упругое напряжение, напряжение фон Мизеса и любые другие типы напряжения, о которых могут думать инженеры, обычно обозначаются как сигма. Однако сигма в верхнем регистре наиболее популярна для обозначения «суммы» любых значений.
Больше стресса! Тау обычно используется для обозначения определенного типа напряжения, называемого напряжением сдвига, а также постоянной распространения, коэффициента Томсона, постоянной времени, временного фазового смещения и коэффициента передачи.
Ипсилон (Y)Прописные буквы Ипсилон часто используется в астрофизике и обозначает отношение массы к свету.
Phi (φ) При работе с круглыми объектами, такими как трубы, Phi обычно используется для обозначения их диаметра, а также для обозначения углов, коэффициента полезного действия, контактного потенциала, магнитного потока, фазового угла, фазового смещения, и лучистый поток.
Нижний регистр Chi обычно используется в расчете конструкций для обозначения коэффициента снижения изгибающих нагрузок.
Psi (ψ)Psi часто используется в физике для обозначения волновых функций в квантовой механике и даже используется для обозначения планеты Нептун!
Омега (ω)Оставьте лучшее напоследок.Это, безусловно, моя любимая греческая буква, поскольку она обозначает частоту в мире структурной динамики. Эта базовая формула динамики продвинет вас далеко вперед в структурной динамике и инженерии землетрясений, если вы столкнетесь лицом к лицу с такими демонами.
ω 2 = k/m
Конечно, прописная буква также используется для обозначения Ом в электротехнике — я бы не пропустил это.
Итак, краткий обзор научного, математического и инженерного значения всех 24 греческих букв.Дайте нам знать, если мы пропустили значительное использование любого из этих алфавитов через раздел комментариев.
Вы зашли так далеко. Итак, мы предполагаем, что вы любите математику?
| v , v | скорость, скорость | м/с | метров в секунду |
| и , и | ускорение | м/с 2 | метров в секунду в квадрате |
| а с , а с | центростремительное ускорение, центробежное ускорение | м/с 2 | метров в секунду в квадрате |
| г , г | гравитационное поле, ускорение свободного падения | м/с 2 | метров в секунду в квадрате |
| м | масса | кг | килограмм |
| Ф , Ф | сила | Н | ньютон |
| Ж г , | сила тяжести, вес | Н | ньютон |
| Ф Н , | нормальное усилие, нормальное | Н | ньютон |
| Ф ф , | 4 к 4сила трения (статическая, кинетическая) | Н | ньютон |
| мк с , мк к | коэффициент трения (статический, кинетический) | безразмерный | |
| р , р | импульс | кг м/с | килограмм метр в секунду |
| Дж , Дж | импульс | Н с | ньютон секунд |
| Ш | работа | Дж | джоулей |
| Е | энергия, общая энергия | Дж | джоулей |
| К , | кинетическая энергия (поступательная, вращательная) | Дж | джоулей |
| У , | потенциальная энергия (гравитационная, пружинная) | Дж | джоулей |
| В г | гравитационный потенциал | Дж/кг | джоулей на килограмм |
| η | эффективность | безразмерный | |
| П | мощность | Вт | Вт |
| ω , ω | скорость вращения, скорость вращения | рад/с | радиан в секунду |
| α , α | ускорение вращения | рад/с 2 | радиан на секунду в квадрате |
| т , т | крутящий момент | Н·м | ньютон-метр |
| я | момент инерции | кг м 2 | килограмм метр в квадрате |
| л , л | угловой момент | кг м 2 /с | килограмм-метр в квадрате в секунду |
| Х , Х | угловой импульс | Н·м·с | ньютон метр секунд |
| к | жесткость пружины | Н/м | ньютонов на метр |
| П | давление | Па | паскалей |
| о | нормальное напряжение | Па | паскалей |
| т | напряжение сдвига | Па | паскалей |
| р | плотность, объемно-массовая плотность | кг/м 3 | килограмм на кубический метр |
| о | удельная массовая плотность, поверхностная массовая плотность | кг/м 2 | килограмм на квадратный метр |
| λ | линейная массовая плотность | кг/м | килограмм на метр |
| Ф Б , | плавучесть, выталкивающая сила | Н | ньютон |
| q м | массовый расход | кг/с | кг в секунду |
| q В | объемный расход | м 3 /с | кубических метров в секунду |
| Ф Д , | сопротивление, аэродинамическое сопротивление, сопротивление воздуха | Н | ньютон |
| К , К Д | коэффициент аэродинамического сопротивления, коэффициент аэродинамического сопротивления | безразмерный | |
| η | вязкость, динамическая вязкость | Па с | паскалей секунды |
| ν | кинематическая вязкость | м 2 /с | квадратных метров в секунду |
| млн лет | число Маха | безразмерный | |
| Ре | число Рейнольдса | безразмерный | |
| Пт | фроуд номер | безразмерный | |
| Е | модуль Юнга, модуль упругости | Па | паскалей |
| Г | модуль сдвига, модуль жесткости | Па | паскалей |
| К | объемный модуль, модуль сжатия | Па | паскалей |
| ε | линейная деформация | безразмерный | |
| γ | деформация сдвига | безразмерный | |
| θ | объемная деформация | безразмерный | |
| γ | поверхностное натяжение | Н/м | ньютонов на метр |
Объясните это любителю математики
Спейс-Нидл, Сиэтл, Вашингтон
23 декабря 2011 г.
Сидя в кофейне в 1959 году, Эдвард Э.Карлсон воображал и набрасывал башню будущего, которая возвышалась над Всемирной выставкой 1962 года в Сиэтле. После многих итераций и участия архитектора Джона Грэма появилась форма, вдохновленная летающей тарелкой, которую мы знаем (и, по крайней мере, некоторые из нас любят). 1
Башня Спейс-Нидл в Сиэтле имеет высоту 605 футов. Целое блюдце не вращается. Вращается только участок шириной 14 футов рядом с окнами ресторана SkyCity. Двигатель мощностью 1,5 л.с. приводит в движение вращение, а вращающаяся секция совершает 1 оборот каждые 47 минут.Кроме того, ресторан находится на высоте 500 футов и имеет диаметр 94,5 фута.
Если это похоже на создание сюжетной проблемы, так и должно быть. Меление, которое я сделал у подножия Спейс-Нидл, связано с угловой скоростью. Угловая скорость используется в расчетах скорости объекта, вращающегося вокруг фиксированной точки. Мы делаем это различие «угловой» скоростью, потому что когда речь идет о круговом движении, случаются забавные вещи.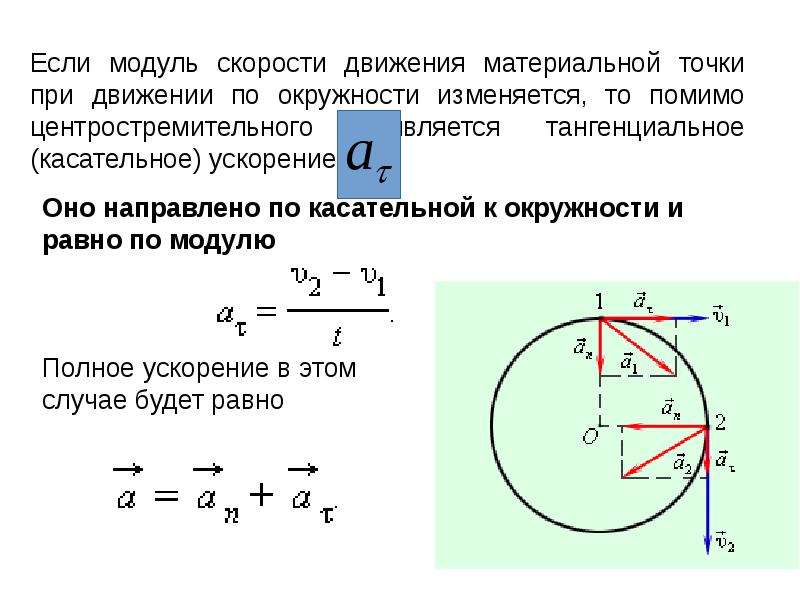
Греческая буква омега, ω, используется для обозначения угловой скорости.
Это обозначение пришло из исчисления, где ω можно рассматривать как производную, мгновенную скорость изменения. Буква d используется для изменения и представляет собой эволюцию использования греческой буквы дельта, Δ. Уравнение просто говорит, что ω – это скорость мгновенного углового изменения, dΦ , по отношению к мгновенному изменению времени.
Работа с угловой скоростью часто связана с векторами. 2 Векторы — это математические объекты, используемые в физике, поскольку они содержат две важные части информации: величину и направление.Графически стрелка используется для представления вектора. Длина стрелки определяется величиной вектора, а направление, на которое указывает стрелка, определяется направлением вектора. В случае скорости величина или длина вектора представляет скорость.
Угловая скорость измеряется в радианах в секунду. Радианы — это альтернативный способ измерения углов.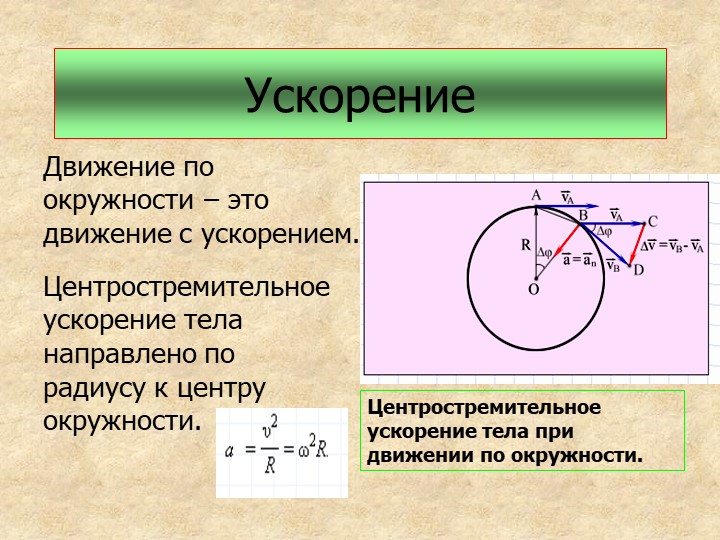 Вместо того, чтобы основываться на, казалось бы, произвольном числе (360) 3 , радианы основаны на том, что мы знаем о окружностях.Радиан супер! Вот краткое руководство:
Вместо того, чтобы основываться на, казалось бы, произвольном числе (360) 3 , радианы основаны на том, что мы знаем о окружностях.Радиан супер! Вот краткое руководство:
Мы знаем, что длину окружности C можно найти с помощью C = 2π r . Окружность радиусом 1 единица имеет длину окружности 2π. Тогда 360° в некотором смысле эквивалентны 2π. 180° переводится в 1π. И наш дорогой друг 90° можно преобразовать в π/2 радиана. (Небольшой тест: чему равен радиан для угла 45°?)
Опять же, угловая скорость измеряется в радианах в секунду. Используя то, что мы узнали из краткого руководства, один оборот равен 2π радианам.Если мы умножим число оборотов в секунду, которое вращается объект, на 2π, мы получим скорость вращения объекта, то есть его угловую скорость.
В случае с лентой пола, вращающейся в ресторане в Спейс-Нидл, пока мы знаем, что для совершения одного оборота требуется 47 минут. Преобразуем эту скорость в радианы в секунду. Поскольку в минуте 60 секунд, один оборот совершается каждые 47 × 60 = 2820 секунд.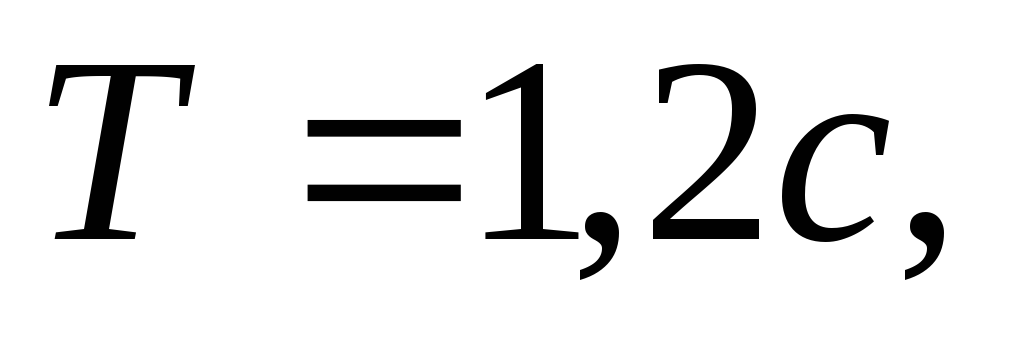 Затем каждую секунду совершается 1/2820 оборота.Умножение на 2π даст угловую скорость.
Затем каждую секунду совершается 1/2820 оборота.Умножение на 2π даст угловую скорость.
Секция пола в Спейс-Нидл имеет угловую скорость ω = π/1410 рад/с ≈ 0,002 рад/с. Но это еще не все.
Большинству из нас приходилось вращаться вокруг фиксированной точки. Я предполагаю, что 95% читателей играли на классическом игровом оборудовании, известном как карусель. Как вы помните, ваше ощущение того, насколько быстро вы движетесь, зависело от того, насколько близко или далеко вы находились от центра карусели.Это было не только ваше чувство. По мере удаления от центра ваше тело перемещается на большее расстояние за то же время. Как преодолеть большее расстояние за то же время? Вы идете быстрее.
Как математики и ученые, мы хотели бы объяснить это явление. Для этого нас интересует движение перпендикулярно радиусу от центра вращения. Это направление, в котором вы бы летели, если бы отпустили карусель, несмотря на ощущение, что вас отбрасывает наружу.Мгновенная линейная скорость, которую мы хотим, является произведением расстояния от оси вращения, r , и угловой скорости.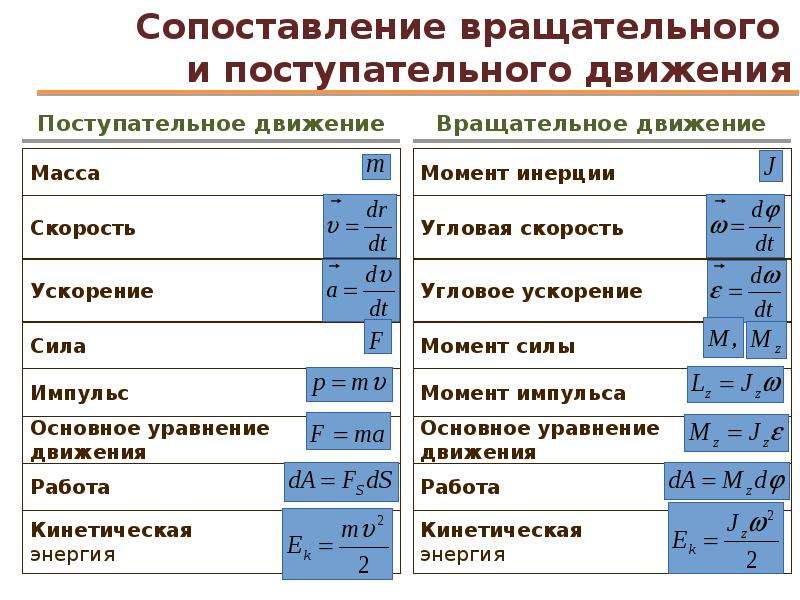
Поскольку радиус ресторана равен 94,5 / 2 = 47,25 фута, мгновенная линейная скорость человека, стоящего (совсем) возле окон ресторана, составляет около 0,105 фута/с.
При переводе в мили в час мгновенная линейная скорость равна 0,072 мили/ч. Чтобы дать этому некоторый контекст, на поверхности Земли мы вращаемся 1 оборот или 2π радиан / день.Один день равен 86 400 секунд.
Для человека, стоящего на экваторе, его линейная скорость из-за вращения Земли составляет от одной четверти до одной трети мили в секунду.
Это около 1037,511 миль/ч. По сравнению с вращением Земли пол ресторана движется очень медленно. Да, вы замечаете вращение пола в ресторане, потому что вы поворачиваетесь, а вещи вокруг вас — нет. А на поверхности земли все вращается вместе с вами.
Фотографии сделаны Карен Ассери http://karenussery.com/.
1. Чтобы узнать больше о Space Needle, посетите http://en.wikipedia.org/wiki/Space_Needle и http://www. spaceneedle.com/discover/funfacts.html.
spaceneedle.com/discover/funfacts.html.
2. В Интернете есть отличные ресурсы по математике и физике. Я ссылался на следующие сайты при разборе деталей угловой скорости:
http://en.wikipedia.org/wiki/Angular_velocity
http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html
http://www.sparknotes.com/testprep/books/sat2/physics/chapter10section3.rhtml
Да, верно. Я не разобрался со всем этим, прежде чем решил записать угловую скорость в Сиэтле. Моя подруга Карен, фотограф этой прогулки, посоветовала мне нарисовать мелом что-то конкретное здесь, в Сиэтле, и Спейс-Нидл просто продолжал стоять там, пытаясь притвориться невинным.
3. Учитывая, что мы все выросли на 360, это, вероятно, не кажется произвольным, и на самом деле это не так.Будь то приблизительное количество дней в году или вавилонская шестидесятеричная система счисления (основание 60), деление круга на 360 частей имеет определенный смысл.
Нравится:
Нравится Загрузка. ..
..
Математика? Для меня это все греческий
Почему в математике так много греческого языка?
Знаете ли вы, что…
α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω
- Греческий (ελληνκα), вероятно, древнейший европейский язык (разговорный 4000 лет и письменный 3000 лет)
- Греческий язык использовался на Ближнем Востоке и даже в Индии в эллинистический период (с 330 г. до н.э. по 100 г. н.э.).Раннехристианские писатели использовали греческий язык, и в одном отрывке говорится, что Бог есть «Альфа и Омега» (Α и Ω, первая и последняя буквы греческого алфавита), что означает, что Он есть начало и конец 90 982.
- Это был официальный язык Византийской империи (римская цивилизация с центром в Константинополе – современный Стамбул в Турции – с 380 по 1483 год н.э.), которая простиралась на большую часть Средиземноморья и Ближнего Востока
- Важно отметить (из-за его общего использования в математике ), что греческий язык широко использовался для публикации научных открытий во время европейского Возрождения (15 век)
Общеупотребительные греческие буквы, используемые в математике
Вероятно, первая греческая буква, с которой сталкивается любой из нас, — это π ( pi ), значение, которое получается при делении длины окружности на ее диаметр. Пи было выбрано для обозначения «периметра».
Пи было выбрано для обозначения «периметра».
Тригонометрия широко использует θ ( тета ) в качестве переменной для углов, а также в статистике.
Второе место по углам занимает phi (нижний регистр: φ, верхний регистр: Φ). Фи также является символом, используемым для золотого сечения (1,618… См. Математика красоты.)
Первые 3 буквы греческого алфавита, α ( альфа ), β ( бета ) и γ ( гамма ) также используются в тригонометрии в качестве переменных для углов.Вы также столкнетесь с гаммой в верхнем регистре (Γ) как с переменной или как с именем функции.
24-я и последняя буква греческого алфавита, омега (ω, верхний регистр: Ω) обычно используется в электричество . Единицей измерения сопротивления является ом (Ом), а угловая скорость объекта, вращающегося вокруг оси, записывается как ω, а единицами измерения обычно являются радианы в секунду.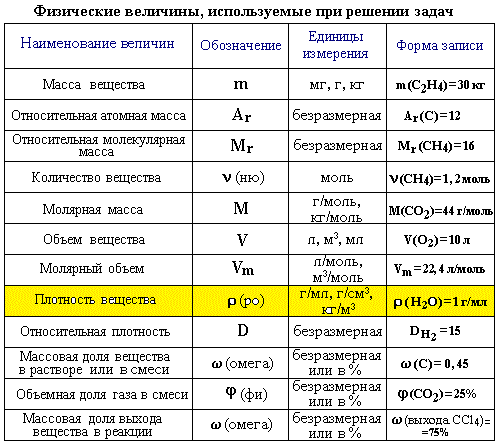 (См. Применение радианов.) О-мега означает «большой О».
(См. Применение радианов.) О-мега означает «большой О».
В научной нотации мы используем mu (μ) для префикса «микро» или 10 -6 .Так, например, человеческий волос имеет ширину около 50 мкм.
Дельта (δ, верхний регистр: Δ) часто используется, когда пишут о дифференцировании в исчислении. Это часто означает «небольшое изменение» количества. Таким образом, δ x (или Δ x ) означает «небольшое изменение x ». Пятая греческая буква ε ( эпсилон ) также используется в исчислении для обозначения «чрезвычайно малое количество — почти нуль».
Следующим идет лямбда (λ, верхний регистр: Λ), который используется для длины волны периодической волны.
Вы встретите сигма в вероятности и статистике . Сигма верхнего регистра (Σ) используется для «суммы» (см. «Обозначение суммирования»), а нижний регистр (σ) используется для стандартного отклонения показателя совокупности в статистике.
Плотность объекта представлена rho (ρ, верхний регистр: Ρ). Ро также используется в сферических полярных координатах для представления радиуса.
Реже используемые греческие буквы
Обычно вы видите только следующие греческие буквы в математике университетского уровня.Как таковые, их труднее запомнить (а некоторые из них трудно произнести!). Надеюсь, этот список греческих букв (с их обычным произношением названий букв в английском языке, не обязательно так, как их произносят греки) поможет вам.
Zeta , произносится как zeeta: Ζ, ζ — 6-я буква алфавита (не последняя)
Эта , произносится как «эта»: Η, η
Йота , произносится как «глаз-о-та»: Ι, ι — используется в английском выражении «ни на йоту разницы» для обозначения «почти идентичны».
Каппа : Κ, κ
Nu , произносится как «ноо»: Ν, ν
Xi , произносится как «вздох»: Ξ, ξ
Омикрон : Ο, ο — О-микрон означает «маленький О».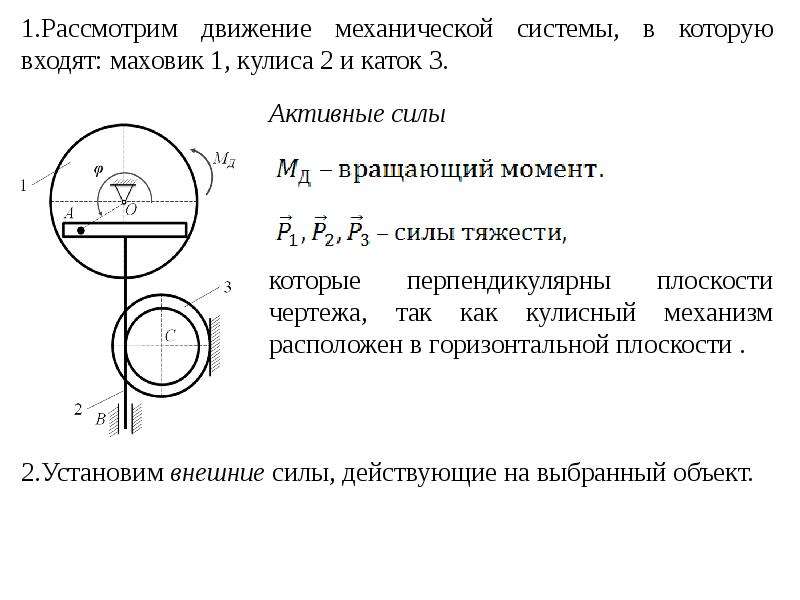 (Помните О-мега или «большое О» выше?)
(Помните О-мега или «большое О» выше?)
Тау , рифмуется со словом «как»: Τ, τ — см. Цепь Серии RL для одного использования Тау в качестве единицы времени.
Ипсилон , произносится как «упс-и-лон»: Υ, υ
Чи , произносится как «кай» рифмуется с «глаз»: Χ, χ
Psi , произносится как «вздох» (да, то же, что и Xi): Ψ, ψ — в словах «психология» и «психиатрия» — буква «р» обычно не произносится.
Утопия
Итак, теперь, после всего этого, надеюсь, вы находитесь в математической утопии . Слово «утопия» происходит от греческого «нигде».
См. 7 комментариев ниже.
Источники: |
5.
 3 Угловое ускорение – Биомеханика движений человека
3 Угловое ускорение – Биомеханика движений человекаУгловое ускорение обозначается греческой буквой альфа (α). Угловое ускорение представляет собой скорость изменения угловой скорости во времени. Другой способ подумать об этом — как быстро что-то ускоряется или замедляется.
ускорение (α) = Δω/Δt
Единицы измерения: рад/с 2 или градус/с 2 . Когда скорость увеличивается, ускорение происходит в том же направлении вращения, чтобы увеличить скорость.Когда скорость уменьшается, должно быть ускорение в направлении, противоположном движению, действующее как тормоз, чтобы уменьшить скорость.
Ускорение имеет направление. Если объект движется в направлении против часовой стрелки (+) и набирает скорость, ускорение положительное. Если скорость уменьшается, ускорение отрицательно. Если объект движется по часовой стрелке (-) и набирает скорость, ускорение отрицательно. Если скорость уменьшается, ускорение положительно.
Пример 1. Расчет углового ускорения и замедления велосипедного колеса
Предположим, подросток кладет свой велосипед на спину и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об/мин за 5,00 с. (a) Рассчитайте угловое ускорение в рад/с 2 . (b) Если теперь она ударит по тормозам, вызывая угловое ускорение -87,3 рад/с 2 , сколько времени понадобится колесу, чтобы остановиться?
Стратегия для (а)
Угловое ускорение можно найти непосредственно из его определения в [latex]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}[/latex], поскольку даны конечная угловая скорость и время .Мы видим, что Δω — это 250 об/мин, а Δ t — это 5,00 с.
Решение для (а)
Вводя известную информацию в определение углового ускорения, получаем
[латекс]\begin{array}{lcl} \boldsymbol{\alpha} & \boldsymbol{=} & \boldsymbol{\frac{\Delta\omega}{\Delta{t}}} \\ {} & \ boldsymbol{=} & \boldsymbol{\frac{250\textbf{об/мин}}{5.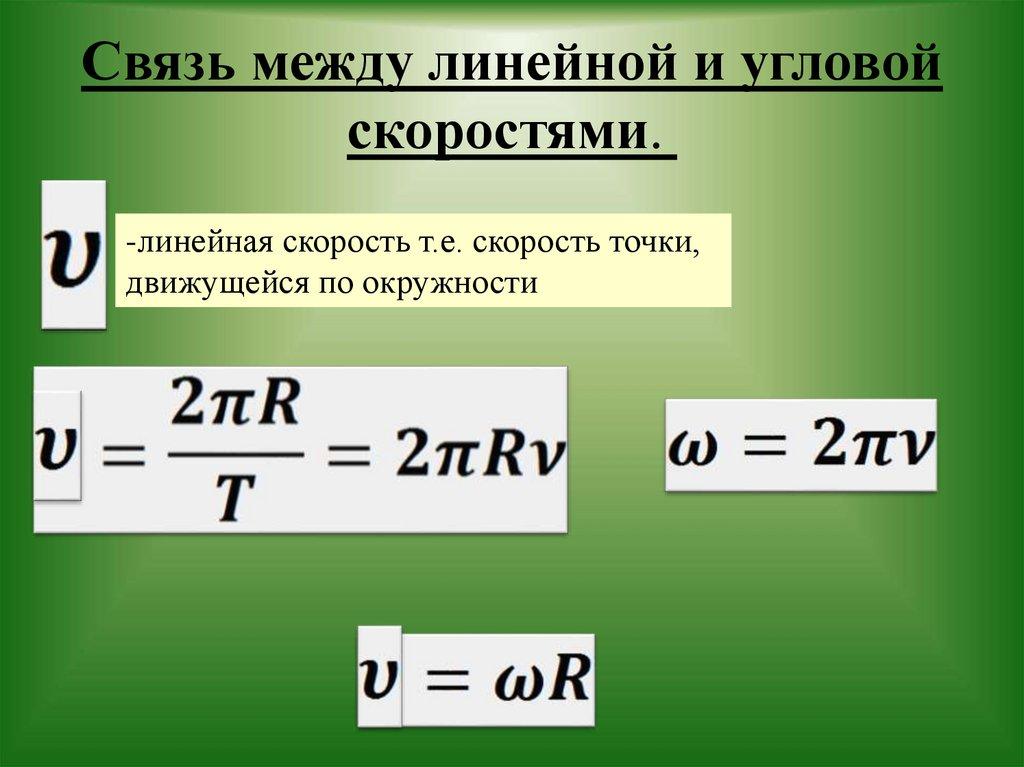 00\textbf{с.}}} \end{массив}[/latex]
00\textbf{с.}}} \end{массив}[/latex]
Поскольку Δω выражается в оборотах в минуту (об/мин) и нам нужны стандартные единицы измерения рад/с 2 для углового ускорения, нам нужно преобразовать Δω из об/мин в рад/с:
[латекс]\begin{array}{lcl} \boldsymbol{\Delta\omega} & \boldsymbol{=} & \boldsymbol{250\frac{\textbf{rev}}{\textbf{min}}\cdotp\ frac{2\pi\textbf{ рад}}{\textbf{об}}\cdotp\frac{1\textbf{ мин}}{60\textbf{ сек}}} \\ {} & \boldsymbol{=} & \boldsymbol{26.2} \end{массив}[/латекс]
Стратегия для (б)
В этой части нам известны угловое ускорение и начальная угловая скорость. Мы можем найти время остановки, используя определение углового ускорения и решив для Δ t , что даст
[латекс]\boldsymbol{\Delta{t}\:=}\boldsymbol{\frac{\Delta\omega}{\alpha}}.[/latex]
Решение для (б)
Здесь угловая скорость уменьшается с 26.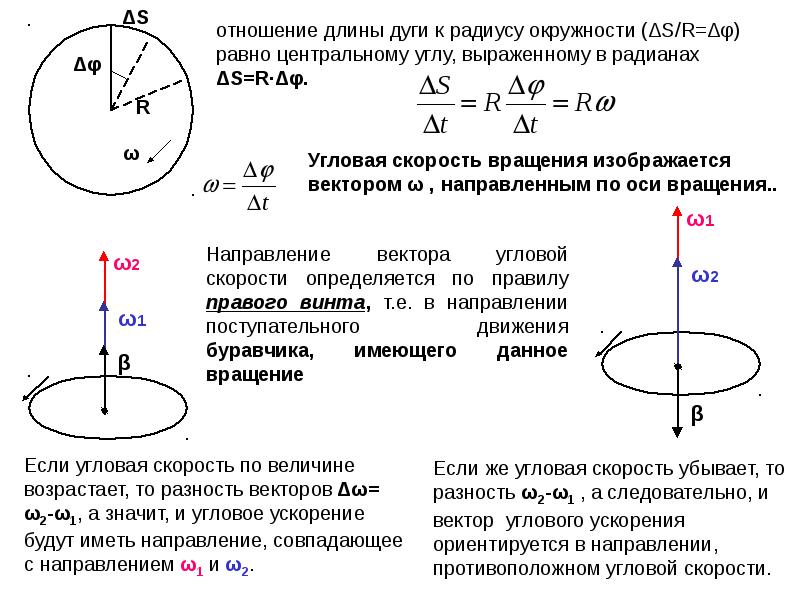 2}} \\ {} & \boldsymbol{=} & \boldsymbol{0,300\textbf{ с.}} \end{массив}[/latex]
2}} \\ {} & \boldsymbol{=} & \boldsymbol{0,300\textbf{ с.}} \end{массив}[/latex]
Обсуждение
Обратите внимание, что угловое ускорение, когда девушка крутит колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.
Если бы велосипед в предыдущем примере находился на своих колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение равно касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением a t .
Таким образом, линейное ускорение называется тангенциальным ускорением a t .
Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Мы знаем , что при круговом движении центростремительное ускорение a c относится к изменениям направления скорости, но не к ее величине.Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3. Таким образом, a t и a c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t напрямую связано с угловым ускорением [латекс]\жирныйсимвол{\альфа}[/латекс] и связано с увеличением или уменьшением скорости, но не с ее направлением.
Тангенциальное ускорение a t напрямую связано с угловым ускорением [латекс]\жирныйсимвол{\альфа}[/латекс] и связано с увеличением или уменьшением скорости, но не с ее направлением.
Теперь мы можем найти точное соотношение между линейным ускорением a t и угловым ускорением [латекс]\boldsymbol{\alpha}[/латекс]. Поскольку линейное ускорение пропорционально изменению величины скорости, оно определено как
.[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta{v}}{\Delta{t}}.}[/латекс]
Для кругового движения обратите внимание, что v = r ω , так что
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}. }[/latex]
}[/latex]
Радиус r является постоянным для кругового движения, поэтому Δ( r ω)= r (Δω) . Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r}\boldsymbol{\frac{\Delta\omega}{\Delta{t}}.}[/latex]
По определению [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}.[/латекс] Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha},[/латекс]
или
[латекс] \boldsymbol{\alpha\:=}\boldsymbol{\frac{a_{\textbf{t}}}{r}.}[/latex]
Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес велосипеда, тем больше ускорение велосипеда.Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении [латекс]\boldsymbol{\alpha}[/латекс].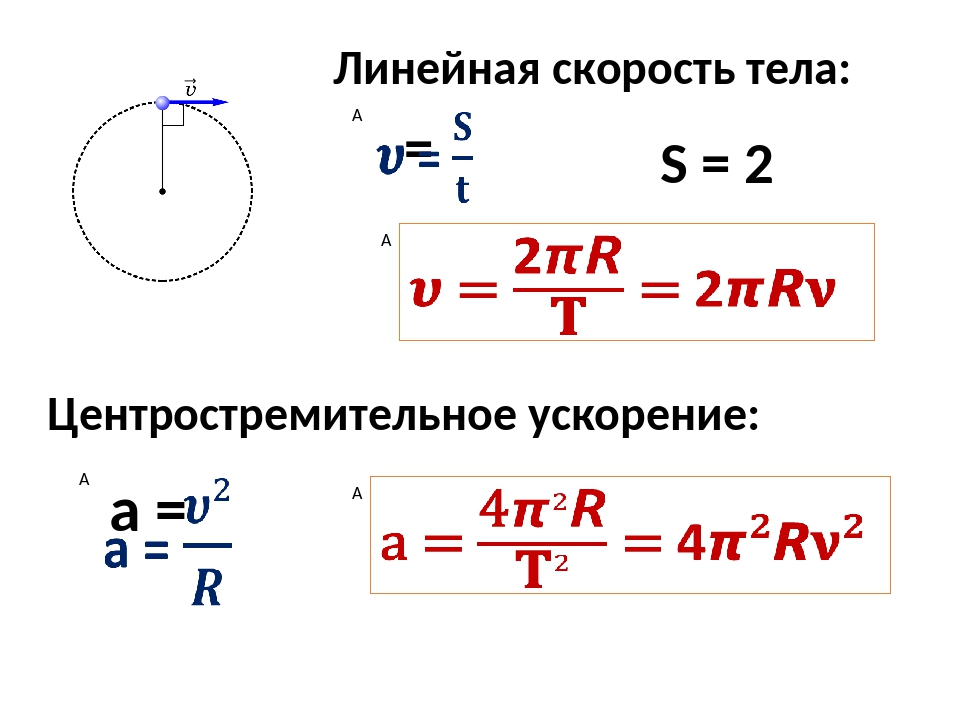
До сих пор мы определили три величины вращения — θ , ω и [латекс]\жирныйсимвол{\альфа}[/латекс]. Эти величины аналогичны поступательным величинам x , v и a . В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Поворотный | Трансляционное | Отношения |
|---|---|---|
| [латекс]\boldsymbol{\theta}[/латекс] | [латекс]\boldsymbol{x}[/латекс] | [латекс] \boldsymbol{\theta=\frac{x}{r}}[/латекс] |
| [латекс]\boldsymbol{\omega}[/латекс] | [латекс]\boldsymbol{v}[/латекс] | [латекс]\boldsymbol{\omega=\frac{v}{r}}[/латекс] |
| [латекс]\boldsymbol{\alpha}[/латекс] | [латекс]\boldsymbol{a}[/латекс] | [латекс] \boldsymbol{\alpha=\frac{a_{\textbf{t}}}{r}}[/latex] |
Таблица 1. Вращательные и поступательные величины. Вращательные и поступательные величины. | ||
- Равномерное круговое движение — это движение с постоянной угловой скоростью [латекс]\жирныйсимвол{\омега=\фракция{\Delta\theta}{\Delta{t}}}.[/latex]
- При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t} }}.[/латекс]
- Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]\жирныйсимвол{а_{\текстбф{т}}=\фракция{\Delta{v}}{\Delta{t} }}.[/латекс]
- Для кругового движения обратите внимание, что v = r ω , так что
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}}.[/latex]
- Радиус r постоянен для кругового движения, поэтому Δ( r ω)= r Δω .
 Таким образом,
Таким образом,[латекс]\boldsymbol{a_{\textbf{t}}=r}\boldsymbol{\frac{\Delta\omega}{\Delta{t}}}.[/latex]
- По определению, Δω/Δ t = [латекс]\жирныйсимвол{\альфа}[/латекс].Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha}[/латекс]
или
[латекс]\boldsymbol{\alpha=}\boldsymbol{\frac{a _{\textbf{t}}}{r}}.[/latex]
Задачи и упражнения
4: Необоснованные результаты
Вам известно, что баскетболист вращает мяч с угловым ускорением 100 рад/с 2 . а) Чему равна конечная угловая скорость мяча, если мяч стартует из состояния покоя и ускорение длится 2.00 с? б) Что неразумного в результате? (c) Какие посылки являются неразумными или непоследовательными?
Глоссарий
- угловое ускорение
- скорость изменения угловой скорости во времени
- изменение угловой скорости
- разница между конечным и начальным значениями угловой скорости
- тангенциальное ускорение
- ускорение в направлении касательной к окружности в интересующей точке при круговом движении
Решения
Задачи и упражнения
4:
.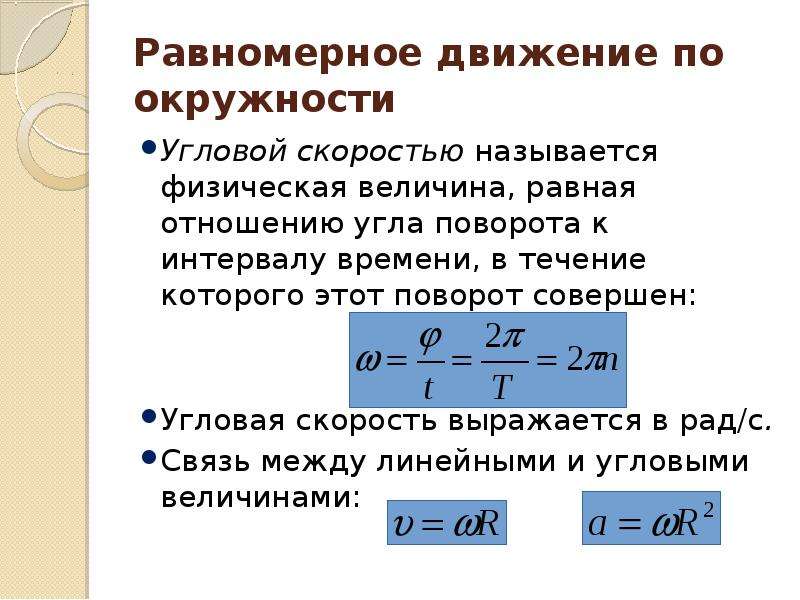


 Таким образом,
Таким образом,