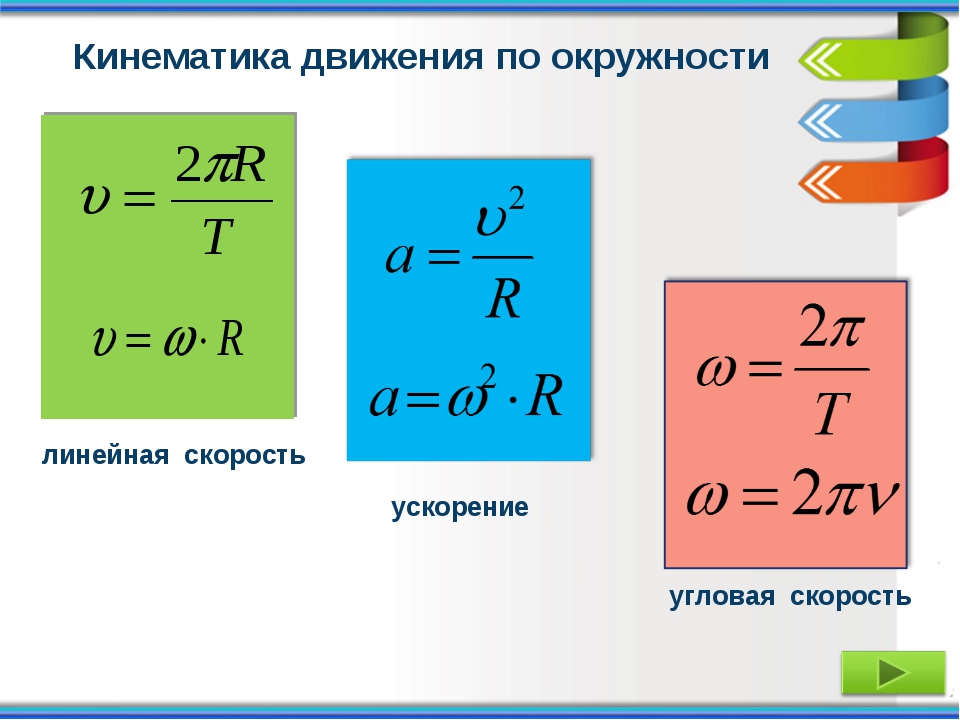
Период через скорость и радиус: Как можно найти период обращения зная радиус окружности и скорость движения тела?

Содержание

Радиус окружности — что такое, формула, как найти ⚪

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных.

Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a² + b², где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Сгубивший динозавров астероид проливает свет на зарождение жизни

23 марта 2017

Автор фото, Science Photo Library

Подпись к фото,

Во времена падения Чиксулубского астероида магнитное поле Земли имело противоположную полярность

Мексиканский кратер Чиксулуб, возникший на месте падения астероида 65 млн лет назад, проливает свет на появление микроорганизмов на Земле, сообщают специалисты Лунарного и планетарного института в Хьюстоне.

Ученые пробурили 829-метровую воронку вглубь 180-километрового кратера. В первую очередь палеонтологи изучили стены кратера, примерно половина которого сейчас скрыта под водами Мексиканского залива, а также примерно 600-метровым слоем морских отложений.

65 млн лет назад произошло событие, приведшее к исчезновению за короткий по геологическим меркам период около 70-75% всех земных видов и, в частности, динозавров, не относящихся к пернатым. Это событие ассоциируется многими учеными со столкновением с космическим телом в Чиксулубе.

Сильнейшее столкновение вызвало пожары, землетрясения и мощные цунами. Как полагают геологи, выброшенные в атмосферу облака пыли и газа могли на несколько лет вызвать глобальное похолодание на Земле, что ускорило процесс вымирания.

Команда исследовала образцы почвы с разных глубин в мае-июне прошлого года. Команда геологов и палеонтологов намеревалась исследовать так называемое «пиковое кольцо» — сердцевину кратера, где горные породы максимально сместились в результате удара астероида.

Как замечают специалисты, тщательно изученные отложения показывают, что кратер стал своего рода гигантской геотермальной системой, где горячая жидкость выливалась сквозь трещины и разломы.

«Это впечатляет, поскольку мы используем Чиксулуб для моделирования других крупных [геологических] событий из самой ранней истории Земли, когда эти системы могли быть колыбелью для химической [добиологической] эволюции и «горячими точками» эволюции самых первых проявлений жизни на нашей планете», — заметил доктор Дэвид Кринг из Лунарного и планетарного института в американском Хьюстоне.

Автор фото, Science Photo Library

Подпись к фото,

Падение астероида пережили порядка 20-25% видов живых существ на планете; тираннозавры в число счастливчиков не вошли

Столкновение метеорита с Землей, по словам специалиста, должно было породить очень крупную подводную систему горячих источников. Нынешние горячие ключи на месте падения метеорита бьют уже более 2 млн лет.

Центральная часть кратера на мексиканском полуострове Юкатан составляет 15 километров в диаметре.

С языка майя название «Чиксулуб» переводится неоднозначно: «блохастый дьявол», «украшенный рог» или «демон клещей» — в зависимости от трактовки.

Эксперт по палеомагнетизму Ратгерского университета в Нью-Джерси профессор Соня Тику заметила, что изученный материал позволяет ученым определить нижнюю границу периода существования подводных источников.

На Земле каждые несколько тысяч лет меняется направление магнитного поля. На момент падения астероида в Чиксулубе оно имело обратную намагниченность по отношению к нынешнему.

«Одна вещь нас особенно заинтриговала: в горной породе мы нашли фрагменты с нормальной намагниченностью — того же направления магнитного поля, что существует сейчас. Эти породы получили свою магнетизацию позднее, во времена, когда установилась нормальная направленность поля — впервые с момента падения метеорита на Землю это произошло спустя 300 тысяч лет. Таким образом, мы понимаем, как и когда горячая жидкость выходила на поверхность через кратер», — заметила ученая на брифинге в Лунарном и планетарном институте.

«Изучив гидротермальную систему, мы смогли определить минералогический состав горячих ключей», — добавила профессор Тику.

Автор фото, Science Photo Library

Подпись к фото,

Катаклизмы, вызванные падением астероида, могли носить самый разнообразный характер, о чем ученые строят всевозможные догадки

Система горячих ключей изначально была слишком горячей даже для самых жаростойких микроорганизмов. Однако со временем воды «пикового кольца» охладели, создав условия для появления одноклеточных организмов, аналогичных тем, что живут в вулканах, которые принялись осваивать растворенные в жидкости соединения.

«Мы не знаем, насколько разнообразна их популяция. Может ли быть, что два вида оставались неизменными миллионы лет? Или мы узнаем, что там имела место бурная эволюция, и мы увидим 15, 30 или 50 видов?» — задалась вопросом Тику.

На данный момент остается загадкой, почему в ходе климатической катастрофы, связанной с падением метеорита, с исторической сцены сошли динозавры, при этом широкий ряд других видов рептилий, а также птиц и животных пережили это эпохальное событие вполне благополучно.

«Мы не знаем, почему выжили птицы, черепахи и некоторые другие рептилии. Но, основываясь на пробуренной породе, мы сможем узнать больше об энергии [соударения] и траектории [движения], и все это приблизит нас к разгадке», — резюмировала специалист по палеомагнетизму.

Проект по бурению кратера в Чиксулубе проводился Европейским консорциумом по исследовательскому бурению океана (ECORD) при поддержке Международной континетнальной научной буровой программы (ICDP) в рамках Международной океанической исследовательской программы (IODP).

Решение задач по физике №11. Физические основы механики. Кинематика.

51. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением аr = 5 см/с2. Через какое время t после начала движения нормальное ускорение аn точки будет: а) равно тангенциальному; б) вдвое больше тангенциального? Решение:

1.52. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аr. Найти тангенциалъное ускорение аr точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки V = 79,2 см/с.

Решение:

1.53. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аr . Найти нормальное ускорение аn точки через время t = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 10 см/с.
Решение:

1.54. В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость ф вращения электрона вокруг ядра и его нормальное ускорение а„. 6 м/с.
Решение:

1.55. Колесо радиусом R = 10 см вращается с угловым ускорением E — 3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения:
а) угловую скорость w ;

б) линейную скорость v;
в) тангенциальное ускорение аt;
г) нормальное ускорение an;
д) полное ускорение а;
е) угол а, составляемый вектором полного ускорения с радиусом колеса.
Решение:

| Гость

спасибо большущее))))))))**********

| Гость

помогли)

| Гость

Спасибочки за решения…

| Гость

Спасибо!!!!

| Гость

Спасибо

| Гость

Спасибо

| Гость

ай саул эээ

| Гость

большое спасибо))))))

| Гость

Выручили, спасибо!!!

| Гость

спасибо

| Гость

Спасибо большое)

| Гость

спасибо

| Гость

ссылки битые, поправьте

Равномерное круговое движение

Равномерное круговое движение: движение по круговой траектории с постоянной скоростью.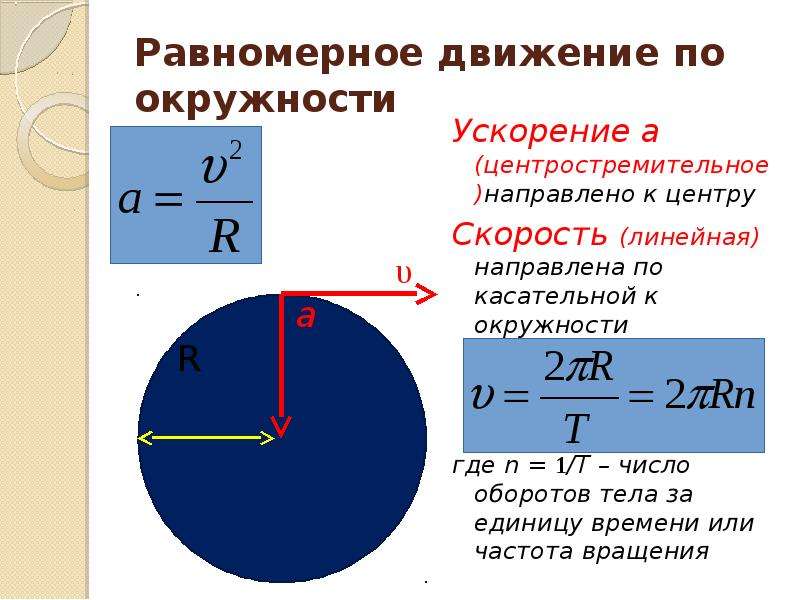

Здесь задействовано ускорение?

Да
Нет

Да — скорость меняется, потому что меняется ее направление.

Мяч вращается по кругу. Если отпустить нить, когда мяч находится в показанном положении, по какой траектории пойдет мяч?

Если отпустить струну, нет силы, которая могла бы отклонить траекторию мяча, поэтому он будет двигаться по прямой, следуя траектории 2.

Основные определения

r = радиус кругового пути

T = период, время одного обхода

v = 2πr/T

Как и при прямолинейном движении, соотношение между a и v такое же, как и между v и r:

а = 2πv/T

Объединение этих двух уравнений дает нам:

центростремительное ускорение: a _c = v ² /r

Угловые переменные

Для движения по круговым траекториям может быть полезно описать движение с использованием угловых переменных.Вместо того, чтобы спрашивать, какое расстояние было пройдено, мы иногда спрашиваем, на какой угол что-то повернулось.

Есть эквивалентные вопросы для скорости и ускорения.

Расстояние: s = rθ

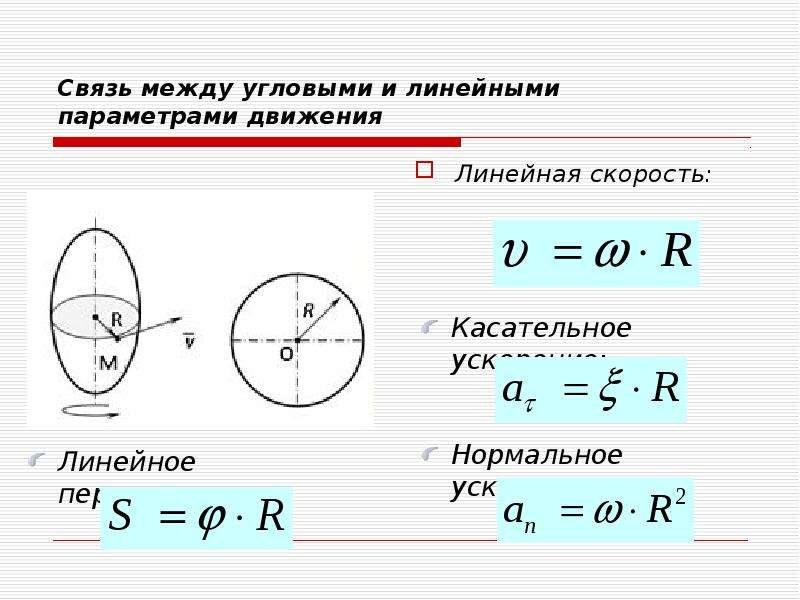
Скорость: v = rω

Ускорение: a _t = rα

Это ускорение включает ускорение или замедление объекта при его движении по круговой траектории и равно нулю при равномерном круговом движении. А направлена по касательной к окружности, значит, это тангенциальное ускорение.Это сильно отличается от центростремительного ускорения, которое действует в радиальном направлении.

Диаграммы свободного тела

Имея в виду, что диаграмма свободного тела показывает все силы, действующие на объект, и что эти силы возникают в результате взаимодействия между этим объектом и другими объектами, как выглядит диаграмма свободного тела для Земли на ее примерно круговой орбите вокруг Солнца?

Единственное взаимодействие, о котором нам нужно беспокоиться, это сила гравитации.Солнце оказывает на Землю гравитационную силу, направленную в сторону Солнца.

Зная расстояние до Солнца и время, за которое Земля совершает оборот вокруг Солнца, мы можем рассчитать ускорение, которое испытывает Земля.

r = 150 млн км = 1,5 х 10 ¹¹ м

Т = 1 год = π х 10 ⁷ с

v = 2π r / t = 3 x 10 ⁴ м/с = 30000 м/с = 30 км/с.

а _с = v ² /r = 9 х 10 ⁸ / 1.5 x 10 ¹¹ = 6 x 10 ^-3 м/с ²

Довольно маленький, но в самый раз, чтобы держать нас на орбите.

Центростремительное ускорение

Центростремительное ускорение — это особая форма ускорения, когда объект совершает равномерное круговое движение. Это:

а _с = v

2 / р

и направлен к центру круга.

Второй закон Ньютона можно записать так:

Σ F = ma = mv ² /r

Я предпочитаю НЕ использовать фразу «центростремительная сила», потому что она заставляет вас думать, что существует магическая сила, которая возникает, когда объект совершает равномерное круговое движение.Такого нет, и, на мой взгляд, никогда не следует помещать центростремительную силу на диаграмму свободного тела.

Когда объект совершает равномерное круговое движение, определенно существует результирующая сила, направленная к центру круга, но эта сила исходит от одной или нескольких стандартных сил, которые мы уже обсуждали. В зависимости от ситуации это может быть сила тяжести, нормальная сила, натяжение, трение, некоторая их комбинация или даже комбинация этих компонентов.

Использование уравнений кругового движения — Физика средней школы

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Видео-вопрос: Определение орбитальной скорости по радиусу и периоду для круговых орбит

Стенограмма видео

Спутник вращается вокруг Земли на радиус орбиты 10 000 километров. Его орбитальный период равен 2,8 часы. Как быстро спутник движущийся? Дайте ответ ближайшему километр в секунду.

Чтобы ответить на этот вопрос, давайте подумайте, что именно здесь спрашивают. Мы хотим знать, как быстро это спутник движется, а это значит, что мы хотим выяснить скорость спутника. И найти его нам дано только два других числа: радиус орбиты спутника вокруг Земли, 10 000 километров, что является расстоянием от спутника до центра Земли, и его орбитальный период 2.8 часов, именно столько времени требуется, чтобы завершить один полный орбита.

Теперь, используя эти два значения, радиус и период, нам нужно найти скорость. Для этого давайте посмотрим на определение скорости. Скорость равна расстоянию объект перемещается за время, необходимое для прохождения этого расстояния, что в данном случае будет расстоянием, которое спутник проходит за период обращения.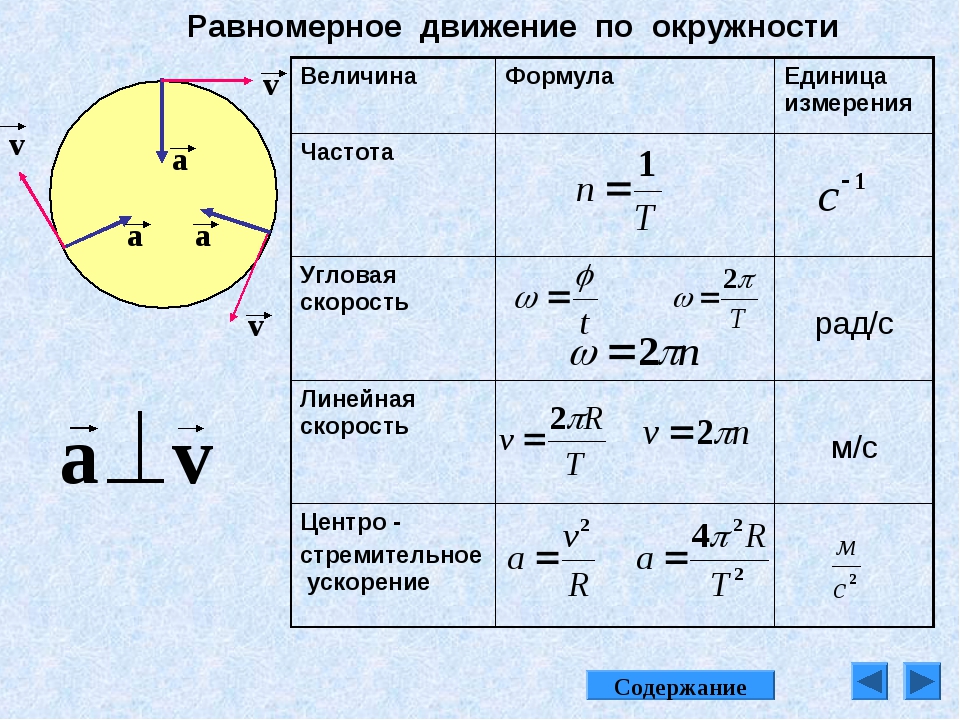

Здесь нужно быть осторожным хотя. Расстояние, которое проходит спутник это не радиус. Радиус — это всего лишь расстояние между спутником и центром Земли. Мы хотим найти расстояние, на котором спутник проходит одну полную круговую орбиту. Мы можем найти это, используя орбитальную радиус в уравнении для длины окружности, два 𝜋𝑟, где 𝑟 — радиус круга, на который мы смотрим.

Окружность круга это длина его периметра, что означает, что это то же самое, что и расстояние совершите полный оборот вокруг этого круга, сделав расстояние два 𝜋, умноженное на 10 000 километров.

Это означает, что все, что нам нужно сделать сейчас, это подставляем в орбитальный период и все готово, да? Ну, не совсем. Нам нужен ответ для скорости в километров в секунду, а не километров в час.Итак, нам нужно преобразовать период обращения от часов до секунд.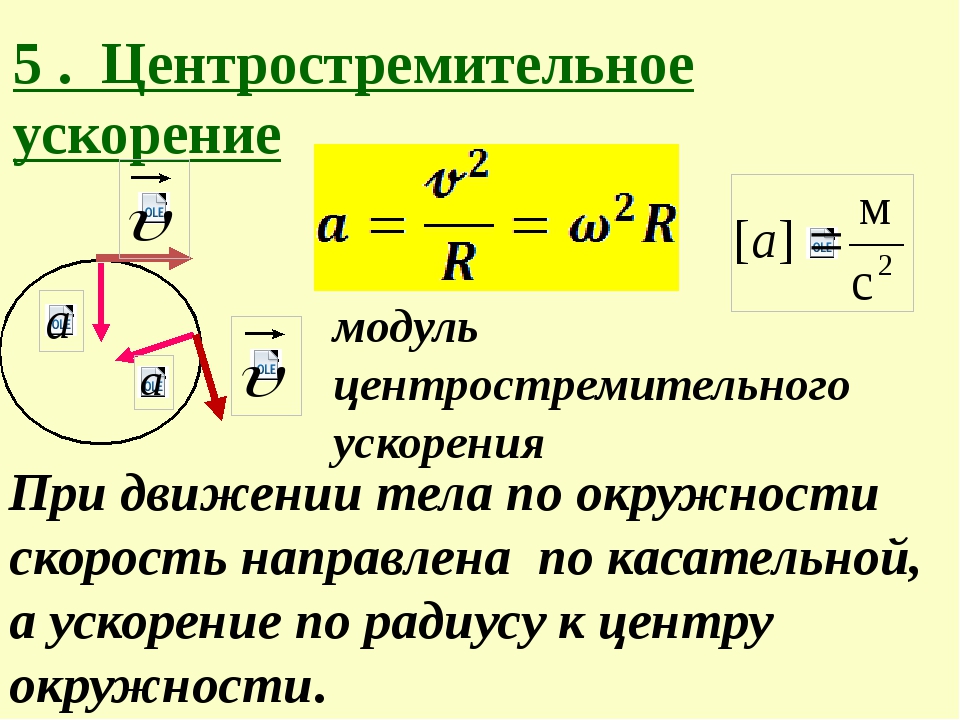 В одном часе 60 минут и 60 секунд в одной минуте. Таким образом, умножая это первое соотношение на 2,8 часа единицы часов отменяются. И 2,8 умножить на 60 минут равно до 168 минут. Умножая это на следующее В этом случае минуты отменяются, и 60 секунд, умноженные на 168, составляют 10 080 секунд.

Теперь, когда у нас есть этот номер, мы можно подставить его в уравнение, которое у нас есть для скорости, что делает наше уравнение вторым 𝜋 умножить на 10 000 километров и разделить на 10 080 секунд.Расчет и оплата Обратите внимание на наши единицы, мы находим ответ равным 6,23 километра в секунду. Затем округляем до ближайшего километр в секунду, мы находим, что ответ на вопрос, как быстро движется этот спутник составляет шесть километров в секунду.

Равномерное круговое движение

Центростремительное ускорение

Движение объекта по круговой траектории с постоянной скоростью известно как равномерное круговое движение (UCM).Объект в UCM постоянно меняет направление, а поскольку скорость является вектором и имеет направление, можно сказать, что объект, подвергающийся UCM, имеет постоянно изменяющуюся скорость, даже если его скорость остается постоянной. И если скорость объекта меняется, он должен ускоряться. Следовательно, объект, подвергающийся UCM, постоянно ускоряется. Этот тип ускорения известен как центростремительное ускорение .

Вопрос : Если автомобиль ускоряется, увеличивается ли его скорость?
Ответ : Это зависит.Его скорость может увеличиваться, или он может ускоряться в направлении, противоположном его скорости (замедляясь). Или его скорость может оставаться постоянной, но при этом увеличиваться, если он движется равномерно по окружности.

Не менее важно определить направление ускорения объекта, поскольку ускорение является вектором. Для этого нарисуем объект, движущийся против часовой стрелки по круговой траектории, и покажем вектор его скорости в два разных момента времени.Поскольку мы знаем, что ускорение — это скорость изменения скорости объекта во времени, мы можем определить направление ускорения объекта, найдя направление изменения его скорости, Δv.

Чтобы найти изменение скорости Δv, мы должны вспомнить, что .

Следовательно, нам нужно найти разность векторов v _f и v _i графически, которую можно переписать в виде .

Вспомните, что для графического сложения векторов мы выстраиваем их в линию, кончик к хвосту, а затем рисуем результирующий вектор от начальной точки (хвоста) нашего первого вектора до конечной точки (конца) нашего последнего вектора.

Значит, вектор ускорения должен указывать в указанном выше направлении. Если я покажу этот вектор обратно на нашу исходную окружность, выстроив ее прямо между начальным и конечным векторами скорости, легко увидеть, что вектор ускорения указывает на центр окружности.

Вы можете повторить эту процедуру из любой точки круга… куда бы вы ни пошли, вектор ускорения всегда указывает на центр круга. На самом деле слово центростремительный в центростремительном ускорении означает «наведение по центру!»

Итак, теперь мы знаем направление ускорения объекта (к центру круга), но как насчет его величины? Величина центростремительного ускорения объекта находится в справочной таблице и определяется по формуле:

Круговая скорость

Так как же найти скорость объекта, движущегося по круговой траектории? Формула скорости, которую мы узнали из кинематики, по-прежнему применима.

Однако мы должны быть осторожны при использовании этого уравнения, чтобы понять, что объект, движущийся по круговой траектории, движется по окружности окружности. Следовательно, если бы объект совершил один полный оборот по окружности, расстояние, которое он проходит, было бы равно длине окружности.

Давайте рассмотрим пример задачи:

Вопрос : Миранда едет на своей машине по часовой стрелке по круговой трассе радиусом 30 м.Она проходит 10 кругов по трассе за 2 минуты. Найдите общее расстояние, пройденное Мирандой, среднюю скорость и центростремительное ускорение.
Ответ :

Центростремительная сила

Если объект, движущийся по круговой траектории, имеет внутреннее ускорение, второй закон Ньютона говорит нам, что должна быть результирующая сила, направленная также к центру окружности.Этот тип силы, известный как центростремительная сила, может быть силой гравитации, натяжением, приложенной силой или даже силой трения.

ПРИМЕЧАНИЕ. При решении задач с круговым движением важно понимать, что центростремительная сила на самом деле не является новой силой, центростремительная сила — это просто ярлык или группа, которую мы применяем к силе, чтобы указать, что ее направление направлено к центру круг. Это означает, что вы никогда не захотите обозначать силу на диаграмме свободного тела как центростремительную силу, F _c .Вместо этого назовите силу, направленную по центру, как можно конкретнее. Если сила возникает из-за натяжения, обозначьте силу F _T. Если сила трения вызывает направленную по центру силу, обозначьте ее F _f и так далее.

Мы можем объединить уравнение для центростремительного ускорения со 2-м законом Ньютона, чтобы получить 2-й закон Ньютона для кругового движения. Напомним, что 2-й закон Ньютона гласит:

Для объекта, движущегося по круговому пути, должна существовать результирующая (центростремительная) сила, направленная к центру кругового пути, чтобы вызвать (центростремительное) ускорение, направленное к центру кругового пути.Тогда мы можем пересмотреть второй закон Ньютона для этого конкретного случая следующим образом:

Тогда, вспоминая нашу формулу для центростремительного ускорения как:

Мы можем сложить их вместе, заменив _на в нашем уравнении, чтобы получить объединенную форму 2-го закона Ньютона для равномерного кругового движения:

Конечно, если объект движется по круговой траектории и центростремительная сила устранена, объект будет продолжать двигаться по прямой линии в любом направлении, в котором он двигался в момент снятия силы.

Вопрос : Бегущий назад 800 Н поворачивает угол по круговой траектории r = 1 м со скоростью 8 м/с. Найдите массу бегущего, центростремительное ускорение и центростремительную силу.
Ответ : Дано mg=800N, r=1м, v=8м/с; Найти m, ac, Fc

Попробуем еще:

Еще одна примерная задача, на этот раз включающая только алгебраические операции:

Частота и период

Для объектов, движущихся по круговым траекториям, мы можем охарактеризовать их движение по окружности, используя термины частота (f) и период (T).Частота объекта — это количество оборотов, которое объект совершает за полную секунду. Измеряется в единицах [1/с] или Герцах (Гц). Точно так же период объекта — это время, необходимое для совершения одного полного оборота. Поскольку период представляет собой временной интервал, он измеряется в секундах. Мы можем связать период и частоту, используя уравнения:

Вопрос : Игрушечный поезд массой 500 г проходит 10 кругов по кругу за 1 мин 40 с.Если диаметр пути равен 1 м, найдите центростремительное ускорение поезда (a _c ), центростремительную силу (F _c ), период (T) и частоту (f).
Ответ :

Давайте посмотрим на другой пример:

Вертикальное круговое движение

Объекты перемещаются по кругу как по вертикали, так и по горизонтали.Поскольку скорость этих объектов обычно непостоянна, технически это не равномерное круговое движение , но наши навыки анализа UCM по-прежнему применимы.

Рассмотрим американские горки, движущиеся по вертикальной петле радиусом 10 м. Вы путешествуете по петле вверх ногами, но не падаете с американских горок. Как это возможно? Мы можем использовать наше понимание UCM и динамики, чтобы выяснить это!

Нижняя часть круга

Для начала давайте сначала посмотрим на подстаканник, когда машина находится в нижней части петли.На диаграмме свободного тела сила тяжести на каботажном судне, также известная как его вес, тянет его вниз, поэтому мы рисуем вектор, указывающий вниз, обозначенный «mg». Противодействующей этой силе является нормальная сила толкающих вверх рельсов подставки, которую мы обозначаем F _N.

Поскольку каботажное судно движется по круговой траектории, мы можем проанализировать его с помощью разработанных нами инструментов для равномерного кругового движения. Второй закон Ньютона остается в силе, поэтому мы можем написать:

Обратите внимание: поскольку мы говорим о круговом движении, мы примем соглашение о том, что силы, направленные к центру круга, положительны, а силы, направленные от центра круга, отрицательны. В этот момент вспомните, что сила, которую вы «чувствуете», когда находитесь в движении, на самом деле является нормальной силой. Итак, находя нормальную силу, когда вы начинаете двигаться по кругу, мы находим, что

Поскольку мы знаем, что результирующая сила всегда равна массе, умноженной на ускорение, поэтому результирующая центростремительная сила равна массе, умноженной на центростремительное ускорение, мы можем заменить F _{NET _c} следующим образом:

Из полученного уравнения видно, что нормальная сила теперь равна весу плюс дополнительный член от центростремительной силы кругового движения.Когда мы движемся по круговой траектории в нижней части петли, мы чувствуем себя тяжелее своего веса. Говоря простым языком, мы чувствуем дополнительные «перегрузки». Сколько g мы чувствуем, может быть получено с немного большим количеством манипуляций. Если мы перепишем наше уравнение для нормальной силы, вытянув массу, применив распределительное свойство умножения, то получим:

Обратите внимание, что в скобках указано стандартное ускорение свободного падения, g, плюс член от центростремительного ускорения ().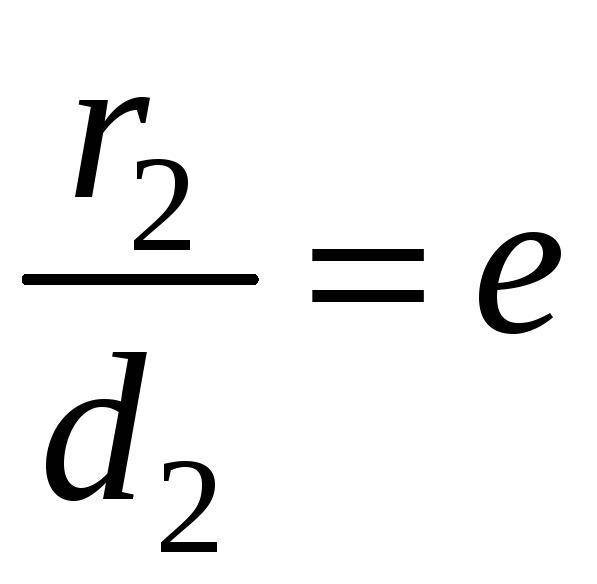

Этот дополнительный термин представляет собой дополнительную перегрузку, ощущаемую человеком. Например, если _c равно g (9,81 м/с ² ), можно сказать, что человек в тележке испытал два g (1g от центростремительного ускорения и 1g от гравитационного поля Земли). Если бы _c было равно 3*g (29,4 м/с ² ), человек испытал бы в общей сложности четыре g.

Расширив этот анализ на аналогичную ситуацию в другом контексте, попробуйте представить вместо американских горок массу, вращающуюся по вертикальному кругу на веревке.Вы можете заменить нормальную силу натяжением струны в нашем анализе. Поскольку сила больше в нижней части круга, вероятность разрыва струны выше всего, когда масса находится в нижней части круга!

Вершина круга

В верхней части цикла мы имеем совершенно иную картину. Теперь нормальная сила от рельсов подставки должна давить на тележку, хотя все еще в положительном направлении, поскольку теперь вниз направлена к центру кругового пути. Однако в этом случае вес объекта также указывает на центр круга, поскольку гравитационное поле Земли всегда притягивает к центру Земли. Наша диаграмма свободного тела выглядит значительно иначе, и поэтому наше приложение ко второму закону Ньютона для кругового движения также значительно отличается.

Поскольку сила, которую вы чувствуете, на самом деле является нормальной силой, мы можем найти нормальную силу и разложить результирующую центростремительную силу, как показано:

Из уравнения видно, что нормальная сила теперь равна центростремительной силе за вычетом вашего веса.Если бы центростремительная сила была равна вашему весу, вы бы чувствовали себя невесомыми. Обратите внимание, что это также точка, где нормальная сила точно равна 0. Это означает, что рельсы дорожки больше не давит на тележку американских горок… если бы центростремительная сила была хоть немного меньше (скорость автомобиля была бы чуть меньше), нормальная сила FN была бы меньше 0. Поскольку рельсы физически не могут тянуть тележку в отрицательном направлении (от центра круга), это означает, что вагон падает с рельса. и у пассажира повозки скоро будет очень, очень плохой день.Только поддерживая высокую скорость, тележка может успешно преодолевать петлю… если двигаться слишком медленно, тележка падает.

Чтобы оставаться в безопасности, настоящие американские горки на самом деле имеют колеса с обеих сторон рельсов, чтобы предотвратить падение тележки, если она когда-либо замедляется в верхней части петли, хотя подставки спроектированы таким образом, что на самом деле это никогда не происходит.

Равномерное круговое движение

Равномерное круговое движение
Далее: Центростремительное ускорение Вверх: Круговое движение Предыдущий: Введение Предположим, что объект совершает круговую орбиту радиусом с равномерной тангенциальной скоростью.

Мгновенное положение объекта удобнее всего задавать в терминах угол . См. рис. 57. Например, мы могли бы решить, что соответствует к местоположению объекта в , и в этом случае мы бы написали

(245)

где называется угловой скоростью объекта. Для равномерно вращающийся объект, угловая скорость — это просто угол, под которым объект поворачивается за одну секунду.

**Рисунок 57:** *Круговое движение.*

Рассмотрим движение объекта в интервале времени между и . За это время объект поворачивается на угол , и вычерчивает дугу окружности длиной . См. рис. 57. Совершенно очевидно, что длина дуги прямо пропорциональна углу : но что такое константа пропорциональности? Ну и угол соответствует длине дуги . Следовательно, угол должна соответствовать длине дуги

(246)

На этом этапе удобно определить новую угловую единицу, известную как радиан (обозначение рад). Угол измеренный в радианах, связан с углом, измеренным в градусах, через следующую простую формулу:

(247)

Таким образом, соответствует радианам, соответствует радианам, соответствует радианам и соответствует до 1 радиана.Когда измеряется в радианах, уравнение. (246) упрощает сильно давать

(248)

Отныне в этом курсе все углы измеряются в радианах по умолчанию .

Рассмотрим движение объекта на коротком промежутке между моментами времени и . В этом интервале объект поворачивается на небольшой угол и очерчивает короткую дугу длины , где

(249)

В настоящее время ( я.е. , расстояние, пройденное за единицу времени) это просто тангенциальная скорость , тогда как ( т.е. , угол поворота за единицу времени) — это просто угловая скорость . Таким образом, разделив уравнение (249) через , получаем

(250)

Обратите внимание, однако, что эта формула справедлива только в том случае, если угловая скорость измеряется в радиан в секунду . Отныне в этом конечно, все угловые скорости измеряются в радианах в секунду по умолчанию .

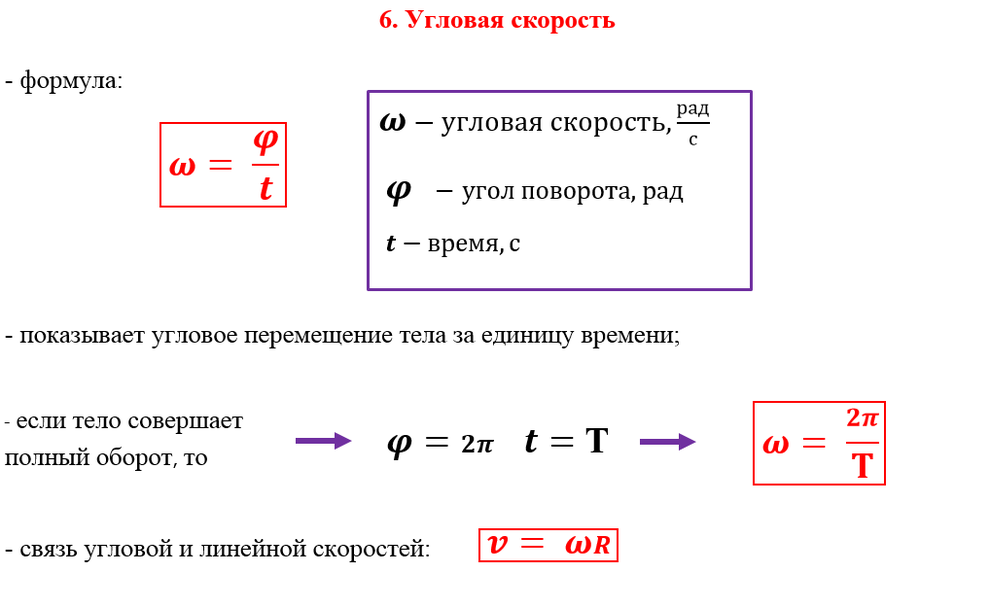
Объект, вращающийся с равномерной угловой скоростью, проходит через радиан за 1 секунду. Следовательно, объект поворачивается на радианы ( т.е. , он выполняет полный круг) в

(251)

секунды. Здесь период повторения кругового движения. Если объект выполняет полный цикл ( т.е. , переворачивается) за секунды, тогда количество циклов, выполняемых в секунду, равно

(252)

Здесь частота повторения , , движения измеряется в циклов в секунду — иначе известный как герц (символ Гц).

В качестве примера предположим, что объект совершает равномерное круговое движение, радиус , на частоте ( т. е. , объект выполняет полный вращения 50 раз в секунду). Период повторения этого движения просто

(253)

Кроме того, угловая частота движения определяется выражением

(254)

Наконец, тангенциальная скорость тела равна

(255)

Далее: Центростремительное ускорение Вверх: Круговое движение Предыдущий: Введение

Ричард Фицпатрик 2006-02-02

Центростремительное ускорение

Центростремительное ускорение ЦЕНТРОСТРЕМЕННОЕ УСКОРЕНИЕ
(Пересмотрено 4/07)
Я. Введение
Цель этого упражнения — проверить уравнение для центростремительного ускорения,
а = v ² /r,
для объекта, движущегося с постоянной скоростью v по окружности радиусом r. Мы также проверим, что направление вектора ускорения направлено к центру окружности. Воспользуемся графическим методом векторной арифметики.
I. Введение
Предположим, что объект изначально имеет вектор скорости v _A , а через время Dt имеет вектор скорости v _B .Тогда его среднее ускорение за этот период равно
a _avg = ( v _B — v _A )/Dt.
Направление a _avg совпадает с направлением v _B — v _A . Мы также будем называть эту разность скоростей Dv .
a _ср = Dv /Dt.
Чтобы найти мгновенное ускорение объекта в одной точке P, мы хотели бы взять две точки, очень близкие по времени.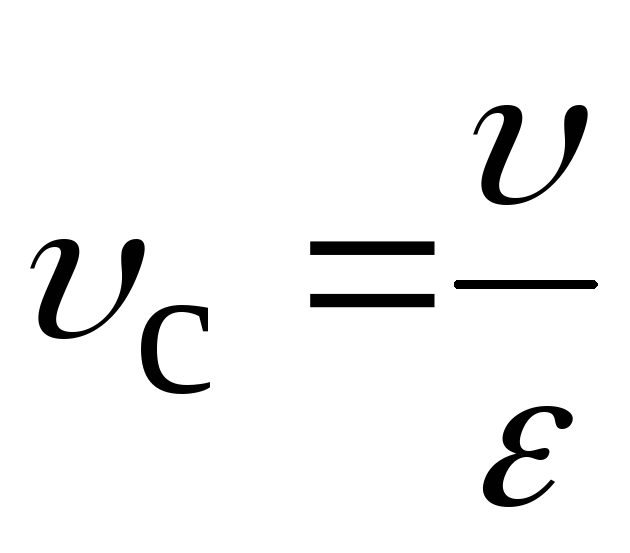 Dt будет очень маленьким, и разность векторов Dv тоже будет очень маленькой. Однако вычислять разность векторов таким образом нецелесообразно, потому что небольшие ошибки в рисовании векторов приведут к большим ошибкам в разности векторов. Следовательно, в этой лабораторной работе мы возьмем довольно большую разницу во времени и все же увидим, что направление и величина среднего ускорения оказываются достаточно близкими к ожидаемым значениям.
II. Разделение работы
Учащиеся будут работать в группах по два , но каждый учащийся будет строить свои собственные конструкции.Вы будете использовать циркуль, чтобы нарисовать дугу окружности на миллиметровой бумаге. Мы хотим найти ускорение тела при его движении на угол q, опирающийся на центр окружности. Будем делать построения для q равных 30, 40, 50, 60, 70, 80, 90, 100, 110 и 120 градусов. Каждая группа будет делать только два из этих углов. Инструктор попросит некоторые группы сделать 30 и 80 градусов, другие группы сделать 40 и 90 градусов и т. д., чтобы у нас была работа для всех этих углов. Позже вы запишете свои результаты на доске и вместе посмотрите на рассчитанные средние ускорения.
В группе из двух человек оба ученика должны построить оба угла. Когда у вас есть результаты, вы можете их сравнить. Если кажется, что есть существенная разница, попытайтесь выяснить, почему, а если не можете, спросите у инструктора.
III. Строительство
Установите компас на радиус ровно 10 см. Держите миллиметровку вертикально, поместите центр круга с левой стороны и нарисуйте дугу, начинающуюся прямо под центром и продолжающуюся вокруг вашего значения q.

Мы будем думать об этой дуге как о масштабном рисунке части круга, где масштаб 1 см равен 1 м в реальном движении.
1 см на пространственной диаграмме = 1 м в реальном пространстве.
Запишите радиус окружности в метрах.
Точка А, начальная позиция движения, должна быть прямо под центром, чтобы радиус-вектор от центра к А был вертикальным.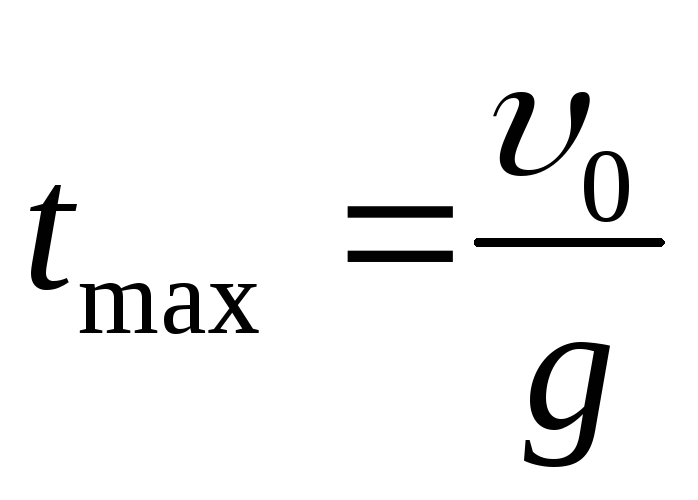 Вектор скорости, v _A , является касательной к кривой в точке A, и поэтому должен быть проведен горизонтально.(Важная теорема плоской геометрии состоит в том, что касательная к окружности перпендикулярна радиусу в точке касания.) Изобразите вектор скорости длиной 10 см. На диаграмме скоростей примем 1 см равным 1 м/с.
1 см на диаграмме скоростей = 1 м/с реальной скорости.
Запишите скорость вашего движения в м/с.
Теперь найдите точку B, конечное положение движения, используя транспортир. Это угол q вокруг дуги из A. Проведите радиус-вектор из центра в B и проведите касательную к окружности в точке B.
Примечание. Чтобы нарисовать касательную, попробуйте , а не , провести линию, пересекающую окружность только в одной точке. Лучше использовать транспортир, чтобы провести перпендикуляр к радиусу.
Нарисуйте вектор скорости v _B вдоль этой касательной длиной 10 см. (Помните, что мы рассматриваем равномерное круговое движение, поэтому скорость постоянна.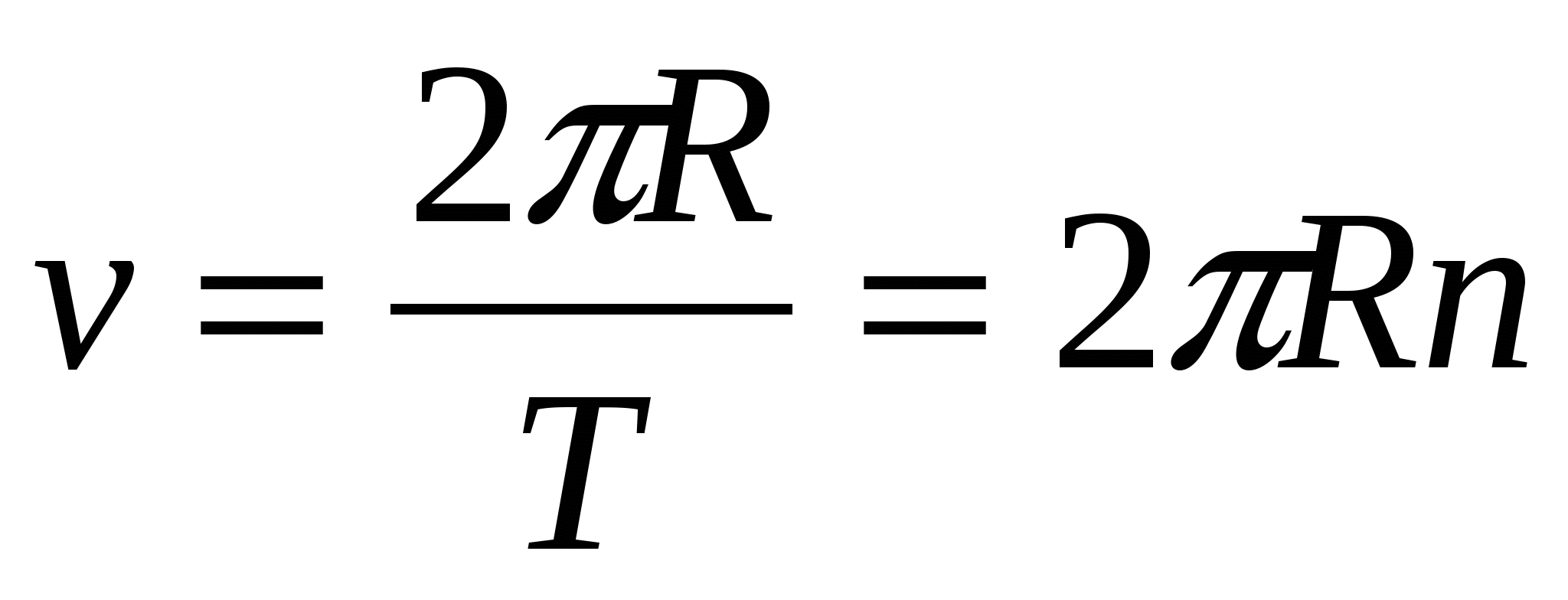 ) Теперь нарисуйте вектор -v _A с хвостом на голове v _B .Вектор -v _A по определению противоположен вектору v _A , поэтому он горизонтален на бумаге и имеет длину 10 см. Теперь используйте определение суммирования векторов, чтобы построить v _B + (-v _A) , что, в свою очередь, равно v _B — v _A или Dv .
IV. Направление ускорения
Направление Dv — это направление ускорения.Ваш вектор указывает на центр круга?
Помните, что вектор скорости не имеет местоположения в пространстве. У него есть только длина и направление. (50 миль в час на север в Чикаго — это та же скорость, что и 50 миль в час на север в Нью-Йорке.) Найденное вами ускорение — это среднее ускорение объекта при его перемещении из точки A в точку B. Таким образом, этот вектор можно рассматривать следующим образом: для переместите его в точку где-то между A и B. Выберите точку на полпути от A до B и переместите свой Dv так, чтобы его хвост оказался в этой точке.Чтобы переместить его, используйте технику, описанную в части VII этой статьи. Теперь он указывает на центр круга?
V. Величина ускорения
Используя две шкалы (для расстояния и для скорости), вы можете вычислить величину ускорения:
Сначала вспомните свои значения r (в метрах) и v (в м/с).
Затем найдите величину Dv на диаграмме: Измерьте длину вектора линейкой в см и переведите в м/с.Теперь вам нужно найти временной интервал Dt.
Сначала найдите период T для одного полного круга, учитывая, что длина окружности равна 2pr, а ваша скорость равна v. Это время будет в секундах.
Затем найдите время, Dt, чтобы пройти от А до Б, для вашего строительства. Для этого используйте тот факт, что длина дуги от A до B составляет часть q/360 полной окружности (где q в градусах). Следовательно, Dt является той же долей периода. Найдите дробь.
Найти Dt.
Вычислить величину ускорения,
a _avg = Dv /Dt, Это будет в м/с ².
То, что вы нашли, используя определение ускорения как скорость изменения скорости , есть среднее ускорение от точки А до точки В. Формула мгновенного ускорения такова: v ² /r. Рассчитайте и это значение.
VI. Сбор результатов
Чтобы уменьшить количество рассматриваемых данных, два студента в группе должны усреднить два своих результата для каждого угла. Затем поместите на доске их значения q и _avg . Затем все учащиеся лаборатории должны скопировать таблицу и построить график зависимости _{среднего} от q, используя все точки. (Точек будет около 20.) Нарисуйте плавную кривую как можно ближе ко всем точкам (не обязательно прямую линию, если только она не выглядит как прямая линия).Затем экстраполируйте кривую к q = 0. Этот предел, поскольку расстояние (и время) от точки A до точки B становится очень маленьким, является мгновенным ускорением.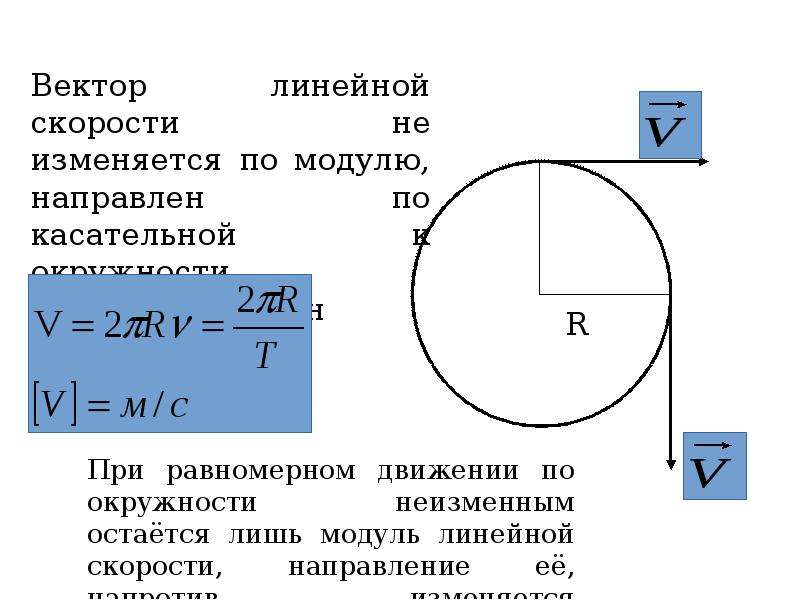 Отметьте теоретическое значение v ² /r на вертикальной оси. Какова процентная разница между вашим значением и этим теоретическим значением?
VII. Примечание по перемещению вектора:
Важным свойством вектора является то, что он не имеет местоположения в пространстве. Если у вас есть вектор в точке P (как показано ниже), вы можете перерисовать его в точке Q с тем же величина и направление, и это один и тот же вектор.

На практике вы можете измерить угол b между вектором и горизонтальной линией в точке P. Затем вы используете транспортир, чтобы построить тот же угол в точке Q; затем нарисуйте вектор в точке Q, сделав его такой же длины, как и в точке P.
Круговая скорость
Круговая скорость

Рассчитать Прозрачный
⚠️ Сообщить о проблеме
Вы когда-нибудь наблюдали за вращающимся вентилятором или колесом движущегося велосипеда? Каждая точка на них совершает круговое движение вокруг центра вращения. Такое движение частиц, при котором движение объекта происходит по круговой траектории, называется круговым движением.
Что такое равномерное круговое движение?
О любой частице, которая движется по окружности с постоянной скоростью, говорят, что она совершает равномерное круговое движение. Главный аспект равномерного кругового движения заключается в том, что направление движения частицы постоянно меняется в каждый момент времени. Направление частицы находится в мгновенном тангенциальном направлении.
Скажем, при равномерном круговом движении направление всегда меняется, но величина круговой скорости остается постоянной в каждый момент времени.
Может ли быть неравномерное круговое движение?
Да, может быть. При таком неравномерном круговом движении скорость частицы непостоянна. Например, когда вы вращаете объект, привязанный к веревке, по вертикальной окружности, вы, должно быть, заметили, что движение происходит быстрее, когда объект находится внизу, где сила тяжести увеличивает его скорость, и медленнее в самом верхнем положении, где сила тяжести действует против этого.
Другой особый вид кругового движения — это когда объект вращается вокруг себя, что также известно как вращательное движение.Волчок является примером такого кругового движения.
Теперь я напомню, что движение небесных тел круговое, так как движение, свойственное сфере, есть вращение по кругу. – Николай Коперник
Переменные в круговом движении
Движение частицы, совершающей круговое движение, определяется определенным набором переменных, как определено ниже:
Угловое смещение:
Обозначаемый Δθ, это угол, под которым вектор положения частицы образует центр траектории кругового движения.
Это также отношение линейного перемещения к радиусу в любой данный момент времени. Единицей углового смещения является радиан.
Угловое смещение (Δθ) = (ΔS/r)
Угловая скорость
Скорость изменения углового смещения (Δθ). Измеряется в рад/с и является векторной величиной.
Угловая скорость (ω) = Δθ/Δt
Угловое ускорение
Скорость изменения угловой скорости (dω). Измеряется в рад/с2 и является скалярной величиной.
Угловое ускорение (α) = dω/dt = d2θ / dt2
Как рассчитывается круговая скорость?
Формула для расчета круговой скорости формула:
v _c = 2πr / T
Где r — радиус круговой орбиты
T — период времени.
Если вы знаете угловую скорость ω, вы можете рассчитать круговую скорость как:
v _c = ω r
Где ω — угловая скорость,
r — радиус кругового пути
Пример задачи для понимания расчета круговой скорости
Рассчитайте круговую скорость камня, привязанного к нити длиной 1 м, если его вращать с угловой скоростью 45 рад/с
Решение
Здесь:
Угловая скорость ω = 45 рад/с
Радиус = 1 м
Мы знаем, что формула для круговой скорости дается выражением v _c = ω r
v _c = 45 × 1
= 45 м /с.
Примеры равномерного кругового движения
Камень, привязанный к веревке и закрученный горизонтально
Стрелки часов
Круглый объект, движущийся по полу с постоянной скоростью
Шины дорожного катка или автомобиля, движущегося с постоянной скоростью
Вращающиеся лопасти потолочного вентилятора.
Искусственный спутник, вращающийся вокруг Земли на фиксированной высоте.
Электроны в атоме движутся вокруг ядра.
Карусель
Вы знаете?
Закон Ньютона применим и к круговому движению. Посмотрим как:
Согласно первому закону движения Ньютона любой объект будет продолжать находиться в состоянии движения, если на него не воздействует внешняя сила. В случае кругового движения эта сила есть не что иное, как центростремительная сила или сила, продолжающая тянуть тело к центру.
Например, когда вы крутите камень, привязанный к веревке, удерживая его рукой, ваша рука оказывает на камень центростремительную силу через веревку.Именно эта сила заставляет камень двигаться по кругу. Интересно, не так ли? Чтобы узнать больше о центростремительной силе, посетите нашу страницу калькулятора центростремительного ускорения.
Чем вам поможет бесплатный онлайн-калькулятор круговой скорости CalculatorHut?
CalculatorHut содержит более 100 научных, медицинских и других калькуляторов, специально разработанных для упрощения расчетов. Мы работаем с одной идеей — разработать удобный бесплатный онлайн-инструмент для расчетов для студентов, профессионалов, финансовых энтузиастов, людей, заботящихся о своем здоровье, и всех, кто имеет дело с числами в своей повседневной жизни.
Круговая скорость является незаменимым понятием для любого студента-физика. С помощью нашего калькулятора вы можете легко рассчитать любой параметр формулы круговой скорости и получить мгновенный результат. Бесплатный калькулятор круговой скорости CalculatorHut также является полезным инструментом для перекрестной проверки результатов, полученных во время вычислений, и изучения концепций кругового движения.
Вы знаете? CalculatorHut — это центр бесплатных онлайн-калькуляторов. Ознакомьтесь с нашим широким ассортиментом калькуляторов по математике, физике, химии, финансам, здравоохранению, транспортным средствам и другим.
Если у вас есть учебный блог или веб-сайт, посвященный физике, и вы хотите, чтобы какой-либо из наших калькуляторов был встроен в виде виджета на ваш веб-сайт, напишите нам слово по адресу calculatehut@gmail. com, и мы разработаем для вас виджет абсолютно бесплатно!
CalculatorHut также имеет бесплатное приложение для своих пользователей! Просто загрузите приложение CalculatorHut на свой мобильный телефон и ура, у вас в руках огромный выбор бесплатных онлайн-калькуляторов. С CalculatorHut вы можете выполнять любые расчеты на ходу!
С CalculatorHut вы всегда можете наслаждаться простыми расчетами всех видов, потому что мы стремимся сделать научные расчеты простыми и легкими! CalculatorHut упрощает ваши расчеты!
Гравитация объясняет движение планет; но оно не может объяснить, кто приводит планеты в движение.- Исаак Ньютон.
.