Период вращения формула: Ничего не найдено для %25D0%25Bc%25D0%25B5%25D1%2585%25D0%25B0%25D0%25Bd%25D0%25B8%25D0%25Ba%25D0%25B0 %25D0%25Bf%25D0%25B5%25D1%2580%25D0%25B8%25D0%25Be%25D0%25B4 %25D0%25Be%25D0%25B1%25D1%2580%25D0%25B0%25D1%2589%25D0%25B5%25D0%25Bd%25D0%25B8%25D1%258F
Период вращения вокруг земли формула. Во сколько раз период обращения искусственного спутника, совершающего движение. Расчет скорости движения спутника вокруг Земли
Цель: научиться вычислять период обращения спутника вокруг планеты в зависимости от ее массы, размеров и вида спутника.
Ход работы:
1. Перечертите в тетрадь таблицу, представленную в нижней части таблицы.
2. Выполните расчеты периода обращения для каждого спутника для каждой планеты и представьте результат в таблице на странице. Известно, что планета, тяжелее Земли в 2 раза, больше ее по размерам в 1,4 раза, а планета, меньшая Земли по массе, в размерах равна 0,8 размера Земли. Данные необходимо брать из информационного окна на странице «Моделирование движения спутника». Радиус Земли принять равным 6400 км. Ответ следует выразить в минутах, округлять до целого числа.
3. Проверьте полученные вами данные. Для этого нажмите кнопку «Проверить результаты».
4. В случае наличия ошибок, исправьте их.
5. Полученные верные данные запишите в таблицу в тетради.
6. Сделайте вывод о том, как зависит период обращения спутника от размеров планеты и от вида спутника.
В космосе гравитация обеспечивает силу, из-за которой спутники (такие, как Луна) вращаются по орбитам вокруг более крупных тел (таких, как Земля). Эти орбиты в общем случае имеют форму эллипса, на чаще всего, этот эллипс не сильно отличается от окружности. Поэтому в первом приближении можно считать орбиты спутников круговыми. Зная массу планеты и высоту орбиты спутника над Землей, можно рассчитать, какой должна быть скорость движения спутника вокруг Земли .
Расчет скорости движения спутника вокруг Земли
Вращаясь по круговой орбите вокруг Земли, спутник в любой точке своей траектории может двигаться только с постоянной по модулю скоростью, хотя направление этой скорости будет постоянно изменяться. Какова же величина этой скорости? Её можно рассчитать с помощью второго закона Ньютона и закона тяготения.
Для поддержания круговой орбиты спутника массы в соответствии со вторым законом Ньютона потребуется центростремительная сила: , где — центростремительное ускорение.
Как известно, центростремительное ускорение определяется по формуле:
где — скорость движения спутника, — радиус круговой орбиты, по которой движется спутник.
Центростремительную силу обеспечивает гравитация, поэтому в соответствии с законом тяготения:
где кг — масса Земли, м 3 ⋅кг -1 ⋅с -2 — гравитационная постоянная.
Подставляя все в исходную формулу, получаем:
Выражая искомую скорость , получаем, что скорость движения спутника вокруг Земли равна:
Это формула скорости, которую должен иметь спутник Земли на заданном радиусе (т.е. расстоянии от центра планеты) для поддержания круговой орбиты. Скорость не может меняться по модулю, пока спутник сохраняет постоянный орбитальный радиус, то есть пока он продолжает обращаться вокруг планеты по круговой траектории.
При использовании полученной формулы следует учитывать несколько деталей:
Искусственные спутники Земли, как правило, обращаются вокруг планеты на высоте от 500 до 2000 км от поверхности планеты. Рассчитаем, с какой скоростью должен двигаться такой спутник на высоте 1000 км над поверхностью Земли. В этом случае км. Подставляя числа, получаем:
Материал подготовлен , Сергеем Валерьевичем
Для определения двух характерных «космических» скоростей, связанных с размерами и полем тяготения некоторой планеты. Планету будем считать одним шаром.
Рис. 5.8. Различные траектории движения спутников вокруг Земли
Первой космической скоростью называют такую горизонтально направленную минимальную скорость, при которой тело могло бы двигаться вокруг Земли по круговой орбите, то есть превратиться в искусственный спутник Земли.
Это, конечно идеализация, во-первых планета не шар, во-вторых, если у планеты есть достаточно плотная атмосфера, то такой спутник — даже если его удастся запустить — очень быстро сгорит. Другое дело, что, скажем спутник Земли, летающий в ионосфере на средней высоте над поверхностью в 200 км имеет радиус орбиты отличающийся от среднего радиуса Земли всего, примерно, на 3 %.
Другое дело, что, скажем спутник Земли, летающий в ионосфере на средней высоте над поверхностью в 200 км имеет радиус орбиты отличающийся от среднего радиуса Земли всего, примерно, на 3 %.На спутник, движущийся по круговой орбите радиусом (рис. 5.9), действует сила притяжения Земли, сообщающая ему нормальное ускорение
Рис. 5.9. Движение искусственного спутника Земли по круговой орбите
По второму закону Ньютона имеем
Если спутник движется недалеко от поверхности Земли, то
Поэтому для на Земле получаем
Видно,что действительно определяется параметрами планеты:её радиусом и массой.
Период обращения спутника вокруг Земли равен
где — радиус орбиты спутника, а — его орбитальная скорость.
Минимальное значение периода обращения достигается при движении по орбите, радиус которой равен радиусу планеты:
так что первую космическую скорость можно определить и так: скорость спутника на круговой орбите с минимальным периодом обращения вокруг планеты.
Период обращения растет с увеличением радиуса орбиты.
Если период обращения спутника равен периоду обращения Земли вокруг своей оси и их направления вращения совпадают, а орбита расположена в экваториальной плоскости, то такой спутник называется геостационарным .
Геостационарный спутник постоянно висит над одной и той же точкой поверхности Земли (рис. 5.10).
Рис. 5.10. Движение геостационарного спутника
Для того чтобы тело могло выйти из сферы земного притяжения, то есть могло удалиться на такое расстояние, где притяжение к Земле перестает играть существенную роль, необходима вторая космическая скорость (рис. 5.11).
Второй космической скоростью называют наименьшую скорость, которую необходимо сообщить телу, чтобы его орбита в поле тяготения Земли стала параболической, то есть чтобы тело могло превратиться в спутник Солнца.
Рис. 5.11. Вторая космическая скорость
Для того чтобы тело (при отсутствии сопротивления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы кинетическая энергия тела на поверхности планеты была равна (или превосходила) работу, совершаемую против сил земного притяжения. Напишем закон сохранения механической энергии Е такого тела. На поверхности планеты, конкретно — Земли
Напишем закон сохранения механической энергии Е такого тела. На поверхности планеты, конкретно — Земли
Скорость получится минимальной,если на бесконечном удалении от планеты тело будет покоиться
Приравнивая эти два выражения,получаем
откуда для второй космической скорости имеем
Для сообщения запускаемому объекту необходимой скорости (первой или второй космической) выгодно использовать линейную скорость вращения Земли, то есть запускать его как можно ближе к экватору, где эта скорость составляет, как мы видели, 463 м/с (точнее 465,10 м/с). При этом направление запуска должно совпадать с направлением вращения Земли — с запада на восток. Легко подсчитать, что таким способом можно выиграть несколько процентов в энергетических затратах.
В зависимости от начальной скорости , сообщаемой телу в точке бросания А на поверхности Земли, возможны следующие виды движения (рис. 5.8 и 5.12):
Рис. 5.12.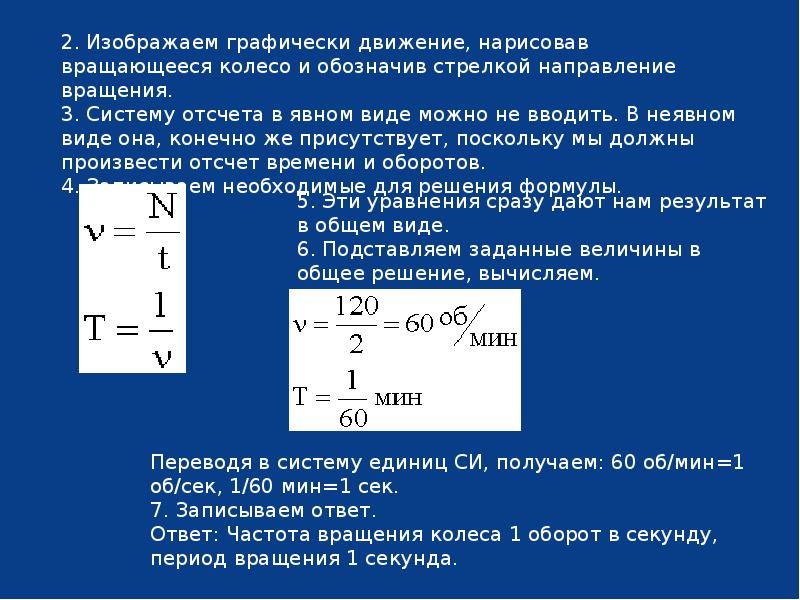 Формы траектории частицы в зависимости от скорости бросания
Формы траектории частицы в зависимости от скорости бросания
Совершенно аналогично рассчитывается движение в гравитационном поле любого другого космического тела,например, Солнца. Чтобы преодолеть силу притяжения светила и покинуть Солнечную систему,объекту,покоящемусю относительно Солнца и находящемуся от него на расстоянии, равном радиусу земной орбиты (см. выше), необходимо сообщить минимальную скорость , определяемую из равенства
где , напомним, это радиус земной орбиты, а — масса Солнца.
Отсюда следует формула, аналогичная выражению для второй космической скорости, где надо заменить массу Земли на массу Солнца и радиус Земли на радиус земной орбиты:
Подчеркнем, что — это минимальная скорость, которую надо придать неподвижному телу, находящемуся на земной орбите, чтобы оно преодолело притяжение Солнца.
Отметим также связь
с орбитальной скоростью Земли . Эта связь, как и должно быть — Земля спутник Солнца, такая же, как и между первой и второй космическими скоростями и .
На практике мы запускаем ракету с Земли, так что она заведомо участвует в орбитальном движении вокруг Солнца. Как было показано выше, Земля движется вокруг Солнца с линейной скоростью
Ракету целесообразно запускать в направлении движения Земли вокруг Солнца.
Скорость, которую необходимо сообщить телу на Земле, чтобы оно навсегда покинуло пределы Солнечной системы, называется третьей космической скоростью .
Скорость зависит от того, в каком направлении космический корабль выходит из зоны действия земного притяжения. При оптимальном запуске эта скорость составляет приблизительно = 6,6 км/с.
Понять происхождение этого числа можно также из энергетических соображений. Казалось бы, достаточно ракете сообщить относительно Земли скорость
в направлении движения Земли вокруг Солнца, и она покинет пределы Солнечной системы. Но это было бы правильно, если бы Земля не имела собственного поля тяготения. Такую скорость тело должно иметь, уже удалившись из сферы земного притяжения.
В этом уравнении мы можем выразить потенциальную энергию тела на поверхности Земли (второе слагаемое в левой части уравнения) через вторую космическую скорость в соответствии с полученной ранее формулой для второй космической скорости
Отсюда находим
Дополнительная информация
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 325–332 (§61, 62): выведены формулы для всех космических скоростей (включая третью), решены задачи о движении космических аппаратов, законы Кеплера выведены из закона всемирного тяготения.
http://kvant.mirror1.mccme.ru/1986/04/polet_k_solncu.html — Журнал «Квант» — полет космического аппарата к Солнцу (А. Бялко).
http://kvant.mirror1. mccme.ru/1981/12/zvezdnaya_dinamika.html — журнал «Квант» — звездная динамика (А.Чернин).
mccme.ru/1981/12/zvezdnaya_dinamika.html — журнал «Квант» — звездная динамика (А.Чернин).
http://www.plib.ru/library/book/17005.html — Стрелков С.П. Механика Изд. Наука 1971 г. — стр. 138–143 (§§ 40, 41): вязкое трение, закон Ньютона.
http://kvant.mirror1.mccme.ru/pdf/1997/06/kv0697sambelashvili.pdf — журнал «Квант» — гравитационная машина (А. Самбелашвили).
http://publ.lib.ru/ARCHIVES/B/»»Bibliotechka_»»Kvant»»/_»»Bibliotechka_»»Kvant»».html#029 — А.В. Бялко «Наша планета — Земля». Наука 1983 г., гл. 1, пункт 3, стр. 23–26 — приводится схема положения солнечной системы в нашей галактике, направления и скорости движения Солнца и Галактики относительно реликтового излучения.
Период обращения спутника
«…Период обращения (спутника): промежуток времени между двумя последовательными прохождениями спутником характерной точки его орбиты…»
Источник:
(Извлечение)
Официальная терминология . Академик.ру . 2012 .
Смотреть что такое «Период обращения спутника» в других словарях:
период обращения спутника — palydovo sūkio periodas statusas T sritis radioelektronika atitikmenys: angl. period of a satellite; satellite revolution period vok. Satellitenumdrehungsperiode, f; Umlaufzeit eines Satelliten, f rus. период обращения спутника, m pranc. période… … Radioelektronikos terminų žodynas
period of a satellite; satellite revolution period vok. Satellitenumdrehungsperiode, f; Umlaufzeit eines Satelliten, f rus. период обращения спутника, m pranc. période… … Radioelektronikos terminų žodynas
Период обращения (спутника) — 1. Промежуток времени между двумя последовательными прохождениями спутником характерной точки его орбиты Употребляется в документе: МСЭ 2007 год … Телекоммуникационный словарь
период обращения — Время полного обращения спутника вокруг Земли, определяемое как интервал времени между двумя последовательными проходами спутника через одну и ту же точку орбиты. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь… … Справочник технического переводчика
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
Период Изоляции — Барраяр (англ. Barrayar) вымышленная планета, место действия большинства романов научно фантастического цикла «Сага о Форкосиганах» Лоис МакМастер Буджолд. В широком смысле межзвёздная Барраярская империя с центром на этой планете.… … Википедия
Barrayar) вымышленная планета, место действия большинства романов научно фантастического цикла «Сага о Форкосиганах» Лоис МакМастер Буджолд. В широком смысле межзвёздная Барраярская империя с центром на этой планете.… … Википедия
период — сущ., м., употр. часто Морфология: (нет) чего? периода, чему? периоду, (вижу) что? период, чем? периодом, о чём? о периоде; мн. что? периоды, (нет) чего? периодов, чему? периодам, (вижу) что? периоды, чем? периодами, о чём? о периодах 1. Периодом … Толковый словарь Дмитриева
Запуск первого спутника — Первый в мире искусственный спутник Земли Передовица «Правды», посвящённая запуску спутника Спутник 1 первый искусственный спутник Земли, был запущен на орбиту в СССР 4 октября 1957 года. Кодовое обозначение спутника ПС 1 (Простейший Спутник 1).… … Википедия Википедия
Равномерное движение материальной точки по окружности. Период вращения
Более 5000 лет назад жрецы древнего Вавилона, наблюдая за Луной, определили такой хорошо известный нам интервал времени, как неделя. Как они это сделали? В чем особенность движения Луны? Встречается ли на Земле подобное движение? В данном параграфе вы найдете ответы на эти и многие другие вопросы.
Как они это сделали? В чем особенность движения Луны? Встречается ли на Земле подобное движение? В данном параграфе вы найдете ответы на эти и многие другие вопросы.
Знакомимся с движением по окружности
Попробуйте представить линию, вдоль которой движутся ребенок, кружащийся на карусели, носок в барабане стиральной машины во время отжима, кончик ножа блендера при изготовлении коктейля или смузи. Уверены, что вы легко определили: этой линией является окружность. Итак, в перечисленных случаях имеем дело с движением по окружности; простейшим является равномерное движение по окружности. Далее, говоря о равномерном движении по окружности любого физического тела, будем считать это тело материальной точкой.
Равномерно по окружности движутся, например, кабинки колеса обозрения. Близким к равномерному движению по окружности является движение планет вокруг Солнца (рис. 12.1, а), естественного спутника (Луны) или искусственных спутников вокруг Земли* (рис. 12.1, б).
Приведите примеры движения по окружности. В каких случаях это движение можно считать равномерным? Можно ли считать движение точек обода колеса велосипеда относительно его рамы равномерным движением по окружности? Обоснуйте свой ответ.
Точнее — планеты и спутники движутся по эллиптическим орбитам.
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь.
Определяем период вращения
Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные равные интервалы времени. Например, кончик секундной стрелки часов, двигаясь равномерно вдоль циферблата, повторяет свое движение через каждые 60 с (рис. 12.2).
Любое периодическое движение характеризуется такими физическими величинами, как период и частота. При равномерном движении по окружности говорят о периоде вращения и частоте вращения.
Период вращения — это физическая величина, равная времени, за которое материальная точка, равномерно движущаяся по окружности, совершает один оборот.
Период вращения обозначают символом T.
Единица периода вращения в СИ — секунда:
Период вращения равен одной секунде, если за одну секунду совершается один оборот.
Кончик секундной стрелки часов совершает один оборот за 60 с, поэтому период его вращения, как и каждой точки секундной стрелки, равен 60 с (( = 60 с).
Подумайте, каковы периоды вращения точек минутной и часовой стрелок часов. Когда взбивают молочный коктейль блендером, каждая точка его ножа за 30 с делает 6000 оборотов (рис. 12.3). Чтобы определить время одного оборота, нужно
Таким образом, чтобы определить период вращения Т, следует подсчитать количество оборотов N. совершенных за интервал времени t, и воспользоваться формулой:
Определяем частоту вращения
Указывая технические характеристики устройств, используют не период вращения, а частоту вращения (рис. 12.4).
12.4).
Частота вращения — это физическая величина, которая равна количеству оборотов за единицу времени.
Частоту вращения обозначают символом п и определяют по формуле:
где t — время вращения; N — количество оборотов за данное время. Единица частоты вращения в СИ — оборот в секунду:
Учитывая, что
приходим к выводу, что период вращения и частота вращения являются взаимно обратными величинами:
Чем больше период вращения тела, тем меньше его частота вращения, и наоборот.
I Попробуйте рассчитать частоту, с которой вращаются точки ножа блендера (см. рис. 12.3).
Узнаем, как возникли единицы времени: сутки и неделя
Как измерить время? Ответ на этот вопрос подсказала людям сама природа. Дело в том, что многие движения, происходящие в природе, являются периодическими, а период такого движения может служить единицей времени. Например, вращение Земли вокруг своей оси — периодическое движение. Ежедневный восход (закат) Солнца, обусловленный этим движением, подсказал нашим предкам единицу времени сутки, которые равны периоду вращения Земли вокруг своей оси.
Ежедневный восход (закат) Солнца, обусловленный этим движением, подсказал нашим предкам единицу времени сутки, которые равны периоду вращения Земли вокруг своей оси.
Несколько единиц времени были получены в древнем Вавилоне. Наблюдая за ночным небом, жрецы заметили, что «молодая» Луна появляется на небосклоне приблизительно каждые 28 суток. Периодическое рождение лунного диска служило своего рода вечными «часами». Так возникла единица времени месяц*. За это время Луна, вращаясь вокруг Земли, проходит полный цикл изменения фаз: новолуние, первая четверть, полнолуние, последняя четверть (рис. 12.5). Именно поэтому жрецы разделили лунный месяц на четыре части (по количеству лунных фаз) и получили семь дней — единицу времени, которая называется неделя.
Определяем скорость равномерного движения по окружности
Кроме периода вращения и его частоты важной характеристикой движения по окружности является скорость движения. Если тело равномерно движется по окружности, то за время, равное периоду вращения (= Т , тело совершает один оборот, то есть проходит путь, равный длине окружности. Длину окружности l можно вычислить по известной вам из математики формуле: I = 2лИ, где л = 3,14 — математическая константа; К — радиус окружности.
Длину окружности l можно вычислить по известной вам из математики формуле: I = 2лИ, где л = 3,14 — математическая константа; К — радиус окружности.
Зная путь и время, за которое этот путь пройден, получаем формулу для расчета скорости равномерного движения по окружности:
Сейчас, как правило, используют понятие календарного месяца, который не зависит от фаз Луны и длится от 28 до 31 суток.
Именно об этой скорости идет речь, когда, например, определяют скорость движения человека, кружащегося на карусели, говорят о скорости полета искусственных спутников Земли и т. д.
Подводим итоги
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь. Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные одинаковые интервалы времени.
Период вращения Т — физическая величина, равная времени, в течение которого материальная точка, равномерно движущаяся по окружности, совершает один оборот. Единица периода вращения в СИ — секунда (с).
Единица периода вращения в СИ — секунда (с).
Частота вращения п — это физическая величина, которая равна количеству оборотов за единицу времени. Единица частоты вращения в СИ — оборот в секунду (об/с, или 1/с).
Период вращения Т и частоту вращения п определяют по формулам:
где t — время наблюдения; N — количество оборотов за это время. Частота вращения и период вращения — взаимно обратные величины:
Контрольные вопросы
1. Какое движение называют равномерным движением по окружности?
2. Какое движение называют периодическим? Почему равномерное движение по окружности является периодическим? 3. Какие физические величины характеризуют периодическое движение? 4. Дайте определение периода вращения. 5. Как вычислить период вращения? 6. Дайте определение частоты вращения. 7. Как вычислить частоту вращения, если известен период вращения? 8. Наблюдение за каким процессом послужило причиной появления таких единиц времени, как месяц и неделя?
Упражнение № 12
1. За 18 секунд колесо автомобиля сделало 24 оборота. Определите период вращения точки на ободе колеса.
За 18 секунд колесо автомобиля сделало 24 оборота. Определите период вращения точки на ободе колеса.
2. Какова частота вращения точек патрона электродрели, если за минуту патрон совершает 900 оборотов?
3. На лопасть отключенного вентилятора прикрепили маленькую наклейку со смайликом. С какой частотой будет вращаться смайлик, если лопасти вентилятора будут совершать один оборот за 0,2 с?
4. Известно, что вентилятор микропроцессора персонального компьютера вращается с частотой 3600 об/мин. Определите период вращения точек лопастей вентилятора.
5. Мальчик кружился на карусели 5 мин. За это время он совершил 100 оборотов. В каком случае можно утверждать, что период вращения мальчика был равен 3 с? Ответ обоснуйте.
6. Четыре шестерни скреплены зубцами так, как показано на рис. 1. Шестерня 1 имеет 9 зубцов, шестерня 2 — 15 зубцов, шестерня 3 — 8 зубцов, шестерня 4 — 16 зубцов. Шестерни 2 и 3 закреплены на общем валу. Определите период вращения шестерни 4, если частота вращения шестерни 1 равна 5 об/с. Определите скорость, с которой вращается стакан, стоящий на краю поворотного столика СВЧ-печи.
Определите скорость, с которой вращается стакан, стоящий на краю поворотного столика СВЧ-печи.
ЛАБОРАТОРНАЯ РАБОТА № 4
Тема. Измерение периода и частоты вращения.
Цель: измерить период и частоту вращения тела при его равномерном движении по окружности.
Оборудование: пластиковый шарик или другое небольшое тело (пуговица, ключ и т. п.), которое можно легко закрепить на нити; лист бумаги с изображением окружности радиусом 15 см; крепкая нерастяжимая нить длиной 50-60 см; секундомер; линейка.
УКАЗАНИЯ К РАБОТЕ Подготовка к эксперименту
1. Убедитесь, что вы знаете ответы на следующие вопросы.
1) Какое движение называют равномерным движением по окружности?
2) По какой формуле вычисляют период равномерного движения тела по окружности? По какой формуле вычисляют частоту вращения?
2. Прикрепите шарик (или другое небольшое тело) к нити. На свободном конце нити сделайте петлю, за которую вы будете держать нить, вращая тело в горизонтальной плоскости.
Эксперимент
Строго придерживайтесь инструкции по безопасности (см. форзац). Результаты измерений сразу заносите в таблицу.
1. Возьмите за петлю нить с телом. Расположите руку над центром изображенной окружности.
Не меняя положения руки, заставьте тело двигаться так, чтобы траектория его движения совпадала с окружностью.
2. Измерьте время t, за которое тело выполняет 10 оборотов; 15 оборотов.
Обработка результатов эксперимента
Определите период и частоту вращения тела при его равномерном движении по окружности. Результаты занесите в таблицу.
Анализ эксперимента и его результатов
Проанализировав эксперимент, сделайте вывод, в котором укажите: 1) какое движение вы изучали; 2) значение каких величин определяли;
3) какие результаты получили; 4) какие факторы влияли на точность результатов.
Творческое задание
В плохо освещенном помещении благодаря особенностям зрения человек может различать события как отдельные, если интервал времени между ними составляет более 0,2-0,3 с. С какой частотой нужно двигать по окружности «бенгальский огонь», чтобы увидеть светящееся кольцо?
С какой частотой нужно двигать по окружности «бенгальский огонь», чтобы увидеть светящееся кольцо?
Задание «со звездочкой»
Запишите результаты измерения периода вращения тела в виде:
Это материал учебника Физика 7 класс Барьяхтар, Довгий
Период обращения спутника — Энциклопедия по машиностроению XXL
Решение. Период обращения спутника — это время, за которое он совершает один полный оборот по орбите. Это время равно 1 ч 36 мин, или 96 мин. [c.275]Если в это время происходит п-е затмение того же спутника Юпитера, то на Земле оно будет зарегистрировано с опозданием на R- -r)l секунд. Поэтому, если период обращения спутника вокруг Юпитера t, то промежуток времени Тх, протекший между первым и п-и затмениями ли, равен [c.419]
Зная длину окружности радиуса R+H, получим формулу для периода обращения спутника вокруг Земли
[c. 363]
363]
Двумя месяцами позднее, 3 апреля 1966 г. в 21 час 44 мин по московскому времени был выведен на окололунную орбиту первый искусственный спутник Луны — Луна-10 . Угол наклонения орбиты спутника к плоскости лунного экватора был равен 72°2 , максимальное удаление от лунной поверхности (в апоселении) составляло около 1000 км, минимальное удаление (в периселении) — около 380 км период обращения спутника вокруг Луны определился равным 2 час 58 мин. До 30 мая, когда был полностью израсходован бортовой запас электроэнергии, со спутником проведено 219 сеансов радиосвязи. Полученная при этом информация позволила определить напряженность магнитного поля и пространствен- [c.432]
Период обращения спутников Земли зависит от высоты их полета (табл. 2.2). [c.90]
| Таблица 2.2 Период обращения спутников Земли |
 Период обращения спутника 90 мин. Определите нормальное ускорение спутника. Радиус Земли 6400 км. (9 м/с .)
[c.304]
Период обращения спутника 90 мин. Определите нормальное ускорение спутника. Радиус Земли 6400 км. (9 м/с .)
[c.304]Периоды обращения спутников Земли [c.990]
Период обращения спутника зависит от средней высоты полета. В случае движения по круговой орбите скорость движения спутника постоянна и равна первой космической скорости на данной высоте [14]. [c.990]
В этом параграфе будет идти речь только об эллиптическом движении. Периодом обращения спутника вокруг притягивающего центра называют время Т между двумя последовательными моментами прохождения спутника через его перицентр. Пусть т— время, прошедшее с момента /о прохождения спутника через перицентр Я, 5 — площадь, заметенная радиусом-вектором спутника в течение [c.80]
Когда спутник совершит один полный оборот вокруг притягивающего центра, то от момента го прохождения через перицентр пройдет время Т (где Т — период обращения спутника), а радиус-вектор спутника успеет замести весь эллипс и притом один раз. Площадь этого эллипса, как известно, равна шЬ, следовательно,
[c.80]
Площадь этого эллипса, как известно, равна шЬ, следовательно,
[c.80]
Эта формула позволяет найти период обращения спутника, если известна большая полуось его орбиты и гравитационный параметр К. Из формулы (1) видно, что при изменении эксцентриситета орбиты или ее малой полуоси Ь или фокального параметра р период спутника не изменится только изменение большой полуоси влияет на период обращения спутника (при данном К)- Формулу (1) можно переписать и так [c.81]
Поэтому (см. (7)) период обращения спутника Т зависит только от абсолютной величины скорости, но не от ее направления если в какой-то точке пространства стартует малый спутник с некоторой эллиптической скоростью VQ, то при любом направлении вектора скорости спутник вернется в точку старта через одно и то же время (если только он по пути не столкнется с центральным телом). [c.83]
Советский спутник Электрон-2 , запущенный в январе 1964 года для исследования радиационных поясов Земли, имел в день запуска перигей ную высоту // = 460 км. Период обращения спутника составлял
[c.86]
Период обращения спутника составлял
[c.86]
Положим в этом равенстве 0 = 2я тогда % = Т, где Г — период обращения спутника вокруг притягивающего центра. В этом случае формула (6) дает [c.105]
По этим формулам можно найти дуги % и осо. Выбор нужного значения уро среди различных дуг, удовлетворяющих условию (3), можно произвести на основании дополнительных сведений о движении спутника, например по тому, каков был период обращения спутника Т, проходил ли спутник над пунктом Л с юга на север или наоборот, и т. п. Аналогично обстоит дело с выбором дуги ао. [c.160]
Задача 2. Искусственный спутник Земли в момент времени находился в своем перигее Я, который (в этот момент) оказался над пунктом А земной поверхности, имеющим географические координаты (фо, А,о) (рис. 4.10). Известны следующие элементы орбиты спутника угол у наклона плоскости орбиты к плоскости экватора период обращения спутника 7, эксцентриситет орбиты 8. Требуется указать те моменты /, когда спутник будет находиться над пунктами с широтой ф. Какова будет в каждый такой момент времени долгота А, подспутниковой точки
[c.162]
Требуется указать те моменты /, когда спутник будет находиться над пунктами с широтой ф. Какова будет в каждый такой момент времени долгота А, подспутниковой точки
[c.162]
Эти формулы и позволяют вычислить оставшийся срок жизни спутника, если, помимо обычно публикуемых сведений об орбите, известна еще быстрота уменьшения периода обращения спутника —дТ/(И). [c.298]
Приведем пример 9 ноября 1957 года перигей первого искусственного спутника находился на высоте 210 км, апогей — на высоте 810 км. Быстрота уменьшения периода обращения спутника составляла 2,94 секунды за сутки. Легко подсчитать, что а = 6880 /сж, Г = 5610 сек. [c.298]
Спутник движется по круговой околоземной орбите радиуса го, делая один оборот за время Т. В результате приложения радиального импульса скорости и он переходит на эллиптическую орбиту. Определить период обращения спутника по эллиптической орбите. [c.137]
Таким образом, период вынужденных колебаний равен половине периода обращения спутника по орбите в вы-
[c. 142]
142]
Здесь Т — период обращения спутника. [c.207]
Так как ориентация спутника изменяется, то меняется И эффективная площадь сечения (средняя по периоду кувыркания спутника), поэтому меняются величина силы торможения и период обращения по орбите. На рис. 87 изображено (сплошной линией) наблюдаемое изменение периода обращения спутника Экспло-рер-1У . Наряду с этим на рис. 87 изображено изменение эффективной площади при прохождении через пери- [c.351]
Найдем теперь период обращения спутника по эллиптической орбите. Исходя из интеграла площадей, имеем [c.112]
Среднее значение функции ДСф) за период обращения спутника легка вычисляется [c.603]
Возмущенное движение спутников. Вследствие возмущений траектория ИСЗ существенно изменяется за конечный промежуток времени. В этом случае для расчета траектории используют приближенный метод, предполагая, что в течение периода обращения спутник движется по эллипсу, а параметры, определяющие его размеры и ориентацию в пространстве, изменяются адиабатически медленно МТ [c. 47]
47]
Пусть теперь Т есть аномалистический период обращения спутника. Тогда, поскольку [c.272]
Для того чтобы найти плотность по этой формуле, нужно знать скорость изменения аномалистического периода обращения спутника. [c.272]
Ранее мы видели, что под влиянием сопротивления атмосферы высота перигея, эксцентриситет и период обращения спутника монотонно уменьшаются. Со временем они достигают некоторых критических значений, при которых спутник может совершить одно-два обращения вокруг Земли. Критические значения элементов орбиты зависят от коэффициента х, пропорционального отношению площади поперечного сечения к массе спутника. Чем больше этот коэффициент, тем больше критический период обращения и критическая высота перигея. На практике, однако, можно считать, что спутник прекращает свое существование, когда высота перигея достигает 120— 150 км, а период обращения равен 86,5—88,0 минут. При этом существенным обстоятельством является то, что в конце своей жизни спутник движется по почти круговой орбите, т. е. критическое значение эксцентриситета оказывается весьма близким к нулю. Поэтому при определении продолжительности жизни спутника можно принять за критический момент тот момент времени, когда эксцентриситет его орбиты тождественно равен нулю.
[c.273]
е. критическое значение эксцентриситета оказывается весьма близким к нулю. Поэтому при определении продолжительности жизни спутника можно принять за критический момент тот момент времени, когда эксцентриситет его орбиты тождественно равен нулю.
[c.273]
Период обращения спутника по круговой орбите Т = Например, для рассчитанного выше случая, когда == 6,7-10 /ш и = 7,8 кмкек, период Т 91 Спутник движется по орбите, в плоскости которой лежит центр Земли (в одном из фокусов эллипса). Поэтому сила тяготения, действующая на спутник и направленная к центру Земли, также лежит в плоскости орбиты и не может изменить положения этой плоскости относительно Солнца и звезд. Дело здесь обстоит так же, как и с плоскостью качании маятника Фуко, установленного на полюсе ( 27). Плоскость орбиты сохраняет неизменным свое положение относительно Солнца и звезд, а Земля вращается под нею вокруг своей оси ).
 Если за один оборот Земли вокруг своей оси спутник делает много оборотов по своей орбите, то траектория спутника относительно Земли представляет собой ряд витков , сдвинутых по экватору на тот угол, на который Земля успевает повернуться за один оборот спутника. Угол, который образуют вптки с экватором, зависит от угла между плоскостью орбиты и осью Земли (который можно считать неизменным, поскольку можно счи1ать, что плоскость орбиты сохраняет свое положение относительно Солнца и звезд),
[c.330]
Если за один оборот Земли вокруг своей оси спутник делает много оборотов по своей орбите, то траектория спутника относительно Земли представляет собой ряд витков , сдвинутых по экватору на тот угол, на который Земля успевает повернуться за один оборот спутника. Угол, который образуют вптки с экватором, зависит от угла между плоскостью орбиты и осью Земли (который можно считать неизменным, поскольку можно счи1ать, что плоскость орбиты сохраняет свое положение относительно Солнца и звезд),
[c.330]Формулы (10) и (II) иногда записывают в ином виде, удобном в случае малого эксцентриситета 8. Пусть экваториальный радиус планеты (/ э) и большая полуось орбиты спутника а) измеряются в км, а гравитационный параметр К имеет размерность км 1сек тогда период обращения спутника (Т) составляет 2па» /р К сек. [c.281]
Периодические колебания произвольного спутника при произвольных эксцентриситетах. Если оба параметра уравнения (2.3.5)—и е — произвольны (не малы), то анализ движения представляется весьма затруднительным однако такой анализ можно провести, широко использовав расчеты на вычислительных машинах. Такое иссдедование было проведено В. А. Злато-устовым, Д. Е. Охоцимским, В. А. Сарычевым, А. П. Торжевским и изложено в их совместной работе [37]. Как уже было указано, наибольший интерес представляют периодические решения, ибо устойчивые периодические движения могут быть использованы в качестве номинальных движений для системы гравитационной стабилизации на эллиптических орбитах. В работе [37] исследуются нечетные периодические решения с периодом, равным периоду обращения спутника по
[c.96]
Такое иссдедование было проведено В. А. Злато-устовым, Д. Е. Охоцимским, В. А. Сарычевым, А. П. Торжевским и изложено в их совместной работе [37]. Как уже было указано, наибольший интерес представляют периодические решения, ибо устойчивые периодические движения могут быть использованы в качестве номинальных движений для системы гравитационной стабилизации на эллиптических орбитах. В работе [37] исследуются нечетные периодические решения с периодом, равным периоду обращения спутника по
[c.96]
С точки зрения механики осреднение по гр эквивалентно пренебрежению в решении высокочастотными колебаниями весьма малой амплитуды, которые накладываются на более плавные колебания, описываемые уравнениями (5.4.12). Высокочастотные колебания, обусловленные влиянием гр, назовем вибрационными колебаниями. Уравнения (5.4.12) в общем случае не интегрируются, так как U зависит от v. Эти уравнения описывают весьма медленные вековые и долгопериодические эффекты движения, а также периодические эффекты, обусловленные влиянием v. Период этих периодических колебаний соизмерим с периодом обращения спутника по орбите. Вековые и долгопериодические члены изменяются весьма медленно по сравнению со скоростью движения центра масс спутника по орбите. Для их выявления можно осреднить уравнения движения не только по гр, но и по v. Независимое осреднение по каждой фазовой переменной (гр, v) допустимо, если частоты этих переменных несоизмеримы, что мы всегда будем предполагать. Такое двойное осреднение уравнений (5.4.3) сводится к осреднению по v уравнений
[c.187]
Период этих периодических колебаний соизмерим с периодом обращения спутника по орбите. Вековые и долгопериодические члены изменяются весьма медленно по сравнению со скоростью движения центра масс спутника по орбите. Для их выявления можно осреднить уравнения движения не только по гр, но и по v. Независимое осреднение по каждой фазовой переменной (гр, v) допустимо, если частоты этих переменных несоизмеримы, что мы всегда будем предполагать. Такое двойное осреднение уравнений (5.4.3) сводится к осреднению по v уравнений
[c.187]
 Не учитывая ни долгопериодических, ни короткопериодических возмущений, следует правые части упомянутых уравнений осреднить по обоим аргументам а и Ф. Придем к соотношениям вида
[c.592]
Не учитывая ни долгопериодических, ни короткопериодических возмущений, следует правые части упомянутых уравнений осреднить по обоим аргументам а и Ф. Придем к соотношениям вида
[c.592]Математика движения спутников
Урок 4: Планетарные и Спутниковое движениеМатематика спутника Движение
Движение объектов подчиняется законам Ньютона. В те же простые законы, которые управляют движением объектов на Земле также простираются до небес, чтобы управлять движением планет, луны и другие спутники. Математика, описывающая движение спутника — та же математика, представленная для круговые движения в Уроке 1.В в этой части Урока 4 мы рассмотрим разнообразие математических уравнений, описывающих движение спутники.
Рассмотрим спутник
с массой M села на орбиту центрального тела с
масса массы M Central . Центральное тело могло быть
планета, солнце или другая большая масса, способная
вызывая достаточное ускорение на менее массивном поблизости
объект. Если спутник движется по кругу, то
чистая центростремительная сила, действующая на
этот орбитальный спутник задается соотношением
Центральное тело могло быть
планета, солнце или другая большая масса, способная
вызывая достаточное ускорение на менее массивном поблизости
объект. Если спутник движется по кругу, то
чистая центростремительная сила, действующая на
этот орбитальный спутник задается соотношением
Эта чистая центростремительная сила является результатом гравитационного сила, притягивающая спутник к центральному body, и может быть представлен как
F грав = (G * M сб. * M Центральный ) / 2Поскольку F grav = F net , указанное выше выражения для центростремительной силы и гравитационной силы равны.Таким образом,
(M сб. *)
v 2 ) / R = (G * M сб. * M Центральный ) / R 2
*)
v 2 ) / R = (G * M сб. * M Центральный ) / R 2 Обратите внимание на то, что масса спутника присутствует на обоих стороны уравнения; таким образом, его можно отменить, разделив через M сб . потом обе части уравнения можно умножить на R , оставив следующие уравнение.
против 2 = (G * M Центральный ) / RВзяв квадратный корень из каждой стороны, остается следующее уравнение скорости спутника, движущегося вокруг центральное тело в круговом движении
, где G = 6,67 x
10 -11 Н м 2 / кг 2 , м центральный =
масса центрального тела, вокруг которого находится спутник
орбиты, а R =
радиус орбиты спутника.
Подобные рассуждения могут быть используется для определения уравнения ускорения нашего спутник, который выражается массой и радиусом орбита. Величина ускорения спутника равна ускорение свободного падения спутника при любом место, на орбите которого он движется. В уроке 3 уравнение ускорения свободного падения было задано как
г = (G * M центральный ) / R 2Таким образом, ускорение спутник, движущийся по кругу вокруг некоторого центрального тела, является определяется следующим уравнением
где G = 6.67 х
10 -11 Н м 2 / кг 2 , м центральный =
масса центрального тела, вокруг которого находится спутник
орбиты, а R =
средний радиус орбиты спутника.
Окончательное уравнение, которое полезно в описывающее движение спутников — это форма Ньютона. Третий закон Кеплера. Поскольку логика разработки уравнения было представлено в другом месте, здесь будет представлено только уравнение.Период спутник ( T ) и среднее расстояние от центрального тела ( R ) связаны следующее уравнение:
где T = период спутника, R = средний радиус орбиты спутника (расстояние от центр центральной планеты), и G = 6,67 x 10 -11 Н м 2 / кг 2 .
Есть важная концепция очевидна во всех трех из этих уравнений — период, скорость и ускорение обращения по орбите спутник не зависят от массы спутника.
Ни одно из этих трех уравнений не имеет
переменная M спутник в них. Период, скорость и ускорение спутника
зависит только от радиуса орбиты и массы
центральное тело, вокруг которого вращается спутник.Просто в
в случае движения снаряда по земле масса
снаряд не влияет на ускорение в сторону
земля и скорость в любой момент. Когда воздух
сопротивление незначительно, и все силы, кроме гравитации,
не существует, масса движущегося объекта становится
нефакторный. Так обстоит дело с орбитальными спутниками.
Период, скорость и ускорение спутника
зависит только от радиуса орбиты и массы
центральное тело, вокруг которого вращается спутник.Просто в
в случае движения снаряда по земле масса
снаряд не влияет на ускорение в сторону
земля и скорость в любой момент. Когда воздух
сопротивление незначительно, и все силы, кроме гравитации,
не существует, масса движущегося объекта становится
нефакторный. Так обстоит дело с орбитальными спутниками.
Чтобы проиллюстрировать полезность вышеизложенного уравнения, рассмотрите следующие практические задачи.
| Практическая задача
# 1 Спутник желает облететь Землю на
высота 100 км (примерно 60 миль) над
поверхность земли. |
Как и большинство других задач в физике, эта задача начинается с выявление известной и неизвестной информации и выбор соответствующее уравнение, способное разрешить неизвестное. За Эта проблема, известные и неизвестные перечислены ниже.
| Выдано / Известно: R = R земля + высота = 6.47 х 10 6 м M земля = 5.98×10 24 кг G = 6,67 x 10 -11 Н м 2 / кг 2 | Неизвестный: v = ??? а = ??? Т = ??? |
Обратите внимание, что радиус спутника
орбиту можно найти, зная радиус Земли
и высота спутника над землей. Как показано в
диаграмма справа, радиус орбиты для
спутник равен сумме радиуса Земли и
высота над землей. Эти две величины могут быть добавлены к
дают радиус орбиты. В этой задаче 100 км должны
сначала преобразовать в 100 000 м перед добавлением к
радиус земли. Уравнения, необходимые для определения
неизвестны те, которые перечислены выше. Мы начнем с
определение орбитальной скорости спутника с помощью
следующее уравнение:
Как показано в
диаграмма справа, радиус орбиты для
спутник равен сумме радиуса Земли и
высота над землей. Эти две величины могут быть добавлены к
дают радиус орбиты. В этой задаче 100 км должны
сначала преобразовать в 100 000 м перед добавлением к
радиус земли. Уравнения, необходимые для определения
неизвестны те, которые перечислены выше. Мы начнем с
определение орбитальной скорости спутника с помощью
следующее уравнение:
Замена и решение следующие:
v = КОРЕНЬ [(6.67 х 10 -11 с.ш. м 2 / кг 2 ) * (5,98 x 10 24 кг) / (6,47 x 10 6 м) ]v = 7,85 x 10 3 м / с
Ускорение можно определить по одному из следующие уравнения:
| (1) а = (G * M центральный ) / R 2 | (2) а = v 2 / R |
Уравнение (1) было получено выше. Уравнение (2) является общим уравнением для
круговое движение. Любое уравнение можно использовать для
рассчитать ускорение; использование уравнения (1) будет
продемонстрировано здесь.
Уравнение (2) является общим уравнением для
круговое движение. Любое уравнение можно использовать для
рассчитать ускорение; использование уравнения (1) будет
продемонстрировано здесь.
a = (6,67 x 10 -11 N м 2 / кг 2 ) * (5.98×10 24 кг) / (6,47 x 10 6 м) 2
а = 9.53 м / с 2
Обратите внимание, что это ускорение немного меньше, чем 9,8 м / с 2 ожидаемое значение на поверхности земли. Как обсуждалось в Уроке 3, увеличенное расстояние от центра земли снижает значение г.
Наконец, период можно рассчитать, используя следующие уравнение:
Уравнение можно переписать к следующему виду
T = КОРЕНЬ [(4 * pi 2 * R 3 ) / (G * M центральный )]Замена и решение следующие:
Т = КОРЕНЬ [(4 * (3. 1415) 2 * (6,47 х
10 6 м) 3 ) /
(6,67 x 10 -11 Н
м 2 / кг 2 ) * (5.98×10 24 кг) ]
1415) 2 * (6,47 х
10 6 м) 3 ) /
(6,67 x 10 -11 Н
м 2 / кг 2 ) * (5.98×10 24 кг) ]T = 5177 с = 1,44 часы
| Практическая задача
# 2 Период Луны примерно 27.2 дней (2.35×10 6 с). Определить радиус орбиты Луны и орбитальной скорости Луна. (Дано: M земля = 5.98×10 24 кг, R земля = 6.37 x 10 6 м) |
Как и практическая задача №2, эта задача начинается с
идентификация известных и неизвестных значений. Они показаны
ниже.
Они показаны
ниже.
| Выдано / Известно: T = 2.35×10 6 с M земля = 5.98×10 24 кг G = 6,67 x 10 -11 Н м 2 / кг 2 | Неизвестный: R = ??? v = ??? |
Радиус орбиты можно рассчитать, используя следующие уравнение:
Уравнение можно переписать к следующему виду
R 3 = [(Т 2 * Г * М центральный ) / (4 * pi 2 )]Замена и решение следующие:
R 3 = [((2. 35х10 6 с) 2 * (6,67 x
10 -11 с.ш.
м 2 / кг 2 ) * (5.98×10 24 кг) ) /
(4 * (3,1415) 2 )]
35х10 6 с) 2 * (6,67 x
10 -11 с.ш.
м 2 / кг 2 ) * (5.98×10 24 кг) ) /
(4 * (3,1415) 2 )]R 3 = 5,58 x 10 25 м 3
Взяв кубический корень из 5,58 x 10 25 м 3 , радиус можно определить так:
R = 3.82 х 10 8 мОрбитальная скорость спутника может быть вычислена из любое из следующих уравнений:
| (1) v = КОРЕНЬ [ (G * M Центральный ) / R ] | (2) v = (2 * пи * R) / Т |
Уравнение (1) было получено выше. Уравнение (2) является общим уравнением для
круговое движение. Любое уравнение можно использовать для
рассчитать орбитальную скорость; использование уравнения (1) будет
продемонстрировано здесь. Подстановка значений в это
уравнение и решение следующие:
Уравнение (2) является общим уравнением для
круговое движение. Любое уравнение можно использовать для
рассчитать орбитальную скорость; использование уравнения (1) будет
продемонстрировано здесь. Подстановка значений в это
уравнение и решение следующие:
v = 1.02 х 10 3 м / с
| Практическая задача
# 3 Геостационарный спутник — это спутник, который
вращается вокруг Земли с периодом обращения 24
часов, что соответствует периоду земного
вращательное движение. |
Как и в предыдущей задаче, решение начинается с идентификация известных и неизвестных значений. Это показано ниже.
| Выдано / Известно: T = 86400 с М земля = 5. R земля = 6,37 x 10 6 м G = 6,67 x 10 -11 Н м 2 / кг 2 | Неизвестный: ч = ??? |
Неизвестное в этой проблеме высота спутника над поверхностью земли.Но уравнения с переменной h нет. Решение затем включает сначала определение радиуса орбиты и использование это значение R и R земли, чтобы найти высоту спутник над землей. Как показано на диаграмме на справа радиус орбиты спутника равен сумма радиуса Земли и высоты над земной шар. Радиус орбиты можно найти, используя следующие уравнение:
Уравнение можно переписать к следующему виду
R 3 = [(Т 2 * Г * М центральный ) / (4 * pi 2 )]Замена и решение следующие:
R 3 = [((86400 с) 2 * (6. 67 x 10 -11 Н
м 2 / кг 2 ) * (5.98×10 24 кг) ) /
(4 * (3,1415) 2 )]
67 x 10 -11 Н
м 2 / кг 2 ) * (5.98×10 24 кг) ) /
(4 * (3,1415) 2 )]R 3 = 7,54 x 10 22 м 3
Взяв кубический корень из 7,54 x 10 22 м 3 , радиус можно определить так:
R = 4,23 х 10 7 мРадиус орбиты указывает расстояние, на которое спутник идет из центра Земли.Теперь, когда радиус орбиты найден, высота над землей можно рассчитать. Поскольку поверхность Земли равна 6,37 x 10 6 м от его центра (это радиус Земля), высота спутника должна составлять
4,23 x 10 7 м — 6,37 x 10 6 м = 3,59 х 10 7 м над поверхностью земли. Так что высота
спутник 3. 59 х 10 7 м .
59 х 10 7 м .
1. Спутник вращается вокруг Земли. Какой из следующие переменные будут влиять на скорость спутник?
- Масса спутника
- высота над поверхностью земли
- масса земли
2.Используйте информацию ниже и отношения выше для расчета соотношения T 2 / R 3 для планеты о Солнце, Луна о Земле и спутники Сатурна около планеты Сатурн. Значение G равно 6.67×10 -11 Н · м 2 / кг 2 .
вс | M = 2,0 x 10 30 кг |
| земной шар | М = 6. 0 x 10 24 кг 0 x 10 24 кг |
| Сатурн | M = 5,7 x 10 26 кг |
- T 2 / R 3 для планет
около солнца
- T 2 / R 3 для Луны около Земли
- T 2 / R 3 для лун около Сатурн
3.Мимас — спутник Сатурна. Средний радиус орбиты
Мимаса составляет 1,87×10 8 м, а его период обращения составляет
примерно 23 часа (8,28×10 4 с). Использовать
T 2 / R 3 соотношение для определения массы
Сатурн.
4. Спутник находится на низкой околоземной орбите на высоте 220 метров. км над земной поверхностью. Учитывая следующую информацию, определить орбитальную скорость спутника.
| G = 6,67 x 10 -11 Нм 2 / кг 2 M Земля = 5,98 x 10 24 кг R земля = 6,37 x 10 6 м |
5.Космический шаттл вращается вокруг Земли на высоте 400 км над ее уровнем.
поверхность. Используйте информацию, указанную в предыдущем вопросе
для определения орбитальной скорости и орбитального периода
космический шаттл.
Кривая вращения Млечного Пути
Дополнительная информация с сайта www.astronomynotes.com
Теперь, когда у нас есть представление о размере, звездном населении и общее представление о Млечном Пути как о галактике, давайте рассмотрим еще одно свойство, которое мы можем определить для Млечного Пути: его массу.В большинстве случаев, когда мы намереваемся вычислить массу астрономического объекта, мы возвращаемся к версии третьего закона Кеплера Ньютона:
P2 = (4π 2 x a3) / G (m1 + m2) Солнце вращается вокруг центра Галактики, поэтому, в принципе, если мы можем измерить расстояние Солнца от Центра Галактики и его период обращения, это означает, что мы можем оценить сумма масс Солнца и Галактики (по крайней мере, та часть Галактики, которая находится внутри орбиты Солнца). Поскольку мы ожидаем, что масса Галактики намного превысит массу Солнца, мы можем принять вычисленное нами значение за массу Галактики. Итак, каков ответ? Насколько массивна наша галактика?
Итак, каков ответ? Насколько массивна наша галактика?
Расстояние от Солнца до центра Галактики можно измерить с помощью нескольких различных методов, но сделать это сложно. Исследователи по-прежнему расходятся во мнениях относительно точного значения, но оно составляет примерно 8 кпк (то есть 8000 парсеков). Есть связанное с этим, но тоже сложное измерение, и это скорость Солнца по отношению к Центру Галактики. Это примерно 200 км / сек, что позволяет нам оценить период обращения Солнца вокруг Галактического центра следующим образом:
- Предположим, что Солнце движется по круговой орбите с радиусом 8000 парсеков.
- Вычислите длину окружности орбиты Солнца: c = 2πr = (2π) * (8000 пк) * (3,1 x 1013 км / пк) = 1,6 x 1018 км.
- Вычислите период орбиты, взяв длину окружности и разделив ее на скорость: P = 1,6 x 1018 км / 200 км / сек = 8,0 x 1015 сек ≈ 250 миллионов лет.
Если принять большую полуось орбиты Солнца равной 8 килопарсек, а период обращения 250 миллионов лет, вы можете определить, что масса Млечного Пути по отношению к орбите Солнца составляет примерно 10 11 масс Солнца, или в 100 миллиардов раз больше массы Солнца.
Теперь сравним и сопоставим движения планет в Солнечной системе и движения звезд в Галактике. То, что мы сделали выше, чтобы вычислить период орбиты Солнца, заключалось в использовании уравнения:
орбитальный период (P) = окружность орбиты (2πr) / орбитальная скорость (v)Мы можем изменить это уравнение и вычислить орбитальную скорость для любого объекта с учетом его периода и большой полуоси. Если мы применим это к планетам в Солнечной системе, вы обнаружите, что по мере удаления от Солнца орбитальная скорость объекта уменьшается.Ниже представлен двухмерный график, который я создал для орбитальных скоростей планет (и Плутона) как функции их расстояния от Солнца. Каждая точка помечена первой буквой названия объекта (например, V = Венера). Этот тип графика (орбитальная скорость как функция расстояния от центра) называется кривой вращения .
Рис. 8.16: График орбитальных скоростей планет Солнечной системы, показывающий, как они уменьшаются быстрее, чем линейно для объектов, более удаленных от Солнца.
Кредит: Крис Пальма
Поведение планет Солнечной системы, показанное на этом графике, часто называют Кеплеровским вращением . Ясно, что Галактика Млечный Путь сложнее Солнечной системы. Есть по крайней мере 100 миллиардов объектов, газовых облаков и пыли, и в центре нет ни одной доминирующей массы. Однако астрономы ожидали, что по мере того, как вы удаляетесь от центра Галактики, скорости звезд должны уменьшаться подобно кеплеровскому вращению, наблюдаемому у планет Солнечной системы.Однако астрономы заметили, что существует значительная разница между прогнозируемой формой кривой вращения Млечного Пути и тем, что фактически измеряется. См. Изображение ниже.
Рис. 8.17: Кривая вращения типичной спиральной галактики: предсказанная ( A ) и наблюдаемая ( B ). Расхождение кривых связано с темной материей.
Сплошная линия, обозначенная буквой B, представляет собой схематическую кривую вращения, подобную той, которая измеряется для Млечного Пути. Пунктирная линия, обозначенная A, представляет собой прогнозируемую кривую вращения, отображающую кеплеровское вращение. Кривая вращения B говорит нам о том, что наша модель Млечного Пути пока что-то упускает. Чтобы объекты, далекие от центра Галактики, двигались быстрее, чем предполагалось, должна быть значительная дополнительная масса вдали от центра Галактики, оказывающая гравитационное притяжение на эти звезды. Это означает, что Млечный Путь должен включать в себя очень массивный компонент, намного превышающий размер видимого диска Галактики.Мы не видим никаких компонентов в видимом свете или любой другой части электромагнитного спектра, поэтому этот массивный ореол должен быть темным. Сегодня мы называем это «гало темной материи» Галактики, и мы обсудим темную материю больше в нашем уроке по космологии.
Пунктирная линия, обозначенная A, представляет собой прогнозируемую кривую вращения, отображающую кеплеровское вращение. Кривая вращения B говорит нам о том, что наша модель Млечного Пути пока что-то упускает. Чтобы объекты, далекие от центра Галактики, двигались быстрее, чем предполагалось, должна быть значительная дополнительная масса вдали от центра Галактики, оказывающая гравитационное притяжение на эти звезды. Это означает, что Млечный Путь должен включать в себя очень массивный компонент, намного превышающий размер видимого диска Галактики.Мы не видим никаких компонентов в видимом свете или любой другой части электромагнитного спектра, поэтому этот массивный ореол должен быть темным. Сегодня мы называем это «гало темной материи» Галактики, и мы обсудим темную материю больше в нашем уроке по космологии.
Возвращаясь к изображению Млечного Пути, которое мы изучали ранее, гало из проволочного каркаса на самом деле означает размер гало темной материи. На изображении ниже сравните масштаб диска с масштабом ореола темной материи.
Рис. 8.18: Схематическая диаграмма гало темной материи Млечного Пути, полученная из Partiview / Digital Universe Atlas, представленная каркасной сферой, которая полностью охватывает тонкий диск Млечного Пути и намного больше его.
Вращение тела — обзор
1.6.2 Перенос напряжений Рейнольдса
Точная формула для Pk, Eq. (1.46) следует из рассуждений в формуле. (1,47). Иные, но аналогичные рассуждения дают формулу
(1.53) Pij = −τik∂U‾j∂xk − τjk∂U‾i∂xk
для компонента тензора напряжений Рейнольдса τij, производимого компонентами. Перенос напряжений Рейнольдса Модели имеют форму Ур. (1.45) с ϕ = τij, но член Pϕ разбивается на две части. Первый представляет собой переход между турбулентностью и средним потоком; второй представляет собой перенос между различными компонентами напряжения Рейнольдса. Следовательно, уравнение переноса записывается
(1.54) DτDt = P + Π − ετ − ∇⋅Fϕ
, в котором P — добыча по среднему потоку (уравнение. (1.53)), а Π — перераспределение между компонентами. Об этом свидетельствуют трассы Πii = 0 и Pii = 2Pk. Тензор перераспределения , Π , берет отклонение от одного компонента и добавляет его к другому, сохраняя общую постоянную.
(1.53)), а Π — перераспределение между компонентами. Об этом свидетельствуют трассы Πii = 0 и Pii = 2Pk. Тензор перераспределения , Π , берет отклонение от одного компонента и добавляет его к другому, сохраняя общую постоянную.
В параллельном сдвиговом потоке, U‾ (y), уравнение. (1.53) дает
(1.55) P11 = −2u′v′‾∂U‾∂y; P12 = −v′2‾∂U‾∂y;
,и все остальные Pij равны нулю. Второй из них показывает, почему u′v′‾ <0, когда ∂yU‾> 0, как в формуле вихревой вязкости Eq.(1.35). Первое из уравнений (1.55) показывает, как энергия среднего потока передается только в u′2‾. Он перераспределяется в v′2‾ и w′2‾ с помощью члена перераспределения, следовательно, 11 <0 и Π22, Π33> 0.
В качестве другого примера рассмотрим жидкость во вращении твердого тела с угловой скоростью ΩF против часовой стрелки. По отношению к фиксированной системе отсчета абсолютная скорость увеличивается на U = −ΩFy, V = ΩFx и
(1,56) P11 = 2u′v′‾ΩF; P22 = −2u′v′‾ΩF; P12 = (v ′ 2‾ − u′2‾) ΩF
добавлено в производство. (Если бы турбулентность была изотропной, все это исчезло бы.Изотропия.)
(Если бы турбулентность была изотропной, все это исчезло бы.Изотропия.)
При вращающемся параллельном сдвиговом потоке два вклада в добычу, уравнения. (1.55) и (1.56) складываются, чтобы получить
P11 = −2u′v′‾ (∂U‾∂y − ΩF); P22 = −2u′v′‾ΩF; P12 = −v′2‾∂ U‾∂y− (u′2‾ − v′2‾) ΩF.
Сумма первых двух показывает, что вращение не оказывает прямого влияния на производство турбулентной кинетической энергии. Однако это косвенно влияет на производство.
В сдвиговом потоке с ∂U‾ / ∂y> 0 напряжение сдвига Рейнольдса u′v′‾ отрицательно и u′2‾> v′2‾.Возмущение, вызванное положительным вращением, увеличивает величину P12, что увеличивает величину u′v′‾, соответственно увеличивая добычу на k . Положительное вращение — против часовой стрелки, что противодействует сдвигу; так, вращение против сдвига увеличивает интенсивность турбулентности; вращение со сдвигом уменьшает его. Этот анализ вращения переносится на влияние кривизны линий тока на турбулентность: вогнутая кривизна увеличивает образование турбулентности, выпуклая кривизна уменьшает ее.
В дополнение к ротационному вкладу в добычу добавляется неинерциальный член, если поток решается во вращающейся системе отсчета. Это вносит вклад в уравнение. (1.54), что совпадает с формулой. (1.56). Важно отличать вклад вращения в производство от его вклада через неинерционные члены в уравнении переноса напряжения Рейнольдса.
Но есть простое объяснение влияния вращения на сдвиговый поток, в котором они объединяются в одно ускорение Кориолиса.Возвращаясь к уравнениям. (1.31), которые представляют собой уравнения для независимых возмущений x , и отбрасывая вязкий член, но добавляя ускорение Кориолиса,
(1,57) dudt = 2ΩFv − Svdvdt = −2ΩFu
, где S представляет ∂yU‾. Комбинируя уравнения. (1.57) и определение параметра вращения R≡ − 2ΩF / S дает
d2udt2 = −R (R + 1) S2u.
Общее решение u = exp (± −R (R + 1) St). Таким образом, если −1  Следовательно, экспоненциальный рост происходит, когда вращение противодействует сдвигу. Однако при сильном вращении R <−1, так что рост прекращается. Когда R <-1 или R> 0, решение является колебательным; но при добавлении вязкости раствор превращается в затухающие колебания.
Следовательно, экспоненциальный рост происходит, когда вращение противодействует сдвигу. Однако при сильном вращении R <−1, так что рост прекращается. Когда R <-1 или R> 0, решение является колебательным; но при добавлении вязкости раствор превращается в затухающие колебания.
Если R = 0 или −1, решением будет u = u0 + u˙0t, что предполагает, что решение все еще растет, хотя и алгебраически, а не экспоненциально. Действительно, R = 0 — это (однородный) сдвиг без вращения, при котором турбулентная энергия действительно растет.
Коэффициент R (R + 1) дает максимальный рост при R = −1 / 2, что верно, но он дает скорость роста, симметричную относительно R = −1 / 2, а это не так.Тем не менее, из этого анализа можно сделать некоторые выводы. Переформулированные как уравнения эволюции напряжений Рейнольдса, Eqs. (1.57) становится
(1.58), где τ = St. Первые два уравнения можно заменить на
(1.59) 12d (u2‾ + v2‾) dτ = −uv‾12d (u2‾ − v2‾) dτ = −uv‾ (2R + 1)
, которое показывает, что вращение не влияет напрямую на рост кинетической энергии, и это вращение создает анизотропию, если R = −1 / 2.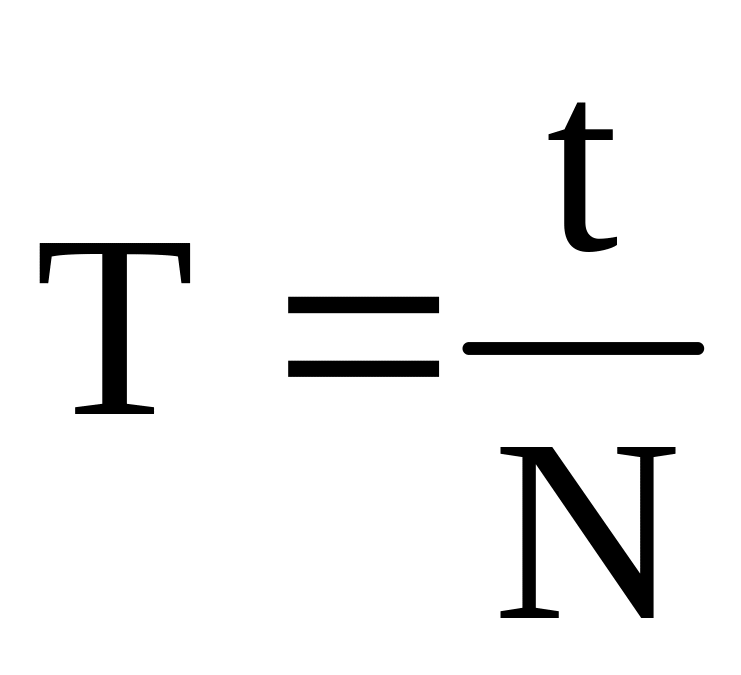 Энергия будет расти, только если uv‾ <0. При этом условии, учитывая уравнение. (1.58) v2‾ может расти, только если R <0, а u2‾ может расти, только если R> −1.
Энергия будет расти, только если uv‾ <0. При этом условии, учитывая уравнение. (1.58) v2‾ может расти, только если R <0, а u2‾ может расти, только если R> −1.
10.2 Кинематика вращательного движения — College Physics chapters 1-17
Сводка
- Соблюдайте кинематику вращательного движения.
- Составьте кинематические уравнения вращения.
- Оцените стратегии решения проблем для вращательной кинематики.
Просто используя нашу интуицию, мы можем начать видеть, как вращательные величины, такие как [латекс] \ boldsymbol {\ theta}, \: \ boldsymbol {\ omega}, [/ latex] и [латекс] \ boldsymbol {\ alpha} [ / latex] связаны друг с другом.Например, если колесо мотоцикла имеет большое угловое ускорение в течение довольно длительного времени, оно быстро вращается и совершает много оборотов. Говоря техническим языком, если угловое ускорение колеса [латекс] \ boldsymbol {\ alpha} [/ latex] велико в течение длительного периода времени [латекс] \ boldsymbol {t}, [/ latex], то конечная угловая скорость [ latex] \ boldsymbol {\ omega} [/ latex] и угол поворота [latex] \ boldsymbol {\ theta} [/ latex] большие.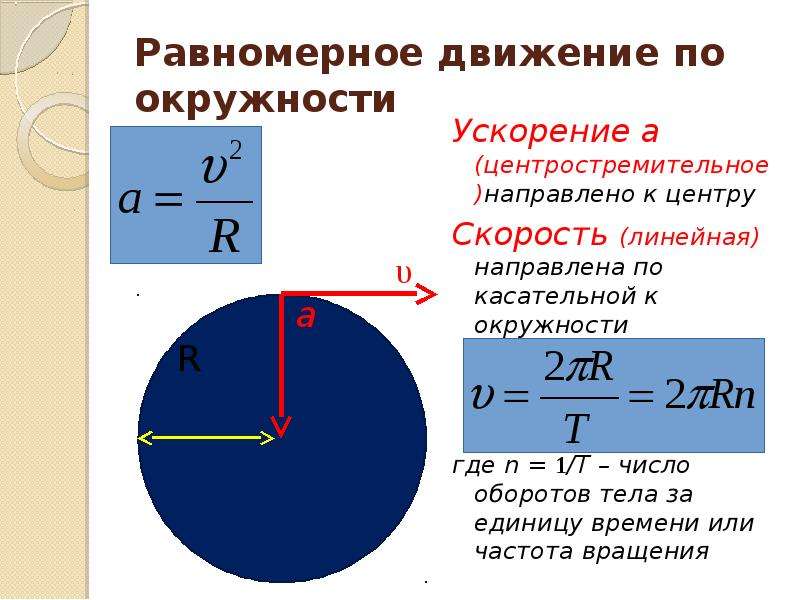 Вращательное движение колеса в точности аналогично тому, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.
Вращательное движение колеса в точности аналогично тому, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.
Кинематика — это описание движения. Кинематика вращательного движения описывает отношения между углом вращения, угловой скоростью, угловым ускорением и временем. Давайте начнем с поиска уравнения, связывающего [латекс] \ boldsymbol {\ omega}, \: \ boldsymbol {\ alpha}, [/ latex] и [латекс] \ boldsymbol {t}. [/ Latex] Чтобы определить это уравнение, напомним знакомое кинематическое уравнение поступательного или прямолинейного движения:
[латекс] \ boldsymbol {v = v_0 + at \ textbf {(константа a)}} [/ latex]
Обратите внимание, что во вращательном движении [латекс] \ boldsymbol {a = a _ {\ textbf {t}}}, [/ latex] и мы будем использовать символ [латекс] \ boldsymbol {a} [/ latex] для тангенциального или линейного ускорение с этого момента.Как и в линейной кинематике, мы предполагаем, что [латекс] \ boldsymbol {a} [/ latex] является постоянным, что означает, что угловое ускорение [латекс] \ boldsymbol {\ alpha} [/ latex] также является константой, потому что [латекс] \ boldsymbol {a = r \ alpha}. [/ latex] Теперь давайте заменим [latex] \ boldsymbol {v = r \ omega} [/ latex] на [latex] \ boldsymbol {a = r \ alpha} [/ latex ] в линейное уравнение выше:
[/ latex] Теперь давайте заменим [latex] \ boldsymbol {v = r \ omega} [/ latex] на [latex] \ boldsymbol {a = r \ alpha} [/ latex ] в линейное уравнение выше:
[латекс] \ boldsymbol {r \ omega = r \ omega_0 + r \ alpha {t}}. [/ Latex]
Радиус [латекс] \ boldsymbol {r} [/ latex] сокращается в уравнении, давая
[латекс] \ boldsymbol {\ omega = \ omega_0 + at \ textbf {(константа a),}} [/ latex]
где [латекс] \ boldsymbol {\ omega_0} [/ latex] — начальная угловая скорость.Это последнее уравнение представляет собой кинематическое соотношение между [latex] \ boldsymbol {\ omega}, \: \ boldsymbol {\ alpha}, [/ latex] и [latex] \ boldsymbol {t} [/ latex], то есть он описывает их отношения без ссылки на силы или массы, которые могут повлиять на вращение. По форме он аналогичен своему переводному аналогу.
ПОДКЛЮЧЕНИЕ
Кинематика вращательного движения полностью аналогична поступательной кинематике, впервые представленной в главе 2 «Одномерная кинематика». Кинематика занимается описанием движения без учета силы или массы. Мы обнаружим, что поступательные кинематические величины, такие как смещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.
Кинематика занимается описанием движения без учета силы или массы. Мы обнаружим, что поступательные кинематические величины, такие как смещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.
Исходя из четырех кинематических уравнений, которые мы разработали в главе 2 «Одномерная кинематика», мы можем вывести следующие четыре кинематических уравнения вращения (представленные вместе с их аналогами для поступательного движения):
| ротационный | Трансляционный | |
|---|---|---|
| [латекс] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ латекс] | [латекс] \ boldsymbol {x = \ bar {v} t} [/ латекс] | |
| [латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}} [/ латекс] | [латекс] \ boldsymbol {v = v_0 + at} [/ латекс] | (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) |
| [латекс] \ boldsymbol {\ omega = \ omega_0 {t} + \ frac {1} {2} \ alpha {t} ^ 2} [/ латекс] | [латекс] \ boldsymbol {x = v_0t + \ frac {1} {2} at ^ 2} [/ latex] | (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) |
| [латекс] \ boldsymbol {\ omega ^ 2 = \ omega_0 ^ 2 + 2 \ alpha \ theta} [/ латекс] | [латекс] \ boldsymbol {v ^ 2 = v_0 ^ 2 + 2ax} [/ латекс] | (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) |
Таблица 2.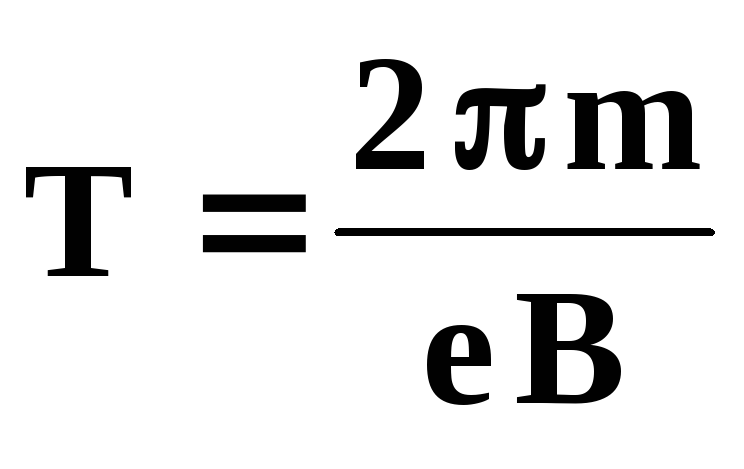 Вращательные кинематические уравнения. Вращательные кинематические уравнения. | ||
В этих уравнениях индекс 0 обозначает начальные значения ([latex] \ boldsymbol {\ theta_0}, \: \ boldsymbol {x_0}, [/ latex] и [latex] \ boldsymbol {t_0} [/ latex] — начальные значения), а средняя угловая скорость [латекс] \ boldsymbol {\ bar {\ omega}} [/ latex] и средняя скорость [латекс] \ boldsymbol {\ bar {v}} [/ latex] определяются следующим образом :
[латекс] \ boldsymbol {\ bar {\ omega} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ omega_0 + \ omega} {2}} [/ latex] [латекс] \ textbf {и } \ boldsymbol {\ bar {v} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v_0 + v} {2}}.[/ латекс]
Уравнения, приведенные выше в таблице 2, могут использоваться для решения любой задачи вращательной или поступательной кинематики, в которой [latex] \ boldsymbol {a} [/ latex] и [latex] \ boldsymbol {\ alpha} [/ latex] являются постоянными.
СТРАТЕГИЯ РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ВРАЩАТЕЛЬНОЙ КИНЕМАТИКИ
- Изучите ситуацию, чтобы определить, задействована ли кинематика вращения (вращательное движение) .
 Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.
Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение. - Определите, что именно необходимо определить в проблеме (определите неизвестные) . Набросок ситуации полезен.
- Составьте список того, что дано или может быть выведено из проблемы, как указано (укажите известные) .
- Решите соответствующее уравнение или уравнения для количества, которое необходимо определить (неизвестное) . Может быть полезно думать в терминах трансляционного аналога, потому что теперь вы знакомы с таким движением.
- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения . Обязательно используйте радианы для углов.
- Проверьте свой ответ, чтобы узнать, разумен ли он: Имеет ли смысл ваш ответ ?
Пример 1: Расчет ускорения рыболовной катушки
Глубоководный рыбак ловит большую рыбу, которая отплывает от лодки, выдергивая леску из своей рыболовной катушки. 2} [/ latex] в течение 2,00 с, как показано на рисунке 1.
2} [/ latex] в течение 2,00 с, как показано на рисунке 1.
(а) Какова конечная угловая скорость мотовила?
(b) С какой скоростью леска покидает катушку по истечении 2,00 с?
(c) Сколько оборотов делает катушка?
(d) Сколько метров лески сошло с катушки за это время?
Стратегия
В каждой части этого примера стратегия такая же, как и для решения задач линейной кинематики. В частности, идентифицируются известные значения, и затем ищется взаимосвязь, которая может использоваться для решения неизвестных.
Решение для (а)
Здесь даны [латекс] \ boldsymbol {\ alpha} [/ latex] и [latex] \ boldsymbol {t} [/ latex] и необходимо определить [latex] \ boldsymbol {\ omega} [/ latex]. Самым простым в использовании уравнением является [латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}} [/ latex], потому что неизвестное уже на одной стороне, а все остальные термины известны. Это уравнение утверждает, что
[латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}. 2) (2.00 \ textbf {s}) = 220 \ textbf {рад / с.}} [/ Latex]
2) (2.00 \ textbf {s}) = 220 \ textbf {рад / с.}} [/ Latex]
Решение для (b)
Теперь, когда [латекс] \ boldsymbol {\ omega} [/ latex] известен, скорость [латекс] \ boldsymbol {v} [/ latex] проще всего определить с помощью соотношения
[латекс] \ boldsymbol {v = r \ omega,} [/ латекс]
, где радиус [латекс] \ boldsymbol {r} [/ латекс] катушки задан равным 4,50 см; таким образом,
[латекс] \ boldsymbol {v = (0,0450 \ textbf {m}) (220 \ textbf {rad / s}) = 9.90 \ textbf {m / s.}} [/ Latex]
Еще раз обратите внимание, что радианы всегда должны использоваться в любых вычислениях, касающихся линейных и угловых величин.Кроме того, поскольку радианы безразмерны, мы имеем [latex] \ boldsymbol {\ textbf {m} \ times \ textbf {rad} = \ textbf {m}}. [/ Latex]
Решение для (c)
Здесь нам предлагается найти количество оборотов. Поскольку [latex] \ boldsymbol {1 \ textbf {rev} = 2 \ pi \ textbf {rad}}, [/ latex], мы можем узнать количество оборотов, найдя [latex] \ boldsymbol {\ theta} [/ latex] в радианах.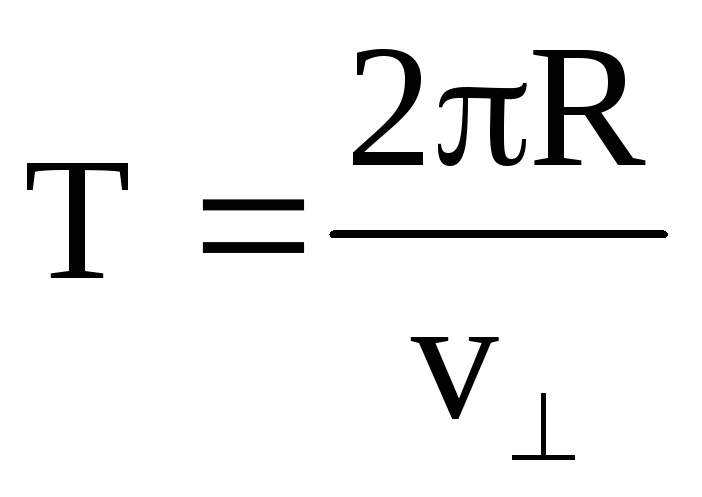 2}.2 = 220 \ textbf {рад.}} \ End {array} [/ latex]
2}.2 = 220 \ textbf {рад.}} \ End {array} [/ latex]
Преобразование радианов в обороты дает
[латекс] \ boldsymbol {\ theta = (220 \ textbf {rad})} [/ latex] [латекс] \ boldsymbol {\ frac {1 \ textbf {rev}} {2 \ pi \ textbf {rad}}} [/ latex] [latex] \ boldsymbol {= 35.0 \ textbf {rev.}} [/ latex]
Решение для (d)
Длина лески [latex] \ boldsymbol {x}, [/ latex] в метрах может быть получена через ее связь с [latex] \ boldsymbol {\ theta}: [/ latex]
[латекс] \ boldsymbol {x = r \ theta = (0.0450 \ textbf {m}) (220 \ textbf {rad}) = 9.90 \ textbf {m}}. [/ Latex]
Обсуждение
Этот пример показывает, что отношения между вращательными величинами очень похожи на отношения между линейными величинами. Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После раскручивания в течение двух секунд катушка вращается со скоростью 220 рад / с, что составляет 2100 об / мин. 2}} [/ latex] [латекс] \ boldsymbol {= 0.733 \ textbf {s.}} [/ Latex]
2}} [/ latex] [латекс] \ boldsymbol {= 0.733 \ textbf {s.}} [/ Latex]
Обсуждение
Обратите внимание, что следует проявлять осторожность со знаками, указывающими направление различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда лопается из-за участвующих в ней ускорений, и рыбаки часто позволяют рыбе плавать некоторое время, прежде чем тормозить катушку. Уставшая рыба будет медленнее, требуя меньшего ускорения.
Пример 3: Расчет медленного ускорения поездов и их колес
Большие грузовые поезда очень медленно ускоряются.2}. [/ Latex] После того, как колеса сделали 200 оборотов (предполагая отсутствие пробуксовки): (a) Как далеко поезд продвинулся по рельсам? б) Какова конечная угловая скорость колес и линейная скорость поезда?
Стратегия
В части (a) нас просят найти [latex] \ boldsymbol {x}, [/ latex], а в (b) нас просят найти [latex] \ boldsymbol {\ omega} [/ latex] и [ латекс] \ boldsymbol {v}. [/ latex] Нам даны количество оборотов [латекс] \ boldsymbol {\ theta}, [/ latex] радиус колес [латекс] \ boldsymbol {r}, [/ латекс ] и угловое ускорение [латекс] \ boldsymbol {\ alpha}.[/ латекс]
[/ latex] Нам даны количество оборотов [латекс] \ boldsymbol {\ theta}, [/ latex] радиус колес [латекс] \ boldsymbol {r}, [/ латекс ] и угловое ускорение [латекс] \ boldsymbol {\ alpha}.[/ латекс]
Решение для (а)
Расстояние [латекс] \ boldsymbol {x} [/ latex] очень легко найти из соотношения между расстоянием и углом поворота:
[латекс] \ boldsymbol {\ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {x} {r}}. [/ Latex]
Решение этого уравнения для [latex] \ boldsymbol {x} [/ latex] дает
[латекс] \ boldsymbol {x = r \ theta}. [/ Latex]
Перед использованием этого уравнения мы должны преобразовать количество оборотов в радианы, потому что мы имеем дело с соотношением между линейными и вращательными величинами:
[латекс] \ boldsymbol {\ theta = (200 \ textbf {rev})} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi \ textbf {rad}} {1 \ textbf {rev}}} [/ латекс] [латекс] \ boldsymbol {= 1257 \ textbf {рад. 2 + 2 \ alpha \ theta} [/ латекс]
2 + 2 \ alpha \ theta} [/ латекс]
Извлечение квадратного корня из этого уравнения и ввод известных значений дает
[латекс] \ begin {array} {lcl} \ boldsymbol {\ omega} & \ boldsymbol {=} & \ boldsymbol {[0 + 2 (0.{1/2}} \\ {} & \ boldsymbol {=} & \ boldsymbol {25.1 \ textbf {rad / s.}} \ End {array} [/ latex]
Мы можем найти линейную скорость поезда, [latex] \ boldsymbol {v}, [/ latex] через его связь с [latex] \ boldsymbol {\ omega}: [/ latex]
[латекс] \ boldsymbol {v = r \ omega = (0.350 \ textbf {m}) (25.1 \ textbf {rad / s}) = 8.77 \ textbf {m / s.}} [/ Latex]
Обсуждение
Пройденное расстояние довольно велико, а конечная скорость довольно мала (чуть менее 32 км / ч).
Существует поступательное движение даже для чего-то, вращающегося на месте, как показано в следующем примере. На рис. 2 изображена муха на краю вращающейся пластины микроволновой печи. В приведенном ниже примере вычисляется общее пройденное расстояние.
Пример 4: Расчет расстояния, пройденного мухой на краю плиты микроволновой печи
Человек решает использовать микроволновую печь, чтобы разогреть обед.При этом муха случайно влетает в микроволновку, приземляется на внешний край вращающейся пластины и остается там. Если тарелка имеет радиус 0,15 м и вращается со скоростью 6,0 об / мин, рассчитайте общее расстояние, пройденное мухой за 2,0-минутный период приготовления. (Игнорируйте время запуска и замедления.)
Стратегия
Сначала найдите общее количество оборотов [latex] \ boldsymbol {\ theta}, [/ latex], а затем линейное расстояние [latex] \ boldsymbol {x} [/ latex], пройденное.[latex] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ latex] можно использовать для поиска [latex] \ boldsymbol {\ theta} [/ latex], потому что [latex] \ boldsymbol {\ bar {\ omega}} [/ latex] задано 6,0 об / мин.
Решение
Ввод известных значений в [latex] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ latex] дает
[латекс] \ boldsymbol {\ theta = \ bar {\ omega} t = (6.0 \ textbf {rpm}) (2.0 \ textbf {min}) = 12 \ textbf {rev}.} [/ Latex]
Как всегда, необходимо преобразовать обороты в радианы перед вычислением линейной величины, такой как [latex] \ boldsymbol {x} [/ latex], из угловой величины, такой как [latex] \ boldsymbol {\ theta}: [/ latex]
[латекс] \ boldsymbol {\ theta = (12 \ textbf {rev})} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi \ textbf {rad}} {1 \ textbf {rev}}} [/ латекс] [латекс] \ boldsymbol {= 75.4 \ textbf {rad}.} [/ Latex]
Теперь, используя соотношение между [latex] \ boldsymbol {x} [/ latex] и [latex] \ boldsymbol {\ theta}, [/ latex], мы можем определить пройденное расстояние:
[латекс] \ boldsymbol {x = r \ omega = (0.15 \ textbf {m}) (75.4 \ textbf {rad}) = 11 \ textbf {m}}. [/ Latex]
Обсуждение
Неплохая поездка (если выживет)! Обратите внимание, что это расстояние — это полное расстояние, пройденное мухой.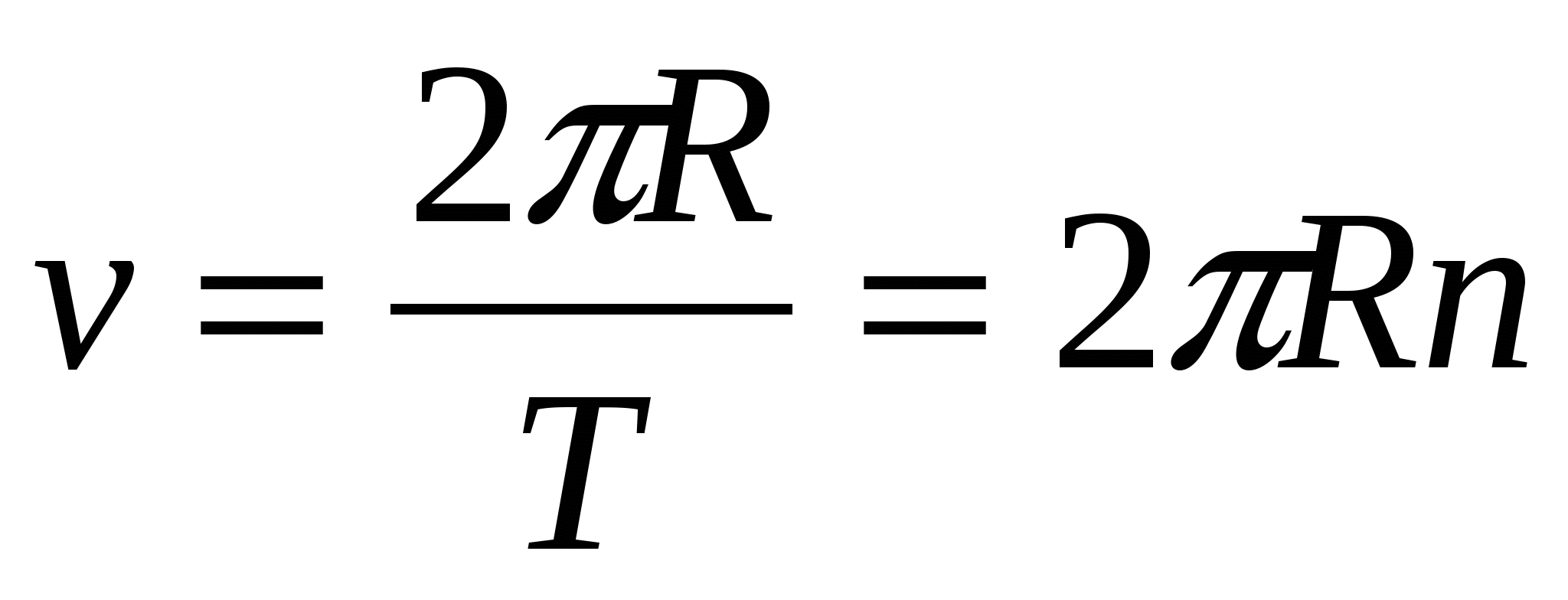 Смещение фактически равно нулю для полных оборотов, потому что они возвращают муху в исходное положение.Различие между общим пройденным расстоянием и перемещением было впервые отмечено в главе 2 «Одномерная кинематика».
Смещение фактически равно нулю для полных оборотов, потому что они возвращают муху в исходное положение.Различие между общим пройденным расстоянием и перемещением было впервые отмечено в главе 2 «Одномерная кинематика».
Проверьте свое понимание
1: Кинематика вращения имеет множество полезных взаимосвязей, часто выражаемых в форме уравнений. Являются ли эти отношения законами физики или они просто описательны? (Подсказка: тот же вопрос относится к линейной кинематике.)
Задачи и упражнения
1: С помощью струны гироскоп ускоряется из состояния покоя до 32 рад / с за 0.40 с.
(а) Каково его угловое ускорение в рад / с 2 ?
(б) Сколько оборотов он совершает в процессе?
2: Предположим, на компакт-диске оказался кусок пыли. Если скорость вращения компакт-диска составляет 500 об / мин, а пылинка находится на расстоянии 4,3 см от центра, какое общее расстояние проходит пыль за 3 минуты? (Игнорируйте ускорения из-за вращения компакт-диска. )
)
3: Гироскоп замедляется с начальной скорости 32.2}. [/ Latex]
(a) Каково угловое ускорение его шин радиусом 0,280 м, если предположить, что они не скользят по тротуару?
(b) Сколько оборотов делают шины перед остановкой, учитывая их начальную угловую скорость [латекс] \ boldsymbol {95.0 \ textbf {rad / s}} [/ latex]?
(c) Сколько времени нужно автомобилю, чтобы полностью остановиться?
(d) Какое расстояние машина проезжает за это время?
(e) Какова была начальная скорость автомобиля?
(f) Кажутся ли полученные значения разумными, учитывая, что эта остановка происходит очень быстро?
Рисунок 3.2}, [/ latex] какое угловое ускорение у йо-йо?(б) Какова угловая скорость через 0,750 с, если она начинается из состояния покоя?
(c) Внешний радиус йо-йо составляет 3,50 см. Каково тангенциальное ускорение точки на краю?
Глоссарий
- кинематика вращательного движения
- описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем.

Решения
Проверьте свое понимание
1: Кинематика вращения (как и линейная кинематика) носит описательный характер и не отражает законы природы.2} [/ латекс]
б) 450 рад / с
в) 21,0 м / с
Расчет периода экономической ротации для равновозрастных насаждений в Хорватии Расчет периода экономической ротации для одновозрастных насаждений в Хорватии ISSN 1 8 4 7-6 4 8 1
S. Posavec, K. Beljan, S. Krajter, D Першун
110
Целевой севооборот обычно основан на физиологической
зрелости деревьев. В разновозрастных лесах возраст рубки
для лесных деревьев основан на диаметре дерева
и спелости рубки, т.е.е. оптимальный диаметр
дерева; когда дерево станет достаточно зрелым, чтобы его можно было использовать
. Зрелость рубок означает, что возраст, когда чистая приведенная стоимость леса
максимальна, тогда как стоимость
может включать стоимость древесины и недревесных пород.
Это утверждение относится к спелой древесине, а не к старому
приросту и прореживанию [8]. Объем древесины, подлежащей рубке
, должен учитывать спрос рынка —
кет, но также и мощность леса, при этом
необходимо учитывать производственные возможности,
наряду с сохранением или увеличение лесного фонда [9].
Определение экономически наиболее выгодного периода рентабельности
— это инвестиционная проблема, а также проблема (управленческой) инвентаризации, связанная с
конкретным землепользованием [10].
Хозяйственный оборот древостоя достигается при достижении максимального дохода
, т. Е. При производстве
ценных запасов древесины. Увеличение стоимости запаса древостоя на
более стабильно, чем прирост
.Максимальное значение роста происходит после
максимума приращения стоимости древесины. Возраст экологической зрелости
может быть определен с помощью тангенса угла
, взятого из начала системы координат на
кривой стоимости древостоя или определения возраста
, при котором будет достигнут максимально возможный доход
по расчету.
В одновозрастных лесах экономическая зрелость приводит к
очень долгой ротации, особенно для тех древесных пород
, цена которых растет пропорционально возрасту.В случае леса дуба черешчатого (Quercus robur L.)
значение
увеличивается пропорционально кубу диаметра
на высоте груди [11]. По мере увеличения диаметра элитных деревьев
значение также увеличивается или остается неизменным. Это означает, что дубы черешчатые
нельзя рубить, пока они здоровые, а их стоимость
постоянно увеличивается.
Чтобы обеспечить устойчивый доход от леса
, необходимо найти ответ на вопрос, как, где и
, когда следует рубить древесину в лесу и как будет восстанавливать древостой
.Устойчивый урожай составит
, если лес не был вырублен более чем на
годового прироста.
В этой статье мы анализируем, можно ли
определить экономический оборот для одновозрастного леса
на основе природных и экономических параметров. Сравнение
Сравнение
между периодом ротации, используемым в хорватской лесохозяйственной практике
, и периодом экономической ротации составило
.
МАТЕРИАЛ И МЕТОДЫ
Бук обыкновенный (Fagus sylvatica L.) является наиболее распространенным видом деревьев в Хорватии, занимая площадь 744 796
га. Он занимает наибольшую долю в хорватском запасе древостоя
(36%) [12].
Буковые леса классифицируются в соответствии с менеджментом —
возрастом типов леса для хозяйственного производства
качественных бревен (фанерный, лущеный и распиловочный)
и древесины для химической обработки. Одновозрастная система управления
всегда дает лучший круглый лес, чем выборочная
.
Из-за длительного периода производства (и ротации)
цены на продукцию подвержены влиянию инфляции. Цены на пиломатериалы
сортиментов и стоимость рабочей силы не равны на протяжении
периода производства (в данном случае 100 лет) и их
сложно рассчитать точно. В связи с различными ограничениями долгосрочных расчетов было использовано допущение о постоянных
В связи с различными ограничениями долгосрочных расчетов было использовано допущение о постоянных
постоянных ценах на продукты, лесохозяйственные и административные
затрат.В расчетах инфляция
будет равна нулю. Таким образом, средние затраты и цены на
товаров и услуг будут постоянными во времени.
Объектами исследования являются 14 буков обыкновенных
насаждений размером 1 га, по одному в декаду. Research
Стендынаходятся на первой площадке класса качества и управляются с помощью системы управления одновозрастным
. Источником данных был
«Справочник лесоуправления», из которого были даны данные о развитии запаса древостоя, текущем годовом приросте
(CAI) и среднегодовом приросте (MAI) из таблицы
до конца ротации. (Таблица 1) было взято
.
Таблицы урожайности используются для сравнения реального состояния запасов
в реальном лесу при нормальных условиях.
Расчет производится на основе установленной тарифной последовательности
, полученной из таблиц двойного объема
единиц и кривой высот. Диаметр груди
Диаметр груди
рост измерялся методом тотальной калибровки. В четных
старых насаждениях, выделенных на рубку в последующие
лет, все деревья были обмерены.
Возраст
Древостой
Объем
(м3 / га)
Текущий годовой
прирост
(м3 / га / год)
Среднегодовой
прирост
(м3 / га / год)
20100 12,0 5,5
30185 13,0 7,7
40 254 13,3 9,0
50 310 13,9 9,9
60 367 13,1 10,5
70 419 12,4 10,9
80 469 11,6 11,1
90 516
100 55 11,1 9000 9,4 11,1
110 591 8.6 10,9
120 618 7,8 10,7
130 637 6,7 10,5
140 646 6,6 10,2
150 654 10,0
ТАБЛИЦА 1
Характеристики стенда (CAI- Текущий годовой
Прирост, MAI- Средний годовой прирост) [13 ]
Вращение и гравитация
Вращение и гравитация
Равномерное круговое движение означает, что частица движется с постоянной скоростью по кругу.
Для такого случая скорость не является постоянным , даже если скорость постоянна. Следовательно, частица имеет ускорение. Почему?
Ответ : ускорение возникает из-за того, что направление v постоянно меняется как v остается параллельным касательной к окружности.
На основании свойств подобных треугольников (т.е. соотношение соответствующие стороны равны), докажем, что величина ускорения равна предоставлено,
a = v 2 / r, где r — радиус окружности.
Это называется центростремительный (поиск по центру) ускорение, потому что a всегда указывает на центр круга. В приведенной выше формуле скорость определяется выражением
.в = 2пр / Т,
, где T — период движения, т. е.е.
время один раз обойти круг.
е.е.
время один раз обойти круг.
Вооружен приведенными выше формулами центростремительного ускорения и скорость, второй закон Ньютона движения, и третий закон Кеплера движения планет (T 2 пропорционально r 3 ),
Ньютонов Вселенский закон всемирного тяготения следует,
F = G M m / r 2 .
Эта формула дает величину гравитационной силы, F, одна масса, M, действует на другую массу, m, когда две массы находятся на расстоянии из r друг от друга. Символ G называется всемирным тяготением. постоянный. Его значение
G = 6,67×10 -11 Н-м 2 / кг 2 .
Примеры [ в классе]
оборотов
оборотОборотов
Предположим, вы заменяете подшипники в колесе вашего
велосипед. Чтобы проверить, хорошо ли вы поработали, вы держите ось.
вертикально и покрутите. Ось в центре колеса
стационарный. Колеса в целом нет поступательное движение . Но колесо крутится
ось. Каждая точка колеса совершает круговое движение вокруг
ось вращения. Такое движение вокруг оси вращения есть
называется вращательным движением .
Чтобы проверить, хорошо ли вы поработали, вы держите ось.
вертикально и покрутите. Ось в центре колеса
стационарный. Колеса в целом нет поступательное движение . Но колесо крутится
ось. Каждая точка колеса совершает круговое движение вокруг
ось вращения. Такое движение вокруг оси вращения есть
называется вращательным движением .
Расширенный объект может иметь трансляционные и вращательное движение.Любое движение протяженного объекта можно увидеть как сочетание поступательного движения центр масс и вращательное движение вокруг центра масс.
Фильм о подбрасывании губки
Пример:
Квадрат из пенопласта имеет синий светодиод возле CM и красный светодиод у его края. Если мы бросим губку мы можем легко наблюдать параболическое движение ЦМ и вращательное движение вокруг ЦМ.
Как описать вращательное движение?
Предположим, вы сделали отметку мелом на ободе колеса и вы
первоначально сориентируйте колесо так, чтобы отметка была обращена к вам. Это ваша справочная ориентация. В угловое положение колеса описывает его ориентацию
относительно этой эталонной ориентации. Когда колесо вращается, это
угловое положение меняется. Угловой смещение измеряет, как далеко он повернулся от своего
справочная ориентация.Это часто
удобно ориентировать систему координат так, чтобы ось z
совпадает с осью вращения, а ось x определяет
справочная ориентация. Тогда угловое смещение
θ из
точка P на колесе — это угол θ прямой от оси вращения
в точку P делает с осью абсцисс.
Это ваша справочная ориентация. В угловое положение колеса описывает его ориентацию
относительно этой эталонной ориентации. Когда колесо вращается, это
угловое положение меняется. Угловой смещение измеряет, как далеко он повернулся от своего
справочная ориентация.Это часто
удобно ориентировать систему координат так, чтобы ось z
совпадает с осью вращения, а ось x определяет
справочная ориентация. Тогда угловое смещение
θ из
точка P на колесе — это угол θ прямой от оси вращения
в точку P делает с осью абсцисс.
Углы могут измеряться в градусах или градусах. радианы. 360 градусов = 2π радиан. При описании вращательного движения наиболее удобно измерять углы в радианах.
Чтобы узнать, насколько быстро вращается колесо, мы измеряем его угловая скорость ω. Средняя угловая скорость определяется выражением
ω ср. = (θ f — θ i ) / (t f — t и ) = Δθ / Δt.
Каждая точка колеса имеет одинаковую угловую скорость. В единицы угловой скорости — рад / с или с -1 , т. к. радианы безразмерны.
Предположим, вы поворачиваете ось прялки из с вертикального на горизонтальный.Колесо все так же крутится угловая скорость, но его угловая скорость ω изменилась. Угловой Скорость имеет величину и направление. Его величина — это угловая скорость, а направление — это направление оси вращения. Однако есть тонкость, которую мы надо позаботиться. Предположим, что ось вращения вертикальный. Какое направление вращения? Колесо крутится по часовой стрелке или против часовой стрелки, если смотреть сверху? Просто говорю ось вертикальна не говорит нам смысла вращения.
Чтобы указать направление вращения, мы используем соглашение, называемое Правое правило . Если пальцы
вашей правой руки изгибаются, чтобы указать, в какую сторону
поворачиваясь, большой палец правой руки указывает в
направление оси вращения. Это направление
угловая скорость ω .
Это направление
угловая скорость ω .
Пожалуйста, нажмите на изображении ниже для трехмерного просмотра!
Проблема:
Какова средняя угловая скорость, в радианах в секунду,
(a) Земли на своей орбите вокруг
Солнце и
(b) Луна на своей орбите вокруг Земли?
Решение:
- Рассуждение:
Земля обращается вокруг Солнца один раз в год.
Луна обращается вокруг Земли за 27,3 дня - Детали расчета:
а) угловая скорость Земли на орбите вокруг Солнца равна ω = 2π / год = 2π / (365 * 24 * 60 * 60 с) = 2 * 10 -7 / с.
(b) угловая скорость Луны на орбите вокруг Земли составляет ω = 2π / (27,3 дня) = 2π / (27,3 * 24 * 60 * 60 с) = 2,7 * 10 -6 / с.
Угловое ускорение
Угловое ускорение α определяется как скорость изменения угловая скорость.Среднее угловое ускорение равно
. α = ( ω 2 — ω 1 ) / (т 2 — т 1 )
= Δ ω / Δt.
Угловая скорость изменяется, когда частота вращения увеличение или уменьшение и при изменении оси вращения направление. Угловое ускорение — вектор.
Если поменять количество оборотов
колесо делает в секунду, затем каждая точка на колесе
имеет угловое ускорение.Предположим, что точки угловой скорости в
z-направлении, и за интервал времени в одну секунду мы изменяем угловую скорость
колесо от π / s до 2π / s. Среднее угловое ускорение составляет
α = ( ω 2 — ω 1 ) / (т 2 — t 1 ) = ((2π / с
— π / с) к / (1 с) = (π / с 2 ) к ,
то есть имеет величину π / s и указывает в направлении оси z.
Если повернуть ось
вращение с вертикали на горизонталь, затем каждая точка на колесе
имеет угловое ускорение.Предположим, что колесо вращается с угловым
скорость (2π / с) к относительно оси Z. Если за время 1 с переориентировать ось вращения с
вертикально на горизонтальное, так что теперь колесо вращается с угловой скоростью (2π / с) i вокруг оси x, затем
дано среднее угловое ускорение
на
α = ( ω 2 — ω 1 ) / (т 2 — t 1 ) = ((2π / с i — 2π / с к ) / (1 с).

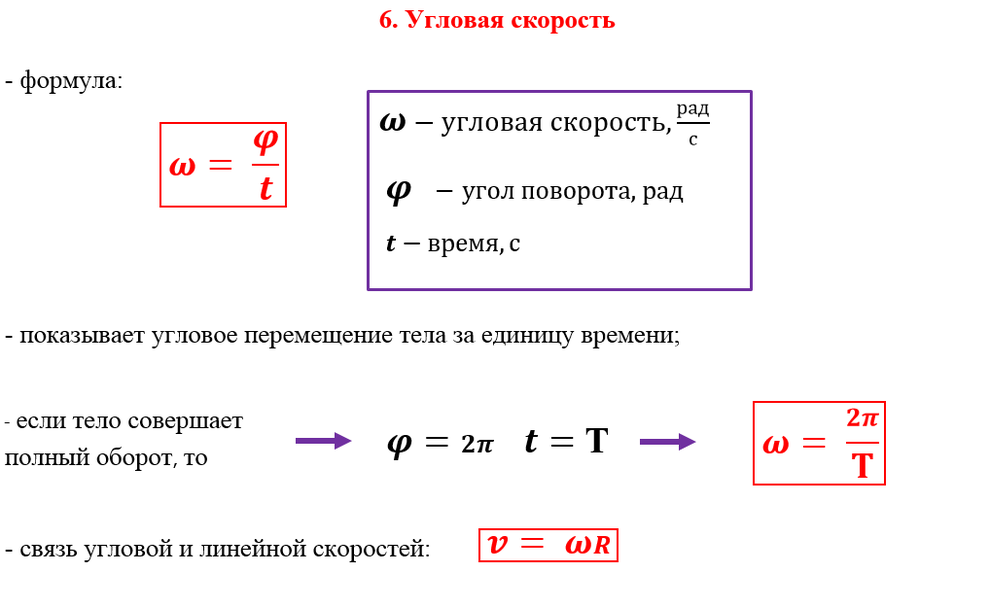 Определите скорость,
ускорение и период обращения спутника.
(Дано: M земля = 5.98×10 24 кг, R земля = 6.37 х 10 6 м)
Определите скорость,
ускорение и период обращения спутника.
(Дано: M земля = 5.98×10 24 кг, R земля = 6.37 х 10 6 м)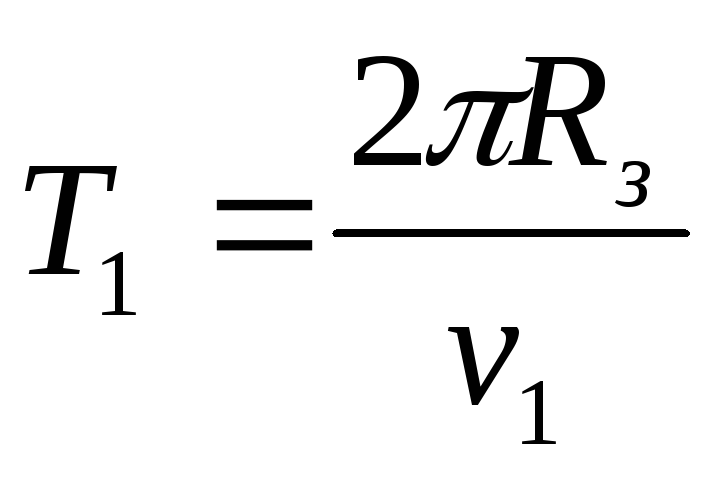 Особый класс
геостационарные спутники — геостационарные
спутник.Геостационарный спутник вращается вокруг
Земля за 24 часа по орбитальной траектории, которая
параллельно воображаемой плоскости, проведенной через
Экватор Земли. Такой спутник появляется
постоянно закреплен над тем же местом на
Земной шар. Если геостационарный спутник хочет выйти на орбиту
Земля за 24 часа (86400 с), то как высоко
над поверхностью земли он должен располагаться?
(Дано: M земля = 5.98×10 24 кг, R земля = 6,37 x 10 6 м)
Особый класс
геостационарные спутники — геостационарные
спутник.Геостационарный спутник вращается вокруг
Земля за 24 часа по орбитальной траектории, которая
параллельно воображаемой плоскости, проведенной через
Экватор Земли. Такой спутник появляется
постоянно закреплен над тем же местом на
Земной шар. Если геостационарный спутник хочет выйти на орбиту
Земля за 24 часа (86400 с), то как высоко
над поверхностью земли он должен располагаться?
(Дано: M земля = 5.98×10 24 кг, R земля = 6,37 x 10 6 м)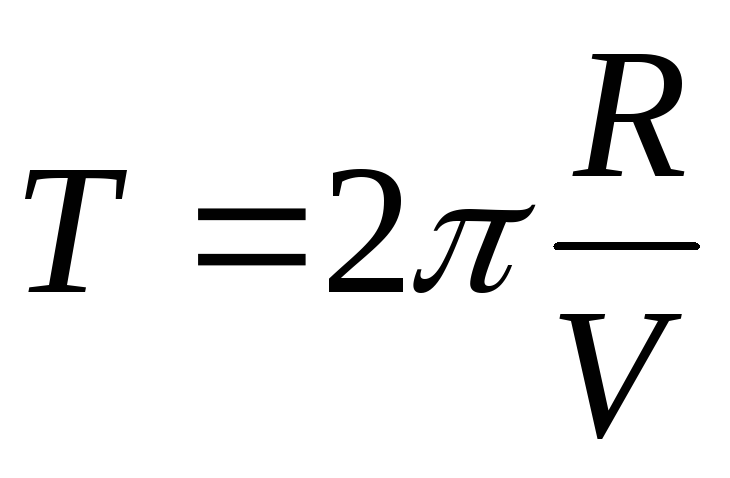 98×10 24 кг
98×10 24 кг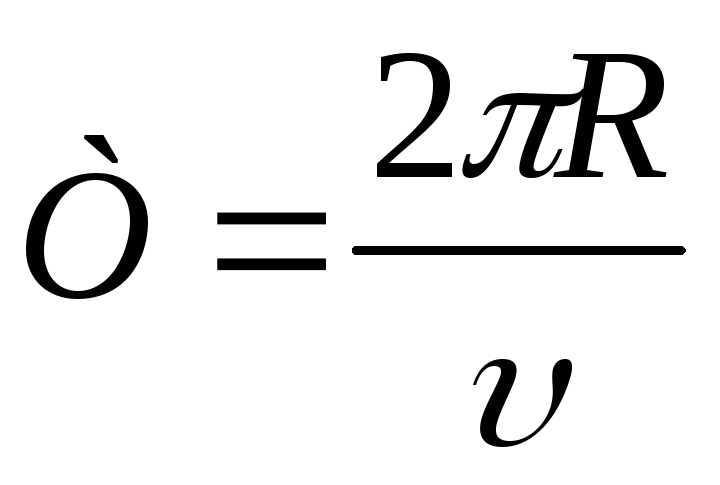 Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.
Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.