Планетарный механизм тмм: Кинематика зубчатых механизмов — Лекции и примеры решения задач технической механики

Кинематический анализ редуктора — Лекции и примеры решения задач технической механики

Среди заданных зубчатых редукторов имеются планетарные, составные и замкнутые дифференциальные механизмы. В планетарных (W=1) и дифференциальных (W=2) передачах оси отдельных колес (сателлитов) являются подвижными.

Для решения задачи необходимо разделить механизмы на части, выделив планетарные и дифференциальные, и для каждой части написать уравнение передаточного отношения, используя соответствующий метод.

При решении планетарных и дифференциальных механизмов применяется метод обращения движения (метод остановки водила) – всем звеньям придается дополнительная угловая скорость (-ω_H) в результате чего получается обычный механизм с неподвижными осями колес, так как водило Н будет иметь скорость ω_H—ω_H=0. Общее передаточное отношение сложного механизма определяется решением полученной системы уравнений.

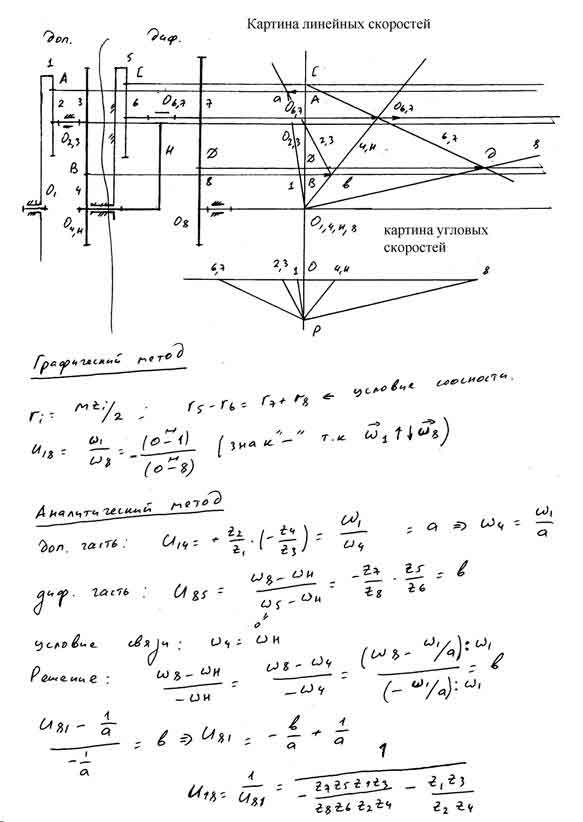
В задании входным звеном является колесо «а», выходным – звено I, поэтому искомым является передаточное отношение i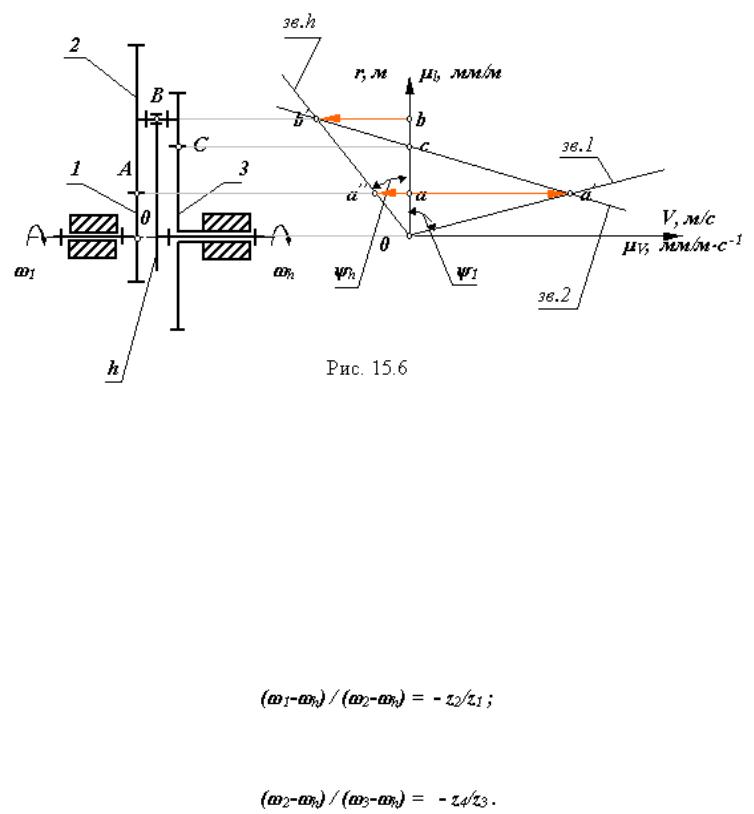

a1 В рассматриваемом примере (рисунок 12) ось колес 8-8′ является подвижной (8-8′ – сателлиты). Они входят в зацепление с колесами 7 и 9, которые называются центральными.

Рисунок 12 — Схема редуктора

Таким образом колеса 7, 8, 8′, 9 и водило Н (звено, соединяющее ось сателлитов с центральной осью) составляют планетарную передачу, а весь механизм делится на три части:  – обычная зубчатая пара, 7, 8, 8′, 9 – планетарная часть, 10, 11,1 – обычная (рядовая) передача.

Запишем уравнения для рядовых передач:

Для планетарной части, после остановки водила “Н”, колеса 7, 8, 8′, 9 будут иметь скорость соответственно: ω₇—ω_H, ω₈—ω_H, ω_8′—ω_H, ω₉—ω_H а передаточное отношение между центральными колесами

Из (1) ω_b=-8/9ω_aа из (2) ω₁₀=-4ω

1 и с учетом ω_b=ω₇; ω_H=ω₁₀; ω₉=0 подставляем в уравнение (3):

Преобразуем (4), разделив почленно числитель и знаменатель на ω₁:

Геометрический расчет пары зубчатых колес, нарезанных стандартным инструментом реечного типа >
Курсовой проект по ТММ >

Механизм с двумя внешними зацеплениями.

u⁽⁴⁾_1–Н = 20 ÷ 50 приη = 0.99

Входное звено – водило;

Выходное – первое колесо.

u⁽⁴⁾_1–Н = 1 / u⁽⁴⁾_Н–1

Например, если u⁽⁴⁾_Н–1= 20, тоu⁽⁴⁾_1–Н = 1 /20 .

1. Графический способ.

Выберем точку Fна входном звене так, чтобыO

1F = O₂B.

Точка Сдля данной схемы может располагаться как выше, так и ниже точкиА. В зависимости от положения точкиСплан скоростей будет разный.

ψ₁иφ₂– направлены в разные стороны от вертикали. Следовательно, водило и колесо 1 вращаются в разные стороны.

2. Аналитический способ.

Применим метод обращения движения.

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4

Запишем передаточное отношение через число зубьев:

Минусовой механизм

Планетарный механизм с двумя внешними зацеплениями.

Механизм Давида

Применяется в приборных устройствах, так как u⁽⁴⁾_Н–1до10 000.

Недостаток – низкий К.П.Д

1. Графический способ.

Выберем на водиле НточкуFтак, чтобыO₂F=O₁A(валыO₁иO₂соосны). ТочкаСможет быть выше или ниже точкиА.

FF’– произвольный отрезок (линейная скорость точкиF).

Для колес 2 и 3 точка С– МЦС.

2. Аналитический способ.

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4

Минусовой механизм.

Синтез (проектирование) планетарных механизмов.

Под синтезом в этом курсе будем понимать подбор (определение) чисел зубьев планетарных механизмов при условии, что зубчатые колеса нулевые, а радиальный габарит механизма минимальный.

Расчет на прочность не проводим, но он обязательно должен быть проведен при проектировании.

При проектировании конструктор обязан выполнить ряд условий:

1. Отклонение от заданного передаточного отношения не должно превышать 10% (5%).

2. Обеспечить отсутствие подреза у нулевых зубчатых колес:

У колес с внешними зубьями z₁, z₂, z₃ ≥18;

У колес с внутренними зубьями z ≥85.

Если колеса не нулевые, то z_minдо7или до56.

3. Обеспечить отсутствие заклинивания в зацеплении сателлит – коронная шестерня.

Заклинивания нет, если z_кш – z_сат ≥ 8

4. Обеспечить выполнение условия соосности входного и выходного звеньев.

5. Необходимо обеспечить выполнение условие соседства (окружности вершин соседних сателлитов не должны касаться друг друга).

6. Обеспечить выполнение условия сборки. Определить условие сборки, исходя из чертежа невозможно, необходимо проверить выполнение этого условия по уравнению (см. далее).

Проектирование однорядного планетарного механизма.

Дано: u⁽⁴⁾_1–Н = 6

m = 1 мм

k = 3– количество сателлитов

Определить: z₁, z₂, z₃ – ?

при минимальном радиальном габарите;

колеса – нулевые.



Зададимся числом зубьев z₁так, чтобы выполнялось условие 2, тогдаz₁ = 18, z₃ = 5 ^. 18 = 90 ≥ 85.

Условие соосности записывается в виде

О₁В = О₂В

r₁ + r₂ = r₃ – r₂

z₁ + z₂ = z₃ – z₂

Получим условие соседства.

Условие соседства: окружности вершин соседних сателлитов не касаются друг друга

В_IB_II > 2 r_a2 (1)

Рассмотрим треугольник O₁B_Iq:

B_IB_II = 2B

Iq

2B_Iq = B_IB_II = m(z₁ + z₂) (2)

r_a2 = r₂ + xm + h_a*m – ∆ym

Т. к. колеса нулевые, то xm = 0и∆ym = 0

r_a2 = r₂ + h_a*m

r_a2=(z₂+2h_a*)

2r_a2 = m(z₂ + 2h_a*) (3)

Подставим (3), (2) в (1)

(4)

Уравнение соседства справедливо для всех схем, только для схем 2, 3 и 4 в знаменателе стоит правая или левая часть условия соосности, а в числителе вместо z₂

ставят число зубьев наибольшего из сателлитов.

Условие сборки:

Будем считать, что каждый последующий блок сателлитов устанавливается в позицииВ_I.

Чтобы освободить место, нужно повернуть водило на угол (360^о / k).

При установке 1–го сателлита зубья центральных колес ориентированы относительно оси симметрии.

Если на дуге АВукладывается целое число шагов, то при повороте водила на угол(360^о/k) зубья центральных колес будут ориентированы относительно оси симметрии точно так же, как и при установке первого сателлита.

Если на указанной дуге не укладывается целое число шагов, то при повороте водила на угол (360^о / k) зуб 1–го колеса не встанет на то же место и тогда, чтобы установить следующий сателлит, нужно от позицииВ

IIсделатьрдополнительных оборотов водила, чтобы за счет выборки углового шага правильно ориентировать зубья центральных колес.

Уравнение сборки имеет вид:

= (1 + kp) = γ,гдеγ– целое число.

Для нашего случая: 18^.6 (1+ 3р) / 3 = 36 (1+3р)

Условие сборки выполняется при р = 0.

После подбора чисел зубьев определяют радиусы делительных окружностей колес:

мм

мм

мм

По полученным данным строится схема механизма в масштабе и проверяется выполнение передаточного отношения.

5.3.2 Проектирование планетарного механизма со смешанным зацеплением.

Дано:

m=1 мм

Определить:

z1, z2, z3, z4

при условии:

k=3

радиальные габариты – min

колеса – нулевые.

Исходная формула:

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4= 1 +

= u⁽⁴⁾_1–Н – 1 = 21 – 1 = 20

Представим число (20/1) в виде произведений сомножителей:

Где С₁~z₁при этомС₁, С₂, С₃, С₄– взаимно

С₂~z₂простые числа, то есть не имеют

С₃~z₃общих делителей.

С₄~z₄

Указываются все возможные разложения

1: С₁= 4 С₂= 1 С₃= 1 С₄= 5

Запишем условие соосности данного редуктора

О₁В=О₂В

r₁ + r₂ = r₄ – r₃

m ( z₁ + z₂ ) = m ( z₄ – z₃ )

В результате преобразований

z₁ = C₁ ( C₄ – C₃ ) q

z₄ = C₄ ( C₁ + C₂ ) q

где q– коэффициент пропорциональности – любое число но такое, чтобыzбыло целым.

тогда

z₂ = C₂ ( C₄ – C₃ ) q

z₃ = C₃ ( C₁ + C₂ ) q

z₁ = 1 ( 5 – 1 ) q = 4q z₁ = 20

z₂ = 4 ( 5 – 1 ) q = 16q z₂ = 80

z₃ = 1 ( 1 + 4 ) q = 5q z₃ = 25

z₄ = 5 ( 1 + 4 ) q =25q z₄ = 125

qназначается так, чтобы не было подреза, напримерq = 5.

Проверяем выполнение условия соседства:

0,87 > 0,82

Условие соседства выполняется.

Проверяем выполнение условия сборки:

= (1 + kp) = γ (a)

20 ^. 21( 1+3p) / 3 = 140 при p = 0

Для передач со сдвоенными сателлитами формула (а) не является общей. Общей формулой является:

– целое

Условие сборки выполняется.

Если хотя бы одно из условий не выполняется, то необходимо рассмотреть следующий вариант разложения на простые множители.

Если, перебрав все возможные варианты разложения, не удалось подобрать числа зубьев, то допускается изменить заданное передаточное отношение в пределах 10 %.

Для других схем числа зубьев подбираются по формулам, представленным в таблице:

	2 внутренних зацепления Схема 3	2 внешних зацепления Схема 4
Условие соосности	z1 – z2 = z4 – z3	z1 + z2 = z4 + z3
z1	C1 ( C4 – C3 ) q	C1 ( C4 + C3 ) q
z2	C2 ( C4 – C3 ) q	C2 ( C4 + C3 ) q
z3	C3 ( C1 – C2 ) q	C3 ( C1 + C2 ) q
z4	C4 ( C1 – C2 ) q	C4 ( C1 + C2 ) q

18 Проектирование многопоточных планетарных механизмов » СтудИзба

Лекция 18

Проектирование многопоточных планетарных механизмов

Постановка задачи синтеза.

При проектировании многопоточных планетарных механизмов необходимо, кроме требований технического задания, выполнять ряд условий связанных с особенностями планетарных и многопоточных механизмов. Задача проектирования и в этом случае может быть разделена на структурный и кинематический синтез механизма. При структурном синтезе определяется структурная схема механизма, при кинематическом – определяются числа зубьев колес, так как радиусы зубчатых прямо пропорциональны числам зубьев 

Для типовых механизмов первая задача сводится к выбору схемы из набора типовых схем. При этом руководствуются рекомендуемым для схемы диапазоном передаточных отношений и примерными оценками ее КПД. Для рассматриваемых схем эти данные приведены в таблице 17.1. После выбора схемы механизма необходимо определить сочетание чисел зубьев его колес, которые обеспечат выполнение условий технического задания — для редуктора это передаточное отношение и величина момента сопротивления на выходном валу. Передаточное отношение задает условия выбора относительных размеров зубчатых колес — чисел зубьев колес, крутящий момент задает условия выбора абсолютных размеров — модулей зубчатых зацеплений. Так как для определения модуля необходимо выбрать материал зубчатой пары и вид его термообработки, то на первых этапах проектирования принимают модуль зубчатых колес равным единице, то есть решают задачу кинематического синтеза механизма в относительных величинах.

При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при заданном числе силовых потоков (или числе сателлитов k) и заданном передаточном отношении u необходимо подобрать числа зубьев колес z_i, которые обеспечат выполнение ряда условий.

Условия подбора чисел зубьев. Вывод расчетных формул для условий соосности, соседства и сборки:

Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:

·        заданное передаточное отношение с требуемой точностью

·        соосность входного и выходного валов механизма

·        свободное размещение (соседство) нескольких сателлитов

·        сборку механизма при выбранных числах зубьев колес

·        отсутствие подрезания зубьев с внешним зацеплением

·        отсутствие заклинивания зубьев во внутреннем зацеплении

·        минимальные относительные габариты механизма.

Рассмотрим эти условия подробнее на примере двухрядного планетарного механизма с одним внешним и одним внутренним зацеплением.

Рис. 18.1

1. Обеспечение заданного передаточного отношения с требуемой точностью:

Принимаем требуемую точность ± 5%, тогда для рассматриваемой схемы механизма :

2. Обеспечение соосности входного и выходного валов:

Для этого необходимо чтобы межосевое расстояние в передаче внешнего зацепления (первый ряд) равнялось межосевому расстоянию в передаче внутреннего зацепления (второй ряд), то есть :

a_wI = a_wII ; a_wI= r_w1 + r_w2 = r₁ + r₂ ; a_wII = r_w4 — r_w3 = r₄ — r₃.

Обычно в планетарных механизмах применяются зубчатые колеса без смещения, для которых x_i = 0 и r_wi = r_i = z_i m / 2.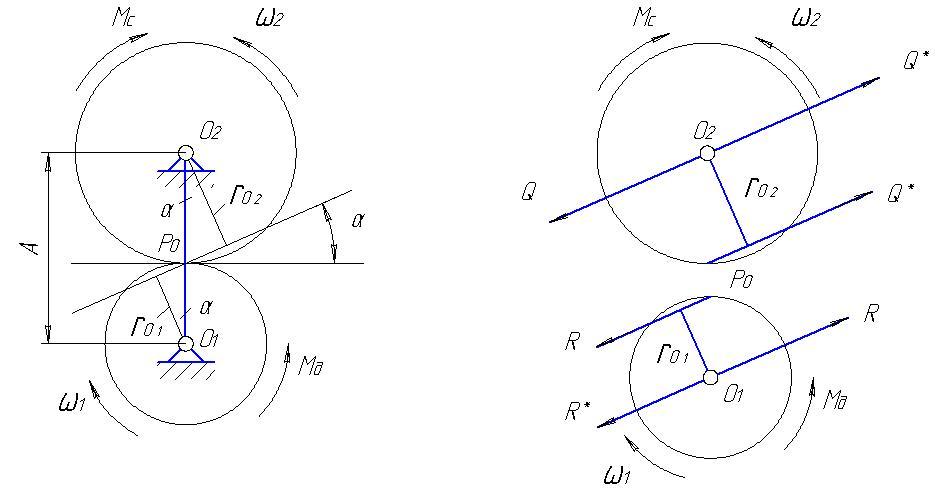

Тогда :

r₁ + r₂= r₄ — r₃   => m_I(z₁ + z₂) = m_II (z₄ — z₃).

Принимаем, что m_I = m_II = m, и получаем условие соосности для данной схемы механизма

3. Обеспечение условия соседства сателлитов (при числе сателлитов k > 1):

Сателлиты размещаются на окружности радиуса a_w. Вершины зубьев сателлитов не будут мешать движению друг друга, если выполняется условие :

max ( d_a2,3 ) < l_B2B3.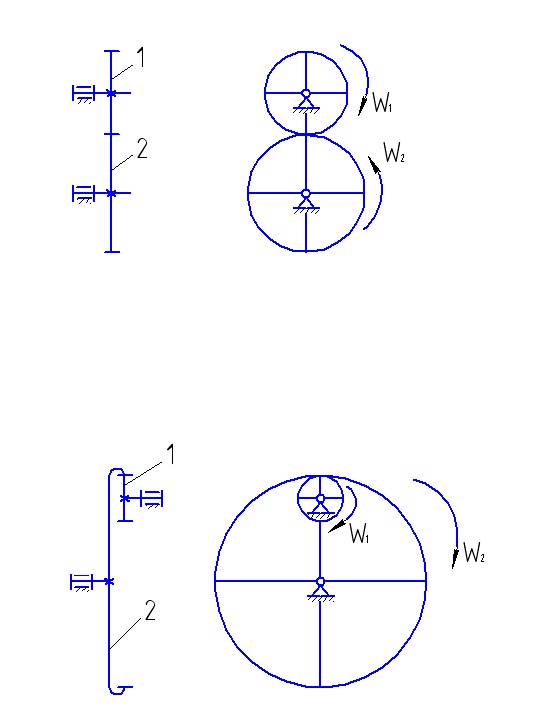

Для зубчатых колес без смещения ( h_a^*= 1, x_2,3 = 0, 2y = 0 ) максимальный из диаметров сателлитов равен

max ( d_a2,3 ) = max [( z_2,3 + 2  h_a^* + 2  x_2,3 — 2y) m ] = max[( z_2,3 + 2)  m ].

Расстояние между осями сателлитов :

l_B2B3 = 2   a_w sin ( j_h / 2 ) = 2  (r₁ + r₂)  sin ( p / k ). = (z₁ + z₂)  m  sin ( p / k ).

Подставим полученные выражения в неравенство и получим условие соседства:

max [( z_2,3 + 2)  m ] < (z₁ + z₂)  m  sin (p / k).

sin ( p /k ) > max [( z2,3 + 2)/ (z1 + z2) ]

4. Обеспечить возможность сборки механизма с подобранными числами зубьев колес при заданном числе сателлитов k > 1:

Для вывода формулы условия сборки воспользуемся следующим методом:

Допустим, что все сателлиты устанавливаются на оси водила в одном и том же положении – точке В₁. После установки первого сателлита, зубья колес z₁и z₄определенным образом установились относительно зубьев венцов сателлита. Тогда установить второй сателлит в этом же положении будет можно, если после поворота водила на угол _h колесо z₁повернется на целое число угловых шагов В. При этом зубья колес z₁ и z₄установятся относительно зубьев венцов сателлита так же, как и при установке первого сателлита.

Угол поворота водила:_h= 2   / k

Угловой шаг первого колеса: ₁ = 2 / z₁

Угол на который повернется первое колесо при повороте водила на угол _h :

      ₁ = _h u_1h  =>  ₁ = 2    u_1h / k

Число угловых шагов ₁ в угле ₁ => B = ₁ / ₁, где B — произвольное целое число.

Подставляем все эти выражения в формулу для B и после преобразований получаем :

2   u_1h z₁ / (k  2 ) = B   =>

u1h z1 / k = B.

Поворачивать водило можно на угол j_hплюс произвольное число p полных оборотов водила, то есть:

_h= 2   / k + 2  р = 2   / k ( 1 + k  р).

С учетом этого, формула для условия сборки примет следующий вид:

U1h * z1 / k ( 1 + k * р) = B.

 

5. Обеспечить отсутствие подрезания колес с внешними зубьями зубьев:

Это условие обеспечивается, если для всех колес с внешними зубьями выполняется неравенство z_i > z_min.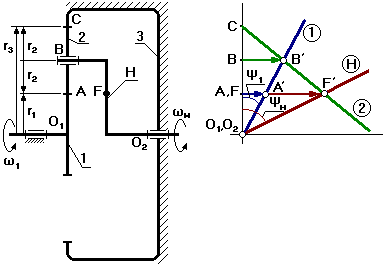

6. Обеспечить отсутствие заклинивания во внутреннем зацеплении:

Это условие для передачи внутреннего зацепления, состоящей из колес без смещения, можно обеспечить при выполнении следующих неравенств:

z с внеш. зуб. > 20, z с внутр. зуб. > 85, zd = z с внутр. зуб — z с внеш. зуб. > 8.

7. Обеспечить минимальные габариты механизма.

Для рассматриваемой схемы условие обеспечения минимального габаритного размера R можно записать так 
R = min [ max ( z₁ + 2  z₂ ), (k_K z₄) ], где k_K — коэффициент, учитывающий особенности конструкции зубчатого колеса с внутренними зубьями.

Подбор чисел зубьев по методу сомножителей.

Рассмотрим один из методов, используемых при подборе чисел зубьев планетарного редуктора, — метод сомножителей. Метод позволяет объединить в расчетные формулы некоторые из условий подбора (условия 1, 2, 5 и 6). Выполнение остальных условий для выбранных чисел зубьев проверяется. Из первого условия выразим внутреннее передаточное отношение механизма. Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма.

u₁₄ ^h = (z₂ * z₄)/(z₁ * z₃) = [ u_1h / ( 0.95 … 1.05 ) – 1] = (B * D)/(A * C).

Разложим внутреннее передаточное отношение u₁₄^hна сомножители — некоторые целые числа A, B, C и D. При этом сомножитель A соответствует числу зубьев z₁ , B — z₂ , C — z₃ и D — z₄.Сомножители могут быть произвольными целыми числами, комбинация (BD) / (AC) которых равна u₁₄^h.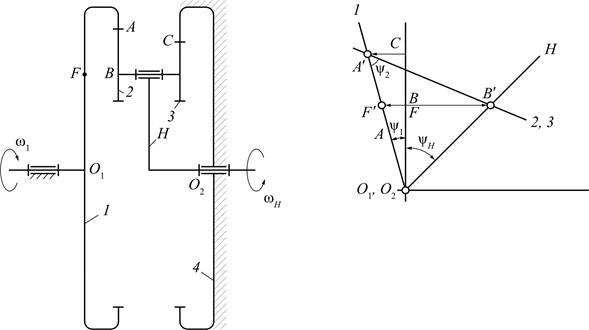

Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями:

B / A = z₂ / z₁ = 1 … 6 —внешнее зацепление,

D / C = z₄ / z₃ = 1.1 … 8 – внутреннее зацепление.

Включим в рассмотрение условие соосности:

z₁ + z₂ = z₄ — z₃

и выразим его через сомножители:

a  ( A + B) = b  ( D – C ).

Если принять, что коэффициенты a и b равны:

a = ( D – C ), b = (A + B),

то выражение превращается в тождество.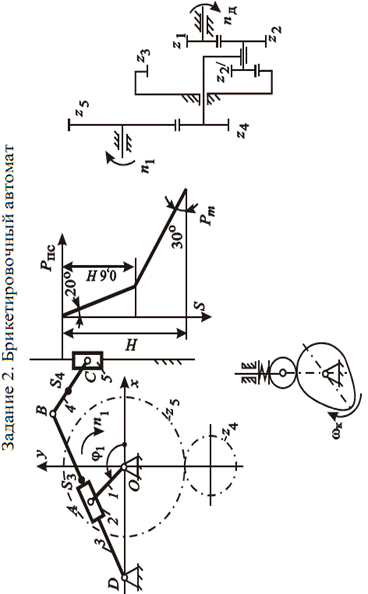

Из этого тождества можно записать:

z₁= ( D – C )  A  q

z₃= ( A + B )  C  q

z₂= ( D – C )  B  q

z₄= ( A + B )  D  q

где q — произвольный множитель, выбором которого обеспечиваем выполнение условий 5 и 6.

Зубья колес планетарного механизма, рассчитанные по этим формулам, удовлетворяют условиям 1, 2, 5 и 6. Проверяем эти зубья по условиям 3 (соседства) и 4 (сборки) и если они выполняются, считаем этот вариант одним из возможных решений. Если после перебора рассматриваемых сочетаний сомножителей получим несколько возможных решений, то проводим их сравнение по условию 7. Решением задачи будет сочетание чисел зубьев, обеспечивающее минимальный  габаритный размер R.

Примеры подбора чисел зубьев для типовых планетарных механизмов.

1. Двухрядный планетарный редуктор с одним внешним и с одним внутренним зацеплением.

Дано: Схема планетарного механизма, u_1h = 13, k = 3.

Определить: z_i

Внутреннее передаточное отношение механизма:

u₁₄ ^h = (z₂ z₄) / (z₁ z₃) = [ u_1h / ( 0.95 … 1.05 ) – 1] = 12 = (B  D)/(A  C) = 3  4 / (1  1) = 2  6 / (1  1)= 4  3 / (1  1) = …

Для первого сочетания сомножителей:

z₁= ( D – C )  A  q = ( 4 – 1 )  1  q = 3  q ;                    z₁= 18 > 17;
z₂= ( D – C )  B  q = ( 4 – 1 )  3  q = 9  q ;      q = 6;    z₂= 54 > 17;
z₃= ( A + B )  C  q = ( 3 + 1 )  1  q = 4  q;                     z₃= 24 > 20;
z₄= ( A + B )  D   q = ( 3 + 1 )  4  q = 16  q;                                     z₄= 96 > 85;

Проверка условия соседства:

sin (  / k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin (  / 3 ) > (54 + 2)/(18+54)

0. 866 > 0.77 — условие выполняется.

Проверка условия сборки:

 ( u_1h z₁ / k )  ( 1 + k p) = B;

(13 18/3)  ( 1 + 3 р) = В — целое при любом p.

Условие сборки тоже выполняется. То есть, получен первый вариант решения!
Габаритный размер R = (18 + 2 Ч 54) = 126.

Для второго сочетания сомножителей:

z₁= ( D – C )  A  q = ( 6 – 1 )  1  q = 5  q ;                    z₁= 45 > 17;
z₂= ( D – C )  B  q = ( 6 – 1 )  2  q = 10  q ;    q = 9;    z₂= 90 > 17;
z₃= ( A + B )  C  q = ( 2 + 1 )  1  q = 3  q;                     z₃= 27 > 20;
z₄= ( A + B )  D  q = ( 2 + 1 )  6 8 q = 18  q;                                   z₄= 162 > 85;

Проверка условия соседства:

sin (  / k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin (  / 3 ) > (90 + 2)/(45+90)

0. 866 > 0.681 — условие выполняется.

Проверка условия сборки:

( u_1h  z₁ / k )  ( 1 + k  р) = B

(12  45 / 3)  ( 1 + 3 р) = В — целое при любом р.

Условие сборки тоже выполняется и получен второй вариант решения!
Габаритный размер R = (45 + 2  90) = 225.

Для третьего сочетания сомножителей:

z₁= ( D – C )  A  q = ( 3 – 1 ) 1  q = 2  q ; z₁= 18 > 17;
z₂= ( D – C )  B   q = ( 3 – 1 )  4  q = 8  q ; q = 9; z₂= 72 > 17;
z₃= ( A + B )  C   q = ( 1 + 4 )  1  q = 5  q; z₃= 45 > 20;
z₄= ( A + B )  D   q = ( 1 + 4 )  3  q = 15  q;                 z₄= 135 > 85;

Проверка условия соседства:

sin ( / k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin ( / 3 ) > (70 + 2)/(18+72)

0. 866 > 0.8 — условие выполняется.

Проверка условия сборки:

( u_1h  z₁ / k )  ( 1 + k  р) = B; (13  18/3)  ( 1 + 3 р) = В — целое при любом р.

Условие сборки тоже выполняется и получен третий вариант решения.
Габаритный размер R = (18 + 2  72) = 162.

Из рассмотренных трех вариантов наименьший габаритный размер получен в первом. Этот вариант и будет решением нашей задачи.

2. Однорядный механизм с одним внутренним и одним внешним зацеплением.
Дано:

схема планетарного механизма, u_1h = 7; k = 3.
Определить: z_i  = ?.

Для однорядного планетарного механизма задача подбора чисел зубьев решается без применения метода сомножителей. Задаемся для первого колеса числом зубьев больше 17 и кратным u_1h или k.

В нашем примере принимаем:

z₁ = 18 > 17.

Тогда из формулы передаточного отношения можно определить число зубьев третьего колеса:

u_1h= ( 1 + z₃ / z₁ )  (0.95 … 1.05)

z₃ = [u_1h/ (0.95…1.05) — 1]  z₁

z₃ = [ 7_{/ (0.95…1.05) — 1]  18 = 108}

Число зубьев второго колеса определим из условия соосности:
z₁ + z₂ = z₃ — z₂

z₂ = ( z₃ — z₁ ) / 2 = ( 108 — 18 ) / 2 = 45

Проверка условия соседства:

sin ( / k ) > max [( z₂ + 2)/ (z₁ + z₂) ]

sin ( / 3 ) > (45 + 2)/(18+45)

0. 866 > 0.73 — условие выполняется.

Проверка условия сборки:

( u_1h  z₁ / k )  ( 1 + k  р) = B

(7  18/3)  ( 1 + 3 р) = В целое при любом р.

В данном случае нет необходимости сравнивать варианты по габаритам, так как мы приняли минимально допустимую величину z₁, то получим редуктор минимальных размеров.

3. Двухрядный механизм с двумя внешними зацеплениями. (рис. 18.3)

Дано: схема планетарного механизма, u_h2 = -24; k =3.

Определить: z_i — ?.

Рис. 16.3

Внутреннее передаточное отношение  механизма:
u_1h= 1 / u_h2
u₁₄ ^h = (z₂ z₄)/(z₁ z₃) = [ 1 — u_1h / ( 0. 95 … 1.05 ) ] = 25/24 = (B  D)/(A  C) = 5

  5 / (4  6) = 5  5 / (6  4)= 25  1 / (12  2) = …

Условие соосности для этой схемы:

z₁ + z₂ = z₄ + z₃

и выразим его через сомножители:

  ( A + B) =   ( D + C ).

Принимаем коэффициенты и :

 = ( D + C ),  = (A + B).

и получаем для сочетания сомножителей обведенного рамкой:

z₁= ( D + C )  A  q = ( 1 + 2 )  12  q = 36  q ;                           z₁= 36 > 17;
z₂= ( D + C )  B  q = ( 1 + 2 )  25  q = 75  q ;         q = 1;        z₂= 75 > 17;
z₃= ( A + B )  C  q = ( 12 + 25 )  2  q = 74  q;                          z₃= 74 > 17;
z₄= ( A + B )  D  q = ( 12 + 25 )  1  q = 37  q;                                 z₄= 37 > 17;

Проверка условия соседства:

 sin  (/ k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ];

sin ( / 3 ) > (75 + 2)/(36+75)

0. 866 > 0.694 — условие выполняется.

Проверка условия сборки:

 ( u_1h  z₁ / k )  ( 1 + k  р) = B;

[18 / (-24 3)]  ( 1 + 3 р) = В — целое при р=1.

Условие сборки тоже выполняется. То есть, получен первый вариант решения.

Габаритный размер R = (36 + 2  75) = 186.

Аналогичным образом рассматриваются другие сочетания сомножителей и из вариантов, удовлетворяющих первым шести условиям, выбирается тот, который обеспечивает наименьшие габариты.

4. Двухрядный механизм с двумя внутренними зацеплениями.
 Дано:

схема планетарного механизма (рис. 18.4), u_1h = 55;  k = 2.

Определить: z_i  =?.

Внутреннее передаточное отношение механизма:

u_1h= 1 / u_h2;

u₁₄ ^h= (z₂  z₄)/(z₁  z₃) = [ 1 — u_1h/ ( 0. 95 … 1.05 ) ] = 54 / 55 = (B  D)/(A  C) = 6  9 / (11  5) = 18  3 / (55 * 1) = …

Условие соосности для этой схемы:

z₁ — z₂ = z₄ — z₃

и выразим его через сомножители:

 ( A — B) =   ( D — C )

Принимаем коэффициенты  и из условия тождественности :

 = ( D — C ),  = (A — B)

и получаем для сочетания сомножителей обведенного рамкой:

z₁= ( D — C )  A  q = ( 3 — 1 )  55  q = 110  q ;                             z₁= 110 > 85;
z₂= ( D — C )  B  q = ( 3 — 1 )  18  q = 36  q ;                  q = 1;    z₂= 36 > 20;
z₃= ( A — B )  C  q = ( 55 — 18 )  1  q = 37  q;                               z₃= 37 > 20;
z₄= ( A — B )  D  q = ( 55 — 18 )  3  q = 111  q;                                z₄= 111 > 85;

Проверка условия соседства:

sin (/k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin (/2 ) > (37 + 2)/(110 — 36)

1. 0 > 0.527 — условие выполняется.

Проверка условия сборки:

( u_1h  z₁ / k )  ( 1 + k  р) = B;

[110 / (55  2)]  ( 1 + 3 р) = В — целое при любом р.

Условие сборки тоже выполняется. То есть, получен первый вариант решения.
         Аналогичным образом рассматриваются другие сочетания сомножителей и из вариантов, удовлетворяющих первым шести условиям, выбирается тот, который обеспечивает наименьшие габариты.

Оптимальный синтез планетарных механизмов при автоматизированном проектировании.

При автоматизированном проектировании с помощью компьютера можно за относительно небольшой промежуток времени получить большое количество возможных решений задачи. Сопоставляя эти решения между собой находят то, которое удовлетворяет всем требованиям наилучшим образом. При этом перебор вариантов осуществляется в пределах заданных ограничений на параметры (в данном случае на числа зубьев колес) по какой-либо стратегии или чаще случайным образом. Программы оптимального синтеза могут использовать рассмотренные выше методы (например, метод сомножителей), а могут просто перебирать допустимые сочетания параметров и проверять их на соответствие заданным условиям. Использование компьютерных программ для синтеза планетарных механизмов позволяет существенно сократить время проектирования и существенно улучшить качественные показатели спроектированных механизмов.

Планетарные дифференциальные механизмы с W=2.

На практике в качестве механизмов с двумя подвижностями наиболее часто применяются планетарные зубчатые механизмы или как их еще называют планетарные дифференциалы. Это название справедливо для механизмов, в которых входной энергетический поток разделяется на два выходных потока. Если входные энергетические потоки суммируются на выходе в один выходной поток, то такие механизмы следует называть суммирующими или интегральными.

Все рассмотренные типовые схемы механизмов можно выполнить с двумя подвижностями. Рассмотрим в качестве примера двухрядный механизм с одним внешним и одним внутренним зацеплением (рис.18.5).

Рис. 16.5

         По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z₂и z₁

(₁ — _h) / (₂ — _h) = — z₂ / z₁

для внутреннего зацепления колес z₄и z₃

(₂ — _h) / (₃ — _h) = z₄ / z₃ .

Перемножим, правые и левые части этих уравнений, и получим соотношение между угловыми скоростями механизма с двумя подвижностями

[(₁ — _h) / (₂ — w_h)]  [(₂—_h)/ (₃—_h)] = — z₂  z₄ / ( z₁  z₃)

(₁ — _h) / (₃ — _h) = — z₂  z₄ / ( z₁  z₃) = u₁₃^(h)

u₁₃ ^(h) ₃ — u₁₃ ^(h) _h = ₁ — _h

Чтобы из механизма с двумя подвижностями получить одноподвижный механизм необходимо либо остановить одно из подвижных звеньев, либо связать между собой функционально ( например, простой зубчатой передачей ) два подвижных звена. Механизмы, образованные по второму способу, называются замкнутыми дифференциалами. Схема такого замкнутого дифференциального механизма приведена на рис.18.6.

Рис 16.6

         Контрольные вопросы к лекции N18.

1.     Как формулируется задача кинематического синтеза планетарного механизма?

2.     Какие основные условия необходимо выполнить при синтезе многосателитного планетарного механизма? Перечислите их.

3.     Запишите условие соседства для однорядного планетарного механизма с K=3 ?

4.     Как обеспечивается условие сборки многосателитного планетарного механизма?

5.     Как определяются числа зубьев (любой из схем) планетарного механизма методом сомножителей?

6.     Определите числа зубьев однорядного планетарного механизма с  и К=3.

7.     Как устанавливаются кинематические зависимости в дифференциальном планетарном механизме графическим способом?

ТММ. Пресс-автомат для холодного выдавливания

омский сельскохозяйственный институт — филиал федерального государственного бюджетного образовательного учреждения высшего образования «Новосибирский государственный аграрный университет
Кафедра Агроинженерия
Курсовой проект по десциплине: Теория механизмов и машин
На тему: Кинематический анализ механизма

Курсовой проект содержит: 32 листа пояснительной записки, 4 чертежа А1.
Содержание
Задание
Введение
1. Кинематический анализ механизма
1.1. Проектирование кривошипно-ползунного механизма
1.2. Структурное исследование механизма
1.3. Построение схемы механизма
1.4. Кинематические диаграммы точки Е
1.5. Построение планов скоростей механизма
1.6 Построение планов ускорений механизма
2. Силовой расчет рычажного механизма
2.1. Определение силы РС
2.2 Определение масс и моментов инерции звеньев
2.3. Определение сил инерции звеньев
2.4. Определение реакций в кинематических парах групп Ассура II класса 2-го вида
2.5. Силовой расчет ведущего звена механизма
2.7. Определение уравновешивающей силы методом Жуковского
3. Проектирование кинематической схемы планетарного редуктора и построение картины эвольвентного зацепления
4. Синтез кулачкового механизма
Заключение
Список литературы

Объектом исследования является механизм пресс-автомата для холодного выдавливания.
Пресс-автомат для холодного выдавливания
а — рычажный механизм перемещения ползуна с пуансоном; б — график силы сопротивления, приложенной к пуансону; в — схема планетарной и простой ступени редуктора; г — схема кулачкового механизма перемещения матриц; д — синусоидальный закон изменения аналога ускорения толкателя

Состав: Синтез кулачкового механизма, Планетарный редуктор, Рычажный механизм, Кинематический механизм, ПЗ

Софт: КОМПАС-3D 14

Планетарный редуктор | KHK Gears

Трансмиссия и планетарный механизм

Многие «шестерни» используются для автомобилей, но они также используются для многих других машин. Наиболее типичным из них является «трансмиссия», которая передает мощность двигателя на шины. В общих чертах, трансмиссия автомобиля играет две роли: первая — замедлять высокую скорость вращения, создаваемую двигателем для передачи на шины; другой — изменить передаточное число в соответствии с ускорением / замедлением или скоростью движения автомобиля.

Скорость вращения автомобильного двигателя в общем состоянии движения составляет 1000 — 4000 оборотов в минуту (17 — 67 в секунду). Поскольку невозможно вращать шины с одинаковой скоростью вращения для работы, необходимо снизить скорость вращения, используя соотношение числа зубьев шестерни. Такая роль называется замедлением; Соотношение скорости вращения двигателя и шин называется передаточным числом.

Тогда почему необходимо изменять передаточное число в соответствии с ускорением / замедлением или скоростью движения? Это связано с тем, что веществам требуется большая сила, чтобы начать движение, однако им не требуется такая большая сила, чтобы продолжать движение после того, как они начали движение. Автомобиль можно назвать хорошим примером. Однако двигатель по своей природе не может так точно изменять свою мощность. Следовательно, один регулирует его выход, изменяя передаточное число, используя трансмиссию.

Передача движущей силы через шестерни очень напоминает принцип рычага (рычага). Отношение числа зубьев шестерен, находящихся в зацеплении друг с другом, можно рассматривать как отношение длины плеч рычагов. То есть, если передаточное число велико, а скорость вращения на выходе мала по сравнению с входной, выходная мощность при передаче (крутящий момент) будет большой; с другой стороны, если скорость вращения на выходе не такая низкая по сравнению со скоростью на входе, выходная мощность (крутящий момент) будет небольшой.Таким образом, изменение передаточного числа с помощью трансмиссии во многом похоже на принцип перемещения вещей.

Тогда как трансмиссия изменяет передаточное число? Ответ кроется в механизме, называемом планетарной зубчатой ​​передачей.

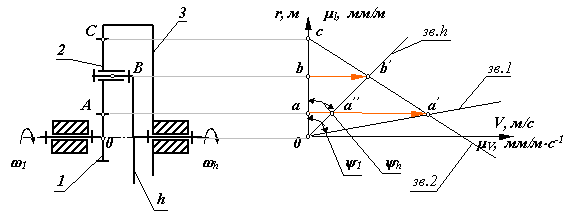
Механизм планетарной передачи — это зубчатый механизм, состоящий из 4 компонентов, а именно солнечной шестерни A, нескольких планетарных шестерен B, внутренней шестерни C и водила D, соединяющего планетарные шестерни, как показано на графике ниже.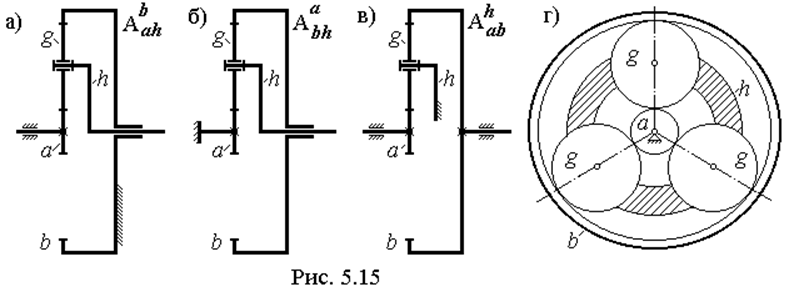 Он имеет очень сложную структуру, что затрудняет его проектирование или производство; он может реализовать высокое передаточное число с помощью шестерен, однако этот механизм подходит для редукционного механизма, который требует как небольших размеров, так и высоких характеристик, например, трансмиссии для автомобилей.

График 17.1: Устройство планетарного редуктора

Механизмы планетарной передачи обладают способностью изменять передаточное число, выбирая, какой из компонентов должен быть зафиксирован.
Например, предположим, что внутренняя шестерня C зафиксирована, входная ось соединена с солнечной шестерней A, а водило выходной оси D. Когда солнечная шестерня A вращается один раз, планетарная шестерня B будет вращаться несколько раз. Если внутренняя шестерня C не зафиксирована, а вместо нее фиксировано водило D, когда планетарная шестерня B вращается один раз, внутренняя шестерня C будет вращаться несколько раз.Это означает, что когда солнечная шестерня A вращается один раз, внутренняя шестерня C будет вращаться один раз.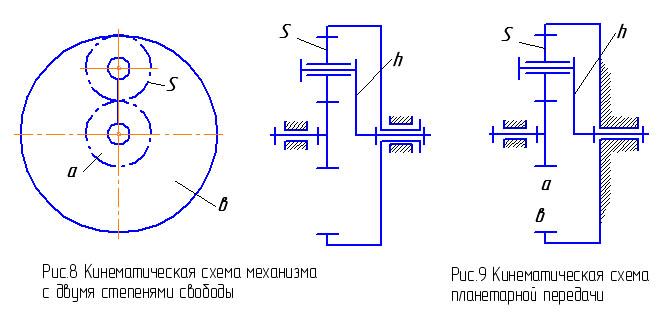 Но поскольку на самом деле внутренняя шестерня C зафиксирована, а водило D будет находиться в движении, весь механизм планетарной шестерни следует рассматривать только во времени вращения. Затем солнечная шестерня A повернется раз, а водило D —
раз, что приведет к уменьшению передаточного числа.
Затем предположим, что водило D зафиксировано, входная ось соединена с солнечной шестерней A, а внутренняя шестерня сателлита выходной оси C. В этом случае планетарная шестерня B будет вращаться только для передачи движущей силы в качестве второстепенной шестерни.Кроме того, поскольку внутренняя шестерня C будет вращаться в направлении, обратном солнечной шестерне A, передаточное число будет равным.
Таким образом, фиксируя и вращая компоненты зубчатого механизма, трансмиссия изменяет передаточное число, не требуя большого механизма.

Приложение — планетарная передача

Эта статья воспроизводится с разрешения автора.
Masao Kubota, Haguruma Nyumon, Tokyo: Ohmsha, Ltd. , 1963.

Планетарная шестерня — это зубчатая передача, состоящая из шестерни (солнечной шестерни), которая зафиксирована или вращается вокруг фиксированного центра, а шестерня (планетарная шестерня) вращается вокруг центра, который вращается вокруг солнечной шестерни.На рис. 12.9 показана простейшая планетарная передача. Когда шестерня A (число зубьев α) зафиксирована (неподвижная солнечная шестерня) и рычаг C вращается в направлении ωc, а шестерня B (планетарная шестерня, число зубцов b) вращается во время вращения.

Рис 12.9 Очень простая планетарная передача

Считая угловую скорость пространства, в котором он вращается, равной ωb, получим соотношение между ωb и ωc. Во-первых, скорость v2 в центре O2 планетарной шестерни B равна ωc на O1O2.С другой стороны, точка P зафиксирована, потому что шестерня A не вращается. Поскольку шестерня B вращается вокруг точки B с угловой скоростью со скоростью ωb, v2 = ωb на PO2. Следовательно,

ωb / ωc = O1O2 / PO2 = a + b / b
(12,3)

В качестве альтернативы вы можете рассмотреть следующее: рассматривать вращение, когда шестерня A и B находится в зацеплении, а рычаг C фиксируется, как нормальное зацепление, затем дать A обратное вращение, в то время как A, B и C взаимно зафиксированы. Затем поворот A становится 0 (фиксированным), а поворот B и C показан в таблице 12.1.
Таблица 12.1

	А	B	C
Против C	1	— а / б	0
С C	-1	-1	-1	(+
	0	— (1 + а / б)	-1

Когда C вращает -1 оборот, B вращает — (a + b) / b, и это соответствует результату формулы 12.3.

Рис. 12.10 Планетарная шестерня обратного хода с внешней шестерней

Рис. 12.10 показывает типичную планетарную шестерню обратного хода, которая поворачивается назад и передает вращение от неподвижной солнечной шестерни концентрической вращающейся солнечной шестерне через планетарную шестерню. Вы можете получить большое передаточное число, используя небольшую машину. Этот механизм используется для понижающей / ускоряющей передачи. На картинке выше зацепление представляет собой солнечную шестерню A -> планетарную шестерню B -> планетарную шестерню C (соединенную с шестерней B) -> солнечную шестерню D (концентрическую, но не соединенную с шестерней B) и шестерню A фиксируется, а рычаг E вращается.

Чтобы получить передаточное число, сначала зафиксируйте рычаг E и получите вращение каждой шестерни за один оборот шестерни A, затем вычислите количество оборотов каждой шестерни, задав шестерне A -1 оборот, как в таблице 12.2.

Таблица 12.2

	А	B	C	D	E
Против E	+1	— а / б	— а / б	ac / bd	0
С E	-1	–1	-1	–1	-1	(+
	0	— (1 + а / б)	— (1 + а / б)	— (1-ак / бд)	-1

Следовательно, если угловая скорость плеча равна ωe, угловая скорость ωd солнечной шестерни D выражается с помощью следующей формулы:

ωd = — (ac / bd — 1) ωe
(12. 4)

В этом случае D обратно пропорционально E, когда ac> bd, D и E синхронно вращаются, когда ac

Существуют различные формы планетарной передачи в дополнение к вышеперечисленным, например, с внутренним зацеплением, как на рис. 12.11 и в таблице 12.3, или с коническим зубчатым колесом, как на рис. 12.12.

Когда какая-либо внешняя шестерня заменяется внутренней шестерней, используйте знак минус для радиуса делительной окружности в формуле для передаточного числа.

Рис. 12.11 Обратно-планетарный редуктор с внутренним зацеплением

Рис. 12.12 Планетарный редуктор с угловым редуктором

Таблица 12.3

фиксированная передача	ведущая шестерня	ведомая шестерня	число оборотов s1	число оборотов s2	число вращения	число оборотов оси p1, p2
s2	а	s1	p2s1 + p1s2 / p2s1	0	1	s2 / p2
s1	а	s2	0	p2s1 + p1s2 / p1s2	1	s1 / p1
s2	s1	а	1	0	p2s1 / p2s1 + p1s2	p2s1 / p2s1 + p1s2 * s2 / p2
s1	s2	а	0	1	p1s2 / p2s1 + p1s2	p1s2 / p2s1 + p1s2 * s1 / p1

Ссылки по теме:
Gear Systems

Типы планетарных редукторов, которые мы можем поставить и. ..

Типы планетарных зубчатых передач — это своего рода планетарная зубчатая передача , принцип , в которой используется зацепление с циклоидальным штифтом, а также усовершенствованная конструкция и новая конструкция. Редуктор может широко использоваться в различном передаточном оборудовании, таком как: подъемное, транспортное, горнодобывающее, металлургическое, нефтехимическое, текстильное, печатное и красящее, легкая промышленность, фармацевтика, пищевое оборудование.

Во-вторых, структура

Все трансмиссии Типов планетарных передач можно разделить на три части: входную часть, часть замедления и выходную часть, которые делятся на четыре типа в зависимости от структуры: горизонтальные, вертикальные, двухосные и прямые. -сопряженный. Помимо производства стандартных редукторов, наш завод также может удовлетворить потребности пользователей в нестандартном проектировании и производстве.

Редуктор с прямым подключением состоит из специального двигателя серии Y и специального двигателя серии Y, таких как двигатель повышенной безопасности YA, взрывозащищенный двигатель YB, двигатель с регулируемой скоростью YCT и двигатель с тормозом YEJ.

В-третьих, характеристики планетарных передач:

1. Передаточное число большое: передаточное число составляет 1 / 9–1 / 87 при замедлении; передаточное число составляет 1 / 99-1 / 5133 при двухступенчатом замедлении; передаточное число составляет 1 / 5841–1 / 658503, когда необходимо замедление третьей ступени; Можно использовать больше комбинаций

2. Высокая эффективность передачи: средний КПД может достигать более 90% из-за зацепления зацепляющегося циклоидного редуктора

.

3.Малый размер и легкий вес: поскольку принят принцип типов планетарных зубчатых передач, типы планетарных зубчатых передач входной и выходной валы находятся на одной оси, и есть уникальная особенность, которая напрямую интегрирована с двигателем, планетарный циклоидальный редуктор имеет компактную конструкцию и небольшой объем. Маленький, легкий

4. Низкий уровень отказов и длительный срок службы: основные детали трансмиссии машины изготовлены из подшипниковой стали, поэтому механические характеристики хорошие, износостойкость хорошая, а трение качения используется для уменьшения неисправностей и повышения качества обслуживания. жизнь длинная.

5. Работа надежна и стабильна: планетарный циклоидный редуктор имеет несколько зубьев в процессе передачи, поэтому он стабилен, надежен и прост в обслуживании.

6. Простота разборки и установки, простота ремонта: благодаря разумной конструкции, простой разборке и сборке, простоте обслуживания

7. Типы планетарных зубчатых передач Машина также обладает высокой перегрузочной способностью, ударопрочностью и малым моментом инерции, что подходит для частого запуска и обратного вращения.

С наилучшими пожеланиями,

Лэнс (Директор по маркетингу; г-н)

NER GROUP CO., LIMITED

Yantai Bonway Manufacturer Co. , Ltd

Тел .: + 86-535-6330966

мобильный: + 86-18563806647

http://www.sogears.com/

Tweets by gearboxmotor

https://www.facebook.com/sogearsgroup

Viber / Line / Whatsapp / Wechat: 008618563806647

Эл. Почта: [email protected]; Skype ID: qingdao411

Адрес: No.5 Wanshoushan Road, Яньтай, провинция Шаньдун, Китай (264006)

Планетарные редукторы от нашей компании

Завод планетарных редукторов

, каталог планетарных редукторов, планетарные редукторы Цены , планетарные редукторы в Китае, прецизионные редукторы, планетарные редукторы с самой высокой плотностью крутящего момента на продажу, Экономичный планетарный поворотный привод, гидравлический двигатель Сервопривод

• Самые популярные запросы по теме

изображений, стоковых фотографий и векторных изображений планетарной передачи

В настоящее время вы используете более старую версию браузера, и ваш опыт может быть не оптимальным. Пожалуйста, подумайте об обновлении. Учить больше. ImagesImages homeCurated collectionsPhotosVectorsOffset ImagesCategoriesAbstractAnimals / WildlifeThe ArtsBackgrounds / TexturesBeauty / FashionBuildings / LandmarksBusiness / FinanceCelebritiesEditorialEducationFood и DrinkHealthcare / MedicalHolidaysIllustrations / Clip-ArtIndustrialInteriorsMiscellaneousNatureObjectsParks / OutdoorPeopleReligionScienceSigns / SymbolsSports / RecreationTechnologyTransportationVectorsVintageAll categoriesFootageFootage homeCurated collectionsShutterstock SelectShutterstock ElementsCategoriesAnimals / WildlifeBuildings / LandmarksBackgrounds / TexturesBusiness / FinanceEducationFood и DrinkHealth CareHolidaysObjectsIndustrialArtNaturePeopleReligionScienceTechnologySigns / SymbolsSports / RecreationTransportationEditorialAll categoriesMusicMusic ГлавнаяПремиумBeatШаблоныШаблоныДомашняя страницаСоциальные медиаШаблоныFacebook ОбложкаFacebook Mobile CoverInstagram StoryTwitter BannerYouTube Channel ArtШаблоны печатиВизитная карточкаСертификатКупонFlyerПодарочный сертификатРедакцияГлавная редакцияEnterta inmentNewsRoyaltySportsToolsShutterstock EditorMobile appsPluginsImage resizerFile converterCollage makerColor schemesBlogBlog homeDesignVideoContributorNews

---

PremiumBeat blogEnterprisePricing

Вход

Зарегистрироваться

Меню

FiltersClear allAll изображений

• Все изображения
• Фото
• Vectors
• Иллюстрации

% PDF-1. 6 % 80 0 объект > endobj xref 80 65 0000000016 00000 н. 0000002330 00000 н. 0000002466 00000 н. 0000002529 00000 н. 0000003068 00000 н. 0000003861 00000 н. 0000004620 00000 н. 0000005398 00000 п. 0000006236 00000 п. 0000006347 00000 п. 0000006383 00000 п. 0000006430 00000 н. 0000006554 00000 н. 0000007374 00000 н. 0000007460 00000 н. 0000008222 00000 п. 0000008884 00000 н. 0000009569 00000 н. 0000010175 00000 п. 0000010855 00000 п. 0000010938 00000 п. 0000011613 00000 п. 0000012964 00000 п. 0000014114 00000 п. 0000015300 00000 п. 0000016501 00000 п. 0000017236 00000 п. 0000017355 00000 п. 0000017961 00000 п. 0000018619 00000 п. 0000019763 00000 п. 0000019876 00000 п. 0000021075 00000 п. 0000021534 00000 п. 0000021756 00000 п. 0000021870 00000 п. 0000022218 00000 п. 0000022565 00000 п. 0000022994 00000 п. 0000023509 00000 п. 0000023934 00000 п. 0000024593 00000 п. 0000025417 00000 п. 0000031188 00000 п. 0000041255 00000 п. 0000042075 00000 п.