Работа через кпд – Мощность и КПД в физике, формулы и примеры

Мощность и КПД в физике, формулы и примеры

Понятие мощности

Единицей измерения мощности в системе СИ является ватт.

Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина или механизм.

В случае равномерного прямолинейного движения также справедлива формула:

   

где — сила, совершающая работу, — скорость движения тела.

Коэффициент полезного действия, КПД

Все механизмы или двигатели предназначены для выполнения определенной механической работы, которую называют полезной работой. Однако любой машине приходится совершать большую по величине работу, так как вследствие действия сил трения некоторая часть подводимой к машине энергии не преобразовывается в механическую работу.

Эффективность работы машины или механизма характеризуют коэффициентом полезного действия.

Коэффициент полезного действия (КПД) – это отношение полезной работы , совершенной машиной или механизмом, ко всей затраченной работе (энергии , подведенной к системе):

   

Также справедливы следующие формулы:

   

   

где и полезная и затраченная мощности соответственно.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Мощность и коэффициент полезного действия — урок. Физика, 8 класс.

Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.

Среднее значение мощности — это работа, выполненная за единицу времени.

Величина мощности прямо пропорциональна величине совершённой работы \(A\) и обратно пропорциональна времени \(t\), за которое работа была совершена.

Мощность \(N\) определяют по формуле:

N=At.

 

Единицей измерения мощности в системе \(СИ\) является \(Ватт\) (русское обозначение — \(Вт\), международное — \(W\)).

Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.

Пример:

Мощность двигателя автомобиля равна примерно \(90 л.с. = 66240 Вт\).

Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля \(F\) и скорость его движения (v).

N=F⋅v

Эту формулу получают, преобразуя основную формулу определения мощности.

 

Ни одно устройство не способно использовать \(100\) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.  

Пример:

Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах \(40 — 45\) %. Таким образом, получается, что только около \(40\) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.

Если мы заправим в бак автомобиля \(20\) литров бензина, тогда только \(8\) литров будут расходоваться на перемещение автомобиля, а \(12\) литров сгорят без совершения полезной работы.

Коэффициент полезного действия обозначается буквой греческого алфавита \(«эта»\) η, он является отношением полезной мощности \(N\) к полной или общей мощности Nполная.

 

Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.

 

Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%.

 

Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы \(A\) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:

 

η=AAполная⋅100%.

 

Коэффициент полезного действия всегда меньше \(1\), или \(100\) % (η < 1, или η < \(100\) %).

 

Источники:

E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp.

(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)

www.yaklass.ru

Расчет коэффициента полезного действия: формулы для электрической цепи

Для оценки эффективности расхода энергии на выполнение работы необходимо выяснить, как найти КПД. Полученные сведения пригодятся для оптимизации параметров электрических компонентов цепи, рычагов и других передаточных механизмов. С помощью предварительных вычислений можно увеличить длительность действия автономного источника питания, решить другие практические задачи.

Формула КПД поясняет основные определения

Что такое КПД источника тока

Неподвижный заряд не выполняет работу. Уменьшение энергетического запаса в аккумуляторе происходит за счет химических реакций. Фактически это свидетельство несовершенства конструкции.

После подключения источника к проводникам с подключенной нагрузкой заряды перемещаются по цепи, выполняя определенную работу. Полезная составляющая мощности (Pпол) определяется параметрами внешнего контура. Полная (Pп) – содержит совокупные затраты. Если электротехник пользуется привычными терминами, он быстро установит для коэффициента полезного действия формулу:

КПД = Рпол/Рп = (U*I)/(Е*I) = U/E.

Для чего нужен расчет КПД

Наглядный пример недостаточно эффективного устройства – классическая лампа накаливания. Пропускание тока через вольфрамовую спираль повышает температуру проводника. В рабочем режиме значительное количество потребляемой мощности расходуется на генерацию излучения. Однако к видимой части диапазона относится только небольшая часть спектра. Так как вырабатываемая теплота не выполняет полезного действия, соответствующие энергетические затраты следует узнавать по излишним.

Если выразить КПД через мощность в этом случае, следует одновременно учесть долговечность. Эта методика повышает точность оценки, так как подразумевает необходимость периодической замены испорченного излучателя.

В типовом рабочем режиме лампа накаливания нагревает нить до 2600-2800К. При таком значении срок службы составляет 900-1200 часов, КПД – от 5 до 7%. Увеличить эффективность в 2-5 раз можно повышением температуры до 3400-3600К. Однако в этом варианте долговечность уменьшается до 5-6 часов. Подобные практические характеристики нельзя признать удовлетворительными.

Сравнение эффективности и других параметров разных типов ламп

Эта таблица демонстрирует превосходство экономичных источников света. Срок службы современных светодиодов измеряется десятками тысяч часов. Даже на завершающих этапах рабочих циклов обеспечиваются высокая яркость и качественное распределение спектральных составляющих.

Нахождение тока в полной цепи

Для изучения эффективности потребления энергии в электротехнике можно использовать базовые формулы. В полной цепи по базовому определению рассматривают источник тока (I) с внутренним сопротивлением (r). Подключенная нагрузка потребляет определенную мощность. Она характеризуется электрическим сопротивлением R.

Прохождение тока по такой цепи обеспечивает энергия источника, которая определена значением электродвижущей силы (ЭДС – E). Ее можно выразить как отношение выполненной сторонними силами работы (A) по передвижению заряда (q) с положительным знаком по соответствующему контуру. С учетом известной формулы

I= q/t несложно определить зависимость между рассматриваемыми величинами:

А = E * I * t,

где t – контрольный временной интервал.

Отдельно можно рассмотреть участки с внутренним и внешним сопротивлением. Каждый из них выделяет определенное законом Джоуля-Ленца количество теплоты Q = I2 * R * t. Так как энергия не пропадает бесследно, можно сделать правильный вывод о равенстве Q = A. Подставив значения в исходное выражение, получают:

E = I*R + I*r.

ЭДС полной цепи вычисляется сложением двух падений напряжений на внутреннем и внешнем участке. Элементарное преобразование позволяет узнать силу тока в соответствующем проводнике:

I = E/ (R+r).

Расчет КПД электрической цепи

После определения основных параметров можно перейти к изучению эффективности системы. Для вычисления КПД обозначение потребления электроэнергии удобно сделать по стандартным формулам.

Определить мощность можно по следующим соотношениям силы тока, напряжения, электрического сопротивления

Выполняемая работа в цепи определяется количеством перемещенных зарядов, а также скоростью данного процесса. Для объективной оценки последнего параметра измерения выполняют с учетом определенных временных интервалов (Δt). Работу и мощность можно определить следующими формулами:

• A = P * Δt;
• P = A / Δt.

Как и в классической механике, работу можно измерить в джоулях (Дж). Мощность, по стандартам СИ, указывают в ваттах (Вт). Зависимость между отмеченными единицами:

Вт = Дж/ с (для электрических цепей вольт * ампер).

Для обозначения КПД символ «η» применяют в типовых формулах. Базовое определение с учетом приведенных замечаний можно преобразовать следующим образом:

η = A / Q * 100%,

где:

• A – выполненная работа;
• Q – энергия, полученная из источника.

Как найти КПД, формула для полной цепи

Любое подключенное устройство характеризуется определенными потерями. Резистор выделяет тепло. Трансформатор тратит часть энергии на преобразование электромагнитных волн. На примере лампы накаливания показана низкая эффективность изделия. С применением КПД увеличивают объективность оценки разных систем, подключаемых потребителей, генераторов. В следующем пункте представлена технология проверки силовых агрегатов.

Методика и порядок измерений

Идеальные условия можно рассматривать только в теории. Для корректной оценки замкнутой системы необходимо учитывать энергетические потери на выполнение необходимой работы. Ниже показано, как определить КПД механических силовых агрегатов с применением разных исходных данных.

Движению поршня в блоке цилиндров двигателя внутреннего сгорания препятствует сила трения. Поступательно-возвратные движения в ходе стандартного цикла преобразуются во вращение вала с дополнительными потерями. Высокая температура не выполняет в данном случае полезные функции. Чтобы не допустить разрушения агрегата, необходимо поддерживать определенный тепловой режим. Приходится обеспечить циркуляцию охлаждающей жидкости с помощью помпы.

Понятно, что в подобном случае сделать общий КПД расчет с учетом каждого компонента конструкции непросто. Однако можно узнать в ходе эксперимента с высокой точностью, какое количество топлива (масса – m) придется затратить на 100 км пробега машины за соответствующее время (t). Далее нужно взять из сопроводительной документации (справочников) следующие данные:

• мощность мотора – Рм;
• удельную теплоту бензина – У.

В этом варианте для расчета КПД двигателя формула преобразуется следующим образом: 

η = (Pм * t) / (У * m).

Для отображения результата в % итоговое значение умножают на 100.

Если мощность силового агрегата не известна, определять эффективность можно по массе авто (Mа). Измерять ее несложно с помощью промышленных весов (на станции техосмотра, элеваторе). В ходе эксперимента разгоняются с места до контрольной скорости (v). Массу топлива вычисляют по объему (переведенному из литров в м кв.), который умножают на плотность (справочная величина в кг на куб. м).

В этом случае КПД расчет находят по формуле:

η = (Mа * v2)/(2 * У * m).

Следует перевести предварительно скорость из км/час в м/с.

Проще измеряется эффективность электродвигателя с паспортной мощностью (P). Его подключают к источнику питания с известным напряжением (U). После выхода на стабильную частоту вращения фиксируют значение тока (I) в цепи. Далее применяют классическую формулу:

η = P/ (U * I).

Если сопроводительная документация отсутствует, технические параметры берут с официального сайта производителя. Однако и в этом случае следует понимать ограниченную точность подобных данных. В процессе эксплуатации характеристики могут ухудшиться за счет естественного износа. Погрешность увеличивается после длительной интенсивной эксплуатации, при подключении редуктора или другого переходного устройства.

Значительно улучшить точность можно с применением простой методики:

• устанавливают на вал шкив с закрепленным тросом;
• поднимают на контрольную высоту (h) груз c массой m;
• секундомером фиксируют время (t) на выполнение этой работы;
• мультиметром измеряют напряжение (U) и силу тока (I) на клеммах источника питания и в разрыве цепи, соответственно.

Для нахождения КПД в физике формула выглядит следующим образом:

η = (m * h * g)/(I * U * t),

где g – это гравитационная постоянная (9,80665).

Эффективность любого силового агрегата определяют по соотношению полезной работы к расходованной энергии. Чтобы корректно определять класс техники, пользуются переводом в проценты. Следует подчеркнуть, что значение больше 100% обозначает ошибку в расчетах. Создатель подобного агрегата станет «властелином мира», так как изобретет вечный двигатель.

Видео

amperof.ru

Конспект «Механическая работа, мощность и КПД»

Механическая работа, мощность и КПД механизма

1. Механическая работа (или работа силы над телом) – физическая величина, равная по модулю произведению силы на путь, пройденный телом вдоль направления этой силы. Если вектор силы перпендикулярен направлению движения тела, то совершаемая этой силой работа равна нулю; если вектор силы сонаправлен с направлением движения тела, то работу силы считают положительной; если вектор силы противоположен направлению движения тела, то работу силы считают отрицательной.

• В случае, когда точка приложения силы перемещается в направлении действия силы, механическая работа А равна произведению модуля F силы на путь s, пройденный точкой приложения силы: А = Fs.
• Единица работы в СИ 1 Джоуль (Дж) = 1 Нм.
• «Золотое правило» механики с использованием понятия работы: никакой простой механизм не дает выигрыша в работе.

Таблица «Механическая работа, мощность и КПД»

 

---

2. Коэффициент полезного действия (КПД) – физическая величина, равная отношению полезной работы к полной совершённой работе. КПД показывает долю полезной работы от полной и, как и все доли, всегда имеет положительный знак и не имеет «своей» единицы для измерения. Значение КПД обычно выражают в процентах, которое нужно переводить в десятичную дробь для дальнейших вычислений.

• Коэффициентом полезного действия (КПД) механизма называют отношение полезной работы А_пол к совершенной А_сов, выраженное в процентах: η = А_пол/А_сов · 100%.
• КПД любого реального механизма меньше 100 % (из-за трения и из-за того, что сами механизмы и их части имеют некоторую массу).

3. Мощность действия – физическая величина, равная отношению механической работы ко времени, за которое она была совершена. Мощность характеризует быстроту (скорость) совершения работы. Мощность принято вычислять только для тех действий, в которых механическая работа положительна.

• Мощностью N называют отношение совершенной работы А к промежутку времени t, за который эта работа совершена: N = A/t
• Единица мощности в СИ 1 ватт (Вт) = 1 Дж/с.
• Мощность можно выразить через силу и скорость с помощью формулы N = Fv.

---

Схема «Механическая работа. Мощность»

 

---

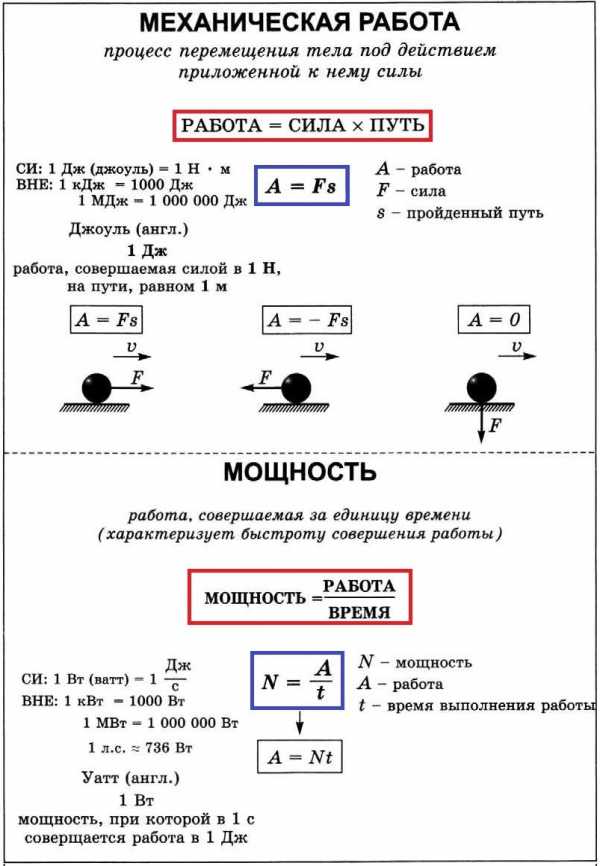
Конспект урока по физике в 7 класса «Механическая работа и энергия».

Смотреть задачи: 1) на механическую работу,  2) механическую мощность, 3) на КПД простых механизмов.

Следующая тема: «Простые механизмы. Блоки»

uchitel.pro

Как найти коэффициент полезного действия

10 января 2012

Автор КакПросто!

Коэффициент полезного действия показывает отношение полезной работы, которая выполняется механизмом или устройством, к затраченной. Часто за затраченную работу принимают количество энергии, которое потребляет устройство для того, чтобы выполнить работу.

Статьи по теме:

Вам понадобится

• — автомобиль;
• — термометр;
• — калькулятор.

Инструкция

Для того чтобы рассчитать коэффициент полезного действия (КПД) поделите полезную работу Ап на работу затраченную Аз, а результат умножьте на 100% (КПД=Ап/Аз∙100%). Результат получите в процентах.

При расчете КПД теплового двигателя, полезной работой считайте механическую работу, выполненную механизмом. За затраченную работу берите количество теплоты, выделяемое сгоревшим топливом, которое является источником энергии для двигателя. Пример. Средняя сила тяги двигателя автомобиля составляет 882 Н. На 100 км пути он потребляет 7 кг бензина. Определите КПД его двигателя. Сначала найдите полезную работу. Она равна произведению силы F на расстояние S, преодолеваемое телом под ее воздействием Ап=F∙S. Определите количество теплоты, которое выделится при сжигании 7 кг бензина, это и будет затраченная работа Аз=Q=q∙m, где q – удельная теплота сгорания топлива, для бензина она равна 42∙10^6 Дж/кг, а m – масса этого топлива. КПД двигателя будет равен КПД=(F∙S)/(q∙m)∙100%= (882∙100000)/( 42∙10^6∙7)∙100%=30%.

В общем случае чтобы найти КПД, любой тепловой машины (двигателя внутреннего сгорания, парового двигателя, турбины и т.д.), где работа выполняется газом, имеет коэффициент полезного действия равный разности теплоты отданной нагревателем Q1 и полученной холодильником Q2, найдите разность теплоты нагревателя и холодильника, и поделите на теплоту нагревателя КПД= (Q1-Q2)/Q1. Здесь КПД измеряется в дольных единицах от 0 до 1, чтобы перевести результат в проценты, умножьте его на 100.

Чтобы получить КПД идеальной тепловой машины (машины Карно), найдите отношение разности температур нагревателя Т1 и холодильника Т2 к температуре нагревателя КПД=(Т1-Т2)/Т1. Это предельно возможный КПД для конкретного типа тепловой машины с заданными температурами нагревателя и холодильника.

Для электродвигателя найдите затраченную работу как произведение мощности на время ее выполнения. Например, если электродвигатель крана мощностью 3,2 кВт поднимает груз массой 800 кг на высоту 3,6 м за 10 с, то его КПД равен отношению полезной работы Ап=m∙g∙h, где m – масса груза, g≈10 м/с² ускорение свободного падения, h – высота на которую подняли груз, и затраченной работы Аз=Р∙t, где Р – мощность двигателя, t – время его работы. Получите формулу для определения КПД=Ап/Аз∙100%=(m∙g∙h)/(Р∙t) ∙100%=%=(800∙10∙3,6)/(3200∙10) ∙100%=90%.

Видео по теме

Источники:

• как определить кпд

Совет полезен?

Статьи по теме:

www.kakprosto.ru

Работа, мощность, энергия — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Механическая работа

К оглавлению…

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:

Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.

Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:

Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (F_упр = kx).

 

Мощность

К оглавлению…

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

По этой формуле рассчитывается средняя мощность, т.е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:

По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.

КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:

Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.

Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).

В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:

 

Кинетическая энергия

К оглавлению…

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):

То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Е_к = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.

Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.

Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.

Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:

Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.

 

Потенциальная энергия

К оглавлению…

Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:

Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:

Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.

Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.

Потенциальная энергия растянутой пружины рассчитывается по формуле:

где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x₁, тогда при переходе в новое состояние с удлинением x₂ сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.

 

Коэффициент полезного действия

К оглавлению…

Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).

КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.

В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.

В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.

Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.

Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.

 

Закон сохранения механической энергии

К оглавлению…

Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):

Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:

Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.

Алгоритм решения задач на закон сохранения энергии:

1. Найти точки начального и конечного положения тела.
2. Записать какой или какими энергиями обладает тело в данных точках.
3. Приравнять начальную и конечную энергию тела.
4. Добавить другие необходимые уравнения из предыдущих тем по физике.
5. Решить полученное уравнение или систему уравнений математическими методами.

Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.

 

Разные задачи на работу

К оглавлению…

Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:

1. Работу можно найти по формуле: A = FS∙cosα. Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
2. Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
3. Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
4. Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
5. Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.

 

Закон сохранения энергии и динамика вращательного движения

К оглавлению…

Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:

1. Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
2. Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
3. Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
4. В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
5. Провести остальные необходимые математические операции для получения окончательного результата.

При решении задач надо помнить, что:

• Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.
• При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
• Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.

 

Неупругие соударения

К оглавлению…

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).

 

Абсолютно упругий удар

К оглавлению…

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.

 

Законы сохранения. Сложные задачи

К оглавлению…

Несколько тел

В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.

Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:

1. выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
2. записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
3. учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
4. при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда

В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.

Столкновения с тяжёлой плитой

Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью u_н. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:

Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:

Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров

В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.

educon.by

Тема 1.14. Работа и мощность. Коэффициент полезного действия.

⇐ ПредыдущаяСтр 19 из 21Следующая ⇒

 

Иметь представление о мощности при прямолинейном и кри­волинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия.

Знать зависимости для определения мощности при поступа­тельном и вращательном движениях, КПД.

Уметь рассчитать мощность с учетом потерь на трение и сил инерции.

Мощность

Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.

Мощность — работа, выполненная в единицу времени:

Единицы измерения мощности: ватты, киловатты,

Мощность при поступательном движении (рис. 16.1)

Учитывая, что S/t = v_cp, полу­чим

где F — модуль силы, действующей на тело; v_ср — средняя скорость движения тела.

 

Средняя мощность при поступательном движении равна про­изведению модуля силы на среднюю скорость перемещения и на ко­синус угла между направлениями силы и скорости.

 

Мощность при вращении (рис. 16.2)

 

Тело движется по дуге радиуса r из точки М₁ в точку M₂

Работа силы:

где М_вр — вращающий момент.

Учитывая, что

получим

где ω_cp — средняя угловая скорость.

 

Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость.

 

Если при выполнении работы усилие машины и скорость дви­жения меняются, можно определить мощность в любой момент вре­мени, зная значения усилия и скорости в данный момент.

 

Коэффициент полезного действия

 

Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений. Таким образом, машина (механизм) кроме полезной работы со­вершает еще и дополнительную работу.

Отношение полезной работы к полной работе или полезной мощ­ности ко всей затраченной мощности называется коэффициентом по­лезного действия (КПД):

Полезная работа (мощность) расходуется на движение с задан­ной скоростью и определяется по формулам:

Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери.

Чем выше КПД, тем совершеннее машина.

Примеры решения задач

 

Пример 1. Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.

Решение

1. Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки.

Полезная мощность определяется по формуле

Р = Fv cos α.

В данном случае α = 0; груз движется поступательно.

2. Скорость подъема груза

3. Необходимое усилие равно весу груза (равномерный подъем).

6. Полезная мощность Р = 3000 • 4 = 12 000 Вт.

7. Полная мощность. затрачиваемая мотором,

 

Пример 2. Судно движется со скоростью 56 км/ч (рис. 16.4). Двигатель развивает мощность 1200 кВт. Определить силу сопротивления во­ды движению судна. КПД машины 0,4.

Решение

1. Определяем полезную мощность, используемую на движение с заданной скоростью:

2. По формуле для полезной мощности можно определить движущую силу судна с учетом условия α = 0. При равномерном дви­жении движущая сила равна силе сопротивления воды:

Fдв = Fcопр.

3. Скорость движения судна v = 36 * 1000/3600 = 10 м/с

4. Сила сопротивления воды

 

Сила сопротивления воды движению судна

Fcопр. = 48 кН

 

Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощ­ность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.

 

Решение

1. Резание осуществляется за счет трения между точильным камнем и обрабатываемой деталью:

Пример 4. Для того чтобы поднять волоком по наклонной плоскости на высоту H = 10 м станину массой т == 500 кг, воспользовались электрической лебедкой (рис. 1.64). Вращающий момент на выходном барабане лебедки М = 250 Н-м. Ба­рабан равномерно вращается с частотой п = 30 об/мин. Для подъема станины лебедка ра­ботала в течение t = 2 мин. Определить коэффициент по­лезного действия наклонной плоскости.

 

Решение

 

Как известно,

где А_п.с. — полезная работа; А_дв — работа движущих сил.

В рассматриваемом примере полезная работа — работа силы тяжести

Вычислим работу движущих сил, т. е. работу вра­щающего момента на выходном валу лебедки:

Угол поворота барабана лебедки определяется по уравнению равномерного вращения:

где

Тогда

Подставив в выражение работы движущих сил число­вые значения вращающего момента М и угла поворота φ, получим:

 

Коэффициент полезного действия наклонной плоскости составит

 

Контрольные вопросы и задания

 

1. Запишите формулы для расчета работы при поступательном и вращательном движениях.

2. Вагон массой 1000 кг перемещают по горизонтальному пути на 5 м, коэффициент трения 0,15. Определите работу силы тяжести.

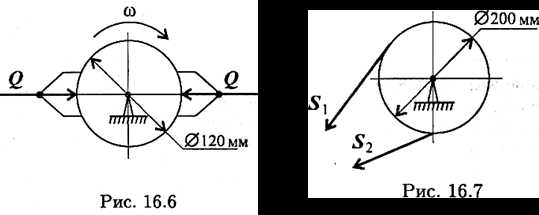
3. Колодочным тормозом останавливают барабан после отклю­чения двигателя (рис. 16.6). Определите работу торможения за 3 обо­рота, если сила прижатия колодок к барабану 1 кН, коэффициент трения 0,3.

4. Натяжение ветвей ременной передачи S₁ = 700 Н, S₂ = 300 Н (рис. 16.7). Определите вращающий момент передачи.

5. Запишите формулы для расчета мощности при поступатель­ном и вращательном движениях.

6. Определите мощность, необходимую для подъема груза весом 0,5 кН на высоту 10 м за 1 мин.

7. Определите общий КПД механизма, если при мощности дви­гателя 12,5 кВт и общей силе сопротивления движению 2 кН ско­рость движения 5 м/с.

8. Ответьте на вопросы тестового задания.

Тема 1.14. Динамика. Работа и мощность

ЛЕКЦИЯ 17



infopedia.su