Размерность угловой скорости в си: HTTP 429 — too many requests, слишком много запросов

Угловая скорость — frwiki.wiki

«Скорость вращения» перенаправляется сюда. Для других значений см Скорость (значения) и Вращение .

«Угловая частота» перенаправляется сюда. Для других значений, см. Частота (значения) .

Угловая скорость (или скорость вращения ) представляет собой величину , которая представляет собой отношение от угла поворота в момент . Это является аналогом, для вращательного движения , от скорости для поступательного движения .

• Когда время ограничено, мы говорим о средней угловой скорости .
• Когда время бесконечно мало, мы говорим о мгновенной угловой скорости или просто об угловой скорости . Затем угловая скорость определяется как производная по времени от углового положения вращающегося объекта. Производная по времени от угловой скорости — это угловое ускорение .

Резюме

• 1 шт.
  • 1.1 Эквивалентность единиц
• 2 измерение
• 3 Вектор угловой скорости
• 4 Примечания и ссылки
• 5 См. Также
  • 5.1 Библиография
  • 5.2 Статьи по теме

Единицы измерения

Единица угловой скорости в Международной системе является радиан в секунду (рад / с или рад с ^-1 ). Его не следует выражать в герцах (Гц), до которых нельзя привести радиан в секунду.

В области промышленной механики и повседневной жизни это часто выражается в оборотах в минуту (об / мин).

Вы также можете использовать градусы в секунду и обороты в секунду.

Эквивалентность единиц

Полный оборот, совершенный за период T , равен 2π радиан. Следовательно, пройден радиан . Угловая скорость, которая описывает количество угловых единиц, пройденных за единицу времени, является обратной, поскольку частота f является обратной по отношению к периоду. Другими словами: Т2π{\ displaystyle {\ frac {T} {2 \ pi}}}ωзнак равно2πТзнак равно2πж{\ displaystyle \ omega = {\ frac {2 \ pi} {T}} = 2 \ pi f}

ωзнак равноdθdтзнак равно2πТзнак равно2πж{\ displaystyle \ omega = {\ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}} = {\ frac {2 \ pi} {T}} = 2 \ pi f}

В международной системе единиц время выражается в секундах, а частота — в герцах . {- 1}}это размерность частоты .

1{\ displaystyle 1}выражает плоский угол , безразмерную величину .

Поскольку углы являются безразмерными величинами, их можно передать просто в с ^-1 , но этого следует избегать, если единица измерения угла не является совершенно ясной.

Вектор угловой скорости

Иногда используется вектор угловой скорости . Это вектор: ω→{\ displaystyle {\ vec {\ omega}}}

• перпендикулярно плоскости вращения;
• ориентированы так, чтобы движение было в положительном направлении, обычно задаваемом правилом правой руки  ;
• норма которого равна ω .

Таким образом, вектор угловой скорости определяет как ось, вокруг которой вращается объект, так и скорость его вращения. Это не совсем вектор, а псевдовектор , поскольку симметричное в зеркале инвертировано.

Использование вектора угловой скорости позволяет применять методы вычисления вектора к объектам, вращающимся относительно друг друга.

Он позволяет составлять угловые скорости путем сложения векторов и вычислять линейные скорости из угловых скоростей.

Циркулярный перевод:

В объекте, вращающемся вокруг опоры, который сам вращается, сложение векторов угловой скорости дает движение объекта.

Если два вектора угловой скорости направлены в одном направлении, но в противоположном направлении, их сложение дает нулевой вектор. Объект описывает круг, не меняя ориентации, в круговом поступательном движении .

Примечания и ссылки

1. ↑ Dubesset 2000 , стр.  4 ( онлайн ), стр.  122 ( онлайн ).
2. ↑ Dubesset 2000 , стр.  104.
3. ↑ «На практике символы rad и sr используются по мере необходимости» , Международное бюро мер и весов , Единицы со специальными названиями и специальными символами .

Смотрите также

Библиография

 : документ, использованный в качестве источника для этой статьи.

• Ричард Тайлле , Лоик Злодей и Паскаль Февр , Физический словарь , Брюссель, Де Бок ,2013, 3 ^е  изд. , Х-899  с. ( ISBN  978-2-8041-7554-2 , читать онлайн ) :
  • п.  561 , «Пульсация» ,
  • п.  723 «Угловая скорость» ,
  • [ Дик. Phys. , изд. 2008  (страница консультации по 23 июля 2014)] ( ( ISBN  978-2-8041-5688-6 ) (уведомление BnF п ^о  FRBNF41256105 ) , соответственно.
    P.  405 и стр.  523 .
• Мишель Дюбессе , Руководство Международной системы единиц: лексика и преобразования , Париж, Technip, колл.  «Публикации Французского нефтяного института  »,2000 г., 169  с. ( ISBN  2-7108-0762-9 , уведомление BnF п ^о  FRBNF37624276 , читать онлайн )

Статьи по Теме

• Момент (механический)
• Вектор угловой скорости
• Аналогия между вращением и перемещением

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

3.

3.2.Угловая скорость

Если за промежуток времени тело совершит поворот на угол , то средняя угловая скорость тела за этот промежуток времени равна: .

Угловая скорость в данный момент времени называется величина, к которой стремится средняя угловая скорость ω_ср, когда промежуток времени Δt→0.

, или

. (3.5)

Таким образом, угловая скорость в данный момент времени численно равна первой производной от угла поворота по времени. Знак определяется направлением вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки ω>0, а когда по ходу часовой стрелки, ω<0. Размерность угловой скорости = с^-1, так как радиан – величина безразмерная.

Условимся угловую скорость изображать в виде вектора , численная величина которого равна и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Такой вектор определяет сразу модуль угловой скорости, ось вращения и направление вращения тела вокруг оси.

3.3.3. Угловое ускорение

Угловое ускорение характеризует изменение угловой скорости с течением времени. Если за промежуток угловая скорость изменилась на , то среднее угловое ускорение тела за этот промежуток времени будет численно равно .

Угловым ускорением в данный момент времени называется величина, к которой стремится значение , когда промежуток времени Δt→0, следовательно:

, или

. (3.6)

Итак, угловое ускорение тела в данный момент времени численно равно первой производной от угловой скорости или второй производной от угла поворота тела.

Размерность углового ускорения [ε]=1/c² =с^-2

Если модуль угловой скорости с течением времени возрастает, то движение называется ускоренным, если убывает – то замедленным. Легко видеть, что вращение будет ускоренным, если ω и ε имеют одинаковые знаки, и замедленным, если ω и ε имеют разные знаки.

Угловое ускорение тела (по аналогии с угловой скоростью) можно изобразить вектором , направленным вдоль оси вращения. При этом направление совпадает с направлением , если движение ускоренное (рис. 3.4) и противоположно направлению , если движение замедленное (рис. 3.5)

Pис. 3.4 Рис. 3.5

Ускоренное вращение Замедленное вращение

3.3.4. Равномерное и равнопеременное вращение

Вращение тела с постоянной угловой скоростью ω = const называется равномерным.

Найдем закон равномерного вращения. При условии, что при t = 0, φ = φ_0. Из (3.5) имеем . Проинтегрировав это уравнение в пределах слева от φ до φ₀, справа от 0 до t, получим: , oткуда

. (3.7)

Выражение (3.7) является уравнением равномерного вращения тела.

Из уравнения (3.7) находим , то есть угловая скорость равномерного вращения тела равна отношению приращения угла поворота за некоторый промежуток времени к величине этого промежутка времени.

В технике угловая скорость измеряется числом оборотов в минуту и обозначается n. Так как, один оборот равен 2π рад, то зависимость между угловой скоростью [n] = об/мин и [ω] = с^—1 при φ₀ = 0 имеет вид

. (3.8)

Пример 1. Определить угловую скорость Земли вокруг ее оси, выраженной в с^—1.

Решение: .

Вращение тела при котором угловое ускорение постоянно (ε=const) во все время движения, называется равнопеременным.

Найдем закон равнопеременного вращения, если при t=0, φ=φ₀, ω=ω₀. Из (3.6) имеем: . Это уравнение проинтегрируем в пределах, соответствующих начальному моменту t₀ и произвольному моменту времени t. Получим , или

. (3.9)

Подставим полученное выражение в уравнение , тогда . Интегрируя его в соответствующих пределах, получим: , или

(3.10)

Пример 2. Вал начитает вращаться из состояния покоя. В первые 10 с он совершает 200 оборотов. Каковы его угловые скорость и ускорение по истечении 20 с?

Решение. Так как вал начинает вращаться из состояния покоя, то . В этом случае уравнения (3.9) и (3.10) при = 0 имеют вид

, (а)

. (б)

Из уравнения (б) находим , где φ = 2π N. Подставляя числовые значения, находим:

с^—2, с^—1.

Конвертер угловой скорости и частоты вращения • Механика • Определения единиц измерения • Онлайн-конвертеры единиц измерения

Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица

радиан в секунду

A радиан в секунду (рад·с⁻¹, рад/с) — единица измерения скорости вращения или угловой скорости в системе СИ и СГС. Радиан в секунду также является единицей угловой частоты. Один радиан в секунду определяется как изменение ориентации объекта на один радиан каждую секунду.

радиан/день

радиан в день (рад·д⁻¹, рад/д) — метрическая единица скорости вращения или угловой скорости. Радиан в сутки также является единицей угловой частоты. Один радиан в день определяется как изменение ориентации объекта на один радиан каждые 24 часа.

радиан/час

A радиан в час (рад·ч⁻¹, рад/ч) — метрическая единица скорости вращения или угловой скорости. Радиан в час также является единицей угловой частоты. Один радиан в час определяется как изменение ориентации объекта на один радиан каждый час.

радиан/минута

радиан в минуту (рад·мин⁻¹, рад/мин) — метрическая единица скорости вращения или угловой скорости. Радиан в минуту также является единицей угловой частоты. Один радиан в минуту определяется как изменение ориентации объекта на один радиан каждую минуту.

градус/день

A градус в день (градус·d⁻¹, градус/d) — метрическая единица скорости вращения или угловой скорости. Градус в сутки также является единицей угловой частоты. Один градус в день определяется как изменение ориентации объекта на один градус каждые 24 часа.

градус/час

A градус в час (градус·ч⁻¹, градус/ч) — метрическая единица скорости вращения или угловой скорости. Градус в час также является единицей угловой частоты. Один градус в час определяется как изменение ориентации объекта на один градус каждый час.

град/мин

A градус в минуту (градус·мин⁻¹, град/мин) — метрическая единица скорости вращения или угловой скорости. Градус в минуту также является единицей угловой частоты. Один градус в минуту определяется как изменение ориентации объекта на один градус каждую минуту.

градуса в секунду

A градусов в секунду (градус·с⁻¹, градус/с) — метрическая единица скорости вращения или угловой скорости. Градус в секунду также является единицей угловой частоты. Один градус в секунду определяется как изменение ориентации объекта на один градус каждую секунду.

оборотов в сутки

оборотов в сутки (r·d⁻¹, r/d, 1/d, d⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в сутки также является единицей угловой частоты. Один оборот в день определяется как изменение ориентации объекта на один полный оборот каждые 24 часа.

оборотов в час

оборотов в час (r·h⁻¹, r/h, 1/h, h⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в час также является единицей угловой частоты. Один оборот в час определяется как изменение ориентации объекта на один полный оборот каждый час.

оборотов в минуту

оборотов в минуту (об/мин⁻¹, об/мин, 1/мин, мин⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в минуту также является единицей угловой частоты. Один оборот в минуту определяется как изменение ориентации объекта на один полный оборот каждую минуту.

оборотов в секунду

оборотов в секунду (r·s⁻¹, r/s) — метрическая единица скорости вращения или угловой скорости. Оборот в секунду также является единицей угловой частоты. Один оборот в секунду определяется как изменение ориентации объекта на один полный оборот каждую секунду.

оборотов в год

оборотов в год (r·y⁻¹, r/y, 1/y, y⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в год также является единицей угловой частоты. Один оборот в год определяется как изменение ориентации объекта на один полный оборот каждый год.

оборотов в месяц

оборотов в месяц (об/м⁻¹, об/м, 1/м, м⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в месяц также является единицей угловой частоты. Один оборот в месяц определяется как изменение ориентации объекта на один полный оборот каждый месяц.

оборота в неделю

оборотов в неделю (r·w⁻¹, r/w, 1/w, w⁻¹) — метрическая единица скорости вращения или угловой скорости. Оборот в неделю также является единицей угловой частоты. Один оборот в неделю определяется как изменение ориентации объекта на один полный оборот каждую неделю.

градус/год

A градус в год (градус·г⁻¹, градус/год) — метрическая единица скорости вращения или угловой скорости. Градус в год также является единицей угловой частоты. Один градус в год определяется как изменение ориентации объекта на один градус каждый год.

градус/месяц

A градус в месяц (градус·м⁻¹, градус/м) — метрическая единица скорости вращения или угловой скорости. Градус в месяц также является единицей угловой частоты. Один градус в месяц определяется как изменение ориентации объекта на один градус каждый месяц.

градус/неделя

A градус в неделю (градус·w⁻¹, градус/w) — метрическая единица скорости вращения или угловой скорости. Градус в неделю также является единицей угловой частоты. Один градус в неделю определяется как изменение ориентации объекта на один градус каждую неделю.

радиан/год

A радиан в год (рад·г⁻¹, рад/год, 1/год, y⁻¹) — метрическая единица скорости вращения или угловой скорости. Радиан в год также является единицей угловой частоты. Один радиан в год определяется как изменение ориентации объекта на один радиан каждый год.

радиан/месяц

A радиан в месяц (рад·м⁻¹, рад/м, 1/м, м⁻¹) – метрическая единица скорости вращения или угловой скорости. Радиан в месяц также является единицей угловой частоты. Один радиан в месяц определяется как изменение ориентации объекта на один радиан каждый месяц.

радиан/неделя

A радиан в неделю (рад·вт⁻¹, рад/в, 1/в, вт⁻¹) — метрическая единица скорости вращения или угловой скорости. Радиан в неделю также является единицей угловой частоты. Один радиан в неделю определяется как изменение ориентации объекта на один радиан каждую неделю.

Преобразование единиц с помощью преобразователя угловой скорости и частоты вращения

Компактный калькулятор Полный калькулятор определений единиц измерения

У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и вы получите ответ от опытных технических переводчиков в считанные минуты.

Расчеты для преобразователя угловой скорости и частоты вращения выполнены с использованием математики с сайта unitconversion.org.

условных единиц — Единица угловой скорости

Заданный вопрос 4 года 11 месяцев назад

Модифицированный 4 года, 11 месяцев назад

Просмотрено 795 раз

$\begingroup$

На этот вопрос уже есть ответы здесь :

Почему радианы более естественны, чем любые другие угловые единицы? (7 ответов)

Закрыт 4 года назад.

Почему угловая скорость $\omega$ всегда указывается в $rad/sec$? Что-то не так, если я напишу в $градусах/сек$? Если нет, то почему почти во всех книгах он указан как $rad/sec$??

• условные обозначения
• единицы
• размерный анализ
• угловая скорость

$\endgroup$

3

$\begingroup$

$w $ — это угловая скорость, а не угловое смещение. Вы можете записать это в град/сек, если хотите. Причина, по которой используются рад/сек, заключается в том, что тождества $\frac{d}{dx}\cos(x) = -\sin(x) $ и $ \frac{d}{dx}\sin(x) = \ cos(x)$ справедливы только тогда, когда x измеряется в радианах. 9{i\pi\omega t/180}$. Эти дополнительные факторы вступят в силу, когда вы будете брать производные или выполнять интегралы, а также решать любые дифференциальные уравнения, поэтому вскоре я буду на коленях умолять вернуть радианы.

Но, если вы не находитесь в классе, где инструктор требует, чтобы вы использовали радианы в секунду (и не поймите меня неправильно — если бы вы были в моем классе, я бы сделал это требованием), тогда вы’ Вы вольны сделать свою жизнь настолько неудобной, насколько захотите.

$\endgroup$

4

$\begingroup$

Радиан — стандартная единица измерения угла.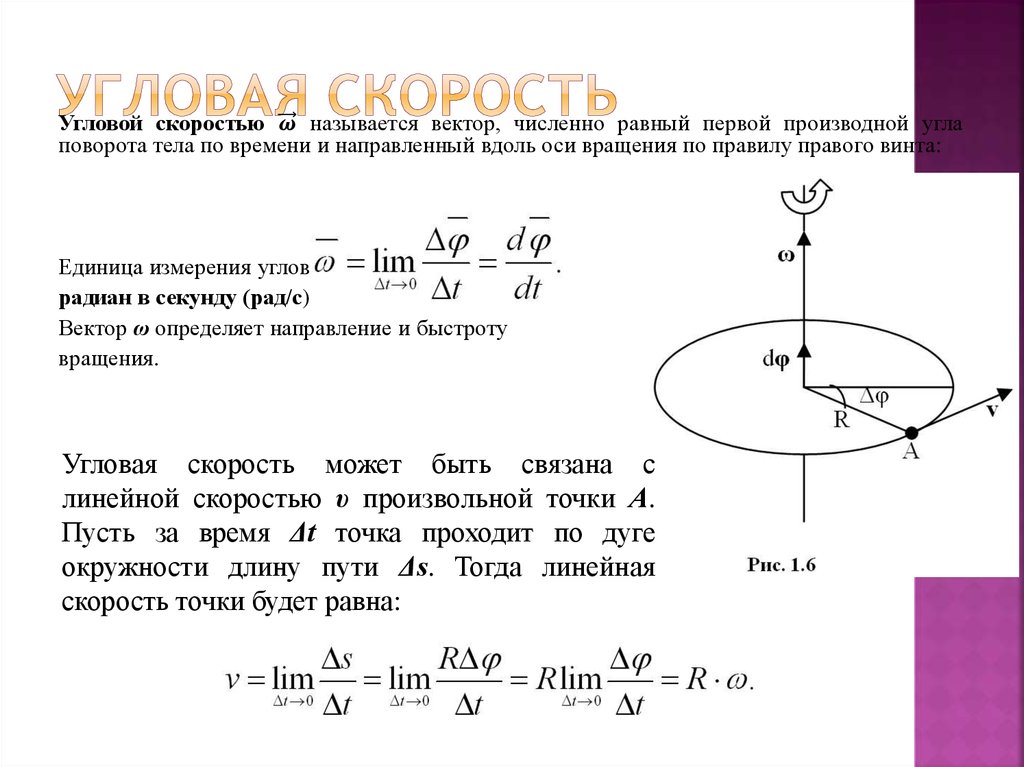 Угловая скорость — это просто угол, на который проходит частица или тело в единицу времени. Вы можете задать ему любую разумную единицу, которая, очевидно, должна обозначать угол, пройденный за единицу времени. Поэтому вы можете использовать единицу измерения $град/с$.

Единица измерения $рад/с$ обычно используется, потому что это единица СИ, а соотношение типа $v=\omega r$ выводится для угловой скорости в $рад/с$.

$\endgroup$

$\begingroup$

Вы можете писать угловую скорость как угодно, если это имеет смысл и вы указываете единицы измерения. Вы можете свободно записывать это как градусы в секунду, обороты в час или что-то в этом роде. Причина, по которой ω выражается в рад/сек, заключается в том, что с ним гораздо проще проводить дифференцирование и интегрирование (находить угловое ускорение или угловое смещение). Дифференциация треугольников с единицами измерения, отличными от радианов, не будет работать.