С знак – Знак копирайта — Википедия

Содержание

Знак копирайта — Википедия

Материал из Википедии — свободной энциклопедии

Знак копирайта
©
Изображение

	copyright sign
Юникод	U+00A9
HTML-код	или
UTF-16	0xA9
	%C2%A9
Мнемоника	`©`

Знак охраны авторского права используется с именем физического или юридического лица, которому принадлежат авторские права. Также может быть указан объект защиты авторского права. Указывается год публикации или диапазон дат.

В русской типографике употребление символа регулируется ГОСТ Р 7.0.1—2003^[1].

Бернская конвенция[править | править код]

Отсутствие знака не означает, что произведение не защищено авторскими правами, так как согласно Бернской конвенции, авторское право возникает в момент создания произведения, и для защиты авторских прав не требуется регистрация произведения или соблюдение каких-либо иных формальностей.

Знак охраны авторского права не создаёт дополнительных прав. Он только уведомляет, что авторские права принадлежат указанному физическому или юридическому лицу.

Всемирная конвенция об авторском праве[править | править код]

В странах, присоединившихся только к Всемирной конвенции об авторском праве, наличие знака является определяющим для предоставления защиты авторских прав, в соответствии с п. 1 ст. III указанной конвенции в редакции 24 июля 1971 года.

Знак копилефта
🄯
Изображение

	copyleft symbol
Юникод	U+1F12F
HTML-код	или
UTF-16	0x1F12F
	%F0%9F%84%AF

Знак Share-alike

По причине отсутствия символа в Юникоде его невозможно вывести в совместимых со стандартом компьютерных шрифтах; в отдельных случаях вместо него могут быть использованы схожие по начертанию графемы.

Знак общественного достояния

По причине отсутствия символа в Юникоде его невозможно вывести в совместимых со стандартом компьютерных шрифтах; в отдельных случаях вместо него могут быть использованы схожие по начертанию графемы.

Перевёрнутый вокруг вертикальной оси знак охраны авторского права является символом копилефта. В отличие от символа авторского права, символ копилефта не имеет юридического значения.

Символ копилефта с наконечником стрелки в верхнем конце буквы C используется в качестве символа лицензий Share-alike проекта Creative Commons.

Перечёркнутый обратной косой чертой символ копирайта обозначает, что произведение не защищено никаким известным авторским правом^[2] и поэтому находится в общественном достоянии. Данный символ также был разработан Creative Commons^[3]^[4].

Символ копирайта включён в стандарт Юникод начиная с самой первой версии во втором по счёту блоке Дополнение к латинице — 1 (англ. Latin-1 Supplement) под шестнадцатеричным кодом U+00A9 и называется copyright sign. В HTML символ может быть набран с помощью мнемоники ©

. Отдельно от символа копирайта в блоке Обрамлённые буквы и цифры (англ. Enclosed Alphanumerics) Юникода присутствует схожий символ «C в круге» Ⓒ, который, однако, предназначен для использования в качестве маркера списка.

Символ копилефта отсутствовал в Юникоде до версии 11.0, вышедшей в июне 2018 года, в которой символ был добавлен в блок Дополнение к обрамлённым буквам и цифрам (англ. Enclosed Alphanumeric Supplement) под кодом U+1F12F и названием copyleft symbol.

Символы Share-alike и общественного достояния по состоянию на версию 12.1 не включены в стандарт, хотя подана заявка на их включение^[5].

Ввод с клавиатуры[править | править код]

В операционной системе Microsoft Windows, чтобы напечатать знак на клавиатуре, нужно ввести комбинацию Alt+0169. Этот символ также включён в типографскую раскладку Ильи Бирмана, где для его набора надо нажать AltGr+c. Однако есть более простой способ напечатать знак: перевести на печать латиницей, далее печатать: левая скобка, «с», правая скобка, пробел. Символ появится автоматически после нажатия клавиши пробела.

В операционной системе Mac OS X, чтобы напечатать знак на клавиатуре, нужно ввести комбинацию ⌥ Option+G.

В X Window System (Linux), чтобы напечатать знак на клавиатуре, нужно ввести комбинацию Compose+o+c.

ru.wikipedia.org

7 известных символов, о значении которых мы и не догадывались

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Каждый день мы видим тысячи знаков и обозначений. А некоторые из них даже используем для выражения самых сильных чувств, когда не можем подобрать слова. Но задумывались ли вы, откуда они возникли? И правильно ли вообще мы их используем?

AdMe.ru решил подробно в этом разобраться и собрал для вас 7 самых известных символов, о значении и происхождении которых известно далеко не каждому.

Амперсанд (знак &)

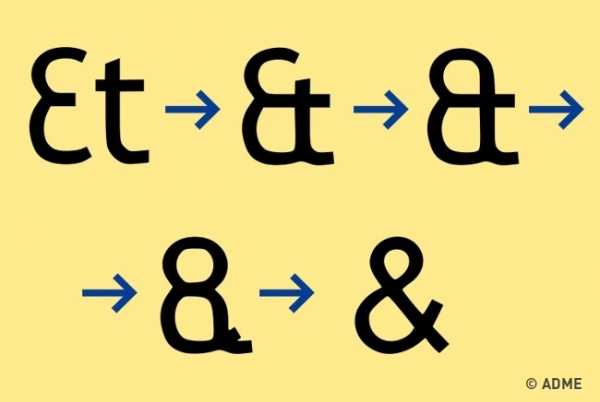
Знак амперсанд (&) обозначает латинский союз et (или английский and), то есть «и». Такую лигатуру придумали еще в Древнем Риме. Тирон, который был личным секретарем Цицерона, изобрел свою систему сокращений для ускорения письма, называемую «тироновскими знаками».

Впоследствии этот знак настолько прижился в Европе и Америке, что долгое время стоял на последнем месте в английском алфавите, а пропадать начал только к началу ХХ века. Само слово «амперсанд» — это сокращение фразы And per se and. Когда детям произносили буквы алфавита, то после z учитель говорил: Аnd per se and — «И само по себе «и». Перед буквой, совпадающей по произношению со словом, говорили per se («сама по себе», «как таковая»).

Со временем от букв et форма символа изменилась до такой степени, что возник такой знак.

Сердце

А вот тут все сложнее. Несмотря на то что «любовь живет в сердце», все знают, что с настоящим сердцем у символа сердечка не так уж много общего. Но существует несколько гипотез о его происхождении.

Пара лебедей, подплывающих навстречу друг другу, в момент касания образует форму сердца. В культурах многих народов эти птицы являются символом любви, верности и преданности, так как сформированная пара остается вместе на всю жизнь.
Другая гипотеза говорит, что изначально знак был символом женского начала. Сам он изображает форму женского таза. Древние греки даже построили специальный храм

www.adme.ru

Таблица математических символов — Википедия

Символ (TeX) (Команда (TeX))	Символ (Юникод)	Название	Значение	Пример
		Произношение
		Раздел математики
⇒{\displaystyle \Rightarrow } (\Rightarrow) →{\displaystyle \rightarrow } (\rightarrow) ⊃{\displaystyle \supset } (\supset)	⇒ → ⊃	Импликация, следование	A⇒B{\displaystyle A\Rightarrow B} означает «если A{\displaystyle A} верно, то B{\displaystyle B} также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже. ) (⊃ может использоваться вместо ⇒ или для обозначения надмножества, см. ниже.).	x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4} верно, но x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2} неверно (так как x=−2{\displaystyle x=-2} также является решением).
		«влечёт» или «если…, то» или «отсюда следует»
		везде
⇔{\displaystyle \Leftrightarrow } (\Leftrightarrow)	⇔	Равносильность	A⇔B{\displaystyle A\Leftrightarrow B} означает «A{\displaystyle A} верно тогда и только тогда, когда B{\displaystyle B} верно».	x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y}
		«если и только если» или «равносильно»
		везде
∧{\displaystyle \wedge } (\wedge)	∧	Конъюнкция	A∧B{\displaystyle A\wedge B} истинно тогда и только тогда, когда A{\displaystyle A} и B{\displaystyle B} оба истинны.	(n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, если n{\displaystyle n} — натуральное число.
		«и»
		Математическая логика
∨{\displaystyle \vee } (\vee)	∨	Дизъюнкция	A∨B{\displaystyle A\vee B} истинно, когда хотя бы одно из условий A{\displaystyle A} и B{\displaystyle B} истинно.	(n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, если n{\displaystyle n} — натуральное число.
		«или»
		Математическая логика
¬{\displaystyle \neg } (\neg)	¬	Отрицание	¬A{\displaystyle \neg A} истинно тогда и только тогда, когда ложно A{\displaystyle A}.	¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)}
		«не»
		Математическая логика
∀{\displaystyle \forall } (\forall)	∀	Квантор всеобщности	∀x,P(x){\displaystyle \forall x,P\left(x\right)} обозначает «P(x){\displaystyle P\left(x\right)} верно для всех x{\displaystyle x}».	∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n}
		«Для любых», «Для всех», «Для всякого»
		Математическая логика
∃{\displaystyle \exists } (\exists)	∃	Квантор существования	∃x,P(x){\displaystyle \exists x,\;P\left(x\right)} означает «существует хотя бы один x{\displaystyle x} такой, что верно P(x){\displaystyle P\left(x\right)}»	∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (подходит число 5)
		«существует»
		Математическая логика
={\displaystyle =}	=	Равенство	x=y{\displaystyle x=y} обозначает «x{\displaystyle x} и y{\displaystyle y} обозначают одно и то же значение».	1 + 2 = 6 − 3
		«равно»
		везде
:={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } (:\Leftrightarrow) =def{\displaystyle {\stackrel {\rm {def}}{=}}} (\stackrel{\rm{def}}{=})	:= :⇔	Определение	x:=y{\displaystyle x:=y} означает «x{\displaystyle x} по определению равен y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означает «P{\displaystyle P} по определению равносильно Q{\displaystyle Q}»	ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}\left(x\right):={1 \over 2}\left(e^{x}+e^{-x}\right)} (определение гиперболического косинуса) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (определение исключающего «ИЛИ»)
		«равно/равносильно по определению»
		везде
{,}{\displaystyle \{,\}}	{ }	Множество элементов	{a,b,c}{\displaystyle \{a,\;b,\;c\}} означает множество, элементами которого являются a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}.	N={1,2,…}{\displaystyle \mathbb {N} =\{1,\;2,\;\ldots \}} (множество натуральных чисел)
		«Множество…»
		Теория множеств
{\|}{\displaystyle \{\|\}}	{\|}	Множество элементов, удовлетворяющих условию	{x\|P(x)}{\displaystyle \{x\,\|\,P\left(x\right)\}} означает множество всех x{\displaystyle x} таких, что верно P(x){\displaystyle P\left(x\right)}.	{n∈N\|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,\|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}}
		«Множество всех… таких, что верно…»
		Теория множеств
∅{\displaystyle \varnothing } (\varnothing) {}{\displaystyle \{\}}	∅ {}	Пустое множество	{}{\displaystyle \{\}} и ∅{\displaystyle \varnothing } означают множество, не содержащее ни одного элемента.	{n∈N\|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,\|\,1<n^{2}<4\}=\varnothing }
		«Пустое множество»
		Теория множеств
∈{\displaystyle \in } (\in) ∉{\displaystyle \notin } (\notin)	∈ ∉	Принадлежность/непринадлежность к множеству	a∈S{\displaystyle a\in S} означает «a{\displaystyle a} является элементом множества S{\displaystyle S}» a∉S{\displaystyle a\notin S} означает «a{\displaystyle a} не является элементом множества S{\displaystyle S}»	2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} }
		«принадлежит», «из» «не принадлежит»
		Теория множеств
⊆{\displaystyle \subseteq } (\subseteq) ⊂{\displaystyle \subset } (\subset)	⊆ ⊂	Подмножество	A⊆B{\displaystyle A\subseteq B} означает «каждый элемент из A{\displaystyle A} также является элементом из B{\displaystyle B}». A⊂B{\displaystyle A\subset B} обычно означает то же, что и A⊆B{\displaystyle A\subseteq B}. Однако некоторые авторы используют ⊂{\displaystyle \subset }, чтобы показать строгое включение (то есть ⊊{\displaystyle \subsetneq }).	(A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} }
		«является подмножеством», «включено в»
		Теория множеств
⊇{\displaystyle \supseteq } (\supseteq) ⊃{\displaystyle \supset } (\supset)	⊇ ⊃	Надмножество	A⊇B{\displaystyle A\supseteq B} означает «каждый элемент из B{\displaystyle B} также является элементом из A{\displaystyle A}». A⊃B{\displaystyle A\supset B} обычно означает то же, что и A⊇B{\displaystyle A\supseteq B}. Однако некоторые авторы используют ⊃{\displaystyle \supset }, чтобы показать строгое включение (то есть ⊋{\displaystyle \supsetneq }).	(A∪B)⊇A{\displaystyle (A\cup B)\supseteq A} R⊇Q{\displaystyle \mathbb {R} \supseteq \mathbb {Q} }
		«является надмножеством», «включает в себя»
		Теория множеств
⊊{\displaystyle \subsetneq } (\subsetneq)	⊊	Собственное подмножество	A⊊B{\displaystyle A\subsetneq B} означает A⊆B{\displaystyle A\subseteq B} и A≠B{\displaystyle A\neq B}.	N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} }
		«является собственным подмножеством», «строго включается в»
		Теория множеств
⊋{\displaystyle \supsetneq } (\supsetneq)	⊋	Собственное надмножество	A⊋B{\displaystyle A\supsetneq B} означает A⊇B{\displaystyle A\supseteq B} и A≠B{\displaystyle A\neq B}.	Q⊋N{\displaystyle \mathbb {Q} \supsetneq \mathbb {N} }
		«является собственным надмножеством», «строго включает в себя»
		Теория множеств
∪{\displaystyle \cup } (\cup)	∪	Объединение	A∪B{\displaystyle A\cup B} означает множество, содержащее все элементы из A{\displaystyle A} и B{\displaystyle B}

ru.wikipedia.org

как набрать с клавиатуры.

Копирайт или цитирование.

…

инструкция:

1. Нажмите и удерживайте Alt
2. С правой (!) стороны клавиатуры (боковая цифровая клавиатура) наберите четыре цифры — 0169
3. Отпустите Alt
4. Появится ©
…
Не формально, а по жизни —
пишущие в социальных сетях используют (с) после фразы, взятой в кавычки, указывая этим, что текст является цитатой, кого-то: «… не помню кого.»
…
/ PhDrDAK

Бонус:
[советую набирать при Eng установки клавиатуры]

Нажимаете и удерживаете Alt
и сбоку на цифровой клавиатуре набирайте —

0128 — — евро €
0133 — — многоточие … (как один знак,а не как три точки)
0146 — — апостроф ’
0149 — — жирная точка •
0153 — — символ товарного знака ™
0163 — — фунт £
0165 — — йена ¥
0167 — — параграф §
0169 — — знак копирайта ©
0174 — — символ зарегистрированного товарного знака ®
0176 — — знак градуса °
0177 — — плюс\минус ±

— это обычный способ ввода ASCII символов с клавиатуры!

/ PhDrDAK, 2015

P.S.   Знак копирайт на айфоне
Совет — иные способы я считаю более сложными.
Итак:
Скопируйте отсюда копирайт ©
Далее зайдите в Настройки > Основные > Клавиатура > Сокращения
> нажмите +
> и добавьте:
Фраза — ©
Сокращение — (с) (или сами придумайте)
ВАЖНО:

Необходимо писать не в «сокращение» (с), а в «фразу» ©. Не запутайтесь.

P.S.S.
Можно облегчить себе жизнь,
вместо того. чтобы цифры 4 раза нажимать —

нажмите
Ctrl и Alt одновременно и справа Стрелочка вправо [рядом с 0]
…
С Приветом!
phdrdak.blogspot.com
О ©, ™, ® и (ↄ) в этих ваших интернетах.
Здравствуйте девуши и юношки! Не похоже на меня, но все же решил написать познавательную статейку. Статейка данная о таких известных и часто используемых знаках как (с),™, (R) и чуть мене известный (ↄ).
Многие интернет-обыватели очень любят ставить эти знаки после, допустим, своего имени (тм, например, или (R)), или после какой-нибудь невьбнно умной цитаты ((с)), но, как выяснилось, не многие знают что же данные знаки означают. Ниже хочу немного прояснить ситуацию и поделиться кое какой инфой о них (возможно где-то я не прав, и что-то упустил… простите — человек я, грешен и местами глуп).
Итак, начнем со Знака охраны авторских прав — (с) (латинская буква «с» от английского «copyright» — т.е. «авторское право», если по российски). Что же означает данный символ, и для чего гномеки живущие во вконтактике ставят его в конце цитат, стихов и прочих продуктов ментального онанизма? А ставят они его для того, что бы указать на то, что это копипаста (мопед не мой…), а в ответ на вопрос: «почему именно Знак охраны авторского права?» ссылаются на Лурк.

Великий Лурк гласит:
«(c), а также (ц); клеймо, которое ставят на контенте, неумело подражая копирастскому символу ©; объекту утреннего фапа Тёмы (имеется ввиду теплое и нежное отношение к закону об авторском праве многих издателей и «творителей», а в частности намекают на Артемия Лебедева). Самостоятельно
на форумах и в прочих интернетах применяется для выделения и подчеркивания некоей общеизвестной цитаты. Обычно предполагается, что и аффтар цитаты также широко известен, и поэтому не указывается, а сама цитата служит аргументом...»
«Иногда после © автор пишет своё имя или ник, какбе пытаясь сказать нам, что он имеет мозг и даже умеет печатать.«
То есть (с) здесь означает то, что текст, под которым ставится данная закорючка, является копией, и разместивший ее человек не автор текста. Здесь так принято, да… и это довольно забавно, так как изначально (с) был (да, собственно и до сих пор считается таковым в некоторых кругах) символом обозначающим заявление об авторстве текста (или иного продукта умственного труда).
Цитата из Вики:
«Знак охраны авторского права используется с именем физического или юридического лица, которому принадлежат авторские права.«
Цитата не из Вики:
«Значок необходим для того,чтобы показать ваше исключительное право на произведение, на недоступность свободного копирования третьими лицами. Значок © рекомендуется ставить внизу сайта или после каждого поста в блоге.«
«…Знак охраны авторского права действует только в том случае, если вместе с ним указано имя физического или юридического лица, которому принадлежит право на опубликованный материал.»
Таким образом, Паша Барсуков пишет себе на стеночку в ВК: «ДАО, которое может быть выражено словами, не есть постоянное дао. (с)» таким образом заявляя свои авторские права на цитату из Дао Де Цзин и запрещает его копирование третьими лицами о_О. Другое дело когда текст размещает некто Хрен
Хренов, так как скорее всего это все же ник, а не имя физического лица (впрочем, бывает нам и не так не везет с именами) и потому данный знак силы не имеет и может расцениваться как пресловутое обозначение копипасты.
Итак (с) ставится одними для обозначения копипасты (откуда это пошло для меня загадка) и это является скорее мемом, нежели является заявлением об авторском праве (т.е. совершенно противопложенно по смыслу).
Далее у нас идут «™» и «(R)», которые многим нравится ставить возле своего имени. Тут все гораздо проще для меня, ибо про данные модные значки хорошо написано на Лурке.
Цитата:
«™ (англ. Trade Mark, рус. торговая марка) — знак. Чем-то напоминает ©, используется после названия какого-нибудь продукта, чтобы подчеркнуть,
что это название зарегистрировано и использовать его нельзя. В этой России знак ™ не значит совсем ничего, вообще. По закону использовать можно знак ®, слова «товарный знак» или «зарегистрированный товарный знак».
То есть если вы хотите придать своему имени, лицу, левой руке или иной части тела статус товарного знака, который без вашего согласия ни кто не может использовать, клеить на майки, рисовать в подъездах и на иконах, но при этом вы сами сможете его продавать, сдавать в аренду, и всячески выблядываться то ставьте (R). Единственный нюанс: знак (R) не будет иметь ни какой силы (кроме придания некого смыслового оттенка объекту к которому он прилагается, конечно же (о смыслах в статье с лурка)) если его не зарегистрировать в соответствующих органах. Знак ™, как мы выяснили, в России вообще ни какой силы не имеет в принципе. Такие дела.
Ну, и о известном в меньшей степени (ↄ) (видимо потому как символ «(ↄ)» ввести немного сложнее нежели «©» так как он не доступен в юникоде, что обьясняется конспиративной теорией как «из-за не любви к этому знаку информационных корпораций и издателей (пояснение ниже)»). Ртом произносится данный знак как «копилефт» (copyleft — игра слов… copyleft, copyright — понятненько, да?).
Знак (ↄ) в противоположенность (с) не запрещает использовать продукт умственного труда без ведома автора, а наоборот — запрещает коммерческое использование оного и всяческое ограничение его (и его модификаций, продуктов созданных на его базе) распространения кому бы то ни было. История знака довольно интересна, и как бы намекает о том, почему же этот знак не так любят в интернетах. Концепция копилефта зародилась в начале 80-х прошлого века. Автором ее считается Ричард Столлман (хотя есть мнение, что ее автором мог быть и наш соотечественник — Евгений Леонидович Косарев — ведущий научный сотрудник НИИ имени Капицы (тогда), так как в то же самое время им была озвучена концепция подобная Столпановской). Концепция эта была разработана применительно к программному обеспечению и ставя перед собой задачу свободного распространения ПО для ускорения научных процессов в обществе и поддержания чистоты исследований от коммерческих целей один из ее пунктов гласил о том, что не только ПО предназначенное для свободного распространения (и соответственно заверенная знаком (ↄ) ) должно распространяться бесплатно, но и программы созданные на ее основе, ее модификации и апгрейды так же должны распространяться свободно и никто не имеет права ограничивать к ним доступ. Понятно, что данная концепция не была поддержана информационными гигантами, да и вообще всеми теми, кто зарабатывает на ограничении доступа к информации (или же на предоставлении оного). И уж тем более, не особо были рады таким мыслям те, кто любит заниматься продажей плагиата, обходя закон об авторском
праве с помощью различных уловок.
Конечно, концепция копилефта была разработана для ПО, и применяется (спорно, полулегально ибо далеко не всегда признается (а если и признается, то
понимается всеми по разному), не имеет юридической силы) к ПО, но мой извращенный ум умудряется применить ее и к данному тексту, ибо я, как автор, не желаю ограничивать доступ к нему каким либо способом, и считаю его достоянием всех людей. Ставя в окончании текста (ↄ) я заявляю о том, что как автор разрешаю его свободное распространение, и запрещаю какое либо ограничение доступа к нему (хоть он и даром ни кому не нужен, но тем не менее фишечка мне нравится, да знак напоминает энсо, что не может меня не радовать;)).
Текст мой говно — оно и ясно, но тем не менее здесь я попытался объяснить кое-какие моменты по некоторым часто применяемым в интернет-среде знакам. Надеюсь, юзер, я чем-то помог тебе, а возможно, даже обогатил твой багаж знаний и внес маленький вклад в твою ориентацию
(вот так и приходит на ум всякое непотребство какое ныне связывают с этим словом, однако я имею в виду не сэксуальную ориентацию) по этому миру.
Для тех кто любит вышеописанные значки: ©, ™, ®, (ↄ).
Данный текст написан во благо всех живых существ. ОМ, ребята!
(ↄ) Лука Криворуков
dzen-rusist.livejournal.com
ЗНАК — это… Что такое ЗНАК?
знак — знак, а … Русский орфографический словарь
знак — знак/ … Морфемно-орфографический словарь
ЗНАК —         материальный предмет (явление, событие), выступающий в качестве представителя некоторого др. предмета, свойства или отношения и используемый для приобретения, хранения, переработки и передачи сообщений (информации, знаний). Различают… … Философская энциклопедия
знак — сущ., м., употр. очень часто Морфология: (нет) чего? знака, чему? знаку, (вижу) что? знак, чем? знаком, о чём? о знаке; мн. что? знаки, (нет) чего? знаков, чему? знакам, (вижу) что? знаки, чем? знаками, о чём? о знаках 1. Знаком называется… … Толковый словарь Дмитриева
% (знак) — % % знак, чаще всего обозначающий проценты. Происхождение обозначения … Википедия
знак — Признак, примета, отличие; значок, мета (метка), отметка, клеймо, печать, штемпель, тавро, тамга; буква, цифра, черточка; знамение, предзнаменование, предвестие, предвестник, сигнал, симптом; девиз, пароль, лозунг, символ, эмблема, вензель, герб … Словарь синонимов
ЗНАК —         материальный объект (артефакт), выступающий в коммуникативном или трансляционном процессе аналогом другого объекта (предмета, свойства, явления, понятия, действия), замещающий его. 3. является осн. средством культуры, с его помощью… … Энциклопедия культурологии
ЗНАК — муж. признак, примета, отличие; предзнаменование; предвестие; чувственое доказательство, свидетельство; чувственое изъявление, обнаружение чего либо. Знак таможни, клеймо. отличия, орден. от раны, рубец. Подать знак рукой, шапкой, помаячить. Знак … Толковый словарь Даля
знак — предмет (явление), служащий представителем другого предмета, явления, процесса. Наука о З. семиотика, возникшая во второй половине XIX начале ХХ в., связанная с именами Ч. Пирса, Ч. Морриса, Ф. де Соссюра, Г. Фреге, Р. Карнапа и др. и традиционно … Большая психологическая энциклопедия
ЗНАК — ЗНАК, а, муж. 1. Пометка, изображение, предмет, к рыми отмечается, обозначается что н. Условный з. Дорожные знаки (на автомобильных дорогах, на улицах: информирующие об особенностях дороги, о правилах движения). Товарный з. (на товаре, изделии,… … Толковый словарь Ожегова
dic.academic.ru
Таблица математических символов — это… Что такое Таблица математических символов?
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования.
Кроме указанных символов, иногда используются их зеркальные отражения, например, обозначает то же, что и
Знаки операций или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.
Символ (TeX) Символ (Unicode) Название Значение Пример
Произношение
Раздел математики
⇒
→
⊃
Импликация, следование означает «если верно, то также верно».
(→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.)
(⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). верно, но неверно (так как также является решением).
«влечёт» или «если…, то»
везде
⇔ Равносильность означает « верно тогда и только тогда, когда верно».
«если и только если» или «равносильно»
везде
∧ Конъюнкция истинно тогда и только тогда, когда и оба истинны. , если — натуральное число.
«и»
Математическая логика
∨ Дизъюнкция истинно, когда хотя бы одно из условий и истинно. , если — натуральное число.
«или»
Математическая логика
¬ Отрицание истинно тогда и только тогда, когда ложно .
«не»
Математическая логика
∀ Квантор всеобщности обозначает « верно для всех ».
«Для любых», «Для всех»
Математическая логика
∃ Квантор существования означает «существует хотя бы один такой, что верно » (подходит число 5)
«существует»
Математическая логика
= Равенство обозначает « и обозначают одно и то же значение». 1 + 2 = 6 − 3
«равно»
везде
:=
:⇔
Определение означает « по определению равен ».
означает « по определению равносильно » (Гиперболический косинус)
(Исключающее или)
«равно/равносильно по определению»
везде
{ , } Множество элементов означает множество, элементами которого являются , и . (множество натуральных чисел)
«Множество…»
Теория множеств
{ | }
{ : }
Множество элементов, удовлетворяющих условию означает множество всех таких, что верно .
«Множество всех… таких, что верно…»
Теория множеств
∅
{}
Пустое множество и означают множество, не содержащее ни одного элемента.
«Пустое множество»
Теория множеств
∈
∉
Принадлежность/непринадлежность к множеству означает « является элементом множества »
означает « не является элементом множества »
«принадлежит», «из»
«не принадлежит»
Теория множеств
⊆
⊂
Подмножество означает «каждый элемент из также является элементом из ».
обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
«является подмножеством», «включено в»
Теория множеств
⊇
⊃
Надмножество означает «каждый элемент из также является элементом из ».
обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
«является надмножеством», «включает в себя»
Теория множеств
⊊ Собственное подмножество означает и .
«является собственным подмножеством», «строго включается в»
Теория множеств
⊋ Собственное надмножество означает и .
«является собственным надмножеством», «строго включает в себя»
Теория множеств
∪ Объединение означает множество элементов, принадлежащих или (или обоим сразу).
«Объединение … и …», «…, объединённое с …»
Теория множеств
⋂ Пересечение означает множество элементов, принадлежащих и , и .
«Пересечение … и … », «…, пересечённое с …»
Теория множеств
\ Разность множеств означает множество элементов, принадлежащих , но не принадлежащих .
«разность … и … », «минус», «… без …»
Теория множеств
→ Функция означает функцию с областью определения и областью прибытия (областью значений) . Функция , определённая как
«из … в»,
везде
↦ Отображение означает, что образом после применения функции будет . Функцию, определённую как , можно записать так:
«отображается в»
везде
N или ℕ Натуральные числа означает множество или реже (в зависимости от ситуации).
«Эн»
Числа
Z или ℤ Целые числа означает множество
«Зед»
Числа
Q или ℚ Рациональные числа означает
«Ку»
Числа
R или ℝ Вещественные числа, или действительные числа означает множество всех пределов последовательностей из
( — комплексное число: )
«Эр»
Числа
C или ℂ Комплексные числа означает множество
«Це»
Числа
<
> Сравнение обозначает, что строго меньше .
означает, что строго больше .
«меньше чем», «больше чем»
Отношение порядка

≤ или ⩽
≥ или ⩾ Сравнение означает, что меньше или равен .
означает, что больше или равен .
«меньше или равно»; «больше или равно»
Отношение порядка
≈ Приблизительное равенство с точностью до означает, что 2,718 отличается от не больше чем на . с точностью до .
«приблизительно равно»
Числа
√ Арифметический квадратный корень означает неотрицательное действительное число, которое в квадрате даёт .
«Корень квадратный из …»
Числа
∞ Бесконечность и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел.
«Плюс/минус бесконечность»
Числа
| | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества обозначает абсолютную величину .
обозначает мощность множества и равняется, если конечно, числу элементов .
«Модуль»; «Мощность»
Числа и Теория множеств
∑ Сумма, сумма ряда означает «сумма , где принимает значения от 1 до », то есть .
означает сумму ряда, состоящего из .

«Сумма … по … от … до …»
Арифметика, Математический анализ
∏ Произведение означает «произведение для всех от 1 до », то есть
«Произведение … по … от … до …»
Арифметика
! Факториал означает «произведение всех натуральных чисел от 1 до включительно, то есть

« факториал»
Комбинаторика
∫ Интеграл означает «интеграл от до функции от по переменной ».
«Интеграл (от … до …) функции … по (или d)…»
Математический анализ
df/dx
f'(x) Производная или означает «(первая) производная функции от по переменной ».
«Производная … по …»
Математический анализ

Производная -го порядка или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ».
«-я производная … по …»
Математический анализ
dic.academic.ru

С знак – Знак копирайта — Википедия