Скорость через частоту вращения – Формула расчета частоты вращений

1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки

Видеоурок: Движение по окружности

Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки

Движение по окружности

Траектория движения — окружность.

Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.

Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое. Основные характеристики движения

1. Линейная скорость

Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.
Так как траектория движения точки — окружность, то в качестве пути в числителе находится формула длины перемещения.

Поэтому формула мгновенной скорости приобретает следующий вид, где Т — период:

2. Центростремительное ускорение

Направлено перпендикулярно к линейной скорости на протяжении всего движения.

Центростремительное ускорение определяется по формуле:

3. Период вращения

Период вращения — это величина, определяющая время, за которое тело делает одно полное вращение.

Период — это скалярная величина. Основной единицей периода является [Т]=1с.  

Период определяется по формуле:

где N — количество оборотов, t — время, за которое они были совершены.

4. Частота вращения

Определяет, насколько часто совершаются обороты в единицу времени.

Частота — скалярная величина. Измеряется в [n] = 1с^-1.

Частота определяется по формуле:

5. Угловое перемещение

Угловое перемещение — величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.

Данная величина может измеряться в градусной или радианной мере углов.

6. Угловая скорость

Это значение, которое определяет, насколько изменяется угловое перемещение со временем.

Измеряется в 1 рад/с.Определяется по формуле:
где
— угловая скорость материальной точки, 1/с
— угол поворота радиус — вектора, рад— промежуток времени, с

Угловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:

cknow.ru

Движение материальной точки по окружности. Угловая скорость и угловое ускорение и их связь с линейными характеристиками движения

Движение по окружности – частный случай криволинейного движения. Скорость тела в любой точке криволинейной траектории направлена по касательной к ней (рис.2.1). Скорость как вектор при этом может изменяться и по модулю (величине) и по направлению. Если модуль скорости

остается неизменным, то говорят оравномерном криволинейном движении.

Пусть тело движется по окружности с постоянной по величине скоростью из точки 1 в точку 2.

Рис.2.1

При этом тело пройдет путь, равный длине дуги ℓ₁₂между точками 1 и 2 за времяt. За это же времяtрадиус- векторR, проведенный из центра окружности 0 к точке, повернется на угол Δφ.

Вектор скорости в точке 2 отличается от вектора скорости в точке 1 по направлениюна величину ΔV:

;

Для характеристики изменения вектора скорости на величину δv введем ускорение :

(2.4)

Вектор в любой точке траектории направлен по радиусуRкцентруокружности перпендикулярно к вектору скоростиV₂. Поэтому ускорение, характеризующее при криволинейном движении изменение скоростипо направлению, называютцентростремительным или нормальным. Таким образом, движение точки по окружности с постоянной по модулю скоростью являетсяускоренным.

Если скорость изменяется не только по направлению, но и по модулю (величине), то кроме нормального ускорения

вводят еще икасательное (тангенциальное) ускорение, которое характеризует изменение скорости по величине: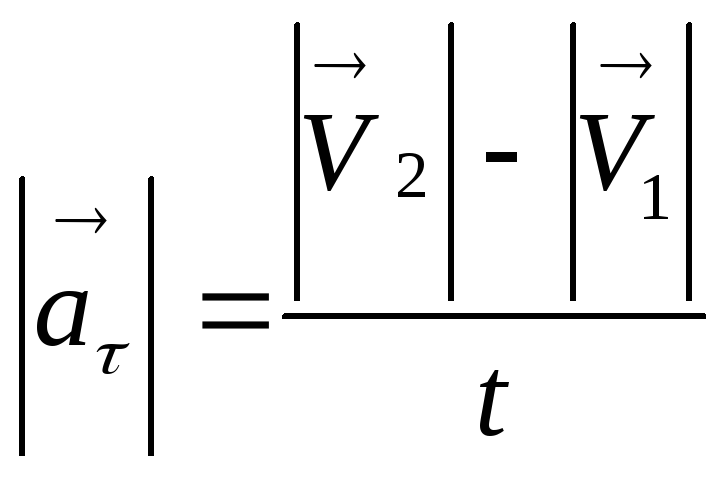

или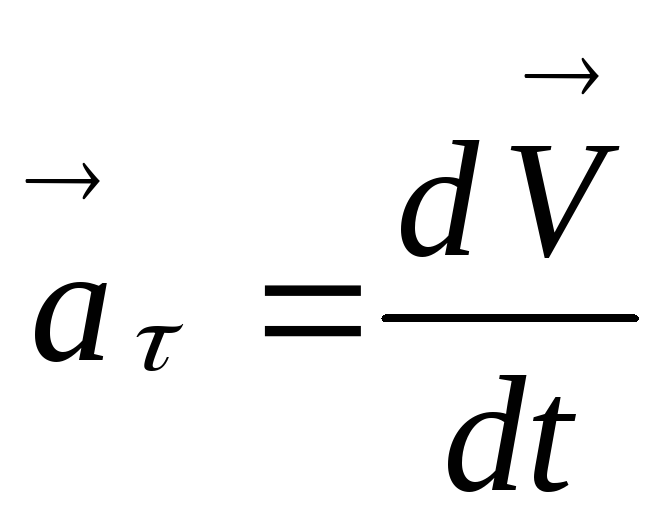

Направлен вектор по касательной в любой точке траектории (т.е. совпадает с направлением вектора). Угол между векторамии

равен 90⁰.

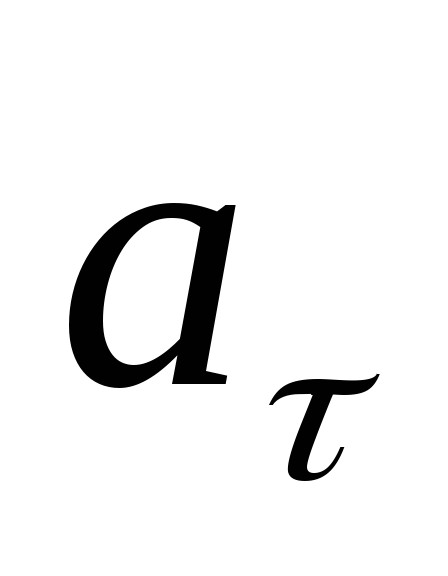
Полное ускорение точки, движущейся по криволинейной траектории, определяется как векторная сумма (рис.2.1.).

.

Модуль вектора .

Угловая скорость и угловое ускорение

При движении материальной точки по окружностирадиус-векторR, проведенный из центра окружности О к точке, поворачивается на угол Δφ (рис.2.1). Для характеристики вращения вводятся понятия угловой скорости ω и углового ускорения ε.

Угол φ можно измерять в радианах. 1 радравен углу, который опирается на дугу ℓ, равную радиусуRокружности, т.е.

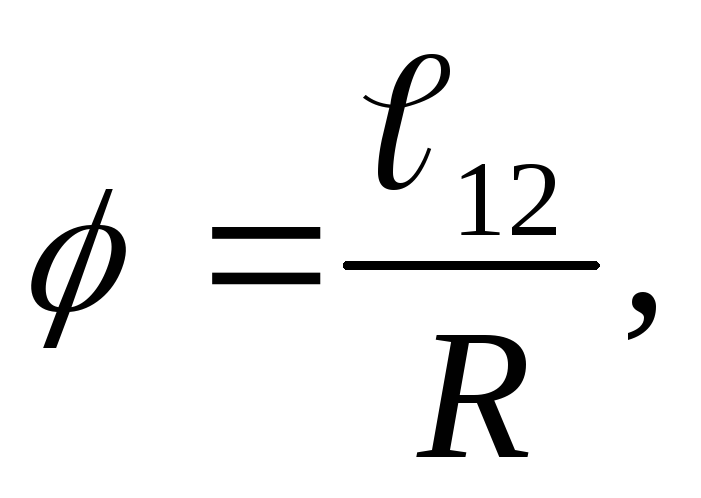или

ℓ₁₂ = Rφ(2.5.)

Продифференцируем уравнение (2.5.)

(2.6.)

Величина dℓ/dt=V_мгн. Величину ω =dφ/dtназываютугловой скоростью(измеряется в рад/с). Получим связь между линейной и угловой скоростями:

V = ωR, (2.7)

Величина ω векторная. Направление вектораопределяетсяправилом винта (буравчика): оно совпадает с направлением перемещения винта, ориентированного вдоль оси вращения точки или тела и вращаемого в направлении поворота тела (рис.2.2), т.е.

.

Рис.2.2

Угловым ускорениемназывается векторная величина производная от угловой скорости (мгновенное угловое ускорение)

, (2.8.)

Вектор совпадает с осью вращения и направлен в туже сторону, что и вектор, если вращение ускоренное, и в противоположную, если вращение замедленное.

Число оборотов n тела в единицу времени называют частотой вращения.

Время Т одного полного оборота тела называют периодом вращения. При этом R опишет угол Δφ=2π радиан

n=1/T

С учетом сказанного

, (2.9)

Уравнение (2.8) можно записать следующим образом:

(2.10)

Тогда тангенциальная составляющая ускорения

а_=R(2.11)

Нормальное ускорение а_nможно выразить следующим образом:

с учетом (2.7) и (2.9)

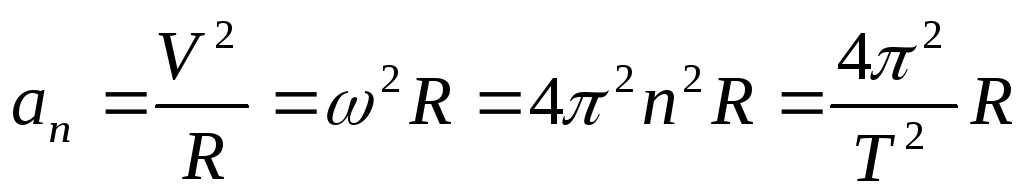(2.12)

Тогда полное ускорение .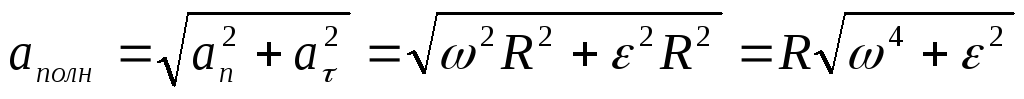

Для вращательного движения с постоянным угловым ускорением можно записать уравнение кинематики по аналогии с уравнением (2.1) – (2.3) для поступательного движения:

,

.

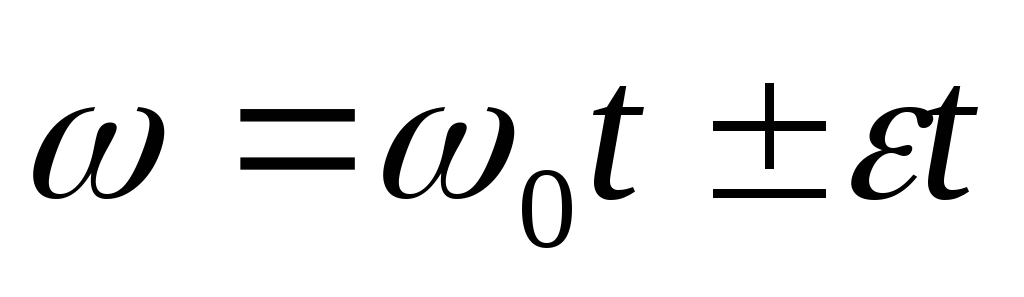studfile.net

Равномерное движение по окружности | Физика для всех

Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.

При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости Тангенциальное ускорение в этом случае отсутствует (a_r = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) a_n или а_ЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.

Модуль центростремительного ускорения равен

a_ЦС=v² / R

Где v – линейная скорость, R – радиус окружности

Рис. 1.22. Движение тела по окружности.

Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то

1 радиан= l / R

Так как длина окружности равна

l = 2πR

то

360^о = 2πR / R = 2π рад.

Следовательно

1 рад. = 57,2958^о = 57^о18’

Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:

ω = φ / t

Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:

v= l / t

Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением

l = Rφ

где R – радиус окружности.

Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:

v = l / t = Rφ / t = Rω или v = Rω

Рис. 1.23. Радиан.

Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.

n = 1 / T

За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда

T = 2π / ω

То есть угловая скорость равна

ω = 2π / T = 2πn

Центростремительное ускорение можно выразить через период Т и частоту обращения n:

a_ЦС = (4π²R) / T² = 4π²Rn²

av-mag.ru