Скорость движения формула: формула, единица измерения, как рассчитать через обороты в минуту и радиус

формула, единица измерения, как рассчитать через обороты в минуту и радиус

Что такое линейная скорость, единицы измерения

Определение

Скоростью при равномерном движении тела называют физическую величину, с помощью которой определяют путь, преодоленный телом за единицу времени.

В международной системе СИ единицей измерения линейной скорости является производная от двух основных единиц:

• метр;
• секунда.

В международной системе СИ скорость измеряется в метрах в секунду (м/с). За единицу скорости принимают скорость равномерного движения, при которой путь в один метр тело преодолеет в течение одной секунды. Кроме того, скорость можно измерять в:

• км/ч;
• км/с;
• см/с.

Связь между линейной и угловой скоростями

Скорость точки, которая совершает круговое движение, называется линейной скоростью, чтобы отделить это понятие от термина угловая скорость.

Во время вращения абсолютно твердое тело в разных точках будет обладать неодинаковыми линейными скоростями, но значение угловой скорости остается стабильным.

Источник: class-fizika.ru

Можно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет:

2πR

Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:

\(v=\frac{2\pi R}{T}=2\pi RV\)

Зная, что:

\(\omega =2\pi V\)

получим справедливое равенство:

\(v=\omega R\)

Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения. К примеру, точки, которые движутся по земному экватору v=463 м/с, а точки, расположенные на широте города Санкт-Петербург, движутся со скоростью v=233 м/с. При нахождении на полюсах планеты скорость уменьшается до v=0.

{2}R\)

Таким образом, рассматривают пару простейших движений, характерных для абсолютно твердого тела, включая поступательное и вращательное. При этом стоит отметить, что определить любое сложное движение, которое совершает абсолютно твердое тело, можно с помощью суммы двух независимых движений:

• поступательное;
• вращательное.

С помощью закона независимости движений описывают сложное движение абсолютно твердого тела.

Формулы для нахождения линейной скорости

Тело движется равномерно тогда, когда его скорость характеризуется постоянной величиной. Формула для расчета скорости такого движения будет иметь следующий вид:

V = st

где s является пройденным путем, то есть длиной линии;

t представляет собой время, в течение которого тело преодолевало указанный путь.

Определение

Линейной скоростью V называют физическую величину, которая демонстрирует путь, пройденный телом в течение определенного времени.

Основной формулой для определения линейной скорости является следующее равенство:

V = St

где S является путем,

t обозначает время, в течение которого тело преодолело путь S.

Иной вариант уравнения имеет такой вид:

V = lt

где l является путем,

t обозначает время, в течение которого тело преодолело дугу l.

В некоторых научных источниках скорость обозначают с помощью маленькой буквы v. Другим уравнением для расчета линейной скорости является равенство:

\(v=2\pi RT\)

В данном случае 2π представляет собой полную окружность и составляет 360 угловых градусов. Вектор скорости направлен по касательной к траектории движении тела.

Модуль скорости

Числовое значение скорости может быть разным в зависимости от выбранной единицы измерения. Кроме числового значения, скорость характеризуется направлением. Числовое значение, которым обладает скорость, в физике называют ее модулем. {2}}{R}\)

\(v=\sqrt{aR}=\sqrt{40\times 3}=10.9\) м/с

Ответ: линейная скорость равна 10,9 м/с.

Задача №2

Поезд совершает равномерное движение. В течение 4 часов он преодолевает путь в 219 километров. Требуется рассчитать скорость движения поезда.

Решение:

Исходя из основной формулы для расчета линейной скорости, получим:

\(v=\frac{S}{t}=\frac{219}{4}=54.75\) км/ч

Ответ: скорость движения поезда составит 54.75 км/ч или 15.2 м/с.

Задача №3

Транспортное средство, работая на двигателе внутреннего сгорания, в течение 2,5 часов преодолевает расстояние в 213 километров. Требуется определить скорость движения транспорта.

Решение:

С помощью уравнения расчета скорости можно записать решение задачи:

\(v=\frac{S}{t}=\frac{213}{2,5}=85.2\) км/ч

Ответ: Скорость движение транспортного средства составляет 85.2 км/ч или 23.7 м/с.

Формула путь без времени и как ее выводить

Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.

Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).

Рис.1. Так выглядит формула, по которой можно вычислить путь тела, не зная, сколько времени занимало движение

Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.

Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.

Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.

Выводим формулу пути без времени

Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.

В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону). {2}} \right)\) – ускорение тела;

\( \large S \left( \text{м} \right)\) – путь, пройденный телом;

\(\large t \left( c \right)\) – время, за которое тело прошло этот путь.

В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.

Что сделать, чтобы получить формулу пути, в которой отсутствует время:

• сначала получить выражение для времени t из уравнения для скорости;
•  затем в формулу пути подставить полученное выражение вместо времени t.

Выражаем время из формулы для скорости

Выпишем формулу, связывающую начальную и конечную скорость тела:

\[ \large v  = v_{0} + a \cdot t \]

Избавимся в правой части от начальной скорости, обозначенной символом \( v_{0}\). Для этого из обеих частей уравнения вычтем число \( v_{0}\). Получим такую запись:

\[ \large v — v_{0} = a \cdot t \]

Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». {2}\]

Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.

Упрощаем выражение, расположенное до знака «плюс» в правой части

Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:

\[\large v_{0} \cdot \frac{ v — v_{0}}{a} \]

Умножим числитель дроби на число \(v_{0}\).

Для этого:

• сначала числитель обособим скобками;
• затем запишем число \(v_{0}\) перед скобками;
• а потом внесем это число внутрь скобок.

В числитель дроби, обособленный с помощью скобок помещаем число \(v_{0}\):

\[\large v_{0} \cdot \frac{ (v — v_{0})}{a} = \frac{ v_{0} \cdot (v — v_{0})}{a} \]

Теперь необходимо умножить скобку на число \(v_{0}\).  На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.

Рис. 2. Чтобы умножить скобку на число, нужно умножить каждое слагаемое в скобке на это число

Нужно к каждой скорости в скобках дописать число \(v_{0}\), умножая его на эти скорости. {2}}{2a} }\]

Скорость в физике — это… Формула скорости

Эта тема будет полезна не только учащимся средней школы, но даже взрослым. Кроме того, статья будет интересна родителям, желающим объяснить своим детям простые вещи из естественных наук. Среди очень важных тем – это скорость в физике.

Довольно часто ученики не могут разобраться в решении задач, отличить имеющиеся виды скоростей, а еще сложнее понять научные определения. Здесь мы рассмотрим все на более доступном языке, чтобы было не только все ясно, но даже интересно. А вот запомнить некоторые вещи все же придется, так как технические науки (физика и математика) требуют заучивать наизусть формулы, единицы измерения и, конечно же, значения символов в каждой формуле.

Где встречается?

Для начала вспомним, что данная тема относится к такому разделу физики как механика, подразделу «Кинематика». Кроме того, изучение скорости на этом не заканчивается, оно будет и в последующих разделах:

• оптика,
• колебания и волны,
• термодинамика,
• квантовая физика и так далее.

Также понятие скорость встречается в химии, биологии, географии, информатике. В физике тема «скорость» встречается чаще всего и изучается углубленно.

Кроме того, данное слово употребляется в повседневной жизни всеми нами, особенно среди автомобилистов, водителей транспортной техники. Даже опытные кулинары иногда используют фразу, например, «взбить яичные белки миксером на средней скорости».

Что такое скорость?

Скорость в физике – это кинематическая величина. Означает расстояние, которое преодолевается телом за какой-то промежуток времени. Допустим, молодой человек движется от дома к магазину, преодолевая двести метров за одну минуту. Напротив, его старенькая бабушка пройдет тем же маршрутом за шесть минут мелкими шажками. То есть парень перемещается намного быстрее своей пожилой родственницы, так как развивает скорость гораздо больше, делая очень быстрые длинные шаги.

То же самое стоит сказать про автомобиль: одна машина едет быстрее, а другая медленнее, потому что скорости движения разные. Позднее мы рассмотрим многочисленные примеры, связанные с этим понятием.

Формула

На уроке в школе обязательно рассматривается формула скорости в физике для того, чтобы было удобно решать задачи.

• V – это, соответственно, скорость движения;
• S – расстояние, которое преодолевается телом при перемещении от одной точки в пространстве до другой;
• t – время перемещения.

Следует запомнить формулу, потому что она пригодится в будущем при решении множества задач и не только. Например, вам может стать интересно, с какой скоростью дойдете от дома до работы или места учебы. Но вы заранее можете узнать расстояние по карте в смартфоне или на компьютере, либо по бумажному варианту, зная масштаб и имея при себе линейку. Далее вы засекаете время, перед тем, как начать движение. Придя на место назначения, смотрите, сколько минут или часов потребовалось пройти без остановки.

В чем измеряется?

Скорость чаще всего измеряется по системе единиц СИ. Ниже представлены не только единицы, но и примеры того, где они применяются:

• км/ч (километр в час) — транспорт;
• м/с (метр в секунду) — ветер;
• км/с (километр в секунду) – космические объекты, ракеты;
• мм/ч (миллиметр в час) — жидкости.

Давайте для начала разберемся, откуда взялась дробная черта и почему единица измерения именно такая. Обратите внимание по физике на формулу скорости. Что вы видите? В числителе стоит S (расстояние, путь). В чем измеряется расстояние? В километрах, метрах, миллиметрах. В знаменателе, соответственно, t (время) – часы, минуты, секунды. Отсюда и единицы измерения величины именно такие, как представлены в начале данного раздела.

Закрепим с вами изучение формулы скорости в физике следующим образом: какое расстояние преодолеет тело за конкретный промежуток времени? Например, человек пройдет 5 километров за 1 час. Итого: скорость движения человека – 5 км/ч.

От чего зависит?

Нередко учителя задают ученикам вопрос: «От чего зависит скорость?».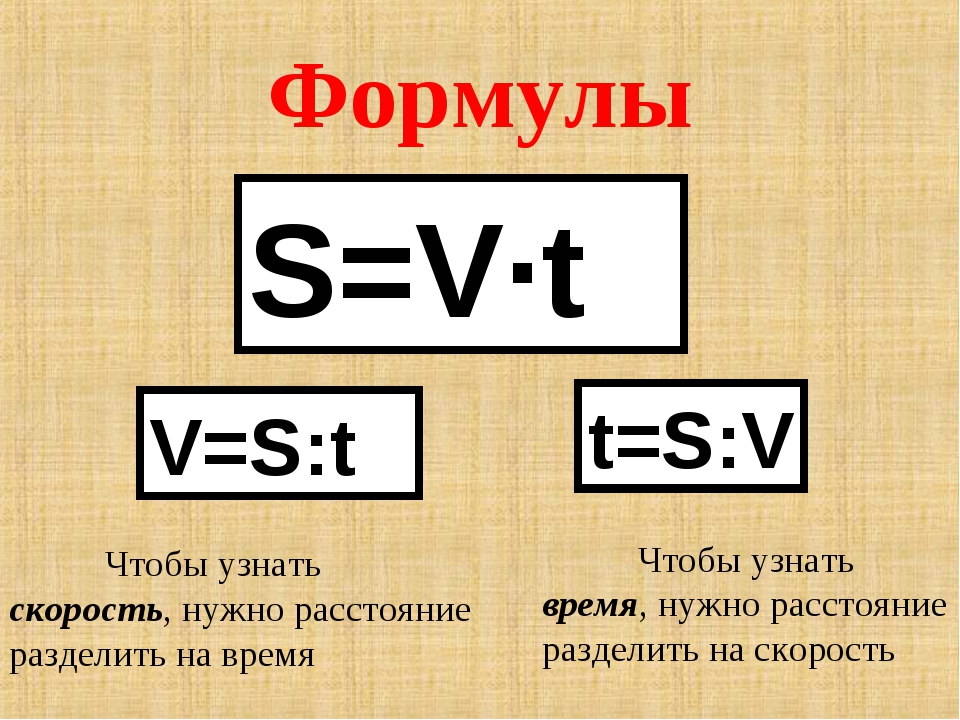 Школьники часто теряются и не знают, что сказать. На самом деле, все очень просто. Достаточно посмотреть на формулу, чтобы всплыла подсказка. Скорость тела в физике зависит от времени движения и расстояния. Если неизвестен хотя бы один из этих параметров, решить задачу будет невозможно. Кроме того, в примере можно встретить другие виды скоростей, о которых речь пойдет в следующих разделах этой статьи.

Во многих задачах по кинематике приходится строить графики зависимости, где по оси Х – время, а по оси Y – расстояние, путь. По таким изображениям можно легко оценить характер скорости движения. Стоит отметить, что во многих профессиях, связанных с транспортом, электрическими машинами часто применяются графики. Например, на железной дороге.

В нужный момент измеряем скорость

Есть еще одна тема, которая пугает учеников средней школы, — мгновенная скорость. В физике это понятие встречается как определение величины скорости в мгновенный промежуток времени.

Давайте рассмотрим простой пример: машинист ведет поезд, его помощник наблюдает за скоростью движения время от времени. Вдалеке виднеется знак ограничения скорости. Следует проконтролировать, с какой скоростью движется поезд именно сейчас. Помощник машиниста сообщает в 16 часов 00 минут, что скорость равна 117 км/ч. Это и есть мгновенная скорость, зафиксированная ровно в 4 часа вечера. Через три минуты скорость стала 98 км/ч. Это тоже мгновенная скорость относительно 16 часов 03 минут.

Начало движения

Без начальной скорости физика не представляет практически ни одно движение транспортной техники. Что это за параметр? Это скорость, с которой начинает движение объект. Допустим, машина не может начинать движение моментально со скоростью 50 км/ч. Ей нужно разогнаться. Когда водитель нажимает педаль, автомобиль плавно начинает движение, например, со скоростью сначала 5 км/ч, потом постепенно 10 км/ч, 20 км/ч и так далее (5 км/ч и есть начальная скорость).

Конечно, можно совершить резкий старт, какой бывает у бегунов-спортсменов, при ударе теннисного мяча ракеткой, но все равно всегда существует начальная скорость. Ее нет по нашим меркам только у звезд, планет и спутников нашей Галактики, так как мы не знаем, когда началось движение и каким образом. Ведь до самой смерти космические объекты не могут останавливаться, они всегда в движении.

Равномерная скорость

Скорость в физике – это совокупность отдельных явлений и характеристик. Различают также равномерное и неравномерное движение, криволинейное и прямолинейное. Давайте приведем пример: человек идет по прямой дороге с одинаковой скоростью преодолевая из точки А в точку В расстояние 100 метров.

С одной стороны, это можно назвать прямолинейной и равномерной скоростью. Но если присоединить человеку очень точные датчики скорости, маршрута, то можно заметить, что разница все же есть. Неравномерная скорость – это когда скорость регулярно или постоянно меняется.

В быту и технике

Скорость движения в физике существует всюду. Даже микроорганизмы перемещаются, пусть и с очень медленной скоростью. Стоит отметить, что существует вращение, которое характеризуется также скоростью, но имеет единицу измерения – об/мин (обороты в минуту). Например, скорость вращения барабана в стиральной машине. Данная единица измерения употребляется всюду, где есть механизмы и машины (двигатели, моторы).

В географии и химии

Даже вода имеет скорость движения. Физика всего лишь является дочерней наукой в сфере процессов, происходящих в природе. Допустим, скорость ветра, волны в море – это все измеряется привычными физическими параметрами, величинами.

Наверняка, многие из вас знакомы с фразой «скорость химической реакции». Только в химии это имеет иное значение, так как имеется в виду, за какое время произойдет тот или иной процесс. Например, марганцовка быстрее растворится в воде, если взболтать сосуд.

Скорость-невидимка

Существуют невидимые явления. Например, мы не можем видеть, как перемещаются частицы света, различных излучений, как распространяется звук. Но если бы не было движения их частиц, то никакое бы из этих явлений не существовало в природе.

Информатика

Практически каждый современный человек сталкивается с понятием «скорость» во время работы на компьютере:

• скорость Интернета;
• скорость загрузки страниц;
• быстрота загрузки процессора и так далее.

Примеров скорости движения в физике можно привести огромное множество.

Внимательно прочитав статью, вы познакомились с понятием скорости, узнали, что она из себя представляет. Пусть данный материал поможет вам углубленно изучить раздел «Механика», проявить к нему интерес и побороть страх при ответах на уроках. Ведь скорость в физике – это часто встречающееся понятие, которое легко запомнить.

Конспект «Неравномерное движение. Средняя скорость»

Неравномерное движение.
Средняя скорость

Неравномерное движение

— это движение, при котором за равные промежутки времени тело проходит разные пути.

Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.

 

Средняя путевая скорость — скалярная неотрицательная величина.

Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения , совершённого телом, к длительности этого промежутка времени.

Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.

Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.

Пример решения задач на среднюю скорость при неравномерном движении

Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?

Ответ: 70 км/ч

---

Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»

---

Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:

 

Формула средней скорости движения

 

 

Рассмотрим одну из самых простейших задач, которые можно встретить в школьной программе. Итак немного теории

 

Средняя скорость движения —  это отношение полного пути пройденного объектом на общее время затраченное на это путешествие

 

 

Естественно предположить, что если объект часть общего пути прошел за одно время,  другую часть  за другое время, а третью за третье время, то  средняя скорость  будет являтся отношением  всех частей пути на все затраченное время.

 

 

А если  известно  например  части пути и скорость объекта на каждом пути ?  Не среднее арифметическое же брать от всех скоростей… хотя очень часто  именно так и поступают впервые большинство учеников, да и взрослых тоже

 

На самом деле, при известных частях пути и скоростей на участке формула будет следующая

 

 

наверняка догадались как она получилась из предыдущей формулы.

 

Если в задании пути буду обозначаться как часть от общего ( например,  первая половина пути, 2/3 пути и т.п.) то, учитывая  что сумма таких частей будет равна всему пути ( равной единице), то средняя скорость  будет определятся как

 

Пример: 

Автомобиль проехал первую треть дороги со скоростью 60 км/ч, вторую треть дороги со скоростью 120 км/ч, третью треть дороги со скоростью 40 км/ч. найдите среднюю скорость.

Решение:

 

Ответ: 60 км/час

 

 

И последний вариант формулы на среднюю скорость это когда известно время и скорость на каждом из участков.

 

 

Правда есть еще четвертый вариант, но он практически никогда не встречается в задачах. Это когда встречаются комбинированные данные, например: Пешеход, преодолевает путь из точки А в точку Б. Первую половину пути пешеход прошел со скоростью 5 км/час а вторую половину пути за 1 час. Какое расстояние  между А и Б, если средняя скорость пешехода, со всеми остановками и перекурами, была 3 км/час

 

Смотрим вот на эту формулу    и думаем

 

Части пути нам известны, то есть общее расстояние нам известно и принимается за единицу ( половина пути+половина пути равна единице пути)

Теперь со временем

На первом участке время легко вычислить ( половину пути разделить на 5 км/ч). Получаем одну десятую пути.  Не пугайтесь что получилось «время  равно одной десятой пути». Оно потом понадобится..

Время на втором участке известно и равно 1 час

 

Напишем нашу формулу по полученным данным

 

 

 

Выразим расстояние от точки А до точки Б через среднюю скорость и получим

 

 

Поставим значение средней скорости  получим что общее расстояние которое преодолел пешеход равно  4 километра и почти 286 метров

 

Сложновато? Зато интересно и увлекательно.

 

Из последней формулы  вытекает  «парадоксальный» вывод: При средней скорости приближающейся к 10 км/час  расстояние между точками А и Б становится неприлично большим и уходит в бесконечность, а при 11 км/час расстояние вообще  становится отрицательным.

 

Что хотелось бы по этому поводу сказать. не всегда надо бездумно подвергать анализу последнюю формулу, особенно когда знаменатель  обращается в ноль.

Взяв предыдущую формулу  — мы бы увидели что  при средней скорости в 10 км/ч , расстояние просто будет неопределено. То есть при заданных условиях средняя скорость никак не может быть больше 10 км/час.

 

 

• Фразеологический словарь выражения чувств и эмоций >>

2.5. Расчёт скорости движения автомобиля

Для всех ступеней коробки передач и дополнительной коробки рассчиты­ваются значения скорости движения автомобиля в зависимости от частоты вращения коленчатого вала двигателя (по согласованию с руководителем рас­чёт может производиться только для высшей ступени дополнительной короб­ки).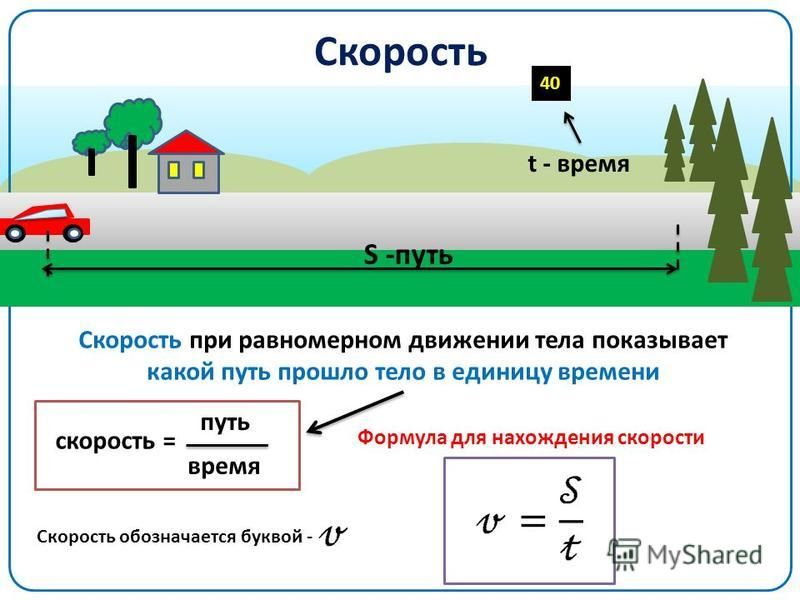

Расчёт ведётся по формуле

где v — скорость автомобиля, км/ч;

n — частота вращения коленчатого вала дви­гателя, об/мин;

r_К — радиус качения, м;

и₀ — передаточное число главной переда­чи;

и_к — передаточное число рассчитываемой ступени коробки передач;

и_д — пе­редаточное число рассчитываемой ступени дополнительной (раздаточной) ко­робки.

Значения частоты вращения коленчатого вала берутся теми же, что и при построении внешней скоростной характеристики.

Рассчитанные значения v_t заносятся в столбец 4 табл. 2.1. Графики зави­симости скорости движения автомобиля от частоты вращения коленчатого вала двигателя представляют собой серию лучей, выходящих под разными углами из начала координат рисунок 2. 2.

Рис. 2.2 Зависимости скорости движения автомобиля от частоты вращения коленчатого вала по передачам.

2.6. Тяговая характеристика и тяговый баланс автомобиля

Тяговая характеристика представляет собой зависимость силы тяги авто­мобиля от скорости движения по передачам. Значения силы тяги Р_Т рассчиты­ваются в отдельных точках по формуле

(2.26)

где М_К — крутящий момент двигателя, Нм;

η_Т — КПД трансмиссии.

Результаты расчёта Р_Т заносятся в столбец 7 табл. 2.1, и по ним строятся графики зависимости Р_Т =f(V) по передачам.

Тяговый баланс автомобиля описывается уравнением тягового или силово­го баланса

Р_Т = Рд + Рв + Ри , (2.27)

где Р_Т — сила тяги автомобиля, Н;

Р_д — суммарная сила сопротивления дороги, Н;

Р_в — сила сопротивления воздушной среды, Н;

Р_и — сила инерции автомоби­ля, Н.

Величина Р_д определяется по выражению

Р_д = G_aψ, (2.28)

где G_a — полный вес автомобиля, Н; ψ — суммарный коэффициент сопротивления дороги.

Суммарный коэффициент сопротивления дороги является величиной, за­висящей от скорости автомобиля. Однако учёт этой зависимости сильно ос­ложняет выполнение тягового расчёта и в то же время не даёт важного для практики уточнения. Поэтому при выполнении тягового расчёта рекомендуется принять значение ψ постоянным, равным тому значению, которое было рассчи­тано для максимальной скорости движения автомобиля при определении мощ­ности двигателя, необходимой для движения на режиме максимальной скоро­сти, т.е. принять везде ψ=ψ_v.

При каком-то одном выбранном значении ψ величина Р_д остаётся постоян­ной для всех расчётных точек на всех передачах. Поэтому значение Р_д подсчитывается один раз и в таблицу не заносится. На графике тяговой характеристи­ки зависимость P_Т=f(v) представляется в виде прямой, параллельной оси абс­цисс.

Рис. 2.3 Тяговая характеристика автомобиля.

Сила сопротивления воздушной среды Р_в составляет величину

(2.29)

где с_х — коэффициент продольной аэродинамической силы;

р_в — плотность воздуха, кг/м³ ;

к_в — коэффициент обтекаемости, кг/м³;

F — лобовая площадь авто­мобиля, м ;

v_в — скорость воздушного потока относительно автомобиля, км/ч.

При расчёте можно задать ρ_в=1,225 кг/м . Скорость воздушного потока обычно принимается равной скорости движения автомобиля.

Значения Р_в рассчитываются для всех точек и заносятся в столбец 5 табл. 2.1. График зависимости Р_в от скорости представляет собой параболу, проходящую через начало координат.

Для удобства дальнейшего анализа этот график смещают вверх на ве­личину, равную Р_д (в принятом для сил масштабе). Фактически при таком построении этот график выражает зависимость (P_в+P_d)=f(v).

Сила инерции автомобиля Р_и после расчёта Р_д и Р_в может быть определена как замыкающее слагаемое силового баланса

(2.30)

На графике значение Р_и определяется отрезком прямой, проведённой для нужного значения скорости параллельно оси ординат, между точками пересечения этой прямой графиков P_Т=f[v) и (P_д+P_в)=f(v). Если заданная скорость может быть обеспечена на нескольких передачах, то каждой из этих передач будет соответствовать своё значение силы инерции. Рассчи­танные значения Р_и следует занести в столбец 6 табл. 2.1.

Значение Р_Т заносится в столбец 7 табл. 2.1. Тяговая характеристика автомобиля представлена на рис. 2.3.

Формула средней скорости

Формула средней скорости используется для нахождения единой скорости, при которой объект движется с фиксированным и постоянным темпом.

Например, машина едет 3 часа. Он проходит 30 миль за первый час, 45 миль за второй час и 75 миль за третий час.

Скорость в первый час = 30 миль / час

Скорость во второй час = 45 миль / час

Скорость в третий час = 75 миль / час

У нас есть три разных скорости в трехчасовом путешествии.

Если мы хотим найти среднюю скорость для всего трехчасового путешествия, мы должны найти соотношение между общим пройденным расстоянием и общим затраченным временем.

То есть постоянная скорость = (30 + 45 + 75) / 3

= 150/3

= 50 миль / час

На основании приведенного выше примера формула для определения средней скорости приведена ниже.

Если человек едет из пункта А в пункт Б с некоторой скоростью, скажите «х» миль в час. Он возвращается из пункта B в пункт A с другой скоростью, скажем, «y» миль в час.В обоих направлениях он преодолевает одинаковое расстояние, но с разной скоростью.

Затем формула для определения средней скорости для всей поездки приведена ниже.

Формула средней скорости — примеры

Пример 1:

Дэвид ехал 3 часа со скоростью 50 миль в час, 2 часа со скоростью 60 миль в час и 5 часов со скоростью 70 миль в час. Какова была его средняя скорость за все путешествие?

Ответ:

Шаг 1:

Формула для средней скорости

= Общее расстояние / Общее затраченное время.

А также формула для расстояния:

= Скорость ⋅ Время

Шаг 2:

Расстояние, пройденное за первые 3 часа, составляет

= 50 ⋅ 3

= 150 миль

Расстояние, пройденное за следующие 2 часа

= 60 ⋅ 2

= 120 миль

Расстояние, пройденное за последние 5 часов

= 70 ⋅ 5

= 350 миль

Шаг 3:

Тогда общее расстояние равно

= 150 + 120 + 350

= 620 миль

Общее время

= 3 + 2 + 5

= 10 часов

Шаг 4:

Итак, средняя скорость

= 620 / 10

= 62

Итак, средняя скорость на всем пути составляет 62 мили в час.

Пример 2:

Хосе перемещается из места A в место B с определенной скоростью. Когда он возвращается из пункта B в пункт A, его скорость составляет 60 миль в час. Если средняя скорость за все путешествие составляет 72 мили в час, найдите его скорость, когда он едет из пункта A в пункт B.

Ответ:

Шаг 1:

Пусть «a» будет скоростью от места A до B.

Скорость от места B до A = 60 миль / час

Шаг 2:

Здесь, в обе стороны он преодолевает одинаковое расстояние.

Тогда формула для определения средней скорости:

= 2xy / (x + y)

Шаг 3:

x —-> Скорость от места A до B

x = a

y —-> Скорость от точки B до точки A

y = 60

Шаг 4:

Дано: Средняя скорость 72 мили / час.

(2 ⋅ a ⋅ 60) / (a ​​+ 60) = 72

120a = 72 (a + 60)

120a = 72a + 4320

48a = 4320

a = 90

Итак, скорость от места А до Б — 90 миль в час.

Пример 3:

Дэвид перемещается из места A в место B с определенной скоростью. Когда он возвращается с места B на место A, он увеличивает свою скорость в 2 раза. Если постоянная скорость на протяжении всего пути составляет 80 миль в час, найдите его скорость, когда он едет из точки А в точку Б.

Ответ:

Шаг 1:

Пусть «а» будет скорость от места A до B.

Тогда скорость от места B до A = 2a

Шаг 2:

Расстояние, пройденное в обоих направлениях (от A до B и от B до A), одинаково.

Итак, формула для определения средней скорости:

= 2xy / (x + y)

Шаг 3:

x —-> Скорость от места A до B

x = a

y —-> Скорость от места B до A

y = 2a

Шаг 4:

Дано: Средняя скорость = 80 миль / час

(2 ⋅ a ⋅ 2a) / ( a + 2a) = 80

4a² / 3a = 80

4a / 3 = 80

a = 60

Итак, скорость от места A до B составляет 60 миль в час.

Пример 4:

Человеку требуется 5 часов, чтобы добраться из пункта A в пункт B со скоростью 40 миль в час. Он возвращается из места B в место A с 25% увеличенной скоростью. Найдите среднюю скорость для всего пути.

Ответ:

Шаг 1:

Скорость (от A до B) = 40 миль / час

Скорость (от B до A) = 50 миль / час (увеличение на 25%)

Шаг 2:

Расстояние, пройденное в обоих направлениях (от A до B и от B до A), одинаково.

Итак, формула для определения среднего расстояния:

= 2xy / (x + y)

Шаг 3:

x —-> Скорость от места A до B

x = 40

y —-> Скорость от точки B до точки A

y = 50

Шаг 4:

Средняя скорость = (2 ⋅ 40 ⋅ 50) / (40 + 50)

Средняя скорость = 44,44

Итак, средняя скорость за весь путь составляет около 44,44 миль / час.

Пример 5:

Скорость (от A до B) = 20 миль / час,

Скорость (от B до C) = 15 миль / час,

Скорость (от C до D) = 30 миль / час

Если расстояния от A до B, от B до C и от C до D равны и путь от A до B занимает 3 часа, найдите среднюю скорость от A до D.

Ответ:

Шаг 1:

Формула для определения расстояния:

= Скорость ⋅ Время

Расстояние от A до B составляет

= 20 ⋅ 3

= 60 миль

Дано: Расстояние от A до B, от B до C и C к D равны.

Общее расстояние от A до D составляет

= 60 + 60 + 60

= 180 миль

Шаг 2:

Формула для определения времени:

= Расстояние / Скорость

Время (от A до B ) = 60/20 = 3 часа

Время (от B до C) = 60/15 = 4 часа

Время (от C до D) = 60/30 = 2 часа

Общее время, прошедшее от A до D, составляет

= 3 + 4 + 2

= 9 часов

Шаг 3:

Формула для определения средней скорости:

= Общее расстояние / Общее время

= 180/9

= 20

Итак, средняя скорость от A до D составляет 20 миль в час.

Чтобы получить больше проблем на средней скорости,

Нажмите здесь

Помимо вышеперечисленного, если вам нужны другие данные, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Проблемы со словами на квадратных уравнениях

Алгебраные задачи на четыре слова
2

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Проблемы со словами по цене за единицу

Word задачи по сравнению ставок

Преобразование общепринятых единиц в текстовые задачи

Преобразование в метрические единицы в текстовых задачах

Word задачи по простому проценту

Word по сложным процентам

Word по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Разметка и разметка задачи

Проблемы с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы с линейными неравенствами в словах

Соотношение и пропорции Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами на постоянной скорости

Проблемы со словами на средней скорости

Проблемы со словами на сумму углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Домен и диапазон рациональных функций

Домен и диапазон рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Нахождение квадратного корня с помощью long di видение

L. Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении 17 степени 23 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Постоянная скорость

Постоянная скорость также называется равномерной скоростью, при которой что-то движется с фиксированной и постоянной скоростью или движется с некоторой средней скоростью.

Например, автомобиль едет 3 часа. Он проходит 30 миль за первый час, 45 миль за второй час и 75 миль за третий час.

Скорость в первый час = 30 миль / час

Скорость во второй час = 45 миль / час

Скорость в третий час = 75 миль / час

У нас есть три разных скорости в трехчасовом путешествии.

Если мы хотим найти постоянную скорость для всего трехчасового путешествия, мы должны найти соотношение между общим пройденным расстоянием и общим затраченным временем.

То есть постоянная скорость = (30 + 45 + 75) / 3

= 150/3

= 50 миль / час

На основе приведенного выше примера формула для определения постоянной скорости приведена ниже.

Если человек едет из пункта А в пункт Б с некоторой скоростью, скажите «х» миль в час. Он возвращается из пункта B в пункт A с другой скоростью, скажем, «y» миль в час. В обоих направлениях он преодолевает одинаковое расстояние, но с разной скоростью.

Затем формула для определения постоянной скорости для всего пути приведена ниже.

Постоянная скорость — Примеры

Пример 1:

Дэвид ехал 3 часа со скоростью 50 миль в час, 2 часа со скоростью 60 миль в час и 4 часа со скоростью 70 миль в час. Какова была его постоянная скорость на протяжении всего путешествия?

Решение:

Шаг 1:

Формула для постоянной скорости = Общее расстояние / Общее затраченное время.

А также для for distance = Rate x Time

Step 2:

Расстояние, пройденное за первые 3 часа:

= 50 x 3

= 150 миль

Расстояние, пройденное за следующие 2 часа:

= 60 x 2

= 120 миль

Расстояние, пройденное за последние 4 часа:

= 70 x 5

= 350 миль

Шаг 3:

Тогда общее расстояние будет

= 150 + 120 + 350

= 620 миль

Общее время

= 3 + 2 + 5

= 10 часов

Шаг 4:

Итак, постоянная скорость

= 620/10

= 62 мили в час

Следовательно, постоянная скорость на всем пути составляет 62 мили в час.

Пример 2:

Человек едет из Нью-Йорка в Вашингтон со скоростью 45 миль в час и возвращается в Нью-Йорк со скоростью 55 миль в час. Какая постоянная скорость на всем пути?

Ответ:

Шаг 1:

Здесь в обе стороны он преодолевает одинаковое расстояние.

Тогда формула для определения средней скорости:

= 2xy / (x + y)

Шаг 2:

x —-> Скорость, с которой он едет из Нью-Йорка в Вашингтон

x = 45

y —-> Скорость, с которой он едет из Нью-Йорка в Вашингтон

y = 55

Шаг 3:

Итак, средняя скорость

= (2 ⋅ 45 ⋅ 55) / (45 + 55)

= 4950/100

= 49.5

Итак, постоянная скорость на всем пути составляет 45 миль в час.

Пример 3:

Человеку требуется 10 часов, чтобы добраться до места и вернуться обратно, пройдя оба пути. Он мог бы выиграть 2 часа, катаясь в обе стороны. Расстояние, пройденное за весь путь, составляет 18 миль. Найдите постоянную скорость на протяжении всего пути, если он идет пешком и возвращается верхом.

Решение:

Шаг 1:

Дано: Человеку требуется 10 часов, чтобы добраться до места и вернуться, пройдя оба пути.

То есть

Ходьба + Ходьба = 10 часов

2 ⋅ Ходьба = 10 часов

Ходьба = 5 часов

Дано: Он мог бы выиграть 2 часа, катаясь в обе стороны.

То есть

Верховая езда + езда = 8 часов

2 ⋅ Верховая езда = 8 часов

Верховая езда = 4 часа

Шаг 2:

Если он идет пешком и возвращается верхом, время требуется им:

Ходьба + верховая езда = 5 + 4

Ходьба + верховая езда = 9 часов

Шаг 3:

Общее время = 9 часов

Общее пройденное расстояние = 18 миль

Шаг 4:

Итак, средняя скорость составляет

= Общее расстояние / Общее время

= 18/9

= 2

Итак, требуемая постоянная скорость составляет 2 мили в час.

Пример 4:

Лили требуется 3 часа, чтобы добраться от места A до места B со скоростью 60 миль в час. Ей требуется 2 часа, чтобы добраться от места B до C с увеличением скорости на 50%. Найдите постоянную скорость от точки A до C.

Решение:

Шаг 1:

Скорость (от A до B) = 60 миль / час

Скорость (от B до C) = 90 миль / час (увеличение на 50%)

Шаг 2:

Формула для определения расстояния:

= Скорость ⋅ Время

Расстояние от A до B составляет

= 60 ⋅ 3

= 180 миль

Расстояние от От B до C

= 90 ⋅ 2

= 180 миль

Общее расстояние, пройденное от A до B, составляет

= 180 + 180

= 360 миль

Общее время, пройденное от A до B, составляет

= 3 + 2

= 5 часов

Шаг 3:

Формула для определения средней скорости:

= Общее расстояние / Общее время

= 360/5

= 72

Итак, постоянная скорость с места От А до Б — 72 мили / час.

Пример 5:

Человеку требуется 5 часов, чтобы добраться из пункта A в пункт B со скоростью 40 миль в час. Он возвращается из места B в место A с 25% увеличенной скоростью. Найдите постоянную скорость на всем пути.

Решение:

Шаг 1:

Скорость (от A до B) = 40 миль / час

Скорость (от B до A) = 50 миль / час (увеличение на 25%)

Шаг 2:

Расстояние, пройденное в обоих направлениях (от A до B и от B до A), одинаково.

Итак, формула для определения среднего расстояния:

= 2xy / (x + y)

Шаг 3:

x —-> Скорость от места A до B

x = 40

y —-> Скорость от точки B до точки A

y = 50

Шаг 4:

Средняя скорость = (2 ⋅ 40 ⋅ 50) / (40 + 50)

Средняя скорость = 44,44

Итак, постоянная скорость на протяжении всего пути составляет около 44,44 миль / час.

Пример 6:

Расстояние от A до B = 200 миль,

Расстояние от B до C = 300 миль,

Расстояние от C до D = 540 миль

Скорость от B до C составляет 50% больше, чем от A до B. Скорость от C до D на 50% больше, чем от B до C. Если скорость от A до B составляет 40 миль в час, найдите постоянную скорость от A до D.

Решение:

Шаг 1:

Скорость (от A до B) = 40 миль / час

Скорость (от B до C) = 60 миль / час (на 50% больше)

Скорость (от C до D) = 90 миль / час (на 50% больше)

Шаг 2:

Формула для определения времени:

= Расстояние / время

Время (от A до B) = 200/40 = 5 часов

Время (B до C) = 300/60 = 5 часов

Время (от C до D) = 540/90 = 6 часов

Общее время, затраченное от A до D, составляет

= 5 + 5 + 6

= 16 ho urs

Общее расстояние от A до D составляет

= 200 + 300 + 540

= 1040 миль

Шаг 3:

Формула для определения средней скорости:

= Общее расстояние / Общее время

= 1040/16

= 65

Итак, средняя скорость от A до D составляет 65 миль в час.

Помимо вышеперечисленного, если вам нужны другие вещи, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Проблемы со словами на квадратных уравнениях

Алгебраные задачи на четыре слова
2

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Проблемы со словами по цене за единицу

Word задачи по сравнению ставок

Преобразование общепринятых единиц в текстовые задачи

Преобразование в метрические единицы в текстовых задачах

Word задачи по простому проценту

Word по сложным процентам

Word по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Разметка и разметка задачи

Проблемы с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы с линейными неравенствами в словах

Соотношение и пропорции Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами на постоянной скорости

Проблемы со словами на средней скорости

Проблемы со словами на сумму углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Домен и диапазон рациональных функций

Домен и диапазон рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Нахождение квадратного корня с помощью long di видение

L.Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении 17 степени 23 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Скорость, дистанция, время, калькулятор

Использование калькулятора

Рассчитайте скорость, расстояние или время по формуле d = st, расстояние равно скорости, умноженной на время.Калькулятор скорости, дистанции и времени может решить неизвестные sdt значение для двух известных значений.

Время можно ввести или рассчитать в секундах (с), минутах (мин), часах (час) или часах и минутах и ​​секундах (чч: мм: сс). Видеть ярлыки для форматов времени ниже.

Чтобы найти расстояние, используйте формулу для расстояния d = st, или расстояние равно скорости, умноженной на время.

расстояние = скорость x время

Скорость и скорость аналогичны, поскольку они оба представляют собой расстояние в единицу времени, например мили в час или километры в час.Если ставка r совпадает со скоростью с , r = s = d / t. Вы можете использовать эквивалентную формулу d = rt, что означает, что расстояние равно скорости, умноженной на время.

расстояние = скорость x время

Чтобы найти скорость или коэффициент, используйте формулу для скорости s = d / t, что означает, что скорость равна расстоянию, разделенному на время.

скорость = расстояние / время

Чтобы найти время, используйте формулу для времени t = d / s, что означает, что время равно расстоянию, разделенному на скорость.

время = расстояние / скорость

Форматы ввода времени чч: мм: сс

В качестве разделителей можно использовать тире (-), точку (.) Или двоеточие (:), при этом всегда необходимо использовать 2 разделителя. Например, 15-06-22, 15.06.22 и 15:06:22 все интерпретируются как 15 часов 6 минут 22 секунды или 15:06:22.

Разрешенные ограничения на вход:

• часы 0 до 999
• минут 0 до 59
• секунд от 0 до 59

Ярлыки формата времени

Х..

5 ..

5 часов: 0 минут: 0 секунд

05:00:00

X.Y.

5.22.

5 часов: 22 минут: 0 секунд

05:22:00

X.Y.Z

5.22.10
5.01.15
5.3.6

5 часов: 22 минут: 10 секунд
5 часов: 1 минута: 15 секунд
5 часов: 3 минут: 6 секунд

05:22:10
05:01:15
05:03:06

.Ю.

.22.

22 минуты

00:22:00

.Y.Z

. 22,15

22 минуты: 15 секунд

00:22:15

..Z

..5

5 секунд

00:00:05

X..Z

5..05

5 часов: 0 минут: 5 секунд

05:00:05

Связанные калькуляторы

Для физических расчетов скорости, смещения и скорости используйте наш Калькулятор смещения для решения смещения с , средняя скорость v или время t .2

Использование калькулятора

Этот калькулятор смещения находит пройденное расстояние или смещение (я) объекта, используя его начальную скорость (u), ускорение (a) и время (t) пройденного пути. Используемое уравнение: s = ut + ½at ² ; ниже, чтобы показать, как найти решение для каждой отдельной переменной. Калькулятор можно использовать для определения s, u, a или t.

Уравнения смещения для этих расчетов:

Смещение (с) объекта равно скорости (u), умноженной на время (t), плюс 1/2 ускорения (a), умноженное на квадрат времени (t ² ).2 \)

Где:
с = смещение
u = начальная скорость
a = ускорение
t = время

Используйте стандартную гравитацию a = 9,80665 м / с ² для уравнений, в которых гравитационная сила Земли используется как скорость ускорения объекта. 2 \)

Где:
с = смещение
v _i = начальная скорость
a = ускорение
t = время

Расчет смещения, используемый в калькуляторе:

Решая различные переменные, мы можем использовать следующие формулы:

• Учитывая u, t и вычислить s
  По заданной начальной скорости, времени и ускорению рассчитайте смещение.
  • s = ut + ½ при ² : найти s
• Даны s, t и вычислить u
  При заданном смещении, времени и ускорении вычисляется окончательная скорость.
  • u = s / t — ½at: решить относительно u
• Учитывая a, u и s, вычислить t
  Время вычисляется с учетом ускорения, начальной скорости и смещения.
  • ½at ² + ut — s = 0: найти t, используя формулу корней квадратного уравнения
• Для заданных s, t и u вычислить
  Рассчитать ускорение по заданному смещению, времени и начальной скорости.
  • a = 2s / t ² — 2u / t: вычислить

Задача смещения 1:

Автомобиль, движущийся со скоростью 25 м / с, начинает ускоряться со скоростью 3 м / с ² в течение 4 секунд.Как далеко уезжает машина за 4 секунды разгона?

Три переменные, необходимые для определения расстояния, представлены как u (25 м / с), a (3 м / с ² ) и t (4 секунды).

с = ut + ½ при ²
с = 25 м / с * 4 с + ½ * 3 м / с ² * (4 с) ² = 124 метра

Задача смещения 2:

Самолету с начальной скоростью 20 м / с требуется 8 секунд, чтобы достичь конца взлетно-посадочной полосы.Если самолет ускоряется со скоростью 10 м / с ² , какова длина взлетно-посадочной полосы?

с = ut + ½ при ²
с = 20 м / с * 8 с + ½ * 10 м / с ² * (8 с) ² = 600 метров

Предварительный расчет скорости подачи проволоки, скорости перемещения и напряжения

Цех хотел бы сократить время разработки новых сварных швов MIG. Есть ли способ предварительно рассчитать скорость подачи проволоки, скорость движения и напряжение, чтобы приблизить их до первого сварного шва?

Да, можно рассчитать начальную скорость подачи проволоки и скорость движения.Это очень частый вопрос от производителей, выполняющих сварку сплошной проволокой или порошковой проволокой. Большинство профессионалов в области сварки знают скорость подачи проволоки (WFS), при которой процесс проходит хорошо, исходя из их опыта, или могут быстро получить WFS, выполнив рекомендуемые производителем процедуры.

Однако определение скорости перемещения сварного шва определенного размера оказывается итеративным и трудоемким процессом. Понимая несколько концепций и выполняя некоторые вычисления с помощью нескольких простых формул, мы можем определить, по крайней мере, хорошую отправную точку для процедуры сварки, которая обеспечивает желаемый сварной шов.

СКОРОСТЬ НАЛОЖЕНИЯ
Важно помнить, что скорость наплавки прямо пропорциональна скорости, с которой проволока определенного диаметра выходит из сварочного пистолета во время сварки. Скорость наплавки не имеет никакого отношения ни к скорости движения пистолета, ни к настройке напряжения на станке. Скорость наплавки — это просто мера того, сколько фунтов проволоки выходит из сварочной горелки за определенный промежуток времени, обычно измеряется в фунтах / час.

Если скорость подачи проволоки увеличивается, скорость наплавки увеличивается.Мы также понимаем, что если мы сохраним скорость подачи проволоки и перейдем на проволоку большего диаметра, скорость наплавки также увеличится. При таком понимании расчет скорости наплавки оказывается очень мощным упражнением, дающим вам число, которое можно использовать для расчета основных параметров сварки. Давайте посмотрим на формулу и пример:

Расчет скорости наплавки
Скорость наплавки (фунт / час) = 13,1 × (диаметр проволоки) ² × (скорость подачи проволоки) × (эффективность)
— Диаметр проволоки в дюймах (дюймах)
— Скорость подачи проволоки в дюймах в минуту (ipm)
— КПД (1.0 для сплошной проволоки, 0,85 для порошковой проволоки)
— Этот расчет только для стали
— например : Диаметр проволоки = 0,045 дюйма (1,2 мм) сплошной проволоки, WFS = 300 дюймов в минуту

Скорость наплавки = 13,1 × (0,045) ² × (300) × (1,0) = 7,96 фунта / час

Расчет скорости движения с учетом скорости наплавки
Зная скорость наплавки, мы можем рассчитать скорость движения в дюймах в минуту (ipm) для конкретного сварного шва. Предположим, мы хотим сделать угловой шов стали 3/8 дюйма (предположим, что усиление 10% или 0.4125 дюймов), используя сплошную проволоку 0,045 дюйма на скорости 300 дюймов в минуту, вес металла шва на фут можно рассчитать, умножив плотность стали (0,283 фунта / дюйм ³ ) на объем металла шва на фут следующим образом:

Расчет веса сварного шва на стопу
Объем сварочного металла / фут = 1/2 × b × h × 12 дюймов = 1/2 × 0,4125 дюймов × 0,4125 дюймов × 12 дюймов = 1,02 дюймов ³

Вес металла шва / фут 3/8 дюйма углового шва = (0,283 фунта / дюйм ³ ) × (1,02 дюйма ³ ) = 0.2887 фунт / фут

Из приведенного ниже расчета мы видим, что скорость перемещения для однопроходного углового шва 3/8 дюйма будет 5,52 дюйма в минуту, 11,03 дюйма в минуту для двухходового углового шва или 16,55 дюйма в минуту для трехходового сварного шва.

Расчет скорости перемещения
Скорость перемещения = (скорость наплавки) × (количество проходов) / 5 × (вес сварочного металла на фут {фунт / фут}) =
Скорость перемещения = {7,96 x 1} / {5 x 0,2887} = 5,52 изобр. / Мин,

РАСЧЕТ СКОРОСТИ ПОДАЧИ ПРОВОЛОКИ СО СКОРОСТЬЮ НАПЛАВЛЕНИЯ
Предположим, что требуется выполнение угловых швов со скоростью 12 фунтов / час с использованием 0.045 в сварочной проволоке. Мы можем рассчитать WFS, используя приведенные ниже формулы и вес сварочной проволоки на фут в Таблица 1 .

Расчет скорости подачи проволоки
Скорость подачи проволоки = (скорость наплавки) / 5 × (вес проволоки на фут {фунт / фут}) = (12) / 5 × (0,0054) = 444,4 дюйм / мин

Конечно, скорость перемещения для однопроходного углового шва 3/8 дюйма при скорости наплавки 12 фунтов / час будет составлять 8,31 дюйм / мин, как рассчитано ниже:
Скорость перемещения = (скорость наплавки) × (количество проходов) / 5 × (вес наплавленного металла {фунт./ фут}) = (12) × (1) / 5 × (0,2887) = 8,31 изобр. / мин

УПРОЩЕНИЕ
Коэффициент преобразования Бартона (см. , таблица 2, ) немного упрощает работу с угловыми сварными швами. В приведенном ниже примере коэффициент преобразования используется для расчета скорости перемещения при 5,57 дюйм / мин для того же углового шва 3/8 дюйма с использованием сплошной проволоки 0,045 дюйма.

Скорость перемещения = 7,96 × 0,7 = 5,57 дюймов / мин (0,2887)

Вес металла шва на фут можно рассчитать для любого типа соединения путем вычисления объема и умножения на плотность металла шва (например,0,283 фунта / дюйм ³ для стали). Однако значения, представленные в таблицах с 3 по 6 , устраняют необходимость в вычислениях. Эти значения взяты из Таблицы 12-1 в «Справочнике по дуговой сварке » компании Lincoln Electric Co. и показывают вес металла сварного шва на фут для нескольких распространенных типов соединений, сваренных со сталью. В следующих примерах расчетов используются Таблицы 3–6 .

РАСЧЕТ ОБРАЗЦА № 1
Пластина 1/2 дюйма, сварной шов с V-образной канавкой, угол наклона 90 ° и усиление 1/8 дюйма с использованием 0.052 в сплошной проволоке, 90% Ar / 10% CO ₂ защитный газ. Производитель рекомендует WFS со скоростью 325 изображений в минуту и ​​30 вольт.

Скорость осаждения (фунт / час) = 13,1 × (0,052) ² × (325) × (1,0) = 11,51 фунт / час

Скорость хода для проходов заполнения и укупорки = (11,51) × (6) / 5 × (0,849 + 0,199) = 13,18 дюймов / мин

РАСЧЕТ ОБРАЗЦА № 2
Плоский квадратный сварной шов 3/8 дюйма на подложку с зазором 3/16 дюйма и усилением 1/8 дюйма порошковой проволокой 1/16 дюйма, 75% Ar / 25% CO ₂ защитный газ.Наш процесс отлично работает с WFS со скоростью 285 изображений в минуту и ​​26 вольт.

Скорость наплавки (фунт / час) = 13,1 × (1/16 дюйма) ² × (285) × (0,85) = 12,39 фунта / час

Скорость перемещения для проходов заполнения и укупорки = (12,39) × (1) / 5 × (0,239 + 0,053) = 8,49 дюймов / мин

РАСЧЕТ ОБРАЗЦА № 3
Какой должна быть моя скорость подачи проволоки, если я хочу сделать толстый угловой шов 1/4 дюйма при скорости перемещения 20 дюймов в минуту с использованием сплошной проволоки 0,045 дюйма и 90% Ar / 10% CO ₂ защитный газ?

Изменив приведенный выше расчет скорости перемещения для расчета скорости наплавки, мы получим:
Скорость наплавки = 5 × скорость перемещения × (вес сварочного металла {фунт / фут}) / (количество проходов) = 5 × 20 дюймов в минуту × ( 0.165) / 1 = 16,5 фунтов / час

Изменив расчет скорости наплавки выше для определения скорости подачи проволоки, мы получим:
Скорость подачи проволоки = скорость наплавки / 13,1 × (диаметр проволоки) ² × (Эффективность) = 16,5 / 13,1 × (0,045 дюйма .) ² × (1) = 622 дюйм / мин

РЕЗЮМЕ
Использование математики и этих простых формул может сократить время разработки сварных швов и улучшить документацию, предшествующую WPS. Эти расчеты приблизят вас, но, возможно, придется внести некоторые изменения, чтобы добиться желаемого сварного шва.Наличие хорошей отправной точки для разработки процедуры сварки сократит время и сократит количество догадок в цехе.

Калькулятор средней скорости

— вычисляет среднюю скорость. скорость в миль / ч, км / ч и т. д.

Используйте этот калькулятор скорости, чтобы легко вычислить среднюю скорость транспортного средства: автомобиля, автобуса, поезда, велосипеда, мотоцикла, самолета и т. д. с заданным расстоянием и временем в пути. Возвращает мили в час, км в час, метры в секунду и т. Д.

Формула средней скорости

Расчет средней скорости прост: учитывая пройденное расстояние и время, которое потребовалось, чтобы преодолеть это расстояние, вы можете рассчитать свою скорость по следующей формуле:

Скорость = Расстояние / Время

Метрическая единица результата будет зависеть от введенных вами единиц.Например, если вы измерили расстояние в метрах, а время в секундах, результат вычислителя средней скорости будет фут / с. Если расстояние измерялось в милях, а время — в часах, то вывод будет в милях в час (миль / ч, миль / ч) и так далее для км / ч, м / с и т. Д. — все это поддерживается нашим инструментом.

Как рассчитать среднюю скорость автомобиля?

Допустим, вы проехали определенное расстояние на своей машине и хотите вычислить ее среднюю скорость. Самый простой способ сделать это — использовать приведенный выше калькулятор скорости, но при желании вы также можете выполнить вычисления самостоятельно.В любом случае нужно знать расстояние. Если вы отметили расстояние на одометре, вы можете использовать это число. Другие варианты — использовать карту (например, Google Maps) и измерить пройденное расстояние на основе вашего фактического пути (не по прямой, если вы не путешествовали по воздуху, и в этом случае это было бы хорошим приближением) или использовать GPS. чтение, если вы пользовались навигацией на протяжении всей поездки. Тогда вам нужно знать время в пути. Обязательно вычтите из общей продолжительности поездки любые остановки и остановки.

Например, если общее пройденное расстояние составило 250 миль, а время, которое потребовалось, составляло 5 часов, тогда средняя скорость была 250/5 = 50 миль в час (миль в час). Если расстояние составляло 200 километров и на его преодоление уходило 4 часа, то скорость составляла 200/4 = 50 км / ч (километров в час).

Нахождение примеров средней скорости

Пример 1: Используя приведенное выше уравнение, найдите скорость поезда, который проехал 120 миль за 2 часа 10 минут, сделав четыре остановки, каждая продолжительностью примерно две.5 минут. Сначала вычтите время, проведенное на остановках поезда: 2,5 х 4 = 10 минут. 2:10 минус 10 минут оставляет 2 часа в пути. Затем примените формулу средней скорости, чтобы получить 120 миль / 2 часа = 60 миль в час (миль в час).

Пример 2: Велосипедист едет на работу и с работы, преодолевая 10 км в каждую сторону. Дорога на работу заняла 25 минут, а обратная — 35 минут. Какая средняя скорость велосипедиста? Сначала сложите время, чтобы получить 1 час. Также сложите расстояние: 5 + 5 = 10 километров.Наконец, замените в формуле, чтобы получить в среднем 10/1 = 10 км / ч (километров в час).

Средняя скорость относительно средней скорости

Средняя скорость (вычисляемая данным калькулятором) и средняя скорость не обязательно одно и то же, хотя в определенных сценариях они могут совпадать. Это базовая физика, но многих это сбивает с толку. Вот вкратце различия.

Скорость — это скалярное значение, тогда как скорость — это величина вектора.