Скорость движения по окружности формула: Движение по окружности, теория и онлайн калькуляторы
Движение по окружности | fizmatuski.narod.ru
Движение по окружности
Движение по окружности – частный случай криволинейного движения.
При движении по окружности движение может быть:
- С постоянной по величине скоростью V=const
- С одинаково изменяющейся по величине скоростью Δ V= const
- С неодинаково изменяющейся по величине скоростью, ΔV разное, изменяется не одинаково.
!!! Но при этом во всех 3-х случаях V изменяется по направлению (всегда). Движение по окружности – это периодически повторяющееся движение.
Основными характеристиками такого движения являются:
— период – это время 1 полного оборота (t – все время, N – число оборотов за время t)
— частота – число оборотов за 1с. (Гц)
l = 2πR – путь за 1 поворот (длина окружности) (м)
L = 2πRN – путь за N оборотов (м).
1.Рассмотрим движение с постоянной по величине скоростью. По определению, скорость это путь, пройденнфй телом за единицу времени:
— это путевая скорость движения тела по окружности. Зная значения величин, входящих в эту формулу, получим формулы скорости, которые выражают зависимость от основных характеристик движения по окружности:
ω = 2πn – циклическая частота или угловая скорость (число оборотов за 2π секунды), измеряется в (Гц = рад/с).
(Гц)
Аналогия: тело со V тело проходит путь L, со скоростью ω проходит угловой путь φ (поворачивается на угол).
Угловое расстояние: φ = ωt или φ = 2πN
— ускорение, которое показываем изменение направления скорости ( но не величины) т.к. всегда перпендикулярна и направлена к центру окружности, то это ускорение называется центростремительным:
— формула, определяющая центростремительное ускорение.Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения:
— формулы для вычисления центростремительного ускорения через основные характеристики.
Рассмотрим частные случаи движения тел по окружности:
1. Движение по одному кругу, но по окружностям разного радиуса:
Если т.А и т.В двигаются синхронно то они вместе совершают 1 оборот, значит Т1 = Т2 (периоды их оборотов одинаковы), а из этого следует
=> n1 = n2 => ω1 = ω2, Зная связь между линейной и угловой скоростями, между ускорением и угловой скоростью, получим выражения:
2. Рассмотрим случай, когда два тела совершают круговые движения, но связаны ременной или зубчатой передачей
ременная связь или зубчатая связь
В этом случае скорости движения двух тел равны (нет провисания ремня ): V1 = V2
Зная формулы, связывающие линейную скорость с периодом вращения и с ускорением, получим:
2.Более сложный случай, когда скорость изменяется по величине.
— это средняя путевая скорость движения тела по окружности, где её изменение по величине характеризуется тангенциальным ускорением: ат , изменение скорости по направлению характеризуется центростремительным ускорением ац , которое в каждой точке разное, так как разной будет скорость движения по величине: . Эти два ускорения взаимно перпендикулярны т.к. ац направлено к центру окружности, а ат — по касательной ( если разгон, то по направлению скорости, если торможение, то в противоположную сторону).Так как тангенциальное ускорение не изменяется, а центростремительное изменяется, то будет изменяться и общее ускорение
Изменение скорости приведёт к изменению связанных с ним характеристик: периода, частоты и угловой скорости вращения.
Вернуться к конспектам урока
Уравнение движение по окружности. Равномерное движение по окружности
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.
Положение тела на окружности определяется радиусом-вектором \(~\vec r\), проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).
За время Δt тело, двигаясь из точки А в точку В , совершает перемещение \(~\Delta \vec r\), равное хорде АВ , и проходит путь, равный длине дуги l .
Радиус-вектор поворачивается на угол Δφ . Угол выражают в радианах.
Скорость \(~\vec \upsilon\) движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью . Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:
\(~\upsilon = \frac{l}{\Delta t}. \)
\)
Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью :
\(~\omega = \frac{\Delta \varphi}{\Delta t}.\)
В СИ единицей угловой скорости является радиан в секунду (рад/с).
При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.
Положение тела можно определить, если известен модуль радиуса-вектора \(~\vec r\) и угол φ , который он составляет с осью Ox (угловая координата). Если в начальный момент времени t 0 = 0 угловая координата равна φ 0 , а в момент времени t она равна φ , то угол поворота Δφ радиуса-вектора за время \(~\Delta t = t — t_0 = t\) равен \(~\Delta \varphi = \varphi — \varphi_0\). Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности :
\(~\varphi = \varphi_0 + \omega t.
Оно позволяет определить положение тела в любой момент времени t . Учитывая, что \(~\Delta \varphi = \frac{l}{R}\), получаем\[~\omega = \frac{l}{R \Delta t} = \frac{\upsilon}{R} \Rightarrow\]
\(~\upsilon = \omega R\) — формула связи между линейной и угловой скоростью.
Промежуток времени Τ , в течение которого тело совершает один полный оборот, называется периодом вращения :
\(~T = \frac{\Delta t}{N},\)
где N — число оборотов, совершенных телом за время Δt .
За время Δt = Τ тело проходит путь \(~l = 2 \pi R\). Следовательно,
\(~\upsilon = \frac{2 \pi R}{T}; \ \omega = \frac{2 \pi}{T} .\)
Величина ν , обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения :
\(~\nu = \frac{1}{T} = \frac{N}{\Delta t}.\)
Следовательно,
\(~\upsilon = 2 \pi \nu R; \ \omega = 2 \pi \nu .\)
Литература
Аксенович Л.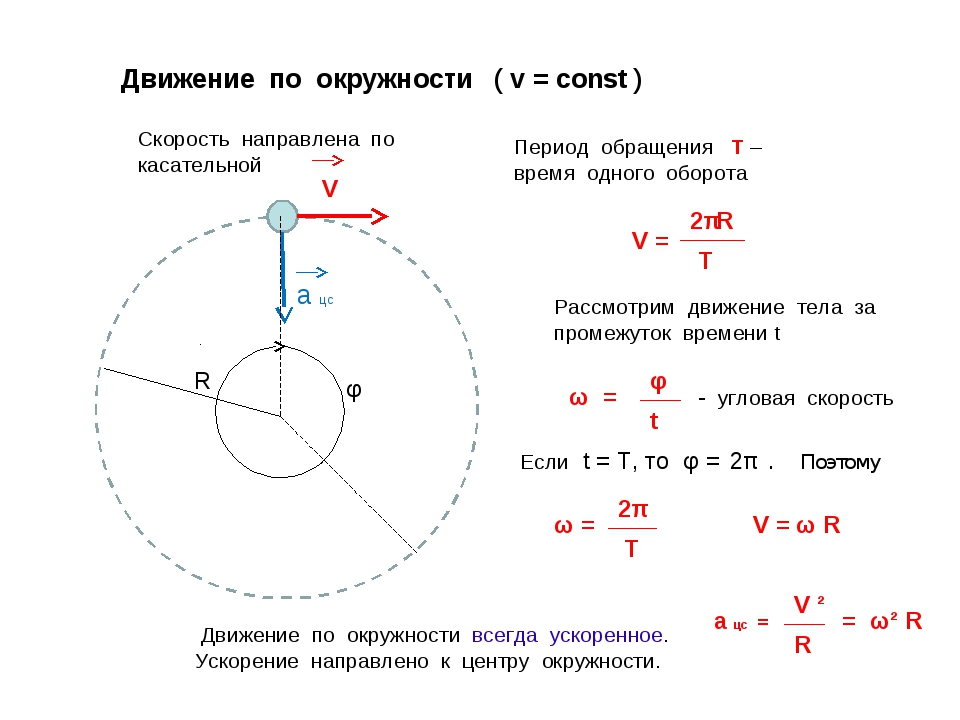 А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 18-19.
А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 18-19.
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назватьравномерным , оно являетсяравноускоренным .
Угловая скорость
Выберем на окружности точку1 . Построим радиус. За единицу времени точка переместится в пункт2 . При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращенияT — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют
линейной. Направление вектора
линейной скорости всегда совпадает с касательной к окружности. Например,
искры из-под точильного станка двигаются, повторяя направление мгновенной
скорости.
Направление вектора
линейной скорости всегда совпадает с касательной к окружности. Например,
искры из-под точильного станка двигаются, повторяя направление мгновенной
скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть периодT .Путь , который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив
и для вращательного движения. Если движение тела или системы отсчета не является
равномерным, то закон применяется для мгновенных скоростей. Например, скорость
человека, идущего по краю вращающейся карусели, равна векторной сумме линейной
скорости вращения края карусели и скорости движения человека.
Если движение тела или системы отсчета не является
равномерным, то закон применяется для мгновенных скоростей. Например, скорость
человека, идущего по краю вращающейся карусели, равна векторной сумме линейной
скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона
причиной любого ускорения является сила. Если движущееся тело
испытывает центростремительное ускорение, то природа сил,
действием которых вызвано это ускорение, может быть различной.
Например, если тело движется по окружности на привязанной к нему
веревке, то действующей силой является сила упругости.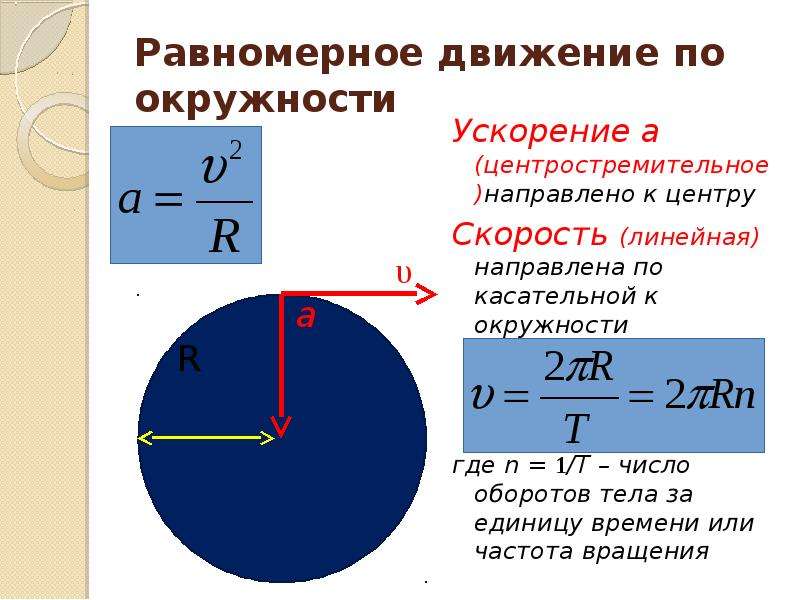
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
 Равномерное движение по окружности. Система отсчёта. Траектория, перемещение, путь, уравнение движения, скорость, ускорение, связь линейной и угловой скорости.
Равномерное движение по окружности. Система отсчёта. Траектория, перемещение, путь, уравнение движения, скорость, ускорение, связь линейной и угловой скорости. интерференция…)
интерференция…) Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор.
Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор. Среднее квадратическое отклонение (ошибка). Таблица определения погрешностей косвенных измерений различных функций.
Среднее квадратическое отклонение (ошибка). Таблица определения погрешностей косвенных измерений различных функций.Равномерное движение по окружности – это простейший пример . Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость .
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости в этом случае отсутствует (a r = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение () a n или а ЦС. В каждой точке вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен
a ЦС =v 2 / R
Где v – линейная скорость, R – радиус окружности
Рис. 1.22. Движение тела по окружности.
Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то
Угол поворота измеряется в радианах. равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то
1 радиан= l / R
Так как длина окружности равна
l = 2πR
360 о = 2πR / R = 2π рад.
Следовательно
1 рад. = 57,2958 о = 57 о 18’
Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:
ω = φ / t
Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:
v= l / t
Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением
l = Rφ
где R – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
v = l / t = Rφ / t = Rω или v = Rω
Рис. 1.23. Радиан.
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.
n = 1 / T
За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда
T = 2π / ω
То есть угловая скорость равна
ω = 2π / T = 2πn
Центростремительное ускорение можно выразить через период Т и частоту обращения n:
a ЦС = (4π 2 R) / T 2 = 4π 2 Rn 2
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆ l = R ∆ φ
Если угол поворота мал, то ∆ l ≈ ∆ s .
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду (р а д с).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.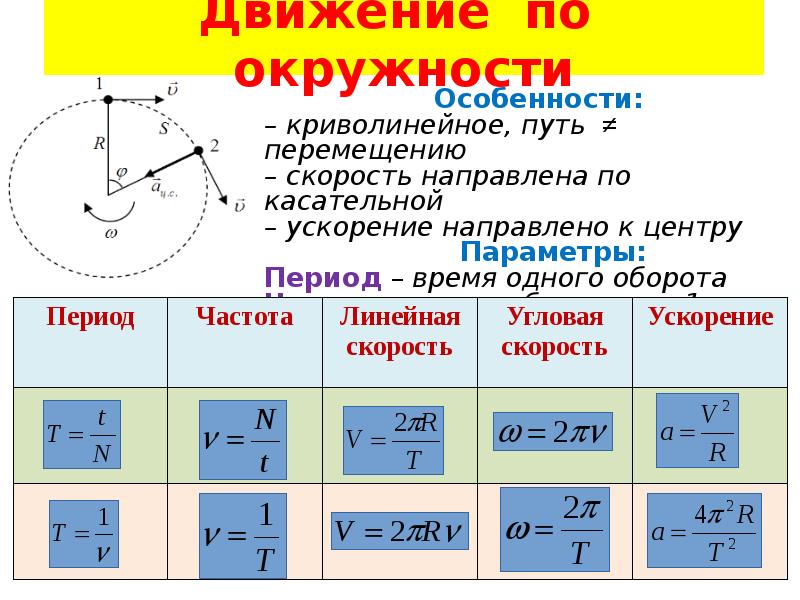
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
a n → = — ω 2 R → .
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Равномерное движение по окружности
Как известно, год, но Земле длится примерно 365 дней и соответствует периоду обращения земли вокруг Солнца. Период обращения Т — это время одного оборота. Проще всего его найти в случае равномерного кругового движения – он будет равен отношению длины окружности l=2пR к скорости, с которой движется тело:
T=(2пR)/v
Скорость V в этой формуле называется линейной. Она показывает путь, пройденный телом за единицу времени. Помимо линейной движение по окружности характеризуется также угловой скоростью w.
 Угловая скорость выражает не путь, а угол, на который поворачивается радиус-вектор частицы за единицу времени, и потому она определяется следующим образом: w=a/t. Поскольку одному обороту соответствует угол a=2п радиан и время t=T, то угловую скорость можно представить в виде:
Угловая скорость выражает не путь, а угол, на который поворачивается радиус-вектор частицы за единицу времени, и потому она определяется следующим образом: w=a/t. Поскольку одному обороту соответствует угол a=2п радиан и время t=T, то угловую скорость можно представить в виде:
T=(2пR)/T=v/R
При равномерном движений по окружности неизменным остаётся лишь модуль линейной скорости, направлений её, напротив, изменяется непрерывно. Этого достаточно, чтобы ускорение было отлично от нуля. Правда, оно будет характеризовать не быстроту изменения её числового значения скорости (оно не меняется), а быстроту изменения её направления. Чтобы выяснить, от чего зависит модуль этого ускорения, заметим: чем больше скорость движения (по одной и той же окружности), тем быстрее изменяется направление вектора скорости и, следовательно, тем больше должно быть ускорение. Если же при неизменной скорости увеличивать радиус окружности, то каждый её участок (проходит за данное время) будет все более приближаться к прямой линий, а движение – всё больше походить на равномерное прямолинейное.
 Но про равномерное прямолинейном движении а =0. Поэтому с ростом радиуса окружности модуль ускорения должен уменьшаться.
Таким образом, можно предположить, что при равномерном круговом движении ускорение тела прямопропорционально скорости движения и обратно пропорционально радиусу окружности, т.е. ровно отношению v/R. Однако размерность этого отношения (1/с) отличаются от размерности ускорения (м/с2). Чтобы добиться совпадения их размерностей, достаточно скорость в рассматриваемом отношений на её квадрат. Разделив (м/с)2 на (м), мы действительно получим (м/с2). Линейная скорость равна:V=wR Следовательно,
Но про равномерное прямолинейном движении а =0. Поэтому с ростом радиуса окружности модуль ускорения должен уменьшаться.
Таким образом, можно предположить, что при равномерном круговом движении ускорение тела прямопропорционально скорости движения и обратно пропорционально радиусу окружности, т.е. ровно отношению v/R. Однако размерность этого отношения (1/с) отличаются от размерности ускорения (м/с2). Чтобы добиться совпадения их размерностей, достаточно скорость в рассматриваемом отношений на её квадрат. Разделив (м/с)2 на (м), мы действительно получим (м/с2). Линейная скорость равна:V=wR Следовательно,
ац=v2/R=w2R=Vw
Строго говоря, в правую часть формулы нужно было бы добавить безразмерный коэффициент пропорциональности. Однако расчёты показывают, что он равен единице. Приведенная выше формула позволяет определить модуль ускорения. Поскольку ускорение – величина векторная, она характеризуется не только числовым значением, но и направлением.
 Куда же оно направленно при равномерном движении по окружности? Понятно, что не в ту же сторону, что и скорость (это привело бы к её увеличению, и движение перестало бы быть равномерным), но и не в противоположную сторону. Ускорение тела в данном случае всё время направлено под прямым углом к вектору скорости, а именно к центру окружности, по которой движется тело.
Данное обстоятельство помогло установить причину обращения Земли (а также других планет) вокруг Солнца. До Галилея и Ньютона эта причина (сила) связывалась со скоростью тела. Но смотреть в направлении движения Земли бесполезно. Ничего особенного мы там не увидим. Если же посмотреть в сторону ускорения нашей планеты, можно увидеть там Солнце. Поэтому именно Солнце естественно считать тем источником силы, который заставляет двигаться Землю.
Куда же оно направленно при равномерном движении по окружности? Понятно, что не в ту же сторону, что и скорость (это привело бы к её увеличению, и движение перестало бы быть равномерным), но и не в противоположную сторону. Ускорение тела в данном случае всё время направлено под прямым углом к вектору скорости, а именно к центру окружности, по которой движется тело.
Данное обстоятельство помогло установить причину обращения Земли (а также других планет) вокруг Солнца. До Галилея и Ньютона эта причина (сила) связывалась со скоростью тела. Но смотреть в направлении движения Земли бесполезно. Ничего особенного мы там не увидим. Если же посмотреть в сторону ускорения нашей планеты, можно увидеть там Солнце. Поэтому именно Солнце естественно считать тем источником силы, который заставляет двигаться Землю.
теория, как решать, примеры на равноускоренное
Человек регулярно сталкивается с разными видами движения. Перемещение тела по окружности позволяет понять многие физические процессы. На основе закономерностей такого явления работают разнообразные механизмы. Рассчитать характеристики движения по окружности достаточно просто, если знать и уметь применять несколько основных формул.
Перемещение тела по окружности позволяет понять многие физические процессы. На основе закономерностей такого явления работают разнообразные механизмы. Рассчитать характеристики движения по окружности достаточно просто, если знать и уметь применять несколько основных формул.
Движение тела по окружности — какими законами описывается
Движением по окружности в теории называют вращение какой-либо материальной точки или тела относительно оси, неподвижной в выбранной системе отсчета и не проходящей через центр тела.
Тело может двигаться по окружности двумя способами:
- равномерно;
- неравномерно.
Равномерное движение тела характеризуется постоянной угловой скоростью. Для описания такого перемещения применяют следующие формулы:
- угловая скорость: \(\omega =\frac{2\pi }{T}\)
- скорость движения: \(V =\frac{2\pi R}{T}=\omega R\)
- угол поворота: \(\phi =2\pi \frac{t}{T}=\omega t\)
- ускорение: \(\frac{2\pi v}{T}=\omega ^{2}R\)
Неравномерное движение возможно при переменной угловой скорости тела. {2}R\)
{2}R\)
В представленных уравнениях используются такие параметры, как:
- Т — период вращения;
- t — время;
- ω — угловая скорость;
- R — радиус;
- at — тангенциальное ускорение;
- an — центростремительное или полное ускорение.
При отсутствии специальных оговорок, в процессе решения задач движение тела по окружности принимают за равномерное. Для расчета пройденного пути используют формулу:
\(S=\frac{v}{t}\)
где:
- S является расстоянием, которое преодолело тело;
- v представляет собой скорость движения тела;
- t определяет время движения.
Таким образом, справедливы выражения:
\(v=\frac{S}{t}\)
\(t =\frac{v}{S}\)
Величины, которые применяют для решения задач, характеризуются положительными значениями:
S > 0, v > 0, t > 0
При решении задач принято все величины переводить в единицы измерения, согласно системе СИ.
Секретом заданий на движение тела по окружности является то, что обгоняющий будет преодолевать на 1 круг больше при первом обгоне. Данное расстояние считается на n кругов больше, если первый объект обогнал другого в n-ый раз.
Источник: phototass3.cdnvideo.ruЗадачи на движение по окружности от простых до сложных
Задачи на движение тела по окружности отличаются по степени сложности. Можно рассмотреть примеры простых заданий.
Задача 1
Длина круговой трассы составляет 8 километров. Из ее точки в один момент времени в одинаковом направлении выехали два автомобиля. Первый автомобиль развил скорость 114 км/ч и, спустя 20 минут после начала движения, обогнал второй автомобиль на один круг. Требуется определить скорость, с которой двигался второй автомобиль. Ответ необходимо представить в км/ч.
Решение
Известно, что старт произошел одновременно для обоих автомобилей. Через 20 минут после начала движения первое транспортное средство опережало второе на один круг. Таким образом, в течение 20 минут или 1/3 часа первый автомобиль преодолел на 1 круг больше, то есть на 8 км больше. За час первый автомобиль проехал на 8*3=24 км больше, чем второй. Скорость второго транспортного средства на 24 км/ч меньше по сравнению с первым, и равна 114-24=90 км/ч.
Таким образом, в течение 20 минут или 1/3 часа первый автомобиль преодолел на 1 круг больше, то есть на 8 км больше. За час первый автомобиль проехал на 8*3=24 км больше, чем второй. Скорость второго транспортного средства на 24 км/ч меньше по сравнению с первым, и равна 114-24=90 км/ч.
Ответ: второй автомобиль двигался со скоростью 90 км/ч.
Задача 2
Из пункта А круговой трассы выехал велосипедист, а спустя полчаса стартовал мотоциклист. Через 10 минут после начала пути водитель мотоцикла догнал велосипедиста в первый раз. Спустя еще 30 минут мотоциклист догнал велосипедиста повторно. Требуется определить, какова скорость мотоциклиста, в том случае, когда длина трассы составляет 30 км. Ответ необходимо представить в км/ч.
Решение
В первую очередь требуется перевести минуты в часы. Скорости мотоциклиста и велосипедиста можно обозначить х и у. В первый раз водитель мотоцикла обогнал велосипедиста, спустя 10 минут или 1/6 часа после начала движения. До этого момента велосипедист находился в движении 40 минут или 2/3 часа.
До этого момента велосипедист находился в движении 40 минут или 2/3 часа.
Можно упростить запись условий задачи:
велосипедист: v = х, t = 2/3, S = 2/3*х;
мотоциклист: v = у, t = 1/6, S = 1/6*у.
Велосипедист и мотоциклист преодолели одинаковый путь:
\(\frac{1}{6}y=\frac{2}{3}x\)
Спустя 30 минут или 1/2 часа после первого обгона мотоциклист выполнил второй обгон велосипедиста.
Таким образом:
велосипедист: v = х, t = 1/2, S = 1/2*х;
мотоциклист: v = у, t = 1/2, S = 1/2*у.
Требуется определить расстояния, которые преодолели гонщики. Мотоциклист обогнал велосипедиста, то есть проехал больше на один круг. Это является ключевым моментом в данной задаче. Один круг составляет 30 километров. Второе уравнение будет иметь вид:
\(\frac{1}{2}y-\frac{1}{2}x=30\)
Далее необходимо решить полученную систему:
у = 4х
у – х = 60
Таким образом, х = 20, у = 80.
Ответ: скорость мотоциклиста равна 80 км/ч.
Бывают задания на движение тела по окружности с повышенной степенью сложности. Как правило, подобные примеры при невозможности проведения экспериментов требуют сложных вычислений.
Задача 3
На часах со стрелками время 8 часов 00 минут. Требуется определить, через сколько минут минутная стрелка в четвертый раз догонит часовую стрелку.
Решение
Спустя один час минутная стрелка преодолевает один круг, а часовая проходит лишь 1/12 циферблата. Допустим, что скорости равны 1 круг в час и 1/12 круга в час соответственно. Начало движения приходится на 8.00. Необходимо определить время, в течение которого минутной стрелке в первый раз удастся догнать часовую.
Минутная стрелка преодолеет на 2/3 круга больше. Исходя из этого, можно записать уравнение:
\(1*t-\frac{1}{12}t=\frac{2}{3}\)
Таким образом, спустя 8/11 часа стрелки совпадут. Предположим, что через время z стрелки совпадут повторно. Минутная стрелка преодолеет расстояние 1*z, а часовая 1/12*z. При этом минутной стрелкой будет пройдено на один круг больше. Можно записать уравнение:
При этом минутной стрелкой будет пройдено на один круг больше. Можно записать уравнение:
\(1*z-\frac{1}{12}z=1\)
Решение данного уравнения будет таким:
\(z=\frac{12}{11}\)
Таким образом, через 12/11 часа стрелки совпадут повторно. Спустя еще 12/11 часа они встретятся вновь и так далее. Поэтому при старте в 8.00 в четвертый раз минутная стрелка догонит часовую через:
\(\frac{8}{11}+3\frac{12}{11}\) часа
Ответ: минутная и часовая стрелки совпадут в четвертый раз через \(\frac{8}{11}+3\frac{12}{11}\)часа.
Нередко при решении задач на движение по окружности требуется рассчитать среднюю скорость тела. Важно, что данная величина не совпадает со средним арифметическим скоростей. Средняя скорость определяется с помощью формулы:
\(v=\frac{S_{0}}{t_{0}}\)
где v является средней скоростью;
S0 представляет собой общий путь;
t0 определяет общее время.
При наличии двух участков пути средняя скорость рассчитывается по формуле:
\(v=\frac{S_{1}+S_{2}}{t_{1}+t_{2}}\)
Наиболее сложными задачами считаются примеры с пятизначными дискриминантами. Рассмотрим алгоритм действий в таком случае.
Рассмотрим алгоритм действий в таком случае.
Задача 4
Пара гонщиков участвует в соревновании. Путь, который требуется преодолеть, равен 60 кругам кольцевой трассы в 3 км. После одновременного старта первый гонщик пересек финиш раньше, чем второй на 10 минут. Требуется рассчитать среднюю скорость второго гонщика. Известно, что впервые первый участник обогнал второго на круг, спустя 15 минут после начала движения. Ответ требуется записать в км/ч.
Решение
Первый участник гонки, находясь в движении 15 минут, догнал второго гонщика на первом круге. Таким образом, в течение 15 минут он преодолел на 1 круг или на 3 км больше, чем второй. За час первый гонщик проехал 3*4=12 километров больше. При этом скорость его движения на 12 км/ч превышает скорость второго гонщика. 10 минут соответствует ¼ часа. Можно записать уравнение:
\(\frac{180}{x}-\frac{180}{x+12}=\frac{1}{6}\)
Далее необходимо преобразовать выражение к квадратному уравнению:
\(x^{2}+12x-12960=0\)
Таким образом, получен пятизначный дискриминант. Есть более простой вариант решения задачи. Можно записать уравнение:
Есть более простой вариант решения задачи. Можно записать уравнение:
\(\frac{180}{x}-\frac{180}{x+12}=\frac{1}{6}\)
В нем 180 можно поделить на 12. Заменим х=12z:
\(\frac{180}{12z}-\frac{180}{12z+12}=\frac{1}{6}\)
\(\frac{15}{z}-\frac{15}{z+1}=\frac{1}{6}\)
\(\frac{90}{z}-\frac{90}{z+1}=1\)
Данное равенство можно преобразить в квадратное уравнение. Целый положительный корень такого выражения z=9. Тогда получим:
\(х=12z=108\)
Ответ: средняя скорость второго гонщика равна 108 км/ч.
Нахождение линейной скорости при движении по окружности
Любая точка, находящаяся на окружности, перемещается с некоторой скоростью. Данная величина называется линейной скоростью. Вектор линейной скорости всегда совпадает по направлению с касательной к окружности. К примеру, стружка из точильного станка движется, повторяя направление мгновенной скорости.
Источник: msk.edu.uaМожно рассмотреть какую-то точку на окружности, совершившую один оборот. При этом было затрачено время равное периоду Т. Расстояние или путь, пройденный точкой, представляет собой длину рассматриваемой окружности.
При этом было затрачено время равное периоду Т. Расстояние или путь, пройденный точкой, представляет собой длину рассматриваемой окружности.
Задачи на тему равномерное движение по окружности
Задача 1
Радиус выпуклого моста равен 90 м. Требуется определить скорость, с которой автомобиль должен пройти его середину, чтобы пассажир на мгновение ощутил невесомость.
Решение
Согласно условиям задачи:
R = 90 м
N = 0
Сила реакции опоры обладает нулевым значением, так как пассажир в состоянии невесомости не оказывает давление на сиденье автомобиля.
Источник: static-interneturok.cdnvideo.ruРешение задачи необходимо представить в системе отсчета, которая связана с Землей. Человек совершает движение вместе с автомобилем. Ускорение при этом направлено вниз. На пассажира действует сила притяжения Земли, которая будет центростремительной:
\(mg=m\frac{v^{2}}{R}\)
Таким образом:
\(v=\sqrt{\frac{Rmg}{m}}=\sqrt{Rg}=\sqrt{90*10}=30\) м/с
Ответ: скорость автомобиля составляет 30 м/с. {2}=gl*\sin \alpha *\tan \alpha \)
{2}=gl*\sin \alpha *\tan \alpha \)
\(v=\sqrt{gl*\sin \alpha *\tan \alpha }=\sqrt{10*0.6*\frac{\sqrt{3}}{2}*\sqrt{3}}=3\) м/с
Ответ: скорость шарика составляет 3 м/с.
Задача 4
Необходимо определить максимальную скорость мотоцикла по горизонтальной плоскости, который описывает при этом дугу окружности с радиусом 100 м. Коэффициент трения резины о плоскость составляет 0,4.
Источник: static-interneturok.cdnvideo.ruРешение
Во время поворота мотоцикл наклоняется к центру поворота. На транспортное средство оказывают действие:
- сила тяжести \(m\vec{g}\);
- сила реакции опоры \(\vec{N}\);
- сила трения \(\vec{F_{tr}}\);
- сила тяги \(\vec{F_{t}}\);
- сила сопротивления \(\vec{F_{c}}\).
Данные силы в сумме составляют:
\(m\vec{g}+\vec{N}+\vec{F_{tr}}+\vec{F_{t}}+\vec{F_{c}}= m\vec{a}\)
Согласно выражениям:
\(m\vec{g}+\vec{N}=0\)
\(\vec{F_{t}}+\vec{F_{c}}=0\)
Получим:
\(\vec{F_{tr}}= m\vec{a}\)
Сила трения составляет:
\(F_{tr}= \mu mg\)
Таким образом:
\(\mu mg=ma= m\frac{v^{2}}{R}\)
\(v=\sqrt{\frac{\mu mgR}{m}}=\sqrt{\mu gR}=\sqrt{0. 4*10*100}=20\) м/с
4*10*100}=20\) м/с
Ответ: максимальная скорость равна 20 м/с.
Источник: avatars.mds.yandex.netЗадачи разной сложности по теме движения тела по кружности часто встречаются не только в школьной программе, но и во время обучения в вузе. Знание основных закономерностей позволит быстро найти решение примера любой сложности. Если в процессе расчетов возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.
Движение по окружности: формулы и расчеты
Перемещение тел по окружности достаточно распространено в нашей жизни и в природе. Яркими примерами этого типа перемещения являются вращения ветровых мельниц, планет вокруг своих звезд и колес транспортных средств. В данной статье рассмотрим, какими формулами движение по окружности тел описывается.
Перемещение по окружности и по прямой линии в физике
В физике вопросами движения занимается кинематика. Она устанавливает связь между величинами, описывающими этот процесс. В динамике также уделяется внимание движению, однако она ориентирована на описание причин его возникновения. Другими словами, если для кинематики главными физическими величинами являются путь и скорость, то для динамики — это действующие на тела силы.
В динамике также уделяется внимание движению, однако она ориентирована на описание причин его возникновения. Другими словами, если для кинематики главными физическими величинами являются путь и скорость, то для динамики — это действующие на тела силы.
В физике принято выделять два идеальных типа траекторий движения:
- прямая линия;
- окружность.
Математический аппарат для описания движения по обоим типам траекторий развит настолько хорошо, что понимание формул, например для прямолинейного движения, автоматически приводит к пониманию выражений для движения по окружности. Единственная принципиальная разница между формулами указанных типов перемещения заключается в том, что для движения по окружности удобно использовать угловые характеристики, а не линейные.
Далее в статье будем рассматривать исключительно кинематические формулы движения по окружности тел, не вдаваясь в подробности динамики.
Угловые характеристики движения: угол поворота
Прежде чем записывать формулы движения по окружности в физике, следует ввести величины, которые будут фигурировать в этих формулах.
Начнем с угла поворота. Будем обозначать его греческой буквой θ (тета). Поскольку вращение предполагает движение точки вдоль одной и той же окружности, то значение угла поворота θ за определенный промежуток времени можно использовать для определения количества оборотов, которое сделала эта точка. Напомним, что вся окружность равна 2*pi радиан, или 360o. Тогда формула для числа оборотов n через угол θ примет вид:
n = θ/(2*pi)
Здесь и далее во всех формулах угол выражается в радианах.
Пользуясь известным углом θ, также можно определить линейное расстояние, которое точка прошла вдоль окружности. Это расстояние будет равно:
L = θ*r
Здесь r — радиус рассматриваемой окружности.
Угловая скорость и ускорение
Кинематические формулы движения по окружности точки предполагают также использование понятий угловой скорости и углового ускорения. Обозначим первую буквой ω (омега), а вторую буквой α (альфа).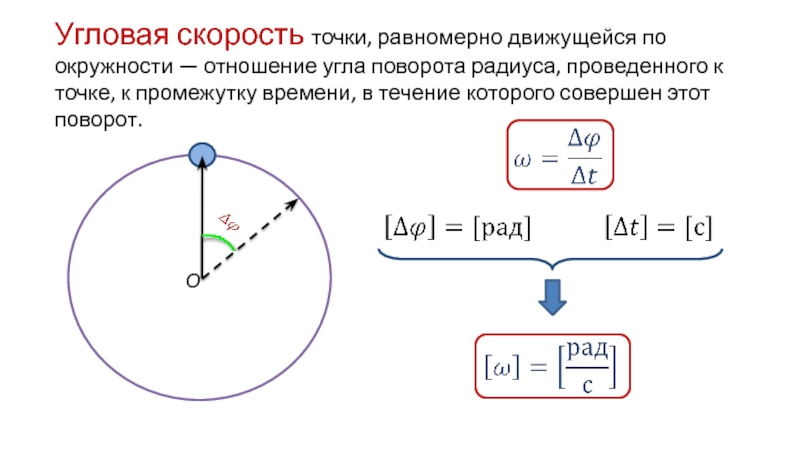
Физический смысл угловой скорости ω прост: эта величина показывает, на какой угол в радианах поворачивается точка за каждую секунду времени. Данное определение имеет следующее математическое представление:
ω = dθ/dt
Эта формула скорости движения по окружности записана в дифференциальной форме. Полученная с ее помощью величина ω называется мгновенной скоростью. Ее удобно использовать, если движение не является равномерным, то есть происходит с переменной скоростью.
Угловое ускорение α — это величина, которая описывает быстроту изменения скорости ω, то есть:
α = dω/dt
Угловое ускорение измеряется в радианах в секунду квадратную (рад/с2). Так, 1 рад/с2 означает, что тело увеличивает за каждую секунду времени скорость на 1 рад/с.
Учитывая выражение для ω, записанное выше, равенство можно представить в такой форме:
α = d2θ/dt2
В зависимости от особенностей движения по окружности величина α может быть постоянной, переменной или нулевой.
Равномерное движение
Когда на вращающееся тело не действует никакая внешняя сила, то угловая скорость будет оставаться постоянной сколь угодно длительное время. Такое движение получило название равномерного вращения. Оно описывается следующей формулой:
θ = ω*t
В этом выражении переменными являются всего две величины: t и θ. Скорость ω = const.
Следует отметить один важный момент: нулю равна лишь равнодействующая внешних сил на тело, внутренние же силы, действующие в системе, нулю не равны. Так, внутренняя сила заставляет вращающееся тело изменять свою прямолинейную траекторию на криволинейную (окружность). Эта сила приводит к появлению центростремительного ускорения. Последнее не изменяет ни скорость ω, ни линейную скорость v, оно лишь изменяет направление движения.
Равноускоренное движение по окружности
Формулы для этого типа перемещения можно получить непосредственно из приведенных математических выражений для величин ω и α. Равноускоренное движение предполагает, что за более-менее длительный промежуток времени модуль и направление ускорения α не изменяются. Благодаря этому можно проинтегрировать дифференциальное выражение для α и получить следующие две формулы:
Равноускоренное движение предполагает, что за более-менее длительный промежуток времени модуль и направление ускорения α не изменяются. Благодаря этому можно проинтегрировать дифференциальное выражение для α и получить следующие две формулы:
ω = ω0 + α*t;
ω = ω0 — α*t
Очевидно, что в первом случае движение будет равноускоренным, во втором — равнозамедленным. Величина ω0 здесь — это некоторая начальная скорость, которой вращающееся тело обладало до появления ускорения.
Для равноускоренного движения не существует конечной скорости, поскольку она может возрастать сколь угодно долго. Для равнозамедленного движения конечным состоянием будет прекращение вращения, то есть ω = 0.
Теперь запишем формулы для определения угла θ при движении с постоянным ускорением. Эти формулы получаются, если произвести двойное интегрирование по времени для выражения α через θ. Получаются следующие выражения:
θ = ω0*t + α*t2/2;
θ = ω0*t — α*t2/2
То есть центральный угол θ, на который тело повернется за время t, будет равен сумме двух слагаемых. Первое слагаемое — это вклад в θ равномерного движения, второе — равноускоренного (равнозамедленного).
Первое слагаемое — это вклад в θ равномерного движения, второе — равноускоренного (равнозамедленного).
Связь между угловыми и линейными величинами
При рассмотрении понятия угла поворота θ уже была приведена формула, которая его связывает с линейным расстоянием L. Здесь же рассмотрим аналогичные выражения для скорости ω и ускорения α.
Линейная скорость v при равномерном движении определяется как расстояние L, пройденное за время t, то есть:
v = L/t
Подставляя сюда выражение для L через θ, получаем:
v = L/t = θ/t*r = ω*r
Мы получили связь между линейной и угловой скоростью. Важно отметить, что удобство использования угловой скорости связано с тем, что она не зависит от радиуса окружности. В свою очередь, линейная скорость v возрастает линейно с увеличением r.
Остается записать связь между линейным ускорением a и его угловым аналогом α. Чтобы это сделать, запишем выражение для скорости v при равноускоренном движении без начальной скорости v0. Получаем:
Получаем:
v = a*t
Подставляем сюда полученное выражение связи между v и ω:
ω*r = a*t =>
a = ω/t*r = α*r
Как и скорость, линейное ускорение, направленное по касательной к окружности, зависит от радиуса.
Ускорение центростремительное
Выше уже было сказано несколько слов об этой величине. Здесь приведем формулы, которые можно использовать для ее вычисления. Через скорость v выражение для центростремительного ускорения ac имеет вид:
ac = v2/r
Через угловую скорость его можно записать так:
ac = ω2*r2/r = ω2*r
Величина ac не имеет никакого отношения к тангенциальному ускорению a. Центростремительное ускорение обеспечивает поддержание вращающегося тела на одной окружности.
Задача на определение угловой скорости вращения планеты
Известно, что ближе всего к солнцу находится Меркурий. Полагая, что он вращается по окружности вокруг светила, мы можем определить его угловую скорость ω.
Полагая, что он вращается по окружности вокруг светила, мы можем определить его угловую скорость ω.
Для решения задачи следует обратиться к справочным данным. Из них известно, что планета делает полный оборот вокруг светила за 87 дней 23,23 часа земных. Это время называется периодом обращения. Учитывая, что движение происходит с постоянной угловой скоростью, запишем рабочую формулу:
θ = ω*t =>
ω = θ/t
Остается перевести время в секунды, подставить значение угла θ, соответствующее полному обороту (2*pi), и записать ответ: ω = 8,26*10-7 рад/c.
Неравномерное движение по окружности в физике
Неравномерное движение по окружности:
Вы в 7 классе ознакомились с равномерным движением по окружности. В данной теме мы рассмотрим неравномерное движение по окружности. Вспомним физические величины, которые описывают равномерное движение по окружности (рис. 1.2).
Величина, численно равная пути, пройденному за единицу времени равномерно двигающейся по дуге окружности материальной точкой, называется линейной скоростью и определяется следующим выражением:
2. Отношение угла поворота радиуса окружности при равномерном движении по окружности ко времени поворота называется угловой скоростью:
Отношение угла поворота радиуса окружности при равномерном движении по окружности ко времени поворота называется угловой скоростью:
Угловая скорость, также как и линейная скорость, считается векторной величиной. Ее направление определяется по правилу правого винта. То есть, если головку винта вращать по направлению вращения тела, то поступательное движение его укажет направление вектора углового перемещения, или угловой скорости (рис. 1.3).
В большинстве случаев тела, совершающие вращательные движения, меняют скорость вращения. Например, в начале движения автомобиля до достижения им определенной скорости или в момент торможении до полной остановки, колеса автомобиля совершают вращательные движения с разной скоростью.
Движение, при котором угловая скорость предмета, совершающего вращательное движение, изменяется по времени называется переменным вращательным движением.
Среди переменных вращательных движений встречаются движения, в которых угловая скорость за любые равные промежутки времени меняется на равные значения. Например, колеса автобуса, который приближается к остановке или отъезжает от нее, совершают равнопеременное вращательное движение. В таких движениях ритм изменения угловой скорости описывается физической величиной, называемой угловым ускорением.
Например, колеса автобуса, который приближается к остановке или отъезжает от нее, совершают равнопеременное вращательное движение. В таких движениях ритм изменения угловой скорости описывается физической величиной, называемой угловым ускорением.
Величина, измеряемая отношением изменения угловой скорости ко времени, за которое произошло это изменение, называется угловым ускорением.
Угловое ускорение при равнопеременном движении с течением времени не меняется, так как угловая скорость такого движения тоже меняется за равные промежутки времени на равные значения. Если начальная угловая скорость двигающейся материальной точки равна , угловая скорость через промежуток времени равна , то изменение угловой скорости будет: . Тогда уравнение (1.12) приобретает вид:
Исходя из этого, единица измерения углового ускорения будет равна . Из выражения (1.13) можно вывести формулу для определения угловой скорости в любой момент времени:
Если угловая скорость в ходе движения растет равномерно, вращательное движение будет равноускоренным (рис.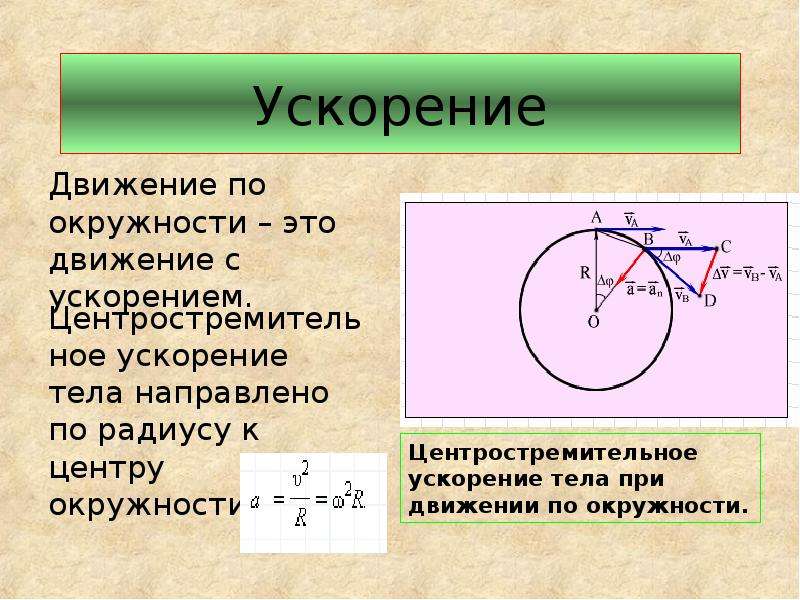 1.4 а). Если угловая скорость вращательного движения в ходе вращения равномерно уменьшается, такое вращательное движение называется равномерно замедленным (рис. 1.4 б).
1.4 а). Если угловая скорость вращательного движения в ходе вращения равномерно уменьшается, такое вращательное движение называется равномерно замедленным (рис. 1.4 б).
Из-за того, что при вращательном движении угловая скорость является векторной величиной, угловое ускорение тоже считается векторной величиной. Так как, в формуле (1.13) является скалярной величиной. В случае , вектор и угловое ускорение совпадает с направлением угловой скорости, а в случае будет, и вектор противонаправлен вектору .
В уравнении равнопеременного прямолинейного движения достаточно заменить пройденный путь на угол поворота , скорость на угловую скорость , ускорение на угловое ускорение чтобы получить уравнение равномерно изменяющегося вращательного движения. Сопоставление этих уравнений для данных видов движения приводится в следующей таблице:
При вращательном движении встречаются случаи, когда меняется количественная величина линейной скорости материальной точки.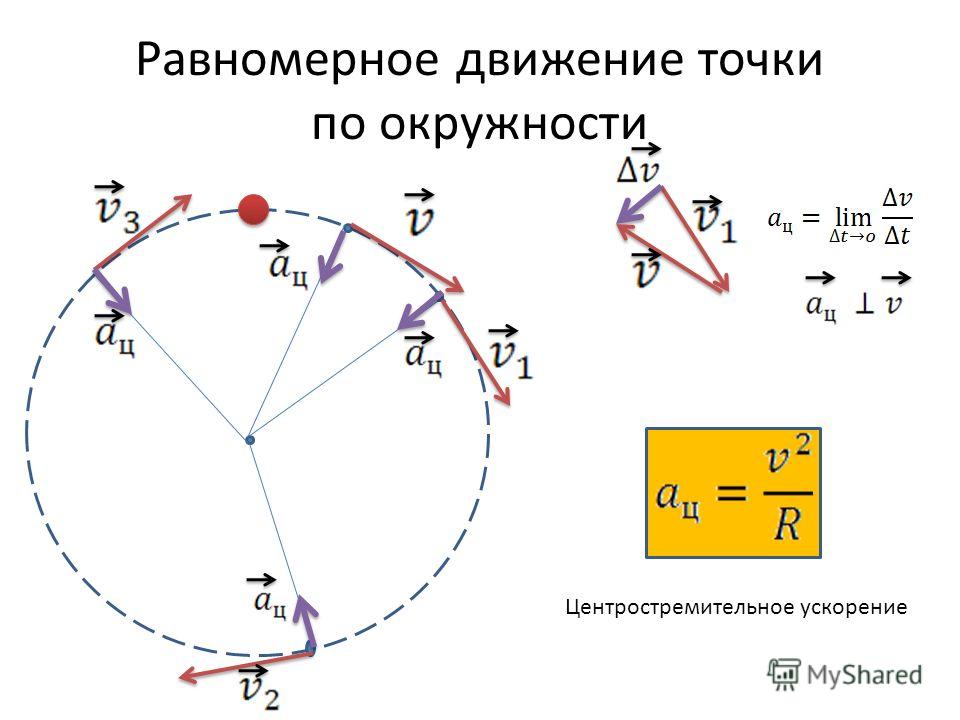 В таких случаях в связи с изменением линейной скорости материальной точки возникает ускорение. Из-за того, что это ускорение появилось в результате изменения количественных величин скорости, его направление совпадает с направлением скорости. Поэтому оно называется касательным, т.е. тангенциальным ускорением и его можно выразить формулой:
В таких случаях в связи с изменением линейной скорости материальной точки возникает ускорение. Из-за того, что это ускорение появилось в результате изменения количественных величин скорости, его направление совпадает с направлением скорости. Поэтому оно называется касательным, т.е. тангенциальным ускорением и его можно выразить формулой:
Таким образом, если меняется линейная скорость материальной точки, совершающей вращательное движение, ее общее ускорение можно определить по формуле:
здесь .
Формула угловой скорости движения тела по окружности. Движение материальной точки по окружности. Угловая скорость и угловое ускорение и их связь с линейными характеристиками движения. Угловая скорость и угловое ускорение
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назватьравномерным , оно являетсяравноускоренным .
Угловая скорость
Выберем на окружности точку1 .
Построим радиус.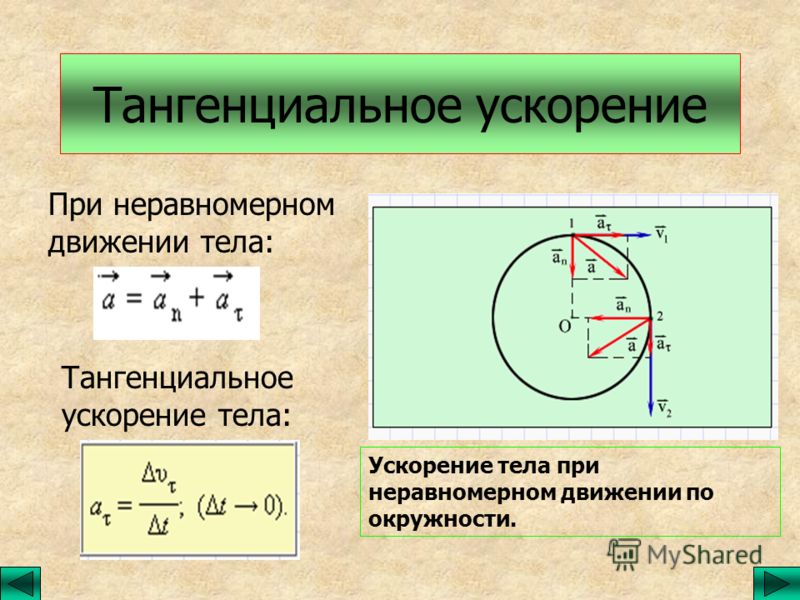 За единицу времени точка переместится в пункт2 .
При этом радиус описывает угол. Угловая скорость численно равна углу поворота
радиуса за единицу времени.
За единицу времени точка переместится в пункт2 .
При этом радиус описывает угол. Угловая скорость численно равна углу поворота
радиуса за единицу времени.
Период и частота
Период вращенияT — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной.Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть периодT .Путь , который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору
скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных
вращательных движениях: суточном (вокруг своей оси) и
орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца
составляет 1 год или 365 суток. Вокруг своей оси Земля вращается
с запада на восток, период этого вращения составляет 1 сутки или
24 часа. Широтой называется угол между плоскостью экватора и
направлением из центра Земли на точку ее поверхности.
Широтой называется угол между плоскостью экватора и
направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна
Теперь перейдем в неподвижную
систему, связанную с землей. Полное ускорение точки А останется
прежним и по модулю, и по направлению, так как при переходе от
одной инерциальной системы отсчета к другой ускорение не
меняется. С точки зрения неподвижного наблюдателя траектория
точки А — уже не окружность, а более сложная кривая (циклоида),
вдоль которой точка движется неравномерно.
Движение по окружности – частный случай криволинейного движения. Скорость тела в любой точке криволинейной траектории направлена по касательной к ней (рис.2.1). Скорость как вектор при этом может изменяться и по модулю (величине) и по направлению. Если модуль скоростиостается неизменным, то говорят оравномерном криволинейном движении.
Пусть тело движется по окружности с постоянной по величине скоростью из точки 1 в точку 2.
При этом тело пройдет путь, равный длине дуги ℓ 12 между точками 1 и 2 за времяt. За это же времяtрадиус- векторR, проведенный из центра окружности 0 к точке, повернется на угол Δφ.
Вектор скорости в точке 2 отличается от вектора скорости в точке 1 по направлению на величину ΔV:
;
Для характеристики изменения вектора скорости на величину δv введем ускорение:
(2.4)
Вектор
в любой точке траектории направлен по
радиусуRкцентру окружности перпендикулярно к вектору
скоростиV 2 . Поэтому
ускорение,
характеризующее при криволинейном
движении изменение скоростипо направлению, называютцентростремительным
или нормальным .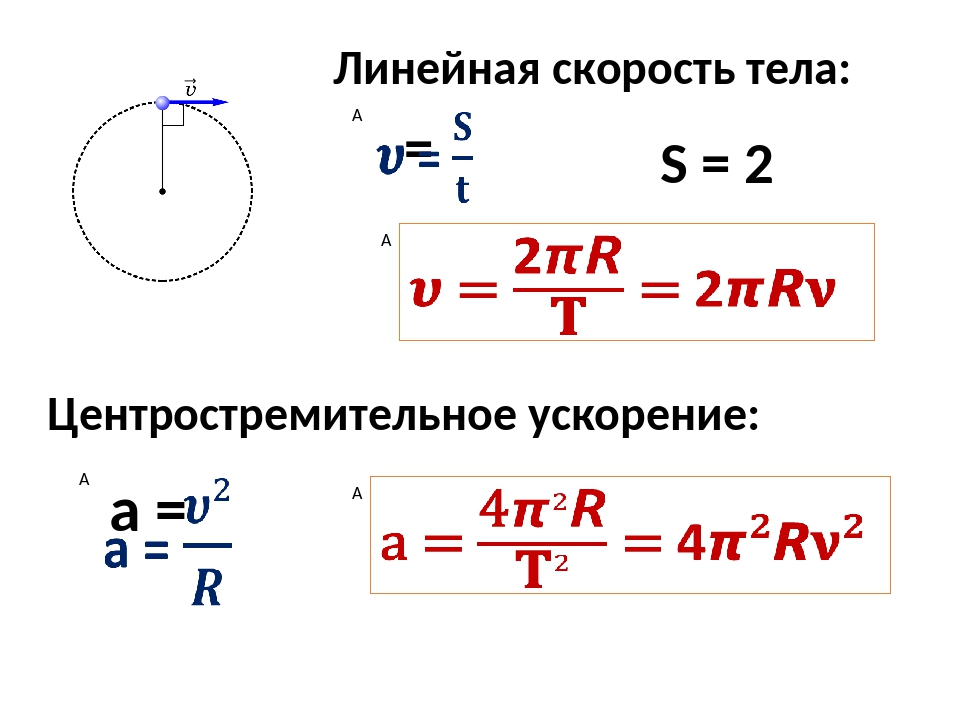 Таким образом, движение
точки по окружности с постоянной по
модулю скоростью являетсяускоренным .
Таким образом, движение
точки по окружности с постоянной по
модулю скоростью являетсяускоренным .
Если скорость изменяется не только по направлению, но и по модулю (величине), то кроме нормального ускорениявводят еще икасательное (тангенциальное) ускорение, которое характеризует изменение скорости по величине:
или
Направлен вектор по касательной в любой точке траектории (т.е. совпадает с направлением вектора). Угол между векторамииравен 90 0 .
Полное ускорение точки, движущейся по криволинейной траектории, определяется как векторная сумма (рис.2.1.).
.
Модуль вектора
.
Угловая скорость и угловое ускорение
При движении материальной точки по окружности радиус-векторR, проведенный из центра окружности О к точке, поворачивается на угол Δφ (рис.2.1). Для характеристики вращения вводятся понятия угловой скорости ω и углового ускорения ε.
Угол φ можно измерять в радианах. 1 рад равен углу, который опирается на дугу
ℓ, равную радиусуRокружности, т. е.
е.
илиℓ 12 = R φ (2.5.)
Продифференцируем уравнение (2.5.)
(2.6.)
Величина dℓ/dt=V мгн. Величину ω =dφ/dtназываютугловой скоростью (измеряется в рад/с). Получим связь между линейной и угловой скоростями:
Величина
ω векторная. Направление вектораопределяетсяправилом винта (буравчика) :
оно совпадает с направлением перемещения
винта, ориентированного вдоль оси
вращения точки или тела и вращаемого в
направлении поворота тела (рис.2.2), т.е.
.
Угловым ускорением называется векторная величина производная от угловой скорости (мгновенное угловое ускорение)
, (2.8.)
Вектор совпадает с осью вращения и направлен в туже сторону, что и вектор, если вращение ускоренное, и в противоположную, если вращение замедленное.
Число оборотов n тела в единицу времени называют частотой вращения .
Время Т одного полного оборота тела
называют периодом вращения .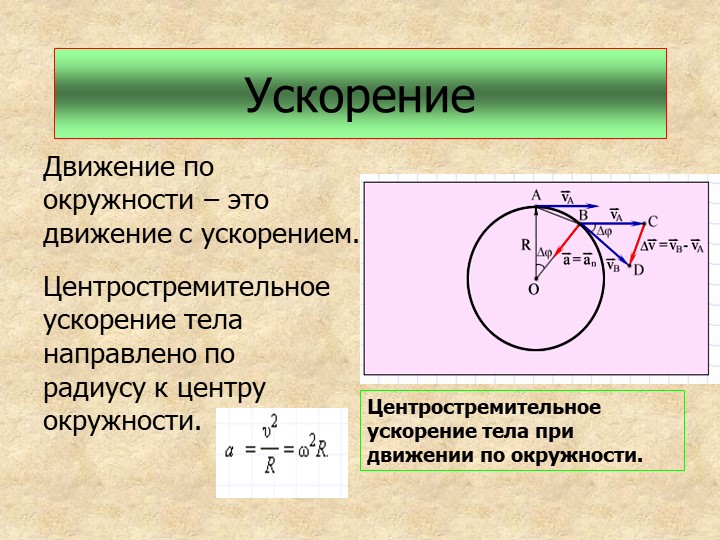 При этом R опишет
угол Δφ=2π радиан
При этом R опишет
угол Δφ=2π радиан
С учетом сказанного
, (2.9)
Уравнение (2.8) можно записать следующим образом:
(2.10)
Тогда тангенциальная составляющая ускорения
а =R(2.11)
Нормальное ускорение а n можно выразить следующим образом:
с учетом (2.7) и (2.9)
(2.12)
Тогда полное ускорение .
Для вращательного движения с постоянным угловым ускорением можно записать уравнение кинематики по аналогии с уравнением (2.1) – (2.3) для поступательного движения:
,
.
1 . Колесо при вращении имеет угловую скорость 10π рад/с. После торможения, за минуту его скорость уменьшилась до 6π рад/с. Найдите угловое ускорение колеса.
2 . Маховик начал вращаться равноускоренно и за 10 с достиг угловой скорости 10π рад/с. Определите угловое ускорение маховика.
3 . Укажите направление тангенциального ускорения в точках A , B , C , D при движении по окружности по часовой стрелке (рис. 1), если:
1), если:
а) если скорость увеличивается;
б) уменьшается.
4 . Определите тангенциальное ускорение колеса радиуса 30 см, если он начинает тормозить с угловым ускорением 0,2 рад/с 2 .
5 . Определите угловое ускорение вала электродвигателя радиуса 0,5 см, если его тангенциальное ускорение равно 1 см/с 2 .
6 . Сравните формулы, описывающие равноускоренное движение по прямой и по окружности, и, используя метод аналогии, заполните таблицу.
| № | Величины и формулы | Равноускоренное движение по прямой (линейные величины) | Равноускоренное движение по окружности (угловые величины) |
|---|---|---|---|
| 1 | Скорость начальная | υ 0 | |
| 2 | Скорость конечная | υ | |
| 3 | Перемещение | Δr | |
| 4 | Ускорение | a | |
| 5 | Формула для расчета ускорения | \(~a_x = \frac{\upsilon_x — \upsilon_{0x}}{t}\) | |
| 6 | Формула для расчета скорости.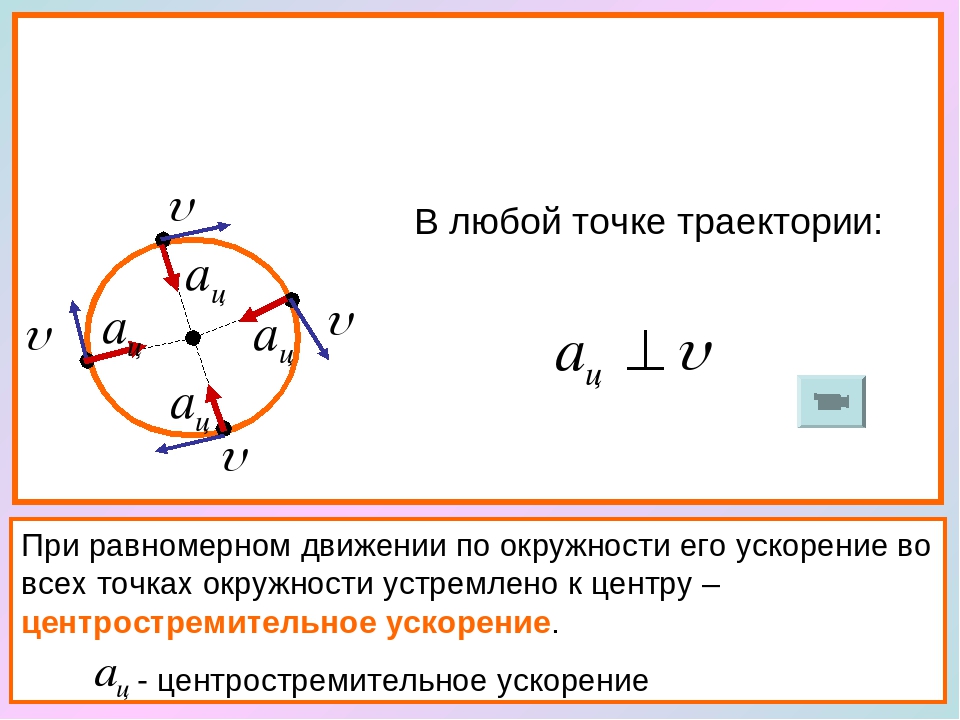 2_{0x}}{2 a_x}\) ; 2_{0x}}{2 a_x}\) ; |
7 . Маховик начал вращаться равноускоренно и через 10 с стал вращаться с периодом 0,2 с. Определите:
б) угловое перемещение, которое он сделает за это время.
8 . Маховик, вращающийся с частотой 2 Гц, останавливается в течении 1,5 мин. Считая движение маховика равнозамедленным, определите:
а) угловое ускорение маховика;
б) угловое перемещение маховика до полной остановки.
9 . Диск вращается с угловым ускорением 2 рад/с 2 . Определите угловое перемещение диска при изменении частоты вращения от 4 Гц до 1,5 Гц?
10 . Колесо, вращаясь равнозамедленно, при торможении уменьшило свою частоту за 1 мин от 5 Гц до 3 Гц. Найдите угловое перемещение, которые совершило колесо за время торможения.
Уровень
C1 . Маховик начинает вращаться равноускоренно из состояния покоя и за первые 2 мин делает 3600 оборотов. Найдите угловое ускорение маховика.
2 .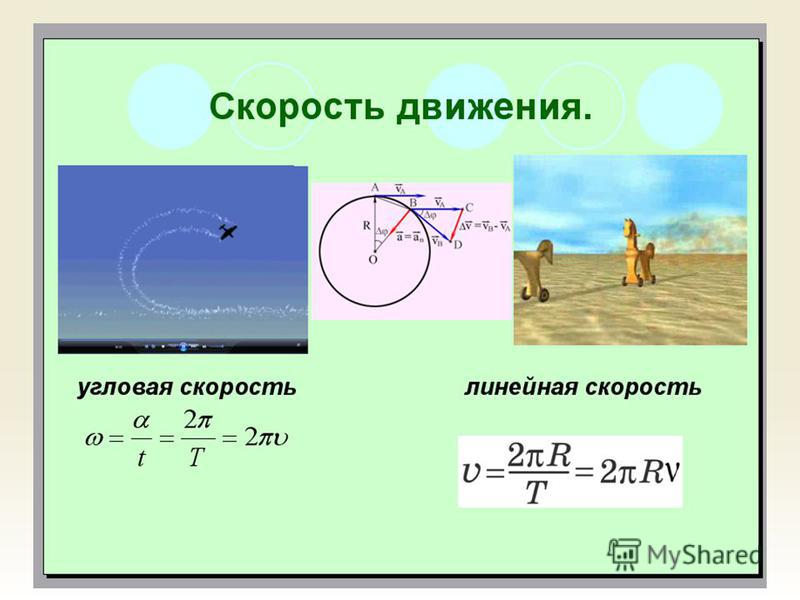 Ротор электродвигателя начинает вращаться из состояния покоя равноускоренно и за первые 5 с делает 25 оборотов. Вычислите угловую скорость ротора в конце пятой секунды.
Ротор электродвигателя начинает вращаться из состояния покоя равноускоренно и за первые 5 с делает 25 оборотов. Вычислите угловую скорость ротора в конце пятой секунды.
3 . Пропеллер самолета вращается с частотой равной 20 Гц. В некоторый момент времени выключают мотор. Сделав 80 оборотов, пропеллер останавливается. Сколько времени прошло с момента выключения мотора до остановки, если вращение пропеллера считать равнозамедленным?
4 . Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найдите угловое ускорение колеса.
5 . Материальная точка движется по окружности. Когда центростремительное ускорение точки становится равным 3,2 м/с 2 , угол между вектором полного и центростремительного ускорений равен 60°. Найдите тангенциальное ускорение точки для этого момента времени.
6 . Точка движется по кривой с постоянным тангенциальным ускорением 0,5 м/с 2 . Определите полное ускорение точки на участке кривой с радиусом кривизны 3 м в момент времени, когда линейная скорость равна 2 м/с.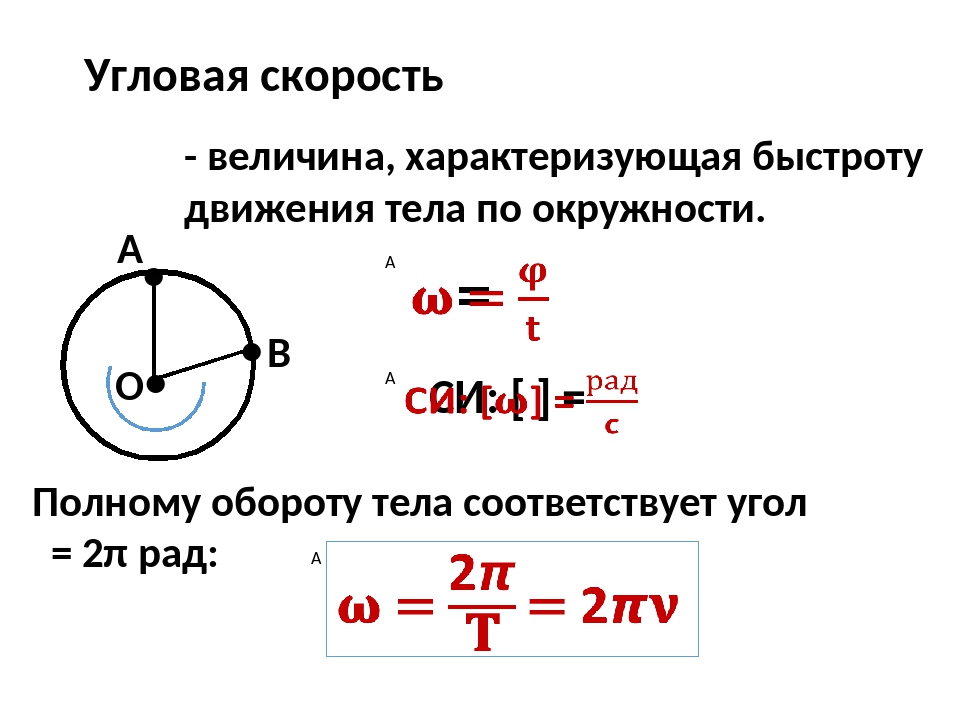
7 . Небольшое тело начинает движение по окружности радиусом 30 м с постоянным по модулю тангенциальным ускорением 5 м/с 2 . Найдите полное ускорение тела через 3 с после начала движения.
8 . Диск радиусом 10 см, находящийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 0,5 рад/с 2 . Найдите полное ускорение точек на окружности диска в конце второй секунды после начала вращения.
9 . Угол поворота колеса радиусом 0,1 м изменяется по закону φ =π · t . Найдите угловую и линейную скорости, центростремительное и тангенциальное ускорения точек обода колеса.
10 . Колесо вращается по закону φ = 5t – t 2 . Найдите в конце первой секунды вращения угловую скорость колеса, а также линейную скорость и полное ускорение точек, лежащих на ободе колеса. Радиус колеса 20 см.
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆ l = R ∆ φ
Если угол поворота мал, то ∆ l ≈ ∆ s .
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду (р а д с).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
a n → = — ω 2 R → .
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
4.4: Круговое движение — линейная и угловая скорость
Радианы и длина дуги могут применяться для исследования кругового движения . В физике средняя скорость объекта определяется как:
\ [\ nonumber
\ text {средняя скорость} ~ = ~ \ frac {\ text {пройденное расстояние}} {\ text {time elapsed}}
\]
Итак, предположим, что объект движется по окружности радиуса \ (r \), преодолевая расстояние \ (s \) за период времени \ (t \), как на рисунке 4.4.1. Тогда имеет смысл определить (среднюю) линейную скорость \ (\ nu \) объекта как:
\ [\ nu ~ = ~ \ frac {s} {t} \ label {eqn: linspeed} \]
Пусть \ (\ theta \) будет углом, заметенным объектом за этот период времени. Затем мы определяем (среднюю) угловую скорость \ (\ omega \) объекта как:
Затем мы определяем (среднюю) угловую скорость \ (\ omega \) объекта как:
\ [\ omega ~ = ~ \ frac {\ theta} {t} \ label {eqn: angspeed} \]
Угловая скорость — это скорость, с которой центральный угол, охватываемый объектом, изменяется при движении объекта по окружности, и, таким образом, она измеряется в радианах в единицу времени.Линейная скорость измеряется в единицах расстояния в единицу времени (например, футов в секунду). Слово линейный используется потому, что выпрямление дуги, пройденной объектом по окружности, приводит к линии такой же длины, так что можно использовать обычное определение скорости как расстояния во времени. Обычно мы опускаем слово «средняя» при обсуждении здесь линейной и угловой скорости.
Поскольку длина \ (s \) дуги, отрезанной центральным углом \ (\ theta \) в окружности радиуса \ (r \), равна \ (s = r \, \ theta \), мы видим что
\ [\ nonumber
\ nu ~ = ~ \ frac {s} {t} ~ = ~ \ frac {r \, \ theta} {t} ~ = ~ \ frac {\ theta} {t} \; \ cdot \; r ~,
\]
так, чтобы мы получили следующее соотношение между линейной и угловой скоростью:
\ [\ nu ~ = ~ \ omega \, r \ label {eqn: linang} \]
Пример 4.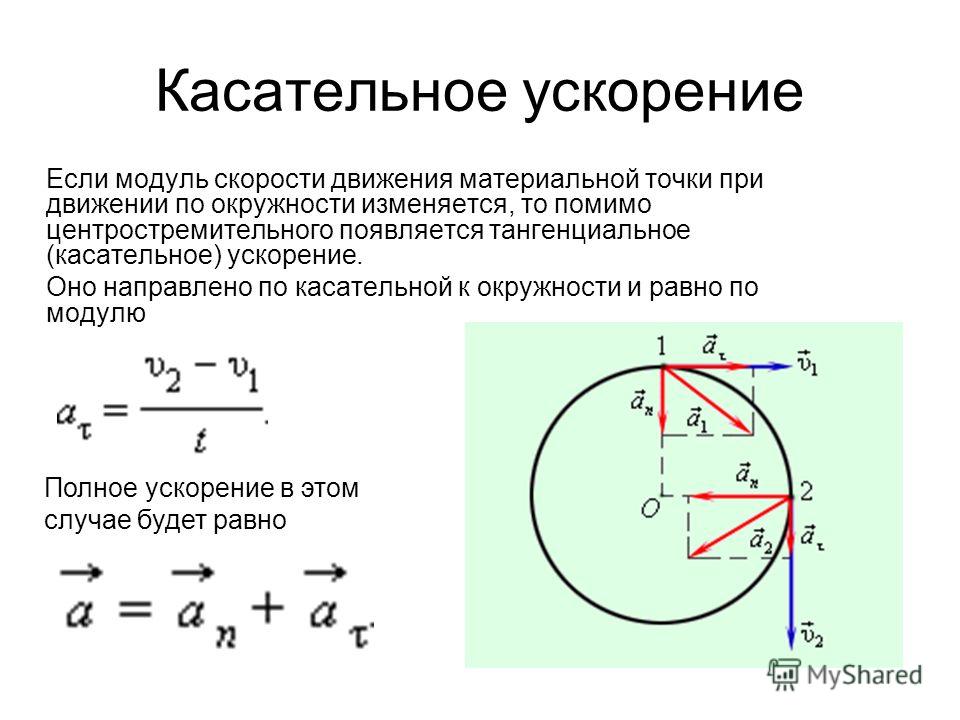 14
14
Объект сметает центральный угол в \ (\ frac {\ pi} {3} \) радиан за \ (0,5 \) секунды, когда он движется по окружности радиуса \ (3 \) м. Найдите его линейную и угловую скорость за этот период времени.
Решение:
Здесь мы имеем \ (t = 0,5 \) сек, \ (r = 3 \) m и \ (\ theta = \ frac {\ pi} {3} \) рад. Таким образом, угловая скорость \ (\ omega \) равна
\ [\ nonumber
\ omega ~ = ~ \ frac {\ theta} {t} ~ = ~ \ frac {\ dfrac {\ pi} {3} ~ \ text { рад}} {0,5 ~ \ text {sec}}
\ quad \ Rightarrow \ quad \ boxed {\ omega ~ = ~ \ frac {2 \ pi} {3} ~ \ text {rad / sec}} ~,
\ ]
и, следовательно, линейная скорость \ (\ nu \) равна
\ [\ nonumber
\ nu ~ = ~ \ omega \, r ~ = ~ \ left (\ frac {2 \ pi} {3} ~ \ text { рад / сек} \ right) \, (3 ~ \ text {m})
\ quad \ Rightarrow \ quad \ boxed {\ nu ~ = ~ 2 \ pi ~ \ text {m / sec}} ~.
\] Обратите внимание, что единицы измерения для \ (\ omega \) — рад / сек, а единицы для \ (\ nu \) — м / сек.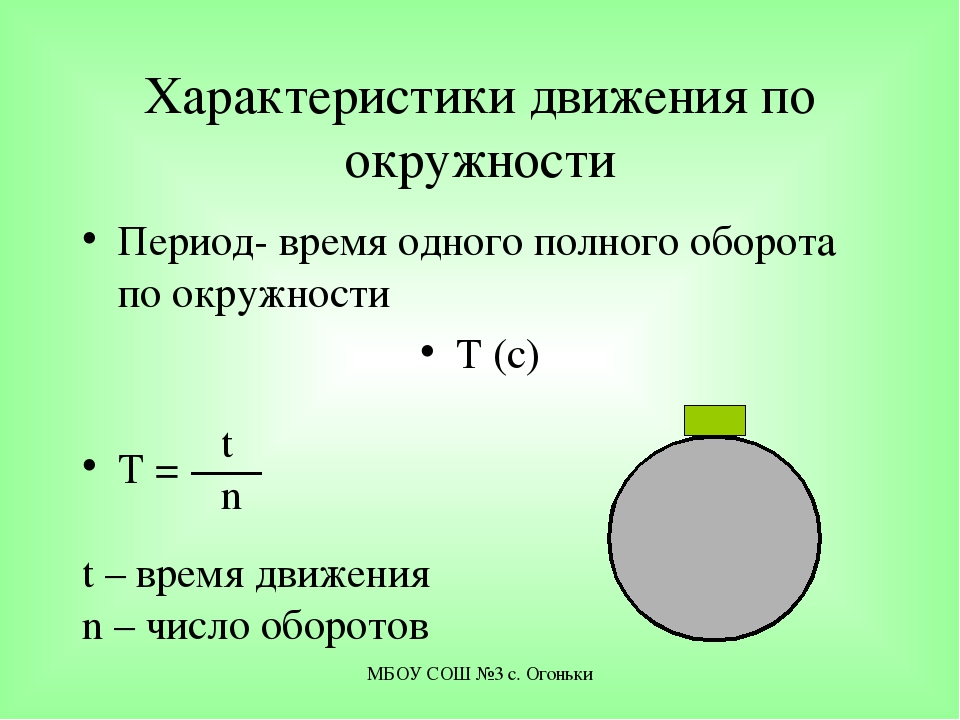 Напомним, что радианы на самом деле безразмерны, поэтому в уравнении \ (\ nu = \ omega \, r \) единицы радиан исчезают.
Напомним, что радианы на самом деле безразмерны, поэтому в уравнении \ (\ nu = \ omega \, r \) единицы радиан исчезают.
Пример 4.15
Объект перемещается на расстояние \ (35 \) футов за \ (2.7 \) секунды по кругу с радиусом \ (2 \) футов. Найдите его линейную и угловую скорость за этот период времени.
Решение:
Здесь мы имеем \ (t = 2.7 \) сек, \ (r = 2 \) ft и \ (s = 35 \) ft.Итак, линейная скорость \ (\ nu \) равна
\ [\ nonumber
\ nu ~ = ~ \ frac {s} {t} ~ = ~ \ frac {35 ~ \ text {feet}} {2.7 ~ \ text { sec}} \ quad \ Rightarrow \ quad
\ boxed {\ nu ~ = ~ 12.96 ~ \ text {ft / sec}} ~,
\]
, поэтому угловая скорость \ (\ omega \) равна
\ [\ nonumber
\ nu ~ = ~ \ omega \, r \ quad \ Rightarrow \ quad 12.96 ~ \ text {ft / sec} ~ = ~ \ omega \, (2 ~ \ text {ft})
\ quad \ Rightarrow \ quad \ boxed {\ omega ~ = ~ 6.48 ~ \ text {рад / сек}} ~.
\]
Пример 4.16
Объект движется с постоянной линейной скоростью \ (10 \) м / сек по окружности радиуса \ (4 \) м. Насколько велик центральный угол за \ (3,1 \) секунды?
Насколько велик центральный угол за \ (3,1 \) секунды?
Решение:
Здесь мы имеем \ (t = 3,1 \) сек, \ (\ nu = 10 \) м / сек и \ (r = 4 \) м. Таким образом, угол \ (\ theta \) задается как
\ [\ nonumber
s ~ = ~ r \, \ theta \ quad \ Rightarrow \ quad \ theta ~ = ~ \ frac {s} {r} ~ = ~ \ frac {\ nu \, t} {r} ~ = ~
\ frac {(10 ~ \ text {m / sec}) \, (3.1 ~ \ text {sec})} {4 ~ \ text {m} } ~ = ~ \ boxed {7.75 ~ \ text {rad}} ~.
\]
Во многих физических приложениях угловая скорость выражается в об / мин. , сокращенно об / мин. Чтобы преобразовать число оборотов в минуту, скажем, в радианы в секунду, обратите внимание, что, поскольку в одном обороте \ (2 \ pi \) радиан, а в одной минуте \ (60 \) секунд, мы можем преобразовать \ (N \) оборотов в минуту в радиан в секунду путем «отмены единиц» следующим образом:
\ [\ require {cancel} \ nonumber
N ~ \ text {rpm} ~ = ~ N ~ \ frac {\ cancel {\ text {rev}}} { \ cancel {\ text {min}}} \; \ cdot \;
\ frac {2 \ pi ~ \ text {rad}} {1 ~ \ cancel {\ text {rev}}}
\; \ cdot \; \ frac {1 ~ \ cancel {\ text {min}}} {60 ~ \ text {sec}} ~ = ~ \ frac {N \ cdot 2 \ pi} {60} ~ \ text {rad / sec}
\ ]
Это работает, потому что все, что мы сделали, это дважды умножили на \ (1 \). Преобразование в другие единицы для угловой скорости работает аналогичным образом. Если пойти в обратном направлении, скажем, от рад / сек до оборотов в минуту, получим:
Преобразование в другие единицы для угловой скорости работает аналогичным образом. Если пойти в обратном направлении, скажем, от рад / сек до оборотов в минуту, получим:
\ [\ nonumber
N ~ \ text {рад / сек} ~ = ~ \ frac {N \ cdot 60} {2 \ pi} ~ \ текст {rpm}
\]
Решение
Представьте себе частицу на внешнем радиусе каждой шестерни. После того как шестерни повернутся в течение некоторого времени \ (t> 0 \), круговое смещение каждой частицы будет одинаковым. Другими словами, \ (s_1 = s_2 \), где \ (s_1 \) и \ (s_2 \) — расстояния, пройденные частицами на шестернях с радиусами \ (r_1 \) и \ (r_2 \) соответственно.
Но \ (s_1 = \ nu_1 \, t \) и \ (s_2 = \ nu_2 \, t \), где \ (\ nu_1 \) и \ (\ nu_2 \) — линейные скорости шестерен с радиусами \ (r_1 \) и \ (r_2 \) соответственно. Таким образом,
\ [\ nonumber
\ nu_1 \, t = \ nu_2 \, t \ quad \ Rightarrow \ quad \ nu_1 = \ nu_2 ~,
\]
, поэтому по уравнению \ ref {eqn: linang} мы получаем фундаментальную соотношение между двумя шестернями:
\ [
\ boxed {\ omega_1 \, r_1 ~ = ~ \ omega_2 \, r_2} \ label {eqn: gears}
\]
Обратите внимание, что это справедливо для любых двух передач. Итак, в нашем случае у нас есть
Итак, в нашем случае у нас есть
\ [\ nonumber
\ omega_1 \, (5) ~ = ~ (25) \, (4) \ quad \ Rightarrow \ quad \ boxed {\ omega_1 ~ = ~ 20 ~ \ text { об / мин}} ~.
\]
Авторы и авторство
Урок 29: Скорость по кругу
Если вам нужно рассчитать центростремительное ускорение объекта, но вы не знаете его скорость, у вас возникнет небольшая проблема.
- Должен быть способ придумать базовую формулу, которая связывает скорость по кругу с некоторыми другими концепциями, которые мы изучили до сих пор.
- Давайте попробуем начать с формулы, которую мы знаем с самого начала курса.
- Поскольку мы смотрим на что-то, вращающееся по кругу, расстояние, которое оно проходит за каждый оборот, равно длине окружности круга.
- Мы подставим это в первую формулу, где расстояние, на которое проходит объект (d), равно длине окружности (C)…
Слово период также используется в других науках, например, в «Периодической таблице элементов» в химии. Он назван так потому, что периодически элементов повторяют одни и те же характеристики.
Он назван так потому, что периодически элементов повторяют одни и те же характеристики.
- Последнее, что нам нужно изменить, это время «t» внизу.
- В физике мы называем время, которое требуется для чего-либо, чтобы завершить один полный цикл или оборот, периодом, который имеет символ «T».
- Для объекта, движущегося по кругу, период — это время, необходимое объекту для того, чтобы обойти его ровно один раз.
- Это дает нам немного другую формулу.
v = скорость (м / с)
π = pi , используйте в расчетах 3,14
r = радиус окружности (м)
T = период (с)
Пример 1. Какова длина руки учащегося, если он может раскачивать ведро по кругу со скоростью 2,72 м / с каждые 1,5 секунды?
v = 2πr / T
r = (vT) / (2π)
= (2,72 x 1,5) / (2π)
r = 0,65 м
Вы также можете объединить эту формулу скорости с формулой ускорения, которую мы уже рассматривали…
Оригинальные формулы
Шаг 1
Шаг 2
Финальная формула
- Этой окончательной формулы нет в вашем листе данных, но вы можете найти ее полезной для решения некоторых задач.

- Вы должны суметь показать, как вы получили эту формулу, поэтому не запоминайте ее вслепую.
Пример 2: Каково ускорение лошади, бегущей по круговой гоночной трассе с радиусом 37 метров каждые 12 секунд?
a c = 4π 2 r / T 2
= 4π 2 (37) / 12 2
a c = 10 м / с 2
Круговое движение (и прочее)
Круговое движение (и прочее)Второй закон Ньютона
применяется к
Плоская кривая
Что обеспечивает центростремительную силу , необходимую для автомобиль сделать поворот на ровной дороге ? Что произойдет, если эта сила будет , а не настоящее время?
Гравитация тянет автомобиль вниз своим весом, w = m g .
Ровная дорога толкает вверх с нормальной силой н и горизонтально с силой трения F frict .
Это сила статического трения ! Когда машина движется и шины вращаются, шины на мгновение в состоянии покоя относительно к дороге. Иначе шины буксуют!
Помните, сила трения может быть любого значения от нуля до максимум F с = с n когда автомобиль едва не скользит.Мы рассмотрим это случай, когда автомобиль едва не скользит. Это означает
F фрикт = F с = с n
На диаграмме справа показаны все эти силы. Там не является вертикальной составляющей ускорения, поэтому мы находим, что
n = m g
, что означает
F net = f s = s m g = m v 2 / r
с г = v 2 / об
с = v 2 / г r
То есть у нас должен быть коэффициент трения покоя с = v 2 / g r, чтобы обеспечить силу трения, позволяющую автомобилю двигаться на скорости v, чтобы сделать это по плоской кривой радиуса r.
Или мы можем найти скорость через этот коэффициент статическое трение,
v 2 = s г г
v = КОРЕНЬ [ s g r]
Это максимальная скорость, с которой может быть снята кривая радиуса r. при коэффициенте статического трения между шинами и дорожным покрытием с .
Если скорость увеличится, радиус r также увеличится! Это означает, что автомобиль не будет следовать намеченной кривой и может съехать с трассы. дорога целиком!
c) Дуг Дэвис, 2001 г .
Какой должен быть коэффициент трения между шины и ровная проезжая часть, позволяющая автомобилю изгибаться по радиусу r = 350 м при скорости 80 км / ч?
; все права защищены
Определение, Введение, Законы, Формула и Пример
При равномерном круговом движении скорость частицы всегда остается постоянной, поэтому тангенциальное ускорение равно нулю.Есть только центростремительное ускорение.
При круговом движении объект движется по круговой траектории. Смещение происходит по кривой окружности. Следовательно, оно измеряется и называется угловым смещением.
Если «s» — это фактический путь, пройденный объектом по окружности r, то связь между «s» и угловым смещением определяется выражением;
s = rΘ
Если мы продифференцируем приведенное выше уравнение относительно времени «t», мы получим
v = rω, где
v = линейная скорость, а
ω = угловая скорость.
Следовательно, угловая скорость вращения или его угловая скорость выражается, как указано ниже, и мы обозначаем экземпляры угловой скорости через ω.
\ (\ omega = {\ Delta \ theta \ over {\ Delta t}} \)
Прочтите о звуковых волнах здесь.
Центростремительное ускорение
- Ускорение, которое отвечает за изменение траектории частицы при круговом движении, и оно происходит по направлению к центру круговой траектории, называется центростремительным ускорением.2 \ over r} \)
Он направлен к центру, как показано на схеме.
- Скорость изменения скорости частицы, движущейся по круговой траектории, называется тангенциальным ускорением.
Обозначается at.
\ (a_t = {dV \ over {dt}} \)
- Он отвечает за изменение скорости частицы.
- Как и при равномерном круговом движении, скорость частицы постоянна. Таким образом, тангенциальное ускорение равно нулю. В этом движении присутствует только центростремительное ускорение.
Чистое ускорение при круговом движении
Чистое ускорение (a) при круговом движении определяется как:
a = ac2 + at2
Угол между чистым ускорением и центростремительным ускорением определяется как:
\ ( tan \ theta = {a_t \ over {a_c}} \)
Прочтите об атомах и ядрах здесь.

Следует помнить
При круговом движении
- Центростремительное ускорение отвечает за круговой путь движения, а
- Тангенциальное ускорение отвечает за изменение скорости движения.
Частота: Величина, обратная периоду времени, называется частотой. Его обозначают ν (nu) или f.
Это часто задаваемые понятия при экзамене по равномерному круговому движению. Вместо того, чтобы пытаться запоминать одно за другим, попрактикуйтесь в имитационных тестах в приложении Testbook, чтобы запомнить их эффективно.
Пример:Q1. Искусственный спутник совершает круговое движение в радиусе 42250 км.Вычислите его скорость, если он совершает оборот вокруг Земли за 24 часа.
A1.
\ (радиус = 42250 км \\\)
\ (время = 24ч = 24 \ times60 \ times60s = 86400с \\\)
\ (скорость = {2 \ pi r \ over {t}} = 3.072 км / с \)
Q2.
 Какое угловое смещение минутной стрелки часов за 30 минут?
Какое угловое смещение минутной стрелки часов за 30 минут?A2. Для минутной стрелки T = 60мин = 60 x 60 = 3600 с, t = 30 x 60 = 1800 с
\ (\ theta = \ omega t \\\)
\ (\, следовательно, \ theta_M = {2 \ pi \ over {T}} \ times t = {2 \ pi \ over {3600}} \ times {1800} = \ pi \ text {rad} \\\)
\ (\ theta_M = 3.14 \ text {rad} \)
Часто задаваемые вопросы о равномерном круговом движении
Q.1 Что такое равномерное круговое движение?
Ans.1 Когда объект движется по круговой траектории с постоянной скоростью, это называется равномерным круговым движением.
Q.2 Что означает тангенциальное ускорение?
Ans.2 Скорость изменения скорости частицы, движущейся по круговой траектории, называется тангенциальным ускорением.
Q.3 Что такое центростремительное ускорение?
Ans.
 3 Ускорение, которое отвечает за изменение траектории частицы при круговом движении по направлению к центру круговой траектории, называется центростремительным ускорением.
3 Ускорение, которое отвечает за изменение траектории частицы при круговом движении по направлению к центру круговой траектории, называется центростремительным ускорением.Q.4 Что такое чистое ускорение?
Ans.4 Это квадратный корень из суммы квадратов центростремительного ускорения и тангенциального ускорения.
Q.5 Что такое частота?
Ans.5 Величина, обратная периоду времени, называется частотой.
Создайте бесплатную учетную запись, чтобы продолжить чтение
Получайте мгновенные оповещения о вакансиях бесплатно!
Получите ежедневный GK и текущие новости Капсула и PDF-файлы
Получите 100+ бесплатных пробных тестов и викторин
Подпишитесь бесплатно Уже есть аккаунт? Войти
Следующая запись
Калькулятор центростремительной силы
Формула центростремительной силы
Формула и уравнение для центростремительной силы:
Центростремительная сила: f = mv 2 r
Некоторые другие формулы, полученные из уравнения центростремительной силы:
Радиус: r = mv 2 f
Скорость: v = √frm
Где
- m = Масса,
- r = Круговой радиус,
- v = Скорость.

Калькулятор центростремительной силы находит центростремительную силу объекта при круговом движении. Другими словами, он вычисляет величину центростремительной силы. Он также может найти центростремительную скорость, массу и радиус объекта, если задана сила.
Если результат вашего расчета отрицательный, это означает, что на объект действует центробежная сила.
Что такое центростремительная сила?
Центростремительная сила — это чистая сила, которая действует на объект, заставляя его двигаться по круговой траектории.Это необходимо, чтобы объект двигался круговыми движениями.
Как найти центростремительную силу?
Чтобы найти центростремительную силу, вы должны иметь скорость, радиус круговой траектории и массу объекта. Если у вас есть угловое ускорение тела, вы все равно можете найти величину центростремительной силы.
- Возьмите скорость в квадрат.
- Умножьте это на массу тела.
- Разделите значение на радиус круга, по которому движется тело.

Пример :
Рассчитайте центростремительную силу объекта, если он движется по окружности с радиусом 5 м, Масса тела 10 кг, и скорость 15 м / с.
Решение:
Поместите указанные значения в уравнение центростремительной силы.
F c = mv 2 / r
F c = 10 × (15) 2 /5
F c = 450 N
Центростремительная и центробежная силы одинаковы?
Оба одинаковые, но противоположные по направлению.Центростремительная сила действует внутрь (тянет объект к центру), а центробежная сила отталкивает его от центра. У обоих одинаковые формулы. Единственная разница в том, что центробежная сила сопровождается отрицательным знаком.
Определение кругового движения — типы, пример и формула
Привет всем! Добро пожаловать в CBSE Digital Education.
 Сегодня мы собираемся обсудить интересную тему об определении кругового движения. CBSE Digital Education предоставляет всю важную информацию, касающуюся определения кругового движения.Прочтите эту статью полностью до конца.
Сегодня мы собираемся обсудить интересную тему об определении кругового движения. CBSE Digital Education предоставляет всю важную информацию, касающуюся определения кругового движения.Прочтите эту статью полностью до конца.Определение кругового движения
Когда объект движется по кругу, называется круговым движением . Движение тела может быть линейным или круговым. Однако они различаются по количеству способов, как указано в таблице ниже:
Линейное движение Вращательное движение Смещение = x Угловое смещение = θ Скорость = dx / dt Угловая скорость, = d / dt Масса M Момент инерции I Сила = Ма Крутящий момент, = Ix Мощность = Fv Мощность, p = τω Ускорение = a = dv / dt Угловое смещение, = d / dt Работа = Fds Работа = τdθ Кинетическая энергия, k = ½ мв 2 Кинетическая энергия, k = ½ Iω 2 Линейный импульс, p = m x v Угловой момент, L = I x ω Типы кругового движения:
Что такое равномерное круговое движение?Он описывает движение тела по круговой траектории с постоянной скоростью.
 Когда тело описывает круговое движение, его расстояние от оси вращения всегда остается постоянным. Хотя скорость тела постоянна, но скорость не постоянна, скорость как векторная величина зависит как от скорости тела, так и от направления его движения. Эта изменяющаяся скорость указывает на наличие ускоренного движения.
Когда тело описывает круговое движение, его расстояние от оси вращения всегда остается постоянным. Хотя скорость тела постоянна, но скорость не постоянна, скорость как векторная величина зависит как от скорости тела, так и от направления его движения. Эта изменяющаяся скорость указывает на наличие ускоренного движения.Центростремительное ускорение постоянной величины всегда направлено к оси вращения. Это ускорение, в свою очередь, создается центростремительной силой , которая также является постоянной по величине и направлена к оси вращения.
В случае вращения вокруг фиксированной оси твердого тела, которое не является пренебрежимо малым по сравнению с радиусом пути, каждая частица тела описывает равномерное круговое движение с той же угловой скоростью, но со скоростью и ускорением отличаются положением относительно оси.
Пример равномерного кругового движения- Искусственный спутник совершает равномерное круговое движение вокруг Земли.

- Земля движется вокруг Солнца равномерно по кругу.
- Велосипедисты, движущиеся по круговой траектории с постоянной скоростью, совершают равномерное круговое движение.
Для движения по окружности радиуса r длина окружности C = 2 r. Если период времени для одного оборота равен Т, угловая скорость вращения также называется , угловой скоростью и единицей измерения является радиан / секунда.
ω = 2π / T = πf = θ / T
Скорость движения тела по кругу:
V = 2π r / T = ωr
Угол заметания за время t указан ниже
θ = 2 πf = ωt
Угловое ускорение частицы указано ниже
α = dω / dt
В случае равномерного кругового движения будет равно нулю. Ускорение из-за изменения направления указано ниже
α = v 2 / r = ω 2 r
Центростремительную и центробежную силу также можно определить с помощью ускорения
F c = ma = mv 2 / r
Рассмотрим тело весом 1 кг, движущееся по кругу радиусом 1 метр с угловой скоростью 1 радиан в секунду, тогда
- Скорость — 1 метр в секунду.

- Ускорение внутрь составляет 1 метр в секунду в квадрате, v 2 / r.
- Импульс тела 1кг.м.с -1 .
- Момент инерции 1 кг.м 2 .
- На него действует центростремительная сила, равная одному метру в секунду в квадрате, что составляет 1 ньютон.
- Период кругового движения составляет 2π секунды за оборот.
- Крутящий момент 1 кг.м 2 .с -1 .
- Кинетическая энергия составляет ½ джоуля.
- Окружность орбиты 2π метра.
- Частота (2π) -1 или 1 / 2π герц (Гц).
Объект, движущийся по круговой траектории с переменной скоростью, считается совершающим неравномерное круговое движение. Если скорость изменяется, в дополнение к нормальному ускорению возникает тангенциальное ускорение.
При неравномерном круговом движении чистое ускорение (a) происходит в направлении Δv, которое направлено внутри круга, но не проходит через его центр, как показано на рисунке.
 Чистое ускорение может быть разделено на два компонента: тангенциальное ускорение и нормальное ускорение, также известное как центростремительное ускорение или ускорение, также известное как центростремительное или радиальное ускорение. Различное тангенциальное ускорение, центростремительное ускорение присутствует как при равномерном, так и при неравномерном круговом движении.
Чистое ускорение может быть разделено на два компонента: тангенциальное ускорение и нормальное ускорение, также известное как центростремительное ускорение или ускорение, также известное как центростремительное или радиальное ускорение. Различное тангенциальное ускорение, центростремительное ускорение присутствует как при равномерном, так и при неравномерном круговом движении.При неравномерном круговом движении нормальная сила не всегда действует в направлении, противоположном весу. При равномерном круговом движении единственной силой, действующей на тело, движущееся по кругу, является центростремительная сила.
При неравномерном круговом движении на тело действуют дополнительные силы из-за ненулевого тангенциального ускорения. Хотя на объект действуют дополнительные силы, сумма всех сил, действующих на объект, должна быть равна центростремительной силе.
Что такое центростремительная сила?Для того чтобы частица могла двигаться круговым движением, на нее должна действовать суммарная сила, направленная к центру.
 Эта сила называется Центростремительной силой.
Эта сила называется Центростремительной силой.Центростремительная сила, F c = ma c = mv 2 / r
F c = mω 2 r = mv 2 / r
a c = ω 2 r = v 2 / r
Это ускорение известно как центростремительное ускорение.
Что такое центробежная сила?Круговое движение — это ускоренное движение. Если мы наблюдаем движение любых частиц в ускоренной системе отсчета, на них действует псевдосила.
- Если частица наблюдается из кадра в круговом движении, на нее действует псевдосила, называемая центробежной силой.
- Псевдосила действует в направлении, противоположном ускорению рамы.
- Центробежная сила — это тенденция объекта улететь от центра кривизны, являющаяся инерцией движения, но центростремительная сила — это сила, которая поддерживает движение объекта с постоянной скоростью по круговой траектории.

- Центробежная сила действует по радиусу круга от центра к объекту, но центростремительная сила действует как радиус круга от объекта к центру.
- Центробежная сила направлена по радиусу от центра к объекту, например, летящему по грязи o
- ff шину или детей выталкивают наружу на вращающемся круговом перекрестке, но центростремительная сила направлена к центру круга, такого как спутник, вращающийся вокруг Земли или планеты.
Надеюсь, вам понравится эта статья о Приглашающих приложениях для определения кругового движения. Если вы хотите задать какие-либо вопросы относительно определения кругового движения, напишите нам в разделе комментариев, и мы ответим вам в ближайшее время.
Нажмите здесь, чтобы узнать больше новостей CBSE
Центростремительная силана вращающейся чашке | Кафедра физики
Перед вращением чашки
- Убедитесь, что вокруг вас достаточно места, чтобы не ударить платформу никого и ничего.

- Поставьте чашку, наполненную водой, в центр доски и убедитесь, что доска выровнена.
- Начните с медленных раскачиваний платформы вперед и назад, чтобы прочувствовать ее.
- Когда вам будет удобно, поверните платформу достаточно быстро, чтобы она двигалась по кругу.
- При изменении ориентации качелей или скорости делайте это медленно и осознанно. Чем больше будет изменений в ускорении, тем больше вероятность того, что вода разольется.
- Когда вы будете готовы остановиться, сделайте это, когда платформа окажется на нижней части поворота.
- Сделайте шаг в том же направлении, в котором движется платформа, чтобы дать ей достаточно времени, чтобы замедлиться.
Объяснение демонстрации
Пример «скрипта»
«Хорошо, у меня есть чашка с водой, которую я собираюсь крутить по кругу над головой. Как вы думаете, ребята, что произойдет? »
(ответы)
«Хорошо, давайте посмотрим, правы ли вы.
 ”
”(Демонстрант продолжает вращать чашу с водой, пока она не окажется над его головой или на его / ее боку, если ему неудобно ходить над головой)
(Пока кружится чашка) «Как вы видите, вода не выходит. Кто-нибудь может сказать мне, почему? »
(ответы)
«Хорошо, все хорошие идеи» (перестает вращаться) Хорошо, причина, по которой вода остается в чашке, — это так называемая центростремительная сила. Все вы, ребята, каким-то образом испытали ту же самую силу ».
(Боязнь недоверия)
«Так сколько из вас, ребята, катались на американских горках, которые переворачиваются вверх ногами?»
(Подъем рук)
«Хорошо, ребята, вы когда-нибудь задумывались, почему вы не упали, когда лежите вверх ногами? (На мгновение молчание) Как я уже сказал, это из-за центростремительной силы американских горок.«
«Итак, все вы, ребята, не катались на американских горках, но все вы катались на машинах, верно?» (Йесес)
«Хорошо, сколько из ваших родителей сделали действительно быстрый поворот, и вы почувствовали, что вас тянут в сторону от машины? (Все думают) »
«Это то же самое, центростремительная сила.



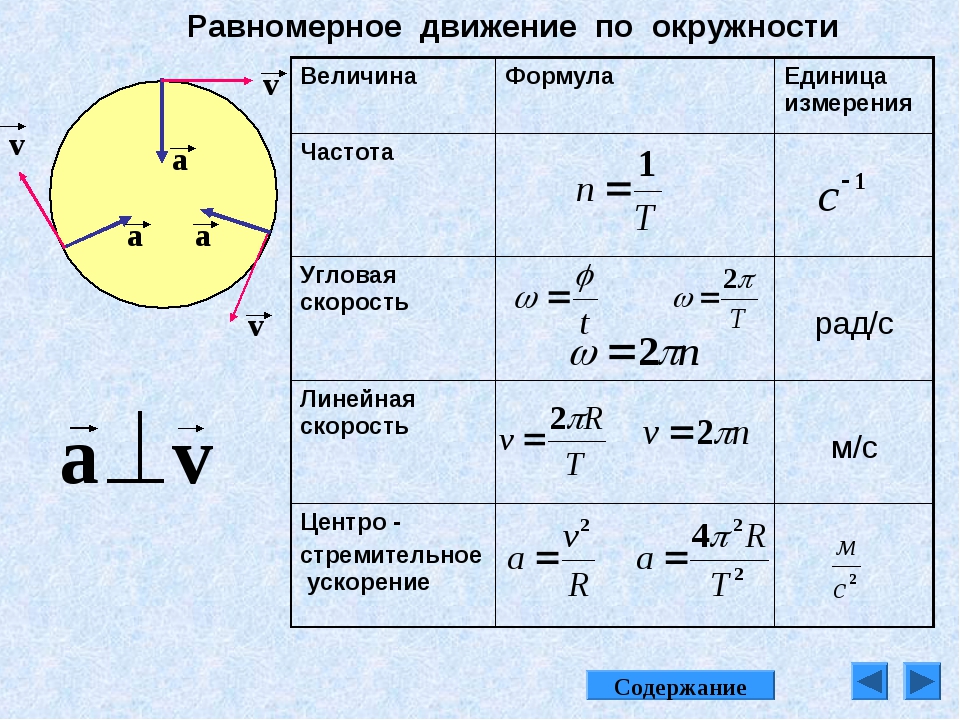 Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения:
Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения: Более сложный случай, когда скорость изменяется по величине.
Более сложный случай, когда скорость изменяется по величине.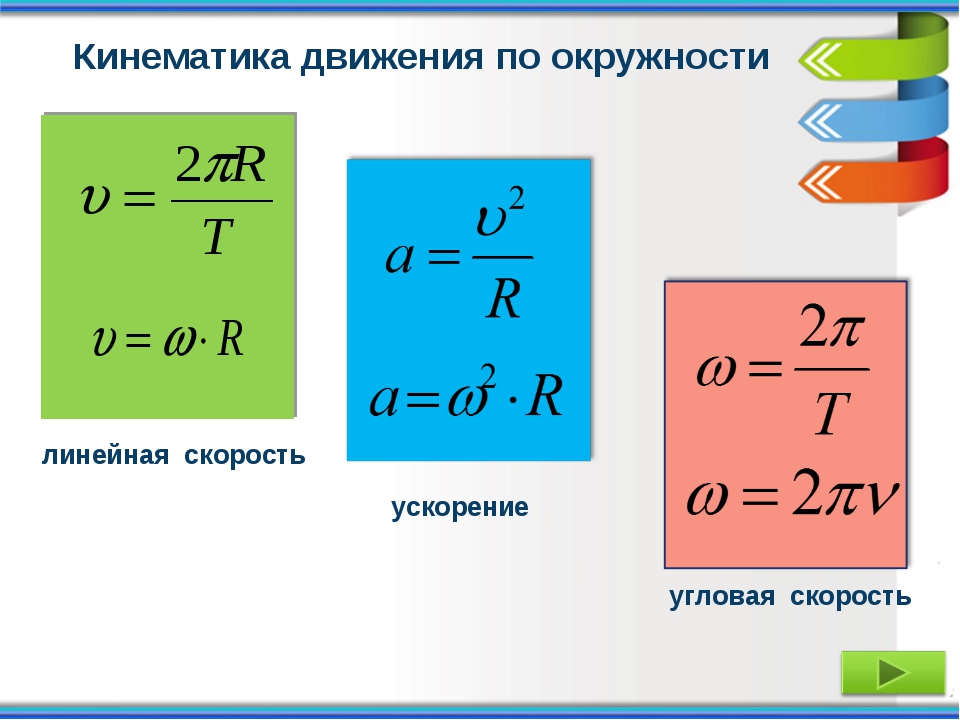
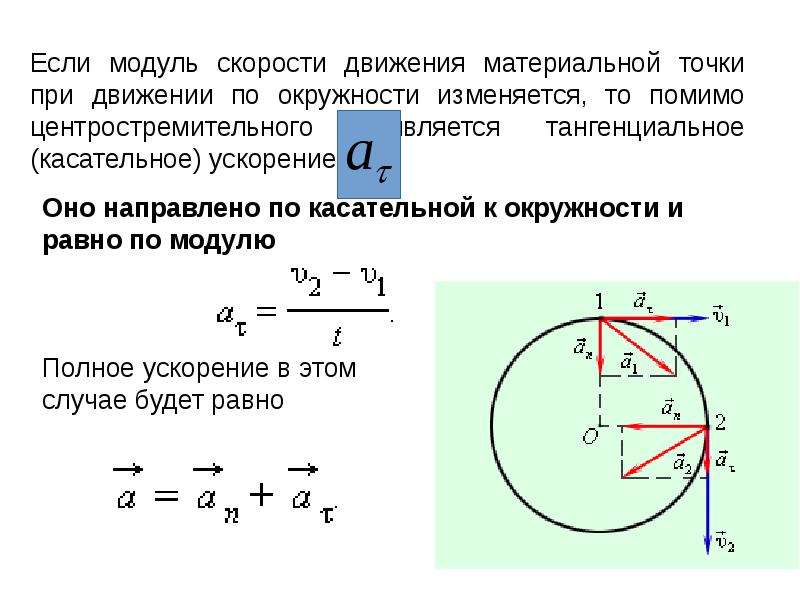
 Ровная дорога толкает вверх с нормальной силой н и горизонтально с силой трения F frict .
Ровная дорога толкает вверх с нормальной силой н и горизонтально с силой трения F frict .
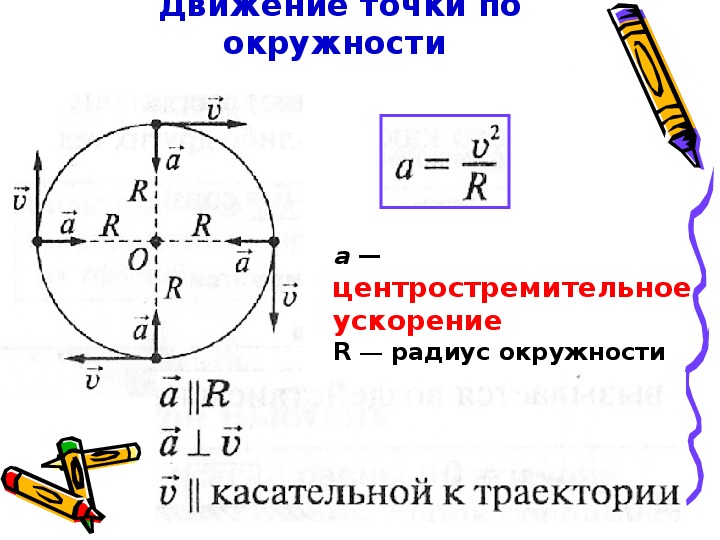 ; все права защищены
; все права защищены
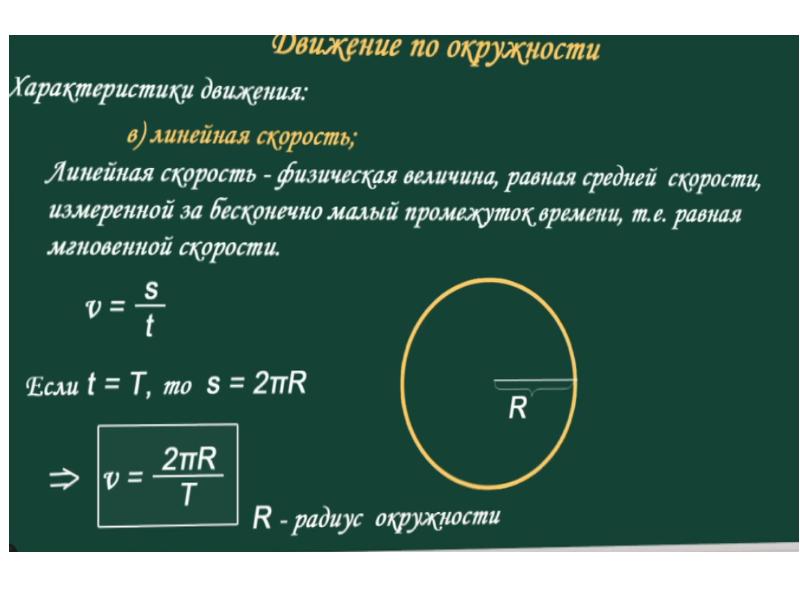 Какое угловое смещение минутной стрелки часов за 30 минут?
Какое угловое смещение минутной стрелки часов за 30 минут?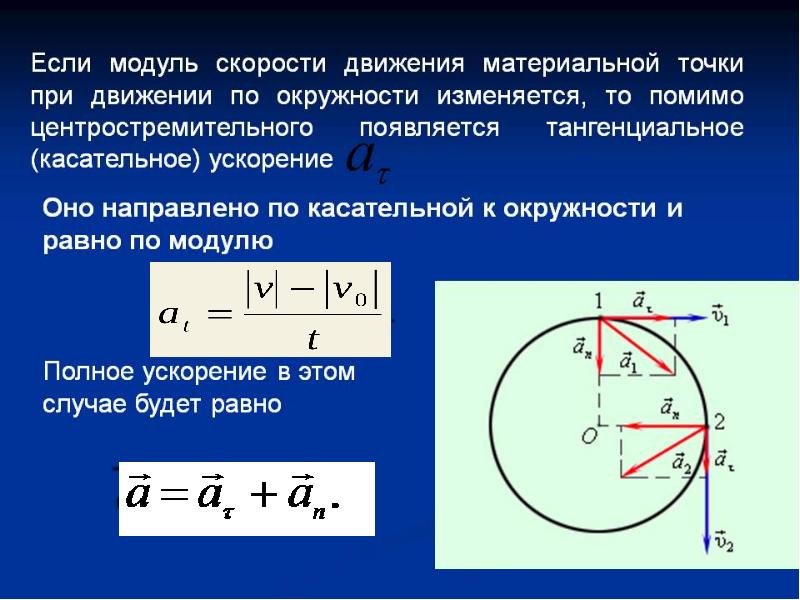 3 Ускорение, которое отвечает за изменение траектории частицы при круговом движении по направлению к центру круговой траектории, называется центростремительным ускорением.
3 Ускорение, которое отвечает за изменение траектории частицы при круговом движении по направлению к центру круговой траектории, называется центростремительным ускорением.

 Сегодня мы собираемся обсудить интересную тему об определении кругового движения. CBSE Digital Education предоставляет всю важную информацию, касающуюся определения кругового движения.Прочтите эту статью полностью до конца.
Сегодня мы собираемся обсудить интересную тему об определении кругового движения. CBSE Digital Education предоставляет всю важную информацию, касающуюся определения кругового движения.Прочтите эту статью полностью до конца. Когда тело описывает круговое движение, его расстояние от оси вращения всегда остается постоянным. Хотя скорость тела постоянна, но скорость не постоянна, скорость как векторная величина зависит как от скорости тела, так и от направления его движения. Эта изменяющаяся скорость указывает на наличие ускоренного движения.
Когда тело описывает круговое движение, его расстояние от оси вращения всегда остается постоянным. Хотя скорость тела постоянна, но скорость не постоянна, скорость как векторная величина зависит как от скорости тела, так и от направления его движения. Эта изменяющаяся скорость указывает на наличие ускоренного движения.

 Чистое ускорение может быть разделено на два компонента: тангенциальное ускорение и нормальное ускорение, также известное как центростремительное ускорение или ускорение, также известное как центростремительное или радиальное ускорение. Различное тангенциальное ускорение, центростремительное ускорение присутствует как при равномерном, так и при неравномерном круговом движении.
Чистое ускорение может быть разделено на два компонента: тангенциальное ускорение и нормальное ускорение, также известное как центростремительное ускорение или ускорение, также известное как центростремительное или радиальное ускорение. Различное тангенциальное ускорение, центростремительное ускорение присутствует как при равномерном, так и при неравномерном круговом движении. Эта сила называется Центростремительной силой.
Эта сила называется Центростремительной силой.

 ”
”