Связь угловой скорости с линейной: Связь между линейной и угловой скоростями.

Линейная и угловая скорость, теория и онлайн калькуляторы

Линейная и угловая скорость, теория и онлайн калькуляторы

Линейная скорость

Определение

Векторная величина равная:

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}=\frac{d\overline{r}}{dt}\left(1\right),\ }\]

называется мгновенной скоростью или просто скоростью.

В выражении (1) $\Delta \overline{r}$ — перемещение материальной точки за отрезок времени равный $\Delta t$. Скорость характеризует быстроту перемещения тела. Мгновенная скорость — это скорость в данный момент времени.

Предельный переход в выражении (1) имеет геометрический смысл. Вектор $\Delta \overline{r}$ направлен вдоль хорды, соединяющей две точки траектории, сближение этих точек ведет к тому, что этот вектор принимает положение касательной к траектории движения в данной точке. Получается, что вектор мгновенной скорости направлен по касательной к траектории движения. При прямолинейном движении вектор скорости направлен по прямой.

Скорость прохождения пути определена аналогично:

\[v={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\left(2\right).\ }\]

Если траектория движения материальной точки — плавная кривая, то чем короче дуга, тем ближе она по длине к длине хорды. В предельном переходе при$\ \Delta t\to 0$ можно считать, что $\Delta s\to \Delta r$. Следовательно,

\[v={\mathop{lim}_{\Delta t\to 0} \frac{\Delta r}{\Delta t}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{dr}{dt}=\frac{ds}{dt}\left(3\right).\ }\ }\]

Если представить радиус — вектор, определяющий положение материальной точки $\overline{r}$ в декартовой системе координат как:

\[\overline{r}=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}+z\left(t\right)\overline{k}\left(4\right),\]

где $\overline{i}$; $\overline{j}$; $\overline{k}$ — единичные орты соответствующих осей координат, постоянные во времени, то подставив правую часть выражения (4) в определение линейной скорости (1), получим:

\[\overline{v}=\overline{i}\frac{dx}{dt}+\overline{j}\frac{dy}{dt}+\overline{k}\frac{dz}{dt}\left(5\right).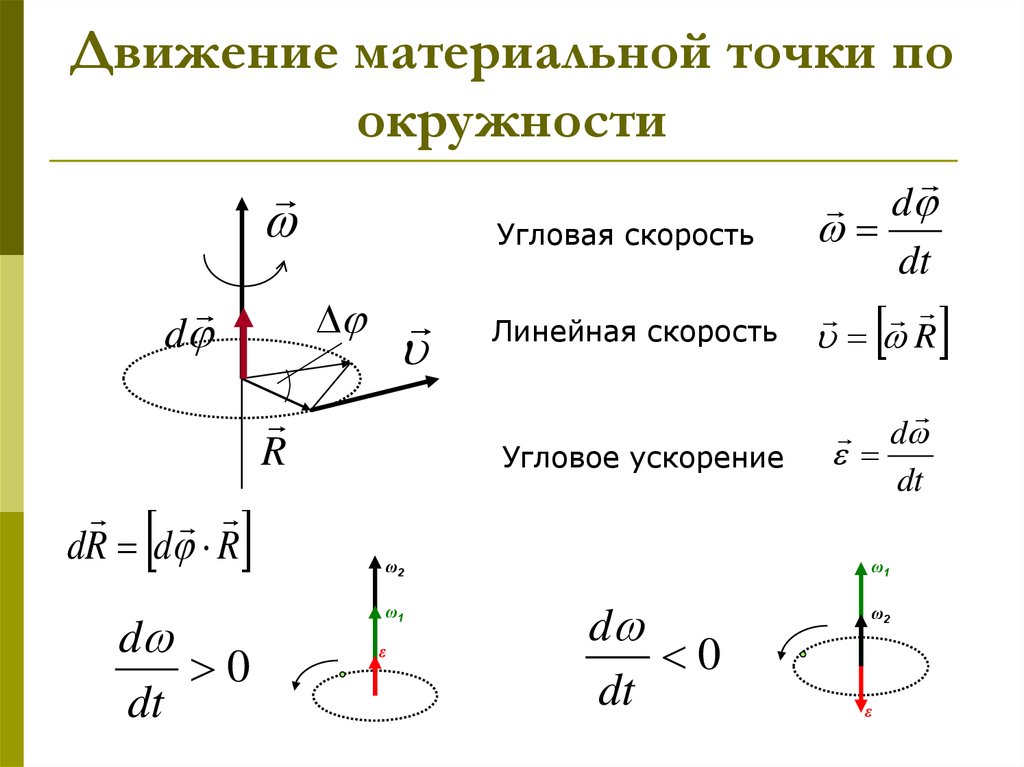 2_z}.\]

Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:

\[\left[v\right]=\frac{\left[s\right]}{\left[t\right]}.\]

В Международной системе единиц (СИ) единицей измерения линейной скорости (в том числе и средней скорости) является метр в секунду:

\[\left[v\right]=\frac{м}{с}.\]

Угловая скорость

Определение

Угловой скоростью называют векторную величину, равную первой производной от угла поворота по времени:

\[\overline{\omega }=\frac{d\overline{\varphi }}{dt}\left(7\right).\]

Вектор угловой скорости направлен по оси вращения по правилу правого винта, то есть как вектор $d\overline{\varphi }.$

Связь между линейной и угловой скоростями задана выражением:

\[v=R\omega \left(8\right). \]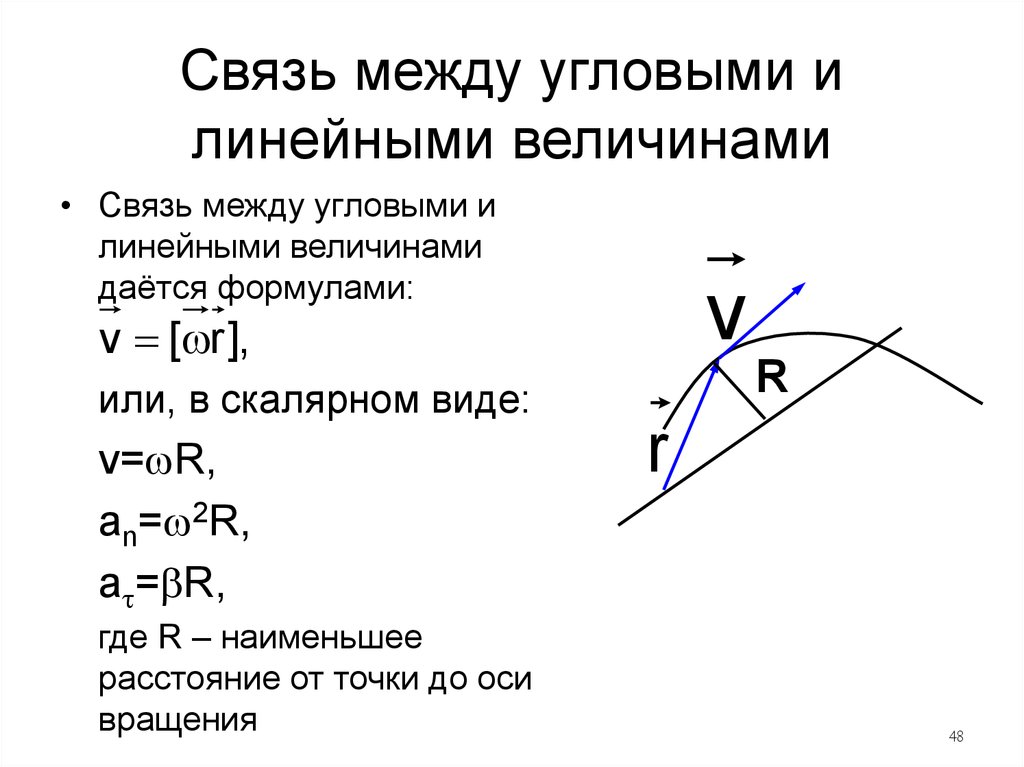

В векторном виде формулу (8) записывают как:

\[\overline{v}=\overline{\omega }\times \overline{R}\left(9\right),\]

$\overline{R}$ — вектор, соединяющий ось вращения и движущуюся точку. Модуль скорости в выражении (9) найдем как:

\[v=\omega R{\sin \alpha \ \left(10\right),\ }\]

где $\alpha $ — угол между вектором угловой скорости и $\overline{R}.$

При равномерном движении по окружности угловая скорость ($\omega =const$), частота и период связаны как:

\[\omega =\frac{2\pi }{T}=2\pi \nu \left(11\right).\]

Единица измерения угловой скорости — это радиан, деленный на секунду:

\[\left[\omega \right]=\frac{рад}{с}.\]

Примеры задач на линейную и угловую скорость

Пример 1

Задание: Цилиндр вращается вокруг неподвижной оси так, что угол поворота изменяется в зависимости от времени как: $\varphi =At^2,\ где\ A=const.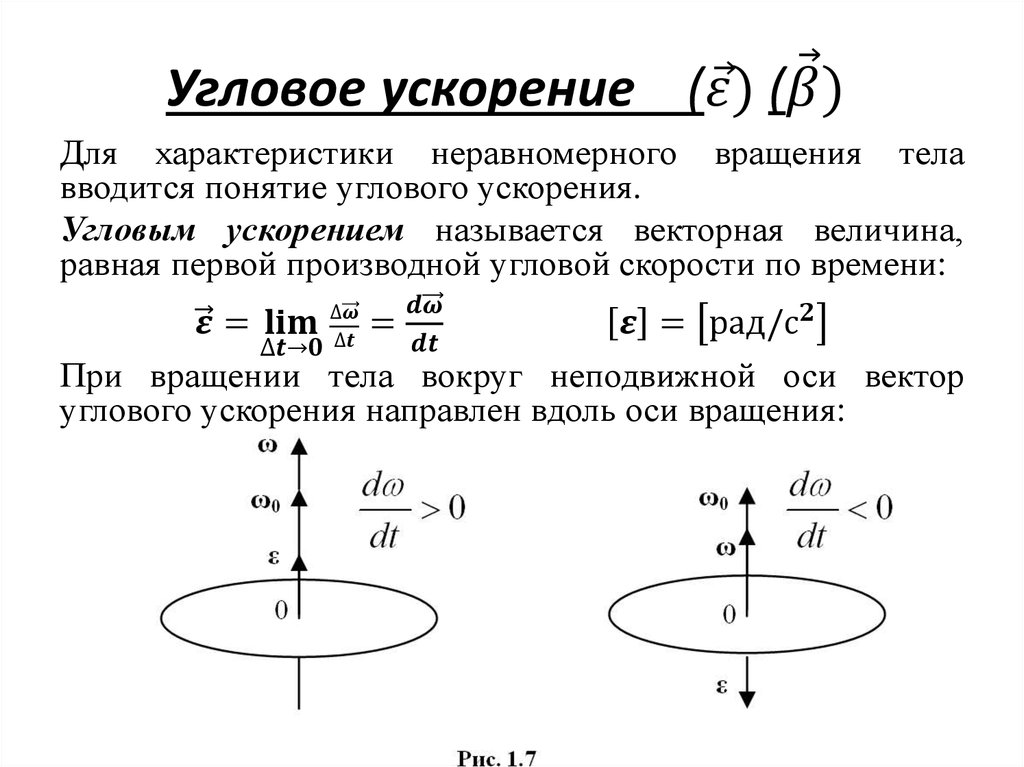 2\right)=2At\ \left(1.2\right).\]

При $t=t’$ угловая скорость цилиндра равна:

\[\omega \left(t’\right)=2At’.\]

Функция $\omega (t)$, как мы видим из уравнения (1.2) является линейной, следовательно, графиком угловой скорости в осях ($\omega ,t$) ,будет прямая, выходящая из начала координат рис.1. Угол наклона прямой характеризует коэффициент $2A$.

   

Пример 2

Задание: Материальная точка движется в плоскости XOY. Ее движение описывают уравнения:

\[ \left\{ \begin{array}{c} x=At, \\ y=At(1+Bt) \end{array} \right. \]

$(A,B-постоянные,\ больше\ нуля)$. Запишите закон изменения скорости движения точки ($\overline{v}(t)$). Каков модуль скорости движения точки?

Решение: Закон движения точки задан в координатной форме. В векторном виде его запишем как:

\[\overline{r}\left(t\right)=x\overline{i}+y\overline{j}=At\overline{i}+At\left(1+Bt\right)\overline{j}\left(2. 2}$

   

Читать дальше: механические колебания и волны.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Линейная скорость через угловую, теория и онлайн калькуляторы

Линейная скорость через угловую, теория и онлайн калькуляторы

Определение

Мгновенной (истинной) скоростью ($\overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}=\frac{d\overline{r}}{dt}\ }\left(1\right).\]

$\Delta \overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $\Delta t$.

Выражение линейной скорости через угловую скорость

Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.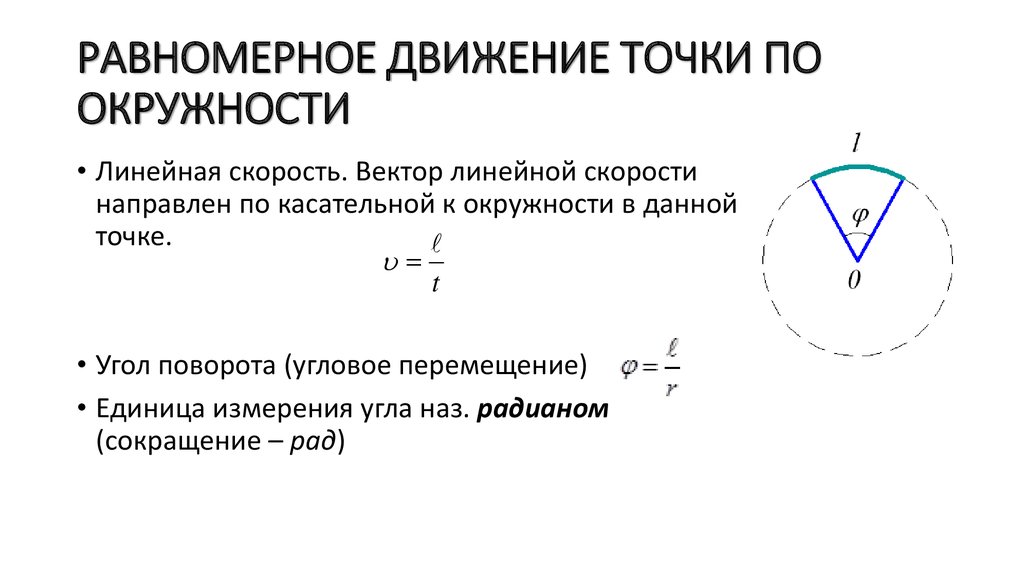

Так как вектор перемещения $\Delta \overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $\Delta \overline{r}$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.

Скорость прохождения пути ($s$) определяют:

\[v={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\left(2\right).\ }\]

Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.

Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($\varphi $), который образует радиус-вектор ($\overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).

Быстроту изменения угла поворота $\varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $\omega $. Угловая скорость равна:

\[\omega =\frac{d\varphi }{dt}\left(3\right).\]

Вращение называют равномерным, если угловая скорость постоянна $\omega =const$. При равномерном вращении $\omega $ можно называть угловой частотой.

Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$\ R=const$, то длину дуги найдем как:

\[s=R\varphi \ \left(4\right).\]

Продифференцируем обе части выражения (4) по времени, имеем:

\[\frac{ds}{dt}=\frac{d\left(R\varphi \right)}{dt}=R\frac{d\varphi }{dt}\left(5\right).\]

Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:

\[v=R\omega \left(6\right). \]

Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ — радиус кривизны траектории в месте нахождения частицы.

В векторном виде выражение (6) записывают так:

\[\overline{v}=\overline{\omega }\times \overline{r}\left(7\right),\]

$\overline{r}$ — вектор, соединяющий ось вращения и движущуюся точку (рис.2). Модуль скорости, используя формулу (7) найдем как:

\[v=\omega r{\sin \alpha \ \left(8\right),\ }\]

где $\alpha $ — угол между вектором угловой скорости и $\overline{r}.$

Угловая скорость через линейную

Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:

\[\omega =\frac{v}{R}\left(9\right).\]

Или используя формулу (8) угловую скорость выразим как:

\[\omega =\frac{v}{r{\sin \alpha \ }}\left(10\right). \]

Примеры задач с решением

Пример 1

Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $\Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($\omega $)?

Решение. Основой для решения задачи будет формула:

\[\omega =\frac{v}{R}\left(1.1\right).\]

Угловые скорости движения точки A и B одинаковы (${\omega }_A={\omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):

\[{\omega }_A=\frac{v_1}{R_1};;\ {\omega }_B=\frac{v_2}{R_2}\left(1.2\right).\]

$R_1$ — расстояние от точки O до точки A; $R_2=R_1-\Delta l$ — расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:

\[\frac{v_1}{R_1}=\frac{v_2}{R_1-\Delta l}\to R_1=\frac{\Delta l\cdot v_1}{v_1-v_2}\left(1. 2=15\ \left(\frac{м}{с}\right).\]

Ответ. $v\left(t’\right)=15\frac{м}{с}$

Читать дальше: масса и плотность вещества.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Угловая скорость и линейная скорость – определение, взаимосвязь и часто задаваемые вопросы

Для студентов, изучающих естественные науки, очень важно точно знать термины. Это означает, что для студентов, изучающих естественные науки, важно знать определения этого термина, потому что это делает его значение очень ясным и кратким. Кроме того, во многих случаях термины кажутся одинаковыми, и поэтому учащиеся путаются в значении, в таких случаях, если учащиеся имеют под рукой определения, они могут легко различить их. И, следовательно, Веданту бесплатно предоставляет то же самое изучающим науку.

Краткий обзор терминов угловая скорость и линейная скорость.

Угловая скорость: Отношение, по которому устанавливается положение одной линии относительно другой линии, называется угловым положением. А скорость, с которой изменяется угловое положение вращающегося тела, называется угловой скоростью.

Линейная скорость: Проще говоря, линейная скорость означает скорость объекта по прямой линии. Иными словами, он показывает время, затрачиваемое объектом на перемещение из точки А в точку Б.

Разница между угловой скоростью и линейной скоростью.

	Угловая скорость	Linear Selocity
Определение 9003 2020202020202020202. говоря, он показывает, с какой скоростью объект вращается, поворачивается и вращается вокруг центральной точки.	Линейная скорость просто показывает скорость, с которой объект перемещается из одной точки в другую по прямому пути.
Основное отличие	• При круговом движении объект имеет угловую скорость вдоль оси окружности. • На протяжении всего кругового движения остается неизменным.	• Линейная скорость объекта при круговом движении определяется по окружности окружности. •В различных точках круга он не остается одним и тем же, то есть разным.
Обозначение	Обозначение угловой скорости взято из греческого алфавита «ω». Иногда используется «Ω». , то есть «v»
Единица измерения	Для измерения угловой скорости используются градусы и радианы.	Для измерения линейной скорости используется единица M/S
Формула	Формула угловой скорости составляет Ом = Δθ/2πr/T 2020202020202020202020202020202. 0202020202020202020202020202020202. . для линейной скорости ω=  ΔS/Δt=  2πr/t

Преимущества наличия определений линейной и угловой скоростей, а также их соотношений

• Для лучшего понимания науки очень важно важно, чтобы студенты имели четкое представление о словах и терминах, используемых в науке, то есть студенты должны иметь хороший научный словарный запас. И лучший способ иметь этот эффективный словарный запас — это иметь в наличии определения и значения терминов. И то же самое касается определения линейной скорости и угловой скорости.

• Понятия линейной скорости и угловой скорости кажутся совершенно разными, если изучить их определения. Но, тем не менее, между ними также существуют некоторые отношения, и, следовательно, Веданту предоставляет то же самое ученикам совершенно бесплатно.

•  Кроме того, иногда учащиеся могут найти концепцию линейной скорости и угловой скорости немного сложной для понимания, поэтому Веданту дает объяснение того же самого простым и ясным языком. То есть вместе с определением дается и объяснение.

• Как только учащиеся хорошо усвоят концепцию линейной скорости и угловой скорости, другие вещи станут довольно простыми. Например, определение линейной и угловой скорости можно легко запомнить, потому что вы уже знаете, что именно это означает. Кроме того, становится довольно легко найти разницу между ними, а также их отношения.

Почему угловое смещение считается осевым вектором?

Мы знаем, что угловое смещение — это угол, на который движется частица при круговом движении. Поскольку направление смещения вдоль оси, поэтому угловое смещение является осевым вектором.

     

Частица, совершающая круговое движение, испытывает два типа смещения; это:

Если ‘r’ — радиус окружности, то отношение между угловым и линейным перемещением будет следующим:  

              

\[S=R\theta \] или \[\theta =\frac{s} {р}\] . . . . . . . (1)

Линейная скорость определяется как скорость изменения линейного смещения. Для частицы P это определяется как:

                    \[V=\frac{\Delta s}{\Delta t}\]…..(2)

Угловая скорость частицы — это скорость изменения углового смещения, т. е. скорость изменения угла. Это дано по:

\ [w = \ frac {\ delta \ theta} {\ delta t} \] ….. (3)

Связь между линейной скоростью и угловой скоростью

Мы мы знаем, что линейная скорость частицы P определяется как: 

                   

\[\mid v \mid =\frac{\Delta (s)}{\Delta t}\]. ….(2), и S = rθ

Теперь, подставляя значение уравнения (1) в (3), получаем:

                    \[v=\frac{\Delta r\theta }{\Delta t}\]…..(2)

Мы знаем, что радиус ‘r’  является постоянной величиной, поэтому получаем:

                 \[v=\frac{\Delta r\theta }{\Delta t}\]…..(2) ( Поскольку \[\frac{\Delta \theta}{\Delta t}\] = w)

⇒ |v| = rω, что является «отношением между линейной и угловой скоростью».

Здесь v зависит от r и ω следующим образом:

ω = скорость вращения объекта, и

r = Линейная скорость частицы в центре будет равна нулю. Когда частица начинает удаляться от центра, линейная скорость начинает увеличиваться. Она максимальна на окружности круга.

Касательная к окружности указывает направление линейной скорости.

Запомнить

Согните пальцы в направлении против часовой стрелки, а большой палец, указывающий наружу (вдоль оси), указывает направление угловой скорости. Точно так же, если вы согните пальцы по часовой стрелке, то большой палец, указывающий внутрь, даст направление ω.

Зависимость угловой скорости от линейной скорости

Для тела, совершающего равномерное круговое движение, соотношение между линейной и угловой скоростью:

                           расстояние частицы от центра круговой траектории и ее угловая скорость.

• Линейная скорость различна в разных точках окружности.

• В центре ноль.

• Минимум между центром и любой точкой на окружности.

• Максимум на окружности круга. Однако угловая скорость остается неизменной во всех точках кругового пути.

От угловой скорости к линейной скорости

Из наших знаний о круговом движении мы можем сделать вывод, что величина линейной скорости частицы, движущейся по окружности, связана с угловой скоростью частицы следующим соотношением:

                        \[r=\frac{v}{w}\]

В любой момент это соотношение применяется к каждой частице, имеющей твердое тело.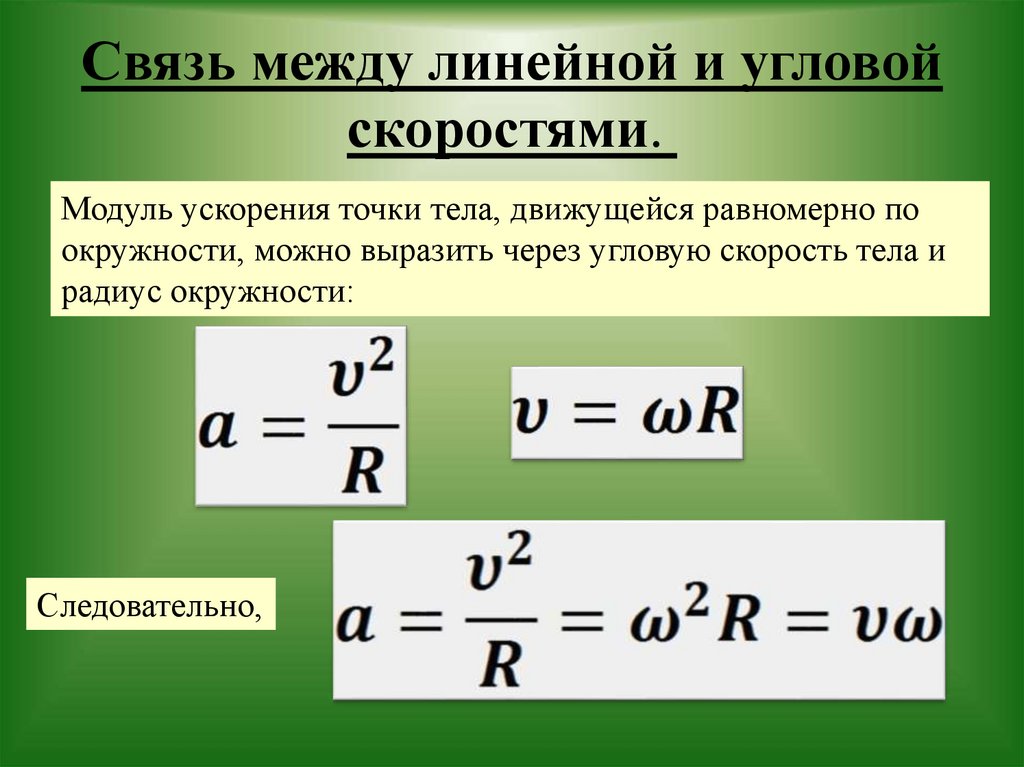

Связь между угловой скоростью и линейной скоростью

Движение описывается как изменение положения в течение определенного периода времени. С точки зрения физики и механики это называется скоростью. Он определяется как изменение позиции за период. Вращательное движение касается тел, которые движутся вокруг фиксированной оси. Эти тела во вращательном движении часто демонстрируют поведение, аналогичное их поведению во время поступательного движения. Например, угловая скорость и скорость при поступательном движении аналогичны, а также крутящий момент-сила и масса-момент инерции.

Угловое вращение

Вращательное движение — это круговое движение вокруг фиксированной оси. Работая над задачами о вращательном движении, мы пытаемся найти сходство между поступательным и вращательным движением и использовать аналогичные переменные. Угол поворота определяется углом, охватываемым телом. Он обозначается обозначением тета(). При вращательном движении объект совершает круговое движение. Длина дуги – это расстояние, пройденное объектом во вращательном движении. Это расстояние и угловой поворот связаны радиусом кривизны.

Обозначим длину дуги буквой «s», а радиус кривизны буквой «r».

θ = s/r 

Угловая скорость

Предположим, что тело вращается вокруг некоторой фиксированной оси. Затем тело меняет свой угол со временем. Обозначая угол через θ, угловая скорость определяется как скорость изменения угла тела. Угловая скорость обозначается ω. Если тело вращается с постоянной скоростью, используется средняя угловая скорость,

В случаях, когда вращательное движение непостоянно, вычисляется мгновенная угловая скорость.

ω = dθ/dt

Как показано на рисунке, угловая скорость направлена ​​к неподвижной оси.

Угловая скорость и линейная скорость

Линейная скорость — это мера расстояния, которое объект проходит за единицу времени. Для объекта, движущегося по кругу, линейная скорость связана с угловой скоростью. Объект, покрывающий угол, также покрывает некоторое расстояние по дуге окружности. Предположим, что линейная скорость частицы P, вращающейся вокруг фиксированной оси, определяется выражением

Известно, что

с = rθ

.

|в| = rω

Примеры задач

Вопрос 1: Найдите угловую скорость мяча, движущегося со скоростью 10 м/с по окружности радиусом 20 м.

Ответ:

Связь между угловой и линейной скоростью мяча определяется выражением, 

|v| = rω

Дано:

v = 10 м/с

r = 20 м

Найти:

ω = ?

v = rω

⇒ 10 = (20)ω

⇒ 0,5 м/с = ω

Вопрос 2. Найдите угловую скорость мяча, движущегося со скоростью 100 м/с по радиусу 5 м. круг.

Ответ:

Связь между угловой и линейной скоростью мяча определяется выражением

|в| = rω

Дано:

v = 100 м/с

r = 5 м

Найти:

ω = ?

v = rω

⇒ 100 = (5)ω

⇒ 20 м/с = ω

Вопрос 3.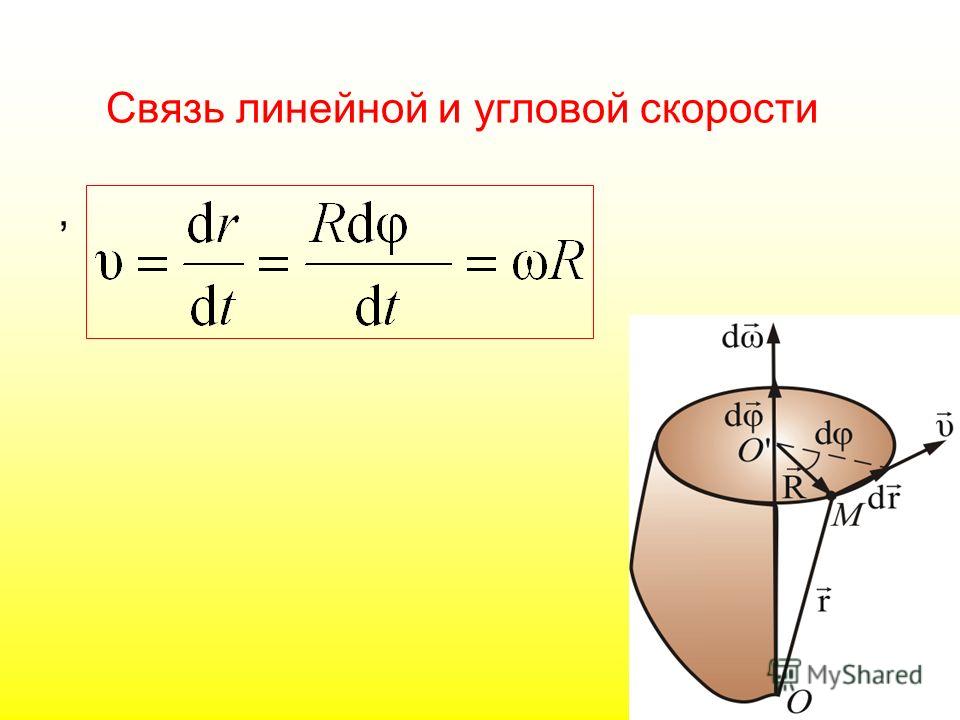 Найти полный круг за 20 секунд. Найдите угловую скорость частицы.

Ответ:

Угловая скорость определяется по формуле0003

= 2π

Время «t» = 20 секунд.

Найти:

ω = (угол)/(время)

⇒ ω = 2π / 20

⇒ ω = π /10 рад/с.

Вопрос 4: Найдите покрытия на 270 градусов за 5 секунд. Найдите угловую скорость частицы.

Ответ:

Угловая скорость определяется выражением

ω = (угол)/(время)

Дано:

9°206 = 93024/9024/9024/9024 = 9024/9024.0003

Время «t» = 5 секунд.

Найти:

ω = (угол)/(время)

⇒ ω = 3π / (4)(5)

⇒ ω = 3π /20 рад/с.

⇒ ω = 0,15π рад/с.

Вопрос 5: Планета движется вокруг своего солнца по кругу. Угловая скорость планеты 0,5 рад/с. Расстояние планеты от Солнца оценивается в 1 00 000 км. Найдите линейную скорость планеты.