Угол вращения это – ОФС.1.2.1.0018.15 Поляриметрия | Фармакопея.рф

Содержание

Удельное вращение — это… Что такое Удельное вращение?

Удельное вращение

Поляриметрия — методы исследования излучения, основанные на измерении:

степени поляризации излучения (света, радиоволн)
оптической активности веществ или их растворов

Поляриметрия используется для исследования излучений, а также в аналитической и структурной химии.

Теория поляриметрии

Оптическая активность веществ очень чувствительна к изменениям пространственной структуры молекул и к межмолекулярному взаимодействию.

Поляризуемость атомов, ионов и молекул определяет степень межмолекулярного взаимодействия и его влияние на оптическую активность среды.

Поляриметрия даёт ценную информацию о природе заместителей в органических молекулах, о строении комплексных неорганических соединений.

Исследование оптической активности веществ

С помощью оптических поляриметров определяют величину вращения плоскости поляризации света при прохождении его через оптически-активные среды (твёрдые вещества или растворы).

Поляриметрия широко применяется в аналитической химии для быстрого измерения концентрации оптически-активных веществ (см. Сахариметрия), для идентификации эфирных масел и в других исследованиях.

Величина оптического вращения в растворах зависит от их концентрации и специфических свойств оптически-активных веществ.
Измерение вращательной дисперсии света (спектрополяриметрия, определение угла вращения при изменении длины волны света позволяет изучать строение веществ.

См. также

Литература

Волькенштейн М. В., Молекулярная оптика, М.-Л., 1951
Джерасси К., Дисперсия оптического вращения, пер. с англ., М., 1962
Терентьев А. П., Органический анализ, М., 1966

Wikimedia Foundation. 2010.

Удельная теплоемкость
Удельная электропроводность

Смотреть что такое «Удельное вращение» в других словарях:

Удельное вращение — см. Вращательная способность химических соединений … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
удельное вращение вещества — Угол, на который поворачивается плоскость поляризации оптического излучения определенной длины волны при прохождении им пути единичной длины в веществе. [ГОСТ 23778 79] Тематики оптика, оптические приборы и измерения EN specific rotation of… … Справочник технического переводчика
удельное вращение раствора — Отношение угла, на который поворачивается плоскость поляризации оптического излучения определенной длины волны при прохождении им пути единичной длины в растворе вещества, к концентрации этого вещества. [ГОСТ 23778 79] Тематики оптика, оптические … Справочник технического переводчика
Удельное вращение некоторых органических веществ
— Вещество Растворитель Удельное вращение* Сахароза Вода +66,462 Глюкоза Вода +52,70 … Химический справочник
относительное удельное вращение вещества — Отношение удельного вращения вещества к плотности этого вещества. [ГОСТ 23778 79] Тематики оптика, оптические приборы и измерения EN relative specific rotation of substance DE relative spezifische Materialdrehung FR rotation relative spécifique… … Справочник технического переводчика
Вращение плоскости поляризации — поперечной волны физическое явление, заключающееся в повороте поляризационного вектора линейно поляризованной поперечной волны вокруг её волнового вектора при прохождении волны через анизотропную среду. Волна может быть электромагнитной,… … Википедия
ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ — ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ, изменение направления (плоскости) колебаний лучей поляризованного света (см. Поляризация оптическая). Этим свойством обладают: 1. Все прозрачные тела, если их поместить в магнитном поле (магнитное В. п. п.). Для… … Большая медицинская энциклопедия
УДЕЛЬНОЕ МАГНИТНОЕ ВРАЩЕНИЕ — то же, что (см. ВЕРДЕ ПОСТОЯННАЯ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия
Вращательная способность химических соединений — Под именем вращательной способности химических соединений подразумевается способность, присущая некоторым из них, отклонять плоскость поляризации светового луча от ее первоначального направления. Допустим, что в луче такого поляризованного света… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Сахарозы — (хим.) название, произведенное от слова сахароза, синонима тростникового сахара; систематически употреблено для обозначения углеводов общей формулы С12Н22О11 только в настоящем Энц. сл. и в 1 м томе соч. Толленса Handb. der Kohlenhydrate (Бресл.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

biograf.academic.ru

Внутренний угол вращения — Справочник химика 21

В этих формулах К — константа, Т — момент вращения, определяемый величиной падающего груза или упругостью ленты подвеса, У — угловая скорость вращения, и Гд — радиусы внутреннего и наружного цилиндров, — эффективная длина цилиндрической части внутреннего тела вращения соответственно погружению его в жидкость, Гд—расстояние от оси вращения до середины зазора между цилиндрами, —угол между осью вращения и серединой конического промежутка. [c.204]
После разрушения смазки по п. 1.3.2 измеряют относительный угол вращения (а) внутреннего цилиндра или конуса измерительного устройства с испытуемой смазкой при градиентах скоростей деформации, указанных в табл. 1.
[c.417]

Влияние температуры на угол вращения было также впервые отмечено Био. Оба явления — влияние растворителя и влияние температуры на оптическое вращение — пытались одно время объяснять с точки зрения теории Таммана (1895), который это влияние связывал с изменением внутреннего давления растворителя или раствора. [c.205]

Определение оптической активности. Угол вращения плоскости поляризации удобно измерять в микрокюветах длиной 2 или 5 см. Они делаются из толстостенной трубочки с внутренним диаметром 1—2 мм. В этом случае определение может быть проведено с минимальным количеством вещества. Наблюдаемый в поляриметре угол вращения пересчитывают с учетом плотности (для жидких веществ) или концентрации (для растворов твердых веществ) на удельное вращение [а]ь . [c.48]

Для испытания применяют ротационный вискозиметр Реотест 2.1 или его последующие модификации с измерительными устройствами — специальным цилиндрическим г и конусом-пли-той. Измерительное устройство заполняют смазкой, термостати-руют при заданной температуре в течение 30 мин, затем разрушают смазку вращением с помощью двигателя. После этого измеряют относительный угол вращения внутреннего цилиндра или конуса измерительного устройства с испытываемой смазкой при определенных градиентах скоростей деформации.

[c.241]

Теперь остается лишь перевести локальные координаты всех узлов в единую систему, связанную с каким-либо одним узлом — первым пли последним. Для этого применяют преобразование Эйринга, описанное в разделе 5 гл. 2 делают два последовательных поворота каждой локальной системы на угол, дополнительный к валентному углу, и на угол вращения вокруг связи главной цепи затем транслируют координаты на длину этой связи. Таким образом, координаты всех атомов оказываются выраженными через внутренние геометрические параметры макромолекулы — длины связей, валентные углы и углы вращения.

[c.322]

При очистке бойком кокс отделяется от стенок трубы слоями. Установлено, что при нормальной очистке около 50% кокса удаляется в виде частиц размером 0,5 мм и около 8% —в виде частиц размером 2,5 мм, остальные частицы (42%) — более крупные. Эффективность очистки зависит от центробежной силы, возникающей при вращении бойка (частота вращения турбинки 3500—5000 об/мин), и силы ударов его граней о кокс. Шарнирное соединение обусловливает сложное движение бойка, при котором он гранями соскабливает с внутренней поверхности трубы кокс, поэтому для ускорения очистки большое значение имеет угол заточки граней бойков. Оптимальный угол заточки грани бойка равен 73°. Заточка осуществляется перед очисткой труб специальным приспособлением. [c.188]

Результаты расчетов иллюстрируются рис. 4,6, где дана зависимость потенциальной энергии олефина от угла между я- и я -ор-биталями (угол внутреннего вращения). Видно, что «триплетное состояние при конфигурации, соответствующей повороту на 90°, энергетически выгодно. Дезактивирование такого возбужденного триплета приведет к основным состояниям, где вновь будет осуществлен поворот на 90° (относительно возбужденного триплета), т. е. к появлению молекул с исходной конфигурацией и с конфигурацией, где осуществлен поворот относительно С—С-связи на 180°, — к цис-гранс-изомеризации. Поэтому схема процессов при активированной фотохимической изомеризации будет следующая [c.68]

В случае разностенности наружного или внутреннего колец подшипника ось вращения коленчатого вала поворачивается на угол бр (фиг. 50,в). Тангенс угла поворота оси вращения коленчатого вала определяется разностенностью (радиальным [c.137]

Погрешность, обусловленная несоосностью поверхностей деталей (фиг. 50). На фиг. 50, г утрировано показано несовпадение осей наружной поверхности стакана и внутренней поверхности отверстия под подшипник. Легко заметить, что несовпадение осей влечет за собой поворот оси вращения коленчатого вала. Угол поворота оси вращения будет максимальным в случае совпадения направления линии эксцентрицитета с плоскостью, проходящей через ось вращения коленчатого вала и ось цилиндра.

[c.138]

В кожухе 4 (рис. 3.19) на валу 1 размещен конический перфорированный барабан 3, внутренняя поверхность которого покрыта листовым ситом. Внутри барабана коаксиально с ним установлено направляющее устройство 2. Оно состоит из пяти секций, образующих с помощью расположенных на наружных поверхностях лопастей 5 каналы для движения суспензии. Барабан и направляющее устройство вращаются с одинаковыми частотами, что является главным отличительным признаком от центрифуги со шнековой выгрузкой осадка. Угол наклона образующей барабана к оси вращения 30—35°, т. е. больше угла трения осадка о сито. Предусмотрена возможность промывки осадка. В центрифуге применены листовые или щелевые колосниковые сита, специально разработанные для машины минимальный размер отверстий листовых сит 20 мкм, колосниковых 50 мкм.

[c.205]

Конструктивно тарельчатые сепараторы (рис. 3.23) аналогичны однокамерным. Пакет тарелок 10 надет на горловину загрузочной воронки и зажат в осевом направлении между раструбом воронки и конической крышкой барабана (в осветляющих сепараторах) или разделительн

www.chem21.info

угол поворота — это… Что такое угол поворота?

3.5 угол поворота (steering angle): Общий угол полного отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальной оси из положения обычного прямолинейного движения в положение поворота.

Примечания

1 Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов

2 Для рулевого управления с поворотными кулаками и трапецией характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота, следовательно, при использовании такого рулевого управления должно быть также указано место измерения угла поворота.

Для определения угла поворота, полученного в случае комбинированного применения кинематических схем, включая систему управления с поворотными кулаками и трапецией, также необходимо указать место измерения угла поворота.

3.5 угол поворота (steering angle): Общий угол полного отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальных осей из положения обычного прямолинейного движения в положение поворота.

Примечания

1. Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов.

2. Для системы рулевого управления Аккерманн (с поворотными кулаками, рычагами и трапецией) характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота. Следовательно, при использовании такого рулевого управления должно быть также указано место измерения угла поворота.

Для определения угла поворота, полученного в случае комбинированного применения кинематических схем, включая систему Аккерманн, также необходимо указать место измерения угла поворота.

4.14. Угол поворота — общий угол отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальных осей из положения обычного прямолинейного движения в положение поворота.

4.14.1. Угол поворота для многоосных машин определяют между колесами первого переднего и последнего заднего мостов.

4.14.2. Для ручного управления с поворотными кулаками и трапецией характерно, что угол поворота колес, расположенных с внутренней стороны поворота, превышает угол поворота колес, расположенных с внешней стороны поворота. Следовательно, для этой системы должно быть также указано место измерения угла поворота.

4.14.3. Угол поворота, полученный в случае комбинированного применения кинематических схем, включая систему управления с поворотными кулаками и трапецией, определяют по п. 4.14, при этом должно быть указано место измерения в соответствии с требованиями п. 4.14.2.

2.4.3 угол поворота: Угол между проекцией продольной оси транспортного средства и линией пересечения плоскости колеса, которая представляет собой центральную плоскость шины, перпендикулярную к оси вращения колеса, и поверхности дороги.

6.19 угол поворота: Угловое перемещение запирающего или регулирующего элемента, исчисленное от закрытого положения затвора.

6.19 угол поворота

Величина углового перемещения запирающего или регулирующего элемента, исчисленная от закрытого положения затвора.

Смотри также родственные термины:

2.3.8 угол поворота ( e): Угол, указывающий расположение светоотражающего материала при помощи соответствующего обозначения с учетом поворота вокруг исходной оси.

6.20 угол поворота номинальный

Величина полного угла поворота без учета допусков.

6.22 угол поворота относительный

Отношение значения текущего угла поворота к номинальному углу поворота.

192 угол поворота рабочего оборудования a

Максимальный угол поворота рабочего оборудования от одного крайнего положения до другого

—

Угол поворота сварного шва b

Угол, который образует поперечная ось шва со своим нулевым положением (см. черт. 3).

6.21 угол поворота текущий

Угол поворота в промежутке от закрытого до полностью открытого положения затвора.

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

normative_reference_dictionary.academic.ru

Кинематика вращательного движения

Лекция

Кинематика вращательного движения

План

Тангенциальное и нормальное ускорение
Радиус кривизны траектории
Угловая скорость, вектор угла поворота, угловое ускорение
Связь линейной и угловой скорости
Связь линейных и угловых характеристик

1. Тангенциальное и нормальное ускорение

Две составляющие ускорения: тангенциальное ускорение и нормальное ускорение.

Тангенциальное ускорение направлено по касательной к траектории

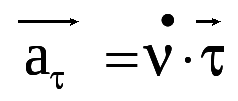
Нормальное ускорение направлено по нормали к траектории

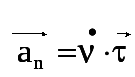
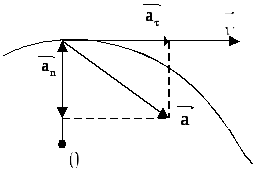
Тангенциальное ускорение характеризует изменение скорости по величине. Если скорость по величине не изменяется, то тангенциальная составляющая равна нулю, а нормальная составляющая ускорения равна полному ускорению.

Нормальное ускорение характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории.

В общем случае полное ускорение:

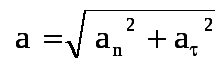
Итак, нормальная составляющая вектора ускорения

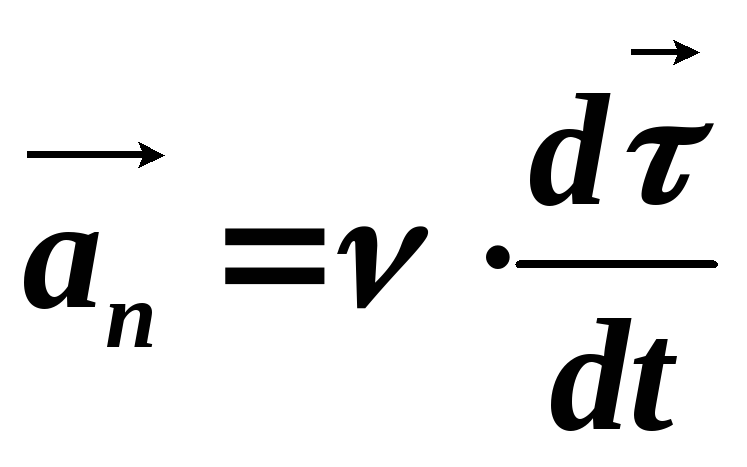
Чтобы выяснить свойства нормального ускорения, надо установить, чем определяется 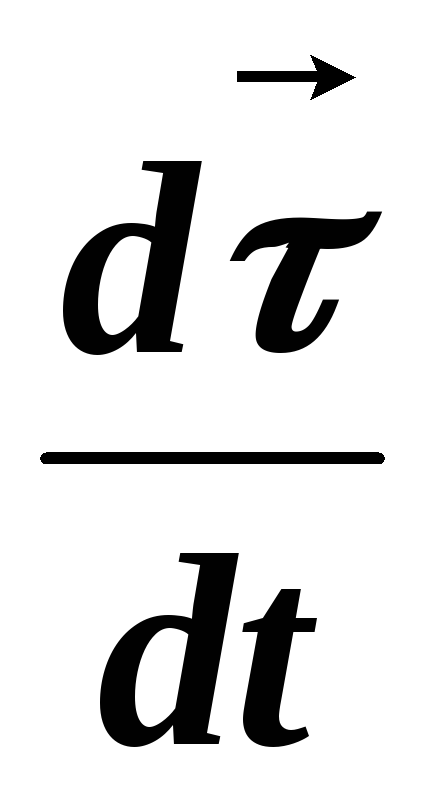, т.е быстрота изменения со временем направления касательной к траектории. Она тем больше (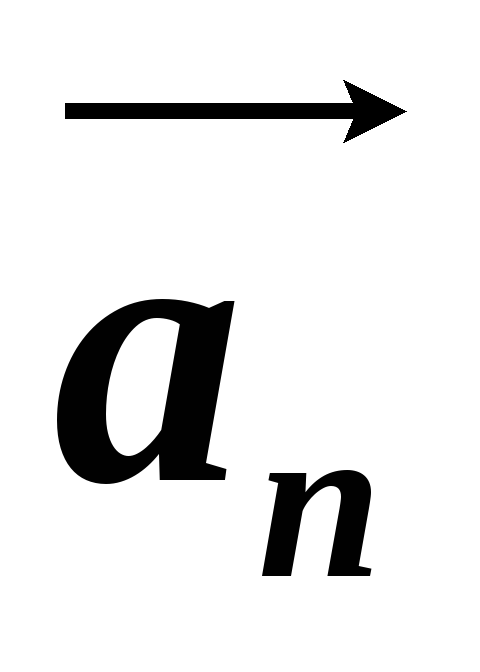), чем больше искривлена траектория и чем быстрее перемещается частица по траектории.

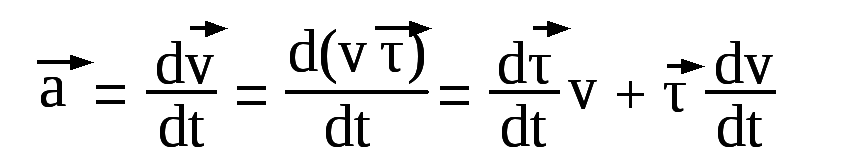
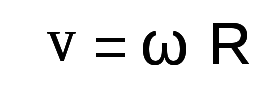
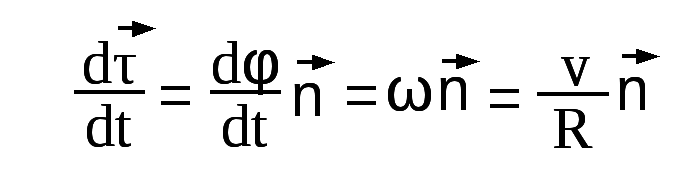
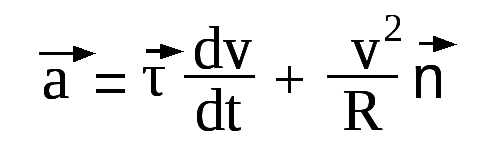
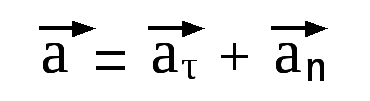
2. Радиус кривизны траектории

Радиус кривизны – это радиус окружности, которая сливается в данном месте с кривой на бесконечно малом её участке.

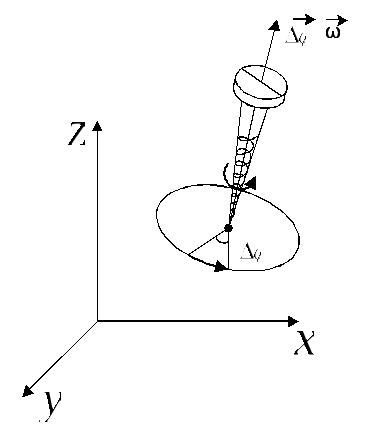
3. Угловая скорость, вектор угла поворота, угловое ускорение.

Любой поворот полностью определяется указанием оси вращения и угла поворота Δφ относительно этой оси. Если поворот осуществляется на малый угол Δφ << 2π, то можно ввести понятие вектор угла поворота.

Вектор 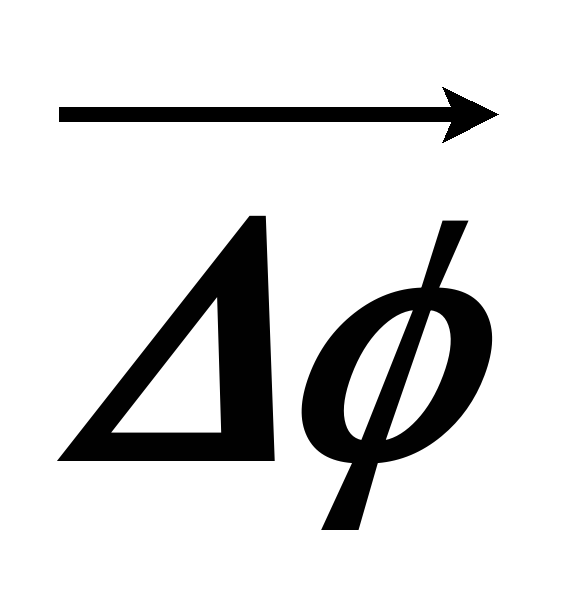направлен вдоль оси вращения, т.е. перпендикулярно плоскости, в которой происходит вращение.

Ориентация этого вектора определяется правилом буравчика.

Абсолютное значение вектора 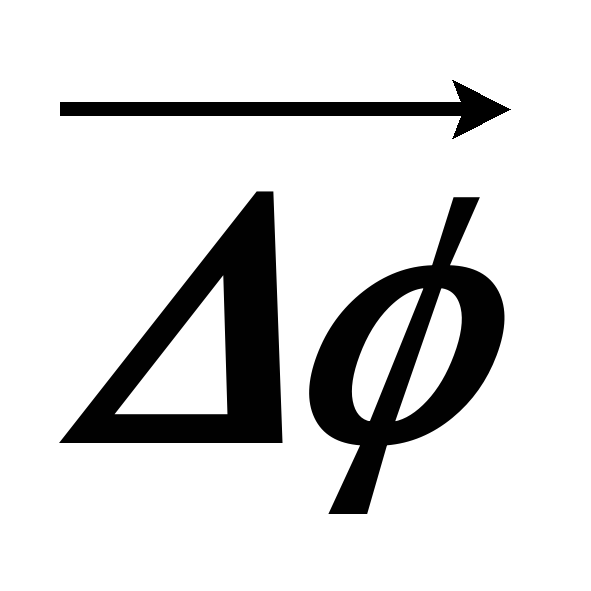равно углу поворота Δφ.

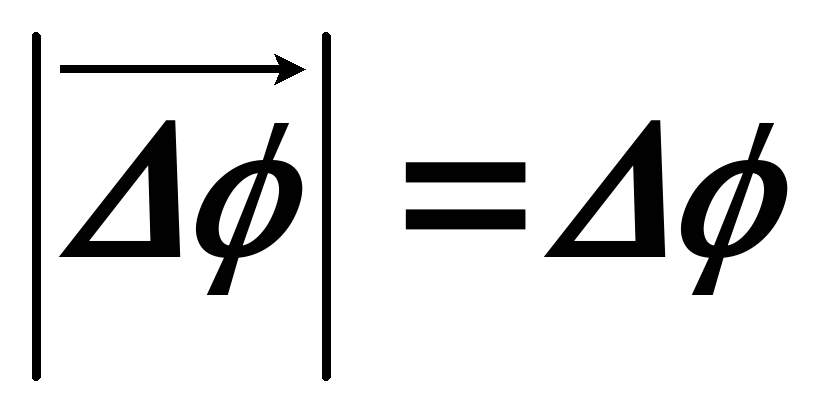
Для того, чтобы величин была вектором, она должна не только направление и абсолютное значение, но и удовлетворять правилу сложения векторов. Это можно показать, что при векторном сложении двух углов поворота правило параллелограмма не выполняется. Оно будет справедливо лишь для малого Δφ << 2π

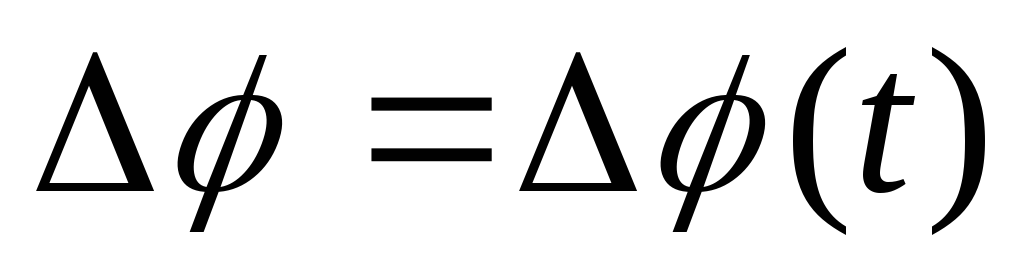
— неполный вектор.

Угловой скоростью называется вектор 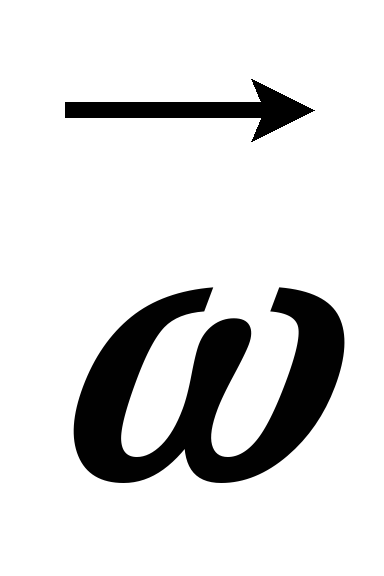, направление которого: определяет ориентацию плоскости вращения и по правилу буравчика направление вращения.

Модуль вектора 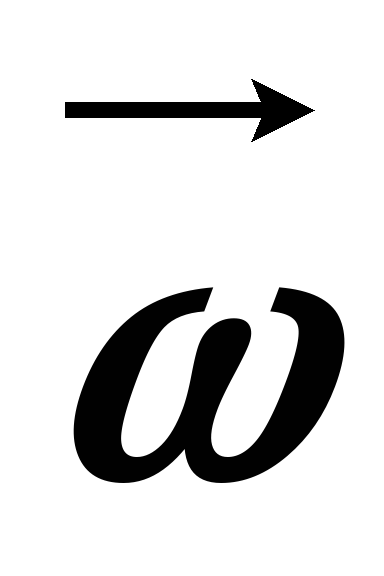равен производной от угла поворота по времени:

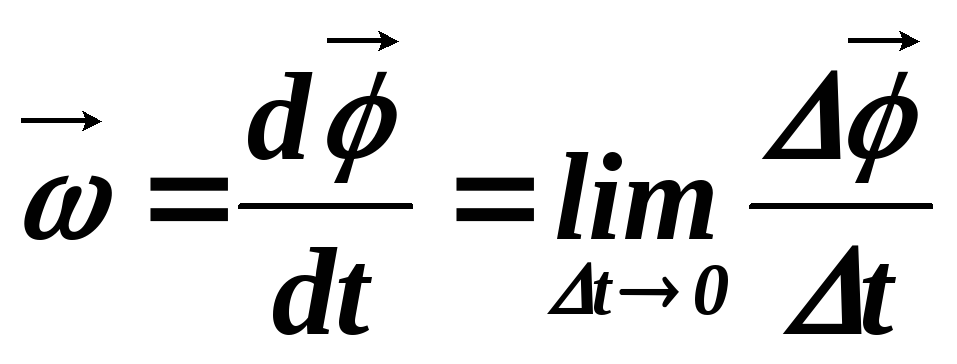
Угловая скорость, в отличие от угла поворота, является полным вектором.

Вектор 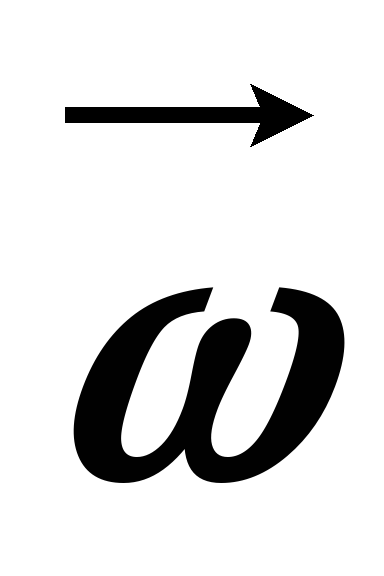может изменяться как за счёт изменения скорости вращения тела вокруг оси (по величине), так и за счёт поворота оси вращения в пространстве (по направлению).

Пусть за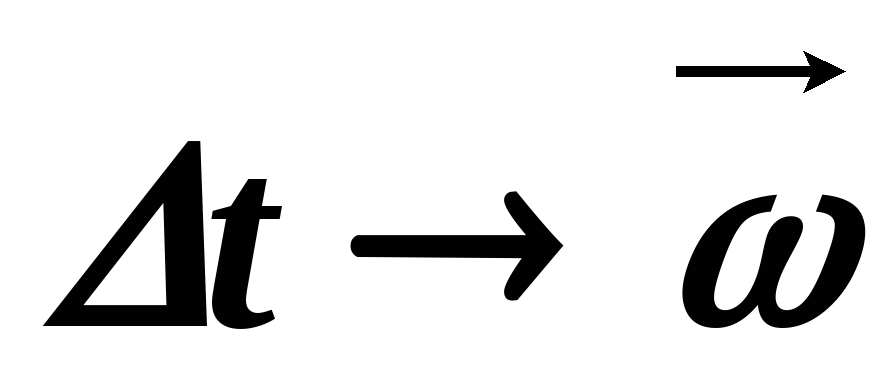

Изменение вектора угловой скорости со временем характеризуется величиной угловое ускорение:

Ускоренное

Замедленное

Модуль углового ускорения измеряется в

Угловое ускорение также как и угловая скорость – псевдовектор.

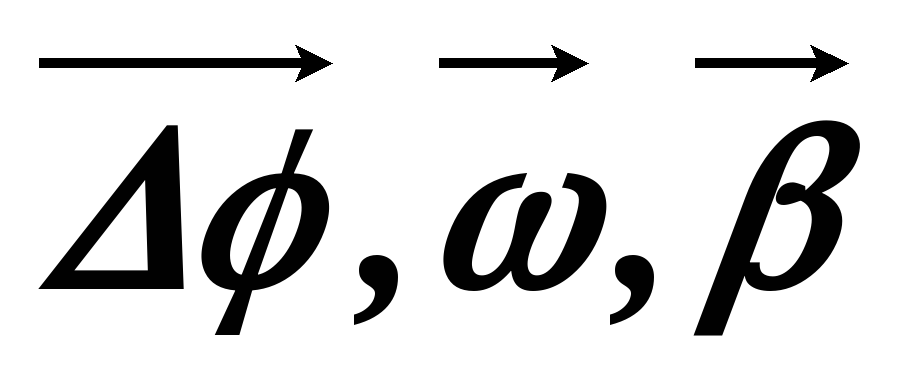— псевдовектора, т.к. направление вектора поворота 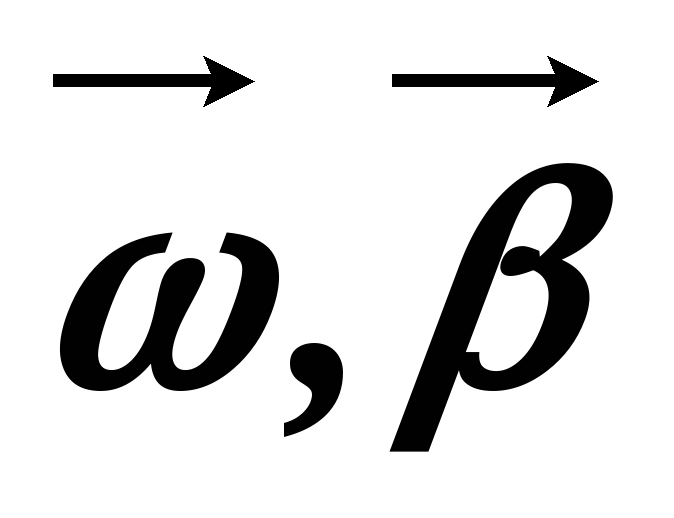связывается с направлением вращения тела.

4. Связь линейной и угловой скорости

Пусть за малый Δt тело повернулось на Δφ. Пусть точки за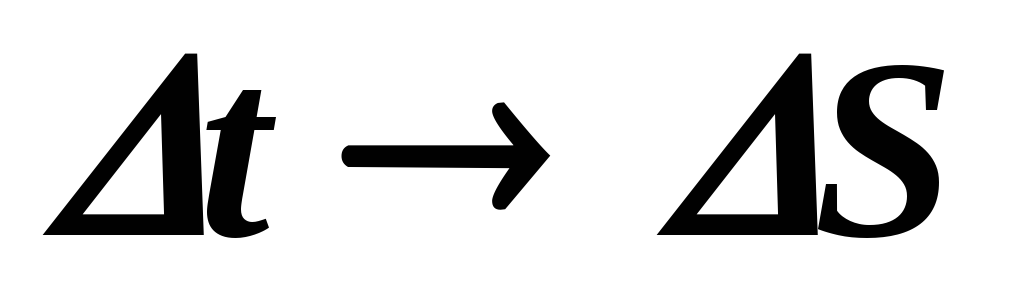

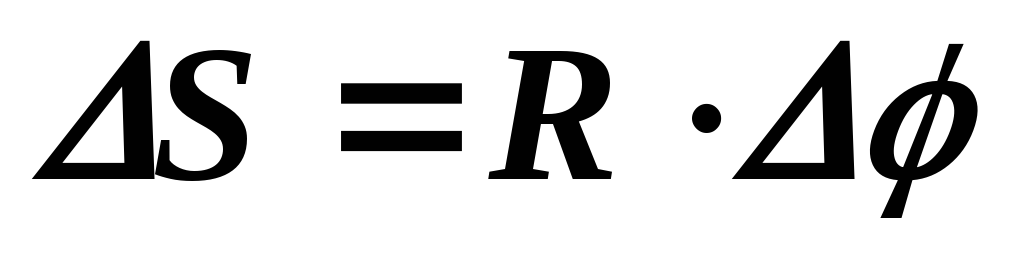
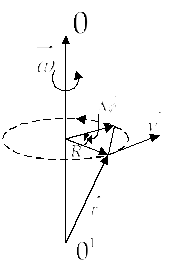
Модуль линейной скорости

Связь векторов линейной и угловой скоростей: положение точки определяется радиусом-вектором , вектор 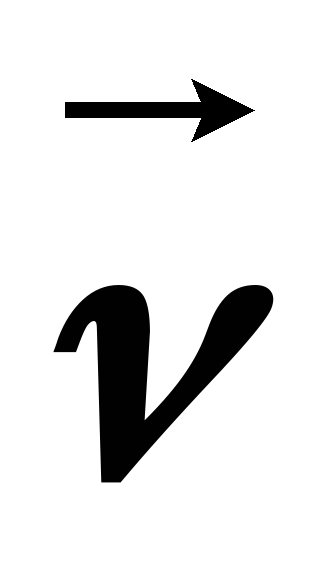из рисунка определяется как векторное произведение 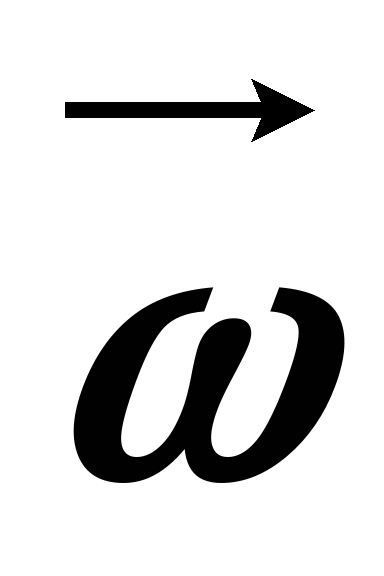и .

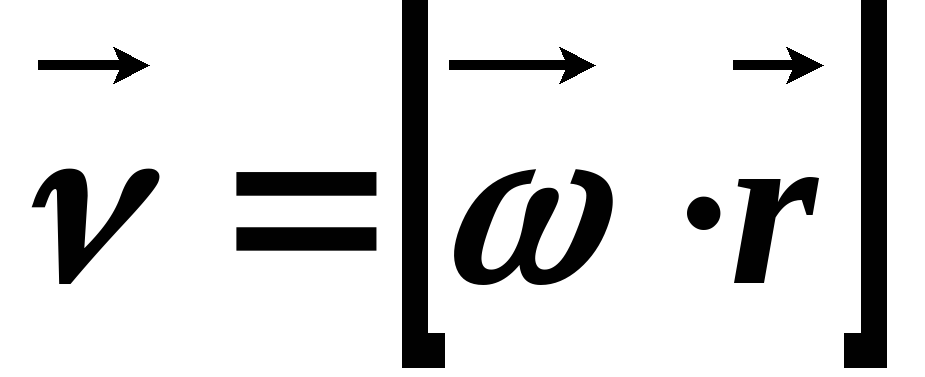
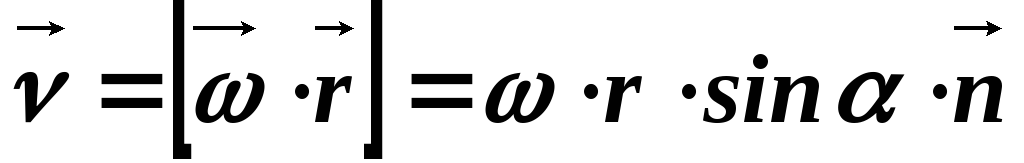
Изменение радиуса-вектора со временем только по направлению называется прецессией.

5. Связь линейных и угловых характеристик

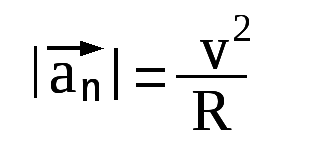
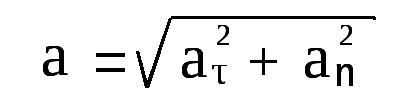
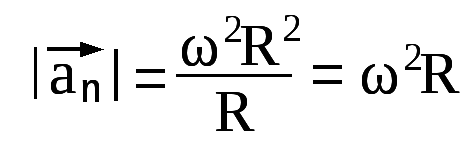
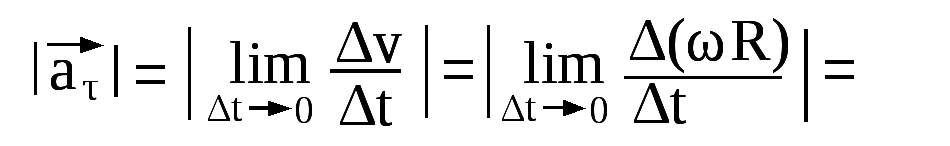
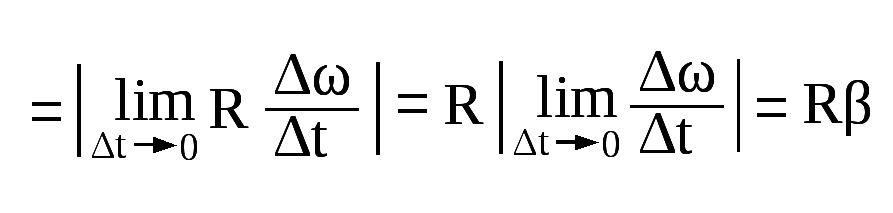
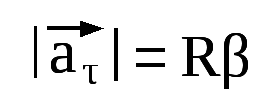
studfile.net

УГОЛ ПОВОРОТА — это… Что такое УГОЛ ПОВОРОТА?

УГОЛ ПОВОРОТА

УГОЛ ПОВОРОТА: внешний угол между направлениями прямых участков жел.-дор. пути при поворотах трассы. У. п. равен центральному углу, вершина к-рого находится в центре круговой кривой, а стороны проходят через тангенсы.

УГОЛ НАБЕГАНИЯ (колеса на рельс)
УГОЛОК ЖЕСТКОСТИ

Смотреть что такое «УГОЛ ПОВОРОТА» в других словарях:

угол поворота — твёрдого тела; угол поворота Угол между двумя последовательными положениями полуплоскости, неизменно связанной с телом и проходящей через его ось вращения … Политехнический терминологический толковый словарь
угол поворота — Угловое перемещение запирающего или регулирующего элемента, исчисленное от закрытого положения затвора. [ГОСТ Р 52720 2007] Тематики арматура трубопроводная … Справочник технического переводчика
угол поворота — 3.5 угол поворота (steering angle): Общий угол полного отклонения, измеряемый между передними и задними колесами при их перемещении относительно одной или более вертикальной оси из положения обычного прямолинейного движения в положение поворота.… … Словарь-справочник терминов нормативно-технической документации
угол поворота ( e) — 2.3.8 угол поворота ( e): Угол, указывающий расположение светоотражающего материала при помощи соответствующего обозначения с учетом поворота вокруг исходной оси. Источник … Словарь-справочник терминов нормативно-технической документации
угол поворота — posūkio kampas statusas T sritis automatika atitikmenys: angl. angle of rotation; turning angle vok. Drehwinkel, m rus. угол поворота, m pranc. angle de rotation, m … Automatikos terminų žodynas
угол поворота — posūkio kampas statusas T sritis fizika atitikmenys: angl. turn angle; turning angle vok. Drehwinkel, m rus. угол поворота, m pranc. angle de rotation, m … Fizikos terminų žodynas
угол поворота — angle of rotation Угол, на который поворачивается любая линия, жестко связанная со звеном и перпендикулярная оси вращения. Шифр IFToMM: 2.2.28 Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
угол поворота растра — Угол, на который необходимо поворачивать проекционный или контактный растры, а также в издательских системах при растрировании изображений для разных красок (как цветных, так и черно белых оригиналов), чтобы при синтезе изображения на оттиске, с… … Справочник технического переводчика
угол поворота твердого тела — угол поворота Угол между двум и последовательными положениями полуплоскости, неизменно связанной с телом и проходящей через его ось вращения. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно… … Справочник технического переводчика
угол поворота растра — Угол, на который необходимо поворачивать проекционный или контактный растр, а также в издательских системах – при растрировании изображений для разных красок (как цветных, так и черно белых оригиналов), чтобы при синтезе изображения на оттиске с… … Краткий толковый словарь по полиграфии

dic.academic.ru

Угол вращения и угловая скорость

Физика > Вращательный угол и угловая скорость

Изучите угол вращения и угловую скорость во вращательном движении: термины и определения, схемы и примеры вращательного движения, формулы, вращение вокруг оси.

Угол вращения – мера удаленности объекта, а угловая скорость измеряет скорость совершаемого им вращения.

Задача обучения

Проследите связь между вращательным углом и дистанцией.

Основные пункты

Когда объект совершает осевые обороты, точки на краю смещаются по дугам.
Угол наклона дуг именуют вращательным углом и обозначают символом тета.
Мера скорости вращения – угловая скорость (омега). Как и в линейной скорости, выступает вектором.

Термин

Радиан – угол, расположенный в центре круга по дуге окружности той же длины, что и радиус круга.

Вращательный угол и угловая скорость

Когда объект совершает осевое вращение, его движение можно описать двумя способами. Точка на его краю будет обладать определенной скоростью и проходить через дугу. Она преодолевает дистанцию ΔS, но удобнее говорить, насколько объект повернулся. Эту величину именуют углом вращения. Его можно измерить в градусах или радианах. Угол вращения связан с ΔS и радиусом в уравнении Δθ = , поэтому удобнее использовать радианы.

Радиус круга поворачивается на угол Δθ, а длина Δs описывается по окружности

Скорость вращения объекта вычисляется угловой скоростью – скорость изменения угла поворота относительно времени. Сам угол не выступает векторной величиной, но угловая скорость является ею. Направление вектора перпендикулярно плоскости вращения. Угол, угловая скорость и угловое ускорение помогают детальнее описать вращательное движение объекта.

Угловая скорость описывает скорость вращения и направление оси, вокруг которой осуществляются обороты. Направление устремляется вдоль оси. Здесь (против часовой стрелки) вектор направляется вверх

Когда ось вращения расположена перпендикулярно вектору позиции, угловую скорость можно рассчитать при помощи линейной скорости (v) на краю вращающегося объекта и разделения на радиус. Это поможет вычислить угловую скорость (ω) в радианах в секунду.

Муха на краю вращающегося тела отображает постоянную скорость (v). Угловая скорость объекта равняется

v-kosmose.com

Часть 6 — Кинематика свободного твердого тела. Природа угловой скорости / Habr

Что такое тензор и для чего он нужен?
Векторные и тензорные операции. Ранги тензоров
Криволинейные координаты
Динамика точки в тензорном изложении
Действия над тензорами и некоторые другие теоретические вопросы
Кинематика свободного твердого тела. Природа угловой скорости
Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
О свертках тензора Леви-Чивиты
Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
Получаем вектор угловой скорости. Работаем над недочетами
Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
Параметры Родрига-Гамильтона в кинематике твердого тела
СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
Нестандартное введение в динамику твердого тела
Движение несвободного твердого тела
Свойства тензора инерции твердого тела
Зарисовка о гайке Джанибекова
Математическое моделирование эффекта Джанибекова

Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.

Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.

Угловая скорость твердого тела — это первая производная от угла поворота тела по времени

А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении
обычно дается следующее определение

Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки

Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат. И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».

При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.

Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.

Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.

Думаю для затравки вполне достаточно, а поэтому — начнем!

Итак, как известно из традиционного вузовского курса теормеха

Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным

Это — самый общий случай движения тела. Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом и сферического вокруг полюса.

Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.

Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.

Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна считается неподвижной и называется базовой, другая жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.

Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.

Рис. 2. Ориентация твердого тела в локальном базисе.

Пусть положение полюса задается вектором

Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.

В точке O₁ задан локальный репер базовой системы координат, образованный тройкой векторов . С движущимся телом связан подвижный репер . Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства

Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор неподвижный относительно связанного репера. Его можно разложить по векторам этого репера

и по векторам базового репера
Каждый вектор связанного репера можно разложить через векторы базового репера
Подставляем (4) в (2) и сравниваем с (3)
Из (5) понятно, что компоненты вектора в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора
или в безиндексной форме
где столбцы матрицы
– контравариантные компоненты векторов связанного репера по отношению к базовому. Точка, как мы уже отмечали в прошлой статье, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор
действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется ортогональным. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат
Правая часть (8) — это локальный метрический тензор

или
Оператор является по сути обыкновенной матрицей поворота координатной системы. И (10) утверждает, что если транспонированную матрицу поворота умножить на метрический тензор, а результат умножить на матрицу поворота мы получим снова метрический тензор. Можно сделать вывод, что

Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.

В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в самой первой статье цикла

Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.

Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.

Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть . Что же, посмотрим. Для этого умножим (10) слева на и справа на

откуда незамедлительно получаем
Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.

Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений

При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый тензором поворота.
Вычислим скорость точки M, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами
Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении
где — скорость полюса; — скорость точки вокруг полюса.

Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать

Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)
Перейдем в (16) к связанной системе координат, домножив (15) слева на
где — компонента оператора обратного преобразования .

Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева

Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости
при этом замечая, что
антисимметричный тензор второго ранга, о котором мы говорили в прошлой статье<. Таким образом, нам бы доказать, что
является антисимметричным тензором второго ранга. Для этого придется доказать, что (19) меняет знак при перестановка индексов (транспонировании). При этом будем учитывать, что метрический тензор — абсолютно симметричный тензор второго ранга и при транспонировании он не меняется. Поэтому исследуем взаимосвязи между матрицами поворота, для чего нам потребуются выражения (10) и (11). Но прежде чем приступить, докажем ещё одно вспомогательное утверждение

Ковариантная производная метрического тензора равна нулю

Обратимся к понятию ковариантной производной вектора, о которой упоминалось в третьей статье. Тогда мы вывели выражения для контравариантных компонент ковариантной производной от вектора
Как как и любой вектор, компоненты данного вектора можно трансформировать в ковариантные умножением и сверткой с метрическим тензором
А можно продифференцировать ковариантные компоненты непосредственно
Сравнивая (21) и (20) мы приходим к выводу, что равенство возможно лишь в случае если верно утверждение леммы

Теперь, перепишем (19) в безиндексном виде, учтя уравнение (11)
Далее, нам нужна связь между оператором поворота и его производной — дифференцируем (10) по времени
или, собирая производные от метрического тензора в правой части
Но, производные от метрического тензора в (24) будут равны нулю, в силу равенства нулю ковариантной производной метрического тензора. Значит правая часть (24) равна нулю
Пользуясь свойствами операции транспонирования, преобразуем (25)

Так как и с учетом (23), получаем

Из (26) непосредственно следует антисимметричность тензора (19)
Ну а коль скоро (19) антисимметричный тензор, то мы смело переписываем (18)
Таким образом мы приходим к выводу, что (19) и (23) есть ни что иное как антисимметричный тензор угловой скорости
Любому антисимметричному тензору можно поставить в соответствие псевдовектор, который мы уже получали в предыдущей статье. Повторим этот результат для тензора угловой скорости
Возможно читателю знаком распространенный подход замены векторного произведения на умножение кососимметричной матрицы, построенной из первого вектора по определенному правилу, на второй вектор. Так вот это правило получается естественным путем, если в качестве инструмента использовать тензорное исчисление. Действительно, вот эта кососимметричная матрица, которой в матричном изложении механики заменяют угловую скорость
Возможно, внимательный читатель увидит, что в полученной матрице знаки противоположны тем, что мы получали в статье, посвященной антисимметричным тензорам. Да, все верно, ведь в той статье мы сворачивали вектор с тензором Леви-Чивиты по его третьему индексу k, тут мы выполняем свертку по среднему индексу j что дает прямо противоположные знаки.

Матрица (30) частенько встречается в литературе, в частности в трудах Д. Ю. Погорелова, но там она вводится как мнемоническое правило. Формула (29) дает четкую связь между вектором угловой скорости и кососимметричной матрицей. Она же дает возможность перейти от (28) к формуле

Что, внезапно, эквивалентно векторному соотношению

В этой статье было много математики. И я вынужден пока ограничится этим материалом — статья вышла длинной и насыщенной формулами. Данная тема будет продолжена и углублена в следующих статьях цикла.

Какой же вывод мы можем сделать сейчас? А вот какой

Угловая скорость твердого тела есть антисимметричный тензор, или, соответствующий ему псевдовектор, порождаемый тензором поворота тела относительно базовой системы координат

Для того чтобы написать эту работу потребовалось перелопатить гору литературы. Основные выкладки выполнены автором самостоятельно. Камнем преткновения были матрицы поворота для случая косоугольных координат. Я не сразу разглядел в соотношении (10) преобразование, оставляющее метрику инвариантной, хотя с учетом ранее написанных статей — следовало бы. Понять эту связь мне помог ужасный по оформлению, но очень толковый сайт «На что похожа математика». Кстати видно, что все соотношения переходят в известные для ортогональных матриц, если метрический тензор сделать единичным.

Разговор о механике твердого тела будет продолжен, а пока — всё. Спасибо за внимание!

Продолжение следует…

habr.com