Формула угла поворота в течение заданного – 7.2. Вращательное движение. Угловая скорость, угловое ускорение

7.2. Вращательное движение. Угловая скорость, угловое ускорение

Движение твердого тела, при котором все его точки перемещаются по окружности, центры которой расположены на перпендикулярной этим окружностям неподвижной прямой, называется вращательным. Неподвижная прямая, на которой лежат центры круговых траекторий то­чек тела, называется его осью вращения. Для образования оси вра­щения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел можно привести движение две­рей или створок окон при их открывании или закрывании.

Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).

Рис. 7.3. К анализу вращательного движения твердого тела

Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя.

Для установления закона вращательного движения тела, по кото­рому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную полуплоскость НП, а внутри тела отметим подвижную полуплоскость, ко­торая вращается около оси вместе с телом, теперь угол φ, образуемый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, т. е. знать закон вращательного движения тела:

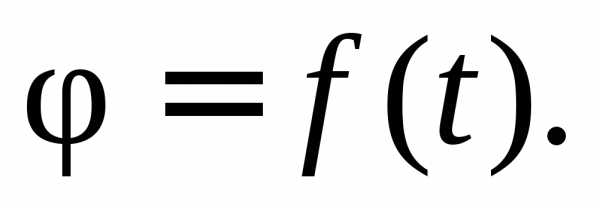
Быстрота изменения угла поворота во времени характеризуется величиной, которая называется угловой скоростью.

Представим, что в некоторый момент времени t положение вращающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело повернулось на угол Δ φ, и величина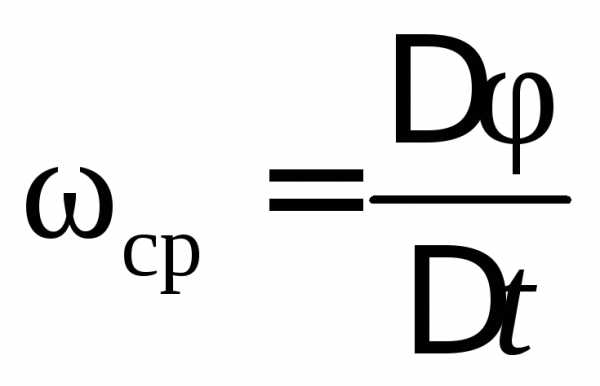

называется средней угловой скоростью.

Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение, обозначаемое . Среднее ускорение ;

.

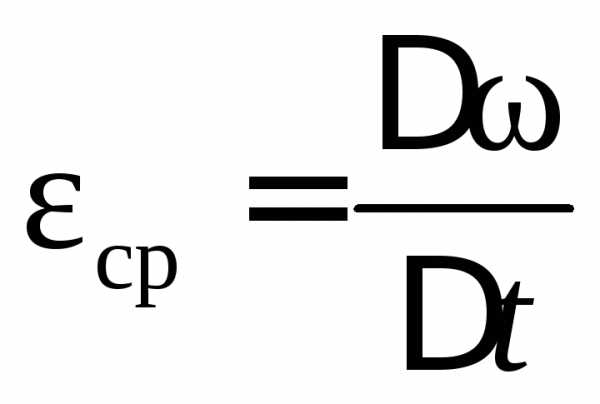Единица углового ускорения 1 рад/с².

Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часовой стрелки – отрицательным.

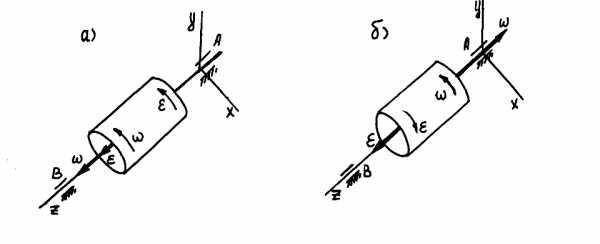
б

а

Рис. 7.4. К определению вида вращательного движения

Векторы и – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора (или ), видеть вращение, происходящее против часовой стрелки.

Если векторы и

направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы и направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).

7.3. Частные случаи вращательного движения

1. Равномерное вращательное движение. Если угловое ускорение 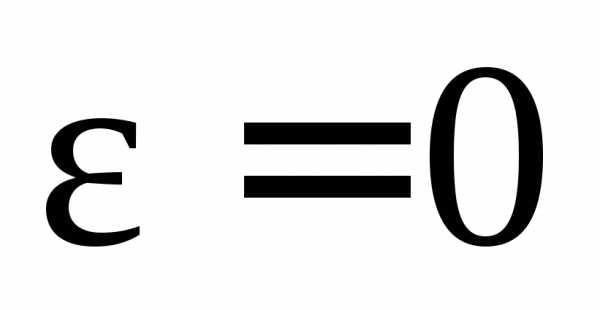и, следовательно, угловая скорость

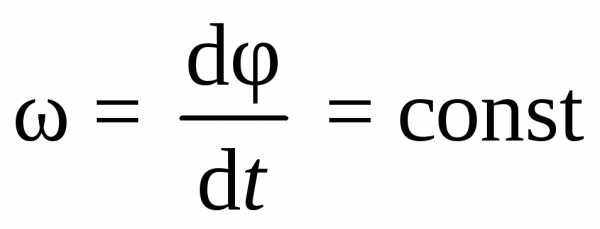, (7.1)

то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных получим

Если при изменении времени от 0 до t угол поворота изменялся от φ₀ (начальный угол поворота) до φ, то, интегрируя уравнение в этих пределах:

получаем уравнение равномерного вращательного движения

,

которое в окончательном виде записывается так:

.

Если , то

.

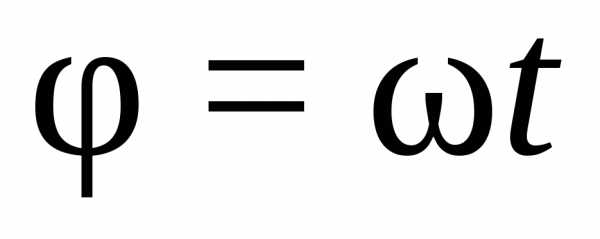Таким образом, при равномерном вращательном движении угловая скорость

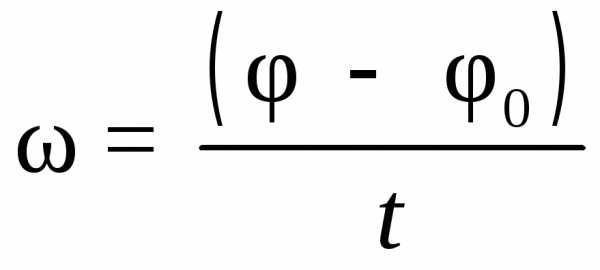или при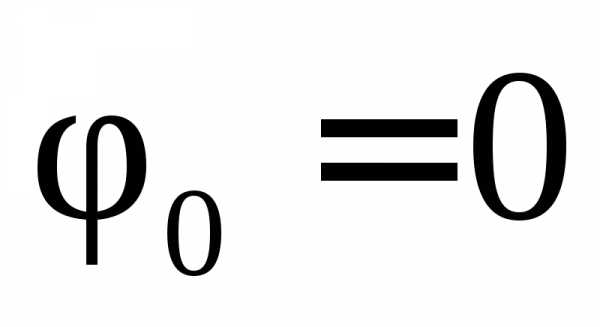

.

2. Равнопеременное вращательное движение. Если угловое ускорение

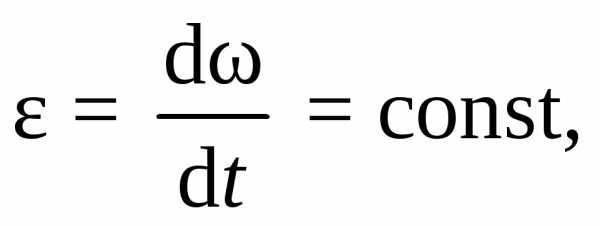(7.2)

то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.2):

и приняв, что при изменении времени от 0 до t угловая скорость изменилась от (начальная угловая скорость) до , проинтегрируем уравнение в этих пределах:

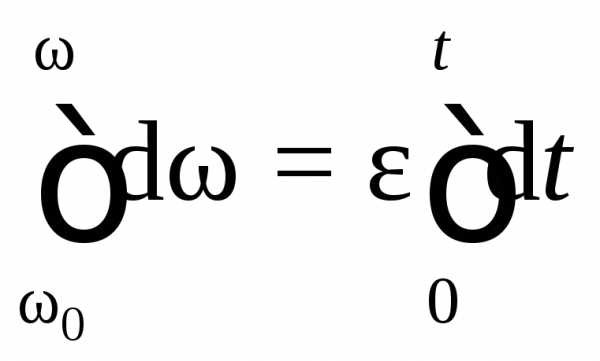или ,

т. е. получим уравнение

(7.3)

выражающее значение угловой скорости в любой момент времени.

Закон равнопеременного вращательного движения 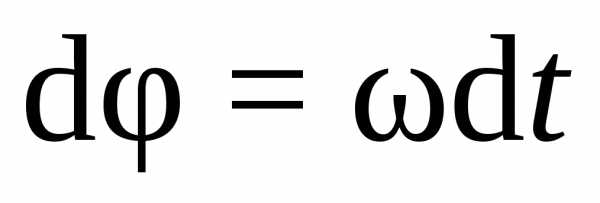или, с учетом уравнения (7.3):

Полагая, что в течение времени от 0 до t угол поворота изменялся от до, проинтегрируем уравнение в этих пределах:

или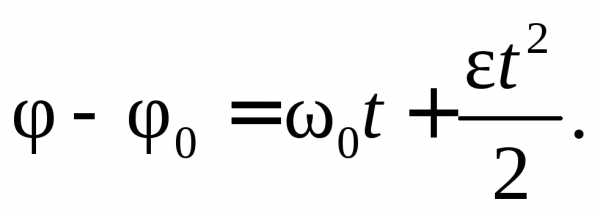

Уравнение равнопеременного вращательного движения в оконча­тельном виде

(7.4)

Первую вспомогательную формулу получим, исключив из формул (7.3) и (7.4) время:

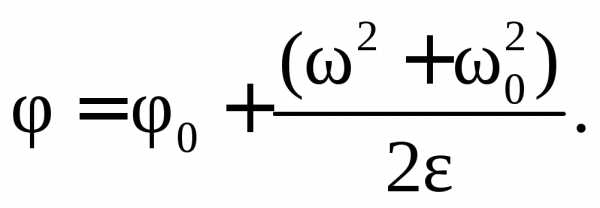(7.5)

Исключив из тех же формул угловое ускорение , получим вторую вспомогательную формулу:

(7.6)

где – средняя угловая скорость при равнопере­менном вращательном движении.

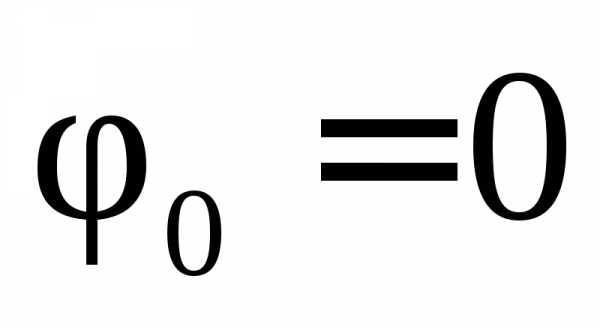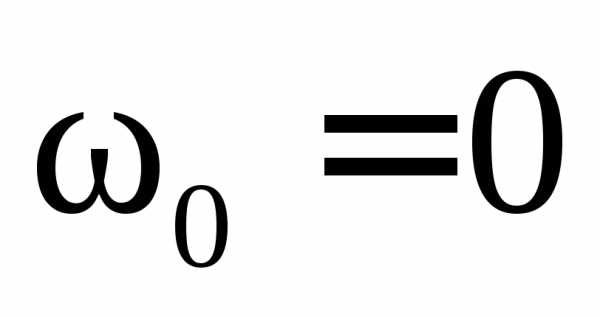Когда и , формулы (7.3)–(7.6) приобретают более простой вид:

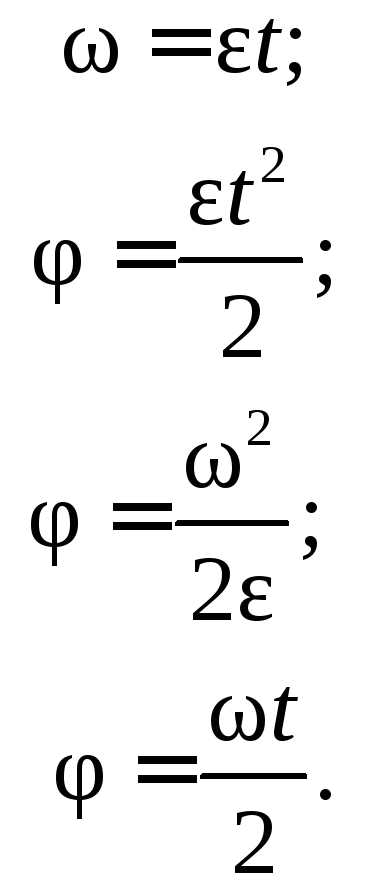
В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.

Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между (с^–1) и n (мин^–1). Так как 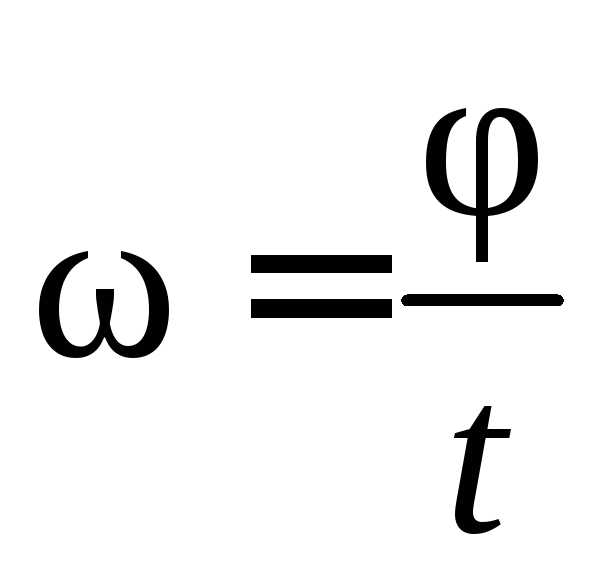, то при n (мин^–1) за t = 1 мин = 60 с угол поворота 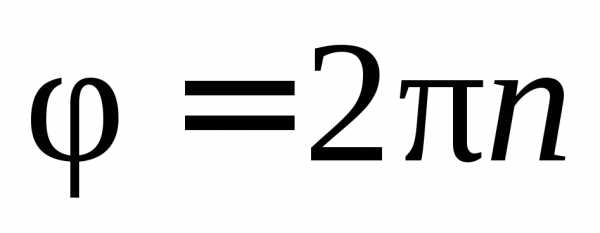. Следовательно:

.

При переходе от угловой скорости

(с^–1) к частоте вращения n (мин^–1) имеем

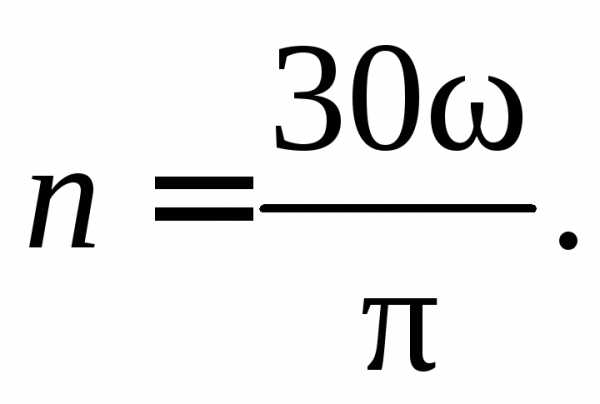
studfiles.net

Как определить прогиб или угол поворота?

Приветствую тебя, читатель моего скромного блога о сопромате. Сегодня я начинаю писать о методиках определения прогибов и углов поворотов поперечных сечений при простом (прямом, поперечном) изгибе. Прогиб — это вертикальное перемещение поперечных сечений изгибаемого элемента. Угол поворота — это поворот сечения на определенный угол.

Планирую рассмотреть несколько методов, посмотрим в действии метод начальных параметров, метод Мора в связке с правилом Верещагина, совместный метод Мора и Симпсона, а также метод конечных разностей. Конечно, это далеко не все методы, которые существуют. Тем, кому данного материала покажется мало, заходите на мой основной сайт, там, в скором будущем, я планирую написать и о других методах.

Что такое прогиб, а что такое угол поворота?

Разберемся, что такое прогиб, а что такое угол поворота. При простом изгибе все поперечные сечения балки перемещаются определенным образом, во-первых они перемещаются вертикально (прогибаются):

Для каждого метода я подготовлю отдельную статью, а данная статья, которую ты сейчас читаешь, будет неким навигатором, содержащая ссылки на эти методы.

Методы определения прогибов и углов поворотов:

1. Метод начальных параметров. Определение перемещений с помощью универсального уравнения, используя которое можно определить любое перемещение для балки постоянного поперечного сечения. 
2. Метод Мора-Верещагина. Также известный как способ перемножения эпюр, предложенный студентом одного московского ВУЗа — А.К.Верещагиным. 

 

sopromats.ru

Вращательное движение

Вращательное движение является периодическим движением.

Период обозначается буквой T.

Чтобы найти период обращения, надо время вращения разделить на число оборотов:

Физическая величина, равная отношению числа полных оборотов тела ко времени, в течение которого эти обороты совершены, называется частотой вращения.

Частота вращения обозначается буквой n.

Чтобы найти частоту вращения, надо число оборотов разделить на время, в течение которого эти обороты совершены:

Частота вращения и период обращения связаны друг с другом как взаимообратные величины: Период измеряется в секундах: [T] = 1 с.

Единица частоты – секунда в минус первой степени: [n] = 1 с^–1.

Эта единица имеет собственное название – 1 герц (1 Гц).

Проведем аналогию между вращательным и поступательным движениями.

Поступательно движущееся тело изменяет свое положение в пространстве относительно других тел.

Тела, совершающие вращательное движение поворачиваются на некоторый угол.

Если за любые равные промежутки времени поступательно движущееся тело совершает равные перемещения, движение называется равномерным.

Если за любые равные промежутки времени вращающееся тело поворачивается на один и тот же угол, то такое вращение называется равномерным. Характеристикой равномерного поступательного движения служит скорость Соответствующей характеристикой вращательного движения служит угловая скорость:

Угловая скорость – это физическая величина, равная отношению угла поворота тела ко времени, в течение которого этот поворот совершен.

Угловая скорость показывает, на какой угол поворачивается тело за единицу времени.

Чтобы получить единицу угловой скорости, нужно в ее определяющую формулу подставить единицу – 1 радиан, и времени – 1 с. Получаем: [ω] = 1

Аналогично можно ввести характеристику неравномерного вращения. Если видом неравномерного поступательного движения является равнопеременное движение, то для вращательного движения можно ввести понятие равнопеременного вращения.

Характеристикой равнопеременного поступательного движения является ускорение:

Соответственно, для вращательного движения можно ввести величину, определяемую отношением изменения угловой скорости ко времени, в течение которого это изменение происходит – угловое ускорение: Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени. Чтобы получить единицу углового ускорения, нужно в его определяющую формулу подставить единицы угловой скорости 1 рад/с и времени – 1 с. Получаем:

Продолжая аналогию дальше, запишем уравнение для перемещения при прямолинейном равноускоренном движении

Так как при вращении перемещению тела соответствует угол вращения, линейной скорости – угловая скорость, линейному ускорению – угловое ускорение, то аналогичное уравнение для вращательного движения будет иметь вид:

Другому уравнению для поступательного движения будет соответствовать уравнение для вращательного движения:

Метод, который использовался в данном случае, называется методом аналогий.

Точки тела, совершающего вращательное движение, поворачиваются относительно оси вращения на некоторые углы и движутся по дугам окружностей, проходя определенные пути. Таким образом, характеристиками вращательного движения являются и угловая, и линейная скорости.

Линейная скорость точки направлена по касательной к окружности, по которой она движется.

Об этом свидетельствует слетающая с колес автомобиля грязь или искры, летящие от металлического предмета, прижатого к наждачному кругу.

Чем дальше от оси вращения находится точка, тем больше ее линейная скорость. Угловая же скорость точек, лежащих на одном радиусе, одинакова. Следовательно, линейная скорость точки прямо пропорциональна радиусу окружности, по которой она вращается.

За время, равное периоду, точка проходит путь, равный длине окружности. Её линейная скорость при этом равна Отношение же угла поворота ко времени поворота на этот угол равно угловой скорости

Таким образом, линейная скорость вращающейся точки связана с ее угловой скоростью соотношением:

При равномерном вращении скорость меняется по направлению, но не изменяется по величине.

Поскольку всякое изменение скорости характеризуется понятием ускорения, то для равномерного вращения следует ввести еще одно ускорение, изменяющееся не по величине, а по направлению. Это ускорение называют центростремительным.

Пусть вращающееся тело в начальный момент времени находится в точке A и скорость его направлена по касательной. В следующий момент времени тело находится в точке B. При этом скорость его изменилось только по направлению и направлена по касательной к окружности.

Найдем вектор разности скоростей, воспользовавшись правилом действия с векторами. Из чертежа видно, что вектор разности направлен в сторону близкую к центру окружности. Чем меньше угол поворота, тем ближе направлен вектор скорости к направлению на центр вращения.

При малом времени движения изменение положения тела незначительно. Поэтому можно считать, что вектор скорости характеризующий изменение скорости по направлению, направлен на центр. Отсюда и происходит название центростремительного ускорения.

Угловое же ускорение, характеризующее изменение скорости по величине, называют еще касательным или тангенциальным ускорением (при неравномерном вращении).

Получим выражение для центростремительного ускорения. Будем считать, что угол поворота очень мал. Соединим точки A и B. Угол MAN = φ по построению.

Мы имеем два равнобедренных треугольника. Треугольник OAB, ребра которого R и AB, и треугольник MAN, ребра которого и

Так как треугольники подобны (по двум сторонам и углу между ними), то можно записать:

Дуга окружности и хорда практически равны из-за малости угла поворота. Поэтому дуга Следовательно, Получим

Разделив правую и левую части последнего уравнения на t, получим:

Отсюда Таким образом,

Полученная формула является формулой для расчета центростремительного ускорения.

Центростремительное ускорение, при движении тела по окружности, равно отношению квадрата скорости к радиусу окружности, по которой движется тело:

files.school-collection.edu.ru

Kvant. Вращательное движение — PhysBook

Кикоин А.К. Формулы кинематики для вращательного движениях //Квант. — 1983. — № 11. — С. 25-26.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Для описания движения материальной точки или поступательного движения твердого тела пользуются следующими кинематическими величинами: перемещением \(~\vec s\), скоростью \(~\vec \upsilon\) и ускорением \(~\vec a\). Сами они и их проекции на оси координат связаны между собой кинематическими формулами. Например, для прямолинейного равномерного движения перемещение от времени зависит так:

\(~\vec s = \vec \upsilon t\) или \(~s_x = \upsilon_x t\),

где t — время, отсчитываемое от некоторого начального момента. При прямолинейном равноускоренном движении с начальной скоростью \(~\vec \upsilon_0\) формулы кинематики имеют вид:

\(~\begin{matrix} \vec \upsilon = \vec \upsilon_0 + \vec a t \\ \vec s = \vec \upsilon_0 t + \frac{\vec a t^2}{2} \end{matrix}\) ,

или

\(~\begin{matrix} \upsilon_x = \upsilon_{0x} + a_x t \\ s_x = \upsilon_{0x} t + \frac{a_x t^2}{2} \\ \upsilon^2_x — \upsilon^2_{0x} = 2 a_x s_x \end{matrix}\) .

Но при вращательном движении тела величинами \(~\vec s\), \(~\vec \upsilon\) и \(~\vec a\) пользоваться неудобно, так как различные точки тела за один и тот же промежуток времени совершают разные перемещения и движутся с различными скоростями и ускорениями. Поэтому для описания вращательного движения вводятся специальные, так называемые угловые величины: угол поворота φ, угловая скорость ω (о них говорится в учебнике «Физика 8») и угловое ускорение \(~\varepsilon = \frac{\omega — \omega_0}{\Delta t} = \frac{\Delta \omega}{\Delta t}\) (о нем в учебнике не говорится). Для различных точек вращающегося тела они одинаковы.

Угловые величины связаны с величинами \(~\vec s\), \(~\vec \upsilon\) и \(~\vec a\), которые, в отличие от угловых, называют линейными, простыми соотношениями:

\(~\begin{matrix} s = r \varphi \\ \upsilon = r \omega \\ a = r \varepsilon \end{matrix}\) .

Здесь s — модуль перемещения данной точки тела (при малых перемещениях s — это длина дуги), r — радиус окружности, по которой она движется, υ — модуль скорости точки, а — модуль касательной проекции ускорения^[1].

Из-за такой простой связи угловых и линейных величин кинематические формулы для вращательного движения во всем подобны кинематическим формулам, приведенным выше.

При равномерном вращении тела (угловая скорость постоянна) зависимость угла поворота φ от времени имеет вид:

\(~\varphi = \omega t\) .

При равноускоренном вращении угловая скорость ω изменяется со временем по формуле

\(~\omega = \omega_0 + \varepsilon t\) ,

где ω _{— начальная угловая скорость. Зависимость угла поворота от времени выражается формулой}

\(~\varphi = \omega_0 t + \frac{\varepsilon t^2}{2}\) .

Точно так же между углом поворота и иловой скоростью существует связь:

\(~\omega^2 — \omega^2_0 = 2 \varepsilon \varphi\) .

Вообще любая формула кинематики вращательного движения тела получается из соответствующей формулы кинематики точки (или поступательного движения тела) простой заменой линейной величины соответствующей угловой.

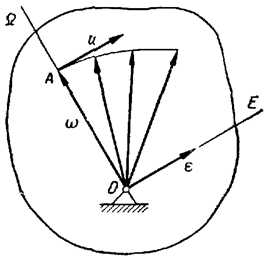
В заключение отметим (в учебнике «Физика 8» об этом не говорится), что величины φ, ω и ε тоже считаются векторными. (Нужно же отличать повороты или вращения по часовой стрелке от поворотов или вращений против часовой стрелки!) Принимается, что векторы угловых величин направлены вдоль оси вращения тела по правилу правого винта: если мысленно вращать правый винт так, как вращается тело, то направление поступательного движения винта укажет направление соответствующего вектора (см. рисунок). Правда, для углового ускорения это правило несколько усложняется: вектор ускорения совпадает по направлению с направлением движения винта, если угловая скорость возрастает по модулю, и направлен в противоположную сторону, если угловая скорость уменьшается.

Примечания

1. ↑ При движении точки по окружности вектор ускорения может иметь две проекции: на направление к центру окружности (центростремительное ускорение) и иа направление касательной к окружности (касательная проекция, представляющая собой быстроту изменения модуля скорости точки).

www.physbook.ru

Определение прогибов углов поворота (сопромат)

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки:

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

sopromato.ru

Билет № 23

1. Учет циркуляции, планирование и выполнение поворота судна, в т.Ч. С учетом течения.

Учет циркуляции.

При прямой задаче, когда после окончания поворота нужно найти положение точки А (рис. 6.6), из которой будет проложен новый курс, достаточно из известной точки начала поворота В отложить перпендикулярно первому курсу величину R_uи провести из полученной точки О, как из центра, окружность циркуляции. Проведем линию нового курса как касательную к этой окружности. Точка касания А будет представлять точку начала следования новым курсом. Если необходимо знать время поворота, то его приближенно можно найти по формуле

где α — угол поворота, град.; — время циркуляции на 180^е.

При обратной задаче можно рекомендовать следующие два приема. Пусть MM₁, — линия проложенного на карте пути судна до поворота, а М₁М₂ — линия пути, на которую нужно выйти после поворота (см. рис. 6.6). Для определения точки В — начала поворота — проведем биссектрису угла ММ₁М₂ и на ней найдем такое положение ножки циркуля, при котором окружность, проведенная радиусом циркуляции R_ц, будет касательной к обоим курсам. Второй прием заключается в проведении двух прямых О₁ и О₂, параллельных старому и новому курсам и отстоящих от них на расстоянии R_u (рис. 6.7).

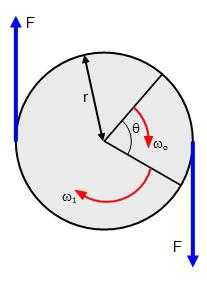
Точка их пересечения будет центром окружности циркуляции, а перпендикуляры из нее на линии обоих курсов определят точки В и А — начало и конец поворота. Команда рулевому о перекладке руля должна быть дана несколько раньше прихода судна в точку В. с учетом предварительного периода циркуляции.

Табличный метод учета циркуляции. Прямая и обратная задачи решаются с использованием величин d₁ или d, выбираемых из таблицы циркуляции. Если из точки М₁ — точки пересечения старого и нового курса — отложить отрезки М₁A = M₁В = d₁то получим точку В — начала поворота — и точку А — окончаний поворота. При прямой задаче из точки В откладывают d₁ получают точку М₁ а затем, отложив по новому курсу d₁ — точку А (рис. 6.8). Так как с приближением к 180° tg(α/2) быстро увеличивается, в таблице циркуляции величина d₁ дана для углов, меньших 150°. В случае, если α>150°, следует использовать величины q = α/2 и d.

При прямой задаче из точки В прокладывают К_ср— промежуточный курс, а по нему откладывают величину d:

где: и — курсы судна до поворота и после него.

При обратной задаче угол α/2 и d откладываются из любой произвольной точки В₁

(рис. 6.9). Через конец отрезка d проводят линию, параллельную , пересечение ее с линией нового курса даст точку А и соответственно точку В — начало поворота.

Планирование и выполнение поворота судна, в т.ч. с учетом течения.

Так как ЛЗП определена условиями плавания, то при расчете поворота решается, как правило, обратная задача: найти точку подачи команды на руль (ТПКР) и точку конца поворота (ТКП) таким образом, чтобы судно, начав поворот на первой ЛЗП₁ вышло бы к моменту окончания поворота на следующую ЛЗП₂ (рис. 20.9,а). Эта задача может быть решена двумя методами — для постоянного угла перекладки руля (δ_Р =const) либо для постоянной угловой скорости поворота (ω_р = const).

При расчете поворотов первым методом рекомендуется планировать δ_Р = 15…20°, так как это позволит впоследствии вносить необходимые коррекции в случае отличия фактической траектории судна от расчетной.

При малых углах перекладки руля затягивается процесс поворота, возрастает влияние внешних факторов (особенно ветра) на поворотливость судна и в итоге увеличиваются погрешности выполнения поворота. При больших углах перекладки руля корректировать движение судна на циркуляции будет трудно, так как руль уже переложен на борт и запаса для ускорения поворота не будет. Кроме того, в стесненных водах вообще избегают перекладки руля на большие углы, потому что ошибки в маневре при большой инерции судна трудно исправить, а вероятность выхода из строя рулевого устройства увеличивается.

Расчет поворота может быть выполнен способами: приближенным способом двух длин, способом окружности (в том числе с учетом «мертвого промежутка») и др. Однако для крупнотоннажных судов наилучшие результаты дает использование диаграмм циркуляции (рис. 20.9,б), входящих в состав информации о маневренных элементах судна (по форме ИМО). Начальная точка каждой диаграммы циркуляции (Т = 00.00) соответствует ТПКР, т. е. никаких дополнительных поправок на «мертвый промежуток» не требуется. Для более точного планирования поворота рекомендуется нанести на диаграммы положения судна, соответствующие углам отворота Δ_к = 10, 20, 30, 60° от первоначального курса. Аргументами для входа в диаграмму циркуляции являются загрузка судна (в грузу или в балласте), сторона поворота и угол перекладки руля (выбор диаграммы) и угол отворота судна (угол разворота ДП судна)

Δ_к = ИК₂ – ИК₁ = ГКК₂ – ГКК₁ (20 30)

На диаграмме циркуляции отыскивается точка а, соответствующая углу отворота Δ_к , и снимаются прямоугольные координаты этой точки, ко, относительно начала координат (ТПКР):

x=ba, y=ca

На навигационной карте поперечное смешение у=са вмещают по перпендикуляру к ЛЗП₁ полученная точка с будет концом поворота (ТКП). Отложив от а назад по ЛЗП прямое смешение х = bа, получим ТПКР, которую необходимо «привязать» к береговым ориентирам контрольными пеленгом и дистанцией (ИП_К, D_K). Кривая циркуляции b—с вписывается от руки, проверяется безопасность прохождения этой кривой с учетом выноса кормы на повороте и полосы, занимаемой судном при криволинейном движении.

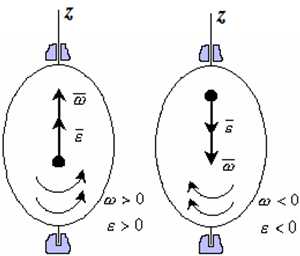
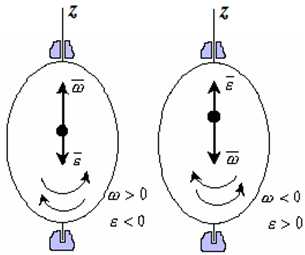
Следует, однако, учитывать, что маневр поворота практически никогда не будет выполнен в полном соответствии с планируемой траекторией. Во-первых, сам процесс движения судна на циркуляции является в значительной степени случайным из-за тенденции поворота (рыскания) судна в момент перекладки руля, характера перекладки руля и «сдерживания» рулевым, что приводит к разбросу траекторий движения судна на циркуляции. Во-вторых, еще более случайный характер придают циркуляции различия в загрузке и посадке судна (по отношению к стандартным), характер изменения глубин

(в особенности на мелководье), влияние ветра на поворотливость судна и смешение судна по течению в процессе циркуляции на величину, пропорциональную времени поворота (рис. 20.10 и 20.11).

Так, на рис. 20.10 кривая 1 показывает циркуляцию судна без воздействия ветра, а кривые 2 и 3 — при встречном и попутном ветре соответственно. Аналогично на рис. 20.11 кривая

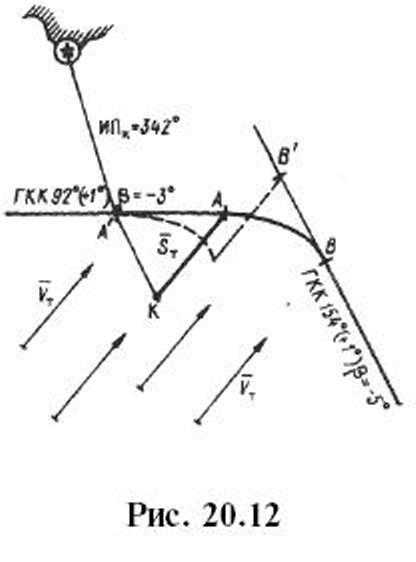
При известных элементах течения ТПКР рассчитывают с учетом сноса судна течением за время t_Δк выполнения циркуляции (рис. 20.12):

(20.31)

Пусть точки А и В — ТПКР и ТКП при отсутствии течения, полученные с помощью диаграммы циркуляции. Величину S_T откладывают от точки А навстречу течению и через полученную определяющую точку К проводят прямую, параллельную ПУ, до пересечения с линией ПУ₁. Полученная точка А’ и будет искомой точкой подачи команды на руль с учетом течения, а расчетная ТКП будет в точке В‘. Следует, однако, иметь в виду, что неточное знание элементов течения резко увеличивает погрешность в выполнении рассчитанного поворота, еще более увеличивая «полосу рассеивания» возможных траекторий движения судов. Таким образом, подтверждается вывод о, том, что поворот судна на новый курс выполняется с невысокой точностью. Поэтому и рекомендуется по возможности избегать поворотов вблизи навигационных опасностей и не входить в узкий канал на циркуляции. Принципиально иным методом планирования и выполнения поворота, позволяющим оперативно учитывать фактическую поворотливость судна, является поворот с фиксированной (заданной) угловой скоростью, рад/с:

или в град./мин

где , — заданный радиус траектории движения судна при по­вороте в метрах и милях соответственно; V_c, V — линейная скорость судна, м/с и узлы соответственно.

Влияние течения может быть скомпенсировано коррекцией задаваемой угловой скорости поворота, град/мин:

так как поворот должен быть выполнен за то же время, но на больший (или меньший) угол.

Технология выполнения поворота заключается в следующем. Сняв с карты заданный радиус циркуляции (например, радиус кривизны речного фарватера), судоводитель рассчитывает требуемую угловую скорость поворота. Не доходя примерно одной длины судна до намеченной точки начала поворота, дают команду на перекладку руля и указывают рулевому требуемую угловую скорость поворота. Наблюдая за показаниями указателя угловой скорости поворота (гиротахометра) и самостоятельно корректируя угол перекладки руля, рулевой добивается постоянства угловой скорости

и тем самым ведет судно по кривой заданного радиуса. Если рулевой будет выдерживать и периодом рыскания τ_Р , с, то судно будет следовать по синусоиде с боковыми отклонениями отно­сительно заданной траектории, м,

Если к моменту прихода в точку начала поворота направление движения центра масс судна будет отличаться от ПУ₁ на величину σ_к , то даже при выполнении условия (20.35) судно будет постепенно удаляться в сторону от заданной траектории на величину, м,

т.е. примерно 30 м на каждую милю плавания S_ц при угловой ошибке = 1°. Необходимо учитывать и существенную (до 30…50% при крутых поворотах) потерю скорости на циркуляции, принимая при расчете среднее значение V. В целом способ достаточно прост и надежен, требуется лишь наличие гиротахометра и опыт работы с ним.

Поворот по окружности заданного радиуса можно выполнить и с помощью абсолютного гидроакустического лага с носовой и кормовой станциями, разнесенными на расстояние l, рассчитав заданное значение алгебраической разности поперечных составляющих скорости судна на носовой и кормовой станциях, уз:

где V_х — продольная составляющая скорости судна; V — абсолютная путевая скорость судна. Для следования по окружности необходимо снимать с лага текущие значения , , мгновенно вычислять их алгебраическую разность, сравнивать эту величину с заданной (20.38) и корректировать соответственно угол перекладки руля. Способ, однако, сложнее, чем при использовании гиротахометра. Перед крутым поворотом рекомендуется планировать уменьшение скорости с тем, чтобы к моменту выхода в ТПКР погасить инерцию судна. Выйдя в ТПКР,на короткое время увеличивают частоту вращения винта дня улучшения управляемости (метод толчка).

studfiles.net

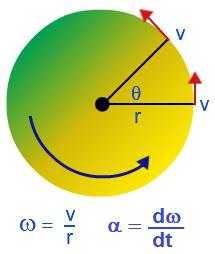
§ 4. Угловая скорость и угловое ускорение

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис.6). Ее положение через промежуток времени t зададим углом . Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Модуль вектора d равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого, винта (рис.6). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

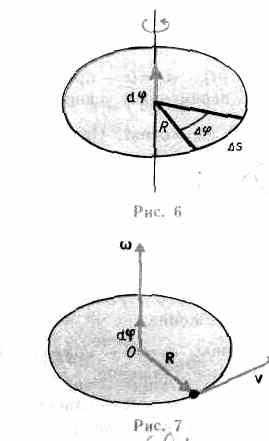
Вектор «в направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор d (рис. 7). Размерность угловой скорости dim=T^-1, a . ее единица — радиан в секунду (рад/с).

Линейная скорость точки (см. рис. 6)

В векторном виде формулу для линейной скорости можно написать как векторное произведение:

При этом модуль векторного произведения, по определению, равен

, а направление совпадает с направлением поступательного движения правого винта при его вращении от  к R.

Если =const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2. Так как промежутку времени t=T соответствует =2, то = 2/Т, откуда

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор

13

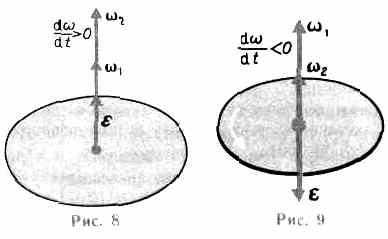
 сонаправлен вектору  (рис.8), при замедленном.— противонаправлен ему (рис. 9).

Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_, нормальное ускорение а_n) и угловыми величинами (угол поворота , угловая скорость (о, угловое ускорение ) выражается следующими формулами:

В случае равнопеременного движения точки по окружности (=const)

где ₀ — начальная угловая скорость.

Контрольные вопросы

• Что называется материальной точкой? Почему в механике вводят такую модель?

• Что такое система отсчета?

• Что такое вектор перемещения? Всегда ли модуль вектора перемещения равен отрезку пути,

пройденному точкой?

• Какое движение называется поступательным? вращательным?

• Дать определения векторов средней скорости и среднего ускорения, мгновенной скорости

и мгновенного ускорения. Каковы их направления?

• Что характеризует тангенциальная составляющая ускорения? нормальная составляющая

ускорения? Каковы их модули?

• Возможны ли движения, при которых отсутствует нормальное ускорение? тангенциальное

ускорение? Приведите примеры.

• Что называется угловой скоростью? угловым ускорением? Как определяются их направления?

• Какова связь между линейными и угловыми величинами?

Задачи

1.1. Зависимость пройденного телом пути от времени задается уравнением s = A+Вt+Сt²+Dt³ (С = 0,1 м/с², D = 0,03 м/с³). Определить: 1) через какое время после начала движения ускорение а тела будет равно 2 м/с²; 2) среднее ускорение <а> тела за этот промежуток времени. [ 1) 10 с; 2) 1,1 м/с²]

1.2. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к горизонту, если максимальная высота подъема тела равна 1/4 дальности его полета. [45°]

1.3. Колесо радиуса R = 0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением  = 2At+5Вt⁴ (A=2 рад/с² и B=1 рад/с⁵). Определить полное ускорение точек обода колеса через t=1 с после начала вращения и число оборотов, сделанных колесом за это время. [а = 8,5 м/с²; N = 0,48]

14

1.4. Нормальное ускорение точки, движущейся по окружности радиуса r=4 м, задается уравнением а_n=А+-Bt+Ct² (A=1 м/с², В=6 м/с³, С=3 м/с⁴). Определить: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t₁=5 с после начала движения; 3) полное ускорение для момента времени t₂=1 с. [ 1) 6 м/с²; 2) 85 м; 3) 6,32 м/с²]

1.5. Частота вращения колеса при равнозамедленном движении за t=1 мин уменьшилась от 300 до 180 мин^-1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. [1) 0,21 рад/с²; 2) 360]

1.6. Диск радиусом R=10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением =A+Bt+Ct²+Dt³ (B = l рад/с, С=1 рад/с², D=l рад/с³). Определить для точек на ободе колеса к концу второй секунды после начала движения: 1) тангенциальное ускорение а_; 2) нормальное ускорение а_n; 3) полное ускорение а. [ 1) 0,14 м/с²; 2) 28,9 м/с²; 3) 28,9 м/с²]

studfiles.net