Как найти количество оборотов – Определение числа оборотов колеса
Вращательное движение (движение тела по окружности) | Формулы и расчеты онлайн
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
между сторонами угла поворота,
r — радиус,
то по определению радиана
\[ φ = \frac{s}{r} \]
Соотношение между единицами угла
\[ \frac[-1.35]{φ_{рад}}{φ_{°}} = \frac[-1.2]{π}{180°} \]
$ 1 рад = 57.3° $ | $ 1° = 17.45 мрад $ | $ 1´ = 291 мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
\[ [n] = [f] = \frac{Обороты}{Секунда} = \frac{(об)}{с} = \frac{1}{c} = Герц \]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
\[ T = \frac{1}{f} = \frac{1}{n} \]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
\[ φ = 2 π N \]
Угловая скорость
Из формулы для одного оборота следует:
\[ ω = 2 π f = \frac{2π}{T} \]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
В помощь студенту
Вращательное движение (движение тела по окружности) |
стр. 421 |
|---|
www.fxyz.ru
Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
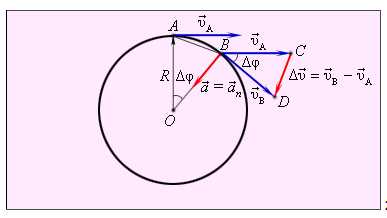
Разница векторов есть . Так как , получим
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
fizmat.by
Формула расчета частоты вращений
При проектировании оборудования необходимо знать число оборотов электродвигателя. Для расчёта частоты вращения есть специальные формулы, различные для двигателей переменного и постоянного напряжения.
Тахометр
Синхронные и асинхронные электромашины
Двигатели переменного напряжения есть трёх типов: синхронные, угловая скорость ротора которых совпадает с угловой частотой магнитного поля статора; асинхронные – в них вращение ротора отстаёт от вращения поля; коллекторные, конструкция и принцип действия которых аналогичны двигателям постоянного напряжения.
Синхронная скорость
Скорость вращения электромашины переменного тока зависит от угловой частоты магнитного поля статора. Эта скорость называется синхронной. В синхронных двигателях вал вращается с той же быстротой, что является преимуществом этих электромашин.
Для этого в роторе машин большой мощности есть обмотка, на которую подаётся постоянное напряжение, создающее магнитное поле. В устройствах малой мощности в ротор вставлены постоянные магниты, или есть явно выраженные полюса.
Скольжение
В асинхронных машинах число оборотов вала меньше синхронной угловой частоты. Эта разница называется скольжение «S». Благодаря скольжению в роторе наводится электрический ток, и вал вращается. Чем больше S, тем выше вращающий момент и меньше скорость. Однако при превышении скольжения выше определённой величины электродвигатель останавливается, начинает перегреваться и может выйти из строя. Частота вращения таких устройств рассчитывается по формуле на рисунке ниже, где:
- n – число оборотов в минуту,
- f – частота сети,
- p – число пар полюсов,
- s – скольжение.
Формула расчёта скорости асинхронного двигателя
Такие устройства есть двух типов:
- С короткозамкнутым ротором. Обмотка в нём отливается из алюминия в процессе изготовления;
- С фазным ротором. Обмотки выполнены из провода и подключаются к дополнительным сопротивлениям.
Регулировка частоты вращения
В процессе работы появляется необходимость регулировки числа оборотов электрических машин. Она осуществляется тремя способами:
- Увеличение добавочного сопротивления в цепи ротора электродвигателей с фазным ротором. При необходимости сильно понизить обороты допускается подключение не трёх, а двух сопротивлений;
- Подключение дополнительных сопротивлений в цепи статора. Применяется для запуска электрических машин большой мощности и для регулировки скорости маленьких электродвигателей. Например, число оборотов настольного вентилятора можно уменьшить, включив последовательно с ним лампу накаливания или конденсатор. Такой же результат даёт уменьшение питающего напряжения;
- Изменение частоты сети. Подходит для синхронных и асинхронных двигателей.
Внимание! Скорость вращения коллекторных электродвигателей, работающих от сети переменного тока, не зависит от частоты сети.
Двигатели постоянного тока
Кроме машин переменного напряжения есть электродвигатели, подключающиеся к сети постоянного тока. Число оборотов таких устройств рассчитывается по совершенно другим формулам.
Номинальная скорость вращения
Число оборотов аппарата постоянного тока рассчитывается по формуле на рисунке ниже, где:
- n – число оборотов в минуту,
- U – напряжение сети,
- Rя и Iя – сопротивление и ток якоря,
- Ce – константа двигателя (зависит от типа электромашины),
- Ф – магнитное поле статора.
Эти данные соответствуют номинальным значениям параметров электромашины, напряжению на обмотке возбуждения и якоре или вращательному моменту на валу двигателя. Их изменение позволяет регулировать частоту вращения. Определить магнитный поток в реальном двигателе очень сложно, поэтому для расчетов пользуются силой тока, протекающего через обмотку возбуждения или напряжения на якоре.
Формула расчёта числа оборотов двигателя постоянного тока
Число оборотов коллекторных электродвигателей переменного тока можно найти по той же формуле.
Регулировка скорости
Регулировка скорости электродвигателя, работающего от сети постоянного тока, возможна в широких пределах. Она возможна в двух диапазонах:
- Вверх от номинальной. Для этого уменьшается магнитный поток при помощи добавочных сопротивлений или регулятора напряжения;
- Вниз от номинальной. Для этого необходимо уменьшить напряжение на якоре электромотора или включить последовательно с ним сопротивление. Кроме снижения числа оборотов это делается при запуске электродвигателя.
Знание того, по каким формулам вычисляется скорость вращения электродвигателя, необходимо при проектировании и наладке оборудования.
Видео
Оцените статью:elquanta.ru
Как определить мощность и частоту оборотов электродвигателя

Возникла необходимость узнать мощность или частоту оборотов вала и другие параметры электродвигателя, но после внимательного осмотра на его корпусе не нашлось таблички (шылдика) с его наименованием и техническими параметрами. Придется определять самому, для этого есть несколько способов и мы их рассмотрим ниже.
Мощность электродвигателя представляет из себя скорость преобразования электрической энергии, ее принято определять в ваттах.Чтоб осознать, как это работает, нам понадобится 2 величины: сила тока и напряжение. Сила тока — численность тока, которое проходит через поперечное сечение за некий отрезок времени, ее принято определять в амперах. Напряжение — значение, равная работе по перемещению заряда меж 2-мя точками цепи, ее принято определять в вольтах.
Для расчета мощности используется формула N = A/t, где:
N — мощность;
А — работа;
t — время.
Часто электродвигатель поступает с завода с уже указанными техническими параметрами. Но заявленная мощность не всегда соответствует фактической, а скорее всего она может значить лишь максимальную мощность электропотока.
Так что если на вашем электроинструменте указана, например, мощность в 500 ват, это совсем не значит что инструмент будит потреблять точно 500 ват.
Электродвигатели производят стандартной дискретной мощности, линейки типа 1.5, 2.2, 4 кВт.
Опытный электрик может легко отличить 1.5 от 2.2 кВт всего лишь взглянув на его габариты. Помимо этого он сможет определить количество оборотов двигателя по размеру статора, количеству пар полюсов и диаметра вала.Еще более опытным в этом деле окажется обмотчик, специалист который занимается перемоткой электродвигателей со 100%-ой уверенностью определит технические параметры вашего электродвигателя.
Если табличка с характеристиками двигателя потеряна для подсчета мощности двигателя нужно измерить силу тока на обмотках ротора и с помощью стандартной формулы найти потребляемую мощность электродвигателя.
Основные способы определения мощности двигателя
Определение мощности по току. Для этого подключаем двигатель в сеть и контролируем напряжение. Затем поочередно, в цепь каждой из обмоток статора включаем амперметр и замеряем потребляемый ток. После того как мы нашли суму потребляемых токов, полученное число необходимо умножить на фиксированное напряжение в результате получим число определяющее мощность электродвигателя в ваттах.
Определяем мощность по габаритам. Нужно измерить диаметр сердечника (с внутренней стороны) и его длину.
Дальше если знаем частоту сети нужно узнать синхронную частоту вращения вала.
Умножаем синхронную частоту вращения вала на диаметр сердечника (в сантиметрах) полученную цифру умножаем на 3.14 затем разделяем на частоту сети умноженную на 120. Полученное значение мощности будит в киловаттах.
Замер по счетчику. Способ считается самым простым. Для этого, для чистоты эксперимента, отключаем все нагрузки в доме. Дальше необходимо включить двигатель на определенное время (например 10 минут) На щетчике будит видно разницу в киловаттах по ней уже легко можно высчитать сколько киловаттах потребляет двигатель. Удобней всего будит воспользоваться портативным электросчетчиком который показывает потребление в киловаттах (ваттах) в режиме реального времени.
Для определения реального показателя мощности, которую выдает двигатель, необходимо найти скорость валового вращения, измеряемую в числе оборотов за секунду, тяговое усилие двигателя.
Частота вращения умножается последовательно на 6,28, показатель силы и радиус вала, который можно вычислить при помощи штангенциркуля. Найденное значение мощности выражается в ваттах.
Определяем рабочее количество оборотов двигателя.
Самый быстрый способ — посчитать количество катушек (катушечных групп) Определяем мощность по расчетным таблицам. С помощью штангенциркуля замеряем диаметр вала, длину мотора (без выступающего вала) и расстояние до оси.Замеряем вылет вала и его выступающую часть, диаметр фланца если он есть, а также расстояние крепежных отверстий. По этим данным с помощью сводной таблицы можно легко определить мощность двигателя и другие характеристики
Определяем мощность по расчетным таблицам. С помощью штангенциркуля замеряем диаметр вала, длину мотора (без выступающего вала) и расстояние до оси.Замеряем вылет вала и его выступающую часть, диаметр фланца если он есть, а также расстояние крепежных отверстий. По этим данным с помощью сводной таблицы можно легко определить мощность двигателя и другие характеристики1,1 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 71 | 80 | 80 |
| Диаметр вала d1, мм | 19 | 22 | 22 |
| Крепление лап по ширине b10, мм | 112 | 125 | 125 |
| Крепление лап по длине L10, мм | 90 | 100 | 100 |
| Крепление фланца по центрам отверстий d20, мм | 165 | 165 | 165 |
| Замок фланца d25, мм | 130 | 130 | 130 |
1,5 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 80 | 80 | 90 |
| Диаметр вала d1, мм | 22 | 22 | 24 |
| Крепление лап по ширине b10, мм | 125 | 125 | 140 |
| Крепление лап по длине L10, мм | 100 | 100 | 125 |
| Крепление фланца по центрам отверстий d20, мм | 165 | 165 | 215 |
| Замок фланца d25, мм | 130 | 130 | 180 |
2,2 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 80 | 90 | 100 |
| Диаметр вала d1, мм | 22 | 24 | 28 |
| Крепление лап по ширине b10, мм | 125 | 140 | 160 |
| Крепление лап по длине L10, мм | 100 | 125 | 140 |
| Крепление фланца по центрам отверстий d20, мм | 165 | 215 | 215 |
| Замок фланца d25, мм | 130 | 180 | 180 |
4 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 100 | 100 | 112 |
| Диаметр вала d1, мм | 28 | 28 | 32 |
| Крепление лап по ширине b10, мм | 160 | 160 | 190 |
| Крепление лап по длине L10, мм | 112 | 140 | 140 |
| Крепление фланца по центрам отверстий d20, мм | 215 | 215 | 265 |
| Замок фланца d25, мм | 180 | 180 | 230 |
elektt.blogspot.com
Напишите пожалуйста как обозначается частота вращения в оборотах и какие нибудь формулы с ней, сразу дам 20 баллов
частота: v(ню)-частота, v=N/t, где N-число оборотов, t-время, за которое было совершено N оборотов<br>v=1/T, Т-период<br>w(омега)-циклическая частота, w=2п/Т=2пv.<br>частота измеряется в оборотах в секунду(об/с) или Герцах(Гц).<br>
rpm — обороты в минуту.<br><br>формул не скажу 🙂
rpm, min^(-1). Ты это имеешь в виду?<br>Или это: ω = 2πf
RPM (revolution per minut) или об/мин. (тоже самое)
Число полных оборотов, совершаемых телом при равн. его движении по окружности в еденицу времени наз. ЧАСТОТОЙ ВРАЩЕНИЯ.<br>n=1/T=w/2п;<br>Т-период вращения, w-угловая скорость,п=3.14<br>еще вопросы-обращайся. У меня справочник пиздатый. Не будет влом — отвечу.
touch.otvet.mail.ru
Как найти число оборотов | О банках и финансах
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то перемещение по окружности нельзя назвать равномерным. оно есть равноускоренным .
Угловая скорость
Выберем на окружности точку 1. Выстроим радиус. За единицу времени точка переместится в пункт 2. Наряду с этим радиус обрисовывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
частота и Период
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
период и Частота взаимосвязаны соотношением
Сообщение с угловой скоростью
Линейная скорость
Любая точка на окружности движется с некоей скоростью. Эту скорость именуют линейной. Направление вектора линейной скорости постоянно совпадает с касательной к окружности.
К примеру, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Разглядим точку на окружности, которая совершает один оборот, время, которое затрачено — это имеется период T. Путь. что преодолевает точка — это имеется протяженность окружности.
Центростремительное ускорение
При перемещении по окружности вектор ускорения неизменно перпендикулярен вектору скорости, направлен в центр окружности.
Применяя прошлые формулы, возможно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (к примеру, это смогут быть точки, каковые лежат на спице колеса), будут иметь однообразные угловые скорости, период и частоту. Другими словами они будут вращаться одинаково, но с различными линейными скоростями. Чем дальше точка от центра, тем стремительнее она будет двигаться.
Закон сложения скоростей честен и для вращательного перемещения. В случае если перемещение тела либо совокупности отсчета не есть равномерным, то закон используется для мгновенных скоростей. К примеру, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости скорости
края движения и вращения карусели человека.
Вращение Почвы
Почва участвует в двух главных вращательных перемещениях: дневном (около собственной оси) и орбитальном (около Солнца). Период вращения Почвы около Солнца образовывает 1 год либо 365 дней. Около собственной оси Почва вращается с запада на восток, период этого вращения образовывает 1 дни либо 24 часа.
Широтой именуется угол между направлением и плоскостью экватора из центра Почвы на точку ее поверхности.
Сообщение со вторым законом Ньютона
В соответствии с второму закону Ньютона обстоятельством любого ускорения есть сила. В случае если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, возможно разной. К примеру, в случае если тело движется по окружности на привязанной к нему веревке, то действующей силой есть сила упругости.
В случае если тело, лежащее на диске, вращается вместе с диском около его оси, то таковой силой есть сила трения. В случае если сила прекратит собственный воздействие, то потом тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Разглядим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Отыщем отличие векторов.
Отличие векторов имеется
. Так как
, возьмём
Перемещение по циклоиде*
В совокупности отсчета, которая связана с колесом, точка равномерно вращается по окружности радиуса R со скоростью
, которая изменяется лишь по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Сейчас перейдем в неподвижную совокупность, связанную с почвой. Полное ускорение точки А останется прошлым и по модулю, и по направлению, поскольку при переходе от одной инерциальной совокупности отсчета к второй ускорение не изменяется. С позиций неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), на протяжении которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Источник: fizmat.by
Как определить обороты электродвигателя
Увлекательные записи:
Подборка статей, которая Вас должна заинтересовать:
Как найти число оборотов колеса
1.3. Кинематика вращательного перемещения жёсткого тела Как уже отмечалось, вращательным перемещением полностью жёсткого тела около неподвижной оси…
Полный оборот планет
Разглядим, за какое время происходит полный оборот планет, в то время, когда они возвращаются на ту же точку зодиака, в которой были. Периоды полного…
Деепричастный оборот. знаки препинания при деепричастном обороте, деепричастии и причастном обороте
July 23, 2015 Что такое деепричастный оборот? Какие конкретно знаки препинания употребляются на письме для выделения деепричастного оборота? Какова роль…
Почему двигатель не набирает, или плохо набирает обороты, не тянет.
В случае если ваш двигатель не набирает, либо не хорошо усиливается , не тянет, чихает и пукает, согласитесь это весьма не приятно. Тут же давайте…
Как найти денежный мультипликатор
мировая экономика их роль и Банки в экономике. Банковский и финансовый мультипликаторы Создатель — Матвеева Татьяна Юрьевна, учитель НИУ-ВШЭ…
Где найти деньги, если их катастрофически не хватает.
Здравствуйте, дорогие читатели. Если вы систематично испытываете проблемы с деньгами и всегда занимаете деньги у друзей, чтобы дотянуть до зарплаты, эта…
kapitalbank.ru
Формула угловой скорости в физике
Определение и формула угловой скорости
ОпределениеКруговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота . Часто используют вектор элементарного поворота , который равен по величине элементарному углу поворота тела замаленький отрезок времени dtи направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.
ОпределениеУгловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой . Математически определение угловой скорости записывают так:
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ( при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
где – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ). Угловая скорость связана с периодом обращения как:
С числом оборотов в единицу времени () угловая скорость связана формулой:
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
где – перпендикулярная к оси вращения компонента радиус-вектора точки (рис.1). Вектор проводят от точки, находящейся на оси вращения к рассматриваемой точке.
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: []=рад/с
В СГС: []=рад/с
Примеры решения задач
ПримерЗадание. Движение тела с неподвижной осью задано уравнением , в рад, t в сек. Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении ( относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.
Решение. Для нахождения модуля угловой скорости применим формулу:
Используем заданную в условии задачи функцию , возьмем производную от нее по времени, получим функцию :
Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):
Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.
Читать дальше: Формула удельного веса.
Вы поняли, как решать? Нет?
Помощь с решением
www.webmath.ru
