Знаки по четным и нечетным числам: Знак «Стоянка запрещена по четным или нечетным числам месяца» — действие, картинка и пояснения к знаку ПДД
Знак «Стоянка запрещена по нечетным числам месяца»
Пункт правил 282.28: знак 328 — «Стоянка запрещена по нечетным числам месяца»;
Пункт правил 136.3: в зоне дорожного знака 327 и, соответственно, по нечетным или четным числам месяца, в зоне действия дорожного знака 328 или 329, а также на всех дорогах территории, въезд на которую обозначен дорожным знаком 522;
Пункт правил 282.30: знак 330 — «Конец всех ограничений». Обозначение конца зоны действия одновременно знаков 318, 319, 321, 323, 325, 326, 327, kurator.lv/images/pravila/znaki/standard/328.png" alt="328" />»>
Пункт правил 283: Если дорожные знаки 328 и 329 установлены на одной и другой стороне дороги, то транспортные средства, которым на следующий день будет запрещена стоянка на этой стороне, должны быть перемещены на другую сторону в период времени с 21.00 до 24.00.
Пункт правил 289: Самоуправления имеют право своим решением устанавливать период времени, в течение которого разрешена загрузка или разгрузка транспортных средств в зоне действия знаков 326, 327, 328 и 329.
Пункт правил 290: Действие знаков 309, 326, 327, kurator.lv/images/pravila/znaki/standard/328.png" alt="328" />»>328 и 329 распространяется только на ту сторону проезжей части, на которой они установлены.
Пункт правил 291: Зона действия знаков 318, 319, 321, 323, 325, 326, 327, 328 и 329 распространяется от места установки знака до ближайшего за ним перекрестка, если перекресток отсутствует, — до знака 519, а если знак 323 установлен перед населенным пунктом, — до знака 518. Зона действия знаков не заканчивается в местах выезда с прилегающих к дороге территорий (двора, места стоянки, автозаправочной станции, предприятия и др.) и в местах, где дорогу пересекает или ответвляется полевая, лесная и т. п. дорога, перед которой не установлены соответствующие знаки приоритета.
Пункт правил 292.1: для знаков 318, 319, 321, 323, 325, 326, 327, kurator.lv/images/pravila/znaki/standard/328.png" alt="328" />»>328 и 329 установкой знака 330 или 803;
Пункт правил 292.4: для знаков 326, 327, 328 и 329 — повторной установкой в конце зоны действия соответствующего знака 326, 327, 328 или 329 вместе со знаком 808. Знак 326 может быть применен совместно с дорожной разметкой 943, а знак 327 — с дорожной разметкой 944. В этих случаях зона действия знаков определяется протяженностью линии дорожной разметки. Зона действия знаков 326, 327, png" alt="328" />»>328 и 329 также заканчивается в местах, где на проезжей части и тротуаре начинается обозначенное знаком 532 или 533 место стоянки.
Пункт правил 298.26: знак 532 — «Место стоянки». Зона действия знака распространяется от места его установки до ближайшего перекрестка за знаком, а если перекресток отсутствует – до знака 532A, 519, 326, 327,
Пункт правил 298.28: знак 533 — «Место платной стоянки». Зона действия знака распространяется от места его установки до ближайшего перекрестка за знаком, а если перекресток отсутствует – до знака 533A, 519, 326, 327,
kurator.lv/images/pravila/znaki/standard/328.png" alt="328" />»>328 или 329. На знаке может быть указана максимальная продолжительность стоянки, за которую можно сразу произвести оплату. В нижней части знака может быть указано направление движения к месту стоянки, находящемуся в непосредственной близости от дороги. На стоянке не действуют запрещения, установленные подпунктами 135.6 и 136.1;Пункт правил 307.4: дополнительные знаки 804, 805 и 806 — «»Зона действия». Указывает направление и зону действия знаков 326, 327, 328 и 329, если остановка или стоянка запрещается вдоль одной стороны площади, фасада здания и т. п.. С дополнительным знаком 804 и 806 указывает также расстояние до объекта, который обозначен знаком 532 или 533, а с дополнительным знаком 805 – зону действия знака 532 и 533, если они установлены параллельно краю стоянки;
Пункт правил 307. 5: дополнительный знак 807 — «Зона действия». Информирует водителя о том, что он находится в зоне действия знака 326, 327, 328 и 329;
5: дополнительный знак 807 — «Зона действия». Информирует водителя о том, что он находится в зоне действия знака 326, 327, 328 и 329;
Пункт правил 307.6: дополнительный знак 808 — «Зона действия». Указывает конец зоны действия знаков 326, 327, 328 и 329;
Пункт правил 307.25: дополнительный знак 841 — «Работает автоэвакуатор». Дополнительный знак устанавливается совместно со знаком 326, 327, 328 и 329, а также без указанных знаков в местах, где стоящие автомобили создают помехи въезду или выезду из дворов и т. п. мест;
п. мест;
Пункт правил 307.26: дополнительный знак 842 — «Прочая информация». Предоставляет информацию, которую не содержат остальные дополнительные знаки (отменяют запрет на остановку и стоянку транспортных средств со специальными разрешениями в зоне действия знаков 326, 327, 328 и 329 (водителю необходимо разместить разрешение в салоне автомобиля у переднего стекла), указывают период времени, в течение которого разрешается погрузить или выгрузить грузы, предоставляет информацию, касающуюся особенностей организации движения велосипедов одностороннее, двустороннее движение, движение на дороге с односторонним движением навстречу общему потоку транспортных средств и т. п.) или маршруты движения велосипедов (на зеленом или синем фоне) и т. п.;
В центре Мурманска заменят дорожные знаки
Общество 1335
Поделиться
В Мурманске на участках проезжей части вдоль домов № 1, 2Б по улице Володарского и дома № 12/2 по улице Челюскинцев будут заменены дорожные знаки.
Таким образом, с 14 января 2021 года на указанном участке проезжей чести дорожные знаки 3.27 «Остановка запрещена» будут заменены на дорожные знаки 3.29 (3.30) «Стоянка запрещена по нечетным (четным) числам месяца».
Автомобилистов просят учесть данную информацию.
Подписаться
- 21 окт
Креативные индустрии Сибири могут получить новый импульс развития благодаря культурным событиям
- 20 окт
Решить кадровую проблему поможет цифровизация
- 17 окт
Новые медиа: кто и как формирует современное инфополе
Что еще почитать
Россиянам рассказали, как избежать проблем с арендой квартиры
199
Белобородько Мария
МурманскКак изменятся правила содержания животных в российских зоомагазинах в 2023 году
152
Белобородько Мария
МурманскЭксперты оценили последствия выхода России из «зерновой сделки» для Украины
30333
Виктор Жданов
Эксперты назвали ближайшие цели спецоперации: Одесса и Киев
14263
Ольга Божьева
Вассерман дал свой рецепт, как прекратить украинские обстрелы Севастополя
28356
Роман Тюкавкин
Что почитать:Ещё материалы
В регионах
Мобилизация в Петербурге: хронология событий и рекомендации
Фото 56518
Санкт-ПетербургЛаврентий Белый
Зерновая сделка приостанавливается из-за теракта в Севастополе
37925
КрымФото: Pixabay.
 com
comЕщё трое арестованы в Москве по делу о подрыве Крымского моста
33104
КрымФото пресс-службы Главы Республики Крым
В Ярославле элитный комплекс остался без воды и отопления
11427
ЯрославльСказка про белого бычка: Какова судьба Северного обхода Пскова
Фото 9806
ПсковЕкатерина Мазепина
Минобоpоны РФ: Севастополь атаковали 9 летательных и 7 морских дронов
9721
Крымфото: crimea.
 mk.ru
mk.ru
В регионах:Ещё материалы
Что такое четные и нечетные числа? Определение, свойства, примеры
Что такое четное число
Число, которое делится на 2 и дает в остатке 0, называется четным числом. Примеры четных чисел: 2, 4, 6, 8, 10 и т. д. Например, предположим, что у вас есть десять шоколадных конфет. Эти шоколадки можно разделить на две группы, в каждой из которых по пять шоколадок. Итак, десять — четное число.
Что такое нечетное число
Однако 11 шоколадок нельзя сгруппировать таким образом, поэтому 11 не является четным числом. Нечетное число — это число, которое не делится на 2. Остаток в случае нечетного числа всегда равен «1». 11 — нечетное число.
Давайте узнаем, что такое четное число:
В следующих разделах мы рассмотрим некоторые дополнительные интригующие методы понимания четных чисел, их особенности и забавные факты о них.
Как определить эти номера?
1. Понимая число в разряде «единицы»
Понимая число в разряде «единицы»
В этом подходе мы анализируем число в разряде «единиц» в целом числе, чтобы проверить, является ли число четным или нечетным. Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами.
2. По группировке
Если число разделить на две группы с одинаковым количеством элементов в каждой, то число будет четным.
Удивительные свойства четных чиселПосмотрите на свойства чисел, такие как сложение, умножение и вычитание.
Свойство сложения- Сложение двух четных чисел дает четное число. Например, 12 + 8 = 20.
- Четное число плюс нечетное число равно нечетному числу. Например, 6 + 7 = 13.
- При сложении двух нечетных чисел получается четное число. Например, 15 + 11 = 26.
- Вычитание двух четных чисел дает четное число.
 Например, 32 – 6 = 26.
Например, 32 – 6 = 26. - Если из нечетного числа вычесть четное, получится нечетное число. Например, 37 – 4 = 33.
- Вычитание двух нечетных чисел дает четное число. Например, 63 – 17 = 46,9.0040
- При умножении двух четных чисел получается четное число. Например, 14 x 2 = 28.
- Четное число, умноженное на нечетное, дает четное число. Например, 10 x 3 = 30.
- Нечетное число, умноженное на другое нечетное число, дает нечетное число. Например, 3 x 5 = 15.
Решенные примеры
Пример 1. Является ли 29510 четным числом?
Решение: Единицы в данном числе равны 0, что является четным числом. Таким образом, число 29510 — четное число.
Пример 2: Чему равна сумма первого и последнего четных чисел от 1 до 100?
Решение: Между 1 и 100 наибольшее четное число равно 98, а наименьшее четное число равно 2.
Итак, искомая сумма равна 98 + 2 = 100. формула суммы первых n четных чисел ряда?Решение: Формула суммы первых n четных чисел равна n * (n + 1).
Практические задачи
Да
NO
Правильный ответ: Да
350 — равномерное число, потому что он точно делится на 2.
5, 23, 147
2, 234
89, 573 , 1257
123, 567, 897
Правильный ответ: 2, 16, 234
2, 16, 234 — номера, деленные на 2.
13
14
15
16
Правильный ответ: 16
Между 20 и 50 16 четных чисел. . (n + 1)
Итак, $S_{n}$ = n(n + 1) = 17(17+1) = 17*18 = 306
Часто задаваемые вопросы
Какое простое число является четным? ?
Единственное простое и четное число — 2.
Какое из чисел 11, 22, 81 и 5 четное?
В данном списке 22 — четное число, так как оно делится на 2.
Какой остаток после деления четного числа на два?
Четное число делится на два точно; следовательно, остаток будет равен 0.
В чем разница между двумя четными числами?
Когда четное число вычитается из другого, всегда получается четное число.
Четные и нечетные числа | Brilliant Math & Science Wiki
Содержание
- Определение
- Четные и нечетные (четные) свойства
- Решение проблем
- Смотрите также
Четное число имеет четность 000, потому что остаток при делении на 222 равен 000, а нечетное число имеет четность 111, потому что остаток при делении на 222 равен 111. Например, 0,2,4,10,−60,2 ,4,10,-60,2,4,10,−6 — все четные числа, потому что при делении на 222 они оставляют остаток 0. Целые числа 1,3,5,11,−71,3,5,11 ,-71,3,5,11,−7 — все нечетные числа, потому что они оставляют остаток 1 при делении на 222.
Каждое целое число либо четное, либо нечетное, и ни одно целое число не является одновременно четным и нечетным. Сюда входит 0, что является четным.
Выясните, является ли 1729 нечетным или четным числом.
Поскольку остаток от деления 1729 на 2 равен 1, 1729 — нечетное число.
ИЛИ\text{ИЛИ}ИЛИ
Число 1729 заканчивается цифрой «9». Таким образом, это нечетное число. □_\квадрат□
Выясните, является ли 1000 нечетным или четным числом.
Поскольку остаток от деления 1000 на 2 равен 0, 1000 — четное число.
ИЛИ\text{ИЛИ}ИЛИ
Число 1000 заканчивается цифрой «0». Таким образом, это четное число. □_\квадрат□
(а) (б) (с) Ничего из вышеперечисленного
Что из следующего верно относительно числа -163?-163?-163?
(а) Это нечетное число.
(b) Это четное число.
(c) Это ни нечетное, ни четное число.
Сколько из следующих 10 чисел являются четными целыми числами?
0,1,−2,3,−1,5,0,−2,4,2×2,−2×3,5,22 \begin{array} {rrrrr} 0, && 1, &&-2, &&3, &&- 1, \\ 5.0, &&-2.4, &&2 \times 2, &&-2 \times 3.5, &&\frac{2}{2} \end{массив} 0,5.0,1,−2.4,− 2,2×2,3,−2×3,5,−1,22
Число 2222452122 четное или нечетное?
Последняя цифра — 2, а 2 — четное число. Итак, 2222452122 — четное число. □_\квадрат□
Ниже приведены свойства четности четных и нечетных чисел:
- четный ± \pm± четный = четный
- нечетное ± \pm± нечетное=четное
- четный ± \pm± нечетный= нечетный
- четный × \times× четный= четный
- четный ×\times× нечетный= четный
- нечетное × \times× нечетное= нечетное
Эти свойства часто полезны для проверки того, является ли равенство ложным, с помощью правил четности арифметики, чтобы увидеть, имеют ли обе стороны одинаковую четность. Применение этих правил становится понятным из следующих примеров и задач:
Применение этих правил становится понятным из следующих примеров и задач:
Если nnn — целое число, какова четность 2n+2?2n+2?2n+2?
Поскольку nnn — целое число, n+1n+1n+1 также является целым числом. Тогда 2n+2=2(n+1)+02n+2 = 2(n+1) + 02n+2=2(n+1)+0 показывает, что четность 2n+22n+22n+2 равна 0 ,0,0, что означает, что 2n+22n+22n+2 всегда четное число. □_\квадрат□
Число (47630750675+453407032)×549068453\влево(47630750675+453407032\вправо) \умножить на 549068453(47630750675+453407032)×549068453 четное или нечетное?
Чтобы ответить на этот вопрос, было бы неразумно умножать эти числа. Вместо этого мы можем применить свойства четных и нечетных чисел.
Поскольку число 476307506754763075067547630750675 оканчивается на 5, оно нечетное. С другой стороны, поскольку 453407032453407032453407032 оканчивается на 2, оно четное. По свойству 3 четное ± \pm± нечетное = нечетное, поэтому 47630750675+45340703247630750675+45340703247630750675+453407032 нечетно.
Поскольку эта сумма умножается на 549068453,549068453,549068453, что является нечетным, все число является нечетным, поскольку свойство 6 дает нечетное × \times× нечетное = нечетное. □_\квадрат□
Вот несколько задач, которые стоит попробовать.
б-аб-аб-а а+ба+ба+б абабаб −ab-ab−ab
Если aaa — отрицательное нечетное число, а bbb — положительное четное число, то какое из следующих чисел должно быть положительным четным числом?
всегда нечетный всегда даже четные или нечетные, в зависимости от значений aaa и bbb 92+a+7) \times (2b+1) (a2+a+7)×(2b+1)
равно __________.\text{\_\_\_\_\_\_\_\_ \_\_}.__________.
Даже это странно Это даже если xxx даже Это даже если yyy даже Даже если xyxyxy отрицательное
Пусть xxx и yyy будут целыми числами. {2}+xy?(x+y)2+xy?
{2}+xy?(x+y)2+xy?
Вот примеры и задачи, мотивированные для улучшения навыков решения задач на четность нечетных и четных чисел. Пройдите их, чтобы достичь целей этого раздела.
Если aaa и bbb целые числа, какова четность a×b?a \times b?a×b?
Мы знаем, что нечетное число, умноженное на нечетное число, остается нечетным, четное число, умноженное на нечетное число, будет четным, а четное число, умноженное на четное число, будет четным. Это можно обобщить как
(четность a) × (четность b) = (четность ab). □ ( \mbox{Четность } a ) \times ( \mbox{Четность } b ) = (\mbox{Четность } ab). \ _\square(Четность a)×(Четность b)=(Четность ab). □
Пусть P P P будет произведением первых 100 простых чисел. Какова четность P? П?П?
Мы видим, что первое простое число — 2, то есть четное. Остальные 99 простых чисел нечетные. Произведение этих 99 простых чисел будет целым числом, скажем, k k k. Умножение четного числа на другое целое всегда дает четное число; поэтому мы можем записать P P P как 2k 2 k 2k.
Деление P P P на 2 не дает остатка, поэтому P P P четно. □_\квадрат □ 92 + k = k (k+1),k2+k=k(k+1), где k kk и (k+1) (k+1)(k+1) имеют разную четность. Тогда по арифметическим правилам четности четность k(k+1) k(k+1)k(k+1) равна 0 00. □_\square□
Да №
Может ли четное число, разделенное на другое четное число, умножить на другое четное число, когда-нибудь получить нечетное число?
Если «да», то найдите три подходящих числа.
Если «нет», то почему? 92 + nn2+n на 2,2,2, мы получим целое число. □_\квадрат □
Попробуйте решить следующие задачи:
Нечет для всех значений aaa и bbb Даже для всех значений aaa и bbb Даже ровно для 1 значения aaa и 1 значения bbb Нечетное ровно для 1 значения aaa и 2 значений bbb
Учитывая, что aaa и bbb — целые числа, какой вывод мы можем сделать о выражении 9{ 2 }+a+2011 \big) ( 2b+1 ) ? (а2+а+2011)(2б+1)?
Произведение цифр числа 38 четно, потому что 3×8=24,3\умножить на 8 = 24,3×8=24.

 com
com mk.ru
mk.ru Например, 32 – 6 = 26.
Например, 32 – 6 = 26.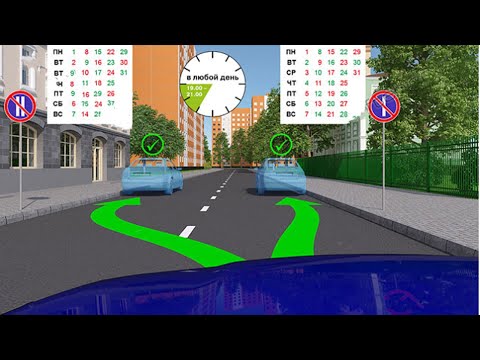 Поскольку эта сумма умножается на 549068453,549068453,549068453, что является нечетным, все число является нечетным, поскольку свойство 6 дает нечетное × \times× нечетное = нечетное. □_\квадрат□
Поскольку эта сумма умножается на 549068453,549068453,549068453, что является нечетным, все число является нечетным, поскольку свойство 6 дает нечетное × \times× нечетное = нечетное. □_\квадрат□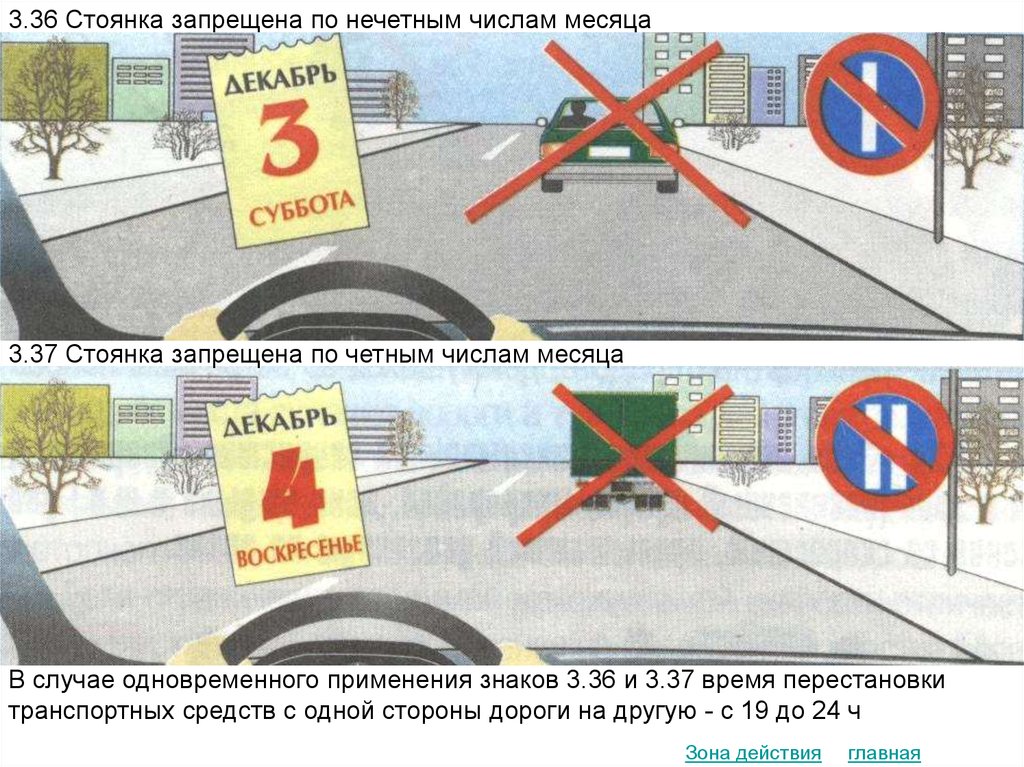 Деление P P P на 2 не дает остатка, поэтому P P P четно. □_\квадрат □
92 + k = k (k+1),k2+k=k(k+1), где k kk и (k+1) (k+1)(k+1) имеют разную четность. Тогда по арифметическим правилам четности четность k(k+1) k(k+1)k(k+1) равна 0 00. □_\square□
Деление P P P на 2 не дает остатка, поэтому P P P четно. □_\квадрат □
92 + k = k (k+1),k2+k=k(k+1), где k kk и (k+1) (k+1)(k+1) имеют разную четность. Тогда по арифметическим правилам четности четность k(k+1) k(k+1)k(k+1) равна 0 00. □_\square□