1 6 1 4: сколько будет 1/4+1/6 — Школьные Знания.com
Десятичные дроби — как решать примеры 5, 6 класс
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной.
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Как решаем:
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ: 16/10 = 1,6.
Пример 2. Перевести 37/1000 в десятичную дробь.
Как решаем:
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный вводный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
и т. д. д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
1% = 1/100 = 0,01
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого.
Преобразование десятичных дробей
Быстрая напоминалка:
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Ответ: 5,4 = 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
Перевести 4,005 в смешанное число.
Как решаем:
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как решаем:
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу.
 Например:
Например:- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.

- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Как решаем:
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
Как решаем:
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.Как решаем:
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
Как решаем:
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Как решаем:
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
Как решаем:
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
I участок | Сазонова Ольга Яковлевна Бухтиярова Евгения Михайловна | Молодежная 4, 6, 7, 8/1, 8/2Молодцова 5, 16 Восточно-Выборгское шоссе 24/,26/1,28/1 |
II участок | Медведева Светлана Станиславовна Суслова Ольга Владимировна | Заречная 1, 2, 3, 4, 5, 6, 7, 7/2, 10, 11, 12, 13, 15, 17Школьная 1, 2/2, 2/3, 3, 5, 6/1, 6/2 ,6/3Сертолово-2 ДНП Омега, Петровское, Слобода, ДПК Ветеран-1, Лесная Поляна |
III участок | Сибилева Галина Михайловна Кукуруза Ольга Ивановна | Ветеранов 1, 3, 3а, 4, 5, 6, 7, 8, 10, 11/1, 11/2, 12,15Ларина 1, 2, 3, 3а, 4, 5, 6, 7, 8, 10, 11Индустриальная Парковая |
IV участок | Бессонова Татьяна Сергеевна Лукьянова Антонина Исаевна | Кленовая 1/1, ½, 3Центральная 2, 4/1, 4/2, 6/1, 6/2, 8/1,8/2ЖСК Модуль 25 км. Общ. Общ.Парковый проезд 5 3 городок |
V участок | Жердева Галина Антоновна Червинская Надежда Федоровна | Молодцова 1, 3, 4, 6, 7/1, 7/2, 7/3Молодежная 1, 2, 3, 3/2, 5Сосновая 1, 2, 3, 4 Ветеранов 8/2 |
VI участок | Мосидзе Манана Вахтанговна Бибик Вера Михайловна | Кожемякина 11/1Молодцова 2, 2/2, 8, 8/2, 9, 10, 13Центральная 1/1 Центральная проходная Нахимовская Песочная |
VII участок | Ширкова Наталья Борисовна Багура Галина Владимировна | Молодцова 11, 15/1, 15/2Кленовая 5, 7Пограничная (кроме Чистого ручья) Центральная 10/1, 10/2,14/4 |
VIII участок | Кутузова Наталья Васильевна Кордон Оксана Юрьевна | Пограничная 4/1,4/2,4/3 Ветеранов 9Ларина 14, 15/1, 15/2 Молодцова 12, 14 Парковый проезд 1, 2/1, 2/2 Центральная ½, 1/3, 3, 5, 7/1,7/2 |
IX участок | Сорока Татьяна Борисовна Полякова Елена Владимировна | Новое Сертолово (Тихвинская, Мира) |
X участок | Викман Виктория Александровна Малышева Татьяна Викторовна м/с | Черная речкаЗолотые куполаСНТ Ромашка, Ягодка |
Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней
Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от
1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет
6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для
решения задач по
теории вероятности,
геометрии и математике! Также на сайте работает
форум, на котором Вы всегда можете
задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет
6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для
решения задач по
теории вероятности,
геометрии и математике! Также на сайте работает
форум, на котором Вы всегда можете
задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1 | 21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024 | 31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049 | 41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576 | 51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625 |
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176 | 71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249 | 81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824 | 91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401 | 101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000 |
Остались вопросы?
Здесь вы найдете ответы. x=3
log2(3)=x
x=3
log2(3)=x
90 в 10 степени
90 в 10 =34867844009999998976.00000
12 в степени 1/3
Сложная формула но в кратце ответ — 6
Слишком сложно?
Таблица степеней не по зубам? Тебе ответит эксперт через 10 минут!
Поликлиника №1 — Центральная Городская Клиническая Больница №6
ПОЛИКЛИНИКА № 1
г. Екатеринбург, ул. Саперов, 3
Call — центр поликлиники № 1:
389 – 26 – 04
телефон регистратора для вызова врача на дом: 257-35-05, 257-06-22
телефон единой городской регистратуры: 204-76-76
Запись через интернет: http://www. medincom.info
medincom.info
e-mail:Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
Заведующая поликлиникой:
Фоменко Надежда Владимировна
Часы приема граждан: четверг с 12-00 до 16-00
телефон: 389-26-43
Старшая медсестра:
Бабушкина Марина Валентиновна
телефон: 257-41-56
Кабинет неотложной помощи — кабинет № 110 (обслуживает вызов на дому)
08:00 – 20:00 (без выходных)
Кабинет неотложной помощи — кабинет № 104 (прием пациентов в поликлинике)
08:00 – 20:00 (кроме субботы и воскресенья)
Кабинет доврачебного приема – кабинет № 414, № 208 (выписка льготных рецептов, выписка направлений на анализы)
08:00 – 20:00 (кроме субботы, воскресенья)
График работы регистратуры: с понедельника по пятницу 07:30 — 20:00
График работы кабинетов приема: с понедельника по пятницу 08:00 — 20:00
Суббота, воскресенье (кабинет дежурного терапевта): 09:00 – 15:00
Как до нас добраться:
Трамвай:
1, 4, 5, 10, 14, 15, 25 – остановка «Декабристов»
Автобус:
23, 46, 50, 57 – остановка «Декабристов»
Маршрутное такси:
024, 012 – остановка «Декабристов»
Терапевтическое отделение № 1
г. Екатеринбург, ул. Постовского, 12а
Екатеринбург, ул. Постовского, 12а
телефон регистратуры: 389-26-04
телефон для вызова врача на дом: 257-35-05, 257-06-22
График работы регистратуры:
с понедельника по пятницу 07:30 — 19:00
График работы кабинетов приема:
с понедельника по среду 08:00 — 20:00,
с четверга по пятницу 08:00 – 19:00
Как до нас добраться:
Автобус:
21, 42, 46, 50, 50А, 76 – остановка «Амундсена» Маршрутное такси:
054, 14, 070, 52 – остановка «Амундсена»
Где находится номер двигателя на Шевроле Круз: 1 4, 1 6, 1 8
Номер мотора Chevrolet Cruze вне зависимости от типа двигателя и поколения модели, располагается на утолщении блока цилиндров силовой установки, рядом с топливным фильтром. Иногда он может быть прикрыт последним, но чаще табличку с номером хорошо видно, если только он не разъеден ржавчиной. Номер может дублироваться на наклейке, которую помещают на корпус установки — обычно такое дублирование встречается на Крузе второго поколения.
Номер может дублироваться на наклейке, которую помещают на корпус установки — обычно такое дублирование встречается на Крузе второго поколения.
В машине еще находится VIN-номер. Он содержит информацию о кузове и защищает авто от злоумышленников. Найти его можно на табличке, которая прикреплена к полу автомобиля в салоне, под ногами у пассажира. Чтобы посмотреть код, нужно поднять обивку пола или пластиковый лючок. Есть и наклейка с VIN-кодом, помещенная на среднюю левую стойку.
Мотор 1 4
В Крузе с модификацией двигателя 1,4 литра, номер установки выбит на табличке, которая расположена на утолщении блока, рядом с масляным фильтром, в верхнем правом углу. Иногда ржавчина сильно покрывает табличку, из-за чего ее бывает сложно найти. В случае с 1,4 мотором, символы хорошо читаются, несмотря на ржавчину.
Мотор 1 6
Номер находится там же — на блоке возле КПП. Именно таким его расположение было с 2010 года. В 2012 г увидела свет новая модификация второго поколения Cruze с доработанными двигателями на 1,6 литра. Это никак не повлияло на расположение символов мотора.
Это никак не повлияло на расположение символов мотора.
Двигатель 1 8
Табличка с маркировкой 1,8-литрового двигателя доставляет автовладельцам больше всего хлопот. Это связано с низким качеством ее изготовления — уже за три года она покрывается ржавчиной так, что очистить ее можно лишь серьезными мерами. Расположена она в том же месте, что и таблички на других моторах, но больше закрыта масляным фильтром. Из-за этого, чтобы ее протереть, придется наматывать тряпочку на тонкую отвертку, поскольку пролезет в зазор только она.
Есть ли разница в расположении номера мотора от типа кузова: хэтчбек или седан
В Крузе это не влияет на положение символов.
Не читается номер силовой установки
Повреждение таблички из-за коррозии, вследствие чего тот просто нельзя прочитать — типичная проблема для данной модели. Чтобы все-таки извлечь номер, необходимо протереть тряпочкой табличку, предварительно нанеся на нее специальный антикоррозионный раствор. Использовать в этих целях наждачную бумагу категорически нельзя.
Использовать в этих целях наждачную бумагу категорически нельзя.
Расшифровка кода VIN Круза
В номере содержатся немало важной информации об автомобиле, от места его производства до варианта кузова. Для примера рассмотрим код XUFJА686JC3000000:
- первые три знака обозначают место производства: XUF — для России и KL1 — Корея;
- следующий знак — модель: J – Cruze или N — Lacetti;
- пятый знак — трансмиссия: А — передний привод с автоматической коробкой передач; F — с МКПП;
- шестой и седьмой знаки — тип кузова: 19 – четырехдверный седан с 6 боковыми окнами, 35 – универсал, 68 – 4-х дверный хэтчбэк с 6 боковыми окнами;
- восьмой знак — мотор: B — 1,8 л DOHC, 6 — 1,6 л DOHC;
- девятый знак — экологический класс двигателя: J – ЕВРО4 или 1 – ЕВРО3;
- десятый знак — год выпуска: А — 2010-2011 гг, В — 2013 г или С — 2012 г;
- одиннадцатый знак — кодировка производства;
- следующие шесть знаков — серийный номер кузова.

Специализация: Закончил государственный автомобильный университет, проработал 20 лет на ГАЗ-56, сейчас езжу на жигулях.
Подробнее об авторе Калькулятор — помощник для расчета стоимости, удорожания автокредита на покупку автомобиляОставить отзыв
Модули ЭНМВ-1 для телесигнализации, телеуправления в системах телемеханики
Набор входов и выходов24 дискретных входа wet contact (внешнее питание входа 24 В=) или 24 дискретных входа dry contact (питание входа от устройства 24 В=) / 0 дискретных выходов
24 дискретных входа wet contact (внешнее питание входа 220 В=)/0 выходов
20 выходов SSR Form A (на твердотельном реле)
20 выходов SSR Form A (на твердотельном реле), 2 быстродействующих выхода (TRIP)
0 входов/3 выхода EMR (релейные выходы: включить, отключить, блокировка)
4 входа/3 выхода EMR (релейные выходы: включить, отключить, блокировка)
6 входов/3 выхода EMR (релейные выходы: включить, отключить, блокировка)
4 дискретных входов wet contact (внешнее питание входа 220 В=) / 3 выхода EMR (релейные выходы: включить, отключить, блокировка)
16 дискретных входов wet contact (внешнее питание входа 24 В=) или 16 дискретных входов dry contact (питание входа от устройства 24 В=) / 3 выхода EMR (релейные выходы: включить, отключить, блокировка)
6 дискретных входов wet contact (внешнее питание входа 220 В=) / 3 выхода EMR (релейные выходы: включить, отключить, блокировка)
16 дискретных входов wet contact (внешнее питание входа 220 В=) / 3 выхода EMR (релейные выходы: включить, отключить, блокировка)
16 дискретных входов wet contact (внешнее питание входа 24 В=) или 16 дискретных входов dry contact (питание входа от устройства 24 В=) / 3 выхода на основе электронных ключей
16 дискретных входов wet contact (внешнее питание входа 220 В=) / 3 выхода на основе электронных ключей
8 настраиваемых токовых входов: 0…20 мА; −20…0…20 мА; 0…5 мА; −5…0…5 мА.
2 настраиваемых входа: 2 или 3-проводное подключение Pt100; 100П; Pt500; 500П; Pt1000; 1000П; Термопара Тип K
8 аналоговых входов / 8 дискретных входов wet contact (внешнее питание входа 220 В=)
8 аналоговых входов / 8 дискретных входов wet contact (внешнее питание входа 24 В=)
Интерфейсы1 порт RS-485 (только для модификаций 0/3R, 4/3R, 6/3R)
2 порта RS-485 (только для модификаций 24/0, 0/22, 0/20, 16/3R, 16/6, 8Х8/0, 8P2T/0)
2 порта RS-485, 1 порт Ethernet 100Base-T (только для модификаций 24/0, 0/22, 0/20, 16/3R, 16/6, 8Х8/0, 8P2T/0)
2 порта RS-485, 2 порта Ethernet 100Base-T (только для модификаций 24/0, 0/22, 0/20, 16/3R, 16/6, 8Х8/0, 8P2T/0)
Опьянение и отрезвление — Alkoinfo.
-reshenie-566.jpg) ee
eeСтепени опьянения и время вытрезвления
От чего зависит опьянение?
То, насколько повышается содержание алкоголя в крови, зависит от множества факторов. Однако общее правило заключается в том, что чем больше алкоголя, тем выше его содержание в крови. В то же время многое зависит от темпа употребления: если пить быстро, содержание алкоголя в крови увеличивается сильнее, чем при медленном употреблении. При пустом желудке алкоголь всасывается полностью и быстрее, чем у сытого человека. Крепкие напитки всасываются быстрее, чем легкие, создавая большую концентрацию алкоголя в крови. Важна и масса тела: на худощавых людей то же количество алкоголя оказывает больший эффект. Кроме того, алкоголь по-разному действует на женщин и мужчин. Поскольку в организме женщин обычно содержится меньше воды, при том же количестве выпитого алкоголя его содержание в крови женщины будет выше даже при одинаковой с мужчиной массе тела.
Измерение степени опьянения
Степень опьянения измеряется в промилле.Промилле показывает массу алкоголя в 1000 мл крови. Например, 0,5-процентное опьянение означает, что в 1000 мл циркулирующей в организме крови содержится 0,5 г чистого алкоголя.
Степень опьянения оценивается как по выдыхаемому воздуху, так и с помощью анализа крови. Содержание алкоголя в выдыхаемом воздухе измеряется в миллиграммах на литр. Однако чаще используется понятие промилле. Для того, чтобы миллиграммы на литр выразить в промилле, нужно полученное число умножить на 2,1. Например, опьянение с 0,5 мл/л в выдыхаемом воздухе соответствует около 1,05 процента.
Согласно законодательству Эстонии, различаются следующие степени опьянения:
признаки употребления алкоголя – содержание алкоголя от 0,10 до 0,24 миллиграмма в литре выдыхаемого воздуха, либо от 0,20 до 0,49 промилле в крови;
легкое алкогольное опьянение – содержание алкоголя от 0,1 до 0,75 миллиграмма в литре выдыхаемого воздуха, либо от 0,20 до 1,50 промилле в крови;
умеренное алкогольное опьянение – содержание алкоголя от 0,76 до 1,25 миллиграмма в литре выдыхаемого воздуха, либо от 1,51 до 2,5 промилле в крови;
тяжелое алкогольное опьянение – содержание алкоголя свыше 1,25 миллиграмма в литре выдыхаемого воздуха, либо свыше 2,5 промилле в крови.
Управление транспортным средством в состоянии опьянения – это преступление! Производство о правонарушении проводится в случае, если содержание алкоголя в одном грамме крови водителя составляет 0,20 мг и больше, либо если в одном литре выдыхаемого им воздуха содержится 0,10 мг или больше алкоголя.
Воздействие опьянения на восприятие и поведение
У некоторых людей симптомы опьянения наступают быстрее и легче, чем у других. Есть и люди, у которых уже образовалась толерантность, из-за чего они не способны почувствовать, насколько пьяны.
В общих чертах все же можно определить, как меняется настроение и поведение при разных степенях опьянения.
0,2–0,3 промилле Вы можете чувствовать себя слегка расслабленным, внутренние ограничения несколько ослабляются. После приема алкоголя настроение начинает подниматься.
0,4–0,6 промилле Вы чувствуете тепло и расслабленность. Ваше поведение может быть более вызывающим: речь становится смелее и быстрее, а голос громче, чем обычно. Усиливаются эмоции – хорошее настроение становится еще лучше и точно так же усиливаются отрицательные эмоции. Вы можете ощущать легкую эйфорию. Мыслительные способности и память могут слегка нарушиться, делая вас неосмотрительным.
Усиливаются эмоции – хорошее настроение становится еще лучше и точно так же усиливаются отрицательные эмоции. Вы можете ощущать легкую эйфорию. Мыслительные способности и память могут слегка нарушиться, делая вас неосмотрительным.
0,7–0,9 промилле При этой степени опьянения начинаются нарушения равновесия, двигательных функций, четкости речи, скорости реакции, зрения и слуха. Нарушается самоконтроль и способность рассуждать, вы считаете, что действуете лучше обычного и вам трудно не продолжить пить. Вы можете чувствовать эйфорию.
1,0–1,2 промилле У вас эйфория, хотя моторные функции, координация, скорость реакции и равновесие уже сильно нарушены. То же со способностью рассуждать и с памятью. В действительности вы не помните, сколько порций уже выпили. Ваши эмоции усиливаются. Некоторые люди становятся очень шумными и агрессивными.
1,3–1,5 промилле Отсутствует равновесие, зрение затуманено, возникают трудности с передвижением и с речью. Мышление, восприятие и способность к принятию решений сильно нарушены. Эйфория понемногу проходит и сменяется неприятными чувствами, такими как тревожность, беспокойство, гнев и подавленность.
Мышление, восприятие и способность к принятию решений сильно нарушены. Эйфория понемногу проходит и сменяется неприятными чувствами, такими как тревожность, беспокойство, гнев и подавленность.
1,6–1,9 промилле Вас наполняют сильные отрицательные эмоции, в результате вы можете стать агрессивным – и ненамеренно причинить вред себе или другим. На этой стадии могут образоваться т.н. провалы памяти – мозг больше не фиксирует происходящее. Моторные функции сильно нарушены.
более 2 промилле Вам не скрыть спутанности сознания, бестолковости и неспособности понимать происходящее. Вам нужна помощь, чтобы встать или ходить. Если вы нанесете себе травму, то скорее всего не осознаете этого, поскольку не чувствуете боли. Вас тошнит или рвет (у некоторых эти симптомы могут возникнуть раньше). Поскольку рвотный рефлекс нарушен, есть опасность захлебнуться собственной рвотой. На этой стадии часты провалы памяти, поэтому вы, очевидно, на следующее утро ничего не вспомните.
более 2,5 промилле Сильно нарушены все психические и физические функции, в том числе восприятие. Наступает эмоциональная бесчувственность. Повышен риск захлебнуться собственной рвотой, упасть и нанести себе серьезную травму или стать жертвой другого несчастного случая.
более 3 промилле Вы в полубессознательном состоянии. Вы не понимаете, где находитесь. Вы можете внезапно потерять сознание, вас трудно привести в чувство.
более 3,5 промилле Такая доза алкоголя действует как наркоз, используемый при операциях. Возможно, вы впадете в кому. Дыхание может стать прерывистым.
более 4 промилле Нарушается работа сердца и дыхание. Фактически, вы в коме или уже мертвы.
Время на вытрезвление
В среднем алкоголь выводится из организма человека со скоростью 0,1 промилле в час. Скорость процесса зависит от пола, массы тела, роста и того, сколько было съедено до приема алкоголя. Поэтому следующие таблицы, показывающие время отрезвления, являются информативными и не должны использоваться для расчета, когда можно будет сесть за руль.Проверяйте трезвость алкометром!
Женщина
Здоровая женщина весом 60 кг
| Количество выпитых алкогольных напитков | Приблизительное время, необходимое для полного вытрезвления |
| 1 бокал (0,125 л) вина (12%) | 0,36 промилле (красный 3, оранжевый 1) |
| 1 бутылка (0,33 л) сидра (4,5%) | 0,35 промилле (красный 3, оранжевый 1) |
| 2 бокала (0,3 л) игристого вина (7,5%) | 0,53 промилле (красный 5, оранжевый 1,5) |
| 2 стопки (0,08 л) водки (40%) | 0,77 промилле (красный 7, оранжевый 1,5) |
| 3 бутылки (0,5 л) пива (4,5%) | 1,6 промилле (красный 15, оранжевый 1,5) |
Мужчина
Здоровый мужчина весом 80 кг
| Количество выпитых алкогольных напитков | Приблизительное время, необходимое для полного вытрезвления |
| 1 бокал (0,125 л) вина (12%) | 0,22 промилле (красный 2, оранжевый 1) |
| 1 бутылка (0,5 л) пива (4,5%) | 0,32 промилле (красный 3, оранжевый 1) |
| 2 стопки (0,08 л) водки (40%) | 0,46 промилле (красный 4, оранжевый 1,5) |
| 4 стопки (0,16 л) ликера (35%) | 0,81 промилле (красный 8, оранжевый 1,5) |
| 5 бутылок (2 л) пива (4,5%) | 1,6 промилле (красный 16, оранжевый 2) |
(При калькуляции использована формула Видмарка)
Мифы об алкоголе и действительность
Можно ли ускорить процесс расщепления алкоголя?
95% алкоголя выводится из организма благодаря работе печени. Небольшое количество выделяется с выдыхаемым воздухом, с мочой и через кожу. Единственный способ протрезветь – выждать время.
Небольшое количество выделяется с выдыхаемым воздухом, с мочой и через кожу. Единственный способ протрезветь – выждать время.
Как влияет на отрезвление сауна?
Поскольку менее 5% алкоголя покидает организм с потом и мочой, процесс сжигания алкоголя не ускоряет ни сауна, ни потение в жаркий летний день. Под действием алкоголя ускоряется частота сердцебиения, повышается потребление сердцем кислорода. Одной из причин ускорения сердечной деятельности является расширение кровеносных сосудов. Кровь приливает к коже, давление крови падает, и потому сердце начинает биться сильнее, чтобы снабжать кровью другие органы. Поэтому сауна и у здорового человека может вызвать опасные изменения кровообращения. В состоянии опьянения человек недостаточно хорошо переносит жар сауны и возникающую в ней потерю жидкости.
Как влияют на отрезвление кофе, энергетические напитки или холодный душ?
Содержащийся в кофе кофеин обладает стимулирующим действием, но в действительности лишь бодрит человека, а не снимает опьянение. Аналогично кофе действует и душ: процесс сжигания алкоголя происходит прежде всего в печени, и его скорость изменить невозможно. Совместное употребление алкоголя и энергетических напитков повышает вероятность алкогольного отравления. Оно также может вызвать обезвоживание, сопровождающееся диареей, тошнотой или рвотой, мышечными судорогами, усталостью и головной болью.
Аналогично кофе действует и душ: процесс сжигания алкоголя происходит прежде всего в печени, и его скорость изменить невозможно. Совместное употребление алкоголя и энергетических напитков повышает вероятность алкогольного отравления. Оно также может вызвать обезвоживание, сопровождающееся диареей, тошнотой или рвотой, мышечными судорогами, усталостью и головной болью.
Можно ли быстрее протрезветь за счет тренировки?
Все-таки нельзя. В результате физической нагрузки в мышцах скапливается молочная кислота, которая вызывает боль. Печень не может одновременно выводить алкоголь и молочную кислоту. Поэтому работоспособность мышц будет низкой, а концентрация молочной кислоты – выше нормы. Алкоголь опустошает в печени запасы гликогена, являющегося для организма источником энергии именно при физических нагрузках.
Алкоголь вызывает обезвоживание, снижает уровень энергии, лишает организм витаминов и минералов и понижает уровень тестостерона. Большая физическая нагрузка в состоянии опьянения скорее опасна для здоровья.
Можно ли опьянеть от кефира и конфет?
В кефире и некоторых конфетах в действительности содержится минимум алкоголя (1–2% от общей массы), но столь малое количество не вызывает алкогольного опьянения.
Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби. Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.
В математике дробь — это число, которое представляет собой часть целого. Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, для этих операций с дробями требуется общий знаменатель. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
Наименьшее общее кратное — это первое общее кратное этих трех чисел.
| Кратное 2: 2, 4, 6, 8 10, 12 |
| Кратное 4: 4, 8, 12 |
| Кратное 6: 6, 12 |
Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
Вычитание:
Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель. По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
Дивизион:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число, обратное числу , равно —
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
, например, более громоздко, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной форме дроби, так и в форме смешанных чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.Преобразование между дробями и десятичными дробями:
Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
Точно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный знак представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.
Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.Преобразование общей инженерной дроби в десятичную
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
| 64 th | 32 nd | 16 th | 8 th | 4 th | 2 nd | Decimal | Decimal (дюйм к мм) | |||||
| 1/64 | 0,015625 | 0,396875 | ||||||||||
| 2/64 | 1/32 | 0.03125 | 0,79375 | |||||||||
| 3/64 | 0,046875 | 1,1 | ||||||||||
| 4/64 | 2/32 | 1/16 | 0,0625 | 1,5875 | ||||||||
| 5/64 | 0,078125 | 1. 984375 984375 | ||||||||||
| 6/64 | 3/32 | 0.09375 | 2,38125 | |||||||||
| 7/64 | 0,109375 | 2,778125 | ||||||||||
| 8/64 | 4/32 | 2/16 | 1/8 | 0,125 | 3,175 | |||||||
| 9/64 | 0,140625 | 3,571875 | ||||||||||
| 10/64 | 5/32 | 0.15625 | 3.96875 | |||||||||
| 11/64 | 0,171875 | 4.365625 | ||||||||||
| 12/64 | 6/32 | 3/16 | 0,1875 | 4,7625 | ||||||||
| 13/64 | 0,203125 | 5,159375 | ||||||||||
| 14/64 | 7/32 | 0. 21875 21875 | 5,55625 | |||||||||
| 15/64 | 0,234375 | 5.953125 | ||||||||||
| 16/64 | 8/32 | 4/16 | 2/8 | 1/4 | 0,25 | 6,35 | ||||||
| 17/64 | 0,265625 | 6,746875 | ||||||||||
| 18/64 | 9/32 | 0.28125 | 7,14375 | |||||||||
| 19/64 | 0,296875 | 7,540625 | ||||||||||
| 20/64 | 10/32 | 5/16 | 0,3125 | 7,9375 | ||||||||
| 21/64 | 0,328125 | 8,334375 | ||||||||||
| 22/64 | 11/32 | 0. 34375 34375 | 8,73125 | |||||||||
| 23/64 | 0,359375 | 9.128125 | ||||||||||
| 24/64 | 12/32 | 6/16 | 3/8 | 0,375 | 9,525 | |||||||
| 25/64 | 0,3 | 9, 5 | ||||||||||
| 26/64 | 13/32 | 0.40625 | 10,31875 | |||||||||
| 27/64 | 0,421875 | 10,715625 | ||||||||||
| 28/64 | 14/32 | 7/16 | 0,4375 | 11,1125 | ||||||||
| 29/64 | 0,453125 | 11,509375 | ||||||||||
| 30/64 | 15/32 | 0. 46875 46875 | 11. | |||||||||
| 31/64 | 0,484375 | 12.303125 | ||||||||||
| 32/64 | 16/32 | 8/16 | 4/8 | 2/4 | 1/2 | 0,5 | 12,7 | |||||
| 33/64 | 0,515625 | 13.096875 | ||||||||||
| 34/64 | 17/32 | 0.53125 | 13.49375 | |||||||||
| 35/64 | 0,546875 | 13.8 | ||||||||||
| 36/64 | 18/32 | 9/16 | 0,5625 | 14,2875 | ||||||||
| 37/64 | 0,578125 | 14,684375 | ||||||||||
| 38/64 | 19/32 | 0. 59375 59375 | 15.08125 | |||||||||
| 39/64 | 0.609375 | 15.478125 | ||||||||||
| 40/64 | 20/32 | 10/16 | 5/8 | 0,625 | 15,875 | |||||||
| 41/64 | 0,640625 | 16,271875 | ||||||||||
| 42/64 | 21/32 | 0.65625 | 16,66875 | |||||||||
| 43/64 | 0,671875 | 17,065625 | ||||||||||
| 44/64 | 22/32 | 11/16 | 0,6875 | 17,4625 | ||||||||
| 45/64 | 0,703125 | 17,859375 | ||||||||||
| 46/64 | 23/32 | 0. 71875 71875 | 18,25625 | |||||||||
| 47/64 | 0,734375 | 18,653125 | ||||||||||
| 48/64 | 24/32 | 12/16 | 6/8 | 3/4 | 0,75 | 19,05 | ||||||
| 49/64 | 0,765625 | 19,446875 | ||||||||||
| 50/64 | 25/32 | 0.78125 | 19.84375 | |||||||||
| 51/64 | 0,796875 | 20.240625 | ||||||||||
| 52/64 | 26/32 | 13/16 | 0,8125 | 20,6375 | ||||||||
| 53/64 | 0,828125 | 21,034375 | ||||||||||
| 54/64 | 27/32 | 0. 84375 84375 | 21,43125 | |||||||||
| 55/64 | 0,859375 | 21,828125 | ||||||||||
| 56/64 | 28/32 | 14/16 | 7/8 | 0,875 | 22,225 | |||||||
| 57/64 | 0,8 | 22,621875 | ||||||||||
| 58/64 | 29/32 | 0. | 23,01875 | |||||||||
| 59/64 | 0, 5 | 23,415625 | ||||||||||
| 60/64 | 30/32 | 15/16 | 0,9375 | 23,8125 | ||||||||
| 61/64 | 0,953125 | 24. 209375 209375 | ||||||||||
| 62/64 | 31/32 | 0.96875 | 24.60625 | |||||||||
| 63/64 | 0,984375 | 25.003125 | ||||||||||
| 64/64 | 32/32 | 16/16 | 8/8 | 4/4 | 2/2 | 1 | 25,4 |
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью. Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, т. Е. 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически переводятся в дроби — i.е. 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей, например 1/2: 1/3 .
Звездочка * или × — это символ умножения. 1/2
1/2
• сложение дробей и смешанные числа: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группировка символов — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Задачи с дробями:
следующие математические задачи »
Сложение дробей
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, выполните три простых шага:
- Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают.
- Шаг 2: сложите верхние числа (числители), поместите полученный ответ над знаменателем
- Шаг 3. Упростите дробь (при необходимости)
Пример:
Шаг 1 .Нижние цифры (знаменатели) уже совпадают. Переходите сразу к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
.
1 4 + 1 4 знак равно 1 + 1 4 знак равно 2 4
Шаг 3 . Упростим дробь:
2 4 знак равно 1 2
На картинке это выглядит так:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
… и ты видишь как 2 4 проще как 1 2 ? (см. Эквивалентные дроби.)
Пример:
Шаг 1 : Нижние числа разные. Видите, как ломтики бывают разных размеров?
| 1 3 | + | 1 6 | = | ? | ||
Нам нужно сделать их такими же, прежде чем мы сможем продолжить, потому что не может, добавить их вот так.
Число «6» вдвое больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 2 , например:
| × 2 |
| × 2 |
Важно: вы умножаете как верхний, так и нижний на одинаковую величину,
, чтобы сохранить значение дроби одинаковым
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
| 2 6 | + | 1 6 | ||||
Нижние числа теперь те же, поэтому мы можем перейти к шагу 2.
Шаг 2 : сложите верхние числа и поместите их над тем же знаменателем:
2 6 + 1 6 знак равно 2 + 1 6 знак равно 3 6
На картинке это выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | ||
Шаг 3 : Упростите дробь:
3 6 знак равно 1 2
На картинке весь ответ выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Рифма, которая поможет тебе вспомнить
♫ «Если вашей целью является сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫» Измените нижнее значение с помощью умножения или деления,
Но то же самое и к верхнему,
♫ » И не забудьте упростить,
Пока не пришло время прощаться «
Пример:
1 3 + 1 5
Опять же, нижние цифры разные (срезы разного размера)!
| 1 3 | + | 1 5 | = | ? | ||
Но давайте попробуем разделить их на меньшие размеры, чтобы каждый был одинаковым :
| 5 15 | + | 3 15 | ||||
Первая дробь: умножив верхнюю и нижнюю части на 5, мы получили 5 15 :
| × 5 |
| × 5 |
Вторая дробь: умножив верхнюю и нижнюю части на 3, мы получили 3 15 :
| × 3 |
| × 3 |
Нижние числа теперь те же, поэтому мы можем продолжить и сложить верхние числа:
| 5 15 | + | 3 15 | = | 8 15 | ||
Результат предельно прост, так что вот ответ: 8 15
1 3 + 1 5 знак равно 8 15
Делаем знаменатели одинаковыми
В предыдущем примере, как мы узнали, что нужно разрезать их на 1 / 15 тысяч, чтобы знаменатели совпадали? Мы просто умножили два знаменателя вместе (3 × 5 = 15).
Прочтите о двух основных способах сделать знаменатели одинаковыми здесь:
Они оба работают, используйте тот, который вам больше нравится!
Пример: кексы
Вы хотите приготовить и продать кексы:
- Друг может предоставить ингредиенты, если вы ему дадите 1 / 3 продаж
- А рыночный прилавок стоит 1 / 4 продаж
Сколько это всего?
Нам нужно добавить 1 / 3 и 1 / 4
Первые делают нижние числа (знаменатели) одинаковыми.
Умножить верхнюю и нижнюю часть 1 / 3 на 4 :
| 1 × 4 | + | 1 | = | ? |
| 3 × 4 | 4 | ? |
И умножьте верхнюю и нижнюю часть 1 / 4 на 3 :
| 1 × 4 | + | 1 × 3 | = | ? |
| 3 × 4 | 4 × 3 | ? |
Сейчас делаем расчеты:
| 4 | + | 3 | = | 4 + 3 | = | 7 |
| 12 | 12 | 12 | 12 |
Ответ: 7 12 продаж идет на ингредиенты и рыночные затраты.
Добавление смешанных фракций
У меня есть специальная (более продвинутая) страница по сложению смешанных дробей.
Порядок дробей | 3 класс
Порядок заказа дробей
На последнем уроке вы научились сравнивать дроби.
Давайте воспользуемся этим знанием, чтобы упорядочить, или отсортировать дроби. 👍
Сравнение фракций, обзор
Есть ярлыки для сравнения дробей с одинаковыми числителями и одинаковыми знаменателями.
Когда 2 дроби имеют одинаковый числитель , просто сравните знаменатели .
Чем больше знаменатель , тем меньше дробь .
Помните: Чем больше знаменатель, тем больше частей разбивается на части, поэтому каждая часть меньше.
Когда 2 дроби имеют одинаковый знаменатель , просто сравните числители .
Чем больше числитель , тем больше дробь .
Если у дробей разные числитель или знаменатель, найдите эквивалентных дробей , у которых один и тот же числитель или знаменатель.
Порядок дробей с одинаковыми числителями
Когда упорядочивает дроби с одинаковыми числителями , посмотрите на знаменатели и сравните их по 2 за раз.
👉 Дробь с наибольшим знаменателем является наименьшим .
👉 Дробь с наименьшим знаменателем является наибольшим .
Давайте посмотрим на пример.
Порядок этих дробей от минимум до наибольший :
У дробей одинаковые числители, поэтому вам просто нужно сравнить их знаменатели.
1/6 имеет наибольший знаменатель .
Это означает, что 1/6 — наименьшая дробь . 👍
1/4 имеет второй по величине знаменатель .
Это означает, что 1/4 больше 1/6 .👍
1/2 имеет наименьший знаменатель .
Это означает, что 1/2 — самая большая дробь . 👍
Мы переставили дроби с наименьшее на наибольшее .
1/6 — наименьшее, а 1/2 — наибольшее. 1/4 находится между ними.
Порядок дробей с одинаковыми знаменателями
Когда упорядочивает дроби с одинаковыми знаменателями , посмотрите на числители и сравните их по 2 за раз.
👉Дробь с наименьшим числителем является наименьшим .
👉Дробь с наибольшим числителем является наибольшим числом .
Учимся на примере.
Порядок этих дробей от минимум до наибольший :
У дробей одинаковые знаменатели, поэтому вам просто нужно сравнить их числители.
3/8 имеет наименьший числитель .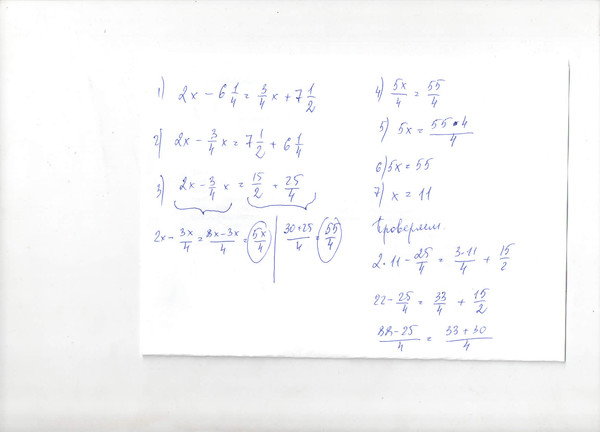
Это означает, что 3/8 — наименьшая дробь . 👍
5/8 имеет второй по величине числитель .
Это означает, что 5/8 больше, чем 3/8 . 👍
7/8 имеет самый большой числитель .
Это означает, что 7/8 — самая большая дробь . 👍
Вот как мы упорядочиваем эти дроби от наименьшего до наибольшего :
Порядок дробей с разными числителями и знаменателями
Когда упорядочивает дроби с различными числителями и знаменателями , запишите дроби как эквивалентных дробей с аналогичными знаменателями.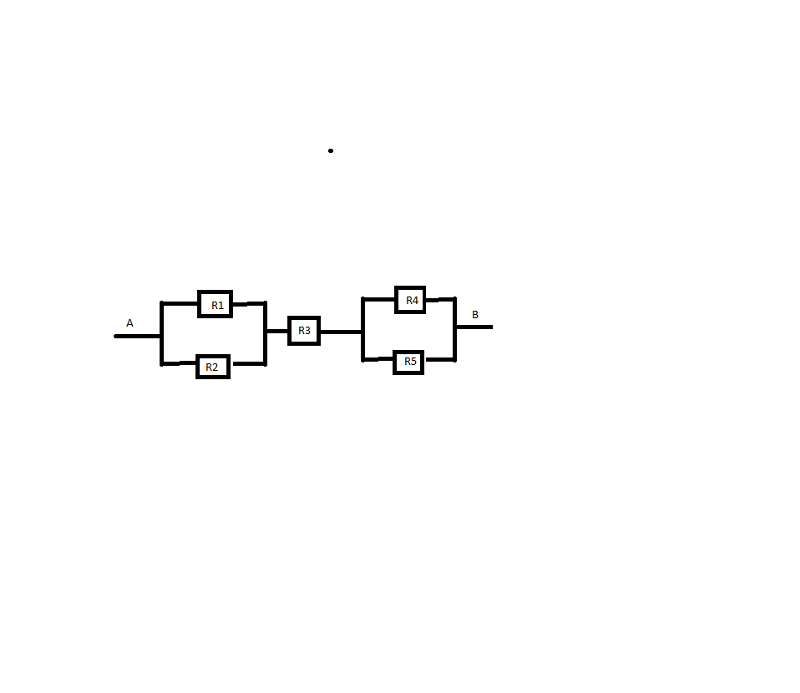
Совет: Как означает «то же самое» . В отличие от означает «другой».
Давайте посмотрим на пример.
Порядок этих дробей от минимум до наибольший :
👉 Сначала найдите эквивалентных дробей для каждой дроби, используя умножение .
👉 Затем выберите эквивалентные дроби, которые имеют одинаковые знаменатели для всех трех дробей.
Будьте осторожны при выборе эквивалентных дробей для сравнения!
Убедитесь, что все они имеют одинаковые знаменатели .
8/12 , 6/12 и 9/12 имеют одинаковые знаменатели.
Теперь, когда мы нашли эквивалентных дробей с совпадающими знаменателями , их легко сравнить!
Посмотрите на числители :
👉Дробь с наименьшим числителем является наименьшим .
👉Дробь с наибольшим числителем является наибольшим числом .
Можете ли вы расположить эти дроби от наименьшей к наибольшей? 🤔
Верно!
Если записать в порядке от минимум до наибольшее , у вас будет 6/12 < 8/12 < 9/12 .
Теперь мы знаем, что …
Отличная работа, научившись заказывать дроби!
Смотри и учись
youtube.com/embed/C1dGmnS7g-4″ frameborder=»0″/>Готовы ли вы попрактиковаться? 💪
фракций: сравнение и сокращение дробей
Урок 2: Сравнение и сокращение дробей
/ ru / fractions / Introduction-to-fractions / content /
Сравнение дробей
Во введении к дробям мы узнали, что дроби — это способ показать часть чего-либо.Дроби полезны, поскольку позволяют нам точно сказать, сколько у нас чего-то есть. Некоторые фракции больше других. Например, что больше: 6/8 пиццы или 7/8 пиццы?
На этом изображении мы видим, что 7/8 больше. Иллюстрация упрощает сравнение этих дробей. Но как бы мы могли это сделать без картинок?
Щелкните слайд-шоу, чтобы узнать, как сравнивать дроби.
Как вы видели, если у двух или более дробей один и тот же знаменатель, вы можете сравнить их, посмотрев на их числители. Как вы можете видеть ниже, 3/4 больше 1/4. Чем больше числитель, тем крупнее дробь.
Как вы можете видеть ниже, 3/4 больше 1/4. Чем больше числитель, тем крупнее дробь.
Сравнение дробей с разными знаменателями
На предыдущей странице мы сравнили дроби, которые имеют одинаковые нижние числа или знаменатели . Но вы знаете, что дроби могут иметь в знаменателе любое число . Что происходит, когда вам нужно сравнить дроби с разными нижними числами?
Например, что из них больше: 2/3 или 1/5? Сложно сказать, просто взглянув на них.В конце концов, 2 больше 1, но знаменатели не совпадают.
Однако если вы посмотрите на картинку, разница очевидна: 2/3 больше 1/5. С иллюстрацией было легко сравнить эти дроби, но как мы могли это сделать без картинки?
Щелкните слайд-шоу, чтобы узнать, как сравнивать дроби с разными знаменателями.
Сравним эти дроби: 5/8 и 4/6.
Прежде чем сравнивать их, нам нужно изменить обе дроби, чтобы они имели одинаковый знаменатель или нижнее число.

Сначала мы найдем наименьшее число, которое можно разделить на оба знаменателя. Мы называем это наименьшим общим знаменателем .
Нашим первым шагом является поиск чисел, которые можно равномерно разделить на 8.
Использование таблицы умножения упрощает эту задачу. Все числа в строке 8 можно разделить поровну на 8.
Теперь давайте посмотрим на наш второй знаменатель: 6.
Мы снова можем использовать таблицу умножения.Все числа в 6-й строке можно разделить поровну на 6.
Давайте сравним две строки. Похоже, есть несколько чисел, которые можно равномерно разделить как на 6, так и на 8.
24 — наименьшее число, которое появляется в обеих строках, поэтому это наименьший общий знаменатель .
Теперь мы собираемся изменить наши дроби, чтобы у них был один и тот же знаменатель: 24.
Для этого нам придется изменить числители так же, как мы изменили знаменатели.

Давайте снова посмотрим на 5/8. Чтобы изменить знаменатель на 24 …
Давайте снова посмотрим на 5/8. Чтобы изменить знаменатель на 24 … нам пришлось умножить 8 на 3.
Поскольку мы умножили знаменатель на 3, мы также умножим числитель или верхнее число на 3.
5 умножить на 3 равно 15. Итак, мы заменили 5/8 на 15/24.
Мы можем это сделать, потому что любое число над собой равно 1.
Итак, когда мы умножаем 5/8 на 3/3 …
Итак, когда мы умножаем 5/8 на 3/3 … мы действительно умножаем 5/8 на 1.
Поскольку любое число, умноженное на 1, равно самому себе …
Поскольку любое число, умноженное на 1, равно самому себе … мы можем сказать, что 5/8 равно 15/24.
Теперь сделаем то же самое с нашей другой дробью: 4/6. Мы также изменили его знаменатель на 24.
Наш старый знаменатель был равен 6.
 Чтобы получить 24, мы умножили 6 на 4.
Чтобы получить 24, мы умножили 6 на 4.Итак, мы также умножим числитель на 4.
4 умножить на 4 равно 16. Итак, 4/6 равно 16/24.
Теперь, когда знаменатели совпадают, мы можем сравнить две дроби, посмотрев на их числители.
16/24 больше 15/24 …
16/24 больше 15/24 … поэтому 4/6 больше 5/8.
Редукция
Что из них больше: 4/8 или 1/2?
Если вы посчитали или даже просто посмотрели на картинку, вы могли бы сказать, что они равны .Другими словами, 4/8 и 1/2 означают одно и то же, даже если они написаны по-разному.
Если 4/8 означает то же самое, что и 1/2, почему бы просто не назвать это так? Половина легче сказать, чем четыре восьмых , и для большинства людей это также легче понять. В конце концов, когда вы едите в ресторане с другом, вы делите счет на половину , а не на восьмых .
Если вы напишете 4/8 как 1/2, вы уменьшите . Когда мы уменьшаем на долю , мы записываем его в более простой форме.Уменьшенные дроби всегда равны , равным исходной дроби.
Мы уже уменьшили 4/8 до 1/2. Если вы посмотрите на примеры ниже, вы увидите, что другие числа также можно уменьшить до 1/2. Эти дроби все равны .
5/10 = 1/2
11/22 = 1/2
36/72 = 1/2
Все эти дроби также приведены к более простой форме.
4/12 = 1/3
14/21 = 2/3
35/50 = 7/10
Щелкните слайд-шоу, чтобы узнать, как уменьшить дроби на , разделив .
Попробуем уменьшить эту дробь: 16/20.
Поскольку числитель и знаменатель четных чисел , вы можете разделить их на 2, чтобы уменьшить дробь.
Сначала мы разделим числитель на 2.
 16, разделенное на 2, будет 8.
16, разделенное на 2, будет 8.Затем мы разделим знаменатель на 2. 20, разделенное на 2, будет равно 10.
We ‘ ve уменьшил 16/20 до 8/10. Можно также сказать, что 16/20 равно 8/10.
Если числитель и знаменатель все еще можно разделить на 2, мы можем продолжить сокращение дроби.
8 разделить на 2 равно 4.
10 разделить на 2 равно 5.
Поскольку нет числа, на которое можно разделить 4 и 5, мы не можем уменьшить 4/5 дальше.
Это означает, что 4/5 — это простейший из из 16/20.
Попробуем сократить еще одну дробь: 6/9.
Хотя числитель четный, знаменатель — нечетное число , поэтому мы не можем уменьшить его путем деления на 2.
Вместо этого нам нужно найти число, на которое можно разделить 6 и 9. Таблица умножения позволит легко найти это число.
Давайте найдем 6 и 9 на той же строке .
 Как видите, 6 и 9 можно разделить на 1 и 3.
Как видите, 6 и 9 можно разделить на 1 и 3.Деление на 1 не изменит эти дроби, поэтому мы будем использовать наибольшее число , на которое можно разделить 6 и 9.
Это 3. Это называется наибольшим общим делителем или GCD .(Вы также можете назвать его наибольшим общим делителем или GCF .)
3 — это GCD из 6 и 9, потому что это наибольшее число , на которое они могут быть разделены.
Итак, мы разделим числитель на 3. 6, разделив на 3, получим 2.
Затем мы разделим знаменатель на 3. 9, разделив на 3, получим 3.
Теперь мы уменьшил 6/9 до 2/3, что является его простейшей формой. Можно также сказать, что 6/9 равно 2/3.
Несводимые фракции
Не все дроби можно уменьшить. Некоторые уже настолько просты, насколько это возможно. Например, вы не можете уменьшить 1/2, потому что нет другого числа, кроме 1, на которое можно разделить 1 и 2. (По этой причине вы не можете уменьшить любую дробь с числителем 1.)
Например, вы не можете уменьшить 1/2, потому что нет другого числа, кроме 1, на которое можно разделить 1 и 2. (По этой причине вы не можете уменьшить любую дробь с числителем 1.)
Некоторые дроби с большими числами также не могут быть уменьшены. Например, 17/36 нельзя уменьшить, потому что нет числа, на которое можно разделить 17 и 36.Если вы не можете найти общих кратных для чисел в дроби, скорее всего, это несократимое .
Попробуй!
Уменьшите каждую дробь до ее простейшего вида.
Смешанные числа и неправильные дроби
На предыдущем уроке вы узнали о смешанных числах . Смешанное число состоит из дробной части и целого числа . Пример — 1 2/3. Вы бы прочитали 1 2/3 так: одна и две трети .
Другой способ записать это — 5/3, или пять третей . Эти два числа выглядят по-разному, но на самом деле они одинаковы. 5/3 — это неправильная дробь . Это просто означает, что числитель на больше, чем на знаменатель.
5/3 — это неправильная дробь . Это просто означает, что числитель на больше, чем на знаменатель.
Бывают случаи, когда вы можете предпочесть использовать неправильную дробь вместо смешанного числа. Смешанное число легко превратить в неправильную дробь. Давайте узнаем как:
Преобразуем 1 1/4 в неправильную дробь.
Во-первых, нам нужно выяснить, сколько частей составляют целое число: 1 в этом примере.
Для этого умножим целое число , 1 на знаменатель, 4.
, 1 умноженное на 4, равно 4.
Теперь добавим это число, 4, к числитель 1.
4 плюс 1 равно 5.
Знаменатель остается прежним.
Наша неправильная дробь — 5/4, или пять четвертей.Таким образом, можно сказать, что 1 1/4 равно 5/4.
Это означает, что пять 1/4 в 1 1/4.
Преобразуем другое смешанное число: 2 2/5.

Сначала умножим целое число на знаменатель. 2 умножить на 5 равно 10.
Затем мы добавим 10 в числитель. 10 плюс 2 равно 12.
Как всегда, знаменатель останется прежним.
Итак, 2 2/5 равно 12/5.
Попробуй!
Попробуйте преобразовать эти смешанные числа в неправильные дроби.
Преобразование неправильных дробей в смешанные числа
Неправильные дроби полезны для математических задач, в которых используются дроби, как вы узнаете позже. Однако их труднее читать и понимать, чем смешанных чисел . Например, гораздо легче представить себе в голове 2 4/7, чем 18/7.
Щелкните слайд-шоу, чтобы узнать, как преобразовать неправильную дробь в смешанное число.
Давайте превратим 10/4 в смешанное число.
Вы можете представить себе любую дробь как деление задачу .
 Просто относитесь к линии между числами как к знаку деления (/).
Просто относитесь к линии между числами как к знаку деления (/).Итак, мы разделим числитель, 10, на знаменатель, 4.
10 разделим на 4 равно 2 …
10 разделим на 4 равно 2 … остаток от 2.
Ответ 2 станет нашим целым числом, потому что 10 можно разделить на 4 дважды .
И остаток , 2 станет числителем дроби, потому что у нас осталось 2 части.
Знаменатель остается прежним.
Итак, 10/4 равно 2 2/4.
Давайте попробуем другой пример: 33/3.
Разделим числитель 33 на знаменатель 3.
33 разделим на 3 …
33 разделим на 3 … равно 11 без остатка.
Ответ, 11, станет нашим целым числом.
Остатка нет, поэтому мы можем видеть, что наша неправильная дробь на самом деле была целым числом. 33/3 равно 11.

Попробуй!
Попробуйте преобразовать эти неправильные дроби в смешанные числа.
/ ru / fractions / сложение-и-вычитание-фракции / content /
Использование моделей для представления дробей и смешанных чисел
Результаты обучения
- Запишите дроби, которые представляют части объектов
- Используйте дробные круги, чтобы получить целые числа
- Используйте модели для визуализации неправильных дробей и смешанных чисел.
Представление частей целого в виде дробей
Энди и Бобби любят пиццу. В понедельник вечером они делят пиццу поровну. Сколько пиццы получает каждый? Вы думаете, что каждый мальчик получает половину пиццы? Верно. Есть одна целая пицца, поровну разделенная на две части, поэтому каждому мальчику достается одна из двух равных частей.
В математике мы пишем [latex] \ frac {1} {2} [/ latex], чтобы обозначать одну из двух частей.
Во вторник Энди и Бобби делят пиццу со своими родителями, Фредом и Кристи, и каждый получает одинаковое количество всей пиццы. Сколько пиццы получает каждый человек? Есть одна целая пицца, поровну разделенная на четыре равные части. У каждого человека есть одна из четырех равных частей, поэтому у каждого есть [латекс] \ frac {1} {4} [/ latex] пиццы.
Сколько пиццы получает каждый человек? Есть одна целая пицца, поровну разделенная на четыре равные части. У каждого человека есть одна из четырех равных частей, поэтому у каждого есть [латекс] \ frac {1} {4} [/ latex] пиццы.
В среду семья приглашает друзей на ужин с пиццей. Всего [латексных] 12 [/ латексных] человек. Если они разделят пиццу поровну, каждый получит [латекс] \ frac {1} {12} [/ латекс] пиццы.
Фракции
Дробь записывается [latex] \ frac {a} {b} [/ latex], где [latex] a [/ latex] и [latex] b [/ latex] — целые числа, а [latex] b \ ne 0 [ /латекс].В дроби [латекс] a [/ латекс] называется числителем, а [латекс] b [/ латекс] — знаменателем.
Дробь — это способ представления частей целого. Знаменатель [латекс] b [/ латекс] представляет собой количество равных частей, на которые все было разделено, а числитель [латекс] a [/ латекс] представляет, сколько частей включено. Знаменатель [латекс] b [/ латекс] не может быть равен нулю, потому что деление на ноль не определено.
На изображении ниже круг разделен на три части равного размера.Каждая часть представляет собой [латекс] \ frac {1} {3} [/ латекс] круга. Такой тип модели называется дробным кругом. Другие формы, такие как прямоугольники, также могут использоваться для моделирования дробей.
Выполнение упражнения по манипуляции математикой Модель дробей поможет вам лучше понять дроби, их числители и знаменатели.
Что означает фракция [латекс] \ frac {2} {3} [/ latex]? Дробь [латекс] \ frac {2} {3} [/ latex] означает две из трех равных частей.
Пример
Назовите долю фигуры, заштрихованную на каждой фигуре.
Решение:
Нам нужно задать два вопроса. Во-первых, сколько там равных частей? Это будет знаменатель. Во-вторых, сколько из этих равных частей закрашены? Это будет числитель.
[латекс] \ begin {array} {cccc} \ text {Сколько там равных частей?} \ Hfill & & & \ text {Есть восемь равных частей} \ text {.} \ Hfill \\ \ text {Как многие закрашены?} \ hfill & & & \ text {Затенены пять частей} \ text {. } \ hfill \ end {array} [/ latex]
} \ hfill \ end {array} [/ latex]
Затенены пять из восьми частей.Следовательно, часть закрашенного круга равна [latex] \ frac {5} {8} [/ latex].
[латекс] \ begin {array} {cccc} \ text {Сколько там равных частей?} \ Hfill & & & \ text {Есть девять равных частей} \ text {.} \ Hfill \\ \ text {Как многие закрашены?} \ hfill & & & \ text {Затенены две части} \ text {.} \ hfill \ end {array} [/ latex]
Затенены две из девяти частей. Следовательно, доля затененного квадрата равна [latex] \ frac {2} {9} [/ latex].
Пример
Растушевка [латекс] \ frac {3} {4} [/ латекс] круга.
Показать решение Решение
Знаменатель [латекс] 4 [/ латекс], поэтому мы разделим круг на четыре равные части ⓐ.
В числителе [латекс] 3 [/ латекс], поэтому заштриховываем три из четырех частей ⓑ.
[латекс] \ frac {3} {4} [/ латекс] круга заштрихован.
Попробовать
Оттенок [латекс] \ frac {6} {8} [/ латекс] круга.
Заштрихуйте [латекс] \ frac {2} {5} [/ latex] прямоугольника.
Показать решениеПосмотрите следующее видео, чтобы увидеть больше примеров того, как записывать дроби с учетом модели.
В предыдущих примерах мы использовали круги и прямоугольники для моделирования дробей. Дроби также можно смоделировать как манипуляторы, называемые плитками с дробями, как показано на изображении ниже. Здесь все моделируется как одна длинная неразделенная прямоугольная плитка. Под ним находятся плитки одинаковой длины, разделенные на разное количество частей одинакового размера.
Мы будем использовать плитки с дробями, чтобы узнать некоторые основные факты о дробях. Обратитесь к плиткам с дробями выше, чтобы ответить на следующие вопросы:
 ) Сколько плиток [latex] \ frac {1} {24} [/ latex] нужно, чтобы сделать одну целую плитку?
) Сколько плиток [latex] \ frac {1} {24} [/ latex] нужно, чтобы сделать одну целую плитку? Требуется [латекс] 24 [/ латекс] двадцать четвертых, поэтому [латекс] \ frac {24} {24} = 1 [/ латекс].
Это приводит нас к собственности одного .
Собственность одного
Любое число, кроме нуля, деленное само на себя, равно единице.
[латекс] \ frac {a} {a} = 1 \ left (a \ ne 0 \ right) [/ latex]
Выполнение задания по манипуляции с математикой «Дроби, эквивалентные единице» поможет вам лучше понять дроби, эквивалентные единице.
Пример
Используйте круги с дробями, чтобы сделать целые, используя следующие детали:
- [латекс] 4 [/ латекс] четверть
- [латекс] 5 [/ латекс] пятый
- [латекс] 6 [/ латекс] шестой
Решение
Попробовать
Используйте дробные круги, чтобы сделать целые из следующих частей: [латекс] 3 [/ латекс] трети.
Используйте дробные круги, чтобы сделать целые части из следующих частей: [латекс] 8 [/ латекс] восьмых.
Показать решениеЧто делать, если у нас больше частей, чем нужно для [латекса] 1 [/ latex] целого? Мы рассмотрим это в следующем примере.
Пример
Используйте круги с дробями, чтобы сделать целые, используя следующие детали:
- [латекс] 3 [/ латекс] половинки
- [латекс] 8 [/ латекс] пятый
- [латекс] 7 [/ латекс] третей
Решение
1.[латекс] 3 [/ латекс] половинки делают [латекс] 1 [/ латекс] целым с оставшейся [латексной] 1 [/ латексной] половиной.
2. [латекс] 8 [/ латекс] пятых делают [латекс] 1 [/ латекс] целым с оставшимися [латексными] 2 [/ латексными] пятыми.
3. [латекс] 7 [/ латекс] трети составляют [латекс] 2 [/ латекс] целые с оставшимися [латексными] 2 [/ латексными] третями.
попробуйте
Используйте дробные круги, чтобы сделать целые из следующих частей: [латекс] 5 [/ латекс] трети.
Показать решениеИспользуйте дробные круги, чтобы сделать целые из следующих частей: [латекс] 5 [/ латекс] половинок.
Показать решениеМодель неправильных дробей и смешанных чисел
В предыдущем примере у вас было восемь равных пятых фишек. Вы использовали пять из них, чтобы сделать одно целое, и у вас осталось три пятых. Давайте воспользуемся дробным обозначением, чтобы показать, что произошло. У вас было восемь частей, каждая пятая, [латекс] \ frac {1} {5} [/ latex], итого у вас было восемь пятых, которые мы можем записать как [латекс] \ frac {8} {5} [/латекс]. Фракция [latex] \ frac {8} {5} [/ latex] составляет одно целое, [latex] 1 [/ latex], плюс три пятых, [latex] \ frac {3} {5} [/ latex], или [латекс] 1 \ frac {3} {5} [/ latex], что читается как одна и три пятых .
Число [латекс] 1 \ frac {3} {5} [/ latex] называется смешанным числом. Смешанное число состоит из целого числа и дроби.
Смешанные числа
Смешанное число состоит из целого числа [latex] a [/ latex] и дроби [latex] \ frac {b} {c} [/ latex], где [latex] c \ ne 0 [/ latex]. Написано это следующим образом.
[латекс] a \ frac {b} {c} \ text {,} c \ ne 0 [/ латекс]
Фракции, такие как [latex] \ frac {5} {4}, \ frac {3} {2}, \ frac {5} {5} [/ latex] и [latex] \ frac {7} {3} [/ latex] называются неправильными дробями.В неправильной дроби числитель больше или равен знаменателю, поэтому его значение больше или равно единице. Если числитель дроби меньше знаменателя, она называется правильной дробью, и ее значение меньше единицы. Такие дроби, как [latex] \ frac {1} {2}, \ frac {3} {7} [/ latex] и [latex] \ frac {11} {18} [/ latex], являются правильными дробями.
Правильные и неправильные дроби
Дробь [латекс] \ frac {a} {b} [/ latex] является правильной дробью, если [latex] a
Выполнение задания по манипуляции с математикой «Моделирование неправильных дробей» и «Смешанные числа» поможет вам лучше понять, как преобразовывать неправильные дроби в смешанные числа.
Пример
Назовите смоделированную неправильную дробь. Затем запишите неправильную дробь как смешанное число.
Решение:
Каждый круг разделен на три части, поэтому каждая часть представляет собой [латекс] \ frac {1} {3} [/ латекс] круга. Четыре части закрашены, поэтому есть четыре трети или [латекс] \ frac {4} {3} [/ latex].На рисунке показано, что у нас также есть один полный круг и одна треть, это [latex] 1 \ frac {1} {3} [/ latex]. Итак, [латекс] \ frac {4} {3} = 1 \ frac {1} {3} [/ latex].
Пример
Нарисуйте фигуру, чтобы смоделировать [латекс] \ frac {11} {8} [/ latex].
Показать решение Решение:
Знаменатель неправильной дроби — [латекс] 8 [/ латекс]. Нарисуйте круг, разделенный на восемь частей, и заштрихуйте их все. Это касается восьми восьмых, но у нас есть [латекс] 11 [/ латекс] восьмых.Мы должны заштриховать три из восьми частей другого круга.
Это касается восьми восьмых, но у нас есть [латекс] 11 [/ латекс] восьмых.Мы должны заштриховать три из восьми частей другого круга.
Итак, [латекс] \ frac {11} {8} = 1 \ frac {3} {8} [/ latex].
Попробовать
Нарисуйте фигуру, чтобы моделировать [латекс] \ frac {7} {6} [/ latex].
Показать решениеНарисуйте фигуру, чтобы моделировать [латекс] \ frac {6} {5} [/ latex].
Показать решениеПример
Используйте модель, чтобы переписать неправильную дробь [latex] \ frac {11} {6} [/ latex] как смешанное число.
Показать решение Решение:
Начнем с [latex] 11 [/ latex] шестых [latex] \ left (\ frac {11} {6} \ right) [/ latex]. Мы знаем, что шесть шестых составляют одно целое.
[латекс] \ frac {6} {6} = 1 [/ latex]
Остается еще пять шестых, то есть [латекс] \ frac {5} {6} \ left (11 \ text {шестые минус} 6 \ text {sixths is} 5 \ text {sixths} \ right) [/ latex].
Итак, [латекс] \ frac {11} {6} = 1 \ frac {5} {6} [/ latex].
В следующем видео мы покажем другой способ рисования модели, представляющей дробь.Вы увидите примеры правильных и неправильных дробей.
Пример
Используйте модель, чтобы переписать смешанное число [латекс] 1 \ frac {4} {5} [/ latex] как неправильную дробь.
Показать решение Решение:
Смешанное число [латекс] 1 \ frac {4} {5} [/ latex] означает одно целое плюс четыре пятых. Знаменатель — [латекс] 5 [/ латекс], поэтому все будет [латекс] \ frac {5} {5} [/ латекс]. Вместе пять пятых и четыре пятых равняются девяти пятым.
Итак, [латекс] 1 \ frac {4} {5} = \ frac {9} {5} [/ latex].
дробей, числовых строк и порядка
дробей, числовых строк и порядка Дроби, числовые строки и порядок
Что не так в следующем примере рекламного заявления?
Всего за один день сэкономьте , , и даже больше ‼! Это распродажа, которую нельзя пропустить ‼!
Каждое значение дроби меньше предыдущего значения, но окончание « и даже больше » означает, что значение каждой дроби становится больше. Утверждение — распространенная ошибка, которую допускают многие люди при использовании дробей. Здесь порядок дробей в утверждении основан на значении знаменателя, а не на истинном значении дроби. В выписке должно быть: Только за один день, за исключением , , и даже больше ‼! , поскольку реклама подразумевает, что на некоторых товарах человек может сэкономить более половины указанной цены.
Утверждение — распространенная ошибка, которую допускают многие люди при использовании дробей. Здесь порядок дробей в утверждении основан на значении знаменателя, а не на истинном значении дроби. В выписке должно быть: Только за один день, за исключением , , и даже больше ‼! , поскольку реклама подразумевает, что на некоторых товарах человек может сэкономить более половины указанной цены.
Мы используем модель числовой линии, чтобы проиллюстрировать порядок дроби для значений от 0 до 1.Мы делим эту длину на две части равного размера и помечаем точку, где сегмент делится, координатой. Расстояние от 0 до представляет собой длину половины всего сегмента от 0 до 1.
Далее мы делим каждую из этих половинок пополам; точки, в которых делится каждый сегмент, представлены дробями и. Как и в случае с эквивалентными дробями из предыдущего сеанса, мы можем пометить точку в как, то есть это еще один способ визуализировать эквивалентные дроби.
Следующие диаграммы иллюстрируют расширение отношений порядка дроби до двенадцатой, шестой, четвертой, трети и половины, а также то, как они соотносятся друг с другом в сегменте от 0 до 1.
Мы объединяем эти числовые линии на иллюстрации ниже в одну числовую линию с координатами, обозначенными в упрощенной форме для каждой дроби на иллюстрации выше.
Когда мы сравниваем значения, то самое левое в числовой строке имеет наименьшее значение.Глядя на диаграмму ниже, мы видим это (значения обведены). Точно так же мы видим это (значения в рамке).
Если бы мы не ссылались на завершенную числовую прямую, мы все равно могли бы определить эти неравенства, заменив каждую пару дробей на дроби с общими знаменателями .
Примеры:
Так как, и, у нас есть. Двенадцатые — это общий знаменатель для четвертей и третей.
Так как и у нас есть. Шестая часть — это общий знаменатель для половин и шестых.
Шестая часть — это общий знаменатель для половин и шестых.
Отметим также, что мы могли бы сравнить все четыре дроби,,, и, заменив их все на общий знаменатель , равный двенадцатым. Поскольку у нас есть. Преобразуя дробные значения в дроби с общими знаменателями, мы можем легко сравнивать их относительные размеры.
Обратите внимание, что наименьший общий знаменатель — это наименьшее общее кратное (НОК) 2, 3, 4 и 6.Значение НОК (2, 3, 4, 6) равно 12, как показано ниже, с заданным методом пересечения для поиска наименьшего общего кратного.
Напоминание: мы также можем найти наименьшее общее кратное (НОК) путем разложения на простые множители в экспоненциальную форму.
2 = 2 | Взяв наибольшую экспоненту каждого простого множителя, получаем 2 2 · 3 = 4 · 3 = 12. |
Пятеро студентов принесли противни с батончиками одинакового размера для продажи на распродаже выпечки. Все стержни были обрезаны до одинакового размера. К концу продажи были проданы три четверти батончиков Кэри, две трети батончиков Даны, половина батончиков Джейми, пять восьмых батончиков Линн и семь восьмых батончиков Терри. Чья тарелка слитков была продана в среднем?
Медиана набора дробей может быть найдена с помощью того же метода, который мы использовали для набора целых чисел.Помните, что медиану можно найти, сначала упорядочив набор значений, и что хороший метод упорядочения дробных значений — это переписать их с общим знаменателем.
Решение указанной выше проблемы: Сначала мы находим наименьший общий знаменатель, находя наименьшее общее кратное для 4, 3, 2, 6 и 8. Мы находим НОК методом разложения на простые множители.
Затем расположите дроби от наименьшей к наибольшей.
Среднее значение — это значение 3 rd . Возьмем самую простую форму, значит, есть медиана.
Мы обнаружили, что Кэри продал среднее количество баров.
Пример: Найдите среднее значение этого списка:
Решение: Сначала нам нужно отсортировать эти значения от наименьшего к наибольшему. Есть много способов сделать это. Мы могли бы использовать числовую строку, как на предыдущей странице. Здесь мы заменим все эти значения на общий знаменатель:
Теперь разместим их в порядке от наименьшего к наибольшему и выберем медиану.
Поскольку в списке 10 значений, нам нужно найти значение, которое находится посередине между значениями 5 -го и 6 -го . Итак, медиана есть.
Мы можем использовать гистограммы для решения некоторых типов проблем. Например, используйте гистограмму для решения следующей задачи:
У Мисси было 45 долларов. Она потратила своих денег на книгу. Сколько у нее осталось денег?
Она потратила своих денег на книгу. Сколько у нее осталось денег?
Решение: Ответ на вопрос «Сколько стоит 45 долларов?» дает нам сумму, которую она потратила.Сумма, которая у нее останется, будет суммой, оставшейся после того, как будет снята сумма, которую она потратила.
У нас есть эта 1 единица за 9 долларов. Итак, 2 единицы будут стоить 18 долларов, а 3 единицы — 27 долларов.
У Мисси осталось 27 долларов после того, как она потратила 18 долларов из своих 45 долларов.
Одним из способов оценки решений проблем, связанных с дробями, является использование 0, и 1 в качестве ключевых точек или якорей, чтобы помочь нам визуализировать относительный размер дробей между 0 и 1.Это хорошие ориентиры или ориентиры, которые следует учитывать при оценке решений.
Пример: ближе к 0, или 1?
Решение : Сначала мы замечаем, что это эквивалентно половине, поэтому оно больше по значению, чем. Затем мы замечаем, что числитель 5 максимально приближен к знаменателю 6, но не достигает. Итак, делаем вывод, что ближе к единице.
Затем мы замечаем, что числитель 5 максимально приближен к знаменателю 6, но не достигает. Итак, делаем вывод, что ближе к единице.
Пример: ближе к 0, или 1?
Решение: Сначала мы замечаем, что это эквивалентно.Делаем вывод, что немного больше половины.
Пример: Оцените значение суммы для.
Решение: Оцениваем значение суммы равным 3, т.к.
Обратите внимание, что символ ≈ означает , примерно равный . Этот символ следует использовать каждый раз, когда в ходе вычислений делается оценка или приближение.
Шутка или цитата
Порядок — это первый закон Небес.
Очерк о человеке IV — Папа, Александр (1688-1744 )


 Например:
Например:

 Промилле показывает массу алкоголя в 1000 мл крови. Например, 0,5-процентное опьянение означает, что в 1000 мл циркулирующей в организме крови содержится 0,5 г чистого алкоголя.
Промилле показывает массу алкоголя в 1000 мл крови. Например, 0,5-процентное опьянение означает, что в 1000 мл циркулирующей в организме крови содержится 0,5 г чистого алкоголя. Проверяйте трезвость алкометром!
Проверяйте трезвость алкометром!

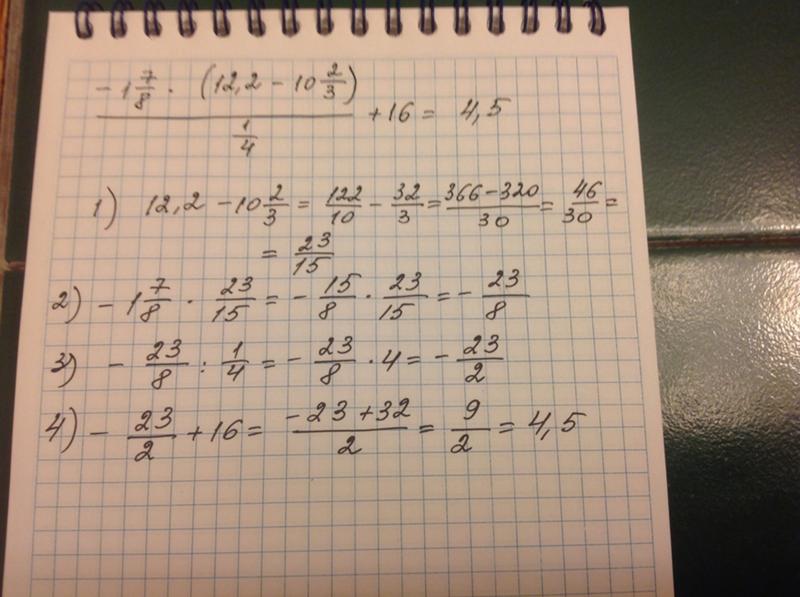 Чтобы получить 24, мы умножили 6 на 4.
Чтобы получить 24, мы умножили 6 на 4. 16, разделенное на 2, будет 8.
16, разделенное на 2, будет 8. Как видите, 6 и 9 можно разделить на 1 и 3.
Как видите, 6 и 9 можно разделить на 1 и 3.
 Просто относитесь к линии между числами как к знаку деления (/).
Просто относитесь к линии между числами как к знаку деления (/).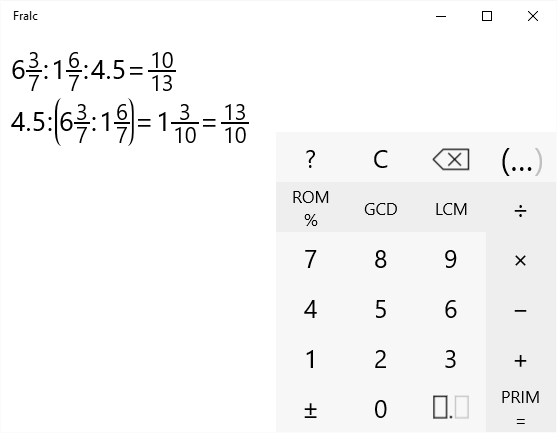
 Итак, LCM (2, 3, 4, 6) = 12.
Итак, LCM (2, 3, 4, 6) = 12.