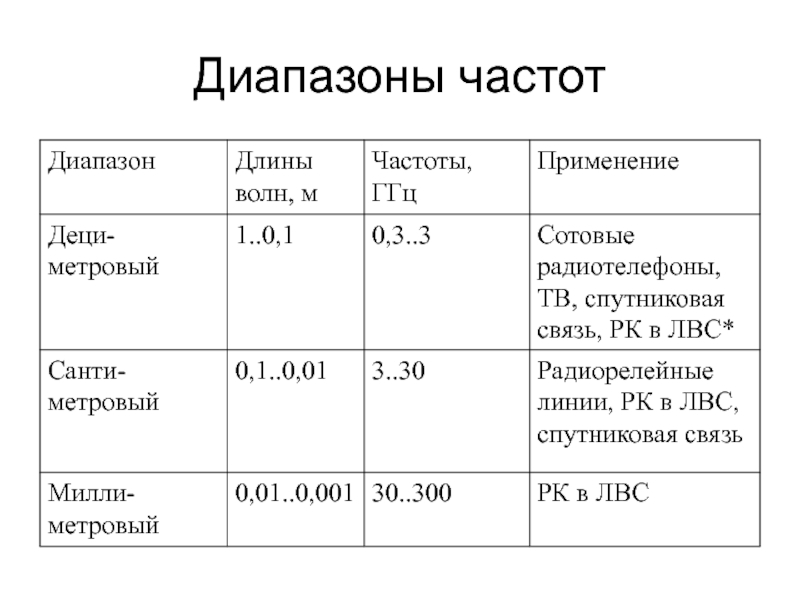
Что такое диапазон к: Недопустимое название — Викисловарь
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Комиссия по радиочастотам рассмотрит еще один диапазон для 5G в России
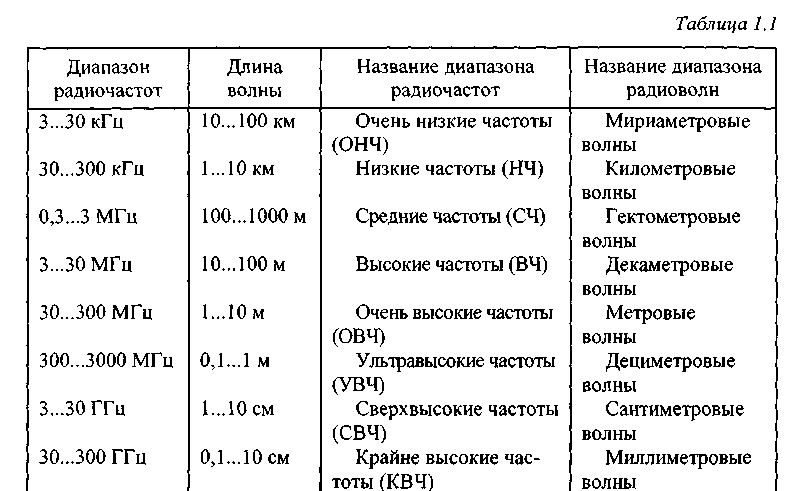
Российские операторы связи могут получить частоты еще в одном диапазоне для строительства сетей пятого поколения. В IV квартале 2021 г. Государственная комиссия по радиочастотам планирует рассмотреть результаты проведения научных, исследовательских, опытных, экспериментальных и конструкторских работ на пилотной зоне сетей 5G в диапазоне 6–7 ГГц. Это следует из протокола плана работы комиссии на следующий год (с копией документа ознакомились «Ведомости»).
В IV квартале 2021 г. Государственная комиссия по радиочастотам планирует рассмотреть результаты проведения научных, исследовательских, опытных, экспериментальных и конструкторских работ на пилотной зоне сетей 5G в диапазоне 6–7 ГГц. Это следует из протокола плана работы комиссии на следующий год (с копией документа ознакомились «Ведомости»).
К проведению исследований в указанном диапазоне планируется привлечь китайского производителя коммуникационного оборудования и электроники Huawei. Компания предоставит свое оборудование и специалистов, объяснил человек, близкий к Huawei.
В Минцифре отказались от комментариев.
Согласно протоколу, результаты исследований могут быть предложены Россией в качестве дополнительного радиочастотного спектра для сетей 5G на Всемирной конференции радиосвязи в 2023 г. (проводится раз в четыре года).
В подавляющем большинстве стран мира стандартом для 5G принят диапазон 3,4–3,8 ГГц. Он оптимален с точки зрения массового покрытия сетями 5G крупных городов, подтверждают представители операторов. Именно эти частоты обеспечивают высокие скорости передачи данных при относительно небольшом количестве базовых станций, на них ориентируются производители сетевого и абонентского оборудования. Однако в России эти частоты заняты спутниковой связью, которой пользуются госведомства, в том числе силовые структуры. Поэтому в России основным для 5G был выбран диапазон 4,4–4,9 ГГц.
Именно эти частоты обеспечивают высокие скорости передачи данных при относительно небольшом количестве базовых станций, на них ориентируются производители сетевого и абонентского оборудования. Однако в России эти частоты заняты спутниковой связью, которой пользуются госведомства, в том числе силовые структуры. Поэтому в России основным для 5G был выбран диапазон 4,4–4,9 ГГц.
Диапазон 4,4–4,9 ГГц не является глобально-гармонизированным, говорит представитель пресс-службы «Мегафона». О своих намерениях рассматривать его для 5G заявили в ходе Всемирной конференции радиосвязи 2019 г. только отдельные страны, в основном страны Африки и Юго-Восточной Азии, продолжает он. Однако до развертывания сетей дело не дошло, в этих странах, как и в Европе, массовые запуски проходят в основной полосе 3,4–3,8 ГГц, объясняет представитель оператора.
Диапазон 4,4–4,9 ГГц используется для работы воздушной и морской пограничных служб Эстонии, Латвии, Литвы и Польши, поэтому строительство базовых станций возможно лишь на удалении 300 км от сухопутной границы и 450 км – от морской. В эту зону попадает и Санкт-Петербург: расстояние от города до российско-эстонской границы составляет всего 134 км. Тестируемый диапазон 6–7 ГГц сможет обеспечить связь пятого поколения как раз в этих районах, объясняет человек, близкий к Huawei. Однако он также не сможет быть основным, поскольку дальность работы базовых станций в нем намного меньше, чем в диапазоне 3,4–3,8 ГГц, и меньше, чем в диапазоне 4,4–4,9 ГГц, а значит, станции нужно будет устанавливать еще чаще, что, в свою очередь, увеличивает стоимость развертывания сети, предупреждает человек, близкий к одному из крупных операторов связи.
В эту зону попадает и Санкт-Петербург: расстояние от города до российско-эстонской границы составляет всего 134 км. Тестируемый диапазон 6–7 ГГц сможет обеспечить связь пятого поколения как раз в этих районах, объясняет человек, близкий к Huawei. Однако он также не сможет быть основным, поскольку дальность работы базовых станций в нем намного меньше, чем в диапазоне 3,4–3,8 ГГц, и меньше, чем в диапазоне 4,4–4,9 ГГц, а значит, станции нужно будет устанавливать еще чаще, что, в свою очередь, увеличивает стоимость развертывания сети, предупреждает человек, близкий к одному из крупных операторов связи.
Сейчас в диапазоне 6–7 ГГц работают преимущественно средства фиксированной радиосвязи и радиорелейные линии связи (РРЛ), говорят представители «Мегафона» и Тele2. В США, например, диапазон 6 ГГц рассматривается американской Федеральной комиссией по связи (FCC) как стандарт для технологии WiFi 6, добавляет эксперт НИИ радио Евгений Девяткин.
Для работы мобильной связи он не выделялся, знают они. Международный союз электросвязи рассматривает диапазон 6–7 ГГц исключительно как полосу расширения для уже выделенных полос частот сетей мобильной связи поколений 2–5 G, говорит представитель «Мегафона». То, что регулятор задумывается о полосе 6425–7100 МГц, – положительная инициатива, но только на среднюю и дальнюю перспективу, рассуждает представитель Tele2 Дарья Колесникова. Единственное преимущество диапазона 6–7 ГГц – дополнительная емкость к 3,5 ГГц, но для полноценного запуска 5G в России он никак не может стать основным, подтверждает она.
Международный союз электросвязи рассматривает диапазон 6–7 ГГц исключительно как полосу расширения для уже выделенных полос частот сетей мобильной связи поколений 2–5 G, говорит представитель «Мегафона». То, что регулятор задумывается о полосе 6425–7100 МГц, – положительная инициатива, но только на среднюю и дальнюю перспективу, рассуждает представитель Tele2 Дарья Колесникова. Единственное преимущество диапазона 6–7 ГГц – дополнительная емкость к 3,5 ГГц, но для полноценного запуска 5G в России он никак не может стать основным, подтверждает она.
Что такое диапазон слуха?
Диапазон слышимости относится к различным частотам, которые могут быть услышаны людьми или животными. Частота, которую можно слышать, меняется на протяжении всей нашей жизни, и для измерения звуков, которые может слышать человек, используется тест, известный как аудиограмма. Существует значительная разница между диапазоном слуха людей и млекопитающих, что объясняет, почему люди не могут слышать звуки, издаваемые определенными животными.
Диапазон слышимости людей составляет от 20 до 20 000 герц (Гц). К тому времени, когда люди достигают подросткового возраста, этот верхний диапазон значительно снижается, при этом большая часть устного общения происходит между 200 и 8000 Гц. Частоты 1000–3500 Гц являются наиболее чувствительными для человеческого уха. Ультразвук относится к звукам выше диапазона слуха, в то время как звук ниже диапазона известен как инфразвук.
Аудиометр используется для проверки слуха людей. Эта часть оборудования позволяет субъекту слушать различные частоты через специальные наушники. Минимальная кривая слышимости используется для сравнения результатов теста. Эта кривая представляет обычный слуховой диапазон.
Альтернативным методом определения диапазона слуха человека является поведенческий тест на слух, известный как аудиометрия. Этот тест включает в себя диапазон тонов с определенной высотой и интенсивностью. Субъект поднимает руку в знак того, что услышал звук. Затем тестер записывает звук с наименьшей интенсивностью, который может слышать субъект.
Собаки имеют больший диапазон слуха, чем люди. Они могут слышать звуки от 40 до 60000 Гц. В зависимости от породы, уши собак имеют минимум 18 мышц, что позволяет им наклонять и вращать уши, чтобы усилить звук. Звуки, которые кажутся человеку громкими, пугают собак, которые хорошо реагируют на ультразвуковые сигналы во время тренировочных свистков. Домашние породы — идеальные сторожевые собаки, поскольку их диапазон слуха позволяет им ясно слышать злоумышленников.
Диапазон слуха мышей составляет от 1000 до 90000 Гц. Хотя они не могут слышать те же низкие частоты, что и люди, они могут общаться с помощью звуков, не слышимых человеку. Это также полезно, когда под атакой. Мыши могут послать предупреждающие звуки другим грызунам без слуха хищника.
У дельфинов-афалин есть диапазон слышимости от 250 до 150000 Гц. Однако дельфины по-разному общаются с другими морскими млекопитающими, такими как киты. В то время как киты используют сигналы и стоны низкой частоты, дельфины используют более высокие частоты щелчков и свистков.
ДРУГИЕ ЯЗЫКИ
Как рассчитать дальность: 4 шага (с иллюстрациями)
Об этой статье
В соавторстве:
Академический наставник
Эта статья была написана в соавторстве с Дэвидом Джиа. Дэвид Джиа — академический репетитор и основатель LA Math Tutoring, частной репетиторской компании, базирующейся в Лос-Анджелесе, Калифорния. Обладая более чем 10-летним опытом преподавания, Дэвид работает со студентами всех возрастов и классов по различным предметам, а также консультирует при поступлении в колледж и готовит к экзаменам SAT, ACT, ISEE и другим.Набрав 800 баллов по математике и 690 баллов по английскому языку на SAT, Дэвид получил стипендию Дикинсона в Университете Майами, где он получил степень бакалавра делового администрирования. Кроме того, Дэвид работал инструктором по онлайн-видео для таких компаний, выпускающих учебники, как Larson Texts, Big Ideas Learning и Big Ideas Math. Эта статья была просмотрена 343 548 раз.
Соавторы: 12
Обновлено: 11 февраля 2022 г.
Просмотров: 343 548
Резюме статьиX«Диапазон» — это термин, используемый в статистике для описания разницы между самым высоким и самым низким значениями в наборе данных.Чтобы рассчитать диапазон, перечислите все числа в вашем наборе данных по порядку. Затем определите самые высокие и самые низкие числа в наборе. Например, если ваш набор данных состоит из чисел 23, 40, 57 и 95, то наименьшее число будет 23, а наибольшее — 95. Затем вычтите наименьшее число из наибольшего, чтобы найти разницу. В этом случае 95-23 даст вам диапазон 72. Как только вы рассчитаете диапазон, не забудьте пометить его, чтобы избежать путаницы. Например, напишите R (или Range) = 72.Чтобы узнать, как упорядочение вашего множества может помочь вам найти другие вычисления, читайте дальше!
- Печать
- Отправить фанатскую почту авторам

Что такое диапазон в математике? — Определение и значение — Видео и стенограмма урока
Домен и диапазон
Вход и выход функции называются доменом и диапазоном функции. Домен относится к пластиковым блокам из приведенного выше примера, а диапазон будет созданными игрушками.2
Независимо от того, какое значение мы подставим вместо x , f( x ) всегда будет положительным, потому что любое число, умноженное само на себя, положительно.
Следовательно, мы бы сказали, что диапазон этой функции — все положительные числа.
Определение диапазона
Существует три способа определить диапазон функции: по значениям, по графику и по правилам.
Из значений
Функция может быть записана в виде списка значений
{(5,3), (2,7), (1,-3), (-2,9)}
Диапазон этой простой функции есть второе число из каждой пары, или список выходных значений.2, вы также использовали значения для определения диапазона. Хотя вы, возможно, не записали их, вы взяли конкретные числа и подставили их в функцию, чтобы получить представление о том, каким будет результат.
Хотя вы, возможно, не записали их, вы взяли конкретные числа и подставили их в функцию, чтобы получить представление о том, каким будет результат.
Из графика
При построении графика функции значения y обозначают диапазон этой функции. Часто можно определить диапазон, посмотрев на график.
Из этого графика видно, что диапазон функции находится между -1 и 1.2). Эта функция будет инвертирована из-за отрицательного знака и будет иметь диапазон, равный всем отрицательным числам.
Другими функциями, которые обычно подчиняются этим правилам, являются квадратный корень и абсолютные значения. Они также имеют диапазон, равный всем положительным числам. Просто обратите внимание на отрицательные знаки и другие включения, которые могут изменить диапазон.
Обозначение
Диапазон функции можно записать словами, но для большей математической корректности его следует записать в виде неравенства или с использованием интервальной записи. 2, записав диапазон в виде неравенства, вы должны иметь:
2, записав диапазон в виде неравенства, вы должны иметь:
y > 0, потому что y равно всем положительным числам.
На экране отображается диапазон, выраженный с использованием интервальной записи:
Давайте рассмотрим практическую задачу. Найдите диапазон следующей функции; дайте ответ словами, в виде неравенства и с использованием интервальной записи:
Диапазон этой функции находится между -1 и 1.
Записывается в виде неравенства:
Обозначение интервала = {-1, 1}
Резюме урока
Функция определяет определенное отношение между входом и выходом. Входы называются доменом , а выходы — диапазоном . Вы можете определить диапазон функции, введя значения, посмотрев на график или следуя определенным математическим правилам.
Диапазон | Специально создан для распределенных команд
Люди уже некоторое время работают в области командной координации и совместной работы.Наконец, Рейндж понял это правильно. Интеграция отличает Range от других и делает его бесценным инструментом для моей команды.
Интеграция Range в наш повседневный рабочий процесс была потрясающей. Это позволяет разговорам и встречам сосредоточиться на том, как люди работают, а не на том, над чем они работают.
Элиас Джулиан
Дизайнер продукта
Вопросы по построению команды дают нам возможность общаться на личном уровне. Они помогают нашим лидерам моделировать уязвимость и развивать эмпатию.
Используя Range, наша команда инженеров может сделать наши встречи эффективными и по-прежнему знать, что все делают. Кроме того, я могу легко видеть, кому нужна помощь, и проверять, как люди себя чувствуют.
Крис Тауэр
Вице-президент по проектированию
Решает все проблемы повседневного стояния. Легко отслеживать историю, общаться с коллегами и давать мне напоминания о будущих задачах.
Легко отслеживать историю, общаться с коллегами и давать мне напоминания о будущих задачах.
Даниэла Л.
Дизайнер продукта
С регистрацией Range не имеет значения, находимся ли мы в разных городах или странах, мы по-прежнему знаем, над чем работают друг друга, и план на день.
Габриэль Маркондес
Инженер
Флаги диапазона помогли моим командам быстрее выявлять и разблокировать блокираторы.
Kayla Roebuck
Scrum Master
С напоминанием Slack о регистрации каждое утро и цепочками сообщений команде было легко начать использовать Range.
Мерсер Боррис
Инженер-программист
С Range проще организовывать повторяющиеся групповые встречи, что означает, что они более эффективны и короче.
Адам Уитлок
Инженер по надежности сайта
Range стал незаменимым средством для повышения производительности, прозрачности, доверия и связанности.
Адам Ваксман
Директор по дизайну продукции
Ассортимент потрясающий. Они часто добавляют новые функции, дизайн и функциональность чрезвычайно интуитивно понятны, и у них отличное обслуживание клиентов. Они всегда ищут то, что пользователи хотят видеть в их продукте, и ясно, что они прислушиваются.
Они часто добавляют новые функции, дизайн и функциональность чрезвычайно интуитивно понятны, и у них отличное обслуживание клиентов. Они всегда ищут то, что пользователи хотят видеть в их продукте, и ясно, что они прислушиваются.
Кевин Э.
Специалист по маркетингу роста
Как рассчитать диапазоны: обзор статистики AP®
Статистика имеет привычку брать слова, которые мы знаем и любим, и превращать их во что-то совершенно другое. Возьмем, к примеру, диапазон. Хотя этот термин может напомнить вам старую мелодию «Дом на хребте», определение диапазона в математике включает в себя гораздо меньше оленей и антилоп. К счастью для вас, этот обзор AP® Statistics призван избавить вас от путаницы.Читайте дальше, чтобы узнать, что такое диапазон и почему он важен, как рассчитать диапазон и как ответить на вопросы, связанные с диапазоном, на экзамене AP® Stats. К концу этой статьи вы будете чувствовать себя на стрельбище как дома!
Что такое диапазон?
Ниже приведено изображение того, что вы можете себе представить, когда слышите слово «хребет» — широкий открытый участок земли. В некотором смысле можно установить связь со значением диапазона в математике: это протяженность вашего набора данных, расстояние от одной стороны вашего распределения до другой.Это описательная статистика , именно так она и звучит — она помогает описать форму распределения. В этом случае диапазон говорит нам, насколько широким или разбросанным является распределение. Точно так же, как это предпочитали на Диком Западе, диапазон — это простая идея, и вычислить диапазон так же просто. Что подводит нас прямо к следующему пункту…
В некотором смысле можно установить связь со значением диапазона в математике: это протяженность вашего набора данных, расстояние от одной стороны вашего распределения до другой.Это описательная статистика , именно так она и звучит — она помогает описать форму распределения. В этом случае диапазон говорит нам, насколько широким или разбросанным является распределение. Точно так же, как это предпочитали на Диком Западе, диапазон — это простая идея, и вычислить диапазон так же просто. Что подводит нас прямо к следующему пункту…
Как рассчитать диапазон
В своей самой простой форме диапазон — это просто числовое расстояние между наименьшим и наибольшим значениями в вашем распределении.На данный момент расчет, вероятно, очевиден: вы просто вычитаете наименьшее число из наибольшего! Просто для удовольствия, давайте попробуем пример. Допустим, у нас есть класс из 5 учеников, и их тест AP® Stats только что был возвращен.
| Студент 1 | Студент 2 | Студент 3 | Студент 4 | Студент 5 |
| 90% | 75% | 82% | 98% | 40% |
Первый шаг — определить наименьшее и самое большое значения — легко! Поскольку это так просто, мы могли бы упорядочить данные в числовом порядке, так как это может помочь нам позже, если мы захотим вычислить другие вещи, например медиану (см. наш пост о медиане для обзора этой концепции).
| Студент 5 | Студент 2 | Студент 3 | Студент 1 | Студент 4 |
| 40% | 75% | 82% | 90% | 98% |
Затем мы берем наше наибольшее значение и вычитаем наше наименьшее значение:
98 – 40 = 58
Итак, наш диапазон составляет 58%. Это так просто! На самом деле диапазон можно выразить и другим, еще более простым способом: от 40% до 98%.
Это так просто! На самом деле диапазон можно выразить и другим, еще более простым способом: от 40% до 98%.
В то время как первый метод более распространен, второй способ выражения диапазона полезен, когда задача также требует, чтобы вы знали точные значения конечных точек, а не только расстояние между ними. Какую версию вы используете, будет зависеть от проблемы.
Почему мы рассчитываем диапазон?
Как видите, диапазон дает нам представление о том, насколько распространено наше распределение.Различные показатели разброса, включая диапазон, называются в AP® Stats показателями «дисперсии». Термин дисперсия относится к тому, насколько ваши результаты отличаются от — все ли они довольно похожи и собраны вместе, или они сильно различаются? Давайте рассмотрим несколько примеров, чтобы лучше понять концепцию дисперсии.
Во-первых, представьте, что ваш класс проходит невероятно простой тест. Все в классе, вероятно, справятся очень хорошо. Очки могут выглядеть так:
Очки могут выглядеть так:
| Студент 1 | Студент 2 | Студент 3 | Студент 4 | Студент 5 |
| 98% | 100% | 99% | 100% | 97% |
В данном случае диапазон составляет 100 – 97 = 3.
Далее предположим, что те же учащиеся сдают другой чрезвычайно сложный тест, и все справляются плохо. Очки могут выглядеть так:
| Студент 1 | Студент 2 | Студент 3 | Студент 4 | Студент 5 |
| 65% | 67% | 66% | 67% | 64% |
Когда мы рассчитаем наш диапазон: 67 – 64 = 3.
Диапазон в обоих случаях одинаков, даже несмотря на то, что баллы сильно различаются! Это потому, что форма распределения не изменилась, она просто сместилась влево. Другими словами, диапазон отражает не 90 229 абсолютных 90 230 значений ваших баллов, а только 90 229 относительных 90 230 различий между ними. В обоих этих примерах баллы расположены близко друг к другу. Другой способ сказать, что это низкая дисперсия. И наоборот, в первом примере выше у нас были низкие и высокие оценки.В этом случае дисперсия намного больше. Изображение ниже иллюстрирует это: тощее распределение имеет низкую дисперсию (и, следовательно, небольшой диапазон), в то время как жирное распределение имеет высокую дисперсию (и большой диапазон).
Источник изображения: Wikimedia CommonsПроблемы с использованием стандартного диапазона
У каждой статистики есть свои плюсы и минусы – каждая полезна в одних ситуациях, но не в других. Например, в предыдущем посте мы обсуждали, как среднее значение зависит от экстремумов, поэтому мы можем захотеть использовать медиану в случаях, когда распределение асимметрично или имеет выбросы. Стандартный диапазон сталкивается с аналогичной проблемой. Рассмотрим следующее. Представьте ситуацию, аналогичную предыдущему примеру, в которой у нас есть очень сложный тест, и все 5 учащихся справляются с ним довольно плохо. Однако на этот раз предположим, что мы добавим шестого ученика, который отлично справился (мне попахивает мошенником…). Данные могут выглядеть так:
Стандартный диапазон сталкивается с аналогичной проблемой. Рассмотрим следующее. Представьте ситуацию, аналогичную предыдущему примеру, в которой у нас есть очень сложный тест, и все 5 учащихся справляются с ним довольно плохо. Однако на этот раз предположим, что мы добавим шестого ученика, который отлично справился (мне попахивает мошенником…). Данные могут выглядеть так:
| Студент 1 | Студент 2 | Студент 3 | Студент 4 | Студент 5 | Студент 6 |
| 65% | 67% | 66% | 67% | 64% | 100% |
Затем вычисляем диапазон: 100 – 64 = 36.
С добавлением этого единственного выброса диапазон подскочил с 3% до 36%! Это новое число является очень плохим индикатором разницы в наших оценках. Если бы мы смотрели только на это число, мы бы ожидали, что оценки будут довольно разбросанными. Тем не менее, 5 из 6 баллов по-прежнему расположены близко друг к другу, и только один находится далеко друг от друга. Этот пример иллюстрирует, как выбросы влияют на диапазон.
Если бы мы смотрели только на это число, мы бы ожидали, что оценки будут довольно разбросанными. Тем не менее, 5 из 6 баллов по-прежнему расположены близко друг к другу, и только один находится далеко друг от друга. Этот пример иллюстрирует, как выбросы влияют на диапазон.
Введите межквартильный диапазон (IQR)
Вот где в игру вступает межквартильный диапазон.IQR — это когда вы берете диапазон, но игнорируете верхние 25% и нижние 25% данных, чтобы исключить любые выбросы. В результате он идентифицирует средние 50% вашего набора данных и может предоставить лучшее описание дисперсии ваших данных.
Источник изображения: Wikimedia CommonsКогда вы слышите «квартили», подумайте о «четвертях» или делении баллов на четыре равные части. Вы выполняете этот процесс, используя ту же технику, которую мы использовали для нахождения медианы. Вот шаги, как рассчитать межквартильный размах:
• Расположите данные в порядке номеров.
• Найдите медиану (которая также { Q }_{ 2 }) — теперь ваши данные разделены пополам
• Найти «медиану» для каждой из половин ({Q}_{1} и {Q}_{3})
• IQR — это диапазон между { Q }_{ 1 } и { Q }_{ 3 } — просто вычтите меньшее из большего, как мы делали раньше.
Разделительные линии ваших квартилей называются {Q}_{1}, {Q}_{2} и {Q}_{3}. Сначала может показаться странным, что их всего 3, но представьте, что вы берете небольшую веревку и разрезаете ее на 4 части.Сколько разрезов вам придется сделать? Только 3, так как в результате последнего разреза получится 2 куска.
Давайте попробуем это на конкретном примере. На этот раз мы будем использовать 11 студентов, чтобы упростить математику. Ниже представлены результаты тестов 11 учеников.
| Студент 1 | Студент 2 | Студент 3 | Студент 4 | Студент 5 | Студент 6 | Студент 7 | Студент 8 | Студент 9 | Студент 10 | Студент 11 |
| 70% | 98% | 67% | 82% | 100% | 85% | 79% | 89% | 87% | 84% | 86% |
Во-первых, мы переставляем данные в числовом порядке:
| Студент 3 | Студент 1 | Студент 7 | Студент 4 | Студент 10 | Студент 6 | Студент 11 | Студент 9 | Студент 8 | Студент 2 | Студент 5 |
| 67 | 70 | 79 | 82 | 84 | 85 | 86 | 87 | 89 | 98 | 100 |
Затем мы находим медиану, а также {Q}_{1} и {Q}_{3}.
| Студент 3 | Студент 1 | Студент 7 | Студент 4 | Студент 10 | Студент 6 | Студент 11 | Студент 9 | Студент 8 | Студент 2 | Студент 5 |
| 67 | 70 | 79 | 82 | 84 | 85 | 86 | 87 | 89 | 98 | 100 |
Как видите, { Q }_{ 2 } — это значение прямо посередине, а { Q }_{ 1 } и { Q }_{ 3 } — значения посередине соответствующих половин. .Теперь IQR — это просто диапазон от {Q}_{1} до {Q}_{3}.
.Теперь IQR — это просто диапазон от {Q}_{1} до {Q}_{3}.
89 – 79 = 10
В этом примере большинство баллов находится в диапазоне 79-89%, но пара студентов получила гораздо более низкие баллы, а пара — намного более высокие. Эти оценки являются выбросами и расширили бы наш диапазон, чтобы он был намного больше. В результате IQR дает более точную картину наших данных в этом случае.
В приведенном выше примере было легко найти квартили, но что, если наши данные не делятся легко? Например, представьте, что у нас снова есть 5 точек данных.
| Студент 5 | Студент 2 | Студент 3 | Студент 1 | Студент 4 |
| 40 | 75 | 82 | 90 | 98 |
В этом случае медиану найти несложно, но наши { Q }_{ 1 } и { Q }_{ 3 } попадут между двумя значениями. Чтобы обойти это, мы используем ту же логику, что и в случае с медианой — вы просто находите число, которое находится непосредственно между этими значениями, взяв среднее значение.
Чтобы обойти это, мы используем ту же логику, что и в случае с медианой — вы просто находите число, которое находится непосредственно между этими значениями, взяв среднее значение.
\dfrac{40+75}{2}=57,5.
{ Q }_{ 3 } находится между двумя последними значениями, поэтому:\dfrac{90+98}{2}=94.
Тогда наш IQR равен
{Q}_{3} – {Q}_{1}: 94 – 57,5 = 36,5.
Использование диапазонов на экзамене AP® Statistics
Наиболее распространенной причиной расчета диапазона на экзамене AP® Stats является ящичковая диаграмма, также известная как диаграмма «ящик и стержень» (см. пример на изображении выше).Блочные диаграммы дают подробное описание ваших данных, поскольку они включают несколько различных значений: стандартный диапазон, IQR и медиану. «Прямоугольник» представляет IQR, линия в центре прямоугольника представляет собой медиану, а «стебли» представляют собой полный диапазон. Это представление позволяет зрителю получить точную картину дисперсии, а также выбросов и обеспечивает меру центрального значения.
Это представление позволяет зрителю получить точную картину дисперсии, а также выбросов и обеспечивает меру центрального значения.
Из этого обзора AP® Stats вы теперь знаете, что такое диапазон, как рассчитывать диапазоны и IQR, почему они важны и как их использовать на экзамене AP®! К этому моменту вы должны иметь представление об основных методах описания распределений, включая показатели центральной тенденции и дисперсии.Закрепив эти основополагающие концепции, вы заложили основу для остальной части статистики AP®!
Хотите узнать больше о статистике AP®?Ознакомьтесь с другими нашими статьями о статистике AP® .
Вы также можете найти тысячи практических вопросов на Albert.io. Albert.io позволяет вам настроить учебный процесс так, чтобы он ориентировался на практику, в которой вам больше всего нужна помощь. Мы дадим вам сложные практические вопросы, которые помогут вам освоить статистику AP®.
Начните тренироваться здесь .
Вы учитель или администратор, заинтересованный в повышении успеваемости учащихся AP® Statistics?
Узнайте больше о наших школьных лицензиях здесь .
Меры дисперсии
J Pharmacol Pharmacother. 2011 г., октябрь-декабрь; 2(4): 315–316.
С. Маникандан
Помощник редактора, JPP
Помощник редактора, JPP
Адрес для корреспонденции: S.Маникандан, кафедра фармакологии, Медицинский колледж Индиры Ганди и больница научно-исследовательского института, Кадиркамам, Пондичерри, Индия. Электронная почта: moc.liamg@100nadnakinamsrdАвторское право: © Журнал фармакологии и фармакотерапии Это статья с открытым доступом, распространяемая в соответствии с условиями Creative Commons Attribution-Noncommercial-Share Alike 3.0 Unported, что разрешает неограниченное использование, распространение и воспроизведение. на любом носителе при условии правильного цитирования оригинальной работы.
ВВЕДЕНИЕ
Меры центральной тенденции неадекватны для описания данных. Два набора данных могут иметь одно и то же среднее значение, но они могут быть совершенно разными. Таким образом, для описания данных необходимо знать степень изменчивости. Это определяется мерами рассеивания. Размах, межквартильный размах и стандартное отклонение — три обычно используемые меры дисперсии.
ДИАПАЗОН
Диапазон — это разница между самым большим и самым маленьким наблюдениями в данных.Основное преимущество этой меры дисперсии состоит в том, что ее легко вычислить. С другой стороны, у него много недостатков. Он очень чувствителен к выбросам и не использует все наблюдения в наборе данных.[1] Более информативно указывать минимальное и максимальное значения, а не диапазон.
МЕЖКВАРТИЛЬНЫЙ ДИАПАЗОН
Межквартильный диапазон определяется как разница между 25 и 75 процентилями (также называемыми первым и третьим квартилем). Следовательно, межквартильный диапазон описывает средние 50% наблюдений. Если межквартильный размах большой, это означает, что средние 50% наблюдений разнесены далеко друг от друга. Важным преимуществом межквартильного диапазона является то, что его можно использовать в качестве меры изменчивости, если крайние значения не регистрируются точно (как в случае открытых интервалов классов в частотном распределении).[2] Другая выгодная особенность заключается в том, что на него не влияют экстремальные значения. Основным недостатком использования межквартильного диапазона в качестве меры дисперсии является то, что он не поддается математическим манипуляциям.
Следовательно, межквартильный диапазон описывает средние 50% наблюдений. Если межквартильный размах большой, это означает, что средние 50% наблюдений разнесены далеко друг от друга. Важным преимуществом межквартильного диапазона является то, что его можно использовать в качестве меры изменчивости, если крайние значения не регистрируются точно (как в случае открытых интервалов классов в частотном распределении).[2] Другая выгодная особенность заключается в том, что на него не влияют экстремальные значения. Основным недостатком использования межквартильного диапазона в качестве меры дисперсии является то, что он не поддается математическим манипуляциям.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ
Стандартное отклонение (SD) является наиболее часто используемой мерой дисперсии. Это мера разброса данных о среднем значении. SD представляет собой квадратный корень из суммы квадратов отклонений от среднего, деленный на количество наблюдений.
Эта формула является определяющей и для расчетов используется более простая формула. Вычислительная формула также позволяет избежать ошибок округления при расчете.
Вычислительная формула также позволяет избежать ошибок округления при расчете.
В обеих этих формулах n — 1 используется вместо n в знаменателе, так как это дает более точную оценку SD населения.
Причина, по которой стандартное отклонение является очень полезной мерой дисперсии, заключается в том, что если наблюдения относятся к нормальному распределению, то [3] 68% наблюдений лежат между средним значением ± 1 стандартное отклонение 95% наблюдений лежат между средним значением ± 2 стандартного отклонения и 99,7% наблюдений лежат между средним значением ± 3 SD
Другим преимуществом SD является то, что наряду со средним значением его можно использовать для обнаружения асимметрии. Недостаток стандартного отклонения в том, что это неподходящая мера дисперсии искаженных данных.
НАДЛЕЖАЩЕЕ ИСПОЛЬЗОВАНИЕ МЕР РАСПРЕДЕЛЕНИЯ
Стандартное отклонение используется в качестве меры дисперсии, когда среднее значение используется как мера центральной тенденции (т. е. для симметричных числовых данных).
е. для симметричных числовых данных).
Сноски
Источник поддержки: Нет
Конфликт интересов: Не объявлено.
ССЫЛКИ
1. Swinscow TD, Campbell MJ. (индийский) 10-е изд. Нью-Дели: Viva Books Private Limited; 2003. Статистика с нуля. [Google Академия]2. Сундарам К.Р., Двиведи С.Н., Шринивас В. 1-е изд. Нью-Дели: B.I Publications Pvt Ltd; 2010. Принципы и методы медицинской статистики. [Google Академия]3. Граветтер Ф.Дж., Валлнау Л.Б. 5-е изд. Бельмонт: Уодсворт – Обучение Томсона; 2000.Статистика для поведенческих наук. [Google Академия]4. Доусон Б., Трапп Р.Г. 4-е изд. Нью-Йорк: Мак-Гроу Хилл; 2004. Базовая и клиническая биостатистика. [Google Scholar]математических функций и отношений, чем они отличаются и как найти домен и диапазон.
Итак, что такое «отношение»?
В математике отношение — это просто набор упорядоченных пар.
Примечание: {} — это символ «набора»
. Некоторые примеры отношений включают
Некоторые примеры отношений включают- {(0, 1) , (55, 22), (3, -50)}
- {(0, 1), (5, 2), (-3, 9)}
- {(-1, 7), (1, 7), (33, 7), (32, 7)}
- {(-1, 7)}
- {3, 1, 2}
- {(0, 1, 2), (3,4,5)} (эти числа сгруппированы по 3, поэтому не упорядочены и, следовательно, не являются отношениями)
- {-1, 7, 3,4,5,5}
Еще раз: Отношение — это просто набор упорядоченных пар.Нет абсолютно ничего особенного в числах, которые находятся в отношении. Другими словами, любая группа чисел является отношением, если эти числа идут парами.
Что делает отношение
функцией ? Функции представляют собой особый вид отношений.
На первый взгляд функция выглядит как отношение.
ОтветВ математике функция отличается от отношения тем, что каждое значение x в функции имеет одно и только ОДНО значение y.
Поскольку отношение #1 имеет ТОЛЬКО ОДНО значение y для каждого значения x, это отношение является функцией.
С другой стороны, отношение #2 имеет ДВА различных значения y ‘a’ и ‘c’ для одного и того же значения x ‘5’ .Следовательно, отношение № 2 не удовлетворяет определению математической функции.
У учителей несколько учеников
Если мы поместим учителей в домен, а учеников в диапазон, мы получим функцию , а не , потому что у одного и того же учителя, как у мистера Джино ниже, есть более 1 ученика в классе.
Аналогия матерей и дочерей
Чтобы попытаться понять эту концепцию, нужно подумать о том, как матери и их дочери могут быть представлены как функция.
Каждый элемент домена, каждая дочь , может иметь только 1 мать (элемент в диапазоне).
Некоторым людям полезно думать о домене и диапазоне как о людях, состоящих в романтических отношениях. Если каждое число в домене является человеком, а каждое число в диапазоне — другим человеком, то функция — это когда у всех людей в домене есть 1 и только 1 парень/девушка в диапазоне.
Сравните два отношения ниже. Они отличаются всего одним числом, но только одно из них является функцией.
Как это сделать проще всего?
Найдите повторяющихся элементов в домене . Как только элемент в домене повторяется, будьте осторожны!
Функция ВПР
Совет: Попробуйте использовать новую функцию XLOOKUP, улучшенную версию VLOOKUP, которая работает в любом направлении и возвращает точные совпадения по умолчанию, что делает ее более простой и удобной в использовании, чем ее предшественница.
Используйте функцию ВПР, когда вам нужно найти что-то в таблице или диапазоне по строке. Например, найдите цену автомобильной детали по номеру детали или найдите имя сотрудника на основе его идентификатора сотрудника.
В простейшей форме функция ВПР говорит:
=ВПР(Что вы хотите найти, где вы хотите это найти, номер столбца в диапазоне, содержащем возвращаемое значение, возвращает приблизительное или точное совпадение – указывается как 1/ИСТИНА или 0/ЛОЖЬ).
Совет: Секрет ВПР заключается в организации данных таким образом, чтобы искомое значение (фрукты) находилось слева от возвращаемого значения (количество), которое вы хотите найти.
Технические характеристики
Используйте функцию ВПР для поиска значения в таблице.
Синтаксис
ВПР (искомое_значение, массив_таблиц, номер_индекса_столбца, [диапазон_просмотра])
Например:
=ВПР(A2,A10:C20,2,ИСТИНА)
=ВПР(«Фонтана»,B2:E7,2,ЛОЖЬ)
=ВПР(A2,’Сведения о клиенте’!A:F,3,ЛОЖЬ)
Имя аргумента | Описание |
|---|---|
искомое_значение (обязательно) | Значение, которое вы хотите найти. Например, если таблица-массив охватывает ячейки B2:D7, то искомое_значение должно находиться в столбце B. Искомое_значение может быть значением или ссылкой на ячейку. |
table_array (обязательно) | Диапазон ячеек, в котором ВПР будет искать искомое_значение и возвращаемое значение. Вы можете использовать именованный диапазон или таблицу, а также имена в аргументах вместо ссылок на ячейки. Первый столбец в диапазоне ячеек должен содержать искомое_значение . Узнайте, как выбирать диапазоны на листе. |
col_index_num (обязательно) | Номер столбца (начиная с 1 для крайнего левого столбца table_array ), который содержит возвращаемое значение. |
range_lookup (необязательно) | Логическое значение, указывающее, хотите ли вы, чтобы VLOOKUP находил приблизительное или точное совпадение:
|
Как начать
Для построения синтаксиса ВПР вам понадобятся четыре элемента информации:
Значение, которое вы хотите найти, также называемое искомым значением.
Диапазон, в котором находится искомое значение. Помните, что значение поиска всегда должно быть в первом столбце диапазона, чтобы функция ВПР работала правильно. Например, если искомое значение находится в ячейке C2, диапазон должен начинаться с C.
.Номер столбца в диапазоне, который содержит возвращаемое значение.
 Например, если вы укажете диапазон B2:D11, вы должны считать B первым столбцом, C вторым и так далее.
Например, если вы укажете диапазон B2:D11, вы должны считать B первым столбцом, C вторым и так далее.Дополнительно можно указать TRUE, если требуется приблизительное соответствие, или FALSE, если требуется точное соответствие возвращаемого значения. Если вы ничего не укажете, значением по умолчанию всегда будет TRUE или приблизительное совпадение.
Теперь соберите все вышеперечисленное вместе следующим образом:
=ВПР(искомое значение, диапазон, содержащий искомое значение, номер столбца в диапазоне, содержащем возвращаемое значение, приблизительное совпадение (ИСТИНА) или точное совпадение (ЛОЖЬ)).
Примеры
Вот несколько примеров ВПР:
Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
Объединение данных из нескольких таблиц на один рабочий лист с помощью функции ВПР
Вы можете использовать функцию ВПР для объединения нескольких таблиц в одну, если одна из таблиц имеет общие поля со всеми остальными. Это может быть особенно полезно, если вам нужно поделиться книгой с людьми, у которых есть более старые версии Excel, которые не поддерживают функции данных с несколькими таблицами в качестве источников данных — путем объединения источников в одну таблицу и изменения источника данных функции данных на новая таблица, функция данных может использоваться в более старых версиях Excel (при условии, что сама функция данных поддерживается более старой версией).
Это может быть особенно полезно, если вам нужно поделиться книгой с людьми, у которых есть более старые версии Excel, которые не поддерживают функции данных с несколькими таблицами в качестве источников данных — путем объединения источников в одну таблицу и изменения источника данных функции данных на новая таблица, функция данных может использоваться в более старых версиях Excel (при условии, что сама функция данных поддерживается более старой версией).
Здесь столбцы A–F и H содержат значения или формулы, которые используют только значения на листе, а остальные столбцы используют функцию ВПР и значения столбца A (код клиента) и столбца B (поверенный) для получения данных из других таблиц. |
Скопируйте таблицу с общими полями на новый лист и дайте ей имя.
Щелкните Данные > Инструменты обработки данных > Отношения , чтобы открыть диалоговое окно Управление отношениями.

Для каждой из перечисленных взаимосвязей обратите внимание на следующее:
Поле, связывающее таблицы (указано в скобках в диалоговом окне).Это lookup_value для вашей формулы ВПР.
Имя связанной таблицы поиска. Это table_array в вашей формуле ВПР.
Поле (столбец) в связанной таблице поиска, которое содержит данные, которые вы хотите добавить в новый столбец. Эта информация не отображается в диалоговом окне «Управление отношениями» — вам придется просмотреть связанную таблицу поиска, чтобы увидеть, какое поле вы хотите получить.Вы хотите отметить номер столбца (A = 1) — это col_index_num в вашей формуле.
Чтобы добавить поле в новую таблицу, введите формулу ВПР в первый пустой столбец, используя информацию, полученную на шаге 3.

В нашем примере столбец G использует Attorney ( lookup_value ) для получения данных Bill Rate из четвертого столбца ( col_index_num = 4) из таблицы Attorneys worksheet, tblAttorneys ( 9 table) ) по формуле =ВПР([@Attorney],tbl_Attorneys,4,FALSE) .
Формула также может использовать ссылку на ячейку и ссылку на диапазон. В нашем примере это будет =ВПР(A2,’Адвокаты’!A:D,4,FALSE ).
Продолжайте добавлять поля, пока не получите все необходимые поля. Если вы пытаетесь подготовить книгу, содержащую функции данных, которые используют несколько таблиц, измените источник данных функции данных на новую таблицу.
Общие проблемы
Проблема | Что пошло не так |
|---|---|
Возвращено неверное значение | Если range_lookup имеет значение TRUE или опущено, первый столбец необходимо отсортировать по алфавиту или по номерам. |
#Н/Д в ячейке |
Дополнительные сведения об устранении ошибок #Н/Д в функции ВПР см. в разделе Как исправить ошибку #Н/Д в функции ВПР. |
#ССЫЛКА! в ячейке | Если col_index_num больше, чем количество столбцов в table-array , вы получите #REF! значение ошибки. Для получения дополнительной информации о разрешении ошибки #REF! ошибки в функции ВПР см. Как исправить ошибку #ССЫЛКА! ошибка. |
#ЗНАЧ! в ячейке | Если table_array меньше 1, вы получите ошибку #ЗНАЧ! значение ошибки. Дополнительные сведения об устранении ошибки #VALUE! ошибки в ВПР, см. Как исправить ошибку #ЗНАЧ! ошибка в функции ВПР. |
#ИМЯ? в ячейке | #ИМЯ? значение ошибки обычно означает, что в формуле отсутствуют кавычки. Чтобы найти имя человека, убедитесь, что вы используете кавычки вокруг имени в формуле. Например, введите имя «Фонтана» в =ВПР(«Фонтана»,B2:E7,2,ЛОЖЬ). Дополнительные сведения см. |
#РАЗЛИВ! в ячейке | Этот конкретный #РАЗЛИВ! ошибка обычно означает, что ваша формула полагается на неявное пересечение для значения поиска и использует весь столбец в качестве ссылки. Например, =ВПР( A:A ,A:C,2,ЛОЖЬ). Вы можете решить эту проблему, привязав ссылку поиска с помощью оператора @ следующим образом: =ВПР( @A:A ,A:C,2,FALSE).Кроме того, вы можете использовать традиционный метод ВПР и обратиться к одной ячейке, а не ко всему столбцу: = ВПР( A2 ,A:C,2,FALSE). |
Лучшие практики
Сделай это | Почему |
|---|---|
Использовать абсолютные ссылки для range_lookup | Использование абсолютных ссылок позволяет заполнить формулу так, чтобы она всегда обращалась к одному и тому же точному диапазону поиска. Узнайте, как использовать абсолютные ссылки на ячейки. |
Не сохранять значения чисел или дат в виде текста. | При поиске значений числа или даты убедитесь, что данные в первом столбце table_array не хранятся в виде текстовых значений. В противном случае функция ВПР может вернуть неверное или неожиданное значение. |
Сортировать первый столбец | Сортировка первого столбца table_array перед использованием ВПР, когда range_lookup имеет значение TRUE. |
Использовать подстановочные знаки | Если range_lookup имеет значение FALSE, а lookup_value является текстом, вы можете использовать подстановочные знаки — вопросительный знак (?) и звездочку (*) — в lookup_value . Например, =VLOOKUP(«Fontan?»,B2:E7,2,FALSE) будет искать все экземпляры Fontana с последней буквой, которая может отличаться. |
Убедитесь, что ваши данные не содержат ошибочных символов. | При поиске текстовых значений в первом столбце убедитесь, что данные в первом столбце не содержат начальных и конечных пробелов, непоследовательного использования прямых (‘ или «) и фигурных (‘ или «) кавычек или непечатаемых символов. , В этих случаях функция ВПР может вернуть непредвиденное значение. Чтобы получить точные результаты, попробуйте использовать функцию CLEAN или TRIM для удаления конечных пробелов после табличных значений в ячейке. |
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
Краткая справочная карта: освежение VLOOKUP
Краткая справочная карта: советы по устранению неполадок функции ВПР
Как исправить ошибку #VALUE! ошибка в функции ВПР
Как исправить ошибку #Н/Д в функции ВПР
Обзор формул в Excel
Как избежать неработающих формул
Обнаружение ошибок в формулах
Функции Excel (по алфавиту)
функций Excel (по категориям)
ВПР (бесплатная предварительная версия)


 Значение, которое вы хотите найти, должно находиться в первом столбце диапазона ячеек, указанного вами в аргументе table_array .
Значение, которое вы хотите найти, должно находиться в первом столбце диапазона ячеек, указанного вами в аргументе table_array . Диапазон ячеек также должен включать возвращаемое значение, которое вы хотите найти.
Диапазон ячеек также должен включать возвращаемое значение, которое вы хотите найти. Это метод по умолчанию, если вы его не укажете. Например, =ВПР(90;A1:B100;2;ИСТИНА).
Это метод по умолчанию, если вы его не укажете. Например, =ВПР(90;A1:B100;2;ИСТИНА). Например, если вы укажете диапазон B2:D11, вы должны считать B первым столбцом, C вторым и так далее.
Например, если вы укажете диапазон B2:D11, вы должны считать B первым столбцом, C вторым и так далее.

 Если первый столбец не отсортирован, возвращаемое значение может оказаться неожиданным. Либо отсортируйте первый столбец, либо используйте FALSE для точного совпадения.
Если первый столбец не отсортирован, возвращаемое значение может оказаться неожиданным. Либо отсортируйте первый столбец, либо используйте FALSE для точного совпадения.
 в разделе Как исправить ошибку #NAME! ошибка.
в разделе Как исправить ошибку #NAME! ошибка.
 Знак вопроса соответствует любому одиночному символу. Звездочка соответствует любой последовательности символов. Если вы хотите найти фактический вопросительный знак или звездочку, введите тильду (~) перед символом.
Знак вопроса соответствует любому одиночному символу. Звездочка соответствует любой последовательности символов. Если вы хотите найти фактический вопросительный знак или звездочку, введите тильду (~) перед символом.