Движение по круговому движению: Как правильно проезжать перекресток с кольцевым движением? | АВТОМОБИЛИ
Телеканал «Краснодар» публикует список приоритетного движения на перекрестках с круговым движением
В кубанской столице таких перекрестков 19 и только на шести из них приоритет получают автомобилисты, которые движутся непосредственно по «кругу».
1. ул. Ставропольская – ул. Старокубанская – частичное;
2. ул. Старокубанская – ул. Сормовская – кольцо главное;
3. ул. Лизы Чайкиной – ул. Сормовская – кольцо главное;
4. ул. Сормовская – ул. Дежнева – кольцо второстепенное;
5. ул. Красных Партизан – ул. Академика Лукьяненко – частичное;
6. ул. Красных Партизан – ул. Тургенева – кольцо второстепенное;
7. ул. Красных Партизан – ул. Аэродромная – частичное;
8. ул. Ростовское шоссе – ул. Офицерская – частичное;
9. ул. 40 лет Победы – ул. Российская – частичное;
10. ул. Алма-Атинская – ул. 70 лет Октября – ул. Думенко – частичное;
11. ул. Тургенева – ул. Кубанская – Набережная (под мостом) – частичное;
12.
13. ул. Красных Партизан – Западный обход – частичное;
14. Западный обход – ЖК «Немецкая деревня» — кольцо главное;
15. ул. Тихорецкая – ул. Восточно-Кругликовская – кольцо главное;
16. ул. 3-я Трудовая – а/д «Краснодар – Ейск» — кольцо второстепенное;
17. ул. Захарова – автовокзал «Южный» — кольцо главное;
18. ул. Мира — вокзал «Краснодар-1» — кольцо главное;
19. ул. Дзержинского – ул. Лузана – частичное.
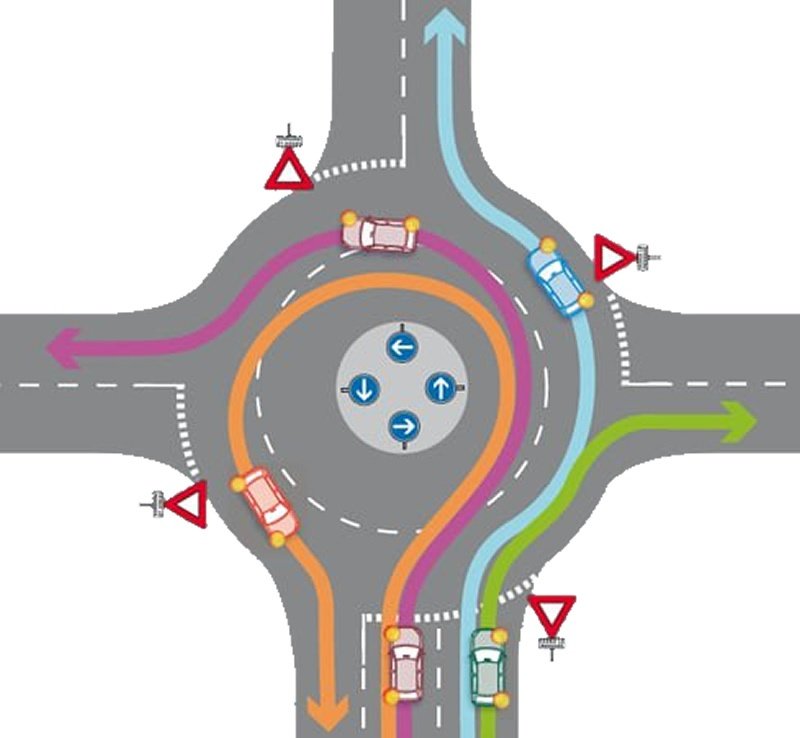
Напомним, в октябре премьер-министр РФ Дмитрий Медведев подписал постановление об изменении правил проезда перекрестков с круговым движением. Если на перекрестке отсутствуют знаки приоритета, при въезде на перекресток с круговым движением водители должны уступить дорогу.
Приоритет на круговом движении есть, только если въезд на такой перекресток обозначен дорожным знаком 4.3 «Круговое движение».
Новые правила не исключают регулирование очередности проезда знаками приоритета.
Круговые движения — Справочник химика 21
Спин-орбитальная связь. Спин-орбитальная связь появляется в результате взаимодействия снинового магнитного момента электрона с магнитным полем, возникающим в результате орбитального движения электрона. Рассмотрим круговое движение электрона по орбитали с радиусом г вокруг ядра с зарядом 2е. В системе координат, связанной с электроном, вращается ядро со скоростью, равной скорости вращения электрона, но только в противополож- [c.228]Добавляют еще столько горячен воды в колбу, чтобы она была заполнена на объема, вынимают воронку и, перемешивая содержимое колбы плавными круговыми движениями, растворяют тетраборат натрия. После этого раствор охлаждают до комнатной температуры и разбавляют его до метки дистиллированной водой.

Таким же образом шлифуют и верхнюю поверхность диска. Проверку притирки и чистоты поверхности диска и торцовой части колец производят путем легкого кругового движения кольца по диску если при этом наблюдается поцарапывание, то протирку кольца повторяют. [c.259]
Колбу С раствором тетрабората натрия ставят под бюретку на лист белой бумаги и понемногу приливают из бюретки раствор НС1, непрерывно перемешивая жидкость плавным круговым движением колбы. Нужно уловить момент, когда от одной капли соляной кислоты первоначально чисто-желтый раствор приобретет чуть розоватый оттенок —как раз такой, как у приготовленного свидетеля. [c. 298]
298]
Разновидностью струйных тарелок являются кольцевые или тангенциальные тарелки. На таких тарелках просечки ориентированы тангенциально, и пары, выходя из них, сообщают жидкости круговое движение. Под действием напора и центробежных сил жидкость движется от центра к периферии. С кругового слива на периферии жидкость поступает по переточным трубам в центр на расположенную ниже тарелку. [c.146]
При круговом движении жидкости на ее поверхности под действием центробежной силы образуется воронка (рис. 10-4), глубина которой возрастает с увеличением числа оборотов. Образование воронки ведет к ухудшению использования емкости сосуда.
Молекулы сольватной оболочки сохраняют колебательное движение преимущественно в радиальном направлении, круговое движение в оболочке и ограниченное вращательное движение. [c.418]
Для этого лист шкурки кладут на плоскую поверхность, смачивают изооктаном и круговыми движениями шлифуют все шесть сторон пластинки, удаляя пятна и дефекты. [c.236]
[c.236]
Предположив, что круговое движение механизма, приводящего в действие пульсатор, равномерное, путь жидкости в колонне и интегралы можно найти аналитическим путем. Из теории кривошипного механизма возьмем исходное уравнение для определения хода пульсатора как функции угла а. Пути частичек в колонне в связи с этим определяются уравнением [c.357]
Принцип действия вихревых насосов следующий (рис. 1.2, а). В кольцевой полости 1, соединенной с всасывающим и нагнетательным патрубками, жидкость увлекается в круговое движение благодаря интенсивной передаче импульса ее частиц, движущихся Б межлопаточных ячейках рабочего колеса 2, потоку жидкости в примыкающем к нему канале. Вследствие неуравновешенности центробежных сил, действующих на частицы жидкости [c.11]
Расчет по методу В. А. Олевского В. Л. Олевский предложил следующие оптимальные параметры работы грохота с круговым движением [c. 219]
219]
Работа, затрачиваемая на подбрасывание материала, за одно колебание = пг,,и72, где —масса материала, находящегося на ситах, кг v — скорость поверхности сита в момент подбрасывания, м/с (для грохота с прямолинейными колебаниями v = соЛ, для грохота с круговым движением v = (ог). [c.221]
На НПЗ обычно применяются горизонтальные или аэрируемые песколовки. Если расход воды не превышает 70 тыс. м /сут, можно применять горизонтальные песколовки с круговым движением воды. При больших расходах сточных вод следует применять песколовки с прямолинейным движением воды (рис. 6.14). [c.574]
При малых числах оборотов мешалки жидкость совершает круговое движение, т. е. вращается по окружностям, лежащим в горизонтальных плоскостях, в которых движутся лопасти. В этих условиях отсутствует смешивание различных слоев жидкости и интенсивность перемешивания низкая. [c.355]
Процесс разделения происходит следующим образом. Сепарируемая жидкость подается в полость тарелкодержателя, откуда поступает через отверстия а в зазор между нижними тарелками здесь жидкость перемещается вокруг оси вращающегося барабана до планок 5 и 4. Затем она устремляется в вырезы б, через отверстия а расположенных выше тарелок попадает в образуемые ими зазоры и продолжает свое круговое движение до следующих планок 5 и 4. Направление движения сепарируемой жидкости (показано на рисунке стрелками) перпендикулярно направлению центробежных сил, что благоприятствует разделению. [c.241]
Сепарируемая жидкость подается в полость тарелкодержателя, откуда поступает через отверстия а в зазор между нижними тарелками здесь жидкость перемещается вокруг оси вращающегося барабана до планок 5 и 4. Затем она устремляется в вырезы б, через отверстия а расположенных выше тарелок попадает в образуемые ими зазоры и продолжает свое круговое движение до следующих планок 5 и 4. Направление движения сепарируемой жидкости (показано на рисунке стрелками) перпендикулярно направлению центробежных сил, что благоприятствует разделению. [c.241]
На рис. 21 показана щековая дробилка с верхним подвесом щеки. Верхний ее конец посажен непосредственно на эксцентрик приводного вала, нижний опирается на нажимную плиту 12и подтягивается к ней тягой 10 через пружину 9. При такой схеме установки щеки верхний ее конец совершает круговое движение, а нижний — по [c.44]
Пренебрегаем силами трения ротора о воздух и учитываем только силы сопротивления, возникающие при круговом движении подшипника вала горловой опоры. Естественно, что значение этих сил сопротивления зависит от конструкции горловой опоры.
Естественно, что значение этих сил сопротивления зависит от конструкции горловой опоры.
Другим типом пылеуловителя, характеризующегося также очень низким перепадом давления, является экранный пылеуловитель О.Е. р [544] (рис. У-9). Основным его элементом является У-образный профиль, где струи запыленного газа, образованные в промежутках между этими профилями, сталкиваются с основой У-образного элемента. Газовый поток либо отталкивается от основы, либо движется по кругу вдоль кривой составляющей элемента. При столкновениях и круговом движении пыль отделяется от газового потока и попадает в пылесборник, расположенный внизу. В ряде случаев для облегчения удаления пыли из У-образных каналов прибегают к обстукиванию или вибрации. С этой же целью может применяться впрыскивание жидкости, что к тому же предотвращает повторный унос пыли газовым потоком. [c.233]
Смешение жидкостей — хорошо известная операция в химической технологии. Промышленность выпускает смесители разнообразных размеров — от малых, с рабочей емкостью -Принцип образования смесей можно пояснить с помош,ью рис.
Равномерного смешения можно достичь, установив вблизи стенок сосуда вертикальные отбойные перегородки, которые отклоняют жидкость вверх. Далее, при использовании мешалки пропеллерного типа частицы жидкости приобретают импульсы как в горизонтальном, так и в вертикальном направлениях (см. рис. 1.3, а), что способствует смешению. Перемешивание эффективно, когда течение становится турбулентным во всем объеме аппарата. Применение турбинной мешалки (см. рис. 1.3, б) позволяет значительно увеличить скорость кругового движения. Центробежные силы разбрасывают частицы жидкости по всему объему смесителя, чем достигается большая эффективность перемешивания.
Выводы об отсутствии скольжения были подтверждены также в статье японского исследователя Снро-Сано [23]. Он приходит к выводу что, частица, находящаяся внутри вращающегося цилиндра, испытывает воздействие со стороны стен цилиндра, и пока не достигнет поверхности слоя зернистого материала, она совершает круговое движение оставаясь неподвижной относительно стен цилиндра, а следовательно относительно и остальных частиц в слое. [c.70]
При непрерывном врашении КСП слой остается в этом положении все время. Круговое движение совершают совместно стенки КСП и частицы в слое, оставаясь в то же время неподвижными друг относительно друга. [c.72]
Турбинные м еш а л к и. Их относят к быстроходным, рабо-тгющим по принципу центробежного насоса, т. е. они всасывают жидкость в середину и за счет центробежной силы отбрасывают ее к периферии. Таким образом, в отличие от лопастных, рамных и якорных мешалок, сообщающих жидкости в основном круговое движение, турбинные сообщают радиальное. Турбинные мешалки делают открытыми и закрытыми. По конструкции закрытые мало 01личаются от колеса центробежного насоса и подразделяются на мешалки одностороннего и двустороннего всасывания. Открытая мешалка представляет собой диск с радиально расположенными лопатками, она более проста по конструкции и поэтому чаще применяется. Турбинные мешалки обеспечивают весьма интенсивное перемешивание. Их можно применять при широком диапазоне вязкостей и плотностей перемешиваемых жидкостей, для подъема тяжелых суспензий, получения эмульсий, ири химических процессах и др. Не рекомендуется применять турбинные мешалки для аппаратов большой емкости. В аппаратах с турбинными мешалками обязательна установка отражательных перегородок (вертикальных планок, которые устанавливаются радиально около стенок аппарата) если они отсутствуют, то образуется глубокая воронка, иногда доходящая до дна аппарата, и перемешивание ухудшается. Обычно устанавливают четыре перегородки в виде радиально расположенных вертикальных планок шириной не более 0,1 В, где Ь — диаметр аппарата.
Турбинные мешалки делают открытыми и закрытыми. По конструкции закрытые мало 01личаются от колеса центробежного насоса и подразделяются на мешалки одностороннего и двустороннего всасывания. Открытая мешалка представляет собой диск с радиально расположенными лопатками, она более проста по конструкции и поэтому чаще применяется. Турбинные мешалки обеспечивают весьма интенсивное перемешивание. Их можно применять при широком диапазоне вязкостей и плотностей перемешиваемых жидкостей, для подъема тяжелых суспензий, получения эмульсий, ири химических процессах и др. Не рекомендуется применять турбинные мешалки для аппаратов большой емкости. В аппаратах с турбинными мешалками обязательна установка отражательных перегородок (вертикальных планок, которые устанавливаются радиально около стенок аппарата) если они отсутствуют, то образуется глубокая воронка, иногда доходящая до дна аппарата, и перемешивание ухудшается. Обычно устанавливают четыре перегородки в виде радиально расположенных вертикальных планок шириной не более 0,1 В, где Ь — диаметр аппарата. [c.230]
[c.230]
Песколовки служат для задержания крупных минеральных примесей и нефтепродуктов. Расчетное время прибывания стоков — 30 с. Как правило, применяются железобетонные песколовки горизонтального типа с круговым движением воды (из условия более удобного сбора нефтепродукта). Изготовляются такие песколовки по типовым проектам. Производительность их колеблется от 1400 до 64000 м /сутки. [c.190]
При этом частицы в круговом движении достигают угла естественного откоса и выходят на поверхность слоя. Дальше они совершать круговое движение не могут и скатываются по поверхности слоя. Пройдя середину хорды они накрывают собой частицы лежащие до того на поверхности и последние начинают круговое движение, как бы ныряя в слой. [c.72]
Как было показано выше, под воздействием результирующей силы, [уравнение (169)] частицы движутся вместе с потоком в проточной его части, поперек его или участвуют в круговом движении в циркуляционной зоне. [c.197]
[c.197]
Песколовки могут быть горизонтальные, в которых хедкооть движется в горизонтальном направлении с прямолинейным или круговым движением воды, или вертикальные, в которых жидкость движется снизу вверх, есть песколовки с поступательно-вращательным движением воды (винтовые песколовки). [c.58]
Присутствие мути легче всего обнаруллист черной бумаги (или на выкрашенную черной краской поверхность стола) и, глядя в него сверху, слегка взбалтывать содержимое стакана плавными круговыми движениями. При этом на дне его собирается некоторое количество прошедшего сквозь фильтр осадка, котстрый становится хорошо заметным. Если фильтрат оказался мутным, нужно снова профильтровать его через тот >Kt фильтр, повторяя это до тех пор, пока поры фильтра не забьются частицами осадка и жидкость не станет совершенно прозрачной. [c.167]
Стиракрил применяется для нанесения на металлические поверхности для компенсации изиоса. Приготовление раствора стиракрила производится непосредствеипо перед его использованием путем смешения порошка и жидкости в течение 2 мин круговыми движениями палочки в одну сторону. Металлические поверхности перед ианесепие.м стиракрила тщательно обезжириваются органическим растворителем. Для предупреждения приставания стиракрила к новерхностп пресс-([юрмы эта поверхность покрывается силиконовым маслом или тонкой пленкой парафина. Бутакрил 176 [c.176]
Приготовление раствора стиракрила производится непосредствеипо перед его использованием путем смешения порошка и жидкости в течение 2 мин круговыми движениями палочки в одну сторону. Металлические поверхности перед ианесепие.м стиракрила тщательно обезжириваются органическим растворителем. Для предупреждения приставания стиракрила к новерхностп пресс-([юрмы эта поверхность покрывается силиконовым маслом или тонкой пленкой парафина. Бутакрил 176 [c.176]
Улита сделана из чугуна СЧ 16-36 и состоит из двух половин, скрепляемых болтами. Поверхность улиты выполнена в виде спирали с наклонными плоскостями. Она имеет съемный колпак, через который поступает воздух в центральную часть нечи при помощи специального вентилятора, остальная часть воздуха поступает с боков улиты при помощи второго вентилятора через выходящую из печи известь. Колпак на улите лучше применять остроконечный вместо плоского и несколько смещенный по отношению оси улиты. Колпак Б этом случае будет совершать круговое движение, что будет способствовать разрыхлению образовавшихся козлов. [c.185]
[c.185]
Конструкции инерционных грохотов. Ииерциопный грохот с круговым движением (рис. 7.12) состоит из кор ба /, установленного на фундаменте на пружинах 6, вала 4 с закрепленными на нем дебалансами 3 (снабженными набором пластин 9), вращающегося от электродвигателя 2 при помощи клиновых ремней и 1икива 5. Тяжелые инерционные грохоты обычно снабжают двумя или тремя пружинами [c.214]
Тарелки, которые можно отнести также к перекрестно-прямоточным, изображены на рис. 60. В данных конструкциях ввиду наличия составляющей скорости газа, направленной в сторону движения жидкости, достигается увеличение производительности по сравнению с обычными ситчатыми тарелками. В последнем случае одностороннее направление потока паров осуществляется за счет отверстий, расположенных преимущественно с одной стороны 5-образного элемента. Отогнутые кромки элемента иод отверстиями создают увеличенную скорость газа при входе в отверстие, что способствует более равномерному вступлению тарелки в работу. К перекрестно-прямоточным провальным тарелкам можно отнести тарелки тииа Киттеля [164]. Движение жидкости на одной такой тарелке происходит по спирали от центра к периферии, на другой — ио радиусу от периферии к центру. Столь сложное движение жидкости осуществляется за счет кинетической энергии паров, так как пары выходят под определенным углом к основанию тарелки благодаря направлению просечки у листов основания. Слив жидкости на одной тарелке осуществляется у периферии, на другой — в центре. Организованное движение жидкости создает места ее скопления и увеличивает статическое давление жидкости в этих местах, что так же, как и на ситчатых волнистых тарелках, повышает их производительность. Кроме того, круговое движение пара в межтаре-лочном пространстве создает благоприятные условия для сепарации жидкости. Тарелки Киттеля в США имеют ограниченное применение и широко используются в других капиталистических странах. Текущие затраты на колонну с тарелками Киттеля составляют в среднем 65— [c.
К перекрестно-прямоточным провальным тарелкам можно отнести тарелки тииа Киттеля [164]. Движение жидкости на одной такой тарелке происходит по спирали от центра к периферии, на другой — ио радиусу от периферии к центру. Столь сложное движение жидкости осуществляется за счет кинетической энергии паров, так как пары выходят под определенным углом к основанию тарелки благодаря направлению просечки у листов основания. Слив жидкости на одной тарелке осуществляется у периферии, на другой — в центре. Организованное движение жидкости создает места ее скопления и увеличивает статическое давление жидкости в этих местах, что так же, как и на ситчатых волнистых тарелках, повышает их производительность. Кроме того, круговое движение пара в межтаре-лочном пространстве создает благоприятные условия для сепарации жидкости. Тарелки Киттеля в США имеют ограниченное применение и широко используются в других капиталистических странах. Текущие затраты на колонну с тарелками Киттеля составляют в среднем 65— [c. 136]
136]
Кроме массы и заряда ядро обладает третьей харакгеристикоп —моментом количества движения, который обусловлен его вращением вокруг оси—спином. Поскольку ядро заряжено, его враш,ение вокруг собственной оси приводит к круговому движению заряда, что формально аналогично электрическому току, протекающему в витке провода (рнс. 20). Этот круговой ток (солеиоид). создает магнитное поле, так что вращающееся ядро ведет себя подобно крощечиому магниту, ось которого совпадает с осью спина. Это обуславливает появление у ядр. ( магнитного допольного. момента . [c.37]
Эксцентриковый вал приводится во враш ательиое движение от электродвигателя 6 через клипоремеиную пару 8. При враш,ении эксцентрикового вала короб совершает круговые движения в вертикальной плоскости (частота 600—900 об/мин). При этом материал на сите встряхивается и рассеивается. Для лучшего продвижения [c.268]
При высоких скоростях вращения мешалок перемешиваемая жидкость вовлекается в круговое движение п вокруг вала образуется воронка, глубина которой увеличивается с возрастанием числа оборотов и уменьшением плотности и вязкости среды. Для предотвращения образования воронки в аппарате помещают отражательные перегородки, которые, кроме того, способствуют возникновению вихрей и увеличению турбулентности системы. 06-Рис VI-4 Лопастн 1я разоваиие воронки можно предотвратить и при мешалка. » ПОЛНОМ заполнении жидкостью аппарата, т. е. при отсутствии воздушной прослойки между перемешиваемой жидкостью и крышкой аппарата, а также при установке вала мешалки эксцентрично к оси аппарата или применении аппарата прямоугольного сечения. [c.254]
Для предотвращения образования воронки в аппарате помещают отражательные перегородки, которые, кроме того, способствуют возникновению вихрей и увеличению турбулентности системы. 06-Рис VI-4 Лопастн 1я разоваиие воронки можно предотвратить и при мешалка. » ПОЛНОМ заполнении жидкостью аппарата, т. е. при отсутствии воздушной прослойки между перемешиваемой жидкостью и крышкой аппарата, а также при установке вала мешалки эксцентрично к оси аппарата или применении аппарата прямоугольного сечения. [c.254]
Движение круговое — Энциклопедия по машиностроению XXL
Рассмотрим однородное тяжелое тело вращения, центр тяжести О которого закреплен неподвижно относительно Земли, Силами, действующими на тело, являются притяжение Земли и реакция Q точки подвеса G Размеры прибора настолько малы, что силы притяжения Землею отдельных частиц тела можно считать параллельными и пропорциональными их массам. Эти силы имеют равнодействующую A, приложенную в центре тяжести G. Последний не будет абсолютно неподвижным, так как центр тяжести участвует в движении Земли. Обозначим через J ускорение, каким обладает в каждый момент эта точка G. Исследуем движение тела относительно осей Gx y z с абсолютно неизменными направлениями и с началом в точке G. Мы можем рассматривать эти оси как неподвижные при условии присоединения к реально действующим на различные точки системы силам только переносных сил инерции. Эти последние, равные —mj, параллельны между собой и пропорциональны массам. Они имеют равнодействующую Ф, приложенную в центре тяжести G. Движение тела относительно осей Gx y z будет совпадать с движением тела вращения, закрепленного в абсолютно неподвижной точке G своей оси и находящегося под действием сил, имеющих равнодействующую, проходящую через неподвижную точку. Но это движение было подробно изучено. Ось Go плоскости максимума площадей неизменна, т. е. направлена все время на одну и ту же звезду, а ось вращения ротора гироскопа описывает равномерным движением круговой конус вокруг этого направления.
Последний не будет абсолютно неподвижным, так как центр тяжести участвует в движении Земли. Обозначим через J ускорение, каким обладает в каждый момент эта точка G. Исследуем движение тела относительно осей Gx y z с абсолютно неизменными направлениями и с началом в точке G. Мы можем рассматривать эти оси как неподвижные при условии присоединения к реально действующим на различные точки системы силам только переносных сил инерции. Эти последние, равные —mj, параллельны между собой и пропорциональны массам. Они имеют равнодействующую Ф, приложенную в центре тяжести G. Движение тела относительно осей Gx y z будет совпадать с движением тела вращения, закрепленного в абсолютно неподвижной точке G своей оси и находящегося под действием сил, имеющих равнодействующую, проходящую через неподвижную точку. Но это движение было подробно изучено. Ось Go плоскости максимума площадей неизменна, т. е. направлена все время на одну и ту же звезду, а ось вращения ротора гироскопа описывает равномерным движением круговой конус вокруг этого направления. Наконец, движение относительно Земли есть результат наложения суточного вращения на это простое движение.
[c.258]
Наконец, движение относительно Земли есть результат наложения суточного вращения на это простое движение.
[c.258]
В установившемся движении (круговая орбита) функция W имеет стационарное значение [c.163]
Это значит, что частица перемещается по параллельному кругу, совершая так называемое движение кругового конического маятника название происходит от того, что если маятник реализован с помощью грузика, подвешенного на нити, то в рассматриваемом случае движения нить описывает круговой конус. Определим для изучаемого движения закон изменения угла ср. Прежде всего из второго из уравнений (21.26) при [c.206]
Ползун jf, скользящий по неподвижной направляющей а, выполнен в виде круговой кулисы с центром в точке А, по которой скользит ползун 2, входящий BG вращательную пару В со штангой 3, скользящей в неподвижной направляющей Ь. При движении круговой кулисы 1 по неподвижной направляющей а штанга 3 движется возвратнопоступательно в неподвижной направляющей Ь,
[c.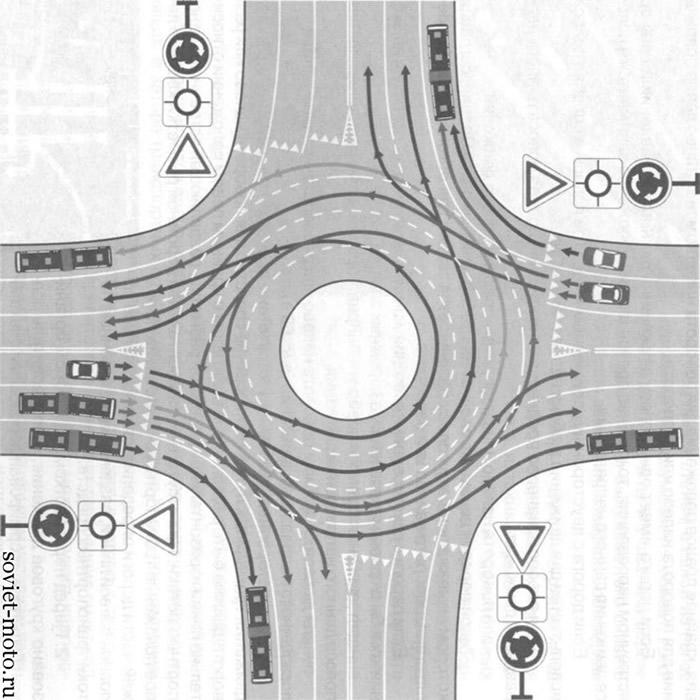 33]
33]
Далее, при отдельных звеньях механизмов поставлены стрелки, иллюстрирующие формы их движения прямые— при поступательном движении, круговые — при вращательном, прямые двойные — при возвратно-посту-пательном движении и круговые двойные — при возврат-но-вращательном. [c.10]
Поверхности с постоянной профильной производящей и винтовой направляющей (в изделиях с резьбой) образуются с заменой относительного движения по винтовой направляющей с углом подъёма а (сложной в изготовлении и использовании) — составляющими его движениями — круговым и прямо- [c.397]
Движение подачи при нарезании дол-бяками разделяется на два движение радиальной подачи — врезание долбяка на глубину зуба мм на 1 оборот заготовки) и движение круговой подачи — встречное вращение заготовки относительно долбяка. Круговая подача задается как длина дуги по делительной окружности долбяка на один двойной ход его мм на дв. ход). [c.109]
Физический маятник.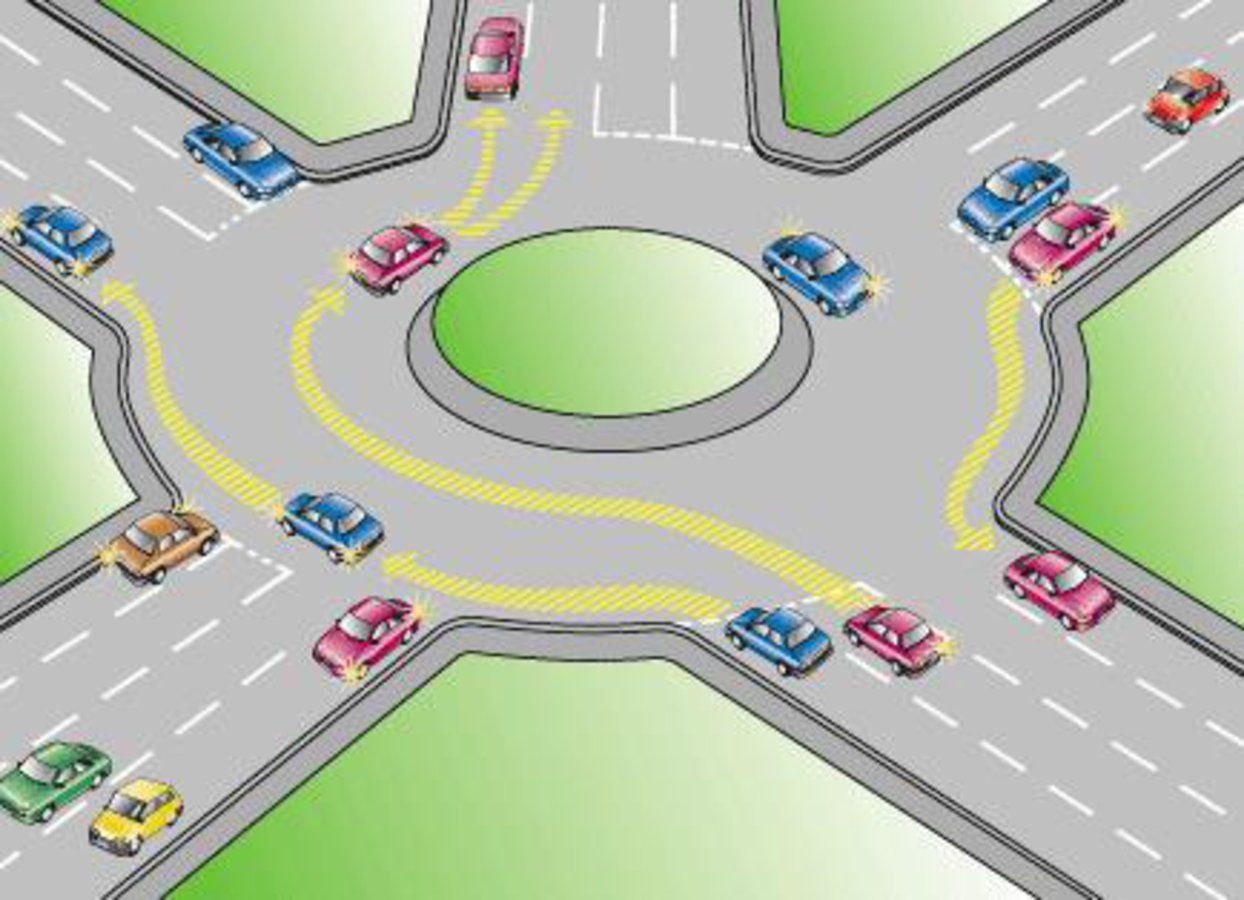 Физ. М. обычно наз. твёрдое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса (рис. 1, б). Движение такого М. вполне аналогично движению кругового матем. М. Период конечных или малых колебаний физ. М. определяется соответственно ф-лами (2) или (3), в к-рых I следует заменить величиной
[c.76]
Физ. М. обычно наз. твёрдое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса (рис. 1, б). Движение такого М. вполне аналогично движению кругового матем. М. Период конечных или малых колебаний физ. М. определяется соответственно ф-лами (2) или (3), в к-рых I следует заменить величиной
[c.76]
На долбежных станках главное движение резания — возвратно-поступательное в вертикальной плоскости — сообщают ползуну, на котором установлен резцедержатель с резцом. Длина хода ползуна обычно не превышает 200 мм. Заготовку закрепляют на столе станка, который имеет прерывистое движение продольной и поперечной подач. Кроме того, стол имеет движение круговой подачи относительно своей вертикальной оси. [c.378]
Карусельно-фрезерный станок показан на рис. 6.60, д. На станине 1 смонтирована стойка 2, по вертикальным направляющим которой перемещается фрезерная головка 3 с двумя шпинделями, один из которых предназначен для чистовой обработки.
 На круглом столе 4 (карусели) с вертикальной осью вращения в приспособлениях устанавливают заготовки. Круглый стол имеет салазки 5 для установки его на направляющих станины. Заготовки устанавливают и снимают со стола без остановки станка фрезерование ведется непрерывно при медленновращающемся столе (движение круговой подачи).
[c.390]
На круглом столе 4 (карусели) с вертикальной осью вращения в приспособлениях устанавливают заготовки. Круглый стол имеет салазки 5 для установки его на направляющих станины. Заготовки устанавливают и снимают со стола без остановки станка фрезерование ведется непрерывно при медленновращающемся столе (движение круговой подачи).
[c.390]Особенностью барабанно-фрезерных станков является наличие барабана с горизонтальной осью вращения. На гранях барабана в приспособлениях устанавливают заготовки, которым медленным вращением барабана сообщают движение круговой подачи. Станки имеют одну или несколько головок. [c.390]
Горизонтальные плоскости по методу непрерывного фрезерования обрабатывают на карусельно-фрезерных станках торцовыми фрезами (рис. 6.66, с). Заготовки устанавливают в приспособлениях, равномерно расположенных по окружности стола, и сообщают им движение круговой подачи. Заготовка сначала проходит черновую обработку (размер Hi), а затем фрезой, установленной во втором шпинделе, обрабатывается окончательно (размер Яг). [c.397]
[c.397]
Подачу измеряют в миллиметрах на один оборот заготовки и выбирают из нормативов по режимам резания в зависимости от числа зубьев, требуемых шероховатости и точности обработки. При обработке однозаходной модульной червячной фрезой необходимо, чтобы за время одного оборота фрезы заготовка, на которой требуется получить z зубьев, повернулась на 1/z часть окружности. Согласованное и непрерывное вращение заготовки и фрезы является обкаточным движением. Таким образом, для нарезания цилиндрических колес с прямыми зубьями необходимы три движения главное вращательное движение резания червячной фрезы, движение круговой подачи заготовки (делительное движение) и движение вертикальной подачи фрезы. Для согласования этих движений на станке настраивают кинематические цепи скоростную, делительную и вертикальной подачи. [c.403]
Для формообразования косого зуба необходимы три движения главное вращательное движение резания фрезы, движение вертикальной подачи фрезы и ускоренное (или замедленное) вращательное движение круговой подачи заготовки, ко-
[c.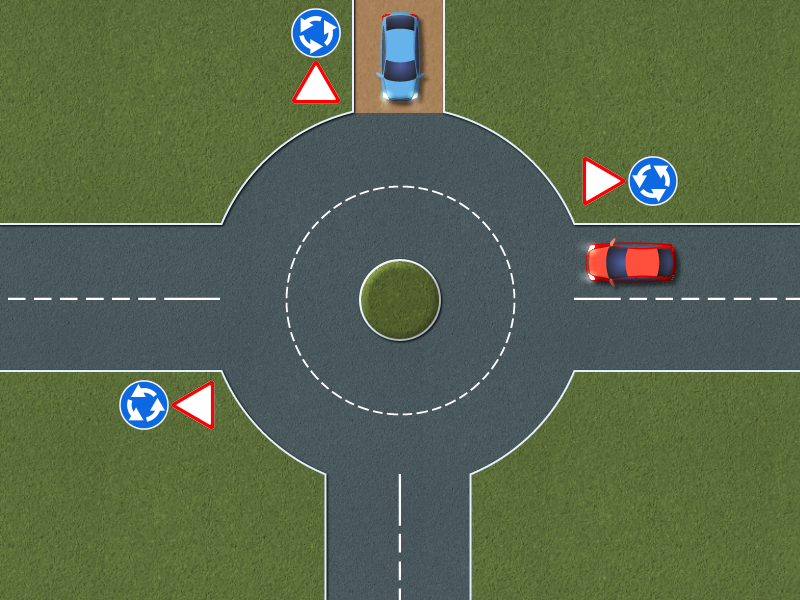 404]
404]
Для нарезания червячных колес необходимы три движения главное вращательное движение резания червячной фрезы, движение круговой подачи заготовки и движение радиальной подачи заготовки. Первые два движения осуществляют настройкой тех же кинематических цепей, что и при нарезании колес с прямыми и косыми зубьями. Для нарезания зуба на полную высоту по всей ширине колеса заготовке сообщают движение радиальной подачи, настраивая кинематическую цепь горизонтальной подачи. Цепь горизонтальной подачи связывает перемещение заготовки в горизонтальной плоскости с ее вращением. [c.405]
Вращение долбяка (движение круговой подачи долбяка) и вращение заготовки (движение круговой подачи заготовки) являются движениями обкатки. [c.405]
Движение круговой подачи выражается длиной дуги делительной окружности долбяка, на которую он поворачивается за один двойной ход (мм/дв. ход). Поперечным перемещением суппорта долбяку
[c. 405]
405]
Долбяку и заготовке сообщают те же движения, что и при нарезании колес с прямыми зубьями. Дополнительно долбяку сообщают вращательное движение (дополнительное движение круговой подачи), обусловленное углом наклона зубьев и согласованное с его возвратно-поступательным движением. Дополнительное вращение долбяка обеспечивается установкой на шпинделе станка винтовых направляющих (копиров). Угол наклона винтовой линии копира должен соответствовать углу наклона зубьев нарезаемого колеса. [c.406]
Вращение заготовки (движение круговой подачи заготовки) и люльки с резцами (движение круговой подачи люльки) является движением обкатки и должно соответствовать передаточному отношению [c.407]
Возвратно-поступательное перемещение стола для движения продольной подачи производят с помощью гидроцилиндра и поршня. Движение круговой подачи D. заготовки обеспечивает специаль-
[c. 413]
413]
Наибольшее распространение получили методы шлифования на центрах. Для повышения точности обработки центры устанавливают неподвижно. Движение круговой подачи заготовки обеспечивается за счет поводкового устройства. Возможно консольное закрепление заготовок в кулачковых патронах. [c.414]
В заключение рассмотрим задачу об образовании слоя расплава при движении кругового цилиндра нормально к своей образующей в твердой плавящейся среде. Сферический аналог этой задачи в приближении Стокса и без учета вязкой диссипации в слое рассмотрен в [6]. Согласно рис. 13, в этом случае 7 = 7г/2 — ж/i , где Я — радиус сечения цилиндра, аж — расстояние от передней точки вдоль окружности. Соотношения (1.13) принимают при этом вид (вновь пренебрегаем оттоком тепла в твердую среду) [c.200]
Движение кругового цилиндра перпендикулярно собственной оси, расположенной посредине между стенками и параллельно им, порождает двумерную задачу. Представляют интерес два случая 1) когда цилиндр движется параллельно стенкам и 2) когда он движется перпендикулярно стенкам. [c.396]
[c.396]
Тогда нелинейные уравнения движения кругового кольца запишем в виде [c.217]
Фактически вращение нарезаемой заготовки вокруг своей оси представляет движение круговой подачи. Инструмент помимо дви- [c.213]
Константы интегрирования Ап.) Вп определяются из начальных условий (7.2) движения круговой трехслойной пластины с [c.409]
Константы An, Bn определяются из начальных условий движения круговой трехслойной вязкоупругой пластины [c.426]
Движение круговой подачи (враш ение заготовки) осуш.ествляют [c.195]
Изготовление косозубых колес производят косозубыми долбя-ками (рис. 171, в). Угол наклона зубьев долбяка должен быть равен углу наклона зубьев нарезаемого колеса, а направления зубьев должны быть разноименными. Долбяку сообщают дополнительное вращение для образования винтового зуба. Дополнительное вращение долбяку задают винтовыми направляющими копирных втулок. Одну из них (рис. 171, а) жестко крепят к шпинделю, а другую (рис. 171, б) — к червячному колесу, сообщающему долбяку медленное вращательное движение круговой подачи.
[c.228]
Одну из них (рис. 171, а) жестко крепят к шпинделю, а другую (рис. 171, б) — к червячному колесу, сообщающему долбяку медленное вращательное движение круговой подачи.
[c.228]
Эти станки применяют для обработки цилиндрических, конических и фасонных отверстий и торцов. Основной размер этих станков — наибольший диаметр шлифуемой детали. По компоновочному расположению шлифовального шпинделя различают горизонтальные и вертикальные станки, а по характеру движения круговой подачи — обычные, бесцентровые и планетарные. В обычных станках заготовку крепят самоцентрирующимися трехкулачковыми патронами с ручным или механизированным приводами, в бесцентровых — электромагнитным патроном с прижимом по торцу. Вращение обеспечивается плоскоременной передачей от электродвигателя — до 2000 мин» пневмоприводом — до 80 ООО мин» электрошпинделем, питаемым током повышенной частоты от генераторов или тиристорных преобразователей, — от 48 ООО до 144 ООО мин гидроприводом (винтовыми гидродвигателями) — до 35 ООО мин . В универ-
[c.255]
В универ-
[c.255]
Движение круговой подачи — вращение шпинделя бабки 12 осуществляется от трехскоростного электродвигателя М2 через [c.274]
Движение круговой подачи осуществляется гидроцилиндром 20t на штоке которого нарезана рейка. Рейка поворачивает реечную шестерню Zg, на оси которой установлено водило с собачкой храпового механизма. От храпового колеса через блок zjz или z-,/za вращение поступает на механизм реверса 21 и далее через червячную передачу планетарный механизм (в этом случае муфта Ml [c.282]
Блок рассмотрел движение кругового, квадратного к линейного источника по полупространству при постоянном (q = qo) и параболическом [ = о(1—л )] распределении теплового H t04HHKa в зоне контакта. Им получены формулы для расчета температуры в зубчатых зацеплениях [c.115]При круглом ш.гтифовании (рис. 6.79, б) движение продольной подачи обеспечивается возвратно-поступательным перемещением заготовки. Подача (мм/об. заг.) соответствует осевому перемещению заготовки за один ее оборот. Вращение заготовки является движением круговой подачи.
[c.411]
Подача (мм/об. заг.) соответствует осевому перемещению заготовки за один ее оборот. Вращение заготовки является движением круговой подачи.
[c.411]
Заготовки больших размеров и массы шлифовать описанными выше методами нерационально. В этих случаях применяют планетарное шлифование (рис. 6.83, б). Заготовку закрепляют на столе станка неподвижно. Шлифовальный круг вращается вокруг своей оси, а также вокруг оси отверстия, что аналогично движению круговой подачи (положение круга, совершившего в планетарном движении пол-оборота, показано штриховой линией). Планетарным шлифованием можно обра-батьшать внутренние фасонные и торцовые поверхности, а также отверстия, положения которых определенным образом связаны друг с другом (например, на деталях типа корпусов). [c.416]
Затылование шлифованием при обработке червячных, резьбовых и реечнък фрез осуществляется со скоростью резания = 18… 40 м/с. Заготовка вращается со скоростью движения круговой подачи не [c.
 291]
291]Такаиси [34] рассматривал задачу о движении кругового цилиндра параллельно одиночной плоской стенке и перпендикулярно своей собственной оси. В предельном случае больших Ыа Ь — расстояние от стенки до оси цилиндра, а — радиус цилиндра) сопротивление на единицу длины равно [c.398]
Еще раньше, в Послании к Инголи Галилей, обсуждая устройство мира (т. е. Солнечной системы), утверждал, что если небесные тела по природе своей должны двигаться каким-либо движением, то таковым может быть только движение круговое но невозможно, чтобы природа дала кому-либо из входящих в нее тел наклонность двигаться по прямой [c.94]
Движение круговой подачи — вращение шпинделя 1 — осущест- [c.201]
Движение круговой подачи — относительный поворот долбяка на один двойной ход шпинделя — осуществляемое по кинематической цепи, связывающей кривошип кулисного механизма с червячной передачей шпкнделя. Уравнение кинематического баланса цепи круговой подачи при чистовом зубонарезании
[c.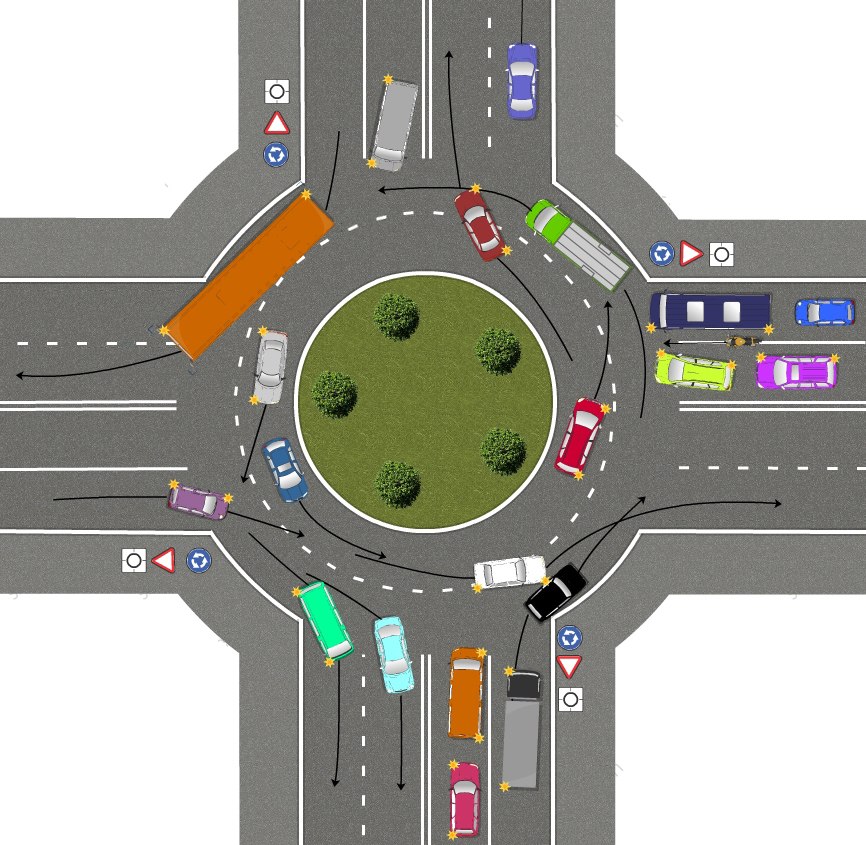 226]
226]
Итогом первого движения является постоянный угол атаки, в то время как итог второго движения — круговое колебание с частотой и с центром в нуле это круговое колебание есть движение Эйлер9—Пуансо ракеты в безвоздушном пространстве (рис. 16). [c.159]
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
4.5: Равномерное круговое движение — Физика LibreTexts
Цели обучения
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.

- Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение.Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или \(\frac{d\vec{v}}{dt}\) ≠ 0. Это показано на рисунке \(\PageIndex{1}\). Когда частица движется против часовой стрелки за время \(\Delta\)t по круговой траектории, ее вектор положения перемещается от \(\vec{r}(t)\) до \(\vec{r}(t + \Delta t )\). Вектор скорости имеет постоянную величину и касается пути при изменении от \(\vec{v}\)(t) до \(\vec{v}\left(t + \Delta t\right)\), меняет только свое направление.Поскольку вектор скорости \(\vec{v}(t)\) перпендикулярен вектору положения \(\vec{r}\)(t), треугольники, образованные векторами положения и \(\Delta \vec{ r}\), а векторы скорости и \(\Delta \vec{v}\) подобны. Кроме того, с
В этом случае вектор скорости меняется, или \(\frac{d\vec{v}}{dt}\) ≠ 0. Это показано на рисунке \(\PageIndex{1}\). Когда частица движется против часовой стрелки за время \(\Delta\)t по круговой траектории, ее вектор положения перемещается от \(\vec{r}(t)\) до \(\vec{r}(t + \Delta t )\). Вектор скорости имеет постоянную величину и касается пути при изменении от \(\vec{v}\)(t) до \(\vec{v}\left(t + \Delta t\right)\), меняет только свое направление.Поскольку вектор скорости \(\vec{v}(t)\) перпендикулярен вектору положения \(\vec{r}\)(t), треугольники, образованные векторами положения и \(\Delta \vec{ r}\), а векторы скорости и \(\Delta \vec{v}\) подобны. Кроме того, с
\[|\vec{r}(t) | = | \vec{r} (t + \Delta t)| \номер\]
и
\[| \vec{v} (т)| = | \vec{v} (t + \Delta t)|, \nonumber \]
два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
.\[\dfrac{\Delta v}{v} = \dfrac{\Delta r}{r}\]
или
\[\Delta v = \dfrac{v}{r} \Delta r. {2}}{r} \ldotp\]
{2}}{r} \ldotp\]
Направление ускорения также можно найти, заметив, что когда \(\Delta\)t и, следовательно, \(\Delta \theta\) приближаются к нулю, вектор \(\Delta \vec{v}\) приближается к направлению перпендикулярно \(\vec{v}\).{2}}{r} \ldotp \label{4.27}\]
Направление вектора ускорения — к центру окружности (рисунок \(\PageIndex{2}\)). Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему индекс \(с\). Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».
Рисунок \(\PageIndex{2}\): Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении.Вектор скорости также показан и касается окружности. Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения.
Пример \(\PageIndex{1}\): создание ускорения в 1 g
Реактивный самолет летит со скоростью 134,1 м/с по прямой линии и делает разворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение в 1 g по направлению к центру круговой траектории?
Стратегия
Зная скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.{2}} = 1835\; т = 1,835\; км \ldotp\]
Значение
Чтобы создать у пилота большее ускорение, чем g, реактивный самолет должен либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.
Упражнение 4.5
Маховик имеет радиус 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение 900,0 см/с 2 ?
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в таблице \(\PageIndex{1}\).
Типичные центростремительные ускорения приведены в таблице \(\PageIndex{1}\).
| Объект | Центростремительное ускорение (м/с 2 или коэффициенты g) |
|---|---|
| Земля вокруг Солнца | 5,93 x 10 -3 |
| Луна вокруг Земли | 2,73 x 10 -3 |
| Спутник на геосинхронной орбите | 0.233 |
| Внешний край компакт-диска при воспроизведении | 5,75 |
| Струя в барабане | (2-3 г) |
| Американские горки | (5 г) |
| Электрон на орбите протона в простой боровской модели атома | 9,0 x 10 22 |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана ее вектором положения \(\vec{r}(t)\). На рисунке \(\PageIndex{3}\) показана частица, совершающая круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол \(\theta\) с осью x. Вектор \(\vec{r}(t)\), составляющий угол \(\theta\) с осью x, показан со своими компонентами вдоль осей x и y. Величина вектора положения равна \(A = |\vec{r}(t)|\), а также является радиусом окружности, так что с точки зрения его компонентов
На рисунке \(\PageIndex{3}\) показана частица, совершающая круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол \(\theta\) с осью x. Вектор \(\vec{r}(t)\), составляющий угол \(\theta\) с осью x, показан со своими компонентами вдоль осей x и y. Величина вектора положения равна \(A = |\vec{r}(t)|\), а также является радиусом окружности, так что с точки зрения его компонентов
\[\vec{r} (t) = A \cos \omega \hat{i} + A \sin \omega t \hat{j} \ldotp \label{4.28}\]
Здесь \(\omega\) — константа, называемая угловой частотой частицы. Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду. Угол \(θ\), который имеет вектор положения в любой конкретный момент времени, равен \(\omega\)t.
Если \(T\) — период движения или время совершения одного оборота (\(2 \pi\, рад\)), то
Рисунок \(\PageIndex{3}\): Вектор положения частицы в круговом движении с его компонентами вдоль осей x и y. Частица движется против часовой стрелки. Угол \(\theta\) – это угловая частота \(\omega\) в радианах в секунду, умноженная на \(t\).
Частица движется против часовой стрелки. Угол \(\theta\) – это угловая частота \(\omega\) в радианах в секунду, умноженная на \(t\).Скорость и ускорение можно получить из функции положения дифференцированием:
\[\vec{v} (t) = \frac{d \vec{r} (t)}{dt} = -A \omega \sin \omega t \hat{i} + A \omega \cos \ омега т \шляпа{j} \ldotp \label{4.29}\]
Из рисунка \(\PageIndex{3}\) видно, что вектор скорости касается окружности в месте нахождения частицы с величиной A\(\omega\).{2} \vec{r}\)(t).
Пример \(\PageIndex{2}\): круговое движение протона
Протон имеет скорость 5 x 10 6 м/с и движется по окружности в плоскости xy радиусом r = 0,175 м. Каково его положение в плоскости xy в момент времени t = 2,0 x 10 −7 с = 200 нс? При t = 0 положение протона составляет 0,175 м \(\hat{i}\), и он вращается против часовой стрелки. Нарисуйте траекторию.
Раствор
Из приведенных данных протон имеет период и угловую частоту:
\[T = \frac{2 \pi r}{v} = \frac{2 \pi (0.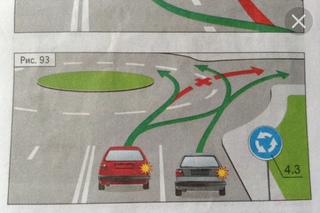 {−7}\, мс = 200\, нс\). Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
{−7}\, мс = 200\, нс\). Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы по оси x. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно быть с постоянной скоростью.Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени.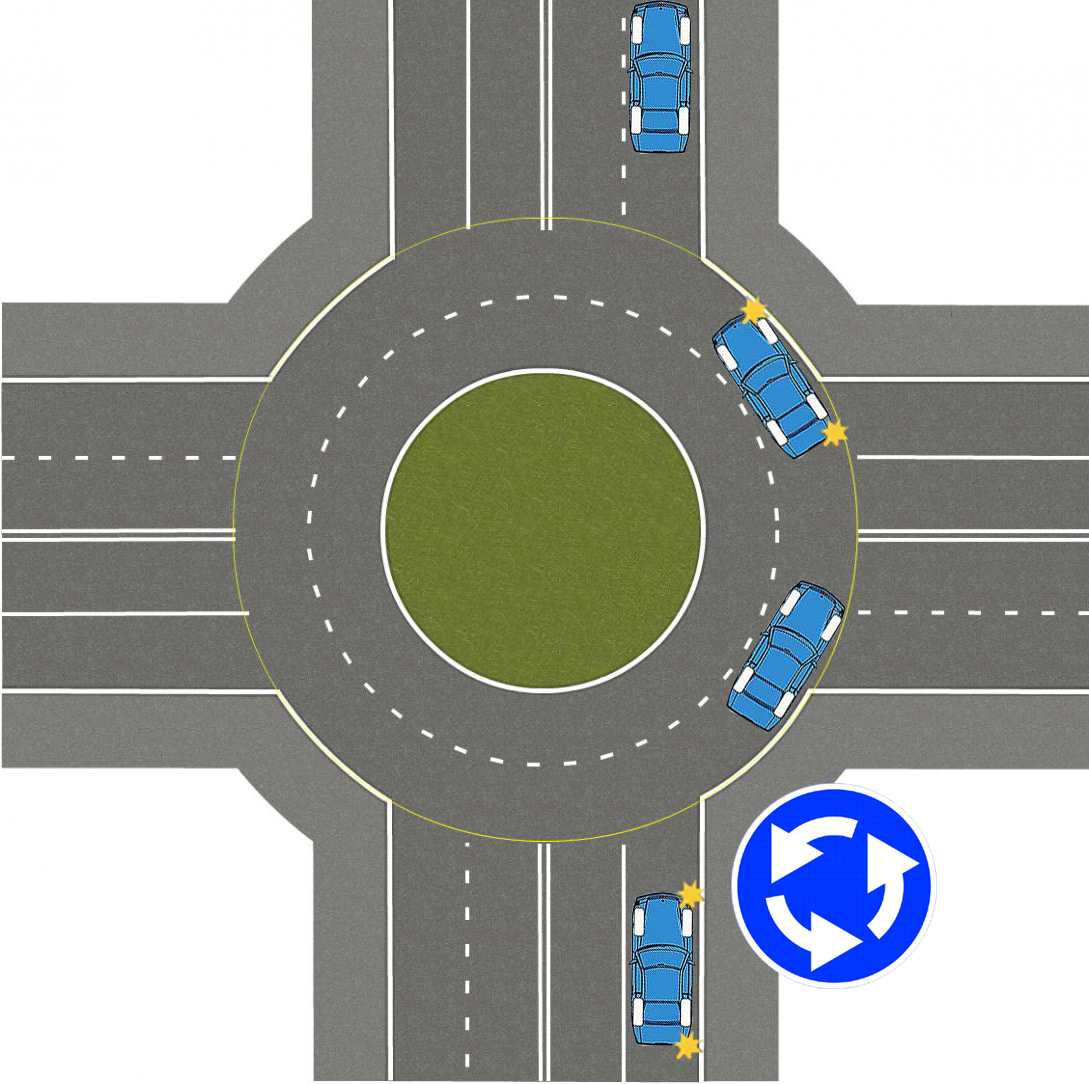 Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
\[a_{T} = \frac{d |\vec{v}|}{dt} \ldotp \label{4.31}\]
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение , которое представляет собой векторную сумму центростремительного и тангенциального ускорений:
\[\vec{a} = \vec{a}_{c} + \vec{a}_{T} \ldotp \label{4.32}\]
Векторы ускорения показаны на рисунке \(\PageIndex{5}\). Обратите внимание, что два вектора ускорения \(\vec{a}_{c}\) и \(\vec{a}_{T}\) перпендикулярны друг другу, при этом \(\vec{a}_{c }\) в радиальном направлении и \(\vec{a}_{T}\) в тангенциальном направлении. Полное ускорение \(\vec{a}\) указывает на угол между \(\vec{a}_{c}\) и \(\vec{a}_{T}\).
Чему равно полное ускорение частицы в момент времени t = 2,0 с?
Стратегия
Нам известны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение. Направление центростремительного ускорения направлено к центру окружности. Найдем величину тангенциального ускорения, взяв производную по времени от |v(t)| используя уравнение \ref{4.{2}\]
и \(\theta\) = tan −1 \(\left(\dfrac{3.1}{1.5}\right)\) = 64° от касательной к окружности. См. рисунок \(\PageIndex{6}\).
Рисунок \(\PageIndex{6}\): Векторы тангенциального и центростремительного ускорения. Чистое ускорение \(\vec{a}\) представляет собой векторную сумму двух ускорений.Значение
Направления центростремительных и тангенциальных ускорений удобнее описывать в полярной системе координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге.
Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс, а также многие другие авторы. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Круговое движение | PhysicsCentral
Руководство для учителя
Введение
Мы уже рассматривали движение предметов, падающих в одном направлении, когда вы его бросаете, или в двух направлениях как часть маятника.Мы также рассмотрели, что происходит, когда объекты падают, одновременно двигаясь в горизонтальном направлении. В этом последнем упражнении мы объединяем все эти знания, чтобы увидеть, что происходит, когда объекты движутся по кругу: во время движения постоянно происходят изменения в горизонтальном и вертикальном направлении, заставляя объект двигаться по круговому пути. Примерами кругового движения являются карусели или карусели в парках, автомобиль, движущийся по кругу, луна, вращающаяся вокруг Земли, или Земля, вращающаяся вокруг Солнца.
Примерами кругового движения являются карусели или карусели в парках, автомобиль, движущийся по кругу, луна, вращающаяся вокруг Земли, или Земля, вращающаяся вокруг Солнца.
В этой статье Кэтрин Джонсон работала над поиском подходящего момента для выключения двигателя спутника, чтобы он приземлился в определенном месте на Земле. Спутники в космосе вращаются вокруг Земли так же, как Луна вращается вокруг Земли. Для этого конкретного уравнения Джонсон работал с элементарной небесной механикой, разделом астрономии, который имеет дело с объектами в космосе. Уравнение, которое она использовала, — это уравнение, в котором сначала рассматривается тело (такое, как наш спутник), на которое действует радиальная сила притяжения, пропорциональная обратному квадрату расстояния.r=p1+ e cos θ Это сложное уравнение является лишь началом в определении расстояния от спутника до центра Земли. Хотя вы можете подумать, что эллипс — это форма, отличная от круга, на самом деле круги — это особый тип эллиптической формы. Объект, который движется по кругу, будет иметь ту же среднюю скорость и высоту, что и объект на эллиптической орбите.
Объект, который движется по кругу, будет иметь ту же среднюю скорость и высоту, что и объект на эллиптической орбите.
Для получения дополнительной информации и идей о том, как реализовать задание в классе, посмотрите видео.
Ключевые термины
Масса: Мера количества материала (или материи) объекта.Не путать с весом или объемом. Это мера того, сколько существует фактического материала, а не того, насколько он велик или насколько сильно что-то его тянет.
Вес: Масса (количество вещества) умножается на силу притяжения планеты (гравитация). Это означает, что ваш вес на Луне будет составлять 1/6 от земного (гравитация на Луне в 0,166 раза больше, чем на Земле). Однако ваша масса останется прежней.
Сила: Толчок или притяжение объекта ощущается из-за взаимодействия с другими объектами.Если взаимодействие прекращается, то силы нет. Формально это определяется как произведение массы на ускорение.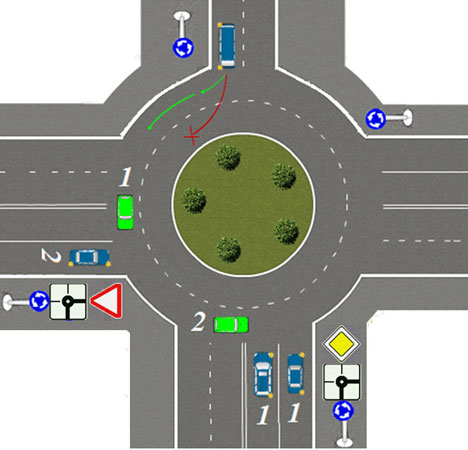 Например, гравитация — это сила, которая представляет собой притяжение Земли ко всем объектам.
Например, гравитация — это сила, которая представляет собой притяжение Земли ко всем объектам.
Центростремительная сила: Общее название любой силы, которая тянет объекты по круговой траектории.
Сила сопротивления: Общее название любой силы, препятствующей движению объектов. Например, сопротивление воздуха, которое мы наблюдали при падении объектов в первом упражнении, или сопротивление, которое вы чувствуете, плавая в бассейне, когда вода вас замедляет.
Скорость: Мера того, насколько быстро что-то движется в определенном направлении. Не путать со скоростью, которая показывает, насколько быстро что-то движется. «Машина ехала со скоростью 65 миль в час на юг по I-95» — это мера скорости. «Американские горки двигались со скоростью 65 миль в час, когда Билли заболел» — это мера скорости.
Тангенциальная скорость: Мгновенная скорость по прямой линии объекта, движущегося по кругу.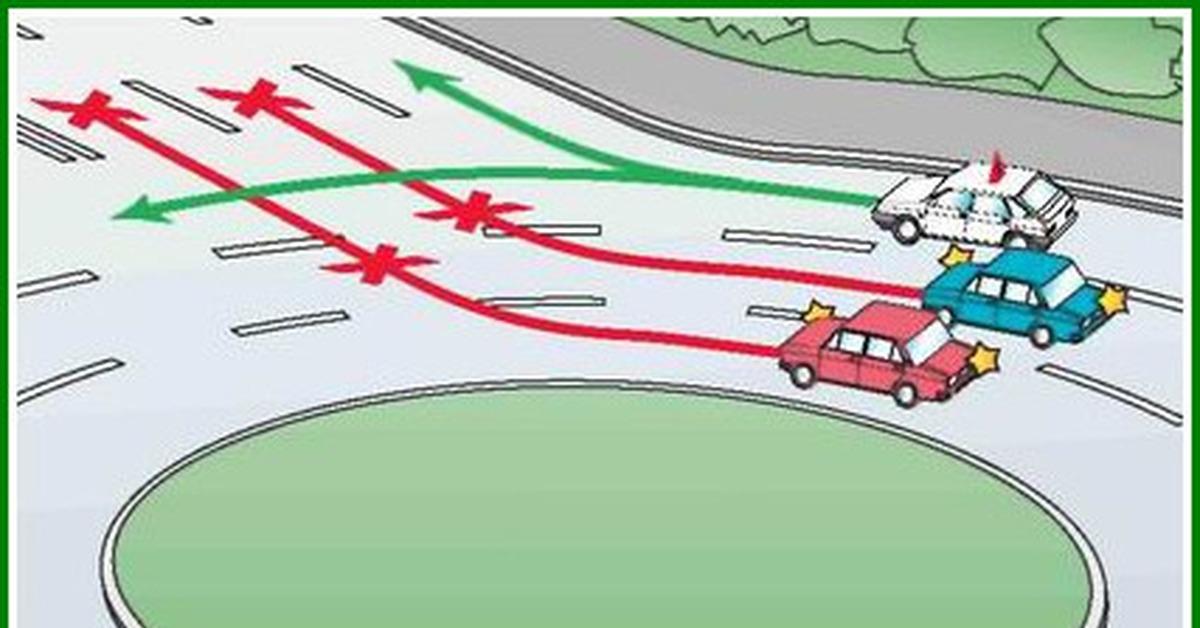 Говорят, что оно мгновенное, потому что при круговом движении направление постоянно меняется, поэтому есть ускорение и сила.
Говорят, что оно мгновенное, потому что при круговом движении направление постоянно меняется, поэтому есть ускорение и сила.
Ускорение: Скорость изменения скорости. Когда что-то ускоряется, меняется скорость или направление движения. Положительное изменение ускорения означает, что объект движется быстрее, скорость автомобиля увеличивается с 30 миль в час до 40 миль в час. Отрицательное изменение означает, что объект движется медленнее, скорость автомобиля увеличивается с 40 до 30 миль в час. Наконец, изменение направления скорости объекта без изменения скорости, например, если автомобиль движется на север и поворачивает на восток, продолжая движение, то автомобиль ускорился, потому что направление скорости автомобиля изменилось.Помните, что скорость — это вектор с направлением и величиной, поэтому изменения любого (или обоих) этих факторов вызовут ускорение.
КЛЮЧЕВОЙ ВОПРОС:
Что происходит, когда центростремительная сила удаляется?
Перед занятием учащиеся должны знать
- Определения силы, скорости и ускорения
- Гравитация Земли заставляет предметы падать и всегда притягивает прямо к полу
- Сила равна массе, умноженной на ускорение, а ускорение означает изменение скорости или направления скорости объекта.

ПОСЛЕ занятия студенты должны знать
- Какие переменные и силы влияют на круговое движение, а какие не влияют.
- Сила, вызывающая круговое движение, направлена к центру окружности. Скорость объекта не меняется, но направление движения постоянно меняется.
- Понимать направление движения объекта, движущегося по кругу, и направление движения, как только он покидает круг.
Наука о круговом движении
В случае с падающими предметами из предыдущей деятельности мы узнали, что силы, воздействующие на предметы, представляют собой силу тяжести, тянущую предметы вниз, и силу сопротивления, толкающую предметы в направлении, противоположном падению. В случае с маятником существовала сила, вызванная натяжением нити, и сила тяжести, тянущая объекты вниз. В случае кругового движения существует сила, которая притягивает объекты внутрь, к центру круга.Мы называем это центростремительной силой. Существование силы говорит нам о наличии ускорения: даже если объект движется с постоянной скоростью, как Луна вокруг Земли, ускорение проявляется в виде изменения направления скорости без изменения скорость.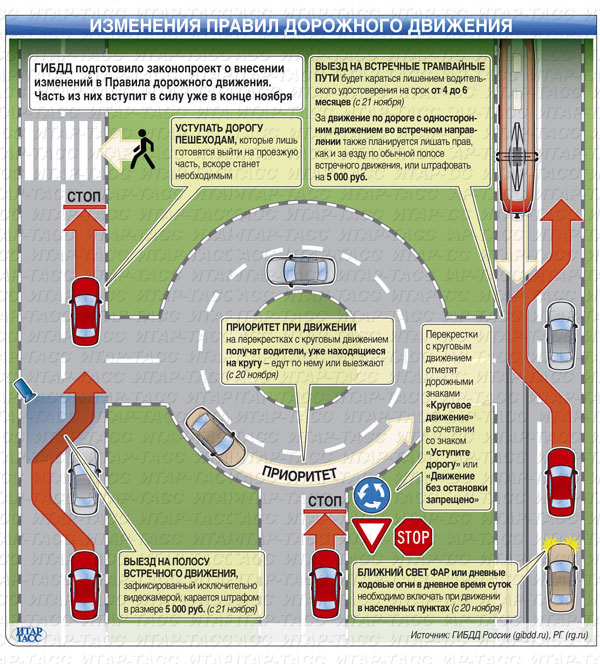 Каким бы ни был объект, если он движется по кругу, на него действует сила, заставляющая его отклоняться от прямолинейного пути, ускоряться внутрь и двигаться по круговому пути. В случае, когда Луна вращается вокруг Земли, сила земного притяжения притягивает Луну к Земле, поскольку она также движется вперед, вызывая круговое движение.Слово «центростремительный» означает только поиск центра, поэтому центростремительная сила — это любая сила, которая тянет объект по круговой траектории. В качающемся йо-йо это веревка, которая удерживает йо-йо и тянет его к точке поворота. В случае вращающихся вокруг планет или лун это сила гравитации, притягивающая вращающийся объект к объекту, вокруг которого они вращаются, что означает, что сила гравитации Земли притягивает Луну внутрь.
Каким бы ни был объект, если он движется по кругу, на него действует сила, заставляющая его отклоняться от прямолинейного пути, ускоряться внутрь и двигаться по круговому пути. В случае, когда Луна вращается вокруг Земли, сила земного притяжения притягивает Луну к Земле, поскольку она также движется вперед, вызывая круговое движение.Слово «центростремительный» означает только поиск центра, поэтому центростремительная сила — это любая сила, которая тянет объект по круговой траектории. В качающемся йо-йо это веревка, которая удерживает йо-йо и тянет его к точке поворота. В случае вращающихся вокруг планет или лун это сила гравитации, притягивающая вращающийся объект к объекту, вокруг которого они вращаются, что означает, что сила гравитации Земли притягивает Луну внутрь.
Эксперимент 1
Материалы
- мячи разных размеров и из разных материалов (используйте разные мячи из предыдущих экспериментов, чтобы увидеть, есть ли разница)
- пластины с бортиком
Материалы можно заменить любыми маленькими шариками или даже сделать из пластилина. Для тарелки вы можете использовать картон, чтобы сделать обод. Идея состоит в том, чтобы создать стену, которая будет направлять движение мяча, и вы также можете вырезать в ней отверстие, чтобы увидеть, что произойдет, когда мяч вылетит через отверстие.
Для тарелки вы можете использовать картон, чтобы сделать обод. Идея состоит в том, чтобы создать стену, которая будет направлять движение мяча, и вы также можете вырезать в ней отверстие, чтобы увидеть, что произойдет, когда мяч вылетит через отверстие.
Настройка
В классе попросите учащихся работать в группах. Дайте им время подумать о примерах кругового движения и обсудите с классом, какие силы участвуют в движении мяча. Решите всем классом, как вы собираетесь проверять, есть ли сила, заставляющая мяч двигаться по кругу — наука происходит в сообществе!
Чтобы понять, что происходит, когда вы удаляете центростремительную силу, учащиеся сначала должны понять, что заставляет объекты двигаться по окружности.Например, шарик можно заставить двигаться по кругу, если толкнуть шарик, удерживаемый круглым объектом, например тарелкой. Мрамор будет следовать по круговой траектории, потому что поверхность мрамора давит на поверхность пластины.
Возьмите тарелку с бортиком и положите на тарелку один из шариков.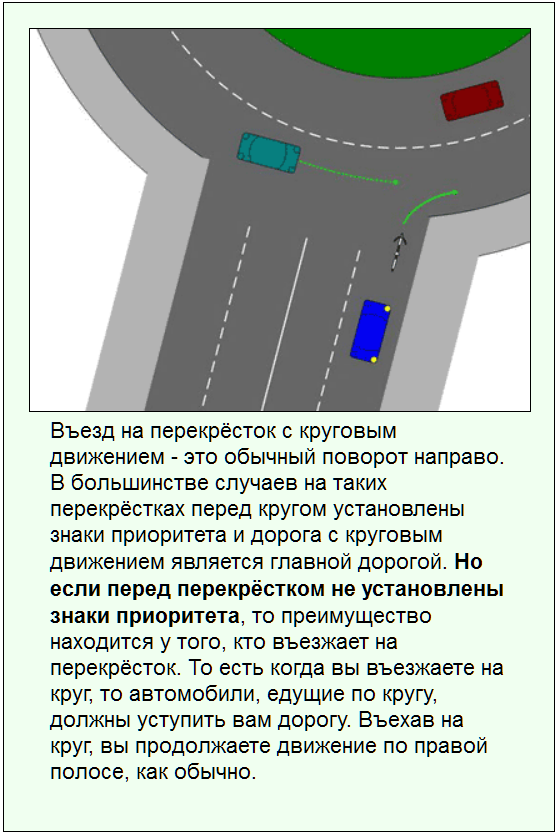 Слегка толкните мяч и наблюдайте за траекторией движения.
Слегка толкните мяч и наблюдайте за траекторией движения.
Подумайте, какие силы вызывают движение — вы можете предложить учащимся подумать о контакте мяча с тарелкой и о том, чем он отличается от силы воздуха, соприкасающейся с падающим листом бумаги, в первом задании.Подумайте о том, каково направление движения, направление скорости и как это связано с направлением силы.
Используйте вторую тарелку и сделайте надрез по краю тарелки. Повторите предыдущие шаги: слегка толкните мяч и наблюдайте за его движением.
Мяч все еще движется по кругу? Что происходит с мячом, когда он попадает в вырезанную часть? Попросите учащихся нарисовать предсказание, в каком направлении будет двигаться мяч, когда он выйдет из выреза.
Всегда ли мяч выходит через вырез? Изменяется ли оно в зависимости от того, насколько быстро или медленно движется мяч? Когда мяч вылетает, он всегда следует одной и той же траектории или она меняется в зависимости от того, как быстро он движется?
Эксперимент 2: вращение вифлбола
Во втором эксперименте мы просим учащихся спланировать эксперимент, чтобы проверить, в каком направлении полетит виффлбол, если вы отпустите веревку во время его вращения. Как и в первом эксперименте, мы хотим, чтобы учащиеся поразмышляли над тем, какие силы действуют на виффлбол, когда они его крутят, и что произойдет, если они отпустят веревку.Они также должны учитывать, будет ли мяч вести себя по-разному, если они будут вращать его вертикально или горизонтально. Обратите внимание, что если они дадут мячу дополнительный толчок, прежде чем отпустить струну, это повлияет на движение виффлбола. Учащиеся должны понимать разницу между тем, чтобы просто отпустить мяч, и тем, чтобы дать ему дополнительный толчок. Идея двух экспериментов состоит в том, чтобы понять движение объектов по кругу и то, как при круговом движении сила на самом деле вызывается постоянным изменением направления скорости.
Как и в первом эксперименте, мы хотим, чтобы учащиеся поразмышляли над тем, какие силы действуют на виффлбол, когда они его крутят, и что произойдет, если они отпустят веревку.Они также должны учитывать, будет ли мяч вести себя по-разному, если они будут вращать его вертикально или горизонтально. Обратите внимание, что если они дадут мячу дополнительный толчок, прежде чем отпустить струну, это повлияет на движение виффлбола. Учащиеся должны понимать разницу между тем, чтобы просто отпустить мяч, и тем, чтобы дать ему дополнительный толчок. Идея двух экспериментов состоит в том, чтобы понять движение объектов по кругу и то, как при круговом движении сила на самом деле вызывается постоянным изменением направления скорости.
Мы снова просим студентов подумать, на какие вопросы они пытаются ответить, посмотреть, какие материалы у них есть, и спланировать эксперимент, используя эти материалы, чтобы ответить на вопрос исследования. Мы просим студентов использовать научный метод в качестве ориентира для планирования эксперимента.
Научный метод состоит из пяти основных шагов плюс один шаг обратной связи:
- Проведите наблюдение.
- Задать вопрос.
- Сформулируйте гипотезу или проверяемое объяснение.
- Сделать прогноз на основе гипотезы.
- Проверить предсказание.
- Итерация: используйте результаты для выдвижения новых гипотез или прогнозов.
Предупреждение
Убедитесь, что вокруг вас достаточно места, чтобы размахивать вифлболом.
Материалы
- Строка
- Шарик для вифле
- Камера для записи эксперимента (опционально)
Материалы можно заменить любым небольшим предметом, к которому можно привязать веревку или даже сделать из пластилина.
Возьмите веревку и прикрепите ее к вифлболу. Убедитесь, что веревка натянута так, чтобы вифлбол не слетел.
Вращайте веревку с прикрепленным к ней вифлболом. Попробуйте вращать его в горизонтальном и вертикальном направлениях. Попросите учащихся предсказать, куда улетит вифлбол, если они отпустят веревку, и изменится ли направление в зависимости от положения руки/ваффлбола, когда они отпустят веревку.
Попросите учащихся предсказать, куда улетит вифлбол, если они отпустят веревку, и изменится ли направление в зависимости от положения руки/ваффлбола, когда они отпустят веревку.
Подготовьте камеру к записи
Проведите несколько тестов, отпуская струну, когда вы вращаете струну вертикально и горизонтально.Сохраняя круговое движение, вам нужно вращать виффлбол как можно медленнее, чтобы ваша группа действительно могла определить правильную точку выпуска. Позвольте струне двигаться в разных положениях, например, при вращении вверх или вниз, или когда она находится дальше всего от вас при вращении по горизонтали. Вифлбол движется в разных направлениях? Имеет ли значение, вращаетесь ли вы по часовой стрелке или против часовой стрелки?
Проверьте свою догадку с помощью шарика для вифлинга. Проведите эксперимент несколько раз, чтобы убедиться, что вы знаете, что происходит на самом деле.
Учащиеся должны подумать о предметах, движущихся по кругу, и определить, в каком направлении действует сила и в каком направлении находится скорость.
Научные стандарты следующего поколения
Стандарт производительности NGSS HS-PS2-1, в котором второй закон Ньютона применяется к движению объекта по кругу, MP8 и SP3.
HS-ESS1-4. Используйте математические или вычислительные представления, чтобы предсказать движение орбитальных объектов в Солнечной системе.
Соответствующая деятельность по расширению
https://colab.research.google.com/drive/198i8UxglkqkBV2Ed8l0JPXlvSgwSyIGg?usp=sharing
Упражнение, связанное с Кэтрин Джонсон: Математика для кругового движения
Предлагаемые ресурсы
Равномерное круговое движение: Ускоренный курс физики #7
Математика кругового движения
Механика: движение, силы, энергия и гравитация, от частиц до планет
Моделирование
Гравитация и орбиты
Движение в 2D
Революция божьей коровки
4.4 Равномерное круговое движение — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.

- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
- Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна.Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или [latex]d\mathbf{\overset{\to }{v}}\text{/}dt\ne 0.[/latex] Это показано на рисунке.Когда частица движется против часовой стрелки во времени [латекс]\Delta t[/латекс] по круговой траектории, ее вектор положения перемещается из [латекс]\mathbf{\overset{\to }{r}}(t)[/латекс] to [latex]\mathbf{\overset{\to }{r}}(t+\Delta t).[/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex]\mathbf{ \overset{\to }{v}}(t)[/latex] to [latex]\mathbf{\overset{\to }{v}}(t+\Delta t),[/latex] меняет только свое направление. Поскольку вектор скорости [латекс]\mathbf{\overset{\to }{v}}(t)[/latex] перпендикулярен вектору положения [латекс]\mathbf{\overset{\to }{r}}( t), [/latex] треугольники, образованные векторами положения и [latex]\Delta \mathbf{\overset{\to }{r}},[/latex] и векторами скорости и [latex]\Delta \mathbf {\overset{\to}}{v}}[/latex] похожи.
Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или [latex]d\mathbf{\overset{\to }{v}}\text{/}dt\ne 0.[/latex] Это показано на рисунке.Когда частица движется против часовой стрелки во времени [латекс]\Delta t[/латекс] по круговой траектории, ее вектор положения перемещается из [латекс]\mathbf{\overset{\to }{r}}(t)[/латекс] to [latex]\mathbf{\overset{\to }{r}}(t+\Delta t).[/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex]\mathbf{ \overset{\to }{v}}(t)[/latex] to [latex]\mathbf{\overset{\to }{v}}(t+\Delta t),[/latex] меняет только свое направление. Поскольку вектор скорости [латекс]\mathbf{\overset{\to }{v}}(t)[/latex] перпендикулярен вектору положения [латекс]\mathbf{\overset{\to }{r}}( t), [/latex] треугольники, образованные векторами положения и [latex]\Delta \mathbf{\overset{\to }{r}},[/latex] и векторами скорости и [latex]\Delta \mathbf {\overset{\to}}{v}}[/latex] похожи. Кроме того, поскольку [латекс]|\mathbf{\overset{\to }{r}}(t)|=|\mathbf{\overset{\to }{r}}(t+\Delta t)|[/latex] и [латекс]|\mathbf{\overset{\to }{v}}(t)|=|\mathbf{\overset{\to }{v}}(t+\Delta t)|,[/latex] два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
Кроме того, поскольку [латекс]|\mathbf{\overset{\to }{r}}(t)|=|\mathbf{\overset{\to }{r}}(t+\Delta t)|[/latex] и [латекс]|\mathbf{\overset{\to }{v}}(t)|=|\mathbf{\overset{\to }{v}}(t+\Delta t)|,[/latex] два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
[латекс]\frac{\Delta v}{v}=\frac{\Delta r}{r}[/latex] или [латекс]\Delta v=\frac{v}{r}\Delta r.[ /латекс]
Рисунок 4.18 (a) Частица движется по окружности с постоянной скоростью, с векторами положения и скорости в моменты времени [latex]t[/latex] и [latex]t+\Delta t.{2}}{r}.[/латекс] Направление ускорения также можно найти, заметив, что по мере того, как [латекс]\Delta t[/латекс] и, следовательно, [латекс]\Дельта \тета[/латекс] приближаются к нулю, вектор [латекс]\Дельта \mathbf{ \overset{\to }{v}}[/latex] приближается к направлению, перпендикулярному [латексу]\mathbf{\overset{\to }{v}}.[/latex] В пределе [латекс]\Delta t\ на 0,[/латекс] [латекс]\Delta \mathbf{\overset{\to} {v}}[/латекс] перпендикулярно [латексу]\mathbf{\overset{\to} {v}}.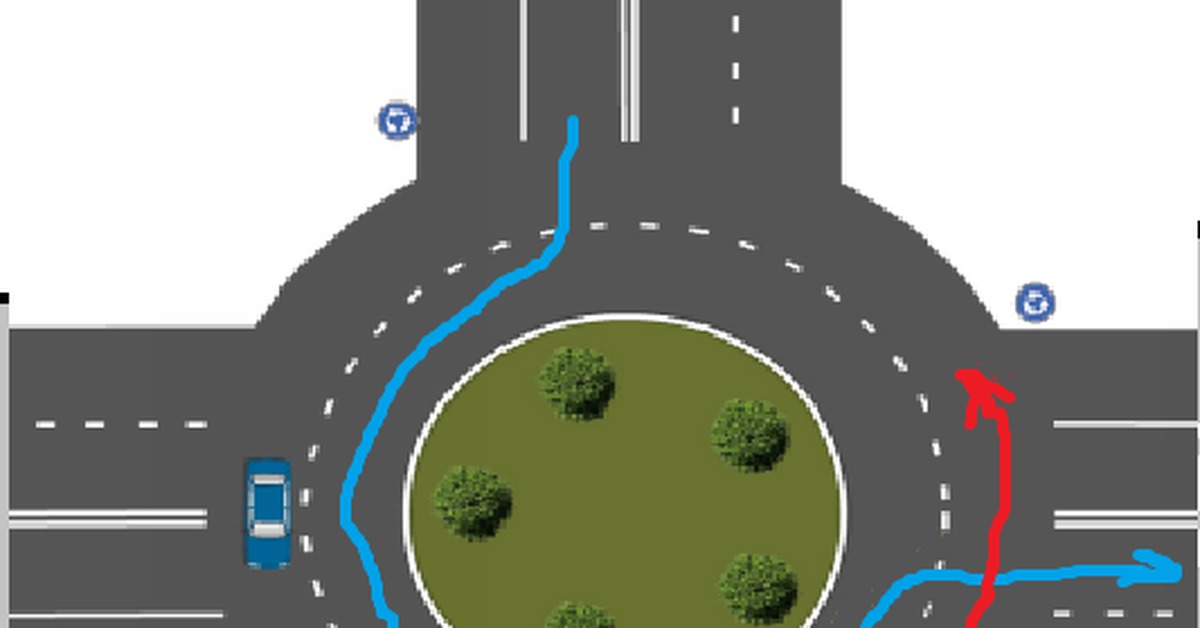 [ /latex] Поскольку [latex]\mathbf{\overset{\to }{v}}[/latex] касается окружности, ускорение [latex]d\mathbf{\overset{\to }{v}}\ text{/}dt[/latex] указывает на центр круга.{2}}{r}.[/латекс]
[ /latex] Поскольку [latex]\mathbf{\overset{\to }{v}}[/latex] касается окружности, ускорение [latex]d\mathbf{\overset{\to }{v}}\ text{/}dt[/latex] указывает на центр круга.{2}}{r}.[/латекс]
Направление вектора ускорения — к центру окружности (рисунок). Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему нижний индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».
Рисунок 4.19 Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении.Вектор скорости также показан и касается окружности.Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения.
Пример
Создание ускорения 1
g Реактивный самолет летит со скоростью 134,1 м/с по прямой линии и делает разворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение 1 g по направлению к центру круговой траектории?
Каким должен быть радиус окружности, чтобы пилот и реактивный самолет получили центростремительное ускорение 1 g по направлению к центру круговой траектории?
Стратегия
Зная скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.{2}}=1835\,\text{м}=1,835\,\text{км}\text{.}[/latex]
Значение
Чтобы создать у пилота большее ускорение, чем g , реактивный самолет должен либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.
Проверьте свое понимание
Маховик имеет радиус 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение [латекс]900.{2}?[/латекс]
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в следующей таблице.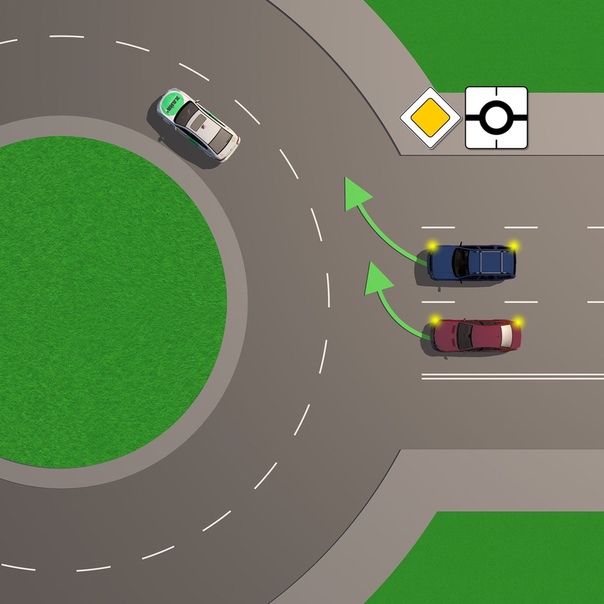
| Объект | Центростремительное ускорение (м/с 2 или коэффициенты g ) |
|---|---|
| Земля вокруг Солнца | [латекс]5,93\раз {10}^{-3}[/латекс] |
| Луна вокруг Земли | [латекс]2. {22}[/латекс] {22}[/латекс] |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана вектором ее положения [латекс]\mathbf{\overset{\to }{r}}(t).[/latex] На рисунке показана частица, совершающая круговое движение против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [latex]\mathbf{\overset{\to }{r}}(t)[/latex], образующий угол [latex]\theta[/latex] с осью x-, показан с компонентами вдоль x – и y — оси.Величина вектора положения равна [латекс] A = |\ mathbf {\ overset {\ to }{r}} (t) | [/ латекс], а также радиусу окружности, так что с точки зрения его компонентов ,
[латекс]\mathbf{\overset{\to}}{r}}(t)=A\,\text{cos}\,\omega t\mathbf{\hat{i}}+A\,\text{ sin}\,\omega t\mathbf{\hat{j}}.[/latex]
Здесь [латекс]\омега[/латекс] — константа, называемая угловой частотой частицы. Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду.Угол [латекс]\тета[/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс]\омега t[/латекс].
Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду.Угол [латекс]\тета[/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс]\омега t[/латекс].
Если T — это период движения или время совершения одного оборота ([латекс]2\пи[/латекс] рад), то
[латекс]\omega =\frac{2\pi }{T}.[/latex]
Рисунок 4.20 Вектор положения частицы в круговом движении с его компонентами вдоль осей x и y. Частица движется против часовой стрелки. Угол [латекс]\тета[/латекс] — это угловая частота [латекс]\омега[/латекс] в радианах в секунду, умноженная на t.Скорость и ускорение можно получить из функции положения дифференцированием:
[латекс] \ mathbf {\ overset {\ to {v}} (t) = \ frac {d \ mathbf {\ overset {\ to {r}} (t)} {dt} = \ text {− } A \ omega \, \ text {sin} \, \ omega t \ mathbf {\ hat {i}} + A \ omega \, \ text {cos} \, \ omega t \ mathbf {\ hat {j}} .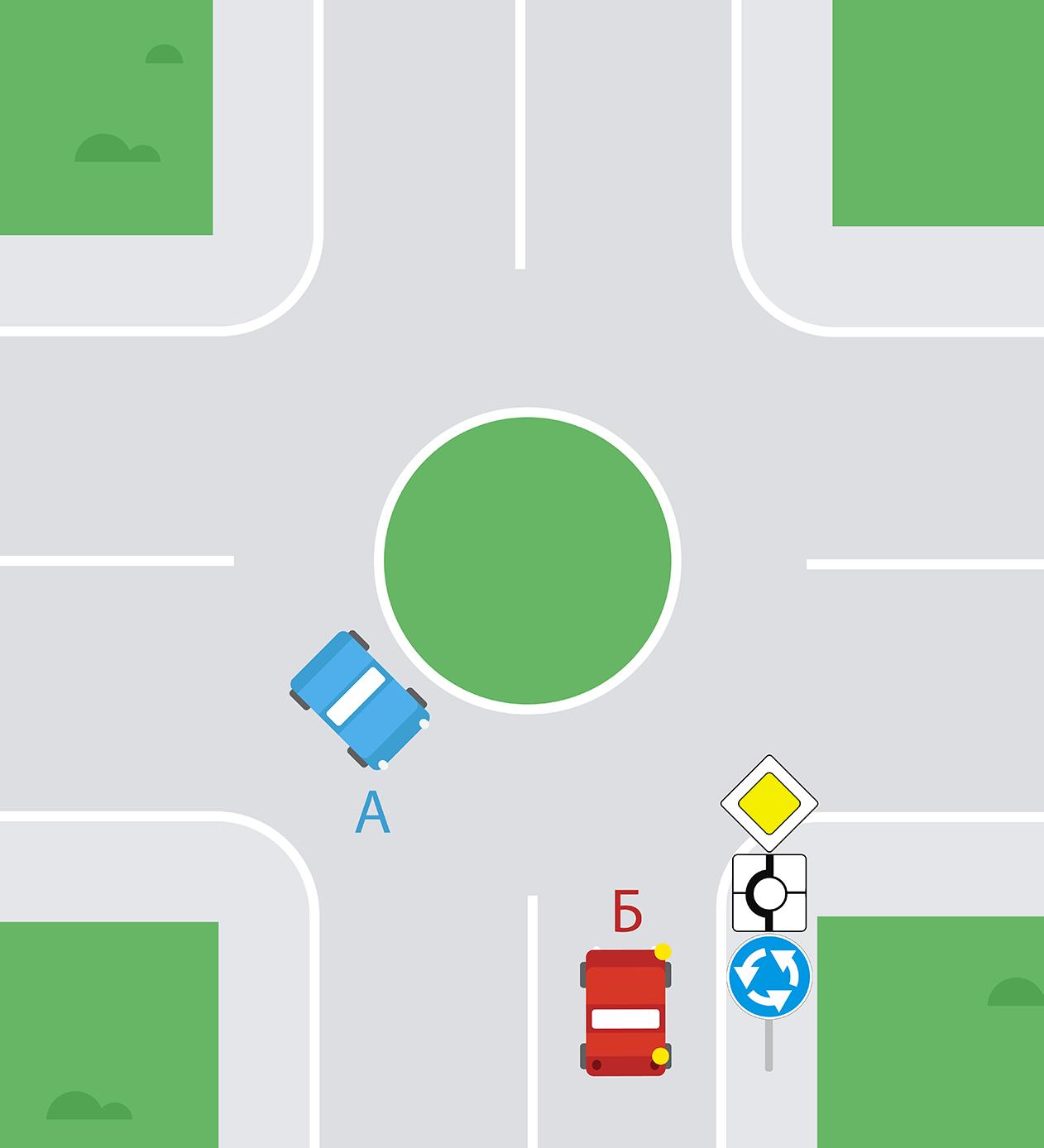 {2} \, \ text {sin} \, \ омега т \ mathbf {\ шляпа {j}}.{-7}\text{s}=200\,\text{ns}\text{.}[/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
{2} \, \ text {sin} \, \ омега т \ mathbf {\ шляпа {j}}.{-7}\text{s}=200\,\text{ns}\text{.}[/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы на оси x-. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно быть с постоянной скоростью.Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени.Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени.Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
[латекс] {a} _ {\ text {T}} = \ frac {d | \ mathbf {\ overset {\ to {v}} |} {dt}. [/latex]
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение , которое представляет собой векторную сумму центростремительного и тангенциального ускорений:
[латекс] \ mathbf {\ overset {\ to {a}} = {\ mathbf {\ overset {\ to {a}}} _ {\ text {C}} + {\ mathbf {\ overset {\ на {a}}}_{\text{T}}.[/латекс]
Векторы ускорения показаны на рисунке. Обратите внимание, что два вектора ускорения {a}}}_{\text{T}}[/latex] перпендикулярны друг другу, при этом [latex]{\mathbf{\overset{\to}}{a}}}_{\text{C}} [/latex] в радиальном направлении и [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}[/latex] в тангенциальном направлении. Полное ускорение [латекс]\mathbf{\overset{\to }{a}}[/latex] указывает на угол между [латекс]{\mathbf{\overset{\to }{a}}}_{\text {C}}[/латекс] и [латекс]{\mathbf{\overset{\to}}{a}}}_{\text{T}}.[/латекс]
Полное ускорение [латекс]\mathbf{\overset{\to }{a}}[/latex] указывает на угол между [латекс]{\mathbf{\overset{\to }{a}}}_{\text {C}}[/латекс] и [латекс]{\mathbf{\overset{\to}}{a}}}_{\text{T}}.[/латекс]
Пример
Общее ускорение во время кругового движения
Частица движется по окружности радиусом r = 2,0 м. На интервале времени от до = 1.{2}},\enspace{c}_{1}=4.0\,\text{m}\text{/}\text{s,}\enspace{c}_{2}=6.0\,\text{ m}\cdot\text{s}\text{.}[/latex]
Чему равно полное ускорение частицы при т = 2,0 с?
Стратегия
Нам известны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение.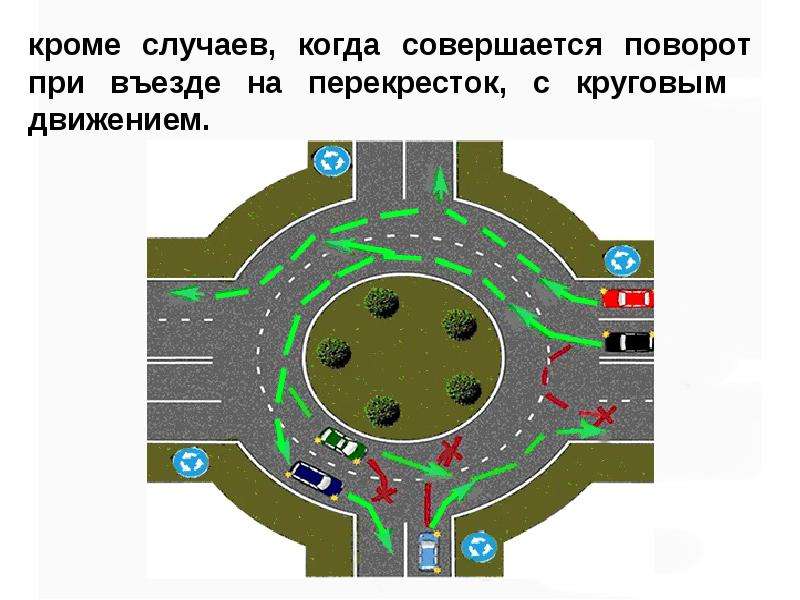 Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекс]|v(t)|[/латекс] с помощью рисунка и оценив ее при t = 2.\circ[/latex] от касательной к окружности. См. рисунок.
Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекс]|v(t)|[/латекс] с помощью рисунка и оценив ее при t = 2.\circ[/latex] от касательной к окружности. См. рисунок.
Значение
Направления центростремительных и тангенциальных ускорений удобнее описывать в полярной системе координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге.{2}\text{/}р.[/латекс]
 Это ускорение называется тангенциальным ускорением [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}.[/latex] величина скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности.Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
Это ускорение называется тангенциальным ускорением [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}.[/latex] величина скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности.Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.Концептуальные вопросы
Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?
Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?
Проблемы
Маховик вращается со скоростью 30 об/с. {2} = r \ enspace {a} _ { \текст{С}}=78.4,\enspace v=8.85\,\text{m}\text{/}\text{s}[/latex]
{2} = r \ enspace {a} _ { \текст{С}}=78.4,\enspace v=8.85\,\text{m}\text{/}\text{s}[/latex]
[латекс]T=5,68\,\text{s,}[/latex], что составляет [латекс]0,176\,\text{rev}\text{/}\text{s}=10,6\,\text{rev }\текст{/}\текст{мин}[/латекс]
Бегун, участвующий в забеге на 200 м, должен обежать конец дорожки, имеющей дугу окружности с радиусом кривизны 30,0 м. Бегун начинает гонку с постоянной скоростью. Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы?
Каково ускорение Венеры по направлению к Солнцу, если предположить, что она движется по круговой орбите?
Показать решениеВенере 108 лет.{2}[/латекс]
Экспериментальная реактивная ракета летит вокруг Земли по экватору прямо над ее поверхностью. С какой скоростью должна двигаться струя, если модуль ее ускорения равен g ?
Вентилятор вращается с постоянной скоростью 360,0 об/мин.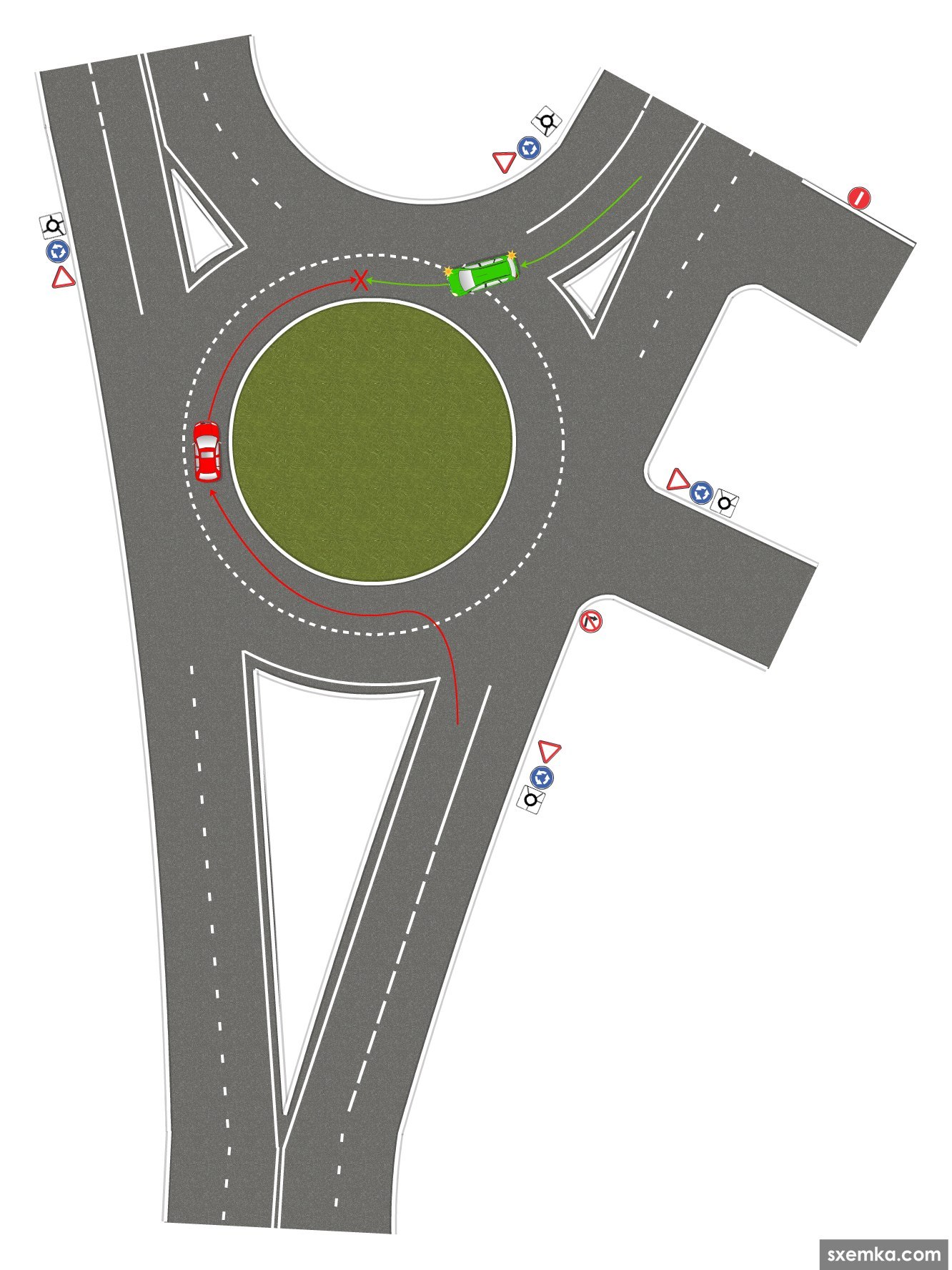 Чему равно ускорение точки одной из его лопастей на расстоянии 10,0 см от оси вращения?
Чему равно ускорение точки одной из его лопастей на расстоянии 10,0 см от оси вращения?
[latex]360\,\text{rev}\text{/}\text{min}=6\,\text{rev}\text{/}\text{s}[/latex]
[латекс]v=3.{2}.[/latex] Как далеко точка от оси вращения секундной стрелки?
Глоссарий
- угловая частота
- [латекс]\омега,[/латекс] скорость изменения угла, с которым объект движется по круговой траектории
- центростремительное ускорение
- составляющая ускорения объекта, движущегося по окружности, направленная радиально внутрь к центру окружности
- тангенциальное ускорение
- величина которого есть скорость изменения скорости во времени.Его направление касается окружности.
- общее ускорение
- векторная сумма центростремительного и тангенциального ускорений
Равномерное круговое движение
Равномерное круговое движениеСледующий: Рабочий пример 11.
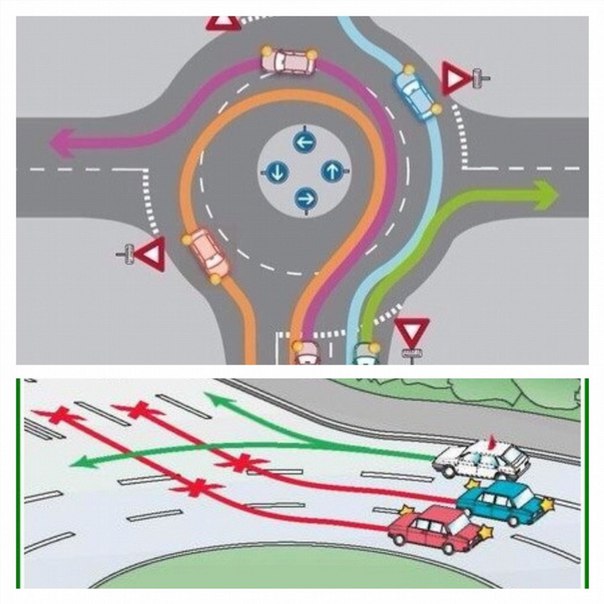 1: Поршень Вверх: Колебательное движение Предыдущий: Составной маятник Рассмотрим объект, совершающий равномерное круговое движение радиусом . Давайте установим
декартова система координат, начало которой совпадает с центром окружности,
и который таков, что движение ограничено плоскостью.Как показано на рис. 99, мгновенное положение объекта может быть удобно
параметризованный в терминах угла .
1: Поршень Вверх: Колебательное движение Предыдущий: Составной маятник Рассмотрим объект, совершающий равномерное круговое движение радиусом . Давайте установим
декартова система координат, начало которой совпадает с центром окружности,
и который таков, что движение ограничено плоскостью.Как показано на рис. 99, мгновенное положение объекта может быть удобно
параметризованный в терминах угла . Поскольку объект совершает равномерное круговое движение, мы ожидаем, что угол увеличится линейно со временем. Другими словами, мы можем написать
| (536) |
где — угловая частота вращения ( i.е. , число радиан, через которое объект вращается в секунду).
 Здесь для удобства принято, что при .
Здесь для удобства принято, что при . Из простой тригонометрии можно записать — и -координаты объекта
соответственно. Отсюда, объединяя предыдущие уравнения, получаем
Здесь использовано тригонометрическое тождество . Сравнение двух приведенных выше уравнений со стандартным уравнением простого гармонического движения, уравнение(505), показывает, что наш объект совершает простое гармоническое движение одновременно по обеим — и -оси. Обратите внимание, однако, что эти два движения ( т.е. , радианы) вне фазы . При этом амплитуда движения равна радиусу окружности. Ясно, что существует тесная связь между простым гармоническим движением и круговое движение.
Следующий: Рабочий пример 11.1: Поршень Вверх: Колебательное движение Предыдущий: Составной маятник Ричард Фицпатрик 2006-02-02
Механика с анимацией и фильмом.
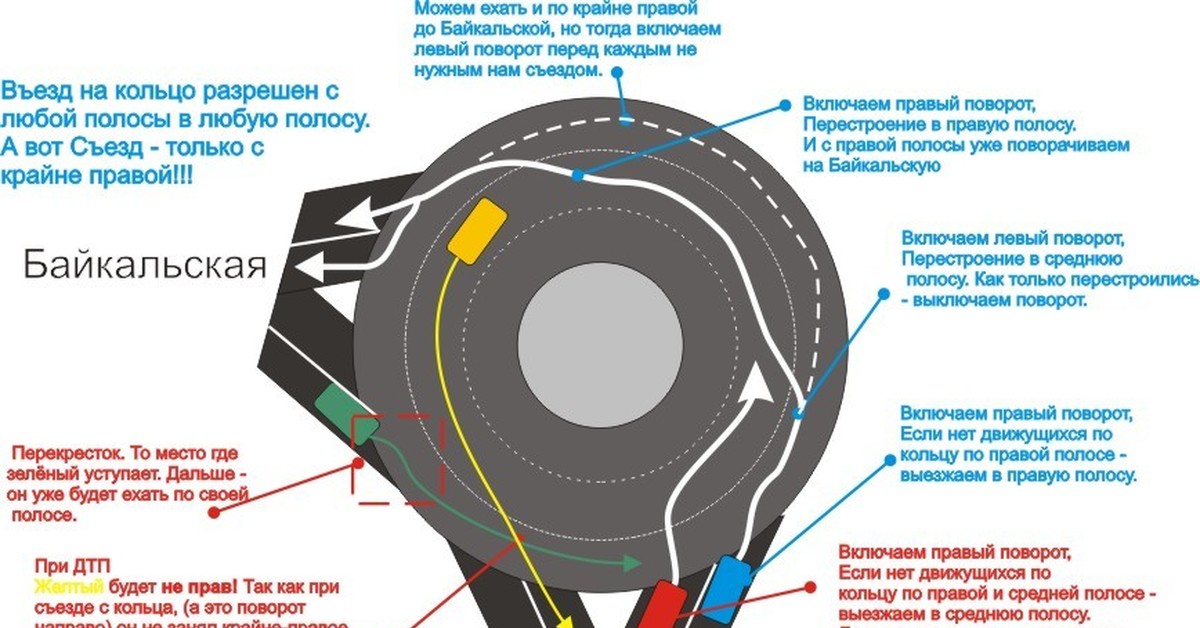 Приведенная ниже анимация представлена в модуле «Круговое движение» и воспроизводится здесь для тех, кто хотел бы просмотреть ее в замедленном режиме.
Приведенная ниже анимация представлена в модуле «Круговое движение» и воспроизводится здесь для тех, кто хотел бы просмотреть ее в замедленном режиме.Автомобиль движется с постоянной скоростью по холму, на вершине которого радиус кривизны в вертикальной плоскости составляет 30 м, как показано на рисунке. Найдем критическую скорость v crit , при которой автомобиль теряет контакт с дорогой.
Следуя по дороге с постоянной скоростью, автомобиль совершает равномерное круговое движение. Следовательно, на вершине холма его ускорение направлено вниз, и его величина равна v 2 /r.Какие силы действуют на него? Его вес является одной из таких сил. Как правило, существует также нисходящая составляющая силы, с которой воздух воздействует на автомобиль*. Для нашего случая эта вторая сила пренебрежимо мала по сравнению с весом. (См. Сопротивление воздуха, чтобы получить верхний предел.)
Итак, на вершине холма вес является единственной силой, направленной вниз, поэтому максимальное ускорение вниз равно g, что, как мы видели в модуле Снаряд, составляет 9,8 м. с −2 . Теперь нисходящее центростремительное ускорение, когда автомобиль находится на вершине холма, равно v 2 /r, и это ускорение не может быть больше, чем g.Таким образом, критические ускорение и скорость равны
с −2 . Теперь нисходящее центростремительное ускорение, когда автомобиль находится на вершине холма, равно v 2 /r, и это ускорение не может быть больше, чем g.Таким образом, критические ускорение и скорость равны
- a крит = v крит 2 /r = g.
- v крит = √(rg) = 17 мс −1 = 62 к.ч.

* Гоночные автомобили часто имеют большую фольгу, эффект которой на высокой скорости состоит в том, чтобы обеспечить направленную вниз силу и, таким образом, увеличить силу трения при прохождении поворотов, торможении и даже ускорении. Некоторые трамваи имеют миниатюрную версию этой фольги.Они имеют несколько возможных функций. Во-первых, они определяют стиль водителя, что может служить предупреждением для других водителей. Во-вторых, они увеличивают сопротивление и расход бензина, что выгодно нефтяным компаниям (по крайней мере, в краткосрочной перспективе). Оказывают ли они значительное влияние на создание направленной вниз силы? Принимая вес автомобиля равным 20 кН, увеличение силы, направленной вниз, на 10 % потребует, чтобы фольга прилагала вниз 2 кН. Я не рекомендую следующий эксперимент, но если он может приложить 2 кН, то он должен упруго выдерживать вес нескольких человек, стоящих на нем.
Физика Риджентс Равномерное круговое движение
Центростремительное ускорение
Движение объекта по круговой траектории с постоянной скоростью известно как равномерное круговое движение (UCM). Объект в UCM постоянно меняет направление, и, поскольку скорость является вектором и имеет направление, можно сказать, что объект, подвергающийся UCM, имеет постоянно изменяющуюся скорость, даже если его скорость остается постоянной. И если скорость объекта меняется, он должен ускоряться.Следовательно, объект, подвергающийся UCM, постоянно ускоряется. Этот тип ускорения известен как центростремительное ускорение .
Объект в UCM постоянно меняет направление, и, поскольку скорость является вектором и имеет направление, можно сказать, что объект, подвергающийся UCM, имеет постоянно изменяющуюся скорость, даже если его скорость остается постоянной. И если скорость объекта меняется, он должен ускоряться.Следовательно, объект, подвергающийся UCM, постоянно ускоряется. Этот тип ускорения известен как центростремительное ускорение .
Вопрос : Если автомобиль ускоряется, увеличивается ли его скорость?
Ответ : Это зависит. Его скорость может увеличиваться, или он может ускоряться в направлении, противоположном его скорости (замедляясь). Или его скорость может оставаться постоянной, но при этом увеличиваться, если он движется равномерно по окружности.
Не менее важно определить направление ускорения объекта, поскольку ускорение является вектором. Для этого нарисуем объект, движущийся против часовой стрелки по круговой траектории, и покажем вектор его скорости в два разных момента времени. Поскольку мы знаем, что ускорение — это скорость изменения скорости объекта во времени, мы можем определить направление ускорения объекта, найдя направление изменения его скорости, Δv.
Поскольку мы знаем, что ускорение — это скорость изменения скорости объекта во времени, мы можем определить направление ускорения объекта, найдя направление изменения его скорости, Δv.
Чтобы найти изменение скорости Δv, мы должны вспомнить, что .
Следовательно, нам нужно найти разность векторов v f и v i графически, которую можно переписать в виде .
Вспомните, что для графического сложения векторов мы выстраиваем их в линию, кончик к хвосту, а затем рисуем результирующий вектор от начальной точки (хвоста) нашего первого вектора до конечной точки (конца) нашего последнего вектора.
Значит, вектор ускорения должен указывать в указанном выше направлении. Если я покажу этот вектор обратно на нашу исходную окружность, выстроив ее прямо между начальным и конечным векторами скорости, легко увидеть, что вектор ускорения указывает на центр окружности.
Вы можете повторить эту процедуру из любой точки круга. .. куда бы вы ни пошли, вектор ускорения всегда указывает на центр круга. На самом деле слово центростремительный в центростремительном ускорении означает «центростремительный»!
.. куда бы вы ни пошли, вектор ускорения всегда указывает на центр круга. На самом деле слово центростремительный в центростремительном ускорении означает «центростремительный»!
Итак, теперь мы знаем направление ускорения объекта (к центру круга), но как насчет его величины? Величина центростремительного ускорения объекта находится в справочной таблице и определяется по формуле:
.Круговая скорость
Так как же найти скорость объекта, движущегося по круговой траектории? Формула скорости, которую мы узнали из кинематики, по-прежнему применима.
Однако мы должны быть осторожны в использовании этого уравнения, чтобы понять, что объект, движущийся по круговой траектории, движется по окружности окружности. Следовательно, если бы объект совершил один полный оборот по окружности, расстояние, которое он проходит, было бы равно длине окружности.
Давайте рассмотрим пример задачи:
Вопрос : Миранда едет на своей машине по часовой стрелке по круговой трассе радиусом 30 м.
Она проходит 10 кругов по трассе за 2 минуты. Найдите общее расстояние, пройденное Мирандой, среднюю скорость и центростремительное ускорение.
Ответ :
Центростремительная сила
Если объект, движущийся по круговой траектории, имеет внутреннее ускорение, второй закон Ньютона говорит нам, что должна быть результирующая сила, направленная также к центру окружности. Этот тип силы, известный как центростремительная сила, может быть силой гравитации, натяжением, приложенной силой или даже силой трения.
ПРИМЕЧАНИЕ. При решении задач с круговым движением важно понимать, что центростремительная сила на самом деле не является новой силой, центростремительная сила — это просто ярлык или группа, которую мы применяем к силе, чтобы указать, что ее направление направлено к центру круг. Это означает, что вы никогда не захотите обозначать силу на диаграмме свободного тела как центростремительную силу Fc. Вместо этого назовите силу, направленную по центру, как можно конкретнее. Если напряжение вызывает силу, обозначьте силу FT. Если сила трения вызывает силу, направленную по центру, обозначьте ее Ff и так далее.
Вместо этого назовите силу, направленную по центру, как можно конкретнее. Если напряжение вызывает силу, обозначьте силу FT. Если сила трения вызывает силу, направленную по центру, обозначьте ее Ff и так далее.
Мы можем объединить уравнение для центростремительного ускорения со 2-м законом Ньютона, чтобы получить 2-й закон Ньютона для кругового движения. Напомним, что 2-й закон Ньютона гласит:
Для объекта, движущегося по круговому пути, должна существовать результирующая (центростремительная) сила, направленная к центру кругового пути, чтобы вызвать (центростремительное) ускорение, направленное к центру кругового пути. Тогда мы можем пересмотреть второй закон Ньютона для этого конкретного случая следующим образом:
Тогда, вспоминая нашу формулу для центростремительного ускорения как:
Мы можем сложить их вместе, заменив на в нашем уравнении, чтобы получить объединенную форму 2-го закона Ньютона для равномерного кругового движения:
Конечно, если объект движется по круговой траектории и центростремительная сила устранена, объект будет продолжать двигаться по прямой линии в любом направлении, в котором он двигался в момент устранения силы.
Вопрос : Бегущий назад с усилием 800 Н совершает поворот по круговой траектории r=1 м со скоростью 8 м/с. Найдите массу бегущего, центростремительное ускорение и центростремительную силу.
Ответ : Дано mg=800N, r=1м, v=8м/с; Найти m, a c , F c
Попробуем еще:
Еще одна примерная задача, на этот раз связанная только с алгебраическими манипуляциями:
Частота и период
Для объектов, движущихся по круговым траекториям, мы можем охарактеризовать их движение по окружности, используя термины частота (f) и период (T).Частота объекта — это количество оборотов, которое объект совершает за полную секунду. Измеряется в единицах [1/с] или Герцах (Гц). Точно так же период объекта — это время, необходимое для совершения одного полного оборота. Поскольку период представляет собой временной интервал, он измеряется в секундах. Мы можем связать период и частоту, используя уравнения:
Поскольку период представляет собой временной интервал, он измеряется в секундах. Мы можем связать период и частоту, используя уравнения:
Вопрос : Игрушечный поезд массой 500 г проходит 10 кругов по кругу за 1 мин 40 с.Если диаметр пути равен 1 м, найдите центростремительное ускорение поезда (a c ), центростремительную силу (F c ), период (T) и частоту (f).
Ответ :
Давайте посмотрим на другой пример:
Вертикальное круговое движение
Объекты перемещаются по кругу как по вертикали, так и по горизонтали. Поскольку скорость этих объектов обычно непостоянна, технически это не 90 514 равномерное 90 515 круговое движение, но наши навыки анализа UCM по-прежнему применимы.
Рассмотрим американские горки, движущиеся по вертикальной петле радиусом 10 м. Вы путешествуете по петле вверх ногами, но не падаете с американских горок. Как это возможно? Мы можем использовать наше понимание UCM и динамики, чтобы выяснить это!
Вы путешествуете по петле вверх ногами, но не падаете с американских горок. Как это возможно? Мы можем использовать наше понимание UCM и динамики, чтобы выяснить это!
Внизу круга
Для начала давайте сначала посмотрим на подстаканник, когда машина находится в нижней части петли. На диаграмме свободного тела сила тяжести, действующая на каботажное судно, также известная как его вес, тянет его вниз, поэтому мы рисуем вектор, указывающий вниз, с надписью «mg.«Противодействующей этой силе является нормальная сила толкающих вверх рельсов каботажного судна, которую мы обозначаем F N .
Поскольку каботажное судно движется по круговой траектории, мы можем проанализировать его с помощью разработанных нами инструментов для равномерного кругового движения. Второй закон Ньютона остается в силе, поэтому мы можем написать:
. Обратите внимание: поскольку мы говорим о круговом движении, мы примем соглашение, согласно которому силы, направленные к центру круга, положительны, а силы, направленные от центра круга, отрицательны. В этот момент вспомните, что сила, которую вы «чувствуете», когда находитесь в движении, на самом деле является нормальной силой. Итак, находя нормальную силу, когда вы начинаете двигаться по кругу, мы находим, что
В этот момент вспомните, что сила, которую вы «чувствуете», когда находитесь в движении, на самом деле является нормальной силой. Итак, находя нормальную силу, когда вы начинаете двигаться по кругу, мы находим, что
Поскольку мы знаем, что результирующая сила всегда равна массе, умноженной на ускорение, поэтому результирующая центростремительная сила равна массе, умноженной на центростремительное ускорение, мы можем заменить F NETc следующим образом:
Из полученного уравнения видно, что нормальная сила теперь равна весу плюс дополнительный член от центростремительной силы кругового движения.Когда мы движемся по круговой траектории в нижней части петли, мы чувствуем себя тяжелее своего веса. Говоря простым языком, мы чувствуем дополнительные «перегрузки». Сколько g мы чувствуем, может быть получено с немного большим количеством манипуляций. Если мы перепишем наше уравнение для нормальной силы, вытянув массу, применив распределительное свойство умножения, то получим:
Обратите внимание, что в скобках указано стандартное ускорение свободного падения, g, плюс член от центростремительного ускорения (). Этот дополнительный термин представляет собой дополнительную перегрузку, которую ощущает человек. Например, если c равно g (9,81 м/с 2 ), можно сказать, что человек в тележке испытывает два g (1g от центростремительного ускорения и 1g от гравитационного поля Земли). Если бы c было равно 3×g (29,4 м/с 2 ), человек испытал бы в общей сложности четыре перегрузки.
Этот дополнительный термин представляет собой дополнительную перегрузку, которую ощущает человек. Например, если c равно g (9,81 м/с 2 ), можно сказать, что человек в тележке испытывает два g (1g от центростремительного ускорения и 1g от гравитационного поля Земли). Если бы c было равно 3×g (29,4 м/с 2 ), человек испытал бы в общей сложности четыре перегрузки.
Расширив этот анализ до аналогичной ситуации в другом контексте, попробуйте представить вместо американских горок массу, вращающуюся по вертикальному кругу на веревке.Вы можете заменить нормальную силу натяжением струны в нашем анализе. Поскольку сила больше в нижней части круга, вероятность разрыва струны выше всего, когда масса находится в нижней части круга!
Вершина круга
В верхней части цикла у нас совершенно другая картина. Теперь нормальная сила от рельсов подставки должна давить на тележку, хотя все еще в положительном направлении, поскольку теперь вниз направлена к центру кругового пути. Однако в этом случае вес объекта также указывает на центр круга, поскольку гравитационное поле Земли всегда притягивает к центру Земли. Наша диаграмма свободного тела выглядит значительно иначе, и поэтому наше приложение ко второму закону Ньютона для кругового движения также значительно отличается.
Однако в этом случае вес объекта также указывает на центр круга, поскольку гравитационное поле Земли всегда притягивает к центру Земли. Наша диаграмма свободного тела выглядит значительно иначе, и поэтому наше приложение ко второму закону Ньютона для кругового движения также значительно отличается.
Поскольку сила, которую вы чувствуете, на самом деле является нормальной силой, мы можем найти нормальную силу и разложить результирующую центростремительную силу, как показано:
Из уравнения видно, что нормальная сила теперь равна центростремительной силе за вычетом вашего веса.Если бы центростремительная сила была равна вашему весу, вы бы чувствовали себя невесомыми. Обратите внимание, что это также точка, в которой нормальная сила точно равна 0. Это означает, что рельсы дорожки больше не давят на тележку американских горок … если бы центростремительная сила была хоть немного меньше (скорость автомобиля была чуть меньше), нормальная сила F N была бы меньше 0. Поскольку рельсы физически не могут тянуть тележку в отрицательном направлении (от центра круга), это означает, что вагон падает. с рельсов, и у пассажира тележки будет очень, очень плохой день.Только поддерживая высокую скорость, тележка может успешно преодолевать петлю… если двигаться слишком медленно, тележка падает.
Поскольку рельсы физически не могут тянуть тележку в отрицательном направлении (от центра круга), это означает, что вагон падает. с рельсов, и у пассажира тележки будет очень, очень плохой день.Только поддерживая высокую скорость, тележка может успешно преодолевать петлю… если двигаться слишком медленно, тележка падает.
Чтобы оставаться в безопасности, настоящие американские горки на самом деле имеют колеса с обеих сторон рельсов, чтобы предотвратить падение тележки, если она когда-либо замедляется в верхней части петли, хотя подставки спроектированы таким образом, что на самом деле это никогда не происходит.
Круговое движение
Тело, которое проходит равные расстояния за равные промежутки времени по окружности, имеет постоянную скорость, но не постоянную скорость.Это потому, что скорость является вектором и, следовательно, имеет не только направление, но и величину
. Скорость точки P направлена по касательной в точке P. Скорость остается постоянной, но скорость изменилась. Мы знаем, что если скорость меняется со временем, то шарик на нити тоже ускоряется.
Скорость остается постоянной, но скорость изменилась. Мы знаем, что если скорость меняется со временем, то шарик на нити тоже ускоряется.
Радиан
углов можно измерять как в радианах, так и в градусах. Угол в радианах определяется по формуле. Если с = r , то θ = 1 рад. Следовательно, 1 рад — это угол, стягиваемый в центре окружности дугой, длина которой равна радиусу.Когда с = 2 π r , тогда θ = 2 π радиан = 360°. Следовательно, 1 рад = 360°/2 π=57,3°
.θ = с / r (1)
Поскольку мы часто имеем дело с углами и тригономическими функциями, полезное приближение, которое часто используется, состоит в том, что для малых углов &theta , sin θ и tan θ = θ , где θ измеряется в радианах .
&theta = sin &theta = tan θ для малых углов, где тета измеряется в радианах.
Угловая скорость
Скорость тела, движущегося по окружности, может быть задана либо его скоростью по касательной в любой момент времени (линейная скорость), либо угловой скоростью. Это угол, заметаемый в единицу времени радиусом, соединяющим тело с центром. Измеряется в [рад с -1 ]
Это угол, заметаемый в единицу времени радиусом, соединяющим тело с центром. Измеряется в [рад с -1 ]
Далее, угловая скорость — это время, за которое частица проходит один оборот, деленное на период. ω = 2 π / Т
ω = θ / t (2)
Происхождение
Рассмотрим тело, равномерно движущееся из A в B за время t так, что OA поворачивается на малый угол θ.
Угловая скорость ω тела относительно O равна ω=θ/ t .
Если дуга AB имеет длину с и v — постоянная скорость тела, v = с / t
Но с = r θ 9 9
Итак, v = r θ / t и ω = θ/ t ,
, следовательно, v = rω
v = r / ω (3)
Ускорение
Выражение для ускорения тела, движущегося по окружности радиусом r и движущегося с постоянной скоростью v , получается следующим образом. Если он перемещается из A в B за короткий промежуток времени δ t , то, поскольку скорость = расстояние x время, дуга AB = v δ t .
Если он перемещается из A в B за короткий промежуток времени δ t , то, поскольку скорость = расстояние x время, дуга AB = v δ t .
Также по определению угла в радианах дуга AB = r δθ = v δt .
Итак, v δt / r = δθ .
Векторы v A и v B представляют скорости в этих точках. Изменение скорости между A и B, полученное путем вычитания v A из v B .
Изменение скорости = v A и v B . Правило параллаграмма или правило треугольника. В результате получается XZ. Поскольку один вектор (- v A ) перпендикулярен OA, а другой v B перпендикулярен OA, а другой v B перпендикулярен OB, поэтому ∠ XYZ = ∠ AOB = δθ
Если δt мало, то и δθ мало. Тогда длина XZ на рисунке будет почти такой же, как X’Y’ в b) X’Z’=rδθ, но также δθ=vδt/r.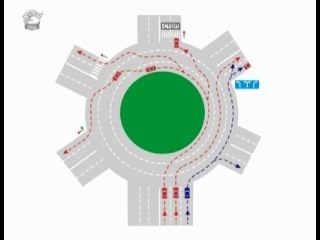 Следовательно, X’Z’=v 2 /r δt.
Следовательно, X’Z’=v 2 /r δt.
a=изменение скорости/интервала времени = (v 2 δt/r)/δt=v 2 /r. Следовательно, a=v 2 /r также a=ω 2 r.
a = v 2 / r (4)
а = r ω 2 (5)
Направление ускорения направлено к центру O, как можно видеть, если δt сделать так, чтобы A и B почти совпадали; Тогда XZ перпендикулярна v A (или v B ) вдоль AO или BO.Мы говорим, что тело имеет центростремительное ускорение (то есть ищет центр). Имеет ли тело, движущееся равномерно по окружности, постоянное ускорение?
Центростремительная сила
Поскольку тело, движущееся по окружности (или дуге окружности), ускоряется, то из 2-го закона Ньютона следует, что на него должна действовать сила, вызывающая ускорение. Эта сила также будет направлена к центру и называется центростремительной силой. Это заставляет тело отклоняться от прямолинейного движения, которому оно должно следовать естественным путем.Величина центростремительной силы определяется как:
Это заставляет тело отклоняться от прямолинейного движения, которому оно должно следовать естественным путем.Величина центростремительной силы определяется как:
F = ma = mv 2 / r (6)
Где м — масса тела, а v — скорость по круговой траектории радиусом r . Если угловая скорость тела равна ω, мы также можем сказать, что v = rω .
F = мА = mrω 2 (7)
Другие примеры кругового движения будут рассмотрены в следующих разделах.Во всех случаях важно понимать, что силы, действующие на тело, должны создавать результирующую силу величины mv 2 / r по направлению к центру.
Экспериментальное измерение центростремительной силы
Поворотная платформа вращается электродвигателем, заставляя тележку известной массы м двигаться от центра поворотной платформы. Движению тележки противодействует пружина, создающая центростремительную силу, необходимую для удержания тележки на месте.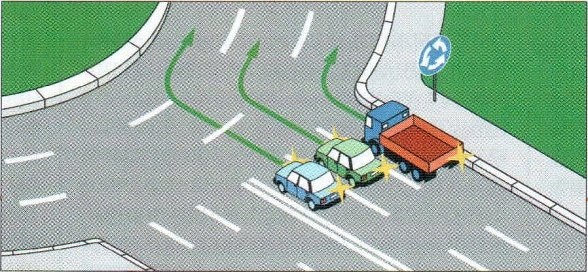 По мере увеличения скорости поворотной платформы пружина растягивается до тех пор, пока тележка не достигнет упора на конце рельсов. Когда грузовик просто врезается в грузовик, удлинение пружины имеет известную длину. Скорость поворотного стола можно найти, измерив время, за которое поворотный стол совершает десять оборотов, и разделив его на десять. Скорость тогда 2π/ t . Мы знаем m и радиус и, следовательно, удлинение пружины. Мы также можем измерить силу, необходимую для получения такого же удлинения, используя пружинные весы, и сравнить две силы.
По мере увеличения скорости поворотной платформы пружина растягивается до тех пор, пока тележка не достигнет упора на конце рельсов. Когда грузовик просто врезается в грузовик, удлинение пружины имеет известную длину. Скорость поворотного стола можно найти, измерив время, за которое поворотный стол совершает десять оборотов, и разделив его на десять. Скорость тогда 2π/ t . Мы знаем m и радиус и, следовательно, удлинение пружины. Мы также можем измерить силу, необходимую для получения такого же удлинения, используя пружинные весы, и сравнить две силы.
Скругление изгиба
Если автомобиль движется по круговому повороту с постоянной скоростью по горизонтальной дороге, результирующая сила, действующая на него, должна быть направлена к центру. т.е. это должна быть центростремительная сила. Эта сила возникает из-за взаимодействия автомобиля с воздухом и дорогой. Направление силы, действующей со стороны воздуха, будет более или менее противоположно мгновенному направлению движения. Другой более важной горизонтальной силой является сила трения, оказываемая дорогой внутрь на шины автомобиля.Равнодействующая этих двух сил и есть центростремительная сила. Если центростремительная сила меньше силы, стремящейся вытащить автомобиль, произойдет занос. Безопасное прохождение поворотов, не зависящее от трения, достигается за счет наклона дороги. Задача состоит в том, чтобы найти угол θ, при котором поворот должен быть креном, чтобы центростремительная сила, действующая на автомобиль, полностью возникала из составляющей нормальной силы, N дороги.
Другой более важной горизонтальной силой является сила трения, оказываемая дорогой внутрь на шины автомобиля.Равнодействующая этих двух сил и есть центростремительная сила. Если центростремительная сила меньше силы, стремящейся вытащить автомобиль, произойдет занос. Безопасное прохождение поворотов, не зависящее от трения, достигается за счет наклона дороги. Задача состоит в том, чтобы найти угол θ, при котором поворот должен быть креном, чтобы центростремительная сила, действующая на автомобиль, полностью возникала из составляющей нормальной силы, N дороги.
Рассматривая автомобиль как частицу и разлагая N по вертикали и горизонтали, мы имеем, так как N sin θ является центростремительной силой. N sin θ = mv 2 / r где м и v — масса, скорость и r — радиус изгиба соответственно. Также предполагается, что автомобиль остается в той же горизонтальной плоскости, поэтому горизонтальное ускорение отсутствует, поэтому N cos θ = мг .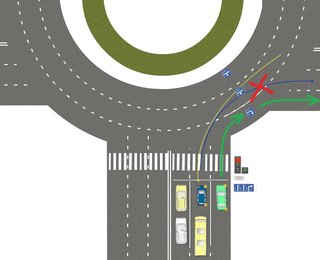 Разделив оба уравнения, tan θ = v 2 / rg
Разделив оба уравнения, tan θ = v 2 / rg
Изгиб железнодорожного пути также имеет наклон. При этом для того, чтобы при определенной скорости не приходилось оказывать поперечного усилия наружным рельсом на гребни колес поезда, иначе рельсы деформируются.Горизонтальную составляющую нормальных усилий рельсов на поезде обеспечивает центростремительная сила.
Самолет
Рисунок. Самолет с креном использует горизонтальную составляющую подъемной силы, чтобы обеспечить центростремительную силу для поворота.
Самолет в прямолинейном горизонтальном полете испытывает подъемную силу, перпендикулярную поверхности его крыльев, которая уравновешивает его вес, mg . Чтобы сделать разворот, элероны работают так, что крен самолета и горизонтальная составляющая подъемной силы создают центростремительную силу, необходимую для поворота самолета.Подъемная сила всегда перпендикулярна крыльям, поэтому вес самолета должен поддерживаться вертикальной составляющей подъемной силы. Поскольку это немного меньше, чем вес самолета, самолет будет терять высоту, если подъемная сила не будет увеличена за счет увеличения скорости или поднятия носа самолета.
Поскольку это немного меньше, чем вес самолета, самолет будет терять высоту, если подъемная сила не будет увеличена за счет увеличения скорости или поднятия носа самолета.
Ротор
Ротор часто можно увидеть на ярмарке. Цилиндр диаметром около 4 метров приводится во вращение. Пассажиры стоят внутри цилиндра у стены, пока он вращается.Вращательное движение заставляет пассажиров прижиматься к стенке ротора. Когда ротор вращается достаточно быстро, дно цилиндра опускается, а пассажиры остаются прижатыми к стенкам. Показаны силы, действующие на пассажира высотой м . N — это нормальная сила и центростремительная сила, необходимая для того, чтобы он двигался по кругу. Следовательно, если r — радиус ротора, а v — скорость пассажиров, то N = mv 2 /r.Если F — это сила трения, действующая вверх между пассажиром и стенкой ротора, поскольку вертикальное движение пассажира отсутствует. F = мг . Если μ — коэффициент предельного трения между пассажиром и стеной, мы имеем F = μН . Следовательно, мкН = мг , мкН = мг/Н = г/об 2 . Обратите внимание, что это не зависит от массы m .
Следовательно, мкН = мг , мкН = мг/Н = г/об 2 . Обратите внимание, что это не зависит от массы m .
Типичное значение μ между одеждой и стенкой ротора (с брезентовой подкладкой) составляет около 0.40, поэтому, если r=2m. v=5 мс -1 . Какой будет угловая скорость?
Так как v = rω , &омега =7/2 =3,5 рад с -1 . Число оборотов в минуту = (3,5 рад -1 x 60 сек)/2π рад=210/2π=105/π
Зацикливание цикла
Рассмотрим ведро с водой, когда оно находится в верхней части петли А. Если вес воды мг меньше, чем mv 2 / r , нормальная сила Н дна петли ведро на воде.Однако, если ведро качается медленнее, чем mg , будет mv 2 / r , а остаточная часть веса заставляет воду покидать ведро.
Центрифуги и стиральные машины
Одежда повреждается в стиральной машине из-за высокой силы тяжести
Космический лифт
Одно применение центростремительной силы и кругового движения обнаружено в космическом лифте. Он был предложен русским ученым Юрием Арцутановым в 1960 году как возможный способ попасть в космос.Он работает по принципу, что при обращении вокруг Земли над экватором объект с периодом 24 часа будет оставаться в том же положении над Землей (см. Геостационарные спутники). Если бы с объекта нужно было спустить веревку, то кабина лифта могла бы подняться по веревке в космос без необходимости в ракете. Поскольку веревка имеет массу, дополнительный вес веревки заставит удерживающий ее спутник притянуться к Земле. Однако противовес, вращающийся вокруг Земли на большем расстоянии, чем геостационарная высота, будет двигаться быстрее, чтобы оставаться в том же положении над экватором, центростремительная сила противовеса может быть уравновешена весом веревки.В результате веревка остается на месте, и космический лифт становится возможным.
Он был предложен русским ученым Юрием Арцутановым в 1960 году как возможный способ попасть в космос.Он работает по принципу, что при обращении вокруг Земли над экватором объект с периодом 24 часа будет оставаться в том же положении над Землей (см. Геостационарные спутники). Если бы с объекта нужно было спустить веревку, то кабина лифта могла бы подняться по веревке в космос без необходимости в ракете. Поскольку веревка имеет массу, дополнительный вес веревки заставит удерживающий ее спутник притянуться к Земле. Однако противовес, вращающийся вокруг Земли на большем расстоянии, чем геостационарная высота, будет двигаться быстрее, чтобы оставаться в том же положении над экватором, центростремительная сила противовеса может быть уравновешена весом веревки.В результате веревка остается на месте, и космический лифт становится возможным.
Несмотря на то, что теория верна, предстоит решить серьезные технические проблемы, прежде чем космический лифт станет реальностью. Во-первых, это свойства материала веревки.

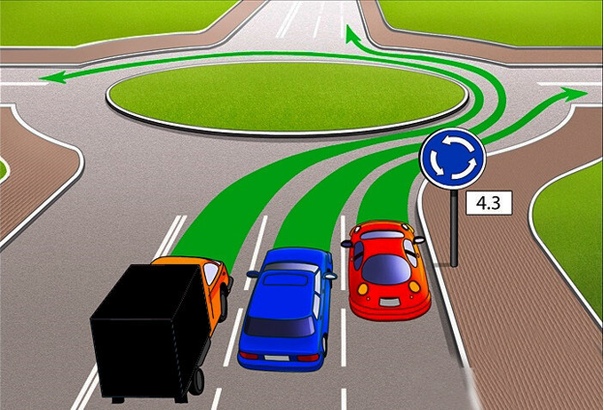 2 Железнодорожный переезд без шлагбаума в Правилах дорожного движения
2 Железнодорожный переезд без шлагбаума в Правилах дорожного движения 3.2 Многопутная железная дорога в Правилах дорожного движения
3.2 Многопутная железная дорога в Правилах дорожного движения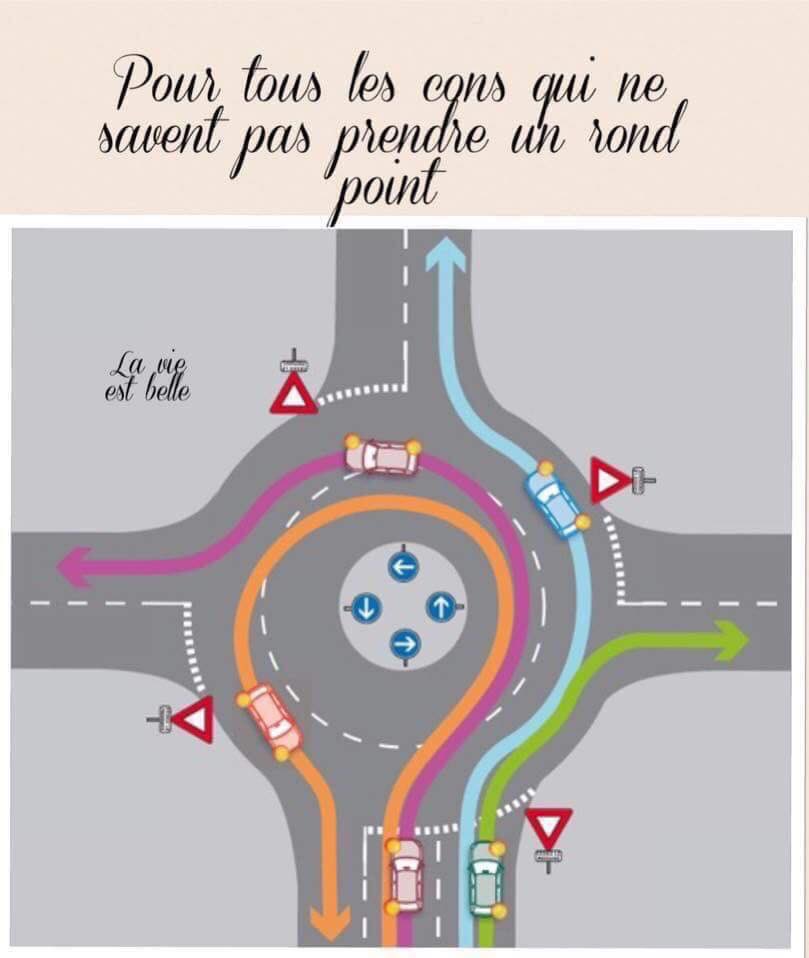
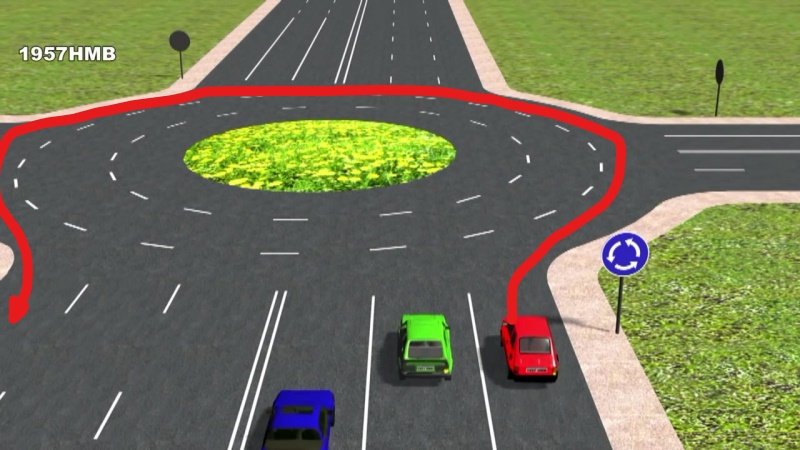
 8 Светофорное регулирование информирует водителей о приближении к регулируемому перекрёстку, правила проезда которого изложены в разделе 13 ПДД.
8 Светофорное регулирование информирует водителей о приближении к регулируемому перекрёстку, правила проезда которого изложены в разделе 13 ПДД.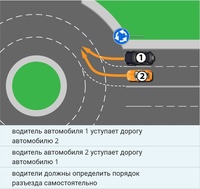 10 Выезд на набережную информирует водителей о приближении к опасному участку дороги — набережной или берегу, движение по которым требует повышенного внимания.
10 Выезд на набережную информирует водителей о приближении к опасному участку дороги — набережной или берегу, движение по которым требует повышенного внимания. 12.1-2 Опасные повороты в Правилах дорожного движения
12.1-2 Опасные повороты в Правилах дорожного движения 13 Крутой спуск в Приложении 1 к ПДД
13 Крутой спуск в Приложении 1 к ПДД
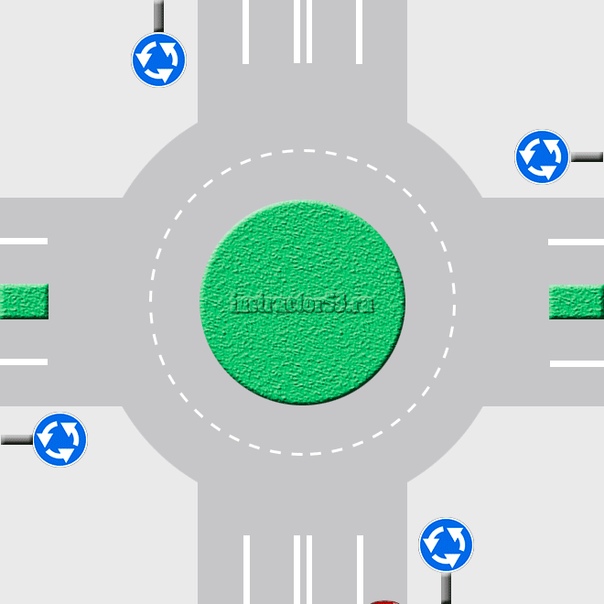 21 Двустороннее движение в Правилах дорожного движения
21 Двустороннее движение в Правилах дорожного движения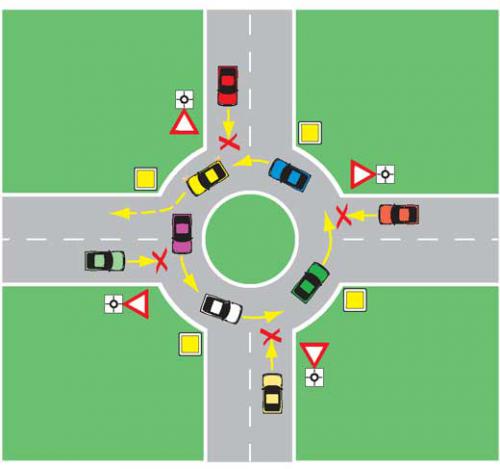 23 Дети в Правилах дорожного движения
23 Дети в Правилах дорожного движения 25 Дорожные работы в Правилах дорожного движения
25 Дорожные работы в Правилах дорожного движения 27 Дикие животные в Правилах дорожного движения
27 Дикие животные в Правилах дорожного движения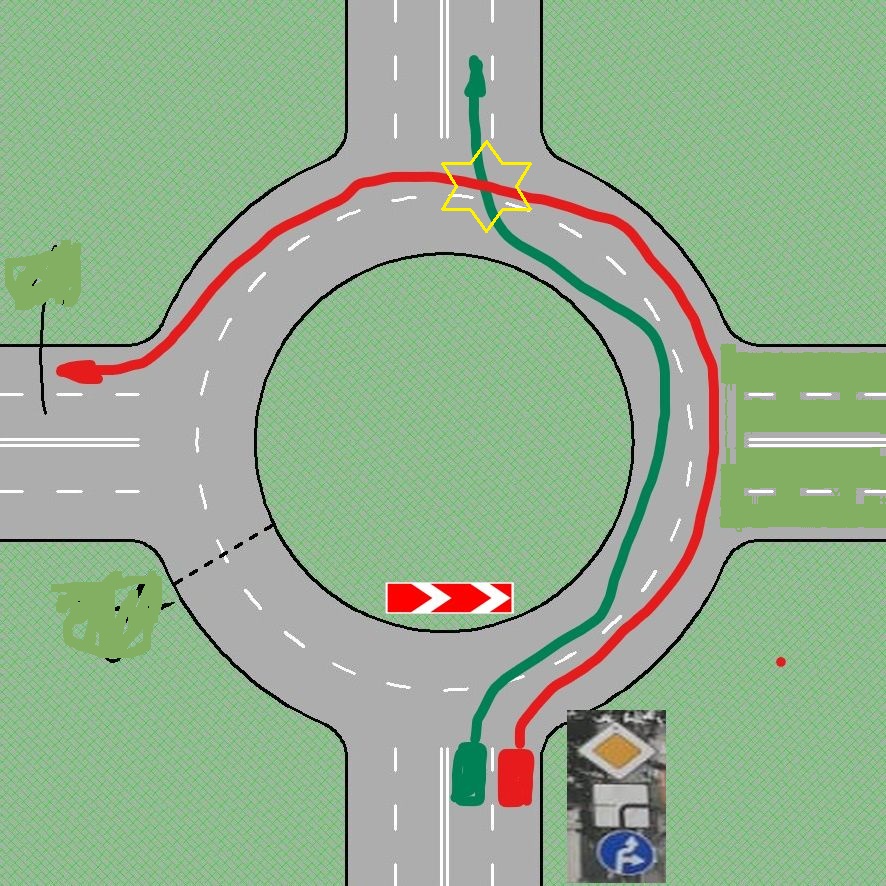 29 Боковой ветер в Правилах дорожного движения
29 Боковой ветер в Правилах дорожного движения 31 Тоннель в Правилах дорожного движения
31 Тоннель в Правилах дорожного движения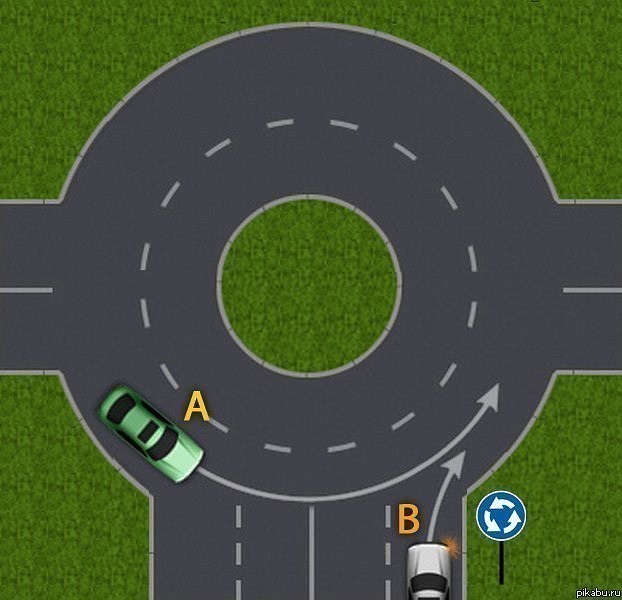 Направление объезда направо ремонтируемого участка дороги.Предупреждающие дорожные знаки 1.34.2 Направление поворота налево малого радиуса в Приложении 1 к ПДД. Направление движения налево на закруглении дороги малого радиуса с ограниченной видимостью. Направление объезда налево ремонтируемого участка дороги.Предупреждающие дорожные знаки 1.34.3 Направления поворота на развилке и налево, и направо в Приложении 1 к ПДД. Направления движения на Т-образном перекрестке или разветвлении дорог. Направление объезда налево или направо ремонтируемого участка дороги.
Направление объезда направо ремонтируемого участка дороги.Предупреждающие дорожные знаки 1.34.2 Направление поворота налево малого радиуса в Приложении 1 к ПДД. Направление движения налево на закруглении дороги малого радиуса с ограниченной видимостью. Направление объезда налево ремонтируемого участка дороги.Предупреждающие дорожные знаки 1.34.3 Направления поворота на развилке и налево, и направо в Приложении 1 к ПДД. Направления движения на Т-образном перекрестке или разветвлении дорог. Направление объезда налево или направо ремонтируемого участка дороги.


 Она проходит 10 кругов по трассе за 2 минуты. Найдите общее расстояние, пройденное Мирандой, среднюю скорость и центростремительное ускорение.
Она проходит 10 кругов по трассе за 2 минуты. Найдите общее расстояние, пройденное Мирандой, среднюю скорость и центростремительное ускорение.