Формула нахождения угловой скорости: 404 — Страница не найдена
Линейная скорость: формула расчета нахождения
С точки зрения физики абсолютного покоя не существует. Каждое тело и частицы, которые его составляют, находятся в постоянном движении друг относительно друга. Важной кинематической величиной, характеризующей движение, является скорость. В данной статье приведем формулы линейной скорости для различных типов перемещения тел в пространстве.
Что такое линейная скорость?
Речь идет о физической величине, которая показывает, какое расстояние в пространстве проходит тело за единицу времени. Как правило, скорость обозначают буквой v¯, где символ черты говорит о том, что она является векторной величиной. Измеряется скорость в метрах в секунду (м/с), километрах в час (км/ч), милях в час (мил/ч) и других единицах, предполагающих отношение расстояния ко времени.
Вектор скорости v¯ показывает направление реального перемещения тела. Этим он отличается от вектора ускорения, который направлен в сторону действующей силы, но не в сторону движения тела, хотя они могут совпадать.
Мгновенная и средняя скорости
Как найти линейную скорость? Формулу, согласно определению величины, можно записать следующую:
v¯ = dl¯/dt.
Где dl¯ — вектор перемещения тела за время dt. Эта скорость называется мгновенной, поскольку рассчитывается за чрезвычайно короткий промежуток времени dt. Мгновенная скорость в действительности является величиной не стабильной и постоянно меняющейся. Например, представим, что по дороге движется автомобиль. На первый взгляд можно полагать, что в любой момент времени его мгновенная скорость будет постоянной, однако, это не так. Мгновенная скорость испытывает колебания. Если спидометр автомобиля достаточно чувствителен, то он фиксирует эти колебания.
Формула линейной скорости средней ничем не отличается от таковой для мгновенной, однако, измеряется она за более длительный промежуток времени Δt:
v¯ = Δl¯/Δt, где Δt>>dt.
В примере с автомобилем выше, хотя мгновенная скорость испытывает колебания, средняя скорость остается постоянной с определенной точностью на всем участке пути Δl¯.
При решении задач, как правило, используют среднюю скорость. Мгновенная же величина имеет смысл только в случае движения с ускорением.
Равномерное движение по прямой линии
Это идеализированный тип движения, который предполагает, что тело в течение некоторого промежутка времени движется вдоль прямой в пространстве. При этом скорость тела не меняется. Обозначая пройденный путь символом l, получаем формулу:
l = v*t.
Здесь v = const.
Этот тип движения рассматривался еще философами Античной Греции. Они полагали, что для движения тел необходимо прикладывать некоторую силу, поэтому естественным состоянием всех окружающих объектов является покой. Только с приходом эпохи Возрождения благодаря работам Галилея и Ньютона было показано, что если на тело не воздействуют внешние силы, то равномерность и прямолинейность его движения не нарушается.
Скорость при движении по прямой с ускорением
Когда появляется внешняя сила, то ее действие на тело приводит к изменению скорости тела. В динамике эта ситуация описывается вторым законом Ньютона:
В динамике эта ситуация описывается вторым законом Ньютона:
F¯ = m*a¯.
Если действие силы F¯ происходит на покоящееся изначально тело массой m, то формула нахождения линейной скорости в любой момент времени t примет вид:
v¯ = a¯*t.
В данном случае обе векторные величины направлены в одну и ту же сторону. Эта формула может применяться для описания разгона какого-либо транспортного средства.
Теперь предположим, что автомобиль двигался с некоторой скоростью v0¯, а затем начал останавливаться. В этой случае соответствующее кинематическое уравнение примет вид:
v¯ = v0¯ + a¯*t.
Поскольку модуль скорости |v¯| авто будет уменьшаться со временем, в скалярной форме это равенство запишется так:
v = v0 — a*t.
В данном случае вектора скорости и ускорения направлены в противоположных направлениях.
Все формулы линейной скорости, приведенные в этом пункте, описывают прямолинейное движение с постоянным ускорением.
Вращение тел
Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
M = I*α.
Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
ω = θ/t.
Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
ω = α*t.
Для измерения всех угловых величин используются радианы.
Формула линейной скорости вращения
Выше отмечалось, что вращение удобно описывать в угловых характеристиках. Тем не менее в некоторых случаях важно знать, чему равна линейная скорость по окружности. Формула для этого случая приведена ниже:
Тем не менее в некоторых случаях важно знать, чему равна линейная скорость по окружности. Формула для этого случая приведена ниже:
v = ω*r.
Здесь r — радиус окружности, равный расстоянию от любой точки траектории тела до оси вращения. Связывающую линейную и угловую скорость формулу получить несложно самостоятельно. Для этого достаточно рассмотреть, какое расстояние по окружности преодолеет тело за известное время t.
Приведенное выражение можно использовать для вычисления линейных скоростей космических тел, например, нашей Земли, вращающейся вокруг Солнца.
Линейная скорость и центростремительное ускорение
Скорость является величиной векторной. Это означает, что тело получает ускорение не только при изменении модуля величины v, но и при изменении ее направления. Последняя ситуация реализуется во время вращения. Вектор мгновенной скорости тела всегда направлен по касательной к окружности. Если за равные промежутки времени тело описывает равные углы относительно центра вращения, то такое движение является равномерным с точки зрения модуля скорости.
Отклонение от прямолинейного движения во время вращения происходит за счет действия центростремительной силы, вызывающей центростремительное ускорение. Оно направлено всегда перпендикулярно скорости, поэтому изменить ее модуль не может. Ускорение центростремительное ac можно вычислить по формуле:
ac = v2/r.
Абсолютная величина ускорения ac показывает, насколько велики центробежные силы, связанные с инерцией вращающегося тела. Практическим примером является занос автомобиля во время крутого поворота. Заметим, что с уменьшением радиуса ac растет медленнее, чем с увеличением линейной скорости.
Задача на определения линейной скорости нашей планеты
Каждый человек понимает, что если автомобиль движется со скоростью 100 км/ч, то эта цифра является достаточно большой в сравнении со скоростями, с которыми люди сталкиваются в повседневной жизни. Любопытно сравнить указанную цифру со скоростью вращения Земли по своей орбите.
Для оценки этой скорости возьмем следующие данные:
- радиус орбиты — 150 млн км;
- период одного оборота — 365 земных дней.
Для определения требуемой величины воспользуемся формулой линейной и угловой скорости:
v = ω*r.
Значение ω через период T определяется так:
ω = 2*pi/T.
Тогда для v приходим к равенству:
v = 2*pi*r/T.
Подставляя данные из условия задачи, получим линейную скорость 107,5 тысяч км/ч! Эта цифра означает, что наша Земля перемещается в космическом пространстве в 1000 раз быстрее, чем автомобиль движется по дороге. Мы не чувствуем этой гигантскую скорости, поскольку силы гравитации Земли увлекают за собой атмосферу так, что она находится в покое относительно поверхности планеты.
Мгновенный центр скоростей в теоретической механике
Содержание:
Мгновенный центр скоростей:
В каждый момент времени при плоском движении фигуры в ее плоскости, если Обозначим ее
Для доказательства этой теоремы достаточно указать способ нахождения мгновенного центра скоростей, если известны по модулю и направлению скорость какой-либо точки плоской фигуры и угловая скорость этой фигуры в рассматриваемый момент времени. Пусть вращение происходит по часовой стрелке ( и ) (рис. 46). Скорость точки плоской фигуры равна нулю, если скорость полюса и скорость от вращения вокруг полюса в этой точке равны по модулю, но противоположны по направлению. Эти точки лежат на перпендикуляре к скорости в точке . В других точках векторная сумма двух векторов не может быть равна нулю.
Пусть вращение происходит по часовой стрелке ( и ) (рис. 46). Скорость точки плоской фигуры равна нулю, если скорость полюса и скорость от вращения вокруг полюса в этой точке равны по модулю, но противоположны по направлению. Эти точки лежат на перпендикуляре к скорости в точке . В других точках векторная сумма двух векторов не может быть равна нулю.
Рис. 46
Итак, если , то .
Ho
следовательно,
Таким образом, мгновенный центр скоростей находится на перпендикуляре к скорости , проведенном из точки , на расстоянии .
Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени мгновенным центром является уже другая точка плоской фигуры.
Если мгновенный центр известен, то, приняв его за полюс и учитывая, что скорость его в этом случае равна нулю, согласно (3) и (4), для точки фигуры имеем
где —расстояние от точки до мгновенного центра скоростей.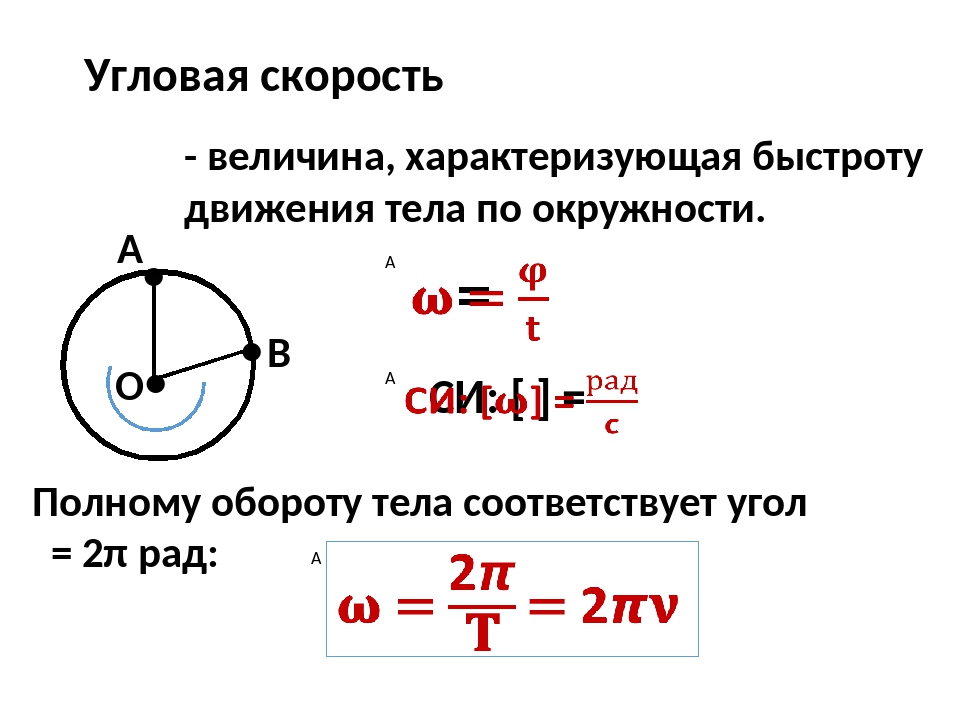
По направлению скорость в этом случае перпендикулярна отрезку . Для точки , аналогично,
причем скорость перпендикулярна отрезку .
Из (5) и (6) имеем
и
Следовательно, если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью .
Для нахождения скоростей точек тела при его плоском движении обычно предварительно находят мгновенный центр скоростей. Но можно применить формулу, выражающую зависимость между скоростями двух точек тела.
Рассмотрим способы нахождения мгновенного центра скоростей. Существует два основных способа его нахождения: из механических условий задачи и по скоростям точек плоской фигуры.
В некоторых случаях удается сразу указать точку плоской фигуры, скорость которой в рассматриваемый момент равна нулю. Эти точки в таких задачах и являются мгновенными центрами скоростей. Так, в случае качения без скольжения одного тела по поверхности другого неподвижного тела точка соприкосновения поверхностей тел и является мгновенным центром скоростей.
Эти точки в таких задачах и являются мгновенными центрами скоростей. Так, в случае качения без скольжения одного тела по поверхности другого неподвижного тела точка соприкосновения поверхностей тел и является мгновенным центром скоростей.
Рис. 47
Рис. 48
Например, при качении без скольжения колеса по неподвижной прямой линии (см. рис. 52) и одного колеса по неподвижному другому колесу (см. рис. 61) мгновенный центр скоростей находится в точках соприкосновения колеса с прямой и соответственно колеса с колесом. В общем случае, если известны скорости двух точек плоской фигуры (рис. 47), мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек.
В том случае, когда точки лежат на общем перпендикуляре к скоростям этих точек, скорости точек параллельны и концы их лежат на одной прямой, проведенной через мгновенный центр скоростей (рис. 48 и 49), так как скорости точек пропорциональны расстояниям от этих точек до мгновенного центра скоростей. Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны (рис. 50), то имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению. Угловая скорость плоской фигуры при мгновенном поступательном движении равна нулю, и в этом случае, согласно формуле (7), мгновенный центр скоростей находится в бесконечности.
Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны (рис. 50), то имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению. Угловая скорость плоской фигуры при мгновенном поступательном движении равна нулю, и в этом случае, согласно формуле (7), мгновенный центр скоростей находится в бесконечности.
Рис. 49
Рис. 50
Рис. 51
Рис. 52
Заметим, что при мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны. Невозможен случай, когда скорости двух точек, не лежащих на общем перпендикуляре к скоростям, не равны друг другу по модулю, но параллельны (рис. 51), так как для него не выполняется теорема о проекциях скоростей двух точек тела на прямую, соединяющую эти точки.
Пример:
Колесо радиусом (рис.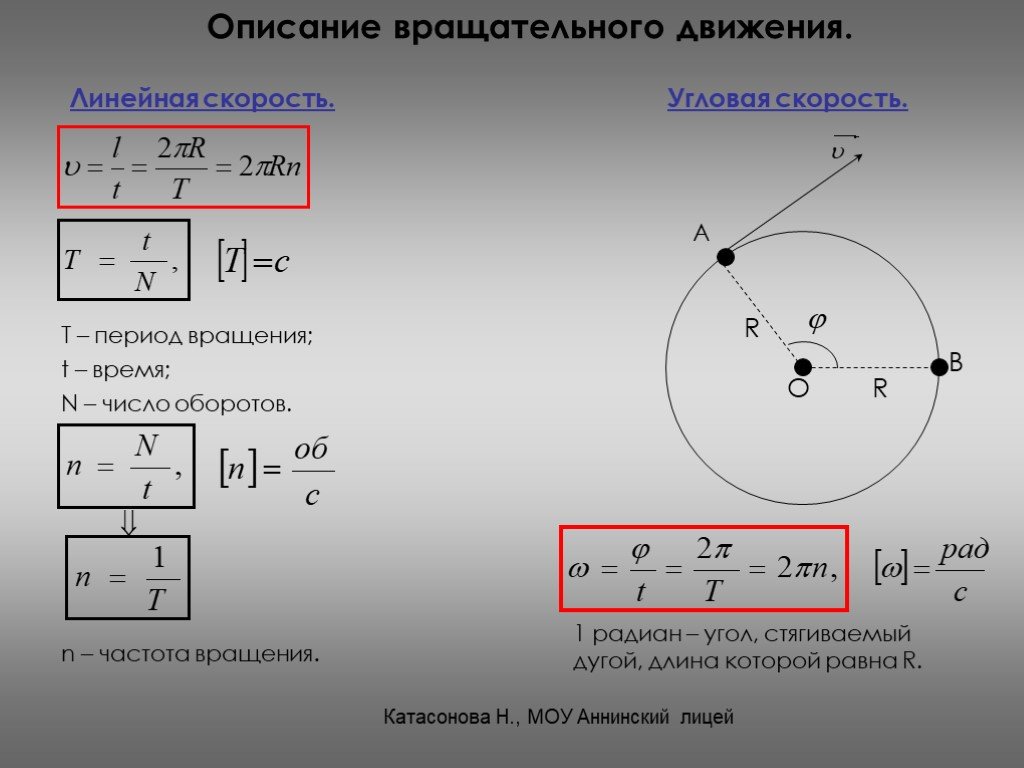
Решение. Мгновенный центр скоростей в этом случае находится в точке соприкосновения колеса с прямой. Угловая скорость колеса определяется по формуле (7):
По формуле (5) для скоростей указанных точек имеем
так как
Скорости точек колеса направлены по перпендикулярам к отрезкам прямых, соединяющих мгновенный центр скоростей с рассматриваемыми точками.
Вычисление угловой скорости при плоском движенииУгловую скорость плоской фигуры при плоском движении можно вычислить, согласно ее определению, как
Затем ее можно определить по формуле (7):
Чтобы определить угловую скорость, надо скорость какой-либо точки плоской фигуры разделить на расстояние от этой точки до мгновенного центра скоростей. Направление вращения определяем по направлению скорости какой-либо точки, считая, что плоская фигура в данный момент вращается вокруг мгновенного центра скоростей с угловой скоростью .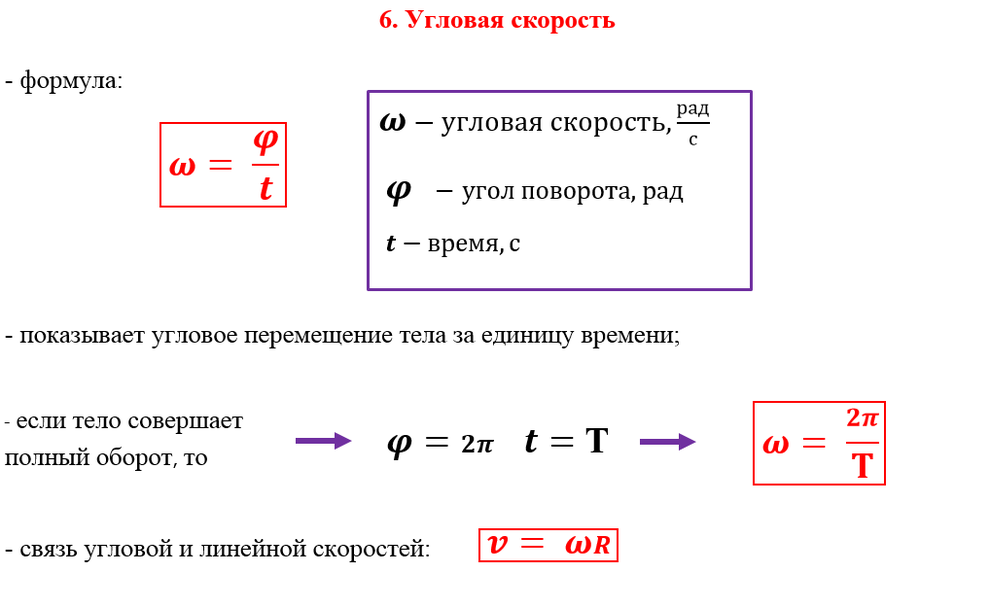
Рис. 53
Угловую скорость при плоском движении можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс, например или . Тогда угловая скорость, согласно формуле (4),
Знак угловой скорости определяют по направлению относительной скорости какой-либо точки фигуры от вращения фигуры вокруг другой ее точки, выбранной за полюс.
Применяют и другие способы определения угловой скорости. Так, если предварительно установить зависимость угла поворота плоской фигуры от линейных и угловых величин других плоских фигур тождественным соотношением, то, дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость. Этот способ используют часто для нахождения зависимости угловых скоростей отдельных звеньев плоских механизмов.
Пример:
В кривошипно-шатунном механизме (рис. 53) даны длины кривошипа , шатуна и расстояние от оси вращения кривошипа до направляющей ползуна . Установить зависимость между угловыми скоростями кривошипа и шатуна при любом положении механизма.
53) даны длины кривошипа , шатуна и расстояние от оси вращения кривошипа до направляющей ползуна . Установить зависимость между угловыми скоростями кривошипа и шатуна при любом положении механизма.
Решение. Положение кривошипа определяется углом , а шатуна — углом . До тех пор пока , справедливо тождество
Дифференцируя это тождество по времени, получим
Но ; следовательно,
Полученное соотношение и является искомой зависимостью между угловыми скоростями кривошипа и шатуна. При имеем частный случай кривошипно-шатунного механизма. Если дополнительно , то и .
Направления вращений кривошипа и шатуна противоположны. При вращении кривошипа против часовой стрелки шатун вращается по часовой стрелке.
Ускорения точек тела при плоском движенииРассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом и относительного вращательного вокруг , по теореме о сложении ускорений для точки имеем
Рис. 54
54
Так как переносное движение является поступательным вместе с точкой фигуры, то переносное ускорение
Относительное ускорение точки от вращения вокруг полюса обозначим . После этого формула (9) принимает вид
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.
Ускорение от относительного вращательного движения вокруг полюса, как и в случае вращения тела вокруг неподвижной оси, состоит из касательной и нормальной составляющих и :
причем
и _________
Касательное относительное ускорение направлено по перпендикуляру к отрезку в сторону дуговой стрелки углового ускорения (рис. 54, а). Нормальное относительное ускорение соответственно направлено по линии от точки к полюсу . Наконец, полное относительное ускорение составляет с отрезком угол , тангенс которого можно определить по формуле
Из формулы (15) следует, что угол для всех точек плоской фигуры одинаков. При угол от ускорения к отрезку надо откладывать против часовой стрелки. При его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (10) и (11) можно построить в выбранном масштабе многоугольник ускорений для точки (рис. 54, б).
При угол от ускорения к отрезку надо откладывать против часовой стрелки. При его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (10) и (11) можно построить в выбранном масштабе многоугольник ускорений для точки (рис. 54, б).
Формулу (10), определяющую зависимость ускорений двух точек плоской фигуры, можно получить непосредственным дифференцированием векторного равенства для скоростей, справедливого в любой момент времени. Имеем
Продифференцируем по времени обе части этого равенства, учитывая изменения векторных величин относительно неподвижной системы координат (полные производные). Получаем
Здесь — ускорения точек и относительно неподвижной системы координат; — угловое ускорение плоской фигуры. У вектора постоянный модуль; следовательно, его производная по времени выражается в форме
Объединяя полученные результаты, получаем
Рассуждения, аналогичные тем, которые проведены для скорости , позволяют сделать вывод о том, что
т. е. являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки . Следовательно,
е. являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки . Следовательно,
Пример:
Колесо радиусом катится со скольжением по неподвижной прямой, совершая плоское движение (рис. 55). Ускорение центра колеса в рассматриваемый момент времени , а угловая скорость и угловое ускорение колеса и . Дуговые стрелки для и направлены по часовой стрелке, т. е. и . Определить в этот момент времени ускорения точек , и , расположенных на концах вертикального и горизонтального диаметров обода колеса.
Решение. Ускорение точки , приняв за полюс точку , определим по формуле
и аналогичным формулам для точек и . Для касательного и нормального ускорений точки от вращения колеса вокруг точки имеем
Рис. 55
Ускорение перпендикулярно отрезку и направлено в сторону, указываемую дуговой стрелкой , а ускорение направлено от точки к точке , принятой за полюс. Аналогично направлены ускорения для точек и .
Аналогично направлены ускорения для точек и .
Так как для точки ускорения и направлены по одной прямой, то, предварительно их сложив, получим две перпендикулярные составляющие ускорения и, следовательно,
Для точки
так как
Окончательно для точки имеем
Для точки соответственно
В том случае, когда колесо катится без скольжения, точка является мгновенным центром скоростей и скорость точки в любой момент времени равна нулю. Скорость точки в этом случае можно определить по формуле
Дифференцируя по времени обе части этого тождества и приравнивая результат дифференцирования, получим
или
так как точка движется прямолинейно, и
Учитывая, что
имеем
Следовательно, при качении колеса по прямой без скольжения
т. е. ускорение мгновенного центра скоростей, скорость которого равна нулю, не равно нулю.
Если угловое ускорение не задано, то при отсутствии скольжения колеса по прямой его можно определить по формуле
модуль скорости формула — The Modula Shcol
Модуль угловой скорости определяют по формуле. Для нахождения метаморфозы скорости определитесь с типом движения.
Для нахождения метаморфозы скорости определитесь с типом движения.
Opredelit Modul Napravleniya Skorosti Tochki Pri Ravnomernom Dvizhenii Vdol Osi Ox Ee Shkolnye Znaniya Com
Формула нахождения модуля перемещения.
модуль скорости формула. Под равномерным движением тела подразумевается что скорость тела постоянна. Модуль числа 10 равен 10-ти верно так же как модуль числа -10. Скажем 10 -10.
Чем больше ускорение тем быстрее меняется скорость тела. Этих формул хватит чтобы сдать ЕГЭ или ОГЭ на высокий балл а. Модуль вектора ускорения показывает на сколько меняется модуль вектора скорости в каждую единицу времени.
Для нахождения модуля угловой скорости применим формулу. Скажем 25 5 5 25 то есть 20 — 20. Это является основным свойством модулей.
Из формулы 16 становится ясным физический смысл скорости. W ft где f угол поворота t время в течение которого происходило вращение. Здесь собраны все основные формулы по физике с 7 по 11 класс.
проекция скорости на ось равна изменению проекции соответствующей. Модуль средней скорости по пути равняется openυ S Δt υ S t. Для того чтобы найти модуль начальной скорости при помощи угломера замеряйте угол к горизонту под которым тело начинает двигаться.
Если требуется найти модуль скорости в момент времени t1 просто подставьте это значение в уравнение и посчитайте v. Она непосредственно выражается. Как вы знаете из 9-го класса модуль вектора это его длина в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Помимо того a b b a потому что расстояние от точки a до точки b и расстояние от b до a равны друг другу. Формула скорости равнозамедленного движения прямолинейного. Теперь найдем модуль вектора скорости материальной точки.
V v 0 at в этой формуле все величины являются скалярами а не векторами. Определение направления и модуля скорости. Помимо того a b b a потому что расстояние от точки a до точки b и расстояние от b до a равны друг другу.
Таблица содержит основные формулы по механике — модуль вектора скорости ускорение мгновенное модуль вектора ускорения угловая скорость и другие формулы. Модуль перемещения r x2 y2 z212 t2 t4 t612 при t2 c r 4 16 6412 91 м. Таким же образом можно найти время подставив известную.
Из формулы 15 определяется выражение для проекции скорости. А вот теперь если мы приравняем правые части и выразим из них скорость и возьмем квадратЧисло Авогадро на массу молекулы получается Молярная масса то у нас и получится формула для средней квадратичной скорости молекулы газа. Vfrac s t s это пройденный телом путь то есть длина линии t время то есть промежуток времени за который пройден путь.
Когда задача требует найти скорость в начальный момент времени подставьте в функцию t0. Omegafracd varphid t11 Используем заданную в условии задачи функцию varphit возьмем производную от нее по времени получим функцию omegat. Скажем 25 5 5 25 то есть 20 — 20.
При этом модуль вектора скорости находят при помощи формулы. Vx2y2z25В цилиндрических координатах модуль скорости вычисляют при помощи формулы. Мгновенная скорость характеризует движение в.
Vx2y2z25В цилиндрических координатах модуль скорости вычисляют при помощи формулы. Мгновенная скорость характеризует движение в.
2 Модуль вектора скорости v 2 2 4 z 2 y 2v 1 4 9t. Скорость v физическая величина численно равна пути s пройденного телом за единицу времени t. При помощи рулетки или дальномера замеряйте расстояние на котором тело упадет на поверхность земли.
Основываясь на определении скорости мы можем утверждать что скорость является вектором. Модуль числа 10 равен 10-ти верно так же как модуль числа -10. 1 Так как вектор скорости v drdt то dr vdt и r t 0 v dt t 0 i 2tj 3t2kdt ti t2j t3k.
Najti Modul Vektora Srednej Skorosti Dvizheniya Youtube
Reshenie K Koncu Pervoj Sekundy Ravnozamedlennogo Dvizheniya Modul Skorosti Tela
Dmsh Samrina Rf
Какова угловая скорость Земли вокруг Солнца? Как нам это получить?
ВОПРОС №256
предыдущий | следующийВопрос задан: Захи Асир
Ответить
Расчет угловой скорости Земли — обманчиво простая задача. Причина для это просто — угловая скорость определяется как угол, образовавшийся за определенное время.
Причина для это просто — угловая скорость определяется как угол, образовавшийся за определенное время.Мы знаем, что Земля вращается вокруг Солнца, полный оборот составляет 2 радиана (360 градусов). Мы также знаем, что это занимает год (примерно 365 дней), что составляет примерно 3,2×10 7 секунд.
Следовательно = 2 / 3,2×10 7 = 2,0×10 -7 рад/с. Мы вычислили угловую скорость.
Однако, если мы можем измерить расстояние до Солнца, мы также можем вычислить скорость Земли относительно Солнца.Хотя, если мы не определим направление, это более технически известный как скорость. Это можно сделать, ознакомившись с определением радиан. Радиан – это единица, которая связывает радиус дуги, длину дуги и угол, образуемый дугой. Формула для этого: s = r x (где s — длина дуги, r — радиус и угол). Итак, если мы знаем радиус Орбиту Земли (1,5×10 11 м) мы можем заменить угловой скоростью из нашего предыдущего уравнения чтобы дать v = x r (где v — скорость, угловая скорость и r — радиус).
Итак, Земля движется в пространстве (относительно Солнца) по адресу: v = 2,0×10 -7 x 6,4×10 6 = 3,0×10 4 м/с
Отвечает: Эдвард Рейн, студент бакалавриата по физике, Кембридж, Великобритания.
По какой формуле рассчитывается угловая скорость? – Greedhead.net
По какой формуле рассчитывается угловая скорость?
Угловая скорость — это скорость изменения позиционного угла объекта по отношению ко времени, поэтому w = тета / t, где w = угловая скорость, тета = позиционный угол и t = время.
Как найти конечную угловую скорость?
Конечная угловая скорость может быть рассчитана по определению углового момента L = Iω. ω=LI=L12MR2 ω знак равно L я знак равно L 1 2 M р 2 . ω=9,75×10−2 кг⋅м2/с(0,500)(4,00 кг)(0,260 м)=0,721 рад/с ω=9,75×10−2 кг⋅м2/с (0,500) (4,00 кг) (0,260 м) = 0,721 рад/с.
Что представляет собой уравнение ОТО для угловой скорости скорости?
Связь между угловой скоростью и линейной скоростью определяется уравнением ω = V/r.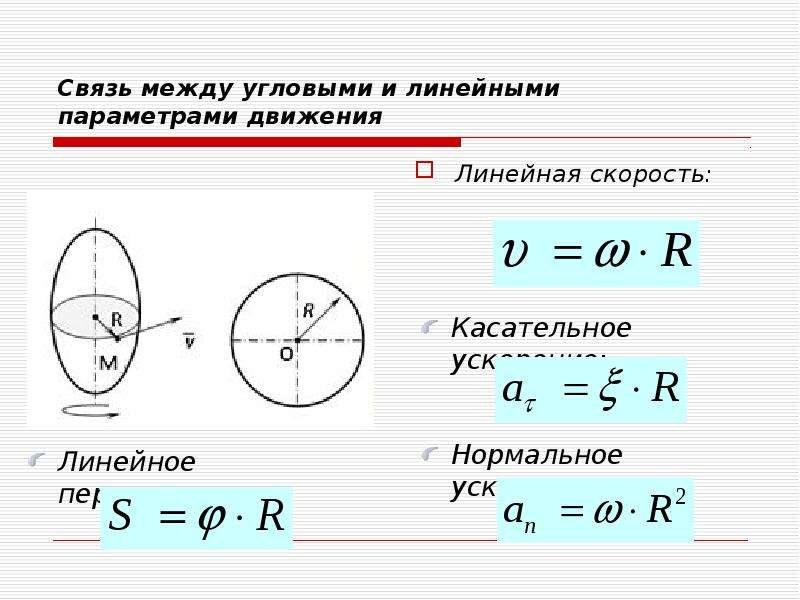
Чему равно произведение угловой скорости?
В более математических терминах единичный вектор угловой скорости может быть записан как векторное произведение вектора положения частицы или любой точки на объекте и его мгновенной скорости. Как упоминалось в предыдущем разделе, угловые величины также ведут себя как векторы.
Как найти угловую скорость с оборотами?
оборотов в минуту можно преобразовать в угловую скорость в градусах в секунду, умножив число оборотов в минуту на 6, поскольку один оборот равен 360 градусам, а в минуте 60 секунд.Если скорость вращения равна 1 об/мин, угловая скорость в градусах в секунду будет равна 6 градусам в секунду, поскольку 6, умноженное на 1, равно 6.
Пример угловой скорости?
Менее распространен, чем линейная скорость, поскольку относится только к объектам, движущимся по круговой траектории. Например, шарик рулетки на колесе рулетки, гоночный автомобиль на круговой траектории и колесо обозрения — все это примеры угловой скорости.
Как рассчитать изменение углового момента?
Линейный импульс (p) определяется как масса (m) объекта, умноженная на скорость (v) этого объекта: p = m*v.С небольшим упрощением угловой момент (L) определяется как расстояние объекта от оси вращения, умноженное на линейный импульс: L = r*p или L = mvr.
Как увеличить угловую скорость?
Ключевые моменты
- Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость.
- Угловая скорость ω аналогична линейной скорости v.
- Мы можем записать соотношение между линейной скоростью и угловой скоростью двумя разными способами: v=rω или ω=v/r.
Как рассчитать угловую скорость по частоте?
Но иногда мы говорим об угловой скорости, которая является вектором. Следовательно, формула угловой скорости такая же, как уравнение для угловой частоты. Его единицей СИ является рад/сек… Формула угловой частоты.
| \омега | угловая частота волны |
|---|---|
| ф | обычная частота волны |
Чему равно произведение угловой скорости на радиус?
Рисунок 11. 1. 3: Определение вектора →r и угловой скорости →w для частицы со скоростью →v, вращающейся вокруг оси в общем направлении. Вектор угловой скорости перпендикулярен как вектору скорости, так и вектору →r, поскольку он определяется как их векторное произведение.
1. 3: Определение вектора →r и угловой скорости →w для частицы со скоростью →v, вращающейся вокруг оси в общем направлении. Вектор угловой скорости перпендикулярен как вектору скорости, так и вектору →r, поскольку он определяется как их векторное произведение.
Как считать обороты?
Для этого используйте формулу: обороты в минуту = скорость в метрах в минуту / длина окружности в метрах. По примеру число оборотов в минуту равно: 1877/1.89 = 993 оборота в минуту.
Как рассчитать угловую скорость?
Умножьте угловую скорость в градусах в минуту на 60, чтобы преобразовать в градусы в час. В этом примере вы должны умножить 10 800 на 60, чтобы получить 648 000 градусов в час. Умножьте количество оборотов в минуту на 6,28 (что примерно в два раза больше числа пи), чтобы найти угловую скорость в радианах в минуту.
Какова формула конечной угловой скорости?
Угловая скорость — это мера того, насколько быстро объект движется под углом.Это изменение угла движущегося объекта (измеряется в радианах), деленное на время. Угловая скорость имеет величину (значение) и направление. Угловая скорость = (конечный угол) – (начальный угол)/время = изменение положения/времени. ω = (θf – θi) / t.
Угловая скорость имеет величину (значение) и направление. Угловая скорость = (конечный угол) – (начальный угол)/время = изменение положения/времени. ω = (θf – θi) / t.
В каких единицах измеряется угловая скорость?
Единицы угловой скорости измеряются в градусах в секунду (°/с) или оборотах в секунду (RPS). Угловая скорость — это просто измерение скорости вращения. Гироскоп LPY503 на доске.Гироскопы, подобные приведенному выше, могут использоваться для определения ориентации и используются в большинстве автономных навигационных систем.
В чем разница между линейной скоростью и угловой скоростью?
Для поддержания угловой скорости всегда требуется сила, но постоянная линейная скорость не требует силы.
youtube.com/embed/d5VXZGinKSk?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Radians против градусов
Radian — это, полученная Si, полученная SI Угол, где
2 θ = D / R (1)
где
θ = Radian
d = расстояние по окружности, измеренное по дуге (м, дюймы)
r = радиус по окружности (м, дюймы)
Поскольку длина окружности равна 2 π r, и радиус Круг R — радианы в полном кругу можно рассчитать до
θ = 2 π R / R
= 2 π
= ~ 6 .283185
Один Radian можно выразить в градусах как
1 RAD = 360 o / (2 π) = ~ 57.29578 O (2A)
Один Radian можно выразить в революциях как
1 Rev = 1 / (2 π) = ~ 0. 16 (2A)
16 (2A)
Одной из степеней можно выразить в радианах как
1 O = 2 π / 360 O = ~ 0 .01745 радиан (2c)
Примечание! — радианы используются по умолчанию в угловых выражениях на большинстве компьютерных языков.
Радиан определяется как угол, образуемый в центре окружности дугой окружности, длина которой равна радиусу окружности.
| градусов | 0 O | 30 O | 45 O | 60 O | 75 O | o | 180 O | 270 O | 360011 | 360 O |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | π / 12 | π / 4 | π / 4 | π / 3 | 5π / 12 | π/2 | π | 3π/2 | 2π | |
| 0 | 0. 26 26 | 0,52 | 0,79 | 1,05 | 1,31 | 1,57 | 3,14 | 4,71 | 6,28 |
радиан в градусы конвертер
градусов в радианы конвертер
угловой скорости
Преобразование угловой скорости (Ω) на другие агрегаты
- ω = 1 RAD / S = 9,55 R / MIN (RPM) = 0,159 R / S (RPS) (3)
1 RPM к радианам и градусам в секунду преобразователь
1 (DEG / S) | |||
|---|---|---|---|
| 0 | 0.0 | 0 | |
| 10 | 1,0 | 60 | |
| 20 | 2,1 | 120 | |
| 30 | 3,1 | 180 | |
| 40 | 4,2 | 240 | |
| 50 | |||
| 50 | 5. 2 2 | 300 | |
| 60 | 60 | 360 | |
| 70 | 7.3 | 420 | |
| 80084 | |||
| 80 | 8.4 | 480 | 480 |
| 90 | 9.4 | 540 | |
| 100 | |||
| 600 | 600 | 6003 |
Загрузка и печати Угловая скорость
Пример — Угловая скорость 100 RAD / S
Угловая скорость 100 рад/с может, как указано в приведенной выше таблице, быть оценена прибл. 950 об/мин и 5700 град/с .
Формула измерения угловой скорости с калькулятором
Определение угловой скорости, формула и примеры: Угловая скорость применяется к объектам, которые движутся по круговой траектории.Я узнаю все об угловой скорости, изучив три типа формул, которые мы можем использовать для пошагового расчета этого типа скорости.
Вы также можете прочитать мой предыдущий пост, например, калькулятор Mifflin St Jeor с уравнением и формулой
Что такое угловая скорость?
Угловая скорость применяется к объектам, которые движутся по круговой траектории. Я изучу определение угловой скорости, а также изучу основные 3 типа различных формул, которые я могу использовать для расчета этого типа скорости.
Кроме того, я объясню правильное использование калькулятора угловой скорости для определения кругового движения объекта. Вы сможете рассчитать не только угловую скорость, но и угол поворота, радиальную скорость объекта и линейную скорость в любой момент времени с помощью бесплатного калькулятора угловой скорости.
Угловая скорость встречается реже, чем линейная скорость, потому что она применяется только к объектам, которые движутся по круговому пути. Например, гоночный автомобиль на круговой трассе, шарик рулетки на колесе рулетки или аттракцион — все они имеют угловую скорость.
Угловая скорость объекта — это угловое смещение объекта, а также соблюдайте ограничение по времени. Когда объект движется по круговой траектории, центральный угол, соответствующий положению объекта на окружности, изменяется. Угловая скорость, представленная w, представляет собой скорость изменения этого угла, а также соблюдение ограничения по времени.
Что такое угловая скоростьНапример, аттракцион может вращаться на pi/6 радиан каждую минуту. Следовательно, угловая скорость аттракциона будет пи/6 радиан в минуту.
Линейная скорость
Прежде чем я перейду к угловой скорости, я сначала просмотрю линейную скорость. Линейная скорость применяется к объекту или частице, движущейся по прямой линии. Это скорость изменения положения объекта, а также соблюдение ограничения по времени.
Одним из наиболее распространенных примеров линейной скорости является ваша скорость, когда вы едете по дороге. Ваш спидометр показывает вашу скорость или скорость в милях в час. Это скорость изменения вашей позиции, а также соблюдение ограничения по времени, другими словами, ваша скорость — это ваша линейная скорость.
Это скорость изменения вашей позиции, а также соблюдение ограничения по времени, другими словами, ваша скорость — это ваша линейная скорость.
Линейную скорость можно рассчитать шаг за шагом, используя хорошую формулу vel_fml = sec_vel / time_scale , где vel_fml = линейная скорость, sec_vel = пройденное расстояние , а time_scale = время , необходимое для прохождения расстояния. Для простого примера, если я проехал 120 миль за 2 часа, то для расчета своей линейной скорости я подставил sec_vel = 120 миль, а также time_scale = 2 часа в свою формулу линейной скорости, чтобы получить vel_fml = 120/2 = 60. миль в час .
Формула угловой скорости
angular_velocityУгловая скорость — это оценка того, насколько быстро объект перемещается под углом. Это изменение угла движущегося объекта (выражается в радианах), деленное на время. Угловая скорость имеет меру (значение) и регулирование.
angular-velocityУгловая скорость = (конечный угол) - (начальный угол) / время = изменение положения/времени ω = (θf - θi) / шкала_времени ω = угловая скорость θf = конечный угол θi = начальный угол масштаб_времени = время Δθ = краткая форма для «изменения угла».Формулы угловой скорости
Существуют основные 3 типа формул, которые я могу использовать для пошагового получения угловой скорости.
Опция 1
Первый исходит прямо из определения. Угловая скорость — это скорость изменения позиционного угла объекта с соблюдением ограничения по времени, поэтому w = theta / time_scale, где w = угловая скорость, theta = позиционный угол и time_scale = время.
Зависимость угловой скорости от угловой частоты
Угловая скорость в зависимости от угловой частотыЕдиницы измерения угловой скорости
Единицы угловой скоростиРадиан
Прежде чем перейти к угловой скорости, я должен рассмотреть еще одну вещь, а именно радианы.Когда мы имеем дело с угловой скоростью, мы используем радианную оценку угла, поэтому важно, чтобы мы были знакомы с радианной оценкой. Техническое определение оценки радиана — это длина дуги, определяемая углом, деленная на радиус круга, частью которого является угол, где указание означает быть противоположным углу и простираться от одной точки окружности до другой, оба отмечены углом. Это говорит нам о том, что угол тета = s / r радиан, где s = длина дуги, соответствующей тета, а r = радиус круга, частью которого является тета.
Это говорит нам о том, что угол тета = s / r радиан, где s = длина дуги, соответствующей тета, а r = радиус круга, частью которого является тета.
Поскольку большинству из нас удобно оценивать угол в градусах, удобно, что мы можем легко преобразовать градусную оценку в радианную, умножив градусную оценку на пи / 180. Например, 45 градусов угол имеет радианную оценку 45 (пи / 180), что равно пи / 4 радианам.
Как найти угловую скорость Земли?
Как найти угловую скорость Земли-1Угловая скорость против линейной скорости
Опираясь на предыдущую задачу, представьте себя на очень большой карусели, а также в маловероятном радиусе 10 километров (10 000 метров).Эта карусель совершает один полный оборот каждые 1 минуту 40 секунд или каждые 100 секунд.
Простой вывод о разнице между угловой скоростью, которая не зависит от расстояния от оси вращения, и линейной круговой скоростью, которая не зависит, состоит в том, что 2 человека, испытывающие одно и то же ω , могут испытывать совершенно разные физические переживания. Если вы находитесь в 1 метре от центра, если это предполагается, большая карусель, ваша формула угловой линейной (посторонней) угловой скорости:
Если вы находитесь в 1 метре от центра, если это предполагается, большая карусель, ваша формула угловой линейной (посторонней) угловой скорости:
(менее 3 дюймов) в секунду
Пример: ωr = (2π радиан/100 с)(1 м) = 0.0628 м/с, или 6,29 см
, но если вы находитесь на краю этого монстра, ваша базовая линейная скорость:
ωr = (2π радиан/100 с)(10 000 м) = 628 м/с.
Это более применимо 1406 миль в час, быстрее пули. просто моменты!
Физические величины, зависящие от угловой скорости
Физические величины, зависящие от угловой скоростиСохранение углового момента
Сохранение углового моментаУчебники по веб-программированию Пример с демонстрацией
Чтение :
Резюме
Вы также можете прочитать об AngularJS, ASP. NET, VueJs, PHP.
NET, VueJs, PHP.
Надеюсь, вы поняли формулу угловой скорости .
Я хотел бы получать отзывы о моем блоге infinityknow.com.
Всегда приветствуются ваши ценные отзывы, вопросы или комментарии по поводу этой статьи.
Если вам понравился этот пост, не забудьте поделиться им.
По какой формуле рассчитывается угловая скорость? – Restaurantnorman.com
По какой формуле рассчитывается угловая скорость?
Угловая скорость — это скорость изменения позиционного угла объекта по отношению ко времени, поэтому w = тета / t, где w = угловая скорость, тета = позиционный угол и t = время.
Как найти минимальную угловую скорость?
Бусинка свободно скользит по вертикальной круглой рамке радиуса R и приходит в равновесие, когда cosθ=g/Rω². Минимальное значение угловой скорости получается равным √g/R, что мы можем узнать, уравновешивая гравитационную и центростремительную силы с нормальной реакцией на валик от рамы.
Как найти угловую скорость в рад с?
ω = v/r, где ω — греческая буква омега. Единицами угловой скорости являются радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v/r дает м/с, деленное на м, или с-1, а это означает, что радианы технически являются безразмерной величиной.
Что из следующего имеет максимальную угловую скорость?
Таким образом секундная стрелка имеет максимальную угловую скорость.
Как найти угловую скорость с оборотами?
оборотов в минуту можно преобразовать в угловую скорость в градусах в секунду, умножив число оборотов в минуту на 6, поскольку один оборот равен 360 градусам, а в минуте 60 секунд. Если обороты в минуту равны 1 об/мин, то угловая скорость в градусах в секунду будет равна 6 градусам в секунду, поскольку 6 умножить на 1 равно 6.
Как найти максимальную скорость при круговом движении?
Для объекта вблизи поверхности земли F = mg и r = 6,4*106 м. Скорость орбитального объекта находится из mg = mv2/r, v2 = gr = (9,8 м/с2)(6,4*106 м). У нас v = 7919 м/с, или примерно 8000 м/с.
Скорость орбитального объекта находится из mg = mv2/r, v2 = gr = (9,8 м/с2)(6,4*106 м). У нас v = 7919 м/с, или примерно 8000 м/с.
Как найти угловую скорость класса 11?
Угловая скорость и ее соотношение с линейной скоростью
- Средняя угловая скорость = ΔΘ/Δt.
- Мгновенная угловая скорость, ω = dΘ/dt.
- v = w r , где v – линейная скорость частицы, движущейся по окружности радиусом r.
- Все части движущегося тела имеют одинаковую угловую скорость при чистом вращательном движении.
Какова формула линейной скорости?
Линейная скорость v точки P равна пройденному ею расстоянию, деленному на прошедшее время. То есть v=ст. Расстояние s — это длина дуги, и мы знаем, что s=rθ.
Как найти максимальную скорость до того, как струна порвется?
Тетива может выдержать массу 25 кг до разрыва, т.е.е. мы можем позволить массе до 25 кг висеть на струне у поверхности земли. Таким образом, максимальное натяжение струны равно Fmax = mg = (25 кг)(9,8 м/с2) = 245 Н.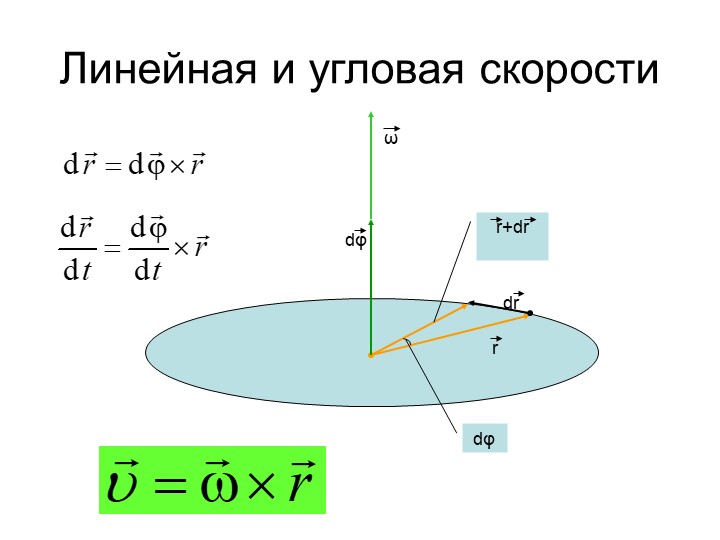 Зная Fmax = 245 Н и F = mv2/r, мы можем найти vmax.
Зная Fmax = 245 Н и F = mv2/r, мы можем найти vmax.
Как найти угловую скорость класса 9?
Теперь рассмотрим другой гоночный автомобиль, едущий по круговой трассе со скоростью 110 км/ч, а радиус трассы равен 0,2 км. Теперь найдите угловую скорость автомобиля. w = 110/0,2 = 550 радиан в час.Итак, угловая скорость автомобиля 550 радиан в час.
Как рассчитать угловую скорость? – М.В.Организинг
Как рассчитать угловую скорость?
ω = v/r, где ω — греческая буква омега. Единицами угловой скорости являются радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v/r дает м/с, деленное на м, или с-1, а это означает, что радианы технически являются безразмерной величиной.
Каково угловое смещение колеса?
Угловое смещение определяется как угол, на который объект движется по круговой траектории.Это угол в радианах между начальным и конечным положениями. Формула углового смещения Вопросы: 1) Бегун движется по круговой дорожке диаметром 8,5 м.
В чем разница между линейным и угловым перемещением?
Угловое смещение не является длиной (не измеряется в метрах или футах), поэтому угловое смещение отличается от линейного смещения. Когда объект вращается на угловое смещение phi, точка на краю диска перемещается на расстояние sa по круговой траектории.
Какая связь между линейным и угловым перемещением?
Уравнение и иллюстрация ниже демонстрируют, что линейное смещение любой точки на вращающемся теле пропорционально радиусу вращения (r; расстояние до этой точки от оси вращения) и угловому смещению вращающегося тела.
В чем разница между угловой скоростью и угловым ускорением?
Скорость изменения угловой скорости движущегося объекта во времени. Ускорение – это изменение скорости движущегося объекта во времени. Если объект движется по окружности, то его скорость называется угловой скоростью. Угловое ускорение также известно как вращательное ускорение.
Ускорение – это изменение скорости движущегося объекта во времени. Если объект движется по окружности, то его скорость называется угловой скоростью. Угловое ускорение также известно как вращательное ускорение.
Как найти максимальное угловое ускорение?
Угловое ускорение α определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом: α = ΔωΔt α = Δ ω Δ t , где Δω — изменение угловой скорости, а Δt — изменение во времени.
На что вам указывает отрицательное угловое ускорение?
Отрицательная угловая скорость (ω) означает, что частица вращается против часовой стрелки. Таким образом, отрицательное угловое ускорение (α) представляет собой «толчок» в направлении против часовой стрелки. Если α и ω имеют один и тот же знак, тело будет ускоряться, в противном случае замедляться (и в конечном итоге двигаться в обратном направлении).
Угловое ускорение отрицательное или положительное?
В двух измерениях угловое ускорение является псевдоскаляром, знак которого считается положительным, если угловая скорость увеличивается против часовой стрелки или уменьшается по часовой стрелке, и отрицательным, если угловая скорость увеличивается по часовой стрелке или уменьшается против часовой стрелки…. Угловое ускорение.
Угловое ускорение.
| Радиан на секунду в квадрате | |
|---|---|
| Символ | рад/с2 |
Как найти угловую скорость по касательному ускорению?
Тангенциальное ускорение = радиус вращения * его угловое ускорение. Она всегда измеряется в радианах на секунду в квадрате. Его размерная формула [T-2].
Имеет ли круговое движение тангенциальное ускорение?
Диаграмма неравномерного кругового движения: При неравномерном круговом движении величина угловой скорости изменяется во времени.Изменение направления объясняется радиальным ускорением (центростремительным ускорением), которое определяется следующим соотношением: ar=v2r a r = v 2 r .
Какая сила вызывает тангенциальное ускорение?
Горизонтальная составляющая силы создаст тангенциальное ускорение, которое заставит объект ускоряться вдоль оси x. Это означает, что изменятся как направление, так и величина скорости объекта, и поэтому объект будет совершать неравномерное круговое движение.
Что такое тангенциальная составляющая ускорения?
Касательная составляющая — это часть ускорения, касательная к кривой, а нормальная составляющая — часть ускорения, перпендикулярная (или ортогональная) к кривой.2}.
Что такое центростремительная и тангенциальная составляющие ускорения?
Центростремительное ускорение всегда направлено к центру вращения и имеет величину aC=v2/r. а C знак равно v 2 / р . Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности.
Может ли быть одновременно тангенциальное и центростремительное ускорение?
Если присутствует неравномерное круговое движение, вращающаяся система имеет угловое ускорение, и мы имеем как линейное центростремительное ускорение, которое изменяется (поскольку v t изменяется), так и линейное тангенциальное ускорение.
Что такое нормальное ускорение при круговом движении?
Нормальное или центростремительное ускорение измеряет изменение направления скорости во времени. Он задается выражением: a → n = v 2 ρ u → n.
Он задается выражением: a → n = v 2 ρ u → n.
Является ли центростремительное ускорение таким же, как ускорение?
Центростремительное ускорение, ускорение тела, движущегося по окружности. Поскольку скорость является векторной величиной (то есть она имеет и величину, и скорость, и направление), когда тело движется по круговой траектории, его направление постоянно меняется, и, таким образом, изменяется его скорость, создавая ускорение.
Какова формула ускорения при движении по окружности?
Уравнения
| Уравнение | Разбивка символа |
|---|---|
| v = r ω v = r \omega v=rω | v v v — линейная скорость, r — радиус, ω — угловая скорость. |
| T = 2 π ω = 1 f T = \dfrac{2\pi}{\omega} = \dfrac{1}{f} T=ω2π=f1 | T T T — период, ω — угловая скорость, f — частота |
Может угловая скорость отрицательная?
Первое определение Угловая скорость положительна при вращении против часовой стрелки и отрицательна при вращении по часовой стрелке. Противоречие: Согласно второму определению, когда угловое смещение уменьшается, угловая скорость отрицательна, а по первому определению угловая скорость положительна.
Противоречие: Согласно второму определению, когда угловое смещение уменьшается, угловая скорость отрицательна, а по первому определению угловая скорость положительна.
Когда тело покоится или вращается с постоянной угловой скоростью?
если тело покоится или вращается с равномерной угловой скоростью, то угловое ускорение будет равно нулю, в этом случае крутящий момент, действующий на тело, будет равен нулю и почему naseebnu0091780 ждет вашей помощи.
Пропорциональна ли угловая скорость радиусу?
Средняя угловая скорость пропорциональна угловому смещению и обратно пропорциональна времени.v v v — линейная скорость, r — радиус, ω — угловая скорость.
Почему угловая скорость увеличивается с уменьшением радиуса?
Поскольку угловой момент в этом случае сохраняется, он должен оставаться неизменным, поэтому, когда фигурист уменьшает свой радиус, скорость вращения должна увеличиваться, поскольку они не могут увеличивать свою массу, поэтому фигурист вращается быстрее.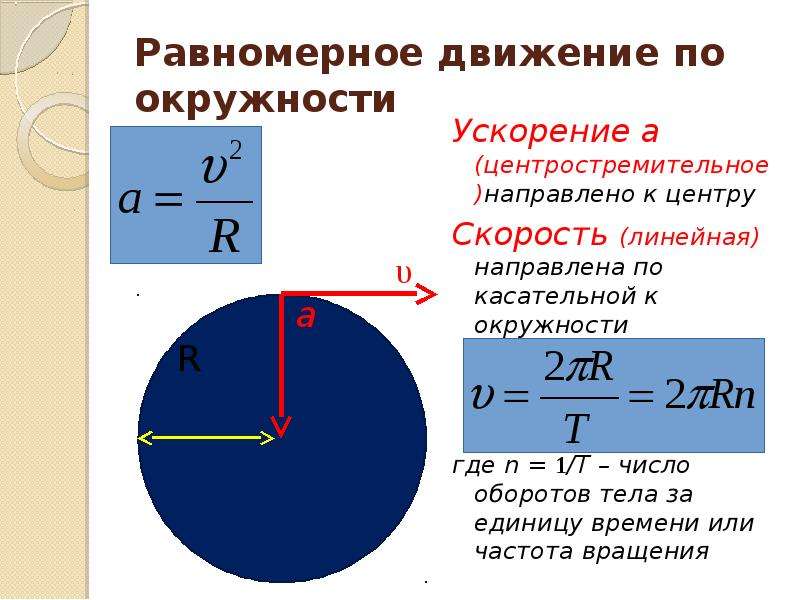 {-2} с−2.Если t (берется время), предоставляются v (конечная скорость) и u (начальная скорость). Тогда формула ускорения: v = u+at. v² = u² + 2ас.
{-2} с−2.Если t (берется время), предоставляются v (конечная скорость) и u (начальная скорость). Тогда формула ускорения: v = u+at. v² = u² + 2ас.
Какова формула линейной скорости?
Мы можем использовать исчисление, чтобы доказать формулу линейной скорости, которая равна v=rω. Рассмотрим тело, движущееся с постоянной скоростью v по окружности радиуса r. Предположим, что тело проходит линейное расстояние △x за короткое время △t и образует угол △θ в центре.
Каким символом обозначается линейная скорость?
Когда объект движется по прямому пути, связанная с ним скорость называется линейной скоростью.Он определяется как отношение пройденного расстояния ко времени. Обозначается с помощью V или Vl и измеряется в единицах СИ м/с. Это векторная величина.
Какая связь между линейной скоростью и угловой скоростью Класс 9?
Разница между линейной скоростью и угловой скоростью Мы определяем линейную скорость как скорость изменения линейного перемещения. Мы определяем угловую скорость как скорость изменения углового смещения. При круговом движении линейная скорость частицы соответствует окружности.
Мы определяем угловую скорость как скорость изменения углового смещения. При круговом движении линейная скорость частицы соответствует окружности.
Какая размерная формула угловой скорости?
Таким образом, угловая скорость размерно представлена как [M0 L0 T-1].
Что является примером линейной скорости?
Объяснение: Линейная скорость определяется как расстояние за период времени. Например, если человек пробежал 1 милю или примерно 1600 метров за 7 минут, он преодолел бы около 230 метров в минуту.
Что такое угловая скорость в тригонометрии?
Угловая скорость – это отношение оборотов, совершаемых в единицу времени.Угловая скорость. Угловая скорость вращающегося объекта – это изменение угла объекта, деленное на изменение во времени.
Является ли скорость такой же, как линейная скорость?
Опубликовано 7 лет назад. Прямая ссылка на сообщение Алана «Линейная скорость — это скорость по прямой линии (измерение…») Линейная скорость — это скорость по прямой линии (измеряется в м/с), а угловая скорость — это изменение угла во времени (измеряется в рад/с, которые также могут быть преобразованы в градусы).
Как преобразовать об/мин в рад-с?
Чтобы преобразовать число оборотов в минуту в радианы в секунду, умножьте частоту на коэффициент преобразования.Частота в радианах в секунду равна числу оборотов в минуту, умноженному на 0,10472.
Угловая скорость выше линейной скорости?
Линейная скорость всегда больше угловой скорости. Линейная скорость может быть измерена в милях в час. Угловая скорость – это угол, на который поворачивается точка за заданный интервал времени. Угловая скорость может быть измерена в радианах.
Постоянна ли угловая скорость в SHM?
Важно отметить, что угловая скорость SHM непостоянна, тогда как угловая частота постоянна.Угловая скорость в угловом СГМ получается либо как решение уравнения движения, либо путем дифференцирования выражения углового смещения по времени.
От чего зависит угловая скорость?
Если объект поворачивается на больший угол за заданное время, он имеет большую угловую скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Единицами угловой скорости являются радианы в секунду (рад/с).
Постоянна ли угловая скорость при круговом движении?
Таким образом, когда объект движется по кругу с постоянной скоростью, он подвергается постоянному линейному ускорению, чтобы поддерживать движение по кругу.Однако его угловая скорость постоянна, так как он постоянно проходит по дуге постоянной длины в единицу времени. Постоянная угловая скорость по окружности называется равномерным круговым движением.
угловая скорость | Британика
угловая скорость , временная скорость, с которой объект вращается вокруг оси или с которой изменяется угловое смещение между двумя телами. На рисунке это смещение представлено углом θ между линией на одном теле и линией на другом.
В технике углы или угловые смещения обычно выражаются в градусах или оборотах (360°), а угловые скорости — в оборотах в минуту (об/мин). В математике и физике углы обычно выражаются в радианах, а угловые скорости — в радианах в секунду.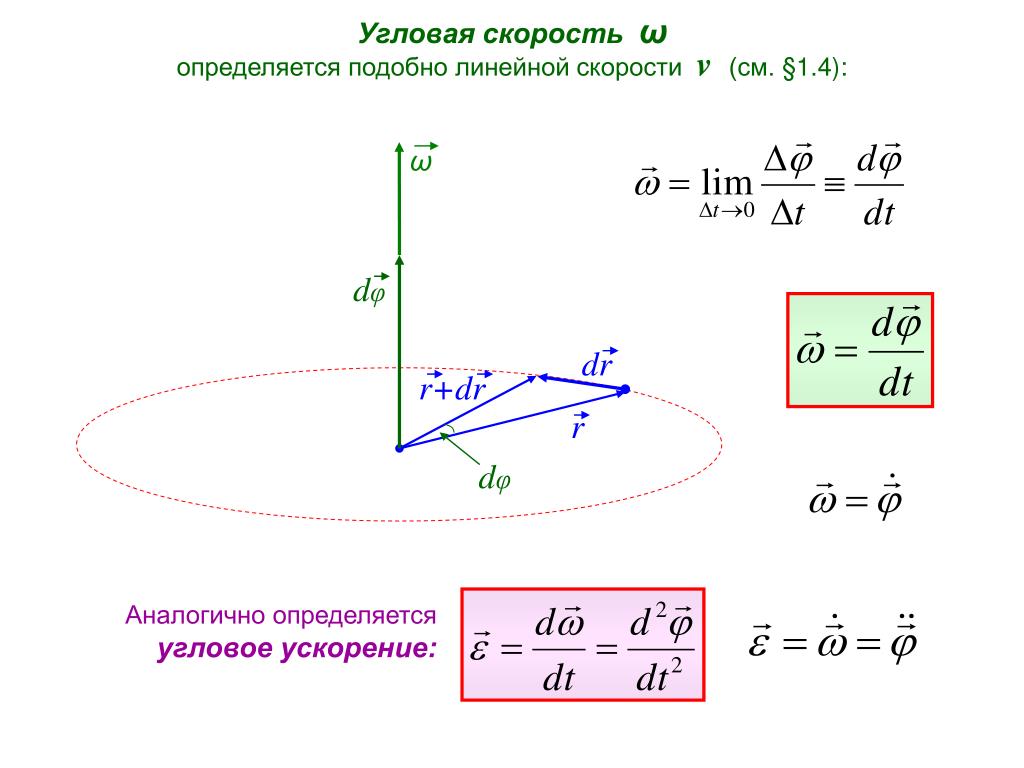 Эти меры связаны через следующие коэффициенты преобразования: 1 градус равен π /180 (около 0,0175) радиан; 1 об/мин равен π /30 (около 0,105) радиана в секунду.
Эти меры связаны через следующие коэффициенты преобразования: 1 градус равен π /180 (около 0,0175) радиан; 1 об/мин равен π /30 (около 0,105) радиана в секунду.
Британская викторина
Наука: правда или вымысел?
Вас увлекает физика? Устали от геологии? С помощью этих вопросов отделите научный факт от вымысла.
Во многих ситуациях угловая скорость — обычно обозначаемая греческой буквой омега ( ω ) — одинаково хорошо рассматривается как частота, и выбор терминов зависит от конкретного аспекта рассматриваемой системы. Так, в электротехнике скорость вращения генератора может быть выражена в оборотах в минуту, тогда как переменный электрический ток, производимый генератором, будет описываться в терминах его частоты.
Угловое ускорение представляет собой скорость изменения угловой скорости во времени и обычно обозначается как α и выражается в радианах в секунду за секунду.

