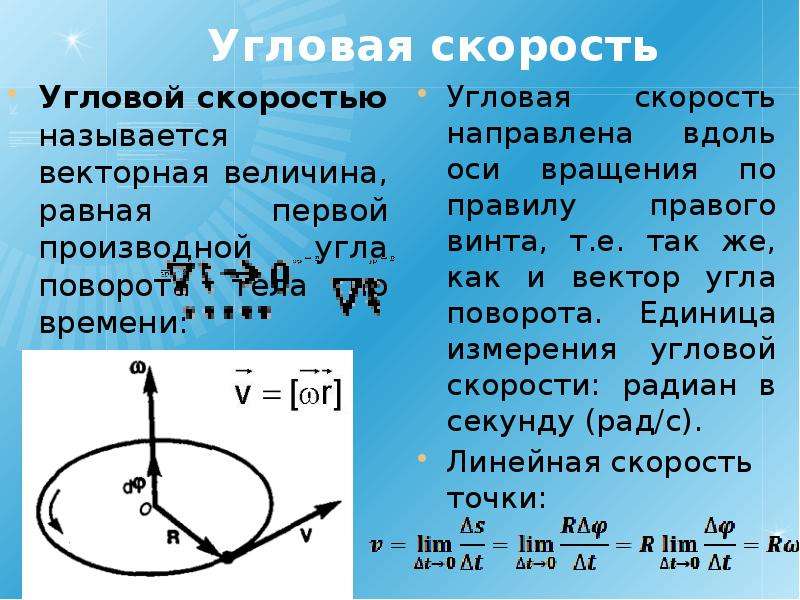
Формула определения угловой скорости: Формула угловой скорости
вращение Земли вокруг своей оси и вокруг Солнца
Движение нашей планеты в космическом пространстве можно охарактеризовать двумя типами вращения: вокруг собственной оси и вокруг Солнца. В данной статье рассматривается понятие угловой скорости, приводятся необходимые формулы для вычисления этой величины, а также дается расчет скорости угловой вращения Земли вокруг своей оси и вокруг нашей звезды.
Что такое угловая скорость вращения?
Когда рассматривают перемещение тела в пространстве на большие расстояния, то, как правило, пренебрегают его размерами. В этом случае вводят понятия пути и скорости его движения. Если же решают задачу движения тела вокруг некоторой точки или оси вращения, то пройденный путь всегда равен длине соответствующей окружности, а линейная скорость перемещения заменяется использованием скорости угловой.
Угловая скорость вращения представляет собой угол, на который тело поворачивается вокруг соответствующей оси за единицу времени. Исходя из этого определения, единицей измерения рассматриваемой величины будут радианы в секунду (рад/с). Также можно использовать градусы в секунду (˚/c). Обозначается угловая скорость греческой буквой омега ω.
Также можно использовать градусы в секунду (˚/c). Обозначается угловая скорость греческой буквой омега ω.
Основные формулы
Прежде чем переходить к вопросу, чему равна скорость вращения Земли угловая, следует познакомиться с основными формулами, описывающими эту величину.
Как известно, угловая мера всей окружности составляет 360 ˚ или 2×π радиан, где π = 3,1416. Если тело совершает вокруг оси полный оборот за время T, тогда можно записать следующее выражение:
ω = 2×π /T = 2×π ×f.
Время T называют периодом обращения, а величина f = 1/T показывает, сколько оборотов тело сделает за единицу времени, то есть характеризует частоту его вращения.
Еще одной важной формулой для угловой скорости является выражение, объединяющее линейную скорость и радиус вращения:
ω = v/r.
Если проверить единицу измерения ω в этом выражении, то получаем те же радианы в секунду (с-1). Формула показывает, что чем меньше расстояние от оси вращения до тела (r), и чем больше его скорость линейная (v), тем больше будет ω.
Из этой формулы можно легко выразить величину v: v = ω×r. Поскольку угловая скорость является величиной постоянной для некоторого рассматриваемого тела, то быстрее будут двигаться те точки, которые находятся дальше от оси вращения.
Рассмотренные формулы и понятия используем для определения скорости угловой вращения Земли вокруг оси и вокруг Солнца.
Вращение нашей планеты вокруг оси
Каждый человек знает, что планета, на которой он живет, вращается вокруг своей оси, причем экваториальная плоскость Земли наклонена под углом 23˚ к плоскости эклиптики.
Как рассчитать угловую скорость вращения вокруг своей оси Земли? Для этого можно воспользоваться совершенно любой из формул, которые приведены были выше. Поскольку мы знаем, что один оборот вокруг оси происходит за 24 часа, то для расчета следует использовать выражение с периодом T. Получаем:
ω = 2×π/T = 2×3,1416/(24×3600) = 7,27×10-5 рад/с.
Здесь значение периода T было переведено в секунды. Полученное значение является небольшим.
Полученное значение является небольшим.
Представляет интерес рассчитать, с какой линейной скоростью движутся точки на поверхности планеты на широте 0˚ (экватор). Экваториальный радиус Земли равен 6 378 000 м. Подставляя это значение в формулу для скорости, получим:
v = ω×r = 7,27×10-5×6 378 000 = 463,8 м/с = 1670 км/ч.
Полученное значение является большим в сравнении со скоростями, которые мы наблюдаем в жизни. Человек эту скорость не ощущает, поскольку вращается вместе с воздухом и почвой под ногами с одной скоростью, то есть он покоится относительно них.
Рассмотренное вращение Земли приводит не только к возникновению явления дня и ночи, но и к появлению так называемой силы Кориолиса, которая оказывает влияние на некоторые земные процессы, например, изменяет направление ветров.
Вращение Земли по своей орбите
Рассчитаем теперь угловую скорость вращения Земли вокруг Солнца. Для этого воспользуемся следующими данными: точное значение сидерического периода обращения нашей планеты по орбите составляет 365 дней 6 часов 9 минут и 9,7632 секунды, то есть T = 31558149,7632 секунд.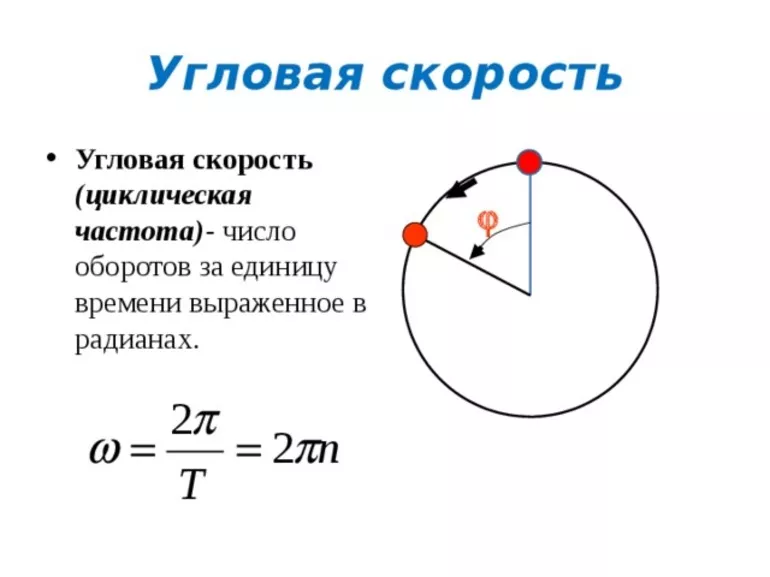 Теперь можно воспользоваться формулой:
Теперь можно воспользоваться формулой:
ω = 2×π/T = 2×3,1416/(31558149,7632) = 1,991×10-7 рад/с.
То есть угловая орбитальная скорость нашей планеты меньше на 1,5 порядка, чем аналогичная величина для вращения вокруг собственной оси. Вычислим линейную скорость, учитывая, что средний радиус орбиты равен 149 597 871 000 метров:
v = ω×r = 1,991×10-7×149 597 871 000 = 29784,8 м/с = 107 225 км/ч.
С этой огромной скоростью наша планета движется в космическом пространстве вокруг Солнца.
С орбитальным движением планеты и наклоном ее оси связано существование времен года в Северном и Южном полушариях.
Угловая скорость и ускорение. Связь между угловыми и линейными характеристиками движения
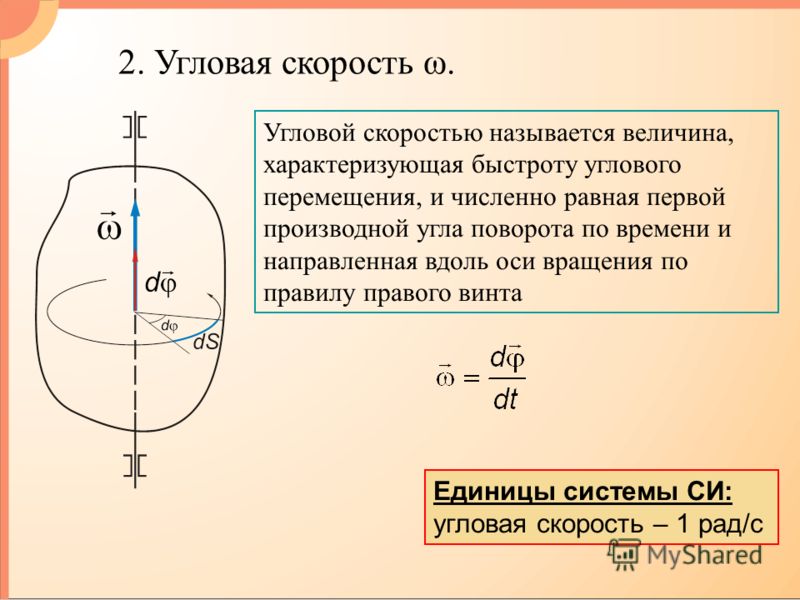
Скорости движения различных точек тела, вращающегося вокруг неподвижной оси, различаются. Поэтому для описания вращения твердого тела вводят угловые величины, относящиеся ко всему телу в целом, а не к отдельным его точкам. Такими величинами являются угол поворота j, угловая скорость и угловое ускорение тела.
Такими величинами являются угол поворота j, угловая скорость и угловое ускорение тела.
Вектор угловой скорости тела определяют в виде:
, (1.18)
где dt – промежуток времени, за который тело совершает поворот . Вектор совпадает по направлению с вектором .
Изменение вектора со временем характеризуют вектором углового ускорения , который определяют в виде
. (1.19)
Направление вектора совпадает с направлением приращения вектора .
Единицей угловой скорости в СИ является радиан в секунду (рад/с), а единицей углового ускорения – радиан на секунду в квадрате (рад/с2).
Используя определения (1.18) и (1.19), получим выражения для проекций угловой скорости и углового ускорения w
; . (1.20)
Рис. 1.7
Формулы для расчета w(t) и j(t). можно получить интегрированием (1. 20)
20)
j(t) = wzt + j0 ; wz(t) = ezt + wz0 . (1.21)
Выразим скорость произвольной точки твердого тела, вращающегося вокруг неподвижной оси, через угловую скорость . Пусть положение точки М относительно некоторой точки О оси вращения характеризуется радиусом-вектором r (рис. 1.10). Разделим обе части формулы (1.17) на dt. Т. к. и , то искомое выражение примет вид
, (1.22)
Модуль вектора скорости в формуле (1.22)
u = wR, (1.23)
где R – радиус окружности, по которой движется точка М.
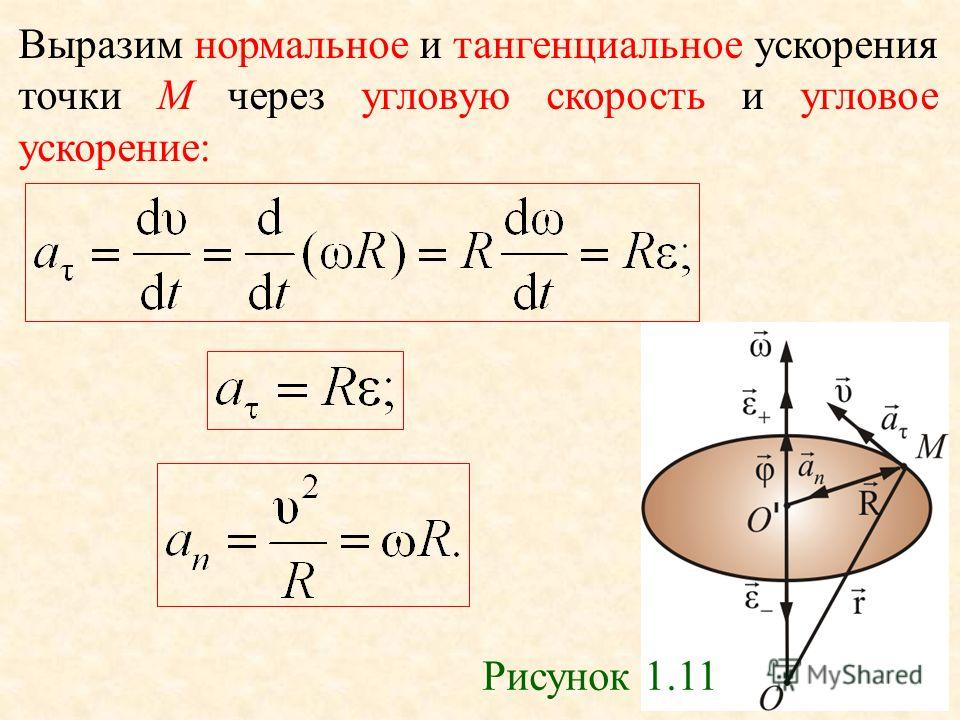
Найдем полное ускорение точки М. Для этого продифференцируем (1.22) по времени
Þ . (1.24)
В данном случае ось вращения неподвижна, и векторы и параллельны. Вектор представляет собой тангенциальное ускорение . Вектор является нормальным ускорением . Модули этих ускорений равны:
Модули этих ускорений равны:
at = eR; an = w2R.
Модуль полного ускорения
.
Для решения задач, в которых вращение тела является равномерным, используются также понятия периода и частоты вращения. Периодом вращения Т называют промежуток времени, в течение которого тело, вращаясь с постоянной угловой скоростью w, совершает один полный оборот, т. е. поворачивается на угол j = 2p. Частотой вращения
Þ . (1.25)
Число оборотов в единицу времени равно:
; или w = 2pn. (1.26)
Пример. Тело брошено под углом a к горизонту с начальной скоростью u0. Найти тангенциальное и нормальное ускорения в начале траектории (точке О), а также радиус кривизны в этой точке.
Найти тангенциальное и нормальное ускорения в начале траектории (точке О), а также радиус кривизны в этой точке.
На брошенное тело действует только сила тяжести. Поэтому вектор полного ускорения равен вектору ускорения свободного падения, который разложим на две составляющих – тангенциальную и нормальную (рис. 1.11). Угол между векторами и равен a, т. к. направление вектора перпендикулярно направлению вектора , а направление вектора совпадает с направлением . Тогда модули векторов и равны
; .
Рис. 1.11
Радиус кривизны в начальной точке траектории О получим, переписав формулу (1.17) для модуля вектора и выразив радиус R
Þ .
Определение скоростей и ускорений при вращательном движении
Основные законы и формулы, применяемые при решении задач
Вращательное движение вокруг неподвижной оси
Рассмотри твердое тело, вращающееся вокруг неподвижной оси z. Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t:
Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t:
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.
Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.
Скорость точки при вращательном движении тела вокруг неподвижной оси
Рассмотрим точку A, принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .
Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA. При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .
Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA. При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .
Ускорение точки при вращательном движении тела вокруг неподвижной оси
Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.
Полное ускорение точки A, или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.
Поступательное прямолинейное движение
Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x. При – противоположно этой оси.
Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x. При – противоположно.
Соприкосновение тел без проскальзывания
Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.
Пример решения задачи
Условие задачи
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r1 = 2 см, R1 = 4 см, у колеса 2 – r2 = 6 см, R2 = 8 см, у колеса 3 – r3 = 12 см, R3 = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s5 = t3 – 6t (см). Положительное направление для s5 – вниз.
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.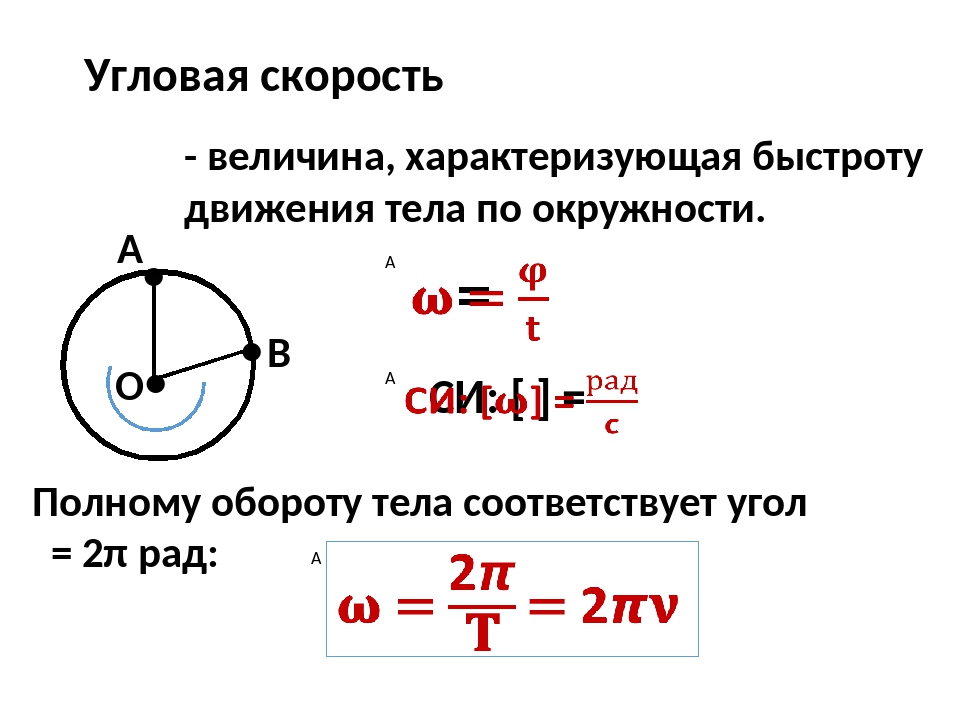
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t3 – 6t (см).
Решение
Определение скорости и ускорения груза 5
Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t, находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.
Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с2.
Определение угловых скоростей и ускорений колес
Решение задачи
Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t. Дифференцируя по t, находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с–1;
с–2.
Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с–1;
с–2.
Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с–1;
с–2.
Итак, мы нашли:
ω1 = 5. 3333 с–1, ω2 = 1.3333 с–1, ω3 = 0.5 с–1, ε1 = 10.6667 с–2, ε2 = 2.6667 с–2, ε3 = 1 с–2.
3333 с–1, ω2 = 1.3333 с–1, ω3 = 0.5 с–1, ε1 = 10.6667 с–2, ε2 = 2.6667 с–2, ε3 = 1 с–2.
Определение скоростей точек A и C
Точка A лежит на окружности радиуса R1 с центром в точке O1, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.
Точка C лежит на окружности радиуса R3 с центром O3 на оси вращения. Скорость этой точки:
см/с.
Определение ускорения точки B
Точка B лежит на окружности радиуса R2 с центром O2, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с2.
Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
По абсолютной величине оно равно
см/с2.
Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с2.
Определение ускорения рейки 4
Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с:
см/с2.
Ответ
см/с; см/с; с–2; см/с2; см/с2.
Автор: Олег Одинцов. Опубликовано:
Угловая скорость. Связь векторов линейной и угловой скоростей.
Стр 1 из 3Следующая ⇒Угловая скорость. Связь векторов линейной и угловой скоростей.
Связь векторов линейной и угловой скоростей.
Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
Легко найти связь между линейной скоростью
т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности.
При вращательном движении действуют: тангенциальное и центростремительное ускорения.
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
Центробежное ускорение можно вычислить по формуле:
Угловое ускорение. Связь линейных и угловых величин.
Угловое ускорение — физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
Существует связь между тангенциальным и угловым ускорениями:
где R — радиус кривизны траектории точки в данный момент времени
Тангенциальное ускорение направлено по касательной в траектории движения тела, а нормальное — перпендикулярно ему.
13. Сформулируйте первый закон Ньютона.
Существуют такие системы отсчёта, относительно которых материальная точка, при отсутствии внешних воздействий, сохраняет состояние покоя или равномерного прямолинейного движения.
Что такое замкнутая механическая система.
Замкнутая механическая система, потенциальная энергия которой имеет минимальное значение и в которой отсутствуют движения тел, находится в состоянии равновесия.
20. Радиус-вектор, скорость, импульс, закон движения центра масс.
Радиус-вектор точки — это вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.
Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат.
Скорость — физическая величина, характеризующая движение тела в пространстве. Физический смысл — Изменение координаты в единицу времени.
Импульс тела — это векторная величина, равная произведению массы тела на его скорость: . Специальных единиц измерения импульса нет. Размерность импульса — это просто произ- ведение размерности массы на размерность скорости: [p] = [m] · [v] = кг · м /с .
Воспользовавшись законом изменения импульса, получим закон движения центра масс:
dP/dt = M∙dVc/dt = ΣFi
Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы.
Энергия и работа. В чём разница?
Термин «работа» в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа — физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением:
А = Fs cos a.
Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos
1 джоуль — это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину «мощность».
Для определения быстроты совершения работы вводят величину «мощность».
Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:
Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт — мощность, при которой совершается работа в 1 Дж за 1 секунду.
Сформулируйте закон Гука.
Закон Гука — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским учёным Робертом Гуком.
Закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Угловая скорость. Связь векторов линейной и угловой скоростей.
Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
Легко найти связь между линейной скоростью точки v, ее угловой скоростью ω и радиусом r окружности, по которой она движется.
т. е. линейная скорость при движении по окружности равна угловой скорости, умноженной на радиус окружности.
При вращательном движении действуют: тангенциальное и центростремительное ускорения.
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
Центробежное ускорение можно вычислить по формуле:
Читайте также:
Угловой путь и угловое ускорение.
Угловое ускорение – это физическая величина равная отношению изменения угловой скорости к интервалу времени, за который оно произошло.
– угловое ускорение в этом движении – величина постоянная, так как = const:
ср = мгн = const.
; . (45)
Единица измерения углового ускорения:
[e] = .
Если вращение около закрепленной оси (рис. 36), то направления векторов углового ускорения и угловой скорости совпадают при равноускоренном вращении (w > w0) и противоположны при равнозамедленном вращении (w < w0).
Рис. 36
Таким
образом, направления векторов и аналогичны
направлениям векторов и .
Соотношения между и (46)
аналогичны соотношениям между и (21;
22; 23).
Формула мгновенной угловой скорости, как следует из формулы (45), равна:
.
– формула модуля угловой скорости:
. (46)
– формула углового пути при равнопеременном движении точки по окружности (см. формулу (44) равен:
. (47)
Подставив в эту формулу значения средней скорости и мгновенной скорости , получим другую формулу углового пути для этого движения:
. (48)
Еще одну формулу углового пути можно получить, подставив в формулу (47) значения и интервала времени (из формулы (46)):
. (49)
Итак, угловой путь, угловая скорость и угловое ускорение (47, 48, 49) связаны между собой так же, как и соответствующие им линейные величины S, v и a (24, 26, 29).
– Уравнение равнопеременного движения материальной точки по окружности. Из формулы (48) следует, что
. (50)
Угловая скорость. Связь с моментом силы.
Углова́я
ско́рость — векторная физическая
величина, характеризующая скорость
вращения тела. Вектор угловой скорости
по величине равен углу
поворота тела в единицу времени:
Вектор угловой скорости
по величине равен углу
поворота тела в единицу времени:
,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]).
Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Момент силы — производная по времени от момента импульса,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
,
То есть если I постоянная, то
,
где
α — угловое
ускорение, измеряемое в радианах в секунду за
секунду.
Второй закон Ньютона и его выражение через импульс.
Второй закон Ньютона: ускорение, приобретаемое материальной точкой, пропорционально вызываемой его силе, совпадает с ней по направлению и обратно пропорционально его массе материальной точки:
Импульс тела – векторная величина, численно равна произведению массы тела на его скорость и имеющая направление скорости тела:
,
где m – масса тела, — скорость тела.
Второй закон Ньютона в импульсной форме (при ):
Как рассчитать формулу угловой скорости
Формула угловой скорости : В физике угловая скорость относится к тому, насколько быстро объект вращается или вращается относительно другой точки, то есть насколько быстро угловое положение или ориентация объекта изменяется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и угловая скорость вращения. Угловая скорость вращения указывает на то, насколько быстро твердое тело вращается относительно центра вращения.
Угловая скорость вращения указывает на то, насколько быстро твердое тело вращается относительно центра вращения.
Орбитальная угловая скорость относится к тому, насколько быстро точечный объект вращается вокруг фиксированного начала координат, то есть скорость изменения его углового положения относительно начала координат во времени. Обычно угловая скорость измеряется в углах в единицу времени, например радиан в секунду. Единица измерения угловой скорости в системе СИ выражается в радианах / сек, причем радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ представлены как 1 / сек . Угловая скорость обычно обозначается символом омега ( ω , иногда Ω ).По соглашению, положительная угловая скорость означает вращение против часовой стрелки, а отрицательная — по часовой стрелке.
Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = 360/24 = 15 градусов в час, или 2π / 24 ≈ 0,26 радиана в час. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega}. Таким образом, с радиусом орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 × 0.26 ≈ 11000 км / час. Угловая скорость положительна, поскольку спутник движется на восток вместе с вращением Земли (против часовой стрелки над северным полюсом).
Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega}. Таким образом, с радиусом орбиты 42 000 км от центра Земли скорость спутника в космосе составляет v = 42 000 × 0.26 ≈ 11000 км / час. Угловая скорость положительна, поскольку спутник движется на восток вместе с вращением Земли (против часовой стрелки над северным полюсом).
В трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, а ее направление указывает перпендикулярно плоскости мгновенного вращения или углового смещения. Ориентация угловой скорости условно задается правилом правой руки.
Формула для угловой скорости
В простейшем случае кругового движения по радиусу {\ displaystyle r} с положением, заданным угловым смещением {\ displaystyle \ phi (t)} от оси x, орбитальная угловая скорость представляет собой скорость изменения угла с относительно времени: {\ displaystyle \ omega = {\ tfrac {d \ phi} {dt}}}. Если {\ displaystyle \ phi} измеряется в радианах, расстояние от оси x вокруг круга до частицы равно {\ displaystyle \ ell = r \ phi}, а линейная скорость равна {\ displaystyle v (t) = {\ tfrac {d \ ell} {dt}} = r \ omega (t)}, так что {\ displaystyle \ omega = {\ tfrac {v} {r}}}.
Если {\ displaystyle \ phi} измеряется в радианах, расстояние от оси x вокруг круга до частицы равно {\ displaystyle \ ell = r \ phi}, а линейная скорость равна {\ displaystyle v (t) = {\ tfrac {d \ ell} {dt}} = r \ omega (t)}, так что {\ displaystyle \ omega = {\ tfrac {v} {r}}}.
В общем случае частицы, движущейся в плоскости, орбитальная угловая скорость — это скорость, с которой вектор положения относительно выбранного начала координат «выметает» угол. На диаграмме показан вектор положения {\ displaystyle \ mathbf {r}} от начала координат {\ displaystyle O} до частицы {\ displaystyle P} с его полярными координатами {\ displaystyle (r, \ phi)}. (Все переменные являются функциями времени {\ displaystyle t}.) Частица имеет линейное разделение скорости как {\ displaystyle \ mathbf {v} = \ mathbf {v} _ {\ |} + \ mathbf {v} _ {\ perp }}, с радиальным компонентом {\ displaystyle \ mathbf {v} _ {\ |}}, параллельным радиусу, и поперечно-радиальным (или тангенциальным) компонентом {\ displaystyle \ mathbf {v} _ {\ perp}} перпендикулярно радиусу. Когда радиальная составляющая отсутствует, частица движется вокруг начала координат по окружности; но когда нет поперечно-радиального компонента, он движется по прямой от начала координат. Поскольку при радиальном движении угол остается неизменным, только поперечно-радиальная составляющая линейной скорости вносит вклад в угловую скорость.
Когда радиальная составляющая отсутствует, частица движется вокруг начала координат по окружности; но когда нет поперечно-радиального компонента, он движется по прямой от начала координат. Поскольку при радиальном движении угол остается неизменным, только поперечно-радиальная составляющая линейной скорости вносит вклад в угловую скорость.
Угловая скорость ω — это скорость изменения углового положения относительно времени, которую можно вычислить из поперечной радиальной скорости как:
- {\ displaystyle \ omega = {\ frac {d \ phi} {dt}} = {\ frac {v _ {\ perp}} {r}}.}
Здесь поперечная радиальная скорость {\ displaystyle v _ {\ perp}} — это величина со знаком {\ displaystyle \ mathbf {v} _ {\ perp}}, положительная для движения против часовой стрелки, отрицательная для движения по часовой стрелке. Если взять полярные координаты для линейной скорости {\ displaystyle \ mathbf {v}}, получаем величину {\ displaystyle v} (линейную скорость) и угол {\ displaystyle \ theta} относительно радиус-вектора; в этих терминах {\ displaystyle v _ {\ perp} = v \ sin (\ theta)}, так что
- {\ displaystyle \ omega = {\ frac {v \ sin (\ theta)} {r}}.
 {\ perp} = (- y, x)}.
{\ perp} = (- y, x)}.В двух измерениях угловая скорость — это число со знаком плюс или минус, указывающее ориентацию, но не указывающее в направлении. Знак обычно считается положительным, если радиус-вектор вращается против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда угловая скорость может быть названа псевдоскалярной, числовой величиной, которая меняет знак при инверсии четности, такой как инвертирование одной оси или переключение двух осей.
Читайте также: Формула трехчлена идеального квадрата
Как рассчитать угловую скорость по оборотам?
оборотов в минуту можно преобразовать в угловую скорость в градусах в секунду, умножив оборотов в минуту на 6, так как один оборот составляет 360 градусов и 60 секунд в минуту.Если об / мин равно 1 об / мин , угловая скорость в градусах в секунду будет 6 градусов в секунду, так как 6 умноженное на 1 равно 6.

Какова формула угловой скорости?
Чтобы получить нашу вторую формулу для угловой скорости , мы понимаем, что тета дается в радианах, а определение радианной меры дает theta = s / r. Таким образом, мы можем подставить theta = s / r в нашу первую формулу угловой скорости .Это дает w = (s / r) / t.
Обороты — это то же самое, что и угловая скорость?
Угловая скорость составляет скорость вращения . Что-то крутится. Это сокращение от количества оборотов в минуту. Другие связанные единицы, которые выражают то же свойство , — градусы в секунду и радианы в секунду.

Формула средней угловой скорости
Во-первых, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-либо другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругам или их частям.Вы можете вспомнить из геометрии или тригонометрии, что длина окружности равна его диаметру, умноженному на константу пи, или πd . (Значение пи составляет около 3,14159.) Это чаще всего выражается в терминах радиуса окружности r , который составляет половину диаметра, в результате чего длина окружности 2πr .
Кроме того, вы, вероятно, где-то по пути узнали, что круг состоит из 360 градусов (360 °). Если вы переместитесь на расстояние S по окружности, то угловое смещение θ будет равно S / r.Таким образом, один полный оборот дает 2πr / r, что оставляет 2π. Это означает, что углы меньше 360 ° могут быть выражены в пи, или, другими словами, в радианах.

Взяв всю эту информацию вместе, вы можете выразить углы или части круга в единицах, отличных от градусов:
1 радиан = (360 ° / 2π) = 57,3 °,
В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно в секунду.
Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r от центра круга, причем направление v всегда перпендикулярно радиусу круга, тогда угловую скорость можно записать
, где ω — греческая буква омега. Единицы угловой скорости — радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v / r дает м / с, деленные на m, или с -1 , что означает, что радианы технически являются безразмерной величиной.
Формула центростремительного ускорения Угловая скорость
Формула углового ускорения выводится так же, как и формула угловой скорости: это просто линейное ускорение в направлении, перпендикулярном радиусу круга (эквивалентно его ускорение по касательной к круговой траектории в любой точке) делится на радиус круга или части круга, который составляет:
, потому что для кругового движения a t = ωr / t = v / t.

α , как вы, наверное, знаете, это греческая буква «альфа». Индекс «t» здесь означает «касательную».
Как ни странно, однако, вращательное движение может иметь другой вид ускорения, называемый центростремительным («центростремительное») ускорением. Это дается выражением:
Это ускорение направлено к точке, вокруг которой вращается рассматриваемый объект. Это может показаться странным, поскольку объект не приближается к этой центральной точке, поскольку радиус r фиксирован.Думайте о центростремительном ускорении как о свободном падении, при котором нет опасности удара объекта о землю, потому что сила, притягивающая объект к нему (обычно сила тяжести), в точности компенсируется тангенциальным (линейным) ускорением, описываемым первым уравнением в эта секция. Если бы a c не было равно a t , объект либо улетел бы в космос, либо вскоре врезался бы в середину круга.

Читайте также: Средняя и мгновенная скорость изменения
Формула угловой скорости Физика
Прежде чем мы перейдем к угловой скорости, мы сначала рассмотрим линейную скорость. Линейная скорость применяется к объекту или частице, движущимся по прямой линии. Это скорость изменения положения объекта во времени.
Линейная скорость может быть рассчитана по формуле v = с / t , где v = линейная скорость, с = пройденное расстояние и t = время, необходимое для преодоления расстояния. Например, если я проехал 120 миль за 2 часа, то для расчета моей линейной скорости я бы вставил с = 120 миль и t = 2 часа в свою формулу линейной скорости, чтобы получить v = 120 / 2 = 60 миль в час.Один из наиболее распространенных примеров линейной скорости — это ваша скорость при движении по дороге. Ваш спидометр показывает вашу скорость или показатель в милях в час. Это скорость изменения вашего положения относительно времени, другими словами, ваша скорость — это ваша линейная скорость.

Перед тем как перейти к угловой скорости, нам нужно рассмотреть еще одну вещь — радианы. Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой.Техническое определение радиан. — это длина дуги, образованной углом, деленная на радиус круга, частью которого является угол, где подразумеваемый означает, что она противоположна углу и проходит от одной точки на круг к другому, оба отмечены углом. Это говорит нам о том, что угол тета = с / r радиан, где с = длина дуги, соответствующей тета, и r = радиус круга, частью которого является тета.
Формула угловой скорости в линейную скорость Поскольку большинство из нас привыкли к градусному измерению углов, удобно, что мы можем легко преобразовать градус в радиан, умножив градус на пи / 180. Например, угол 45 градусов имеет мера в радианах 45 (пи / 180), что равно пи / 4 радиана.
Читайте также: Формула линейной интерполяции
Угловая скорость и угловое ускорение ГЛАВА 9 ВРАЩЕНИЕ.
 Угловая скорость и угловое ускорение.! уравнения вращательного движения
Угловая скорость и угловое ускорение.! уравнения вращательного движения 1 Угловая скорость и угловое ускорение ГЛАВА 9 ВРАЩЕНИЕ! r i ds i dθ θ i Угловая скорость и угловое ускорение! уравнения вращательного движения Крутящий момент и Момент инерции! Закон Ньютона для вращения Определение момента инерции Кинетическая энергия вращения! мощность Катящиеся объекты (без проскальзывания) Длина дуги, перемещаемая i-м элементом во вращающемся жестком недеформируемом диске, составляет: ds i = r i dθ, где dθ в радианах.Угловая скорость вращающегося диска определяется как: ω = dθ dt, поэтому линейная скорость i-го элемента (в направлении касательной) равна: v i = ds i dt = r iω.
2 Какая связь между угловой и линейной скоростью двух точек на одном диске? ОБСУЖДЕНИЕ ПРОБЛЕМА [9.
 1]: у вас есть друг, который живет в Миннесоте, а вы живете во Флориде. Когда Земля вращается, ваша линейная скорость принадлежит ей, а ваша угловая скорость — ее.RMM0VD.mov Угловая скорость ω одинакова для всех точек на диске, но линейная (или касательная) скорость — нет. Посмотрите, v = rω, так как r> r 1, то v> v 1. A: меньше; равно B: равно; больше, чем C: больше, чем; меньше D: меньше; больше, чем E: больше, чем; равно
1]: у вас есть друг, который живет в Миннесоте, а вы живете во Флориде. Когда Земля вращается, ваша линейная скорость принадлежит ей, а ваша угловая скорость — ее.RMM0VD.mov Угловая скорость ω одинакова для всех точек на диске, но линейная (или касательная) скорость — нет. Посмотрите, v = rω, так как r> r 1, то v> v 1. A: меньше; равно B: равно; больше, чем C: больше, чем; меньше D: меньше; больше, чем E: больше, чем; равно3 Если угловая скорость изменяется, возникает угловое ускорение … Угловое ускорение диска равно: α = dω dt = d dt. dθ dt = d θ dt, а тангенциальное ускорение i-го элемента равно: a it = dv i dt = r i dω dt = r iα.Но поскольку i-й элемент движется по кругу, он испытывает радиальное (центростремительное) ускорение :! r i a ir (= a ic) = v i r i = r i ω. Результирующее линейное ускорение равно dθ Угловая скорость (ω) (вектор)! а! ds i a i it θ i! воздух! а ир а! Это! а я = а ир + а это. Размерность: ω 1 [T] (проверьте: v i = r i ω [L] 1 [T] = [L] [T]). Единицы: рад / с Угловое ускорение (α) (вектор) Размер: α 1 [T] Единицы: рад / с
4 СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМ И ВРАЩАТЕЛЬНЫМ ДВИЖЕНИЕМ Линейное движение a постоянное Вращательное движение α constant v = v! + при ω = ω! + αt (!) = v! t + 1 при (θ θ!) = ω! t + 1 αt v = v! + а (!) ω = ω! + α (θ θ!) Видите ли, они очень похожи на вопрос 9.
 1: Диск радиусом 1 см, первоначально находящийся в состоянии покоя, начинает вращаться вокруг своего носа с постоянным угловым ускорением 3,00 рад / с. Через 5 с, каковы (а) угловая скорость диска и (б) тангенциальное и центростремительное ускорение точки на периметре диска? (c) Сколько оборотов сделал диск за эти 5 с?
1: Диск радиусом 1 см, первоначально находящийся в состоянии покоя, начинает вращаться вокруг своего носа с постоянным угловым ускорением 3,00 рад / с. Через 5 с, каковы (а) угловая скорость диска и (б) тангенциальное и центростремительное ускорение точки на периметре диска? (c) Сколько оборотов сделал диск за эти 5 с?5 r r = 0,1 м: ω! = 0: θ! = 0: t = 5 с α = 3,00 рад / с. ω = ?: θ = ?: a t = ?: a c =? а) ω = ω! + αt = (3,00 рад / с) (5 с) = 15.0 рад / с. (б) v i = r i ω = (0,1 м) (15,0 рад / с) = 1,80 м / с (линейный). тангенциальное ускорение: a t = r i α = (0,1 м) (3,00 рад / с) = 0,36 м / с. центростремительное ускорение: ac = ri ω (Проверить … ac = vr = (0,1 м) (15,0 рад / с) = 7,0 м / с. = (1,80 м / с) 0,1 м = 7,0 м / с.) применения ремень или цепь натягивается или наматывается на шкив или шестерню … vtvtat R Когда струна (цепь или ремень) удаляется (или добавляется), ее мгновенная скорость совпадает с тангенциальной скоростью на ободе колесо, при условии отсутствия проскальзывания: i.
 е., v t = Rω. (в) (θ θ!) = ω! t + 1 αt = 1 (3,00 рад / с) (5 с) = 37,5 рад, n = 37,5 рад π = 5,97 об. Кроме того, при тех же условиях мгновенное ускорение струны такое же, как тангенциальное ускорение на ободе колеса: то есть a t = dv t dt = R dω dt = Rα.
е., v t = Rω. (в) (θ θ!) = ω! t + 1 αt = 1 (3,00 рад / с) (5 с) = 37,5 рад, n = 37,5 рад π = 5,97 об. Кроме того, при тех же условиях мгновенное ускорение струны такое же, как тангенциальное ускорение на ободе колеса: то есть a t = dv t dt = R dω dt = Rα.6 Как мы видели в главе 4, сила вызывает изменение движения. Однако сила не всегда вызывает изменение вращательного движения. Именно крутящий момент вызывает изменение вращательного движения.Рассмотрим массу m, прикрепленную к безмассовому жесткому стержню, который вращается вокруг ais O. Показанная сила F заставит массу вращаться. O Величина крутящего момента, создаваемого силой F, действующей на m, равна: τ = lf = (r sin θ) f, где l называется плечом рычага. Плечо рычага — это перпендикулярное расстояние от оси вращения (O) до линии действия силы. ПРИМЕЧАНИЕ: если «F проходит через O, т. Е. L = 0, то τ = 0 и не будет изменений во вращательном движении. Lr θ m» F l = r sin θ Размер: τ [L] [M] [L ] [T] Единица: N m = [M] [L] [T] (вектор) Сформируйте радиальную и тангенциальную составляющие силы: O l Тогда τ = lf = (r sin θ) f = r (fsin θ) я.
 е., τ = rf t. Примечание: радиальная составляющая F r, проходящая через проход вращения, не создает крутящего момента и, следовательно, не вызывает вращения; только тангенциальная составляющая F t создает крутящий момент, который приводит к вращению. rm «FF t = F sin θ O lr θ m» FF r = F cosθ
е., τ = rf t. Примечание: радиальная составляющая F r, проходящая через проход вращения, не создает крутящего момента и, следовательно, не вызывает вращения; только тангенциальная составляющая F t создает крутящий момент, который приводит к вращению. rm «FF t = F sin θ O lr θ m» FF r = F cosθ7 F t = F sin θ O rl θ m «FF r = F cosθ Закон Ньютона s nd говорит нам, что тангенциальная составляющая силы F t вызывает тангенциальное ускорение при, т. Е. F t = ma t.τ = rf t = mra t. Но, как было сказано ранее, тангенциальное (линейное) ускорение связано с угловым ускорением α, а именно: a t = rα. τ = mra t = mr α. Таким образом, крутящий момент (τ) вызывает угловое ускорение (α). Сверху для каждого отдельного массового элемента имеем O r i Δm i τ i = (Δm i) r i α, где τ i — чистый крутящий момент на i-м элементе. Суммируя все элементы, общий чистый крутящий момент на объекте равен: τ net = i τ i = i (δm i) ri α = (Δm i) r (ii) α = Iα, где мы называем I = (Δm i) rii МОМЕНТ ИНЕРЦИИ.Это закон Ньютона для вращения, то есть τ net = Iα.
 Жесткий объект, который вращается вокруг аэродрома, можно представить как набор небольших отдельных элементов с массой Δm i (), каждый из которых движется по круговой траектории с радиусом r i, где r i отсчитывается от аэродрома вращения. Чистый вечный крутящий момент, действующий на тело, вызывает угловое ускорение α этого тела, задаваемое Iα, где I — момент инерции. (а именно: F net = i F i = ma.)
Жесткий объект, который вращается вокруг аэродрома, можно представить как набор небольших отдельных элементов с массой Δm i (), каждый из которых движется по круговой траектории с радиусом r i, где r i отсчитывается от аэродрома вращения. Чистый вечный крутящий момент, действующий на тело, вызывает угловое ускорение α этого тела, задаваемое Iα, где I — момент инерции. (а именно: F net = i F i = ma.)8 Момент инерции… так о чем все это? Размерность: I [M] [L] Единицы: кг · м (скаляр) Каждый объект имеет момент инерции относительно оси вращения. Его значение зависит не только от массы, но и от того, как масса распределяется вокруг этого прохода. Для дискретного набора из n объектов момент инерции относительно вращения ais равен: Для непрерывного объекта: I = Предел Δm i 0 I = n I n = n m n r n. i (Δm i) r i = r dm, Вопрос 9: Найти момент инерции однородного тонкого стержня длины l и массы M, вращающегося вокруг оси, перпендикулярной стержню, и через его центр.y l, где m является функцией r.

9 ярдов [1] Убедитесь, что момент инерции стержня массы M и длины l относительно одного конца равен y. Стержень представляет собой сплошной объект, поэтому момент инерции равен I = r dm = = l dm. . = l Масса на единицу длины стержня равна M l, поэтому масса d 0 l I = 1 3 Ml. маленький элемент длины d равен dm = (M l) d. Подставляя вместо dm, интеграл принимает вид I = = l = M l () M l d = M l = l () l3 3 () 3 4 (l3) 4 = 1 1 Ml.l l [] Покажите себе, что момент инерции стержня массы M и длины l около a составляет одну треть расстояния от одного конца y d l 3 0 l 3 I = 1 9 Ml.
10 r Момент инерции определяется как I = r dm. Рассмотрим r 1 Вопрос 9.3: Найдите момент инерции круглого диска, показанного ниже, вращающегося вокруг оси, перпендикулярной плоскости, и через ее центр. Масса диска 1,50 кг. 10 см 0 см кольцо радиусом r и шириной dr.Если масса объекта равна M, масса кольца равна dm = M πrdr π r r 1 (), где r 1 и r — внутренний и внешний радиусы объекта. Затем, подставив вместо dm, r I = r M πrdr π rr 1 = r 1 M rr (1) r 4 4 r () = M rr (1) r = r1 rr 1 r 3 dr M rr (1) r 4 r 4 (1) = M rr (1) rr (1) r + r (1) = 1 M r + r (1).

11 I = 1 M r + r (1) = 1 (1,50 кг) ((0,0 м) + (0,10 м)) = кг · м. [1] Если r 1 = 0, то I disk = 1 MR, где R — радиус диска (= r).R Конечно, но каково значение «я»? Помните, из главы 4 … Массовая мера сопротивления изменению линейного движения, например, насколько сложно начать или остановить линейное движение. Момент инерции — мера сопротивления изменению вращательного движения, то есть насколько сложно начать или остановить вращательное движение. [] Для тонких обручей r 1 r = R, тогда I обруч = 1 M R () = MR. R При одинаковой толщине дисков моменты инерции не зависят от толщины. Таким образом, эти выемки также относятся к цилиндрам и трубкам.Одинаковые моменты инерции Различные моменты инерции RMM04VD1.MOV
12 Значения момента инерции для простых форм … Тонкий стержень I = 1 1 ML Плита I = 1 1 M (a + b) LL Тонкий стержень I = 1 3 ML Полый цилиндр I = 1 M (R + r) aba Плита I = 1 3 Ma b Полая сфера I = 3 MR Вопрос 9.4: Линейка длиной 1 м имеет массу 0,5 кг. К 100-сантиметровому концу линейки прикрепляется груз весом 5 кг.
 Каков его момент инерции относительно конца 0 см? Тонкостенный цилиндр I = MR Сплошной цилиндр I = 1 MR Твердая сфера I = 5 MR
Каков его момент инерции относительно конца 0 см? Тонкостенный цилиндр I = MR Сплошной цилиндр I = 1 MR Твердая сфера I = 5 MR13 b O O Комбинированный момент инерции равен I = I линейка + I масса, где I линейка и I масса рассчитываются относительно O O.Поскольку a >> b, мы предполагаем, что линейка метра представляет собой стержень (а именно: вопрос 9.) с I = 1 3 млн лет назад около 0 O. I линейка = 1 3 млн лет = 1 (0,5 кг) (1 м) 3 = кг · м . Момент инерции массы 5 кг относительно O O равен I mass = ma = (5,0 кг) (1 м) = 5,0 кг · м. Таким образом, суммарный момент инерции линейки и массы равен I линейке + I масса = кг · м. ПРОБЛЕМА ДЛЯ ОБСУЖДЕНИЯ 5 кг [9.]: Пара линейок для счетчиков размещается так, чтобы их нижний конец был прижат к стене. К верхнему концу одной из линейок прикреплена большая масса. Если одновременно отпустить линейки счетчиков и позволить упасть, какая из них упадет на пол первой? A: Измерительная линейка с массой.B: Измерительная линейка без массы. C: Они падают на пол одновременно.

14 Теорема о перпендикулярном ais: Теорема о параллельном ais: I cm I d Обычно момент инерции задается для ais, проходящего через центр масс (см) объекта. Что, если объект вращается вокруг айсиса, для которого нам неизвестен момент инерции? Момент инерции относительно общего (параллельного) ais определяется как: I = I cm + Md, где I cm — момент инерции относительно центра масс, M — масса объекта, а d — расстояние между aes. .Примечание: два угла поворота должны быть параллельны. Рассмотрим плоский объект (например, тонкий диск или лист) в плоскости y. По определению, момент инерции относительно оси z (перпендикулярно плоскости объекта) равен I z = imiri = mi (ii + yi) = miii + imiyi Но miii = I, то есть момент инерции относительно, и imiyi = I y, т.е. момент инерции относительно y. Пример диска: z z y i r i m i y I z = I + I y. Примечание: объект должен быть плоским y I z = 1 MR. Но по симметрии I = I y.I = I y = 1 4 MR.
15 м 3 кг 4 кг м 3 м Вопрос 9.5: Четыре массы в углах квадрата в м см м с длиной стороны L = м соединены безмассовыми стержнями.
 Масса m 1 = m 3 = 3 кг и m = m 4 = 4 кг. 4 кг 3 кг D Найдите (а) момент инерции относительно оси z, (b) момент инерции zz относительно оси, которая перпендикулярна плоскости ансамбля и проходит через центр масс системы, (c) момент инерции относительно -ais, который проходит через м 3 и м 4.(a) Момент инерции относительно оси z: I z = mirii = (3 кг) (м) + (4 кг) (м) + (3 кг) (м) + (4 кг) (0) = 56 кг м. y L m 1 m L (b) По симметрии центр масс находится в центре квадрата. I см = m i r i i = (3 кг) (м) + (4 кг) (м) м 4 м 3 + (3 кг) (м) + (4 кг) (м) = 8 кг м. Проверьте, используя теорему о параллельности z I z = I cm + MD I cm = I z MD = (56 кг м) (14 кг) (м) = 8 кг м.
Масса m 1 = m 3 = 3 кг и m = m 4 = 4 кг. 4 кг 3 кг D Найдите (а) момент инерции относительно оси z, (b) момент инерции zz относительно оси, которая перпендикулярна плоскости ансамбля и проходит через центр масс системы, (c) момент инерции относительно -ais, который проходит через м 3 и м 4.(a) Момент инерции относительно оси z: I z = mirii = (3 кг) (м) + (4 кг) (м) + (3 кг) (м) + (4 кг) (0) = 56 кг м. y L m 1 m L (b) По симметрии центр масс находится в центре квадрата. I см = m i r i i = (3 кг) (м) + (4 кг) (м) м 4 м 3 + (3 кг) (м) + (4 кг) (м) = 8 кг м. Проверьте, используя теорему о параллельности z I z = I cm + MD I cm = I z MD = (56 кг м) (14 кг) (м) = 8 кг м.16 y м 3 кг 4 кг z м 4 кг 3 кг (c) Поскольку ансамбль является плоским и ограничен плоскостью y, мы можем использовать теорему о перпендикуляре ais, т.е.е., I z = I + I y. Но по симметрии I = I y. I = 1 I z = 1 (56 кг м) Проверить: I = m i r i i = 8 кг м. = (3 кг) (м) + (4 кг) (м) = 8 кг м. Вопрос 9.6: Четыре тонких стержня, каждая длиной l и массой M, расположены так, что образуют квадрат в плоскости y, как показано, с началом координат aes в центре квадрата.
 (a) Используя теорему о параллельности ais, покажите, что I z = 4 3 Ml. (b) Следовательно, найдите I и I y. z l l y
(a) Используя теорему о параллельности ais, покажите, что I z = 4 3 Ml. (b) Следовательно, найдите I и I y. z l l y17 z l l y (a) Используя теорему о параллельности ais, мы имеем для каждого стержня I z = I cm + Md, где I cm — момент инерции через центр масс каждого стержня, а d = l.I z (всего) = ml + m l = ml. (b) Поскольку объект плоский, мы можем использовать теорему о перпендикуляре ais, т.е.I z = I + I y. Но в силу симметрии I = I y. I = I y = 1 I z = 3 мл. В главе 6 мы видели, что линейно движущийся объект имеет поступательную кинетическую энергию … объект, вращающийся вокруг ais, имеет кинетическую энергию вращения … ω O viri Δm i Если твердый объект вращается с угловой скоростью ω, кинетическая энергия i-й элемент: K i = 1 (Δm i) vi = 1 (Δm i) (ri ω), поскольку vi = ri ω.Итак, полная кинетическая энергия вращения равна: 1 K = i K i = i (Δm i) r i ω = 1 Iω. * K rot = 1 Iω является аналогом K trans = 1 mv.
18 Для вращения (или замедления) объекта требуется крутящий момент .
 .. но крутящий момент включает в себя силу … Когда сила прилагается на расстоянии, выполняется работа, определяемая выражением: O! r ds dθ! F dw =! F d! s = F.dscos γ = F cos γ.ds F t γ! F θ F r γ + θ = 90 «F t = F cos γ Вопрос 9.7: Двигатель развивает крутящий момент 400 Н · м при 3700 об / мин. Какую мощность развивает двигатель? = F t.ds = F t.rdθ = τ.dθ (Дж или Нм). Мощность — это скорость, с которой работает крутящий момент, то есть P = dw = τ dθ dt dt = τω (ватт). dw = τ.dθ является аналогом dw = F.ds. P = τω является аналогом P = Fv.
.. но крутящий момент включает в себя силу … Когда сила прилагается на расстоянии, выполняется работа, определяемая выражением: O! r ds dθ! F dw =! F d! s = F.dscos γ = F cos γ.ds F t γ! F θ F r γ + θ = 90 «F t = F cos γ Вопрос 9.7: Двигатель развивает крутящий момент 400 Н · м при 3700 об / мин. Какую мощность развивает двигатель? = F t.ds = F t.rdθ = τ.dθ (Дж или Нм). Мощность — это скорость, с которой работает крутящий момент, то есть P = dw = τ dθ dt dt = τω (ватт). dw = τ.dθ является аналогом dw = F.ds. P = τω является аналогом P = Fv.19 Крутящий момент τ = 400 Н · м. Угловая скорость ω = 3700 об / мин π (3700 об / мин) = = рад / с. 60 с / мин Изначально мощность P = τω = (400 Н · м) (387,5 рад / с) = Вт. Но 746 Вт = 1 л.с. P = Вт 746 Вт / л.с. = 08 л.с. Вопрос 9.8: Электродвигатель передает на вал точильного камня постоянный крутящий момент 10 Н · м.Если момент инерции точильного камня равен кг · м и система запускается из состояния покоя, найдите (а) кинетическую энергию вращения точильного камня через 8,0 с, (б) работу, выполненную двигателем за это время, и (в) средняя мощность, отдаваемая двигателем.

20 (a) Чтобы найти кинетическую энергию вращения, нам нужно знать угловую скорость ω. Поскольку τ = Iα, α = τ I = 10 Н · м · кг · м = 5,0 рад / с. Точильный камень запускается из состояния покоя (ω! = 0), поэтому ω = αt = (5,0 рад / с) (8.0 с) = 40 рад / с. K = 1 Iω = 1 (кг · м) (40 рад / с) = 1600 Дж. (B) Есть два способа определить работу, выполняемую двигателем. (i) По теореме о работе-кинетической энергии мы ожидаем, что двигатель отработал 1600 Дж работы. (ii) Мы можем использовать выемку W = τθ, но нам нужно найти θ, то есть угол, на который точильный камень повернулся за 8,0 с. (c) Средняя мощность — это общая проделанная работа, разделенная на общий временной интервал, то есть P av = ΔW = 1600 Дж Δt 8,0 с = 00 Вт. Примечание: полученное нами ранее значение P = τω фактически является мгновенной мощностью.Мы не можем использовать это углубление здесь, поскольку ω не является постоянным. Обратите внимание, что мгновенная мощность линейно увеличивается от нуля при t = 0 до (10 Н · м) (40 рад / с) = 400 Вт при t = 8,0 с.
 θ = ω! t + 1 αt = 1 (5,0 рад / с) (8,0 с) = 160 рад (= 5,46 об). W = τθ = (10 Н · м) (160 рад) = 1600 Дж.
θ = ω! t + 1 αt = 1 (5,0 рад / с) (8,0 с) = 160 рад (= 5,46 об). W = τθ = (10 Н · м) (160 рад) = 1600 Дж.21 Если жесткий объект подвешен к произвольной точке O и может свободно вращаться вокруг этой точки, он будет поворачиваться до тех пор, пока центр масс не окажется вертикально ниже точки подвеса.y r cm cm O cm Mg v cm ω v cm v = 0 Рассмотрим шар, цилиндр, колесо или диск), катящиеся по поверхности без скольжения. Точка контакта с поверхностью имеет нулевую мгновенную скорость относительно поверхности. Скорость см равна v см (= rω = v), скорость точки наверху равна v см (= v). Если направление y вертикально и точка подвеса не находится в центре масс, объект будет испытывать чистый крутящий момент, равный τ = Mg см, где см — составляющая центра масс. Следовательно, объект будет вращаться, пока cm = 0, т.е.Т. е. точка подвеса находится в направлении выше центра масс. Поскольку объект имеет ту же линейную скорость, что и cm, то есть v, общая кинетическая энергия равна: K tot = 1 mv + 1 Iω поступательное + вращательное, где ω = v r.
 Итак, когда мяч скатывается с холма … v, ω Гравитационная потенциальная энергия поступательная энергия + энергия вращения
Итак, когда мяч скатывается с холма … v, ω Гравитационная потенциальная энергия поступательная энергия + энергия вращения22 Рассмотрим катание сферы, цилиндра и обруча по склону. У них одинаковая скорость внизу? h v Для каждого объекта закон сохранения энергии дает: mgh = 1 mv + 1 Iω, а без проскальзывания v = Rω, где R — радиус объекта.После манипуляции находим: v gh =. 1 + I mr Для максимальной скорости: I наименьшее значение. Итак, в гонке между объектами, катящимися по склону, порядок будет (1) сфера, () цилиндр, (3) обруч, и он полностью не зависит от m и R! v gh = 1 + I mr Для твердой сферы I = 5 mr. v = gh 1 +, то есть v = 10gh 5 7. RMA07VD.MOV Поскольку это не зависит от m и R, шар для боулинга и шар для пула будут иметь одинаковые скорости в нижней части склона, несмотря на их разные массы и радиусы!
23 Вопрос 9.9: Однородный цельный шар массы M и радиуса R катится, не сползая вниз по наклонной поверхности под углом θ к горизонту. Найдите (а) силу трения, действующую в точке контакта с поверхностью, и (б) ускорение центра масс мяча в терминах M, R, g и θ.
 ПРИМЕЧАНИЕ: в точке контакта должно быть трение, иначе мяч соскользнет по склону! θ (a) Изобразите диаграмму свободного тела всех сил, действующих на мяч. Используйте закон Ньютона вниз по наклонной поверхности: f O R Mg N θ Mg sin θ f = Ma cm… (i) где см — ускорение центра масс. Чтобы получить вдавление на см, мы берем крутящий момент около O, центра шара. τ = fr = Iα, т.е. α = fr I, где I — момент инерции шара, а α — его угловое ускорение. (ПРИМЕЧАНИЕ: нормальная сила N и сила веса Mg не влияют на крутящий момент, поскольку их линии действия проходят через O.) Без проскальзывания a cm = Rα = fr I (ii) Подставляя cm в уравнение (i) , получаем Mg sin θ f = M fr I = MfR 5 MR = 5 f.
ПРИМЕЧАНИЕ: в точке контакта должно быть трение, иначе мяч соскользнет по склону! θ (a) Изобразите диаграмму свободного тела всех сил, действующих на мяч. Используйте закон Ньютона вниз по наклонной поверхности: f O R Mg N θ Mg sin θ f = Ma cm… (i) где см — ускорение центра масс. Чтобы получить вдавление на см, мы берем крутящий момент около O, центра шара. τ = fr = Iα, т.е. α = fr I, где I — момент инерции шара, а α — его угловое ускорение. (ПРИМЕЧАНИЕ: нормальная сила N и сила веса Mg не влияют на крутящий момент, поскольку их линии действия проходят через O.) Без проскальзывания a cm = Rα = fr I (ii) Подставляя cm в уравнение (i) , получаем Mg sin θ f = M fr I = MfR 5 MR = 5 f.24 мг sin θ = 5 f + f = 7 f, т.е.е., f = Mg sin θ. 7 Обратите внимание, что это сила статического трения (потому что нет скольжения). (b) Подставляя f в уравнение (ii), мы получаем a cm = fr I = Mg sin θ 7 5 MR R = 5 gsin θ. 7 Вы можете показать себе, что если мы положим I = βmr, где β = 1 для обруча, β = 1 для диска и т.
 Д., То получится общее сжатие для силы статического трения, действующей на объект, катящийся по склону, с отсутствие скольжения, а ускорение центра масс составляет: Mg sin θ f = 1 + β 1 и a cm = gsin θ 1 + β. Вопрос 9.10: Предположим, вы можете выбрать колеса любого дизайна для гоночной машины в мыльном дерби. Если указан общий вес автомобиля, какую конструкцию колес вам следует выбрать, если вы хотите иметь больше шансов на победу в гонке?
Д., То получится общее сжатие для силы статического трения, действующей на объект, катящийся по склону, с отсутствие скольжения, а ускорение центра масс составляет: Mg sin θ f = 1 + β 1 и a cm = gsin θ 1 + β. Вопрос 9.10: Предположим, вы можете выбрать колеса любого дизайна для гоночной машины в мыльном дерби. Если указан общий вес автомобиля, какую конструкцию колес вам следует выбрать, если вы хотите иметь больше шансов на победу в гонке?25 Полная механическая энергия автомобиля составляет: поступательная кинетическая энергия + вращательная кинетическая энергия. Сохранение энергии дает: Mgh = K trans + K rot = 1 Mv + 1 Iω, где M — полная масса автомобиля, а I — момент инерции колес.С четырьмя колесами радиуса r, например, мы имеем, используя условие отсутствия проскальзывания, () vr K rot = 1 (4I) ω = 1 4 βmr Mgh = 1 Mv + βmv, т. Е. V = Mgh (M + 4βм). = βmv, Итак, для максимальной скорости (v) у подножия холма (и большей средней скорости) с M fied мы хотим, чтобы m и β были как можно меньше.
 Обратите внимание: результат не зависит от радиуса колес (r). Таким образом, цельнолитые колеса (β = 1) — хороший выбор с массой, сконцентрированной как можно ближе к элю. F h R Вопрос 9.11: По битку наносится удар горизонтальным кием на расстоянии h выше центра шара.Если биток должен катиться без скольжения, что такое h? Выразите свой ответ радиусом R шара. Вы можете предположить, что сила трения стола о шар незначительна по сравнению с приложенной силой F.
Обратите внимание: результат не зависит от радиуса колес (r). Таким образом, цельнолитые колеса (β = 1) — хороший выбор с массой, сконцентрированной как можно ближе к элю. F h R Вопрос 9.11: По битку наносится удар горизонтальным кием на расстоянии h выше центра шара.Если биток должен катиться без скольжения, что такое h? Выразите свой ответ радиусом R шара. Вы можете предположить, что сила трения стола о шар незначительна по сравнению с приложенной силой F.26 F h R f Чистый крутящий момент относительно центра равен τ = Fh fr. Как было сказано ранее, при наличии прилипания v cm = Rω, т.е. a cm = dv cm dt = R dω dt = Rα. Используя закон Ньютона F + f = ma cm. Если F >> f, то F ma cm и τ Fh = Iα.F m = a cm = Rα = R Fh I, т.е. h = Для твердой сферы I = 5 mr. h> 5 R h = 5 R. верхний отжим I mr. h <5 R обратное вращение SLIP m 30 кг 0 кг m 1 м Вопрос 9.1: 30-килограммовая гиря, показанная выше, высвобождается из состояния покоя с расстояния метров над землей. Моделируя шкив как однородный диск с радиусом 10 см и массой 5 кг, найдите (а) скорость массы 30 кг непосредственно перед тем, как она ударится о землю, (б) угловую скорость шкива в этот момент, ( c) натяжение двух струн и d) время, за которое 30-килограммовый блок достигнет земли.
 Предположим, что подшипники в шкиве не имеют трения и между струной и шкивом нет проскальзывания.
Предположим, что подшипники в шкиве не имеют трения и между струной и шкивом нет проскальзывания.27 ω ω 0 кг м 1 м 30 кг м v м 1 м v 0 кг м 1 м 30 кг м v м 1 м v У нас есть поступательное и вращательное движение. Момент инерции шкива: I = 1 mr = 1 (5 кг) (0,10 м) = 0,05 кг · м. (a) Используя закон сохранения энергии, когда m ударяется о землю m gh = 1 m 1v + m 1 gh + 1 m v + 1 Iω. Угловая скорость шкива ω = v R, поэтому (30 кг) (9.81 м / с) (м) = 1 (0 кг) v + (0 кг) (9,81 м / с) (м) + 1 (30 кг) v + 1 (0,05 кг vm) (0,10 м) продолжение .. То есть 589 = 10v v + 1,3vv = 197 = 0,74 м / с. 6.3 (b) ω = v R = .74 = 7.4 рад / с (c) T 1 T m 1 g a m g Каково восходящее ускорение m 1? a Нарисуйте диаграммы свободного тела для масс. v = ах. a = v (0,74 м / с) = h (м) = 1,88 м / с.
28 T 1 T m 1 gamga Тогда T 1 m 1 g = m 1 a, т. Е. T 1 = m 1 (g + a) = 34 Н. Также T mg = m (a), т. Е. T = m (ga) = 38 Н.(d) (y y!) = h = 1 ат. t = h a = (м) = 1,46 с м / с
Формула угловой скорости kitab — kitaplar
Формула угловой скорости kitab — kitaplar — Формула угловой скорости ile ilgili kitaplar.
Bilmeden yaplan hata yanllktr, bilerek yaplan hata ise ihanettir. Б. БРЕХТ [Пайла]
Калькулятор преобразованияBölümler Эдебият Дефтери
• Kurallar
• Ярдым
• İletişimДиер
• Edebiyat TV
• Kütüphane
• Burçlar
• Bebek isimleriDier
• Ря Табирлери,
• simlerEdebiyatdefteri.  com, 2020. Bu sayfada yer alan bilgilerin her hakk, aksi ayrca belirtilmedii srece Edebiyatdefteri.com’a aittir. Sitemizde yer alan iir ve yazlarn telif haklar air ve yazarlarn kendilerine veya yeya verdikleri kiilere aittir. Sitemiz привет бир ekilde kr amac gtmemektedir ve sitemizde yer alan tm materyaller yalnzca bilgilendirme ve eitim amacyla sunulmaktadr.
com, 2020. Bu sayfada yer alan bilgilerin her hakk, aksi ayrca belirtilmedii srece Edebiyatdefteri.com’a aittir. Sitemizde yer alan iir ve yazlarn telif haklar air ve yazarlarn kendilerine veya yeya verdikleri kiilere aittir. Sitemiz привет бир ekilde kr amac gtmemektedir ve sitemizde yer alan tm materyaller yalnzca bilgilendirme ve eitim amacyla sunulmaktadr.Sitemizde yer alan iirler, ykler ve diğer eserlerin telif hakları yazarların kendilerine veya butki verdikleri kişilere aittir. Eserlerin izin alınmadan kopyalanması ve kullanılması 5846 sayılı Fikir ve Sanat Eserleri Yasası na göre suçtur.Ayrca sitemiz Telif Haklar kanuna gre korunmaktadr. Herhangi бир zelliinin ksmende olsa kullanlmas ya da kopyalanmas sutur. Эдебият — iirler — Китап
герц (Гц) в рад / сек
КалькуляторГерц в рад / сек
Введите частоту в герцах и нажмите кнопку Calc :
Калькулятор преобразованиярад / с в Гц ►
Как рассчитать рад / сек по герцу
1 Гц = 2π рад / с = 6.
 2831853 рад / с
2831853 рад / сили
1 рад / с = 1 / 2π Гц = 0,1591549 Гц
Герц в рад / с формула
Угловая частота или угловая скорость ω в радианах в секунду (рад / с) равна 2π умноженной на частоту f в герцах (Гц):
ω (рад / с) = 2π × f (Гц)
Пример
Вычислить угловую скорость в рад / с для частоты 300 Гц:
ω (рад / с) = 2π × 300 Гц = 1884.956 рад / с
Таблица преобразованияГерц в рад / сек
Калькулятор преобразованияГц
(Гц)рад в секунду
(рад / с)0 Гц 0 рад / с 1 Гц 6,28 рад / с 2 Гц 12,57 рад / с 3 Гц 18,85 рад / с 4 Гц 25,13 рад / с 5 Гц 31,42 рад / с 6 Гц 37.70 рад / с 7 Гц 43,98 рад / с 8 Гц 50,27 рад / с 9 Гц 56,55 рад / с 10 Гц 62,83 рад / с 20 Гц 125,66 рад / с 30 Гц 188,50 рад / с 40 Гц 251,33 рад / с 50 Гц 314,16 рад / с 60 Гц 376.  99рад / с
99рад / с70 Гц 439,82рад / с 80 Гц 502,65рад / с 90 Гц 565,49рад / с 100 Гц 628,32рад / с 200 Гц 1256,64рад / с 300 Гц 1884,96рад / с 400 Гц 2513,27рад / с 500 Гц 3141,59рад / с 600 Гц 3769.91рад / с 700 Гц 4398,23рад / с 800 Гц 5026,55рад / с 900 Гц 5654,87рад / с 1000 Гц 6283,19рад / с 2000 Гц 12566,37рад / с 3000 Гц 18849,56рад / с 4000 Гц 25132,74рад / с 5000 Гц 31415.93рад / с 6000 Гц 37699,11рад / с 7000 Гц 43982,30рад / с 8000 Гц 50265,48рад / с 9000 Гц 56548,67рад / с 10000 Гц 62831,85рад / с рад / с в Гц ►
См.



 {\ perp} = (- y, x)}.
{\ perp} = (- y, x)}.



 Угловая скорость и угловое ускорение.! уравнения вращательного движения
Угловая скорость и угловое ускорение.! уравнения вращательного движения  1]: у вас есть друг, который живет в Миннесоте, а вы живете во Флориде. Когда Земля вращается, ваша линейная скорость принадлежит ей, а ваша угловая скорость — ее.RMM0VD.mov Угловая скорость ω одинакова для всех точек на диске, но линейная (или касательная) скорость — нет. Посмотрите, v = rω, так как r> r 1, то v> v 1. A: меньше; равно B: равно; больше, чем C: больше, чем; меньше D: меньше; больше, чем E: больше, чем; равно
1]: у вас есть друг, который живет в Миннесоте, а вы живете во Флориде. Когда Земля вращается, ваша линейная скорость принадлежит ей, а ваша угловая скорость — ее.RMM0VD.mov Угловая скорость ω одинакова для всех точек на диске, но линейная (или касательная) скорость — нет. Посмотрите, v = rω, так как r> r 1, то v> v 1. A: меньше; равно B: равно; больше, чем C: больше, чем; меньше D: меньше; больше, чем E: больше, чем; равно 1: Диск радиусом 1 см, первоначально находящийся в состоянии покоя, начинает вращаться вокруг своего носа с постоянным угловым ускорением 3,00 рад / с. Через 5 с, каковы (а) угловая скорость диска и (б) тангенциальное и центростремительное ускорение точки на периметре диска? (c) Сколько оборотов сделал диск за эти 5 с?
1: Диск радиусом 1 см, первоначально находящийся в состоянии покоя, начинает вращаться вокруг своего носа с постоянным угловым ускорением 3,00 рад / с. Через 5 с, каковы (а) угловая скорость диска и (б) тангенциальное и центростремительное ускорение точки на периметре диска? (c) Сколько оборотов сделал диск за эти 5 с? е., v t = Rω. (в) (θ θ!) = ω! t + 1 αt = 1 (3,00 рад / с) (5 с) = 37,5 рад, n = 37,5 рад π = 5,97 об. Кроме того, при тех же условиях мгновенное ускорение струны такое же, как тангенциальное ускорение на ободе колеса: то есть a t = dv t dt = R dω dt = Rα.
е., v t = Rω. (в) (θ θ!) = ω! t + 1 αt = 1 (3,00 рад / с) (5 с) = 37,5 рад, n = 37,5 рад π = 5,97 об. Кроме того, при тех же условиях мгновенное ускорение струны такое же, как тангенциальное ускорение на ободе колеса: то есть a t = dv t dt = R dω dt = Rα. е., τ = rf t. Примечание: радиальная составляющая F r, проходящая через проход вращения, не создает крутящего момента и, следовательно, не вызывает вращения; только тангенциальная составляющая F t создает крутящий момент, который приводит к вращению. rm «FF t = F sin θ O lr θ m» FF r = F cosθ
е., τ = rf t. Примечание: радиальная составляющая F r, проходящая через проход вращения, не создает крутящего момента и, следовательно, не вызывает вращения; только тангенциальная составляющая F t создает крутящий момент, который приводит к вращению. rm «FF t = F sin θ O lr θ m» FF r = F cosθ Жесткий объект, который вращается вокруг аэродрома, можно представить как набор небольших отдельных элементов с массой Δm i (), каждый из которых движется по круговой траектории с радиусом r i, где r i отсчитывается от аэродрома вращения. Чистый вечный крутящий момент, действующий на тело, вызывает угловое ускорение α этого тела, задаваемое Iα, где I — момент инерции. (а именно: F net = i F i = ma.)
Жесткий объект, который вращается вокруг аэродрома, можно представить как набор небольших отдельных элементов с массой Δm i (), каждый из которых движется по круговой траектории с радиусом r i, где r i отсчитывается от аэродрома вращения. Чистый вечный крутящий момент, действующий на тело, вызывает угловое ускорение α этого тела, задаваемое Iα, где I — момент инерции. (а именно: F net = i F i = ma.)

 Каков его момент инерции относительно конца 0 см? Тонкостенный цилиндр I = MR Сплошной цилиндр I = 1 MR Твердая сфера I = 5 MR
Каков его момент инерции относительно конца 0 см? Тонкостенный цилиндр I = MR Сплошной цилиндр I = 1 MR Твердая сфера I = 5 MR
 Масса m 1 = m 3 = 3 кг и m = m 4 = 4 кг. 4 кг 3 кг D Найдите (а) момент инерции относительно оси z, (b) момент инерции zz относительно оси, которая перпендикулярна плоскости ансамбля и проходит через центр масс системы, (c) момент инерции относительно -ais, который проходит через м 3 и м 4.(a) Момент инерции относительно оси z: I z = mirii = (3 кг) (м) + (4 кг) (м) + (3 кг) (м) + (4 кг) (0) = 56 кг м. y L m 1 m L (b) По симметрии центр масс находится в центре квадрата. I см = m i r i i = (3 кг) (м) + (4 кг) (м) м 4 м 3 + (3 кг) (м) + (4 кг) (м) = 8 кг м. Проверьте, используя теорему о параллельности z I z = I cm + MD I cm = I z MD = (56 кг м) (14 кг) (м) = 8 кг м.
Масса m 1 = m 3 = 3 кг и m = m 4 = 4 кг. 4 кг 3 кг D Найдите (а) момент инерции относительно оси z, (b) момент инерции zz относительно оси, которая перпендикулярна плоскости ансамбля и проходит через центр масс системы, (c) момент инерции относительно -ais, который проходит через м 3 и м 4.(a) Момент инерции относительно оси z: I z = mirii = (3 кг) (м) + (4 кг) (м) + (3 кг) (м) + (4 кг) (0) = 56 кг м. y L m 1 m L (b) По симметрии центр масс находится в центре квадрата. I см = m i r i i = (3 кг) (м) + (4 кг) (м) м 4 м 3 + (3 кг) (м) + (4 кг) (м) = 8 кг м. Проверьте, используя теорему о параллельности z I z = I cm + MD I cm = I z MD = (56 кг м) (14 кг) (м) = 8 кг м. (a) Используя теорему о параллельности ais, покажите, что I z = 4 3 Ml. (b) Следовательно, найдите I и I y. z l l y
(a) Используя теорему о параллельности ais, покажите, что I z = 4 3 Ml. (b) Следовательно, найдите I и I y. z l l y .. но крутящий момент включает в себя силу … Когда сила прилагается на расстоянии, выполняется работа, определяемая выражением: O! r ds dθ! F dw =! F d! s = F.dscos γ = F cos γ.ds F t γ! F θ F r γ + θ = 90 «F t = F cos γ Вопрос 9.7: Двигатель развивает крутящий момент 400 Н · м при 3700 об / мин. Какую мощность развивает двигатель? = F t.ds = F t.rdθ = τ.dθ (Дж или Нм). Мощность — это скорость, с которой работает крутящий момент, то есть P = dw = τ dθ dt dt = τω (ватт). dw = τ.dθ является аналогом dw = F.ds. P = τω является аналогом P = Fv.
.. но крутящий момент включает в себя силу … Когда сила прилагается на расстоянии, выполняется работа, определяемая выражением: O! r ds dθ! F dw =! F d! s = F.dscos γ = F cos γ.ds F t γ! F θ F r γ + θ = 90 «F t = F cos γ Вопрос 9.7: Двигатель развивает крутящий момент 400 Н · м при 3700 об / мин. Какую мощность развивает двигатель? = F t.ds = F t.rdθ = τ.dθ (Дж или Нм). Мощность — это скорость, с которой работает крутящий момент, то есть P = dw = τ dθ dt dt = τω (ватт). dw = τ.dθ является аналогом dw = F.ds. P = τω является аналогом P = Fv.
 θ = ω! t + 1 αt = 1 (5,0 рад / с) (8,0 с) = 160 рад (= 5,46 об). W = τθ = (10 Н · м) (160 рад) = 1600 Дж.
θ = ω! t + 1 αt = 1 (5,0 рад / с) (8,0 с) = 160 рад (= 5,46 об). W = τθ = (10 Н · м) (160 рад) = 1600 Дж. Итак, когда мяч скатывается с холма … v, ω Гравитационная потенциальная энергия поступательная энергия + энергия вращения
Итак, когда мяч скатывается с холма … v, ω Гравитационная потенциальная энергия поступательная энергия + энергия вращения ПРИМЕЧАНИЕ: в точке контакта должно быть трение, иначе мяч соскользнет по склону! θ (a) Изобразите диаграмму свободного тела всех сил, действующих на мяч. Используйте закон Ньютона вниз по наклонной поверхности: f O R Mg N θ Mg sin θ f = Ma cm… (i) где см — ускорение центра масс. Чтобы получить вдавление на см, мы берем крутящий момент около O, центра шара. τ = fr = Iα, т.е. α = fr I, где I — момент инерции шара, а α — его угловое ускорение. (ПРИМЕЧАНИЕ: нормальная сила N и сила веса Mg не влияют на крутящий момент, поскольку их линии действия проходят через O.) Без проскальзывания a cm = Rα = fr I (ii) Подставляя cm в уравнение (i) , получаем Mg sin θ f = M fr I = MfR 5 MR = 5 f.
ПРИМЕЧАНИЕ: в точке контакта должно быть трение, иначе мяч соскользнет по склону! θ (a) Изобразите диаграмму свободного тела всех сил, действующих на мяч. Используйте закон Ньютона вниз по наклонной поверхности: f O R Mg N θ Mg sin θ f = Ma cm… (i) где см — ускорение центра масс. Чтобы получить вдавление на см, мы берем крутящий момент около O, центра шара. τ = fr = Iα, т.е. α = fr I, где I — момент инерции шара, а α — его угловое ускорение. (ПРИМЕЧАНИЕ: нормальная сила N и сила веса Mg не влияют на крутящий момент, поскольку их линии действия проходят через O.) Без проскальзывания a cm = Rα = fr I (ii) Подставляя cm в уравнение (i) , получаем Mg sin θ f = M fr I = MfR 5 MR = 5 f. Д., То получится общее сжатие для силы статического трения, действующей на объект, катящийся по склону, с отсутствие скольжения, а ускорение центра масс составляет: Mg sin θ f = 1 + β 1 и a cm = gsin θ 1 + β. Вопрос 9.10: Предположим, вы можете выбрать колеса любого дизайна для гоночной машины в мыльном дерби. Если указан общий вес автомобиля, какую конструкцию колес вам следует выбрать, если вы хотите иметь больше шансов на победу в гонке?
Д., То получится общее сжатие для силы статического трения, действующей на объект, катящийся по склону, с отсутствие скольжения, а ускорение центра масс составляет: Mg sin θ f = 1 + β 1 и a cm = gsin θ 1 + β. Вопрос 9.10: Предположим, вы можете выбрать колеса любого дизайна для гоночной машины в мыльном дерби. Если указан общий вес автомобиля, какую конструкцию колес вам следует выбрать, если вы хотите иметь больше шансов на победу в гонке?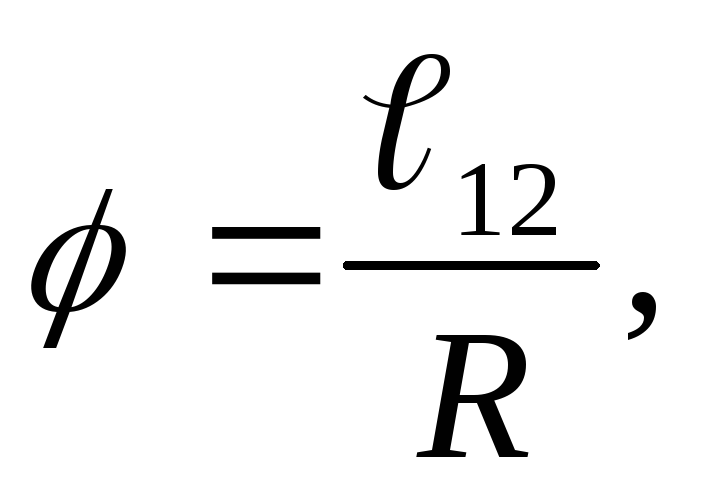 Обратите внимание: результат не зависит от радиуса колес (r). Таким образом, цельнолитые колеса (β = 1) — хороший выбор с массой, сконцентрированной как можно ближе к элю. F h R Вопрос 9.11: По битку наносится удар горизонтальным кием на расстоянии h выше центра шара.Если биток должен катиться без скольжения, что такое h? Выразите свой ответ радиусом R шара. Вы можете предположить, что сила трения стола о шар незначительна по сравнению с приложенной силой F.
Обратите внимание: результат не зависит от радиуса колес (r). Таким образом, цельнолитые колеса (β = 1) — хороший выбор с массой, сконцентрированной как можно ближе к элю. F h R Вопрос 9.11: По битку наносится удар горизонтальным кием на расстоянии h выше центра шара.Если биток должен катиться без скольжения, что такое h? Выразите свой ответ радиусом R шара. Вы можете предположить, что сила трения стола о шар незначительна по сравнению с приложенной силой F. Предположим, что подшипники в шкиве не имеют трения и между струной и шкивом нет проскальзывания.
Предположим, что подшипники в шкиве не имеют трения и между струной и шкивом нет проскальзывания.
 com, 2020. Bu sayfada yer alan bilgilerin her hakk, aksi ayrca belirtilmedii srece Edebiyatdefteri.com’a aittir. Sitemizde yer alan iir ve yazlarn telif haklar air ve yazarlarn kendilerine veya yeya verdikleri kiilere aittir. Sitemiz привет бир ekilde kr amac gtmemektedir ve sitemizde yer alan tm materyaller yalnzca bilgilendirme ve eitim amacyla sunulmaktadr.
com, 2020. Bu sayfada yer alan bilgilerin her hakk, aksi ayrca belirtilmedii srece Edebiyatdefteri.com’a aittir. Sitemizde yer alan iir ve yazlarn telif haklar air ve yazarlarn kendilerine veya yeya verdikleri kiilere aittir. Sitemiz привет бир ekilde kr amac gtmemektedir ve sitemizde yer alan tm materyaller yalnzca bilgilendirme ve eitim amacyla sunulmaktadr. 2831853 рад / с
2831853 рад / с 99рад / с
99рад / с