Формула периода вращения: Период обращения | Все Формулы

Период обращения | Все Формулы

    \[ \]

Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения

    \[\LARGE T=\frac{2\pi }{\omega }=\frac{1}{n }\]

Сидерические периоды обращения планет Солнечной системы:

Период обращения (меркурий, венера, солнце, земля)

Найдем период обращения:

Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле

    \[\Large T=\frac{1}{n }\]

Найдем частоту обращения:

Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:

    \[\Large \omega =\frac{n}{T}\]

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).

В формуле мы использовали :

T — Период обращения

    \[ \omega\]

— Частота обращения

n — Число оборотов

Период вращения — Википедия с видео // WIKI 2

Период вращения космического объекта — время, которое требуется объекту для совершения полного оборота вокруг своей оси относительно звёзд.

Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности.

Период вращения Земли относительно точки весеннего равноденствия называется звёздными сутками[1].

Периоды вращения некоторых объектов:

ОбъектПериод
Солнце25,379995 дня[2][3]25.379995

 

Меркурий58,6462 дня[4]58.6462

 

Венера243,0187 дня (ретроградное)
[4]		243.0187

 

Земля0,99726968 дня[4]0.99726968

 

Луна27,321661 дня[5]27.321661

 

Марс1,02595675 дня[4]1.02595675

 

Юпитер0,41354 дня[4]0.41354

 

Сатурн0,44401 дня[4]0.44401

 

Уран0,71833 дня (ретроградное)[4]0.71833

 

Нептун0,67125 дня[4]0.67125

 

Плутон6,38718 дня (ретроградное)[4]6.38718

 

Энциклопедичный YouTube

  • 1/5

    Просмотров:

    15 724

    2 248

    2 807

    385

    2 107

  • ✪ Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.

  • ✪ Подробнее о времени

  • ✪ 1.1.6 Кинематика криволинейного движения

  • ✪ EU-2 Комета Чурюмова-Герасименко (67P)

  • ✪ Астрономия 36. Пульсар — нейтронная звезда — Академия занимательных наук

См. также

Примечания

  1. ↑ К. В. Куимов. Вращение Земли и продолжительность суток (рус.). Астронет (6 февраля 2008). Дата обращения 20 июля 2010.
  2. ↑ P. K. Seidelmann, V. K. Abalakin, M. Bursa, M. E. Davies, C. de Bergh, J. H. Lieske, J. Oberst, J. L. Simon, E. M. Standish, P. Stooke, P. C. Thomas. Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites: 2000 (англ.) // Celestial Mechanics and Dynamical Astronomy : journal. — 2002. — Vol. 82, no. 1. — P. 86.
  3. ↑ Равен 360° делить на коэффициент при d в выражении для W.
  4. ↑ 1 2 3 4 5 6 7 8 9 Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — С. 296. — ISBN 0-387-98746-0.
  5. ↑ Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — С. 308. — ISBN 0-387-98746-0.
Эта страница в последний раз была отредактирована 7 июля 2020 в 00:38.
Движение по окружности, период обращения и частота.

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Таким образом,

 Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

    \[T = \frac{t}{N}.\]

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: 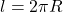l = 2 \pi R. Итак,

    \[\nu = \frac{l}{T} = \frac{2 \pi R}{T}.\]

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

    \[\nu=\frac{1}{T}\]

Частоту в СИ измеряют в

    \[\frac{1}{c}(c^{-1})\]

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

  1. Приведите два-три примера криволинейного движения.
  2. Приведите два-три примера равномерного движения по кругу.
  3. Что такое вращательное движение? Приведите примеры такого движения.
  4. Как направлена ​​мгновенная скорость при движении по кругу Приведите два-три примера.

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: 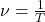\nu=\frac{1}{T} Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Равномерное движение по окружности. Скорость, ускорение

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.

Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:

. (1)

Частота обращения — это величина, обратная периоду:

.

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.

 

Угловая скорость.

 

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

\nu = 1/0,1 = 10
Рис. 1. Равномерное движение по окружности

 

Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

. (2)

Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому

. (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

. (4)

 

Закон движения.

 

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

.

Но из формулы (2) имеем: . Следовательно,

. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

 

Центростремительное ускорение.

 

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

С учётом формул (5) имеем:

(6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

(7)

где — радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

(8)

Выразим угловую скорость из (4)

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

.

 

Период и частота обращения | Физика

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот.

Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле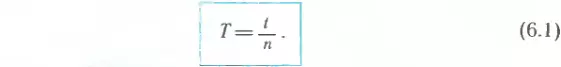
Формула периода обращения

Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.

Другой характеристикой равномерного движения по окружности является частота обращения.

Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле
Формула частоты обращения

Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.

Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому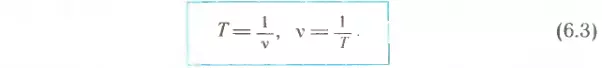
Отношение периода и частоты обращения

Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l

окр = 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Период обращения, выраженный через длину окружности

Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.

Видео, не по теме но интересно

1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?

Период обращения | Все формулы

Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения


Сидерические периоды обращения планет Солнечной системы:

Найдем период обращения:

Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле

Найдем частоту обращения:

Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).

В формуле мы использовали :

— Период обращения

— Частота обращения

— Число оборотов

Формула угловой скорости в физике

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота . Часто используют вектор элементарного поворота , который равен по величине элементарному углу поворота тела замаленький отрезок времени dtи направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой . Математически определение угловой скорости записывают так:

Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ( при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

где – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ). Угловая скорость связана с периодом обращения как:

С числом оборотов в единицу времени () угловая скорость связана формулой:

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.

Формула, связывающая линейную и угловую скорости

Линейная скорость точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:

где – перпендикулярная к оси вращения компонента радиус-вектора точки (рис.1). Вектор проводят от точки, находящейся на оси вращения к рассматриваемой точке.

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: []=рад/с

В СГС: []=рад/с

Примеры решения задач

Пример

Задание. Движение тела с неподвижной осью задано уравнением , в рад, t в сек. Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении ( относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.

Решение. Для нахождения модуля угловой скорости применим формулу:

Используем заданную в условии задачи функцию , возьмем производную от нее по времени, получим функцию :

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

Скорость вращения

— видео по физике от Brightstorm

Скорость, с которой объект вращается или вращается, называется , скорость вращения . В отличие от линейной скорости, она определяется тем, сколько оборотов совершает объект за период времени. Формула для скорости вращения: Скорость вращения = вращения / время , но линейная скорость = расстояние / время .

Хорошо, давайте поговорим о скорости вращения, у скорости вращения действительно есть 2 компонента.Одним из них является линейная скорость, которая также называется тангенциальной скоростью, и это в основном расстояние, объект движется с течением времени, хорошо. Если он будет вращаться по круговой орбите, если мы выпустим его с этой орбиты, он продолжит тангенциально двигаться с этой точки с определенной скоростью, хорошо. Другая скорость, которую имеет объект, — это скорость вращения, скорость вращения — это число вращений за раз. Итак, давайте рассмотрим пример, который часто задают: скажем, у нас есть 2 очка на записи, и запись вращается с определенной скоростью, например, 33 оборота в минуту, хорошо.Что ж, если мы сравним скорость этих двух объектов, то все будет по-другому, если мы говорим о тангенциальной, линейной или тангенциальной скорости относительно скорости вращения вправо. Так что, если мы посмотрим на них обоих, они оба имеют скорость вращения 33 оборота в минуту.

Но если мы посмотрим на скорость, с которой они движутся, на рекордную линейную скорость, то мы увидим, что линейная скорость на самом деле связана с радиальным расстоянием и скоростью вращения. Поэтому, если я скажу, что a — это x, а b — в 2 раза с точки зрения нашего радиального расстояния, то с точки зрения радиуса от центра справа мы можем видеть, что b будет двигаться намного быстрее, чем a.Вот почему 2 объекта могут иметь одинаковую скорость вращения, но очень разные линейные скорости.

,

Формула линейной скорости (вращающийся объект)

Линейная скорость точки на вращающемся объекте зависит от ее расстояния от центра вращения. Угловая скорость — это угол, через который объект движется в течение определенного времени. Угловая скорость имеет единицы радиан в секунду (рад / с). В полном круге 2π радианов. На расстоянии r от центра вращения точка на объекте имеет линейную скорость, равную угловой скорости, умноженной на расстояние r. Единицами линейной скорости являются метры в секунду, м / с.

линейная скорость = угловая скорость х радиус вращения

v = ωr

v = линейная скорость (м / с)

ω = угловая скорость (радианы / с)

r = радиус вращения (м)

Формула линейной скорости (вращающийся объект) Вопросы:

1) Электрическая дрель включена и вращается со скоростью 10,0 оборотов в секунду (об / с). Диаметр бурового долота составляет 4,00 мм. Какова линейная скорость точки на поверхности бурового долота, в метрах в секунду?

Ответ: Первый шаг — найти угловую скорость бурового долота.Обороты в секунду должны быть переведены в радианы в секунду. В полном круге 2π радианов.

ω = 10,0 об / с

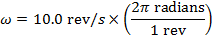
Расстояние между центром вращения и точкой на поверхности бурового долота равно радиусу. Диаметр бурового долота указан в миллиметрах. Радиус в метрах составляет

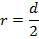
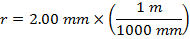
∴r = 0,002 м

Используя формулу v = ωr, линейная скорость точки на поверхности бурового долота равна

.

v = ωr

∴v = (62.8 радиан / с) (0,002 м)

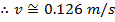
Линейная скорость точки на поверхности бурового долота составляет приблизительно 0,126 м / с. Радианы являются «заполнителями», поэтому они не учитываются при записи решенного значения для линейной скорости.

2) Еще один вопрос.

Внутри автомобильного колеса подключен датчик, который измеряет линейную скорость. Датчик находится на расстоянии 0,080 м от центра вращения. В этом положении датчик считывает, что линейная скорость колеса равна 8.00 м / с. Если радиус колеса составляет 0,220 м, какова линейная скорость на внешней кромке колеса?

Ответ: Линейная скорость отличается на разных расстояниях от центра вращения, но угловая скорость везде одинакова на колесе. Чтобы решить эту проблему, сначала найдите угловую скорость, используя линейную скорость в положении датчика, 0,080 м. Формула v = ωr может быть переупорядочена для решения для угловой скорости ω:

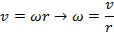
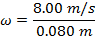
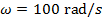
Это также угловая скорость на внешней кромке колеса, где радиус равен r = 0.220 м. Формула v = ωr может быть снова использована для определения линейной скорости на этом радиусе:

v = ωr

v = (100 рад / с) (0,220 м)

мкВ = 22,0 м / с

Линейная скорость автомобильного колеса на внешней кромке составляет 22,0 м / с.

период ротации — это … Что такое период ротации?

  • Период вращения — Период вращения астрономического объекта — это время, необходимое для завершения одного оборота вокруг своей оси вращения относительно фоновых звезд. Он отличается от солнечного дня планеты, который включает в себя дополнительное дробное вращение, необходимое… Wikipedia

  • период вращения — существительное период вращения… Викисловарь

  • Пульсар с питанием от вращения — это один из основных классов пульсаров.Пульсар с питанием от вращения — это быстро вращающаяся нейтронная звезда, электромагнитное излучение которой наблюдается через регулярные интервалы или импульсы. Он отличается от других типов пульсаров тем, что источник … Википедия

  • Ротация в офисе — Ротация в офисе, или срок полномочий, восходит к американской революции, а до этого — к демократиям и республикам древности. Совет 500 в древних Афинах ежегодно менял свой состав, как и эфорат в…… Википедии

  • Вращение — Эта статья о движении физического тела.Для других целей, см. Вращение (значения). Многогранник, напоминающий сферу, вращающуюся вокруг оси. Вращение — это круговое движение объекта вокруг центра (или точки) вращения. A…… Википедия

  • Вращение вокруг фиксированной оси — Вращательное движение может происходить вокруг более чем одной оси одновременно и может включать такие явления, как колебание и прецессия. Вращение вокруг фиксированной оси является частным случаем вращательного движения, которое не включает эти явления.Кинематика… Википедия

  • Номер поворота — В этой статье рассказывается о числе оборотов, которое иногда называют номером обмотки карты или просто номером обмотки. Есть другое значение для числа обмоток, которое появляется в комплексном анализе. В математике число вращения — это…… Википедия

  • вращение — вращение [rəuˈteıʃən US rou] n 1.) [U], когда что-то вращается с круговым движением вокруг центральной точки вращения ▪ вращение Земли вокруг своей оси вокруг / вокруг ▪ вращение планеты вокруг солнца 2.) один полный…… словарь современного английского языка

  • период — / груша ею, / н. 1. довольно большой промежуток времени, который имеет значение в жизни человека, в анамнезе и т. Д. Из-за его особых характеристик: период болезни; период большой прибыльности для компании; период социального…… Универсалиум

  • вращение — 1. Поворот или движение тела вокруг своей оси. 2. Рецидив в регулярном порядке определенных событий, таких как симптомы периодического заболевания.3. В медицинском образовании период времени по конкретной услуге или специальности… Медицинский словарь

  • ротация — / rəυ teɪʃ (ə) n / существительное акт смены по очереди ♦ заполнение поста председателя по очереди, чтобы каждый член группы действовал в качестве председателя в течение определенного периода, а затем передает этот пост другому члену ♦ два директора уходят на пенсию поочередно два директора уходят на пенсию…… словарь банковского дела и финансов

    • ,
    Формула частоты период время частота цикла в секунду Герц Гц амплитуда длительность периодический период времени к угловой частоте Формулярная длина волны Акустическое уравнение Соотношение длины волны Гц Миллисекунды мс Расчет вычисления калькулятор t = 1 / f Гц Герц к мс T к f рабочему листу Формула частоты период время частота цикл в секунду герц Гц амплитуда длительность периодический период времени к угловой частоте формулярная длина волны акустическое уравнение отношение длина волны Гц миллисекунда мс расчет вычислить калькулятор t = 1 / f Гц герц до мс T to f рабочий лист — sengpielaudio Sengpiel Berlin


    Заполните серое поле выше и нажмите на панель расчета соответствующего столбца.

    Частота означает колебания (циклы) в секунду в Гц = герц = 1 / с.
    1 секунда = 1 с = 1000 мс | 1 мс = 0,001 с | 1 мкс = 0,000001 с
    cps = циклов в секунду


    Чтобы использовать калькулятор, просто введите значение.
    Калькулятор работает в обоих направлениях знака × .

    Осциллограф: Ввод коробок (Div.) и время (Y) дают частоту.

    Формула за период (продолжительность цикла) T

    Физическая ценность символ блок аббревиатура формула
    Продолжительность цикла T = 1 / f секунда с T = λ / c
    Частота f = 1 / T герц Гц = 1 / с f = c / λ
    Длина волны λ метр м λ = с / ф
    Скорость волны с метра в секунду м / с c = λ × f

    Преобразование времени — со временем

    Формулы и уравнения для частоты и длины волны

    Формула для частоты: f (частота) = 1/ T (период).
    f = c / λ = скорость волны c (м / с) / длина волны λ (м).
    Формула для времени: T (период) = 1/ f (частота).
    Формула для длины волны составляет λ (м) = с / ф
    λ = c / f = скорость волны c (м / с) / частота f (Гц).

    Единица герц (Гц) когда-то называлась cps = циклов в секунду.


    c = λ × f λ = c / f = c × T f = c / λ
    дифференцировать скорость среды:
    Скорость звука или скорость света
    Выберите: Скорость звука в воздухе при температуре 20 ° C: c = 343 м / с
    или скорость радиоволн и света в вакууме: с = 299 792 458 м / с.

    Скорость распространения электрических сигналов по оптоволокну составляет около 9/10
    скорость света, то есть ≈ 270 000 км / с.
    Скорость распространения электрических сигналов по медным кабелям составляет около 2/3
    скорость света, то есть ≈ 200 000 км / с.

    Скорость звука с = 343 м / с также равна 1235 км. / ч, 767 миль в час, 1125 фут / с.

    Волна состоит из четырех частей:
    длина волны, период, частота и амплитуда
    Изменение частоты (герц, Гц) никогда не меняет амплитуду и наоборот

    Угловая частота составляет ω = 2 π × f

    Дано уравнение: у = 50 грех (5000 т)
    Определите частоту и амплитуду.
    Ответ: амплитуда 50 и ω = 5000.
    Таким образом, частота составляет f = 1/ T = ω /2 π = 795,77 Гц.

    Чтобы использовать калькулятор, просто введите значение.
    Калькулятор работает в обоих направлениях знака × .

    Преобразование : частота в длину волны и наоборот


    Синусоида или синусоида и период T
    В физике и электротехнике для синусоидального процесса часто используется
    угловая частота ω вместо частоты f .Скорость или частота вращения
    размер при — предпочтительно механических — вращающихся движениях, указывающий частоту
    революций. Например, это важная функция для двигателей. Это будет дано в
    1 / мин, в оборотах в минуту или в об / мин.


    На оси и показано звуковое давление p (амплитуда звукового давления).
    Если график показывает на оси x время t , мы видим период T = 1/ f .
    Если график показывает на оси x расстояние d , мы видим длину волны λ .
    Наибольший прогиб или удлинение называется амплитудой и .


    Амплитуда абсолютно не связана с частотой…
    тоже ничего с длиной волны.

    ● Волновые графики ●
    Волны могут быть изображены как функция времени или расстояния. Одна частота
    волна будет выглядеть как синусоида (синусоида) в любом случае. С расстояния
    На графике можно определить длину волны. Из графика времени, период
    и частота может быть получена. От обоих вместе, скорость волны может быть
    определяется.Источник:
    http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html


    В акустике выражение для синусоиды записано в виде
    y = A sin (2 πf T + φ ). Где ω = 2 π f и A — амплитуда и
    где f — частота волны, измеренная в герцах.
    Сравнение математической формы y = A sin ( B T + φ ):
    С этой акустической формой мы видим, что | B | = 2 π f . Отсюда у нас
    частота ф = | B | / 2 № и период T = 2 № / | B | = 1/ f .


    СИ кратных для герц (Гц)
    Значение Символ Наименование Значение Символ Наименование
    10 -1 Гц дГц децигерц 10 1 Гц дГц декагерц
    10 -2 Гц кГц сантигерц 10 2 Гц Гц гектогерц
    10 −3 Гц МГц миллигерц 10 3 Гц кГц килогерц
    10 −6 Гц мкГц микрогерц 10 6 Гц МГц мегагерц
    10 −9 Гц НГц наногерц 10 9 Гц ГГц гигагерц
    10 −12 Гц pHz пикогерц 10 12 Гц ТГц терагерц
    10 −15 Гц ФГц фемтогерц 10 15 Гц Фц петахерц
    10 −18 Гц Гц аттогерц 10 18 Гц Гц exahertz
    10 −21 Гц зГц Цептогерц 10 21 Гц ZHz Цеттахерц
    10 −24 Гц Гц йогерц 10 24 Гц ГГц йоттагерц
    Общие префиксные единицы выделены жирным шрифтом.

    Типичный вопрос: какова связь между длиной волны, температурой и частотой?

    Объясните связь между расстоянием, временем и частотой при определении
    длина волны или: каково уравнение с частотой, расстоянием и временем?

    Скорость = расстояние / время
    Скорость = длина волны × частота
    следовательно,
    Длина волны × частота = расстояние / время
    следовательно,
    Длина волны = расстояние / (время × частота)

    Калькулятор Masterclock (тактовая частота)

    Чтобы использовать калькулятор, просто введите значение.
    Калькулятор работает в обоих направлениях знака × .

    Калькулятор с опорной частотой

    Для настройки вниз можно изменить опорную частоту и настройку фортепиано.

    100 центов эквивалентны полутону (полутону).

    Названия нот: английская и немецкая системы для сравнения

    Расчеты гармоник по основной частоте


    ,

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *