Формула расчета скорости движения: Формула расчета скорости движения

Формула средней скорости движения

Формула средней скорости движения: V = S / t
где
V — средняя скорость тела
S — пройденный путь
t — время, за которое был пройден весь путь

Пример 1
Автомобиль проехал первую треть всего пути со скоростью 60 км/ч, а оставшееся расстояние со скоростью 40 км/ч. Найдите среднюю скорость движения автомобиля.

Решение
Обозначим длину всего пути S, скорость на 1-м участке V₁, а скорость на 2-м участке V₂. Тогда время, затраченное на прохождение первого участка будет
t₁ = S / 3 / V₁ = S / 3 / 60 = S / 180
а на прохождение второго участка
t₂ = S * 2 / 3 / V₂ = S * 2 / 3 / 40 = S / 60
Отсюда общее время прохождения пути будет

t = t₁ + t₂ = S / 180 + S / 60 = (S + 3 * S) / 180 = S * 4 / 180 = S / 45
Используя формулу средней скорости, получим
V = S / t = S / (S / 45) = 45

Ответ
Средняя скорость автомобиля 45 км/ч

Пример 2
Первую половину пути автомобиль двигался со скоростью 120 км/ч. Ещё четверть пути — со скоростью 90 км/ч. С какой скоростью он проехал оставшийся участок, если средняя путевая скорость составила 96 км/ч.

Решение
Введем обозначения: S — длина всего пути, V₁, V₂ и V₃ — скорость на 1-м, 2-м и 3-м участках соответственно, V — средняя скорость.

Длина 3-го участка составит S₃ = S — S/2 — S/4 = S/4
Теперь вычислим время, затраченное на прохождение каждого участка
t₁ = S / 2 / V₁ = S / 2 / 120 = S / 240
t₂ = S / 4 / V₂ = S / 4 / 90 = S / 360
Общее время пути
t = S / V = S / 96
Теперь вычисляем время прохождения последнего участка
t₃ = t — t₁ — t₂ = S / 96 — S / 240 — S / 360 = S * 15 / 1440 — S * 6/ 1440 — S * 4 / 1440 = S * 5 / 1440 = S / 288
И, наконец, вычисляем по формуле скорость на 3-м участке
V₃ = S₃ / t₃ = S / 4 / t₃ = S / 4 / (S / 288) = 288 / 4 = 72

Ответ
Скорость автомобиля на третьем участке 72 км/ч

Скорость движения молекул -Скорость в физике

К оглавлению раздела На главную

Расчёт скорости движения молекул.

Введение. Температура, как мера средней кинетической энергии молекул

Попробуем получить нетривиальные результаты, используя уравнение Клайперона-Менделеева и основное уравнение МКТ.

Введем понятие средней кинетической энергии молекул:

(1)

Преобразуем основное уравнение МКТ с учетом формулы (1):

т.е. основное уравнение МКТ запишем так (2)

Воспользуемся уравнением К.-М. в таком виде:

(3)

Сравним уравнения (2) и (3) и получим, что

или (4)

Как понимать формулу (4)?

Мы выяснили, что от температуры зависит величина средней кинетической энергии молекул. Поэтому говорят, что температура — мера средней кинетической энергии молекул. Это утверждение мы доказали на для идеального газа, но оказывается оно справедливо и для других агрегатных сосятояний вещества.

Среднеквадратичная скорость движения молекул.

Интересен вопрос о скорости движения молекул газа. В газен царит полный хаос, молекулы движутся по всем направлениям с самыми разными скоростями.

Оказывается, что

1. в газе есть молекулы с очень маленькими скоростями и с очень большими, но их сравнительно мало.
2. Средняя проекция скорости на любое направление для всего газа равна 0 (иначе, в газе существовали бы потоки).
3. Оказывается у молекул есть средняя скорость (по модулю), которая зависит от температуры, и основная часть молекул имеет модуль скорости близкий к ней. Эту скорость мы не можем вычислить, но можем легко посчитать среднеквадратичную скорость движения молекул газа, которая отличается от средней скорости коэффициентом порядка 1.

Определение. Среднеквадратичная скорость молекул равна квадратному корню из среднего квадрата скорости молекул:

(5)

Вычислим среднеквадратичную скорость из средней кинетической энергии молекул, которую мы легко можем сосчитать:

(6)

С учетом уравнения (4) получим:

(7)

Посчитаем, например, среднюю скорость молекул газа в классной комнате:

T=300K, m_o=M/N_a, М=0,029 г/моль. С учетом этого имеем:

Расчет скорости, пути и времени движения

Расчёт пути и времени движения

«Движение – это жизнь»

Аристотель

В данной теме будем применять приобретённые знания о механическом движении на практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь – это физическая величина, равная длине траектории, по которой двигалось тело, в течение данного промежутка времени. Путь является скалярной величиной, то есть, не имеет направления. Скорость при равномерном движении – это величина, равная отношению пройденного пути к промежутку времени, за который этот путь пройден.

                                                              

Скорость является векторной величиной, то есть, характеризуется как числовым значением, так и направлением.

Средняя скорость при неравномерном движении – это величина, равная отношению всего пройденного пути к общему времени в пути.

                                                  

Задача 1. Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?

В первую очередь, необходимо научиться правильно оформлять задачи по физике. При решении любой задачи нужно писать «дано». То есть, в левой части листа необходимо записать слово «дано», после которого ставится двоеточие, а дальше в столбик перечисляете все исходные данные, которые указаны в условии задачи. В нашем случае – это скорость и время в пути. После этого, нужно очеркнуть данные и ниже (уже под линией)

записать, что необходимо найти. В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем непосредственно к решению задачи.

А теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть, сколько километров автомобиль проходит за час. А время в условии дано в минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в часы.

В общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами измерения, можно (и даже нужно) переводить данные в систему СИ сразу после того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в км/ч необходимо

                                                      1 м/с = 3,6 км/ч

                                                    1 км/ч = 1/3,6 м/с

Время в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому, чтобы перевести минуты в секунды, нужно минуты умножить на 60. После того, как перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее пишитсяе само решение. Решение и ответ будут одинаковыми. Однако

рекомендуется переводить данные в систему СИ.

Задача 2. Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.

Получившееся выражение, в котором остались, только те величины, которые были даны изначально, называется расчетной формулой. Только в расчетную формулу необходимо подставлять числовые значения, а до этого, все делается в буквенном виде.

Задача 3. Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя скорость?

Сразу хочется обратить ваше внимание на распространенную ошибку. Среднюю скорость нельзя находить как среднее арифметическое разных скоростей на разных участках движения. В этом можно убедиться с помощью простых расчетов: если подсчитать среднюю скорость, как среднее арифметическое скоростей, то получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю скорость как отношение всего пройденного пути к общему времени в пути. В результате получим 214,3 м/с. Получается вроде небольшая разница. В результате неверных расчётов за каждую секунду, пройденное расстояние увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное расстоянии будет больше на 8,6 км, а это существенно.

Задача 4. Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть своего пути велосипедист проехал за 3 минуты. За какое время велосипедист проехал вторую часть, если общий путь составил 2 км?

Задача 5. Определите по графику скорость равномерного движения тела.

Здесь, конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не нужно. В таких заданиях, в первую очередь нужно посмотреть на оси графика: какие величины они обозначают и в каких единицах измеряются. Вертикальная ось – обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах. Значит, это график зависимости пройденного пути от времени. При равномерном движении скорость постоянна, значит, можно путь, пройденный за определенный промежуток времени, разделить на это время и, таким образом, найти скорость. Для наибольшей точности желательно найти точку, на графике, наиболее близкую к пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие координаты, то есть, на значения пути и времени. Для этого из точки опускаем перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.

Основные выводы:

В качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.

Разработка урока по физике 7 класса «Расчет скорости и средней скорости»

Қазақстан Республиқасының білім және ғылым министрлігі

Ақмола облысы

«Сандықтау ауданының білім бөлімі» ММ

Министерство науки и образования Республики Казахстан

Акмолинская область

ГУ «Сандыктауский отдел образования»

Разработка урока

по физике 7 класса на тему:

«Расчет скорости и средней скорости»

в рамках обновленного содержания образования

(районный семинар учителей физики)

Дайындаған /Подготовила: учитель физики

КГУ «Белгородская ОШ» Беренкова О. В.

а/с. Каменка

2017 жыл/год.

Краткосрочный план урока по физике

Раздел долгосрочного плана:

Механическое движение

Школа: КГУ «Белгородская ОШ»

Дата: 19.10.17г.

ФИО учителя: Беренкова Ольга Владимировна

Класс: 7

Количество присутствующих:

отсутствующих:

Тема урока

Расчет скорости и средней скорости

Тип урока

Изучение нового материала

Цели обучения, которые достигаются на данном уроке (ссылка на учебный план)

7.2.1.4 — вычислять скорость и среднюю скорость движения тел

Цели урока

Все учащиеся смогут: формулировать понятия скорости, путь, время, применять формулу скорости при решении задач, переводить единицы измерения скорости в систему СИ

Большинство учащихся будут уметь: выражать неизвестные величины, использовать формулу расчета скорости, решать задачи на сравнение скоростей равномерного движения, приводить примеры скоростей движения из окружающего мира

Некоторые учащиеся смогут: решать задачи связанные с жизнью

Критерии оценивания

Вычисляют скорость при равномерном движении

Языковые цели

Учащиеся могут:

Обсуждать в группе и в паре, называть метрические системы измерения величин, применять в речи физические термины, дать определения скорости, равномерного и неравномерного движения

Ключевые слова и фразы:

Скорость, равномерное движение, перемещение, время движения, вычислить скорость при равномерном движении,

Воспитание ценностей

Развитие навыков конструктивного общения и взаимодействия, развитие навыков коллективной работы

Межпредметные связи

Математика, биология

Предварительные знания

Траектория движения, перемещение, путь, уравнение движения, время

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

(2 мин)

Организационный момент.

Здравствуйте ребята! Я рада вас приветствовать на уроке.

Меня зовут Ольга Владимировна.

Мотивация:

девиз нашего урока «Кто хочет познать, тот познает».

В конце урока определим ваш уровень познания нового материала. Будьте внимательны и активны на уроке, познавайте сами и помогайте другим.

Тема урока: Расчет скорости и средней скорости

Цели урока: научиться вычислять скорость и среднюю скорость движения тел.

Слайд №2

Слайд №3

Слайд №4

Середина урока

(3 мин)

Этап вызова.

Задание «Найти соответствие».

1)Материальная точка

1)это линия, по которой движется тело.

2)Траектория

2)это направленный отрезок, соединяющий начальное положение с конечным.

3)Путь

3)это движение при котором тело за любые равные промежутки времени совершает одинаковые перемещения, не изменяя направление движения

4)Перемещение

4)это часть траектории за определенный момент времени

5)Прямолинейное равномерное движение

5)это движение при котором тело за любые равные промежутки времени совершает различные перемещения, не изменяя направление движения

6)Прямолинейное неравномерное движение

6)это тело, размерами которого можно пренебречь в данных условиях

Проверь себя!

1)Материальная точка

6)это тело, размерами которого можно пренебречь в данных условиях

2)Траектория

1)это линия, по которой движется тело.

3)Путь

4)это часть траектории за определенный момент времени

4)Перемещение

2)это направленный отрезок, соединяющий начальное положение с конечным.

5)Прямолинейное равномерное движение

3)это движение при котором тело за любые равные промежутки времени совершает одинаковые перемещения, не изменяя направление движения

6)Прямолинейное неравномерное движение

5)это движение при котором тело за любые равные промежутки времени совершает различные перемещения, не изменяя направление движения

Дескриптор:

Все соответствия верны

ФО: «Словесное оценивание» — осуществляет учитель

Слайд №5

Слайд №6

(5 мин)

(5 мин)

(4 мин)

(1 мин)

(3 мин)

(5 мин)

(7 мин)

Изучение новой темы

Мотивация: Кто быстрее всех на свете, Солнца свет (3*10⁸ м/с) или самолет? Чтобы ответить на вопрос, нужно рассмотреть величину характеризующую быстроту движения тела.

Цель: на уроке мы должны рассмотреть физическую величину характеризующую быстроту движения тела при равномерном и неравномерном движении и ввести её единицу измерения.

В форме беседы с элементами проблемного обучения, ввести новые понятия.

На экране фрагмент демонстрирующий движение разных тел (полет самолета, движение автомобиля, движение пешехода). Определите, кто движется быстрее? Поясните ответ.

Величина, характеризующая быстроту движения тел, является скорость.

Если автомобиль за 1 час проезжает 60 км, то говорят, что его скорость 60 км в час.

Что показывает скорость? ( Путь в единицу времени).

Словесная формулировка скорость =.

Обозначение : v- скорость, s – путь, t- время

Формула v=

Скорость – векторная величина, т.к. кроме своего числового значения имеет направление.

Скорость тела при равномерном движении – это величина равная отношению пути ко времени, за которое этот путь пройден.

В Международной системе (СИ) скорость измеряется в метрах на секунду (.

Как перевести в ?

1 =

108 = 108* = 30

Работа в парах

Задание1. Заполните недостающие величины в таблице

Критерии оценивания

Скорость

7 м/с

72 км/ч

Путь

120 см

40 м

Время

1 мин

10 с

Дескрипторы

• Переводит единицы измерения в систему СИ

• Использует формулу определения скорости для расчета скорости движения тел

• Использует формулу определения скорости для расчета пройденного пути

• Использует формулу определения скорости для расчета времени

Проверь себя!

Скорость

0,02м/с

7 м/с

72 км/ч

Путь

120 см

70м

40 м

Время

1 мин

10 с

2с

Учимся оформлять задачи

Задача. Мотоциклист преодолевает расстояние в 9 километров за 30 минут. С какой скоростью он движется?

Дано: СИ Формула: Решение:

S=9 км 9000 м

t=30 мин 1800 с

Найти:

v-?

Ответ: v= 5 м/с

Гимнастика для глаз

Учитель: Как определить скорость неравномерного движения? (Рассуждение учеников).

Вывод: чтобы определить скорость при неравномерном движении, нужно весь путь поделить на всё время движения. Такая скорость называется средней скоростью.

Формула расчета средней скорости. v_ср= .

v_ср

Этап осмысления

Задача.(один уч-ся работает у доски, остальные в тетрадях)

Автобус за первые 2 часа проехал 90 км, а следующие 3 часа двигался со скоростью 50 км/ч. Какова средняя скорость движения автобуса на всем пути?

Дано: Формула: Решение:

t₁=2 ч v_ср S₂ =50км/ч*3ч=150км

S₁=90 км S₂ =v₂*t₂ v_ср = 48км/ч

t₂=3 ч

v₂ = 50 км/ч

v_ср = ? Ответ: v_ср= 48 км/ч

Дескрипторы

• Определяет весь пройденный путь автобуса — определяет затраченное время

• Использует формулу для определения средней скорости движения тела

ФО: Самопроверка « По шаблону»

Формативное оценивание через оказание поддержки ученикам, допустившие ошибки.

Деление на 3 группы –

(на партах учащихся приклеены стикеры, на обратной стороне которых физические величины S, v, t)

Работа в группах

Задание «Кто самый быстрый»

Критерии оценивания

Дескрипторы

• Выражает единицы измерения скорости в СИ

• Сравнивает скорости животных

• Выявляет самого быстрого

ФО: Взаимопроверка в группах по образцу.

Прием «Сигнальные карточки».

Желтый – все верно, красный – есть ошибки.

Задание: «Цепочка».

Критерии оценивания

t₁ =7200c. v₂ = 20м/с. S₃ = 1920м. v₄ = 16c.

Дескрипторы

• Вычисляет время, используя формулу определения скорости

• Переводит единицы измерения расстояния в систему СИ

• Использует формулу определения скорости для расчета скорости движения тел

• Переводит единицы времени в систему СИ

• Использует формулу определения скорости для расчета пройденного пути

• Переводит единицы времени в систему СИ

• Использует формулу определения скорости

• Получает итоговый результат

ФО: Взаимопроверка в группах по образцу и прием

«Две звезды — одно пожелание»

Проверяя работы одноклассников учащиеся комментируют работы друг-друга не оценивая их , а определяя и указывая на 2 положительных момента в решении задачи и на 1 момент, который нужно доработать.

Слайд №7

Слайд №8

Слайд №9

Слайд №10

Слайд №11

bilimland.kz

Слайд №12

Слайд №13

Слайд №14

Карточки

Слайд №15

Слайд №16

Слайд №17

Слайд №18

bilimland.kz

Слайд №19

Слайд №20

Слайд №21

Слайд №22

Карточки

Слайд №23

Слайд №24

Карточки

Слайд №25

Слайд №26

Конец урока

(3 мин)

(2 мин)

Этап рефлексия: Итог совместной работы «схема-паутина»
1)Что нового ты узнал на уроке?
2)Какие уже имеющиеся у тебя знания понадобились в решении задач?
3)Кто и как тебе помогал(и) на уроке при решении задач?
4)Какие знания, полученные на уроке, понадобятся тебе в будущем?
5)Где ты применишь полученные знания?
6)В какой момент урока ты чувствовал себя особенно успешным?
7)С кем тебе было интереснее всего работать в паре/группе? Почему?
8)За что бы ты себя похвалил на уроке?
9)Что изменил бы в своих действиях на уроке?

10)Что бы ты изменил на уроке в последующем?

11)Что тебе понравилось на уроке больше всего?

Домашнее задание: §9 стр. 46-52

1. Задачи из учебника

Упр.7д стр.53

2.Вычислить свою скорость движения, зная расстояние от школы до дома и время движения (по желанию)

Урок окончен,

спасибо за внимание!

Слайд №27

Слайд №28

Слайд №29

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Развитие лидерских качеств при работе в группе, развитие функциональной граммотности, выполнение домашнего задания по желанию

Формативное оценивание: словесное оценивание учителя, «две звезды и одно пожелание», «сигнальные карточки», устные ответы на вопросы

Создание коллаборативной среды

Были ли цели урока/цели обучения реалистичными?

Все ли учащиеся достигли ЦО?

Если нет, то почему?

Правильно ли проведена дифференциация на уроке?

Выдержаны ли были временные этапы урока?

Какие отступления были от плана урока и почему?

Рефлексия по уроку

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?

1:

2:

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?

1:

2:

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?

Работа в парах

ФИ уч-ся 1.___________________________ 2._____________________________

Задание 1. Заполните недостающие величины в таблице

Критерии оценивания

Скорость

7 м/с

72 км/ч

Путь

120 см

40 м

Время

1 мин

10 с

Дескрипторы

• Переводит единицы измерения в систему СИ

• Использует формулу определения скорости для расчета скорости движения тел

• Использует формулу определения скорости для расчета пройденного пути

• Использует формулу определения скорости для расчета времени

Работа в группах

Задание «Кто самый быстрый»

Критерии оценивания

Дескрипторы

• Выражает единицы измерения скорости в СИ

• Сравнивает скорости животных

• Выявляет самого быстрого

Работа в группах

Задание 2: «Цепочка».

Критерии оценивания

Дескрипторы

• Вычисляет время, используя формулу определения скорости

• Переводит единицы измерения расстояния в систему СИ

• Использует формулу определения скорости для расчета скорости движения тел

• Переводит единицы времени в систему СИ

• Использует формулу определения скорости для расчета пройденного пути

• Переводит единицы времени в систему СИ

• Использует формулу определения скорости

• Получает итоговый результат

Формула скорость время расстояние треугольник. Формула нахождения значений скорости, времени и расстояния

Для всех ступеней коробки передач и дополнительной коробки рассчиты­ваются значения скорости движения автомобиля в зависимости от частоты вращения коленчатого вала двигателя (по согласованию с руководителем рас­чёт может производиться только для высшей ступени дополнительной короб­ки).

Расчёт ведётся по формуле

где v — скорость автомобиля, км/ч;

n — частота вращения коленчатого вала дви­гателя, об/мин;

r К — радиус качения, м;

и 0 — передаточное число главной переда­чи;

и к — передаточное число рассчитываемой ступени коробки передач;

и д — пе­редаточное число рассчитываемой ступени дополнительной (раздаточной) ко­робки.

Значения частоты вращения коленчатого вала берутся теми же, что и при построении внешней скоростной характеристики.

Рассчитанные значения v t заносятся в столбец 4 табл. 2.1. Графики зави­симости скорости движения автомобиля от частоты вращения коленчатого вала двигателя представляют собой серию лучей, выходящих под разными углами из начала координат рисунок 2.2.

Рис. 2.2 Зависимости скорости движения автомобиля от частоты вращения коленчатого вала по передачам.

2.6. Тяговая характеристика и тяговый баланс автомобиля

Тяговая характеристика представляет собой зависимость силы тяги авто­мобиля от скорости движения по передачам. Значения силы тяги Р Т рассчиты­ваются в отдельных точках по формуле

где М К — крутящий момент двигателя, Нм;

η Т — КПД трансмиссии.

Результаты расчёта Р Т заносятся в столбец 7 табл. 2.1, и по ним строятся графики зависимости Р Т = f (V ) по передачам.

Тяговый баланс автомобиля описывается уравнением тягового или силово­го баланса

Р Т = Р д + Р в + Р и , (2.27)

где Р Т — сила тяги автомобиля, Н;

Р д — суммарная сила сопротивления дороги, Н;

Р в — сила сопротивления воздушной среды, Н;

Р и — сила инерции автомоби­ля, Н.

Величина Р д определяется по выражению

Р д = G a ψ , (2.28)

где G a — полный вес автомобиля, Н; ψ — суммарный коэффициент сопротивления дороги.

Суммарный коэффициент сопротивления дороги является величиной, за­висящей от скорости автомобиля. Однако учёт этой зависимости сильно ос­ложняет выполнение тягового расчёта и в то же время не даёт важного для практики уточнения. Поэтому при выполнении тягового расчёта рекомендуется принять значение ψ постоянным, равным тому значению, которое было рассчи­тано для максимальной скорости движения автомобиля при определении мощ­ности двигателя, необходимой для движения на режиме максимальной скоро­сти, т.е. принять везде ψ=ψ v .

При каком-то одном выбранном значении ψ величина Р д остаётся постоян­ной для всех расчётных точек на всех передачах. Поэтому значение Р д подсчитывается один раз и в таблицу не заносится. На графике тяговой характеристи­ки зависимость P Т = f (v ) представляется в виде прямой, параллельной оси абс­цисс.

Рис. 2.3 Тяговая характеристика автомобиля.

Сила сопротивления воздушной среды Р в составляет величину

где с х — коэффициент продольной аэродинамической силы;

р в — плотность воздуха, кг/м 3 ;

к в — коэффициент обтекаемости, кг/м 3 ;

F — лобовая площадь авто­мобиля, м;

v в — скорость воздушного потока относительно автомобиля, км/ч.

При расчёте можно задать ρ в =1,225 кг/м. Скорость воздушного потока обычно принимается равной скорости движения автомобиля.

Значения Р в рассчитываются для всех точек и заносятся в столбец 5 табл. 2.1. График зависимости Р в от скорости представляет собой параболу, проходящую через начало координат.

Для удобства дальнейшего анализа этот график смещают вверх на ве­личину, равную Р д (в принятом для сил масштабе). Фактически при таком построении этот график выражает зависимость ( P в + P d )= f ( v ).

Сила инерции автомобиля Р и после расчёта Р д и Р в может быть определена как замыкающее слагаемое силового баланса

(2.30)

На графике значение Р и определяется отрезком прямой, проведённой для нужного значения скорости параллельно оси ординат, между точками пересечения этой прямой графиков P Т = f [ v ) и ( P д + P в )= f ( v ). Если заданная скорость может быть обеспечена на нескольких передачах, то каждой из этих передач будет соответствовать своё значение силы инерции. Рассчи­танные значения Р и следует занести в столбец 6 табл. 2.1.

Значение Р Т заносится в столбец 7 табл. 2.1. Тяговая характеристика автомобиля представлена на рис. 2.3.

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:

Научимся ее находить на примере следующей задачи:

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Сергей Валерьевич

Скоростью является тем, насколько быстро движется точка или же тело. Это векторная величина и для того, чтобы задать скорость, необходимо предварительно задать величину скорости, а также непосредственно направление, в сторону которого она измеряется. Рассмотрит то, как рассчитать скорость.

Обычно, скорость рассматривают вдоль траектории движения тела. Тогда, величина будет определяться как путь, который был пройден в единицу времени. Другими словами говоря, для нахождения скорости тела, путь необходимо разделить на время, за которое он был пройден. И в таком случае, формула скорости движения будет выглядеть так: V=S/t.

Как рассчитать среднюю скорость?

В кинематике это понятие является ничем иным, как усредненной характеристикой скорости частиц за время их движения. Есть два основных способа вычисления средней скорости. Средняя скорость пути — это скорость, в которой длина пути, пройденная телом, соотносится со временем, за которое он был пройден. Такая скорость, в отличие от мгновенной скорости, векторной величиной не является. Если тело одинаковые промежутки времени двигалось с одинаковыми скоростями, средняя скорость будет равняться среднему арифметическому от скоростей. Но, если половина пути была с одной скоростью, а вторая половина – с другой, средняя скорость будет равняться среднему гармоническому от всех взятых отдельно скоростей, которые будут равны между собой на разных участках дороги. Формула вычисления следующая:

Как вычислить среднюю скорость по перемещению?

Среднюю скорость можно вывести и по перемещению, она будет векторной, то есть равной по отношению к времени, за которое его совершили. В таком случае, средняя скорость будет равняться нулю в том случае, если тело реально двигалось. Если же перемещение имело место быть по прямой, то средняя путевая скорость будет равна модулю средней скорости по перемещению. Формула выглядит так:

Как рассчитать скорость по тормозному пути?

Тормозным путем является расстояние, которое транспортное средство проходит с момента влияния на тормозную систему транспорта и до полной остановки. Протяженность тормозного пути зависит и от массы, и от скорости, а также состояния проезжей части, погодных условий, шин и так далее. Кроме того, она зависит и от технологических особенностей транспортного средства. В зависимости от того, какие у транспортного средства тормозные колодки, какая логика работы электронных устройств, и других параметров скорость тормозного пути будет разной. 2/2. Из нее следует, что если на торможение дается одинаковое усилие, то тормозной путь будет прямо пропорционален массе тела и квадратно – скорости.

Единицы измерения, естественно, очень важны для всякого рода расчетов, что касается расчетов скорости движения, то тут единицами измерения будут единицы измерения скорости. Но, важно не только знать их, нужно уметь переводить значения в разные величины. Например, скорость измеряется в метрах на секунду (м/с), как перевести такое значение, например, в километры на секунду? Все просто! В одном метре на секунду содержится шесть тысяч сантиметров в минуту и, соответственно, сто сантиметров в секунду. Кроме того, один метр на секунду это три тысячи шестьсот метров в час и шестьдесят метров в минуту. А три и шесть километра в час — это один метр в секунду. Надеемся, что теперь у прочитавших эту статью не будет возникать вопросов о том, как рассчитать скорость движения.

Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.

Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

• Скорость = путь / время.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

Следовательно, вектор скоростив декартовых координатах можно представить:

где единичные орты. При этом модуль вектора скорости находят при помощи формулы:

В цилиндрических координатах модуль скорости вычисляют при помощи формулы:

в сферической системе координат:

Частные случаи формул для вычисления скорости

Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const). При равномерном движении скорость можно вычислить, применяя формулу:

где s– длина пути, t – время, за которое материальная точка преодолела путь s.

При ускоренном движении скорость можно найти как:

где – ускорение точки, – отрезок времени, в течение которого рассматривается скорость.

Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:

где – начальная скорость движения, .

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: [v]=м/с 2

В СГС: [v]=см/с 2

Примеры решения задач

Пример

Задание. Движение материальной точки А задано уравнением: . Точка начала свое движение при t 0 =0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1. 1) указанный в условии момент времении сравним результат с нулем:

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

Пример

Задание. Скорость материальной точки является функцией от времени вида:

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой.

Рассчитать время если известно расстояние и скорость. Расчет пути, скорости и времени движения

Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.

Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

• Скорость = путь / время.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время {\displaystyle {\text{Скорость}}={\frac {\text{Пройденный путь}}{\text{Время}}}} . Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.

Шаги

По одному значению пути и одному значению времени

• длина пути, пройденного телом;
• время, за которое тело прошло этот путь.
• Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.

1. Формула: , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — пройденный путь, t {\displaystyle t} — время, за которое пройден путь.

   В формулу подставьте пройденный путь. Значение пути подставьте вместо s {\displaystyle s} .

   • В нашем примере автомобиль проехал 150 км. Формула запишется так: v = 150 t {\displaystyle v={\frac {150}{t}}} .

2. В формулу подставьте время. Значение времени подставьте вместо t {\displaystyle t} .

   • В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: .

3. Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).

   • В нашем примере:
     v = 150 3 {\displaystyle v={\frac {150}{3}}}

     Таким образом, если автомобиль проехал 150 км за 3 ч, то он двигался со средней скоростью 50 км/ч.

4. Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • В нашем примере автомобиль проехал 150 км, 120 км и 70 км. Общий пройденный путь: .

5. T {\displaystyle t} ).

   • . Таким образом, формула запишется так: .
6. • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}

     Таким образом, если автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По нескольким значениям скоростей и нескольким значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:

   Запишите формулу для вычисления средней скорости. Формула: v = s t {\displaystyle v={\frac {s}{t}}} , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — общий пройденный путь, t {\displaystyle t} — общее время, за которое пройден путь.

2. Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • Например:
     50 км/ч в течение 3 ч = 50 × 3 = 150 {\displaystyle 50\times 3=150} км
     60 км/ч в течение 2 ч = 60 × 2 = 120 {\displaystyle 60\times 2=120} км
     70 км/ч в течение 1 ч = 70 × 1 = 70 {\displaystyle 70\times 1=70} км
     Общий пройденный путь: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} км. Таким образом, формула запишется так: v = 340 t {\displaystyle v={\frac {340}{t}}} .

3. Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо t {\displaystyle t} ).

   • В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч. Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6} . Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}} .

4. Разделите общий путь на общее время. Вы найдете среднюю скорость.

   • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}
     v = 56 , 67 {\displaystyle v=56,67}
     Таким образом, если автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По двум значениям скоростей и двум одинаковым значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:

   • два или несколько значений скоростей, с которыми двигалось тело;
   • тело двигалось с определенными скоростями в течение равных промежутков времени.
   • Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.

2. Запишите формулу для вычисления средней скорости, если даны две скорости, с которыми тело движется в течение равных промежутков времени. Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}} , где v {\displaystyle v} — средняя скорость, a {\displaystyle a} — скорость тела в течение первого промежутка времени, b {\displaystyle b} — скорость тела в течение второго (такого же, как первый) промежутка времени.

   • В таких задачах значения промежутков времени не важны — главное, чтобы они были равны.
   • Если дано несколько значений скоростей и равные промежутки времени, перепишите формулу так: v = a + b + c 3 {\displaystyle v={\frac {a+b+c}{3}}} или v = a + b + c + d 4 {\displaystyle v={\frac {a+b+c+d}{4}}} . Если промежутки времени равны, сложите все значения скоростей и разделите их на количество таких значений.

3. В формулу подставьте значения скоростей. Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} .

   • Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .

4. Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

   • Например:
     v = 40 + 60 2 {\displaystyle v={\frac {40+60}{2}}}
     v = 100 2 {\displaystyle v={\frac {100}{2}}}
     v = 50 {\displaystyle v=50}
     Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.

Которое потребовалось на этот путь:
v=s/t, где:
v – это скорость,

s – длина пройденного пути, а

t — время
Примечание.
Предварительно, все единицы измерения следует привести к одной системе (желательно СИ).
Пример 1
Разогнавшись до максимальной скорости, автомобиль проехал один километр за полминуты, после чего затормозил и .

Определите максимальную скорость автомобиля.
Решение.
Так как после разгона автомобиль двигался на максимальной скорости, то ее по условиям задачи можно считать равномерной. Следовательно:
s=1 км,

t=0,5 мин.
Приводим единицы измерения времени и пройденного пути к одной системе (СИ):
1 км=1000 м

0,5 мин= 30 сек
Значит, максимальная скорость автомобиля:
1000/30=100/3=33 1/3 м/с, или приблизительно: 33,33 м/с
Ответ: максимальная скорость автомобиля: 33,33 м/с.

Для определения скорости тела при равноускоренном движении необходимо знать начальную скорость и величину или другие связанные параметры. Ускорение может быть и отрицательным (в этом случае это, фактически, торможение).
Скорость равна начальной скорости плюс ускорение, умноженное на время. В виде это записывается следующим образом:
v(t)= v(0)+аt, где:
v(t) – скорость тела в момент времени t

Чему была равна скорость кирпича в момент приземления?
Решение.
Так как направление начальной скорости и ускорения свободного падения совпадают, то скорость кирпича у поверхности земли будет равной:
1+9,8*10=99 м/с.
Сопротивление в такого рода, как правило, не учитывается.

Скорость автомобиля постоянно меняется во время путешествия. Определением того, какая скорость у машины была в тот или иной момент пути, очень часто занимаются как сами автолюбители, так и компетентные органы. Тем более, что способов узнать скорость автомобиля огромное количество.

Инструкция

Самый простой способ определить скорость автомобиля знаком всем еще со школы. Для этого вам нужно зафиксировать количество километров, которое вы проехали, и время, за которое вы это расстояние преодолели. Рассчитывается скорость авто по : расстояние (км.) разделить на время (ч.). Так вы получите искомое число.

Вариант второй используется тогда, когда автомобиль резко остановился, но базовых замеров, как то время и расстояние, никто не проводил. В этом случае скорость автомобиля рассчитывают по его . Для подобных вычислений есть даже своя . Но использоваться она может только в том случае, если при торможении остался на дороге след.

Итак, формула следующим образом: начальная скорость автомобиля равна 0,5 х время нарастания торможения (м/с) х, установившееся замедление авто при торможении (м/с²) + корень из длины тормозного пути (м) х, установившееся замедление автомобиля при торможении (м/с²). Величина под названием «установившееся замедление авто при торможении» фиксированная и зависит только от того, какой асфальт имел место быть. В случае сухой дороги в формулу подставьте число 6,8 — оно прописано в ГОСТе, используемом для расчетов. Для мокрого асфальта данная величина будет равняться 5.

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы , так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать , если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей .

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

v — скорость,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени , за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

t = S: V

15: 3 = 5 (с)

Составим выражение: 5 3: 3 = 5 (с) Ответ: 5 с потребуется слепню.

Реши задачу.

1. Катер, двигаясь со скоростью 32 км/ч, про­шёл путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на лодке, если она движется со скорос­тью 8 км/ч?

2.Велосипедист, двигаясь со скоростью 10 км/ч, проехал путь между деревнями за 4 ч. Сколько

потребуется времени пешеходу, чтобы пройти этот же путь, если он движется со скоростью 15 км/ч?

Составные задачи на время. II тип.

Образец:

Многоножка сначала бежала 3 мин со скоростью 2 дм/м, а потом она побежала со скоростью 3 дм/м. За какое время мно­гоножка пробежала оставшийся путь, если всего она пробежала 15 дм? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (t) Расстояние (S)

С. — 2 дм/мин З мин?дм

П.-3 дм/мин? ? мин?дм 15дм

Составим план решения этой задачи. Что­бы узнать, время многоножки потом, надо узнать какое расстояние она пробежала потом, а для этого надо знать, какое рас­стояние она пробежала сначала.

t п S п S с

S с = V с · t

2 3 = 6 (м) — расстояние, которое пробе­жала многоножка сначала.

S п = S — S с

15 — 6 = 9 (м) — расстояние, которое пробежала многоножка потом.

Чтобы найти время, надо расстояние раз­делить на скорость.

9: 3 = 3(мин)

Ответ: за 3 мин многоножка пробежала оставшийся путь.

Реши задачу.

1. Волк бежал по лесу 3 ч со скоростью 8 км/ч. По полю он бежал со скоростью 10 км/ч. Сколько времени волк бежал по полю, если он пробежал 44 км?

2. Рак до коряги полз 3 мин со скоростью 18 м/мин. Остальной путь он полз со скоростью 16 м/мин. Сколько времени потребовалось раку на остальной путь, если он прополз 118м?

3. Гена добежал до футбольной площадки за 48 с со скоростью 6 м/с, а потом он побежал к школе со скоростью 7 м/с. Через какое время Гена добежит до школы, если он пробежал 477 м?

4. Пешеход шёл до остановки 3 ч со скоростью 5 км/ч, после остановки он пошёл со скорос­тью 4 км/ч. Сколько времени пешеход был в пути после остановки, если он прошёл 23 км?

5. Уж плыл до коряги 10с со скоростью 8 дм/с, а потом он поплыл до берега со скоростью 6 дм/с. За какое время доплыл уж до берега, если он проплыл 122дм?

Составные задачи на скорость. I тип

Образец:

Из норки побежали два ёжика. Один бе­жал 6 с со скоростью 2 м/с. С какой ско­ростью должен бежать другой ёжик, чтобы преодолеть это расстояние за 3 с? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (1) Расстояние (8)

I — 2 м/с 6 с одинаковое

II — ?м/с 3 с

Составим план решения этой задачи. Что­бы найти скорость второго ёжика, надо найти расстояние, которое пробежал пер­вый ёжик.

Чтобы найти расстояние, надо скорость умножить на время.

S = V I · t I

2 · 6 = 12 (м) – расстояние, которое пробежал первый ежик.

Чтобы найти скорость, надо расстояние разделить на время.

V II = S: t II

12:3 = 4(м/с)

Составим выражение: 2 6:3 = 4 (м/с)

Ответ; 4м/с скорость второго ёжика.

Реши задачу.

1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?

2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы пре­одолеть это расстояние за 3 ч?

3. Автобус, двигаясь со скоростью 64 км/ч, про­шёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, что­бы преодолеть это расстояние за 8 ч?

4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстоя­ние за 6 мин?

Составные задачи на скорость. II тип

Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?

Как узнать путь зная скорость и время. Формулы прямолинейного равноускоренного движения

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы , так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать , если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей .

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

v — скорость,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени , за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.

Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

• Скорость = путь / время.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.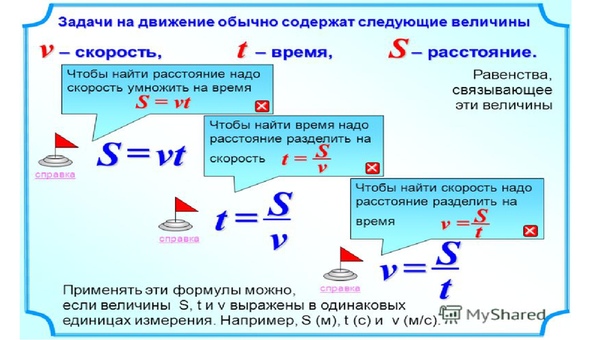

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>

Нужна помощь в учебе?

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>&nbspРасчет пути, скорости и времени движения: равномерное и неравномерное

Обычно равномерное движение очень редко можно встретить в реальной жизни.

Как найти скорость, время и расстояние — формулы и дополнительные параметры

За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.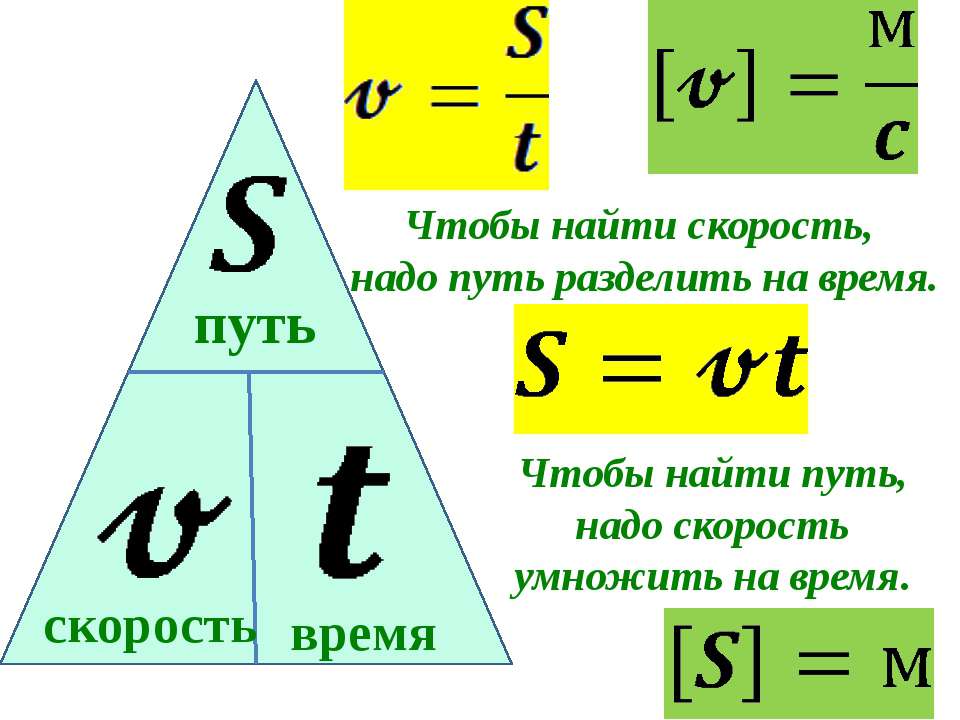

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Нужна помощь в учебе?

Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:&nbsp&nbsp&nbspЯвление инерции: в чем заключается и примеры из жизни

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>&nbspРасчет пути, скорости и времени движения: равномерное и неравномерное

Обычно равномерное движение очень редко можно встретить в реальной жизни.

Как найти скорость, формула

За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Нужна помощь в учебе?

Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:&nbsp&nbsp&nbspЯвление инерции: в чем заключается и примеры из жизни

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>&nbspРасчет пути, скорости и времени движения: равномерное и неравномерное

Обычно равномерное движение очень редко можно встретить в реальной жизни.

Скорость время расстояние

За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Нужна помощь в учебе?

Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:&nbsp&nbsp&nbspЯвление инерции: в чем заключается и примеры из жизни

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>&nbspРасчет пути, скорости и времени движения: равномерное и неравномерное

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением.

Формула пути

Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Нужна помощь в учебе?

Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:&nbsp&nbsp&nbspЯвление инерции: в чем заключается и примеры из жизни

VII = S: tII

12:3 = 4(м/с)

Составим выражение: 2 6:3 = 4 (м/с)

Ответ; 4м/с скорость второго ёжика.

Реши задачу.

1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?

2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы пре­одолеть это расстояние за 3 ч?

3. Автобус, двигаясь со скоростью 64 км/ч, про­шёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, что­бы преодолеть это расстояние за 8 ч?

4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстоя­ние за 6 мин?

Составные задачи на скорость. II тип

Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?

Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Г. -15 км/ч 2 ч?км

Л. — ? км/ч З ч?км 66км

Составим план решения этой задачи. Что­бы узнать скорость движения лыжника по лесу, надо узнать какое расстояние он проехал по лесу, а для этого надо знать какое расстояние он проехал до горки.

Vл Sл Sг

Sг = Vг · tг

15 2 = 30 (км) — расстояние, которое про­ехал лыжник до горки.

Sл = S – Sг

66 — 30 = 36 (км) — расстояние, которое проехал лыжник по лесу.

Чтобы найти скорость, надо расстояние разделить на время.

Vл = Sл: tл

36.: 3 = 12 (км/ч)

Ответ: 12 км/ч скорость лыжника по лесу.

Реши задачу.

1. Ворона летела по полям 3 ч со скоростью 48 км/ч, а потом она летела 2 ч по городу. С какой скоростью ворона летела по городу, если всего она пролетела 244 км?

2. Черепаха ползла до камня 5 мин со скоростью 29 см/мин, а после камня черепаха ползла ещё 4 мин.

Формула скорости — математика 4 класс

С какой скоростью черепах ползла после камня, если она проползла 33 см?

3. Поезд шёл до станции 7 ч со скоростью 63 км/ч, а после станции поезд проехал ещё 4 ч. С какой скоростью поезд проедет путь от станции, если всего он прошёл 741 км?

Составные задачи на расстояние.

Образец:

Травоядный динозавр сначала бежал 3 ч со скоростью 6 км/ч, а потом он бежал ещё 4 ч со скоростью 5 км/ч. Какое расстояние пробежал травоядный динозавр?

Рассуждаем так. Это задача в одном направлении.

Составим таблицу.

Слова « скорость », «время», «расстояние» запишем зеленой ручкой.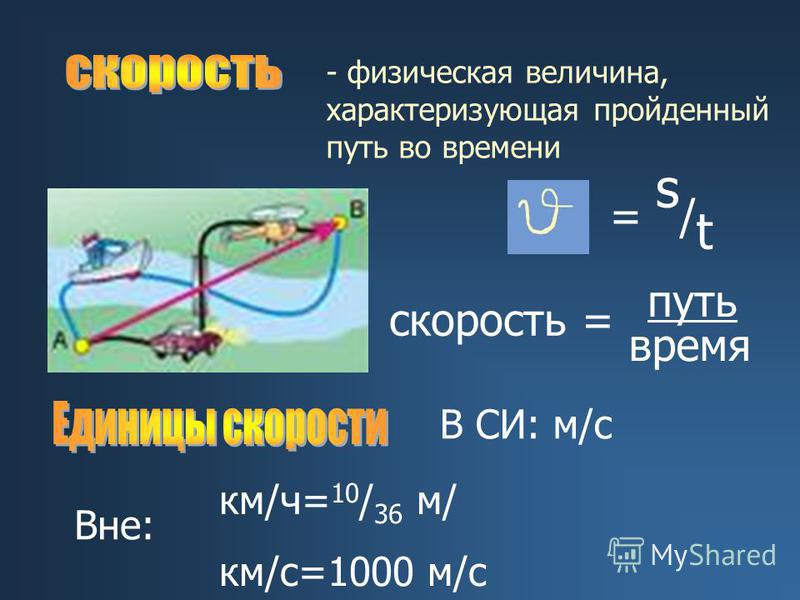

Скорость (V) Время (t) Расстояние (S)

С. — 6 км/ч Зч? км

П. — 5 км/ч 4ч?км? км

Составим план решения этой задачи. Чтобы узнать какое расстояние пробежал динозавр, надо знать, какое расстояние он пробежал, потом и какое расстояние он пробежал сначала.

S Sп Sс

Чтобы найти расстояние, надо скорость умножить на время.

Sс =Vс t с

6· 3 = 18 (км) — расстояние, которое про­бежал динозавр сначала. Чтобы найти расстояние, надо скорость умножить на время.

Sп = Vп tп

5 4 = 20 (км) — расстояние, которое про­бежал динозавр потом.

18 + 20 = 38 (км)

Составим выражение:6 3 + 5 4 = 38(км)

Ответ: 38 км пробежал травоядный динозавр.

Реши задачу.

1. Ракета сначала летела 28 с со скоростью 15 км/с, а оставшийся путь летела 53 с со скоростью 16 км/с. Какое расстояние проле­тела ракета?

2. Утка сначала плыла 3 ч со, скоростью 19 км/ч, а потом она плыла ещё 2 ч со скоро­стью 17 км/ч. Какое расстояние проплыла утка?

3. Кит полосатик сначала плыл 2 ч со скорос­тью 22 км/ч, а потом он плыл ещё 2 ч со ско­ростью 43 км/ч. Какое расстояние проплыл кит полосатик?

4. Теплоход до пристани шёл 3 ч со скоростью 28 км/ч, а после пристани плыл ещё 2 ч со скоростью 32 км/ч. Какое расстояние про­плыл теплоход?

Задачи на нахождение времени совместной работы.

Образец:

Привезли 240 саженцев елей. Первый лесник может посадить эти ели за 4 дня, а второй за 12 дней. За сколько дней оба лесника могут выполнить задание, рабо­тая вместе?

240: 4 = 60 (саж,) за 1 день сажает пер­вый лесник.

240: 12 — 20 (саж.) за 1 день сажает вто­рой лесник.

60 + 20 = 80 (саж.) за 1 день сажают оба лесника. 240:80 = 3(дн.)

Ответ: за 3 дня лесники посадят сажен­цы, работая вместе.

Реши задачу.

1. В мастерской 140 мониторов. Один мастер отремонтирует их за 70 дней, а другой, за 28 дней. За сколько дней оба мастера отре­монтируют эти мониторы, если будут рабо­тать вместе?

2. Было 600 кг горючего. Один трактор израсходовал его за 6 дней, а другой – за 3 дня. За сколько дней тракторы израсходуют это горючее, работая вместе?

3. Надо перевезти 150 пассажиров. Один катер перевезёт их за 15 рейсов, а другой за 10 рейсов. За сколько рейсов эти катера перевезу всех пассажиров, работая вместе?

4. Один ученик может сделать 120 снежинок 60 мин, а другой — за 30 мин. Сколько потребуется времени ученикам, если они будут работать вместе?

5. Один мастер может изготовить 90 шайбочек за 30 мин, другой—‘за 15 мин. За какое вре­мя они изготовят 90 шайбочек при совмест­ной работе?

⇐ Предыдущая234567891011

При прямолинейном равноускоренном движении тело

1. двигается вдоль условной прямой линии,
2. его скорость постепенно увеличивается или уменьшается,
3. за равные промежутки времени скорость меняется на равную величину.

Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с 2 .

Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.

Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:

При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:

Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с 2 . Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:

Получим из этих формул формулы ускорения. В случае ускорения:

at = v – v 0
a = (v – v 0)/t

В случае торможения:

at = v 0 – v
a = (v 0 – v)/t

В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении . Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.

При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.

Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:

s = ½ * (v 0 + v) * t

Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2

Итак, пройденный путь определяется по формуле:

s = v 0 t + at 2 /2

(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)

Если тело начало двигаться равноускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2 /2.

Если вектор ускорения был противоположен скорости, то произведение at 2 /2 надо вычитать.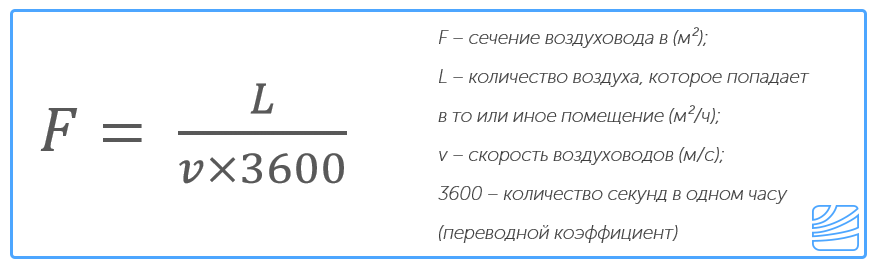 Понятно, что при этом разность v 0 t и at 2 /2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v 0 /a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле.

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.

Скорость

Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая -медленее; один человек идет быстрым шагом, другой — не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то Допустим, что 5 км/ч. То есть за 1 час он прошел 5 километров.

Формула пути (расстояния) — произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время. Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».

Не упустите!

Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:

Человек проехал по тротуару на велосипеде 2 километра за 15 минут.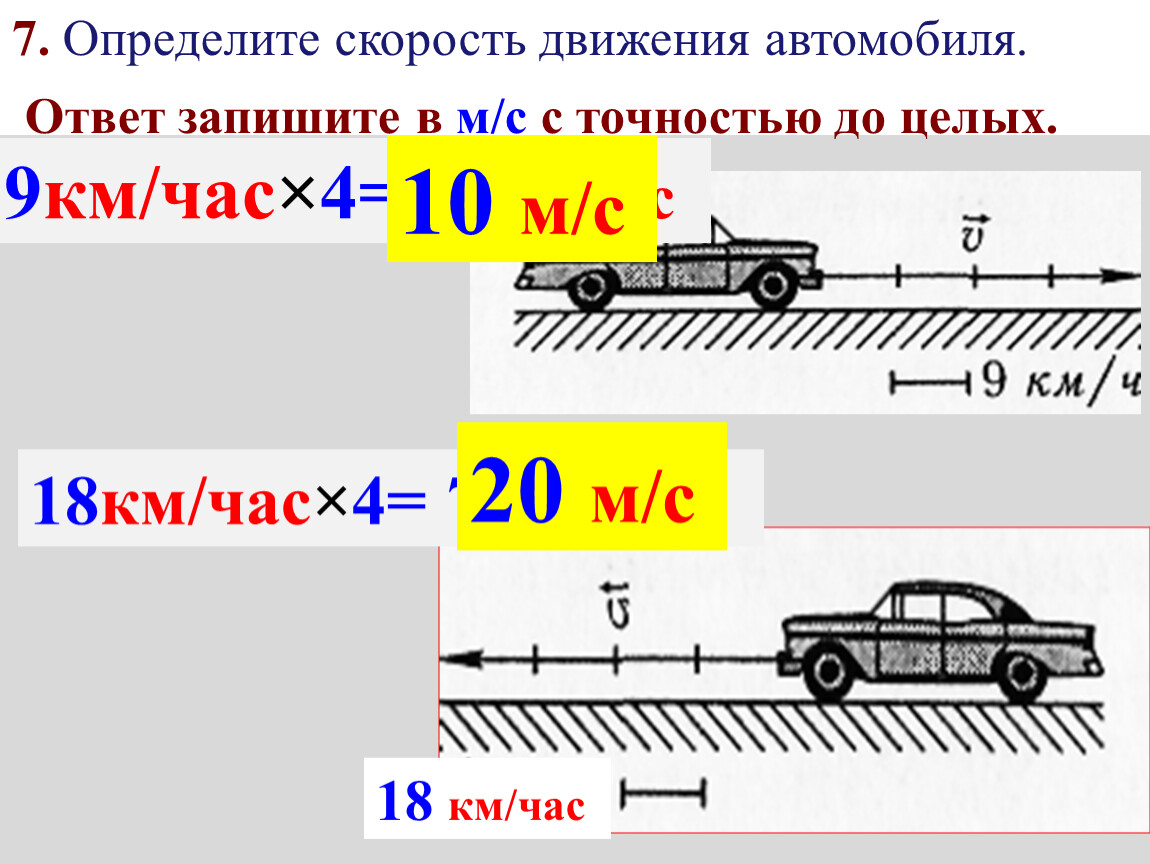 Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.

Вот так легко запоминается формула «скорость, время, расстояние». Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено.

21.3 Скорость и скорость | Движение в одном измерении

Бонгани приходится идти в магазин за молоком. Пройдя \(\text{100}\) \(\text{m}\), он понимает, что ему не хватает денег, и возвращается домой. Если бы ему потребовалось две минуты, чтобы уйти и вернись, подсчитай следующее:

1. Как долго он был вне дома (интервал времени \(\Delta t\) в секундах)?

2. Какое расстояние он прошел (расстояние (\(D\))?

3. Каково было его перемещение (\(\Delta \vec{x}\))?

4. Какова была его средняя скорость (в \(\text{м·с$^{-1}$}\))?

5. Какова была его средняя скорость (в \(\text{м·с$^{-1}$}\))?

Решение пока недоступно

Бриджит наблюдает за прямым участком дороги из окна своего класса. Она может видеть два полюса, которые ранее она находилась на расстоянии \(\text{50}\) \(\text{m}\) друг от друга. Используя свой секундомер, Бриджит замечает, что большинству автомобилей требуется \(\text{3}\) \(\text{s}\) для проезда от одного полюса к другому.

1. Используя уравнение для скорости \(\left({\vec{v}}_{av} = \frac{\Delta \vec{x}}{\Delta t}\right)\), показать всю работу, необходимую для вычисления скорости автомобиля, движущегося слева направо правильно.{-1}$}\), в каком направлении ехал Гольф?

2. Бриджит оставляет включенным секундомер и замечает, что в \(t = \text{5,0}\text{ s}\) такси проходит левый столб в то же время, когда автобус проходит правый столб. В момент \(t = \text{7,5}\text{ s}\) такси проезжает правый столб. {-1}$}\)?

Решение пока недоступно

Кролик перебегает автостраду.{-1}$}\)?

Если на автостраде есть \(\text{3}\) полос, и каждая полоса имеет ширину \(\text{3}\) \(\text{m}\) сколько времени кролику потребуется, чтобы пересечь все три дорожки?

Если машина едет по дальней от кролика полосе, сможет ли кролик пересечь все \(\text{3}\) полосы автострады безопасно?

Решение пока недоступно

От силы к скорости: Что это за волшебство?

Итак, теперь мы знаем, что можем получить очень много увлекательной и полезной информации из простых тестов, проведенных на системе измерения силовой плиты.

Мы также знаем, что сила — это сила, с которой вы что-то толкаете или тянете.

Как же тогда мы можем перейти от знания того, как сильно что-то толкают или тянут, к знанию того, как быстро оно движется? Что ж, это важный вопрос, потому что возможность рассчитать, как быстро что-то движется, позволяет нам рассчитать следующее…

• Как далеко он движется
• Направление движения
• Произведенная работа и мощность, полученная при его перемещении

Теперь, если вы узнали что-то из моих сообщений в блоге, это сила понимания того, откуда берутся ваши данные, и именно из-за трех пунктов, которые я только что перечислил, я думаю, что важно, чтобы вы поняли, как мы получаем скорость из силы.

 

---

Конечно, я понимаю, что математика (да, я англичанин — мы изобрели язык, и мы его так называем) не обязательно всем нравится, но не волнуйтесь, я не математик, так что я Я сделаю все, что в моих силах, чтобы избавить вас от неприятных ощущений в следующем объяснении.

Итак, мы надеемся, что все мы знаем, что если вы знаете, как далеко что-то переместилось, и вы знаете, сколько времени потребовалось для перемещения, мы можем рассчитать его скорость? По сути, мы берем расстояние, которое он переместил, и делим его на то, сколько времени потребовалось для перемещения. Если нас не беспокоит направление, в котором двигался интересующий нас объект, то мы можем назвать результат скоростью. Однако, если нас интересует направление, в котором двигался объект интереса — а давайте признаем, направление является довольно важной частью спорта — тогда мы будем называть его скоростью.

 

Мы могли бы повторить этот процесс, разделив скорость на время, чтобы вычислить ускорение — независимо от того, ускоряется ли интересующий объект, замедляется ли он или движется с постоянной скоростью.Мы все сталкивались с уравнением, которое часто используется для описания второго закона Ньютона…

 

F = м а   

…верно: сила = масса × ускорение. Если мы знаем ускорение интересующего объекта и знаем его массу, мы можем умножить их, чтобы получить силу. Технически это дает нам то, что мы часто называем чистой силой , силой , влияющей на движение. Если мы вернемся к аналогии весов в ванной с силовой пластиной, которую я дал несколько статей в блоге назад, мы можем представить чистую силу как силу минус вес тела. Помните, это потому, что просто стоя на месте, мы прикладываем к земле силу . Однако нас это не трогает. Это делает сила , которая либо больше, либо меньше веса нашего тела.

Численное дифференцирование — это многословный способ сказать, что мы разделили что-то (скажем, как далеко что-то движется) на время (сколько времени требуется, чтобы двигаться).

Противоположностью числового дифференцирования является числовое интегрирование.. просто, правда?

Правильно, вместо того, чтобы делить одни метрики на время для расчета других метрик, мы умножаем их на время.

Если мы знаем, какая сила была приложена к известной массе (наша перемычка — и мы знаем, именно поэтому мы в первую очередь используем силовую пластину, верно?), то мы можем вычислить следующее:

• Чистая сила = сила минус вес тела
• Ускорение = чистая сила ÷ масса тела (вес тела ÷ ускорение свободного падения [9. 81 м/с/с])
• Скорость = ускорение × время
• Перемещение = скорость × время

 

 

Именно поэтому компании, производящие пластины, должны быть открытыми для своих клиентов и работать с полной прозрачностью. Не забудьте задать себе этот действительно важный вопрос:

• Как я могу стать владельцем своих данных, если я не знаю, откуда они взялись?

Конечно, не всегда все так просто. Например, в приведенном выше примере мы вычисляем среднюю скорость.Как правило, программное обеспечение силовой пластины рассчитывает такие показатели, как результирующая сила, ускорение, скорость и смещение, для каждого образца. На самом деле это не усложняет обработку данных, это просто означает, что ваши данные будут интегрироваться по одной строке за раз. Конечно, когда у нас есть скорость, мы можем умножить ее на силу, чтобы получить мощность (часто пушистая, ненужная метрика, но она определенно имеет место быть). Интересно, что если нас интересует, сколько работы было выполнено при подталкивании интересующего объекта к движению, то мы можем интегрировать среднюю мощность фазы по времени (т. г. движение работа = фаза движения средняя мощность × время).

 

 

---

Ну да. Это действительно так. В принудительной обработке данных действительно нет никакого волшебства. Как следствие, никакой секретности тоже быть не должно. Однако мы должны закончить это на предостерегающей ноте…

Расчеты, которые любое программное обеспечение системы измерения силы будет выполнять с вашими данными, будут настолько точными, насколько хороши данные о силе, которые вы ему предоставите.Под этим я подразумеваю, что вы должны убедиться, что вы стандартизируете (см. последнюю статью в блоге) любые задачи, которые ваши спортсмены или клиенты выполняют на ваших силовых плитах. Чем дальше вы позволите своим спортсменам или клиентам уйти от любой стандартизированной задачи , тем менее точными будут ваши данные и тем меньше у вас будет уверенности в них. Так что помните…

• Предоставьте своим спортсменам и клиентам четкие инструкции
• Дайте своим спортсменам и клиентам достаточно времени, чтобы попрактиковаться в задачах, которые вы хотите, чтобы они выполняли
• Следуйте сценарию инструкций для выпуска каждой пробной версии
• Наблюдайте за тем, как ваши спортсмены или клиенты выполняют каждое испытание (и повторяйте его, если оно вас не устраивает

Я надеюсь, что эта статья помогла пролить немного света на элемент системы силовых пластин, который часто кажется окутанным тайной. Помните, если кто-то пытается сказать вам, что это сложнее, чем это, то, вероятно, они либо пытаются вам что-то продать, либо им есть что скрывать. Наверное оба.

Наконец, если у вас есть какие-либо вопросы, напишите мне по электронной почте [email protected]

>> Теперь, когда вы узнали о силе и скорости, прочитайте CMJ Playbook, чтобы узнать, как это применимо к человеческому движению.

 

3.6 Определение скорости и смещения по ускорению – University Physics Volume 1

3 Движение по прямой

Цели обучения

К концу этого раздела вы сможете:

• Выведите кинематические уравнения для постоянного ускорения с помощью интегрального исчисления.
• Использовать интегральную формулировку кинематических уравнений при анализе движения.
• Найдите функциональную форму зависимости скорости от времени по заданной функции ускорения.
• Найдите функциональную форму зависимости положения от времени по заданной функции скорости.

В этом разделе предполагается, что у вас достаточно знаний в области исчисления, чтобы быть знакомым с интегрированием. В разделах «Мгновенная скорость и скорость» и «Среднее и мгновенное ускорение» мы ввели кинематические функции скорости и ускорения с помощью производной.Взяв производную от функции положения, мы нашли функцию скорости, и точно так же, взяв производную от функции скорости, мы нашли функцию ускорения. Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения, а функцию положения из функции скорости.

Кинематические уравнения интегрального исчисления

Начнем с частицы с ускорением a (t) — известная функция времени.Поскольку производная по времени от функции скорости есть ускорение,

   

мы можем взять неопределенный интеграл от обеих частей, найдя

   

где C ₁ — постоянная интегрирования. С

   

, скорость равна

   

Точно так же производная по времени от функции положения является функцией скорости,

   

Таким образом, мы можем использовать те же математические манипуляции, которые мы только что использовали, и найти

.

   

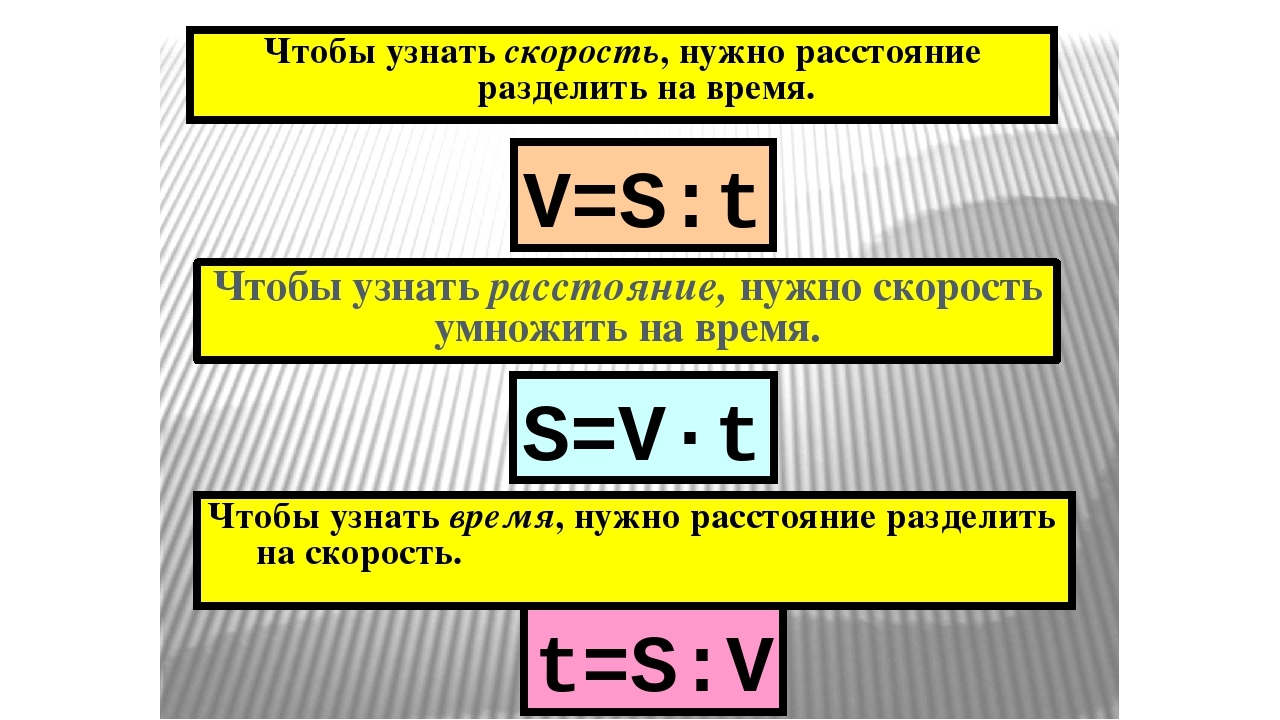
, где C ₂ — вторая постоянная интегрирования.

Мы можем вывести кинематические уравнения для постоянного ускорения, используя эти интегралы. С a ( t ) = a константа, и выполняя интегрирование в (Рисунок), мы находим

   

Если начальная скорость v (0) = v ₀ , то

   

Тогда С ₁ = v ₀ и

   

, что (Уравнение).Подстановка этого выражения в (Рисунок) дает

   

Делая интегрирование, находим

   

Если х (0) = х ₀ , мы имеем

   

так, С ₂ = х ₀ . Подставляя обратно в уравнение для x ( t ), мы, наконец, имеем

   

, что (Уравнение).

Пример

Движение моторной лодки

Моторная лодка движется с постоянной скоростью 5. 0 м/с, когда он начинает замедляться, чтобы прибыть в док. Его ускорение

   

. а) Какова функция скорости моторной лодки? б) В какой момент времени скорость достигает нуля? в) Какова функция положения моторной лодки? г) Каково водоизмещение моторной лодки с момента начала торможения до момента, когда скорость равна нулю? (e) Нарисуйте график функций скорости и положения.

Стратегия

(a) Чтобы получить функцию скорости, мы должны проинтегрировать и использовать начальные условия, чтобы найти постоянную интегрирования.(b) Мы устанавливаем функцию скорости равной нулю и находим t . (c) Точно так же мы должны проинтегрировать, чтобы найти функцию положения, и использовать начальные условия, чтобы найти константу интегрирования. (d) Поскольку начальная позиция принимается равной нулю, нам нужно только оценить функцию позиции в

   

.

Решение

Примем t = 0 за время, когда лодка начинает замедляться.

1. Из функциональной формы ускорения мы можем решить (рисунок), чтобы получить v ( t ): [reveal-answer q=»136447″]Показать ответ[/reveal-answer]
   [скрытый ответ = ”136447″]

      

   При t = 0 имеем v(0) = 5.0 м/с = 0 + C1, поэтому C1 = 5,0 м/с или

   .

      

   .[/скрытый ответ]

2. [reveal-answer q=»967265″]Показать ответ[/reveal-answer]
   [hidden-answer a=»967265″]

      

   [/скрытый ответ]

3. Решите (Рисунок): [reveal-answer q=»251505″]Показать ответ[/reveal-answer]
   [скрытый ответ = ”251505″]

      

   При t = 0 мы устанавливаем x(0) = 0 = x0, так как нас интересует только перемещение с момента, когда лодка начинает замедляться.У нас есть

      

   Таким образом, уравнение для позиции

      

   [/скрытый ответ]

4. [reveal-answer q=”330950″]Показать ответ[/reveal-answer]
   [скрытый-answer a=”330950″]Поскольку начальная позиция принимается равной нулю, мы должны оценить x(t) только тогда, когда скорость равна нулю. Это происходит при t = 6,3 с. Следовательно, смещение равно

      

   [/скрытый ответ]

Рис. 3.30 (a) Скорость моторной лодки как функция времени.Моторная лодка уменьшает скорость до нуля за 6,3 с. В моменты времени, превышающие это значение, скорость становится отрицательной, то есть лодка меняет направление. (b) Положение моторной лодки в зависимости от времени. В момент времени t = 6,3 с скорость равна нулю, и лодка остановилась. В моменты времени, превышающие это, скорость становится отрицательной — это означает, что если лодка продолжает двигаться с тем же ускорением, она меняет направление и направляется обратно к тому месту, где она возникла.

Значение

Функция ускорения линейна во времени, поэтому при интегрировании используются простые полиномы.На (рисунке) мы видим, что если мы расширим решение за точку, где скорость равна нулю, скорость станет отрицательной, и лодка изменит направление. Это говорит нам о том, что решения могут дать нам информацию, выходящую за рамки нашего непосредственного интереса, и мы должны быть осторожны при их интерпретации.

Проверьте свое понимание

Частица стартует из состояния покоя и имеет функцию ускорения

   

. а) Что такое функция скорости? б) Что такое функция положения? в) Когда скорость равна нулю?

[reveal-answer q=»fs-id1168057352922″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168057352922″]

1. Функция скорости представляет собой интеграл функции ускорения плюс постоянная интегрирования.По (рисунок),

      

   Поскольку v (0) = 0, мы имеем C ₁ = 0; Итак,

      

2. По (Рисунок),

      

   . Поскольку x (0) = 0, мы имеем C ₂ = 0 и

   .

      

3. Скорость можно записать как v ( t ) = 5 t (1 – t ), что равно нулю при t = 0 и t = 1 с.

[/скрытый ответ]

Резюме

• Интегральное исчисление дает нам более полную формулировку кинематики.
• Если известно ускорение a ( t ), мы можем использовать интегральное исчисление для получения выражений для скорости v ( t ) и положения x ( t ).
• Если ускорение постоянно, интегральные уравнения сводятся к (Рисунок) и (Рисунок) для движения с постоянным ускорением.

Ключевые уравнения

«>

Рабочий объем
Полный водоизмещение
Средняя скорость
Мгновенная скорость
Средняя скорость
Мгновенная скорость
Среднее ускорение
Мгновенное ускорение
Позиция по средней скорости
Средняя скорость
Скорость от ускорения
Положение по скорости и ускорению
Скорость на расстоянии
Скорость свободного падения
Высота свободного падения
Скорость свободного падения с высоты
Скорость от ускорения
Положение по скорости

Концептуальные вопросы

Когда задана функция ускорения, какая дополнительная информация необходима для нахождения функции скорости и функции положения?

Проблемы

Ускорение частицы изменяется со временем согласно уравнению

   

. Первоначально скорость и положение равны нулю. а) Как зависит скорость от времени? б) Что такое положение как функция времени?

Между t = 0 и t = t ₀ ракета движется прямо вверх с ускорением, равным

   

, где A и B — константы. (a) Если x в метрах, а t в секундах, каковы единицы A и B ? (b) Если ракета стартует из состояния покоя, как изменится скорость между t = 0 и t = t ₀ ? в) Если ее начальное положение равно нулю, каково положение ракеты в зависимости от времени в течение этого же интервала времени?

[reveal-answer q=»fs-id1168055134758″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055134758″]

а.

   

;
б.

   

;

в.

   

[/скрытый ответ]

Скорость частицы, движущейся вдоль оси x-, изменяется со временем по закону

   

, где A = 2 м/с, B = 0,25 м и

   

. Определить ускорение и положение частицы при t = 2,0 с и t = 5.0 с. Предположим, что

   

.

Частица, находящаяся в состоянии покоя, покидает точку отсчета, и ее скорость увеличивается со временем по формуле v ( t ) = 3,2 t м/с. В 5,0 с скорость частицы начинает уменьшаться согласно [16,0 – 1,5( t – 5,0)] м/с. Это уменьшение продолжается до t = 11,0 с, после чего скорость частицы остается постоянной и равной 7,0 м/с. а) Как зависит ускорение частицы от времени? б) Каково положение частицы в точке t = 2.0 с, t = 7,0 с и t = 12,0 с?

[reveal-answer q=»fs-id1168055121296″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055121296″]

а.

   

;
б.

   

[/скрытый ответ]

Дополнительные проблемы

Профессиональный бейсболист Нолан Райан мог подавать бейсбольный мяч со скоростью примерно 160,0 км/ч. При такой средней скорости сколько времени потребовалось мячу, брошенному Райаном, чтобы достичь домашней площадки, что составляет 18.4 м от горки кувшина? Сравните это со средним временем реакции человека на зрительный стимул, которое составляет 0,25 с.

Самолет вылетает из Чикаго и пролетает 3000 км до Лос-Анджелеса за 5 часов. Второй самолет вылетает из Чикаго на полчаса позже и прибывает в Лос-Анджелес в то же время. Сравните средние скорости двух самолетов. Не обращайте внимания на кривизну Земли и разницу в высоте между двумя городами.

[reveal-answer q=»fs-id1168055151090″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055151090″]

Возьмите запад в положительном направлении.

1-й самолет:

   

2-й самолет

   

[/скрытый ответ]

Необоснованные результаты Велосипедист проезжает 16,0 км на восток, затем 8,0 км на запад, затем 8,0 км на восток, затем 32,0 км на запад и, наконец, 11,2 км на восток. Если его средняя скорость равна 24 км/ч, то за какое время он проделал путь? Это разумный срок?

Объект имеет ускорение

   

. В

   

, его скорость

   

.Определить скорости объекта на

   

и

   

.

[reveal-answer q=»fs-id1168055302745″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055302745″]

   

,

   

   

;

   

[/скрытый ответ]

Частица движется вдоль оси x по уравнению

   

м.Каковы скорость и ускорение на

?

   

с и

   

с?

Частица, движущаяся с постоянным ускорением, имеет скорость

   

на

   

с и

   

на

   

с. Чему равно ускорение частицы?

[reveal-answer q=»fs-id1168055307822″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055307822″]

   

[/скрытый ответ]

Поезд движется вверх по крутому склону с постоянной скоростью (см. следующий рисунок), когда его камбуз отрывается и начинает свободно катиться по рельсам.Через 5,0 с камбуз отстает от поезда на 30 м. Каково ускорение камбуза?

Электрон движется прямолинейно со скоростью

   

м/с. Он входит в область длиной 5,0 см, где он испытывает ускорение

   

по той же прямой. а) Какова скорость электрона, когда он вылетает из этой области? б) Сколько времени требуется электрону, чтобы пересечь область?

[reveal-answer q=»fs-id1168055302554″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055302554″]

а.

   

;

б.

   

[/скрытый ответ]

Водитель скорой помощи везет пациента в больницу. Двигаясь со скоростью 72 км/ч, она замечает, что светофор на предстоящем перекрестке загорелся желтым. Чтобы добраться до перекрестка до того, как загорится красный свет, она должна проехать 50 м за 2,0 с. а) Какое минимальное ускорение должна иметь машина скорой помощи, чтобы добраться до перекрестка до того, как загорится красный сигнал светофора? б) С какой скоростью машина скорой помощи доедет до перекрестка?

Мотоцикл, замедляющийся равномерно, охватывает 2. 0 км подряд за 80 с и 120 с соответственно. Вычислите: а) ускорение мотоцикла и б) его скорость в начале и в конце 2-километровой поездки.

[reveal-answer q=»fs-id1168057524743″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168057524743″]

   

;

   

решить одновременно, чтобы получить

   

и

   

, то есть

   

.Скорость в конце пути

   

.
[/скрытый ответ]

Велосипедист проехал из пункта А в пункт Б за 10 мин. В течение первых 2,0 мин пути она поддерживает равномерное ускорение

   

. Затем она движется с постоянной скоростью в течение следующих 5,0 мин. Затем она замедляется с постоянной скоростью так, что через 3,0 мин останавливается в точке B. а) Нарисуйте график зависимости скорости от времени для поездки. б) Чему равно ускорение за последние 3 мин? в) Какое расстояние проехал велосипедист?

Два поезда движутся со скоростью 30 м/с в противоположных направлениях по одному и тому же пути. Инженеры одновременно видят, что они находятся на встречном курсе, и включают тормоза, когда расстояние между ними составляет 1000 м. Предполагая, что оба поезда имеют одинаковое ускорение, каким должно быть это ускорение, чтобы поезда остановились перед столкновением?

[reveal-answer q=»fs-id1168055171872″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055171872″]

   

[/скрытый ответ]

Грузовик длиной 10 м движется с постоянной скоростью 97.0 км/ч проезжает автомобиль длиной 3,0 м, движущийся с постоянной скоростью 80,0 км/ч. Сколько времени проходит между моментом, когда передняя часть грузовика окажется на одном уровне с задней частью автомобиля, и моментом, когда задняя часть грузовика окажется на одном уровне с передней частью автомобиля?

Полицейская машина спряталась недалеко от шоссе. Полицейская машина замечает мчащуюся машину, которая движется со скоростью 40 м/с. В тот момент, когда мчащаяся машина проезжает мимо полицейской машины, полицейская машина разгоняется из состояния покоя со скоростью 4 м/с ² , чтобы догнать мчащуюся машину. Сколько времени потребуется полицейской машине, чтобы догнать мчащуюся машину?

[reveal-answer q=»fs-id1168055306834″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055306834″]

Уравнение для движущегося автомобиля: Этот автомобиль имеет постоянную скорость, которая является средней скоростью, и не ускоряется, поэтому используйте уравнение для перемещения с

.

   

:

   

; Уравнение для полицейской машины: эта машина ускоряется, поэтому используйте уравнение для перемещения с

.

   

и

   

, так как полицейская машина трогается с места:

   

; Теперь у нас есть уравнение движения для каждого автомобиля с общим параметром, который можно исключить, чтобы найти решение.В этом случае мы решаем для

   

. Шаг 1, устранение

   

:

   

; Шаг 2, решение для

   

:

   

. Автомобиль движется с постоянной скоростью 40 м/с, что является его средней скоростью. Ускорение полицейской машины равно 4 м/с ² . Оценивая t , время, за которое полицейская машина догонит мчащуюся машину, мы имеем

   

.
[/скрытый ответ]

Пабло бежит полумарафон со скоростью 3 м/с. Другой бегун, Джейкоб, с такой же скоростью отстает от Пабло на 50 метров. Джейкоб начинает ускоряться со скоростью 0,05 м/с ² . а) Сколько времени потребуется Джейкобу, чтобы поймать Пабло? б) Какое расстояние преодолел Иаков? в) Какова конечная скорость Якова?

Необоснованные результаты Бегун приближается к финишу и находится на расстоянии 75 м; ее средняя скорость в этом положении 8 м/с.В этот момент она замедляется со скоростью 0,5 м/с ² . За какое время она пересечет финишную черту с расстояния 75 м? Это разумно?

[reveal-answer q=»fs-id1168055381859″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055381859″]

При таком ускорении она полностью останавливается за

   

, но пройденное расстояние

   

, что меньше, чем расстояние до финиша, поэтому она никогда не финиширует в гонке.
[/скрытый ответ]

Самолет разгоняется до 5,0 м/с ² за 30,0 с. За это время он преодолевает расстояние 10,0 км. Каковы начальная и конечная скорости самолета?

Сравните расстояние, пройденное объектом, скорость которого изменилась в два раза по сравнению с начальной скоростью, с объектом, скорость которого изменилась в четыре раза по сравнению с начальной скоростью за тот же период времени. Ускорения обоих тел постоянны.

[reveal-answer q=»fs-id1168055323241″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055323241″]

   

   

[/скрытый ответ]

Объект движется на восток с постоянной скоростью и находится в позиции

   

.а) Какое ускорение должен иметь объект, чтобы его полное перемещение стало равным нулю в более позднее время t ? (b) Какова физическая интерпретация решения в случае

?

   

?

Мяч брошен прямо вверх. На своем пути вверх он проходит окно высотой 2,00 м на высоте 7,50 м от земли, и ему требуется 1,30 с, чтобы пройти мимо окна. Какова была начальная скорость мяча?

[reveal-answer q=»fs-id11680553

″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id11680553

″]

   

скорости в нижней части окна.

   

   

[/скрытый ответ]

Монета сбрасывается с воздушного шара, находящегося на высоте 300 м над землей и поднимающегося вверх со скоростью 10,0 м/с. Для монеты найдите (а) максимальную достигнутую высоту, (б) ее положение и скорость через 4,00 с после того, как ее отпустили, и (в) время до того, как она упадет на землю.

Мягкий теннисный мяч падает на твердый пол с высоты 1,50 м и отскакивает на высоту 1,10 м. а) Определите его скорость непосредственно перед ударом об пол.(b) Рассчитайте его скорость сразу после того, как он оторвется от пола на обратном пути вверх. (c) Рассчитайте его ускорение при контакте с полом, если этот контакт длится 3,50 мс

   

(г) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?

[reveal-answer q=»fs-id1168055325521″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055325521″]

а.

   

;
б.

   

;

в.

   

;

д.

   

[/скрытый ответ]

Необоснованные результаты . Капля дождя падает из облака на высоте 100 м над землей. Сопротивлением воздуха пренебречь. Какова скорость капли дождя в момент удара о землю? Это разумное число?

Сравните время нахождения в воздухе баскетболиста, прыгнувшего вертикально с пола на 1,0 м, со временем игрока, прыгнувшего на 0.3 м по вертикали.

[reveal-answer q=»fs-id1168057418927″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168057418927″]

Рассмотрим падение игроков из состояния покоя на высоте 1,0 м и 0,3 м.

0,9 с

0,5 с

[/скрытый ответ]

Предположим, что человеку требуется 0,5 с, чтобы отреагировать и пошевелить рукой, чтобы поймать предмет, который он уронил. (а) Как далеко объект падает на Землю, где

   

(b) Как далеко падает объект на Луне, где ускорение свободного падения составляет 1/6 от земного?

Воздушный шар поднимается над землей с постоянной скоростью 3. 0 м/с. Через минуту после старта с воздушного шара случайно сбрасывается мешок с песком. Вычислите: а) время, за которое мешок с песком достигает земли, и б) скорость мешка с песком в момент удара о землю.

[reveal-answer q=»fs-id1168055469821″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055469821″]

а.

   

с положительным корнем;
б.

   

[/скрытый ответ]

(a) Мировой рекорд был установлен в беге на 100 м среди мужчин на Олимпийских играх 2008 года в Пекине Усэйном Болтом из Ямайки.Болт «перебежал» финишную черту со временем 9,69 с. Если мы предположим, что Болт ускорялся в течение 3,00 с, чтобы достичь своей максимальной скорости, и поддерживал эту скорость до конца гонки, рассчитайте его максимальную скорость и его ускорение. (b) Во время той же Олимпиады Болт также установил мировой рекорд в беге на 200 м со временем 19,30 с. Используя те же предположения, что и для бега на 100 м, какова была его максимальная скорость в этом забеге?

Предмет падает с высоты 75,0 м над уровнем земли. а) Определите путь, пройденный за первую секунду. б) Определить конечную скорость, с которой тело упадет на землю. в) Определите расстояние, пройденное за последнюю секунду движения до удара о землю.

[reveal-answer q=»fs-id1168055273683″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055273683″]

а.

   

;
б.

   

;

в.

   

[/скрытый ответ]

Стальной шар падает на твердый пол с высоты 1.50 м и подборами на высоту 1,45 м. а) Определите его скорость непосредственно перед ударом об пол. (b) Рассчитайте его скорость сразу после того, как он оторвется от пола на обратном пути вверх. (c) Рассчитайте его ускорение при контакте с полом, если этот контакт длится 0,0800 мс

   

(г) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?

Предмет падает с крыши здания высотой h .За последнюю секунду спуска он проходит расстояние ч /3. Рассчитайте высоту здания.

[reveal-answer q=»fs-id11680554″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id11680554″]

   

, ч = общая высота и время падения на землю

   

в т – 1 сек падает 2/3 ч

   

или

   

   

   

т = 5.45 с и ч = 145,5 м. Другой корень меньше 1 с. Проверка на t = 4,45 с

   

м

   

[/скрытый ответ]

Задачи-вызовы

В забеге на 100 м время победителя составляет 11,2 с. Время второго места – 11,6 с. Как далеко занявшая второе место отстаёт от победительницы, когда она пересекает финишную черту? Предположим, что скорость каждого бегуна постоянна на протяжении всего забега.

Положение частицы, движущейся вдоль оси x , изменяется со временем в соответствии с

   

м. Найти: а) скорость и ускорение частицы как функции времени, б) скорость и ускорение в момент времени t = 2,0 с, в) время, когда положение максимально, скорость которого равна нулю, и (e) максимальное положение.

[reveal-answer q=»fs-id1168055269782″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168055269782″]

а.

   

;
б.

   

; в.Наклон функции положения равен нулю или скорость равна нулю. Возможны два решения: t = 0, что дает x = 0, или t = 10,0/12,0 = 0,83 с, что дает x = 1,16 м. Второй ответ является правильным выбором; д. 0,83 с (д) 1,16 м

[/скрытый ответ]

Велосипедист мчится в конце гонки, чтобы одержать победу. Она имеет начальную скорость 11,5 м/с и ускоряется со скоростью 0,500 м/с ² за 7.00 с. а) Какова его конечная скорость? (b) Велосипедист продолжает движение с этой скоростью до финиша. Если она находится в 300 м от финиша, когда начинает разгоняться, сколько времени она сэкономила? (c) Победитель, занявший второе место, был на 5,00 м впереди, когда победитель начал ускоряться, но он не смог ускориться и двигался со скоростью 11,8 м/с до финиша. Какая разница во времени финиша в секундах между победителем и призером? Как далеко от финиша финишировал занявший второе место?

В 1967 году новозеландец Берт Манро установил мировой рекорд на индийском мотоцикле на соляных равнинах Бонневиль в штате Юта (295).38 км/ч. Длина трассы в один конец составила 8,00 км. Темпы ускорения часто описываются временем, которое требуется для достижения 96,0 км/ч из состояния покоя. Если это время составило 4,00 с, и Берт разогнался с такой скоростью, пока не достиг своей максимальной скорости, сколько времени потребовалось Берту, чтобы пройти этот путь?

[reveal-answer q=»fs-id1168057239219″]Показать решение[/reveal-answer]

[скрытый ответ a=”fs-id1168057239219″]

   

, 295,38 км/ч = 82,05 м/с,

   

время разгона до максимальной скорости

   

пройденное расстояние при разгоне

   

на постоянной скорости

   

, значит общее время

   

.

[/скрытый ответ]

Расчет размеров двигателя

Правильный размер и выбор двигателя для вашего оборудования являются ключом к обеспечению производительности, надежности и стоимости оборудования. В дополнение к приведенной ниже информации по правильному подбору двигателя, Oriental Motor предлагает онлайн-инструменты для подбора двигателя, а также помощь сотрудников службы технической поддержки.

Наш персонал службы технической поддержки всегда готов помочь вам правильно подобрать размер и выбрать двигатель в зависимости от вашего индивидуального применения.Просто позвоните по номеру 1-800-GO-VEXTA (468-3982) (с понедельника по пятницу с 7:30 до 17:00 по тихоокеанскому времени).

Процедура выбора

Первый шаг — определить приводной механизм для вашего оборудования. Некоторыми примерами являются прямое вращение, шариковый винт, ремень и шкив или рейка и шестерня. Наряду с типом приводного механизма необходимо также определить размеры, массу, коэффициент трения и т. д., необходимые для расчета нагрузки:

• Размеры и масса (или плотность) груза
• Размеры и масса (или плотность) каждой части
• Коэффициент трения поверхности скольжения каждой движущейся части

Далее необходимо определить требуемые характеристики оборудования:

• Рабочая скорость и время работы
• Расстояние позиционирования и время позиционирования
• Разрешение
• Точность остановки
• Удержание позиции
• Источник питания и напряжение
• Операционная среда
• Особые характеристики и требования, такие как; Открытый цикл, замкнутый цикл, программируемый, обратная связь, рейтинг IP, утверждения агента и т. д.

Чтобы определить требуемую производительность двигателя, необходимо рассчитать три фактора; Момент инерции, крутящий момент и скорость. (См. приведенные ниже разделы по расчетам для каждого из них. )

После того, как вы рассчитаете инерцию, крутящий момент и скорость двигателя, вы выберете тип двигателя на основе требуемых характеристик. Oriental Motor предлагает широкий ассортимент шаговых двигателей, серводвигателей, двигателей переменного тока и бесщеточных двигателей для удовлетворения конкретных потребностей вашего оборудования.

Наконец, после выбора типа двигателя вы сделаете окончательное определение двигателя, подтвердив, что характеристики выбранного двигателя (и редуктора, если применимо) удовлетворяют всем требованиям, таким как механическая прочность, время разгона и момент разгона.

Расчет размеров двигателя

При выборе двигателя необходимо рассчитать три фактора; Момент инерции, крутящий момент и скорость.

Момент инерции

Момент инерции – это мера сопротивления объекта изменению скорости его вращения.

Когда объект просто сидит без движения, момент инерции равен 0.

Когда вы пытаетесь заставить его двигаться, что означает, что вы хотите изменить скорость объекта от 0 до любой, будет эффект момента инерции.

Уравнение основной инерции (Дж) :

Расчет момента инерции для вращающегося объекта

Расчет момента инерции цилиндра

Расчет момента инерции для полого цилиндра

Расчет момента инерции для нецентральной оси

Расчет момента инерции для прямоугольной стойки

Расчет момента инерции объекта в линейном движении

Единицы измерения момента инерции

Единицы инерции обычно используются двумя способами: унций-дюйм² и унций-дюйм² .Первое включает гравитацию, второе — только массу.

Теоретически инерция является фактором массы, поэтому она не должна включать гравитацию, однако практически мы не можем легко измерить массу на Земле.

Oriental Motor обычно обеспечивает инерцию в унциях на дюйм². Затем, когда мы рассчитываем крутящий момент ускорения в разделе «Расчет крутящего момента», мы делим общую инерцию на силу тяжести.

Гравитация = 386 дюймов/с²

• унций на дюйм²  = инерция в зависимости от веса
• унций-в-сек²  = инерция на основе массы

Расчет преобразования унций на дюйм² в унции на секунду²

Крутящий момент

Крутящий момент – это стремление силы вращать объект вокруг оси.Крутящий момент состоит из двух компонентов; составляющая нагрузки (постоянная) и составляющая ускорения.

Компонент момента нагрузки обычно возникает из-за трения и/или силы тяжести и всегда действует на двигатель. Этот компонент обычно можно определить путем расчета или путем установки динамометрического ключа на систему и считывания значения крутящего момента. Когда это невозможно измерить, мы используем некоторые уравнения для расчета приблизительного значения.

Однако ускоряющий момент воздействует на двигатель только при его ускорении или замедлении.Когда двигатель работает с постоянной скоростью, этот компонент исчезает. Измерение составляющей ускорения сложно, не говоря уже об опасности. Если вы хотите, чтобы нагрузка достигла нужной скорости в течение 50 миллисекунд, вполне вероятно, что динамометрический ключ слетит. Поэтому вычисляем составляющую ускорения. Эта составляющая является функцией инерции системы и скорости ускорения. Итак, как только мы определим эти значения, мы сможем вычислить момент ускорения.

Момент нагрузки (  T  )

Загрузить крутящий момент очень просто.

Как вы видите, крутящий момент в этом уравнении является произведением силы и расстояния между силой и центром вращения. Например, если вы хотите удерживать силу, действующую на конец шкива, T = F x r .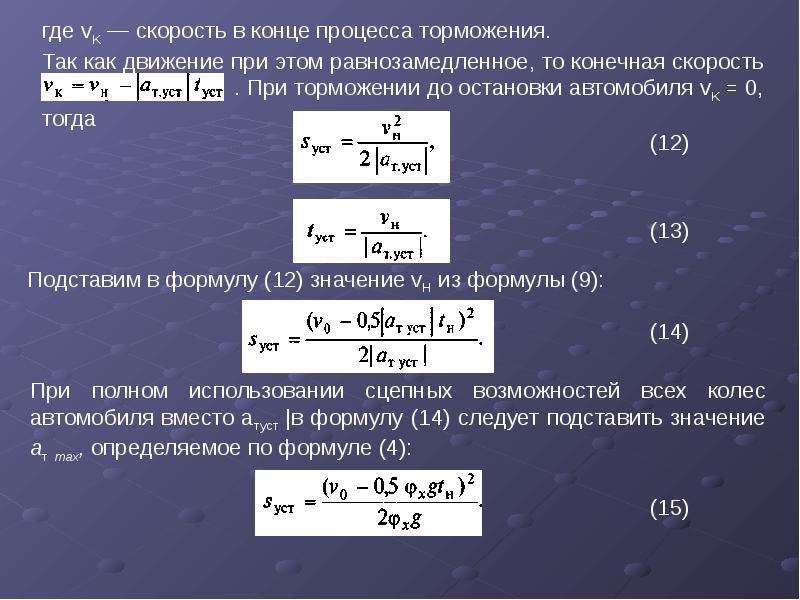 Таким образом, расчет крутящего момента нагрузки определяет силу в системе и логическое расстояние между валом двигателя и местом, где действует сила.

Когда механика становится сложной, нам нужно преобразовать F и r, чтобы она соответствовала механике.

Момент нагрузки — фактическое измерение

Если вы можете измерить силу, это самый точный способ найти силу, так как он учитывает эффективность и коэффициент трения каждой детали.

FB  = Сила, при которой главный вал начинает вращаться

Сил

Есть три типа сил; вертикальные, горизонтальные и наклонные. Сила меняется в зависимости от того, как она действует.

Расчет вертикальной силы

Расчет горизонтальной силы

Расчет силы наклона

Расчет крутящего момента при нагрузке — шарико-винтовая передача

Расчет момента нагрузки — шкив привода

Расчет крутящего момента при нагрузке — канатная или ременная передача, реечный привод

Момент ускорения

Как упоминалось ранее, момент ускорения состоит из инерции и скорости ускорения.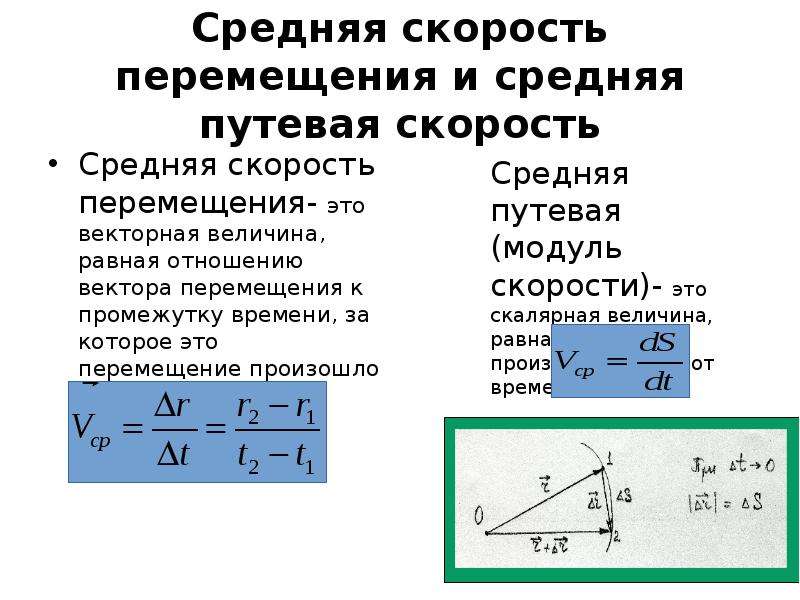 Зная эти два значения, мы можем рассчитать момент ускорения.

Расчет момента ускорения ( Ta  )

Если скорость двигателя изменяется, всегда необходимо устанавливать момент ускорения или момент торможения.

Основная формула одинакова для всех двигателей. Однако используйте приведенные ниже формулы при расчете ускоряющего момента для шаговых двигателей или серводвигателей на основе импульсной скорости.

Общая формула для всех двигателей

При расчете крутящего момента для шаговых или серводвигателей на основе импульсной скорости

Существует два основных профиля движения.Операция ускорения/торможения является наиболее распространенной. Когда рабочая скорость низкая и инерция нагрузки мала, можно использовать операцию пуска/останова.

Расчет требуемого крутящего момента ( TM  )

Требуемый крутящий момент рассчитывается путем умножения суммы момента нагрузки и момента ускорения на коэффициент безопасности.

Расчет эффективного крутящего момента нагрузки ( Trms  ) для серводвигателей и бесщеточных двигателей серии BX

Если требуемый крутящий момент для двигателя меняется со временем, определите, можно ли использовать двигатель, рассчитав эффективный крутящий момент нагрузки.Эффективный момент нагрузки становится особенно важным для режимов работы, таких как операции с быстрым циклом, где часто происходит ускорение/замедление. Рассчитайте эффективный крутящий момент нагрузки при выборе серводвигателей или бесщеточных двигателей серии BX.

Скорость

Скорость определяется путем вычисления расстояния, деленного на время. Для шаговых или серводвигателей также необходимо учитывать время разгона.

Расчет стандартной скорости

Скорость = Расстояние/Время

Для шаговых или серводвигателей

Скорость = Расстояние / (Время — Время ускорения (  t1  )

Хотите узнать больше?

Группа технической поддержки и инженеры по применению Oriental Motor будут работать с вами, чтобы определить лучшее решение для вашей области применения. Опытные члены команды ORIENTAL MOTOR знают технологию вдоль и поперек. Мы найдем правильное решение, основанное на ваших потребностях, и объясним альтернативы. Позвоните 1-800-GO-VEXTA (468-3982), чтобы поговорить с сотрудником группы технической поддержки Oriental Motor.

 

 

Калькулятор кинетической энергии — Рассчитайте кинетическую энергию движущегося объекта

Простой расчет кинетической энергии движущегося объекта. Ввод поддерживает метрические и имперские единицы измерения.Выходная мощность в джоулях (Дж, кДж, МДж), ватт-часах (Втч, кВтч), калориях (Кал, кКал) и футо-фунтах (фут-фунт). Калькулятор также можно использовать для вычисления массы или скорости.

    Быстрая навигация:

1. Использование калькулятора кинетической энергии
2. Формулы кинетической энергии
3. Примеры расчета кинетической энергии

    Использование калькулятора кинетической энергии

Этот калькулятор кинетической энергии полезен для оценки энергии, которую тело приобретает при любом движении. Например, его можно использовать для расчета кинетической энергии человека, транспортного средства (автомобиль, грузовик, поезд), самолета, футбольного мяча, а также для падающих тел, врезающихся в землю. Его также можно использовать для расчета энергии различных видов снарядов. Для расчета кинетической энергии нужно знать только массу и скорость тела. Его ускорение не имеет значения, так как энергия рассчитывается в конкретный момент времени.

Калькулятор KE также можно использовать для решения любых других величин: массы и скорости .Соответствующие поля ввода будут скрыты или отображены при выборе того, для чего вы хотите использовать калькулятор. При решении для массы вам нужно знать скорость и кинетическую энергию, а при решении для скорости вам нужно знать массу и кинетическую энергию объекта.

Выход инструмента при расчете кинетической энергии выражается в джоулях (Дж, кДж, МДж), ватт-часах (Втч, кВтч), калориях (Кал, кКал) и футо-фунтах (фут-фунт). Когда выход инструмента представляет собой массу или скорость, он выражается как в стандартных метрических единицах, так и в имперских, причем единицы автоматически корректируются в зависимости от того, насколько велико или мало полученное значение.

    Формулы кинетической энергии

Формула кинетической энергии ( KE ), выраженная через скорость тела (скорость) ( v ) и его массу ( m ), представляет собой первое уравнение ниже:

, тогда как второе и третье являются преобразованными уравнениями для решения массы или скорости.

Эта формула справедлива в классической механике и для невращающихся твердых точечных объектов (предполагается, что масса объекта существует в одной точке).Если скорость объекта превышает пару процентов от скорости света в вакууме, это плохое приближение согласно релятивистской механике. Это уравнение используется при кодировании этого онлайн-калькулятора кинетической энергии.

    Примеры расчета кинетической энергии

Пример 1: Автомобиль весит 2200 кг (2,2 тонны) и движется со скоростью 40 км/ч. Какова кинетическая энергия автомобиля? Чтобы рассчитать кинетическую энергию, сначала переведите км/ч в метры в секунду: 40 км/ч = 11.11 м/с. Используя приведенное выше первое уравнение кинетической энергии, замените значения для m и v и получите KE = 2200 · (11,11) ² / 2 = 135775,3 Дж или 135,7753 кДж.

Пример 2: Мяч весом 500 грамм имеет кинетическую энергию 500 Дж. Какова скорость мяча? Сначала мы преобразуем 500 граммов в 0,5 кг, а затем заменим в формуле: v = √(2 · 500/0,5) = 44,7214 м/с или 146,7236 футов в секунду.

Пример 3: Самолет движется со скоростью 800 км/ч и имеет кинетическую энергию 2100 МДж (мегаджоулей).Какова масса самолета? Сначала нам нужно преобразовать МДж в Дж: 2 100 · 1 000 000 = 2 100 000 000 Дж. Затем нам нужно преобразовать 800 км/ч в м/с, что равно 222,22(2) м/с. Наконец, мы заменяем в формуле, чтобы получить m = 2 · 2 100 000 000 / 222,22 ² = 85 050 кг = 85,05 тонны.

Конечно, при использовании нашего калькулятора вам не нужно будет выполнять эти преобразования единиц измерения, так как они обрабатываются для вас на лету.

Тонна против тонны, тонны против тонны

При вычислении массы объекта выводятся как тонна (метрическая тонна), так и тонна (короткая тонна).Первый используется во всех странах мира и определен международным органом стандартизации равным 1000 кг. Тонна в настоящее время используется только в Соединенных Штатах и ​​​​равна 2000 фунтов (2000 фунтов).

    Ссылки

[1] Специальная публикация NIST 330 (2008 г.) — «Международная система единиц (СИ)», под редакцией Барри Н. Тейлора и Амблера Томпсона, с. 52

[2] «Международная система единиц» (СИ) (2006 г., 8-е изд.). Bureau international des poids et mesures стр. 142–143. ISBN 92-822-2213-6

куб.

см | Физика и поступательное движение

Поскольку физика MCAT часто опирается на расчеты, эта часть экзамена по физике часто вызывает у учащихся чрезмерный уровень беспокойства. Как репетитор MCAT и репетитор по физике, я могу помочь вам преодолеть беспокойство по поводу этого раздела MCAT. Считайте, что это первое из серии неопределенной продолжительности и частоты, которая поможет демистифицировать те понятия, которые могут пригодиться на уроке физики в день экзамена.

Поступательное движение для MCAT означает, что что-то движется не более чем в двух измерениях, не вращаясь. Это движение можно разбить, описав скорость и ускорение в направлении X (влево-вправо в модели на странице) или в направлении Y (вверх-вниз на странице). Скорость рассчитывается как расстояние, деленное на время, а ускорение — это изменение скорости, деленное на время, необходимое для того, чтобы это изменение произошло.

Например: Автомобиль, который проезжает шестьдесят миль за один час, имеет скорость 60 миль/час. Автомобиль, который разгоняется от нуля до шестидесяти миль в час за 4 секунды, имеет ускорение 15 миль в секунду2. (Примечание: единицы измерения выстраиваются в линию! Скорость [расстояние/время], деленная на время, дает вам единицы измерения расстояния/времени2!)

Есть четыре формулы относительно поступательного движения, которые вы должны обязательно выучить наизусть в день экзамена. Они:

1. d=v _o t+ ¹ / ₂ a*t ²
2. v _о = v _t + a*t
3. d= ¹ / ₂ (v _o + v _t )*t
4. v _x ² =v _o ² +2a*d

 

(d=расстояние, v _o =начальная скорость, v _t =конечная скорость, t=время, a=ускорение)

Легче понять эти уравнения, если вы знаете, откуда они взялись.

1.d=v

_o t+ ¹ / ₂ a*t ²

Первое уравнение разбивает расстояние, которое преодолевает объект, на две составляющие: скорость и ускорение.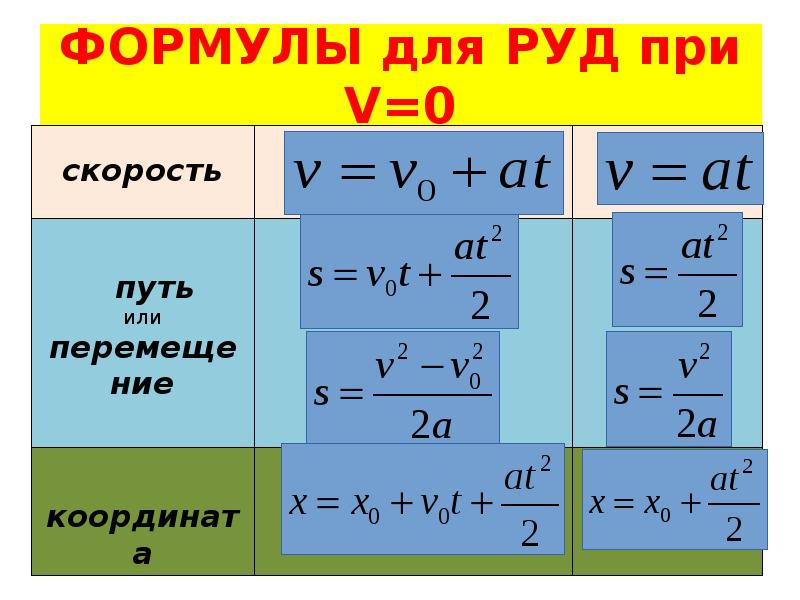 Расстояние, обусловленное начальной скоростью, равно просто скорости, умноженной на время (автомобиль, движущийся со скоростью 30 миль в час в течение 2 часов, проезжает 60 миль [30 миль/час x 2 часа = 60 миль]).

Второй компонент — ускорение. Поскольку ускорение может очень быстро добавить объекту большую скорость (а точнее, потому что именно так работает исчисление), ускорение умножается на КВАДРАТ времени и делится на 2.

2.v

_о =V _T +a*t

Это уравнение определяет ускорение! Скорость движения объекта определяется как скорость, с которой он двигался в начале, плюс скорость ускорения, умноженная на время ускорения. Например, автомобиль, движущийся со скоростью 10 метров в секунду, который затем ускоряется со скоростью 5 метров в секунду ² в течение 2 секунд, по истечении этих 2 секунд будет двигаться со скоростью 40 метров в секунду! (30 метров в секунду + 5 миль в секунду ² * 2 секунды = 40 метров в секунду!)

3.

d= ¹ / ₂ (v _o + v _t )*t

Это уравнение пригодится, когда неизвестно ускорение. Предположим, вы знаете начальную и конечную скорости объекта и время движения. Все это уравнение говорит о том, что пройденное расстояние есть СРЕДНЕЕ значение этих двух скоростей, умноженных на время!

Например: автомобиль начинает движение со скоростью 30 миль в час и через 2 часа движется со скоростью 60 миль в час с постоянным ускорением.Средняя скорость ( ¹ / ₂ [30+60]) составляет 45 миль в час. Так как 45 миль в час раз, 2 часа составляют 90 миль, автомобиль должен был проехать 90 миль! В 95% случаев MCAT предполагает постоянное ускорение.

4. v

_x ² =v _o ² +2a*d

Это уравнение очень полезно, когда время не задано, а ускорение и расстояние не заданы. Это немного сложнее понять интуитивно, но если это полезно, его можно получить, решив уравнение (2) для переменной t, а затем подставив это выражение вместо t в уравнение (3). По сути, если вы знаете начальную скорость объекта, его ускорение и пройденное расстояние, вы можете рассчитать его конечную скорость!

Продолжая решать практические задачи, вы заметите, что ОГРОМНОЕ большинство задач трансляционной физики MCAT — это просто применение этих 4 формул с небольшими вариациями.

Скорость и Скорость

СКОРОСТЬ И СКОРОСТЬ

В последних разделах мы изучили скалярные и векторные понятия. Помимо определений этих понятий, мы попытаемся объяснить термины скорость и скорость.Как упоминалось в последнем разделе, расстояние и смещение — это разные термины. Расстояние — это скалярная величина, а перемещение — векторная величина. Точно так же мы можем классифицировать скорость и скорость. Скорость — это скалярная величина, которая касается только величины, а скорость — векторная величина, которая должна учитывать как величину, так и направление.

СКОРОСТЬ

Скорость можно определить как «насколько быстро что-то движется» или более научно объяснить как «расстояние, пройденное за единицу времени». В повседневной жизни мы используем первое определение и говорим, что более быстрый объект имеет более высокую скорость. Скорость не показывает нам направление движения, она просто дает величину расстояния, пройденного за заданное время. Другими словами, это скалярная величина. Мы используем символ v , чтобы показать скорость. Позвольте мне сформулировать то, о чем мы говорили выше;

Скорость=расстояние/время

Из вышеприведенной формулы можно сказать, что скорость прямо пропорциональна расстоянию и обратно пропорциональна времени.Думаю, пришло время немного поговорить о единицах скорости. Автомобильные транспортные средства обычно используют километр в час (км/ч) в качестве единицы скорости, однако на коротких расстояниях мы можем использовать метр в секунду (м/с) в качестве единицы скорости. В моих примерах и пояснениях я буду использовать м/с в качестве единицы измерения.

Пример : Рассчитайте скорость автомобиля, проехавшего 450 м за 9 секунд.

 

СКОРОСТЬ

Скорость может быть определена как «скорость, имеющая направление».Как вы можете понять из определения, скорость — это векторная величина, имеющая как величину, так и направление. В повседневной жизни мы используем скорость и скорость взаимозаменяемо, но в физике они имеют разные значения. Мы можем определить скорость как «скорость изменения смещения», тогда как «скорость — это скорость изменения расстояния». Когда мы вычисляем скорость, мы смотрим на общее расстояние, однако при вычислении скорости мы должны учитывать направление, и, короче говоря, мы можем просто смотреть на изменение положения, а не на все пройденное расстояние.Если человек проходит 5 м на восток, а затем 5 м на запад, скорость этого человека, рассчитанная путем деления общего пройденного расстояния, равного 10 м, на прошедшее время, однако скорость, рассчитанная путем деления смещения на прошедшее время, равное 0 м, разделенному на прошедшее время, дает нам ноль. Другими словами, если смещение равно нулю, мы не можем говорить о скорости.

Будьте осторожны!! Должно измениться положение объекта, чтобы иметь скорость.

• Мы используем символ ∆, чтобы показать изменение чего-либо.Например, мы можем обозначить изменение положения как ∆X.

 

Пример: Рассчитайте скорость и скорость человека, проходящего 45 м на север и 36 м на юг за 27 секунд.

Сначала мы должны рассчитать пройденное расстояние и перемещение человека, чтобы вычислить скорость и скорость.

Общее пройденное расстояние = 45 м + 6 м = 81 м

Скорость = общее расстояние/время в пути = 81 м / 27 с = 3 м/с

Скорость = перемещение/время = (45-36) м / 27 с = 9 м / 27 с = 0,33 м/с

На этом примере мы показываем, что скорость и скорость — не одно и то же.

Средняя скорость и мгновенная скорость

Движущийся объект не имеет одинаковой скорости во время своего движения.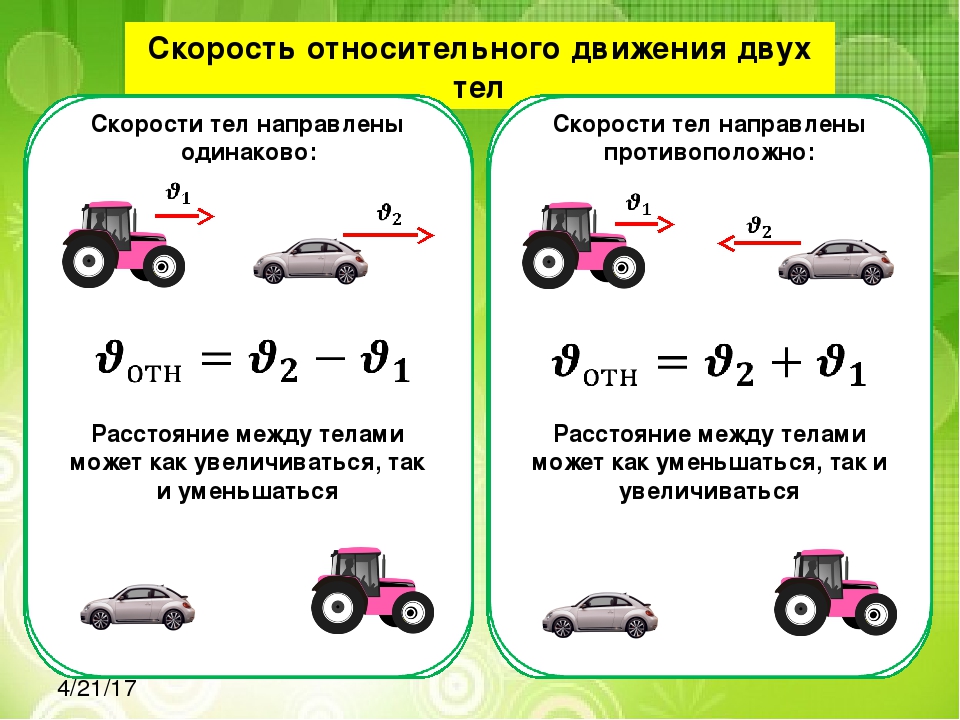 Иногда ускоряется, а иногда замедляется. В данный момент времени то, что мы читаем со спидометра, равно мгновенной скорости . Например, автомобиль, движущийся с постоянной скоростью, едет в другой город, он должен остановиться на красный сигнал светофора в пробке или притормозить при возникновении нежелательных ситуаций на дороге. В конце поездки, если мы хотим узнать среднюю скорость автомобиля, мы делим общее расстояние на общее время поездки.

Предположим, что автомобиль проезжает 500 км за 5 часов. Когда мы вычисляем среднюю скорость, мы видим, что она составляет 100 км/ч. Конечно, машина не едет с постоянной скоростью 100 км/ч. У него много мгновенных скоростей, и 100 км/ч — это среднее значение этих мгновенных скоростей.

Средняя скорость и мгновенная скорость

Мы можем следовать тем же шагам, что и при определении средней и мгновенной скорости, при определении средней и мгновенной скорости. Мгновенная скорость – это скорость в данный момент времени, однако, как и в случае со скоростью, средняя скорость вычисляется со смещением за интервал времени.

Пример Человек, путешествующий на своей машине 150 м на восток и 70 м на запад, рассчитает среднюю скорость и скорость автомобиля, если путешествие занимает 10 секунд.

Средняя скорость=Перемещение/Временной интервал Перемещение=150м-70м=80м

Средняя скорость = 80 м/10 с = 8 м/с на восток

Средняя скорость = общее пройденное расстояние/интервал времени

Средняя скорость = (150м+70м)/10с

Средняя скорость=22 м/с

 

Это хороший пример, который ясно показывает разницу скорости и скорости.Мы должны указать направление со скоростью, поскольку скорость является векторной величиной, однако скорость является скалярной величиной, и мы не учитываем направление.

  Пример: Автомобиль движется по прямой, как показано на приведенном ниже графике.