Формула скорости движения по окружности: Движение по окружности, теория и онлайн калькуляторы
Движение по окружности-Теория.Скорость в физике
На главную Теория Задачи Учёные Интересные статьи Шкала скоростейKинематика равномерного вращения по окружности
При движении по окружности с
постоянной по величине линейной
скоростью v тело испытывает
направленное к центру окружности
постоянное центростремительное
ускорение
aц = v2/R,
где R — радиус окружности.
Вывод формулы для центростремительного ускорения
По определению
На рисунке треугольники,
образованные векторами перемещений
и скоростей, подобны. Учитывая, что
|r1| = |r2| = R и |v1| = |v2| = v, из
подобия треугольников находим:
откуда
Поместим начало координат в
центр окружности и выберем
плоскость, в которой лежит
окружность, за плоскость (x, y).
x = R cos(j + j0), y = R sin(j + j0),
где j0 определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).
В случае равномерного вращения
угол j, измеряемый в радианах,
линейно растет со временем:
j = wt,
где w называется циклической (круговой) частотой. Размерность циклической частоты: [w] = c-1 = Гц.
Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.
Зависимость координат точки на
окружности от времени в случае
равномерного вращения с заданной
частотой можно записать в виде:
x = R cos(wt + j0),
y = R sin(wt + j0).
Время, за которое совершается один оборот, называется периодом T.
Частота
n = 1/T.
Размерность частоты: [n] = с-1 = Гц.
Связь циклической частоты с
периодом и частотой: 2p = wT, откуда
w = 2p/T = 2pn.
Связь линейной скорости и угловой
скорости находится из равенства:
2pR = vT, откуда
v = 2pR/T = wR.
Выражение для
центростремительного ускорения
можно записать разными способами,
используя связи между скоростью,
частотой и периодом:
aц = v2/R = w2R = 4p2n2R = 4p2R/T2.
Связь поступательного и вращательного движений
Основные кинематические
характеристики движения по прямой с
постоянным ускорением: перемещение
s, скорость v и ускорение a. Соответствующие характеристики при
движении по окружности радиусом R:
угловое перемещение j, угловая
скорость w и угловое ускорение a (в
случае, если тело вращается с
переменной скоростью). Из
геометрических соображений
вытекают следующие связи между
этими характеристиками:
Соответствующие характеристики при
движении по окружности радиусом R:
угловое перемещение j, угловая
скорость w и угловое ускорение a (в
случае, если тело вращается с
переменной скоростью). Из
геометрических соображений
вытекают следующие связи между
этими характеристиками:
перемещение sугловое перемещение j = s/R;
скорость vугловая скорость w = v/R;
ускорение aугловое ускорение a = a/R.
Все формулы кинематики
равноускоренного движения по прямой
могут быть превращены в формулы
кинематики вращения по окружности,
если сделать указанные замены.
Например:
s = vtj = wt,
v = v0 + atw = w0 + at.
Связь между линейной и угловой
скоростями точки при вращении по
окружности можно записать в
векторной форме. Действительно,
пусть окружность с центром в начале
координат расположена в плоскости
(x, y). В любой момент времени вектор
R, проведенный из начала координат в
точку на окружности, где находится
тело, перпендикулярен вектору
скорости тела v, направленному по
касательной к окружности в этой
точке. Определим вектор w, который
по модулю равен угловой скорости w и
направлен вдоль оси вращения в
сторону, которая определяется
правилом правого винта: если
завинчивать винт так, чтобы
направление его вращения совпадало с
направлением вращения точки по
окружности, то направление движения
винта показывает направление
вектора w. Тогда связь трех взаимно
перпендикулярных векторов R, v и w
можно записать с помощью векторного
произведения векторов:
Действительно,
пусть окружность с центром в начале
координат расположена в плоскости
(x, y). В любой момент времени вектор
R, проведенный из начала координат в
точку на окружности, где находится
тело, перпендикулярен вектору
скорости тела v, направленному по
касательной к окружности в этой
точке. Определим вектор w, который
по модулю равен угловой скорости w и
направлен вдоль оси вращения в
сторону, которая определяется
правилом правого винта: если
завинчивать винт так, чтобы
направление его вращения совпадало с
направлением вращения точки по
окружности, то направление движения
винта показывает направление
вектора w. Тогда связь трех взаимно
перпендикулярных векторов R, v и w
можно записать с помощью векторного
произведения векторов:
v = wR.Задачи на эту тему
Движение по окружности. Уравнение движения по окружности.
 Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости Кинематика кругового движения
Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости Кинематика кругового движенияТак как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным , оно является равноускоренным .
Угловая скорость
Выберем на окружности точку 1 . Построим радиус. За единицу времени точка переместится в пункт 2 . При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности.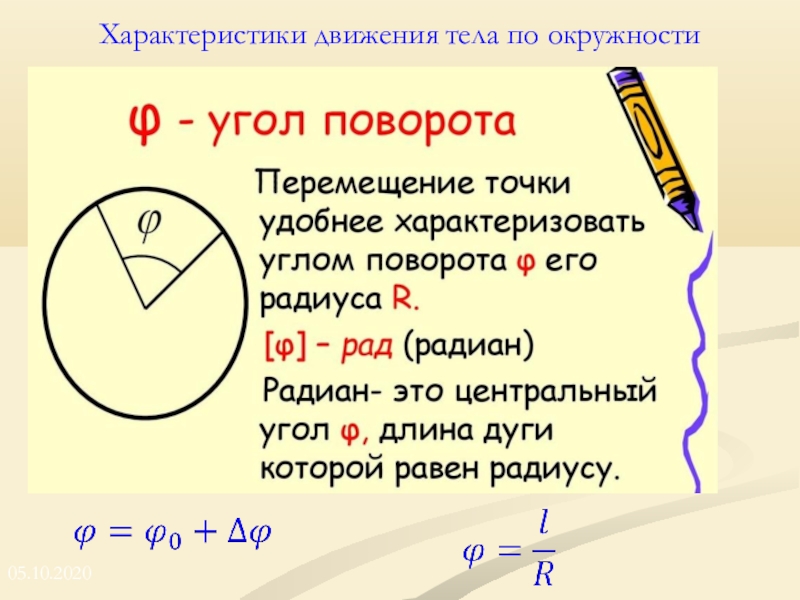 Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T . Путь , который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
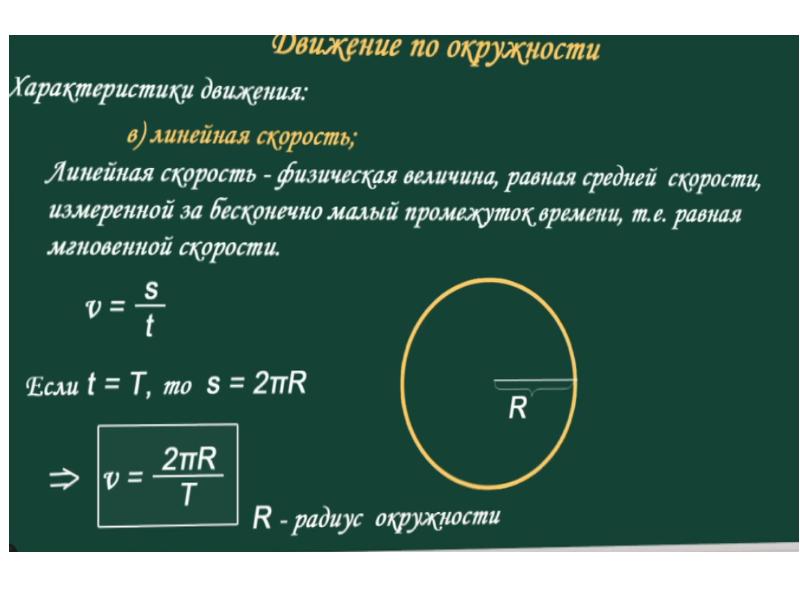
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения.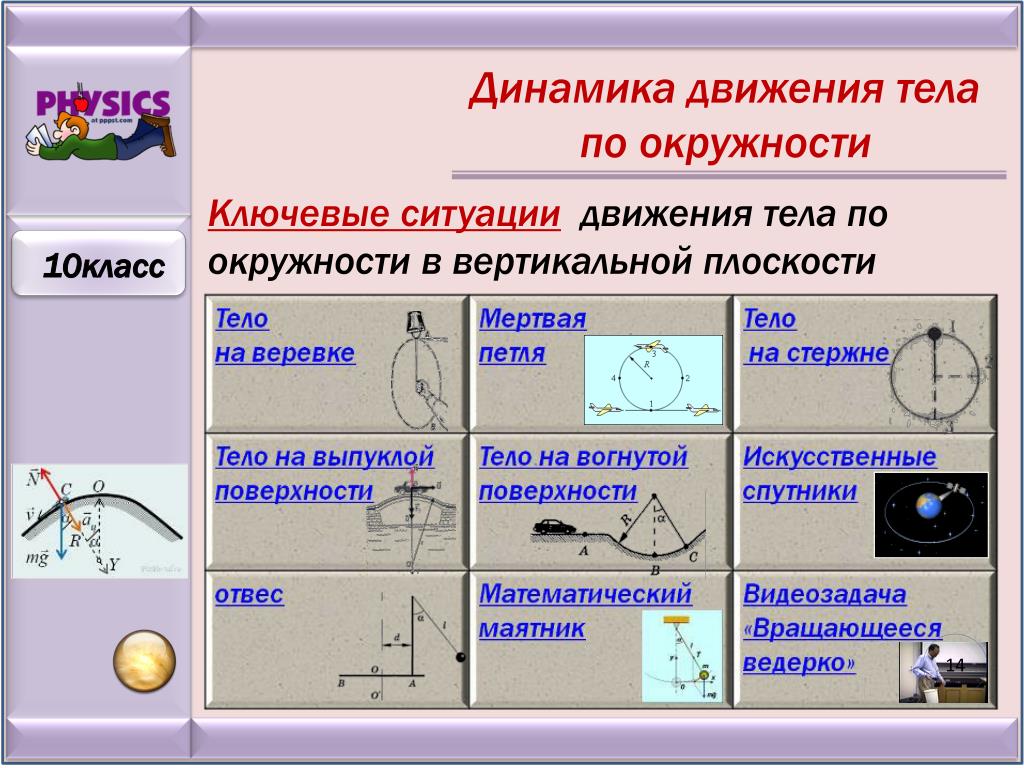 Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна
 Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел
Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел
 Правила Кирхгофа.
Правила Кирхгофа.Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назватьравномерным , оно являетсяравноускоренным .
Угловая скорость
Выберем на окружности точку1 .
Построим радиус. За единицу времени точка переместится в пункт2 . При этом радиус описывает угол. Угловая скорость численно равна углу поворота
радиуса за единицу времени.
При этом радиус описывает угол. Угловая скорость численно равна углу поворота
радиуса за единицу времени.
Период и частота
Период вращенияT — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной.Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть периодT .Путь , который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору
скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных
вращательных движениях: суточном (вокруг своей оси) и
орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца
составляет 1 год или 365 суток. Вокруг своей оси Земля вращается
с запада на восток, период этого вращения составляет 1 сутки или
24 часа. Широтой называется угол между плоскостью экватора и
направлением из центра Земли на точку ее поверхности.
Широтой называется угол между плоскостью экватора и
направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна
Теперь перейдем в неподвижную
систему, связанную с землей. Полное ускорение точки А останется
прежним и по модулю, и по направлению, так как при переходе от
одной инерциальной системы отсчета к другой ускорение не
меняется. С точки зрения неподвижного наблюдателя траектория
точки А — уже не окружность, а более сложная кривая (циклоида),
вдоль которой точка движется неравномерно.
Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности . Это самый простой вид криволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности .
Такое движение совершают точки вращающихся колес, роторов турбин, искуственные спутники, вращающиеся по орбитам и т. д. При равномерном движении по окружности численное значение скорости остается постоянным. Однако направление скорости при таком движении непрерывно изменяется.
Скорость движения тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. В этом можно убедиться, наблюдая за работой точила, имеющего форму диска: прижав к вращающемуся камню конец стального прута можно увидеть отрывающиеся от камня раскаленные частицы. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной к окружности движутся также брызги от колес буксующего автомобиля.
Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной к окружности движутся также брызги от колес буксующего автомобиля.
Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различные направления, тогда как модуль скорости может быть или всюду одинаковым, или изменяться от точки к точке. Но даже если модуль скорости не изменяется, ее все равно нельзя считать постоянной. Ведь скорость — величина векторная, а для векторных величин модуль и направление одинаково важны. Поэтому криволинейное движение всегда ускоренное , даже если модуль скорости постоянен.
При криволинейном движении могут изменяться модуль скорости и ее направление. Криволинейное движение, при котором модуль скорости остается постоянным, называют равномерным криволинейным движением . Ускорение при таком движении связано только с изменением направления вектора скорости.
И модуль, и направление ускорения должны зависеть от формы кривлинейной траектории. Однако нет необходимости рассматривать каждую из ее бесчисленных форм. Представив каждый участок как отдельную окружность с некоторым радиусом, задача нахождения ускорения при криволинейном равномерном движении сведется к отысканию ускорения при равномерном движении тела по окружности.
Однако нет необходимости рассматривать каждую из ее бесчисленных форм. Представив каждый участок как отдельную окружность с некоторым радиусом, задача нахождения ускорения при криволинейном равномерном движении сведется к отысканию ускорения при равномерном движении тела по окружности.
Равномерное движение по окружности характеризуется периодом и частотой обращения.
Время, за которое тело делает один оборот, называют периодом обращения .
При равномерном движении по окружности период обращения определяется делением пройденного пути, т. е. длины окружности на скорость движения:
Величина, обратная периоду, называется частотой обращения , обозначается буквой ν . Число оборотов в единицу времени ν называют частотой обращения :
Из-за непрерывного изменения направления скорости, движущееся по окружности тело имеет ускорение, которое характеризует быстроту изменения ее направления, численное значение скорости в данном случае не меняется.
При равномерном движении тела по окружности ускорение в любой ее точке всегда направлено перпендикулярно скорости движения по радиусу окружности к ее центру и называется центростремительным ускорением .
Чтобы найти его значение, рассмотрим отношение изменения вектора скорости к интервалу времени , за который это изменение произошло. Поскольку угол очень мал, то мы имеем.
12-л. Равномерное движение по окружности
§ 12-л. Равномерное движение по окружности
Завершая изучение основ кинематики, рассмотрим движение, которое является равномерным и ускоренным одновременно, поскольку вектор мгновенной скорости меняется особым образом.
Рассмотрим спутник, равномерно летящий по круговой орбите вокруг Земли: за равные интервалы времени он пролетает равные части пути, поэтому мгновенная скорость спутника сохраняет свой модуль. То есть можно говорить о наличии скорости равномерного движения (см. § 12-д).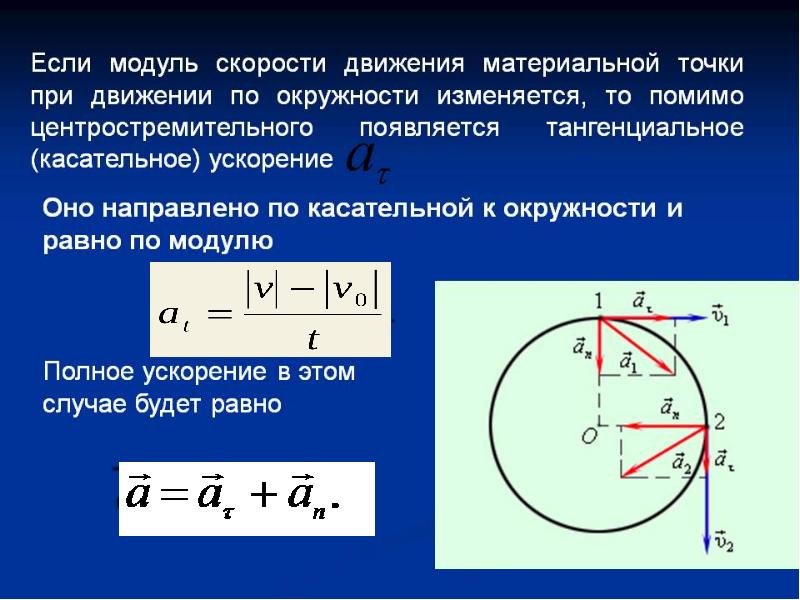 Однако при этом мгновенная скорость непрерывно меняет направление.
Однако при этом мгновенная скорость непрерывно меняет направление.
Найдём, куда направлен вектор изменения мгновенной скорости в двух произвольных точках траектории А и В. Для этого сделаем новый чертёж, обозначив Землю зелёной точкой, а спутник – красной. Выберем вблизи положений спутника А и В пары точек А1, А1 и В1, В2. Изобразим в каждой из них вектор мгновенной скорости спутника (см. чертёж). Пользуясь «правилом треугольника» для нахождения разности двух векторов, построим и обозначим векторы изменения мгновенной скорости (см. правую часть чертежа).
Построение при Δt→0 показывает, что при равномерном движении по окружности вектор изменения мгновенной скорости, оставаясь постоянным по модулю, в любой точке траектории направлен к центру окружности. То есть существует так называемое центростремительное ускорение, сонаправленное с вектором изменения мгновенной скорости и имеющее модуль, который всегда можно вычислить по следующей формуле:
Формула для определения модуля центростремительного ускорения тела, равномерно движущегося по окружности.
| a = | .υ² . | a – модуль центростремительного ускорения, м/с² | |||
| R |
Эта формула выводится из геометрических построений и рассуждений. Они сложны, поэтому мы приводим формулу без вывода. Важно: в отличие от ранее рассмотренных, в этой формуле присутствует не вектор и даже не проекция мгновенной скорости, а её модуль.
В наше время на балконах и крышах домов нередко можно видеть антенны-«тарелки», принимающие спутниковый телевизионный сигнал. Не кажется ли вам удивительным, что спутники, на которые направлены антенны, неподвижно «висят» в небе?
Вспомним: Земля обращается вокруг своей оси за 24 часа. И если спутник будет облетать вокруг нашей планеты с периодичностью 24 часа, то он будет двигаться синхронно с вращением Земли, всё время «пролетая» над одной и той же точкой земной поверхности. Такие спутники и их орбиты называются геостационарными.
Такие спутники и их орбиты называются геостационарными.
Известно: геостационарные орбиты находятся на высоте около 30000 км над поверхностью Земли. Подсчитаем, с какой скоростью летают по ним спутники. Длину орбиты найдём по формуле длины окружности: l = 2πR. Время оборота по орбите 24 часа, а радиус Земли около 6000 км.
| υ = | l | = | 2πR | = | 2 · 3,14 · ( 30000 + 6000 ) км | ≈ 9420 км/ч | |
| Δt | T | 24 ч |
Формула для определения модуля центростремительного ускорения тела, равномерно движущегося по окружности.
В ходе этого рассуждения мы вывели формулу для расчёта модуля скорости тела, равномерно движущегося по окружности: | υ = | 2πR | ||
| T |
Формула для определения модуля центростремительного ускорения тела, равномерно движущегося по окружности.
Тогда модуль центростремительного ускорения тела при его равномерном движении по окружности можно вычислить по формуле: | a = | 4π²R | ||
| T² |
| a = | υ² | = | … | = | 4π²R | = | 4 · 3,14² · ( 30000 + 6000 ) км | ≈ 0,2 м/с² | |
| R | T² | ( 24·60·60 с )² |
Вычисленное значение показывает, что на геостационарной орбите вектор мгновенной скорости спутника, оставаясь постоянным по модулю, ежесекундно меняется на 0,2 м/с по направлению.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxПрезентация «Движение тела по окружности». Презентация по физике на тему «движение тела по окружности» Презентация по физике движение по окружности
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Движение по окружности Учитель физики Федоров Александр Михайлович МОУ Кюкяйская СОШ Сунтарский улус Республика Саха
В окружающей нас жизни мы встречаемся с движением по окружности довольно часто. Так движутся стрелки часов и зубчатые колеса их механизмов; так движутся автомобили по выпуклым мостам и на закругленных участках дорог; по круговым орбитам движутся искусственные спутники Земли.
Мгновенная скорость тела, движущейся по окружности, направлена по касательной к ней в этой точке. Это нетрудно наблюдать.
Это нетрудно наблюдать.
Мы будем изучать движение точки по окружности с постоянной по модулю скоростью. Его называют равномерным движением по окружности. Скорость точки, движущейся по окружности, часто называют линейной скоростью. Если точка движется по окружности равномерно и за время t проходит путь L, равный длине дуги АВ, то линейная скорость (ее модуль) равна V = L/t A B
Равномерное движение по окружности – это движение с ускорением, хотя модуль скорости не меняется. Но направление непрерывно изменяется. Следовательно, в этом случае ускорение а должно характеризовать изменение скорости по направлению. О v a Вектор ускорения а при равномерном движении точки по окружности направлен по радиусу к центру окружности, поэтому его называют центростремительным. Модуль ускорения определяется по формуле: a = v 2 /R, Где v – модуль скорости движения точки, R – радиус окружности.
ПЕРИОД ОБРАЩЕНИЯ Движение тела по окружности часто характеризуют не скоростью движения v, а промежутком времени, за который тело совершает один полный оборот. Эта величина называется периодом обращения. Обозначают ее буквой Т. При расчетах Т выражают в секундах. За время t, равное периоду Т, тело проходит путь, равный длине окружности: L = 2 R. Следовательно, v = L/T=2 R/T. Подставив это выражение в формулу для ускорения получим для него другое выражение: a= v 2 /R = 4 2 R/T 2 .
Эта величина называется периодом обращения. Обозначают ее буквой Т. При расчетах Т выражают в секундах. За время t, равное периоду Т, тело проходит путь, равный длине окружности: L = 2 R. Следовательно, v = L/T=2 R/T. Подставив это выражение в формулу для ускорения получим для него другое выражение: a= v 2 /R = 4 2 R/T 2 .
Частота обращения Движение тела по окружности можно характеризовать еще одной величиной – числом оборотов по окружности в единицу времени. Ее называют частотой обращения и обозначают греческой буквой (ню). Частота обращения и период связаны следующим соотношением: = 1/T Единица частоты – это 1 /c или Гц. Используя понятие частоты, получим формулы для скорости и ускорения: v = 2R/T = 2R; a = 4 2 R/T 2 = 4 2 2 R.
Итак, мы изучили движение по окружности: Равномерное движение по окружности – это движение с ускорением a = v 2 /R . Период обращения — промежуток времени, за который тело совершает один полный оборот. Обозначают ее буквой Т. Частота обращения — число оборотов по окружности в единицу времени. Ее обозначают греческой буквой (ню). Частота обращения и период связаны следующим соотношением: = 1/T Формулы для скорости и ускорения: v = 2R/T = 2R; a = 4 2 R/T 2 = 4 2 2 R.
Ее обозначают греческой буквой (ню). Частота обращения и период связаны следующим соотношением: = 1/T Формулы для скорости и ускорения: v = 2R/T = 2R; a = 4 2 R/T 2 = 4 2 2 R.
СПАСИБО ЗА ВНИМАНИЕ!
По теме: методические разработки, презентации и конспекты
Урок решения задач по теме «Динамика движения по окружности». В процессе решения задач в группах просходит взаимное обучение учащихся….
Урок изучения новой темы с использованием призентации, видеоролики….
Александрова Зинаида Васильевна, учитель физики и информатики
Образовательное учреждение: МБОУ СОШ №5 п. Печенга, Мурманская обл.
Предмет: физика
Класс : 9 класс
Тема урока : Движение тела по окружности с постоянной по модулю скоростью
Цель урока:
дать представление о криволинейном движении, ввести понятия частоты, периода, угловой скорости, центростремительного ускорения и центростремительной силы.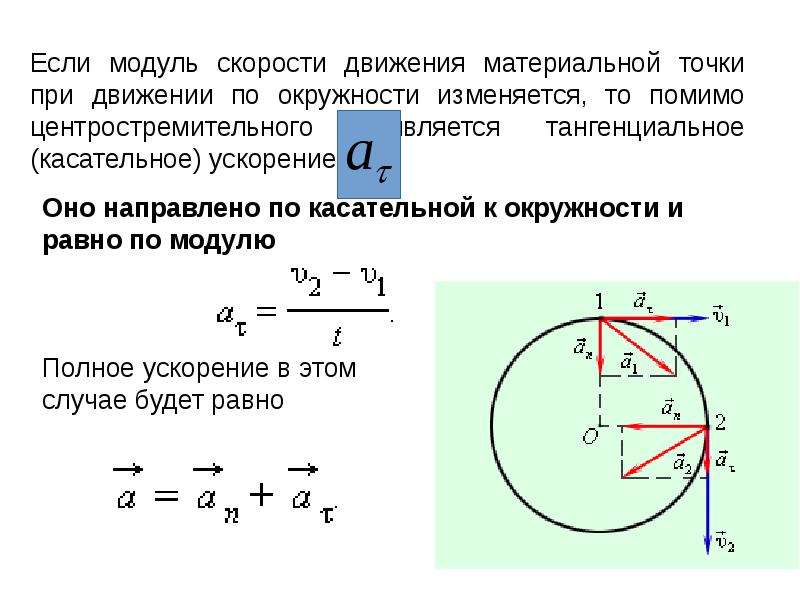
Задачи урока:
Образовательные:
Повторить виды механического движения, познакомить с новыми понятиями: движение по окружности, центростремительное ускорение, период, частота;
Выявить на практике связь периода, частоты и центростремительного ускорения с радиусом обращения;
Использовать учебное лабораторное оборудование для решения практических задач.
Развивающие :
Развивать умения применять теоретические знания для решения конкретных задач;
Развивать культуру логического мышления;
Развивать интерес к предмету; познавательную деятельность при постановке и проведении эксперимента.
Воспитательные :
Формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность;
Воспитывать коммуникативную и информационную культуру учащихся
Оснащение урока:
компьютер, проектор, экран, презентация к уроку « Движение тела по окружности» , распечатка карточек с заданиями;
теннисный шар, волан для бадминтона, игрушечный автомобиль, шарик на нити, штатив;
наборы для эксперимента: секундомер, штатив с муфтой и лапкой, шарик на нити, линейка.
Форма организации обучения: фронтальная, индивидуальная, групповая.
Тип урока: изучение и первичное закрепление знаний.
Учебно-методическое обеспечение: Физика. 9 класс. Учебник. Перышкин А.В., Гутник Е.М. 14-е изд., стер. — М.: Дрофа, 2012 г.
Время реализации урока : 45 минут
1. Редактор, в котором выполнен мультимедиа ресурс: MS PowerPoint
2. Вид мультимедиа ресурса: наглядная презентация учебного материала с использованием триггеров, встроенного видео и интерактивного теста.
План проведения урока
Организационный момент. Мотивация к учебной деятельности.
Актуализация опорных знаний.
Изучение нового материала.
Беседа по вопросам;
Решение задач;
Выполнение исследовательской практической работы.
Подведение итогов урока.
Ход урока
Этапы урока
Временная реализация
Организационный момент. Мотивация к учебной деятельности.
Мотивация к учебной деятельности.
Слайд 1. ( Проверка готовности к уроку, объявление темы и целей урока.)
Учитель. Сегодня на уроке вы узнаете, что такое ускорение при равномерном движении тела по окружности и как его определить.
2 мин
Актуализация опорных знаний.
Слайд 2.
Ф изический диктант:
Изменение положения тела в пространстве с течением времени. (Движение)
Физическая величина, измеряемая в метрах. (Перемещение)
Физическая векторная величина, характеризующая быстроту движения. (Скорость)
Основная единица измерения длины в физике. (Метр)
Физическая величина, единицами измерения которой служат год, сутки, час. (Время)
Физическая векторная величина, которую можно измерить с помощью прибора акселерометра. (Ускорение)
(Ускорение)
Длина траектории . (Путь)
Единицы измерения ускорения (м/с 2 ).
(Проведение диктанта с последующей проверкой, самооценка работ учениками)
5 мин
Изучение нового материала.
Слайд 3.
Учитель. Мы достаточно часто наблюдаем такое движение тела, при котором его траекторией является окружность. По окружности движется, например, точка обода колеса при его вращении, точки вращающихся деталей станков, конец стрелки часов.
Демонстрации опытов 1. Падение теннисного шара, полёт волана для бадминтона, перемещение игрушечного автомобиля, колебания шарика на нити, закреплённого в штативе. Что общего и чем отличаются эти движения по виду? (Ответы учеников)
Учитель. Прямолинейное движение – это движение, траектория которого — прямая линия, криволинейное – кривая. Приведите примеры прямолинейного и криволинейного движения, с которыми вы встречались в жизни. (Ответы учеников)
(Ответы учеников)
Движение тела по окружности является частным случаем криволинейного движения .
Любую кривую можно представить, как сумму дуг окружностей разного (или одинакового) радиуса.
Криволинейным движением называют такое движение, которое совершается по дугам окружностей.
Введём некоторые характеристики криволинейного движения.
Слайд 4. (просмотр видео « скорость.avi» по ссылке на слайде)
Криволинейное движение с постоянной по модулю скоростью. Движение с ускорением, т.к. скорость меняет направление.
Слайд 5 . (просмотр видео «Зависимость центростремительного ускорения от радиуса и скорости. аvi » по ссылке на слайде)
Слайд 6. Направление векторов скорости и ускорения.
(работа с материалами слайда и анализ рисунков, рациональное использование эффектов анимации, заложенных в элементы рисунков, рис 1. )
)
Рис.1.
Слайд 7.
При равномерном движении тела по окружности вектор ускорения всё время перпендикулярен вектору скорости, который направлен по касательной к окружности.
Тело движется по окружности при условии, что вектор линейной скорости перпендикулярен вектору центростремительного ускорения.
Слайд 8. (работа с иллюстрациями и материалами слайда)
Центростремительное ускорение — ускорение, с которым тело движется по окружности с постоянной по модулю скоростью, всегда направлено вдоль радиуса окружности к центру.
a ц =
Слайд 9.
При движении по окружности тело через определённый промежуток времени вернётся в первоначальную точку. Движение по окружности – периодическое.
Период обращения – это промежуток времени Т , в течение которого тело (точка) совершает один оборот по окружности.
Единица измерения периода — секунда
Частота вращения – число полных оборотов в единицу времени.
[ ] = с -1 = Гц
Единица измерения частоты
Сообщение ученика 1. Период — это величина, которая часто встречается в природе, науке и технике. Земля вращается вокруг своей оси, средний период этого вращения составляет 24 часа; полный оборот Земли вокруг Солнца происходит примерно за 365,26 суток; винт вертолёта имеет средний период вращения от 0,15 до 0,3 с; период кровообращения у человека равен примерно 21 — 22 с.
Сообщение ученика 2. Частоту измеряют специальными приборами – тахометрами.
Частота вращения технических устройств: ротор газовой турбины вращается с частотой от 200 до 300 1/с; пуля, вылетевшая из автомата Калашникова, вращается с частотой 3000 1/с.
Слайд 10. Связь периода с частотой:
Если за время t тело совершило N полных оборотов, то период обращения равен:
Период и частота – это взаимообратные величины: частота обратно пропорциональна периоду, а период обратно пропорционален частоте
Слайд 11. Быстроту обращения тела характеризуют угловой скоростью.
Быстроту обращения тела характеризуют угловой скоростью.
Угловая скорость (циклическая частота)- число оборотов за единицу времени, выраженное в радианах.
Угловая скорость – угол поворота, на который поворачивается точка за время t .
Угловая скорость измеряется в рад/с.
Слайд 12. (просмотр видео «Путь и перемещение при криволинейном движении.avi» по ссылке на слайде)
Слайд 13 . Кинематика движения по окружности.
Учитель. При равномерном движении по окружности модуль его скорости не изменяется. Но скорость — векторная величина, и она характеризуется не только числовым значением, но и направлением. При равномерном движении по окружности всё время изменяется направление вектора скорости. Поэтому такое равномерное движение является ускоренным.
Линейная скорость: ;
Линейная и угловая скорости связаны соотношением:
Центростремительное ускорение: ;
Угловая скорость: ;
Слайд 14. (работа с иллюстрациями на слайде)
(работа с иллюстрациями на слайде)
Направление вектора скорости. Линейная (мгновенная скорость) всегда направлена по касательной к траектории, проведенной к той ее точке, где в данный момент находится рассматриваемое физическое тело.
Вектор скорости направлен по касательной к описываемой окружности.
Равномерное движение тела по окружности является движением с ускорением. При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора.
Слайд 15. Центростремительная сила.
Сила, удерживающая вращающееся тело на окружности и направленная к центру вращения, называется центростремительной силой.
Чтобы получить формулу для расчёта величины центростремительной силы, надо воспользоваться вторым законом Ньютона, который применим и к любому криволинейному движению.
Подставляя в формулу значение центростремительного ускорения a ц = , получим формулу центростремительной силы:
F =
Из первой формулы видно, что при одной и той же скорости чем меньше радиус окружности, тем больше центростремительная сила. Так, на поворотах дороги на движущееся тело (поезд, автомобиль, велосипед) должна действовать по направлению к центру закругления тем большая сила, чем круче поворот, т. е. чем меньше радиус закругления.
Так, на поворотах дороги на движущееся тело (поезд, автомобиль, велосипед) должна действовать по направлению к центру закругления тем большая сила, чем круче поворот, т. е. чем меньше радиус закругления.
Центростремительная сила зависит от линейной скорости: с увеличением скорости она увеличивается. Это хорошо известно всем конькобежцам, лыжникам и велосипедистам: чем с большей скоростью движешься, тем труднее сделать поворот. Шофёры очень хорошо знают, как опасно круто поворачивать автомобиль на большой скорости.
Слайд 16.
Сводная таблица физических величин, характеризующих криволинейное движение (анализ зависимостей между величинами и формулами)
Слайды 17, 18, 19. Примеры движение по окружности.
Круговое движение на дорогах. Движение спутников вокруг Земли.
Слайд 20. Аттракционы, карусели.
Сообщение ученика 3. В Средние века каруселями (слово тогда имело мужской род) называли рыцарские турниры. Позднее, в XVIII веке, для подготовки к турнирам, вместо схваток с реальными соперниками, стали использовать вращающуюся платформу, прообраз современной развлекательной карусели, которая тогда же появилась на городских ярмарках.
Позднее, в XVIII веке, для подготовки к турнирам, вместо схваток с реальными соперниками, стали использовать вращающуюся платформу, прообраз современной развлекательной карусели, которая тогда же появилась на городских ярмарках.
В России первый карусель был построен 16 июня 1766 года перед Зимним дворцом. Карусель состоял из четырёх кадрилей: Славянской, Римской, Индийской, Турецкой. Второй раз карусель была построена на том же месте, в том же году 11 июля. Подробное описание этих каруселей приводятся в газете Санкт-Петербургские ведомости 1766 года.
Карусель, распространённая во дворах в советское время. Карусель может приводиться в движение как двигателем (обычно электрическим), так и силами самих крутящихся, которые перед тем как сесть на карусель, раскручивают её. Такие карусели, которые нужно раскручивать самим катающимся, часто устанавливают на детских игровых площадках.
Кроме аттракционов, каруселями часто называют другие механизмы, имеющие сходное поведение — например, в автоматизированных линиях по разливу напитков, упаковке сыпучих веществ или производству печатной продукции.
В переносном смысле каруселью называют череду быстро сменяющихся предметов или событий.
18 мин
Закрепление нового материала. Применение знаний и умений в новой ситуации.
Учитель. Сегодня на этом уроке мы познакомились с описанием криволинейного движения, с новыми понятиями и новыми физическими величинами.
Беседа по вопросам:
Что такое период? Что такое частота? Как связаны между собой эти величины? В каких единицах измеряются? Как их можно определить?
Что такое угловая скорость? В каких единицах она измеряется? Как можно её рассчитать?
Что называют угловой скоростью? Что является единицей угловой скорости?
Как связаны угловая и линейная скорости движения тела?
Как направлено центростремительное ускорение? По какой формуле оно рассчитывается?
Слайд 21.
Задание 1. Заполните таблицу, решив задачи по исходным данным (Рис. 2), затем мы сверим ответы. (Ученики работают самостоятельно с таблицей, необходимо заранее приготовить распечатку таблицы для каждого ученика)
2), затем мы сверим ответы. (Ученики работают самостоятельно с таблицей, необходимо заранее приготовить распечатку таблицы для каждого ученика)
Рис.2
Слайд 22. Задание 2. (устно)
Обратите внимание на анимационные эффекты рисунка. Сравните характеристики равномерного движения синего и красного шара . (Работа с иллюстрацией на слайде).
Слайд 23. Задание 3. (устно)
Колёса представленных видов транспорта за одно и то же время совершают равное количество оборотов. Сравните их центростремительные ускорения. (Работа с материалами слайда)
(Работа в группе, проведение эксперимента, распечатка инструкции для проведения эксперимента есть на каждом столе)
Оборудование: секундомер, линейка, шарик, закреплённый на нити, штатив с муфтой и лапкой.
Цель: исследовать зависимость периода, частоты и ускорения от радиуса вращения .
План работы
Измерьте время t 10 полных оборотов вращательного движения и радиус R вращения, шарика, закреплённого на нити в штативе.
Вычислите период Т и частоту, скорость вращения, центростремительное ускорение Результаты оформите в виде задачи.
Измените радиус вращения (длину нити), повторите опыт ещё 1 раза, стараясь сохранить прежней скорость, прикладывая прежнее усилие.
Сделайте вывод о зависимости периода, частоты и ускорения от радиуса вращения (чем меньше радиус вращения, тем меньше период обращения и больше значение частоты).
Слайды 24 -29.
Фронтальная работа с интерактивным тестом.
Необходимо выбрать один ответ из трёх возможных, если был выбран правильный ответ, то он остаётся на слайде, и начинает мигать зелёный индикатор, неверные ответы исчезают.
Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при уменьшении радиуса окружности в 3 раза?
В центрифуге стиральной машины белье при отжиме движется по окружности с постоянной по модулю скоростью в горизонтальной плоскости. Как при этом направлен вектор его ускорения?
Как при этом направлен вектор его ускорения?
Конькобежец движется со скоростью 10 м/с по окружности радиусом 20 м. Определите его центростремительное ускорение.
Куда направлено ускорение тела при его движении по окружности с постоянной по модулю скоростью?
Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить втрое?
Колесо машины делает 20 оборотов за 10 с. Определите период обращения колеса?
Слайд 30. Решение задач (самостоятельная работа при наличии времени на уроке)
Вариант 1.
С каким периодом должна вращаться карусель радиусом 6,4 м для того, чтобы центростремительное ускорение человека на карусели было равно 10 м/с 2 ?
На арене цирка лошадь скачет с такой скоростью, что за 1 минуту обегает 2 круга. Радиус арены равен 6,5 м. Определите период и частоту вращения, скорость и центростремительное ускорение.
Вариант 2.
Частота обращения карусели 0,05 с -1 . Человек, вращающийся на карусели, находится на расстоянии 4 м от оси вращения. Определите центростремительное ускорение человека, период обращения и угловую скорость карусели.
Точка обода колеса велосипеда совершает один оборот за 2 с. Радиус колеса 35 см. Чему равно центростремительное ускорение точки обода колеса?
18 мин
Подведение итогов урока.
Выставление оценок. Рефлексия.
Слайд 31 .
Д/з: п. 18-19, Упр.18 (2,4).
http :// www . stmary . ws / highschool / physics / home / lab / labGraphic . gif
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
1 2 Равномерное движение по окружности — это такое движение при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности. Равномерное движение по окружности Решение зАдач 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
Равномерное движение по окружности Решение зАдач 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
Период обращения 2 1 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Время одного оборота по окружности называется периодом вращения T N — число оборотов, совершаемых за время t . Единица частоты обращения — 1 оборот в секунду (1 с -1) Частота обращения
3 2 10 1 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Угловая скорость
4 2 10 3 1 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Модуль вектора линейной скорости равен:
5 2 10 3 4 1 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Модуль вектора центростремительного ускорения равен:
6 2 10 3 4 5 1 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Задача. Какова линейная скорость точек на ободе колеса паровой турбины с диаметром колеса 1 м и частотой вращения 300 об/мин? Показать решение
7 2 10 3 4 5 6 1 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Задача. Во сколько раз изменится центростремительное ускорение тела, если оно будет двигаться равномерно по окружности вдвое большего радиуса с той же угловой скоростью? Показать решение
Во сколько раз изменится центростремительное ускорение тела, если оно будет двигаться равномерно по окружности вдвое большего радиуса с той же угловой скоростью? Показать решение
8 2 10 3 4 5 6 7 1 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Задача. Угловая скорость лопастей вентилятора 20π рад/с. Найти число оборотов за 30 мин. Показать решение
1 Вариант 2 Вариант 1. Угловая скорость лопастей вентилятора 20π рад/с. Найти число оборотов за 30 мин. 2 . Частота вращения воздушного винта самолета 1500 об/мин. Сколько оборотов сделает винт на пути 90 км при скорости полета 180 км/ч 2 . Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его колеса, если их радиус 50 см? 1 . На повороте вагон трамвая движется с постоянной по модулю скоростью 5 м/с. Чему равно его центростремительное ускорение, если радиус закругления пути 50 м. 9 2 10 3 4 5 6 7 8 1 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
ОТВЕТЫ 1 Вариант 2 Вариант 1 . 18000. 2 . 45000 2 . 5,31 1 . 0,5 м/с 2 . 1 2 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
0,5 м/с 2 . 1 2 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
1 2 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Показать решение
По теме: методические разработки, презентации и конспекты
Урок решения задач по теме «Динамика движения по окружности». В процессе решения задач в группах просходит взаимное обучение учащихся….
Урок изучения новой темы с использованием призентации, видеоролики….
Работа предназначена для учащихся 10 класса, представлена в двух вариантах. Задания на знания определений, графические задачи и задания на соответствия….
Слайд 2
В механике примеры учат не меньше, чем правила. И. Ньютон
Слайд 3
Загадки страшные природыПовсюду в воздухе висят.Н. Заболоцкий (из поэмы «Безумный волк»)
Слайд 4
А4. Тело движется по окружности по часовой стрелке. Какой из изображенных векторов совпадает по направлению с вектором скорости тела в точке А?
1) 1; 2) 2; 3) 3; 4) 4.
Слайд 5
Слайд 6
Движение тела по окружности с постоянной по модулю скоростью. Тема урока:
Слайд 7
Цели:Повторить особенности криволинейного движения,рассмотреть особенности движения по окружности,познакомиться с понятием центростремительного ускорения и центростремительной силы, периодом и частотой вращения,выяснить связь между величинами.
Слайд 8
Слайд 9
Слайд 10
Слайд 11
Вывод стр. 70
Слайд 12
При равномерном движении по окружности модуль его скорости не изменяется.Но скорость — векторная величина, и она характеризуется не только числовым значением, но и направлением. При равномерном движении по окружности всё время изменяется направление вектора скорости. Поэтому такое равномерное движение является ускоренным.
Слайд 13
Слайд 14
Слайд 15
При равномерном движении тела по окружности вектор ускорения всё время перпендикулярен вектору скорости, который направлен по касательной к окружности.
Слайд 16
Вывод стр. 72
Слайд 17
Слайд 18
Период вращения – время одного оборота по окружности. Частота вращения – число оборотов в единицу времени.
Слайд 19
Кинематика движения по окружности
Модуль скорости не изменяется Модуль скорости изменяется линейная скорость угловая скорость ускорение
Слайд 20
Ответ: 1 1 2
Слайд 21
д/з§ 19 Упр. 18 (1,2) И тут в мой разум грянул блеск с высот, Неся свершенье всех его усилий. А. Данте
Слайд 22
Вариант 1 Вариант 2
Тело движется равномерно по окружности в направлении
по часовой стрелки против часовой стрелки
Как направлен вектор ускорения
при таком движении?
а) 1 ; б) 2 ; в) 3 ; г) 4 .
2. Автомобиль движется с постоянной по модулю скоростью по траектории
рисунка. В какой из указанных точек траектории центростремительное
ускорение
минимально максимально?
3. Во сколько раз изменится центростремительное ускорение, если скорость
материальной точки
увеличить уменьшить
в 3 раза?
а) увеличится в 9 раз; б) уменьшится в 9 раз;
в) увеличится в 3 раза; г) уменьшится в 3 раза.
Слайд 23
Вариант 1 4. Движение материальной точки называется криволинейным, если а) траектория движения окружность; б) её траектория – кривая линия; в) её траектория – прямая линия. 5. Тело массой 1 кг движется с постоянной скоростью 2 м/с по окружности радиусом 1 м. Определить центробежную силу, действующую на тело. Вариант 2 4. Движение тела называется криволинейным, если а) все его точки движутся по кривым линиям; б) некоторые его точки движутся по кривым линиям; в) хотя бы одна его точка двигается по кривой линии. 5. Тело массой 2 кг движется с постоянной скоростью 2 м/с по окружности радиусом 1 м. Определить центробежную силу, действующую на тело.
Слайд 24
Литература Учебники «Физика –9» А.В. Перышкин, М.М. Балашов, Н.М. Шахмаев, Законы физики Б.Н. Иванов Задания ЕГЭ Поурочные разработки по физике В.А. Волков Мультимедийное учебное пособие нового образца (физика, основная школа 7-9 кл. часть 2)
Посмотреть все слайды
Кинематика — что это такое? Что изучает?
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю. |
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость → → → → t — время [с] |
Средняя путевая скорость V ср.путевая = S/t V ср. S — путь [м] t — время [с] |
В чем разница между перемещением и путем? Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории. |
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.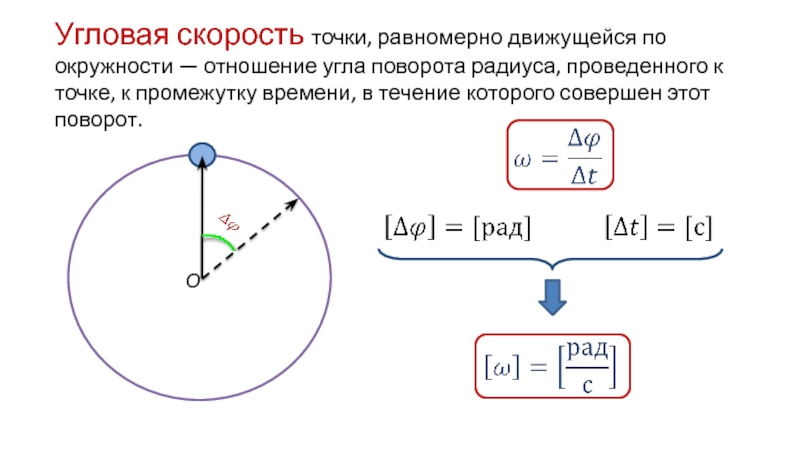 путевая = 210/2,5 = 84 км/ч
путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения x(t) = x0 + vxt x(t) — искомая координата [м] x0 — начальная координата [м] vx — скорость тела в данный момент времени [м/с] t — момент времени [с] |
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси x(t) = x0 — vxt x(t) — искомая координата [м] x0 — начальная координата [м] vx — скорость тела в данный момент времени [м/с] t — момент времени [с] |
Графики
Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
В видео ниже я рассказываю, как строить графики кинематических величин и зачем они нужны.
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. 2.
2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела, когда тело движется вокруг некоторой точки. Очень важно разделить движение по окружности и вращение тела.
При вращательном движении тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.
Ось вращения может располагаться внутри тела и за его пределами.
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с дугами.
При движении по окружности тело двигается вокруг одной точки, а при вращении — все точки тела движутся вокруг оси вращения.
В видеролике ниже рассказано про ускорение при криволинейном движении. Оно складывается из двух составляющих — нормальной и тангенциальной. При равномерном движении по окружности тангенциальная составляющая отсутствует, остается нормальная, которую мы в данном случае называем центростремительной.
Центростремительное ускорение
При движении по окружности модуль скорости постоянен, а вот направление скорости постоянно меняется. {2}}{r}\)
{2}}{r}\)
aц.с. = ω2r – связь центростремительного ускорения с угловой скоростью
Рис. 1. ГДЗ конспекты по физике 9 класс Задание: Движение тела по окружности с постоянной по модулю скоростью
Равномерное круговое движение
Равномерное круговое движениеРавномерное круговое движение
Обзор:
Объект, движущийся по окружности радиусом r
с постоянной скоростью v ускоряется. То
направление вектора его скорости все время меняется, но величина
вектор скорости остается постоянным. Вектор ускорения не может иметь
компонента в направлении вектора скорости, так как такая компонента
вызвать изменение скорости.Поэтому вектор ускорения должен быть
перпендикулярно вектору скорости в любой точке окружности. Этот
ускорение называется радиальным ускорением
или центростремительное ускорение, и оно указывает
к центру круга. Величина центростремительной
вектор ускорения равен a c = v 2 /r.
Какова сила при различных обстоятельствах?
Решим несколько задач, исследуя этот вопрос.
Проблема:
Груз массой 3 кг, прикрепленный к легкой нити, вращается по горизонтальной поверхности без трения. Таблица. Радиус окружности равен 0,8 м, а струна может выдержать массу 25 кг до разрыва. Какой диапазон скоростей может иметь масса перед струной перерывы?
Решение:
- Обоснование:
Масса, прикрепленная к нити, вращается по горизонтали, стол без трения.
Предположим, что масса вращается с постоянной скоростью. это ускорение. Направление ускорения в сторону центр круга, а его величина v 2 /r. В струне есть напряжение. Нить натягивает массу с силой F, направленной к центру окружности. Этот сила F отвечает за центростремительное ускорение, F = mv 2 /r.
Струна может выдержать массу 25 кг до разрыва, т.е.е. мы может позволить массе до 25 кг висеть на веревке рядом с поверхность земли. Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н.
Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н.
Учитывая F max = 245 Н и F = mv 2 /r, мы можем найти v max . - Детали расчета:
v макс. 2 = F макс. об/мин = (250 Н)(0,8 м)/(3кг). v max = 8,1 м/с.
Проблема:
Монета, помещенная на расстоянии 30 см от центра вращающегося горизонтального поворотного стола
когда его скорость 50 см/с.
а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижна?
относительно поворотного стола?
б) Каков коэффициент статического трения между монетой и поворотным столом?
Решение:
- Обоснование:
Когда монета покоится относительно вращающегося поворотного стола, сила статическое трение между монетой и поворотным столом обеспечивает центростремительное ускорение.
Сила трения покоя имеет максимальное значение f с = μ с Н = μ с мг.
Настройка μ с мг = mv 2 /r, мы можем решить для μ s . - Детали расчета:
(a) Сила трения покоя между монетой и поворотным столом обеспечивает центростремительное ускорение.
(b) Величина максимального сила трения покоя равна f с = μ с Н.Этот максимальная сила трения покоя равна mv 2 /r при v = 0,5 м/с. Имеем µ с N = µ с mg = mv 2 /r,
или мк с = v 2 /(rg) = (0,5 м/с) 2 /(0,3 м 9,8 м/с 2 ) = 0,085.
Проблема:
Рассмотрим конический маятник с грузом массой 80 кг на проволоке длиной 10 м, образующей угол.
θ = 5 o с вертикалью. Определить
(а) горизонтальная и вертикальная составляющая силы, действующей со стороны проволоки на
маятник и
(b) центростремительное ускорение боба.
Решение:
- Обоснование:
Диаграмма свободного тела боба показана справа.
Боб не меняет своего вертикального положения, y = константа, v y = a y = 0. Вертикальный компонент T должен иметь величина мг.
Горизонтальная составляющая Т обеспечивает центростремительное (радиальное) ускорение а р . - Детали расчета:
(a) Вертикальный компонент T должен иметь величина мг.
Tcos(5 o ) = мг, T = (80 кг 9,8 м/с 2 )/cos(5 o ) = 787 N
Величина горизонтальной составляющей T равна Tsin(5 o ) = 68,6 Н. Горизонтальная составляющая силы направлена к центру круг.(b) Tsin(5 o ) = ma r , a r = (68,6 Н)/(80 кг) = 0,857 м/с 2 .
Скорость боба находится из a r = v 2 /r, v = (a r r) ½ .
Поскольку r = (10 м)*sin(5 o ), мы имеем v = 0,86 м/с.
Проблема:
Автомобиль массой 1800 кг преодолевает неровность на дороге, идущей по дуге окружности. радиусом 42 м.
радиусом 42 м.
а) С какой силой дорога действует на автомобиль при прохождении автомобиля?
наивысшая точка горки, если автомобиль движется со скоростью 16 м/с?
б) С какой максимальной скоростью может двигаться автомобиль, проезжая через этот горб?
потеря связи с дорогой?
Решение:
- Обоснование:
Показана схема свободного кузова автомобиля.Единственными силами, действующими на автомобиль, движущийся с постоянной скоростью, являются сила тяжести и нормальная сила, действующая на дорогу. Если эти силы равны по величине, автомобиль не разгоняется. Если автомобиль движется по дуга окружности, то она ускоряется. Ускорение равно r = v 2 /р. Следовательно, гравитационная сила должна иметь большую величины, чем нормальная сила.
- Детали расчета:
Нам нужно
мг — n = mv 2 /r, или n = m(g — v 2 /r).
n = (1800 кг)(9,8 м/с 2 — (16 м/с) 2 /(42 m)) = 6669 N(b) Автомобиль теряет контакт с дорогой, когда n становится равным нулю.
 Затем
дорога больше не поддерживает машину. Это происходит, когда g — v 2 /r
= 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3
РС.
Затем
дорога больше не поддерживает машину. Это происходит, когда g — v 2 /r
= 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3
РС.
Модуль 5: Вопрос 1
Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете кривую, которая идеально накрен для скорости вашего автомобиля? Как направлена сила, приложенная на вас возле автокресла?
Обсудите это со своими однокурсниками на форуме!
Гравитация
Массивные объекты обладают инерцией.Требуется сила, чтобы изменить их состояние движение. Все массивные объекты взаимодействуют через силу гравитации . Частица массой m 1 действует с силой F 12 на частицу массой m 2 . Закон тяготения Ньютона дает эту силу как
F 12 = (-G м 1 м 2 /r 12 2 )
( р 12 / р 12 ).
Здесь r 12 — расстояние между частицами 1
и 2, и ( r 12 / r 12 )
Единичный вектор , указывающий от частицы 1 к частице
2.
G — гравитационная постоянная, G = 6,67*10 -11 Нм 2 /кг 2 .
Сила F 21 , действующая на частицу массой m 2 действует на частицу массой m 1 , равно — F 12 , по третьему закону Ньютона. Сила тяжести всегда привлекательный.
Точка в объекте, от которой расстояние r 12 равно измеряется его центр масс.Масса m 1 тянет массу m 2 , и масса m 2 тянет на массу m 1 . Центр масса каждого тела притягивается к центру масс другого объект.
Взвешивание земли
Радиус Земли R = 6368 км. Если вы подниметесь на гору высотой 1000 м,
ваше расстояние от центра земли изменится на (1/6368) * 100 % = 0,016 %
а величина гравитационной силы, действующей на вас, изменится на (1/6368) 2 *100
% = 2. 4*10 -6 %. Для всех объектов вблизи поверхности земли
расстояние от центра почти постоянно, а величина
Поэтому вектор гравитационной силы приблизительно постоянен. За малым
расстояния, когда кривизной земной поверхности можно пренебречь,
направление вектора гравитационной силы также почти постоянно. Это указывает
прямо вниз к центру земли.
4*10 -6 %. Для всех объектов вблизи поверхности земли
расстояние от центра почти постоянно, а величина
Поэтому вектор гравитационной силы приблизительно постоянен. За малым
расстояния, когда кривизной земной поверхности можно пренебречь,
направление вектора гравитационной силы также почти постоянно. Это указывает
прямо вниз к центру земли.
Сила тяжести, действующая на тело массой m на поверхности земли, равна
величина F = мг.Используя закон всемирного тяготения Ньютона, мы пишем GMm/R 2 =
мг, где М — масса Земли. Таким образом, мы имеем M = gR 2 /G.
Используя R = 6,4*10 6 м, находим M = (9,8 м/с 2 )(6,4*10 6 м) 2 /(6,67*10 -11 Н·м 2 /кг 2 ) =
6*10 24 кг.
Орбитальный
Гравитационное притяжение между объектом и землей притягивает объект
к центру земли.Когда объект вращается вокруг Земли,
направление силы тяжести на объекте постоянно меняется. То
радиус Земли настолько велик, что Земля кажется в некоторых местах плоской
наблюдатель, стоящий на поверхности. Когда проблема касается только расстояний, которые
намного меньше радиуса Земли, мы часто пренебрегаем кривизной
земной поверхности и предположим, что сила гравитации направлена в одну и ту же
направление вниз везде.
То
радиус Земли настолько велик, что Земля кажется в некоторых местах плоской
наблюдатель, стоящий на поверхности. Когда проблема касается только расстояний, которые
намного меньше радиуса Земли, мы часто пренебрегаем кривизной
земной поверхности и предположим, что сила гравитации направлена в одну и ту же
направление вниз везде.
Ссылка: Спутник как снаряд
Предположим, что вблизи поверхности земли в
x-направление, как показано на рисунке выше.Первоначально он ускоряется только в
Y-направление. Но по мере движения объекта направление ускорения
изменения. Если начальная скорость объектов достаточно высока, мы должны принять
изменение направления силы учитывать при расчете объектов
траектория. Объект на круговой орбите вокруг Земли находится
постоянно падает к центру земли. Это постоянно
ускорение. Но пока он движется по криволинейной траектории, поверхность
Земля изгибается в сторону от объекта так, что расстояние между Землей и
объект остается постоянным.
Сила тяжести всегда направлена к центру объекта. круговой орбите и отвечает за центростремительное ускорение объект.
F = mv 2 /r
Для объекта вблизи поверхности земли F = mg и r = 6,4*10 6 м. Скорость орбитального объекта находится из mg = mv 2 /r, v 2 = gr = (9,8 м/с 2 )(6,4*10 6 м).Имеем v = 7919 м/с, или примерно 8000 м/с. Требуется объект t = 2πr/v = (6,28*6,4*10 6 м)/(7919 м/с) = 5075 с = 84 мин, чтобы совершить полный оборот по орбите.
Если тот же объект двигался по круговой орбите с большим радиусом, сила
силы тяжести на объекте будет меньше. Поскольку мы удваиваем расстояние от
центра земли сила тяжести уменьшается в 1/4 раза. То
центростремительное ускорение v 2 /r уменьшается в 1/4 раза.Этот
означает, что v 2 должно уменьшиться в 1/2 раза. Имеем v = 5600 м/с
а для совершения оборота по орбите требуется 14355 с = 240 мин.
Объектов на геосинхронных орбитах совершить полный оборот за 24 часа или 86400 с. Следовательно, их скорость равна v = 2πr/(86400 с). Запись GMm/r 2 = mv 2 /r = m(2πr/(86400 с)) 2 /r, или r 3 = GM(86400s) 2 /(4π). мы можем решить это уравнение для радиуса геосинхронной орбиты.С М = 6*10 24 кг имеем r=42260 км. Геосинхронный спутник вращается вокруг 42260 км — 6400 км = 35860 км над поверхностью земли. Радиус его орбиты в 6,6 раза больше радиуса Земли.
Луна совершает один оборот вокруг Земли за 27,3 дня. Мы можем найти расстояние до Луну таким же образом мы нашли расстояние до геосинхронного спутника. Расстояние от Земли до Луны 384400 км.
Проблема:
Когда падающий метеор находится на расстоянии над земной поверхностью в 3 раза больше Радиус Земли, каково ускорение ее свободного падения под действием силы тяжести приложенная к нему сила?
Решение:
- Обоснование:
Сила, действующая на метеор, равна F = ma = GMm/r 2 . Следовательно, a = GM/r 2 .
Следовательно, a = GM/r 2 . - Детали расчета:
a = GM/r 2 , a = (6,67*10 -11 Нм 2 /кг 2 )*(6*10 24 кг)/(4*6,4*10 6 м) 2 = 0,61 м/с 2 .
(Метеор находится на 3 земных радиуса над земной поверхностью, значит, это 4 земных радиуса от его центра.)
Для получения дополнительной информации о равномерном круговом движении изучите это материал из «Кабинета физики».
Ссылка: Движение Характеристики кругового движения
- Скорость и скорость
- Ускорение
- Требование к центростремительной силе
- Запретное F-слово
- Математика кругового движения
Ссылка: Применение кругового движения
- Второй закон Ньютона — Новый взгляд на
- Парк развлечений Физика
- Легкая атлетика
Центростремительное и центробежное ускорение и сила
Центробежная и центробежная сила представляют собой пару сил действия и противодействия, связанную с круговым движением.
Центростремительное ускорение
Скорость — это вектор, указывающий, насколько быстро (или медленно) преодолевается расстояние и направление движения. Так как вектор скорости (направление) тела изменяется при движении по окружности — возникает ускорение.
Это ускорение называется центрипетальным ускорением — и может быть выражена как
A C = V 2 / R
= Ω 2 R 2 R
= (2 π N RPS ) 2 R
= (2 π N RPM /60) 2 R
= = 7 (π N RPM /30) 2 R (1)
, где
A C = Центрипентное ускорение (м / с 2 , Ft / S 2 )
V = Тангенская скорость (м / s, ft / s)
R = круговой радиус (м, футов)
ω = угловая скорость (RAD / S)
N RPS = Революции в секунду (Rev / S, 1 / S)
RPM = Революции на мин (REV / MIN, 1 / MIN)
Центрипетальная сила
Согласно второму времени Ньютона Закон Центрипетальная сила может быть выражена как
= MA C = MA C
= MV 2 / R
= M Ω 2 R
= M (2 Π N S ) 2 R
= M (2 π N RPM /60) 2 R
= M (π N RPM /30) 2 R (2)
, где
F
C = центрипетальная сила (N, LB F )м = масса (кг, слизни )
по третьему закону Ньютона центростремительная сила, действующая на объект, имеет центробежную силу той же величины, действующую в противоположном направлении.
Пример — центростремительное ускорение и сила, действующая на автомобиль по кривой
Метрические единицы
Автомобиль массой 1000 кг движется по кривой радиусом 200 м со скоростью 50467 50472 . Центростремительное ускорение можно рассчитать как
a c = ((50 км/ч) (1000 м/км) (1/3600 ч/с)) 2 / (200 м)
= 0,965 м/с 2
= 0.1 г
, где
1 г = ускорение гравитации (9,81 м / с 2 )
Центрипетальная сила может быть рассчитана как
F C = (1000 кг) ( 0,965 м / с 2 )
= 965 N
= 965 N= 0,97 kn
, связанные с Гравитационной силой — Вес:
F G = (1000 кг) ( 9,81 м/с 2 )
= 9810 Н
= 9. 8 кН
8 кН
Британские единицы
Автомобиль с весом (силой тяжести) 3000 фунтов движется по кривой радиусом 100 футов со скоростью 15 миль/ч .
Масса автомобиля может быть рассчитана как
м = (3000 фунтов) / (32 Ft / S 2 )
= 94 = 94 Slugs Центрипентное ускорение можно рассчитать как a c = ((15 миль/ч)(5280 футов/милю) / (3600 с/ч)) 2 / (100 футов) = 4.84 FT / S 2 Центрипетальная сила может рассчитываться как F C = (94 слизни) (4,84 футов / с 2 ) = 455 фунтов — Этот калькулятор можно использовать, если известна скорость объекта — например, автомобиля на повороте. Уравнение (2) можно изменить, чтобы выразить центростремительную или центробежную силу как функцию числа оборотов в минуту — об/мин — как
Центростремительный (центробежный) калькулятор — скорость
Центростремительная (центробежная) сила — об/мин
9007 0.
 01097 MRN RPM 2 (3)
01097 MRN RPM 2 (3)
, где
N N RPM = Revolution в минуту (RPM)
Centripetal (центробежный) Калькулятор — RPM
Этот калькулятор можно использовать, если известна скорость вращения предмета — как токарная чаша на токарном станке.
Центробежная сила
Сила — это абстракция, представляющая взаимодействие притяжения и выталкивания между объектами.Третий закон Ньютона гласит, что
- для каждой действующей силы существует равная и противоположно направленная сила противодействия
Следовательно, должна существовать равная и противоположно направленная сила противодействия центростремительной силе — Центробежная сила.
Что такое тангенциальная скорость? — Определение и формула — Видео и стенограмма урока
Уравнение
Согласно уравнению, тангенциальная скорость равна расстоянию 2π r , деленному на время T . Таким образом,
Таким образом,
Точка на окружности перемещается на расстояние 2π r за время T .
Другие формы уравнений
Мы можем расширить наше уравнение, взглянув на несколько идей. Эти понятия включают угловую скорость ω и частоту ф.
- угловая скорость , ω, является скоростью вращения. Он измеряет количество радиан (или градусов) в секунду. Обратите внимание, другие названия угловой скорости включают угловую частоту и круговую частоту.
- Другой мерой вращения в секунду является частота , f . Однако есть важное отличие. Частота — это количество циклов в секунду. Цикл относится к одному полному обороту, когда мы вернулись в исходную точку.
Например, если мы делаем 2 полных оборота за 1 секунду, частота составляет 2 цикла в секунду.
Как связаны ω и f ?
- Угловая частота в 2π раз больше частоты.

ω обычно выражается в радианах в секунду. Каждый раз, когда мы совершаем 2π радиан вращения, мы совершаем один полный оборот по окружности. Таким образом, ω, деленное на 2π, представляет собой количество циклов в секунду. Количество циклов в секунду — это частота. Таким образом, ω/(2π) = f и ω = 2π f.
Частота, f, и период, T, также связаны между собой.
- Частота и период обратны друг другу.
Продолжая наш пример, если мы делаем 2 оборота за 1 секунду, то время, чтобы сделать один полный оборот, составляет 1/2 секунды. Период равен 1/2 секунды, а частота равна 2 циклам в секунду. (Обратите внимание, что мы обычно используем герц для единиц цикла в секунду.) Таким образом, T и f обратны друг другу. В виде уравнений
и
Теперь мы готовы разработать другую форму уравнения тангенциальной скорости.
Учитывайте следующее:
В первой строке мы начинаем с нашего более раннего уравнения для тангенциальной скорости с расстоянием (2π r ) в зависимости от времени для одного полного оборота ( T ). Тогда мы записываем деление на T как умножение на 1/ T .
Во второй строке 1/ T заменяется на частоту f.
Далее,
В первой строке мы переставляем 2π r f в 2π f r.
Во второй строке заменяем 2π f на ω.
Таким образом, тангенциальная скорость имеет другую форму: v = ω r.
Пример. Объект вращается с угловой скоростью ω, равной 30 рад/сек, вокруг точки на расстоянии 2 метров. Какова тангенциальная скорость объекта ?
- Используйте уравнение v = ω r .
- Подставьте 30 радиан/сек вместо ω и 2 метра вместо r .

- Упростить.
Краткое содержание урока
Давайте быстро повторим! Для тангенциальной скорости мы описываем движение вдоль края окружности, и направление в любой заданной точке окружности всегда вдоль касательной. Как уравнение , тангенциальная скорость равна:
расстояние, 2π r , деленное на время, T .
Чтобы понять это уравнение и успешно его рассчитать, нам нужно усвоить понятия угловой скорости, омеги и частоты f .2)/р
Силы и движение
Доказательство F = mv²/R
Учебное руководство за 14-16
Метод А
Это следует непосредственно из эксперимента
Зарисовка орбиты спутника и предсказание ее периода
Математика непосредственно следует из наброска, полученного в ходе этого эксперимента и воспроизведенного ниже. Это метод Ньютона.
Это метод Ньютона.
Он в значительной степени опирается на теорему о скрещенных хордах для окружности, которую следует дать.
Окружность представляет собой орбиту спутника радиусом R , движущегося со скоростью v . Спутник перемещается из точки А в точку В за время t . Без силы спутник двигался бы к K с постоянной скоростью.
Теперь «включим» гравитацию, и спутник упадет на расстояние ч за то же время от касательной из точки А в точку В.Неважно, позволите ли вы ему сначала упасть из точки А, а затем продолжите движение в тангенциальном направлении или наоборот. Всем, кто возражает, что падение от К до В происходит не по радиусу, следует еще раз взглянуть на их масштабную диаграмму: почти невозможно увидеть разницу между h и радиальным падением. [Возможно, вам придется говорить о в пределе
.]
Из свойства скрещенных хорд ч (2R- ч ) = x 2
но 2 R >> H Поэтому 2v = x 2 и так h = x 2 2 R (уравнение 1)
теперь x = AK, что почти равно arcAB = v t (уравнение 2)
Объединение 1 и 2, h = ( v t ) 2 2 R (уравнение 3)
h — вертикальное падение, поэтому используя s = ½ a t 2 = h (уравнение 4)
Затем из (уравнение 3) и (уравнение 4)
½ a t 2 = ( v t ) 2 2 R
ведет к a = v 2 R
Использование F = м a затем F = м v 2 R
То же верно для движения во всех местах по кругу. Под вертикалью всегда понимают направление от спутника к центру притягивающего тела.
Под вертикалью всегда понимают направление от спутника к центру притягивающего тела.
Метод Б
Этот метод основан на понимании векторов.
Окружность представляет собой орбиту спутника радиусом R , движущегося со скоростью v . Спутник перемещается из точки А в точку В за время t .
Нарисуйте вектор AP для представления начальной скорости спутника в точке A, которая проходит по касательной в точке A.Нарисуйте второй вектор той же длины, BQ, чтобы представить более позднюю скорость в B.
Перерисовать начальный и последующие векторы, начиная с одной и той же точки D. Оба имеют модуль, равный v . FG, представляющий изменение скорости, должен быть добавлен к старой скорости, чтобы получить новую скорость.
AOB и FDG — подобные треугольники.
изменение скорости v = AB R
ускорение = изменение скорости от A до B = AB x v R x время от A до B = v 2 R
Использование F = м a затем F = м v 2 R
Уравнение F = m v 2 R иллюстрирует эти соотношения:
- чем выше скорость v , тем больше сила, необходимая для удержания объектов на орбите, а значит, тем больше центральное ускорение
- для той же скорости, чем меньше радиус или чем круче кривая, тем больше сила и, следовательно, тем больше должно быть ускорение.

Ускорение увеличивается с увеличением орбитальной скорости, v , но уменьшается с увеличением радиуса, R .
Круговое движение (и прочее)
Второй закон Ньютона
применяется к
Вертикальный круг
Какие силы вступают в игру, когда пилот-пилот переворачивает бочку?
Или, если на то пошло, какие силы вступают в игру, когда вы или я едем на одном из сегодняшние американские горки с холмами, долинами и петлями?
Пожалуйста, сделайте , а не попытку запомнить — и держитесь прямо — уравнения сил, которые мы выведем для различных ситуаций.
Скорее, составьте четкую диаграмму и затем примените F net = m > a c где a c это центростремительное ускорение поэтому оно
— и чистая сила или центростремительная сила — указывает на
центр круга. Вот и все!>
Вот и все!>
Всегда хорошо рисовать, детализировать «свободное тело» диаграммы»! То есть всегда важно а сейчас это особенно важно. Никогда начните с подстановки чисел в уравнения и вычисления ответа. Всегда начните со схемы!
На вершине холма
Единственными силами, действующими на всадника, являются направленные вверх нормальная сила n , действующая на автомобиль, и направленная вниз сила тяжести w , вес всадника. Они складываются вместе, как векторы, чтобы обеспечить чистая сила F чистая где есть центростремительная сила F c , направлен к центру круга. нормальная сила может также называется «кажущимся весом» всадника, поскольку это сила сиденье на гонщика, а также описывает, что «чувствует» гонщик (вдобавок к террору!).
F нетто = w — n = мг — nF нетто = F c = m v 2 / р
мг — n = m v 2 / r
n = мг — m v 2 / r
Что все это значит? Нормальная сила или сила всадника
кажущийся вес на меньше, чем реальный вес всадника на . Сиденье может
не оказывать негативного воздействия на всадника. Если мы подойдем к ситуации, когда
кажущийся вес может стать отрицательным, должна быть хорошая защита Система — ремни безопасности, поясные дуги, плечевые ограничители или что-то в этом роде.
Сортировать.
Сиденье может
не оказывать негативного воздействия на всадника. Если мы подойдем к ситуации, когда
кажущийся вес может стать отрицательным, должна быть хорошая защита Система — ремни безопасности, поясные дуги, плечевые ограничители или что-то в этом роде.
Сортировать.
Мы могли бы спросить, как быстро каботажное судно может двигаться до тех пор, пока всадник просто (едва) теряет контакт с сиденьем. значит нормальная сила между сиденьем и всадником ноль . Это происходит для
n = мг — m v 2 / r = 0м v 2 / r = мг
v 2 / г = г
v 2 = г р
Мы описали это с помощью диаграммы, показывающей гостя на вершине горка американских горок.Те же идеи применимы, конечно, и к пилот правой стороной вверх на вершине «бочки», как показано здесь.
Дно долины
Единственными силами, действующими на всадника, являются направленные вверх
нормальная сила n , действующая на автомобиль, и направленная вниз сила тяжести w , вес всадника. Они складываются вместе, как векторы, чтобы обеспечить
чистая сила F чистая где есть центростремительная сила F c ,
направлен к центру круга.Заметьте, конечно, что
центр круга теперь на выше от всадника. Как всегда нормальный
сила также может быть названа «кажущимся весом» всадника, поскольку это
сила сиденья на гонщика, а также описывает, что гонщик «чувствует»
(помимо террора!).
Они складываются вместе, как векторы, чтобы обеспечить
чистая сила F чистая где есть центростремительная сила F c ,
направлен к центру круга.Заметьте, конечно, что
центр круга теперь на выше от всадника. Как всегда нормальный
сила также может быть названа «кажущимся весом» всадника, поскольку это
сила сиденья на гонщика, а также описывает, что гонщик «чувствует»
(помимо террора!).
F нетто = n — w = n — мгF нетто = F c = m v 2 / р
n — мг = m v 2 / r
n = мг + m v 2 / r
Что все это значит? Нормальная сила или сила всадника
кажущийся вес теперь на больше, чем реальный вес гонщика на .Всадник
чувствуется прижатым к сиденью. И ощущение более общее. всадника
руки и руки трудно двигаться. Кровь всадника даже трудно двигаться. Самолет
пилоты находятся в этой ситуации, когда они выходят из пикирования. Отношение этого
«кажущегося веса» к реальному весу можно описать как кажущееся влияние
сила тяжести или может быть описана как «перегрузка». «g-сил» шесть или семь — значение
видимый вес, в шесть или семь раз превышающий реальный вес, может означать, что
к мозгу не будет поступать достаточное количество крови, и пилот или другой пассажир
— может вырубиться.
Кровь всадника даже трудно двигаться. Самолет
пилоты находятся в этой ситуации, когда они выходят из пикирования. Отношение этого
«кажущегося веса» к реальному весу можно описать как кажущееся влияние
сила тяжести или может быть описана как «перегрузка». «g-сил» шесть или семь — значение
видимый вес, в шесть или семь раз превышающий реальный вес, может означать, что
к мозгу не будет поступать достаточное количество крови, и пилот или другой пассажир
— может вырубиться.
Мы описали это с диаграммой, показывающей гостя на дне долины ролика каботажное судно. Те же идеи применимы, конечно, к пилоту на дне «погружение», как показано здесь.
Перевернутое вверху петли
Теперь и нормальная сила n и вес w направлены в одном направлении, поэтому результирующая сила равна сумме этих двух силы,
F нетто = n + w = n + мгF нетто = F c = m v 2 / р
n + мг = m v 2 / r
n = ( m v 2 / r ) — мг
Что все это значит? Если скорость слишком низкая ,
это уравнение говорит, что нормальная сила будет минус . Что означает негатив
нормальная сила значит? Поскольку сиденье не может дотянуться и оттянуть вас назад, вы
выпадет из машины. И, так как дорожка не может дотянуться и вытащить
назад на машине американских горок, машина упала бы с трассы! Предотвращать
это, американские горки имеют колеса по обеим сторонам трассы ! Мы можем
подумайте о том, чтобы спроектировать поездку так, чтобы нормальная сила просто исчезла, а жертвы
действительно, чувствуешь себя невесомым наверху. Или мы могли бы спроектировать поездку так, чтобы это было нормально
сила равна реальному весу наверху.
Что означает негатив
нормальная сила значит? Поскольку сиденье не может дотянуться и оттянуть вас назад, вы
выпадет из машины. И, так как дорожка не может дотянуться и вытащить
назад на машине американских горок, машина упала бы с трассы! Предотвращать
это, американские горки имеют колеса по обеим сторонам трассы ! Мы можем
подумайте о том, чтобы спроектировать поездку так, чтобы нормальная сила просто исчезла, а жертвы
действительно, чувствуешь себя невесомым наверху. Или мы могли бы спроектировать поездку так, чтобы это было нормально
сила равна реальному весу наверху.
Мы описали это с диаграммой, показывающей гостя на вершине петли американских горок. Те же самые идеи применимы, конечно, к пилоту вверх ногами на вершине рулон, как показано здесь.
Конечно, есть и другие ситуации, которые обеспечивают
вертикальные круги, кроме как просто американские горки. Пилотажные пилоты или военные
пилоты в погружениях и петлях испытывают то же самое. Когда вы едете по холмистой местности
дорога вы испытываете две из этих трех ситуаций.
Когда вы едете по холмистой местности
дорога вы испытываете две из этих трех ситуаций.
Физика раскачивания груза на веревке для развлечения
Хорошо, есть еще кое-что, на что стоит обратить внимание. Как насчет соотношения между угловой скоростью и длиной струны? Глядя на приведенную выше диаграмму силы, видно, что в горизонтальном направлении действует только составляющая силы натяжения. Это означает, что чистая горизонтальная сила не может быть равна нулю. На самом деле оно должно быть равно массе (m 1 ), умноженной на ускорение.В этом случае масса ускоряется вправо, так как движется по окружности. Круговое ускорение будет произведением квадрата угловой скорости (нам нравится использовать для этого символ ω) и радиуса окружности. Обратите внимание, что радиус окружности равен 90 476, а не 90 479 длины строки — вместо этого это длина строки, умноженная на косинус θ (чтобы получить смежную сторону треугольника). Сложив это вместе, я получаю следующее.
Сложив это вместе, я получаю следующее.
Это уравнение говорит о том, что квадрат угловой скорости должен быть пропорционален единице, деленной на длину струны.Это кажется достаточно простым для проверки. Все, что мне нужно сделать, это раскачивать груз веревками разной длины (длина от верха трубки до груза). Я могу сделать это, наблюдая за небольшим кусочком ленты на дне трубки, чтобы убедиться, что длина постоянна. Конечно, мне также нужно поддерживать постоянные массы. Я могу определить угловую скорость, измерив время, за которое масса совершает один оборот. Тогда угловая скорость будет равна 2π, деленной на это время.
Я сделал это для пяти разных длин, используя подвесной груз 50 грамм и качающийся груз 15.8 грамм. Вот график зависимости ω в квадрате от 1/л:
Это выглядит довольно линейно. Но важной частью является наклон. Оглядываясь назад на соотношение между ω 2 и 1/л, константа пропорциональности должна быть M 2 г/м 1 .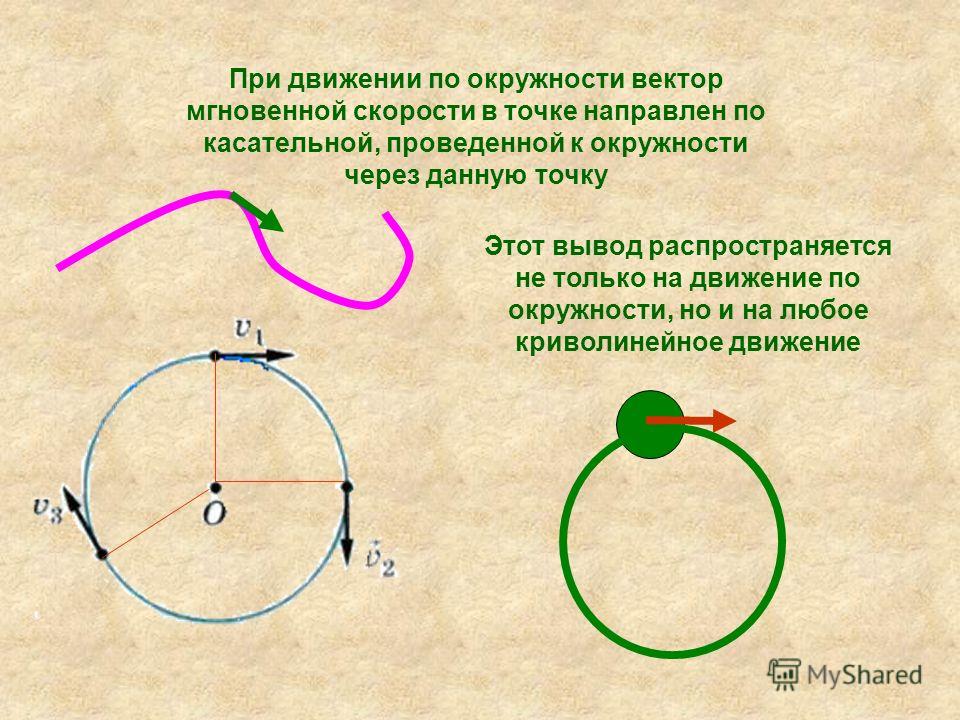 Я знаю массу и знаю g, поэтому эта константа должна быть 31 м/с 2 . Линейная подгонка имеет наклон 43 м/с 2 — не совсем то же самое, но все же близко.
Я знаю массу и знаю g, поэтому эта константа должна быть 31 м/с 2 . Линейная подгонка имеет наклон 43 м/с 2 — не совсем то же самое, но все же близко.
Тем не менее, если бы это был отчет студенческой лаборатории, я думаю, что данные были бы приемлемыми.Я все еще немного обеспокоен тем, что угол поворота не является постоянным, и этот наклон не ближе к ожидаемому значению. У меня есть ощущение, что между струной и вращающимся стеклянным стержнем может быть некоторое трение. Трение в точке контакта означало бы, что натяжение струны при качающейся массе равно не M 2 г, а чему-то другому. Может быть, мне нужно придумать другой метод измерения напряжения.
Честно говоря, это веская причина, по которой вам всегда следует проводить лабораторные эксперименты, даже если вы почти уверены, что знаете, как это работает.Просто никогда не знаешь, как все обернется.
Вращательная кинематика – физика 298
«Мужчины говорят об убийстве времени, а
время тихо убивает их
Дион Бусико Лондон Страхование (1841)
- На сегодняшний день мы рассмотрели
кинематика и динамика частиц, в том числе поступательная
и круговое движение, а также поступательное движение
системы частиц (в частности, твердых тел) с точки зрения
движение центра масс системы (тела).
 В
В последнем случае мы можем представить себе, что вся масса
объект находится в центре масс до внешней
речь идет о поступательных силах.
В
В последнем случае мы можем представить себе, что вся масса
объект находится в центре масс до внешней
речь идет о поступательных силах.
- Следующим шагом является рассмотрение вращения твердого тела вокруг
фиксированная ось вращения. Примечание
что, поскольку мы рассматриваем твердое тело, каждая частица в теле остается неподвижной относительно
остальным .Этот
означает, что при таком вращательном движении каждая частица движется в
окружность, центр которой лежит на оси вращения. В
на диаграмме справа объект вращается вокруг оси z; в
две частицы образца движутся по кругу с радиусом r 1 и р 2 . Если мы можем
описывают круговое движение частицы без непосредственного
относительно его радиуса, то все частицы в системе будут
описывается одной и той же системой уравнений.
 Хотя радиусы частиц различны, их
угловые повороты одинаковы. Следовательно
Это необходимо ввести угловые переменные.
Хотя радиусы частиц различны, их
угловые повороты одинаковы. Следовательно
Это необходимо ввести угловые переменные.
- Угловая скорость (скорость) и Угловое ускорение
Угловая скорость и угловое ускорение определяются аналогично скорость и ускорение.Там средние и мгновенные значения каждого из них.
Угловой ускорение это не то же самое как центростремительное ускорение. Центростремительное ускорение возникает из-за изменение в направлении скорости, угловое ускорение связано с изменением звездной величины скорости (через угол поворота).
Точно как и в поступательном случае, разница между угловыми
скорость и угловая скорость — это направление. Угловой
скорость должна включать направление вращения вокруг оси в
вопрос. За
например, 10 рад/с по часовой стрелке примерно
ось x — угловая скорость,
10 рад/с относительно оси абсцисс
угловая скорость.
Угловой
скорость должна включать направление вращения вокруг оси в
вопрос. За
например, 10 рад/с по часовой стрелке примерно
ось x — угловая скорость,
10 рад/с относительно оси абсцисс
угловая скорость.
- Уравнения кинематики вращения
По прямой аналогии с поступательной кинематикой уравнений, круговое движение вокруг одной оси при постоянном угловое ускорение может быть описано следующими четырьмя уравнения,
где мы сделали замены,
Обратите внимание, что так же, как +x определяется произвольно вправо, положительное значение тета может быть определена как по часовой стрелке или против часовой стрелки.
- Связь между Angular и Трансляционные переменные
Запуск от определение радианной меры путем дифференцирования с относительно времени, мы можем показать, что
, где против тангенциальная скорость, а a — тангенциальная
ускорение.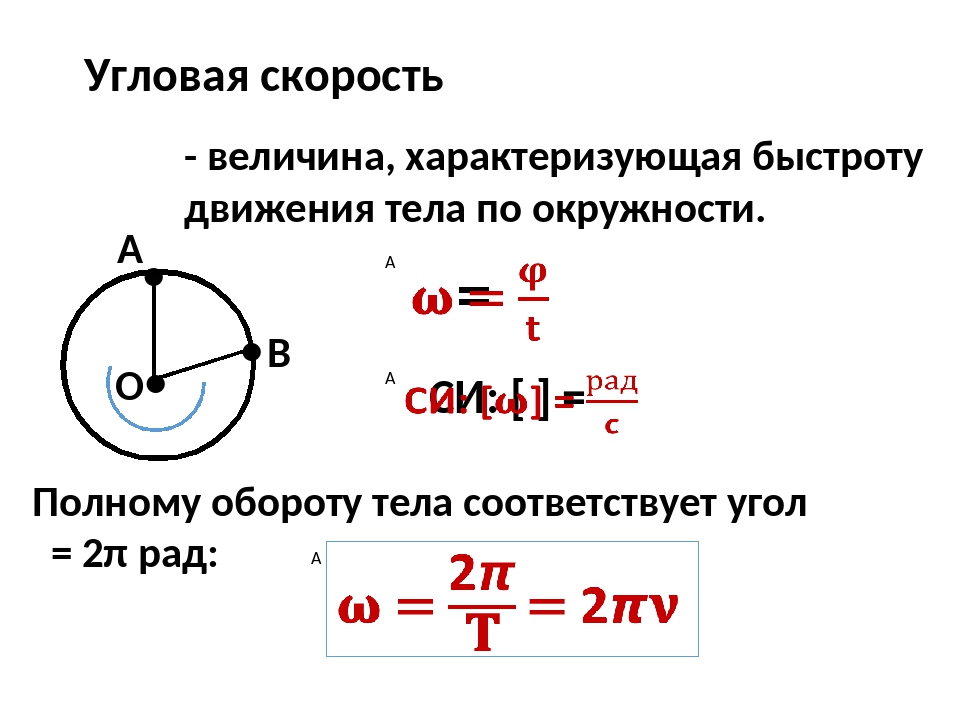
А частица, совершающая круговое движение с переменным углом скорость (неравномерное круговое движение), будет испытывать два компоненты ускорения, тангенциальная составляющая из-за изменение величины его скорости и радиальной (центростремительной) компонент из-за изменения направления его скорости
Сеть ускорение частицы есть векторная сумма этих двух компоненты, как указано ниже.
Возможно одновременное вращение вокруг нескольких осей.
рассматривается аналогично движению снаряда, где мы
расширили наше обсуждение одномерного перевода до двухмерного движения. В авиационных применениях вращение вокруг
три оси описываются как Roll, Шаг и рыскание.
Пример задачи
я не хочу достичь бессмертия своей работой я хочу добиться этого, не умирая
Вуди Аллен Вуди Аллен и его комедия (1975)
Др.C. L. Davis
Физический факультет
University of Louisville
электронная почта : [email protected]
.
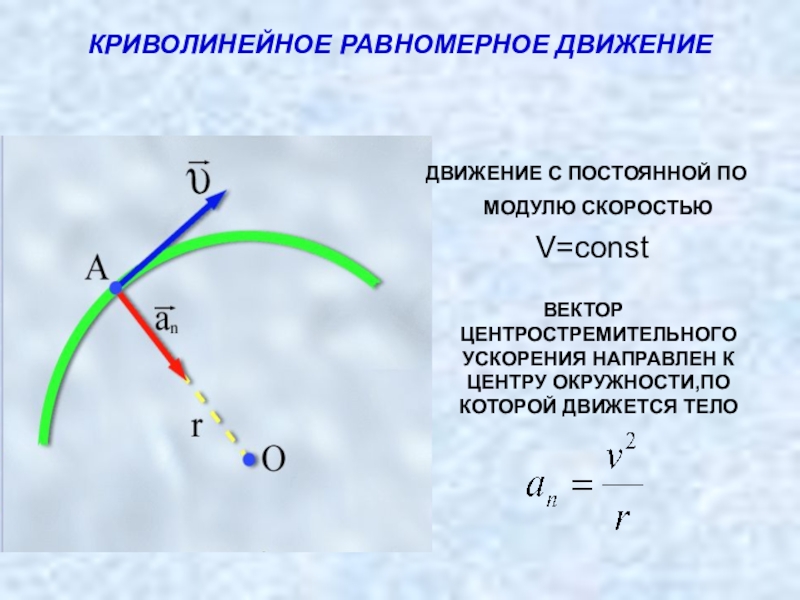

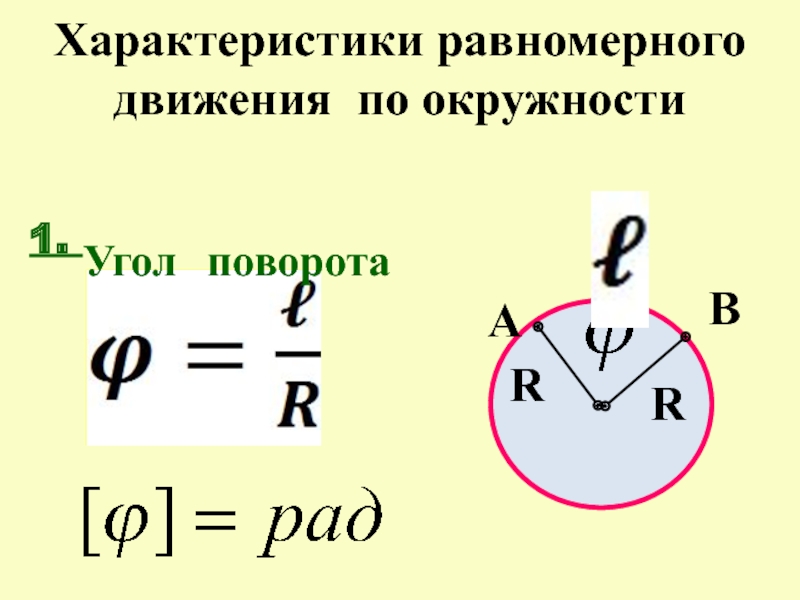

 путевая — средняя путевая скорость [м/с]
путевая — средняя путевая скорость [м/с] Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н.
Максимальное натяжение струны
поэтому F max = mg = (25 кг)(9,8 м/с 2 ) = 245 Н. 

 Затем
дорога больше не поддерживает машину. Это происходит, когда g — v 2 /r
= 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3
РС.
Затем
дорога больше не поддерживает машину. Это происходит, когда g — v 2 /r
= 0, или v 2 = gr = 411,6 м 2 /с 2 , v = 20,3
РС. Следовательно, a = GM/r 2 .
Следовательно, a = GM/r 2 .

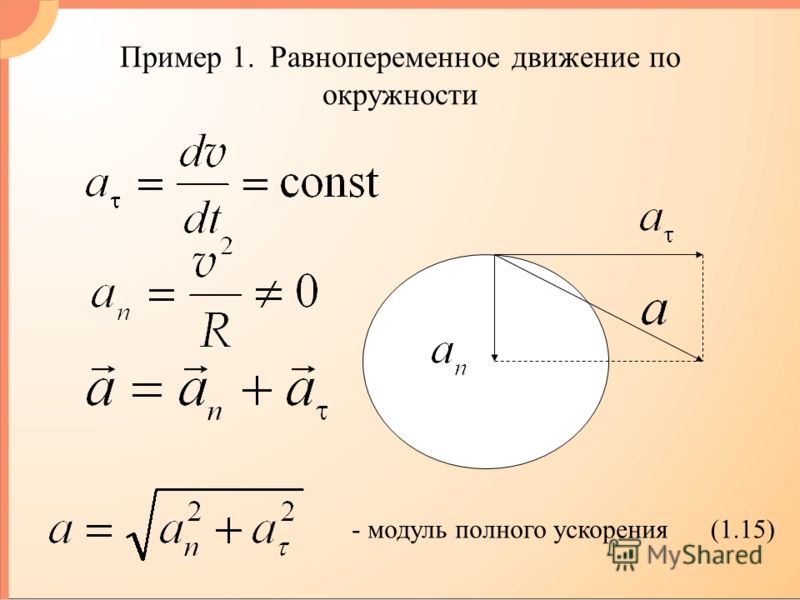
 В
В последнем случае мы можем представить себе, что вся масса
объект находится в центре масс до внешней
речь идет о поступательных силах.
В
В последнем случае мы можем представить себе, что вся масса
объект находится в центре масс до внешней
речь идет о поступательных силах. Хотя радиусы частиц различны, их
угловые повороты одинаковы. Следовательно
Это необходимо ввести угловые переменные.
Хотя радиусы частиц различны, их
угловые повороты одинаковы. Следовательно
Это необходимо ввести угловые переменные.