Формула угла поворота в течение заданного – ( )

7.2. Вращательное движение. Угловая скорость, угловое ускорение

Движение твердого тела, при котором все его точки перемещаются по окружности, центры которой расположены на перпендикулярной этим окружностям неподвижной прямой, называется вращательным. Неподвижная прямая, на которой лежат центры круговых траекторий то­чек тела, называется его осью вращения. Для образования оси вра­щения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел можно привести движение две­рей или створок окон при их открывании или закрывании.

Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).

Рис. 7.3. К анализу вращательного движения твердого тела

Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя.

Для установления закона вращательного движения тела, по кото­рому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную полуплоскость НП, а внутри тела отметим подвижную полуплоскость, ко­торая вращается около оси вместе с телом, теперь угол φ, образуемый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, т. е. знать закон вращательного движения тела:

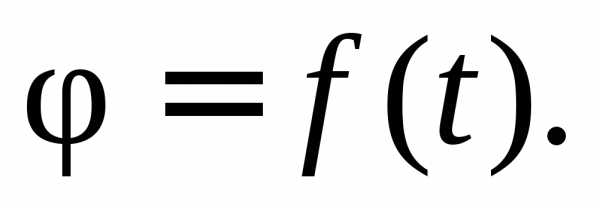
Быстрота изменения угла поворота во времени характеризуется величиной, которая называется угловой скоростью.

Представим, что в некоторый момент времени t положение вращающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело повернулось на угол Δ φ, и величина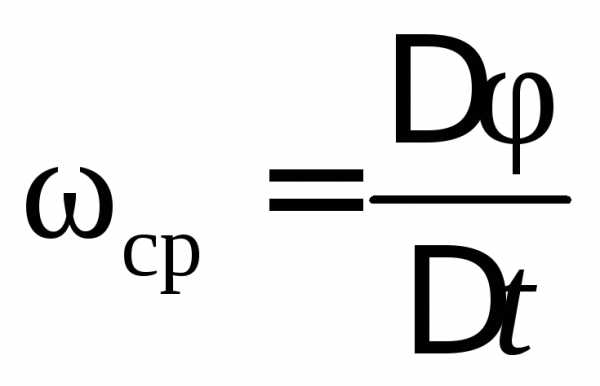

называется средней угловой скоростью.

Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение, обозначаемое . Среднее ускорение ;

.

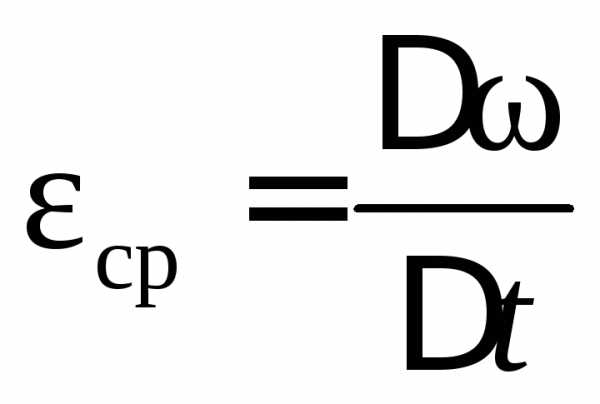Единица углового ускорения 1 рад/с².

Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часовой стрелки – отрицательным.

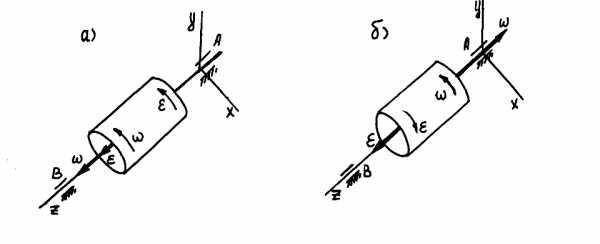
б

а

Рис. 7.4. К определению вида вращательного движения

Векторы и – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора (или ), видеть вращение, происходящее против часовой стрелки.

Если векторы и

направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы и направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).

7.3. Частные случаи вращательного движения

1. Равномерное вращательное движение. Если угловое ускорение 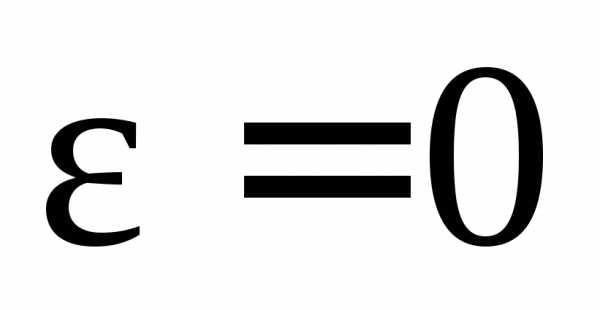и, следовательно, угловая скорость

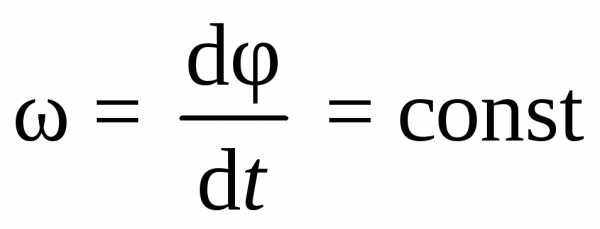, (7.1)

то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных получим

Если при изменении времени от 0 до t угол поворота изменялся от φ₀ (начальный угол поворота) до φ, то, интегрируя уравнение в этих пределах:

получаем уравнение равномерного вращательного движения

,

которое в окончательном виде записывается так:

.

Если , то

.

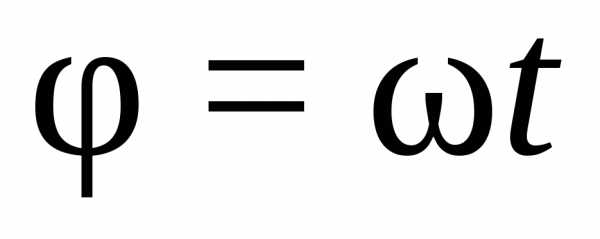Таким образом, при равномерном вращательном движении угловая скорость

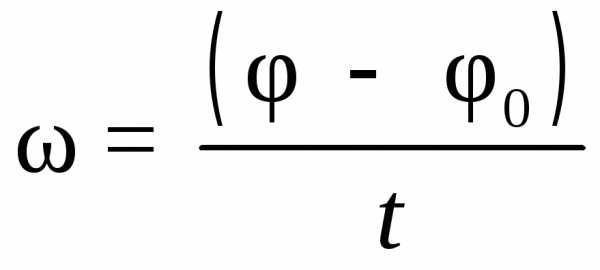или при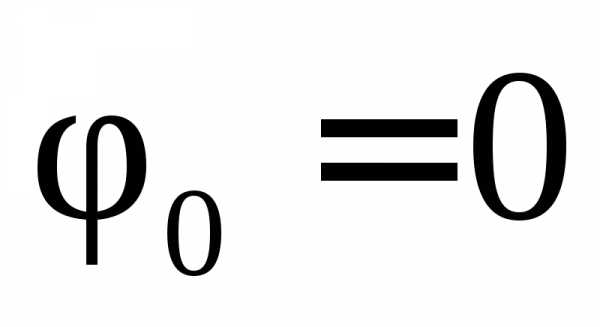

.

2. Равнопеременное вращательное движение. Если угловое ускорение

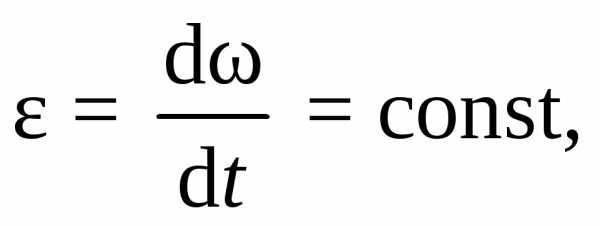(7.2)

то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.2):

и приняв, что при изменении времени от 0 до t угловая скорость изменилась от (начальная угловая скорость) до , проинтегрируем уравнение в этих пределах:

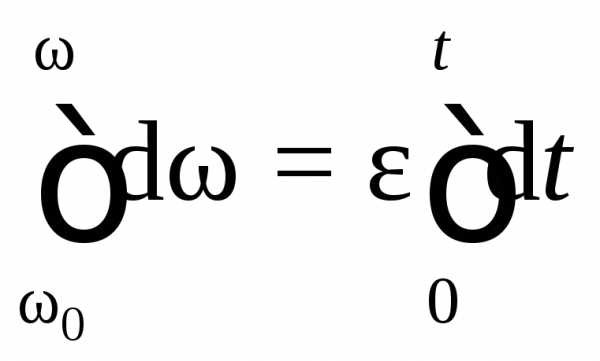или ,

т. е. получим уравнение

(7.3)

выражающее значение угловой скорости в любой момент времени.

Закон равнопеременного вращательного движения 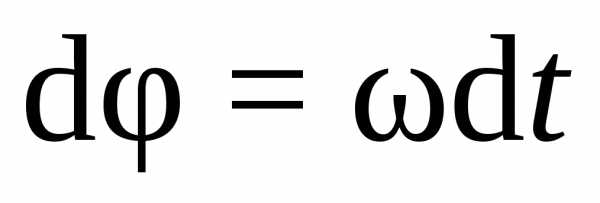или, с учетом уравнения (7.3):

Полагая, что в течение времени от 0 до t угол поворота изменялся от до, проинтегрируем уравнение в этих пределах:

или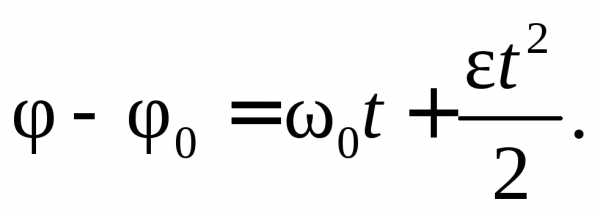

Уравнение равнопеременного вращательного движения в оконча­тельном виде

(7.4)

Первую вспомогательную формулу получим, исключив из формул (7.3) и (7.4) время:

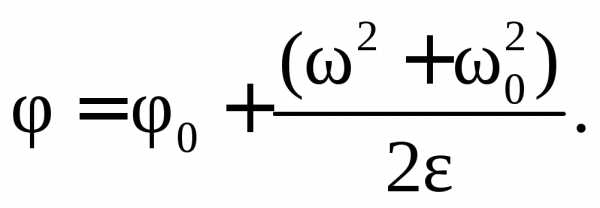(7.5)

Исключив из тех же формул угловое ускорение , получим вторую вспомогательную формулу:

(7.6)

где – средняя угловая скорость при равнопере­менном вращательном движении.

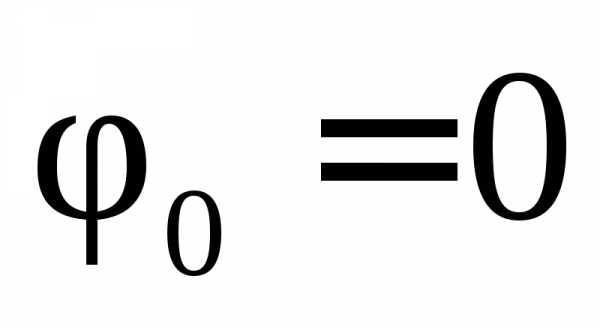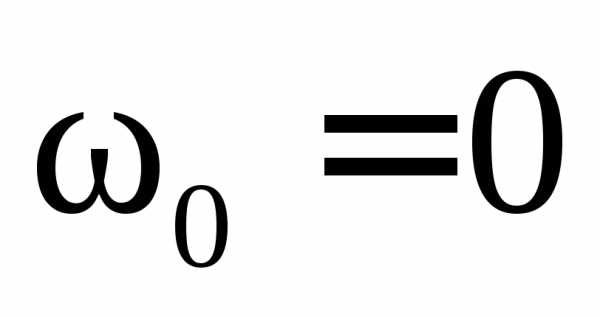Когда и , формулы (7.3)–(7.6) приобретают более простой вид:

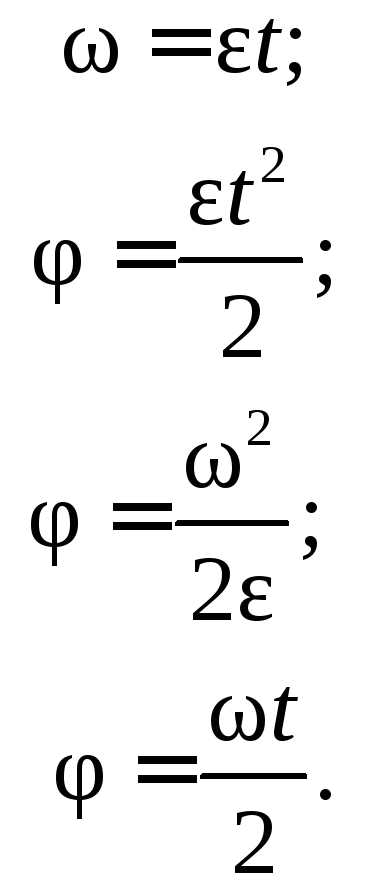
В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.

Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между (с^–1) и n (мин^–1). Так как 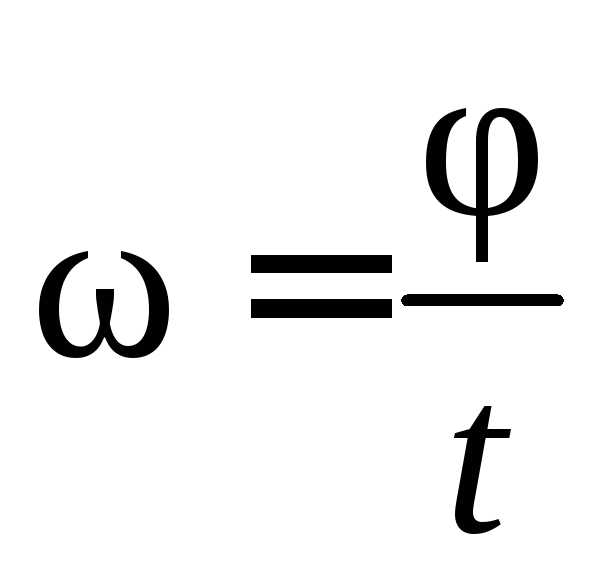, то при n (мин^–1) за t = 1 мин = 60 с угол поворота 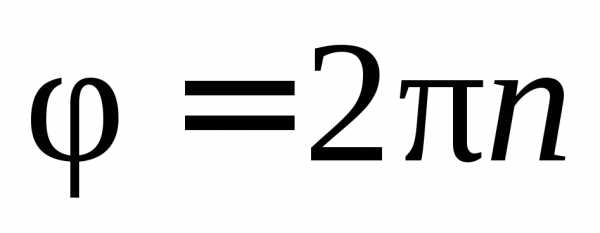. Следовательно:

.

При переходе от угловой скорости

(с^–1) к частоте вращения n (мин^–1) имеем

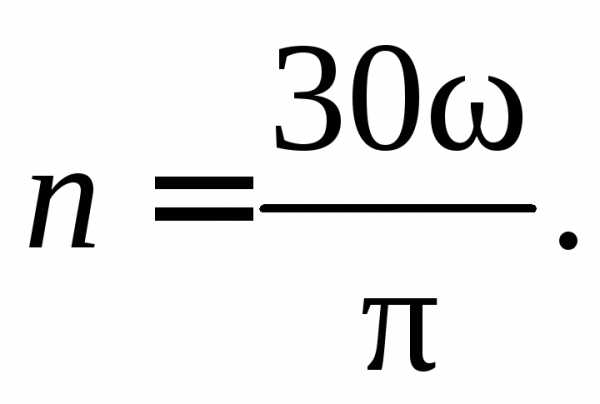
studfile.net

Вращательное движение (движение тела по окружности) | Формулы и расчеты онлайн

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:

Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α

Вращательное движение, характеристики

Вращательное движение	Угловая скорость	Угловое ускорение
Равномерное	Постоянная	Равно нулю
Равномерно ускоренное	Изменяется равномерно	Постоянно
Неравномерно ускоренное	Изменяется неравномерно	Переменное

Угол поворота

Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).

Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана

\[ φ = \frac{s}{r} \]

Соотношение между единицами угла

\[ \frac[-1.35]{φ_{рад}}{φ_{°}} = \frac[-1.2]{π}{180°} \]

$ 1 рад = 57.3° $

$ 1° = 17.45 мрад $

$ 1´ = 291 мкрад $

Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.

Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).

Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).

Число оборотов

Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.

Единица СИ частоты (или числа оборотов)

\[ [n] = [f] = \frac{Обороты}{Секунда} = \frac{(об)}{с} = \frac{1}{c} = Герц \]

В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.

Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.

Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то

Период

\[ T = \frac{1}{f} = \frac{1}{n} \]

Угловое перемещение

Угловое перемещение равно произведению полного числа оборотов на 2π:

\[ φ = 2 π N \]

Угловая скорость

Из формулы для одного оборота следует:

\[ ω = 2 π f = \frac{2π}{T} \]

Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.

В помощь студенту

Вращательное движение (движение тела по окружности)	стр. 421

www.fxyz.ru

Угловая скорость при вращении тела вокруг неподвижной точки

Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.

Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол  Δα вокруг мгновенной оси Ω (рисунок 3.2). 

Рис. 3.2 

Предел, к которому стремится отношение  Δα / Δt, называется угловой скоростью твердого тела в рассматриваемый момент времени

Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.

Угловое ускорение при вращении тела

Угловым ускорением называют степень изменения угловой скорости.

За вектор углового ускорения ε при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости ω в данный момент как по числовой величине, так и по направлению. Такой характеристикой является производная по времени от вектора угловой скорости ω. Таким образом, угловое ускорение определяется так:

     

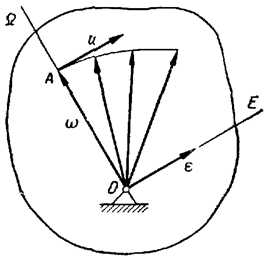
Рис. 3.3

В общем случае угловое ускорение не направлено по мгновенной оси, а, как производная по времени от вектора ω, параллельно касательной к годографу этого вектора. Условимся угловое ускорениеε изображать в любой точке прямой, параллельной этой касательной годографа угловой скорости u, но проходящей через неподвижную точку тела (рисунок 3.3). Прямая, по которой направлен вектор углового ускорения, называется осью углового ускорения и обозначается E.

7

2 Кинематика твердого тела

     В кинематике твердого тела определяются: закон движения и кинематические характеристики тела, а также кинематические характеристики точек тела.

   В данном методическом пособии рассмотрены следующие виды движения твердого тела:

    — поступательное;

    — вращательное;

    — плоскопараллельное.

2.1 Поступательное движение

     Поступательное движение – это движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе.

     На рисунках 2.1,а и 2.1,б приведены примеры поступательного движения: движение прямоугольника в плоскости чертежа, движение каждой кабины колеса обозрения.

а                                  б

Рисунок 2.1

 

Рисунок 2.2

    Исходя из определения поступательного движения, движение твердого тела может быть задано в векторном виде формулой (рисунок 2.2):   

                                                  r_M=r_A ⊕ AM.

   В этой формуле AM —  вектор постоянный по величине и направлению, поэтому производная от него равна нулю. Для скорости и ускорения произвольной точки M  получим:

    То есть скорости и ускорения точек твердого тела при  поступательном движении равны и одинаково направлены, а траектории при наложении совпадают. 

    Для определения кинематических характеристик точек тела достаточно знать закон движения одной из них.

8

 Движение твердого тела, при котором две его точки О и О‘ остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО‘ называют осью вращения.         Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО‘ (рис. 2.12).

Рис. 2.12

       Проследим за некоторой точкой М этого твердого тела. За время  dt  точка М совершает элементарное перемещение  dr.         При том же самом угле поворота  dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная , ни вторая производнаяне могут служить характеристикой движения всего твердого тела.        За это же время dt радиус-вектор , проведенный из точки0‘ в точку М, повернется на угол  dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).         Угол поворота  dφ  характеризует перемещение всего тела за время dt.         Удобно ввести – вектор элементарного поворота тела, численно равныйdφ  и направленный вдоль оси вращения ОО‘ так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора и направление вращения связаны «правилом буравчика»).        Элементарные повороты удовлетворяют обычному правилу сложения векторов:

       Угловой скоростью называется вектор , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении(ивсегда направлены в одну сторону).

.

(2.4.1)

       Если  ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси.  Пусть  v  – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время  dr = Rdφ  (dφ — центральный угол). Тогда, можно получить связь линейной скорости и угловой:

.

(2.4.2)

       В векторной форме .        Вектор ортогонален к векторамии направлен в ту же сторону, что и векторное произведение.        Наряду с угловой скоростью вращения используют понятия периода и частоты вращения.         Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол φ = 2π).         Частота ν – число оборотов тела за 1 секунду.         При вращении с угловой скоростью ω имеем:

,         ,.

       Введем вектор углового ускорения для характеристики неравномерного вращения тела:

.

(2.4.3)

       Вектор направлен в ту же сторону, что ипри ускоренном вращении, анаправлен в противоположную сторону при замедленном вращении(рис. 2.13).

Рис. 2.13

       Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:

	aτ = Rε;	(2.4.4)
		(2.4 5)

       Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота), направлены вдоль оси вращения.         Формулы простейших случаев вращения тела вокруг неподвижной оси:

     равномерное вращение ε = 0;       ω = const;       φ = φ₀ ± ωt,

     равнопеременное вращение .

9

 Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11). 

    При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M₁M₂ ) совершают одинаковые движения.

                                    

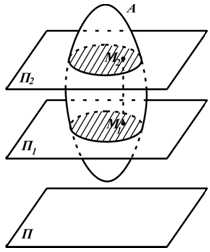
Рисунок 2.11

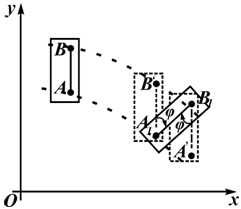
Рисунок 2.12

    Отрезок M₁M₂  движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.

    На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy  из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A  с последующим поворотом на угол φ  вокруг точки A₁. Это же перемещение можно выполнить иначе. 

    Например, перемещая пластинку поступательно с траекторией точки B , с последующим поворотом вокруг B₁  на угол φ. Траектории точек A  и B различны, а угол поворота в обоих случаях  одинаков. 

     Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:

                                 x_A=x_A(t),  y_A=y_A(t),  φ=φ(t).

    Точка A  в этом случае называется полюсом. Если принять за полюс точку B , то получим уравнения:

                                x_B=xB(t),  y_B=yB(t),  φ=φ(t)

    За полюс выбирается точка, закон движения которой известен.

10

ИНЕРЦИАЛЬНАЯ система ОТСЧЕТА — система отсчета, в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения. Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета. Все инерциальные системы отсчета равноправны, т. е. во всех таких системах законы физики одинаковы.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v₀.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x’,y’,z’ системы K’ так что оси x и x’ совпадали, а оси y и y’ , z и z’, были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x’,y’,z’ той же точки в системе K’. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x’+v₀, кроме того, очевидно, что y=y’, z=z’. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t’. Получим совокупность четырёх уравнений : x=x’+v₀t;y=y’;z=z’;t=t’, названных преобразованиями Галилея

Инвариантами преобразования Галилея являются длина тел и промежуток времени между событиями. Именно поэтому понятия длины и промежутка времени играют такую большую роль в классической физике. [4]

Дифференциал dr является инвариантом преобразований Лоренца, т.е. интервалом времени, не зависящим от ситуации — подвижной или неподвижной является исходная система отсчета. Ньютона о существовании некоего универсального, абсолютного времени. [13]

скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно движущейся системы и скорости самой движущейся системы относительно неподвижной

 

В классической механике справедлив механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчета.

Рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), условно будем считать неподвижной, и систему К’ (с координатами x’, y’, z’), движущуюся относительно К равномерно и прямолинейно со скоростью υ₀ (υ₀=const)

Координата точки А по отношению к системе К: х = х’ + 00′, за промежуток времени t от начала отсчета будет:

(3.19)

Уравнения (3.19) носят название преобразования координат и времени Галилея. Отсчет времени начат с момента, когда начало координат обеих систем совпадают. Продифференцировав по времени t, получим выражение правила сложения скоростей в классической механике: υ=υ’+υ₀ (3.20)

Ускорения в обеих системах отсчета одинаковы, а это означает, что поведение тел в обеих системах одинаково: a=a’ (3.21), т.е. из соотношения (3.21) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям Галилея. Механический принцип относительности можно сформулировать еще следующим образом: никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.

11.

studfile.net

Вращательное движение

Вращательное движение является периодическим движением.

Период обозначается буквой T.

Чтобы найти период обращения, надо время вращения разделить на число оборотов:

Физическая величина, равная отношению числа полных оборотов тела ко времени, в течение которого эти обороты совершены, называется частотой вращения.

Частота вращения обозначается буквой n.

Чтобы найти частоту вращения, надо число оборотов разделить на время, в течение которого эти обороты совершены:

Частота вращения и период обращения связаны друг с другом как взаимообратные величины: Период измеряется в секундах: [T] = 1 с.

Единица частоты – секунда в минус первой степени: [n] = 1 с^–1.

Эта единица имеет собственное название – 1 герц (1 Гц).

Проведем аналогию между вращательным и поступательным движениями.

Поступательно движущееся тело изменяет свое положение в пространстве относительно других тел.

Тела, совершающие вращательное движение поворачиваются на некоторый угол.

Если за любые равные промежутки времени поступательно движущееся тело совершает равные перемещения, движение называется равномерным.

Если за любые равные промежутки времени вращающееся тело поворачивается на один и тот же угол, то такое вращение называется равномерным. Характеристикой равномерного поступательного движения служит скорость Соответствующей характеристикой вращательного движения служит угловая скорость:

Угловая скорость – это физическая величина, равная отношению угла поворота тела ко времени, в течение которого этот поворот совершен.

Угловая скорость показывает, на какой угол поворачивается тело за единицу времени.

Чтобы получить единицу угловой скорости, нужно в ее определяющую формулу подставить единицу – 1 радиан, и времени – 1 с. Получаем: [ω] = 1

Аналогично можно ввести характеристику неравномерного вращения. Если видом неравномерного поступательного движения является равнопеременное движение, то для вращательного движения можно ввести понятие равнопеременного вращения.

Характеристикой равнопеременного поступательного движения является ускорение:

Соответственно, для вращательного движения можно ввести величину, определяемую отношением изменения угловой скорости ко времени, в течение которого это изменение происходит – угловое ускорение: Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени. Чтобы получить единицу углового ускорения, нужно в его определяющую формулу подставить единицы угловой скорости 1 рад/с и времени – 1 с. Получаем:

Продолжая аналогию дальше, запишем уравнение для перемещения при прямолинейном равноускоренном движении

Так как при вращении перемещению тела соответствует угол вращения, линейной скорости – угловая скорость, линейному ускорению – угловое ускорение, то аналогичное уравнение для вращательного движения будет иметь вид:

Другому уравнению для поступательного движения будет соответствовать уравнение для вращательного движения:

Метод, который использовался в данном случае, называется методом аналогий.

Точки тела, совершающего вращательное движение, поворачиваются относительно оси вращения на некоторые углы и движутся по дугам окружностей, проходя определенные пути. Таким образом, характеристиками вращательного движения являются и угловая, и линейная скорости.

Линейная скорость точки направлена по касательной к окружности, по которой она движется.

Об этом свидетельствует слетающая с колес автомобиля грязь или искры, летящие от металлического предмета, прижатого к наждачному кругу.

Чем дальше от оси вращения находится точка, тем больше ее линейная скорость. Угловая же скорость точек, лежащих на одном радиусе, одинакова. Следовательно, линейная скорость точки прямо пропорциональна радиусу окружности, по которой она вращается.

За время, равное периоду, точка проходит путь, равный длине окружности. Её линейная скорость при этом равна Отношение же угла поворота ко времени поворота на этот угол равно угловой скорости

Таким образом, линейная скорость вращающейся точки связана с ее угловой скоростью соотношением:

При равномерном вращении скорость меняется по направлению, но не изменяется по величине.

Поскольку всякое изменение скорости характеризуется понятием ускорения, то для равномерного вращения следует ввести еще одно ускорение, изменяющееся не по величине, а по направлению. Это ускорение называют центростремительным.

Пусть вращающееся тело в начальный момент времени находится в точке A и скорость его направлена по касательной. В следующий момент времени тело находится в точке B. При этом скорость его изменилось только по направлению и направлена по касательной к окружности.

Найдем вектор разности скоростей, воспользовавшись правилом действия с векторами. Из чертежа видно, что вектор разности направлен в сторону близкую к центру окружности. Чем меньше угол поворота, тем ближе направлен вектор скорости к направлению на центр вращения.

При малом времени движения изменение положения тела незначительно. Поэтому можно считать, что вектор скорости характеризующий изменение скорости по направлению, направлен на центр. Отсюда и происходит название центростремительного ускорения.

Угловое же ускорение, характеризующее изменение скорости по величине, называют еще касательным или тангенциальным ускорением (при неравномерном вращении).

Получим выражение для центростремительного ускорения. Будем считать, что угол поворота очень мал. Соединим точки A и B. Угол MAN = φ по построению.

Мы имеем два равнобедренных треугольника. Треугольник OAB, ребра которого R и AB, и треугольник MAN, ребра которого и

Так как треугольники подобны (по двум сторонам и углу между ними), то можно записать:

Дуга окружности и хорда практически равны из-за малости угла поворота. Поэтому дуга Следовательно, Получим

Разделив правую и левую части последнего уравнения на t, получим:

Отсюда Таким образом,

Полученная формула является формулой для расчета центростремительного ускорения.

Центростремительное ускорение, при движении тела по окружности, равно отношению квадрата скорости к радиусу окружности, по которой движется тело:

files.school-collection.edu.ru

Вращательное движение и угловая скорость твердого тела :: SYL.ru

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

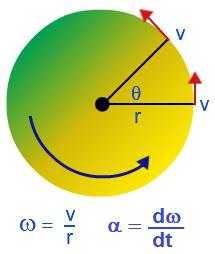
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

φ = φ(t).

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с².

Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ₀ + ωt, где φ₀ – начальное значение угла поворота.

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω₀+ εt, φ = φ₀ + ω₀t + εt²/2.

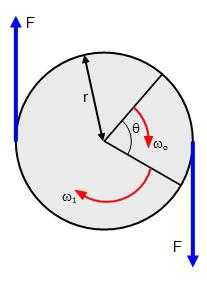
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц= v²/R = (ωR)²/R = ω²R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t= ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R²mβ, β= M/mR² = M/I, где I = mR² — момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10⁴ об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Решение

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω₀— εt.

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω₀/t = 2πn/t.

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с²).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ₀ + ω₀t + εt²/2. Учитывая выражение для углового ускорения и то, что φ₀ = 0, находим: φ(t)= ω₀t/2 = πnt.

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10⁴ (об.).

Ответ: угловое ускорение равно 4,36 рад/с²; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10⁴ об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Решение

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR² = F/mR.

Найдем время, за которое диск остановится: t = ω₀/ε, где ω₀ — начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

www.syl.ru

Вращательное движение твердого тела — Лекции и примеры решения задач технической механики

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П, одна из которых неподвижна, а другая жестко связана с телом.

φ=φ(t) – уравнение вращательного движения твердого тела.

Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.

Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

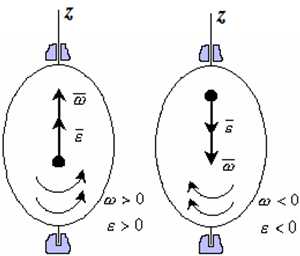
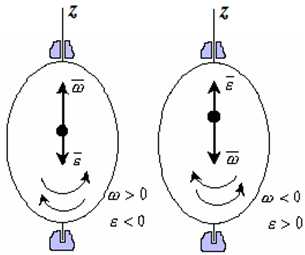
Рис. 1.4

1. Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.
2. При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz.
3. Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.
4. Если ε >0 при
   ω <0, то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны.
5. Если угловая скорость ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения

   φ=φ₀+ωt

6. Если угловое ускорение ε=const, то вращательное движение называется равнопеременным.
   Уравнение равнопеременного вращения и уравнение, выражающее угловую скорость в любой момент времени

   ω=ω₀+εt

   представляют совокупность основных формул вращательного равнопеременного движения тела.

---

isopromat.ru

Вопрос 2. Кинематика вращательного движения. Угловая скорость, угловое ускорение. Связь линейных и угловых величин. Псевдовекторы.

Вопрос 1. Механическое движение. Система отсчёта. Путь, перемещение, траектория. Расчёт пути при равноускоренном движении. Кинематика поступательного движения. Скорость мгновенная, средняя. Модуль скорости. Ускорение и его составляющие.

Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.

Механика Галилея-Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения тел со скоростями, сравнимыми со скоростью света, изучаются релятивистской механикой.

Движение тел происходит в пространстве и во времени. Положение материальной точки определяется по отношению к какому-либо другому телу, называемому телом отсчёта. С ним связана система отсчета – совокупность системы координат и часов, связанных с телом отсчета.

Траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Длина участка АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути и является скалярной функцией времени: . Вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени называется перемещением.

Равноускоренное движение – движение точки с постоянным ускорением. Ускорение – величина, характеризующая быстроту изменения скорости. В равноускоренном движении . Формула расчета скорости при равноускоренном движении в момент времени:

Проинтегрируем эту формулу: — путь при равноускоренном движении.

Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. При поступательном движении все точки тела движутся одинаково, поэтому достаточно изучить движение одной какой-то произвольной точки тела (например, движение центра масс тела). Так же при поступательном движении тело не изменяет ни своего вида, ни строения, одновременные скорости всех точек равны и сонаправлены.

Мгновенная скорость (скорость) — предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при стремлении длительности промежутка времени к нулю. Модуль мгновенной скорости равен первой производной пути по времени.

Средняя скорость (средняя путевая скорость) – отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной. Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.

В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.

Ускорение – величина, характеризующая быстроту изменения скорости по величине и направлению. Ускорение – векторная величина, состоит из двух составляющих – тангенциальной составляющей и нормальной.

Тангенциальная составляющая характеризует изменение скорости по величине и направлена по направлению вектора скорости (если движение равноускоренное) или противоположно вектору скорости (равнозамедленное движение), равна:

Вторая составляющая ускорения называется нормальной и направлена по нормали к траектории к центру ее кривизны (центростремительное ускорение):

При вращательном движении точки тела описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением.

Если точка движется по окружности радиусом R, то через её положение можно задать углом поворота — элементарный угол поворота. Угол поворота – координата точки при вращательном движении; векторная величина, модуль которой равен углу поворота, а направление этого вектора связано с направлением вращения (по правилу правого винта). Сам вектор находится на оси вращения.

Угловая скорость — векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первой производной от угла поворота по времени. Направлен так же, как и вектор.

Если угловая скорость остается постоянной, то вращение будет равномерное, и оно характеризуется периодом вращения (время полного оборота на угол ).

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени.

Векторы, направления которых связаны с направлением вращения, называются псевдовекторами.

Связь линейных и угловых величин:

Вопрос3. Масса, свойство массы. Сила. Инерция. Первый закон Ньютона.

Динамика изучает движение тел, вскрывая причины, придающие движению тел тот или иной характер. Основы динамики составляют 3 закона Ньютона, которые представляют собой обобщение большого числа экспериментальных фактов.

Сила — векторная величина, которая является мерой механического воздействия одного тела на другое.

Вектор силы полностью задаётся точкой приложения, направлением, модулем (величиной).

Направление вектора силы совпадает с направлением ускорения сообщаемого телу данным воздействием. Под действием силы тела либо деформируются, либо изменяют скорость.

Инерция – свойство тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью

Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.

Из этого закона следует:

— Тела обладают свойствами инертности (свойство состоит в стремлении тел сохранить состояние покоя или равномерного прямолинейного движение).

— Система отсчета, в которой материальная точка, свободная от внешних воздействий либо покоится, либо движется равномерно и прямолинейно, называется инерциальной системой отсчета.

Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.

□ Если рассматривать действие различных сил на одно и то же тело, то оказывается, что ускорение прямо пропорционально равнодействующей приложенных сил: и . Можем записать, что. Это соотношение выражает второй закон Ньютона. ■

Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В СИ коэффициент k=1.

Векторная величина, равная произведению массы тела на его скорость и имеющая направление скорости, называется импульсом:

Выражение — второй закон Ньютона в общем виде: скорость изменения импульса материальной точки равна действующей на неё силе.

Принцип независимости сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, как если бы других сил не было вообще.

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют тела друг на друга, всегда равны по модулю и противоположно направлены, действуют вдоль прямой, соединяющей эти точки.

В любой системе тел, силы действуют попарно и являются силами одной природы.

Таким образом, –закон сохранения импульса: импульс замкнутой системы сохраняется, то есть не изменяется с течением времени. Закон сохранения импульса выполняется не только в классической физике. Закон носит универсальный характер и является фундаментальным законом природы.

В классической механике из-за независимости массы от скорости импульс системы может быть выражен через скорость её центра масс. Центром масс системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Её радиус-вектор равен:

Если мы найдём производную от радиус-вектора, то мы найдём скорость, с которой движется центр масс. .

Центр масс системы движется так, как двигалась бы материальная точка с массой равной сумме масс системы тел под действием результирующей внешних сил. Для замкнутой системы сумма внешних сил равна 0, поэтому центр масс замкнутой системы движется равномерно и прямолинейно.

Вопрос 4. Динамика вращательного движения. Момент силы, момент импульса точки, твердого тела относительно оси вращения. Основной закон динамики вращательного движения. Понятие момента инерции точки, тв.тела относительно оси вращ-я.

Основное уравнение динамики вращательного движения:

Производная по времени от момента количества движения механической системы относительно неподвижной точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе: dL/dt=M.

Пример: Вращение системы вокруг неподвижной оси Oz: L_X=L_Y=0, L_Z=J_Z, где –угловая скорость, J_Z -момент инерции системы относительно оси Oz. Уравнение движения: (d/dt)(J_Z)=M_Z. Если система является абсолютно твёрдым телом, то J_Z (d/dt)=M_Z.

Момент импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

Модуль вектора момента импульса:

Моментом импульса материальной точки относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса , не зависит от положения точки О на осиz.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точки тела движется по окружности постоянного радиуса с некоторой скоростью . Скоростьи импульсперпендикулярны этому радиусу, то есть радиус является плечом вектора. Поэтому можем записать, что момент импульса отдельной частицы равени направлен по оси в сторону, определяемую правильном правого винта.

Момент инерции является мерой инертности при вращательном движении. Момент инерции материальной точки относительно оси – это произведение массы этой точки на квадрат расстояния до оси Z.

Моментом инерции тела относительно оси, проходящей через центр масс, называется сумма произведений масс материальных точек на квадрат расстояния их до оси вращения.

Если масса распределена неправильным образом, то тогда определить момент инерции в этом случае можно переходя к интегрированию.

Момент инерции — это величина аддитивная. Момент инерции системы материальных точек равен сумме моментов инерций этих точек, рассчитанных относительно одной и той же оси.

Момент инерции зависит от формы и размеров тела, от материалов, из которых сделано тело, а также от расположения тела относительно оси.

studfile.net