Как найти количество оборотов: Определение числа оборотов колеса — Пример решения задачи

Содержание

Расчет RCF-RPM on-line

Он-лайн калькулятор может быть использован для:

расчета параметра RPM (обороты в минуту) при работе по протоколам к нашим наборам или методикам, приведенным в статьях;
указания универсальной величины центрифугирования RCF (g) в своих публикациях.

Отличие

RCF от RPM

В статьях рекомендуется указывать универсальную величину — относительное ускорение центрифуги (RCF, Relative Centrifugal Force), которая измеряется в g. Это дает возможность воспроизвести методику в любой лаборатории.

Если установить одно и то же значение RCF на разных центрифугах, они будут осаждать образец с одинаковой эффективностью.

Некоторые модели центрифуг не позволяют задать ускорение RCF, на них возможно установить только частоту вращения (RPM, Rotation Per Minute), которая измеряется в оборотах в минуту. RPM характеризует условия центрифугирования только на выбранной модели центрифуги: если установить одно и то же значение RPM на центрифугах с разными роторами, они будут осаждать образец с разной эффективностью.

RCF, RPM и радиус ротора центрифуги связаны формулой:

, где:

RPM — частота вращения в оборотах в минуту,
RCF — относительное ускорение центрифуги в g,
r — радиус ротора в сантиметрах.

Из этой формулы следует два вывода:

Чем больше радиус ротора, тем меньше нужно оборотов в минуту, чтобы поддерживать то же относительное ускорение. Информацию о роторе указывают в руководстве по эксплуатации центрифуги.
Любое изменение частоты вращения сильно влияет на эффективность центрифугирования, поскольку RCF прямо пропорционально квадрату RPM .

Перевести

g в об/мин или наоборот

Радиус ротора (см):

Введите радиус ротора центрифуги в сантиметрах.

RCF (g):

При заполнении поля RCF (g) или RPM (об/мин),
второе значение рассчитается автоматически.

Число оборотов в минуту —

Помимо изображений, принципиальные гидравлические схемы станков содержат технические данные насосов модель, производительность, давление, число оборотов в минуту и мощность электродвигателя привода, а для регулируемых насосов — пределы производительности.

В технических данных гидроаппаратов указывают присоединительные резьбы, условные проходы, давления и допускаемые расходы жидкости. [c.327]
На кинематических схемах станков, кроме условных изображений деталей, применяют также указания в виде текстовых и цифровых надписей. Так, например, валы нумеруются обычно римскими цифрами в порядке передачи движения, считая от привода электродвигателя (рис. 232) для шкивов указывают диаметры и их ширину для зубчатых колес—модуль и число зубьев каждого колеса. У ходовых винтов надписями указывают шаг, число заходов и направление резьбы. Около электродвигателя указывают его мощность и число оборотов в минуту, например N= 1,3 кВт п = 960 об/мин.
[c.276]

На четвертом шпинделе обычно производится отрезание детали. Упомянутое специальное резьбонарезное устройство позволяет дать метчику вращение в том же направлении, в каком вращается и деталь, но с большим числом оборотов в минуту, чем у детали, что позволяет [c. 364]

Частицы воды входят в турбину со скоростью и. Угол между скоростью и и касательной к ротору, проведенной в точке входа частицы, равен а. Внешний диаметр ротора D, его число оборотов в минуту п.

[c.158]

Найти число оборотов в минуту шестерни с числом зубцов 2з = 25, если кривошип ОА вращается вокруг оси О неподвижной шестерни (с числом зубцов zo = 60) с угловой скоростью, соответствующей по = 30 об/мии, и несет на себе ось двойной шестерни с числами зубцов Zi = 40, Z-2 = 50. [c.177]

Ведущий вал I редуктора делает П = 1200 об/мин. Найти число оборотов в минуту ведомого вала II, если неподвижное зубчатое колесо с внутренним зацеплением имеет г = 180 зубцов бегающие шестеренки, спаренные между собой, имеют га—60 [c.178]

Г2 = 20 см и Га = 30 см, спаренных между собой, и шестеренки с внутренним зацеплением радиуса Г4 = 90 см, сидящей на ведомом валу. Ведущий вал и кривошип, несущий оси бегающих шестеренок, делают щ = 1800 об/мин.

Найти число оборотов в минуту ведомого вала. [c.178]

Число оборотов в минуту, max [c.413]

В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через лоб/мин. Найдем зависимость между п об/мин и [c.122]

Вращение шпинделя осуществляется от двухскоростного электродвигателя 18 (число оборотов в минуту 720 или 1430) через коробку скоростей с зубчатыми колесами I—13 и две клиноременные передачи 14—15 и 16—17. Коробка скоростей позволяет получить шесть скоростей шпинделя при прямом, а также при обратном вращении электродвигателя. Настройка этой цепи осуществляется двумя переставными блоками зубчатых колес коробки передач блоком с колесами 5 и блоком с колесами 7, 9, 11. При зацеплении колес 3—4 или 5—6 вал с неподвижно закрепленными колесами 6, 8, 10 может вращаться с двумя скоростями. При зацеплении зубчатых колес 6—7, или 8—9, или 10—11 зубчатые колеса 12—13 и шкив 14 получают шесть скоростей вращения.

[c.356]

Так как величины угловых скоростей пропорциональны числам оборотов в минуту, имеем [c.288]

Определить число оборотов в минуту ведомого вала, если числа зубцов колес 1, 2, 3, 4 соответственно равны 2 = 20 z. = 40 Z3 = 30 24 = 60. [c.186]

Найдем соотнощение между угловой скоростью ш, выраженной в радианах в секунду, и числом оборотов в минуту. Если тело делает п оборотов в минуту, то оно поворачивается за каждую минуту на 2лп радианов, а за секунду—в 60 раз меньше, следовательно, [c.166]

Задача № 160 (№ 29.18,722 М). Посредством ремня (рис. 216) передается мощность 20 л. с. Радиус ременного шкива 50 см, число оборотов в минуту 150.

[c.378]

При проверке на виброустойчивость против поперечных и крутильных колебаний определяют собственную частоту колебаний (критическое число оборотов в минуту) и сравнивают ее с частотой возмущающих сил (фактическим числом оборотов в минуту) для оценки опасности появления резонанса 12 4]. [c.371]

В технике угловая скорость — это частота вращения, выраженная в оборотах в минуту. За 1 мин тело повернется на угол 2лп, если и — число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим [c.127]

Угловая скорость тела в данный момент характеризует скорость изменения во времени угла поворота и равна первой производной по времени от угла поворота. 2. В технике угловую скорость часто задают числом оборотов в минуту. 3. При сложении двух мгновенных вращений твёрдого тела вокруг параллельных осей в одном направлении получается результирующее мгновенное вращение вокруг оси, параллельной данным осям, с угловой скоростью, равной арифметической сумме составляющих угловых скоростей.

[c.91]

В технике угловую скорость равномерного вращения обычно характеризуют числом оборотов в минуту и обозначают эту величину через [c.295]

Построить кривую, абсциссами которой являются числа оборотов в минуту, а ординатами — необходимые диаметры сплошного стального вала, передающего 50 л. с. при допускаемом касательном напряжении 600 кг[см. Число оборотов менять в пределах 16— 16 ООО об/мин. [c.90]

Чугунный стержень АВ длиной /=1,8 м, вращается с постоянной угловой скоростью вокруг вертикальной оси 00 см. рисунок). Определить для этого стержня предельное число оборотов в минуту, если in

[c.299]

При каком числе оборотов в минуту произойдет разрушение [c.300]

П — число оборотов в минуту возмущающей силы (неуравновешенной массы двигателя) [c.55]

Определить числа оборотов в минуту водила Н и сателлита , если вал Oi вращается со скоростью, равной л, = 120 об1мин, [c.74]

Расстояние между центрами станка 445 мм скорость рабочего хода 22 м/мин, обратного 28 м1мин, диапазон бесступенчатых подач 0,03— —0,15 мм дв. ход номинальная тяговая сила станков 3000 кГ (29 430 н) мощность электродвигателя главного привода 14 кет, число оборотов в минуту 1000. [c.345]

Число оборотов в минуту наиболее распространенных усталостных машин обычно порядка 3000 (50 Гц). Поэтому испытание на усталость с целью получения предела выносливости требует продолжительного времени, исчисляемого неделями непрерывной работы машины. За последнее время во многих случаях при Ршс1 исследовании выносливости материалов и конструктив-ных деталей применяют более быстроходные машины — 100—500 Гц, а в некоторых случаях и 20 ООО Гц (ультразвуковые частоты).

[c.595]

При отсчете угла поворота в радианах и измерении времени в секундах угловая скорость измеряется в сел . В технике угловую скорость часто определяют числом оборотов в минуту (п об1мин). Связь между этими единицами измерения дается формулой [c.272]

Задача 1206. В регуляторе, изображенном па рис. 625, грузы А ц В имеют массы по 1 кг каждый, масса муфты 3 кг, длины стержней 10 ем. Определить число оборотов в минуту, которое совершает регулятор, если муфта С поднялась при этом на расстояние s==2 см, а при отсутствии вращения угол а равен нулю. Размерами грузов и муфты, а также трением преггебречь. [c.425]

Определить мощность, если вес гирь известен и равен Q, длина плеча равна I, а число оборотов в минуту п. Подобрать длину плеча так, чтобы мощность выражалась формулой N = Qnein. [c.377]

В технике часто в.место угловой скорости, при равномерном вращении тела (т. е. при ы = onst), пользуются понятием числа оборотов в минуту п (об/мин). Зависимость между угловой скоростью и число.м оборотов в минуту п определяется по формуле [c.111]

Исследования показывают, что число оборотов в минуту (я = ЗОмо/я), необходимое для обеспечения гироскопического эффекта, должно быть больше величины ял JJy , где Jх — соответственно экваториальный [c.74]

Скорость вращения шпинделя

Частота вращения шпинделя относится к характеристикам фрезерного станка и имеет обозначение в об/мин. Это скорость, с которой вращается шпиндель вместе с цанговым патроном и фрезой.

Шпиндели принято разделять на ременные и моторшпиндели (электрошпиндели). Первые характеризуются меньшим крутящим моментом. Конструкция классического шпинделя с ременным приводом имеет в составной части шпиндельный вал с подшипниками. Данный вал способен зажимать либо разжимать фрезу. Мощность и динамика передаются шпинделю от наружного мотора, который инсталлирован рядом с приспособлением посредством ременной передачи. Мощность, вращающий момент и скорость шпинделя зависят от характеристик внешнего двигателя и самой ременной передачи. За счет внешней инсталляции можно варьировать размеры мотора, тем самым изменяя обороты и мощность шпинделя, как в меньшую, так и в большую сторону. Применение шпинделей с ременной передачей возможно для задач, где требуемая скорость вращения шпинделя не превышает значение 12 000 – 15 000 об/мин. Из минусов – это ограничение по скорости в сравнении с электрошпинделем. Также натяжение ремня формирует излишнюю нагрузку на задние подшипники шпинделя, тем самым исчерпывая их ресурс.

Электрошпиндель — это приспособление, которое имеет в своей конструкции три ключевых звена: электрический асинхронный двигатель, патрон для зажима фрезы и подшипник. Предельные частоты вращения электрошпинделей — до 180 тысяч об/мин. Эти шпиндели являются более дорогостоящими по сравнению с ременными.

По количеству оборотов, шпиндели подразделяются:

Высокой мощности от 5 кВт и более: применяются в основном на крупногабаритных станках. Обороты составляют 12000…18000 об/мин. Предназначены для высокопроизводительных работ. Такое количество оборотов является большим минусом при работе с твёрдосплавными фрезами при фрезеровании тонкими фрезами, что существенно снижает общий КПД фрезерного станка.
Средней мощности 1.2…5 кВт: используются во фрезерных станках средних габаритов. Применяются для фрезерования пластиков, дерева и мягких металлов. Обороты составляют 18000…24000 об/мин. Идеально подходят для мелких гравировальных работ.
Малой мощности 0.8 кВт и менее: используются во фрезерных станках малых габаритов. Обороты составляют до 60000…70000 об/мин.

Скорость вращения вычисляется по формуле:

, где

d – диаметр режущей части инструмента (мм),

П – число Пи, постоянная величина равная 3.14;

V – скорость резания (м/мин) – это путь, пройденный точкой режущей кромки фрезы в единицу времени.

d – диаметр режущей части инструмента (мм),

П – число Пи, постоянная величина равная 3.14;

V – скорость резания (м/мин) – это путь, пройденный точкой режущей кромки фрезы в единицу времени.

Если у станка есть преимущество в виде преобразователя частоты (т.е. можно с легкостью варьировать скорость вращения шпинделя), то скорость мотора выбирается исходя из выбора диаметра фрезы и материала заготовки. Но важно знать, что при стремительном снижении скорости вращения потерю момента не миновать. В некоторой степени эта потеря возмещается инвертором благодаря функции поддержания крутящего момента при понижении скорости вращения шпинделя. Можно использовать данные из таблицы при выборе параметров соотношения количества оборотов двигателя к диаметру фрезы:

Диаметр фрезы	Скорость вращения
Свыше 25-50 мм	18 000 об/мин
Более 65-75 мм	12 000 об/мин
До 25 мм	24 000 об/мин
Более 50-65 мм	16 000 об/мин
Более 75 мм	10 000 об/мин

Опытным путем было установлено, что заявленные максимальные обороты в паспорте шпинделя не являются физической границей – абсолютно все высокоскоростные шпиндели без труда разгоняются до 120% от номинальных оборотов, и даже выше. Но при этом следует помнить, что ресурс подшипников может резко снизиться. И очень быстрое вращение не всегда хорошо, так как, например, дерево при фрезеровании образует мелкую пыль, которая затирается между материалом и режущим инструментом, и начинает подгорать. Как следствие, происходит перегрев фрезы и заготовки.

Пример влияния количества оборотов шпинделя при фрезеровании заготовки:

Исходя из вышеизложенного, подытожим, что многоцелевого шпинделя с большим диапазоном оборотов, увы, не существует. И важно оптимальное соотношение размера, мощности и максимальных оборотов шпинделя для решения той или иной задачи. Скорость подачи важно распределять равномерно, так как это существенно влияет на качество обработки. При вычислении оборотов шпинделя для того или иного материала необходимо обращать внимание на скорость резания и диаметр режущей части фрезы для оптимальной работы станка без погрешностей. При «закрытом» фрезеровании, где отвод стружки затруднен (пазы, шпунты, гнезда), миновать прижогов возможно, если на порядок уменьшить частоту вращения. Также необходимо учитывать ресурс подшипников при фрезеровании и искусственно не увеличивать число оборотов шпинделя, в зависимости от номинальных, с целью получения большей производительности.

Количество оборотов в минуту у электродвигателей

Электродвигатель обеспечивает преобразование электрической энергии в механическую. При выборе подходящего электродвигателя требуется учитывать многое: простота конструкции, надежность, стоимость, вес, несложное управление и т.д. В настоящее время электропривод с двигателем постоянного тока стремительно вытесняется асинхронным. Учитывая количество оборотов в минуту, подбирается наиболее подходящий электродвигатель.

Некоторые характеристики электродвигателей

Выбор электродвигателя до 1000 об/мин, как правило, происходит в случае отсутствия необходимости обеспечить вращение вала ротора на высокой скорости. Такой электродвигатель подойдет для установки на лебедку, кран, вибратор, тельфер, на различный подъемный механизм, транспортер и т. д.

Асинхронный электродвигатель до 3000 об/мин следует выбирать для установки на оборудование, на котором вал ротора должен вращаться с достаточно высокой скоростью. Такой электродвигатель может быть установлен на металлообрабатывающий и деревообрабатывающий станок, компрессор, холодильное оборудование и т.д. Нужно отметить, что электродвигатели асинхронные отличаются мощностью, габаритами и массой. Данные характеристики электродвигателей зависят друг от друга. К примеру, в случае увеличения мощности электродвигателя, наблюдается увеличение его массы и габаритов.

Что касается мощности электродвигателя асинхронного, то она может быть от 0,12 кВт до 200 кВт. Выбор электродвигателя той или иной мощности будет напрямую зависеть от размеров и предназначения оборудования, на которое двигатель будет установлен. Вес электродвигателя будет напрямую зависеть от его мощности.

Необходимо помнить о том, что электродвигатель с меньшим количеством оборотов будет отличаться большим весом, в сравнении с электродвигателем с большим количеством оборотов. При этом мощность такого оборудования будет одинаковой. Конструкция электродвигателя подбирается, исходя из климатических условий. Также понадобится учитывать некоторые особенности соединения двигателя с рабочим оборудованием. Купить качественные электродвигатели ответственных производителей Вы можете в нашей компании по разумной цене.

Дата: Воскресенье, 15 Декабрь 2013

Основные определения и формулы

Скорость резания V (м/мин) – это окружная скорость перемещения режущих кромок фрезы. Эта величина определяет эффективность обработки и лежит в рекомендованных для каждого инструментального материала пределах. За один оборот фрезы точка режущей кромки, находящаяся на окружности фрезы диаметра D (мм), сможет пройти путь, равный длине окружности, то есть πD. Для того чтобы определить длину пути, пройденного точкой за одну минуту, нужно умножить длину пути за один оборот на частоту вращения фрезы, то есть πDN (мм/мин). Таким образом, формула для определения скорости резания будет следующей:

V = πDN/1000 (мм/мин).

Частота вращения шпинделя N (об/мин) равняется числу оборотов фрезы в минуту. Вычисляется в соответствии с рекомендованной для данного типа обработки скоростью резания:

N = 1000V/nD (об/мин).

При фрезеровании различают минутную подачу, подачу на зуб и подачу наоборот фрезы.

Подача на зуб Fz (мм/зуб) – величина перемещения фрезы или рабочего стола с заготовкой за время поворота фрезы на один зуб.

Подача на оборот Fo (мм/об) – величина перемещения фрезы или рабочего стола с заготовкой за один оборот фрезы. Подача на оборот равняется произведению подачи на зуб на число зубьев фрезы Z:

Fo = FzZ (мм/об).

Минутной подачей Fm (мм/мин) называется величина относительного перемещения фрезы или рабочего стола с заготовкой за одну минуту. Минутная подача равняется произведению подачи на оборот на частоту вращения фрезы:

Fm = FoN = FzZN (мм/мин).

Глубиной фрезерования h (мм) называется расстояние между обработанной и необработанной поверхностями, измеряемое вдоль оси фрезы.

Шириной фрезерования b (мм) называется величина срезаемого припуска, измеренная в радиальном направлении, или ширина контакта заготовки и инструмента.

Производительность снятия материала Q (см³) – это объем удаляемого материала в единицу времени, определяемый глубиной, шириной обработки и величиной подачи.

Q = (h × b × Fm)/1000.

Western Digital считает скорость вращения жёстких дисков по-своему — обороты зависят от маркетинга

На прошлой неделе участники форума Reddit DataHoarder снова заметили странный маркетинг Western Digital — на этот раз речь идёт о неверном информировании о скорости вращения жёстких дисков WD Red NAS. А участники немецкоязычного форума hardwareluxx.de начали исследовать эту проблему ещё более года назад.

Это напоминает ситуацию, когда Western Digital не раскрывала должным образом использование сомнительной технологии Shingled Magnetic Recording (SMR) в своих накопителях для NAS. Новая проблема заключается в том, что Western Digital называет диски с частотой оборотов шпинделя 7200 в минуту (RPM) «классом 5400 RPM», а собственная прошивка дисков сообщает показатель 5400 RPM через интерфейс SMART.

Участник Reddit Amaroko решил доказать или опровергнуть выводы, сделанные ранее пользователями Сети. Несколько моделей дисков Amaroko отдельно помещал в пустую картонную коробку с микрофоном Blue Yeti, а затем включал диск. Спектральный анализ записанного звука с помощью Adobe Audition показал базовую частоту 120 Гц для двух моделей накопителя WD 8 Тбайт класса 5400 RPM.

Анализ WD Blue указывает на 90 Гц — 5400 RPM

120 циклов в секунду, умноженные на 60 секунд, дают 7200 оборотов в минуту. Другими словами, эти приводы «класса 5400 RPM» в действительности вращаются на скорости 7200 RPM. На первый взгляд может показаться, что это не проблема — кто бы не предпочёл привод с более высокой скоростью вращения шпинделя? Более быстрые шпиндели означают не только потенциально более низкие задержки — они, к сожалению, приводят и к резкому увеличению шума и энергопотребления.

Именно увеличение шума и мощности заставило многих пользователей задуматься о реальной скорости работы шпинделя в дисках Western Digital с заявленными характеристиками 5400 RPM. Они приобрели диски, которые, как они ожидали, будут медленно вращаться, но получили шумные накопители с повышенным тепловыделением.

Анализ WD Elements 8 Тбайт с «классом 5400 RPM» указывает на частоту 120 Гц — 7200 RPM

Сравнивая данные Seagate Barracuda 5400 RPM и Western Digital Red «класса 5400 RPM», который, как показал спектральный анализ звука, на самом деле вращается со скоростью 7200 RPM, можно увидеть явную разницу в энергопотреблении. 8-Тбайт Red потребляет 8,8 Вт против 5,3 Вт у Barracuda в активном состоянии и 800 мВт против 250 мВт у Barracuda в режиме ожидания. Разница здесь, по большей части, не в марке — при вращении на одинаковой скорости диски Western Digital и Seagate потребляют примерно одну и ту же мощность.

По правде говоря, сегодня пользователи попросту не могут купить накопитель ёмкостью 8 Тбайт для NAS, который бы вращался с реальной скоростью в 5400 RPM: и WD Red, и серия Seagate Ironwolf используют шпиндели со скоростью 7200 Western Digital. Но вообще-то показатель «RPM» имеет очень конкретное значение, и в таблице характеристик WD Red нет даже сноски, объясняющей, что на деле означает их «класс производительности 5400 RPM».

Анализ WD MyBook 8 Тбайт с «классом 5400 RPM» указывает на 120 Гц — 7200 RPM

Когда журналисты Anandtech связались с Western Digital в ходе проверки этой истории, представитель компании подтвердил выводы пользователей на форумах Reddit: «класс 5400 RPM» не означает, что привод действительно вращается со скоростью 5400 RPM:

«Для некоторых продуктов Western Digital уже много лет публикует скорость вращения в пределах «класса» или «класса производительности», а не сообщаются конкретные скорости вращения шпинделя. Мы также точно настраиваем выбранные платформы жёстких дисков и соответствующие характеристики, чтобы создать несколько различных вариантов для удовлетворения различных потребностей рынка или сценариев. Поступая таким образом, мы получаем возможность экономить за счёт масштаба производства и предлагать продукцию нашим клиентам по более доступной цене. Как и в случае с каждым продуктом Western Digital, наша информация, включая мощность, акустику и производительность (скорость передачи данных), проверяется на соответствие спецификациям, указанным в технических характеристиках продукта и маркетинговых материалах».

Если провести автомобильную аналогию, это всё равно что продавать 6-цилиндровый седан как «четырёхцилиндровый класс», не указывая прямо, что находится под капотом автомобиля.

Если вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.

Кинематика — Физика — Теория, тесты, формулы и задачи

Основные теоретические сведения

Система СИ

К оглавлению. ..

Основные единицы измерения величин в системе СИ таковы:

единица измерения длины — метр (1 м),
времени — секунда (1 с),
массы — килограмм (1 кг),
количества вещества — моль (1 моль),
температуры — кельвин (1 К),
силы электрического тока — ампер (1 А),
Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).

При выполнении расчетов в системе СИ углы измеряются в радианах.

Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.

Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.

Таблица дольных и кратных приставок в физике:

Путь и перемещение

К оглавлению…

Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.

Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.

Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.

Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.

Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.

Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.

Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.

При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:

где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.

Средняя скорость

К оглавлению…

Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.

Средняя скорость пути – это отношение всего пути ко всему времени движения:

где: L_полн – весь путь, который прошло тело, t_полн – все время движения.

Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:

Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.

При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.

Равноускоренное прямолинейное движение

К оглавлению…

Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:

где: v₀ – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).

Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.

Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».

Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:

Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:

В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):

С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.

Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:

Свободное падение по вертикали

К оглавлению…

На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:

Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.

Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.

Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v₀, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

Горизонтальный бросок

К оглавлению…

При горизонтальном броске с начальной скоростью v₀ движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.

Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна v_x = v₀. А вертикальная возрастает по законам ускоренного движения v_y = gt. При этом полная скорость тела может быть найдена по формулам:

При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:

Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:

Угол между горизонтом и скоростью тела легко найти из соотношения:

Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:

Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:

Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:

При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:

Бросок под углом к горизонту (с земли на землю)

К оглавлению…

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):

Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:

Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.

Сложение скоростей

К оглавлению…

Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:

Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.

Равномерное движение по окружности

К оглавлению…

Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.

Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:

Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:

В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:

При равномерном вращении скорость тела будет определяется следующим образом:

где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:

Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:

Связь между модулем линейной скорости v и угловой скоростью ω:

При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).

Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:

Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.

Кинематика вращательного движения | Физика

Цели обучения

К концу этого раздела вы сможете:

Соблюдайте кинематику вращательного движения.
Составьте кинематические уравнения вращения.
Оценить стратегии решения проблем для вращательной кинематики.

Просто используя нашу интуицию, мы можем начать видеть, как вращательные величины, такие как θ , ω и α , связаны друг с другом. Например, если колесо мотоцикла имеет большое угловое ускорение в течение довольно длительного времени, оно быстро вращается и совершает много оборотов. С технической точки зрения, если угловое ускорение α колеса велико в течение длительного периода времени t , то конечная угловая скорость ω и угол поворота θ будут большими. Вращательное движение колеса в точности аналогично тому, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.

Кинематика — это описание движения. Кинематика вращательного движения описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем. Начнем с поиска уравнения, связывающего ω , α и t . Чтобы определить это уравнение, вспомним знакомое кинематическое уравнение поступательного или прямолинейного движения:

[латекс] v = {v} _ {0} + {at} \\ [/ latex] (константа a )

Обратите внимание, что во вращательном движении a = a _t, и с этого момента мы будем использовать символ a для тангенциального или линейного ускорения. Как и в линейной кинематике, мы предполагаем, что a является постоянным, что означает, что угловое ускорение α также является постоянным, потому что a = rα . Теперь давайте подставим v = rω и a = rα в приведенное выше линейное уравнение:

rω = rω ₀ + крыс.

Радиус r сокращается в уравнении, давая

ω = ω ₀ + ат. (постоянная a )

где ω ₀ — начальная угловая скорость. Это последнее уравнение представляет собой кинематическое соотношение между ω , α и t , то есть оно описывает их соотношение без ссылки на силы или массы, которые могут влиять на вращение. Он также точно аналогичен по форме своему трансляционному аналогу.

Выполнение подключений Кинематика вращательного движения полностью аналогична поступательной кинематике, впервые представленной в «Одномерной кинематике».

Кинематика занимается описанием движения без учета силы или массы. Мы обнаружим, что поступательные кинематические величины, такие как смещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.

Исходя из четырех кинематических уравнений, которые мы разработали в Одномерной кинематике, мы можем вывести следующие четыре кинематических уравнения вращения (представленные вместе с их аналогами для поступательного движения):

Таблица 1. Кинематические уравнения вращения
ротационный	Трансляционный
[латекс] \ theta = \ bar {\ omega} t \\ [/ latex]	[латекс] x = \ bar {v} t \\ [/ latex]
ω = ω ₀ + αt	v = v _o + при	(постоянная α , a )
[латекс] \ theta = {\ omega} _ {0} t + \ frac {1} {2} {\ alpha t} ^ {2} \\ [/ latex]	[латекс] x = {v} _ {0} t + \ frac {1} {2} {\ text {at}} ^ {2} \\ [/ latex]	(постоянная α , a )
ω ² = ω ₀ ² + 2 α θ	v ² = v _o ² + 2ax	(постоянная α , a )

В этих уравнениях индекс 0 обозначает начальные значения ( θ ₀ , x ₀ и t ₀ — начальные значения) и среднюю угловую скорость [латекс] \ bar {\ omega} \\ [/ latex] и средняя скорость [latex] \ bar {v} \\ [/ latex] определяются следующим образом:

[латекс] \ bar {\ omega} = \ frac {{\ omega} _ {0} + \ omega} {2} \ text {и} \ overline {v} = \ frac {{v} _ {0} + v} {2} \\ [/ латекс].

Уравнения, приведенные выше в таблице 1, можно использовать для решения любой задачи вращательной или поступательной кинематики, в которой a и α постоянны.

Стратегия решения проблем вращательной кинематики

Изучите ситуацию, чтобы определить, задействована ли кинематика вращения (вращательное движение) . Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.
Определите, что именно необходимо определить в проблеме (определите неизвестные) .Набросок ситуации полезен.
Составьте список того, что дано или может быть выведено из проблемы, как указано (определить известные) .
Решите соответствующее уравнение или уравнения для количества, которое необходимо определить (неизвестное) . Может быть полезно думать в терминах трансляционного аналога, потому что теперь вы знакомы с таким движением.
Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами . Обязательно используйте радианы для углов.
Проверьте свой ответ, чтобы убедиться, что он разумен: Имеет ли смысл ваш ответ ?

Пример 1. Расчет ускорения рыболовной катушки

Глубоководный рыбак ловит большую рыбу, которая отплывает от лодки, выдергивая леску из своей рыболовной катушки. Вся система изначально находится в состоянии покоя, а леска разматывается с катушки на радиусе 4,50 см от оси вращения. Катушке дается угловое ускорение 110 рад / с ² для 2.00 с, как показано на рисунке 1. (a) Какова конечная угловая скорость барабана? (b) С какой скоростью леска покидает катушку по прошествии 2,00 с? (c) Сколько оборотов делает катушка? (d) Сколько метров лески сошло с катушки за это время?

Стратегия

В каждой части этого примера стратегия такая же, как и для решения задач линейной кинематики. В частности, идентифицируются известные значения и затем ищется взаимосвязь, которая может использоваться для определения неизвестного.

Решение для (a)

Здесь даны α и t , и необходимо определить ω . Самым простым уравнением для использования является ω = ω ₀ + αt , потому что неизвестное уже находится на одной стороне, а все остальные члены известны. Это уравнение утверждает, что

ω = ω ₀ + αt .

Нам также дано, что ω ₀ = 0 (начинается с состояния покоя), так что

ω = 0 + (110 рад / с ²) (2.00 с) = 220 рад / с

Решение для (b)

Теперь, когда известно ω , скорость v легче всего найти, используя соотношение

v = rω ,

, где радиус r барабана задан равным 4,50 см; таким образом,

v = (0,0450 м) (220 рад / с) = 9,90 м / с.

Еще раз обратите внимание, что радианы всегда должны использоваться в любых вычислениях, касающихся линейных и угловых величин. {2} = \ text {220 рад}. \ End {array} \\ [/ latex]

Преобразование радианов в обороты дает

[латекс] \ theta = (220 \ text {rad}) \ frac {1 \ text {rev}} {2 \ pi \ text {rad}} = 35.0 \ text {rev} \\ [/ latex]

Решение для (d)

Количество метров лески — x , которое может быть получено через ее соотношение с θ:

x = rθ = (0,0450 м) (220 рад) = 9,90 м.

Обсуждение

Этот пример показывает, что отношения между вращательными величинами очень похожи на отношения между линейными величинами.Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После раскручивания в течение двух секунд катушка вращается со скоростью 220 рад / с, что составляет 2100 об / мин. (Неудивительно, что барабаны иногда издают высокие звуки.) Длина разыгранной лески составляет 9,90 м, что примерно соответствует тому моменту, когда клюет большая рыба.

Рис. 1. Леска, сходящая с вращающейся катушки, движется линейно. В примерах 10.3 и 10.4 рассматриваются отношения между вращательными и линейными величинами, связанными с рыболовной катушкой.

Пример 2. Расчет продолжительности, когда рыболовная катушка замедляется и останавливается

Теперь давайте посмотрим, что произойдет, если рыбак затормозит вращающуюся катушку, получив угловое ускорение -300 рад / с ². Как долго катушка останавливается?

Стратегия

Нам предлагается найти время t , за которое барабан остановится. Начальные и конечные условия отличаются от условий в предыдущей задаче, в которой использовалась та же рыболовная катушка.Теперь мы видим, что начальная угловая скорость равна ω ₀ = 220 рад / с, а конечная угловая скорость ω равна нулю. Угловое ускорение составляет α = -300 рад / с ². Изучая доступные уравнения, мы видим, что все величины, кроме t , известны в ω = ω ₀ + αt , что упрощает использование этого уравнения.

Решение

Уравнение утверждает

ω = ω ₀ + αt .{2}} = 0 \ text {.} \ Text {733 s} \\ [/ latex].

Обсуждение

Обратите внимание, что следует проявлять осторожность со знаками, указывающими направления различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда ломается из-за участвующих в ней ускорений, и рыбаки часто позволяют рыбе плавать некоторое время, прежде чем затормозить катушку. Уставшая рыба будет медленнее, требуя меньшего ускорения.

Пример 3. Расчет медленного ускорения поездов и их колес

Большие грузовые поезда очень медленно ускоряются. Предположим, что один такой поезд ускоряется из состояния покоя, придавая своим колесам радиусом 0,350 м угловое ускорение 0,250 рад / с ². После того, как колеса совершат 200 оборотов (предположим, что проскальзывания нет): а) Как далеко поезд продвинулся по рельсам? б) Какова конечная угловая скорость колес и линейная скорость поезда?

Стратегия

В части (а) нас просят найти x , а в (b) нас просят найти ω и v . Нам даны число оборотов θ , радиус колес r и угловое ускорение α .

Решение для (a)

Расстояние x очень легко найти из отношения между расстоянием и углом поворота:

[латекс] \ theta = \ frac {x} {r} \\ [/ latex].

Решение этого уравнения для x дает

x = rθ.

Перед использованием этого уравнения мы должны преобразовать количество оборотов в радианы, потому что мы имеем дело с соотношением между линейными и вращательными величинами:

[латекс] \ theta = \ left (\ text {200} \ text {rev} \ right) \ frac {2 \ pi \ text {rad}} {\ text {1 rev}} = \ text {1257} \ текст {рад} \\ [/ латекс].{1/2} \\ & = & \ text {25,1 рад / с.} \ End {array} \\ [/ latex]

Мы можем найти линейную скорость поезда, v , через ее отношение к ω :

v = rω = (0,350 м) (25,1 рад / с) = 8,77 м / с.

Обсуждение

Пройденное расстояние довольно велико, а конечная скорость довольно мала (чуть менее 32 км / ч).

Существует поступательное движение даже для чего-то, вращающегося на месте, как показано в следующем примере.На рис. 2 изображена муха на краю вращающейся пластины микроволновой печи. В приведенном ниже примере вычисляется общее пройденное расстояние.

Рис. 2. На изображении показана микроволновая пластина. Муха совершает обороты, пока еда разогревается (вместе с мухой).

Пример 4. Расчет расстояния, пройденного мухой на краю плиты микроволновой печи

Человек решает использовать микроволновую печь, чтобы разогреть обед. При этом муха случайно влетает в микроволновку, приземляется на внешний край вращающейся пластины и остается там.Если тарелка имеет радиус 0,15 м и вращается со скоростью 6,0 об / мин, рассчитайте общее расстояние, пройденное мухой за 2,0-минутный период приготовления. (Игнорируйте время запуска и замедления.)

Стратегия

Сначала найдите общее количество оборотов θ , а затем пройденное линейное расстояние x .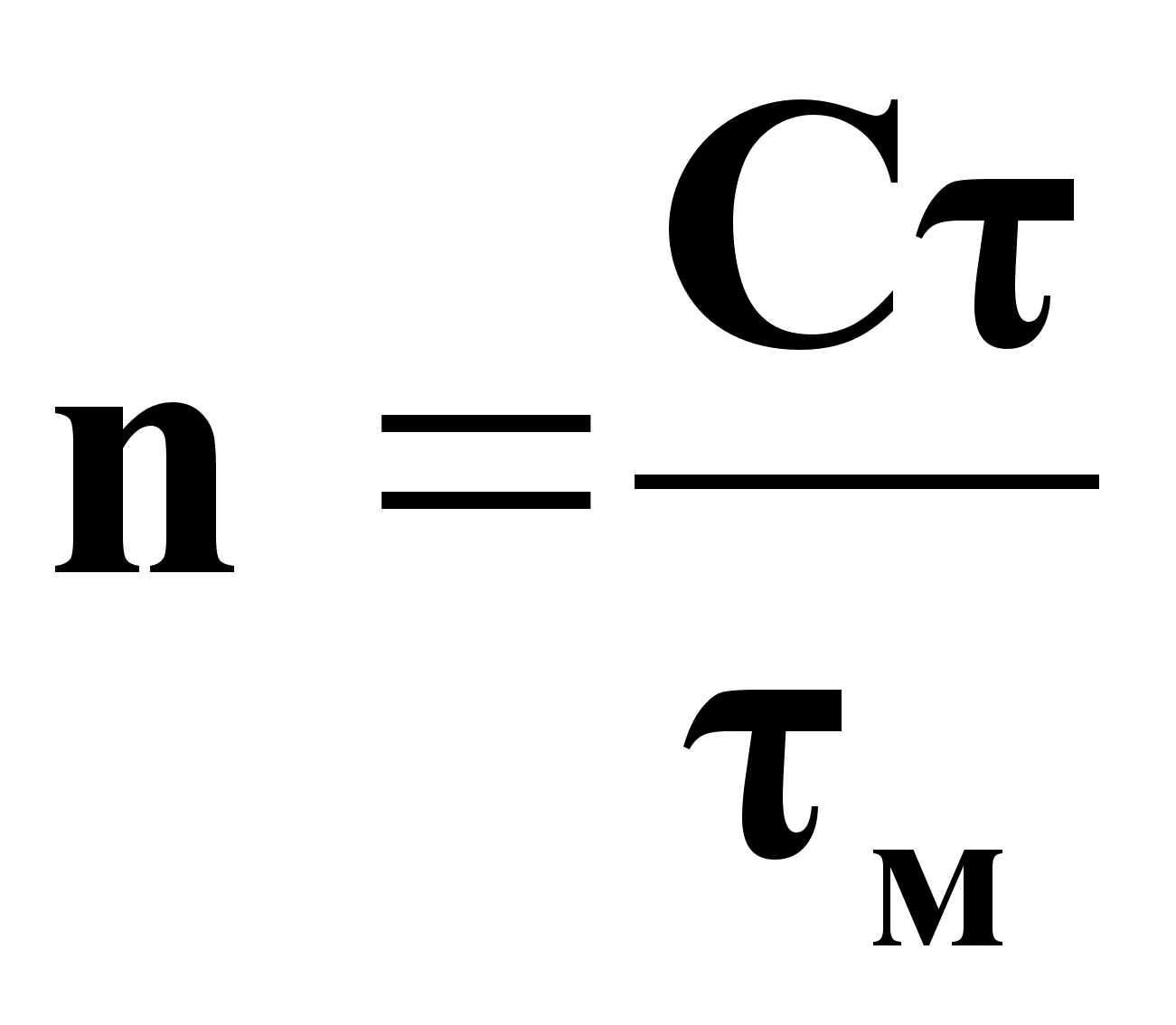 [latex] \ theta = \ bar {\ omega} t \\ [/ latex] можно использовать, чтобы найти θ потому что [latex] \ bar {\ omega} \\ [/ latex] задано равным 6,0 об / мин.

Решение

Ввод известных значений в [latex] \ theta = \ bar {\ omega} t \\ [/ latex] дает

[латекс] \ theta = \ bar {\ omega} t = \ left (\ text {6.0 об / мин} \ right) \ left (\ text {2.0 min} \ right) = \ text {12 rev} \\ [/ latex].

Как всегда, необходимо преобразовать обороты в радианы перед вычислением линейной величины, такой как x , из угловой величины, такой как θ :

[латекс] \ theta = \ left (\ text {12 rev} \ right) \ left (\ frac {2 \ pi \ text {rad}} {\ text {1 rev}} \ right) = 75,4 \ text { рад} \\ [/ латекс].

Теперь, используя соотношение между x и θ , мы можем определить пройденное расстояние:

x = rθ = (0.15 м) (75,4 рад) = 11 м.

Обсуждение

Неплохая поездка (если выживет)! Обратите внимание, что это расстояние — это общее расстояние, пройденное мухой. Смещение фактически равно нулю для полных оборотов, потому что они возвращают муху в исходное положение. Различие между общим пройденным расстоянием и перемещением было впервые отмечено в «Одномерной кинематике».

Проверьте свое понимание

Кинематика вращения имеет множество полезных взаимосвязей, часто выражаемых в форме уравнений.Являются ли эти отношения законами физики или они просто описательны? (Подсказка: тот же вопрос относится к линейной кинематике.)

Решение

Кинематика вращения (как и линейная кинематика) носит описательный характер и не отражает законы природы. С помощью кинематики мы можем описать многие вещи с большой точностью, но кинематика не учитывает причины. Например, большое угловое ускорение описывает очень быстрое изменение угловой скорости без учета его причины.

Сводка раздела

Задачи и упражнения

1. С помощью струны гироскоп из состояния покоя разгоняется до 32 рад / с за 0,40 с. а) Каково его угловое ускорение в рад / с ²? б) Сколько революций происходит в процессе?

2. Допустим, на компакт-диске оказался кусок пыли. Если скорость вращения компакт-диска составляет 500 об / мин, а пылинка находится на расстоянии 4,3 см от центра, какое общее расстояние проходит пыль за 3 минуты? (Игнорируйте ускорения из-за вращения компакт-диска.)

3. Гироскоп замедляется с начальной скорости 32,0 рад / с до 0,700 рад / с ². а) Сколько времени нужно, чтобы успокоиться? б) Сколько оборотов он делает до остановки?

4. При очень быстрой остановке автомобиль замедляется со скоростью 700 м / с ².

(a) Каково угловое ускорение его шин радиусом 0,280 м, если предположить, что они не скользят по тротуару?
(b) Сколько оборотов делают шины перед остановкой, если их начальная угловая скорость равна 95.0 рад / с?
(c) Сколько времени нужно автомобилю, чтобы полностью остановиться?
(d) Какое расстояние машина проезжает за это время?
(e) Какова была начальная скорость автомобиля?
(f) Кажутся ли полученные значения разумными, учитывая, что эта остановка происходит очень быстро?

Рис. 3. Йо-йо — это забавные игрушки, которые демонстрируют значительную физику и созданы для повышения производительности на основе физических законов. (Источник: Beyond Neon, Flickr)

5. Повседневное применение: Предположим, у йо-йо есть центральный вал с цифрой 0.Радиус 250 см и натягивается его веревка.

(a) Если струна неподвижна и йо-йо ускоряется от нее со скоростью 1,50 м / с ², каково угловое ускорение йо-йо?
(b) Какова угловая скорость через 0,750 с, если она начинается из состояния покоя?
(c) Внешний радиус йо-йо составляет 3,50 см. Каково тангенциальное ускорение точки на краю?

Глоссарий

кинематика вращательного движения:: описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем

Избранные решения проблем и упражнения

1.{2} \\ [/ latex] (b) 1.0 rev

3. (а) 45.7 с (б) 116 изм.

5. (а) 600 рад / с ² (б) 450 рад / с (в) 21,0 м / с

Угловая и линейная скорость

и об / мин

Purplemath

По некоторым причинам учебники часто обращаются к вопросам угловой скорости, линейной скорости и оборотов в минуту (об / мин) вскоре после объяснения секторов круга, их площади и длины дуги.

Длина дуги — это расстояние до части окружности; и линейное расстояние, которое преодолевает, скажем, велосипед, связано с радиусом шин велосипеда. Если вы отметите одну точку на передней шине велосипеда (скажем, точку напротив клапана шины) и посчитаете количество оборотов колеса, вы можете найти количество окружностей окружности, на которые переместилась отмеченная точка.

MathHelp.

com

Если вы «раскрутите» эти окружности, чтобы получить прямую линию, то вы найдете расстояние, которое проехал велосипед. Я думаю, что именно из-за такого рода взаимоотношений между различными показателями эта тема часто возникает на данном этапе исследования.

Во-первых, нам нужна техническая терминология и определения.

«Угловая скорость» — это показатель поворота в единицу времени. Он сообщает вам размер угла, под которым что-то вращается за определенный промежуток времени. Например, если колесо вращается шестьдесят раз за одну минуту, то его угловая скорость составляет 120π радиан в минуту. Затем угловая скорость измеряется в радианах в секунду, греческая строчная омега (ω) часто используется в качестве ее названия.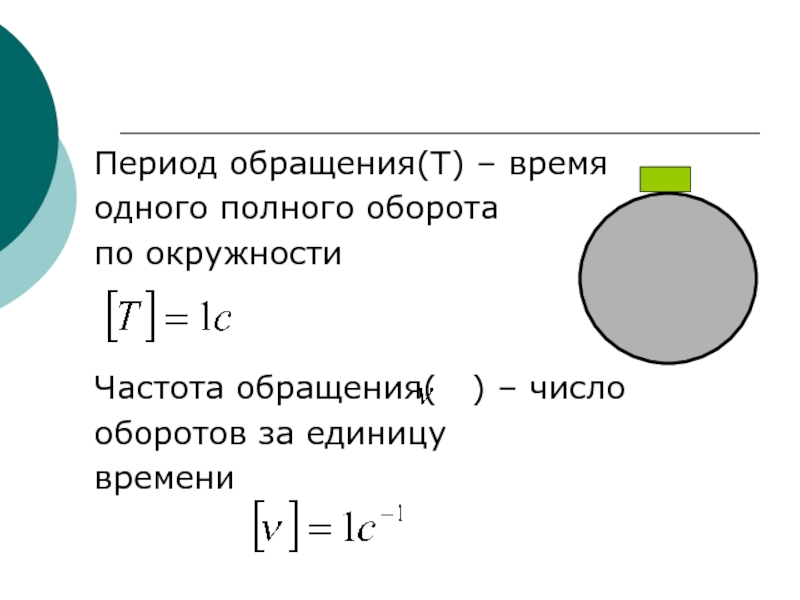

«Линейная скорость» — это мера расстояния в единицу времени. Например, если колесо в предыдущем примере имеет радиус 47 сантиметров, то каждый проход по окружности составляет 94π см, или около 295 см. Поскольку колесо совершает шестьдесят таких оборотов за одну минуту, общая пройденная длина составляет 60 × 94 & pi = 5640π см, или около 177 метров, за одну минуту. (Это примерно 10,6 км / ч или около 6,7 миль / ч)

«Число оборотов в минуту», обычно сокращенно «об / мин», является мерой вращения за единицу времени, но единица времени — всегда одна минута.И вместо того, чтобы указывать угол поворота, он просто дает количество поворотов. Когда вы смотрите на тахометр на приборной панели автомобиля, вы смотрите на текущие обороты двигателя автомобиля. В приведенном выше примере частота вращения будет просто «60».

«Частота» f — это мера вращения (или вибрации) за единицу времени, но единицей времени всегда является одна секунда. Единицей измерения частот является «герц», который обозначается как Гц.

Соотношение между частотой f (в Гц), об / мин и угловой скоростью ω (в радианах) показано ниже (все элементы в любой строке эквивалентны):

Однако вы можете обнаружить, что «угловая скорость» используется взаимозаменяемо (но только неофициально; не учеными) с оборотами в минуту или частотой.Кроме того, некоторые (например, физики) считают, что «угловая скорость» является векторной величиной, а ω — скалярной величиной, называемой «угловой частотой».

Пожалуйста, не запоминайте эти потенциальные слияния и не беспокойтесь о том, какими могут быть «векторы» или «скаляры». Я говорю вам об этом, чтобы предупредить вас, что вы должны уделять очень пристальное внимание тому, как ваш конкретный учебник и ваш конкретный преподаватель определяют различные термины для этого конкретного класса. И знайте, что на следующем уроке термины и определения могут быть другими.

Колесо имеет диаметр 100 сантиметров. Если колесо поддерживает тележку, движущуюся со скоростью 45 километров в час, то какова частота вращения колеса с точностью до целого числа оборотов в минуту?

«Об / мин» — это количество оборотов колеса в минуту.Чтобы выяснить, сколько раз это колесо вращается за одну минуту, мне нужно найти (линейное или прямое) расстояние, пройденное (за минуту) при движении со скоростью 45 км / ч. Затем мне нужно будет найти длину окружности колеса и разделить общее поминутное (линейное) расстояние на это «разовое» расстояние. Количество окружностей, которые умещаются в пределах общего расстояния, — это количество оборотов колеса за этот период времени.

Сначала я переведу (линейную) скорость тележки из км / ч в «сантиметры в минуту», используя то, что я узнал о преобразовании единиц. (Почему «сантиметры в минуту»? Потому что я ищу «обороты в минуту», поэтому минуты — лучшая единица времени, чем часы. Кроме того, диаметр дан в сантиметрах, так что это лучшая единица длины, чем километры. )

Итак, расстояние, пройденное за одну минуту, составляет 75 000 сантиметров. Диаметр колеса — 100 см, поэтому радиус — 50 см, а длина окружности — 100π см. Сколько из этих окружностей (или оборотов колеса) умещается внутри 75 000 см? Другими словами, если бы я снял протектор этого колеса с тележки и разложил его ровно, то получилось бы расстояние 100π см.Сколько из этих длин укладывается на все расстояние, пройденное за одну минуту? Чтобы узнать, сколько из (этого) вписывается в такое количество (этого), я должен разделить (это) на (это), поэтому:

Затем, округляя до ближайшего целого числа оборотов (то есть округляя ответ до целого числа), мой ответ:

Примечание. Эта скорость не такая высокая, как может показаться: чуть меньше четырех оборотов в секунду. Вы можете сделать это на своем велосипеде, не вспотев.Вот еще одно примечание: источник, из которого я получил свою схему для вышеупомянутого упражнения, использовал «угловую скорость» и «ω» для «числа оборотов в минуту». Да, в учебнике алгебры использовались неправильные единицы измерения.

Предыдущее упражнение давало информацию о скорости автомобиля и колесе. Отсюда мы нашли количество оборотов в минуту. Мы можем пойти и другим путем; мы можем начать с числа оборотов в минуту (плюс информацию о колесе) и найти скорость транспортного средства.

Велосипедное колесо имеет диаметр 78 см. Если колесо вращается со скоростью 120 оборотов в минуту, какова линейная скорость велосипеда в километрах в час? Округлите ответ до одного десятичного знака.

Линейная скорость — это расстояние по прямой, которое велосипед проходит за определенный период времени. Они дали мне количество оборотов колеса в минуту. Фиксированная точка на шине (скажем, камешек на протекторе шины) перемещает длину окружности за каждый оборот. Раскручивая это расстояние по земле, велосипед будет двигаться по земле на одинаковое расстояние, по одной окружности за раз, за каждый оборот. Итак, в этом вопросе меня просят найти длину окружности, а затем использовать ее, чтобы найти общее расстояние, пройденное за минуту.

Так как диаметр равен 78 см, то окружность равна C = 78π см.Разматывая путь шины до прямой линии на земле, это означает, что велосипед перемещается на 78π см вперед за каждый оборот шины. Таких оборотов в минуту 120, итого:

(78π см / об) × (120 об / мин) = 9,360π см / мин

Теперь мне нужно преобразовать это из сантиметров в минуту в километры в час:

Велосипед движется со скоростью около 17,6 км / ч.

… или около одиннадцати миль в час.

Предположим, что орбита Земли круглая с радиусом 93 000 000 миль, и пусть «один год» равен 365,25 дням. В этих условиях найдите линейную скорость Земли в милях в секунду. Округлите ответ до одного десятичного знака.

Скорость — это (линейное или эквивалентное прямолинейное) расстояние, пройденное за одну секунду, деленное на одну секунду.Они дали мне информацию за год, так что я начну с этого. Окружность круга с r = 93000000 миль будет линейным расстоянием, которое Земля преодолеет за один год.

C = 2π (93000000 миль) / год = 186000000π миль / год

Это количество миль, пройденных за один год, но мне нужно количество миль, пройденных за одну секунду.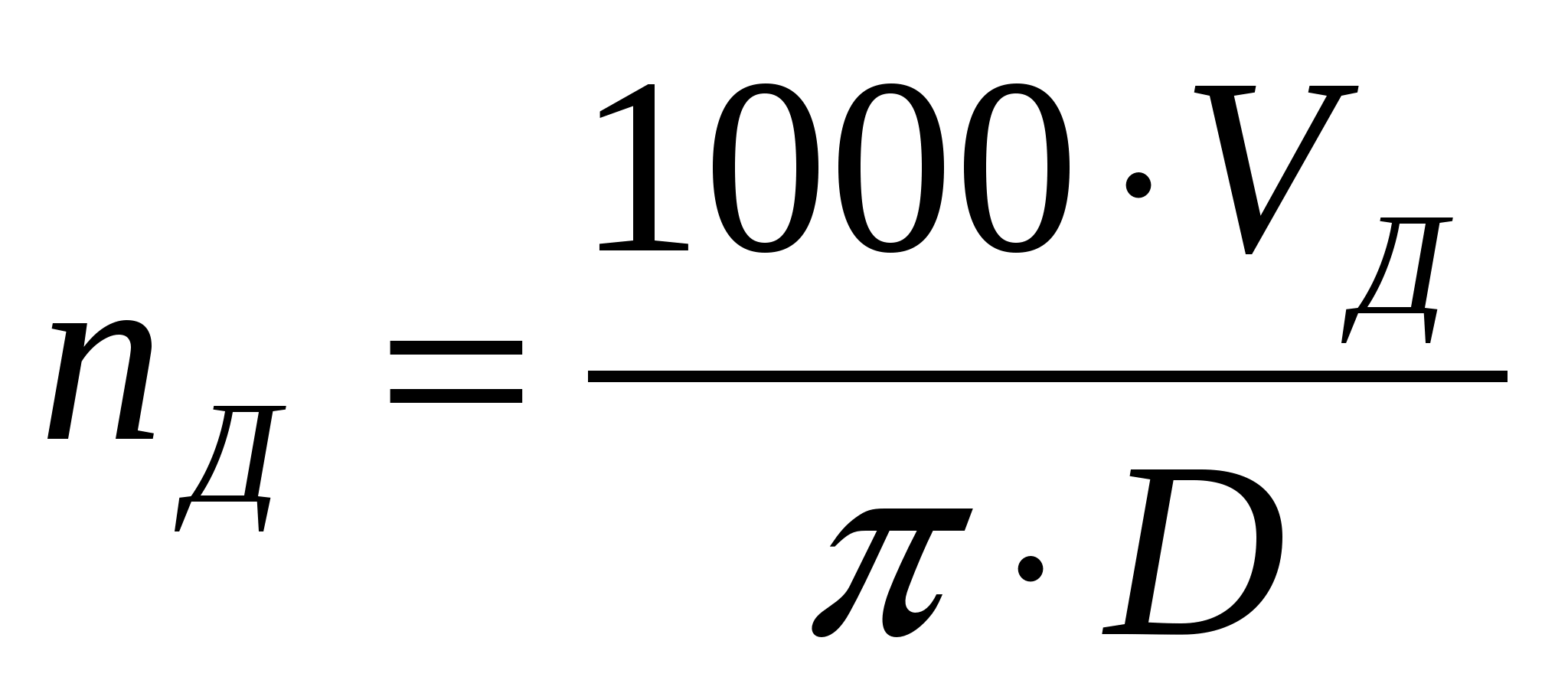 В сутках двадцать четыре часа, в часе шестьдесят минут и в минуте шестьдесят секунд, поэтому общее количество секунд в этом году составляет:

Тогда линейная скорость, представляющая собой общее линейное расстояние, деленное на общее время и выраженное в единицах скорости, равна:

Тогда, округленная до одного десятичного знака, линейная скорость Земли равна:

«Эй!» Я слышу, как ты плачешь.»Когда мы собираемся использовать угловые меры для чего-нибудь?» Хотя многие («большинство»?) Упражнений в вашей книге, вероятно, будут похожи на приведенные выше, иногда вы можете столкнуться с фактическими радианами и градусами.

Поезд движется со скоростью 10 миль в час по кривой радиусом 3000 футов. На какой угол повернется поезд за одну минуту? Округлить до ближайшего целого числа градусов.

«Кривая радиуса 3000 футов» означает, что, если бы я попытался плотно подогнать круг внутри кривой, наилучшим образом подошел бы круг с радиусом r = 3000 футов.Другими словами, я могу использовать факты круга, чтобы ответить на этот вопрос.

Так как радиус кривой выражен в футах и мне нужно найти угол, пройденный за одну минуту, я начну с преобразования скорости миль в час в футы в секунду:

(10 миль / час) (5280 фут / миль) (1 час / 60 мин) = 880 фут / мин

Длина изогнутого пути, который проходит поезд, также является частью окружности круга.Итак, эти 880 футов и есть длина дуги, и теперь мне нужно найти дополнительный угол (подразумеваемого) сектора круга:

Но это значение в радианах (потому что это то, что использует формула длины дуги), и мне нужно, чтобы мой ответ был в градусах, поэтому мне нужно преобразовать:

Поезд поворачивает на угол примерно:

Представьте, что вы стоите в центре этого воображаемого круга (то есть на расстоянии трех тысяч футов от поворота, более чем в полумиле) и наблюдаете, как поезд движется по повороту. Если вы протянете руку на расстоянии вытянутой руки, сожмете кулак и, крепко прижав средние пальцы большим пальцем вниз, приподнимите мизинец и указательный пальцы, расстояние между ними составит около пятнадцати градусов. Поезд вряд ли продвинется дальше. Если бы вы держали кулак на расстоянии вытянутой руки и вытянули мизинец и большой палец, расстояние было бы около двадцати пяти градусов. Поезд не выйдет из ваших пальцев в отведенное время.

(Иногда я узнаю самые крутые вещи, когда исследую проблемы со словами.Опять же, мое определение «крутого» может быть немного грустным ….)

URL: https://www.purplemath.com/modules/sectors3.htm

Равномерное круговое движение

Введение

Равномерное круговое движение — это движение объекта, движущегося с постоянной (равномерной) скоростью по круговой траектории.

Помимо скорости, есть несколько других переменных, которые используются для характеристики движения. Это радиус движения r , угловая скорость ω , период T и частота вращения f . Период — это время, необходимое для того, чтобы объект совершил один оборот движения. Угловая скорость — это угловое смещение в секунду, которое связано с частотой следующим образом: с ω в рад / с.Частота вращения — это количество оборотов в секунду и определяется как: с f в Гц или сек ^-1. скорость объекта является касательной к окружности с величиной v = rω . Ускорение , a направлено к центру круга (центростремительное) с величиной, определяемой следующим образом: с a м / с ². Чтобы объект массой м мог двигаться по окружности с постоянной скоростью, на объект должна действовать чистая центростремительная сила.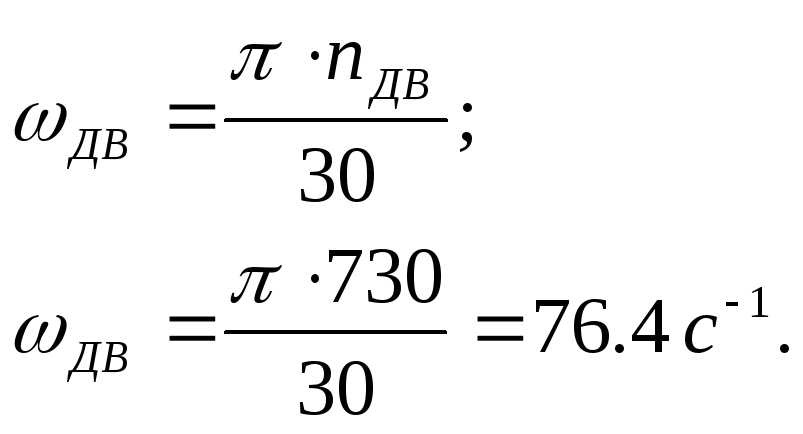

Величина чистой силы F должна быть постоянной и связана с центростремительным ускорением вторым законом Ньютона: с F в Н. Эта центростремительная сила может создаваться за счет натяжения (как в этой лаборатории), трения (как для автомобиля, движущегося по кривой), нормальной силы (как в петлеобразных американских горках) или гравитации (как для движения спутника). В этом эксперименте вы будете измерять период объекта, совершающего равномерное круговое движение с фиксированным радиусом, но с различными значениями F .По периоду можно рассчитать угловую скорость. Используя эти известные значения и приведенные выше уравнения, вы можете найти эмпирическую массу вращающегося объекта и сравнить ее со значением массы, полученным путем непосредственного взвешивания его на весах.

Аппарат UCM

Аппарат UCM состоит из платформы с регулируемой скоростью вращения . На расстоянии r от центра вращения находится узел боковой стойки , на котором висит объект массой м , называемый вращающейся массой (не путать со статической массой ).

Вращающаяся масса прикреплена к пружине на центральной стойке с помощью струны и небольшого шкива. Когда платформа вращается, вращающаяся масса будет перемещаться по круговой траектории из-за силы, прилагаемой к ней струной (посредством натяжения пружины). Поскольку невозможно получить мгновенное считывание этой силы натяжения во время вращения платформы, косвенное измерение этой силы будет производиться с использованием веса статической массы, как показано и объяснено ниже.

Рисунок 1

Когда платформа не вращается, вращающаяся масса не свисает вертикально с боковой стойки, а, скорее, втягивается внутрь за счет натяжения струны и пружины. При проведении эксперимента вы будете регулировать скорость вращения платформы до тех пор, пока вращающаяся масса не будет висеть вертикально на радиусе r . Оранжевый индикаторный диск поможет вам определить, когда вращающаяся масса достигла этого положения.

Рисунок 2

Период вращения измеряется секундомером .

Платформу можно вращать, поворачивая стержень с накаткой вручную.

Процедура

Выравнивание предмета

Если платформа неровная, это отрицательно скажется на ваших результатах. Студенты первой лаборатории недели должны были уже выровнять прибор. Будем надеяться, что с тех пор аппарат не перемещали, и его не нужно будет снова выравнивать. Убедитесь, что ваше устройство выровнено, включив двигатель регулировки скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы.Если ваше устройство необходимо выровнять, выполните следующие действия.

1
Чтобы примерно выровнять платформу, поместите пузырьковый уровень в середину платформы и отрегулируйте два регулировочных винта на основании устройства до тех пор, пока пузырь не будет отцентрирован.
2
Поместите дополнительную массу (~ 500 г) на тот же конец вращающейся платформы, что и вращающаяся масса. Если платформа неровная, тяжелый конец будет качаться в низкую сторону.
3
Отрегулируйте регулировочные винты на ножках основания до тех пор, пока конец платформы не будет качаться равномерно, когда ее осторожно поворачивают вручную.

Установка радиуса

1
Осторожно отсоедините вращающуюся массу от струн. Используйте весы, чтобы взвесить его, и запишите значение массы.
2
Подвесьте вращающуюся гирю к боковой стойке и подсоедините шнур от пружины к гири.Убедитесь, что эта струна проходит под (а не за) маленьким шкивом на центральной стойке.
3
Переместите кронштейн индикатора на центральной стойке в самое нижнее положение.
4
Оттяните вращающуюся массу от центральной стойки, пока оранжевый индикатор не окажется в центре кронштейна. Если струна, поддерживающая вращающийся груз, не является вертикальной, когда индикатор выровнен с кронштейном, боковую стойку следует перемещать внутрь или наружу, пока струна не станет вертикальной. Используйте вертикальную линию на боковой стойке, чтобы облегчить это выравнивание. При затягивании боковой стойки, нажмите на платформу, чтобы убедиться, что она надежно удерживается в вертикальном положении, и избегайте чрезмерного затягивания и поломки пластикового винта с накатанной головкой!
5
Измерьте и запишите радиус, а также оценку погрешности на основе центровки.
6
Теперь ваш аппарат должен быть готов к работе в максимально широком диапазоне центростремительных сил.(Почему это важно?) Центростремительную силу можно изменять, перемещая опору пружины вверх и вниз, при этом другие части устройства остаются на месте. Этот диапазон движение по центральной стойке должно быть не менее 5 см, что соответствует диапазону натяжения пружины примерно 1,2 Н.

Установка величины центростремительной силы

В этой первой части процедуры вы будете использовать метод static (без вращения) для настройки устройства на известное значение центростремительной силы.

1
Присоедините зажимной шкив к концу платформы, ближайшему к вращающейся массе. Прикрепите веревку к вращающейся массе и навесьте известную массу (начиная с 20 г) над зажимным шкивом. Отрегулируйте прижимной шкив вверх или вниз по мере необходимости так, чтобы веревка между шкивом и вращающаяся масса расположена горизонтально. (Почему это важно?)
2
Запишите значение этой статической массы , которая будет определять центростремительную силу.
3
Отрегулируйте опору пружины по вертикали, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора. Теперь устройство должно быть выровнено, чтобы точно знать радиус движения вращающейся массы, когда платформа вращается.

На этом этапе остановитесь и проанализируйте все силы, действующие на вращающуюся массу. Каковы их масштабы и направления? Какие-то силы не совсем вертикальные или горизонтальные? Если да, то как это повлияет на ваши результаты?

Контрольно-пропускной пункт 1:
Прежде чем продолжить, попросите ТА проверить ваше устройство.

Измерение периода

1
Удалите статическую массу и струну из вращающейся массы. (Почему?)
2
Поверните устройство, равномерно поворачивая стержень с накаткой по часовой стрелке. Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.
3
Когда один партнер по лаборатории вращает платформу, другой должен использовать секундомер для измерения времени, необходимого для совершения одного оборота. Сделайте десять таких измерений.
4
Альтернативный метод измерения среднего периода заключается в использовании секундомера для измерения времени для N (например, 10) оборотов и деления на N, чтобы получить T .Сделайте это хотя бы для одного испытания и сравните со значением, полученным с помощью процедуры, приведенной на шаге 3. Какой метод, по вашему мнению, более точен?
5
Прежде чем продолжить, проверьте свои результаты для этой единственной точки данных и убедитесь, что ваше эмпирическое значение для вращающейся массы является разумным. Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.

Контрольно-пропускной пункт 2:
Прежде чем продолжить, попросите технического специалиста проверить ваши данные и результаты расчетов.

Изменение центростремительной силы

Повторите описанную выше процедуру как минимум с пятью различными статическими массами (и, следовательно, пятью различными силами), которые охватывают максимально широкий диапазон значений (обычно от 40 до 150 г).

Анализ

1
Вес статической массы, висящей на шкиве, равен центростремительной силе F , приложенной пружиной. Вычислите эту силу для каждого из пяти испытаний, умножив статическую массу на г и запишите результаты.
2
Для каждой центростремительной силы F вычислите средний период вращения T и его стандартную ошибку.
3
Для каждого значения F рассчитайте ω ² и его неопределенность из
4
Постройте график зависимости ω ² от F (с планками погрешностей) и выполните аппроксимацию методом наименьших квадратов.
5
Определите экспериментальное значение вращающейся массы, м , из наклона вашего графика и уравнения центростремительной силы.Определите пересечение y линейной аппроксимации ваших данных. Это то, чего вы ожидаете?

Обсуждение

Сравните значение м , полученное при подборе кривой, с измеренными значениями вращающейся массы м и радиуса движения r . Есть согласие в пределах неопределенностей? Если вы проведете этот эксперимент осторожно, вы сможете получить результаты с ошибкой менее 3%. Сравните значение интерцепта y с ожидаемым значением.Они согласны? Почему для этого (и большинства других) экспериментов важно получить данные в самом широком диапазоне значений? Каковы потенциальные последствия близкого расположения точек данных? Объясните, как вы собираете данные с помощью этого устройства, чтобы проверить следующую гипотезу: для данного значения величины центростремительной силы F радиус движения r обратно пропорционален квадрату угловой скорости ω .

Диаметр колеса 28 см Сколько оборотов 9 класс по математике CBSE

Подсказка: Нам дан диаметр колеса так; рассчитаем радиус колеса. Как мы знаем, расстояние на один оборот равно длине окружности колеса, которое имеет форму круга \ [2 \ pi r \].Теперь мы поместим значение радиуса в формулу, которая даст нам один оборот, который должно пройти колесо. Теперь, чтобы найти количество оборотов для прохождения 352 м, нужно разделить общее расстояние на расстояние, пройденное за один оборот, и таким образом получить желаемый результат.

Полный пошаговый ответ:

Сначала мы рассмотрим данные, что диаметр колеса 28 см, и построим фигуру

Теперь мы определим значение радиуса, выполнив половину заданного диаметр,
Таким образом, получаем,
\ [
\ Rightarrow r = \ dfrac {{28}} {2} \\
\ Rightarrow r = 14cm \\
\]
Следовательно, радиус колеса равен 14 см. .
Теперь мы найдем расстояние, которое нужно пройти, чтобы сделать один оборот.
Как мы знаем, расстояние, пройденное за один оборот, равно длине окружности колеса, равной \ [2 \ pi r \].
Таким образом, теперь мы подставим значение радиуса в указанную выше окружность,
Таким образом, мы получим,
\ [\ Rightarrow 2 \ pi \ left ({14} \ right) = 88cm \]
Следовательно, чтобы сделать один оборот колесо должно пройти 88 см.
Теперь нам нужно определить количество оборотов, чтобы пройти 352 метра.
Итак, поскольку у нас есть общее пройденное расстояние и расстояние, пройденное за один оборот, мы разделим оба значения одно на одно, чтобы определить количество оборотов.
Кроме того, общее расстояние составляет 352 м, поэтому мы преобразуем его в см, умножив полученное значение на 100.
\ [\ Rightarrow 352 \ times 100 = 35200cm \]
Таким образом, мы получаем
\ [\ Rightarrow \ dfrac { {35200}} {{88}} = 400 \]
Следовательно, количество оборотов, необходимых для преодоления заданного расстояния, равно 400.

Примечание: Мы можем легко определить радиус по заданному диаметру колеса. .Чтобы найти количество оборотов, нам нужно разделить общее расстояние на расстояние, пройденное за один оборот. запомните длину окружности, равную \ [2 \ pi r \]. Перевод единиц измерения с м на см необходим, иначе расчет будет неверным. Сделайте фигуру для более четкого решения. Правильно выполняйте замены в формуле.

Вы в одном шаге от ответа!

Подпишитесь бесплатно!

Регистрируясь, вы также получаете БЕСПЛАТНЫЙ доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам!

оборотов в градусы (от r до °)

Введите угол в оборотах ниже, чтобы преобразовать значение в градусы.

Перевод числа оборотов в градусы

Чтобы преобразовать количество оборотов в градусы, умножьте угол на коэффициент преобразования.

Поскольку один оборот равен 360 градусам, вы можете использовать эту простую формулу для преобразования:

градусы = обороты × 360

Угол в градусах равен оборотам, умноженным на 360.

Например, вот как преобразовать 5 оборотов в градусы, используя формулу выше.

5 r = (5 × 360) = 1800 °

Сколько градусов в революции?

В обороте 360 градусов, поэтому мы используем это значение в приведенной выше формуле.

1 r = 360 °

Обороты и градусы — это единицы измерения угла.Продолжайте читать, чтобы узнать больше о каждой единице измерения.

Один оборот или поворот равен 1 обороту по окружности или 360 °. Обороты обычно используются для измерения скорости вращения, например, при измерении оборотов двигателя транспортного средства в минуту.

Оборот иногда также называют поворотом, циклом или полным вращением.Обороты могут быть сокращены как r , а также иногда сокращены как rev или cyc . Например, 1 оборот можно записать как 1 оборот, 1 оборот или 1 цикл.

Градус — это угол, равный 1/360 оборота или окружности. ^[1] Число 360 имеет 24 делителя, поэтому с ним довольно легко работать. В персидском календарном году также 360 дней, и многие предполагают, что ранние астрономы использовали 1 градус в день.

Градус — это единица измерения угла в системе СИ, используемая в метрической системе. Градус иногда также называют градусом дуги, градусом дуги или градусом дуги. Градусы могут быть сокращены до ° , а также иногда сокращаются до ° . Например, 1 градус можно записать как 1 ° или 1 градус.

В качестве альтернативы десятичной форме градусы также могут быть выражены с помощью минут и секунд.Минуты и секунды выражаются с помощью штрихов (‘) и двойных штрихов (″), хотя для удобства часто используются одинарные и двойные кавычки.

Одна минута равна 1/60 градуса, а одна секунда равна 1/60 минуты.

Транспортиры обычно используются для измерения углов в градусах. Это полукруглые или полукруглые устройства со степенью маркировка, позволяющая пользователю измерить угол в градусах. Узнайте больше о том, как использовать транспортир или загрузите транспортир для печати.

10.2 Вращение с постоянным угловым ускорением — University Physics Volume 1

Learning Objectives

К концу этого раздела вы сможете:

Вывести кинематические уравнения для вращательного движения с постоянным угловым ускорением
Выберите из кинематических уравнений для вращательного движения с постоянным угловым ускорением соответствующие уравнения для решения неизвестных при анализе систем, подвергающихся вращению с фиксированной осью
Используйте решения, найденные с помощью кинематических уравнений, для проверки графического анализа вращения с фиксированной осью с постоянным угловым ускорением

В предыдущем разделе мы определили вращательные переменные углового смещения, угловой скорости и углового ускорения.В этом разделе мы работаем с этими определениями, чтобы вывести отношения между этими переменными, и использовать эти отношения для анализа вращательного движения твердого тела вокруг фиксированной оси при постоянном угловом ускорении. Этот анализ составляет основу кинематики вращения. Если угловое ускорение постоянно, уравнения кинематики вращения упрощаются, подобно уравнениям линейной кинематики, обсуждаемым в разделах «Движение по прямой линии» и «Движение в двух и трех измерениях».Затем мы можем использовать этот упрощенный набор уравнений для описания многих приложений в физике и технике, где угловое ускорение системы постоянно. Кинематика вращения также является предпосылкой для обсуждения динамики вращения далее в этой главе.

Кинематика вращательного движения

Используя нашу интуицию, мы можем начать видеть, как вращательные величины θ, θ, ω, ω, αα и t связаны друг с другом. Например, в предыдущем разделе мы видели, что если маховик имеет угловое ускорение в том же направлении, что и его вектор угловой скорости, его угловая скорость увеличивается со временем, а также увеличивается его угловое смещение.Напротив, если угловое ускорение противоположно вектору угловой скорости, его угловая скорость со временем уменьшается. Мы можем описать эти и многие другие физические ситуации с помощью последовательного набора кинематических уравнений вращения при постоянном угловом ускорении. Такой метод исследования вращательного движения называется кинематикой вращательного движения.

Для начала отметим, что если система вращается с постоянным ускорением, то средняя угловая скорость подчиняется простому соотношению, поскольку угловая скорость линейно увеличивается со временем.Средняя угловая скорость составляет половину суммы начального и конечного значений:

ω– = ω0 + ωf2.ω– = ω0 + ωf2.

10,9

Из определения средней угловой скорости мы можем найти уравнение, которое связывает угловое положение, среднюю угловую скорость и время:

ω– = ΔθΔt.ω– = ΔθΔt.

Решая для θθ, имеем

θf = θ0 + ω – t, θf = θ0 + ω – t,

10,10

, где мы положили t0 = 0t0 = 0. Это уравнение может быть очень полезным, если мы знаем среднюю угловую скорость системы.Тогда мы могли бы найти угловое смещение за заданный период времени. Затем мы находим уравнение, связывающее ωω, αα и t . Чтобы определить это уравнение, начнем с определения углового ускорения:

Мы переставляем это так, чтобы получить αdt = dωαdt = dω, а затем интегрируем обе части этого уравнения от начальных значений до конечных значений, то есть от t0t0 до t и от ω0toωfω0toωf. При равномерном вращательном движении угловое ускорение постоянно, поэтому его можно вывести из интеграла, получив два определенных интеграла:

α∫t0tdt ′ = ∫ω0ωfdω.α∫t0tdt ′ = ∫ω0ωfdω.

Установив t0 = 0t0 = 0, имеем

αt = ωf − ω0.αt = ωf − ω0.

Переставляем это, чтобы получить

ωf = ω0 + αt, ωf = ω0 + αt,

10,11

где ω0ω0 — начальная угловая скорость. Уравнение 10.11 является вращательным аналогом уравнения линейной кинематики vf = v0 + atvf = v0 + at. С помощью уравнения 10.11 мы можем найти угловую скорость объекта в любое заданное время t с учетом начальной угловой скорости и углового ускорения.

Давайте теперь проделаем аналогичную процедуру, начав с уравнения ω = dθdtω = dθdt.Переставляем его так, чтобы получить ωdt = dθωdt = dθ, и снова проинтегрируем обе стороны от начальных до конечных значений, отмечая, что угловое ускорение постоянно и не зависит от времени. Однако на этот раз угловая скорость не является постоянной (в общем случае), поэтому мы подставляем то, что мы получили выше:

∫t0tf (ω0 + αt ′) dt ′ = ∫θ0θfdθ; ∫t0tω0dt + ∫t0tαt′dt ′ = ∫θ0θfdθ = [ω0t ′ + α ((t ′) 22)] t0t = ω0t + α (t22) = θf − θ0 , ∫t0tf (ω0 + αt ′) dt ′ = ∫θ0θfdθ; ∫t0tω0dt + ∫t0tαt′dt ′ = ∫θ0θfdθ = [ω0t ′ + α ((t ′) 22)] t0t = ω0t + α (t22) = θf− θ0,

, где мы положили t0 = 0t0 = 0.Теперь переставляем, чтобы получить

θf = θ0 + ω0t + 12αt2.θf = θ0 + ω0t + 12αt2.

10,12

Уравнение 10.12 — это вращательный аналог уравнения линейной кинематики, найденного в «Движении вдоль прямой линии» для положения как функции времени. Это уравнение дает нам угловое положение вращающегося твердого тела в любой момент времени t с учетом начальных условий (начальное угловое положение и начальная угловая скорость) и углового ускорения.

Мы можем найти уравнение, не зависящее от времени, решив для t в уравнении 10.11 и подставив в уравнение 10.12. Уравнение 10.12 становится

. θf = θ0 + ω0 (ωf − ω0α) + 12α (ωf − ω0α) 2 = θ0 + ω0ωfα − ω02α + 12ωf2α − ω0ωfα + 12ω02α = θ0 + 12ωf2α − 12ω02α, θf − θ0 = ωf2 − ω022α, θf − θ0 = ωf2 − ω022α −ω0α) + 12α (ωf − ω0α) 2 = θ0 + ω0ωfα − ω02α + 12ωf2α − ω0ωfα + 12ω02α = θ0 + 12ωf2α − 12ω02α, θf − θ0 = ωf2 − ω022α

или

ωf2 = ω02 + 2α (Δθ). ωf2 = ω02 + 2α (Δθ).

10,13

Уравнения с 10.10 по 10.13 описывают вращение с фиксированной осью для постоянного ускорения и обобщены в таблице 10.1.

Угловое смещение от средней угловой скорости	θf = θ0 + ω – tθf = θ0 + ω – t
Угловая скорость от углового ускорения	ωf = ω0 + αtωf = ω0 + αt
Угловое смещение от угловой скорости и углового ускорения	θf = θ0 + ω0t + 12αt2θf = θ0 + ω0t + 12αt2
Угловая скорость от углового смещения и углового ускорения	ωf2 = ω02 + 2α (Δθ) ωf2 = ω02 + 2α (Δθ)

Таблица 10.1 Кинематические уравнения

Применение уравнений вращательного движения

Теперь мы можем применить ключевые кинематические соотношения для вращательного движения к некоторым простым примерам, чтобы понять, как уравнения могут применяться в повседневных ситуациях.

Пример 10.4

Расчет ускорения рыболовной катушки

Глубоководный рыбак ловит большую рыбу, которая отплывает от лодки, стягивая леску со своей рыболовной катушки. Вся система изначально находится в состоянии покоя, а леска разматывается с катушки в радиусе 4.50 см от оси вращения. Катушка получает угловое ускорение 110рад / с — 2110рад / с2 в течение 2,00 с (рисунок 10.11).

(а) Какова конечная угловая скорость мотовила через 2 с?

(b) Сколько оборотов делает катушка?

Рисунок 10.11 Леска, сходящая с вращающейся катушки, движется линейно.

Стратегия

Определите известные и сравните с кинематическими уравнениями для постоянного ускорения. Найдите соответствующее уравнение, которое можно решить для неизвестного, используя известные в описании проблемы.

Решение

Нам даны αα и t и мы хотим определить ωω. Самым простым уравнением для использования является ωf = ω0 + αtωf = ω0 + αt, поскольку известны все члены, кроме искомой неизвестной переменной. Нам дано, что ω0 = 0ω0 = 0 (начинается с состояния покоя), поэтому ωf = 0 + (110рад / с2) (2,00 с) = 220рад / с. ωf = 0 + (110рад / с2) (2,00 с) = 220рад / с.
Нас просят найти количество оборотов. Поскольку 1rev = 2πrad1rev = 2πrad, мы можем найти количество оборотов, найдя θθ в радианах.Нам даны αα и t , и мы знаем, что ω0ω0 равно нулю, поэтому мы можем получить θθ, используя θf = θi + ωit + 12αt2 = 0 + 0 + (0.500) (110rad / s2) (2.00s) 2 = 220rad. θf = θi + ωit + 12αt2 = 0 + 0 + (0.500) (110rad / s2) (2.00 с) 2 = 220рад. Преобразование радианов в обороты дает Количество оборотов = (220рад) 1 оборот2πрад = 35,0 оборотов Число оборотов = (220рад) 1 оборот2πрад = 35,0 оборотов

Значение

Этот пример показывает, что отношения между вращательными величинами очень похожи на отношения между линейными величинами. Ответы на вопросы реалистичны.После раскручивания в течение двух секунд катушка вращается со скоростью 220 рад / с, что составляет 2100 об / мин. (Неудивительно, что барабаны иногда издают высокие звуки.)

В предыдущем примере мы рассматривали рыболовную катушку с положительным угловым ускорением. Теперь давайте посмотрим, что происходит с отрицательным угловым ускорением.

Пример 10,5

Расчет продолжительности, когда рыболовная катушка замедляется и останавливается

Теперь рыбак тормозит вращающуюся катушку, достигая углового ускорения -300рад / с2-300рад / с2.Как долго катушка останавливается?

Стратегия

Нас просят найти время t , за которое катушка остановится. Начальные и конечные условия отличаются от условий в предыдущей задаче, в которой использовалась та же рыболовная катушка. Теперь мы видим, что начальная угловая скорость равна ω0 = 220рад / сω0 = 220рад / с, а конечная угловая скорость ωω равна нулю. Угловое ускорение задается как α = −300рад / с2. Α = −300рад / с2. Изучая доступные уравнения, мы видим все величины, но t известны в ωf = ω0 + αtωf = ω0 + αt, что упрощает использование этого уравнения.

Решение

Уравнение состояния

Мы решаем уравнение алгебраически для t , а затем подставляем известные значения, как обычно, давая

t = ωf − ω0α = 0−220,0рад / с − 300,0рад / с2 = 0,733 с. t = ωf − ω0α = 0−220,0рад / с − 300,0рад / с2 = 0,733 с.

Значение

Обратите внимание, что следует проявлять осторожность со знаками, указывающими направления различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда ломается из-за участвующих в ней ускорений, и рыбаки часто позволяют рыбе плавать некоторое время, прежде чем затормозить катушку.Уставшая рыба движется медленнее, требуя меньшего ускорения.

Проверьте свое понимание 10.2

Центрифуга, используемая для экстракции ДНК, вращается с максимальной скоростью 7000 об / мин, создавая на образце «перегрузочную силу», которая в 6000 раз превышает силу тяжести. Если центрифуге требуется 10 секунд для остановки от максимальной скорости вращения: (а) Каково угловое ускорение центрифуги? б) Каково угловое смещение центрифуги за это время?

Пример 10.6

Угловое ускорение воздушного винта

На рис. 10.12 показан график зависимости угловой скорости воздушного винта от времени. Его угловая скорость начинается с 30 рад / с и линейно падает до 0 рад / с в течение 5 секунд. (а) Найдите угловое ускорение объекта и проверьте результат, используя кинематические уравнения. (b) Найдите угол, на который винт вращается в течение этих 5 секунд, и проверьте свой результат, используя кинематические уравнения.

Рисунок 10.12 График зависимости угловой скорости пропеллера от времени.

Стратегия

Поскольку угловая скорость линейно изменяется со временем, мы знаем, что угловое ускорение постоянно и не зависит от переменной времени. Угловое ускорение — это наклон графика зависимости угловой скорости от времени, α = dωdtα = dωdt. Чтобы вычислить наклон, мы читаем непосредственно из рисунка 10.12 и видим, что ω0 = 30rad / sω0 = 30rad / s при t = 0st = 0s и ωf = 0rad / sωf = 0rad / s при t = 5st = 5s. Тогда мы можем проверить результат, используя ω = ω0 + αtω = ω0 + αt.
Используем уравнение ω = dθdt; ω = dθdt; поскольку производная угла по времени — это угловая скорость, мы можем найти угловое смещение, интегрировав угловую скорость, что на рисунке означает взятие площади под графиком угловой скорости. Другими словами: Θ0θfdθ = θf − θ0 = ∫t0tfω (t) dt.∫θ0θfdθ = θf − θ0 = ∫t0tfω (t) dt. Затем мы используем кинематические уравнения для постоянного ускорения, чтобы проверить результат.

Решение

Рассчитывая уклон, получаем α = ω − ω0t − t0 = (0−30.0) рад / с (5,0−0) с = −6,0рад / с2. Α = ω − ω0t − t0 = (0−30,0) рад / с (5,0−0) с = −6,0рад / с2. Мы видим, что это в точности уравнение 10.11 с небольшой перестановкой членов.
Площадь под кривой можно найти, вычислив площадь прямоугольного треугольника, как показано на рисунке 10.13.
Рис. 10.13 Площадь под кривой — это площадь прямоугольного треугольника.
Δθ = площадь (треугольник); Δθ = 12 (30рад / с) (5s) = 75рад. Δθ = площадь (треугольник); Δθ = 12 (30рад / с) (5s) = 75рад. Мы проверяем решение, используя уравнение 10.12: θf = θ0 + ω0t + 12αt2.θf = θ0 + ω0t + 12αt2. Полагая θ0 = 0θ0 = 0, имеем θf = (30,0рад / с) (5,0 с) +12 (−6,0рад / с2) (5,0рад / с) 2 = 150,0−75,0 = 75,0рад. θf = (30,0рад / с) (5,0 с) +12 (−6,0рад / с2) (5,0рад / с) 2 = 150,0−75,0 = 75,0рад. Это подтверждает решение, найденное при нахождении площади под кривой.

Значение

Из части (b) видно, что существуют альтернативные подходы к анализу вращения с фиксированной осью с постоянным ускорением. Мы начали с графического подхода и проверили решение, используя кинематические уравнения вращения.Поскольку α = dωdtα = dωdt, мы могли бы провести такой же графический анализ на кривой зависимости углового ускорения от времени. Площадь под кривой α-по-tα-по-t дает нам изменение угловой скорости. Поскольку угловое ускорение на этом участке постоянно, это несложное упражнение.

BOWL.com | Какая у вас ставка дохода?

Какая у вас ставка?

Всегда будут споры о оборотах и о том, как они влияют на игру в боулинг. Благодаря новым способам доставки мяча, улучшенным характеристикам оборудования и схемам дорожек, которые могут дать преимущество скорости вращения одного игрока перед другим, важно понимать скорость вращения и их характеристики.

Иногда мы зашли так далеко, что классифицируем чью-то игру исключительно по его предполагаемой скорости вращения. Такие заголовки, как «кривошип», «стройщик» и «твинер», часто применяются без точного измерения. Чтобы лучше понять концепцию скорости вращения боулера, нам нужно ответить на несколько основных вопросов.

Учтите, что любой, кто ставит шар для боулинга на дорожку, передает обороты. Что такое революция? Словарное определение вращения: «вращение небесного тела вокруг своей оси». В нашем приложении для боулинга это шар для боулинга, совершающий один оборот вокруг оси.Что такое частота вращения? Скорость вращения — это расчет количества оборотов, совершаемых боулером на шаре. Теперь, с этими основами, мы можем определить, как рассчитать обороты котелка в общей единице, оборотах в минуту (RPM).

об / мин — это частота вращения: количество полных оборотов, совершенных за одну минуту вокруг фиксированной оси. Это применимо, если бы шар для боулинга находился на дорожке в течение одной минуты и все время вращался вокруг одной и той же оси. Если бы это было так, мы бы просто подсчитали, сколько раз он обходится, чтобы получить обороты в минуту.

Академия боулинга USBC объясняет число оборотов в минуту

Даже самые медленные шары для боулинга не выходят на дорожку в течение одной минуты. Средняя скорость мяча 17 миль в час, измеренная по стрелкам, позволяет мячу лететь по дорожке примерно 2-3 секунды. Некоторые люди предлагают просто подсчитывать количество оборотов, пока мяч движется по дорожке, и называть это числом оборотов в минуту, но это измерение числа оборотов за выстрел, а не оборотов в минуту.Лучшее место для фиксации воздействия котелка на мяч — это сразу после высвобождения, когда большой палец и пальцы выходят.

Итак, почему важно знать частоту сердечных сокращений котелка? Понимание скорости вращения поможет классифицировать варианты, например, какой тип шара для боулинга купить, какой тип запястья может потребоваться или какие корректировки и методы применяются с учетом современных технологий.

Процесс расчета оборотов в минуту

Использование видеокамеры или любого записывающего устройства для записи и расчета частоты вращения котелка можно сделать быстро и точно.Сначала определите точку положительной оси боулера (PAP), затем, когда мяч брошен, посмотрите, устойчива ли ось в течение первых двух оборотов, когда мяч находится в воздухе и контактирует с дорожкой. После того, как мы определили ось, поместите полоску ленты от оси до отверстий для пальцев на поверхности мяча. Теперь это один из наших измерительных инструментов.

Используйте видеокамеру, чтобы запечатлеть релиз и воспроизвести видео, где вы можете управлять им по одному кадру за раз.

Начиная с первого кадра после того, как пальцы оторвались от мяча, измерьте, сколько часов часового времени лента покрывает за 10 кадров. Умножьте количество часов, покрытых этими 10 кадрами, на 15, и вы получите свою начальную частоту вращения.

Можно использовать следующие формулы для расчета частоты вращения с помощью видео:

Видеокамеры со скоростью 30 кадров в секунду (стандартный видеоформат NTSC, используемый в основном в Северной Америке): часов на 10 кадров * 15 = об / мин

Другое видео: (Исх.Формат PAL широко используется в Азии и Европе) часов на 10 кадров * (видео кадров в секунду / 30) * 15 = об / мин

Потренируйтесь вычислять частоту вращения.

Расчет RCF-RPM on-line

Отличие

Перевести

Число оборотов в минуту —

Скорость вращения шпинделя

Количество оборотов в минуту у электродвигателей

Некоторые характеристики электродвигателей

Основные определения и формулы

Western Digital считает скорость вращения жёстких дисков по-своему — обороты зависят от маркетинга

Кинематика — Физика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Система СИ

Путь и перемещение

Средняя скорость

Равноускоренное прямолинейное движение

Свободное падение по вертикали

Горизонтальный бросок

Бросок под углом к горизонту (с земли на землю)

Сложение скоростей

Равномерное движение по окружности

Кинематика вращательного движения | Физика

Цели обучения

Пример 1. Расчет ускорения рыболовной катушки

Пример 2. Расчет продолжительности, когда рыболовная катушка замедляется и останавливается

Пример 3. Расчет медленного ускорения поездов и их колес

Пример 4. Расчет расстояния, пройденного мухой на краю плиты микроволновой печи

Проверьте свое понимание

Сводка раздела

Задачи и упражнения

Глоссарий

Избранные решения проблем и упражнения

и об / мин

Purplemath

MathHelp.

Поезд движется со скоростью 10 миль в час по кривой радиусом 3000 футов. На какой угол повернется поезд за одну минуту? Округлить до ближайшего целого числа градусов.

Равномерное круговое движение

Введение

Аппарат UCM

Процедура

Выравнивание предмета

Установка радиуса

Установка величины центростремительной силы

Измерение периода

Изменение центростремительной силы

Анализ

Обсуждение

Диаметр колеса 28 см Сколько оборотов 9 класс по математике CBSE

оборотов в градусы (от r до °)

Перевод числа оборотов в градусы

Сколько градусов в революции?

10.2 Вращение с постоянным угловым ускорением — University Physics Volume 1

Learning Objectives

Кинематика вращательного движения

Применение уравнений вращательного движения

Пример 10.4

Расчет ускорения рыболовной катушки

Стратегия

Решение

Значение

Пример 10,5

Расчет продолжительности, когда рыболовная катушка замедляется и останавливается

Стратегия

Решение

Значение

Пример 10.6

Угловое ускорение воздушного винта

Стратегия

Решение

Значение

BOWL.com | Какая у вас ставка дохода?

Какая у вас ставка?

Добавить комментарий Отменить ответ