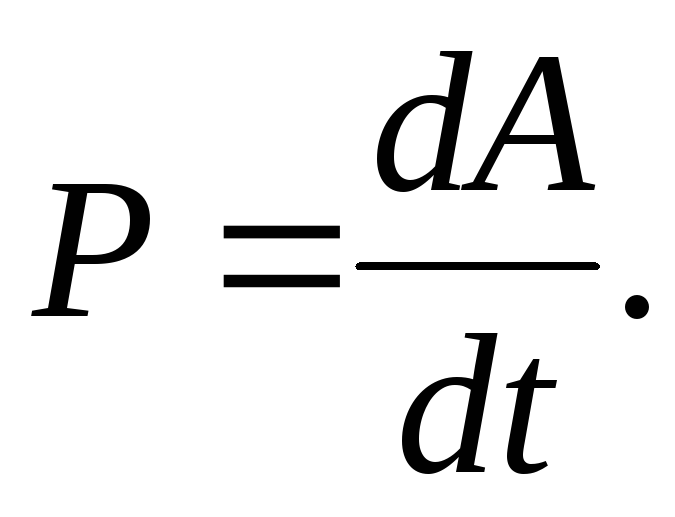Мощность через момент и обороты формула: Пересчет мощности кВт в зависимости от крутящего момента Нм

Ошибка

• Автомобиль — модели, марки
• Устройство автомобиля
• Ремонт и обслуживание
• Тюнинг

• Аксессуары и оборудование
• Компоненты
• Безопасность
• Физика процесса

• Новичкам в помощь
• Приглашение
• Официоз (компании)
• Пригородные маршруты

• Персоны
• Наши люди
• ТЮВ
• Эмблемы

•  
• А
• Б
• В
• Г
• Д
• Е
• Ё
• Ж
• З
• И
• Й
• К
• Л
• М
• Н
• О
• П
• Р
• С
• Т
• У
• Ф
• Х
• Ц
• Ч
• Ш
• Щ
• Ъ
• Ы
• Ь
• Э
• Ю
• Я

Навигация

• Заглавная страница
• Сообщество
• Текущие события
• Свежие правки
• Случайная статья
• Справка

Личные инструменты

• Представиться системе

Инструменты

• Спецстраницы

Пространства имён

• Служебная страница

Просмотры

Перейти к: навигация, поиск

Запрашиваемое название страницы неправильно, пусто, либо неправильно указано межъязыковое или интервики название. Возможно, в названии используются недопустимые символы.

Возврат к странице Заглавная страница.

Если Вы обнаружили ошибку или хотите дополнить статью, выделите ту часть текста статьи, которая нуждается в редакции, и нажмите Ctrl+Enter. Далее следуйте простой инструкции.

Что такое мощность двигателя и крутящий момент. Как рассчитать мощность мотора

Автор Павел Александрович Белоусов На чтение 6 мин. Просмотров 592

Содержание

1. Как рассчитывается мощность двигателя?
2. Видео: Простыми словами без сложных формул и расчетов, что такое мощность, крутящий момент и обороты двигателя.
3. Что такое крутящий момент
4. Что лучше: мощность или крутящий момент

Мощность двигателя – это величина, показывающая, какую работу способен совершить мотор в единицу времени. То есть то количество энергии, которую двигатель передает на трансмиссию за определенный временной промежуток. Измеряется в киловаттах (кВт) или лошадиных силах (л. с.).

Как рассчитывается мощность двигателя?

Расчет мощности мотора проводится несколькими способами. Самый доступный способ – через крутящий момент. Умножаем крутящий момент на угловую скорость – получаем мощность двигателя.

N_дв=M∙ω=2∙π∙M∙n_дв

где:

N_дв – мощность двигателя, кВт;

M – крутящий момент, Нм;

ω – угловая скорость вращения коленчатого вала, рад/сек;

π – математическая постоянная, равная 3,14;

n_дв – частота вращения двигателя, мин-1.

Мощность рассчитывается и через среднее эффективное давление. Камера сгорания имеет определенный объем. Разогретые газы воздействуют на поршень в цилиндре с определенным давлением. Двигатель вращается с некоторой частотой. Произведение объема двигателя, среднего эффективного давления и частоты вращения, поделенное на 120, и даст теоретическую мощность двигателя в кВт.

N_дв=(V_дв∙P_эфф∙n_дв)/120

где:

V_дв – объем двигателя, см3;

P_эфф – эффективное давление в цилиндрах, МПа;

120 – коэффициент, применяемый для расчета мощности четырехтактного двигателя (у двухтактных ДВС этот коэффициент равен 60).

Для расчета лошадиных сил киловатты умножаем на 0,74.

N_(дв л.с.)=N_дв∙0,74

где:

N_дв л.с. – мощность двигателя в лошадиных силах, л. с.

Другие формулы мощности двигателя используются в реальных расчетах реже. Эти формулы включают в себя специфичные переменные. И чтобы измерить мощность двигателя по другим методикам, нужно знать производительность форсунок или массу потребленного двигателем воздуха.

На практике расчет мощности автопроизводители выполняют эмпирическим способом, то есть замеряют на стенде и строят график зависимости по факту, на основании полученных во время испытаний показателей.

Мощность двигателя – величина непостоянная. Для каждого мотора есть кривая, которая отображает на графике зависимость мощности от частоты вращения коленчатого вала. До определенного пика, примерно до 4-5 тысяч оборотов, мощность растет пропорционально оборотам. Далее идет плавное отставание роста мощности, кривая наклоняется. Примерно к 7-8 тысячам оборотов мощность идет на спад. Сказывается перекрытие клапанов на большой частоте вращения коленвала и падение КПД мотора из-за недостаточно интенсивного газообмена.

Чтобы узнать мощность двигателя, обратитесь к инструкции по эксплуатации авто. В разделе с техническими характеристиками мотора будет указана мощность и обороты, при которых она достигает пикового значения. Если мощность указана киловаттах, чтобы рассчитать лошадиные силы двигателя, воспользуйтесь приведенной выше формулой. В некоторых случаях автопроизводитель предоставляет график, на котором есть зависимость мощности двигателя и крутящего момента от частоты оборотов.

Видео: Простыми словами без сложных формул и расчетов, что такое мощность, крутящий момент и обороты двигателя.

Мощность ДВС определяет, насколько быстро автомобиль способен передвигаться или ускоряться (совершать работу). Полезная мощность двигателя рассчитывается с учетом потерь в трансмиссии, то есть указывает, сколько от изначальной мощности мотора по факту доходит до колес авто.

Что такое крутящий момент

Крутящий момент в двигателе автомобиля – это вращающая сила, которая численно равна произведению приложенной силы (давление раскаленных газов на поршень) на плечо (расстояние между осями коренных и шатунных шеек коленчатого вала в проекции, перпендикулярной оси вращения коленвала). Измеряется крутящий момент в ньютонах на метр (Нм).

Крутящий момент ДВС зависит от силы давления на поршень и расстояния между коренными и шатунными шейками. Зависимость здесь прямая. Чем больше плечо и чем больше давление на поршень – тем больше крутящий момент двигателя.

У дизельных двигателей степень сжатия больше. Больше и ход поршня в цилиндре (при равном с бензиновым мотором диаметре цилиндров). А это значит, что и расстояние между коренными и шатунными шейками будет больше. То есть длиннее плечо. За счет большей степени сжатия при рабочем такте у дизелей выше сила, давящая на поршень. Крутящий момент в дизельных моторах при прочих равных больше, чем в бензиновых.

Крутящий момент влияет на то, сколько энергии отдает мотор в текущий момент времени. Крутящий момент есть та величина, которая определяет фактически передаваемую в данный момент времени энергию на трансмиссию. Чем больше момент, тем сильнее тяга двигателя при текущих оборотах.

Что лучше: мощность или крутящий момент

Мощность и крутящий момент двигателя – величины взаимосвязанные. Это хорошо видно в формуле из первого пункта.

Пик крутящего момента на графике зависимости от частоты вращения мотора появляется раньше, чем пик мощности. Это справедливо как для дизельных, так и для бензиновых моторов. Однако у дизелей крутящий момент достигается раньше, и плато (интервал частоты вращения при пиковом значении) длиннее. У бензиновых ДВС мощность выше, хотя для ее достижения нужно раскрутить мотор почти до максимальных оборотов.

Сказать определенно, что лучше: мощность или крутящий момент, нельзя. Все зависит от случая. Трансмиссия современного авто способна трансформировать эти величины под требуемые условия. Поясним на примерах.

Для тяжелой техники, которой важна тяга в широком диапазоне оборотов, важнее крутящий момент. Мотор должен хорошо тянуть. Раскручивать его до предельных оборотов не нужно. Отчасти поэтому почти вся коммерческая техника оснащается дизельными моторами.

В гоночных автомобилях важнее мощность. Моторы этих авто по оборотам пилоты во время заездов держат в красной зоне. Двигатель отдает максимальную мощность. А трансмиссия преобразовывает мощность в тягу.

Для гражданских авто важен стиль вождения. Для езды на автомате подойдут оба мотора. Автоматическая трансмиссия будет держать мотор в диапазоне оборотов, при которых двигатель отдает максимум своего потенциала.

Для агрессивной езды на механике с раскручиванием двигателя в красную зону тахометра лучше подойдет бензиновый мотор. Но в этом случае нужно понимать, что для получения максимальной производительности от мотора потребуется держать его на пике оборотов и часто переключать передачи.

Пик мощности у бензинового ДВС имеет малый диапазон и находится около максимальных оборотов. Для уверенных обгонов и ускорений нужно будет понижать передачу и раскручивать двигатель.

Для размеренной езды, особенно в городе, больше подходит дизель. Для обгона на дизельном авто зачастую не потребуется переходить на пониженную передачу, а высокий крутящий момент в широком диапазоне оборотов позволит реже переключаться.

Печать

	Реставратор для пластика и кожи 5 минут и салон авто как новый.  Посмотрите фото до и после		1490 р.
	Набор для ремонта стекла Ремонт стекла авто своими руками. Спасает от трещин и сколов.		1690 р.
	Зеркало видеорегистратор Vehicle Blackbox DVR видеорегистратор + зеркало заднего вида + камера заднего вида + датчик движения + технология Dual cam + G-Sensor. ..		1990 р.
	Зеркало — бортовой компьютер 12в1 — видеорегистратор, GPS-навигатор, камера, интернет, радар, FM, G-sensor…		1990 р.
	Авточехлы из экокожи Салон будет как новый! Легко чистятся, не трутся, не рвутся.		3990 р.

Уравнение крутящего момента и выходной мощности двигателя постоянного тока

Уравнение крутящего момента и выходной мощности двигателя постоянного тока

• Термин крутящий момент означает «Вращение силы вокруг оси».

T = F × r Ньютон – счетчик

Где T = крутящий момент

F = сила в ньютонах

r = радиус в метрах

• Рассмотрим Якорь радиусом r метра и силой F ньютон действует на него.
• Предположим, что якорь вращается со скоростью N об/мин.
• Когда якорь поворачивается на один оборот, он сокращает расстояние 2πr за время 60/N секунды. Поэтому работа сделано за оборот

= Сила × расстояние

         = F × 2πr

        Но F × r = T

• Итак, работа – сделано / оборот = 2πT Ньютон — метр
• Теперь Сила развита 

= Работа, совершаемая в единицу секунды

= 2πT / ( 60 / Н )

= 2πNT / 60

Где ω = Угловая скорость в радианах/секундах

= 2πN / 60

• Электрическая эквивалент механической мощности, развиваемой якорем, равен

Е _б И _а = 2πNT / 60

Т = ( 60 / 2πН ) E _b I _a …………….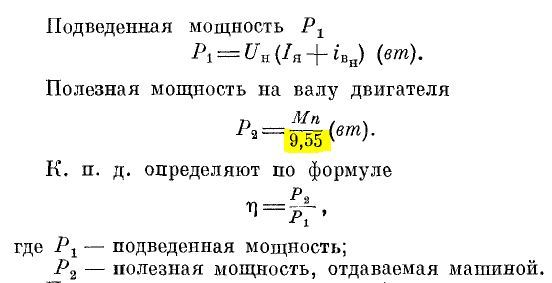 ( 1 )

T = 9.55 (E б I а /Н)


 Если скорость указана в оборотах в секунду (об/с)

T = (9,55/60) (E b I a /N)

• Т = 0,159 ( Е _б I _а /Н)
• В качестве противо-ЭДС Э _б = ФЗНП/60А

Заменитель Е _б в уравнении ( 1 )

Т = ( 60 / 2πН ) (ФЗНП/60А) I _и

= ( 1 / 2π ) ( ФЗНП / А ) I _a Н – м

=  [ 1 / ( 2π × 9,81 ) ] ( ФЗНП / А ) I _a Кг – м

• Количество проводник Z, количество полюсов P и количество параллельных путей A постоянны в двигатель постоянного тока поэтому

T α ФI _a





Вал Крутящий момент

• Крутящий момент на валу Т _ш всегда меньше момента якоря из-за малой величины потери на трение в двигателе.

крутящий момент = Крутящий момент якоря – потери на трение и сопротивление воздуха

Т _ш = T _a – Потери на трение и ветер

Выход мощность

• Выходная мощность = Мощность, развиваемая в якоре

P =  T × ( 2πNT / 60 ) Ватт

• Механический мощность, развиваемая на валу двигателя постоянного тока, всегда меньше, чем на якоре мощность из-за потерь на трение и аэродинамические потери.

стр. _ш = Т _ш × ( 2πНТ / 60 ) Ватт

• Механический мощность, развиваемая на валу, называется тормозной мощностью (л.с.).

Один HP = 735,5 ватт

Р _ш = ( Т _ш ×  2πН / 60 )( 1 / 735,5 ) HP

Вам также может понравиться: 

Система однократного и двойного возбуждения

Части машин постоянного тока

Реакция якоря в генераторе постоянного тока

Характеристики генератора постоянного тока

Принцип работы двигателя постоянного тока




Новое сообщение Старый пост Главная

Подписаться на: Post Comment (Atom)

10.

9: Работа и мощность для вращательного движения

1. Последнее обновление

2. Сохранить как PDF

• Идентификатор страницы

  4685

• OpenStax
• OpenStax

Цели обучения

• Использовать теорему о работе-энергии для анализа вращения, чтобы найти работу, совершаемую над системой, когда она вращается вокруг фиксированной оси при конечном угловом перемещении
• Найдите угловую скорость вращающегося твердого тела, используя теорему работы-энергии
• Найти мощность, передаваемую вращающемуся твердому телу, при заданных приложенных крутящем моменте и угловой скорости
• Суммируйте вращательные переменные и уравнения и свяжите их с их эквивалентами поступательного движения

До сих пор в этом разделе мы подробно рассматривали кинематику и динамику вращения твердых тел вокруг фиксированной оси. В этом последнем подразделе мы определяем работу и мощность в контексте вращения вокруг фиксированной оси, что имеет приложения как к физике, так и к технике. Обсуждение работы и мощности делает наше рассмотрение вращательного движения почти полным, за исключением вращательного движения и углового момента, которые обсуждаются в угловом моменте. Мы начнем этот подраздел с рассмотрения теоремы о работе и энергии для вращения.

Работа для вращательного движения

Теперь, когда мы определили, как вычислить кинетическую энергию для вращения твердых тел, мы можем перейти к обсуждению работы, совершаемой для твердого тела, вращающегося вокруг фиксированной оси. На рисунке \(\PageIndex{1}\) показано твердое тело, которое повернулось на угол d\(\theta\) из точки A в точку B под действием силы \(\vec{F}\). Внешняя сила \(\vec{F}\) приложена к точке P, положение которой равно \(\vec{r}\), и твердое тело вынуждено вращаться вокруг фиксированной оси, перпендикулярной странице и проходит через O. Ось вращения неподвижна, поэтому вектор \(\vec{r}\) движется по окружности радиуса r, а вектор d \(\vec{s}\) перпендикулярен \(\vec{s}\) {р}\).

Рисунок \(\PageIndex{1}\): Твердое тело поворачивается на угол d\(\theta\) из точки A в B под действием внешней силы \(\vec{F}\), приложенной к точке P . {\ theta} \ times \ vec {r}) = d \ vec {\ theta} \ times \ vec {r} + d \ vec {r} \ times \ vec {\ theta} = d \ vec {\ theta} \times \vec{r} \ldotp\]

Обратите внимание, что d\(\vec{r}\) равно нулю, потому что \(\vec{r}\) закреплено на твердом теле от начала координат O до точки P Используя определение работы, получаем

\[W = \int \sum \vec{F}\; \cdotp d \vec{s} = \int \sum \vec{F}\; \cdotp (d \vec{\theta} \times \vec{r}) = \int d \vec{\theta}\; \cdotp (\vec{r} \times \sum \vec{F})\]

, где мы использовали идентификатор \(\vec{a}\; \cdotp (\vec{b} \times \vec{c }) = \vec{b}\;\cdotp (\vec{c} \times \vec{a})\). Заметив, что \((\vec{r} \times \sum \vec{F}) = \sum \vec{\tau}\), мы приходим к выражению для вращательной работы , совершаемой над твердым телом:

\[W = \int \sum \vec{\tau}\; \cdotp d \vec{\theta} \ldotp \label{10. 27}\]

Общая работа, выполненная над твердым телом, представляет собой сумму крутящих моментов, интегрированных по углу, на который тело поворачивается . Дополнительная работа равна

\[dW = \left(\sum_{i} \tau_{i}\right) d \theta \label{10.28}\]

, где мы взяли скалярное произведение в уравнении \ref{ 10.27}, оставив только крутящие моменты вдоль оси вращения. В твердом теле все частицы вращаются на один и тот же угол; таким образом, работа каждой внешней силы равна крутящему моменту, умноженному на общий угол приращения d\(\theta\). Величина \(\left(\sum_{i} \tau_{i}\right)\) — это чистый крутящий момент, действующий на тело из-за внешних сил.

Аналогичным образом мы нашли кинетическую энергию твердого тела, вращающегося вокруг неподвижной оси, путем суммирования кинетической энергии каждой частицы, из которой состоит твердое тело. Поскольку теорема о работе-энергии W _i = \(\Delta\)K _i верна для каждой частицы, она верна и для суммы частиц и всего тела.

Теорема о работе-энергии для вращения

Теорема о работе-энергии для твердого тела, вращающегося вокруг неподвижной оси:

\[W_{AB} = K_{B} — K_{A} \label{10.29{\theta_{B}} \left(\sum_{i} \tau_{i}\right) d \theta \ldotp \label{10.30}\]

Мы даем стратегию использования этого уравнения при анализе вращательного движения.

Стратегия решения задач: теорема о работе и энергии для вращательного движения

1. Определите силы, действующие на тело, и начертите диаграмму свободного тела. Рассчитайте крутящий момент для каждой силы.
2. Рассчитайте работу, совершаемую при вращении тела каждым крутящим моментом.
3. Применить теорему о работе-энергии, приравняв чистую работу, совершаемую телом, к изменению кинетической энергии вращения

Давайте рассмотрим два примера и применим теорему о работе-энергии для анализа вращательного движения.

Пример 10.17: Работа и энергия вращения

Крутящий момент 12,0 Н • м приложен к маховику, который вращается вокруг неподвижной оси и имеет момент инерции 30,0 кг • м ² . Если маховик изначально покоится, какова его угловая скорость после того, как он сделает восемь оборотов?

Стратегия

Применим теорему о работе-энергии. Из описания задачи мы знаем, что такое крутящий момент и угловое смещение маховика. Тогда мы можем найти конечную угловую скорость. 9{2}) — 0 \ldotp\]

Следовательно,

\[\omega_{B} = 6,3\; рад/с \ldotp\]

Это угловая скорость маховика после восьми оборотов.

Значение

Теорема о работе-энергии обеспечивает эффективный способ анализа вращательного движения, связывая крутящий момент с вращательной кинетической энергией.

Пример 10.18: Вращательная работа — шкив

Веревка, намотанная на шкив на рисунке \(\PageIndex{2}\), натягивается с постоянной направленной вниз силой \(\vec{F}\) величиной 50 Н. Радиус R и момент инерции I шкива равны 0,10 м и 2,5 х 10 9 .0306 −3 кг • м ² соответственно. Если струна не проскальзывает, какова угловая скорость шкива после разматывания 1,0 м струны? Предположим, что шкив выходит из состояния покоя.

Рисунок \(\PageIndex{2}\): (a) Нить намотана на шкив радиуса R. (b) Диаграмма свободного тела.

Стратегия

Глядя на диаграмму свободного тела, мы видим, что ни \(\vec{B}\), сила на подшипниках шкива, ни M\(\vec{g}\), вес шкива, создает крутящий момент вокруг оси вращения и, следовательно, не действует на шкив. Когда шкив поворачивается на угол \(\theta\), \(\vec{F}\) действует на расстояние d, такое что d = R\(\theta\). 9{2} \ldotp \end{split}\]

Решив \(\omega\), получим

\[\omega = 200.0\; рад/с \ldotp\]

Мощность для вращательного движения

Мощность всегда упоминается при обсуждении приложений в технике и физике. Мощность для вращательного движения так же важна, как и мощность для линейного движения, и ее можно получить так же, как и для линейного движения, когда сила постоянна. Линейная мощность, когда сила постоянна, равна P = \(\vec{F}\; \cdotp \vec{v}\). Если чистый крутящий момент постоянен в зависимости от углового смещения, уравнение 10. 8.4 упрощается, и чистый крутящий момент можно исключить из интеграла. В последующем обсуждении мы предполагаем, что чистый крутящий момент является постоянным. Мы можем применить определение мощности, полученное в Power, к вращательному движению. Из работы и кинетической энергии мгновенная мощность (или просто мощность) определяется как скорость выполнения работы,

\[P = \frac{dW}{dt} \ldotp\]

Если у нас есть постоянный чистый крутящий момент, уравнение 10.8.4 принимает вид W = \(\tau \theta\), а мощность равна

\ [P = \frac{dW}{dt} = \frac{d}{dt} (\tau \theta) = \tau \frac{d \theta}{dt}\]

или

\[P = \tau \omega \ldotp \label{10.31}\]

Пример 10.19: Крутящий момент гребного винта лодки

Лодочный двигатель, работающий при 9,0 x 10 ⁴ Вт, работает со скоростью 300 об/мин. Какой крутящий момент на карданном валу? 9{4}\; Н\; \cdotp м/с}{31,4\; рад/с} = 2864,8\; Н\; \cdotp m \ldotp\]

Значимость

Важно отметить, что радиан является безразмерной единицей, поскольку его определение представляет собой отношение двух длин. Поэтому он не появляется в решении.

Упражнение 10.8

К ветряной турбине приложен постоянный крутящий момент 500 кН • м, чтобы поддерживать ее вращение со скоростью 6 рад/с. Какая мощность необходима для поддержания вращения турбины?

Вращательные и поступательные отношения Краткий обзор

Вращательные величины и их линейный аналог сведены в три таблицы. В таблице 10.5 приведены вращательные переменные для кругового движения вокруг фиксированной оси с их линейными аналогами и связующим уравнением, за исключением центростремительного ускорения, которое стоит само по себе. В таблице 10.6 приведены уравнения кинематики вращения и поступательного движения. Таблица 10.7 суммирует уравнения динамики вращения с их линейными аналогами.

Таблица 10.5. Вращательные и поступательные переменные: сводка

9{2}}{r}$$

Поворотный	Трансляционное	Отношения
$$\тета$$	$$x$$	$$\тета = \frac{s}{r}$$
$$\омега$$	$$v_{f}$$	$$\omega = \frac{v_{t}}{r}$$
$$\альфа$$	$$a_{t}$$

Таблица 10.

6 – Уравнения кинематики вращения и поступательного движения: сводка 9{\theta_{B}} \left(\sum_{i} \tau_{i}\right) d \theta$$

Поворотный	Трансляционное
$$\theta_{f} = \theta_{0} + \bar{\omega} t$$	$$x = x_{0} + \bar{v} t$$
$$\omega_{f} = \omega_{0} + \alpha t$$	$$v_{f} = v_{0} + at$$	$$W = \int \vec{F}\; \cdotp d \vec{s}$$
$$P = \тау\омега$$	$$P = \vec{F} \cdotp \vec{v}$$

---

Эта страница под названием 10.9: Work and Power for Rotational Motion распространяется под лицензией CC BY 4. 0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. вращательная работа
   2. источник@https://openstax.