От чего зависит амплитудное значение угловой скорости: Гармонические колебания. | Объединение учителей Санкт-Петербурга
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ | ||
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
| |
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
| |
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: |
| |
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
| |
Скорость и ускорение при гармонических колебаниях. | ||
Согласно определению скорости, скорость – это производная от координаты по времени |
| |
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на |
| |
Величина |
| |
Следовательно, для скорости при гармоническом колебании имеем: |
| |
Согласно определению ускорения, ускорение – это производная от скорости по времени:
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят | ||
Величина — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: |
| |
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). | ||
Сравним выражения для смещения и ускорения при гармонических колебаниях:
|
| |
Можно записать: т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. |
| |
Часто бывает удобно записывать уравнения для колебаний в виде: где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: |
| |
Скорость и ускорение гармонических колебаний
Скорость точки, совершающей гармонические колебания
Для того чтобы получить эту зависимость, найдем производную от величины смещения по времени:
Из полученного соотношения видно, что скорость точки, совершающей гармонические колебания, также изменяется по гармоническому закону и опережает по фазе смещение на .
Ускорение точки, совершающей гармонические колебания
Это соотношение получается путем дифференцирования проекции скорости на ось x:
При гармонических колебаниях ускорение точки изменяется по гармоническому закону и опережает по фазе смещение на .
Из последнего соотношения следует, что проекция ускорения на ось x:
или
Так как , последнее соотношение можно переписать в виде:
Последнее уравнение представляет собой дифференциальное уравнение гармонических колебаний, решением которого является синусоидальная зависимость
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Колебания и волны: скорости и ускорения
В этой статье мы вспомним кинематику: то, что скорость – производная координаты, а ускорение – производная скорости или вторая производная координаты. Заодно потренируемся брать производные от сложных функций.
Задача 1. Материальная точка совершает гармонические колебания по закону  . Определить амплитуду, круговую частоту, период и начальную фазу колебаний. Найти амплитуды скорости и ускорения. Построить графики зависимости координаты. скорости и ускорения точки от времени.
. Определить амплитуду, круговую частоту, период и начальную фазу колебаний. Найти амплитуды скорости и ускорения. Построить графики зависимости координаты. скорости и ускорения точки от времени.
Амплитуда равна  , круговая частота (или циклическая, или угловая) равна
, круговая частота (или циклическая, или угловая) равна 
 , период колебаний –
, период колебаний –  с.
с.Скорость – производная координаты. Возьмем производную:
![Rendered by QuickLaTeX.com \[\upsilon=x^{\prime}=A \omega \sin \pi (\frac{2t}{3}+\frac{1}{4})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c17b9f132e51fa8b998d9b100b6a005a_l3.png)

Тогда  м/с.
м/с.
![Rendered by QuickLaTeX.com \[a_{max}= A\omega^2=1,2\left(\frac{2\pi}{3}\right)^2=5,26\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1dbdeefe093467743b465d13806bcc2b_l3.png)
Ответ: амплитуда  , круговая частота
, круговая частота  , начальная фаза
, начальная фаза  , период колебаний –
, период колебаний –  с,
с,  м/с,
м/с,  м/с
м/с
Задача 2. Материальная точка совершает гармонические колебания с частотой  Гц. Амплитуда колебаний А =3 см. Определить скорость точки в момент времени, когда смещение
Гц. Амплитуда колебаний А =3 см. Определить скорость точки в момент времени, когда смещение  см.
см.
Запишем закон колебаний. Так как не указано, по какому закону они совершаются, то выберем косинус.
![Rendered by QuickLaTeX.com \[x=A\cos(\omega t+\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-34624b09d362c9f7fac6573d6e753994_l3.png)
![Rendered by QuickLaTeX.com \[\omega=2 \pi f=\pi\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-beed6ff14eeba6d732b0d7b833d0a777_l3.png)
![Rendered by QuickLaTeX.com \[\frac{x}{A}=\cos(\omega t+\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b13367ee11b01aad871206299f9170dd_l3.png)
![Rendered by QuickLaTeX.com \[\frac{x^2}{A^2}=\cos^2(\omega t+\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4592156098a158b521603ec6bb0255a9_l3.png)
![Rendered by QuickLaTeX.com \[1-\frac{x^2}{A^2}=\sin^2(\omega t+\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-06386d1686cf976584713e17f38da21d_l3.png)
![Rendered by QuickLaTeX.com \[\sin(\omega t+\psi_0)=\sqrt{1-\frac{x^2}{A^2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d47ae69548da3035a0693351e386e94d_l3.png)
Скорость – производная координаты. Возьмем производную:
![Rendered by QuickLaTeX.com \[\upsilon=x^{\prime}=-A \omega \sin (\omega t+\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-353c6f7ce493bbe71c183f1ae29f7987_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon=x^{\prime}=- A \omega \sqrt{1-\frac{x^2}{A^2}}=-\omega \sqrt{A^2-x^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-28b265889bb68e671bf6385a60f32306_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon=-\pi \sqrt{9-2,25}=-8,16\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f4b95ab85c37d58a0d8a9c196c4faefb_l3.png)
Ответ:  см/с.
см/с.
Задача 3. Написать закон гармонического колебания точки, если максимальное ускорение ее  см/с2, период колебаний
см/с2, период колебаний  с и смещение точки от положения равновесия в начальный момент времени
с и смещение точки от положения равновесия в начальный момент времени  см. Колебания совершаются по закону синуса.
см. Колебания совершаются по закону синуса.
![Rendered by QuickLaTeX.com \[x=A\sin(\omega t+\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-182c6119506bdf3aa63138faa07e5e33_l3.png)
![Rendered by QuickLaTeX.com \[\omega=\frac{2\pi}{T}=\frac{2\pi}{2}=\pi\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ee2e91d39048c818518ee579d55d630b_l3.png)
В момент времени  смещение равно 2,5 см:
смещение равно 2,5 см:
![Rendered by QuickLaTeX.com \[x_0=A\sin(\psi_0)= 2,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fa20ab974e0cf5a1e8a1afdf262c001e_l3.png)
Выясним, какая у точки амплитуда колебаний. Для этого определим скорость (первую производную) и ускорение(вторую производную):
![Rendered by QuickLaTeX.com \[\upsilon=x^{\prime}=-A \omega \cos( \omega t+\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-67f65de8c1a12142f121f0f2281462b4_l3.png)

Максимальное ускорение – это амплитуда ускорения, то есть
![Rendered by QuickLaTeX.com \[a_{max}= A\omega^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6cc7cb039d58e4397ceb3392bd8c6503_l3.png)
Откуда  :
:
![Rendered by QuickLaTeX.com \[A=\frac{ a_{max}}{\omega^2}=5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-df02eddb2de62b314af80a7031026c6f_l3.png)
Тогда в момент времени  :
:
![Rendered by QuickLaTeX.com \[x_0=\frac{ a_{max}}{\omega^2}\sin(\psi_0)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-38b0eed5225cefc1c49461613619cda3_l3.png)
Определим начальную фазу:
![Rendered by QuickLaTeX.com \[\sin(\psi_0)=\frac{x_0 \omega^2}{ a_{max}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6369be2a4f7102c35394436a95b294c6_l3.png)
![Rendered by QuickLaTeX.com \[\sin(\psi_0)=\frac{2,5 \pi^2}{49,3}=0,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-be648e94986e022ebf1c43f13132d64b_l3.png)
![Rendered by QuickLaTeX.com \[\alpha=\arcsin(0,5)=30^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4820dcc49dead9c5029c1e92fa4a0355_l3.png)
Закон колебаний тогда будет таким:
![Rendered by QuickLaTeX.com \[x=5\sin(\pi t+\frac{\pi}{6})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ee54a664376be2d1f26ae2ef6fcafe86_l3.png)
Ответ:  см.
см.
Глава 11. Механические колебания и волны
Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где — некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде
(11.1) |
где , и — некоторые числа.
Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний — это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус — периодическая функция с периодом . Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем
(11.2) |
Частотой колебаний тела называется число колебаний, совершаемых в единицу времени. Очевидно, что частота колебаний связана с периодом колебаний по формуле
(11.3) |
Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).
Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.
В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника
(11.4) |
где — коэффициент жесткости пружины, — масса груза. Период колебаний математического маятника определяется следующим соотношением
(11.5) |
где — длина нити, — ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.
Чтобы найти циклическую частоту колебаний груза в задаче 11.1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с — это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c-1 (ответ 2). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний — 0,1 с-1 (ответ 1).
Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11.1.3), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия — одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону — вторая, назад в положение равновесия — третья, из положения равновесия в начальную точку — четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода — две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4).
Величина перемещения тела — расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3).
По определению фаза колебаний — это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в задаче 11.1.5 — 3.
Период — это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (задача 11.1.6) тело затрачивает четвертую часть периода (ответ 3).
Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2. Функция же — тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4).
При гармонических колебаниях скорость тела изменяется по закону , где — амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени (задача 11.1.8). Используя далее известную тригонометрическую формулу, получаем
Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2).
За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2).
Амплитуду колебаний скорости (задача 11.1.10) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где — коэффициент жесткости пружины, — амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где — масса тела, — скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим
(ответ 1), где использовано выражение для круговой частоты колебаний груза на пружине:
По формуле (11.4) получаем в задаче 11.2.1
(ответ 4).
Из формулы (11.5) заключаем (задача 11.2.2), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1).
Часы — это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ 3).
Чтобы найти амплитуду колебаний в задаче 11.2.4, необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим
где — такой угол, что . Из этой формулы следует, что амплитуда колебаний тела — (ответ 4).
В задаче 11.2.5 имеем при см. Откуда см (ответ 2).
Задачи 11.2.6 и 11.2.7 посвящены механическим волнам. Волна – некоторый колебательный процесс, который может распространяться в среде. При этом каждая точка среды совершает колебания около определенного положения и в среднем не перемещается в пространстве. Волна характеризуется периодом (или связанной с ним частотой ), скоростью и длиной волны , которая определяется как минимальное расстояние между точками, колеблющимися в одинаковой фазе. Для решения задач ЕГЭ по этой теме необходимо помнить формулу, дающую связь между параметрами волны
(11.6) |
которую легко запомнить, поскольку эта связь имеет такой же вид как обычное соотношение между расстоянием, скоростью и временем. Например, в задаче 11.2.6 по формуле (11.6) находим длину волны м (ответ 2).
Как следует из рисунка в задаче 11.2.7 длина волны, распространяющейся по шнуру, равна м. Поэтому по формуле (11.6) имеем Гц (ответ 4).
Поскольку в момент максимального отклонения пружинного маятника, механическая энергия системы равна потенциальной энергии пружины, то
где — амплитуда колебаний, — жесткость пружины. Поэтому при увеличении механической энергии пружинного маятника в 2 раза амплитуда колебаний увеличилась в раз (задача 11.2.8 – ответ 1).
Используя известную тригонометрическую формулу, получим в задаче 11.2.9
Эта зависимость представляет собой гармоническую функцию, но колеблющуюся вокруг точки . Амплитудой этих колебаний является множитель перед косинусом — (так как сам косинус меняется в интервале от -1 до 1). Циклической частотой — величина (ответ 4).
Вертикальный пружинный маятник отличается от горизонтального (задача 11.2.10) наличием силы тяжести. Однако сила тяжести приводит только к сдвигу положения равновесия маятника, а возвращающая сила по прежнему будет зависеть от смещения маятника от положения равновесия по закону (так как возвращающей силой будет разность силы упругости и постоянной силы тяжести). Поэтому период колебаний груза на вертикальной и горизонтальной пружине — одинаков (конечно, при условии, что и сам груз и пружины одинаковы). Правильный ответ в задаче — 3.
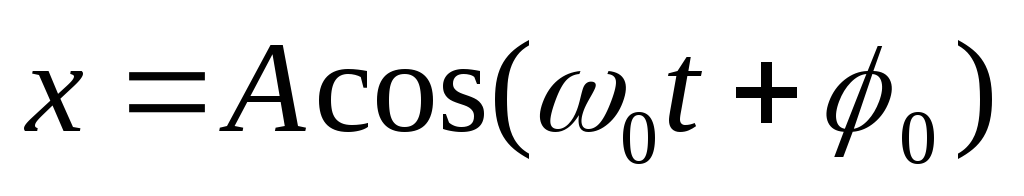
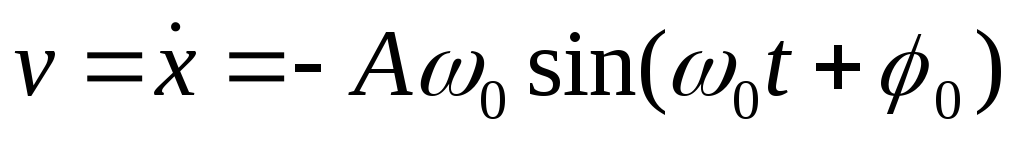 =
=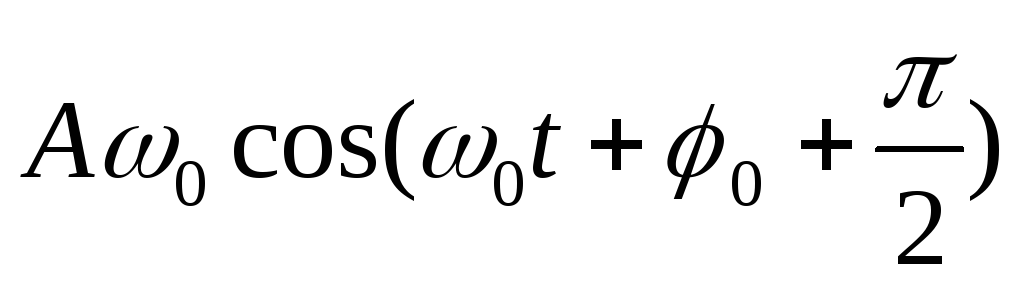
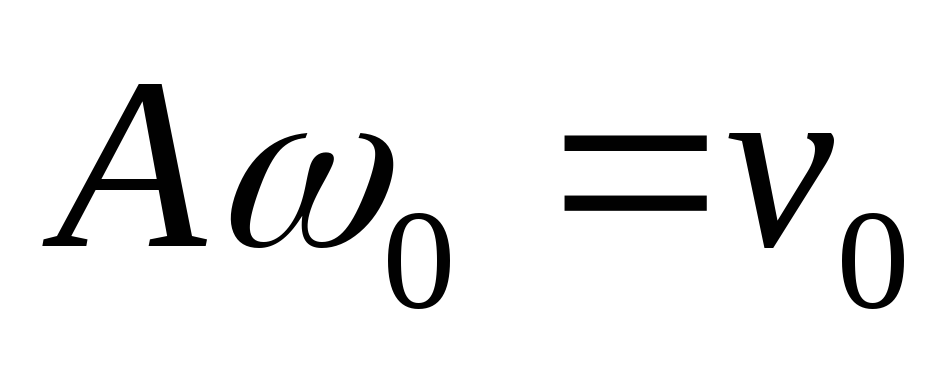 — амплитудное значение скорости
— амплитудное значение скорости
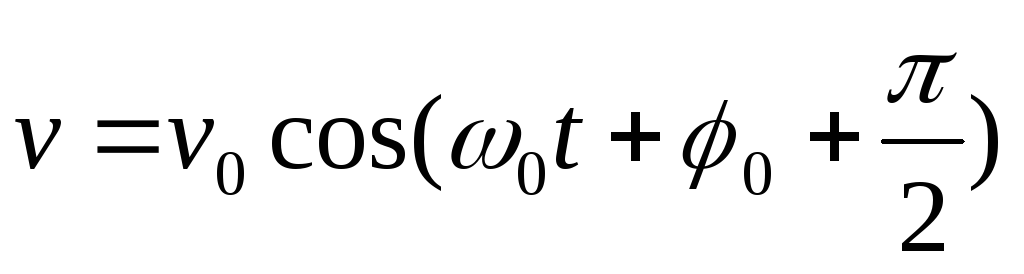
Скорость опережает смещение по фазе на 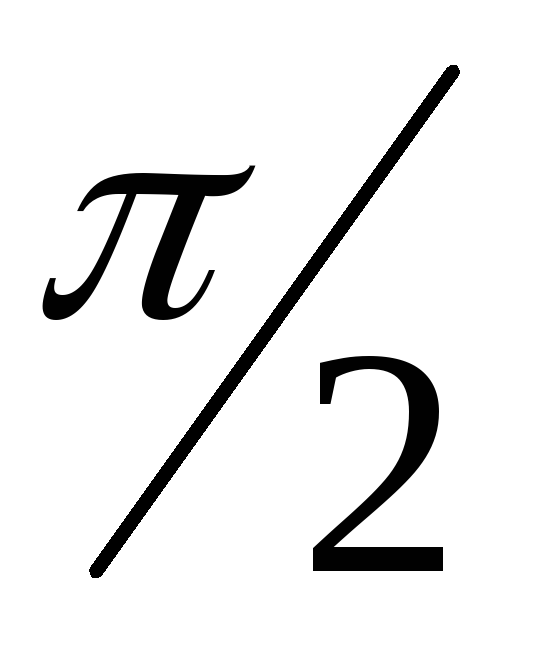 .
.
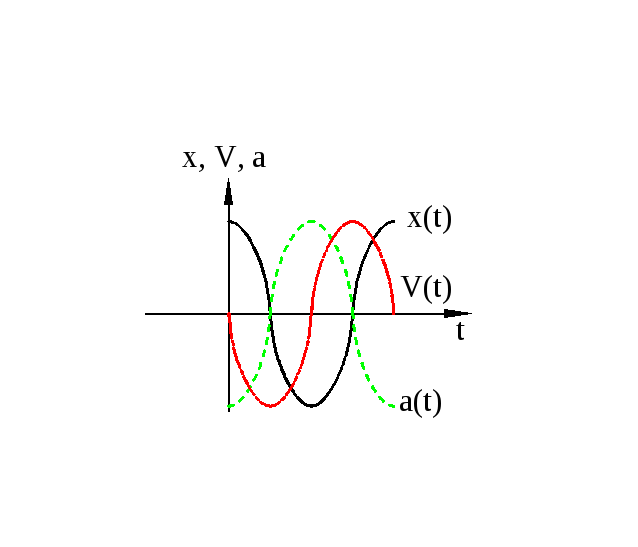
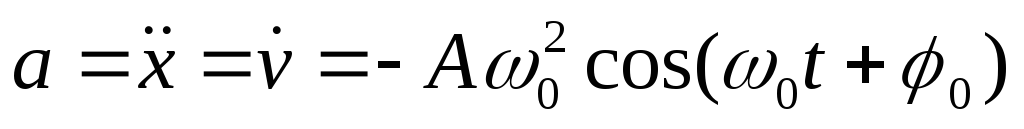 =
=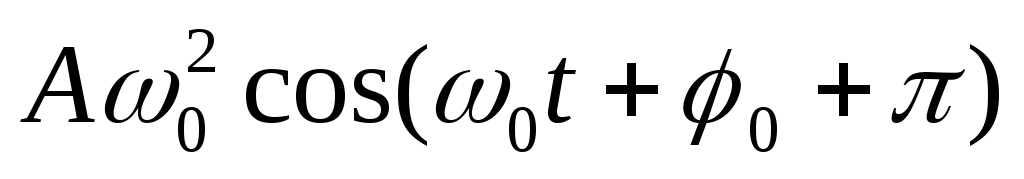
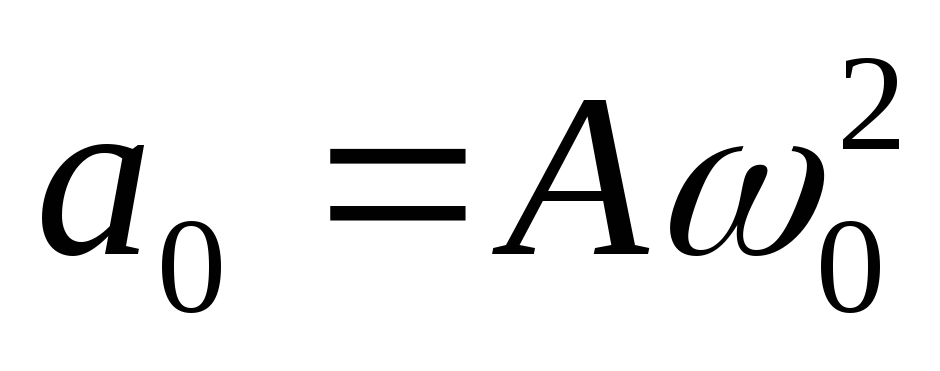
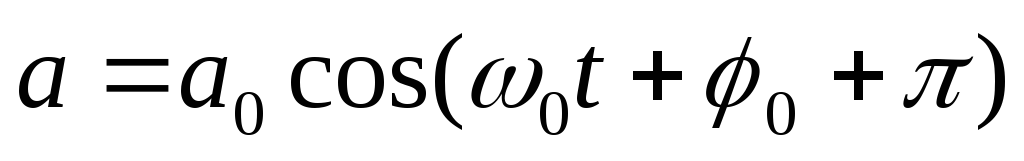
Сдвиг фаз между  и
и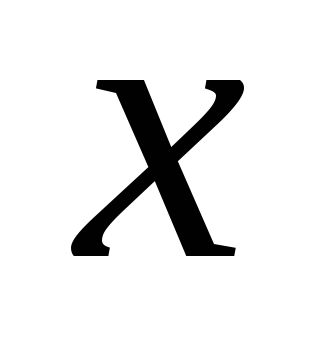 равен
равен ,
они колеблются в противофазах.
,
они колеблются в противофазах.
Сила.
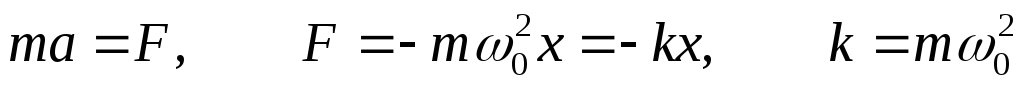
Силы, которые подчиняются закону упругой силы, но по природе своей не являются упругими называются квазиупругими.
Гармонические колебания – это колебания, которые происходят под действием квазиупругой силы, то есть силы, пропорциональной смещению.
Энергия гармонического осциллятора.
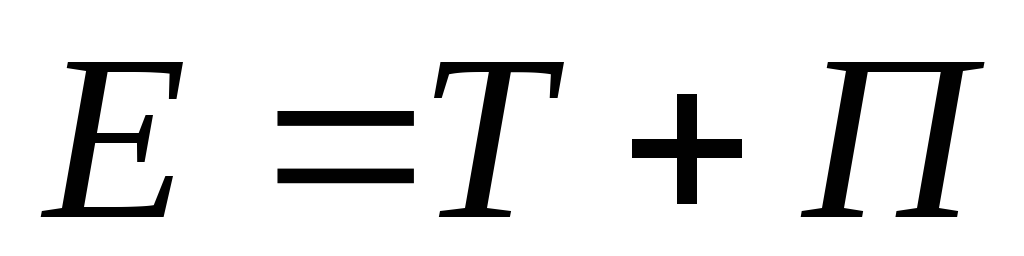
(кинетическая Энергия, Т + потенциальная энергия, П = полной энергии, Е).
Пусть
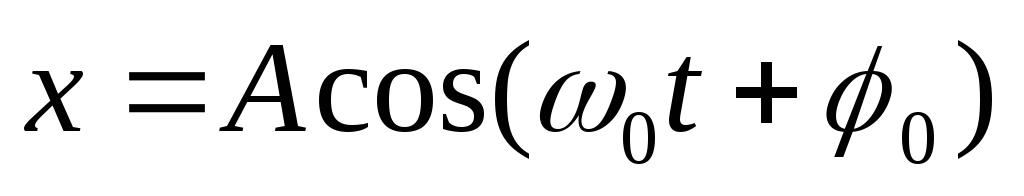
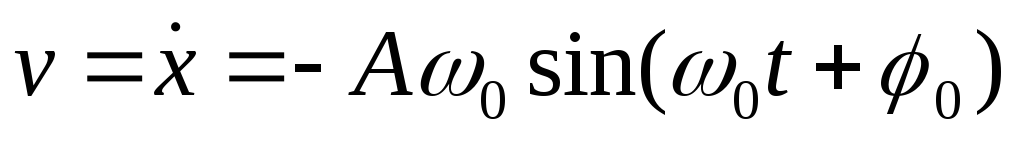 .
.
Тогда
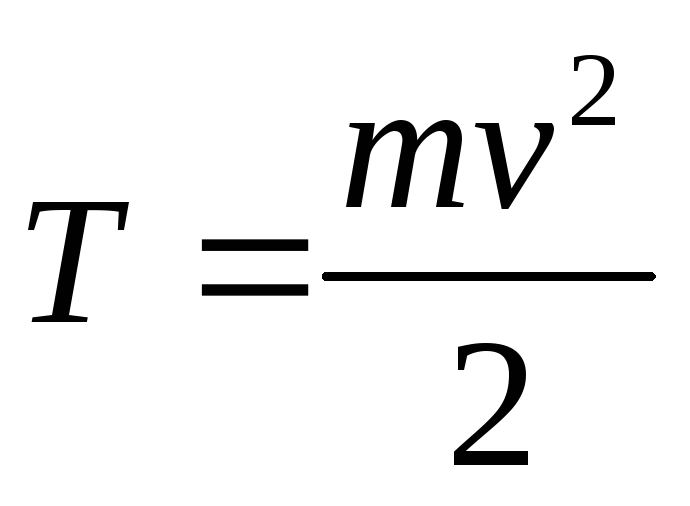 =
=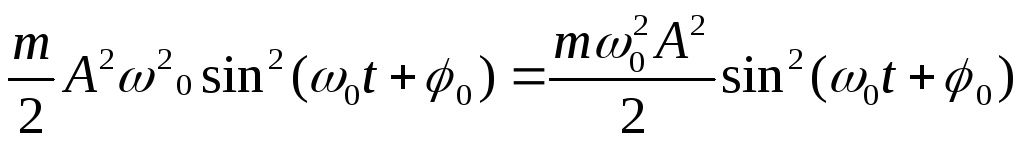
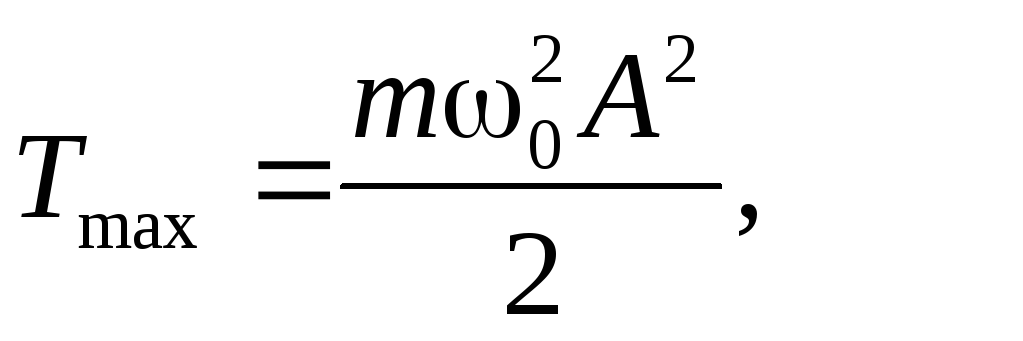
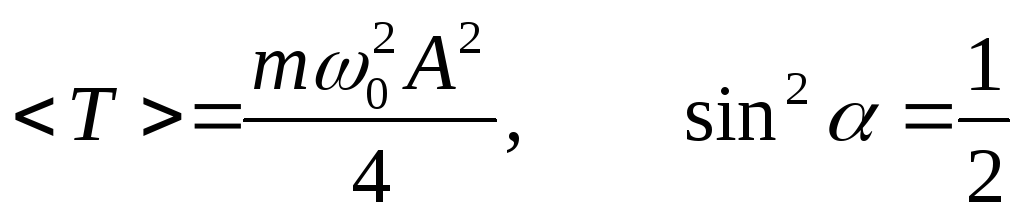
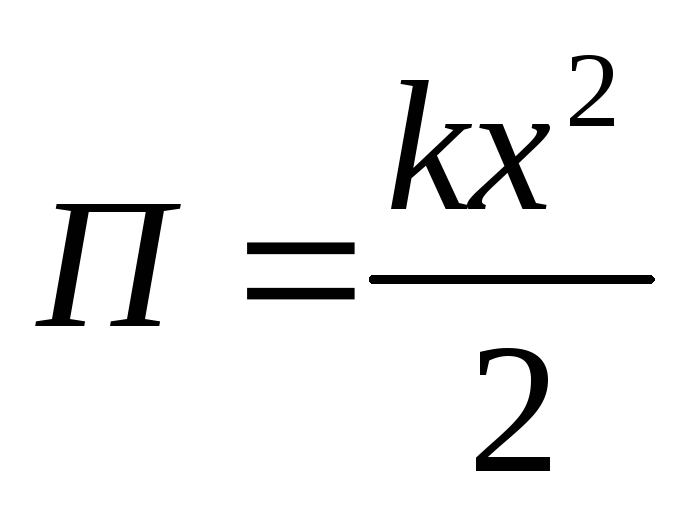 =
=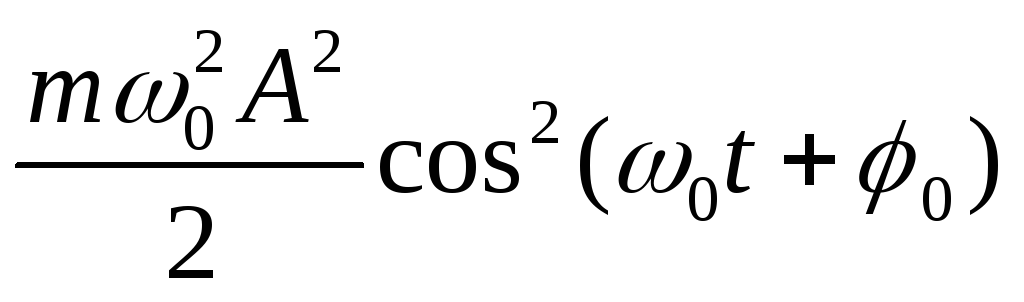
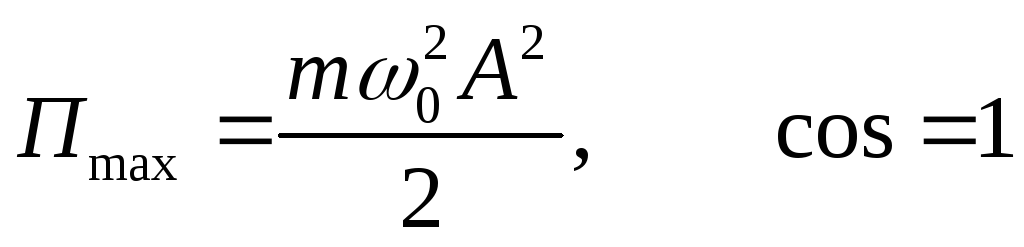
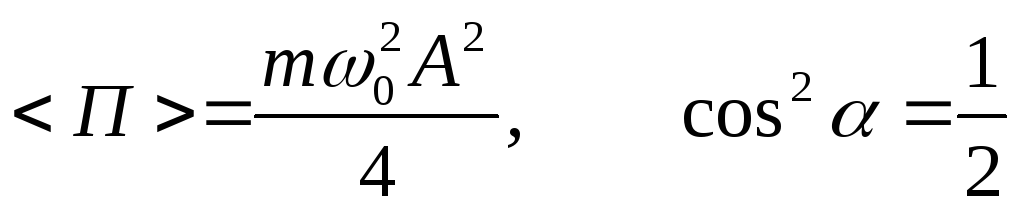
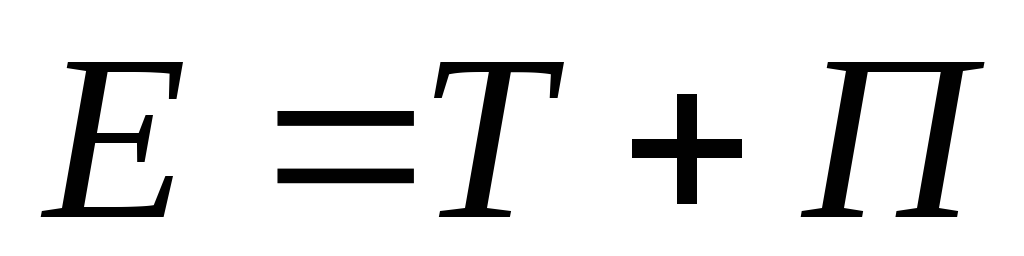 =
=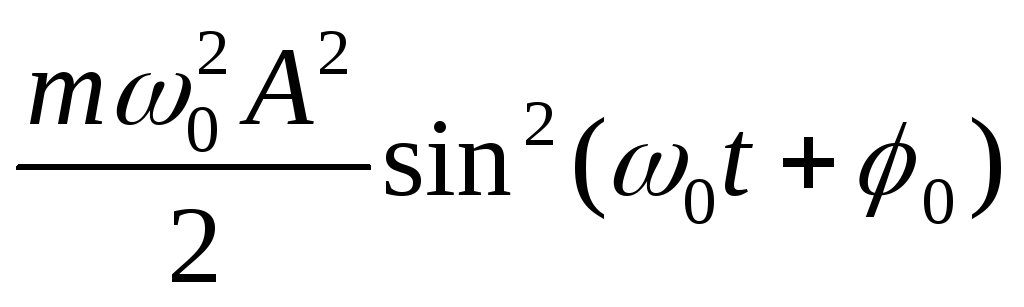 +
+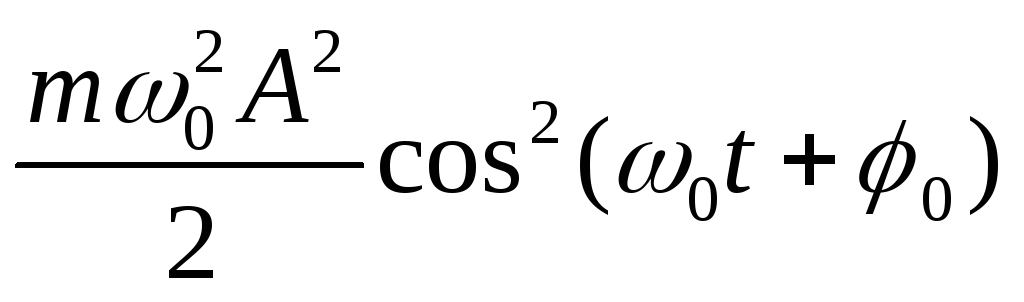 =
=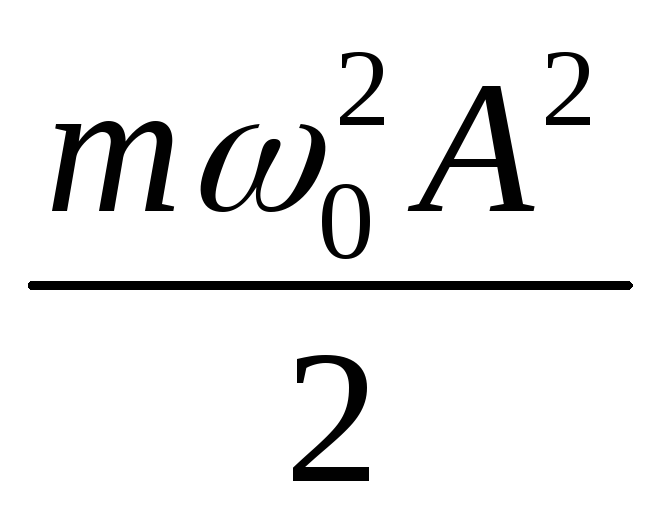 .
.
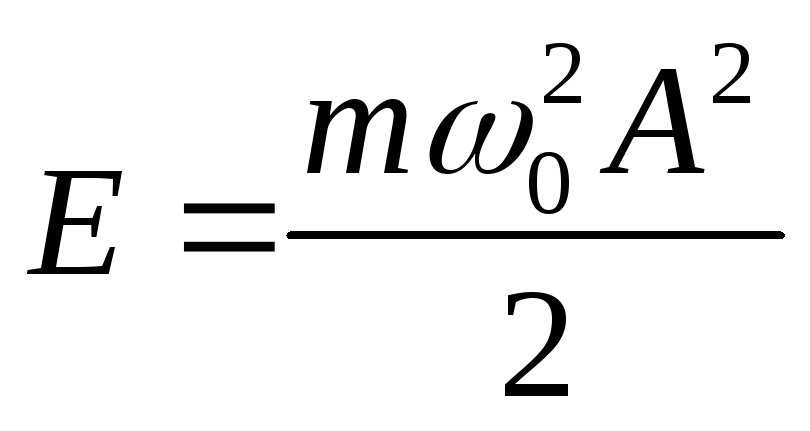
— полная энергия механического осциллятора
не зависит от 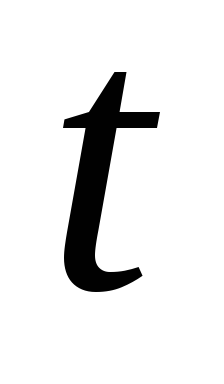 и пропорциональна
и пропорциональна .
Механический осциллятор есть консервативная
система, так как
.
Механический осциллятор есть консервативная
система, так как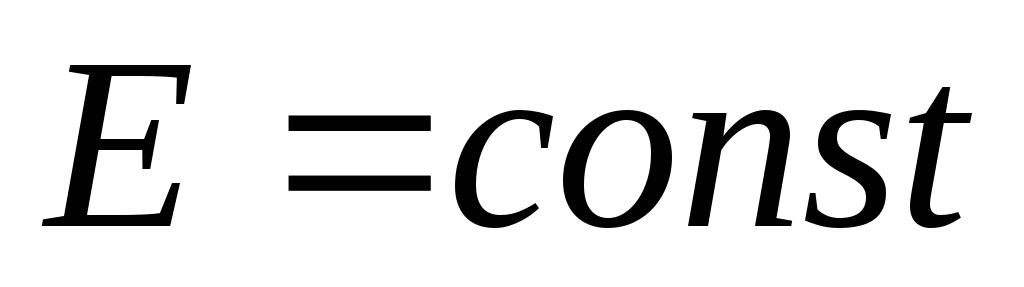 .
.
Выводы:
Кинетическая и потенциальная энергии по отдельности зависят от времени.
Максимальная кинетическая энергия равна максимальной потенциальной энергии и равна полной энергии.
Средняя кинетическая энергия равна средней потенциальной энергии и равна половине полной энергии.
Полная энергия не зависит от времени и пропорциональна квадрату амплитуды.
Лекция 8. Сложение колебаний.
Сложение колебаний – задача сложная и часто пользуются искусственными приемами для ее решения. Представим гармоническое колебание в виде вектора амплитуды.
В момент 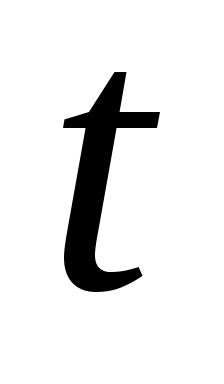 проекция на ось
проекция на ось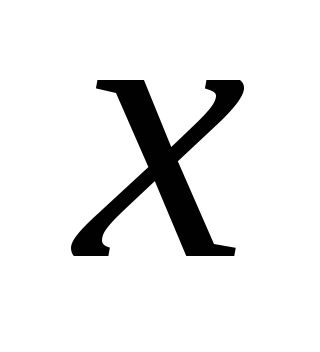 вектора
вектора равна
равна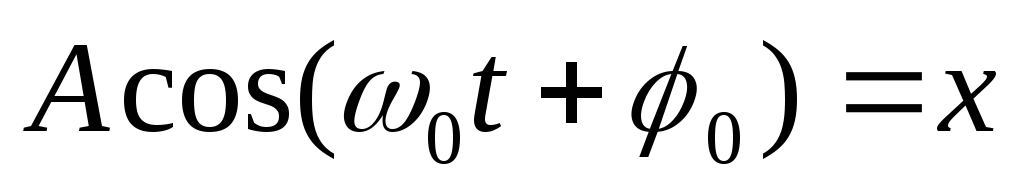 .
Получили уравнение гармонических
колебаний. Итак, всякому гармоническому
колебанию можно сопоставить вектор
амплитуды, вращающийся с угловой
скоростью
.
Получили уравнение гармонических
колебаний. Итак, всякому гармоническому
колебанию можно сопоставить вектор
амплитуды, вращающийся с угловой
скоростью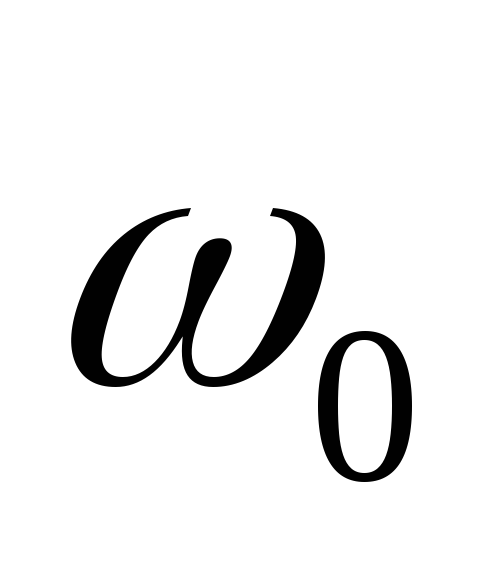 ,
равной круговой частоте колебания.
Тогда проекция этого вектора на ось
,
равной круговой частоте колебания.
Тогда проекция этого вектора на ось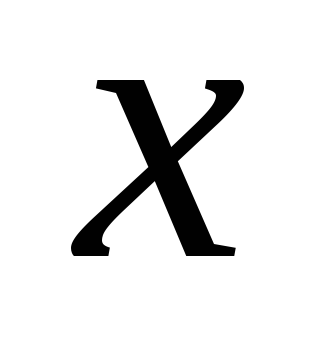 совершает гармонические колебания.
Физического смысла здесь нет, но решение
задачи облегчается.
совершает гармонические колебания.
Физического смысла здесь нет, но решение
задачи облегчается.
Сложение гармонических колебаний одного направления и одной частоты.
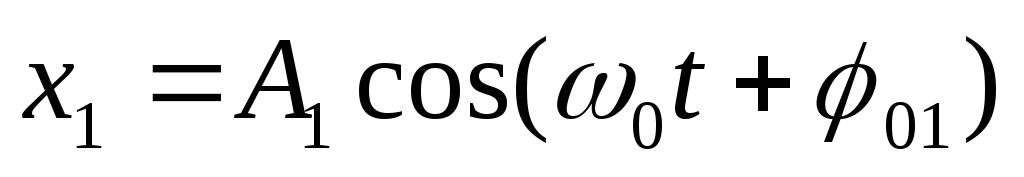
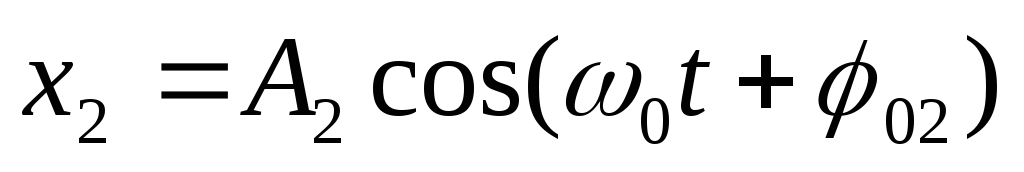 .
.
Изобразим их графически:
Векторы  и
и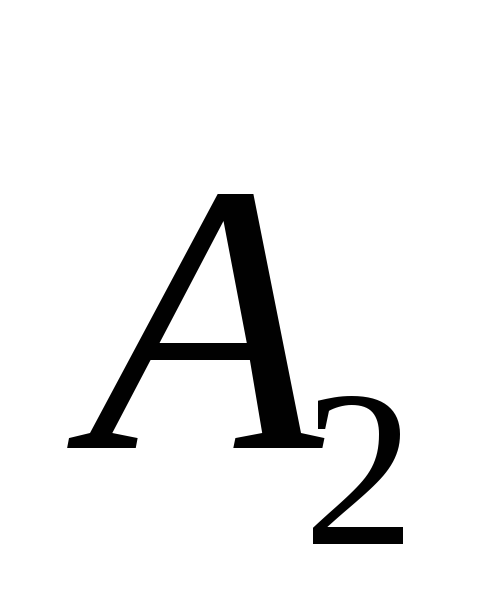 вращаем с
вращаем с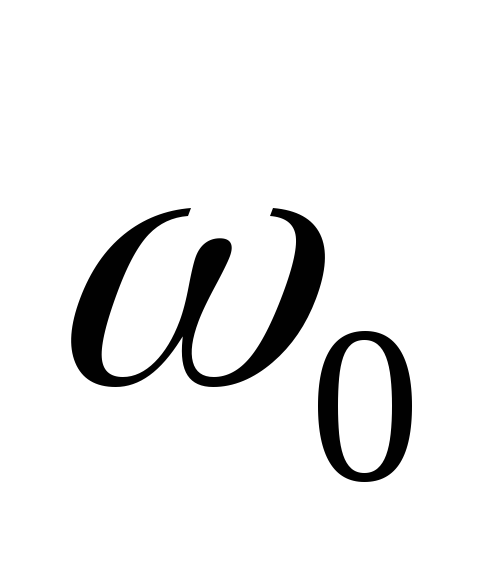 .
Поскольку частоты равны, то параллелограмм,
не деформируясь, вращается с той же
частотой. Длина
.
Поскольку частоты равны, то параллелограмм,
не деформируясь, вращается с той же
частотой. Длина не
меняется. Его проекция совершает
гармонические колебания.
не
меняется. Его проекция совершает
гармонические колебания.
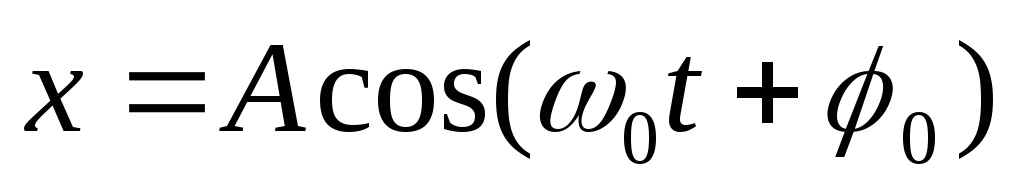 ,
но
,
но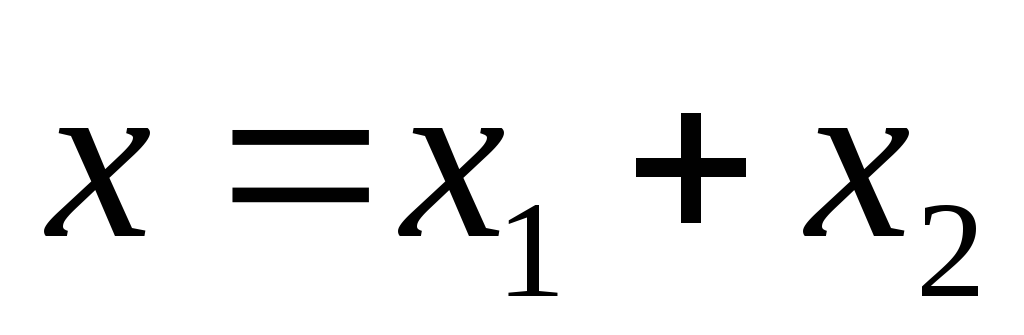 .
.
То есть результирующее колебание гармоническое, имеет ту же частоту, что и слагаемые колебания. Амплитуду находим из начальных условий по формуле
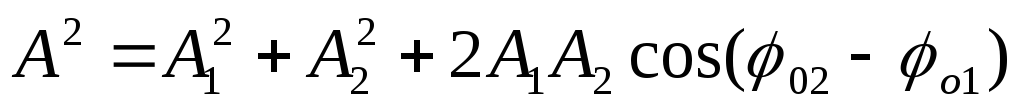
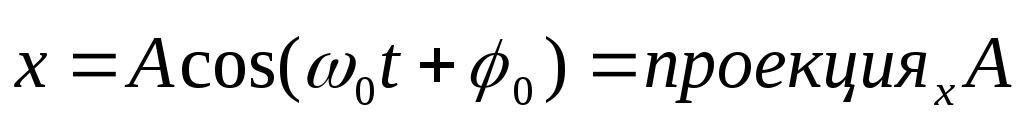 ,
,
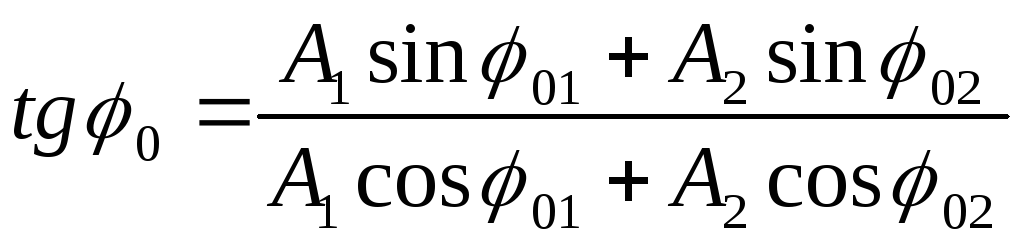
Биения.
Рассмотрим сложение колебаний одинаковой
амплитуды и близких частот 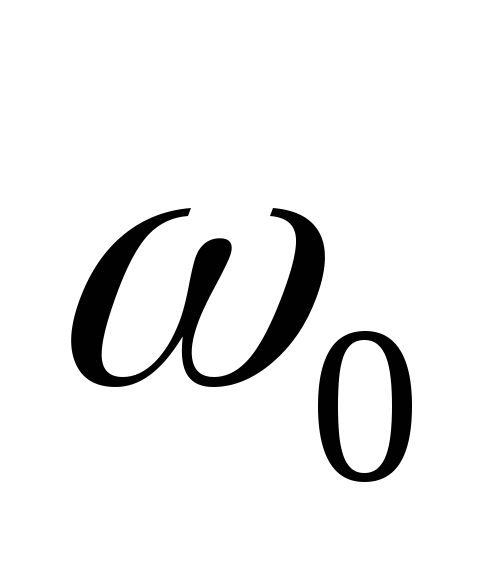 ,
,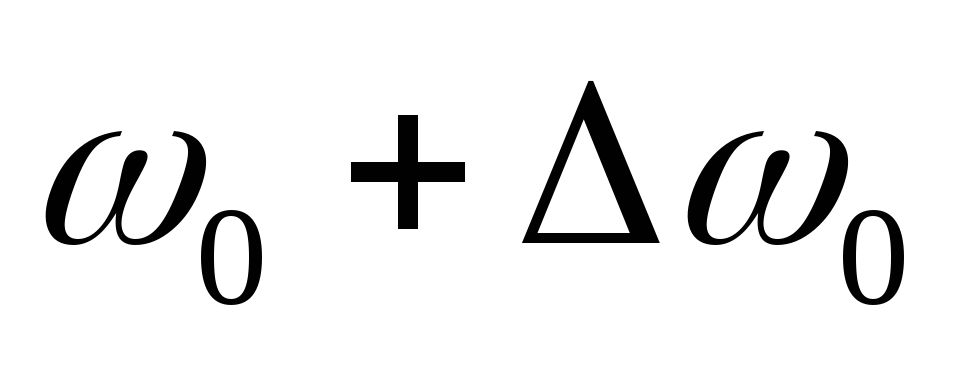 ,.
Решение задачи усложняется.
,.
Решение задачи усложняется.
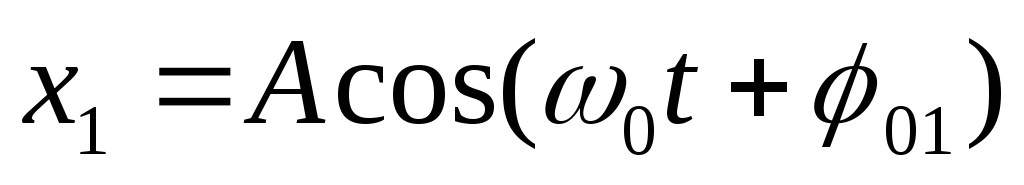
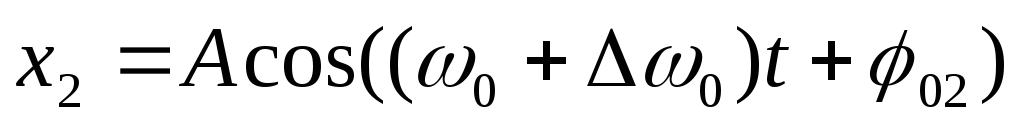 .
.
Если изобразить эти колебания с помощью
вектора амплитуды, то они вращаются с
разными угловыми скоростями, и всегда
будет момент, когда 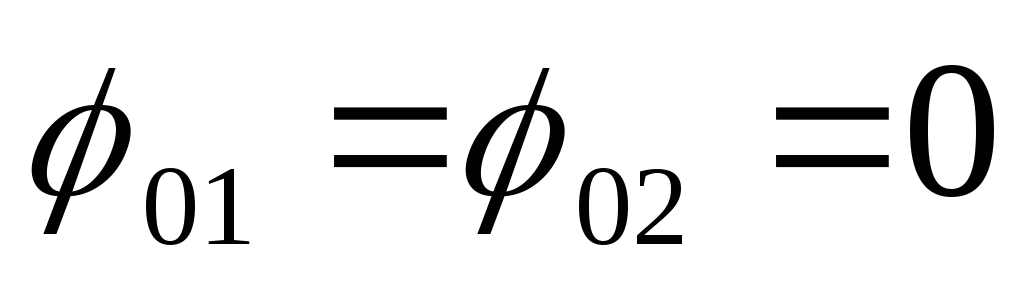 .
Фазы в этот момент принимают за нуль.
Тогда
.
Фазы в этот момент принимают за нуль.
Тогда
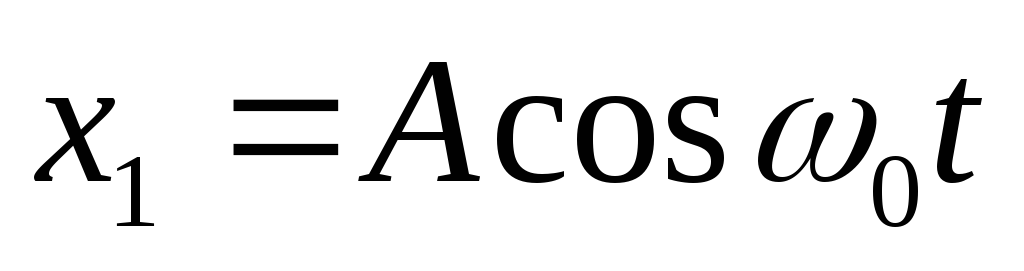
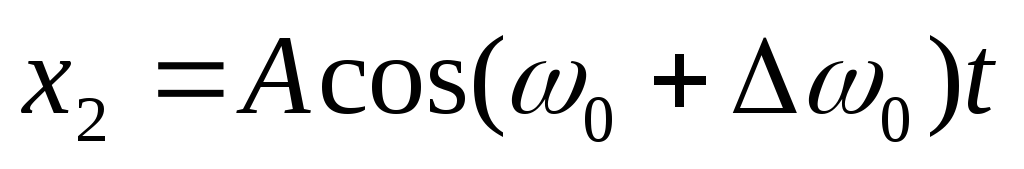 .
.
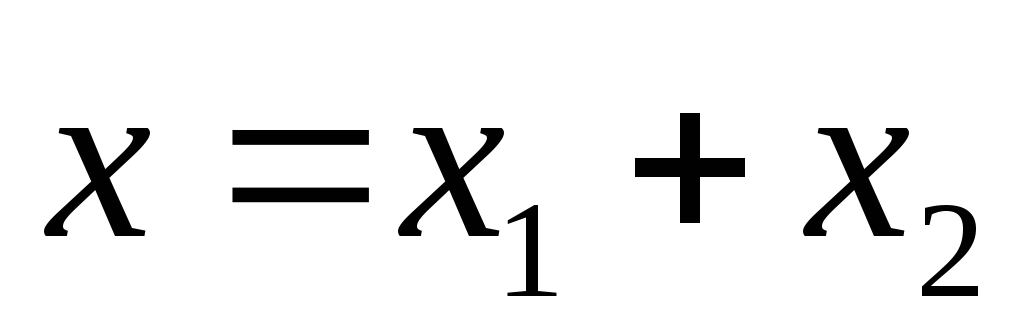 =
=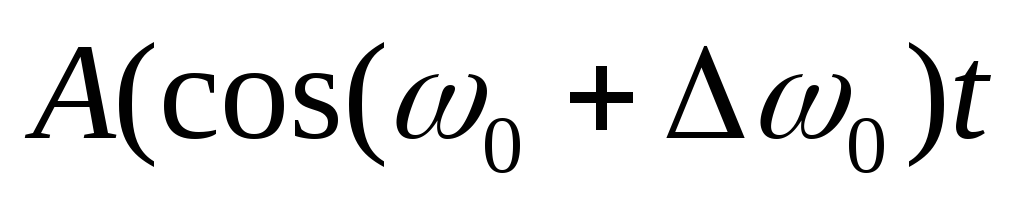
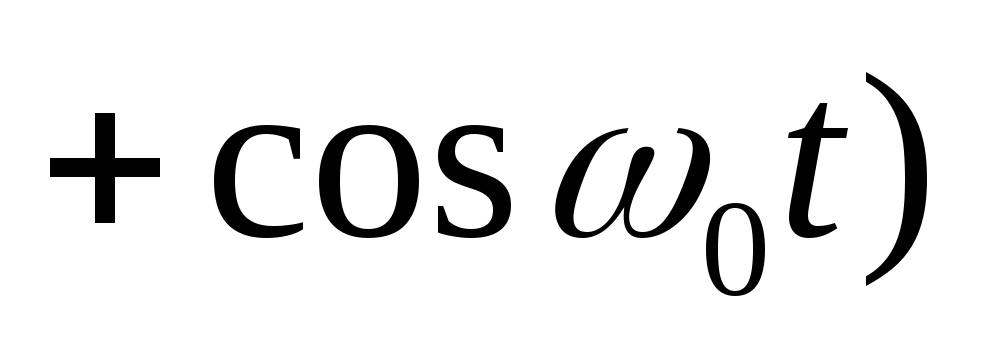 =
=
= 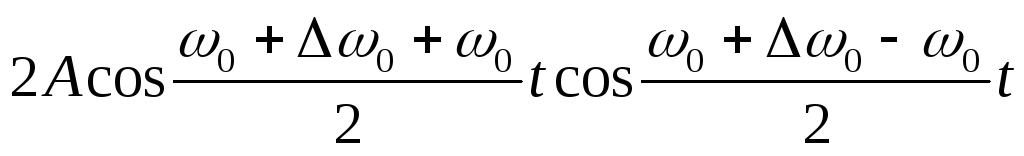 .
.
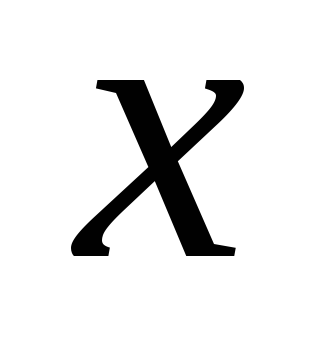 =
=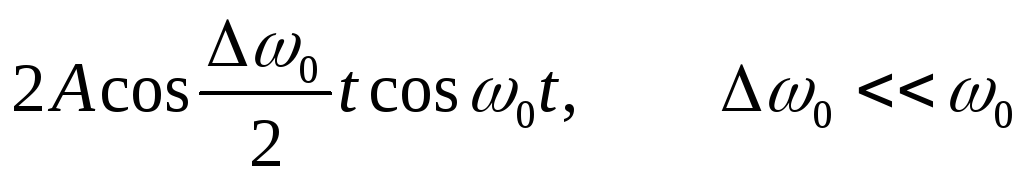
— уравнение биений. Первый множитель медленно меняется, второй – быстро. Уравнение можно представить в виде
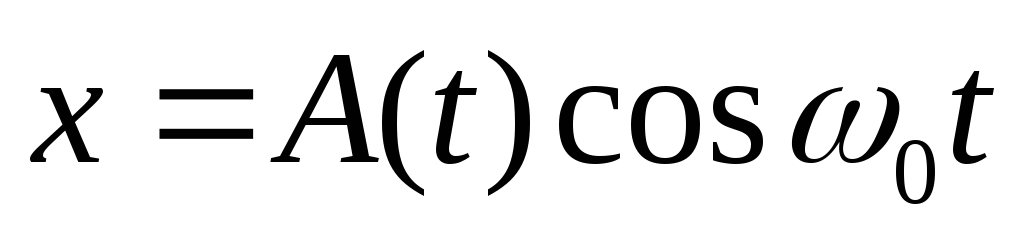
Сравним с уравнением гармонических колебаний
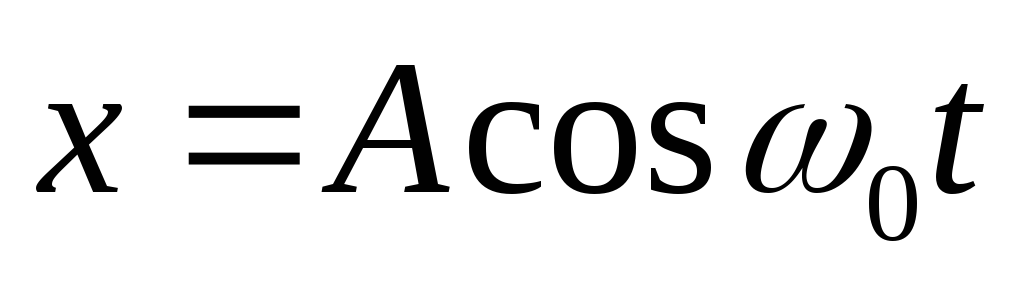 .
.
Уравнение биений – негармоническое,
но 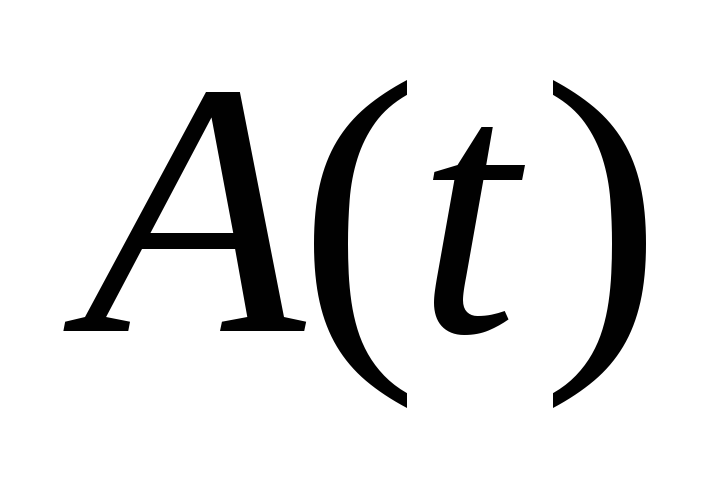 меняется медленно, так как
меняется медленно, так как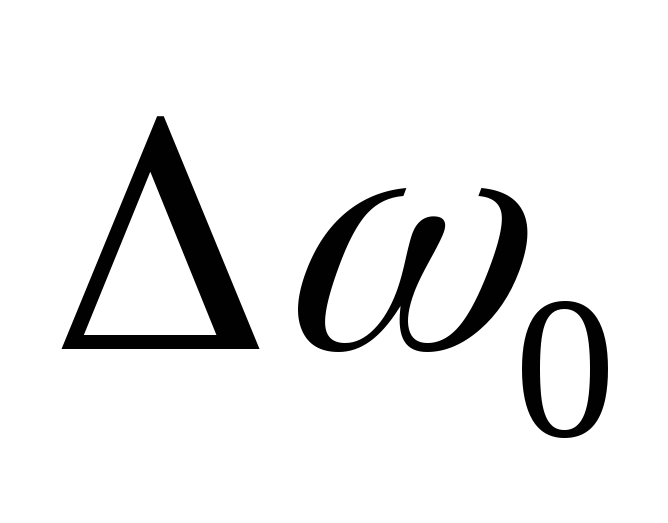 мало.
мало.
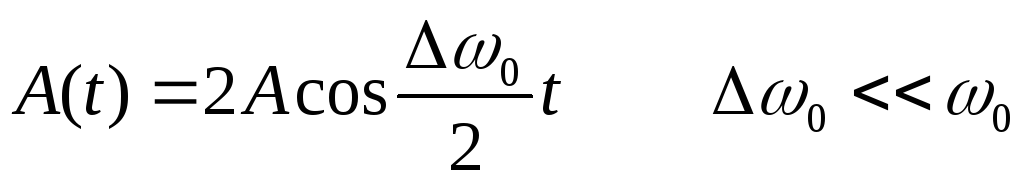 .
.
Поэтому биения – приблизительно
гармонические колебания с медленно
меняющейся амплитудой, 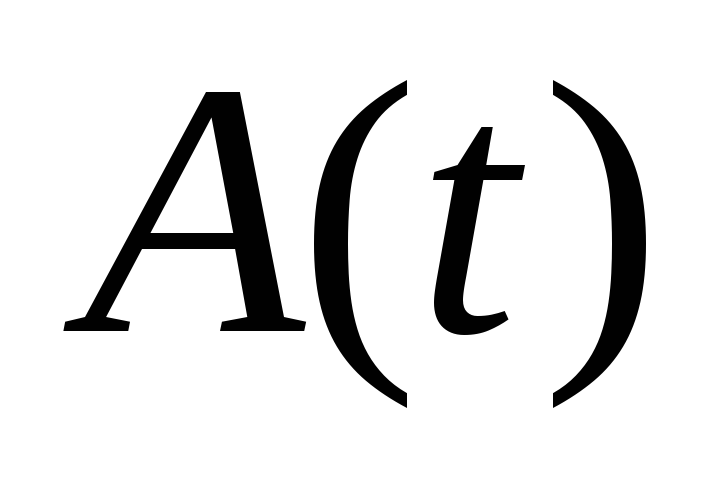 может быть больше и меньше нуля.
может быть больше и меньше нуля.
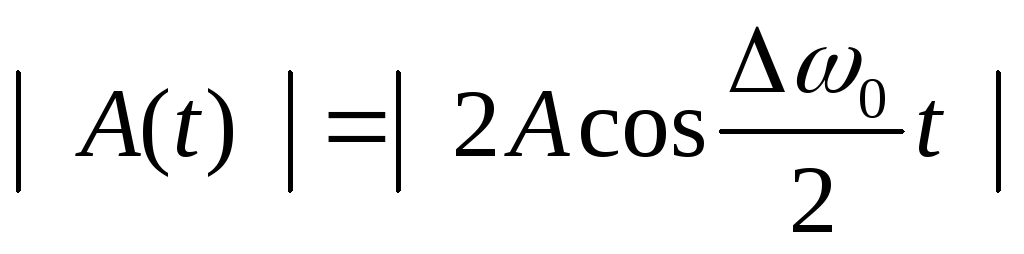 — амплитуда. Для гармонических колебаний
— амплитуда. Для гармонических колебаний
|
|
Амплитуда ограничивает 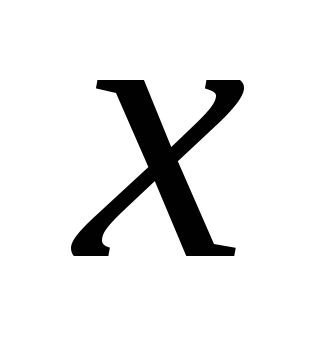 .
(Проводим штрихами симметричную кривую
внизу).Частота
.
(Проводим штрихами симметричную кривую
внизу).Частота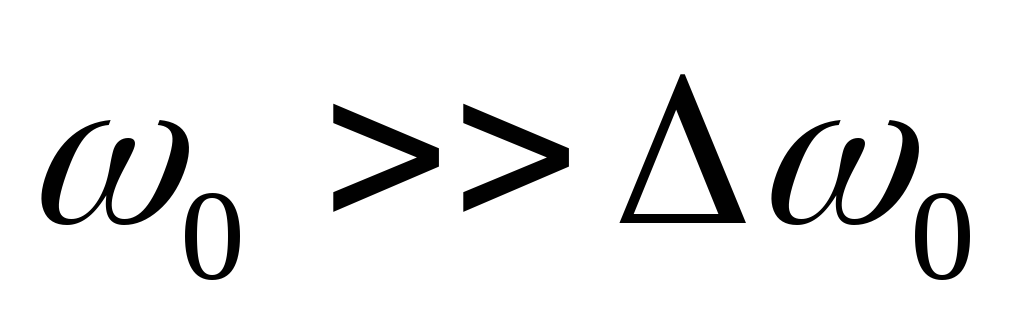 .
.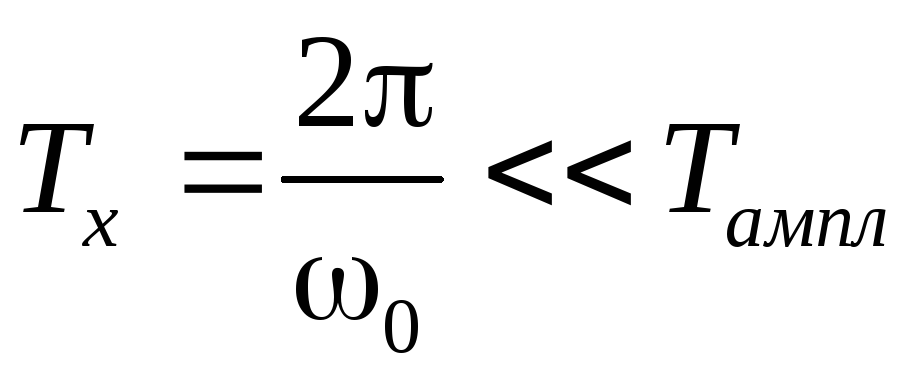 .
Получили биения – усиление и ослабление
колебаний.
.
Получили биения – усиление и ослабление
колебаний.
Метод биений широко применяется на практике. Основан на сравнении искомой частоты с частотой эталона. Метод биений – это один из наиболее точных методов измерения частот, емкостей, индуктивностей. Применяют для настройки музыкальных инструментов.
Значение — угловая скорость
Cтраница 1
Значение угловой скорости ш данного вращающегося твердого тела не зависит от выбора точки В, так как угол Дер, на который поворачивается за данное время Ы радиус ОВ, не зависит от положения точки В. [1]
Значения угловой скорости сошаиб и шшаим можно выразить через среднее арифметическое угловой скорости сокр ( сошаиб со. [2]
Значения угловых скоростей соответствуют полному циклу работы компрессора, при этом исходят из предположения, что вал является абсолютно жестким и угол между кривошипами не изменяется. [3]
Значение угловой скорости, соответствующее резонансу, называется критической угловой скоростью. [4]
Значение угловой скорости тела для данного момента времени может быть положительным или отрицательным в зависимости от того, в какую сторону вращается тело. Когда тело вращается против часовой стрелки, если смотреть с положительного конца оси вращения, то Аф О, dy / dt 0 и угловая скорость со положительна. Если тело вращается по часовой стрелке, то угловая скорость отрицательна. [5]
При значениях угловой скорости меньше сотщ и больше сотах регулятор не реагирует на изменение угловой скорости. Определяя равновесную угловую скорость по формуле (26.7) для г, изменяющегося в пределах хода h, можно построить кривую угловых скоростей вала регулятора ( рис. 26.7) и, следовательно, найти пределы, в которых регулятор реагирует на изменение угловой скорости вала машины. [7]
Так определяются значения угловой скорости со звена приведения механизма. [9]
Так определяются значения угловой скорости ш звена приведения механизма. [11]
Так определяются значения угловой скорости о звена приведения механизма. [13]
Итак, значение угловой скорости тела равно первой производной от угла его поворота по времени. [14]
Критическими называются значения угловых скоростей ротора, при которых амплитуды вынужденных колебаний неограниченно возрастают. [15]
Страницы: 1 2 3 4
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .
Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.
Пружинный маятник.
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):
,
или
.
Это — уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .
Как определить направление угловой скорости
- Образование
- Наука
- Физика
- Как определить направление угловой скорости
Стивен Хольцнер
В физике, когда колесо вращается, оно имеет не только угловую скорость, но и направление. Вот что говорит вам вектор угловой скорости:
Размер вектора угловой скорости говорит вам об угловой скорости.
Направление вектора говорит вам об оси вращения, а также о том, вращение происходит по часовой стрелке или против часовой стрелки.
Можете ли вы определить направление, в котором его угловая скорость,
баллов? Он не может указывать на обод колеса, как это делает тангенциальная скорость, потому что его направление будет меняться каждую секунду. Фактически, единственный реальный выбор для его направления — перпендикулярно колесу.
Направление угловой скорости всегда застает людей врасплох: угловая скорость,
точек вдоль оси колеса (как вы можете видеть на рисунке).
Угловая скорость указывает в направлении, перпендикулярном колесу.
Поскольку вектор угловой скорости указывает, как он делает, он не имеет компонента вдоль колеса. Колесо вращается, поэтому тангенциальная (линейная) скорость в любой точке колеса постоянно меняет направление — за исключением самой центральной точки колеса, где находится основание вектора угловой скорости.Если колесо лежит на земле ровно, голова вектора направлена вверх или вниз от колеса в зависимости от того, в каком направлении вращается колесо.
Правило правой руки можно использовать для определения направления вектора угловой скорости. Оберните правую руку вокруг колеса так, чтобы ваши пальцы указывали в направлении тангенциального движения в любой точке — пальцы на правой руке должны двигаться в том же направлении, что и вращение колеса. Когда вы оборачиваете правую руку вокруг колеса, большой палец указывает в направлении вектора угловой скорости,
На рисунке показано колесо, лежащее ровно и поворачивающееся против часовой стрелки, если смотреть сверху.Оберните пальцы в направлении вращения. Ваш большой палец, который представляет вектор угловой скорости, указывает вверх; он проходит вдоль оси колеса. Если бы вместо этого колесо поворачивалось по часовой стрелке, ваш большой палец — и вектор — должны были бы указывать вниз, в противоположном направлении.
Об авторе книги
Стивен Хольцнер, доктор философии, был ответственным редактором в PC Magazine и преподавал в MIT и Корнелльском университете.Он написал Физика II для чайников , Физика основы для чайников и Квантовая физика для чайников .
,- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Кинетическая энергия вращения
Момент инерцииВот некоторые полезные общие случаи, которые вытекают из интегралов, упомянутых выше.
v = v 0 + в и s = s 0 + v 0 t + ½at 2 и v 2 — v 0 2 = 2a (с — s 0 ) ,
Гироскопы
|
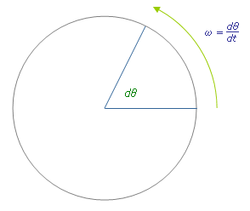 Угловая скорость описывает скорость вращения и ориентацию оси, вокруг которой происходит вращение. Направление вектора угловой скорости будет вдоль оси вращения; в этом случае (вращение против часовой стрелки) вектор указывает на зрителя.
Угловая скорость описывает скорость вращения и ориентацию оси, вокруг которой происходит вращение. Направление вектора угловой скорости будет вдоль оси вращения; в этом случае (вращение против часовой стрелки) вектор указывает на зрителя.В физике угловая скорость определяет угловую скорость, с которой объект вращается вместе с направлением, в котором он вращается.
Это векторная величина. [1] Единица угловой скорости СИ — радианы в секунду. Но его можно измерять и в других единицах (например, градусы в секунду, градусы в час и т. Д.). Когда его измеряют в циклах или оборотах в единицу времени (например, обороты в минуту), его часто называют скоростью вращения, а ее величину — скоростью вращения. Угловая скорость обычно представляется символом омега ( Ω или ω ). Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки.

- ↑ точнее псевдовектор

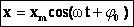
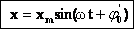
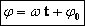 .
.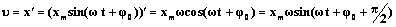
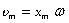 — максимальная скорость колебательного движения (амплитуда колебаний скорости).
— максимальная скорость колебательного движения (амплитуда колебаний скорости).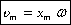
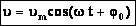 , а для случая нулевой начальной фазы
, а для случая нулевой начальной фазы 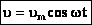 (см. график).
(см. график).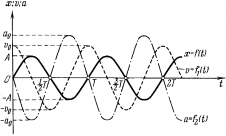
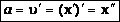 — вторая производная от координаты по времени. Тогда:
— вторая производная от координаты по времени. Тогда: 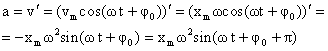 .
.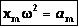
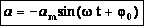 , а для случая нулевой начальной фазы:
, а для случая нулевой начальной фазы: 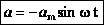 (см. график).
(см. график).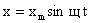 и
и 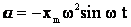 .
.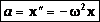
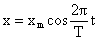 ,
,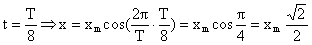 . Аналогично для скорости и ускорения.
. Аналогично для скорости и ускорения.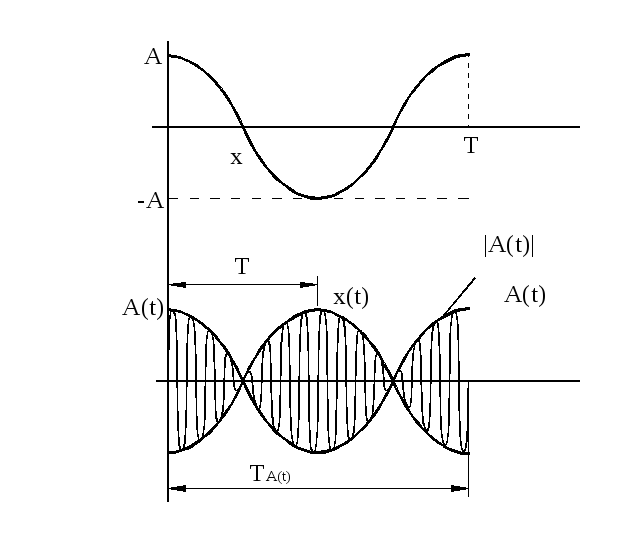
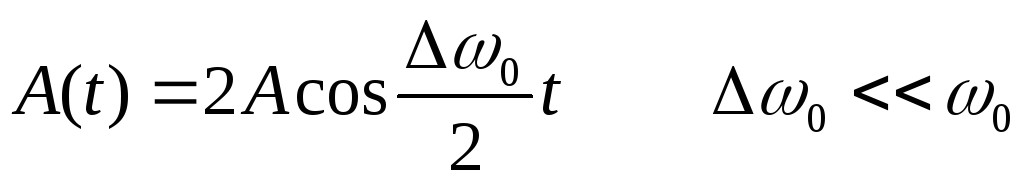
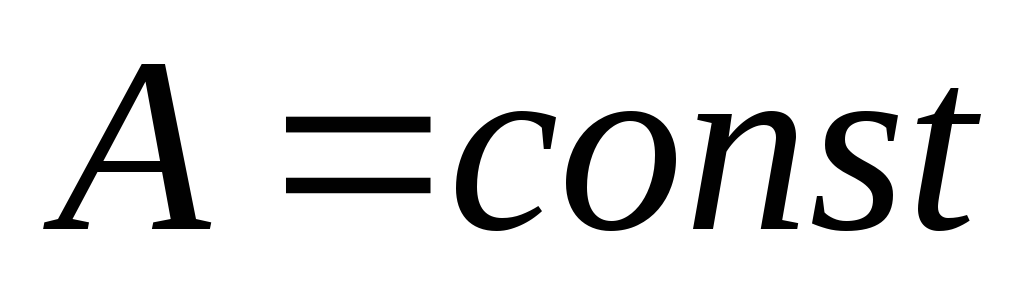
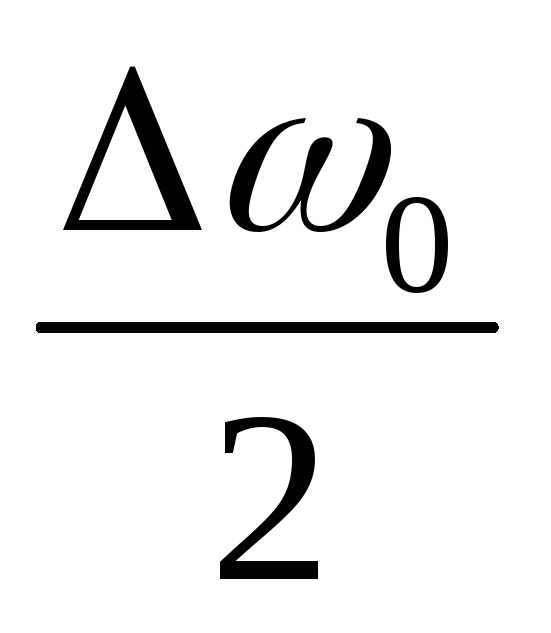 — мало,
— мало,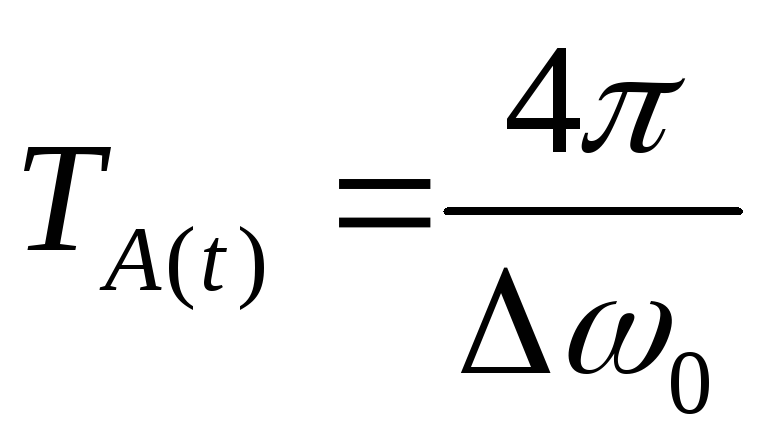 велико.
велико.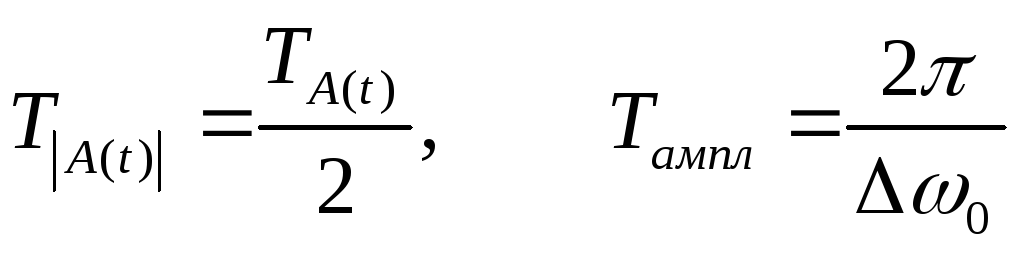 — частота биений.
— частота биений.