Передаточное число планетарной передачи: Волновые зубчатые передачи.
Планетарные редукторы. | PRO-TechInfo
Редукторы с зубчатыми передачами, в которых имеются колеса с перемещающимися осями, называются планетарными. Планетарные передачи позволяют получить большие передаточные числа редукторов при малом числе зубчатых колес. Габариты планетарных редукторов меньше, чем габариты обычных редукторов при одинаковых передаточных числах и нагрузках. Планетарные передачи несколько сложнее в изготовлении.
Кинематические схемы планетарных редукторов.
Планетарные передачи с одновенцовыми (рис. 1 ) и двухвенцовыми (рис. 3) сателлитами, а также многоступенчатые передачи (рис. 2) имеют средние передаточные числа (2…30) и высокий КПД (0,9…0,97).
Одноступенчатый планетарный редуктор.
Рис.1
Валы расположены параллельно установочной плоскости корпуса.
Центральное колесо 1 — ведущее, водило Н — ведомое. Центральное колесо 3 закреплено в корпусе.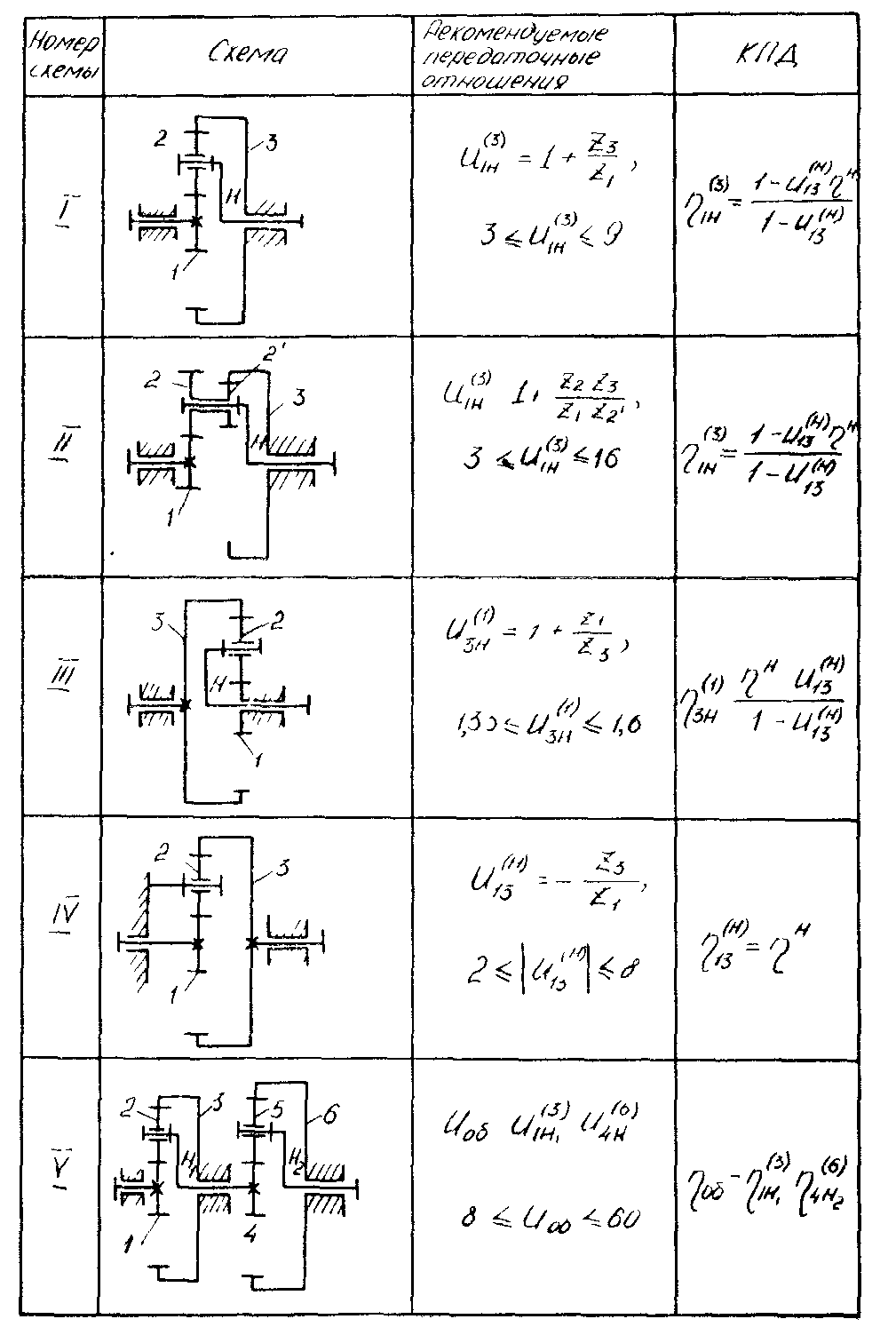
Передаточное число
Ведущий и ведомый валы вращаются в одну сторону.
Двухступенчатый планетарный редуктор. Схема 1.
Рис.2
Валы расположены параллельно установочной плоскости корпуса.
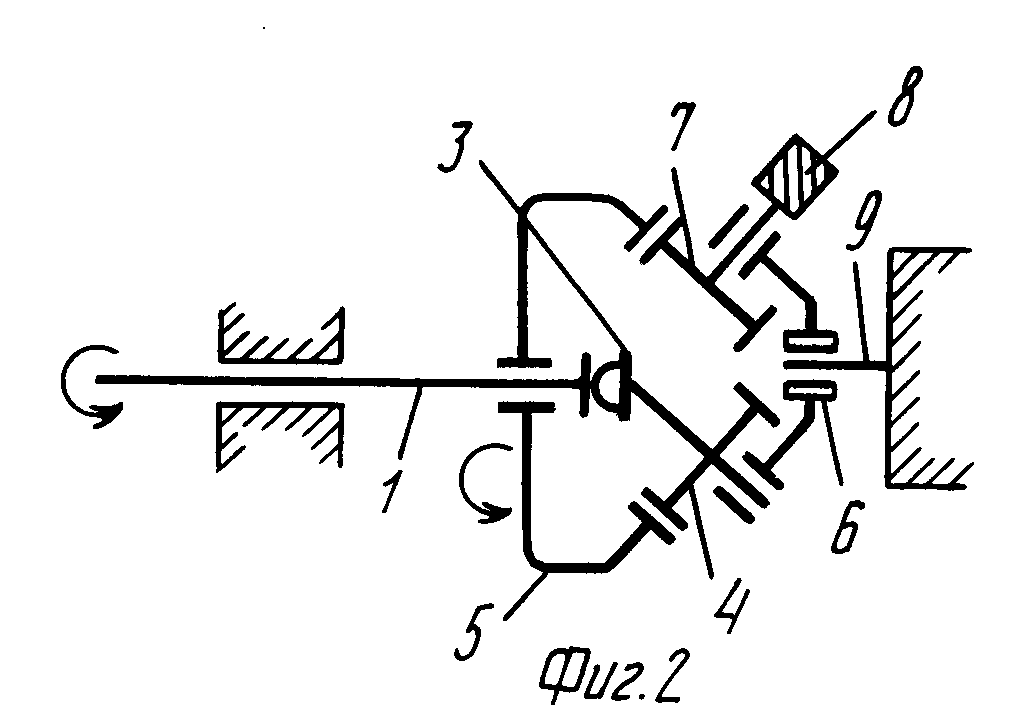
Центральное колесо 1 — ведущее, водило Н2 — ведомое. Центральные колеса 3 и 6 закреплены в корпусе.
Передаточное число
Ведущий и ведомый валы вращаются в одну сторону.
Двухступенчатый планетарный редуктор. Схема 2.
Рис.3
Валы расположены параллельно установочной плоскости корпуса.
Центральное колесо 1 — ведущее, водило Н — ведомое. Центральное колесо 4 закреплено в корпусе. Колеса 2 и 3 жестко соединены между собой.
Передаточное число
Ведущий и ведомый валы вращаются в одну сторону.
Двухступенчатый планетарный редуктор. Схема 3.
Рис. 4
4
Валы расположены параллельно установочной плоскости корпуса.
Центральное колесо 1 — ведущее, центральное колесо 5 — ведомое. Центральное колесо 3 закреплено в корпусе, колеса 2 и 4 жестко соединены между собой.
Передаточное число
Ведущий и ведомый валы вращаются при D5<D3 в одну сторону, при D5>D3 — в противоположные стороны.
Планетарные передачи с тремя центральными колесами (рис. 4) имеют большие передаточные числа (100… 200). С увеличением передаточного числа КПД резко снижается.
Двухступенчатый планетарный редуктор с кривошипом.
Планетарные передачи с кривошипами (рис. 5,6) имеют большие передаточные числа (100…200), но сравнительно низкие КПД.
Рис. 5
Валы расположены параллельно установочной плоскости корпуса.
Водило Н — ведущее, центральное колесо 4 — ведомое. Центральное колесо 2 закреплено в корпусе, колеса
Центральное колесо 2 закреплено в корпусе, колеса
Передаточное число
Ведущий и ведомый валы вращаются при D3<D2 в одну сторону, при D3>D2 — в противоположные стороны.
Одноступенчатый планетарный редуктор с кривошипом.
Рис. 6
Валы расположены параллельно установочной плоскости корпуса.
Водило Н — ведущее, вал с кривошипами К — ведомый. Центральное колесо 2 закреплено в корпусе.
Передаточное число
Ведущий и ведомый валы вращаются в разные стороны.
Кинематическая схема волнового редуктора.
На рис. 7 дана схема волнового зубчатого редуктора.
Рис. 7
Генератор волн Н (кулачок и подшипник с гибкими кольцами) — ведущий, колесо 1 с гибким венцом — ведомое, колесо 2 закреплено в корпусе.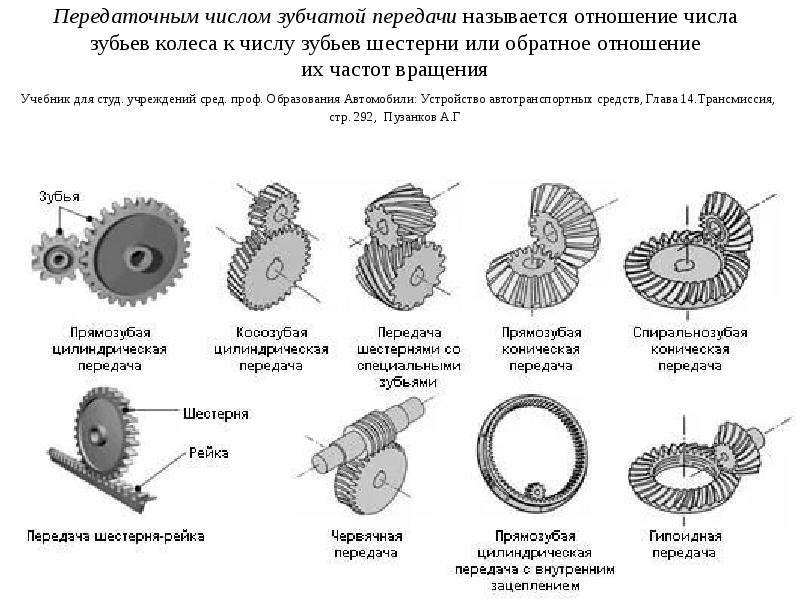
Передаточное число
Чертежи и устройство планетарных редукторов.
Соседние страницы
Планетарная передача | Статья в журнале «Молодой ученый»
Библиографическое описание:
Сарсенов, Б. А. Планетарная передача / Б. А. Сарсенов, Н. А. Максудова. — Текст : непосредственный // Молодой ученый. — 2018. — № 48 (234). — С. 46-48. — URL: https://moluch.ru/archive/234/54101/ (дата обращения: 16.01.2021).
Целью работы является исследование планетарной передачи и кинематический анализ передачи.
Ключевые слова: зубчатое колесо (шестеренка), солнечная шестерня, кольцевая шестерня (корона), сателлит, водило, эпицикл, редуктор, коробка скоростей.
Планетарная передача – механическая передача вращательного движения, имеющая зубчатое колесо с подвижными геометрическими осями.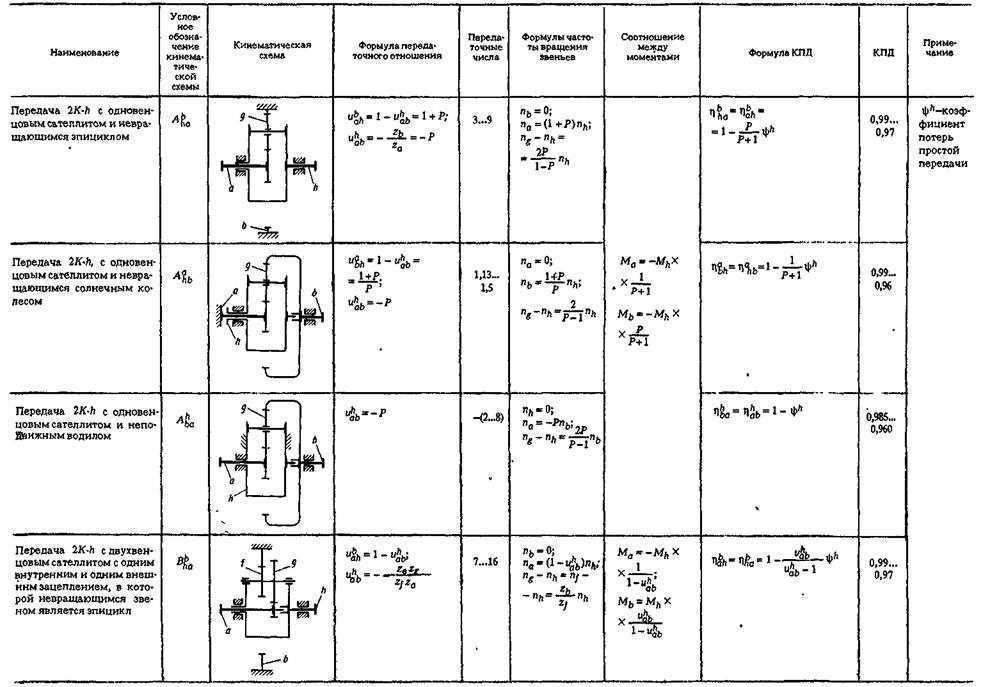
Принцип действия планетарных передач основан на вращении зубчатых колес (шестеренок) и представляет собой несколько взаимосвязанных шестеренок (Рис.1).
Рис. 1. 1 — солнечная шестерня, 2 — кольцевая шестерня (корона), 3 — сателлиты, Н — водило
- Солнечная (центральная) шестерня находится в центре;
- Кольцевая шестерня (корона): внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями. Также ее называют «эпициклом» планетарной передачи;
- Планетарная шестерня (сателлиты) одиночного размера, находящаяся в зацеплении с солнечной шестерней. Число сателлитов в планетарных передачах варьируется от 2 до 6, в зависимости от возможности размещения в механизме, чаще встречаются механизмы с тремя сателлитами, что обеспечивает более равномерное распределение нагрузок.
 Зубчатые колеса планетарной передачи могут быть любого известного типа из курса «Детали машин»: прямозубые, косозубые, червячные, шевронные. Тип зацепления не оказывает влияния на работу планетарной передачи.
Зубчатые колеса планетарной передачи могут быть любого известного типа из курса «Детали машин»: прямозубые, косозубые, червячные, шевронные. Тип зацепления не оказывает влияния на работу планетарной передачи. - Одним из основных элементов планетарной передачи является водило – (Н) – подвижное звено, на котором жестко фиксированы друг относительно друга оси нескольких сателлитов.
После ознакомления с основными деталями планетарной передачи возникает вопрос: а почему подобные механизмы называют планетарными? Ответ простой: сателлиты вращаются вокруг своих осей и вместе с осью – вокруг солнечной шестерни, т. е. совершают движение, подобное движению планет. Отсюда название — планетарные передачи. В международных энциклопедиях встречаются синонимы подобных механизмов: планетарная, дифференциальная или эпициклическая передача.
Как все передаточные механизмы, планетарные передачи служат для преобразования кинематических параметров и передачи движения от двигателя другим механизмам машин. Планетарная передача способна в пределах одной оси изменять, складывать и раскладывать угловые скорости и крутящий момент.
Планетарная передача способна в пределах одной оси изменять, складывать и раскладывать угловые скорости и крутящий момент.
Основной кинематической характеристикой планетарной передачи является передаточное отношение (u). Передаточное отношение такой передачи визуально определить очень сложно, потому что механизм может вращаться различными способами, и для кинематического исследования передачи существуют аналитический и графический методы.
Аналитический метод определения передаточного отношения основан на способе обращения движения, который впервые предложил английский ученый Виллис, поэтому аналитический метод больше всего известен под названием «метод Виллиса».
Суть метода заключается в следующем.
Всей планетарной передаче сообщается дополнительное вращение с угловой скоростью – , равной угловой скорости водила, но обратной направлению. Таким образом, водило Н останавливается, а другие колеса освобождаются; колесо 3 (корона) было неподвижно, а в преобразованном механизме начинается вращаться с угловой скоростью . Обычный планетарный механизм (рис.2,а) превратится в обращенный механизм (рис.2,б)
Обычный планетарный механизм (рис.2,а) превратится в обращенный механизм (рис.2,б)
Рис. 2. 1 — ведущее центральное колесо; 2 — сателлит; 3 — неподвижное центральное колесо; Н — водило
Звенья обращенного механизма будут вращаться с угловыми скоростями:
; ;
Математическое описание передаточного отношения может быть выражено через отношение чисел зубьев (z), угловых скоростей (), частот вращения (n).
Определим передаточное отношение:
а) через угловые скорости:
Но поскольку мы знаем, что 3-звено – это неподвижное центральное колесо (ω3 = 0), то получаем
Отсюда найдем аналогичную формулу для определения передаточного отношения планетарного механизма:
Эта формула справедлива для любой схемы планетарного механизма при наличии неподвижного центрального колеса. Значит, и передаточное отношение от любого планетарного колеса водилу Н при неподвижном опорном колесе j ровно единице минус передаточное отношение от этого же колеса к опорному (центральному) в обращенном механизме, т. е.
е.
= ,
или
+ = 1.
Таким образом, для планетарных механизмов с круглыми колесами сумма передаточных отношений при различных останавливаемых звеньях всегда равна единице.
б) через количество зубьев (z):
; ;
в) через частоты вращения (n):
Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. Допустим, , , — частоты вращения соответственно звеньев 1, 3, Н; а — означает передаточное отношение с направлением движения от 1 к 3 при неподвижном Н. Для обращенного механизма получаем следующую формулу:
=
В реальной ситуации колесо 3 заторможено (= 0), тогда
= =
Широкие кинематические возможности планетарной передачи позволяют использовать данную передачу как редуктор с постоянным передаточным отношением; как коробку скоростей или как дифференциальный механизм.
Литература:
- Иосилевич Г.

- Иванов М. Н., Детали машин. — М.: Высшая школа, 1991.
- Фролов К. В., Попов С. А., Мусатов А. К. и др. Теория механизмов и машин. — М.: Высшая школа, 1987.
Основные термины (генерируются автоматически): планетарная передача, передаточное отношение, обращенный механизм, частота вращения, колесо, кольцевая шестерня, неподвижное центральное колесо, передача, солнечная шестерня, аналитический метод.
Передаточное отношение и передаточное число
Автор admin На чтение 6 мин. Просмотров 1.3k.
Незаменимыми помощниками человека в любой его деятельности являются механизмы. Но сам по себе механизм – просто набор деталей. Для того чтобы он работал, его надо обеспечить энергией. Ее подают от отдельного устройства – двигателя или силовой установки при помощи специальных механизмов, называемых передачами. Так уж сложилось исторически – в технике чаще всего используется вращательное движение, хотя применяются и другие виды. При процессе перехода энергии она может меняться, это изменение происходит в соответствии с тем, какое передаточное отношение имеет механизм.
Так уж сложилось исторически – в технике чаще всего используется вращательное движение, хотя применяются и другие виды. При процессе перехода энергии она может меняться, это изменение происходит в соответствии с тем, какое передаточное отношение имеет механизм.
О том, что при этом происходит
Самый простой пример передачи – от вращающегося колеса водяной мельницы к жернову. При этом зачастую происходит изменение первоначальной энергии, полученной колесом от текущей воды, по величине и направлению. Величину такого изменения будет определять передаточное отношение. Оно описывает одну из важнейших характеристик преобразования энергии при вращательном движении, определяемую как отношение частоты или скорости вращения элемента, получающего энергию, к тем же параметрам элемента, отдающего энергию.
Иными словами, передаточное отношение описывает, как изменяется исходная энергия, получаемая от двигателя или любого другого источника энергии (водяного, ветряного колеса, турбины и т.
 д.), при ее передаче. За всю историю развития техники человечество создало самые разнообразные передачи, для каждой из которых существует передаточное число, являющимся частным от деления скорости ведущего звена на скорость ведомого.
д.), при ее передаче. За всю историю развития техники человечество создало самые разнообразные передачи, для каждой из которых существует передаточное число, являющимся частным от деления скорости ведущего звена на скорость ведомого.Передаточное отношение ременной передачи
Ременной передачей называют два шкива, которые соединяет ремень, как это показано на рисунке. Возможно, что она была одним из первых способов, которые применял человек. Менялся материал, используемый для изготовления ремня, менялась его форма, но неизменным оставалось передаточное отношение, определяемое как частое от деления скорости ведущего вала, на скорость ведомого, или как результат деления числа оборотов этих валов (n1/n2 или ω1/ω2).
Для ременной передачи оно может быть рассчитано с использованием диаметров (радиусов) шкивов. Передаточное число в таком случае также определяется как частное от деления оборотов.
Если при преобразовании энергии число оборотов понижается, то есть передаточное число больше 1, то передача будет понижающей, а само устройство носит название редуктора.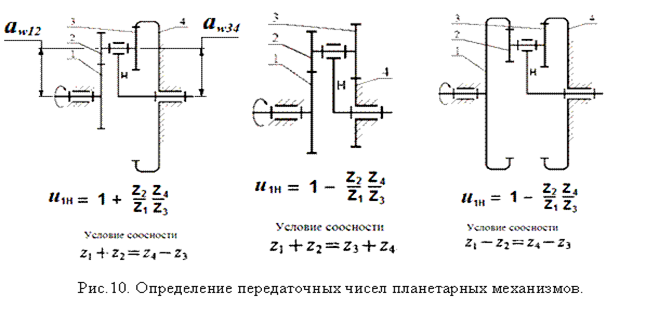 Если результат меньше единицы, то устройство называется мультипликатором, хотя оно также выполняет функции редуктора, только понижающего. Передаточное отношение редуктора позволяет уменьшить число оборотов (угловую скорость), поступающих с ведущего вала на ведомый, увеличив при этом передаваемый момент.
Если результат меньше единицы, то устройство называется мультипликатором, хотя оно также выполняет функции редуктора, только понижающего. Передаточное отношение редуктора позволяет уменьшить число оборотов (угловую скорость), поступающих с ведущего вала на ведомый, увеличив при этом передаваемый момент.
Это свойство редуктора дает возможность добиваться инженерам при проектировании различных устройств изменения параметров передаваемой энергии, а передаточное отношение редуктора служит при этом мощным инструментом в решении поставленной задачи.
Несмотря на значительный возраст, для ременной передачи и сейчас находится работа на автомобиле, она используется как привод генератора, газораспределительного механизма, а также в некоторых других случаях.
Передаточное отношение цепной передачи
В подобной ременной передаче ремень может быть заменен на цепь, в этом случае шкивы также должны быть заменены на звездочки. Полученная передача называется цепной, она знакома каждому, ведь именно такая применяется на велосипедах. Для нее передаточное отношение определяется так же, как для ременной, но можно воспользоваться и соотношением количества зубьев на звездочках (ведущей и ведомой). Однако при таком расчёте передаточное отношение будет обратным, то есть передаточное число определяется делением числа зубьев ведомой звездочки на число зубьев ведущей (z2/z1).
Для нее передаточное отношение определяется так же, как для ременной, но можно воспользоваться и соотношением количества зубьев на звездочках (ведущей и ведомой). Однако при таком расчёте передаточное отношение будет обратным, то есть передаточное число определяется делением числа зубьев ведомой звездочки на число зубьев ведущей (z2/z1).
Отличительной особенностью цепной передачи является повышенный уровень шума, а также износ при работе на высоких скоростях, поэтому ее при необходимости использования лучше всего ставить после уменьшения оборотов. В автомобиле возможно применение цепной передачи для привода ГРМ, правда, ограничением такого применения является повышенный уровень шума при ее работе.
Передаточное отношение зубчатой передачи
Так называется механизм, в котором используются колеса с зубьями, находящимися в зацеплении. Она считается наиболее рациональной и востребованной для машиностроения. Существует множество разнообразных вариантов изготовления подобных колес, отличающихся по расположению осей, форме зубьев, способу их зацепления и т. д. Как в случае с цепной, для зубчатой передаточное число определяется делением числа зубьев шестерен (z2/z1).
д. Как в случае с цепной, для зубчатой передаточное число определяется делением числа зубьев шестерен (z2/z1).
Многообразие вариантов построения зубчатой передачи предоставляет возможность использовать их в разных условиях, от тихоходного редуктора до высокоточных приводов.
Для зубчатой передачи характерны:
- постоянное передаточное число;
- компактность;
- высокий кпд;
- надежность.
Одной из разновидностей зубчатой передачи считается червячная. Она используется в тех случаях, когда передача момента осуществляется между скрещивающимися валами, для чего применяется такой элемент как червяк, представляющий собой винт специальной конструкции с резьбой. Для определения передаточного отношения червячной передачи выполняют деление количества зубьев колеса (червячного) z2 на число заходов резьбы червяка z1.
Планетарная передача
Этот вид зубчатой передачи, содержащей колеса с геометрическими осями, имеющими возможность перемещения. Что она собой представляет, можно понять из приведенного ниже рисунка. По сути дела, это уже конструкция своеобразного планетарного редуктора, включающего в свой состав некоторое число шестерен, взаимодействующих между собой. У каждой из них свое название – солнце, корона, сателлит.
Что она собой представляет, можно понять из приведенного ниже рисунка. По сути дела, это уже конструкция своеобразного планетарного редуктора, включающего в свой состав некоторое число шестерен, взаимодействующих между собой. У каждой из них свое название – солнце, корона, сателлит.
Для такого планетарного редуктора изменение момента зависит от того, какая из его шестерен неподвижна, на какую подан крутящий момент, и с какой он снимается.
При любом использовании планетарного редуктора, один из трех его элементов будет неподвижен. У такого, планетарного варианта построения передач, по отношению к простой зубчатой или ременной, есть возможность получить существенное изменение момента при небольшом количестве колес и габаритах устройства. В автомобиле у подобного планетарного устройства своя сфера применения – в составе АКПП, а также в гибридных транспортных средствах, для обеспечения совместной работы ДВС и электромотора. Широкое применение планетарного редуктора осуществляется в гусеничной технике.

О главной паре
Практически все виды передач используются в автомобиле – крутящий момент от двигателя проходит цепочку различных устройств и претерпевает изменения, начиная от КПП, главной пары, и заканчивая колесами автомобиля. Все передаточные отношения для КПП и главной пары влияют непосредственным образом на динамику автомобиля.
Поэтому с целью
- уменьшения частоты переключения;
- возможности движения при спокойной езде на небольших оборотах двигателя;
- повышения верхнего порога скорости движения,
передаточные отношения, в том числе и для главной пары, должны быть уменьшены. Для улучшения разгонной динамики все должно быть наоборот.
Работа различных механизмов и устройств, в том числе и в автомобиле, не может происходить без преобразования используемой энергии, как по величине, так и по направлению. Оценить и рассчитать величину необходимого изменения, а также его последствия, помогает передаточное отношение.
Что еще стоит почитать
Планетарная передача — Википедия. Что такое Планетарная передача
Планетарная передача с остановленным водилом по сути является двухступенчатой зубчатой передачей с неподвижными осями колес. Планетарная передача (солнечная шестерня остановлена) Планетарная передача (коронная шестерня остановлена) Схема эпициклически движущейся планетыПланетарная передача (далее — ПП) — механическая передача вращательного движения, за счёт своей конструкции способная в пределах одной геометрической оси вращения изменять, складывать и раскладывать подводимые угловые скорости и/или крутящий момент. Обычно является элементом трансмиссии различных технологических и транспортных машин.
Конструктивно ПП всегда представляет собой набор взаимозацепленных зубчатых колёс (не менее 4), часть из которых (не менее 2) имеет общую геометрическую неподвижную ось вращения, а другая часть (также, не менее 2) имеет подвижные оси вращения, концентрически вращающиеся на так называемом «водиле» вокруг неподвижной. Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую, а через зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться относительно первых, но и обкатывать их, тем самым передавая поступательное движение на водило, все звенья ПП, на которые можно подавать/снимать мощность, получают возможность вращаться дифференциально, с тем лишь условием, что угловая скорость любого такого звена не абсолютно хаотична, а определяется угловыми скоростями всех остальных звеньев. В этом плане ПП похожа на планетарную систему, в которой скорость каждой планеты определяется скоростями всех остальных планет системы. Дифференциальный принцип вращения всей системы, а также то, что в своём каноническом виде набор зубчатых колёс, составляющих ПП, собран в некоем подобии солнца и эпициклически движущихся по орбите планет, даёт данной механической передаче такие присущие только ей интернациональные определения, как планетарная, дифференциальная (от лат.
Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую, а через зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться относительно первых, но и обкатывать их, тем самым передавая поступательное движение на водило, все звенья ПП, на которые можно подавать/снимать мощность, получают возможность вращаться дифференциально, с тем лишь условием, что угловая скорость любого такого звена не абсолютно хаотична, а определяется угловыми скоростями всех остальных звеньев. В этом плане ПП похожа на планетарную систему, в которой скорость каждой планеты определяется скоростями всех остальных планет системы. Дифференциальный принцип вращения всей системы, а также то, что в своём каноническом виде набор зубчатых колёс, составляющих ПП, собран в некоем подобии солнца и эпициклически движущихся по орбите планет, даёт данной механической передаче такие присущие только ей интернациональные определения, как планетарная, дифференциальная (от лат.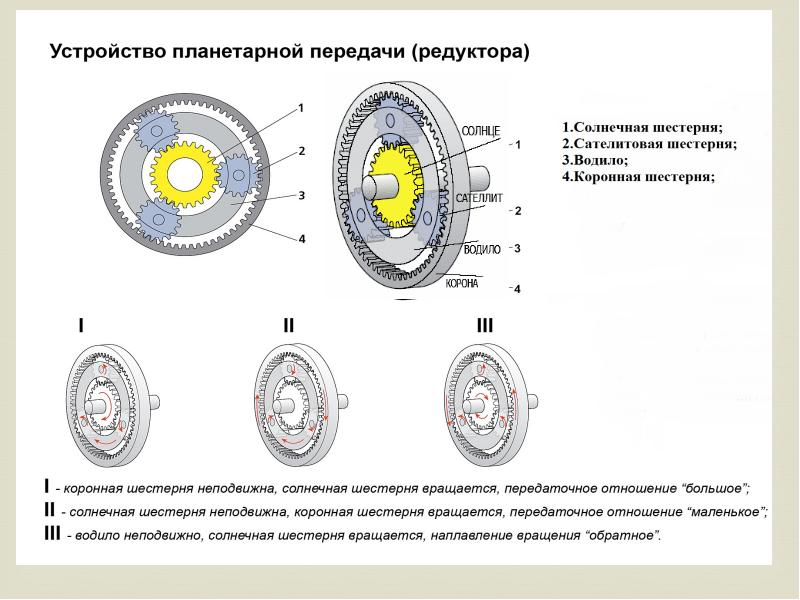 differentia – разность, различие) или эпициклическая, каждое из которых в данном случае есть синонимы.
differentia – разность, различие) или эпициклическая, каждое из которых в данном случае есть синонимы.
С точки зрения теоретической механики планетарная передача — это механическая система с двумя и более степенями свободы. Эта особенность, являющаяся прямым следствием конструкции, есть важное отличие ПП от каких-либо других передач вращательного движения, всегда имеющих только одну степень свободы. И эта особенность наделяет саму ПП тем важным качеством, что в аспекте воздействия на угловые скорости вращения ПП может не только редуцировать эти скорости, но и складывать и раскладывать их, что, в свою очередь, делает её основным механическим исполнительным узлом не только различных планетарных редукторов, но таких устройств, как дифференциалы и суммирующие ПП.
Планетарная передача и планетарный механизм
В русскоязычной инженерной терминологии термины планетарная передача (далее — ПП) и планетарный механизм (далее — ПМ) зачастую предполагаются как синонимы. Отличия в том, что термин ПП обычно используется в контексте принципиального понимания устройства той или иной передачи вращательного движения, особенно если устройство такой передачи не очевидно (скрыто корпусом/картером) или такая передача обладает определёнными уникальными свойствами, присущими только планетарной, и на этом надо акцентировать внимание. А термин ПМ используется для обозначения конкретного зубчато-рычажного механизма, причём существуют критерии, позволяющие чётко описать ПМ как сборочный узел в составе более крупного узла или агрегата и определить, сколько и каких именно использовано ПМ в конкретной передаче вращательного движения.
Отличия в том, что термин ПП обычно используется в контексте принципиального понимания устройства той или иной передачи вращательного движения, особенно если устройство такой передачи не очевидно (скрыто корпусом/картером) или такая передача обладает определёнными уникальными свойствами, присущими только планетарной, и на этом надо акцентировать внимание. А термин ПМ используется для обозначения конкретного зубчато-рычажного механизма, причём существуют критерии, позволяющие чётко описать ПМ как сборочный узел в составе более крупного узла или агрегата и определить, сколько и каких именно использовано ПМ в конкретной передаче вращательного движения.
Состав планетарного механизма
Конструкция ПП/ПМ основана на различных комбинациях из трёх основных и нескольких одинаковых вспомогательных звеньев. Три основные звена с одной общей осью вращения — два центральных зубчатых колеса и водило. Вспомогательные звенья — набор одинаковых зубчатых колёс на подвижных осях вращения и подшипники.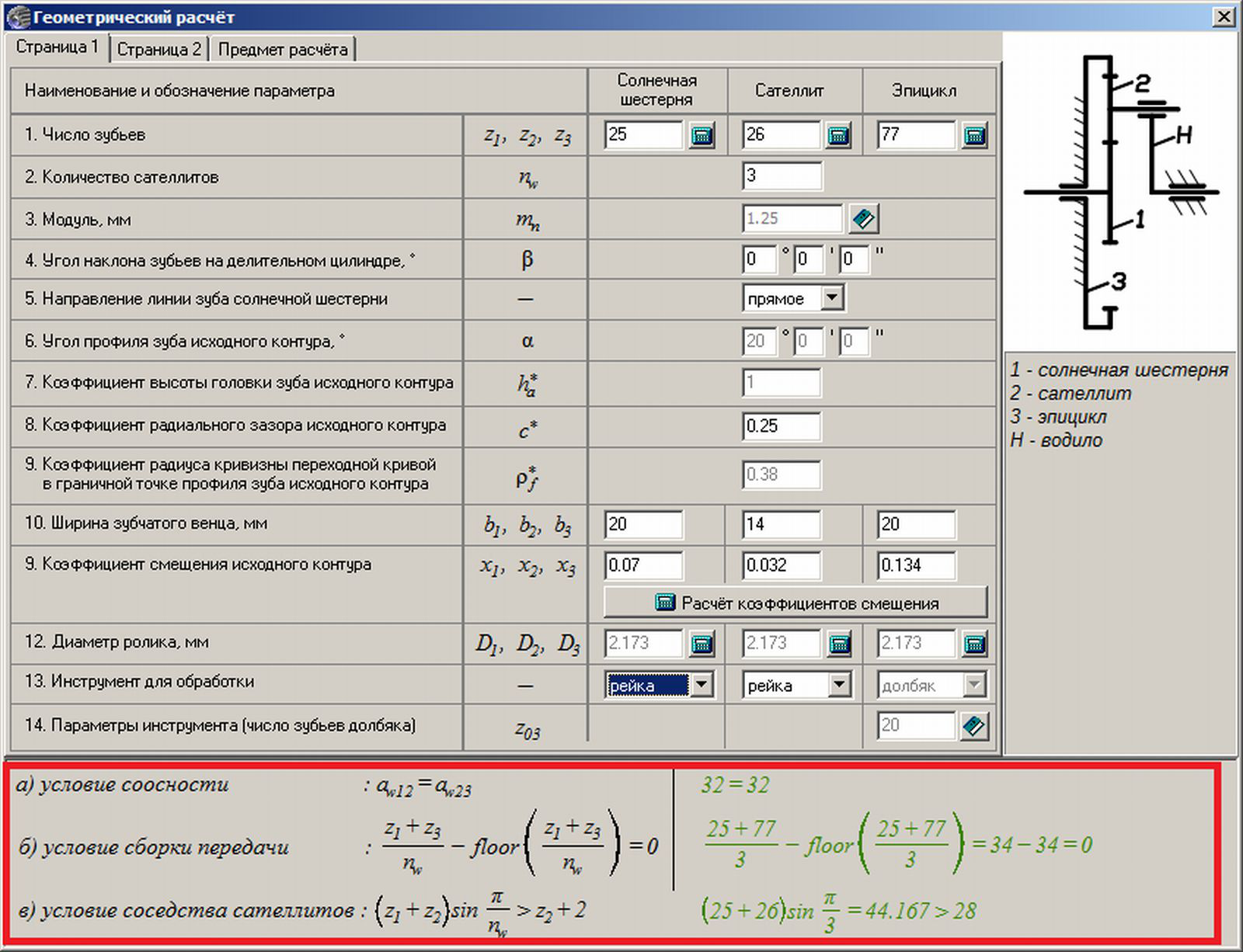
- Малое центральное зубчатое колесо с внешними зубьями называется солнечной шестернёй или солнцем (С).
- Большое центральное зубчатое колесо с внутренними зубьями называется эпициклической шестернёй или эпициклом (Э).
- Водило (В) является основой ПМ — это неотъемлемая деталь абсолютно любого ПМ и краеугольный камень всей идеи передачи вращения через планетарную систему с дифференциальной связью. Водило представляет из себя рычажный механизм — обычно такую пространственную вилку, ось «основания» которой совпадает с осью самого ПМ, а оси «зубцов» с установленными на них сателлитами концентрически вращаются вокруг неё в плоскости/плоскостях расположения центральных зубчатых колёс. Оси «зубцов» — это и есть так называемые подвижные оси или оси сателлитов
- Сателлиты () представляют собой зубчатые колёса (или группы колёс) с внешними зубьями. При этом сателлиты находятся в одновременном и постоянном зацеплении с обоими центральными зубчатыми колёсами ПМ.
 Количество сателлитов в ПМ обычно составляет от двух до шести (чаще всего — три, так как только при трёх сателлитах нет нужды в специальных уравновешивающих механизмах) и точного значения для функциональности ПМ не имеет. В различных ПМ применяются сателлиты одновенцовые (одно простое зубчатое колесо), двухвенцовые (два соосных зубчатых колеса с общей ступицей), трёхвенцовые и так далее. Также сателлиты могут быть парными — то есть, располагающимимся на осях одного водила и зацепленными в паре.
Количество сателлитов в ПМ обычно составляет от двух до шести (чаще всего — три, так как только при трёх сателлитах нет нужды в специальных уравновешивающих механизмах) и точного значения для функциональности ПМ не имеет. В различных ПМ применяются сателлиты одновенцовые (одно простое зубчатое колесо), двухвенцовые (два соосных зубчатых колеса с общей ступицей), трёхвенцовые и так далее. Также сателлиты могут быть парными — то есть, располагающимимся на осях одного водила и зацепленными в паре.
Зубчатые колёса, составляющие ПМ, могут быть любого известного типа: прямозубые, косозубые, шевронные, червячные. Тип зацепления в общем случае не важен и на принципиальную работу ПП влияния не оказывает.
В любом ПМ оси вращения центральных зубчатых колёс и водила всегда совпадают. Однако это не значит, что оси сателлитов всегда будут параллельны основной оси. Как и в случае с простыми зубчатыми передачами, здесь возможны варианты параллельных, скрещивающихся и пересекающихся осей.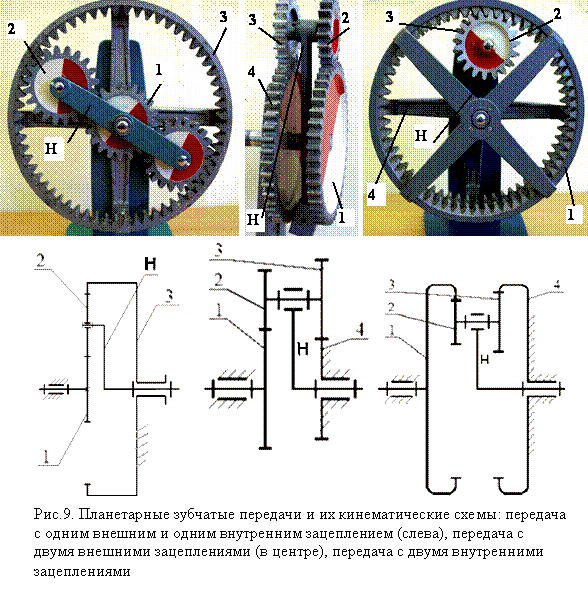 Пример второго варианта — межколёсный дифференциал с коническими зубчатыми колёсами. Пример третьего варианта — самоблокирующийся дифференциал Torsen с червячным зацеплением.
Пример второго варианта — межколёсный дифференциал с коническими зубчатыми колёсами. Пример третьего варианта — самоблокирующийся дифференциал Torsen с червячным зацеплением.
Любой ПМ, независимо простой он или сложный, плоский или пространственный, для своей работоспособности должен иметь одно водило с сателлитами и не менее двух любых центральных зубчатых колёс. Под определением «два любые» подразумевается, что это могут быть не только одно солнце и один эпицикл, но и два солнца и ни одного эпицикла, или два эпицикла и ни одного солнца. Три звена, в том числе водило, есть необходимое и достаточное условие для того, чтобы ПМ мог выполнять функции передачи мощности и сложения/разложения потоков: работать в качестве редуктора (в том числе многоскоростного), в качестве дифференциала или суммирующей ПП. Также три звена есть основа такого русскоязычного технического термина, как Трёхзвенный Дифференциальный Механизм (или ТДМ).
Формально, механизмы, состоящие всего из двух звеньев — из водила и всего-лишь одного центрального зубчатого колеса — также могут именоваться планетарными. Фактически же, такие двухзвенные ПМ трудно разумно приспособить для выполнения какой-либо работы: они не годятся для передачи мощности с одного основного звена на другое и лишь при определённых условиях могут работать как переусложнённая прямая передача. Увеличение числа основных звеньев одного ПМ в большую сторону — до 4 и более — возможно и формально и фактически, однако при этом такие ПМ не приобретают никаких новых свойств, хотя и получают больше теоретически доступных передаточных отношений и могут давать проектируемой ПП определённые компоновочные преимущества.
Фактически же, такие двухзвенные ПМ трудно разумно приспособить для выполнения какой-либо работы: они не годятся для передачи мощности с одного основного звена на другое и лишь при определённых условиях могут работать как переусложнённая прямая передача. Увеличение числа основных звеньев одного ПМ в большую сторону — до 4 и более — возможно и формально и фактически, однако при этом такие ПМ не приобретают никаких новых свойств, хотя и получают больше теоретически доступных передаточных отношений и могут давать проектируемой ПП определённые компоновочные преимущества.
Простые и сложные ПМ, планетарный ряд
Схемы наиболее распространённых сложных планетарных механизмовКритерием деления ПМ на простые и сложные является число составляющих его основных звеньев (именно основных, а число сателлитов — не в счёт). Простой ПМ имеет всего три основных звена: одно водило и два любых центральных зубчатых колеса. Кинематика допускает всего-лишь 7 (семь!) ПМ, подпадающих под это условие: один наиболее распространённый и всем известный, так называемый «элементарный», с набором одновенцовых сателлитов схемы ; три ПМ с двухвенцовыми саттелитами (, , ) и три ПМ с парными взаимозацепленными сателлитами (СВЭ, СВС, ЭВЭ)).
Сложных ПМ гораздо больше чем простых. Их точное число не определено ввиду отсутствия такой нужды, а наиболее распространённые из них приведены на рисунке. Точно так же как и простые ПМ, сложные имеют всего одно водило, но центральных зубчатых колёс может быть три и более. При этом в составе сложного ПМ всегда умозрительно можно выделить несколько простых ПМ (конкретно: три в четырёхзвенном и шесть в пятизвенном), каждый из которых в себя включает два каких-то центральных зубчатых колеса и одно общее водило.
Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой ПМ с набором одновенцовых сателлитов является однорядным. Все три простые ПМ с двухвенцовыми сателлитами — двухрядные. ПМ с парными взаимозацепленными сателлитами схемы СВЭ — однорядный; схем СВС и ЭВЭ — двухрядные. Таким образом, все простые ПМ могут быть или однорядными или двухрядными. Сложные ПМ, в свою очередь, могут быть двух, трёх и четырёхрядные. Верхнее число рядов в сложном ПМ формально не ограничено, хотя фактически уже пятирядные есть большая редкость, хотя в сборках из планетарных механизмов, применяющихся в многоступенчатых планетарных коробках передач, общее число рядов может быть пять и больше. Нередко термины ПМ и планетарный ряд предполагаются как синонимы, но, в общем случае, это неверно: даже если в отдельных случаях оба термина могут обозначать одно и то же, всегда следует помнить, что их смыл несколько разный.
Верхнее число рядов в сложном ПМ формально не ограничено, хотя фактически уже пятирядные есть большая редкость, хотя в сборках из планетарных механизмов, применяющихся в многоступенчатых планетарных коробках передач, общее число рядов может быть пять и больше. Нередко термины ПМ и планетарный ряд предполагаются как синонимы, но, в общем случае, это неверно: даже если в отдельных случаях оба термина могут обозначать одно и то же, всегда следует помнить, что их смыл несколько разный.
Плоские и пространственные ПМ
Свободный дифференциал на основе простого плоского двухрядного ПМ с парными сателлитами Свободный дифференциал на основе пространственного ПМ с коническими шестернямиНаличие в составе одного ПМ более одного планетарного ряда не означает, что он является пространственным. Сколько бы ни было рядов, но если плоскости вращения всех составляющих каждый ряд зубчатых колёс параллельны, то такой ПМ будет оставаться плоским. Критерием отличия плоского ПМ от пространственного является наличие не просто более одной плоскости вращения составляющих его зубчатых колёс, но наличие непараллельных плоскостей их вращения. Плоскости вращения звеньев в пространственном ПМ не обязаны быть строго перпендикулярны друг-другу и могут находиться под любыми произвольными углами. Примером пространственного ПМ может служить конический симметричный дифференциал, наподобие применяющегося в приводе ведущих колёс автомобиля. А вот близкий по конструкции цилиндрический дифференциал, применяющийся там же и выполняющий точно такие же функции, будет оставаться плоским ПМ.
Плоскости вращения звеньев в пространственном ПМ не обязаны быть строго перпендикулярны друг-другу и могут находиться под любыми произвольными углами. Примером пространственного ПМ может служить конический симметричный дифференциал, наподобие применяющегося в приводе ведущих колёс автомобиля. А вот близкий по конструкции цилиндрический дифференциал, применяющийся там же и выполняющий точно такие же функции, будет оставаться плоским ПМ.
Пространственные ПМ по своему функционалу ничем не отличаются от аналогичных по составу плоских ПМ. Выбор того или иного ПМ в качестве основы конкретной ПП есть лишь вопрос экономики или конструкторских предпочтений. Тот же простой межколёсный дифференциал почти всегда выполнен на основе пространственного ПМ не потому, что что плоский не годится, а, скорее, по определённым компоновочным соображениям. Плюс, как это ни странно, пространственный ПМ для выполнения схожих функций может требовать меньшего количества шестерён и деталей вообще. Так, тот же межколёсный дифференциал в пространственном варианте требует всего лишь 4 одинаковые шестерни, из которых две пойдут на два солнца и две — на два саттелита. В случае же плоского варианта, таких шестерён потребуется как минимум шесть, а скорее всего — восемь, и при этом они обязательно будут двух разных типоразмеров.
В случае же плоского варианта, таких шестерён потребуется как минимум шесть, а скорее всего — восемь, и при этом они обязательно будут двух разных типоразмеров.
2 степени свободы ПМ
Уникальной особенностью любого ПМ, отличающей его от всех прочих зубчатых передач, является наличие у него двух степеней свободы. Применительно к простому трёхзвенному ПМ это означает, что понимание угловой скорости вращения любого одного основного звена не даёт однозначного понимания угловых скоростей двух других основных звеньев, даже если известны все передаточные отношения внутри ПМ. Здесь все три основных звена находятся в дифференциальной связи друг с другом и для определения их угловых скоростей надо знать угловые скорости как минимум двух из них. В этом есть важное отличие ПМ от прочих зубчатых механизмов, в которых угловые скорости всех элементов связаны линейной зависимостью, а по угловой скорости одного элемента всегда можно точно определить угловые скорости всех остальных элементов, сколь много их бы не было. И в этом есть основа уникальных свойств, присущих любому ПМ: способность изменять угловые скорости на выходе при неизменных угловых скоростях на входе, способность делить и суммировать потоки мощности и всё это при постоянно зацепленных шестернях.
И в этом есть основа уникальных свойств, присущих любому ПМ: способность изменять угловые скорости на выходе при неизменных угловых скоростях на входе, способность делить и суммировать потоки мощности и всё это при постоянно зацепленных шестернях.
Любой ПМ, независимо от того, простой он или сложный, имеет фактически лишь две степени свободы. Для простого ПМ это подтверждается и визуальным наблюдением за работой такого механизма и уравнением Чёбышева. Для сложных ПМ это визуально не очевидно, а уравнение Чёбышева теоретически может допускать существование для таких ПМ трёх степеней свобод, что подразумевает наличие четырёх звеньев, находящихся в дифференциальной связи друг с другом. Но фактически такие сложные ПМ будут физически неработоспособны в тех практических задачах, ради которых они создаются, а все работоспособные сложные ПМ останутся двухстепенными. Независимо от числа основных звеньев любого работоспособного сложного ПМ, в нём, так же как и в простом ПМ, в дифференциальной связи друг с другом будет находиться только три основных звена, а остальные основные звенья, сколько бы их ни было, будут иметь линейную связь с каким-то одним из трёх вышеупомянутых. Попытки же создания сложных ПМ с тремя (и тем более, с четырьмя) фактическими степенями свободы считаются бесперспективными, а все работоспособные трёх- и четырёхстепенные ПП основаны на сборке последовательно взаимозацепленных двухстепенных ПМ.
Попытки же создания сложных ПМ с тремя (и тем более, с четырьмя) фактическими степенями свободы считаются бесперспективными, а все работоспособные трёх- и четырёхстепенные ПП основаны на сборке последовательно взаимозацепленных двухстепенных ПМ.
Передаточное отношение
Планетарная передача в режиме повышения скорости. Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение различными способами.
При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, а два других служат в качестве ведущего и ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также от того, какой элемент закреплён.
Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как S{\displaystyle S}, а для планетарных шестерён примем это число как P{\displaystyle P}, то передаточное отношение будет определяться формулой SP{\displaystyle {\frac {S}{P}}}, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет −2416{\displaystyle -{\frac {24}{16}}}, или −32{\displaystyle -{\frac {3}{2}}}, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.
Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет A{\displaystyle A} зубьев, то оно будет вращаться с соотношением PA{\displaystyle {\frac {P}{A}}} относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 1664{\displaystyle {\frac {16}{64}}}, или 14{\displaystyle {\frac {1}{4}}}. Таким образом, объединив оба примера, мы получим следующее:
(В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 1664{\displaystyle {\frac {16}{64}}}, или 14{\displaystyle {\frac {1}{4}}}. Таким образом, объединив оба примера, мы получим следующее:
- Один оборот солнечной шестерни даёт −SP{\displaystyle -{\frac {S}{P}}} оборотов планетарных шестерён;
- Один оборот планетарной шестерни даёт PA{\displaystyle {\frac {P}{A}}} оборотов кольцевой.
В итоге, если водило заблокировано, общее передаточное отношение системы будет равно −SA{\displaystyle -{\frac {S}{A}}}.
В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет меньше единицы и составит 1+AS{\displaystyle 1+{\frac {A}{S}}}.
Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно 1(1+AS){\displaystyle {\frac {1}{(1+{\frac {A}{S}})}}} . Это самое большое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.
В этом случае передаточное отношение будет равно 1(1+AS){\displaystyle {\frac {1}{(1+{\frac {A}{S}})}}} . Это самое большое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.
Всё вышесказанное можно описать следующими двумя уравнениями (выведены из условия отсутствия проскальзывания сопрягаемых шестерён и следовательно равенства дуг, проходимых точками, находящихся на окружностях, в единицу времени):
- A(ωa−ωc)=PωpS(ωs−ωc)=−Pωp{\displaystyle {\begin{aligned}A\left(\omega _{a}-\omega _{c}\right)=P\omega _{p}\\S\left(\omega _{s}-\omega _{c}\right)=-P\omega _{p}\end{aligned}}}
Здесь ωa,ωc,ωp,ωs{\displaystyle \omega _{a},\omega _{c},\omega _{p},\omega _{s}} — угловые скорости соответственно: кольцевой шестерни, водила, планетарных шестерён относительно водила, и солнечной шестерни. Первое уравнение характеризует вращение водила относительно кольцевой шестерни, второе — солнечной шестерни относительно водила.
Если исключить из уравнений ωp{\displaystyle \omega _{p}} путём их сложения — получится одно уравнение: Aωa+Sωs=(A+S)ωc{\displaystyle A\omega _{a}+S\omega _{s}=(A+S)\omega _{c}}. Так как числа зубьев шестерён всегда удовлетворяют условию A=S+2P{\displaystyle A=S+2P} (исходя из простых геометрических соотношений, поскольку в диаметр коронной шестерни помещается диаметр солнечной шестерни и два диаметра сателлитов), по-другому это уравнение можно записать как:
(2+n)ωa+nωs−2(1+n)ωc=0{\displaystyle \left(2+n\right)\omega _{a}+n\omega _{s}-2\left(1+n\right)\omega _{c}=0}
Где n — это параметр передачи, равный n=SP{\displaystyle n={S \over P}}, то есть отношению чисел зубьев солнечной и планетарных шестерён.
В нижеуказанной таблице (указывающей выходные скорости различных типов планетарных передач в зависимости от их конструктивных особенностей) приняты следующие условные обозначения:
Формула Виллиса
i0=nP−nSnP−nA{\displaystyle i_{0}={n_{P}-n_{S} \over n_{P}-n_{A}}}, где i0{\displaystyle i_{0}} — передаточное число при заблокированном водиле i0=nSnA=−NANS{\displaystyle i_{0}={n_{S} \over n_{A}}=-{N_{A} \over N_{S}}}, nS{\displaystyle n_{S}} — скорость солнечной шестерни, nP{\displaystyle n_{P}}- скорость водила и nA{\displaystyle n_{A}} — скорость кольцевой шестерни. [2][3]
[2][3]
Управляющие элементы планетарной передачи
Наличие у любых ПМ и их сборок двух и более степеней свободы может использоваться в некоторых типах ПП в качестве основного функционала (здесь имеются ввиду планетарные дифференциалы, разветвители потоков и суммирующие ПП). Однако для работы ПП в режиме редуктора с одним ведущим звеном и одним ведомым всем остальным свободным основным звеньям необходимо задать определённую угловую скорость (в том числе, возможно, нулевую). Лишь в таком случае лишние степени свободы будут сняты, все свободные основные звенья станут опорными, а вся подающаяся на единственное ведущее звено мощность будет снята с единственного ведомого в полном объёме (с поправкой на КПД ПП). Функцию задания необходимых угловых скоростей свободным звеньям выполняют так называемые управляющие элементы ПМ. Таковых элементов два: фрикционы и тормоза.
- Фрикционы соединяют друг с другом два свободных звена ПМ, либо соединяют свободное звено с внешним подводом мощности.
 В обоих случаях при полной блокировке фрикционы обеспечивают паре соединённых элементов некую одинаковую ненулевую угловую скорость. Конструктивно обычно выполнены в виде многодисковых фрикционных муфт, хотя в отдельных случаях возможны и более простые муфты.
В обоих случаях при полной блокировке фрикционы обеспечивают паре соединённых элементов некую одинаковую ненулевую угловую скорость. Конструктивно обычно выполнены в виде многодисковых фрикционных муфт, хотя в отдельных случаях возможны и более простые муфты.
- Тормоза соединяют свободные звенья ПМ с корпусом ПП. При полной блокировке тормоза обеспечивают заторможенному свободному звену нулевую угловую скорость. Конструктивно могут быть аналогичны фрикционам — в виде многодисковых фрикционнных муфт; но широко распространены и более простые конструкции — ленточные, колодочные, однодисковые.
Фрикционы и тормоза по принципу своего действия являются идеальными синхронизаторами угловых скоростей соединяемых элементов. Также они выполняют предохранительные функции и при резких ударных нагрузках могут пробуксовывать, переводя динамические нагрузки в работу сил трения. И также они могут выполнять функцию главной муфты сцепления (главного фрикциона), поэтому зачастую в механических трансмиссиях машин с ПКП главная муфта сцепления вообще не применяется. При том, что тормоза в отличие от фрикционов допускают больше вариантов фактического исполнения, конструкция и тех и других может быть совершенно одинаковой, или, по крайней мере, унифицированной, несмотря на существенное функциональное различие фрикционов и тормозов. Помимо фрикционов и тормозов в работе ПП могут быть задействованы автоматически срабатывающие механизмы свободного хода (другое их название — обгонные муфты или автологи). В русскоязычных кинематических схемах планетарных КП фрикционы, тормоза и муфты свободного хода обычно обозначаются буквами Ф, Т и М.
При том, что тормоза в отличие от фрикционов допускают больше вариантов фактического исполнения, конструкция и тех и других может быть совершенно одинаковой, или, по крайней мере, унифицированной, несмотря на существенное функциональное различие фрикционов и тормозов. Помимо фрикционов и тормозов в работе ПП могут быть задействованы автоматически срабатывающие механизмы свободного хода (другое их название — обгонные муфты или автологи). В русскоязычных кинематических схемах планетарных КП фрикционы, тормоза и муфты свободного хода обычно обозначаются буквами Ф, Т и М.
Применение
Наиболее широкое применение принцип нашёл в планетарных редукторах, автомобильных дифференциалах, бортовых планетарных передачах ведущих мостов тяжёлых автомобилей, кроме того, используется в суммирующих звеньях кинематических схем металлорежущих станков, также в редукторах привода воздушных винтов турбовинтовых двигателей (ТВД) в авиации, также довольно распространены планетарные втулки для велосипедов.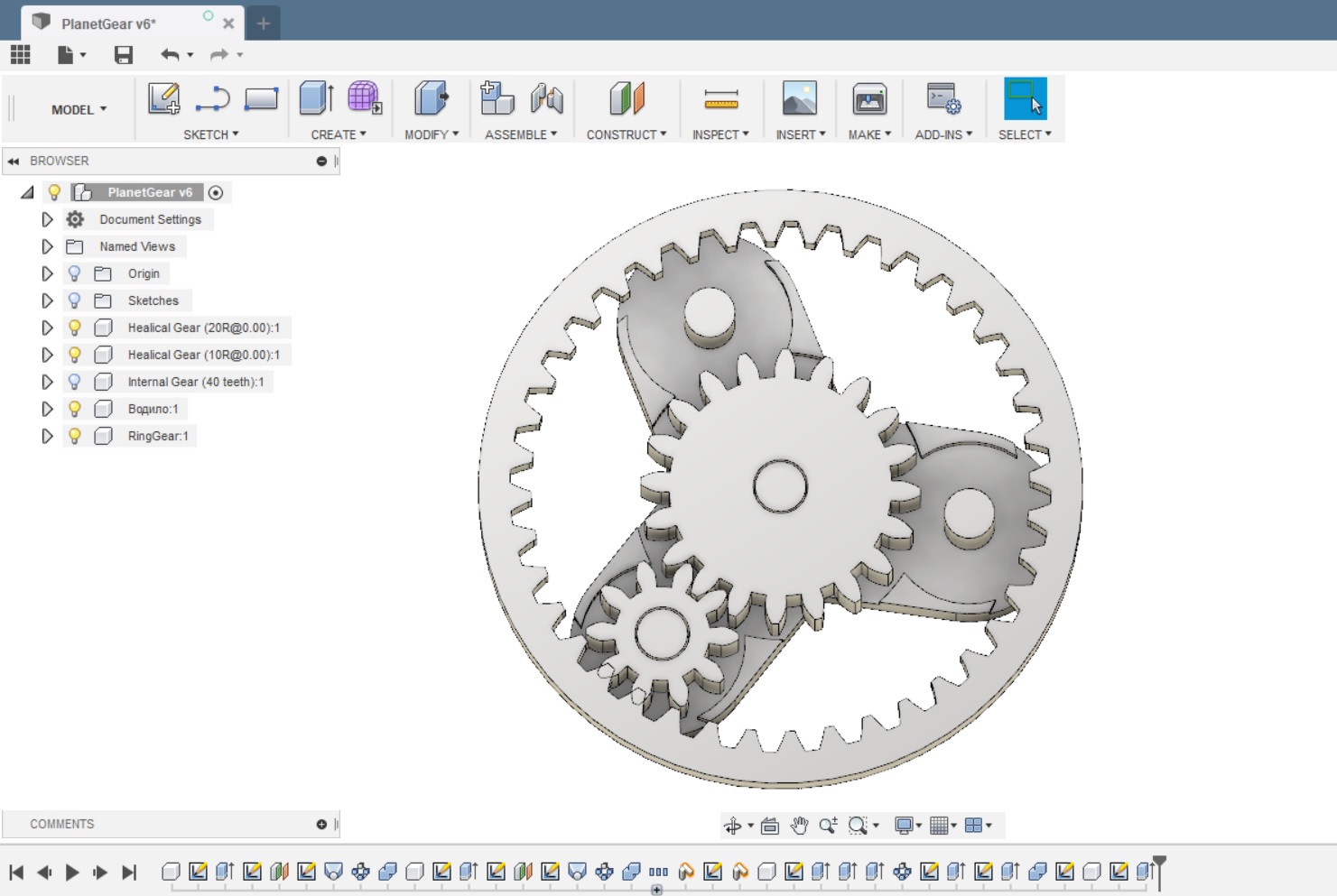
В современных устройствах могут использоваться каскады из нескольких планетарных передач для получения большого диапазона передаточных чисел. На этом принципе работают многие автоматические коробки передач.
Часто планетарные передачи используются для суммирования двух потоков мощности (например, планетарные ряды двухпоточных трансмиссий некоторых танков и др. гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила. Широко применяется данная схема в авиации: в приводе постоянных оборотов электрогенератора планетарный механизм используется для сложения двух различных входных частот вращения с целью получения стабильной выходной. В авиационных электро- и гидроприводах для надёжности используются два мотора, работающие на общий выходной вал через планетарный редуктор, и при отказе одного мотора или цепи управления им работоспособность привода сохраняется, но с двойным уменьшением частоты вращения.
Планетарные передачи также используются в случаях, когда необходимо переменное передаточное отношение (может быть достигнуто торможением, например, водила).
Планетарный механизм поворота
ПМП применяются на гусеничных тракторах и танках для изменения скорости и поворота. В этом случае в трансмиссии к левому и правому ведущим колёсам устанавливается свой планетарный редуктор, коронная шестерня которого приводится от двигателя, с водила передаётся момент на колесо, а солнечная шестерня связана с тормозом той или иной конструкции (как правило, ленточным). Также между коронной шестернёй и выходным валом установлен так называемый блокировочный фрикцион, а на выходном валу (от водила) — ещё один тормоз.
Если тормоз солнечной шестерни и фрикцион выключены, то момент на ведущее колесо трактора не передаётся — корона через сателлиты вращает расторможенную солнечную шестерню, практически не создавая момента на водиле. Для исключения движения трактора в этом случае может быть заторможен основной тормоз (на выходном валу). Если начать затормаживать солнечную шестерню, то сателлиты получат точку опоры и начнут создавать момент на водиле, вращая ведущее колесо трактора. При полностью заторможенной солнечной шестерне ПМП работает как обычный понижающий редуктор. Это первая передача ПМП. При включении блокировочного фрикциона он начнёт передавать момент от двигателя напрямую на водило, минуя редуктор, и при полном включении фрикциона редуктор ПМП будет полностью выведен из работы (заблокирован) — это вторая передача ПМП, работа в качестве прямой передачи.
Таким образом, включение тормоза водила даёт остановку трактора, включение тормоза солнечной шестерни — первую (понижающую) передачу, включение блокировочного фрикциона — вторую.
Преимущества и недостатки
Конструкция передачи со многими сателлитами обеспечивает зацепление большего числа зубцов и потому меньшую нагрузку на каждый зубец. Это позволяет достичь меньших размеров и массы по сравнению с обычной передачей при той же передаваемой мощности.
Соосность ведущих и ведомых валов облегчает компоновку машин и каскадных механизмов.
Сбалансированность сил в передаче приводит к меньшему уровню шума.
Конструкция передачи позволяет достичь больших передаточных отношений при малом числе колёс.
К недостаткам планетарных передач относят повышенные требования к точности изготовления и сборки, а также малый КПД при больших передаточных отношениях.
См. также
Литература
- Антонов А. С., Артамонов Б. А., Коробков Б. М., Магидович Е. И. Планетарные передачи // Танк. — М.: Воениздат, 1954. — С. 422—429. — 607 с.
- Ткаченко В. А. Проектирование многосателлитных планетарных передач / Харьковский государственный университет им. А. М. Горького. — Харьков: Изд-во Харьк. ун-та, 1961. — 186 с. — 7000 экз.
- Кудрявцев В. Н. и др. Планетарные передачи: Справочник / Авт.: В. Н. Кудрявцев, Ю. Н. Кирдяшев, Е. Г. Гинзбург, Ю. А. Державец, А. Н. Иванов, Е. С. Кисточкин, И. С. Кузьмин, А. Л. Филипенков; Под ред. докторов техн. наук В. Н. Кудрявцева и Ю. Н. Кирдяшева. — Л.: Машиностроение. Ленингр. отд-ние, 1977. — 536 с. — 39 000 экз.
Ссылки
Примечания
- ↑ Pattantyús Gépész- és Villamosmérnökök Kézikönyve 3. tom. Műszaki Könyvkiadó, Budapest, 1961. p.632.
- ↑ Bernd Künne. Köhler/Rögnitz Maschinenteile 2. — Vieweg+Teubner Verlag, 2008. — С. 508. — ISBN 3835100920.
- ↑ Berthold Schlecht. Maschinenelemente 2: Getriebe, Verzahnungen und Lagerungen. — Pearson Studium, 2010. — С. 787. — ISBN 3827371465.
| Эта статья также доступна на испанском языке Мне часто задают вопрос, как отработать планетарные передачи с помощью зубчатый шаблон генератора Расчет количества зубьев планетарной передачи на самом деле не так уж и сложен, поэтому я изначально не упомянул, как это сделать. Но, получив вопрос несколько раз, я уточню.Для удобства обозначим R, S и P как количество зубьев на шестернях.
Второе ограничение: То есть количество зубьев коронной шестерни равно количеству зубьев. в средней солнечной шестерне плюс удвоенное количество зубьев планетарной шестерни. В шестеренке слева это будет 30 = 2 × 9 + 12. Теперь представьте, что мы вынимаем одно из колес зеленой планеты и переставляем оставшиеся. быть равномерно распределенными.Все еще того же размера. А теперь представьте, что у колес есть зубья. Зубы торчали бы за линию колеса настолько, насколько они отступают, чтобы линия тангажа шестерен была линией вокруг шестерни. Геометрия остается прежней. Если вы войдете в шестеренчатый генератор и выберите «Показать делительный диаметр», вы увидите, что делительный диаметр представляет собой просто круг что зубы находятся по центру. Делительный диаметр шестерни — это количество зубьев, разделенное на диаметральный шаг.
(большие значения «диаметрального шага» означают меньшие зубья).Программа зубчатого генератора имеет тенденцию относиться к расстоянию между зубьями. Диаметр шага
также может быть рассчитано как расстояние между зубьями * количество зубцов / (2 * π),
где 2 * π = 6.283 … и вот он вставлен. В этом случае планетарные шестерни имеют 12 зубьев, солнечная шестерня — 18, а коронная шестерня — 42 зуба. Итак, применяя R = 2 × P + S Получаем 42 = 2 × 12 + 18 Эти фотографии — часть увлекательно сложной
планетарный редуктор Рональда Уолтерса. Расчет передаточных чисел планетарной передачиРасчет передаточного числа планетарной зубчатой передачи может быть сложной задачей. Обозначим следующее:
(R + S) × T y = R × T r + T s × S Пример:Теперь, обычно в планетарной передаче, одна из шестерен фиксируется.Например, если мы держим коронная шестерня в фиксированном положении, T r всегда будет нулевым. Таким образом, мы можем удалить эти термины из приведенной выше формулы и получить:(R + S) × T y = T s × S Теперь, если мы ведем солнечную шестерню, мы можем изменить формулу для определения оборотов водила Y: Таким образом, передаточное числоS / (R + S) Ограничения на количество зубцов и планетЕсли вы хотите, чтобы планетарные шестерни были расположены равномерно и все зацеплялись за следующий зуб в то же время ваше солнце и зубчатое колесо должны быть равномерно делится на количество планет.Если вы хотите, чтобы они были равномерно распределены, но не обязательно, чтобы все они находились в одной фазе относительно их зубьев, тогда сумма зубьев коронной шестерни и солнца Зубья шестерни должны быть без остатка кратны количеству планет. То есть: (R + S) делится на количество планет. Если, однако, вы хотите расположить планеты неравномерно, это ограничение не действует. применять. Однако угол между планетарными шестернями относительно солнечной шестерни все еще ограничен:
Если вы поместите шестерню внутрь другой шестерни, при этом внутренняя шестерня имеет число зубьев половина числа зубьев коронной шестерни, любая точка на делительном диаметре внутренней шестерни будет двигайтесь вперед и назад по прямой. Латунный стержень на этой фотографии будет перемещаться в гнезде строго слева направо, а
шестерня, к которой она прикреплена, катится внутри зубчатого венца.Это снаряжение действительно прикреплено
к кривошипу, который держит его в движении по краю, хотя только центральная часть
кривошипа видно, поэтому на фото он не похож на кривошип. Фото: См. Также: |
Зубчатые передачи | KHK Gears
Ссылки по теме:
Free Gear Calculator
В этом разделе представлены планетарные зубчатые передачи, гипоциклоидные механизмы и ограниченные зубчатые передачи, которые представляют собой специальные зубчатые передачи, обладающие такими характеристиками, как компактный размер и высокое передаточное число.
17.1 Система планетарной передачи
Базовая форма планетарной передачи показана на рисунке 17.1. Он состоит из солнечной шестерни A, планетарной шестерни B, внутренней шестерни C и водила D.
Рис.17.1 Пример планетарной системы
Входная и выходная оси планетарной передачи находятся на одной линии. Обычно для равномерного распределения нагрузки используются две или более планетарных шестерни. Он компактен в пространстве, но сложен по конструкции. Системы планетарных редукторов нуждаются в высококачественном производственном процессе.Разделение нагрузки между планетарными шестернями, интерференция внутренней шестерни, баланс и вибрация вращающегося водила, опасность заклинивания и т. Д. Являются неотъемлемыми проблемами, которые необходимо решить.
На рисунке 17.1 показана планетарная зубчатая передача типа 2K-H. Солнечная шестерня, внутренняя шестерня и водило имеют общую ось.
(1) Взаимосвязь между шестернями планетарной системы
Чтобы определить соотношение между количеством зубьев солнечной шестерни (za), планетарной шестерни B (zb) и внутренней шестерни C (zc) и количеством планетарных шестерен N в системе, эти параметры должны удовлетворять следующие три условия:
Условие No.1
zc = za + 2 zb (17.1)
Это условие, необходимое для совпадения межосевых расстояний шестерен. Поскольку уравнение справедливо только для стандартной системы зубчатых колес, можно изменять количество зубьев, используя конструкции зубчатых колес с профильным смещением.
Для использования шестерен с профильным смещением необходимо согласовать межосевое расстояние между солнечной шестерней A и планетарной шестерней B, a1, и межосевое расстояние между планетарной шестерней B и внутренними шестернями C, α2.
α1 = α2 (17,2)
Условие No.2
Это условие необходимо для размещения планетарных шестерен, равномерно расположенных вокруг солнечной шестерни. Если желательно неравномерное размещение планетарных шестерен, тогда должно выполняться уравнение (17.4).
Где θ : половина угла между соседними планетарными шестернями (°)
Рис. 17.2 Условия выбора передач
Условие № 3
Удовлетворение этого условия гарантирует, что соседние планетарные шестерни могут работать, не мешая друг другу.Это условие, которое должно быть выполнено для стандартной конструкции шестерни с одинаковым размещением планетарных шестерен. Для других условий система должна удовлетворять соотношению:
Где:
dab : Диаметр кончика планетарной шестерни
α1 : Межосевое расстояние между солнечной и планетарной шестернями
Помимо вышеуказанных трех основных условий, может существовать проблема взаимного взаимодействия между внутреннюю шестерню C и планетарную шестерню B. См. раздел 4.2 Внутренние шестерни (стр. 611–613).
(2) Передаточное число планетарной передачи
В системе планетарной передачи передаточное число и направление вращения должны изменяться в зависимости от того, какой элемент закреплен.Рисунок 17.3 содержит три типичных типа планетарных зубчатых передач:
Рис. 17.3 Планетарный редукторный механизм
(a) Планетарный тип
В этом типе фиксируется внутренняя передача. На входе используется солнечная шестерня, а на выходе — водило D. Передаточное число рассчитывается согласно таблице 17.1.
Таблица 17.1 Уравнения передаточного числа для планетарного типа
Обратите внимание, что направление вращения входной и выходной осей одинаковое.Пример: za = 16, zb = 16, zc = 48, тогда передаточное число = 4.
(b) Тип солнечной энергии
В этом типе солнечная шестерня фиксируется. Внутренняя шестерня C является входом, а ось водила D — выходом. Передаточное число рассчитывается, как в таблице 17.2.
Таблица 17.2 Уравнения передаточного числа для солнечного типа
Обратите внимание, что направления вращения входной и выходной осей одинаковы. Пример: za = 16, zb = 16, zc = 48, тогда передаточное число = 1.33333
(c) Тип звезды
Это тип, в котором фиксируется Carrier D. Планетарные шестерни B вращаются только на фиксированных осях. В строгом понимании этот поезд теряет черты планетарной системы и становится обычным зубчатым колесом. Солнечная шестерня является входной осью, а внутренняя шестерня — выходной. Передаточное отношение:
На Рисунке 2.3 (c) планетарные шестерни являются просто холостыми.
Входная и выходная оси имеют противоположное вращение.
Пример: za = 16, zb = 16, zc = 48,
, тогда передаточное число = -3.
17.2 Гипоциклоидный механизм
При зацеплении внутренней шестерни и внешней шестерни, если разница в количестве зубцов двух шестерен довольно мала, шестерня с профильным переключением может предотвратить столкновение. Таблица 17.3 представляет собой пример того, как предотвратить столкновение в условиях z2 = 50 и разности чисел зубьев двух шестерен от 1 до 8.
Таблица 17.3 Зацепление внутренних и наружных шестерен малой разности чисел зубьев
Все вышеперечисленные комбинации не вызовут эвольвентной интерференции или трохоидной интерференции, но интерференция обрезки все же присутствует.
Для успешной сборки внешнее зубчатое колесо следует собрать, вставив его в осевом направлении. Внутренняя шестерня с профильным смещением и внешняя шестерня, в которой разница в количестве зубьев мала, относятся к области гипоциклических механизмов, которые могут создавать большое передаточное число за один шаг, например 1/100.
На рисунке 17.4 зубчатая передача имеет различие в количестве зубьев всего в 1; z1 = 30 и z2 = 31. Это дает передаточное число 30.
Рис. 17.4 Зацепление внутреннего зубчатого колеса и внешнего зубчатого колеса, в котором разность чисел зубьев равна 1
17.3 Система с ограниченными зубьями
Планетарная зубчатая передача с четырьмя шестернями является примером системы передач с ограничениями. Это замкнутая система, в которой мощность передается от ведущей шестерни через другие шестерни и, в конечном итоге, на ведомую шестерню. Система передачи с замкнутым контуром не будет работать, если шестерни не соответствуют определенным условиям.
Пусть z1, z2 и z3 будут числами зубьев шестерни, как на рисунке 17.5 Создание сетки не может работать, если длина жирной лески (ремня) не делится равномерно на шаг. Уравнение (17.11) определяет это условие.
Рис. 17.5 Система с промежуточной шестерней
На рисунке 17.6 показана ограниченная зубчатая система, в которой зубчатая рейка находится в зацеплении. Жирная линия на рисунке 17.6 соответствует поясу на рисунке 17.5. Если длину ремня нельзя равномерно разделить по шагу, система не работает. Он описывается уравнением (17.12).
Рис.17.6 Зубчатая передача с зубчатой рейкой
Ссылки по теме:
Прямозубые цилиндрические шестерни
Планетарный редуктор
% PDF-1.6 % 1 0 obj > / Метаданные 2 0 R / Страницы 3 0 R / StructTreeRoot 5 0 R / Тип / Каталог >> endobj 2 0 obj > поток 2015-11-05T13: 38-05: 002015-11-05T13: 37: 59-05: 002015-11-05T13: 38-05: 00 Приложение Adobe InDesign CS5 (7.0) / pdfuuid: 15110810-db39-5647-9ce6- 183db7d4c428uuid: eb794bac-032a-8749-8573-fdc4124f4c0e Библиотека Adobe PDF 9.9 конечный поток endobj 3 0 obj > endobj 5 0 obj > endobj 9 0 объект > endobj 10 0 obj > endobj 11 0 объект
Расчет планетарной передачи ZAR5
Расчет планетарной передачи ZAR5 | DeutschПрограммное обеспечение для проектирования планетарных передач
(C) Авторские права 2000-2020, HEXAGON Software, Берлин
Основы для расчета
Программа расчета планетарной передачи ZAR5 рассчитывает геометрию и прочность солнечной, планетарной и кольцевой шестерни (прямозубые или косозубые, эвольвентные зубья) в соответствии с ISO 6336, ISO 1328, DIN 3960, 3961, 3967 и 3990.ZAR5 рассчитывает контакт зубьев для зубчатой пары солнечная планетарная передача и планетарная шестерня.Предварительное измерение
При предварительном выборе размеров ZAR5 создает планетарную шестерню после того, как вы ввели входную / выходную скорость и мощность.
Размеры
Угол давления, угол спирали, нормальный модуль или диаметральный шаг, количество зубцов, ширина грани, коэффициенты модификации дополнения, межосевое расстояние, уменьшение дополнения могут быть отредактированы и оптимизированы в диалоговом окне размеров.
Специальные профили
Чтобы пользователи могли оптимизировать зубчатые передачи с зацеплением с увеличенной глубиной, программа позволяет свободно определять размеры инструмента с нормальным профилем и профилем выступа, с поломкой режущей кромки и без нее.
Распечатка
ZAR5 рассчитывает все данные зубчатой передачи, размеры инструмента, толщину зуба, зазор по бокам, люфт, ширину пролета, размер над / между пальцами и шариками, допуски и допустимые погрешности в соответствии с ISO 1328 или DIN 3961.
Расчет на прочность
Несущая способность в отношении усталостного разрушения корней зуба и точечной коррозии может быть рассчитана для зубчатых пар солнечно-планетарная и планетарно-кольцевая шестерня в соответствии с ISO 6336 или DIN 3990, части 1-3, или DIN 3990, часть 41 (трансмиссия автомобилей ). На диаграмме показаны коэффициенты безопасности и ожидаемый срок службы в зависимости от крутящего момента.
Диаграмма Куцбаха
Диаграмма Куцбаха отображает векторы скорости и относительную скорость.
Вольф диаграмма
Таблица передач для Wolf показывает распределение крутящего момента на 3 вала (2 разностных вала и 1 суммарный вал), а также относительные коэффициенты передачи.
Анимация
Анимация имитирует кинематографию планетарной передачи на экране. Другая анимация показывает контакт зубьев солнечной планетарной передачи и планетарной шестерни.
Производственный чертеж
Вы можете создать чертеж с таблицами всех производственных данных для солнца, планетарной передачи и коронной шестерни.Рисунки можно экспортировать как файлы DXF или IGES или распечатать на любом принтере Windows.
Производственный лист
Другой производственный лист содержит данные о производстве и размеры в предварительно обработанном и законченном состоянии.
Быстрый просмотр
Quick View показывает таблицы с наиболее важными данными о планетарной передаче.
Расчет подшипников каченияЕсли планетарные колеса должны быть установлены на роликовых подшипниках, ZAR5 рассчитывает ожидаемый срок службы шарикоподшипников с канавкой, самоустанавливающихся шарикоподшипников, игольчатых втулок, игольчатых подшипников, цилиндрических роликоподшипников, конических роликоподшипников и самоустанавливающихся роликоподшипников с помощью файлы базы данных, поставляемые с программным обеспечением.
Многоступенчатая планетарная передача
Введите передаточное число и количество ступеней для предварительного расчета многоступенчатой планетарной передачи.
Интерфейс CAD
Интерфейсы DXF и IGES позволяют подключать ZAR5 к системам CAD и DTP. ZAR5 генерирует чертежи рассчитанных передних и боковых высот шестерен, а также таблицы, содержащие данные и размеры шестерен.
Форму зуба с эвольвентами и огибающими можно точно рассчитать и нанести на график в CAD.Отдельный зуб, пространство между зубьями, зубчатое колесо в целом, зубчатый инструмент, планетарная зубчатая передача и вид в разрезе действия зуба могут отображаться на экране или выводиться в виде чертежа САПР.
База данных материалов и профилей зубьев
ZAR5 содержит базы данных с данными о материалах и профилями инструментов, которые могут быть расширены и изменены пользователем.
Спектр нагрузкиZAR5 позволяет определить совокупную нагрузку и рассчитать факторы применения с помощью диаграммы ожидаемого срока службы.
Системные требования
ZAR5 доступен как 32-битное и 64-битное приложение для Windows 10, Windows 8, Windows 7. Если предполагается использование средства CAD, используемая система должна быть оборудована интерфейсом DXF или IGES.
Объем поставки
Пакет ZAR5 состоит из CD-ROM или zip-файла, содержащего программу ZAR5, файлов с примерами приложений, текста справки и вспомогательных файлов изображений, руководства с инструкциями по установке, описания программы и примеров применения, лицензионного соглашения на неопределенный период времени.
Служба информации и обновлений
HEXAGON Программное обеспечение постоянно совершенствуется и обновляется. Лицензированные пользователи могут получать новые версии по цене обновления. Каждой программе предоставляется индивидуальный номер лицензии и пользовательские файлы. За поддержку по электронной почте и горячей линии с зарегистрированных пользователей не взимается дополнительная плата.
Гарантия
HEXAGON гарантирует в течение 24 месяцев, что программное обеспечение будет выполнять описанные функции.
Скачать демо ZAR5 для Windows (869 КБ)
Прейскурант | Заказать | Электронная почта | Главная

 4
4 Зубчатые колеса планетарной передачи могут быть любого известного типа из курса «Детали машин»: прямозубые, косозубые, червячные, шевронные. Тип зацепления не оказывает влияния на работу планетарной передачи.
Зубчатые колеса планетарной передачи могут быть любого известного типа из курса «Детали машин»: прямозубые, косозубые, червячные, шевронные. Тип зацепления не оказывает влияния на работу планетарной передачи.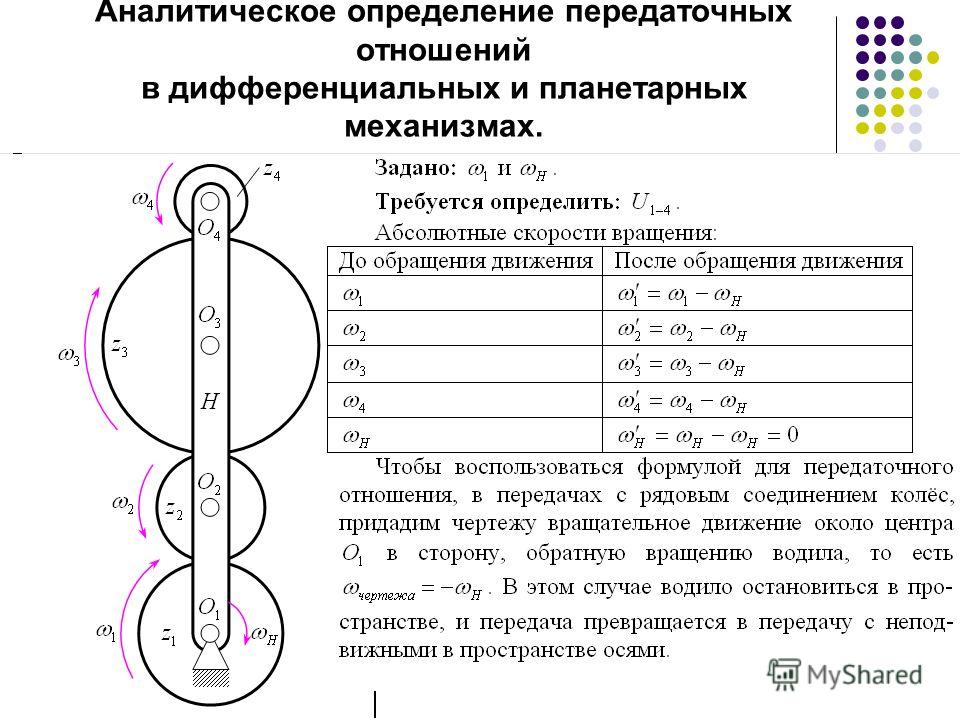
 Количество сателлитов в ПМ обычно составляет от двух до шести (чаще всего — три, так как только при трёх сателлитах нет нужды в специальных уравновешивающих механизмах) и точного значения для функциональности ПМ не имеет. В различных ПМ применяются сателлиты одновенцовые (одно простое зубчатое колесо), двухвенцовые (два соосных зубчатых колеса с общей ступицей), трёхвенцовые и так далее. Также сателлиты могут быть парными — то есть, располагающимимся на осях одного водила и зацепленными в паре.
Количество сателлитов в ПМ обычно составляет от двух до шести (чаще всего — три, так как только при трёх сателлитах нет нужды в специальных уравновешивающих механизмах) и точного значения для функциональности ПМ не имеет. В различных ПМ применяются сателлиты одновенцовые (одно простое зубчатое колесо), двухвенцовые (два соосных зубчатых колеса с общей ступицей), трёхвенцовые и так далее. Также сателлиты могут быть парными — то есть, располагающимимся на осях одного водила и зацепленными в паре. В обоих случаях при полной блокировке фрикционы обеспечивают паре соединённых элементов некую одинаковую ненулевую угловую скорость. Конструктивно обычно выполнены в виде многодисковых фрикционных муфт, хотя в отдельных случаях возможны и более простые муфты.
В обоих случаях при полной блокировке фрикционы обеспечивают паре соединённых элементов некую одинаковую ненулевую угловую скорость. Конструктивно обычно выполнены в виде многодисковых фрикционных муфт, хотя в отдельных случаях возможны и более простые муфты.