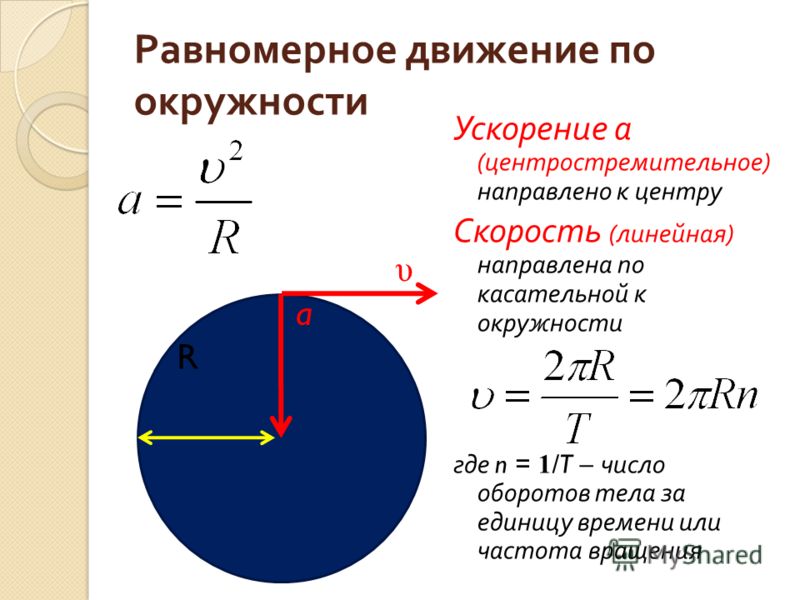
Скорость движения по окружности формула: 1.6. Движение по окружности

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Понятия и определения

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду.

Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

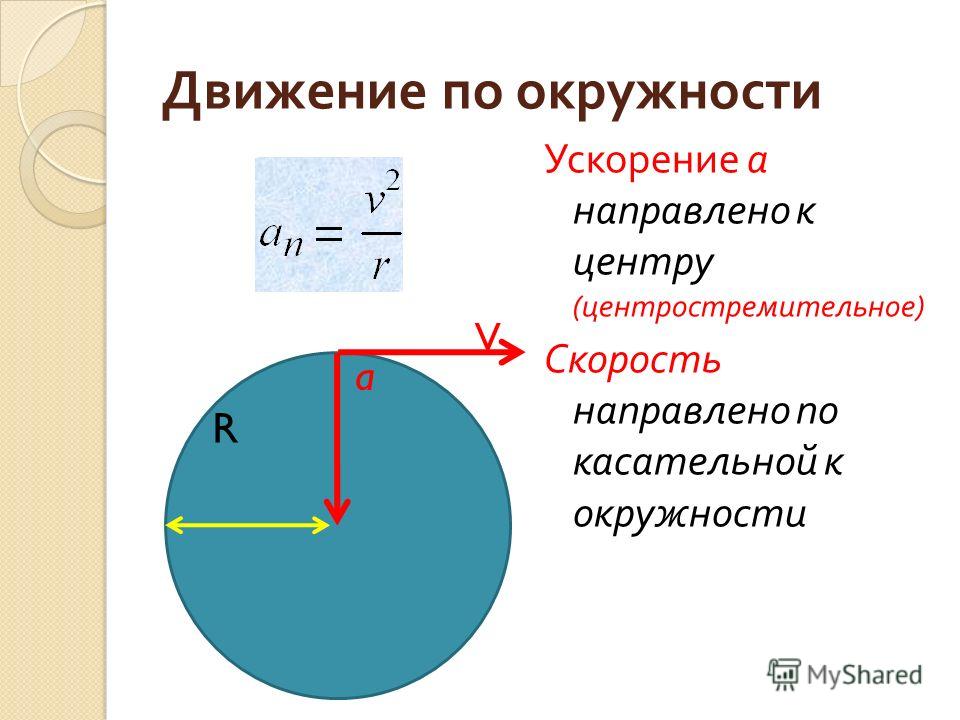
Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с²). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10³ секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10⁶. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения.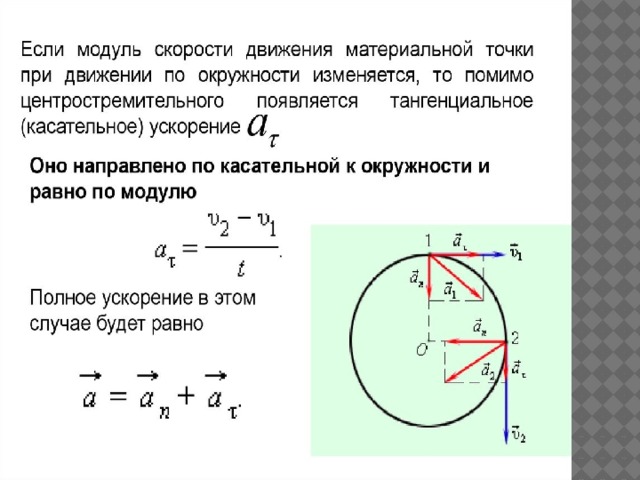 Подставляем данные в формулу:

Задание EF18273 Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…

---

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17763

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

---

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

• Радиус окружности R₁ = R.
• Радиус окружности R₂ = 4R.
• Центростремительное ускорение: a_ц.с. = a₁ = a₂.

Найти нужно ν₂.

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 16.4k | Оценить:

Движение по окружности, теория и онлайн калькуляторы

Движение по окружности, теория и онлайн калькуляторы

Значимым частным случаем перемещения материальной точки по заданной траектории служит движение по окружности. Местоположение точки на окружности можно задавать не при помощи расстояния от некоторой начальной точки (допустим A), а с помощью угла $\varphi $, который образуют радиусы, которые провели из центра окружности (O) к рассматриваемой частице (точка M) и из О в точку начала отсчета (A) (рис.1).

Скорость при движении по окружности

При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($\omega $), которая характеризует быстроту изменения угла $\varphi $:

\[\omega =\frac{d\varphi }{dt}\left(1\right).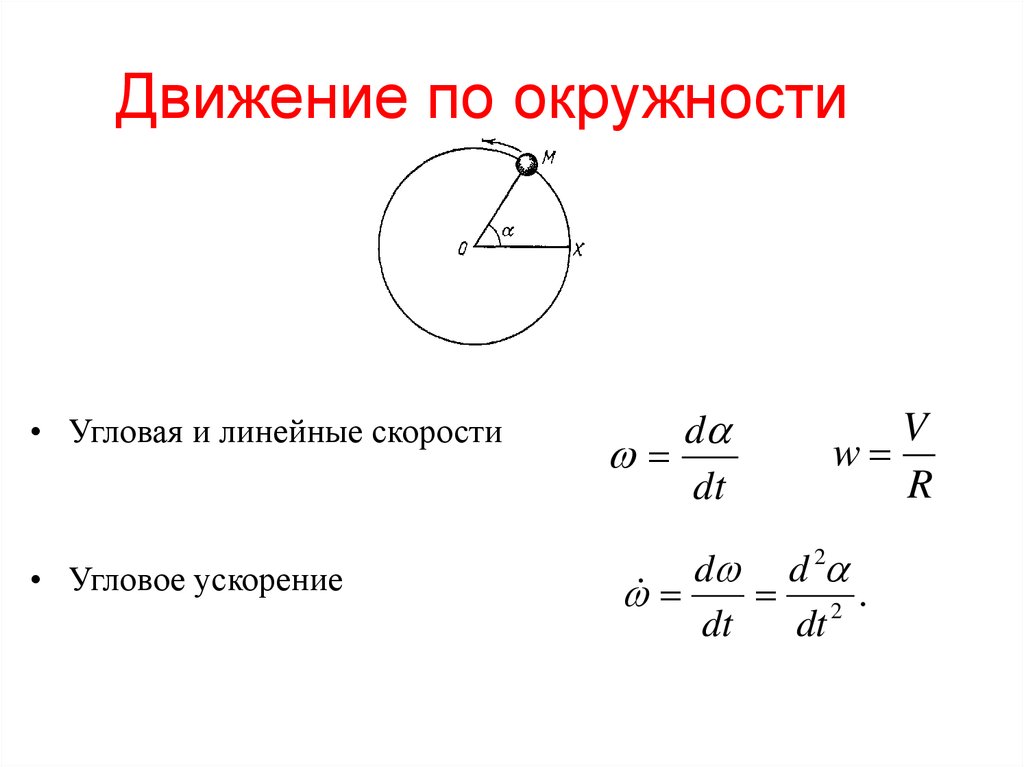

\]

Определим, какова связь между линейной и угловой скоростями. Длину дуги АМ ($s$) (рис.1) можно найти как:

\[s=R\varphi \left(2\right),\]

тогда изменение длины дуги за время$\ \Delta t$ равно$\ \Delta s$:

\[\Delta s=R\Delta \varphi \ \left(3\right).\]

Найдем отношение $\frac{\Delta s}{\Delta t}$, разделив обе части выражения (3) на $\Delta t$:

\[\frac{\Delta s}{\Delta t}=R\frac{\Delta \varphi }{\Delta t}\ \left(4\right).\]

Перейдем к пределу в правой и левой частях равенства (4) при $\Delta t\to 0$, получим:

\[{\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}\ }=R{\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \varphi }{\Delta t}\ }\to v=R\omega \left(5\right).\]

Ускорение материальной точки при движении по окружности

При движении по окружности (как при любом неравномерном криволинейном движении) ускорение можно разложить на две составляющие: тангенциальное ускорение (${\overline{a}}_{\tau }$), которое направлено по касательной к траектории движения точки и характеризующее быстроту изменения модуля скорости $v$ и центростремительной ускорение (${\overline{a}}_n$), направленное к центру кривизны траектории, определяющее быстроту изменения направления скорости.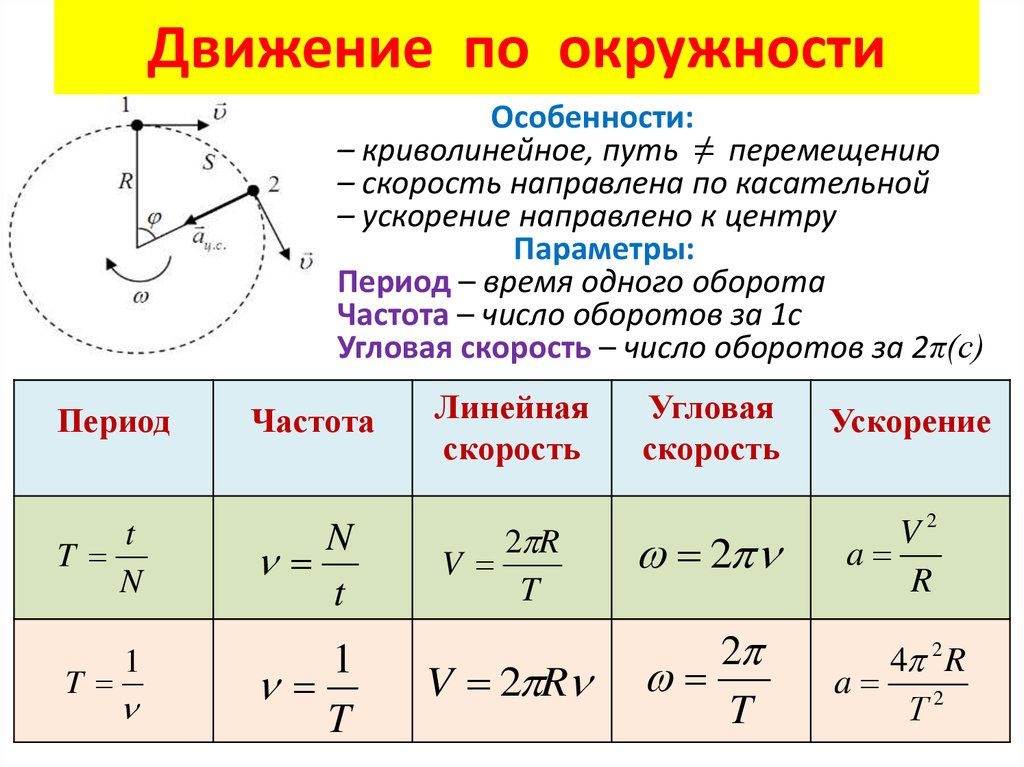

2R\ \left(6\right).\]

При равномерном перемещении по окружности величина центростремительного ускорения постоянна ($a_n=const).\ $Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.

Тангенциальное ускорение при движении по окружности вычисляют, как и при любом криволинейном движении:

\[{\overline{a}}_{\tau }=\frac{d\overline{v}}{dt}\left(7\right).\]

Период и частота — характеристики равномерного движения по окружности

Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения ($T$), который определяют как время совершения материальной точкой полного оборота. Используют и частоту ($\nu$) обращения, которую определяют как величину обратную периоду, равную количеству оборотов за единицу времени:

\[\nu =\frac{1}{T}\left(8\right).\]

При равномерном движении по окружности угловая скорость, частота и период связаны как:

\[\omega =\frac{2\pi }{T}=2\pi \nu \left(9\right). 2\right)$

   

Читать дальше: жесткость пружины.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Математика кругового движения

Существуют три математические величины, которые будут представлять для нас основной интерес при анализе движения объектов по окружности. Этими тремя величинами являются скорость, ускорение и сила. Скорость объекта, движущегося по окружности, определяется следующим уравнением.

Ускорение объекта, движущегося по окружности, можно определить с помощью любого из двух следующих уравнений.

Уравнение справа (выше) получено из уравнения слева заменой выражения для скорости.

Суммарная сила ( F _сеть ), действующая на объект, движущийся по кругу, направлена ​​внутрь. Хотя на объект может действовать более одной силы, векторная сумма всех их должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если она есть), так что внешняя сила уравновешивается, а неуравновешенная сила направлена ​​в центр круга. Суммарная сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:0003

Уравнения в середине (вверху) и справа (вверху) получаются из уравнения слева заменой выражений для ускорения.

Этот набор уравнений кругового движения можно использовать двумя способами:

• как «рецепт» для решения алгебраических задач для решения неизвестной величины.
• как руководство к размышлению о том, как изменение одной величины повлияет на другую величину.

Эти два способа показаны ниже.

 

Уравнения как руководство к мышлению

Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение для второго закона Ньютона определяет, как ускорение связано с результирующей силой и массой объекта.

Связь, выраженная уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. На самом деле, если бы результирующая сила увеличилась в 2 раза, уравнение предсказало бы, что ускорение увеличилось бы в 2 раза. Точно так же, если бы результирующая сила уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшилось бы в 2,9 раза.0003

Уравнение второго закона Ньютона также раскрывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше значение ускорения. С увеличением массы ускорение уменьшается. На самом деле, если бы масса увеличилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса уменьшилась в 2 раза, уравнение предсказало бы, что ускорение уменьшится. увеличить в 2,9 раза0003

Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на другую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Предсказательная способность уравнения усложняется, когда одна из величин, входящих в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее результирующую силу ( F _net ) к скорости ( v ) объекта, движущегося в равномерном круговом движении.

Это уравнение показывает, что результирующая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. Для постоянной массы и радиуса F _сеть пропорциональна скорости ² .

Коэффициент изменения чистой силы равен квадрату коэффициента изменения скорости. Следовательно, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза. А если скорость объекта уменьшится вдвое (уменьшится в 2 раза), необходимая результирующая сила уменьшится в 4 раза.0003

Уравнения как рецепт решения задач

Приведенные выше математические уравнения движения объектов по окружностям можно использовать для решения задач о движении по окружности, в которых необходимо определить неизвестную величину. Процесс решения задачи о круговом движении очень похож на любую другую задачу на уроках физики. Этот процесс включает в себя внимательное прочтение задачи, идентификацию известной и требуемой информации в переменной форме, выбор соответствующего уравнения (уравнений), подстановку известных значений в уравнение и, наконец, алгебраические манипуляции с уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам о круговом движении.

Пример задачи №1 Автомобиль массой 900 кг, движущийся со скоростью 10 м/с, совершает поворот по окружности радиусом 25,0 м. Определить ускорение и результирующую силу, действующую на автомобиль.

Решение этой задачи начинается с идентификации известной и запрашиваемой информации.

Известная информация: м = 900 кг v = 10,0 м/с R = 25,0 м

Запрашиваемая информация: а = ???? F нетто = ????

Для определения ускорения автомобиля используйте уравнение a = v ² / R. Решение выглядит следующим образом:

а = в ² / р

а = (10,0 м/с) ² / (25,0 м)

а = (100 м ² /с ² ) / (25,0 м)

а = 4 м/с ²

Чтобы определить результирующую силу, действующую на автомобиль, используйте уравнение F _net = m•a. Решение заключается в следующем.

F _нетто = м • а

F _нетто = (900 кг) • (4 м/с ² )

F _нетто = 3600 Н

Пример задачи №2 Полузащитник весом 95 кг делает разворот на футбольном поле. Полузащитник прокладывает путь, который представляет собой часть круга радиусом 12 метров. Полузащитник делает четверть оборота по кругу за 2,1 секунды. Определить скорость, ускорение и чистую силу, действующую на полузащитника.

Решение этой задачи начинается с идентификации известной и запрашиваемой информации.

Известная информация: м = 95,0 кг R = 12,0 м Пройдено 1/4 окружности за 2,1 с

Запрашиваемая информация: v = ???? а = ???? F нетто = ????

Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d — одна четвертая длины окружности, а время — 2,1 с. Решение выглядит следующим образом:

v = d/t

v = (0,25 • 2 • пи • R) / t

v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)

v = 8,97 м/с

Для определения ускорения полузащитника воспользуемся уравнением a = v ² /R. Решение будет следующим:

a = v ² /R

а = (8,97 м/с) ² / (12,0 м)

а = (80,5 м ² /с ² ) / (12,0 м)

а = 6,71 м/с ²

Чтобы определить результирующую силу, действующую на полузащитника, используйте уравнение F _нетто = м•а. Решение заключается в следующем.

F _нетто = м*а

F _нетто = (95,0 кг)*(6,71 м/с ² )

F _нетто = 637 Н

 

В уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных реальных сценариев движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.

 

Мы хотели бы предложить…

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием либо нашего интерактивного равномерного кругового движения, либо нашего моделирования горизонтального круга. Вы можете найти их в разделе Physics Interactives на нашем сайте. Интерактивное приложение «Равномерное круговое движение» позволяет учащимся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу. Наше моделирование горизонтального круга моделирует движение трех разных объектов, движущихся по горизонтальному кругу, при этом анализируя влияние, которое изменения переменной могут оказать на движение.

Посетите:  Интерактивное  равномерное круговое движение || Моделирование горизонтального круга

 

Проверьте свое понимание

1. Анна Литикал тренируется дома с демонстрацией центростремительной силы. Она наполняет ведро водой, привязывает его к прочной веревке и раскручивает по кругу. Анна крутит ведро, когда оно наполовину наполнено водой и когда оно на четверть. В каком случае требуется большее усилие, чтобы вращать ведро по кругу? Объясните, используя уравнение как «руководство к мышлению».

 

2. Линкольн Континенталь и Юго делают поворот. Lincoln в четыре раза массивнее Yugo. Если они совершают поворот с одинаковой скоростью, то как соотносятся центростремительные силы, действующие на два автомобиля? Объяснять.

 

3. Cajun Cliffhanger в Great America – это аттракцион, в котором участники выстраиваются вдоль периметра цилиндра и вращаются по кругу с высокой скоростью. Когда цилиндр начинает вращаться очень быстро, пол убирается из-под ног гонщиков. Как влияет удвоение скорости на центростремительную силу? Объяснять.

 

4. Определить центростремительную силу, действующую на ребенка массой 40 кг, который делает 10 оборотов вокруг скалодрома за 29,3 секунды. Радиус ствола составляет 2,90 метра.

 

Перейти к следующему уроку:

Калькулятор кругового движения

Создано Purnima Singh, PhD

Отзыв Стивена Вудинга

Последнее обновление: 05 декабря 2021 г.

Содержание:

• Определение кругового движения
• Что такое равномерное круговое движение?
• Как рассчитать параметры кругового движения?
• Формулы кругового движения
• Часто задаваемые вопросы

Калькулятор кругового движения Omni позволяет вам рассчитать все параметры равномерного кругового движения . Если вы не знаете, что такое равномерное круговое движение, или чувствуете себя подавленным формулами кругового движения, не волнуйтесь! Наш калькулятор кругового движения поможет вам понять концепции равномерного кругового движения в физике.

Читайте дальше, чтобы узнать определение, примеры и формулы кругового движения. Вы также найдете примеры расчета параметров кругового движения (таких как период, частота, скорость и ускорение) с помощью нашего калькулятора равномерного кругового движения.

Определение кругового движения

Когда объект движется по круговому пути , мы называем его движение круговым. Некоторые распространенные примеры кругового движения:

• Гоночный автомобиль движется по круговой кривой;
• Искусственный спутник, вращающийся вокруг Земли;
• Наконечник минутной/секундной стрелки часов; и
• Вращение камня, привязанного к веревке.

Круговое движение объекта может быть либо равномерным круговым движением , либо неравномерным круговым движением .

При круговом движении направление движения непрерывно меняется . В любой момент направление движения тела, движущегося по окружности, лежит по касательной к окружности в этот момент.

Более простой способ визуализировать эту концепцию — представить вращающийся камень, привязанный к веревке; когда струна рвется, камень летит по касательной.

Что такое равномерное круговое движение?

При равномерном круговом движении объект движется по круговой траектории с постоянной скоростью . Это означает, что объект будет проходить равные расстояния по окружности окружности за равные промежутки времени. В неравномерном круговом движении , скорость объекта изменения .

Хотя при равномерном круговом движении скорость постоянна, направление движения постоянно меняется, как мы обсуждали в предыдущем разделе. Следовательно, скорость объекта, совершающего равномерное круговое движение, также непрерывно изменяется (см. рис. 1).

Рис. 1: Скорость, ускорение и угловая скорость при равномерном круговом движении. (Источник: wikimedia.org)

Из-за изменения направления скорости объект испытывает ускорение, называемое центростремительным ускорением .

Из первого закона движения Ньютона мы знаем, что тело не может изменить направление своего движения само по себе. Для этого требуется внешняя сила. Эта внешняя сила , которая удерживает объект, движущийся по круговой траектории , называется центростремительной силой .

Как рассчитать параметры кругового движения?

Давайте посмотрим, как использовать калькулятор равномерного кругового движения для расчета различных физических параметров кругового движения.

1. Используйте раскрывающееся меню . От до выберите набор параметров, которые вы хотите рассчитать. Мы выберем параметр радиус, скорость и ускорение, поскольку мы хотим рассчитать все параметры для этого примера.
2. Введите период времени кругового движения, скажем, 4 секунды в строке 1.
3. Калькулятор отобразит частоту ( 0,25 Гц ) и угловую скорость ( 1,571 рад/с ) кругового движения.
4. Введите радиус кругового пути, скажем, 2 метра , в строке 2. Калькулятор покажет скорость ( 3,142 м/с ) и центростремительное ускорение ( 4,9035 м/с 2 ).

Мы также рекомендуем воспользоваться нашим калькулятором центробежной силы.

Формулы движения по окружности

Рассмотрим объект, движущийся по окружности окружности радиусом r (см. рис. 1) с центром в точке O . Пусть объект перемещается (против часовой стрелки) из P в Q за время t . Физические величины, описывающие это движение, и формулы для кругового движения:

Рис. 1: Движение объекта по круговому пути.

• Угловое смещение (θ) — это угол θ , образуемый в центре радиус-вектором за заданное время. Мы знаем, что:

  угол = дуга/радиус

  … следовательно, для цифры 1 мы можем написать:

  θ = PQ/r

  Единицей углового смещения в системе СИ является радиан ( рад ).

• Период времени (T) — это время, за которое объект совершает один оборот по круговой траектории. Единицей периода времени в СИ является секунда ( с ).

• Частота (ν) — количество оборотов объекта за одну секунду. Единицей частоты в системе СИ является герц ( Гц ).

  ν = 1/Т

• Угловая скорость (ω) — скорость изменения углового смещения во времени, т. е.

  ω = Δθ / Δt

  Единицей угловой скорости в системе СИ является радиан в секунду ( рад/с ).

  Когда объект совершает один оборот (см. рис. 1), угол в центре составляет 2π радиан. Это означает, что за время кругового движения t = T , θ = 2π . Следовательно, мы можем выразить угловую скорость как:

  ω = 2 * π/T

  …или:

  ω = 2 * π * ν

• Угловое ускорение (α) — скорость изменения угловой скорости во времени, т. е.

  α = Δω / Δt

  Единицей углового ускорения в системе СИ является рад/с 2 .

• Центростремительное ускорение ( α c ) — это ускорение объекта, совершающего равномерное круговое движение. Он всегда действует на объект по радиусу и к центру круговой траектории.

  α с = v 2 / r

Часто задаваемые вопросы

Что является постоянным в равномерном движении по окружности?

Скорость постоянна при равномерном круговом движении. Объект движется с постоянной скоростью по круговой траектории в равномерном круговом движении.

Какая центростремительная сила действует на объект, движущийся по окружности?

Центростремительная сила — это сила, которая действует на любой объект, движущийся по окружности . Величина центростремительной силы, действующей на объект, движущийся по окружности, равна произведению его массы на центростремительное ускорение. Центростремительная сила направлена ​​к центру окружности.

Какая связь между линейной скоростью и угловой скоростью?

Для объекта, совершающего равномерное круговое движение, линейная скорость v равна произведению угловой скорости ω и радиуса пути r .

Как найти ускорение при круговом движении?

Чтобы найти центростремительное ускорение при круговом движении, выполните следующие действия:

1. Возьмите квадрат линейной скорости .