Скорость угловая: 404 — Страница не найдена

Содержание

Скорость угловая вращения — Энциклопедия по машиностроению XXL

Для случая, когда оси вращения Oj и Oj звеньев 1 и 2 (рис. 7.1, б) пересекаются в точке О и заданы постоянные угловые скорости и вращения звеньев 1 и 2, передаточное отношение равно [c.138]

Ось Z волчка равномерно описывает вокруг вертикали 0″ круговой конус с углом раствора 29. Угловая скорость вращения оси волчка вокруг оси равна oi, а постоянная угловая скорость собственного вращения волчка равна о. Определить величину и направление абсолютной угловой скорости Q волчка. [c.140]

Коническое зубчатое колесо, ось которого пересекается с геометрической осью плоской опорной шестерни в центре послед[[ей, обегает пять раз в минуту опорную шестерню. Определить угловую скорость Ыг вращения колеса вокруг его оси и угловую скорость (0 вращения вокруг мгновенной оси, если радиус опорной шестерни вдвое больше радиуса колеса 1 = 2г.

[c.142]

Определить в предыдущей задаче угловую скорость равномерного вращения ротора, при которой точка А, находясь в положении В, имеет абсолютное ускорение, равное нулю. [c.162]

Определить угловое ускорение вращающейся кулисы кривошипно-кулисного механизма строгального станка при двух вертикальных и двух горизонтальных положениях кривошипа, если длина кривошипа I = 0,4 м, расстояние между осями кривошипа и кулисы а = 0,3 м, угловая скорость равномерного вращения кривошипа (О = 3 рад/с. (См. рисунок к задаче 22.20.) [c.166]

Дифференциальная передача состоит из двух дисков АВ и ОЕ, центры которых находятся на их общей оси вращения эти диски сжимают колесо ММ, ось которого Н1 перпендикулярна оси дисков. Определить для колеса ММ скорость и центра Н и угловую скорость (Л, вращения вокруг оси Н1, если скорости точек касания колеса с дисками равны Ц] =3 м/с, V2=4 м/с, радиус колеса г = 0,05 м.

[c.183]

Шаровая дробилка состоит из полого шара диаметра (/=10 см, сидящего на оси АВ, на которой заклинено колесо с числом зубцов 24 = 28. Ось АВ закреплена во вращающейся раме / в подшипниках а и Ь. Рама I составляет одно целое с осью D, приводящейся во вращение при помощи рукоятки III. Вращение паровой дробилки вокруг оси АВ осуществляется при помощи зубчатых колес с числами зубцов z = 80, 22 == 43, 23 = 28, причем первое из них неподвижно. Определить абсолютную угловую скорость, угловое ускорение дробилки и скорости и ускорения двух точек Е и F, лежащих в рассматриваемый момент времени на оси D, если рукоятку вращают с постоянной угловой скоростью (О — 4,3 рад/с. [c.188]

Тележка поворотного подъемного крана движется с постоянной скоростью V относительно стрелы. Мотор, вращающий кран, создает в период разгона постоянный момент, равный то- Определить угловую скорость (О вращения крана в зависимости от расстояния х тележки до оси вращения АВ, если масса тележки с грузом равна М, / — момент инерции крана (без тележки) относительно оси вращения вращение начинается в момент, когда тележка находится на расстоянии Хо от оси АВ.

[c.292]

Сохранив условие предыдущей задачи, определить угловую скорость со вращения крана, если мотор создает вращающий момент, равный тц —ао), где /По и а — положительные постоянные. [c.292]

Для определения угловой скорости со вращения тела вокруг мгновенной оси вычислим скорость точки В, считая ее движение сложным. Получим [c.209]

Таким образом, при сложении двух вращений тела вокруг параллельных осей в одинаковых направлениях получается вращение вокруг параллельной оси в том же направлении с угловой скоростью, равной сумме угловых скоростей составляющих вращений. Мгновенная ось полученного вращения делит отрезок

[c.302]

Из того, что пара вращений эквивалентна поступательному движению, следует и обратный вывод поступательное движение твердого тела эквивалентно паре вращений, у которой момент угловых скоростей этих вращений равен поступательной скорости тела. [c.172]

Следовательно, пp сложении вращений вокруг двух осей, пересекающихся в точке О, результирующее движение тела будет мгновенным вращением вокруг оси Ос, проходящей через точку О, и угловая скорость этого вращения будет равна геометрической сумме относительной и переносной угловых скоростей. Мгновенная ось Ос направлена вдоль вектора со, т. е. по диагонали параллелограмма, построенного на векторах oj и Ша-

[c.175]

Определим абсолютное движение тела, получающееся при сложении двух вращательных движений вокруг пересекающихся осей. Пусть твердое тело одновременно вращается вокруг двух мгновенных осей, пересекающихся в точке О (рис. 407), причем его вращение вокруг оси ОК является переносным, а вокруг оси 0L — относительным вращением. Предположим, что угловая скорость переносного вращения тела равна а относительного вращения — [c.323]

Покажем теперь, что геометрическая сумма векторов и т. е. вектор ОС, равна вектору угловой скорости абсолютного вращения тела ы. Для этого проведем из точки О в какую-нибудь точку М тела радиус-вектор / и определим скорость этой точки [c.324]

Таким образом, угловая скорость абсолютного вращения тела равна геометрической сумме угловых скоростей составляющих вращений.

[c.325]

С осью неподвижного конуса. Угловые скорости этих вращений имеют следующую зависимость [c.326]

Модуль угловой скорости переносного вращения со = 2л-15/60 = 0,5л = 1,57 с . [c.327]

Годографом (О является окружность, параллельная основанию неподвижного конуса. Зная модули угловой скорости переносного вращения со,, и относительного вращения конуса II, определим модуль вращательной скорости и [c.327]

На рис. 418, б показано, что абсолютное вращение плоской фигуры направлено против вращения часовой стрелки, т. е. в сторону относительного вращения, угловая скорость которого по модулю больше угловой скорости переносного вращения. [c.337]

Ротор массы М, представляющий собой однородный цилиндр радиуса R и длины /, насажен на вал с перекосом и смешением, так что его ось симметрии отклонена от оси вала на малый случайный угол у а его центр, расположенный посередине между подшипниками, смещен относительно оси вала на случайную величину h. Расстояние между подшипниками равно 2L. Предполагается, что у и к представляют собой независимые случайные величины, угол у имеет нулевое математическое ожидание, расстояние к — математическое ожидание шк и средние квадратические отклонения соответственно равны Оу и ол. Угловая скорость а> вращения ротора вокруг вертикальной оси считается случайной величиной с математическим ожиданием /Нщ и средним квадратическим ртклонением Оа. Определить средние квадратические отклонения и реакций подшипников и / 2-

[c.446]

В технологических процессах интерес представляет случай дисперсной смеси с частицами из ферромагнитного материала в магнитном поле, которое оказывает непосредственное моментное воздействие лишь на частицы (2-я фаза).

Это приводит к их ориентированному мелкомасштабному враш,ению (Mj =5 0) с угловой скоростью 2, кинематически независимой от поля их осреднен-ных скоростей v . Вращение частиц за счет сил трения передается и несущ,ей фазе и приводит к мелкомасштабному с характерным линейным размером, равным размеру частиц, ориентированному вращению несущей жидкости М =7 0), Если магнитное поле не оказывает непосредственного воздействия на несущую фазу, т. е. она остается неполярной, то тензор напряжения в ней будет симметричным, а во второй фазе— несимметричным, причем его несимметрическая часть определяется воздействием внешнего магнитного поля на частицы. Симметричность тензора напряжений несущей фазы вытекает из симметричности тензора микронапряжений o l и совпадения среднеповерхностпых и среднеобъемных величин, что в свою очередь вытекает из регулярности этих величин. Несмотря на эти допущения, уравнения импульса и внутреннего момента несущей фазы могут быть приведены к некоторому виду, где, как и для дисперсной фазы, фигурирует несимметричный тензор поверхностных сил aji (см.

1,6 гл. 3). [c.83]

Последовательное применение этого правила сложения вращений вокруг пересекающихся осей позволяет заменить любое количество вращений вокруг пересекающихся осей одним вращением, угловая скорость которого ш равна векторной сумме угловых скоростей составляюищх вращений, т. е. [c.207]

Вращение вокруг мгновенной оси должно иметь такое направление, чтобы скорость точки О имела такое же направление, что и скорость V. Отсюда получаем совпадение направлений вращения относительного и абсолютного вращений. Следова-гельно, Q = o. Таким образом, при сложении поступательного перепоатго и вращательного относительного движений твердого тела, у которого скорость поступательного движения перпендикулярна оси относительного вращения, эквивалентное абсолютное движение является вращением вокруг мгновенной оси, параллельной оси относительного вращения с угловой скоростью, совпадающей с угловой скоростью относительного вращения.

[c.215]

Модули угловых скоростей прецессии ф и нутации б MajH,i по сравнению с модулем угловой скорости собственного вращения [c.509]

Рассмотрим случай регулярной прецессии гироскопа. Известно, что регулярной прецессией гироскопа называют такое его движение, при котором угловые скорости собственного вращения и прецессии постоянны, прецессия происходит вокруг оси 1ЮСТОЯННОГО направления и угол нутации, т. е. угол между осью собсгвенного вращения и осью прецессии, тоже является постоянным. [c.518]

Следовательно, результатирующее движение тела буц, т поступательным (или мгновенно поступательным) движением со скоростью, численно равной a>i-AB и направленной перпендикул рно плоскости, проходящей ч рез векторы oi и со2 направление вектора v определяется так же, как в статике определялось направление момента т пары сил (см. 9). Иначе говоря, пара вращений эквивалентна поступательному (или мгновенно поступательному) движению со скоростью V, равной моменту пары угловых скоростей этих вращений. [c.171]

Формула (79.12 ), определяющая угловую скорость равнозамедлениого вращения шкива /, имеет вид [c.216]

Вектор е геометрически равен скорости и конца вектора ш (103.2). В данном случае скорость и является вращательной вокруг оси г. Углова я скорость этого вращения определяется как угловая скорость вращения оси конуса ОС вокруг оси 2. Чтобы определить ее модуль, находим расстояние от точки С до оси г [c.284]

Кориолисовым, или поворотным, ускорением называется составля-юшдя абсолютного ускорения точки в сложном движении, равная удвоенному векпюрному произведению угловой скорости переносного вращения на относительную скорость точки [c.299]

Решение. Если подвижную систему отсчета связать с KpHsoujHnoM, то движение точек колеса II будет состоять из переносного вращения вместе с кривошипом вокруг оси О с постоянной угловой скоростью (Og = (Off и относительного движения — вращения вокруг оси А этого колеса. Угловую скорость относительного вращения следует определить. [c.313]

Скользящие векторы угловых скоростей со и перенесем в точку О пересечения мгновенных осей и построим на этих векторах параллелограмм ОАСВ. Покажем, что диагональ ОС этого параллелограмма представляет собой угловую скорость результирующего вращения тела, которое происходит вокруг оси ON. [c.324]

Лл л определения угловой скорости абсолютгюго вращения плоской фигуры III воспользуемся скоростью точки Рг- Приравниваем модули абсолютной скорости точки Рг — вращательной вокруг центра Р и переносной скорости этой точки — вращательной вокруг центра Р [c.337]

Угловая скорость — Справочник химика 21

U — угловая скорость вращения барабана в сек. п — число оборотов барабана в минуту [c.130]

Угловая скорость вращения [c.47]

О — угловая скорость вращения в рад сек [c. 44]

Расчет валов на виброустойчивость, а также уточненный расчет на прочность выполняются по РД РТМ 26-01-72—75. Расчет на виброустойчивость сводится к определению критической частоты вращения и сравнению ее с принятой, Фактические угловые скорости вала не должны совпадать с критическими. В зависимости от соотношения рабочей и первой [c.239]

Угловая скорость радиан в секунду рад/с (1 рад) (1 с) [c.351]

Угловая скорость рад/с теплоты [c.12]

Если оба подшипника жесткие, то критическую угловую скорость вала определяют по формуле [c.274]

Одинарные уплотнения. Принципиальное устройство этих уплотнений показано на рпс. 54. На валу насоса (или на специальной гильзе) устанавливают втулку 4, вращающуюся вместе с ним с такой же угловой скоростью (см. рпс. 54). Крутящий момент от вала к втулке передается через устройство 2. [c.144]

Валы центрифуг по характеру работы разделяют на гибкие и жесткие. Гибкими называют валы, работающие при угловых скоростях, превышающих критическую (со > ю,,р), жесткими — валы, рабочая угловая скорость которых меньше критической (со[c.267]

Для определения первой критической угловой скорости вала Т еобходимо значение коэффициентов (корней частотного уравнения) аь которые -находят по графикам (рис. 225, а, б) в зависимости от приведенной массы Шпр, а 1,ля консольных валов — также и от относительной длины пролета Ь = 1 1, где I — длина пролета между опорами вала 1 — длина консоли. [c.240]

Примечание. Допускается использование смесей пластичных смазок Литол-24 и АМ Карданная с трансмиссионными маслами (50%+50%) для шарниров равных угловых скоростей грузовых автомобилей. [c.25]

В качестве функции отклика обычно выбирают такой параметр, который имеет ясный физический смысл и легко определяется количественно. В ряде случаев функция отклика, как и входные факторы, может представлять собой безразмерный комплекс параметров. Так, при исследовании центробежно-вихревого измельчителя в качестве функции отклика можно выбрать степень измельчения или относительную мощность Л/отн Л /( ы срР), в качестве входных факторов — критерий Фруда, безразмерный комплекс, характеризующий степень загрузки измельчителя материалом (3/((и/ срр), относительный зазор между роторами п т. д. М — мош,ность измельчения, ш — угловая скорость, Q — производительность, 7 ,, — средний радиус верхнего и нижнего роторов, р — плотность материала). [c.18]

Напряжения изгиба, обусловленные действием центробежных сил инерции при вращении вала, можно найти, если известны положения центров масс дисков, закрепленных на валу. При заданной угловой скорости со вала, не совпадающей с критической, рассчитывают деформации у вала, например для вала с двумя дисками по выражениям (3.48)—(3.50), и силы инерции P по формулам, аналогичным [c. 77]

Рассмотрим движение диска, консольно закрепленного на валу (расчетная схема — см. рис. 3.11), последний вращается с угловой скоростью 03. В системе координат Хъ Ух, связанной с диском, моменты инерции массы диска относительно осей J= J 2 1 — = [c.78]

Из теоретической механики известно, что центробежная сила равна произведению массы на 1 вадрат угловой скорости и на радиус вращения [c.46]

Номинальная мощность и угловая скорость выходного вала п]1Ивода аппарата с мешалкой должны соответствовать значени-Я14, указанным в табл. 2.24. [c.108]

Сушилки и холодильники с диаметром барабана более 1200 мм допускается изготовлять с номинальной угловой скоростью 0,85 рал/с (табл. 3.16). Углы наклона барабанов сушилок и холо-дил ) 1иков составляют 1—4″, печей — 1—3°. Число опор у су)иилок две у печей и холодильников может быть две — четыре (в зависимости от длины барабана и его диаметра). [c.144]

Вращающийся дисковый электрод. Особенность вращающегося дискового. электрода (см. рис. 15.6), как это было показано рядом авторов, заключается в постоянстве толщины диффузионного слоя в любыз точках его поверхности, если только бдискового электрода, В то же время величина б является функцией угловой скорости вращения дискового электрода [c.313]

Валы машин, эксплуатируемые в докритической области (угловая скорость которых меньше частоты собственных колебаний), называются жесткими, а валы, эксплуатируемые в закритнческой области ((О > 01 )), — гибкими. Свойством самоцентрирования обладают 7- [c.74]

Центробежные пылеотделители той или иной формы встречаются обычно на многих предприятиях. В центробежных пылеосади-телях (циклонах) поток газа, содержащий пыль, движется с больщой скоростью, при этом угловая скорость твердых частиц достигает значительной величины, что приводит к увеличению центробежной силы. Характерная опасность центробежных пылеосадите-лей обусловлена тем, что в присутствии кислорода нельзя избежать образования зоны взрывоопасной концентрации пыли, так как осаждение твердых частиц сопровождается последовательным уплотнением среды в различных зонах циклона в зависимости от величины частиц. Кроме того, при высоких скоростях пыли в системе сухих центробежных аппаратов образуются большие заряды статического электричества, которые могут служить источником воспламенения горючей и взрывоопасной среды. [c.278]

Для данного насоса угловая скорость и радиус кривошипа — величины постоянные, а изменяется при работе насоса угол поворота кривошипа. Поэтому скорость поршня изменяется на протяжении двойного хода по закону синуса и графически может быть пред-ставл- па в виде синусоиды (рис. 54). [c.103]

Общее требование для всех конструкции центрифуг — хорошая урагшовешенность ротора и устойчивая работа вала. Нарушение устойчивой работы вала происходит в момент, когда угловая скорость вращення становится равной критической угловой скорости вращения, эквивалентной собственной круговой частоте вала. В этот момент наступает резонанс. [c.266]

В ряде случаев, особеипо для гибклх валов, в центрифугах применяют упругие опоры, назначение и сущность которых видны из следующего примера [31. Пусть вал (рис. 227) нагружен массами т, которые расположены с эксцентриситетом е относительно оси вращения. Тогда при вращении вала с некоторой угловой скоростью возникает центробежная сила тсо (е + //), которая изгибает вал и стремится увеличить иервоначальпый эксцентриситет на величину у. По мере приближения угловой скорости вала со к критической величина смещения масс возрастает и становится максимальной при со со р. Дальнейшее увеличение со приводит к тому, что из-за большей устойчивости движения вал займет такое положение, при котором центр масс т окажется на оси вращения, а сам вал будет вращаться около линии, соединяющей оиоры. При этом ирогиб 227. Схема работы ва.ла вала будет равен по величине п про- центрифуги [c.267]

Расчет критической угловой скорости вала центрифуги. Устойчивая работа вала нарушается при приближении его скорости к критической. При этом увеличивается прогиб вала. На рис. 232 приведена схема вала для наиболее типичного случая консольного закреилепия ротора центрифуги. Вал центрифуги совершает двойное вращательное движение. Кроме вращательного движения около собственной изогнутой оси, вал совершает вращательное [c.274]

Рабочая угловая скорость должна быть не более 0,7о)нр для аппаратов, работающих с системами жидкость — жидкость жи, кос1ь — твердое тело , а для систем жидкость — газ —не более 0,6сокр для всех типов мешалок, кроме лопастных, и 0,4о)ьр для лопастных мешалок. Для двухлопастной мешалки, кроме того, не допускается работа в интервале (0,454-0,55)о)кр. [c.241]

Мсследованиямп Б. Г. Холпна установлено, что вращающаяся совместно с перфорпроваппой оболочкой жидкость имеет малую угловую скорость, а для вытекающих из отверстий струй характерно интенсивное сжатие, возрастающее с увеличением частоты вращения. [c.115]

Энергия вращательного движешт е р является функцией угловой скорости ш и момента инерции J [см. уравнение (1,5)1 [c.18]

Характерная особенность рассматриваемой системы — вращение вала, изогнутого в плоскости действия силы инерции, вместе с этой плоскостью. Как следует из формулы (3.43), при угловой скорости вала, равной угловой частоте его собственных колебаний, прогиб вала стремится к бесконечности. Эта скорость называется критической. При угловой скорости вала, превышающей критическую (в закритнческой области), центр масс диска располагается между изогнутой осью вала и осью его вращения и при неограниченном увеличении угловой скорости диска стремится занять положение на оси вращения (рис. 3.19, б) при этом коэффициент и -> (—1). Это явление называется самоцентрированием вала деформация вала при этом уменьшается. [c.74]

Воздействие гироскоиического момента. При большой угловой скорости вала и значительном моменте инерции диска, закрепленного на валу, необходимо учитывать влияние гироскопического момента на критическую скорость вала. [c.78]

Что это — угловая скорость и как ее рассчитывают?

Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а угловая скорость. Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.

Угловая скорость: понятие и формула

Когда материальная точка движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности. Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:

w = φ / t, где:

φ – угол поворота радиуса,

t – период времени вращения.

Единицы измерения величины

В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с – основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):

w = 2π*n,

где n – частота вращения.

В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют правило буравчика, которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит поступательное движение винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.

Примеры расчета

Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:

w = φ / t = 7t / t = 7 с^-1.

Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t. Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π — один полный оборот, получается следующее:

v = 2π*r / t = w * r = 7 * 0. 5 = 3.5 м/с

Вот еще одна задачка на эту тему. Известно, что радиус Земли на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:

w = 2π*n = 2*3,14 *(1/(2 3600)) = 7,268 *10^-5 рад/с.

Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10^-5 *6370 * 1000 = 463 м/с.

Угловая скорость – обзор

3.9 Маховики с переменной инерцией

Необходимость изменения угловой скорости маховика в соответствии с «состоянием заряда» является одним из основных препятствий на пути более широкого использования маховиков. На самом деле, во многих приложениях было бы очень полезно поддерживать фиксированное значение скорости во время цикла зарядки-разрядки, в то время как в других случаях скорость маховика должна увеличиваться во время разрядки и уменьшаться при зарядке аккумулятора. Примером этого требования является применение в транспортных средствах, когда маховик заряжается во время торможения транспортного средства.Конечно, возможно, по крайней мере с теоретической точки зрения, добиться этого при условии, что момент инерции ротора изменяется в зависимости от скорости и состояния заряда.

Главное преимущество «маховиков с переменной инерцией», иногда называемых просто VIF, заключается в том, что они не требуют системы трансмиссии, допускающей бесступенчатое изменение передаточного числа. Этот тип маховика привлекал многих исследователей и изобретателей. Краткое изложение их усилий дано в [77–56].

Уравнение движения маховика переменной инерции можно записать в виде:

(3.244)M=ddt(Jω)=Jω˙+J˙ω

Изменение момента инерции маховика связано с определенной мощностью, положительной, т.е. подводимой к маховику для уменьшения его инерции и отрицательным, если его инерция увеличивается. Значение такой мощности P _i равно:

(3,245)Pi=−12J˙ω2

Энергия, необходимая для изменения момента инерции маховика, может подаваться непосредственно извне или может быть получена из рециркуляция мощности внутри маховика ( рис. 3.64 ).

Рисунок 3.64. Поток мощности в маховиках переменной инерции. P _i : мощность для изменения момента инерции; P _s : мощность на валу маховика; P _L : мощность, которой обменивается нагрузка

В случае Рис. (12Jω2)=12J˙ω2+Jωω˙

и мощность P _с на валу маховика:

(3.247)Ps=PL−Pi=J˙ω2+Jωω˙

Если угловая скорость маховика должна поддерживаться постоянной, абсолютное значение мощности P _i, необходимой для изменения инерции маховик равен мощности, извлекаемой из него:

(3,248)Pi=−PL=−12J˙ω2

и мощности P _s на валу маховика в два раза больше входной/выходной мощности :

(3,249)Ps=2PL=J˙ω2

Скорость изменения инерции маховика, необходимая для придания (или отнятия) фиксированной мощности, легко вычислить из уравнения (3.248).

Другим интересным случаем является маховик, используемый для ускорения инерционной нагрузки. Пусть J _L — момент инерции груза, приведенный к валу маховика. Уравнение равновесия системы:

(3,250)12J˙ω2+Jω˙ω=JLω˙ω

Закон J (ω) легко получить интегрированием:

(3,251)J=(ω0ω )2(J0−JL)−JL

где J ₀ — момент инерции маховика при его скорости ω ₀ .Тогда закон J ( t ) определяется требуемым законом ω( t ), или ускорение определяется законом J ( t ).

Из уравнений (3.245) и (3.251) мощность, необходимая для изменения инерции маховика, равна: P _i /P _L равно:

(3,253)PiPL=(ω0ω)2(J0+JLJL)=J+JLJ0+JL

Поскольку момент инерции уменьшается при ускорении, следует, что значение P _i /P _L меньше единицы, но мощность, необходимая для изменения инерции, остается того же порядка, что и подводимая к нагрузке.В начале разгона они равны.

Закон J (ω) для маховика с переменной инерцией можно изобразить на графике, показанном на рис. 3.65 . Полные линии — изоэнергетические линии; если закон J (ω) находится на одной из этих линий, энергия не извлекается из ротора. Все линии, которые пересекают изоэнергетические линии, связаны с входом или выходом энергии. Некоторые возможные законы J (ω) нанесены на этот же рисунок.

Рисунок 3.65. Момент инерции маховика переменной инерции в зависимости от скорости.

– – – Маховик неподвижный инерционный

– . – . – Маховик с постоянной скоростью

——— Маховик, ускоряющий инерционную нагрузку

Были предложены различные схемы конструкции маховиков с переменной инерцией, и во многих из них используются маховики, заполненные жидкостью. Это решение, которое на первый взгляд кажется весьма привлекательным, однако оно имеет серьезные недостатки, делающие его малоценным с практической точки зрения.

В первую очередь следует ожидать серьезных динамических проблем. Очень большая центробежная сила, действующая на жидкость, делает необходимым использование очень толстого вращающегося сосуда; следовательно, максимальное соотношение между инерцией заполненного и пустого роторов ограничено. Перекачка жидкости к ротору и от него имеет решающее значение; любое изменение количества движения жидкости, если оно не выполнено должным образом, приводит к диссипативным действиям. Насосы и гидромоторы, необходимые для подачи и отвода жидкости, должны иметь мощность того же порядка, что и выходная мощность.Использование гидравлической системы в качестве трансмиссии с переменным передаточным числом с фиксированным инерционным маховиком, вероятно, решит проблему более простым, эффективным и экономичным способом.

Основные концепции некоторых других решений показаны на Рисунок 3.66 . Все эти решения приводят к плотности энергии, которая по своей природе ниже, чем у обычных маховиков, особенно если сравнивать только роторы.

Рисунок 3.66. Некоторые предлагаемые маховики с переменной инерцией, (a) и (b) жесткий элемент, (c) и (d) гибкие провода или волокна; (e) Гибкая лента.

(Ullman, D.G. et al. . [80–72])

Роторы с переменной инерцией можно рассматривать только в том случае, если взаимодействие с нагрузкой позволяет снизить вес или стоимость.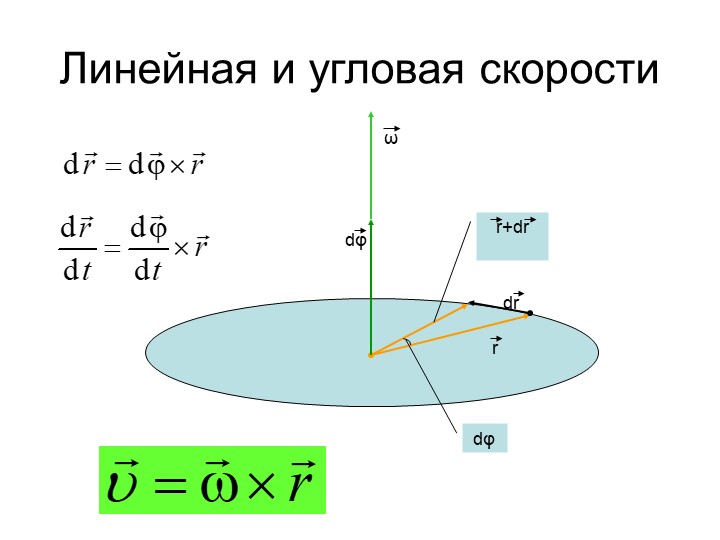 Распространено мнение, что этого можно добиться только за счет гибкости системы путем фиксации определенного закона J (ω).

Выходной крутящий момент снова является функцией углового ускорения, но эта функция отличается от функции, характеризующей ротор с фиксированной инерцией.

Если внутренняя ступица, наружный кожух и нагрузка маховика переменной инерции со спиральной лентой (рис. 3.66( e )) связаны, например, через планетарную передачу, рециркуляция мощности, необходимая для изменения инерции, может быть получена с очень высокой эффективностью, и система довольно проста, по крайней мере, с концептуальной точки зрения. . Уравнения, описывающие поведение ротора такого типа, разработаны в [80–72]. Динамика ускорения фиксированной нагрузки показана на рис. 3.67 .

Рисунок 3.67. История изменения инерции ленточного маховика во времени (рис. 3.66д), ускоряющий фиксированную инерционную нагрузку. Скорости, моменты инерции и моменты как функции времени. Груз находится в состоянии покоя до t = 1 с, затем включается сцепление и проскальзывает до t = 2 с. С этого момента нагрузка напрямую связана с планетарной передачей, к которой также подключен внешний кожух маховика.

(Ullman, D.G. et al. . [80–72])
Маховики с переменной инерцией, возможно, в этой простой версии, в которой поведение определяется фиксированными параметрами, возможны для некоторых приложений, особенно для машин с фиксированным рабочим циклом.Однако они не являются абсолютным решением проблем сопряжения маховик-нагрузка, поскольку для них требуются те же устройства регулирования мощности и контроля скорости, что и для маховиков с фиксированной инерцией.
Границы | Анализ угловой скорости, момента и мощности голеностопных, коленных и тазобедренных суставов при спасении вратаря в прыжке в воду в футболе
Введение
Вратари в футболе играют наиболее специализированную роль в своей команде. Их действия требуют своевременной и резкой корректировки скорости тела, положения и ориентации в ответ на раздражитель. Одна из их наиболее важных задач — защита ворот во время штрафного броска, который обычно выполняется как сейв в прыжке. Спасение в прыжке можно отнести к категории защитного прыжкового навыка, основной целью которого является движение тела в воздухе посредством взрывного отталкивания, достижение и отклонение траектории мяча. Отталкивание, которое присутствует в этих навыках, является обычным паттерном, встречающимся в прыжковых движениях. Предыдущие биомеханические исследования, в которых наблюдались прыжковые движения, показали, что отталкивание должно выполняться в проксимально-дистальной последовательности (Bobbert and van Ingen Schenau, 1988; Pandy and Zajac, 1991; Chiu et al., 2014). Было обнаружено, что движение начинается с тазобедренного сустава, затем переходит в коленный и, наконец, в голеностопный сустав. Тем не менее, в этих исследованиях рассматривались прыжковые задачи, выполняемые посредством одновременных отталкиваний обеих ног, которые нельзя прямо вывести и распространить на последовательные отталкивания, наблюдаемые при спасении вратаря в прыжке в воду (Suzuki et al. , 1987; Spratford et al., 2009; Ибрагим и др., 2019а). Вратарь обычно выполняет спасбросок в прыжке, сначала отталкиваясь контралатеральной ногой, а затем ипсилатеральной ногой, что отличается от вертикального прыжка, когда обе ноги отталкиваются одновременно без какой-либо значительной временной задержки между ними (Ibrahim et al., 2019а).
Практика тренировки вратарей, будь то тренеры по технике или силовой и кондиционной подготовке (S&C), в настоящее время основана на исследованиях вертикальных прыжков и качественных наблюдениях за прыжками в воду, а не на количественных описательных исследованиях. Насколько нам известно, исследование Ibrahim et al. (2019a) был первым, кто устранил этот пробел, проведя полный кинематический и кинетический анализ отталкивания во время ныряния и обнаружив, что вклад контралатерального отталкивания в скорость центра масс (ЦМ) был больше. чем ипсилатеральное отталкивание.Кроме того, было рекомендовано, чтобы тренировка горизонтального бокового движения была более специфичной для выполнения спасбросков при нырянии, поскольку было обнаружено, что горизонтальный линейный импульс больше, чем вертикальный. Тем не менее, для разработки рекомендаций по обучению вратарей по-прежнему требуется более подробная информация о механике прыжка. Мощность суставов нижней части тела, определяемая как произведение моментов в суставах на угловые скорости в суставах, многие считают важным фактором, определяющим результаты в видах спорта, требующих тройного разгибания, то есть разгибания бедер, коленей и лодыжек (Newton and Kramer, 1994; Zink). и другие., 2006; Хори и др., 2007, 2008). Кроме того, оптимальная тренировка для развития силы нижней части тела должна соответствовать принципу специфичности, что означает, что для максимальной передачи выбранные упражнения должны демонстрировать сходство с самой задачей в таких аспектах, как задействованная мускулатура, схема движения, скорость движения и т. д. и диапазон движений (Sheppard et al., 2016). Таким образом, целью данного исследования было определение биомеханических характеристик действий вратаря во время высоких и низких непредвиденных сейвов в прыжках в воду. В частности, мы сравнили время и величину моментов, угловые скорости и силы в голеностопном, коленном и тазобедренном суставах между высоким и низким, а также левым и правым нырянием. Кроме того, в этом исследовании мы стремились улучшить экспериментальную установку по сравнению с предыдущими исследованиями, изучив спасение от ныряния в более реалистичной установке, где шары выстреливались из изготовленной на заказ пушки вместо того, чтобы подвешивать их в стационарное положение.
Основываясь на эмпирических данных предыдущих исследований паттерна координации при вертикальном прыжке, мы сначала предположили, что вратари генерируют силу суставов во время отталкивания каждой ногой в проксимально-дистальной последовательности.Во-вторых, поскольку предыдущее исследование показало, что контралатеральная нога вносит больший вклад, чем ипсилатеральная нога, в общую скорость ЦМ (Ibrahim et al., 2019a), мы предположили, что общая мощность контралатеральной ноги больше, чем у ипсилатеральной ноги. В-третьих, из-за основного характера спасброска в прыжке во фронтальной плоскости мы предположили, что отведение/приведение бедра будет самым большим фактором, влияющим на эффективность спасброска в прыжке с точки зрения пикового момента и мощности.
Материалы и методы
Семь элитных футбольных вратарей, средний возраст ± стандартное отклонение 18 лет.В исследовании принимали участие дети в возрасте 9 ± 3 лет, масса тела 84,9 ± 8,1 кг, рост 186,5 ± 2,1 см, доминирующая нога, определенная как стреляющая 6 правых и 1 левая. Уровень участников во время эксперимента был следующим: два вратаря соревновались в голландской Eredivisie (самый высокий уровень соревнований на национальном уровне), три вратаря — в голландском Eerste Divisie (второй самый высокий уровень соревнований на национальном уровне) и два вратаря в голландской Eredivisie до 17 лет (самый высокий уровень соревнований на национальном уровне для игроков младше 17 лет).Перед проведением эксперимента участники или их родители подписывали форму информированного согласия. Для каждого участника были собраны антропометрические данные, возраст и история травм. Участники не пострадали от каких-либо травм, которые помешали бы им выполнить спасбросок в прыжке с максимальной силой или заставили бы их изменить свою модель движения во время эксперимента. Эксперименты проводились в Adidas miCoach Performance Center футбольного клуба «Аякс». Комитет по этике факультета поведенческих и двигательных наук Амстердамского свободного университета одобрил протокол исследования.
Сбор данных и предварительная обработка
Перед началом измерения участники выполнили специальную программу разминки вратарей со своими тренерами и сделали около 8 спасбросков в прыжках в воду, чтобы ознакомиться с экспериментальной установкой. Затем каждому участнику было приказано среагировать и нырнуть как можно быстрее, чтобы спасти мяч, выпущенный из пушки. Для каждого участника было измерено два успешных прыжка на две высоты (высокая и низкая) по обе стороны от ворот, всего 8 успешных прыжков на участника с 2-минутным временем восстановления между прыжками. Прыжок считался успешным, когда вратарь нырнул и спас мяч, либо ударив его, либо схватив. Порядок погружений был случайным для каждого субъекта.
Шаровая пушка была размещена на одиннадцатиметровой отметке, а передняя часть была закрыта очень легким полосатым занавесом, чтобы предотвратить любое упреждение высоты и борта мяча. Канон мяча калибровался по четырем углам ворот (верхний и нижний углы справа и слева от ворот) перед каждым испытуемым и не смещался в течение всего измерения (рис. 1).Установленная скорость мяча была рассчитана таким образом, чтобы мяч достиг цели за 1,2 ± 0,1 с, в соответствии с результатами недавнего исследования общего времени погружения (время реакции + время движения при погружении), проведенного Ibrahim et al. (2019а). Во время калибровки канона мяча мы нацеливали мяч на положение, аналогичное предыдущему исследованию Ibrahim et al. (2019a), ~70 см медиально от боковой стойки и ~30 см в высоту для низких мячей и ~190 см в высоту для высоких мячей от уровня силовых пластин. Вариабельность конечного положения мяча (при контакте с мячом) оказалась относительно небольшой, со средней стандартной ошибкой ±7 см по горизонтали и ±6 см по вертикали.Поэтому было установлено, что он подходит и надежен для наших анализов, которые не предполагают сравнения времени погружения.
Рисунок 1 . Две принципиальные схемы экспериментальной установки (вид спереди и сверху). Также представлены предполагаемые положения высоких и низких шаров.
Система анализа движения пассивных маркеров (Vicon 612, Оксфорд, Великобритания), состоящая из 10 инфракрасных камер, использовалась для захвата данных 3D-координат 44 маркеров с частотой 200 Гц. Маркеры прикреплялись к разным сегментам тела в виде кластеров (стопы, голени, таз, грудная клетка, голова и предплечья), бедра моделировались между голенью и тазом, а плечи моделировались между грудной клеткой и предплечьями, в для получения модели в полный рост без перекрытия маркеров во время испытаний и ограничения риска приземления на маркеры. Маркеры были прикреплены в виде хорошо узнаваемого рисунка для облегчения маркировки с помощью программного обеспечения Vicon Nexus (версия 1.8.5). Мягкие маркеры использовались на участках, подверженных ударам при приземлении. Анатомические системы координат сегментов отмечались одиночными маркерами и относились к соответствующим кластерам маркеров при измерении в референтном положении (Т-поза). Детали трехмерной модели обратной динамики, которая использовалась в этом исследовании, можно найти в другом месте (Kingma et al., 1996; Faber et al., 2011, 2013; Ибрагим и др., 2016).
Два изготовленных на заказ тензодатчика, 1 × 1 м, силовые пластины (Vrije Universiteit Amsterdam, Амстердам, Нидерланды) использовались для измерения сил реакции опоры (GRF), создаваемых каждой ногой отдельно с частотой 1000 Гц. Каждая силовая пластина была отдельно покрыта искусственной футбольной травой, чтобы предотвратить передачу силы между силовыми пластинами. Рядом с каждой силовой пластиной был помещен матрас, чтобы пол был на одном уровне с силовыми пластинами, а также чтобы вратарь и маркер были в безопасности при каждом приземлении. Две видеокамеры Basler (50 Гц) использовались для записи всех попыток во фронтальной плоскости для визуальной проверки и обнаружения контакта с мячом.
Анализ данных
Все кинематические и кинетические анализы проводились с использованием специального программного обеспечения в MATLAB (R2015b, MathWorks Inc., США). Для сглаживания кинематических сигналов использовался двунаправленный фильтр нижних частот Баттерворта второго порядка с частотой среза 12 Гц. Оптимальная частота отсечки оценивалась по кинематическим данным с использованием уравнения, разработанного Yu et al.(1999). Временные переменные были определены относительно начала погружения, которое было обнаружено с использованием алгоритма, основанного на аппроксимированном обобщенном отношении правдоподобия (AGLR) (Staude and Wolf, 1999). AGLR ранее успешно применялся для обнаружения начала пикирования к висящим шарам (Ibrahim et al., 2019a,b). Он работает путем (1) определения времени срабатывания сигнализации (момент времени, когда сигнал достигает предварительно установленного порога) с использованием скользящего тестового окна, а затем (2) отслеживания сигнала в обратном направлении для определения времени начального изменения с использованием методов максимального правдоподобия (плохой , 1988). Мы использовали порог, равный 20% массы тела вратаря, и три различных входных сигнала [т. е. общую горизонтальную GRF, общую вертикальную GRF и вертикальную GRF контралатеральной ноги (ноги, противоположной ныряющей стороне)]. Начало погружения определяли как среднее двух из трех начал, имеющих наименьшую взаимную разницу.
Моменты контралатеральной (CPF) и ипсилатеральной пиковой силы (IPF) определялись как моменты, когда контралатеральная и ипсилатеральная ноги прикладывали свои максимальные результирующие GRF соответственно.Взлет определялся как момент, когда вертикальная составляющая GRF, суммированная по ногам, падала ниже 10 % веса тела и касания мяча в качестве первого кадра, когда имел место контакт между мячом и вратарем, что было определено по высокоскоростному камеры.
Угловые скорости суставов нижней части тела (тазобедренных, коленных и голеностопных) рассчитывали, сначала выражая матрицу вращения дистального сегмента относительно проксимального, а затем используя уравнение Берме и Каппоццо (1990). Положения центров масс и моменты инерции оценивались по Зациорскому (2002). Кинематика сегментов тела использовалась вместе с GRF для расчета моментов в лодыжках, коленях и бедрах в восходящей динамической модели связанных сегментов (Kingma et al., 1996). Чтобы получить трехмерные компоненты чистых моментов, моменты лодыжки были спроецированы на систему координат стопы (CS), моменты колена были спроецированы на CS голени, а моменты бедра были спроецированы на CS бедра.Сила бедра, колена и лодыжки рассчитывалась путем скалярного умножения угловой скорости и момента соответствующего сустава. После этого общая мощность на ногу была рассчитана путем суммирования мощности по трем суставам для каждой ноги.
Углы тазобедренного сустава были определены как углы Эйлера между бедром и тазом в анатомической системе координат. Последовательность вращения была следующей: сгибание-разгибание, внешнее-внутреннее вращение и отведение-приведение (Wu et al., 2002).
Статистический анализ
Все временные ряды были нормализованы по времени (NT) от начала обнаруженного движения до взлета. Все данные представлены как среднее ± стандартное отклонение. Время и величина пиковой мощности суставов, а также величина пикового чистого момента суставов и пиковой угловой скорости суставов сравнивались между плоскостями движения суставов, между высотами погружения (высокой и низкой) и сторонами (правой и левой) с трехсторонним движением. повторные измерения ANOVA. Плоскость движения сустава представляла собой фактор из 8 уровней: контралатеральное сгибание-разгибание бедра, ипсилатеральное сгибание-разгибание бедра, контралатеральное приведение-отведение бедра, ипсилатеральное приведение-отведение бедра, контралатеральное сгибание-разгибание в колене, ипсилатеральное сгибание-разгибание в колене, контралатеральное сгибание в голеностопном суставе. разгибание, ипсилатеральное сгибание-разгибание голеностопного сустава.Если результаты трехфакторного дисперсионного анализа показывали значительный основной эффект для плоскости движения сустава, использовались попарные сравнения, чтобы определить, между какими конкретными суставами время пиковой мощности значительно отличалось от близлежащего пика в другом суставе.
Величина пиковой мощности на ногу усреднялась по стороне погружения и сравнивалась между ногами (контралатеральной и ипсилатеральной), высотой погружения (высокой и низкой) с двусторонними повторными измерениями ANOVA.
Уровень значимости был установлен на уровне p < 0.05, и сообщалось о частичном эта-квадрате меры размера эффекта (0,01 малый, 0,06 средний, 0,14 большой). Все статистические анализы проводились с использованием IBM SPSS Statistics 20.
.
Результаты
Вратари выполняли высокие и низкие прыжки, используя схожие схемы движений в отталкивании. Они начинали ныряние, шагая сбоку ипсилатеральной ногой по направлению к цели, отталкиваясь контралатеральной ногой и, наконец, отталкиваясь ипсилатеральной ногой.
На рисунках 2, 3 показаны временные ряды сил, моментов и угловых скоростей суставов нижней части тела от начала пикирования до отрыва при высоком и низком пикировании соответственно.Контралатеральное отталкивание длилось от 16 до 75% NT при высоких ныряниях и от 23 до 83% NT при низких ныряниях. Принимая во внимание, что ипсилатеральное отталкивание длилось от 52 до 100% NT при высоких ныряниях и от 53 до 100% NT при низких ныряниях.
Рисунок 2 . Временные ряды, усредненные по субъектам, для силы суставов 90 203 (A–D) 90 204, моментов в суставах 90 203 (E–H) 90 204 и угловых скоростей суставов 90 203 (I–L) 90 204 вратарей, ныряющих, чтобы спасти высокие мячи. Сплошные линии соответствуют контралатеральной ножке, а пунктирные линии — ипсилатеральной ножке.Ось X всех подграфиков представляет собой нормализованное время, выраженное в [%]. Названия (A–D) суставов указывают плоскость движения сустава, а не направление вращения сустава. Знак мощностей суставов отражает выработку (+) и поглощение (-) мощности.
Рисунок 3 . Временные ряды, усредненные по субъектам, для силы суставов 90 203 (A–D) 90 204, моментов суставов 90 203 (E–H) 90 204 и угловых скоростей суставов 90 203 (I–L) 90 204 вратарей, ныряющих, чтобы спасти низкие мячи. Сплошные линии соответствуют контралатеральной ножке, а пунктирные линии — ипсилатеральной ножке. Ось X всех подграфиков представляет собой нормализованное время, выраженное в [%]. Названия (A–D) суставов указывают плоскость движения сустава, а не направление вращения сустава. Знак мощностей суставов отражает выработку (+) и поглощение (–) мощности.
Повторные измерения ANOVA для величины пиковой мощности сустава показали основной эффект для плоскости движения сустава ( p < 0.001, размер большого эффекта = 0,78) и для высоты погружения ( p < 0,01, размер большого эффекта = 0,92), без влияния на сторону погружения. Кроме того, повторные измерения ANOVA для величины пиковых моментов суставов показали основной эффект для плоскости движения сустава ( p < 0,001, большая величина эффекта = 0,84) и для высоты погружения ( p < 0,05, большая величина эффекта = 0,79), при этом нет эффекта для стороны погружения. Кроме того, повторные измерения ANOVA для величины пиковых угловых скоростей суставов показали основной эффект для плоскости движения сустава ( p <0. 001, большой размер эффекта = 0,95), без влияния на сторону погружения и высоту. Сила сгибания-разгибания противоположного бедра была вызвана большим моментом разгибания бедра, который был самым большим суставным моментом из всех ( p <0,05). Однако ипсилатеральная сила сгибания-разгибания бедра характеризовалась большой площадью под кривой, от 63 до 86% NT. Это было вызвано ипсилатеральным моментом разгибания бедра, который был вторым по величине пиком из всех ( p <0,05). Пиковая мощность ипсилатерального дорси-подошвенного сгибания голеностопного сустава была значительно выше, чем сила всех других проанализированных суставов.Это было вызвано четвертым по величине моментом в суставе (момент подошвенного сгибания ипсилатеральной лодыжки), а третьим по величине также было подошвенное сгибание, но контралатеральной лодыжки ( p <0,05). Что касается пиковой мощности на ногу (ипсилатеральная по сравнению с контралатеральной ногой), наблюдалось значительное взаимодействие между высотой ныряния и стороной ноги (90 227 p 90 228 < 0,05). Во время высоких погружений пиковая мощность, генерируемая ипсилатеральной ногой (2294 ± 273 Вт), была значительно выше ( p < 0.05), чем контралатеральная нога (1846 ± 292 Вт). Однако существенной разницы между пиковыми мощностями, генерируемыми ипсилатеральной (1 536 ± 291 Вт) и контралатеральной (1 643 ± 326 Вт) ногами во время низких погружений, не было.
Повторные измерения ANOVA показали значительное влияние плоскости движения сустава на время пиковой мощности ( p <0,001, большая величина эффекта = 0,88), без значительного влияния на сторону или высоту погружения. Во многом в соответствии с гипотетической проксимально-дистальной последовательностью парные сравнения показали, что последовательность пиковой мощности суставов нижних конечностей состояла из 5 основных событий (таблица 1, рис. 4): (1) пиковая мощность контралатерального сгибания-разгибания бедра, (2) пиковая сила сгибания-разгибания контралатерального колена, пиковая сила контралатерального дорси-подошвенного сгибания лодыжки, пиковая сила отведения-приведения контралатерального бедра, (3) пиковая сила сгибания-разгибания бедра на ипсилатеральной стороне и мощность отведения-приведения, (4) пиковая сила ипсилатерального сгибания колена- мощность разгибания и (5) пиковая мощность дорси-подошвенного сгибания ипсилатеральной лодыжки. Время каждого номера события (1–5) значительно отличалось от времени предыдущего и следующего номера события.
Таблица 1 . Время и величины пиковой мощности соединения, а также основные величины пикового суммарного момента соединения и угловой скорости, а также статистические результаты трехфакторных повторных измерений ANOVA.
Рисунок 4 . Время пиковой мощности суставов, усредненное по субъектам, стороне и высоте, выраженное в процентах от общего времени от начала погружения до взлета.Также представлена стандартная ошибка. Стержни сгруппированы, и сила каждого сустава группы значительно отличается от силы других суставов других групп.
Для первого упражнения попарные сравнения (Таблица 1) показали, что пиковая мощность тазобедренного сустава в сагиттальной плоскости, момент разгибания бедра и угловая скорость были выше при прыжках в высоту, чем при прыжках в воду ( p < 0,05). Контралатеральное бедро создавало также больший момент разгибания, чем ипсилатеральное бедро ( p < 0. 05), тогда как угловая скорость ипсилатерального разгибания бедра была больше, чем контралатеральная ( p < 0,05). Во время этой первой фазы мы также рассчитали углы отведения-приведения бедра и поворота внутрь-наружу в момент максимальной мощности тазобедренного сустава, чтобы посмотреть на ориентацию вратаря. Мы обнаружили, что эти углы были почти нулевыми, что указывает на нейтральное положение во фронтальной и поперечной плоскости.
Результат, аналогичный первому событию, был также получен для второго и четвертого события, поскольку контралатеральное колено создавало больший момент разгибания ( p < 0.05) и меньшей угловой скоростью разгибания ( p <0,05), чем ипсилатеральное колено. Ипсилатеральная сила голеностопного сустава в сагиттальной плоскости (пятое событие) была значительно выше ( p < 0,05), чем контралатеральная (во втором событии), и то же самое было очевидно для результирующей пиковой угловой скорости подошвенного сгибания голеностопного сустава ( p < 0,05). Наконец, при высоких ныряниях пиковая сила голеностопного сустава в сагиттальной плоскости и момент подошвенного сгибания были больше, чем при низких ныряниях ( p < 0.05).
Обсуждение
Настоящее исследование было первой попыткой анализа биомеханики броска вратаря в прыжке в воду в футболе с максимально реалистичным моделированием броска с пенальти. В соответствии с нашей первой гипотезой, как контралатеральные, так и ипсилатеральные ноги следовали примерно в проксимально-дистальной последовательности пиковой мощности суставов. Это согласуется с выводами Chiu et al. (2014), анализируя координацию нижних конечностей в задаче вертикального прыжка. Они обнаружили, что проксимально-дистальная последовательность позволяет спортсмену генерировать больший суммарный момент суставных разгибателей бедра, коленного разгибателя и подошвенного сгибателя лодыжки, что приводит к большему угловому ускорению и линейному ускорению таза.Было также высказано предположение, что, если суммарные моменты разгибателей бедра и колена возникают одновременно, это может привести к совместному сокращению антагонистов в колене, что приводит к более медленным угловым ускорениям суставов и более медленным линейным ускорениям таза. Проанализировав последовательность пиковых усилий в суставах, мы определили пять основных событий в ныряющем спасении (таблица 1, рисунок 4): (1) пиковая мощность контралатерального сгибания-разгибания бедра, (2) пиковая контралатеральная мощность сгибания-разгибания колена, пиковая контралатеральная мощность сгибания-разгибания колена, мощность дорси-подошвенного сгибания голеностопного сустава, пиковая мощность отведения-приведения бедра на противоположной стороне, (3) пиковая мощность ипсилатерального сгибания-разгибания бедра и мощность отведения-приведения, (4) пиковая мощность ипсилатерального сгибания-разгибания колена и (5) пиковая мощность ипсилатерального голеностопного сустава сила тыльно-подошвенного сгибания.Время пяти идентифицированных событий пиковой мощности суставов значительно отличалось друг от друга, однако во время второго события несколько суставов достигли своих пиков последовательно, но без существенной разницы во времени. Кроме того, пик силы отведения-приведения контралатерального бедра (2. c; таблица 1) неожиданно оказался последним пиком для контралатеральной ноги и единственным вращением сустава, в котором не соблюдается последовательность проксимально-дистальный. Отведение/приведение контралатерального бедра может быть необходимо для переноса веса тела с противоположной ноги на ипсилатеральную (шаг в сторону), вместо того, чтобы способствовать фактическому отталкиванию, учитывая также, что его суммарный момент в суставе был самым низким по сравнению с другими суставами.Кроме того, относительно большое стандартное отклонение пиковой силы отведения-приведения бедра и других пиковых способностей суставов может отражать индивидуальные технические различия у вратарей элитного уровня.
Анализ пиковой мощности на ногу показал, что не было существенной разницы между ногами при нырянии с целью сохранения лоу-мячей. Напротив, пиковая мощность на ипсилатеральной стороне была больше, чем на контралатеральной, когда ныряли, чтобы сохранить высокие мячи. Это противоречит нашей второй гипотезе, основанной на выводах Ibrahim et al. (2019а). Тем не менее, общая мощность на ногу и мощность в суставах были каким-то образом вводящими в заблуждение переменными, учитывая тот факт, что спасбросок в прыжке характеризуется последовательными отталкиваниями, то есть сначала контралатеральной, а затем ипсилатеральной ногой, что контрастирует с одновременным отталкиванием. например, в вертикальном прыжке. Роль ипсилатеральной и контралатеральной ног можно лучше понять, если рассмотреть компоненты совместной силы по отдельности, то есть моменты в суставах и угловые скорости, в таблице 1.Противоположная нога начинала ныряние с отталкивания, инициируемого моментом разгибания бедра, а затем моментом разгибания колена, оба пиковых суставных момента были значительно больше, чем ипсилатеральные, во время высоких и низких прыжков ( p < 0,05). Кроме того, контралатеральный момент аддукции бедра и момент подошвенного сгибания голеностопного сустава в основном были незначительно больше или в некоторых случаях равны, но никогда не меньше, чем ипсилатеральные (таблица 1). Таким образом, в соответствии с выводами Ibrahim et al.(2019a), суставы контралатеральной ноги создавали больший момент, чем ипсилатеральные, особенно для момента разгибания тазобедренного сустава, который в этом исследовании оказался основным фактором, влияющим на эффективность ныряния. Кроме того, большая мощность ипсилатеральной ноги была обусловлена большей угловой скоростью сустава, достигаемой в ипсилатеральной ноге (таблица 1), и особенно в дистальных суставах (т. е. в ипсилатеральной лодыжке). На основе принципа кинетической связи линейная скорость проксимального конца в модели связанного сегмента (т.э., сегмент таза в этом исследовании) может внести положительный вклад и повысить угловую скорость каждого последующего сустава, полученную в этой модели (Putnam, 1993). Противоположная нога начала нырять и начала отталкиваться из статического положения, то есть без начальной линейной скорости таза, чего не было в случае с ипсилатеральной ногой. Ипсилатеральная нога начинала отталкиваться, после чего таз развивал положительную линейную скорость к цели за счет контралатерального отталкивания. Это могло привести к увеличению угловой скорости и силы суставов ипсилатеральной ноги без необходимости высокой мышечной активации и суставных моментов (Putnam, 1993).
Большой чистый момент разгибания тазобедренного сустава указывает на важность тренировки мышц-разгибателей тазобедренного сустава во время отталкивания в соответствии с предыдущим исследованием прыжков в длину и вертикально с места (Robertson and Fleming, 1987). В то время как моменты разгибания колена и отведения/приведения бедра были самыми низкими, что говорит о том, что они не являются основными факторами, влияющими на эффективность ныряния. Это противоречит нашей третьей гипотезе, которая была основана на обнаружении того, что горизонтальная составляющая силы отталкивания была больше, чем вертикальная составляющая (Ibrahim et al., 2019а). Тем не менее, в текущем исследовании мы показали, что эта горизонтальная скорость СОМ в основном создавалась разгибателями бедра и подошвенными сгибателями голеностопного сустава, а не мышцами приведения/отвода бедра, что было возможно, поскольку тело было наклонено вбок в сторону ныряющего.
В предыдущей работе с вратарями с более низкими уровнями производительности было обнаружено, что вратари ныряют к высоким мячам, сначала делая два перекрестных шага в сторону мяча (Graham-Smith et al., 1999). Напротив, в текущем исследовании мы обнаружили, что элитные вратари не делали перекрестных шагов перед отталкиванием во время высоких прыжков.Они начинали ныряние, шагая сбоку ипсилатеральной ногой по направлению к цели, отталкиваясь контралатеральной ногой и, наконец, отталкиваясь ипсилатеральной ногой. Как и в нашем предыдущем исследовании с подвешенными шарами (Ibrahim et al., 2019a), мы не обнаружили значительного влияния стороны погружения ни на одну из проанализированных переменных (таблица 1). Последнее противоречит результатам другого предыдущего исследования, в котором мячи висели на высокой штанге над линией ворот (Spratford et al., 2009).Одним из ограничений текущего исследования было использование матрасов на площадке приземления по обеим сторонам ворот. Тем не менее, матрацы были необходимы, чтобы выровнять пол с силовыми пластинами, и они использовались для обеспечения безопасности вратаря и маркера при каждом приземлении. Также считалось, что наличие матрасов не повлияет на производительность или схему сохранения при нырянии, вместо этого это позволит вратарю комфортно нырять, не беспокоясь о приземлении и настройке маркера.
В предыдущем исследовании с висящими мячами вместо канона с мячом мы предложили тренерам S&C и техническим тренерам подчеркивать горизонтальные боковые навыки с обеих сторон тела с акцентом на отталкивание контралатеральной ногой (Ibrahim и др., 2019а). Частично это было основано на обнаружении того, что при спасении от ныряния имеется сильный вклад контралатеральной ноги в общую скорость ЦМ и большой горизонтальный линейный импульс. В текущем исследовании мы обнаружили, что основными вращениями суставов, анализируя моменты и силы суставов, являются в основном разгибатели бедра и подошвенные сгибатели голеностопного сустава.Хотя это первоначально кажется противоречащим вышеупомянутому сосредоточению внимания на боковых навыках, следует подчеркнуть, что асимметрия силы сгибания-разгибания ипси- и контралатеральной ноги может привести к большим боковым движениям. Анализ угла отведения/приведения бедра и угла наружной/внутренней ротации бедра в момент максимальной силы разгибания бедра показал, что такая близкая к косой ориентация тела не создается крупными суставными движениями во фронтальной или поперечной плоскостях. Вместо этого он может быть создан полным угловым моментом тела от контралатерального отталкивания и ипсилатерального шага в сторону.
Поэтому вратарям рекомендуется тесно сотрудничать с квалифицированными тренерами по силовой подготовке для развития силы, полагаясь на кинетические результаты текущего исследования в сочетании с кинематическими результатами и рекомендациями нашего предыдущего исследования (Ibrahim et al., 2019a). Силовые упражнения, начинающиеся с разгибания бедра и сопровождаемые разгибанием коленного и голеностопного суставов в проксимально-дистальном направлении (например, силовой толчок и толчок в висе, силовой рывок и силовой рывок в висе, толчок толчком) должны быть включены в тренировка вратаря (Baumann et al. , 1988; Гархаммер, 1993; Гургулис и др., 2000; Чиу и Шиллинг, 2005 г.; Триколи и др., 2005; Кипп и др., 2011). Кроме того, паттерны боковых движений во фронтальной плоскости, приводимые в действие разгибанием бедра противоположной ноги (например, боковые отталкивания, боковые тяги салазок, асимметричные боковые приседания), соответствуют принципу специфичности и могут обеспечить максимальную передачу от тренировок в тренажерном зале. к фактической полевой производительности Sheppard et al., 2016. Будущие интервенционные исследования могут проверить влияние вышеуказанных рекомендаций по обучению наряду с рекомендациями из нашего предыдущего исследования (Ibrahim et al., 2019a), на время прыжка вратаря.
В заключение, вратари выполняют спасбросок в прыжке с использованием последовательности проксимально-дистальных движений на максимальной мощности суставов нижних конечностей. Движение разгибания тазобедренного сустава, особенно контралатеральное разгибание тазобедренного сустава, создавало самый большой пиковый суммарный момент в суставе во время погружения. В целом, суммарные суставные моменты в контралатеральной ноге достигали больших пиков, чем в ипсилатеральной, почти во всех основных суставных движениях. Однако угловые скорости в суставах ипсилатеральной ноги были больше, чем у контралатеральной, что приводило к большей пиковой общей мощности для ипсилатеральной ноги во время высоких прыжков и к таким же пиковым значениям во время низких прыжков.Эти данные могут быть использованы для улучшения рекомендаций по технической и силовой подготовке вратарей.
Заявление о доступности данных
Наборы данных, проанализированные в этой статье, не являются общедоступными, поскольку соответствующие футбольные клубы не давали разрешения на обмен данными. Запросы на доступ к наборам данных следует направлять Рони Ибрагиму, [email protected].
Заявление об этике
Исследования с участием людей были рассмотрены и одобрены Комитетом по этике факультета поведенческих и двигательных наук Свободного университета Амстердама. Письменное информированное согласие на участие в этом исследовании было предоставлено законным опекуном/ближайшим родственником участников.
Вклад авторов
RI участвовал во всем исследовании (обзор литературы, дизайн исследования, экспериментальная установка, измерения, обработка данных, анализ данных и написание рукописи). IK участвовал в разработке дизайна исследования, экспериментальной установки, анализа данных и написании рукописи. В.Б. участвовал в планировании исследования, экспериментальной установке и обработке данных.GF внес свой вклад в разработку дизайна исследования и экспериментальной установки. JD участвовал в анализе данных и написании рукописи.
Конфликт интересов
В.Б. работал в компании AFC Ajax.
Остальные авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Каталожные номера
Бауманн В. , Гросс В., Кваде К., Гальбирц П.и Швирц, А. (1988). Техника рывка тяжелоатлетов мирового класса на чемпионате мира 1985 года. Междунар. Дж. Спорт Биомех. 4, 68–69. doi: 10.1123/ijsb.4.1.68
Полнотекстовая перекрестная ссылка | Академия Google
Берме, Н., и Каппоццо, А. (1990). Биомеханика движений человека: приложения в реабилитации, спорте и эргономике. Уортингтон, Огайо: Bertec Corp, 89–97.
Бобберт, М.Ф., и ван Инген Шенау, Г.Дж. (1988). Координация в вертикальном прыжке. Дж. Биомех. 10, 249–262. дои: 10.1016/0021-9290(88)-3
Полнотекстовая перекрестная ссылка | Академия Google
Чиу, Л. З., Брайантон, М. А., и Мулик, А. Н. (2014). Проксимально-дистальная последовательность в вертикальном прыжке с махом рукой и без него. Дж Прочность Конд. Рез. 28, 1195–1202. doi: 10.1519/JSC.0000000000000388
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Чиу, Л. З., и Шиллинг, Б. (2005). Букварь по тяжелой атлетике: от спорта к спортивной тренировке. Сила конд. Дж. 27, 42–48. дои: 10.1519/00126548-200502000-00008
Полнотекстовая перекрестная ссылка | Академия Google
Фабер, Г. С., Чанг, К., Кингма, И., и Деннерляйн, Дж. (2013). Стиль подъема и пол участника не влияют на оптимальное расположение инерционного датчика для амбулаторной оценки наклона туловища. Дж. Биомех. 46, 1027–1030. doi: 10.1016/j.jbiomech.2012.12.007
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Фабер, Г.С., Кингма И. и ван Дин Дж. Х. (2011). Влияние исходного горизонтального положения объекта на пиковые моменты L5/S1 при подъеме вручную зависит от типа задачи и знакомства с альтернативными стратегиями подъема. Эргономика 54, 72–81. дои: 10.1080/00140139.2010.535019
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Гархаммер, Дж. (1993). Обзор исследований выходной мощности в олимпийском и пауэрлифтинге: методология, прогнозирование производительности и оценочные тесты. Дж. Сила конд. Рез. 7, 76–89. дои: 10.1519/00124278-199305000-00002
Полнотекстовая перекрестная ссылка | Академия Google
Гургулис, В., Аггелусис, Н., Мавроматис, Г., и Гарас, А. (2000). Трехмерный кинематический анализ элитных греческих тяжелоатлетов. J. Спортивные науки. 18, 643–652. дои: 10.1080/02640410050082332
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Грэм-Смит, П., Лис, А., и Ричардсон, Д. (1999).Анализ техники вратарей при выполнении пенальти. J. Спортивные науки. 17, 905–929.
Реферат PubMed
Хори, Н., Ньютон, Р. У., Эндрюс, В. А., Кавамори, Н., МакГиган, М. Р., и Носака, К. (2007). Сравнение четырех различных методов измерения выходной мощности во время подъема на грудь в висе и приседания с прыжком с отягощением. Дж. Сила конд. Рез. 21, 314–320. дои: 10.1519/R-22896.1
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Хори, Н. , Newton, R.U., Andrews, W.A., Kawamori, N., McGuigan, M.R., and Nosaka, K. (2008). Различаются ли результаты в висе на взятие на грудь в прыжках, спринте и смене направления? Дж. Сила конд. Рез. 22, 412–418. doi: 10.1519/JSC.0b013e318166052b
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ибрагим, Р., Фабер, Г. С., Кингма, И., и ван Дин, Дж. Х. (2016). Кинематический анализ броска в хоккее на траве. Спортивная биомеханика. 16, 45–57. дои: 10.1080/14763141.2016.1182207
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ибрагим, Р., Кингма, И., де Боуд, В., Фабер, Г. С., и ван Дин, Дж. Х. (2019a). Кинематический и кинетический анализ сейва вратаря в прыжке в воду в футболе. J. Спортивные науки. 37, 313–321. дои: 10.1080/02640414.2018.1499413
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ибрагим Р., Кингма И., де Боуд В., Фабер Г.С. и ван Дин, Дж.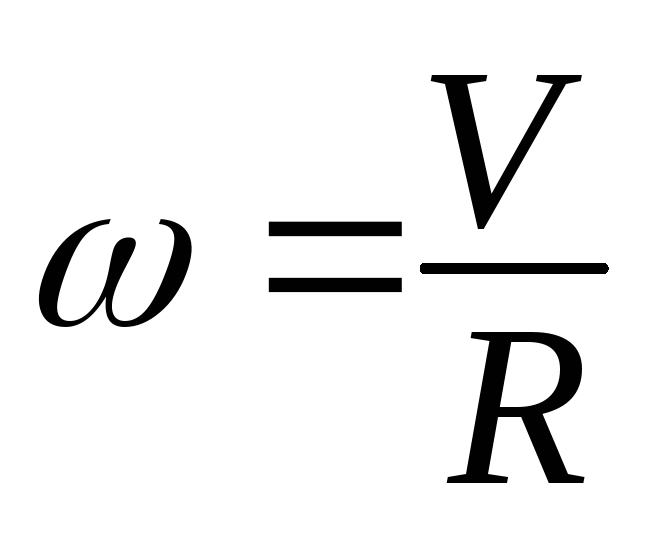 Х. (2019b). Влияние подготовительной позы на сейв вратаря в прыжке в воду в футболе. Спортивные товары для активного образа жизни спереди Масштаб 1:15. doi: 10.3389/fspor.2019.00015
Полнотекстовая перекрестная ссылка | Академия Google
Kingma, I., de Looze, P.M., Toussaint, M.H., Klijnsma, G.H., and Bruijnen, T.B.M. (1996). Проверка трехмерной модели динамического связанного сегмента всего тела. Гул. Мов. науч. 15, 833–860. doi: 10.1016/S0167-9457(96)00034-6
Полнотекстовая перекрестная ссылка | Академия Google
Кипп, К., Харрис, К., и Сабик, М. (2011). Биомеханика нижних конечностей во время упражнений с отягощениями различается в зависимости от сустава и нагрузки. Дж. Сила конд. Рез. 25, 1229–1234. doi: 10.1519/JSC.0b013e3181da780b
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ньютон Р. и Крамер В. (1994). Развитие взрывной мышечной силы: последствия смешанной стратегии тренировок. Сила конд. Дж. 16, 20–31. doi: 10.1519/1073-6840(1994)016<0020:DEMPIF>2.3.СО;2
Полнотекстовая перекрестная ссылка | Академия Google
Бедный, ХВ (1988). Введение в обнаружение и оценку сигналов . Нью-Йорк, штат Нью-Йорк; Берлин; Гейдельберг: Springer, 173–185. дои: 10.1007/978-1-4757-3863-6
Полнотекстовая перекрестная ссылка | Академия Google
Патнэм, Калифорния (1993). Последовательные движения сегментов тела в ударно-бросковом мастерстве: описание и объяснение. Дж. Биомех. 26, 125–135. дои: 10.1016/0021-9290(93)
-р
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Робертсон, Д.Г. и Флеминг Д. (1987). Кинетика прыжков в длину и в длину с места. Кан. Дж. Заявл. Спортивная наука. 12, 19–23.
Реферат PubMed | Академия Google
Шеппард, Дж. М., Триплетт, Т. Н., и Национальная ассоциация силы и физической подготовки (США) (2016). «Разработка программы для тренировок с отягощениями», в Essentials of Strength and Conditioning, 4th Edn. ed TN Triplett (Шампейн, Иллинойс: Human Kinetics), 440.
Спратфорд, В., Меллифонт, Р.и Беркетт, Б. (2009). Влияние направления нырка на характеристики движения элитных футбольных вратарей. Спортивная биомеханика. 8, 235–245. дои: 10.1080/14763140
9526
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Судзуки С., Тогари Х., Исокава М., Охаси Дж. и Огуши Т. (1987). «Анализ движения вратаря в прыжке», в материалах Proceedings of the First World Congress of Science and Football , ed T. Reilly (Liverpool: E&F Spon).468–475.
Академия Google
Триколи В., Ламас Л., Карневале Р. и Угринович К. (2005). Кратковременное влияние на развитие функциональной силы нижней части тела: программы тренировок по тяжелой атлетике и вертикальным прыжкам. Дж. Сила конд. Рез. 19, 433–437. дои: 10.1519/R-14083.1
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ву, Г.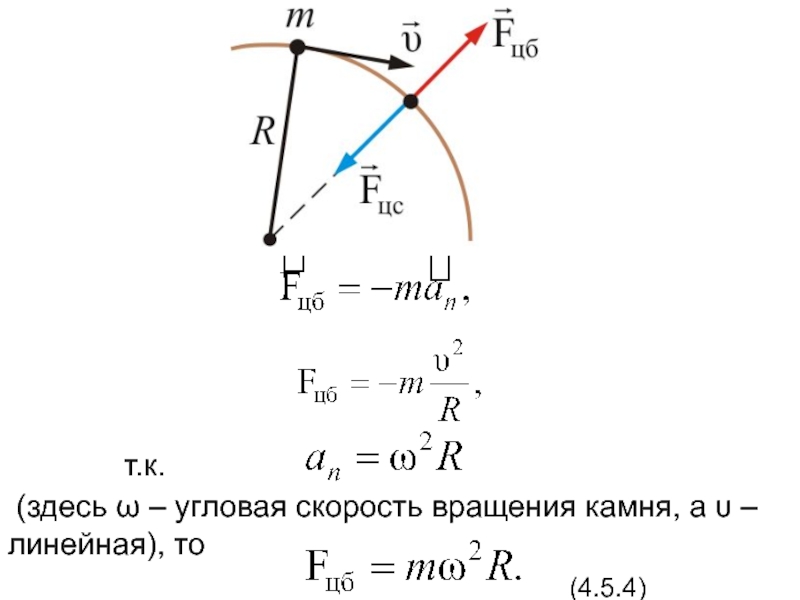 , Зиглер, С., Аллард, П., Киртли, К., Леардини, А., Розенбаум, Д., и соавт. (2002). Рекомендация ISB по определениям системы координат различных суставов для сообщения о движении суставов человека, часть I: лодыжка, бедро и позвоночник. Дж. Биомех. 35, 543–548. doi: 10.1016/s0021-9290(01)00222-6
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ю, Б., Габриэль, Д., Ноубл, Л., и Ан, К. (1999). Оценка оптимальной частоты среза цифрового фильтра нижних частот Баттерворта. J. Appl. Биомех. 15, 318–329. doi: 10.1123/jab.15.3.318
Полнотекстовая перекрестная ссылка | Академия Google
Зациорский В.М. (2002). Кинетика движений человека. Шампейн, Иллинойс: Human Kinetics.
Академия Google
Цинк, А.Дж., Перри, А.С., Робертсон, Б.Л., Роуч, К.Е., и Синьориль, Дж.Ф. (2006). Пиковая мощность, силы реакции опоры и скорость во время выполнения приседаний с различными нагрузками. Дж. Сила конд. Рез .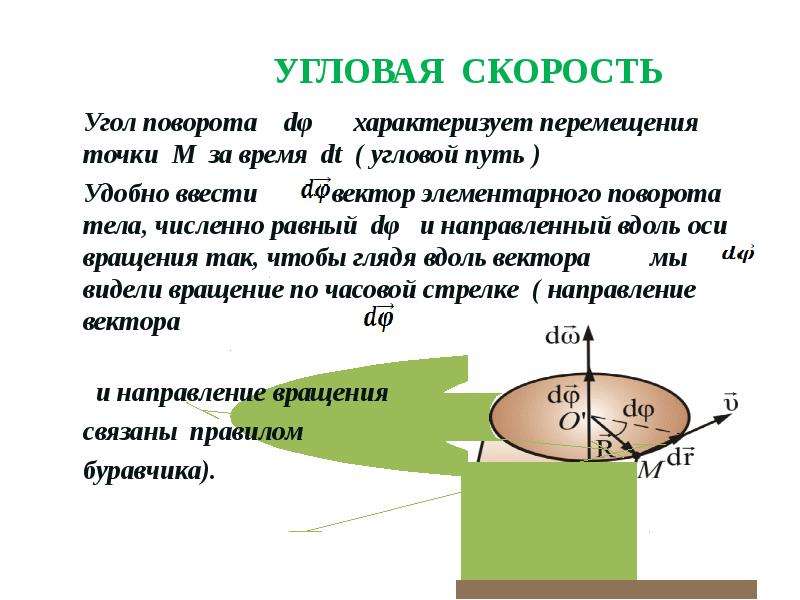 20, 658–664. дои: 10.1519/R-16264.
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
свойств\угловая скорость — calculate.org

Что такое угловая скорость?
Угловая скорость объекта, вращающегося вокруг оси, представляет собой величину, описывающую угловую скорость этого объекта.Угловая скорость считается векторной величиной, хотя ее часто называют псевдовектором. Единицей СИ для угловой скорости является радиан в секунду, а символ угловой скорости обычно представляет собой ω (строчная греческая буква омега). Однако во многих случаях угловая скорость выражается в терминах, более подходящих для рассматриваемой системы. Эти единицы обычно включают градусы в час, обороты в секунду и обороты в минуту.
Вектор угловой скорости всегда проходит перпендикулярно плоскости, в которой вращается объект.Можно определить направление одного вектора угловой скорости, используя правило правой руки. То есть, если мы знаем направление вектора угловой скорости ω, мы можем узнать, вращается ли объект по часовой стрелке или против часовой стрелки, применяя это правило.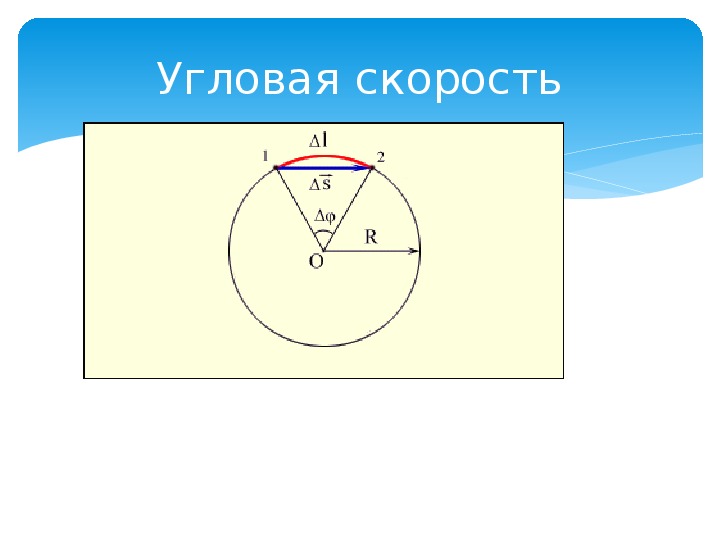 Согните пальцы (почти как кулак) и представьте, что вектор ω направлен вверх к потолку и проходит через вашу правую руку, при этом большой палец также направлен к потолку. Согласно правилу правой руки, объект будет вращаться вокруг начала координат против часовой стрелки в направлении ваших согнутых пальцев.Точно так же, если вы сделаете то же самое и направите большой палец правой руки вниз, вектор ω будет указывать вниз, и объект будет вращаться по часовой стрелке. Вы также можете использовать это правило для определения направления вектора ω, если вы предполагаете, что направление вращения начинается от центра руки и движется наружу к кончикам пальцев.
В двух измерениях для данной частицы p, которая вращается вокруг некоторого начала координат с угловым положением ϕ, эта частица имеет две разные составляющие скорости V.Существует V_perpendicular, который всегда перпендикулярен радиусу между p и началом координат, а также V_parallel, который проходит в том же направлении, что и радиус. Эти два вектора скорости обычно называют кросс-радиальной и радиальной составляющими соответственно. Скорость изменения углового положения частицы p, (dϕ/dt) функционально связана с v _{перпендикулярно} следующим правилом:
v _{перпендикулярно} = r*(dϕ/dt)
В нашей системе также существует угол θ, такой, что θ — это угол между векторами V и v_parallel (также существует другой угол между v _{, перпендикулярным}, и V, такой, что этот угол и θ в сумме составляют 90 градусов).Согласно этому определению, v _{перпендикулярно} связано с θ соотношением:
v _{перпендикулярно} = |V|*sin(θ)
, где |V| является величиной скорости. Мы также предполагаем, что векторная величина ù, представляющая угловую скорость p, также совпадает с изменением углового положения по отношению ко времени (он же dϕ/dt). Другими словами:
ù = dϕ/dt
Теперь, зная это соотношение, мы можем определить ω через величину V путем подстановки, что даст следующее:
ω = (|V|*sin(θ))/|r|
В двух измерениях ω не имеет направления. Тем не менее, если оси x и y поменять местами, ω также изменит свой знак, что означает, что это псевдоскаляр. Однако в трех измерениях ω является псевдовектором, и к нему применяется правило правой руки.
Добавьте эту страницу в закладки в браузере с помощью Ctrl и d или с помощью одного из этих сервисов: (откроется в новом окне)
Энергия и угловой момент
Энергия и угловой момент
Энергия и угловой момент
Если мы нажмем на объект в прямом направлении, пока объект продвигаясь вперед, мы совершаем положительную работу над объектом.Объект ускоряется, потому что мы на это напираем. F = m a . Объект приобретает кинетическую энергию. То поступательная кинетическая энергия объект массой m, центр масс которого движется со скоростью v, равен K = ½mv ² .
Поступательная кинетическая энергия = ½ массы * скорость ²
Кинетическая энергия увеличивается квадратично со скоростью. Когда скорость автомобиля удваивается, его энергия увеличивается в четыре раза.
Вращающийся объект также обладает кинетической энергией. Когда объект вращается относительно его центра масс, его вращательная кинетика энергия равна K = ½Iω ² .
Кинетическая энергия вращения = ½ момента инерции * (угловая скорость) ² .
Когда угловая скорость вращающегося колеса удваивается, его кинетическая энергия увеличивается в четыре раза.
Когда объект имеет поступательное, а также вращательное движение, мы можем посмотреть на движение центра масс и движение вокруг центра масс по отдельности.Полная кинетическая энергия представляет собой сумму поступательной кинетической энергии центра массы (см) и кинетической энергии вращения около см.
Прокатный
Рассмотрим колесо радиуса r и массы m, катящееся по плоской поверхности в x-направление.
Смещение Δx и угловое смещение Δθ связаны соотношением Δx = rΔθ.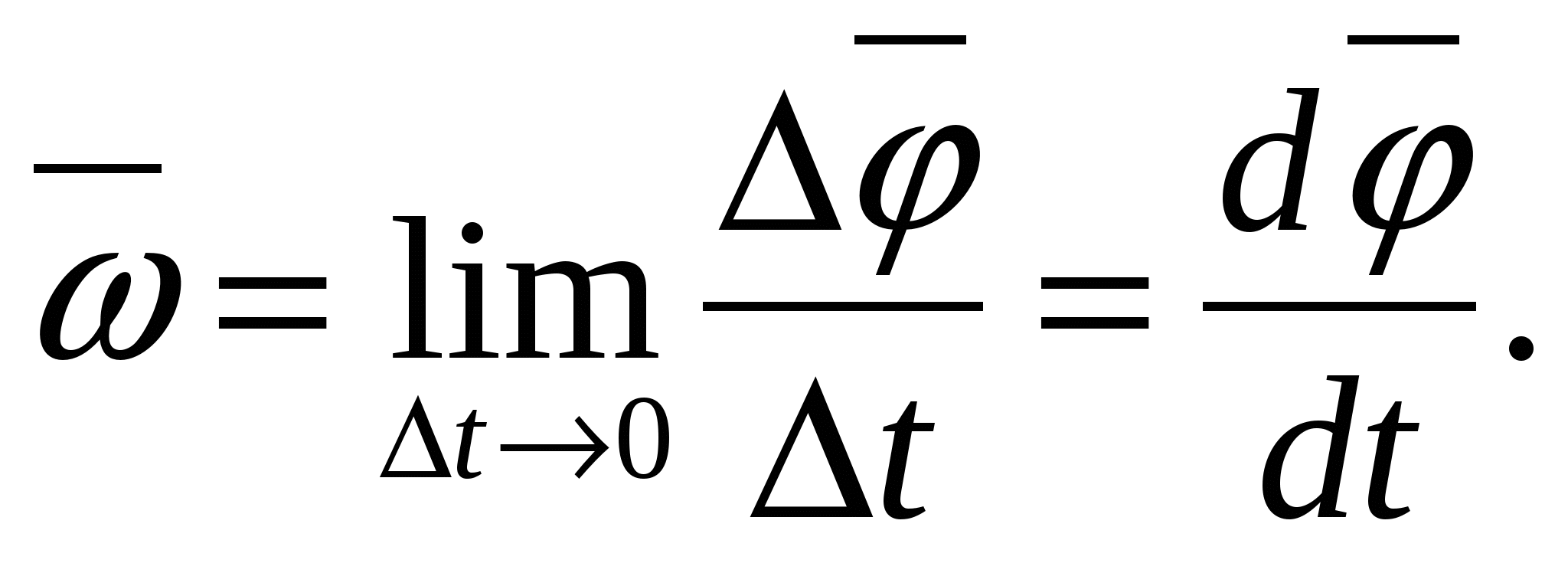
Величины линейной скорости и угловой скорости связаны соотношением v _CM = rω.
Кинетическая энергия диска равна сумме кинетической энергии движения диска. центр масс ½mv _CM ² = ½mr ² ω ² , кинетическая энергия движения вокруг центра масс ½Iω ² .
Общая кинетическая энергия
KE _tot = ½mr ² ω ² + ½Iω ² = ½[mr ² + I]ω ² = ½[m + I/r ² ]v ² .
Пример:
Предположим, что колесо представляет собой однородный диск. Момент инерции I однородного диска относительно оси, перпендикулярной плоскости диска. диск через свой CM равен ½mr ² .
Следовательно, кинетическая энергия диска равна KE _tot = (3/4)mr ² ω ² .
Отношение поступательной кинетической энергии вращения равно E _trans /E _rot = г-н ² /I.
Если два катящихся тела имеют одинаковую кинетическую энергию, то объект с меньшим моментом инерции имеет больший поступательная кинетическая энергия и большая скорость.
Проблема:
Предположим, что диск и кольцо с одинаковым радиусом катятся по наклонной плоскости. h и угол тета. Если они оба стартуют из состояния покоя в t = 0, какой из них достигнет снизу сначала?
Решение:
Подумай сам, а потом посмотри это видеоклип .Был ли ваш ответ правильным?
Модуль 6: Вопрос 2
Предположим, вы разрабатываете гоночный велосипед, и пришло время поработать над колесами. Вам говорят, что колеса должны иметь определенную массу, но вы можете спроектировать их как колеса со спицами (как традиционные велосипедные колеса) или вы можете сделать их как имеющие твердые диски на всем протяжении. Какой дизайн вы бы выбрали, учитывая, что гоночный аспект машины является самым важным? Пожалуйста, объясни!
Обсудите это со своими однокурсниками на форуме!
Пример:
Нажав кнопку ниже, вы может воспроизводить или пошагово просматривать видеоклип кадр за кадром. Каждый шаг соответствует интервалу времени (1/30) с. В обойме такой же крутящий момент действует на объекты с различные моменты инерции. Крутящий момент есть произведение веса и маленькое плечо рычага. Момент инерции линейкообразного объекта изменяется потому что массы добавляются на больших расстояниях от центра. Когда груз пролетит то же самое расстояние Δy, была совершена одна и та же работа, и система имеет одинаковую кинетическую энергию, так как она начинается с отдыха.Пренебрегая трением W = τΔθ = mgΔy = ½Iω ² . Однако система с большим моментом инерции I имеет меньший угловой скорость ω. (Сравните углы, на которые поворачивается линейка за шаг без прикрепленными массами и с массами, прикрепленными в разных местах.)
Проблема:
Три частицы соединены жесткими стержнями ничтожной массы, лежащими вдоль оси Y, как показано.
Если система вращается вокруг оси x с угловой скоростью 2 рад/с, найти
(а) момент инерции относительно оси x и полный вращательный момент кинетическая энергия оценивается по ½Iω ² , и
(b) линейная скорость каждой частицы и общая кинетическая энергия оцениваются от Σ½м _i v _i ² .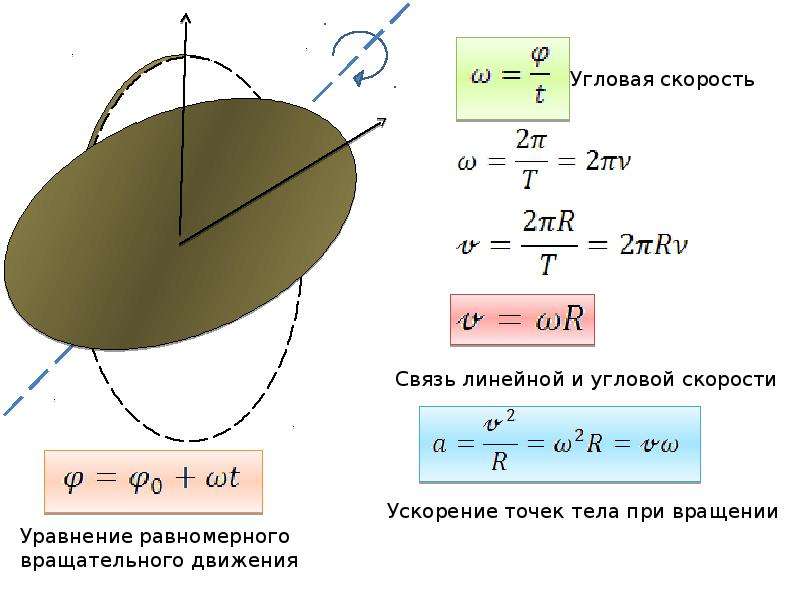
Решение:
Рассуждение:
Момент инерции I = ∑m _i r _i ² . Здесь r _i — перпендикулярное расстояние частицы i от ось х.
Линейная скорость частицы i равна v _i = ωr _i .
Детали расчета:
(a) I = (4 кг)(9 м ² ) ^{+
(2 кг)(4 м ² ) ^{+
(3 кг)(16 м ² ) ^{= 92 кгм ² .
Кинетическая энергия вращения K = ½Iω ² = 46*4/с ² = 184 Дж.
(б) Линейная скорость груза массой 4 кг v = 6 м/с, а его кинетическая энергия равна ½mv ² = 72 Дж.
Линейная скорость груза массой 2 кг v = 4 м/с, а его кинетическая энергия ½mv ² = 16 Дж.
Линейная скорость груза массой 3 кг v = 8 м/с, а его кинетическая энергия ½mv ² = 96 Дж.
Сумма кинетических энергий трех частиц равна 184 Дж.}}}
Угловой момент вокруг оси является мерой вращательного движения объекта относительно этой оси.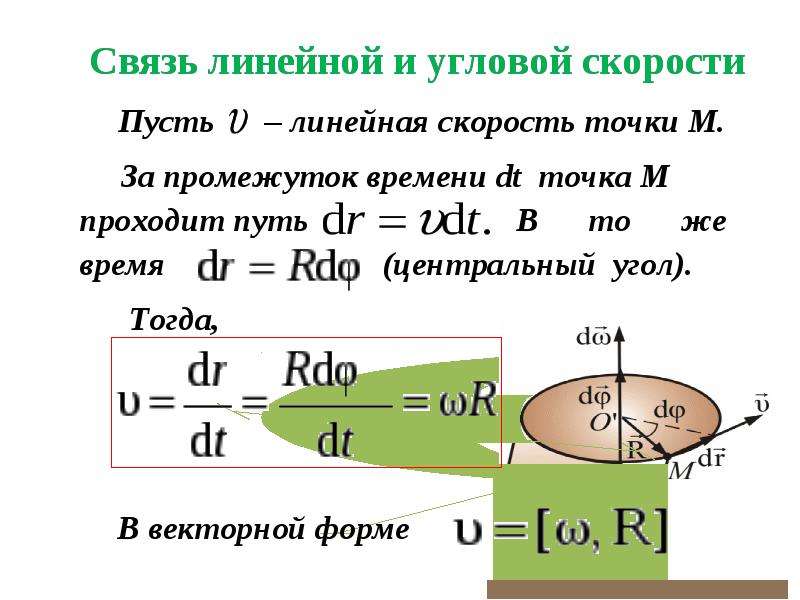 Для вращения вокруг оси симметрии объекта угловой момент L определяется как произведение момент инерции объекта, умноженный на его угловую скорость ω относительно выбранной оси.
L = I ω .
Проблема:
Легкий стержень длиной 1 м вращается в плоскости xy вокруг оси, проходящей через центр стержня.Две частицы массами 4 кг и 3 кг связаны с его заканчивается. Определить момент импульса системы в момент скорость каждой частицы 5 м/с.
Решение:
Рассуждение:
Мы предполагаем, что массой и моментом инерции стержня можно пренебречь.
Пусть ось Z проходит через центр стержня и направлена за пределы страницы.
Момент инерции системы относительно оси z равен I = ∑m _i r _i ² , где r _i — расстояние i-й частицы от центра стержень.
Детали расчета:
Момент инерции системы относительно оси Z равен
3 кг*(0,5 м) ² + 4 кг*(0,5 м) ² = 1,75 кгм ² .
Угловая скорость системы ω = (v/r) k = ((5 м/с)/(0,5 м)) k = (10/с) k .
Здесь k — единичный вектор или указатель направления, указывающий в z-направление (вне страницы).
Угловой момент системы равен L = I ω = (17.5 кгм ² /с) к .
Угловой момент — это вектор. Для одиночной частицы ее направлением является направление углового скорость (определяется правилом правой руки). Угловой момент объекта равен изменили, придав ему угловой импульс . Ан угловой импульс Δ L – изменение углового импульс. Вы придаете объекту угловой импульс, позволяя крутящему моменту воздействовать на него. за промежуток времени Δt.
Δ L = τ Δt
угловой импульс = крутящий момент * время
Если объект имеет много независимо вращающихся частей, полный угловой момент объекта равен сумме угловых импульсы всех его частей.
Проблема:
Обычно вы слегка толкаете дверь шкафа, и она мягко закрывается. за 5 секунд. Но сегодня ты торопишься и напрягаешься в 3 раза больше обычного крутящий момент на нем.
(a) Если вы нажмете на него в течение обычного времени с таким повышенным крутящим моментом, как его угловой момент отличается от обычного значения?
(б) Через какое время дверь шкафа захлопнется после того, как вы поспешите толкать?
Решение:
Обоснование:
(a) Когда вы толкаете дверь, вы создаете крутящий момент (сила, умноженная на плечо рычага). течение определенного времени, и дверь приобретает угловой момент L = I ω .Если увеличить силу в несколько раз 3 и толчок в течение того же времени, угловой момент увеличивается на коэффициент три. Момент инерции двери не меняется, поэтому его угловая скорость должна увеличиться в 3 раза.
(б) угловая скорость = угловое смещение / время, время = угловое перемещение / угловая скорость
Время, необходимое для закрытия двери, уменьшится в три раза.
время = (5 с)/3 = 1,66 с.
Сохранение углового момента
Полный угловой момент отдельного объекта равен постоянным, если на него не действует внешний вращающий момент. объект.Объект не может оказывать крутящий момент на себя. Суммарный угловой момент двух взаимодействующих объектов также постоянна, если на объекты не действует внешний вращающий момент. Третий закон Ньютона говорит нам, что силы, действующие на объекты друг на друга, равны. по величине и противоположно по направлению. То силы взаимодействия создают моменты, равные по величине и противоположные по направление. Эти крутящие моменты изменяют угловой момент каждого объекта на одинаковую величину. сумма, но изменения будут иметь противоположные направления.Когда мы суммируем их находим изменение полного углового момента, получаем ноль.
Если на систему взаимодействующих тел не действует внешний вращающий момент, то их суммарный угловой момент постоянен.
В показанном ниже ролике суммарный момент импульса системы точек вверх. Человек останавливает прялку, и табуретка начинает вращаться.
Ваш браузер не поддерживает видео HTML5.

Несколько первых кадров
Когда человек прикладывает крутящий момент к колесу, колесо прикладывает крутящий момент к персона.Величины угловых моментов колеса и человека изменяются с той же скоростью, но их сумма остается постоянной.
Если у объекта нет ничего внешнего для взаимодействия, он не может изменить свое угловой момент. Однако гибкий объект может менять свое угловое положение.
Пример:
или
Пожалуйста, смотрите.
Проблема:
Женщина весом 60 кг стоит на краю горизонтального поворотного стола и испытывает момент инерции 500 кг м ² и радиусом 2 м.Поворотный стол первоначально находится в состоянии покоя и может свободно вращаться вокруг вертикальной оси без трения через его центр. Затем женщина начинает ходить по краю по часовой стрелке (если смотреть сверху на систему) с постоянной скоростью 1,5 м/с относительно Земли.
(а) В каком направлении и с какой угловой скоростью вращается поворотный стол?
(б) Сколько работы делают женщины, чтобы привести в движение себя и вращающийся стол?
Решение:
Полный угловой момент относительно любой оси во Вселенной сохраняется. Однако угловой момент отдельного объекта изменяется, когда действует чистый крутящий момент. на объекте за конечный интервал времени. И наоборот, если нет чистого крутящего момента действует на тело, то его момент импульса постоянен.
Угол поворота и угловая скорость – Колледж физики
Цели обучения
Задайте длину дуги, угол поворота, радиус кривизны и угловую скорость.
Рассчитайте угловую скорость вращения колеса автомобиля.
В кинематике мы изучали движение по прямой и ввели такие понятия, как перемещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в котором объект проецируется в воздух, подвергаясь действию силы гравитации, и приземляется на расстоянии. В этой главе мы рассмотрим ситуации, когда объект не приземляется, а движется по кривой. Начнем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угловая скорость
Как быстро вращается объект? Мы определяем угловую скорость как скорость изменения угла. В символах это
где угловой поворот происходит за время . Чем больше угол поворота за данный промежуток времени, тем больше угловая скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Угловая скорость аналогична линейной скорости. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся компакт-диске.Эта яма перемещается на длину дуги за время, поэтому ее линейная скорость равна
.
Отсюда мы видим, что . Подставляя это в выражение для дает
Мы записываем это отношение двумя разными способами и получаем два разных понимания:
Первое соотношение в утверждает, что линейная скорость пропорциональна расстоянию от центра вращения, поэтому она наибольшая для точки на ободе (наибольшая), как и следовало ожидать. Мы также можем назвать эту линейную скорость точки на ободе тангенциальной скоростью .Второе соотношение можно проиллюстрировать, рассмотрев шину движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины равна скорости автомобиля. См. (Рисунок). Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой означает большой , потому что . Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (), будет производить большую линейную скорость () для автомобиля.
Оба и имеют направления (следовательно, они являются угловой и линейной скоростями , соответственно).Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается траектории, как показано на (рис.).
Возьми домой эксперимент
Привяжите предмет к концу веревки и раскачивайте его по горизонтальному кругу над головой (раскачивая на запястье). Поддерживайте постоянную скорость при раскачивании объекта и измеряйте угловую скорость движения. Какова примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке.Определите другие круговые движения и измерьте их угловые скорости.
Поскольку объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, ее мгновенная скорость всегда касается окружности. Направление угловой скорости в этом случае – по часовой стрелке.
Исследования PhET: Революция божьей коровки
Вместе с божьей коровкой исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение.Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.
Концептуальные вопросы
Существует аналогия между вращательными и линейными физическими величинами. Какие вращательные величины аналогичны расстоянию и скорости?
Проблемные упражнения
Полуприцепы имеют одометр на одной ступице колеса прицепа. Ступица утяжелена, чтобы не вращаться, но содержит шестерни для подсчета количества оборотов колеса — затем она рассчитывает пройденное расстояние.Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
Микроволновые печи вращаются со скоростью около 6 об/мин. Что это в оборотах в секунду? Какова угловая скорость в радианах в секунду?
Автомобиль с шинами радиусом 0,260 м проезжает 80 000 км, прежде чем они изнашиваются. Сколько оборотов делают шины, если не принимать во внимание заднее движение и изменение радиуса из-за износа?
а) Каков период вращения Земли в секундах? б) Какова угловая скорость Земли? (c) Учитывая, что Земля имеет радиус на экваторе, какова линейная скорость на поверхности Земли?
Бейсбольный питчер выносит руку вперед во время подачи, вращая предплечье вокруг локтя.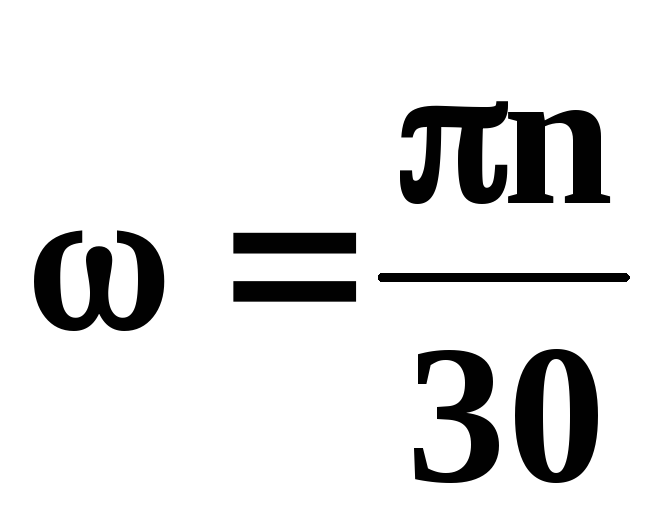 Если скорость мяча в руке питчера 35,0 м/с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
В лакроссе мяч выбрасывается из сетки на конце клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча относительно локтевого сустава равна 30,0 рад/с, а мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
Грузовик с шинами радиусом 0,420 м движется со скоростью 32.0 м/с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об/мин?
Интегрированные концепции При ударе по футбольному мячу бьющий игрок вращает ногу вокруг тазобедренного сустава.
(a) Если скорость носка ботинка кикера составляет 35,0 м/с, а тазобедренный сустав находится на расстоянии 1,05 м от носка ботинка, какова угловая скорость носка ботинка?
(b) Башмак находится в контакте с изначально неподвижным футбольным мячом массой 0,500 кг в течение 20,0 мс. Какая средняя сила действует на футбольный мяч, чтобы придать ему скорость 20?0 м/с?
(c) Найдите максимальную дальность полета мяча, пренебрегая сопротивлением воздуха.
(а) 33,3 рад/с
(б) 500 Н
(в) 40,8 м
Создайте свою собственную проблему
Рассмотрим аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками. Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и наездниками препятствует их скольжению вниз.Составьте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите бесплатную схему тела одного гонщика. Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициент трения между одеждой всадника и стеной.
Глоссарий
длина дуги
, расстояние, пройденное объектом по круговой траектории
яма
крошечное углубление на спиральной дорожке, отформованной в верхней части поликарбонатного слоя компакт-диска
угол поворота
отношение длины дуги к радиусу кривизны на круговой траектории:
радиус кривизны
радиус кругового пути
радиан
единица измерения угла
угловая скорость
, скорость изменения угла, с которым объект движется по круговой траектории
Какова угловая скорость минутной стрелки часов (в радианах в минуту)?
Майкл М. ответил • 24.09.20
Борьба с классами STEM? Я могу помочь!
В полном круге 2*пи радиан, поэтому представьте, что минутная стрелка движется по круговым часам. Он совершает полный оборот вокруг этих круглых часов за 60 минут. Таким образом, угловая скорость минутной стрелки равна 2 * пи / 60 = пи / 30 = (приблизительно) 0,10472 радиана в минуту.
Все еще ищете помощи? Получите правильный ответ, быстро.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ – — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° − ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ е ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А А Â Ã Ä Å Æ Ç Э Э Ê Ë Я Я Я Я Ð С Ò О Ô Õ О Ø О Ш Ù Ú Û О Ý Ÿ Þ а а â г ä å æ ç э э э ë я я я я ð с ò о ô х ö ø œ ш ù ú û ü ý þ ÿ А В Г Δ Е Ζ Η Θ я Κ Λ М N Ξ О Π Р Σ Т Υ Φ Χ Ψ Ом α β γ дельта ε ζ η θ я κ λ мю ν ξ о π р ς о т υ ф х ψ ю ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈〉 ◊
Угловая скорость, ускорение и перемещение
Практические задачи
Вопрос 1: Собака находится на углу круглого вращающегося диска. Изменение угловой скорости составляет 50 рад/с за 15 секунд. Вычислите их угловое ускорение .
а.2,41 рад/с2 б. 4.35 рад/с2c.7.42 рад/с2 d.3.33 рад/с2
Ответ: Правильный вариант (d).
Заданные данные :
Изменение угловой скорости составляет 50 рад/с.
Требуемое время 15 с.
Объяснение:
Мы знаем, что формула углового ускорения:
α=dωdt
Где
ω — угловая скорость.
т это время.
α=5015 рад/с2
α=3,33 рад/с2
Отсюда и далее угловое ускорение равно 3,33 рад/с2.
Вопрос 2: Круглое колесо совершает 180 оборотов в минуту. Чему равна угловая скорость колеса?
2π RAD / S
6π A RAD / S
4π RAD / S
8π RAD / S
9066
Ответ: Правильный вариант (B).
Данные :
Количество оборотов в минуту 180 об/мин.
Объяснение:
Мы знаем, что
1RPM = 2π60 RAD / S
для 180 об / мин, угловая частота может быть выражена как,
ω = 180×2π60
Ω = 6π RAD / S
Отныне , угловая скорость 6π рад/с.
Вопрос 3: Какова единица углового ускорения?
Радиан в секунду
Градус в секунду
Радиан в секунду в квадрате
Ничего из вышеперечисленного
Ответ: Правильный вариант (c).
Пояснение:
Мы знаем, что угловое смещение обозначается как θ в радианах.
Угловое смещение между двумя объектами, которые вращаются вокруг оси относительно времени, называется угловой скоростью.
ω=dθdt
Угловая скорость ω описывается в радианах/с.
Скорость изменения угловой скорости называется угловым ускорением.
α=dωdt=d2θdt2
Угловое ускорение α описывается в радианах/с2.