Угол поворота в физике формула: Угловое перемещение (угол поворота)
Формула угловой скорости в физике
Содержание:
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(\varphi)$ . Часто используют вектор элементарного поворота
$\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела
$(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами.
Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой $\omega$ . Математически определение угловой скорости записывают так:
$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
$$\omega=\frac{\varphi}{t}(2)$$где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:
$$\omega=\frac{2 \pi}{T}(3)$$С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:
$$\omega=2 \pi \nu(4)$$Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.
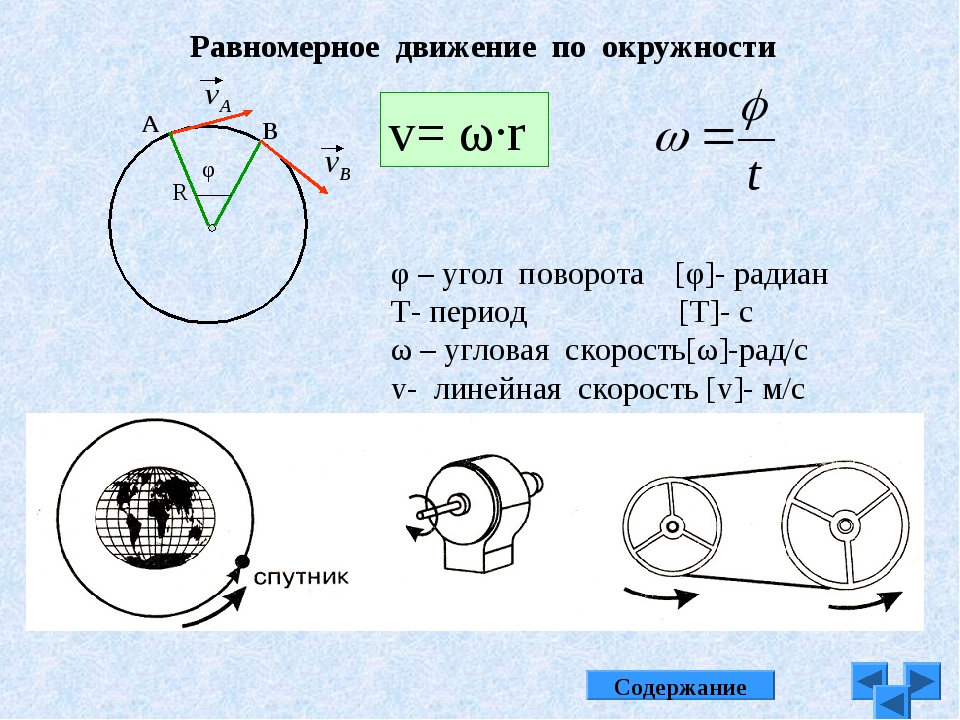
Формула, связывающая линейную и угловую скорости
Линейная скорость $\bar{v}$ точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
где $\bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (\bar{r})$ (рис. {3} \approx 20(\mathrm{rad})$$
{3} \approx 20(\mathrm{rad})$$
Ответ. $\varphi = 20$ рад.
Читать дальше: Формула удельного веса.
Формула угловой скорости в физике
Содержание:
Определение и формула угловой скорости
Определение
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота
$(\varphi)$ . Часто используют вектор элементарного поворота
$\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела
$(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону,
откуда этот поворот виден реализующимся против часовой стрелки.
Определение
Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой $\omega$ . Математически определение угловой скорости записывают так:
$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол,
то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
При этом модуль угловой скорости находят как:
где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:
$$\omega=\frac{2 \pi}{T}(3)$$С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:
$$\omega=2 \pi \nu(4)$$Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость $\bar{v}$ точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
$$\bar{v}=[\bar{\omega} \bar{R}](5)$$где $\bar{R}$ – перпендикулярная к оси вращения компонента радиус-вектора точки
$A (\bar{r})$ (рис. {3} \approx 20(\mathrm{rad})$$
{3} \approx 20(\mathrm{rad})$$
Ответ. $\varphi = 20$ рад.
Читать дальше: Формула удельного веса.
Урок 5. поступательное движение. вращательное движение твердого тела — Физика — 10 класс
Физика, 10 класс
Урок 05. Поступательное движение. Вращательное движение твёрдого тела
Перечень вопросов, рассматриваемых на уроке:
- Поступательное и вращательное движение абсолютно твердого тела.
- Характеристики вращательного движения абсолютно твердого тела.
Глоссарий по теме
1. Абсолютно твердое тело – это тело, расстояние между любыми двумя точками которого остается постоянным при его движении.
2. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе. Одинаковыми остаются при поступательном движении перемещение, траектория, путь, скорость, ускорение.
3. Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения.
4. Угол поворота – угол, на который поворачивается радиус-вектор, соединяющий центр окружности с точкой вращающегося тела.
5. Угловая скорость — отношение угла поворота φ к промежутку времени, в течение которого совершен этот поворот при равномерном движении.
6. Линейная скорость – отношение длины дуги окружности пройденной точкой тела к промежутку времени, в течение которого этот поворот совершен.
7. Период — промежуток времени, за который тело делает один полный оборот.
8. Частота обращения тела – число оборотов за единицу времени
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.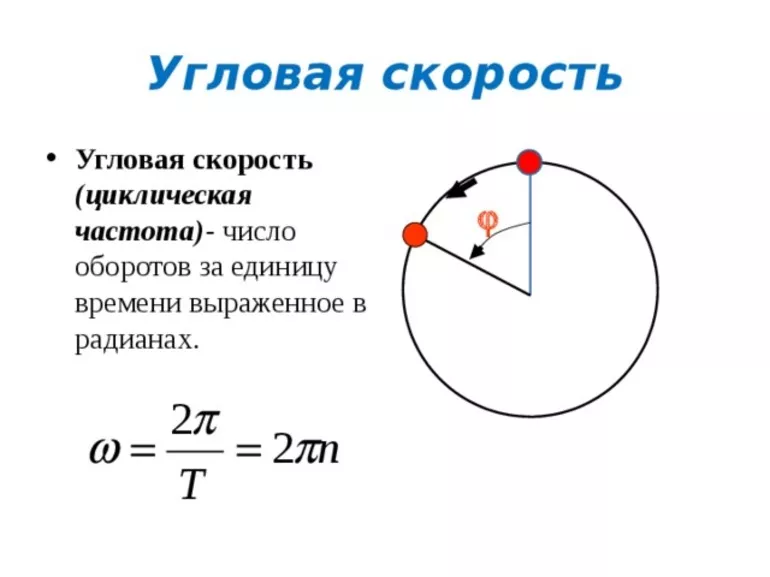 : Просвещение, 2016. – С. 57-61
: Просвещение, 2016. – С. 57-61
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Вы знаете, что в физике для упрощения исследования реальных ситуаций часто используются модели. Одной из механических моделей, используемых при описании движения и взаимодействия тел, является абсолютно твёрдое тело- тело, расстояние между любыми двумя точками которого остаётся постоянным при его движении.
2. Поступательным называется такое движение абсолютно твёрдого тела, при котором любой отрезок, соединяющий любые две точки тела, остаётся параллельным самому себе. Примером поступательного движения может служить свободное падение тел, движение лифта, поезда на прямолинейном участке дороги. При поступательном движении все точки тела описывают одинаковые траектории, совершают одинаковые перемещения, проходят одинаковые пути, в каждый момент времени имеют равные скорости и ускорения.
Для описания поступательного движения абсолютно твёрдого тела достаточно написать уравнение движения одной из его точек.
3. Вращательным движением абсолютно твёрдого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения. При этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения.
Вращательное движение позволяет осуществить непрерывный процесс работы с использованием больших скоростей. Вращающиеся механизмы более компактны и более экономичны, так как потери энергии на преодоление сил трения качения меньше, чем на преодоление сил трения скольжения. Поэтому в современной технике вращательное движение рабочих частей машин всё более вытесняет возвратно-поступательное. Например, вместо ножовочной пилы в технике используют вращающуюся дисковую пилу, поршневые насосы в большинстве случаев вытесняются центробежными.
4. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела ∆φ к промежутку времени ∆t, за которое этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению запишем формулу угловой скорости;
При равномерном вращательном движении угловая скорость у всех точек вращающегося тела одинаковая. Поэтому угловая скорость, так же как и угол поворота, является характеристикой движения всего вращающегося тела, а не только отдельных его частей.
Примером вращательного движения, близкого к равномерному, может служить вращение Земли вокруг своей оси.
Угловая скорость в СИ выражается в радианах в секунду (рад/с).
Один радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
Угловая скорость положительна, если угол между радиусом вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательным, когда он уменьшается
5. Число полных оборотов за единицу времени называют частотой обращения.
Число полных оборотов за единицу времени называют частотой обращения.
Частоту обозначают греческой буквой «ню». Единица измерения частоты является секунда в минус первой степени
Время, за которое тело совершает один полный оборот, называют периодом обращения и обозначают буквой Т.
7. Связь между линейной и угловой скоростями:
8. Связь между ускорением и угловой скоростью:
Итак, мы рассмотрели два простейших движения абсолютно твердого тела – поступательное и вращательное. В жизни мы чаще встречаем сложное движение абсолютно твердого тела, однако, в этом случае любое сложное движение можно представить как сумму двух независимых движений: поступательного и вращательного.
Примеры и разбор типового тренировочного задания
- Ротор мощной паровой турбины делает 100 оборотов за 2 с. Определите угловую скорость.
Дано:
N=100 об.
t = 2 c
Найти: ω.
Решение:
2. Два шкива, соединенные друг с другом ремнем, вращаются вокруг неподвижных осей (см.рис). Больший шкив радиусом 20см делает 50 оборотов за 10 секунд, а частота вращения меньшего шкива 2400 оборотов в минуту. Чему равен радиус меньшего шкива? Шкивы вращаются без проскальзывания.
Дано:
Найти —
Решение:
Из условия задачи ученик видит что, шкивы соединены ремнем, следовательно, линейные скорости их равны:
но частота вращения разная.
Сокращает на 2π обе части.
Отсюда имеем:
и так, как в условии известно , то можем записать:
Отсюда находим радиус второго шкива:
Вторая неизвестная величина
Запишем формулу периода обращения для большего шкива:
так как по условию задачи нам известно число оборотов за 10 секунд.
Подставим в формулу (1) и получим конечную формулу:
Вращательное движение
Страница 1 из 3
Существует большое количество расчетных задач, которые моделируют явления, происходящие в различных вращающихся агрегатах или около них. При постановке подобной численной задачи важно выбрать способ описания вращения в численной модели, который будет корректен с точки зрения физики и оптимален с точки зрения производительности вычислений. FlowVision позволяет задавать вращение различными способами: с помощью вращающейся локальной системы координат; с помощью подвижных тел; с помощью скользящих поверхностей. С целью помочь пользователю разобраться с постановкой такого типа задач, рассмотрены примеры задач разного типа, начиная с физико-математических основ.
При постановке подобной численной задачи важно выбрать способ описания вращения в численной модели, который будет корректен с точки зрения физики и оптимален с точки зрения производительности вычислений. FlowVision позволяет задавать вращение различными способами: с помощью вращающейся локальной системы координат; с помощью подвижных тел; с помощью скользящих поверхностей. С целью помочь пользователю разобраться с постановкой такого типа задач, рассмотрены примеры задач разного типа, начиная с физико-математических основ.
1. Кинематика вращательного движения
1.1. Вращательное движение материальной точки
Вращательное движение материальной точки (м.т.) вокруг неподвижной оси – это движение материальной точки по окружности радиуса R, центр которой лежит на неподвижной относительно данной системы отсчета прямой (ось вращения), перпендикулярной плоскости, в которой лежит траектория точки.
Рис.1.
Вращательное движение тела вокруг неподвижной оси — движение тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. Тело, совершающее вращательное движение, имеет одну степень свободы, и его положение относительно данной системы отсчёта определяется углом поворота φ между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом, проведёнными через ось вращения.
Рис.2.
1.2. Угол поворота
Угол φ считается положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Чтобы знать положение в любой момент времени, надо знать зависимость угла φ от времени t, т.е. φ=f(t).
1.3. Основные кинематические характеристики вращательного движения
Основными кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение .
Угловая скорость и угловое ускорение величины векторные. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. Аналогично углу поворота, когда вращение происходит против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az) ω>0, а когда по ходу часовой стрелки, то ω<0. Таким образом, знак ωопределяет направление вращения.
а) б) в)
Рис.3
1.4. Прочие кинематические характеристики
Скорость точки M на расстоянии R от оси (рис.2):
Тангенциальная составляющая ускорения точки M (рис.3б):
Нормальная составляющая ускорения точки M (рис.3б):
Полное ускорение точки M (рис.3б):
Формула Эйлера (рис.3в):
2. Силы инерции, действующие на материальную точку во вращающейся системе отсчета
2.
 1. Материальная точка, покоящаяся во вращающейся системе отсчета
1. Материальная точка, покоящаяся во вращающейся системе отсчетаЕсли рассмотреть движение вращающейся точки M, то относительно неподвижной системы координат (СК) XYZ (рис.4а) силу, действующую на неё можно определить из второго закона Ньютона: . Относительно вращающейся системы координат X’Y’Z’ точка M неподвижна (рис.4б). Это обеспечивается тем, что равнодействующая сил уравновешивается инерциальной силой (центробежной): .
Рис.4 (а,б)
2.2. Материальная точка, движущаяся во вращающейся системе отсчета
Если же точка движется во вращающейся системе отсчета, то помимо центробежной силы на неё действует ещё одна сила инерции – сила Кориолиса (рис.5). Направление силы Кориолиса определяется правилом правого винта.
Рис. 5.
Таким образом, при переходе от основной неподвижной СК к локальной СК, которая является вращающейся системой отсчета, появляются дополнительные составляющие вектора силы, которые действуют на материальную точку: центробежная сила и сила Кориолиса .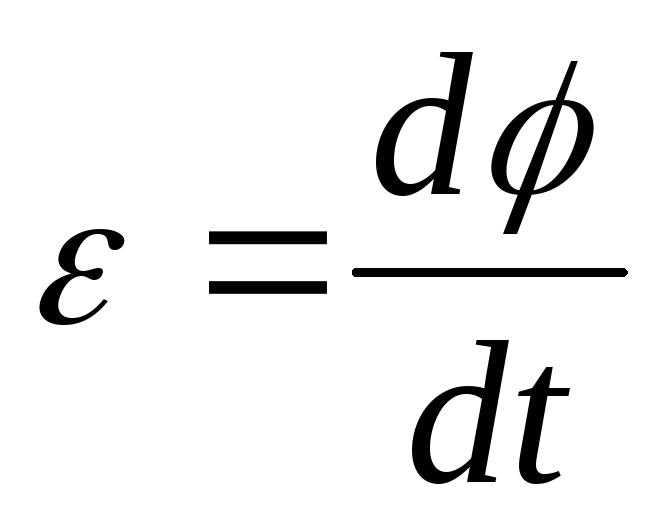
Угловое ускорение
Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.
Основные понятия
Определение 1Угловое ускорение – величина, характеризующая изменение скорости с течением времени.
Пусть рассматриваемый промежуток времени это: Δt=t1-t, а изменение угловой скорости составит Δω=ω1-ω, тогда числовое значение среднего углового ускорения за тот же интервал времени: ε=∆ω∆t=ε. Перейдем к пределу, когда Δt>0, тогда формула углового ускорения будет иметь вид: ε=lim∆t→0∆ω∆t=dωdt=d2φdt=ω˙=φ¨.
Определение 2Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.
Размерность углового ускорения 1T2 (т.е. 1время2). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается рад/с2 или иначе: 1с2(с-2).
Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.
Определение 4Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.
В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.
Рисунок 1. Вектор углового ускорения
Если мы представим угловое ускорение как вектор ε→=dω→dt, имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε→ и ω→ совпадут по направлениям (левая часть
рисунка 1) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка 1).
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЗакон равнопеременного вращения
Определение 5Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным (ε=const).
Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t0 угол вращения равен ϕ=ϕ0; угловая скорость — ω=ω0 (т.е. ω0 является начальной угловой скоростью).
Выражение ε=dωdt=ω˙=φ¨ дает нам возможность сделать запись: dω=εdt. Проинтегрируем левую часть крайней записи в пределах от ω0 до ω, а правую – в пределах от 0 до t, тогда:
ω=ω0+εt, dφ=ω0dt+εtdt.
Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:
Определение 6Закон равнопеременного вращения: φ=φ0+ωt+εt22.
Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.
Вращение является равнозамедленным, когда ω и ε противоположны по знаку.
Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R, тогда: αr=εR. Нормальное ускорение имеет также связь с угловым: an=ω2R. Учтем это выражение и для полного ускорения получим: a=ar2+an2=Rε2+ω4 Для равнопеременного движения: ω=εt; an=ω2R=ε2t2R и a=Rε2+ε4t4=Rε1+ε2t4.
Практические примеры
Пример 1На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.
Рисунок 2
Решение
Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки 2.1. и 2.3. показывают направление псевдовектора вверх, а рисунки 2.2. и 2.4. – вниз.
Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки 2.1. и 2.4.). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2.2. и 2.3.). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
Пример 2Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом R. При этом выражение ϕ=αt3 отражает зависимость угла поворота от времени. Необходимо найти полное ускорение заданной точки как функцию времени.
Решение
Запишем выражения для угловой скорости и углового ускорения заданной точки:
ω=dφdt=3αt2; ε=6αt.
Полное ускорение запишем как:
a=ar2+an2=Rε2+ω4=R36a2t2+81a4t8=3atR4+9a2t6.
Вращательное движение вокруг неподвижной оси — еще один частный случай движения твердого тела.Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4). В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов. Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути. Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол — угол между осью ОХ и радиус-вектором , определяющим положение точки А (см. рис.2.5). Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое — на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел. Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению Угловая скорость выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска — около 140 рад/с1. Угловую скорость можно выразить через частоту вращения, т. е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде: Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1) Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2.1) равен: Если , то , или . Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается. Тем самым мы можем описать положение точек вращающегося тела в любой момент времени. Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так: Так как , то Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли . Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: Следовательно, Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет. Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами , можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени. Знаем мы и направления и , a также форму траекторий точек. |
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Угол поворота и угловая скорость
Цели обучения
К концу этого раздела вы сможете:
- Определите длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Вычислить угловую скорость вращения колеса автомобиля.
В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях.Движение снаряда — это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на рисунке 1 вращается вокруг своего центра — каждая точка в объекте движется по дуге окружности.Рассмотрим линию от центра компакт-диска до его края. Каждая лунка , , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [latex] \ displaystyle \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [ / латекс]
Рис. 1. Все точки на компакт-диске движутся по дугам окружности.Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ за время Δt .
Рис. 2. Радиус круга повернут на угол Δθ . Длина дуги Δs описана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории, как показано на рисунке 2. Обратите внимание, что r — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r . Окружность круга равна 2π r . Таким образом, за один полный оборот угол поворота составляет
°.[латекс] \ displaystyle \ Delta \ theta = \ frac {2 \ pi {r}} {r} = 2 \ pi \\ [/ latex].
Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ равными радиан, (рад), определенным так, что 2π рад = 1 оборот.
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.
| Таблица 1. Сравнение угловых единиц | |
|---|---|
| Градус меры | Мера радиана |
| 30º | [латекс] \ displaystyle \ frac {\ pi} {6} \\ [/ latex] |
| 60º | [латекс] \ displaystyle \ frac {\ pi} {3} \\ [/ latex] |
| 90º | [латекс] \ displaystyle \ frac {\ pi} {2} \\ [/ latex] |
| 120º | [латекс] \ displaystyle \ frac {2 \ pi} {3} \\ [/ latex] |
| 135º | [латекс] \ displaystyle \ frac {3 \ pi} {4} \\ [/ latex] |
| 180º | π |
Рисунок 3.Точки 1 и 2 вращаются на один и тот же угол (Δθ), но точка 2 перемещается на большую длину дуги (Δs), потому что она находится на большем расстоянии от центра вращения (r). {\ circ}} {2 \ pi} \ приблизительно 57.{\ circ} \\ [/ латекс].
Угловая скорость
Насколько быстро вращается объект? Определим угловую скорость ω как скорость изменения угла. В символах это [латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta {t}} \\ [/ latex], где угловой поворот Δ θ происходит за время Δ t . Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω аналогична линейной скорости v . Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги Δ с за время Δ t , поэтому она имеет линейную скорость [латекс] v = \ frac {\ Delta {s}} {\ Delta {t}} \\ [/ латекс].
Из [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex] мы видим, что Δ s = r Δ θ . Подстановка этого в выражение для v дает [latex] v = \ frac {r \ Delta \ theta} {\ Delta {t}} = r \ omega \\ [/ latex].
Мы записываем эту взаимосвязь двумя разными способами и получаем два разных вывода:
[латекс] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex].
Первое соотношение в [latex] v = r \ omega \ text {or} \ omega \ frac {v} {r} \\ [/ latex] утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (наибольшее r ), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью .Вторую взаимосвязь в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины такая же, как скорость v автомобиля. См. Рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой v означает большой ω , потому что v = rω . Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ( ω ), будет создавать для автомобиля большую линейную скорость ( v ).
Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси составляет v , как если бы автомобиль был поднят. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.
Пример 1. Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость 0.Автомобильная шина с радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 4.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем v = 15,0 м / с. Радиус шины задан равным r = 0,300 м. Зная v и r , мы можем использовать второе соотношение в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] для вычисления угловой скорости .
Решение
Для вычисления угловой скорости мы будем использовать следующее соотношение: [latex] \ omega \ frac {v} {r} \\ [/ latex].
Замена известных,
[латекс] \ omega = \ frac {15.0 \ text {m / s}} {0.300 \ text {m}} = 50.0 \ text {rad / s} \\ [/ latex].
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если землеройный комбайн с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его шины вращались медленнее. У них будет угловая скорость [latex] \ omega = \ frac {15.0 \ text {m / s}} {1.20 \ text {m}} = 12.5 \ text {rad / s} \\ [/ latex].
И ω , и v имеют направления (следовательно, это угловая и линейная скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.
Эксперимент на вынос
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5.Когда объект движется по кругу, например муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.
Исследования PhET: Ladybug Revolution
Присоединяйтесь к божьей коровке в исследовании вращательного движения. {\ circ} = 1 \ text { революция} \\ [/ латекс].{\ circ} \\ [/ латекс].
Концептуальные вопросы
- Существует аналогия между вращательными и линейными физическими величинами.Какие вращательные величины аналогичны расстоянию и скорости?
Задачи и упражнения
- Грузовики с полуприцепом имеют одометр на одной ступице колеса прицепа. Ступица утяжеляется таким образом, что она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние. Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
- Микроволновые печи вращаются со скоростью около 6 об / мин.6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
- Бейсбольный питчер выносит руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера составляет 35,0 м / с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
- В лакроссе мяч выбрасывается из сетки на конец клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча около локтевого сустава 30.0 рад / с и мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
- Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
- Комплексные концепции. При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава. (a) Если скорость кончика ботинка кикера составляет 35,0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика ботинка, какова угловая скорость кончика ботинка? (b) Башмак находится в контакте с изначально неподвижным 0.Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность действия футбольного мяча, пренебрегая сопротивлением воздуха.
- Создайте свою проблему. Представьте аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками. Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению.Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную схему тела одного всадника. Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной.
Глоссарий
длина дуги: Δ с , расстояние, пройденное объектом по круговой траектории
яма: крошечное углубление на спиральной дорожке, отформованной в верхней части слоя поликарбоната CD
угол поворота: отношение длины дуги к радиусу кривизны на круговой траектории: [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex]
радиус кривизны: радиус круговой траектории
радиан: единица измерения угла
угловая скорость: ω, скорость изменения угла, под которым объект движется по круговой траектории
Избранные решения проблем и упражнения
1.723 км
3. 5 × 10 7 оборотов
5. 117 рад / с
7. 76,2 рад / с; 728 об / мин
8. (а) 33,3 рад / с; (б) 500 Н; (в) 40,8 м
6.1 Угол вращения и угловая скорость — College Physics
В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии.В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на рис. 6.2 вращается вокруг своего центра, — каждая точка в объекте движется по дуге окружности. Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время.Угол поворота — это величина поворота, аналогичная линейному расстоянию. Угол поворота ΔθΔθ размера 12 {Δθ} {} определяется как отношение длины дуги к радиусу кривизны:
Δθ = Δsr.Δθ = Δsr. размер 12 {Δθ = {{Δs} больше {r}} «.»} {}6,1
Рис. 6.2. Все точки на CD перемещаются по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол ΔθΔθ размер 12 {Δθ} {} за время ΔtΔt размер 12 {Δt} {}. Рисунок 6.3 Радиус круга повернут на угол ΔθΔθ размером 12 {Δθ} {}. Длина дуги ΔsΔs размера 12 {Δs} {} указана на окружности.Длина дуги ΔsΔs размер 12 {Δs} {} — это расстояние, пройденное по круговой траектории, как показано на рисунке 6.3. Обратите внимание, что rr размер 12 {r} {} — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса rr размером 12 {r} {}. Окружность круга равна 2πr2πr размера 12 {2πr} {}.Таким образом, за один полный оборот угол поворота составляет
°. Δθ = 2πrr = 2π, Δθ = 2πrr = 2π. размер 12 {Δθ = {{2πr} over {r}} = 2π «.»} {}6,2
Этот результат является основой для определения единиц измерения углов поворота, ΔθΔθ размер 12 {Δθ} {} до быть радианами (рад), определенными так, что
2πrad = 1 оборот. 2πrad = 1 оборот. size 12 {2π «rad» = «1 оборот»} {}6.3
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 6.1.
| Градус Меры | Мера радиана |
|---|---|
| 30º30º размер 12 {«30» °} {} | π6π6 размер 12 {{{π} больше {6}}} {} |
| 60º60º размер 12 {«60» °} {} | π3π3 размер 12 {{{π} больше {3}}} {} |
| 90º90º размер 12 {«90» °} {} | π2π2 размер 12 {{{π} больше {2}}} {} |
| 120º120º размер 12 {«120» °} {} | 2π32π3 размер 12 {{{2π} больше {3}}} {} |
| 135º135º размер 12 {«135» °} {} | 3π43π4 размер 12 {{{3π} больше {4}}} {} |
| 180º180º размер 12 {«180» °} {} | ππ размер 12 {π} {} |
Таблица 6.1 Сравнение угловых единиц
Рис. 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ размер 12 {Δθ} {}), но точка 2 перемещается по большей длине дуги ΔsΔs размер 12 {влево (Δs вправо)} {}, поскольку находится на большем расстоянии от центра вращения (r) (r) размер 12 {\ (r \)} {}.Если Δθ = 2πΔθ = 2π размер 12 {Δθ = 2π} {} рад, то КД сделал один полный оборот, и каждая точка на КД вернулась в исходное положение. Поскольку в круге или одном обороте 360º360º размер 12 {«360» °} {}, соотношение между радианами и градусами, таким образом, составляет
2πrad = 360º2πrad = 360º размер 12 {2π «rad» = «360» rSup {size 8 {circ}}} {}6.4
так, чтобы
1рад = 360º2π≈57,3º.1рад = 360º2π≈57,3º. размер 12 {1 «rad» = {{«360» rSup {size 8 {circ}}} больше {2π}} = «57» «.» 3 rSup {размер 8 {circ}} «.»} {}6.5
Угловая скорость
Насколько быстро вращается объект? Определим угловую скорость ωω размером 12 {ω} {} как скорость изменения угла. В символах это
. ω = ΔθΔt, ω = ΔθΔt, размер 12 {ω = {{Δθ} над {Δt}} «,»} {}6,6
где угловой поворот ΔθΔθ размер 12 {Δθ} {} происходит за время ΔtΔt размер 12 {Δt} {}.Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ωω размер 12 {ω} {} аналогична линейной скорости vv размером 12 {v} {}. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещает дугу длиной ΔsΔs размером 12 {Δs} {} за время ΔtΔt размером 12 {Δt} {}, и поэтому имеет линейную скорость
v = ΔsΔt.v = ΔsΔt.размер 12 {v = {{Δs} над {Δt}} «.»} {}6,7
Из Δθ = ΔsrΔθ = Δsr размер 12 {Δθ = {{Δs} над {r}}} {} мы видим, что Δs = rΔθΔs = rΔθ размер 12 {Δs = rΔθ} {}. Подставляя это в выражение для размера vv 12 {v} {}, получаем
v = rΔθΔt = rω.v = rΔθΔt = rω. размер 12 {v = {{rΔθ} over {Δt}} = rω «.»} {}6,8
Мы записываем это соотношение двумя разными способами и получаем два разных вывода:
v = rω или ω = vr.v = rω или ω = vr. размер 12 {v = rω« «или» ω = {{v} over {r}} «.»} {}6.9
Первое соотношение в v = rω или ω = vrv = rω или ω = vr размер 12 {v = rω« или «ω = {{v} над {r}}} {} утверждает, что линейная скорость Размер vv 12 {v} {} пропорционален расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (наибольший размер rr 12 {r} {}), как и следовало ожидать. Мы также можем назвать эту линейную скорость vv размером 12 {v} {} точки на ободе тангенциальной скоростью . Второе соотношение в v = rω или ω = vrv = rω или ω = vr размер 12 {v = rω« или «ω = {{v} над {r}}} {} можно проиллюстрировать, рассмотрев шину движущаяся машина.Обратите внимание, что скорость точки на ободе шины такая же, как скорость vv размера 12 {v} {} автомобиля. См. Рисунок 6.5. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой размер vv 12 {v} {} означает большой размер ωω 12 {ω} {}, потому что v = rωv = rω размер 12 {v = rω} {}. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (размер ωω 12 {ω} {}), будет создавать для автомобиля большую линейную скорость (размер vv 12 {v} {}).
Рисунок 6.5 Автомобиль, движущийся вправо со скоростью vv размером 12 {v} {}, имеет шину, вращающуюся с угловой скоростью ωω размером 12 {ω} {}.Скорость протектора шины относительно оси — vv размера 12 {v} {}, такая же, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = rωv = rω size 12 {v = rω} {}, где rr size 12 {r} {} — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.Пример 6.1
Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м / с и 15,0 м / с размером 12 {«15» «.»0`» м / с «} {} (около 54 км / ч 54 км / ч размер 12 {» 54 «» «км / ч»} {}). См. Рис. 6.5.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем v = 15,0 м / с. v = 15,0 м / с. размер 12 {v} {} Радиус шины задан равным r = 0,300 м. r = 0,300 м. размер 12 {r} {} Зная vv размер 12 {v} {} и размер rr 12 {r} {}, мы можем использовать второе соотношение в v = rω, ω = vrv = rω, ω = vr size 12 {v = rω, « ω = { {v} over {r}}} {} для вычисления угловой скорости.
Решение
Для вычисления угловой скорости воспользуемся следующим соотношением:
ω = vr.ω = vr. размер 12 {ω = {{v} over {r}} «.»} {}6,10
Подстановка известных,
ω = 15,0 м / с 0,300 м = 50,0 рад / с. ω = 15,0 м / с 0,300 м = 50,0 рад / с. размер 12 {ω = {{«15» «.» 0 «м / с»} больше {0 «.» «300» «m»}} = «50» «.» 0 «рад / с.»} {}6.11
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с.Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землерой с гораздо большими шинами, скажем, радиусом 1,20 м, двигался с той же скоростью 15,0 м / с, его шины вращались бы медленнее. У них будет угловая скорость
ω = (15,0 м / с) / (1,20 м) = 12,5 рад / с. Ω = (15,0 м / с) / (1,20 м) = 12,5 рад / с. размер 12 {ω = \ («15» «.» 0` «м / с» \) / \ (1 «.» «20» `m \) =» 12 «». » 5` «рад / с.»} {}6.12
Оба размера ωω 12 {ω} {} и vv размера 12 {v} {} имеют направления (следовательно, они имеют угловую и линейную скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 6.6.
Take-Home Experiment
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем).Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рис. 6.6 Когда объект движется по кругу, здесь муха на краю старинной виниловой пластинки, его мгновенная скорость всегда касается круга.Направление угловой скорости в этом случае — по часовой стрелке.
Божья коровка Revolution
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с координатами x, y, скоростью и ускорением жука, используя векторы или графики.
6.1: Угол поворота и угловая скорость
В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение.Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси, например, когда компакт-диск (компакт-диск) на рисунке вращается вокруг своего центра, каждая точка объекта следует по дуге окружности.Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Угол поворота \ (\ Delta \ theta \) определяется как отношение длины дуги к радиусу кривизны:
\ [\ Delta \ theta = \ dfrac {\ Delta s} {r}. \]
Рисунок \ (\ PageIndex {1} \): Все точки на компакт-диске перемещаются по дугам окружности. Ямы вдоль линии от центра к краю все перемещаются на один и тот же угол \ (\ Delta \ theta \) за время \ (\ Delta t \).Рисунок \ (\ PageIndex {2} \): Радиус круга повернут на угол \ (\ Delta \ theta \). Длина дуги \ (\ delta s \) описывается на окружности.Длина дуги \ (\ Delta s \) — это расстояние, пройденное по круговой траектории, как показано на рисунке. Обратите внимание, что r — это радиус кривизны круговой траектории. Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса \ (r \). Окружность круга равна \ (2 \ pi r \).
Таким образом, за один полный оборот угол поворота равен \ [\ Delta \ theta = \ dfrac {2 \ pi r} {r} = 2 \ pi.\]
Этот результат является основой для определения единиц, используемых для измерения углов поворота, \ (\ Delta \ theta \) равными радианам (рад), таким образом, что
\ [2 \ pi \, радианы = 1 \ космический оборот. о \)
Угловая скорость
Насколько быстро вращается объект? Мы определяем угловую скорость \ (\ omega \) как скорость изменения угла. В символах это
.\ [\ omega = \ dfrac {\ Delta \ theta} {\ Delta t}, \]
, где угловое вращение \ (\ Delta \ theta \) происходит за время \ (\ Delta t \). Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с). Угловая скорость \ (\ omega \) аналогична линейной скорости \ (v \).Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги \ (\ Delta s \) за время \ (\ Delta t \), и поэтому имеет линейную скорость
\ [v = \ dfrac {\ Delta s} {\ Delta t}. \]
Из \ (\ Delta \ theta = \ frac {\ Delta s} {r} \) мы видим, что \ (\ Delta s = r \ Delta \ theta \). Подставляя это в выражение для \ (v \), получаем
\ [v = \ dfrac {r \ Delta \ theta} {\ Delta t} = r \ omega. \]
Мы записываем эту взаимосвязь двумя разными способами и получаем два разных вывода:
\ [v = r \ omega, \ или \, \ omega = \ dfrac {v} {r}.\]
Первое соотношение в \ (v = r \ omega, \ или \, \ omega = \ dfrac {v} {r} \) утверждает, что линейная скорость \ (v \) пропорциональна расстоянию от центра вращение, таким образом, оно является наибольшим для точки на ободе (наибольшее значение \ (r \)), как и следовало ожидать. Мы также можем назвать эту линейную скорость \ (v \) точки на ободе тангенциальной скоростью . Второе соотношение в \ (v = r \ omega, \ или \, \ omega = \ dfrac {v} {r} \) можно проиллюстрировать на примере шины движущегося автомобиля.Обратите внимание, что скорость точки на ободе шины такая же, как скорость \ (v \) автомобиля. См. Рисунок. Таким образом, чем быстрее движется машина, тем быстрее вращается шина — большой \ (v \) означает большой \ (\ omega \), потому что \ (v = r \ omega \). Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью \ ((\ omega) \), создаст большую линейную скорость \ ((v) \) для автомобиля.
Рисунок \ (\ PageIndex {4} \): Автомобиль, движущийся со скоростью \ (v \) вправо, имеет шину, вращающуюся с угловой скоростью \ (\ omega \).Скорость протектора шины относительно оси равна \ (v \), как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью \ (v = r \ omega \), где \ (r \) — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.Пример \ (\ PageIndex {1} \): Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью \ (15,0 м / с \) (примерно \ (54 \, км / ч \)). См. Рисунок.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем \ (v = 15.0 м / с \). Радиус шины равен \ (r = 0,300 \, м \). Зная \ (v \) и \ (r \), мы можем использовать второе соотношение в \ (v = \ omega r \), \ (\ omega = \ frac {v} {r} \) для вычисления угловой скорости .
Решение
Для вычисления угловой скорости воспользуемся следующим соотношением:
\ [\ omega = \ dfrac {v} {r}. \]
Замена известных,
\ [\ omega = \ dfrac {15,0 \, м / с} {0,300 \, м} = 50,0 \, рад / с. \]
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50.0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землерой с гораздо большими шинами, скажем, радиусом 1,20 м, двигался с той же скоростью 15,0 м / с, его шины вращались бы медленнее. У них будет угловая скорость
\ [\ omega = (15,0 \, м / с) / (1,20 \, м) = 12,5 \, рад / с. \]
У \ (\ omega \) и \ (v \) есть направления (следовательно, это угловая и линейная скорости соответственно).Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке.
ЭКСПЕРИМЕНТ НА ДОМУ
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке.Определите другие круговые движения и измерьте их угловые скорости.
Рисунок \ (\ PageIndex {5} \): Когда объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.ФЕТ ИССЛЕДОВАНИЯ: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение.Изучите, как круговое движение связано с координатами x, y, скоростью и ускорением жука, используя векторы или графики.
Сводка раздела
- Равномерное круговое движение — это движение по окружности с постоянной скоростью. Угол поворота \ (\ delta \ theta \) определяется как отношение длины дуги к радиусу кривизны:
\ [\ Delta \ theta = \ dfrac {\ Delta s} {r} \]
, где длина дуги \ (\ delta s \) — это расстояние, пройденное по круговой траектории, а \ (r \) — радиус кривизны круговой траектории.о. \]
\ [\ omega = \ dfrac {\ Delta \ theta} {\ Delta t}, \]
, где вращение \ (\ Delta \ theta \) происходит за время \ (\ Delta t \). Единицы угловой скорости — радианы в секунду (рад / с). Линейная скорость \ (v \) и угловая скорость \ (\ omega \) связаны соотношением
\ [v = r \ omega, \ или \, \ omega = \ dfrac {v} {r}. \]
Глоссарий
- длина дуги
- Δs, расстояние, пройденное объектом по круговой траектории
- приямок
- крошечное углубление на спиральной дорожке, отформованной в верхней части слоя поликарбоната CD
- угол поворота
- отношение длины дуги к радиусу кривизны на круговой траектории: \ (Δθ = \ frac {Δs} {r} \)
- радиус кривизны
- радиус круговой траектории
- радиан
- единица измерения угла
- угловая скорость
- \ (ω \), скорость изменения угла, под которым объект движется по круговой траектории
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
6.1 Угол вращения и угловая скорость — Физика колледжа, главы 1-17
Сводка
- Определите длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Вычислить угловую скорость вращения колеса автомобиля.
В главе 2 «Кинематика» мы изучили движение по прямой и ввели такие понятия, как смещение, скорость и ускорение.В главе 3 «Двумерная кинематика» рассматривается движение в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на рисунке 1 вращается вокруг своего центра — каждая точка в объекте движется по дуге окружности.Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота [latex] \ boldsymbol {\ Delta \ theta} [/ latex] как отношение длины дуги к радиусу кривизны:
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {r}}. [/ Latex]
Рисунок 1. Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δ θ за время Δ t . Рис. 2. Радиус круга повернут на угол Δ θ . Длина дуги Δ с описана на окружности.Длина дуги [latex] \ boldsymbol {\ Delta {s}} [/ latex] — это расстояние, пройденное по круговой траектории, как показано на рисунке 2. Обратите внимание, что [latex] \ boldsymbol {r} [/ latex] — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна окружности окружности с радиусом [латекс] \ boldsymbol {r}. [/ Latex] Окружность круга равна [латексу] \ boldsymbol {2 \ pi {r }}. [/ latex] Таким образом, за один полный оборот угол поворота равен
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi {r}} {r}} [/ latex] [латекс] \ boldsymbol {= \: 2 \ pi}. [/ Latex]
Этот результат является основой для определения единиц, используемых для измерения углов поворота, [latex] \ boldsymbol {\ Delta \ theta} [/ latex] равным радианам (рад), таким образом, что
[латекс] \ boldsymbol {2 \ pi \ textbf {rad} = 1 \ textbf {революция}.0} [/ latex]
Если [latex] \ boldsymbol {\ Delta \ theta = 2 \ pi \ textbf {rad}}, [/ latex], то компакт-диск сделал один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение.0}. [/ Latex]
Насколько быстро вращается объект? Мы определяем угловую скорость [латекс] \ boldsymbol {\ omega} [/ latex] как скорость изменения угла. В символах это
.[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ theta} {\ Delta {t}}}, [/ латекс]
, где угловое вращение [латекс] \ boldsymbol {\ Delta \ theta} [/ latex] происходит за время [latex] \ boldsymbol {\ Delta {t}}. [/ Latex] Чем больше угол поворота в данном количество времени, тем больше угловая скорость.Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость [латекс] \ boldsymbol {\ omega} [/ latex] аналогична линейной скорости [латекс] \ boldsymbol {v}. [/ Latex] Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим яму на вращающемся компакт-диске. Эта яма перемещает длину дуги [латекс] \ boldsymbol {\ Delta {s}} [/ latex] за время [латекс] \ boldsymbol {\ Delta {t}}, [/ latex] и поэтому имеет линейную скорость
[латекс] \ boldsymbol {v \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {\ Delta {t}}}.[/ латекс]
Из [latex] \ boldsymbol {\ Delta \ theta = \ frac {\ Delta {s}} {r}} [/ latex] мы видим, что [latex] \ boldsymbol {\ Delta {s} = r \ Delta \ theta }. [/ latex] Подставляя это в выражение для [latex] \ boldsymbol {v} [/ latex], получаем
[латекс] \ boldsymbol {v \: =} [/ latex] [латекс] \ boldsymbol {\ frac {r \ Delta \ theta} {\ Delta {t}}} [/ latex] [латекс] \ boldsymbol {= \: r \ omega}. [/ латекс]
Мы записываем эту взаимосвязь двумя разными способами и получаем два разных вывода:
[латекс] \ boldsymbol {v = r \ omega \ textbf {или} \ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v} {r}}.[/ латекс]
Первое соотношение в [латексе] \ boldsymbol {v = r \ omega \ textbf {or} \ omega \: = \ frac {v} {r}} [/ latex] утверждает, что линейная скорость [латекс] \ boldsymbol { v} [/ latex] пропорционален расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (самый большой [латекс] \ boldsymbol {r} [/ latex]), как и следовало ожидать. Мы также можем назвать эту линейную скорость [латекс] \ boldsymbol {v} [/ latex] точки на ободе тангенциальной скоростью . Вторую взаимосвязь в [latex] \ boldsymbol {v = r \ omega \ textbf {или} \ omega \: = \ frac {v} {r}} [/ latex] можно проиллюстрировать на примере шины движущегося автомобиля.Обратите внимание, что скорость точки на ободе шины такая же, как скорость [latex] \ boldsymbol {v} [/ latex] автомобиля. См. Рис. 4. Таким образом, чем быстрее движется машина, тем быстрее вращается шина — большой [латекс] \ boldsymbol {v} [/ latex] означает большой [латекс] \ boldsymbol {\ omega}, [/ latex], потому что [латекс ] \ boldsymbol {v = r \ omega}. [/ latex] Аналогичным образом, шина большего радиуса, вращающаяся с той же угловой скоростью ([latex] \ boldsymbol {\ omega} [/ latex]), будет иметь большую линейную скорость ( [латекс] \ boldsymbol {v} [/ латекс]) для автомобиля.
Рис. 4. Автомобиль, движущийся со скоростью v вправо, имеет шину, вращающуюся с угловой скоростью ω . Скорость протектора шины относительно оси составляет v , как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω , где r — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.Пример 1: Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется в [латексе] \ boldsymbol {15.0 \ textbf {м / с}} [/ latex] (примерно [латекс] \ boldsymbol {54 \ textbf {км / h}} [/ latex]). См. Рисунок 4.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем [latex] \ boldsymbol {v = 15.0 \ textbf {m / s}}. [/ Latex] Дан радиус шины быть [латексом] \ boldsymbol {r = 0.300 \ textbf {m}}. [/ Latex] Зная [латекс] \ boldsymbol {v} [/ latex] и [latex] \ boldsymbol {r}, [/ latex], мы можем использовать второе соотношение в [latex] \ жирный символ {v = r \ omega, \: \ omega = \ frac {v} {r}} [/ latex] для вычисления угловой скорости.
Решение
Для вычисления угловой скорости воспользуемся следующим соотношением:
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v} {r}}. [/ Latex]
Замена известных,
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {15.0 \ textbf {m / s}} {0.300 \ textbf {m}}} [/ latex] [latex] \ boldsymbol {= \: 50.0 \ textbf {rad / s}}. [/ Latex]
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если бы землерой с гораздо большими шинами, скажем, радиусом 1,20 м, двигался с той же скоростью 15.0 м / с, его колеса будут вращаться медленнее. У них будет угловая скорость
[латекс] \ boldsymbol {\ omega = (15.0 \ textbf {m / s}) / (1.20 \ textbf {m}) = 12.5 \ textbf {rad / s}}. [/ Latex]
У [latex] \ boldsymbol {\ omega} [/ latex] и [latex] \ boldsymbol {v} [/ latex] есть направления (следовательно, они имеют угловую и линейную скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.
ЭКСПЕРИМЕНТ НА ДОМУ
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5. Когда объект движется по кругу, здесь муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.ФЕТ ИССЛЕДОВАНИЯ: РЕВОЛЮЦИЯ БОЖЬЕЙ КОРОВКИ
Рисунок 6. Ladybug RevolutionПрисоединяйтесь к божьей коровке и исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с координатами x, y, скоростью и ускорением жука, используя векторы или графики.
- Равномерное круговое движение — это движение по окружности с постоянной скоростью. Угол поворота [латекс] \ boldsymbol {\ Delta \ theta} [/ latex] определяется как отношение длины дуги к радиусу кривизны:
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {r}}, [/ латекс]
, где длина дуги [latex] \ boldsymbol {\ Delta {s}} [/ latex] — это расстояние, пройденное по круговой траектории, а [latex] \ boldsymbol {r} [/ latex] — это радиус кривизны круговой траектории.0}. [/ Latex]
- Угловая скорость [латекс] \ boldsymbol {\ omega} [/ latex] — это скорость изменения угла,
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ theta} {\ Delta {t}}}, [/ латекс]
, где вращение [латекс] \ boldsymbol {\ Delta \ theta} [/ latex] происходит за время [latex] \ boldsymbol {\ Delta {t}}. [/ Latex] Единицы угловой скорости — радианы в секунду (рад / с). Линейная скорость [латекс] \ boldsymbol {v} [/ latex] и угловая скорость [латекс] \ boldsymbol {\ omega} [/ latex] связаны соотношением
[латекс] \ boldsymbol {v = r \ omega \ textbf {или} \ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v} {r}}.[/ латекс]
Концептуальные вопросы
1: Существует аналогия между вращательными и линейными физическими величинами. Какие вращательные величины аналогичны расстоянию и скорости?
Задачи и упражнения
1: Грузовики с полуприцепом имеют одометр на одной ступице колеса прицепа. Ступица утяжеляется таким образом, что она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние.Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
2: Микроволновые печи вращаются со скоростью около 6 об / мин. Что это в оборотах в секунду? Какова угловая скорость в радианах в секунду?
3: Автомобиль с шинами радиусом 0,260 м проезжает 80 000 км, прежде чем износится. Сколько оборотов делают шины без учета поддержки и изменения радиуса из-за износа?
4: а) Каков период вращения Земли в секундах? б) Какова угловая скорость Земли? (c) Учитывая, что Земля имеет радиус [латекс] \ boldsymbol {6.6 \ textbf {m}} [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
5: Бейсбольный питчер выносит руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера составляет 35,0 м / с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
6: В лакроссе мяч выбрасывается из сетки на конец клюшки путем вращения клюшки и предплечья вокруг локтя.Если угловая скорость мяча относительно локтевого сустава составляет 30,0 рад / с, а мяч находится на 1,30 м от локтевого сустава, какова скорость мяча?
7: Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
8: Интегрированные концепции
При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава.
(a) Если скорость носка башмака кикера равна 35.0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика обуви, какова угловая скорость кончика обуви?
(b) Башмак находится в контакте с первоначально неподвижным футбольным мячом весом 0,500 кг в течение 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с?
(c) Найдите максимальную дальность полета футбольного мяча, пренебрегая сопротивлением воздуха.
9: Создайте свою проблему
Рассмотрим аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками.Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению. Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную схему тела одного всадника. Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной.
Глоссарий
- длина дуги
- [latex] \ boldsymbol {\ Delta {s}}, [/ latex] расстояние, пройденное объектом по круговой траектории
- приямок
- крошечное углубление на спиральной дорожке, отформованной в верхней части слоя поликарбоната CD
- угол поворота
- отношение длины дуги к радиусу кривизны на круговой траектории:
[латекс] \ boldsymbol {\ Delta \ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {s}} {r}} [/ латекс]
- радиус кривизны
- радиус круговой траектории
- радиан
- единица измерения угла
- угловая скорость
- [latex] \ boldsymbol {\ omega}, [/ latex] скорость изменения угла, под которым объект движется по круговой траектории
Решения
Задачи и упражнения
1:
723 км
3:
[латекс] \ boldsymbol {5 \ times10 ^ 7 \ textbf {rotations}} [/ латекс]
5:
117 рад / с
7:
8:
(а) 33.3 рад / с
(б) 500 Н
(в) 40,8 м
Вращательное движение | Блог Гэри Гарбера
До сих пор в этом семестре нашего изучения классической механики мы изучали поступательное движение. Теперь мы приступим к изучению вращательного движения.
У каждой концепции, которую мы до сих пор изучили, есть аналог вращения.
В начале года мы обсуждали, как объект может претерпеть смещение x .Мы также могли повернуть объект на угол θ.
Аналогично, скорость объекта или скорость изменения положения
имеет аналог вращения, скорость вращения, скорость изменения угла
ω = Δθ / Δt
Существует также угловое ускорение, которое представляет собой скорость изменения угловой скорости. Мы можем изучить крутящий момент, который представляет собой силу вращения. Момент инерции (или инерции вращения) — это тенденция объекта оставаться в состоянии покоя или оставаться в состоянии вращательного движения.Основываясь на этом, угловой момент — это инерция вращения в состоянии вращательного движения. У нас также может быть кинетическая энергия вращения!
Если мы предположим, что объект непрерывно вращается, то другой способ взглянуть на вращательное движение — это исследовать период вращения, T . Измеряемый в единицах времени ( миллисекунд, секунды, часы, годы, эоны …), период — это время, необходимое для одного полного оборота. Мы также могли бы описать, как часто объект вращается.Частота объекта, f , на самом деле обратно пропорциональна периоду вращения.
T = 1 / f
и
ф = 1 / т
Метрической единицей измерения частоты является герц ( Гц, ), где 1 Гц = 1 цикл / секунду . Вы, вероятно, знакомы с термином Герц по частотам на шкале радиоприемника, например, WBUR 90,9 МГц или WBZ 1030 кГц .
Пример
Представьте себе маленького мальчика, который пытается вызвать головокружение, быстро вращаясь.Если он вращается с частотой 0,8 Гц, сколько времени ему потребуется, чтобы сделать 1 оборот?
f = 0,8 Гц
T = 1 / f = 1 / 0,8 Гц = 1 / 0,8 циклов в секунду = 1,25 секунд
Другая традиционная единица измерения частоты — оборотов в минуту или оборотов в минуту . Вы можете увидеть это на старомодном проигрывателе, который мог вращаться со скоростью 33 или 45 об / мин на .
А пока рассмотрим двух маленьких человечков LEGO, стоящих на проигрывателе.Когда проигрыватель поворачивается, мы можем описать движение маленьких человечков LEGO с точки зрения их линейной скорости (метры в секунду) или их скорости вращения. Если мы установим проигрыватель на 45 об / мин, то оба LEGO-человечка будут иметь одинаковую скорость вращения. Однако у них разные линейные или тангенциальные скорости. Мы используем слово тангенциальный, потому что, если человек LEGO поскользнется и упадет, его собственная инерция заставит его отлететь от проигрывателя по линии, касающейся его кругового движения!
Мы можем рассчитать линейную скорость для каждого человека, используя уравнение
v = 2πr / Т
где r — радиус окружности, а T — период вращения.Помните, что скорость — это расстояние во времени. В этом случае расстояние за один период вращения оказывается длиной окружности.
Если мужчины расположены на нашем проигрывателе на расстоянии 10 см и 4 см от центральной оси:
Пример
f = 45 об / мин
r = 12 см
Сначала вычисляем период. С 45 об / мин = 0,75 об / с
Таким образом, период вращения равен 1.33 секунд .
Таким образом, скорость будет
v = 2πr / T = 2π (10 см ) / 1,33 с = 47 см / с
Для маленького человечка, стоящего в радиусе 4 см, у него гораздо меньшая линейная скорость, хотя и такая же скорость вращения.
v = 2πr / T = 2π (4 см ) / 1,33 с = 19 см / с
Есть тонкая разница между скоростью вращения и скоростью вращения, которую мы представим позже.
Мы можем определить взаимосвязь между линейной скоростью и угловой скоростью с помощью следующего уравнения
v = ω r
Обратите внимание, что ω, угловая скорость, была определена ранее как изменение угла в единицу времени.
ω = Δθ / Δt
При рассмотрении приведенного выше уравнения возникает интересный вопрос об единицах измерения угловой скорости. До сих пор мы использовали такие термины, как обороты в минуту или обороты в секунду. Но революцию можно было бы определить как ПОЛНЫЙ поворот на 360 °.
Вы, наверное, изучали единицы измерения углов в градусах. Но когда мы обсуждаем угловую скорость, мы обычно не говорим об целом числе оборотов. Таким образом, мы могли бы использовать такие единицы измерения, как градусы в секунду. Однако градус не является метрической единицей вращения. Стандартная единица измерения — радиан.
2π радиан = 360 °
Если мы посмотрим на изображение единичного круга, мы сможем увидеть преобразование между радианами и градусами. Это действительно одно и то же, просто разные единицы.
С одной стороны, единственная разница между частотой и угловой скоростью заключается в единицах измерения. Угловая скорость измеряется в радиан / секунду , а частота измеряется в Гц или оборотов в секунду . Таким образом, мы могли бы выразить алгебраическую связь между этими двумя терминами как
2πf = ω
Используя это, мы могли бы фактически найти угловую скорость нашего проигрывателя, который вращается со скоростью 45 об / мин .
ω = 2πf = 2π (0.75 об / с ) = 4,7 радиан / с
Пример
Давайте еще раз посмотрим на человечков LEGO на проигрывателе. Используя соотношение между линейной скоростью и угловой скоростью, находим
v = ω r
v = 4,7 радиан в секунду x 10 см = 47 см / с
и для человека ближе к центру
v = 4,7 радиан в секунду x 4 см = 19 см / с
Важно отметить, что линейная скорость увеличивается как с угловой скоростью, так и с радиусом
Как рассчитать угловую скорость
Обновлено 15 декабря 2020 г.
Кевин Бек
В повседневном дискурсе «скорость» и «скорость» часто используются как синонимы.Однако в физике эти термины имеют особые и различные значения. «Скорость» — это скорость перемещения объекта в пространстве, и она задается только числом с определенными единицами измерения (часто в метрах в секунду или милях в час). С другой стороны, скорость — это скорость, связанная с направлением. Таким образом, скорость называется скалярной величиной, тогда как скорость — векторной величиной.
Когда машина мчится по шоссе или по воздуху проносится бейсбольный мяч, скорость этих объектов измеряется относительно земли, тогда как скорость включает больше информации.Например, если вы едете в машине со скоростью 70 миль в час по межштатной автомагистрали 95 на восточном побережье Соединенных Штатов, также полезно знать, идет ли она на северо-восток в сторону Бостона или на юг в сторону Флориды. В случае с бейсбольным мячом вы можете захотеть узнать, изменяется ли его координата y быстрее, чем координата x (летающий мяч), или верно ли обратное (линейный привод). Но как насчет вращения шин или вращения (вращения) бейсбольного мяча, когда машина и мяч движутся к своему конечному пункту назначения? Для такого рода вопросов физика предлагает концепцию угловой скорости .
Основы движения
Вещи перемещаются в трехмерном физическом пространстве двумя основными способами: перемещением и вращением. Трансляция — это перемещение всего объекта из одного места в другое, как машина, едущая из Нью-Йорка в Лос-Анджелес. С другой стороны, вращение — это циклическое движение объекта вокруг фиксированной точки. Многие объекты, такие как бейсбольный мяч в приведенном выше примере, демонстрируют оба типа движения одновременно; По мере того, как летающий мяч перемещается по воздуху от домашней пластины к дальнему забору, он также вращается с заданной скоростью вокруг своего собственного центра.
Описание этих двух видов движения рассматривается как отдельные физические задачи; то есть, при расчете расстояния, которое мяч проходит по воздуху, на основе таких вещей, как начальный угол запуска и скорость, с которой он покидает летучую мышь, вы можете игнорировать его вращение, а при вычислении его вращения вы можете рассматривать его как сидящего в одном место для настоящих целей.
Уравнение угловой скорости
Во-первых, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-то другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругу или их части.Вы можете вспомнить из геометрии или тригонометрии, что длина окружности равна его диаметру, умноженному на константу пи, или πd . (Значение пи составляет около 3,14159.) Это чаще всего выражается в терминах радиуса круга r , который составляет половину диаметра, в результате чего окружность 2πr .
Кроме того, вы, вероятно, где-то по пути узнали, что круг состоит из 360 градусов (360 °). Если вы переместитесь на расстояние S по окружности, то угловое смещение θ будет равно S / r.o
В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно в секунду.
Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r от центра круга, причем направление v всегда перпендикулярно радиус круга, то угловая скорость может быть записана в виде
\ omega = \ frac {v} {r}
, где ω — греческая буква омега.Единицы угловой скорости — радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v / r дает м / с, деленные на м, или с -1 , что означает, что радианы технически являются безразмерной величиной.
Уравнения вращательного движения
Формула углового ускорения выводится таким же существенным образом, как и формула угловой скорости: это просто линейное ускорение в направлении, перпендикулярном радиусу окружности (эквивалентно, его ускорение по касательной к круговой траектории в любой точке) делится на радиус круга или части круга, который равен:
\ alpha = \ frac {\ omega} {t}
, потому что для кругового движения:
a_t = \ frac {\ omega r} {t} = \ frac {v} {t}
α , как вы, наверное, знаете, это греческая буква «альфа».2} {r}
Это ускорение направлено к точке, вокруг которой вращается рассматриваемый объект. Это может показаться странным, поскольку объект не приближается к этой центральной точке, поскольку радиус r фиксирован. Думайте о центростремительном ускорении как о свободном падении, при котором нет опасности столкновения объекта с землей, потому что сила, притягивающая объект к нему (обычно сила тяжести), точно компенсируется тангенциальным (линейным) ускорением, описываемым первым уравнением в эта секция.Если бы a c не было равно a t , объект либо улетел бы в космос, либо вскоре врезался бы в середину круга.
Связанные величины и выражения
Хотя угловая скорость обычно выражается, как уже отмечалось, в радианах в секунду, могут быть случаи, в которых предпочтительнее или необходимо использовать вместо этого градусы в секунду или, наоборот, преобразовывать из градусов в радианы до решения проблемы.
Допустим, вам сказали, что источник света вращается на 90 ° каждую секунду с постоянной скоростью. Какова его угловая скорость в радианах?
Сначала запомните, что 2π радиан = 360 °, и установите пропорцию:
\ frac {360} {2 \ pi} = \ frac {90} {\ omega} \ подразумевает 360 \ omega = 180 \ pi \ подразумевает \ omega = \ frac {\ pi} {2}
Ответ — половина пи радиан в секунду.
Если бы вам дополнительно сказали, что световой луч имеет дальность действия 10 метров, какова будет вершина линейной скорости луча v , его угловое ускорение α и его центростремительное ускорение a с ?
Чтобы решить для v , сверху, v = ωr, где ω = π / 2 и r = 10m:
\ frac {\ pi} {2} 10 = 15.2
Зависимость угловой скорости от линейной
Основываясь на предыдущей задаче, представьте себя на очень большой карусели с маловероятным радиусом 10 километров (10 000 метров). Эта карусель совершает один полный оборот каждые 1 минуту 40 секунд или каждые 100 секунд.
Одним из следствий разницы между угловой скоростью, которая не зависит от расстояния от оси вращения, и линейной круговой скоростью, которой нет, является то, что два человека, испытывающие одинаковые ω , могут испытывать совершенно разные физические ощущения. .Если вы окажетесь на расстоянии 1 метра от центра в этой предполагаемой массивной карусели, ваша линейная (тангенциальная) скорость будет:
v_t = \ omega r = \ frac {2 \ pi} {100} (1) = 0,0628 \ text {м / с}
или 6,29 см (менее 3 дюймов) в секунду.
Но если вы находитесь на краю этого монстра, ваша линейная скорость будет:
v_t = \ omega r = \ frac {2 \ pi} {100} (10000) = 628 \ text {m / s}
Это примерно 1406 миль в час, быстрее, чем пуля. Подожди!
Honors Rotational Kinematics
Радианы и градусы
Обычно люди обсуждают вращательное движение в градусах, где один полный оборот по окружности равен 360 °.Когда речь идет о вращательном движении с точки зрения физики, измерение вращательного движения в единицах, известных как радианы (рад), является гораздо более эффективным. Радиан измеряет расстояние вокруг дуги, равное длине радиуса дуги.
До этого момента вы описывали расстояния и смещения в терминах Δx и Δy. Обсуждая угловые смещения, вы должны перейти к описанию поступательного смещения вокруг дуги в терминах переменной s, продолжая использовать символ θ (тета) для обозначения углов и углового смещения.
Расстояние полностью по круговой траектории (360 °), известное как окружность, C, можно найти с помощью ∆s = C = 2𝜋r = 2𝜋 радиан. Следовательно, вы можете использовать это как коэффициент преобразования для перехода между градусами и радианами.
Вопрос: Преобразовать 90 ° в радианы.
Ответ:
Вопрос: Преобразовать 6 радианов в градусы.
Ответ:
Углы также измеряются в оборотах (полные обходы по кругу).Полный единичный оборот равен 360 °, поэтому вы можете записать коэффициенты преобразования для углов поворота и смещений как 360 ° = 2𝜋 радиан = 1 оборот.
Вопрос: Преобразуйте 1,5 оборота в радианы и градусы.
Ответ:
Скорость и ускорение
Вращательная кинематика очень похожа на поступательную кинематику, все, что вам нужно сделать, это изучить вращательные версии кинематических переменных и уравнений.Когда вы изучали кинематику перевода, смещение обсуждалось в терминах Δx. При вращательной кинематике вместо этого вы будете использовать угловую координату θ. Когда в трансляционном мире была введена средняя скорость, вы использовали формулу:
Изучая вращательное движение, вы будете говорить об угловой скорости ω (омега), выраженной в радианах в секунду (рад / с). Поскольку угловая (вращательная) скорость является вектором, определите положительное направление вращения как вращение против часовой стрелки по круговой траектории, а отрицательное направление как по часовой стрелке вокруг траектории.
ПРИМЕЧАНИЕ: Формально направление угловых векторов определяется правилом правой руки. Оберните пальцы правой руки в направлении вращения, скорости или ускорения, а большой палец будет указывать в направлении вектора.
Вопрос: Рекорд вращается на фонографе со скоростью 33 об / мин (оборотов в минуту) по часовой стрелке.Найдите угловую скорость записи.
Ответ:
Обратите внимание, что вектор угловой скорости отрицательный, потому что запись вращается по часовой стрелке.
Вопрос: Найдите величину угловой скорости Земли в радианах в секунду.
Ответ: Осознавая, что Земля совершает один полный оборот каждые 24 часа, мы можем оценить величину угловой скорости Земли как:
Аналогичным образом, когда вы узнали о поступательном ускорении, вы нашли ускорение как скорость изменения поступательной скорости объекта:
Угловое ускорение α (альфа), выраженное в радианах в секунду 2 , представляет собой скорость изменения угловой скорости объекта.Поскольку угловое ускорение также является вектором, вы можете определить его направление как положительное для увеличения угловой скорости в направлении против часовой стрелки и отрицательное для увеличения угловой скорости в направлении по часовой стрелке.
Вопрос: Лягушка едет на одноколесном велосипеде. Если колесо моноцикла начинается в состоянии покоя и равномерно ускоряется против часовой стрелки до угловой скорости 15 об / мин за 6 секунд, найдите угловое ускорение колеса моноцикла.
Ответ: Сначала преобразуйте 15 об / мин в рад / с.
Далее используйте определение углового ускорения.
Снова обратите внимание на положительное угловое ускорение, поскольку колесо велосипеда ускоряется против часовой стрелки.
Вращательные переменные
Объединяя эти определения, вы наблюдаете очень сильную параллель между поступательными кинематическими величинами и вращательными кинематическими величинами.
| Переменная | Трансляционный | Угловой |
|---|---|---|
| Рабочий объем | Δs | Δθ |
| Скорость | v | ω |
| Разгон | а | α |
| Время | т | т |
Также довольно просто переводить между поступательными и угловыми переменными, когда вы знаете радиус (r) интересующей точки на вращающемся объекте.
Вопрос: Рыцарь взмахивает булавой радиусом 1 м за два полных оборота. Что такое поступательное смещение булавы?
Ответ:
Вопрос: Проигрыватель компакт-дисков предназначен для изменения скорости вращения диска, так что точка, считываемая лазером, перемещается с линейной скоростью, равной единице.25 м / с. Какова скорость вращения компакт-диска в об / с, когда лазер считывает информацию с внутренней части диска на радиусе 0,03 м?
Ответ:
Вопрос: Какова скорость вращения компакт-диска в предыдущей задаче, когда лазер считывает крайнюю часть диска (радиус = 0,06 м)?
Ответ:
Уравнения вращательной кинематики
Параллели между поступательным и вращательным движением идут еще дальше.Вы разработали набор кинематических уравнений поступательного движения, которые позволили вам исследовать взаимосвязь между смещением, скоростью и ускорением. Вы можете разработать соответствующий набор соотношений для углового смещения, угловой скорости и углового ускорения. Уравнения имеют ту же форму, что и трансляционные уравнения, все, что вам нужно сделать, это заменить трансляционные переменные на вращательные переменные, как показано в следующей таблице.
Уравнения вращательной кинематики можно использовать так же, как вы использовали уравнения поступательной кинематики для решения задач.Когда вы знаете три кинематические переменные, вы всегда можете использовать уравнения для решения двух других.
Вопрос: Плотник вырезает кусок дерева с помощью мощной циркулярной пилы. Пильный диск ускоряется из состояния покоя с угловым ускорением от 14 рад / с 2 до максимальной скорости 15 000 об / мин. Какова максимальная скорость пилы в радианах в секунду?
Ответ:
Вопрос: Сколько времени нужно пиле для достижения максимальной скорости?
Ответ: Для решения этой задачи можно использовать кинематические уравнения вращения:
Вопрос: Сколько полных оборотов делает пила при разгоне до максимальной скорости?
Ответ:
Вопрос: Предохранительный механизм остановит пильный диск в 0.3 секунды, если рука плотника оторвется от органов управления пилой. Какое угловое ускорение для этого требуется? Сколько полных оборотов пильное полотно сделает за это время?
Ответ: Начните с воссоздания таблицы кинематики вращения.
Сначала найдите угловое ускорение.
Затем найдите угловое смещение.
