Угол вращения: ОФС.1.2.1.0018.15 Поляриметрия | Фармакопея.рф

Содержание

Углы Эйлера — Euler angles

Геометрическое определение классических углов Эйлера. Система xyz (фиксированная) показана синим, система XYZ (повернутая) показана красным. Линия узлов ( N ) отображается зеленым цветом

Эти углы Эйлера имеют три угла , введенный Леонард Эйлер для описания ориентации в виде твердого тела по отношению к неподвижной системе координат .

Они также могут представлять ориентацию мобильной системы отсчета в физике или ориентацию общего базиса в трехмерной линейной алгебре. Позже Питер Гатри Тейт и Джордж Брайан представили альтернативные формы, предназначенные для использования в аэронавтике и технике.

Эквивалентность цепных вращений

Любая целевая ориентация может быть достигнута, начиная с известной эталонной ориентации, используя определенную последовательность собственных вращений, чьи величины являются углами Эйлера целевой ориентации.

В этом примере используется последовательность zx′-z ″ .

Углы Эйлера могут быть определены элементарной геометрией или композицией поворотов. Геометрическое определение демонстрирует, что трех составных элементарных вращений (вращений вокруг осей системы координат ) всегда достаточно для достижения любого целевого кадра.

Три элементарных вращения могут быть внешними (вращения вокруг осей xyz исходной системы координат, которая, как предполагается, остается неподвижной) или внутренними (вращения вокруг осей вращающейся системы координат XYZ , солидарными с движущимся телом, что изменяет его ориентация после каждого вращения элемента).

Углы Эйлера обычно обозначаются как α , β , γ или ψ , θ , φ . Разные авторы могут использовать разные наборы осей вращения для определения углов Эйлера или разные имена для одних и тех же углов. Следовательно, любому обсуждению, использующему углы Эйлера, всегда должно предшествовать их определение.

Без учета возможности использования двух различных соглашений для определения осей вращения (внутренней или внешней) существует двенадцать возможных последовательностей осей вращения, разделенных на две группы:

Собственные углы Эйлера ( z — x — z , x — y — x , y — z — y , z — y — z , x — z — x , y — x — y )
Углы Тейта – Брайана ( x — y — z , y — z — x , z — x — y , x — z — y , z — y — x , y — x — z ) .

Углы Тейта – Брайана также называют карданными углами ; морские углы ; курс , высота и банк ; или рыскание, тангаж и крен . Иногда оба вида последовательностей называют «углами Эйлера». В этом случае последовательности первой группы называются собственными или классическими углами Эйлера.

Правильные углы Эйлера

Слева: карданный набор, показывающий г — х — г последовательность вращения. Внешний каркас показан в основании. Внутренние оси красного цвета. Справа: простая диаграмма, показывающая аналогичные углы Эйлера на диаграмме.

Геометрическое определение

Оси исходного кадра обозначены как х , у , г и осей повернутого кадра , как

X , Y , Z . Геометрическое определение (иногда называемый статический) начинается с определения линии узлов (N) в качестве пересечения плоскостей ху и XY (он также может быть определен как общий перпендикулярно осям Z и Z , а затем записать в виде векторное произведение N = z Z ).

Используя его, можно определить три угла Эйлера следующим образом: × {\ displaystyle \ times}

Углы Эйлера между двумя системами отсчета определяются только в том случае, если обе системы координат имеют одинаковую ручку .

Соглашения по внутреннему вращению

Собственные вращения — это элементарные вращения, которые происходят вокруг осей системы координат XYZ, прикрепленной к движущемуся телу. Следовательно, они меняют свою ориентацию после каждого вращения элемента. Система

XYZ вращается, а xyz фиксируется. Начиная с XYZ, перекрывающего xyz , композиция из трех внутренних вращений может использоваться для достижения любой целевой ориентации для XYZ .

Углы Эйлера могут быть определены внутренними вращениями. Повернутая рамка XYZ может быть представлена первоначально выровненной с xyz , прежде чем претерпеть три элементарных поворота, представленных углами Эйлера. Его последовательные ориентации можно обозначить следующим образом:

x — y — z , или x ₀ — y ₀ — z ₀ (начальный)
x ′ — y ′ — z ′, или x ₁ — y ₁ — z ₁ (после первого поворота)

x ″ — y ″ — z ″, или x ₂ — y ₂ — z ₂ (после второго поворота)
X — Y — Z , или x ₃ — y ₃ — z ₃ (финал)

Для вышеперечисленной последовательности вращений линию узлов N можно просто определить как ориентацию X после первого вращения элемента. Следовательно, N можно просто обозначить x ′. Кроме того, поскольку третье элементное вращение происходит вокруг Z , она не изменяет ориентацию Z .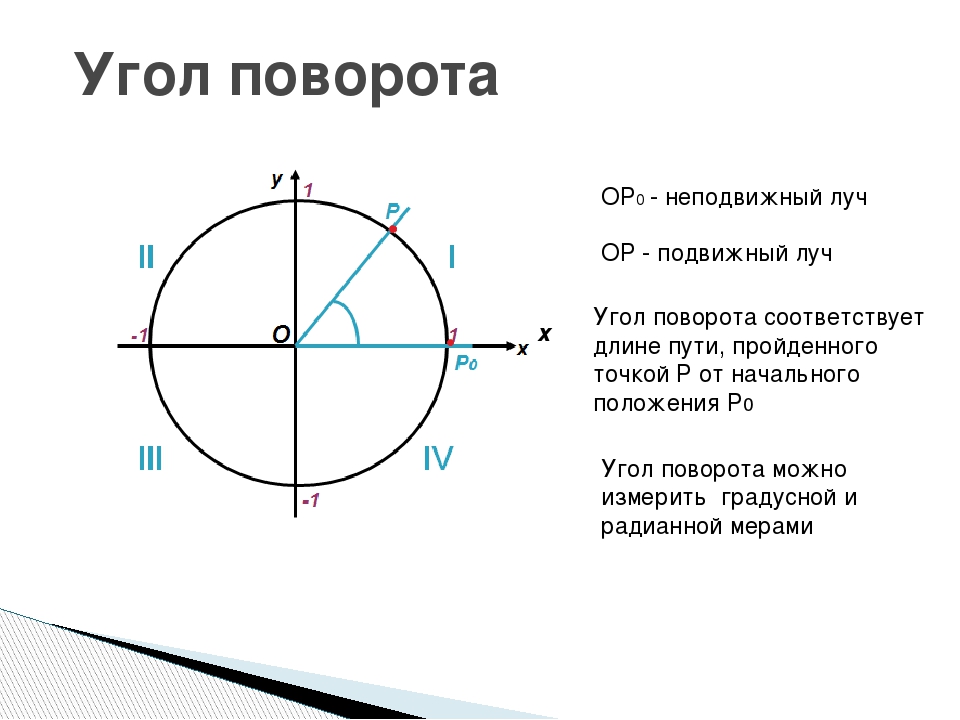 Следовательно, Z совпадает с z ″. Это позволяет упростить определение углов Эйлера следующим образом:

α (или ) представляет вращение вокруг оси z

, φ {\ displaystyle \ varphi}
β (или ) представляет вращение вокруг оси x ‘, θ {\ displaystyle \ theta}
γ (или ) представляет собой вращение вокруг оси z ″. ψ {\ displaystyle \ psi}

Соглашения по внешнему вращению

Внешние вращения — это элементарные вращения, которые происходят вокруг осей фиксированной системы координат xyz . Система XYZ вращается, а xyz фиксируется. Начиная с XYZ, перекрывающего xyz , композиция из трех внешних вращений может использоваться для достижения любой целевой ориентации для XYZ . Углы Эйлера или Тейта – Брайана ( α , β , γ ) представляют собой амплитуды этих вращений элементов. Например, целевая ориентация может быть достигнута следующим образом (обратите внимание на обратный порядок приложения угла Эйлера):

Система XYZ вращается вокруг оси z на угол γ . Х ось теперь под углом гамма относительно х оси.
Система XYZ снова вращается вокруг оси x на β . Z ось теперь под углом р относительно г оси.
Система XYZ совершает третий поворот вокруг оси z на угол α .

В общем, три вращения элемента происходят вокруг z , x и z . Действительно, эту последовательность часто обозначают z — x — z (или 3-1-3). Наборы осей вращения, связанные как с собственными углами Эйлера, так и с углами Тейта – Брайана, обычно называются с использованием этой нотации (подробности см. Выше).

Знаки, диапазоны и условные обозначения

Углы обычно определяются по правилу правой руки .

А именно, они имеют положительные значения, когда они представляют вращение по часовой стрелке, если смотреть в положительном направлении оси, и отрицательные значения, когда вращение появляется против часовой стрелки. Противоположное соглашение (правило левой руки) применяется реже.

О диапазонах (с использованием обозначения интервалов ):

для α и γ диапазон определяется по модулю 2 π радиан . Например, допустимый диапазон может быть [- π , π ] .
для β диапазон покрывает π радиан (но нельзя сказать, что он является модулем π ). Например, это может быть [0, π ] или [- π / 2, π / 2] .

Углы α , β и γ определяются однозначно, за исключением особого случая, когда плоскости xy и XY идентичны, т.е. когда ось z и ось Z имеют одинаковое или противоположное направление. Действительно, если ось

z и ось Z одинаковы, β = 0 и только ( α + γ ) определяется однозначно (не отдельные значения), и, аналогично, если ось z и ось Z противоположны, β = π и только ( α — γ ) определяется однозначно (а не отдельные значения).

Эти неоднозначности известны как блокировка подвеса в приложениях.

Есть шесть возможностей выбора осей вращения для собственных углов Эйлера. Во всех них первая и третья оси вращения совпадают. Шесть возможных последовательностей:

z ₁ — x ′ — z ₂ ″ (внутренние вращения) или z ₂ — x — z ₁ (внешние вращения)
x ₁ — y ′ — x ₂ ″ (внутренние вращения) или x ₂ — y — x ₁ (внешние вращения)
y ₁ — z ′ — y ₂ ″ (собственные вращения) или y ₂ — z — y ₁ (внешние вращения)
z ₁ — y ′ — z ₂ ″ (собственные вращения) или z ₂ — y — z ₁ (внешние вращения)
x ₁ — z ′ — x ₂ ″ (собственные вращения) или x ₂ — z — x ₁ (внешние вращения)
y ₁ — x ′ — y ₂ ″ (внутренние вращения) или y ₂ — x — y ₁ (внешние вращения)

Прецессия, нутация и собственное вращение

Основные движения Земли Эйлера.

Внутренний (зеленый), прецессионный (синий) и нутационный (красный)

Прецессия , нутация и собственное вращение (спин) определяются как движения, полученные путем изменения одного из углов Эйлера, оставляя два других постоянными. Эти движения выражаются не в терминах внешней рамы или в терминах совместно движущейся вращающейся рамы тела, а в виде смеси. Они представляют собой смешанную систему осей вращения , в которой первый угол перемещает линию узлов вокруг внешней оси z , второй вращается вокруг линии узлов N, а третий — собственное вращение вокруг Z , ось, закрепленная в теле. что движется.

Статическое определение подразумевает, что:

α (прецессия) представляет собой вращение вокруг оси z ,
β (нутация) представляет собой вращение вокруг оси N или x ‘,
γ (собственное вращение) представляет собой вращение вокруг оси Z или z ″.

Если β равно нулю, вращения вокруг N нет . Как следствие, Z совпадает с z , α и γ представляют собой вращения вокруг одной и той же оси ( z ), и окончательная ориентация может быть получена с помощью одного поворота вокруг z на угол, равный α + γ .

В качестве примера рассмотрим верх . Вершина вращается вокруг своей оси симметрии; это соответствует его собственному вращению. Он также вращается вокруг своей оси вращения, а его центр масс вращается вокруг оси вращения; это вращение — прецессия. Наконец, верх может раскачиваться вверх и вниз; угол наклона — это угол нутации. Тот же пример можно увидеть с движениями Земли.

Хотя все три движения могут быть представлены оператором вращения с постоянными коэффициентами в некоторой системе отсчета, они не могут быть представлены этими операторами одновременно. При заданной системе отсчета максимум одна из них будет без коэффициентов. Только прецессия может быть выражена в общем виде в виде матрицы в основе пространства без зависимостей других углов.

Эти движения также действуют как карданный подвес. Если мы предположим набор кадров, каждый из которых может перемещаться по отношению к предыдущему только под одним углом, как у подвеса, будет существовать внешний фиксированный кадр, один последний кадр и два кадра посередине, которые называются «промежуточными». кадры ». Два в середине работают как два карданных кольца, которые позволяют последней рамке достигать любой ориентации в пространстве.

Углы Тейта – Брайана

Углы Тейта – Брайана. последовательность z — y ′ — x ″ (собственные вращения; N совпадает с y ‘ ). Последовательность поворота углов: ψ , θ , φ . Обратите внимание, что в этом случае ψ > 90 ° и θ — отрицательный угол.

Второй тип формализма получил название углов Тейта – Брайана в честь Питера Гатри Тейта и Джорджа Х. Брайана . Это соглашение, обычно используемое для аэрокосмических приложений, так что нулевой угол места соответствует горизонтальному положению. Углы Тейта-Брайана представляют ориентацию самолета относительно мировой системы координат. При работе с другими транспортными средствами возможны другие условные обозначения осей .

Определения

Углы Тейта – Брайана. последовательность z — x ′ — y ″ (внутренние вращения; N совпадает с x ′)

Определения и условные обозначения , используемые для Tait-Bryan углов аналогичны тем , которые описаны выше для правильных углов Эйлера ( геометрическое определение , внутреннее определение вращения , внешняя определения вращения ). Единственное отличие состоит в том, что углы Тейта – Брайана представляют собой вращения вокруг трех различных осей (например, x — y — z или x — y ′ — z ″), в то время как правильные углы Эйлера используют одну и ту же ось как для первого, так и для третьего вращения элемента ( например, z — x — z или z — x ′ — z ″).

Это подразумевает другое определение линии узлов геометрической конструкции. В собственном случае углов Эйлера это было определено как пересечение двух гомологичных декартовых плоскостей (параллельных, когда углы Эйлера равны нулю; например, xy и XY ). В случае углов Тейта – Брайана он определяется как пересечение двух негомологических плоскостей (перпендикулярных, если углы Эйлера равны нулю; например, xy и YZ ).

Конвенции

Углы курса, возвышения и крена ( Z — Y ′ — X ″) для самолета, использующего бортовые оси ENU как на борту, так и для наземной станции слежения. Фиксированная система координат x — y — z представляет такую станцию слежения. Бортовые оси Y и Z не показаны. X показан зеленым цветом. Этот рисунок не соответствует правилам RHS: ось y должна быть перевернута, чтобы сформировать правую часть с указанными положительными углами.

Три элементных поворота могут происходить либо вокруг осей исходной системы координат, которая остается неподвижной ( внешние вращения ), либо вокруг осей вращающейся системы координат, которая меняет свою ориентацию после каждого элементарного вращения ( собственные вращения ).

Есть шесть возможностей выбора осей вращения для углов Тейта – Брайана. Шесть возможных последовательностей:

x — y ′ — z ″ (внутренние вращения) или z — y — x (внешние вращения)
y — z ′ — x ″ (внутренние вращения) или x — z — y (внешние вращения)
z — x ‘ — y ″ (внутренние вращения) или y — x — z (внешние вращения)
x — z ′ — y ″ (внутренние вращения) или y — z — x (внешние вращения)
z — y ′ — x ″ (внутренние вращения) или x — y — z (внешние вращения): внутренние вращения известны как рыскание, тангаж и крен
y — x ′ — z ″ (внутренние вращения) или z — x — y (внешние вращения)

Знаки и диапазоны

В главной оси из воздушного судна в соответствии с воздушной нормой DIN 9300.

Обратите внимание , что фиксированная и подвижные рамы должны быть совпадающими с углами нуля. Следовательно, эта норма заставит также согласовать совместимые оси в системе отсчета.

Соглашение Тейта – Брайана широко используется в инженерии с разными целями. На практике существует несколько соглашений об осях для выбора подвижных и фиксированных осей, и эти соглашения определяют знаки углов. Поэтому знаки необходимо изучать в каждом конкретном случае внимательно.

Диапазон углов ψ и φ составляет 2 π радиан. Для θ диапазон охватывает π радиан.

Альтернативные названия

Эти углы обычно берутся как один во внешней системе отсчета ( курс , пеленг ), один во внутренней подвижной системе отсчета ( банк ) и один в средней системе координат, представляя высоту или наклон по отношению к горизонтальной плоскости, что эквивалентно линия узлов для этой цели.

Мнемоника для запоминания названий углов

Для самолета их можно получить за три оборота вокруг его главных осей, если сделать это в правильном порядке. Рыскания получат подшипник, шаг даст возвышение и крен дает угол крена. Поэтому в авиакосмической сфере их иногда называют рысканием, тангажем и креном . Обратите внимание , что это не будет работать , если повороты применяются в любом другом порядке , или если оси самолета начать в любом положении , не эквивалентна системе отсчета.

Углы Тейта – Брайана, следующие за условием z — y ′ — x ″ (внутренние вращения), также известны как морские углы , потому что они могут использоваться для описания ориентации корабля или самолета или углов Кардана в честь итальянского математика и физик Джероламо Кардано , который первым подробно описал карданную подвеску и карданный шарнир .

Углы данного кадра

Проекции вектора Z Проекции вектора Y

Распространенная проблема — найти углы Эйлера заданного кадра. Самый быстрый способ получить их — записать три заданных вектора в виде столбцов матрицы и сравнить их с выражением теоретической матрицы (см.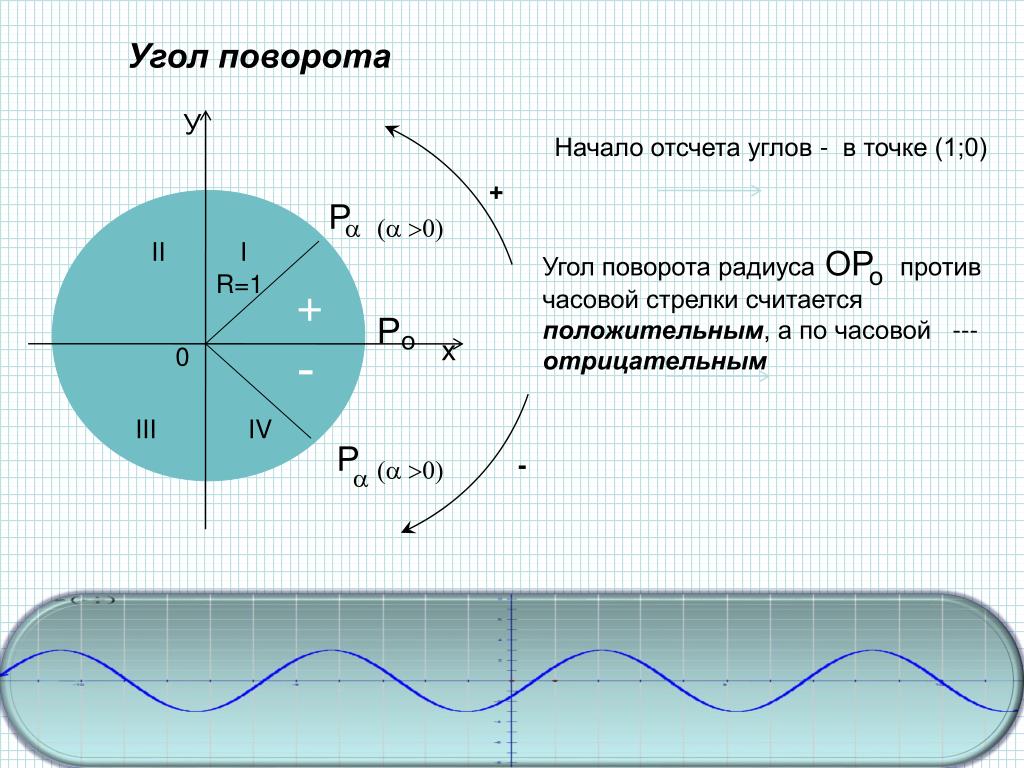 {2}}}).}

Обратите внимание, что функции обратного синуса и косинуса дают два возможных значения аргумента. В этом геометрическом описании действительно только одно из решений. Когда углы Эйлера определены как последовательность поворотов, все решения могут быть действительными, но внутри диапазонов углов будет только одно. Это связано с тем, что последовательность поворотов для достижения целевого кадра не уникальна, если диапазоны не определены ранее.

Для вычислительных целей может быть полезно представить углы с помощью atan2 ( y , x ) . Например, в случае правильных углов Эйлера:

α знак равно atan2 ⁡ ( Z 1 , — Z 2 ) , {\ displaystyle \ alpha = \ operatorname {atan2} (Z_ {1}, — Z_ {2}),}

γ знак равно atan2 ⁡ ( Икс 3 , Y 3 ) . {\ displaystyle \ gamma = \ operatorname {atan2} (X_ {3}, Y_ {3}).}

Преобразование в другие представления ориентации

Углы Эйлера — это один из способов представления ориентации. Есть и другие, и их можно изменить на другие соглашения. Для описания ориентации в трехмерном евклидовом пространстве всегда требуются три параметра . Их можно задавать разными способами, в том числе углы Эйлера; см. диаграммы на SO (3) для других.

Наиболее часто используемым представлением ориентации являются матрицы вращения , ось-угол и кватернионы , также известные как параметры Эйлера – Родригеса , которые обеспечивают еще один механизм для представления трехмерных вращений. Это эквивалентно описанию специальной унитарной группы.

Выражение вращений в 3D в виде единичных кватернионов вместо матриц имеет некоторые преимущества:

Объединение поворотов в вычислительном отношении быстрее и численно более стабильно.
Выделить угол и ось вращения проще.
Интерполяция более проста. См. Например slerp .
Кватернионы не страдают от блокировки кардана, как углы Эйлера.

В любом случае вычисление матрицы вращения — это первый шаг для получения двух других представлений.

Матрица вращения

Любая ориентация может быть достигнута путем составления трех элементарных вращений, начиная с известной стандартной ориентации. Эквивалентно, любая матрица вращения R может быть разложена как произведение трех элементарных матриц вращения. Например:

р знак равно Икс ( α ) Y ( β ) Z ( γ ) {\ Displaystyle Р = Икс (\ альфа) Y (\ бета) Z (\ гамма)}

представляет собой матрицу вращения, которая может использоваться для представления композиции внешних вращений вокруг осей z , y , x (в этом порядке) или композиции собственных вращений вокруг осей x — y ‘- z ″ (в этом порядке). Однако как определение элементарных матриц вращения X , Y , Z , так и их порядок умножения зависят от выбора, сделанного пользователем в отношении определения как матриц вращения, так и углов Эйлера (см., Например, неоднозначность в определении вращения матрицы ). К сожалению, разные наборы соглашений принимаются пользователями в разных контекстах. Следующая таблица была построена в соответствии с этим набором соглашений:

Каждая матрица предназначена для работы путем предварительного умножения векторов — столбцов (см. Неоднозначности в определении матриц вращения ) [ Икс у z ] {\ textstyle {\ begin {bmatrix} x \\ y \\ z \ end {bmatrix}}}
Каждая матрица предназначена для представления активного вращения (составляющая и составляющая матрицы должны воздействовать на координаты векторов, определенных в исходной фиксированной системе отсчета, и давать в результате координаты повернутого вектора, определенного в той же системе отсчета).
Каждая матрица предназначена для представления, в первую очередь, композиции внешних вращений (что соответствует конструктивной оценке матрицы R путем умножения трех истинно элементарных матриц) и, во-вторых, композиции трех неэлементных матриц, представляющих глобально внутренние вращения (вокруг осей вращающейся системы отсчета в обратном порядке).
Принимаются правосторонние системы отсчета, и правило правой руки используется для определения знака углов α , β , γ .

Для простоты в следующей таблице матричных продуктов используется следующая номенклатура:

1, 2, 3 представляют углы α , β и γ , то есть углы, соответствующие первому, второму и третьему поворотам элемента соответственно.
X , Y , Z — это матрицы, представляющие элементарные вращения вокруг осей x , y , z фиксированной системы отсчета (например, X ₁ представляет поворот вокруг x на угол α ).
s и c представляют синус и косинус (например, s ₁ представляет синус α ).

Правильные углы Эйлера	Углы Тейта – Брайана
Икс 1 Z 2 Икс 3 знак равно [ c 2 — c 3 s 2 s 2 s 3 c 1 s 2 c 1 c 2 c 3 — s 1 s 3 — c 3 s 1 — c 1 c 2 s 3 s 1 s 2 c 1 s 3 + c 2 c 3 s 1 c 1 c 3 — c 2 s 1 s 3 ] {\ displaystyle X_ {1} Z_ {2} X_ {3} = {\ begin {bmatrix} c_ {2} & — c_ {3} s_ {2} & s_ {2} s_ {3} \\ c_ {1} s_ {2} & c_ {1} c_ {2} c_ {3} -s_ {1} s_ {3} & — c_ {3} s_ {1} -c_ {1} c_ {2} s_ {3} \\ s_ {1} s_ {2} & c_ {1} s_ {3} + c_ {2} c_ {3} s_ {1} & c_ {1} c_ {3} -c_ {2} s_ {1} s_ {3} \ end {bmatrix}}}	Икс 1 Z 2 Y 3 знак равно [ c 2 c 3 — s 2 c 2 s 3 s 1 s 3 + c 1 c 3 s 2 c 1 c 2 c 1 s 2 s 3 — c 3 s 1 c 3 s 1 s 2 — c 1 s 3 c 2 s 1 c 1 c 3 + s 1 s 2 s 3 ] {\ displaystyle X_ {1} Z_ {2} Y_ {3} = {\ begin {bmatrix} c_ {2} c_ {3} & — s_ {2} & c_ {2} s_ {3} \\ s_ {1} s_ {3} + c_ {1} c_ {3} s_ {2} & c_ {1} c_ {2} & c_ {1} s_ {2} s_ {3} -c_ {3} s_ {1} \\ c_ { 3} s_ {1} s_ {2} -c_ {1} s_ {3} & c_ {2} s_ {1} & c_ {1} c_ {3} + s_ {1} s_ {2} s_ {3} \ end {bmatrix}}}

Правильные углы Эйлера

Углы Тейта – Брайана

Икс 1 Z 2 Икс 3 знак равно [ c 2 — c 3 s 2 s 2 s 3 c 1 s 2 c 1 c 2 c 3 — s 1 s 3 — c 3 s 1 — c 1 c 2 s 3 s 1 s 2 c 1 s 3 + c 2 c 3 s 1 c 1 c 3 — c 2 s 1 s 3 ] {\ displaystyle X_ {1} Z_ {2} X_ {3} = {\ begin {bmatrix} c_ {2} & — c_ {3} s_ {2} & s_ {2} s_ {3} \\ c_ {1} s_ {2} & c_ {1} c_ {2} c_ {3} -s_ {1} s_ {3} & — c_ {3} s_ {1} -c_ {1} c_ {2} s_ {3} \\ s_ {1} s_ {2} & c_ {1} s_ {3} + c_ {2} c_ {3} s_ {1} & c_ {1} c_ {3} -c_ {2} s_ {1} s_ {3} \ end {bmatrix}}}

Икс 1 Z 2 Y 3 знак равно [ c 2 c 3 — s 2 c 2 s 3 s 1 s 3 + c 1 c 3 s 2 c 1 c 2 c 1 s 2 s 3 — c 3 s 1 c 3 s 1 s 2 — c 1 s 3 c 2 s 1 c 1 c 3 + s 1 s 2 s 3 ] {\ displaystyle X_ {1} Z_ {2} Y_ {3} = {\ begin {bmatrix} c_ {2} c_ {3} & — s_ {2} & c_ {2} s_ {3} \\ s_ {1} s_ {3} + c_ {1} c_ {3} s_ {2} & c_ {1} c_ {2} & c_ {1} s_ {2} s_ {3} -c_ {3} s_ {1} \\ c_ { 3} s_ {1} s_ {2} -c_ {1} s_ {3} & c_ {2} s_ {1} & c_ {1} c_ {3} + s_ {1} s_ {2} s_ {3} \ end {bmatrix}}}

Матрица вращения — Rotation matrix

Матрица, представляющая евклидово вращение

В линейной алгебры , A матрица вращения представляет собой матрицу преобразования , которая используется для выполнения вращения в евклидовом пространстве .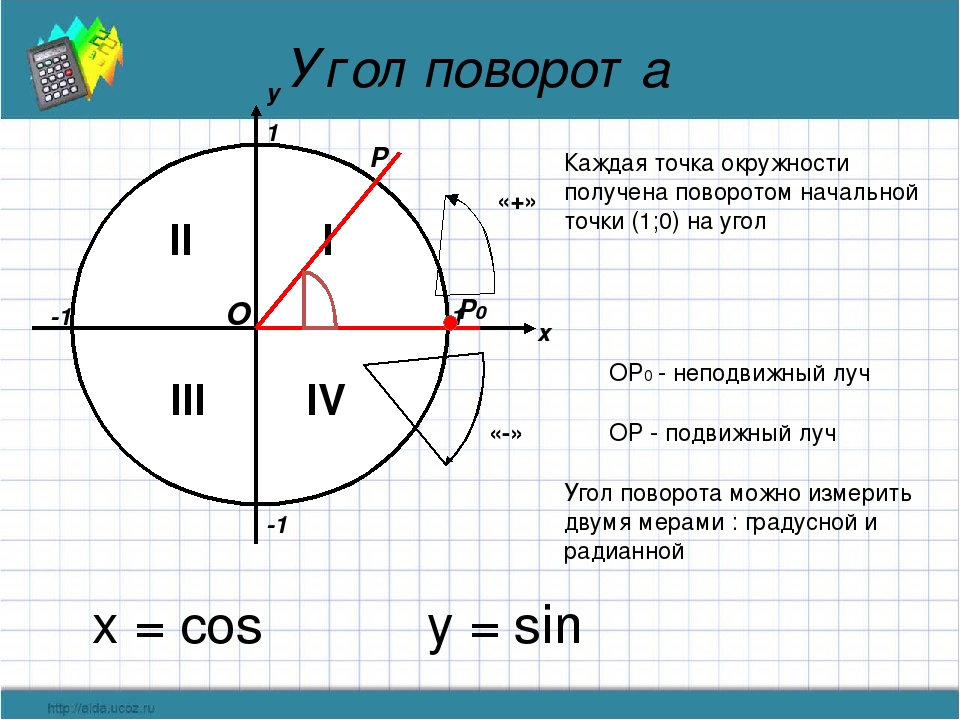 Например, используя приведенное ниже соглашение, матрица

р знак равно [ потому что ⁡ θ — грех ⁡ θ грех ⁡ θ потому что ⁡ θ ] {\ Displaystyle R = {\ begin {bmatrix} \ cos \ theta & — \ sin \ theta \\\ sin \ theta & \ cos \ theta \\\ end {bmatrix}}}

поворачивает точки в плоскости xy против часовой стрелки на угол θ относительно оси x вокруг начала двумерной декартовой системы координат . Чтобы выполнить поворот на плоской точке со стандартными координатами v = (x, y), ее нужно записать как вектор-столбец и умножить на матрицу R :

р v знак равно [ потому что ⁡ θ — грех ⁡ θ грех ⁡ θ потому что ⁡ θ ] ⋅ [ Икс у ] знак равно [ Икс потому что ⁡ θ — у грех ⁡ θ Икс грех ⁡ θ + у потому что ⁡ θ ] . {\ Displaystyle R {\ textbf {v}} \ = \ {\ begin {bmatrix} \ cos \ theta & — \ sin \ theta \\\ sin \ theta & \ cos \ theta \ end {bmatrix}} \ cdot { \ begin {bmatrix} x \\ y \ end {bmatrix}} \ = \ {\ begin {bmatrix} x \ cos \ theta -y \ sin \ theta \\ x \ sin \ theta + y \ cos \ theta \ end {bmatrix}}.

}

Если x и y — координаты конечной точки вектора, где x — косинус, а y — синус, то приведенные выше уравнения становятся формулами тригонометрического суммирования углов . Действительно, матрицу вращения можно рассматривать как формулу тригонометрического суммирования углов в матричной форме. Один из способов понять это — сказать, что у нас есть вектор под углом 30 ° к оси x, и мы хотим повернуть этот угол еще на 45 °. Нам просто нужно вычислить координаты конечной точки вектора при 30 ° + 45 °.

Примеры в этой статье относятся к активному вращению векторов против часовой стрелки в правой системе координат ( y против часовой стрелки от x ) путем предварительного умножения ( R слева). Если какой-либо из них изменяется (например, вращающиеся оси вместо векторов, пассивное преобразование ), то следует использовать инверсию матрицы примера, которая совпадает с ее транспонированием .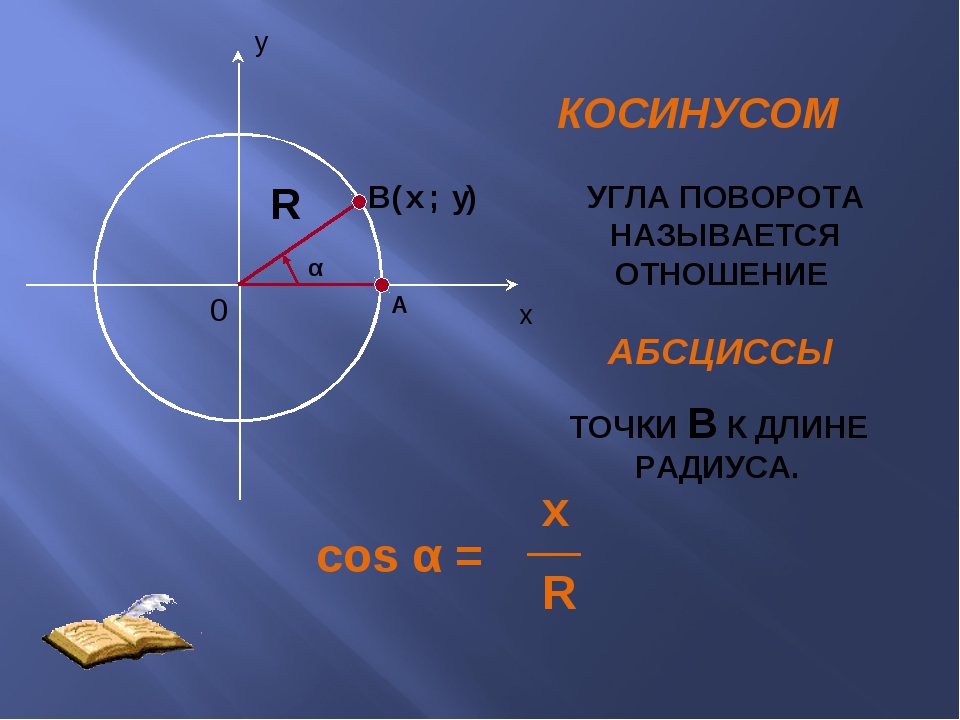

Поскольку умножение матриц не влияет на нулевой вектор (координаты начала координат), матрицы вращения описывают повороты относительно начала координат. Матрицы вращения обеспечивают алгебраическое описание таких вращений и широко используются для вычислений в геометрии , физике и компьютерной графике . В некоторой литературе термин вращение обобщен, чтобы включать неправильные повороты , характеризуемые ортогональными матрицами с определителем -1 (вместо +1). Они сочетают правильный поворот с отражениями (которые меняют ориентацию ). В других случаях, когда не рассматриваются отражения, метка собственно может быть отброшена. В этой статье соблюдается последнее соглашение.

Матрицы вращения — это квадратные матрицы с действительными элементами. Более конкретно, их можно охарактеризовать как ортогональные матрицы с определителем 1; то есть квадратная матрица R является матрицей вращения тогда и только тогда, когда R ^T = R ^-1 и det R = 1 . Множество всех ортогональных матриц размера п с определителем +1 образует группу известный как специальной ортогональной группы SO ( п ) , один из примеров которых является группа вращений SO (3) . Набор всех ортогональных матриц размера n с определителем +1 или -1 образует (общую) ортогональную группу O ( n ) .

В двух измерениях

Поворот вектора против часовой стрелки на угол θ . Вектор изначально выровнен по оси x .

В двух измерениях стандартная матрица вращения имеет следующий вид:

р ( θ ) знак равно [ потому что ⁡ θ — грех ⁡ θ грех ⁡ θ потому что ⁡ θ ] {\ Displaystyle R (\ theta) = {\ begin {bmatrix} \ cos \ theta & — \ sin \ theta \\\ sin \ theta & \ cos \ theta \\\ end {bmatrix}}} .

Это поворачивает векторы-столбцы посредством следующего умножения матриц ,

[ Икс ′ у ′ ] знак равно [ потому что ⁡ θ — грех ⁡ θ грех ⁡ θ потому что ⁡ θ ] [ Икс у ] {\ displaystyle {\ begin {bmatrix} x ‘\\ y’ \\\ end {bmatrix}} = {\ begin {bmatrix} \ cos \ theta & — \ sin \ theta \\\ sin \ theta & \ cos \ theta \\\ end {bmatrix}} {\ begin {bmatrix} x \\ y \\\ end {bmatrix}}} .

знак равно [ 0 1 ] {\ displaystyle \ mathbf {\ hat {y}} = {\ begin {bmatrix} 0 \\ 1 \\\ end {bmatrix}}} θ {\ displaystyle \ theta} [ — грех ⁡ θ потому что ⁡ θ ] {\ displaystyle {\ begin {bmatrix} — \ sin \ theta \\\ cos \ theta \\\ end {bmatrix}}}

Направление

Направление вращения вектора — против часовой стрелки, если θ положительно (например, 90 °), и по часовой стрелке, если θ отрицательно (например, -90 °). Таким образом, матрица вращения по часовой стрелке находится как

р ( — θ ) знак равно [ потому что ⁡ θ грех ⁡ θ — грех ⁡ θ потому что ⁡ θ ] {\ Displaystyle R (- \ theta) = {\ begin {bmatrix} \ cos \ theta & \ sin \ theta \\ — \ sin \ theta & \ cos \ theta \\\ end {bmatrix}} \,} .

Двумерный случай — единственный нетривиальный (т.е. не одномерный) случай, когда группа матриц вращения коммутативна, так что не имеет значения, в каком порядке выполняются множественные вращения. Альтернативное соглашение использует вращающиеся оси, и вышеупомянутые матрицы также представляют вращение осей по часовой стрелке на угол θ .

Нестандартная ориентация системы координат

Поворот на угол θ с нестандартными осями.

Если используется стандартная правая декартова система координат , с осью x вправо и осью y вверх, то вращение R ( θ ) происходит против часовой стрелки. Если используется левая декартова система координат, где x направлен вправо, а y направлен вниз, R ( θ ) — по часовой стрелке. Такие нестандартные ориентации редко используются в математике, но распространены в компьютерной 2D-графике , которая часто имеет начало в верхнем левом углу и ось Y вниз по экрану или странице.

См. Ниже другие альтернативные соглашения, которые могут изменить направление вращения, производимое матрицей вращения.

Общие вращения

Особенно полезными являются матрицы , , на 90 °, 180 ° и 270 ° против часовой стрелки вращения. [ 0 — 1 1 0 ] {\ displaystyle {\ begin {bmatrix} 0 & -1 \\ [3pt] 1 & 0 \\\ end {bmatrix}}} [ — 1 0 0 — 1 ] {\ displaystyle {\ begin {bmatrix} -1 & 0 \\ [3pt] 0 & -1 \\\ end {bmatrix}}} [ 0 1 — 1 0 ] {\ displaystyle {\ begin {bmatrix} 0 & 1 \\ [3pt] -1 & 0 \\\ end {bmatrix}}}

Поворот на 180 ° (в центре), за которым следует положительный поворот на 90 ° (слева), эквивалентен одному отрицательному повороту на 90 ° (положительный 270 °) (справа).

{2} = — 1,} п м знак равно { Икс я + у м : Икс , у ∈ р } {\ Displaystyle P_ {m} = \ {xI + ym: x, y \ in R \}}

г знак равно exp ⁡ ( θ м ) знак равно потому что ⁡ ( θ ) я + м грех ⁡ ( θ ) {\ Displaystyle г \ = \ \ ехр (\ тета м) \ = \ \ соз (\ тета) я + м \ грех (\ тета)} матрица вращения.

Для получения дополнительных сведений о числовых плоскостях в M (2, ℝ) и их типах вращения см. Вещественные матрицы 2 × 2 .

В трех измерениях

Положительный поворот на 90 ° вокруг у -Axis (слева) после того, как один вокруг г ось (средний) дает 120 ° вращение вокруг главной диагонали (справа) с.
В верхнем левом углу находятся матрицы вращения, в правом нижнем углу — соответствующие перестановки куба с началом координат в его центре.

Основные вращения

Базовое вращение (также называемое элементарным вращением) — это вращение вокруг одной из осей системы координат. Следующие три основные матрицы вращения поворачивают векторы на угол θ относительно осей x -, y — или z в трех измерениях, используя правило правой руки, которое кодирует их чередующиеся знаки. (Эти же матрицы могут также представлять вращение осей по часовой стрелке.)

р Икс ( θ ) знак равно [ 1 0 0 0 потому что ⁡ θ — грех ⁡ θ 0 грех ⁡ θ потому что ⁡ θ ] р у ( θ ) знак равно [ потому что ⁡ θ 0 грех ⁡ θ 0 1 0 — грех ⁡ θ 0 потому что ⁡ θ ] р z ( θ ) знак равно [ потому что ⁡ θ — грех ⁡ θ 0 грех ⁡ θ потому что ⁡ θ 0 0 0 1 ] {\ displaystyle {\ begin {alignat} {1} R_ {x} (\ theta) & = {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & \ cos \ theta & — \ sin \ theta \\ [3pt] 0 & \ sin \ theta & \ cos \ theta \\ [3pt] \ end {bmatrix}} \\ [6pt] R_ {y} (\ theta) & = {\ begin {bmatrix} \ cos \ theta & 0 & \ sin \ theta \\ [3pt] 0 & 1 & 0 \\ [3pt] — \ sin \ theta & 0 & \ cos \ theta \\\ end {bmatrix}} \\ [6pt] R_ {z} (\ theta) & = {\ begin {bmatrix} \ cos \ theta & — \ sin \ theta & 0 \\ [3pt] \ sin \ theta & \ cos \ theta & 0 \\ [3pt] 0 & 0 & 1 \\\ end {bmatrix}} \ end {alignat}}}

Для векторов-столбцов каждое из этих вращений основных векторов появляется против часовой стрелки, когда ось, вокруг которой они происходят, указывает на наблюдателя, система координат правая, а угол θ положительный. {\ circ} & 0 \\ 0 & 0 & 1 \\\ end {bmatrix}} {\ begin {bmatrix } 1 \\ 0 \\ 0 \\\ end {bmatrix}} = {\ begin {bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\\ end {bmatrix}} {\ begin {bmatrix} 1 \\ 0 \\ 0 \\\ end {bmatrix}} = {\ begin {bmatrix} 0 \\ 1 \\ 0 \\\ end {bmatrix}}}

Это похоже на вращение, производимое вышеупомянутой двумерной матрицей вращения. См. Ниже альтернативные соглашения, которые могут явно или фактически изменить направление вращения, производимое этими матрицами.

Общие ротации

Другие матрицы вращения могут быть получены из этих трех с использованием матричного умножения . Например, товар

р знак равно р z ( α ) р у ( β ) р Икс ( γ ) знак равно [ потому что ⁡ α — грех ⁡ α 0 грех ⁡ α потому что ⁡ α 0 0 0 1 ] рыскание [ потому что ⁡ β 0 грех ⁡ β 0 1 0 — грех ⁡ β 0 потому что ⁡ β ] подача [ 1 0 0 0 потому что ⁡ γ — грех ⁡ γ 0 грех ⁡ γ потому что ⁡ γ ] рулон {\ Displaystyle R = R_ {z} (\ alpha) \, R_ {y} (\ beta) \, R_ {x} (\ gamma) = {\ overset {\ text {yaw}} {\ begin {bmatrix} \ cos \ alpha & — \ sin \ alpha & 0 \\\ sin \ alpha & \ cos \ alpha & 0 \\ 0 & 0 & 1 \\\ end {bmatrix}}} {\ overset {\ text {pitch}} {\ begin {bmatrix } \ cos \ beta & 0 & \ sin \ beta \\ 0 & 1 & 0 \\ — \ sin \ beta & 0 & \ cos \ beta \\\ end {bmatrix}}} {\ overset {\ text {roll}} {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & \ cos \ gamma & — \ sin \ gamma \\ 0 & \ sin \ gamma & \ cos \ gamma \\\ end {bmatrix}}}}

р знак равно [ потому что ⁡ α потому что ⁡ β потому что ⁡ α грех ⁡ β грех ⁡ γ — грех ⁡ α потому что ⁡ γ потому что ⁡ α грех ⁡ β потому что ⁡ γ + грех ⁡ α грех ⁡ γ грех ⁡ α потому что ⁡ β грех ⁡ α грех ⁡ β грех ⁡ γ + потому что ⁡ α потому что ⁡ γ грех ⁡ α грех ⁡ β потому что ⁡ γ — потому что ⁡ α грех ⁡ γ — грех ⁡ β потому что ⁡ β грех ⁡ γ потому что ⁡ β потому что ⁡ γ ] {\ Displaystyle R = {\ begin {bmatrix} \ соз \ альфа \ соз \ бета & \ соз \ альфа \ грех \ бета \ грех \ гамма — \ грех \ альфа \ соз \ гамма & \ соз \ альфа \ грех \ бета \ cos \ gamma + \ sin \ alpha \ sin \ gamma \\\ sin \ alpha \ cos \ beta & \ sin \ alpha \ sin \ beta \ sin \ gamma + \ cos \ alpha \ cos \ gamma & \ sin \ alpha \ sin \ beta \ cos \ gamma — \ cos \ alpha \ sin \ gamma \\ — \ sin \ beta & \ cos \ beta \ sin \ gamma & \ cos \ beta \ cos \ gamma \\\ end {bmatrix}} }

представляет собой поворот, углы рыскания, тангажа и крена равны α , β и γ соответственно. Более формально это внутреннее вращение , углы Тейта – Брайана которого равны α , β , γ вокруг осей z , y , x соответственно. Аналогичным образом продукт

р знак равно р z ( γ ) р у ( β ) р Икс ( α ) знак равно [ потому что ⁡ γ — грех ⁡ γ 0 грех ⁡ γ потому что ⁡ γ 0 0 0 1 ] [ потому что ⁡ β 0 грех ⁡ β 0 1 0 — грех ⁡ β 0 потому что ⁡ β ] [ 1 0 0 0 потому что ⁡ α — грех ⁡ α 0 грех ⁡ α потому что ⁡ α ] {\ Displaystyle R = R_ {Z} (\ gamma) \, R_ {y} (\ beta) \, R_ {x} (\ alpha) = {\ begin {bmatrix} \ cos \ gamma & — \ sin \ gamma & 0 \\\ sin \ gamma & \ cos \ gamma & 0 \\ 0 & 0 & 1 \\\ end {bmatrix}} {\ begin {bmatrix} \ cos \ beta & 0 & \ sin \ beta \\ 0 & 1 & 0 \\ — \ sin \ beta & 0 & \ cos \ beta \\\ end {bmatrix}} {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & \ cos \ alpha & — \ sin \ alpha \\ 0 & \ sin \ alpha & \ cos \ alpha \\\ end {bmatrix }}}

представляет собой внешнее вращение, чьи (несобственные) углы Эйлера равны α , β , γ относительно осей x , y , z .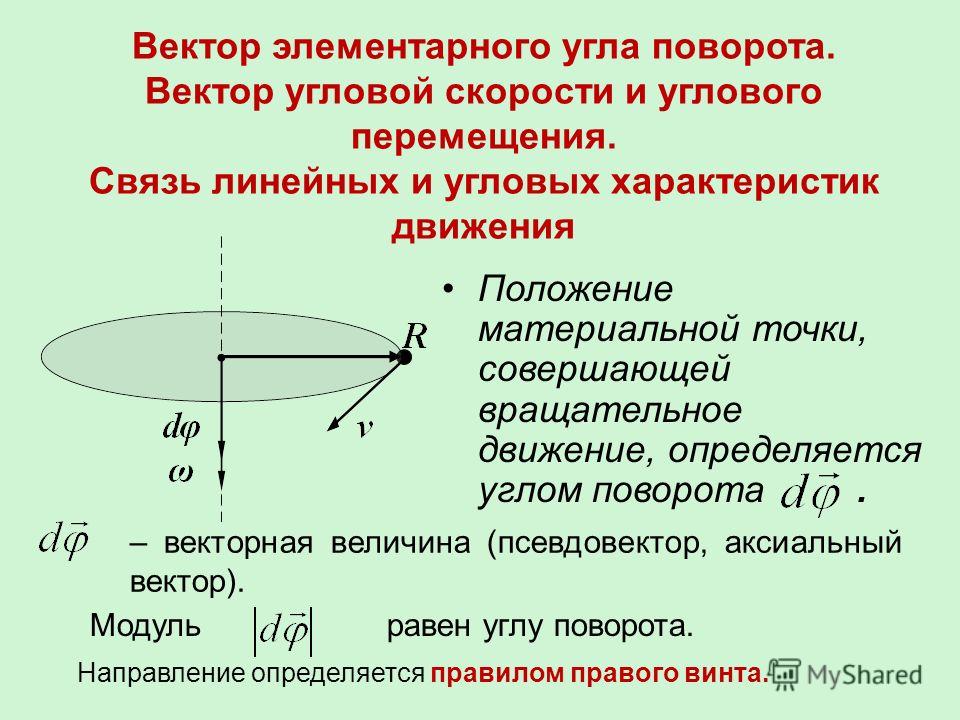

Эти матрицы производят желаемый эффект только в том случае, если они используются для предварительного умножения векторов-столбцов и (поскольку в общем случае умножение матриц не является коммутативным ) только в том случае, если они применяются в указанном порядке (см. Дополнительные сведения в разделе « Неопределенность» ).

Преобразование из матрицы вращения в ось – угол

Каждое вращение в трех измерениях определяется его осью (вектор вдоль этой оси не изменяется вращением), а его угол — величиной вращения вокруг этой оси ( теорема Эйлера о вращении ).

Существует несколько методов вычисления оси и угла из матрицы вращения (см. Также представление оси и угла ). Здесь мы описываем только метод, основанный на вычислении собственных векторов и собственных значений матрицы вращения. Также можно использовать след матрицы вращения.

Определение оси

Поворот R вокруг оси u можно разложить с помощью 3 эндоморфизмов P , ( I — P ) и Q (щелкните, чтобы увеличить).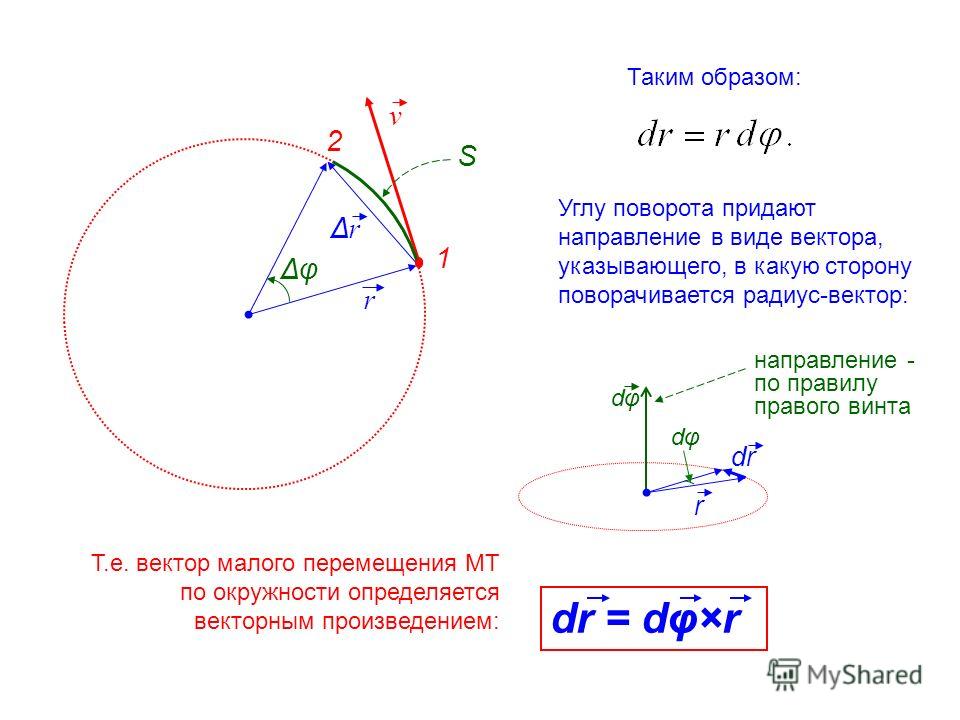

Учитывая матрицу вращения 3 × 3 R , вектор u, параллельный оси вращения, должен удовлетворять

р ты знак равно ты , {\ Displaystyle R \ mathbf {u} = \ mathbf {u},}

так как вращение u вокруг оси вращения должно приводить к u . Выше уравнение может быть решено для U , которое единственно с точностью до скалярного множителя исключением случаев , когда R = I .

Далее уравнение можно переписать

р ты знак равно я ты ⇒ ( р — я ) ты знак равно 0 , {\ Displaystyle R \ mathbf {u} = I \ mathbf {u} \ quad \ Rightarrow \ quad (RI) \ mathbf {u} = 0,}

который показывает , что у лежит в нулевом пространстве от R — I .

Рассматриваемый по — другому, у является собственным вектором из R , соответствующий собственному значению λ = 1 . Каждая матрица вращения должна иметь это собственное значение, два других собственных значения комплексно сопряжены друг с другом. {\ mathrm {T}} \ right).}

Произведение матрица-вектор становится перекрестным произведением вектора на себя, гарантируя, что результат равен нулю:

( р — р Т ) ты знак равно [ ты ]

Зависимость угла вращения от условий измерения

Физико – химическое исследование оптически активных веществ

Измерение вращения плоскости поляризации света оптически активных веществ осуществляется благодаря методу физико – химического исследования – поляриметрии.

Измерения осуществляют с помощью оптических приборов — поляриметров, в которых через систему двух поляризующих призм последовательно проходит луч света.

Так как между концентрацией оптически активного вещества и углом вращения существует пропорциональная зависимость, поляриметрические измерения можно использовать для количественного определения оптически активного вещества.

Оптическое вращение, найденное при помощи поляриметрии, пересчитывают в молекулярное или удельное вращение.

По результатам определения знака и величины вращения плоскости поляризации можно предположить и доказать строение, пространственную конфигурацию вещества, сделать выводы о механизме реакции и др.

Хиральные соединения по разному действуют на плоскополяризованный свет. Энантиомеры хирального вещества оказывают действие на поляризованный свет, поэтому являются оптическими изомерами.

Замечание 1

Если раствор содержит два энантиомера с равными концентрациями, то он не вызывает вращения плоскости поляризации света и его называют рацемической смесью.

Поляриметрия широко применяется:

В производстве антибиотиков (определение пенициллина и энзима пенициллиназы при их совместном присутствии). Пенициллин разрушается энзимом пенициллиназы. Так как продукты разрушения пеницилина не обладают оптической активностью, то оптическая активность раствора уменьшается. Изменение вращения плоскости поляризации позволяет определить изменение содержания пенициллина во времени.
В фармацевтическом производстве для идентификации лекарственных средств.
Для анализа алкалоидов, эфирных масел и др.

Например: Выделенная из камфорного базилика камфора дает правовращающийся раствор в спирте, при этом удельное вращение плоскости поляризации составляет +8,6º, а выделенная из полыни – дает левовращающийся раствор с удельным вращением плоскости поляризации равным -8,6º. Синтетическая камфора не вращает плоскость поляризации.

Факторы, влияющие на угол вращения

Удельное вращение $[\alpha]$ можно выразить через соотношение

$φ=[\alpha]\cdot l \cdot C.$

Тогда для каждого энантиомера величина вращения зависит от:

длины волны света;
толщины образца;
концентрации оптически активного вещества;
природы растворителя;
температуры;
давления (для газов).

Замечание 2

При определении изучении оптической активности вещества учитывают температуру и длину волны ${{\rm [}\alpha {\rm ]}}^t_{\lambda }$.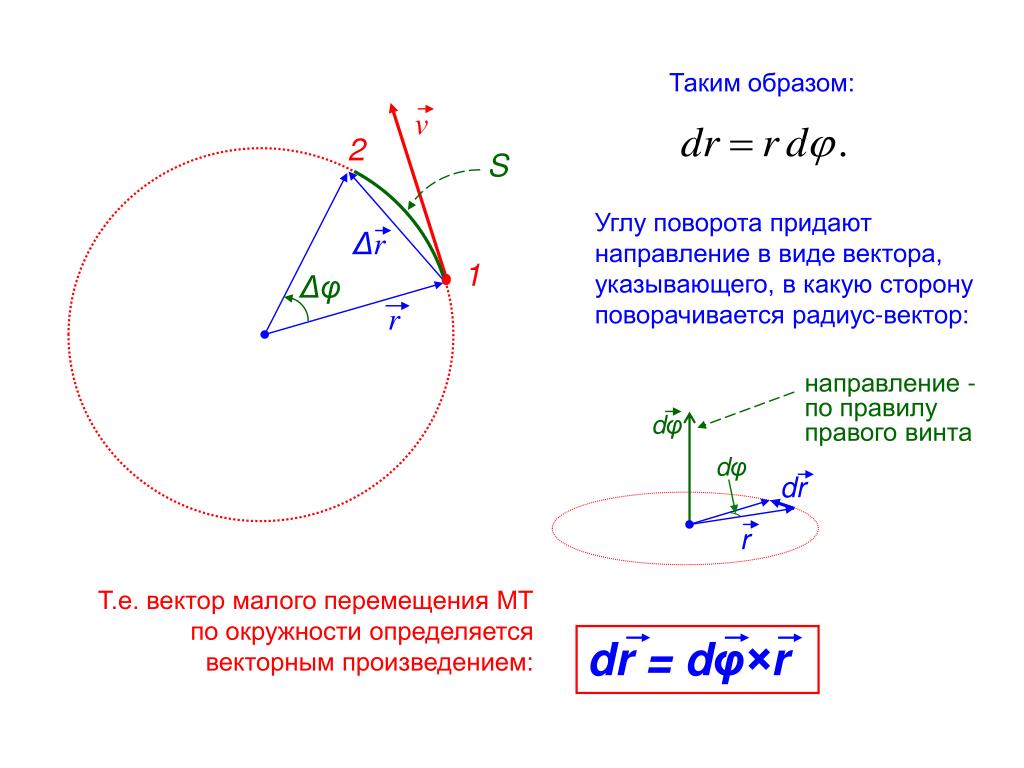 Если вращение измерено при длине волны, которая со

Угол — вращение — плоскость — поляризация

Cтраница 1

Угол вращения плоскости поляризации определяют в поляриметре. В зависимости от природы вещества вра-ни: пне плоскости поляризации может иметь различное направление и неличину. [1]

Угол вращения плоскости поляризации ( 3) зависит от толщины слоя, концентрации раствора, индивидуальных свойств оптически активного вещества. [2]

Угол вращения плоскости поляризации растворами определяется в поляриметре. Основными частями поляриметра являются поляризатор и анализатор. При помощи поляризатора получается поляризованный луч, при помощи анализатора определяется угол вращения плоскости поляризации этого луча. [3]

Угол вращения плоскости поляризации, вызываемый раствором, в котором содержится 1 моль чистого антипода на литр ( мольное вращение) — это стандартная и обязательная характеристика любого оптически активного соединения. Для измерения этой величины тоже применяют несложные оптические приборы — поляриметры. [4]

Угол вращения плоскости поляризации удобно измерять в микрокюветах длиной 2 или 5 см. Они делаются из толстостенной трубочки с внутренним диаметром 1 — 2 мм. В этом случае определение может быть проведено с минимальным количеством вещества. [5]

Угол вращения плоскости поляризации ф — угол, на который повертывается плоскость поляризации при взаимодействии линейно поляризованного оптического излучения с веществом. [6]

Угол вращения плоскости поляризации пропорционален концентрации. Поэтому для времени t минут угол вращения плоскости поляризации а представляет разность между углом вращения плоскости поляризации сахарозы и инвертного сахара. [7]

Угол вращения плоскости поляризации определяют п о л я-р и м е т 0 о м, обстоятельное описание которого дается в курса физики. [9]

Угол вращения плоскости поляризации света зависит от природы исследуемого оптически активного вещества, длины волны излучения и температуры. [11]

Для растворов угол вращения плоскости поляризации р а 1с, где а — постоянная вращения; / — толщина слоя; с — концентрация раствора. [12]

Для растворов угол вращения плоскости поляризации ф I а I / с, где I а — постоянная вращения; / — толщина слоя; с — концентрация раствора. [14]

Следовательно если умножить угол вращения плоскости поляризации на этот постоянный множитель, то сразу получим % сахарозы в испытуемом сахаре. Согласно предложению Вентцке нормальная навеска сахара принята в 26 048 г в

Угол — внутреннее вращение — Большая Энциклопедия Нефти и Газа, статья, страница 1

Угол — внутреннее вращение

Cтраница 1

Угол внутреннего вращения у / характеризует поворот плоскости, проведенной через г — е и ( / — 1) — е звенья цепи, по отношению к плоскости, проведенной через ( г — 1) — е и ( / — 2) — е звенья. Мы будем отсчитывать этот угол от отрянс-положения звеньев, при котором звенья i — 2, I — 1 и / лежат в одной плоскости и г — е звено параллельно ( / — 2) — му. [1]

Угол внутреннего вращения отсчитывается в данном случае от чис-положения. [2]

Если угол внутреннего вращения между треугольниками имеет индекс i, то этот же индекс отнесем и к расстоянию между ними: Длг — — — фг. [3]

Будем отсчитывать угол внутреннего вращения от заслоненной цыс-конформации, в которой четверка атомов С1 — С — С — С1 находится в одной плоскости. [4]

Таким образом, угол внутреннего вращения вычисляется непосредственно из структурных данных; необходимо только задаться длиной связи главной цепи полимера /; при этом угол вращения не зависит от валентного угла. [5]

А — выбранный структурный параметр ( например, длина связи, угол внутреннего вращения) AA ( t) A ( t) — ( Л), ( ДЛ2 ( Л — Л 2 и скобки указывают среднюю величину за время моделирования; в числителе уравнения ( 3) средняя величина включает все значения т за время моделирования. [6]

Произведен расчет скелетных колебаний при пренебрежении внутренними колебаниями СНо-грушш для различных значений угла внутреннего вращения. Угол внутреннего вращения в нолиоксиметилене, определенный из экспериментальных значений частот на основе развитой теории ( — 70 — 100), оказывается в хорошем согласии с моделью Хаггяпса J. Проводится сопоставление вычисленных п наблюденных частот для полпокспметилена. [7]

В — С, то угол между проекциями А — В и С — D и есть угол поворота А и D атомов вокруг связи В — С; этот угол можно описывать как угол между плоскостями, проходящими, с одной стороны, через А, В, С и, с другой — через В, С, D. Угол внутреннего вращения обозначается полностью как 9 ( А ( -, В. Угол внутреннего вращения считается положительным ( 9) или отрицательным ( — 9) в зависимости от того, вправо или влево на меньший угол в направлении к центральному атому А ( или D) нужно довернуть связь, когда смотришь на систему вдоль центральной связи В — С или С — В, чтобы возникла заслоненная конформация; заметим, что несущественно, как при этом смотреть на систему — спереди или сзади.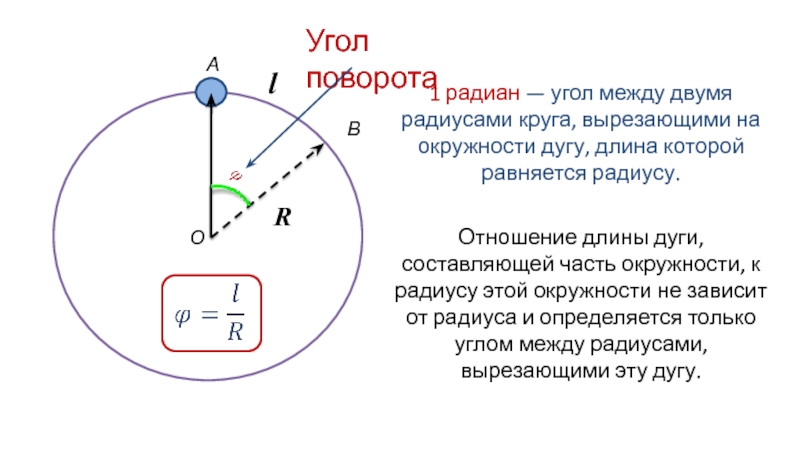 В соответствии с этим определением последовательность положительных углов внутреннего вращения образует правовращающую спираль. [8]

Произведен расчет скелетных колебаний при пренебрежении внутренними колебаниями СН2 — группы для различных значений угла внутреннего вращения. Угол внутреннего вращения

Сферическое движение — Лекции и примеры решения задач технической механики

Сферическим движением твердого тела называют такое движение, при котором одна точка тела остается все время неподвижной. Очевидно, траектории всех точек тела при таком движении располагаются на поверхностях сфер.

Для определения положения тела с неподвижной точкой O в каждый момент времени свяжем две системы координат: неподвижную Ox₁y₁z₁ и подвижную Oxyz, жестко связанную с телом, вращающимся вокруг точки O (рисунок 3.1).

Рис. 3.1

Положение подвижной системы координат относительно неподвижной однозначно определяется тремя углами, называемыми углами Эйлера: ψ — угол прецессии,
θ — угол нутации и
φ — угол собственного вращения.

Линия пересечения подвижной плоскости xOy с неподвижной x₁Oy₁ называется линией узлов OK. Угол прецессии определяет положение линии узлов на неподвижной плоскости x₁Oy₁. Для изменения этого угла тело должно вращаться вокруг оси Oz₁, которую называют осью прецессии.

Угол нутации θ — это угол между осями Oz₁ и Oz. При изменении угла происходит поворот тела вокруг линии узлов, которую также называют осью нутации.

Угол собственного вращения φ — это угол между линией узлов и подвижной осью Ox. При изменении угла φ тело вращается вокруг оси Oz (оси собственного вращения).

Для определения положения тела с одной неподвижной точкой в любой момент времени необходимо задать углы Эйлера как функции времени, т. е.

ψ = ψ(t),
θ = θ(t),
φ = φ(t). (3.1)

Выражения (3.1) называются уравнениями вращения твердого тела вокруг неподвижной точки.

>> Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку

Преобразовать прямые углы в повороты

1 Прямые углы = 0,25 Повороты	10 Прямые углы = 2,5 Повороты	2500 Прямые углы = 625 Обороты
2 Прямые углы = 0,5 Повороты	20 Прямые углы = 5 Повороты	5000 Прямые углы = 1250 Повороты
3 Прямые углы = 0.75 Оборотов	30 Прямые углы = 7,5 Повороты	10000 Прямые углы = 2500 Повороты
4 Прямые углы = 1 Повороты	40 Прямые углы = 10 Обороты	25000 Прямые углы = 6250 Повороты
5 Прямые углы = 1. 25 Оборотов	50 Прямые углы = 12,5 Повороты	50000 Прямые углы = 12500 Повороты
6 Прямые углы = 1,5 Повороты	100 Прямые углы = 25 Обороты	100000 Прямые углы = 25000 Повороты
7 Прямые углы = 1.75 Оборотов	250 Прямые углы = 62,5 Повороты	250000 Прямые углы = 62500 Обороты
8 Прямые углы = 2 Повороты	500 Прямые углы = 125 Повороты	500000 Прямые углы = 125000 Повороты
9 Прямые углы = 2. 25 Оборотов	1000 Прямые углы = 250 Повороты	1000000 Прямые углы = 250000 Повороты

Повернуть изображения (правильно) с OpenCV и Python

Получите мгновенный доступ к коду для этого руководства и всех других 400+ руководств по PyImageSearch.

Внутри вы найдете …

Доступ к централизованным репозиториям кода для все 400+ руководств на PyImageSearch
Предварительно настроенные блокноты Jupyter в Google Colab для более 200 руководств по PyImageSearch (включая блокноты для всех новых еженедельных руководств !)
Подробные видеоуроки для всех новых сообщений в блогах — эти видео включают дополнительные комментарии, методы и советы, которые я не не включаю в текстовые версии моих руководств

Введите свой адрес электронной почты ниже и получите доступ:

Я использовал часть одного из ваших руководств для решения возникшей у меня проблемы с Python и OpenCV. Боролся с этим две недели, но от других экспертов не ответили. Прочтите вашу статью я нашел …. Исправил за два часа. И это тоже было критически важно. Ваши вещи качественные!
Исмаил Томас-Бенге Старший консультант по обеспечению качества и архитектор

PyImageSearch Plus — Получите мгновенный доступ к коду для этого руководства и всех других 400 руководств по PyImageSearch!

Выберите свой тарифный план ниже …

$ 4.95 / мес

49,50 $ / год (экономия 15%)

Доступ к централизованным репозиториям кода для все 400+ руководств на PyImageSearch
Код быстрого доступа для все новых руководств , которые публикуются каждый понедельник
Простая загрузка в один клик для кода, моделей, наборов данных и т. Д.

14,95 $ / мес

149 долларов.50 / год (сэкономьте 15%)

Предварительно сконфигурированные блокноты Jupyter в Google Colab для более 200 руководств по PyImageSearch (включая блокноты для всех новых еженедельных руководств !)
Запускайте все примеры кода в своем веб-браузере. — работает в Windows, macOS и Linux.
Доступ к централизованным репозиториям кода для все 400+ руководств на PyImageSearch
Код быстрого доступа для все новых руководств , которые публикуются каждый понедельник
Простая загрузка в один клик для кода, моделей, наборов данных и т. Д.

74,95 $ / мес

749,50 $ / год (экономия 15%)

Видеоуроки для всех новых сообщений в блоге
Предварительно настроенные блокноты Jupyter в Google Colab для более 200 руководств по PyImageSearch (включая блокноты для всех новых еженедельных руководств !)
Запускайте все примеры кода в своем веб-браузере. — работает в Windows, macOS и Linux.
Доступ к централизованным репозиториям кода для все 400+ руководств на PyImageSearch
Код быстрого доступа для все новых руководств , которые публикуются каждый понедельник
Простая загрузка в один клик для кода, моделей, наборов данных и т. Д.

Доступ к централизованным репозиториям кода для все 400+ руководств в блоге PyImageSearch
Простой код доступа для всех новых руководств , которые публикуются каждый понедельник в 10:00 EST
Простая загрузка в один клик для исходного кода, наборов данных, предварительно обученных моделей и т. Д.
Отменить в любой момент

Легкий доступ к коду, наборам данных и предварительно обученным моделям для всех 400+ руководств в блоге PyImageSearch
Изучите использование Jupyter Notebooks в Google Colab для всех новых руководств , опубликованных на PyImageSearch
Используйте предварительно настроенных сред разработки в Google Colab — больше никаких головных болей и траты времени на настройку среды разработки

Подробные видеоуроки и пошаговые инструкции для всех новых руководств и руководств
Доступ к эксклюзивных предложений моих книг и курсов

Я использовал часть одного из ваших руководств для решения возникшей у меня проблемы с Python и OpenCV. Боролся с этим две недели, но от других экспертов не ответили. Прочтите вашу статью я нашел …. Исправил за два часа. И это тоже было критически важно. Ваши вещи качественные!
Исмаил Томас-Бенге Старший консультант по обеспечению качества и архитектор

Простая проверка пересечения повернутых прямоугольников и окружностей / точек

(нажмите, чтобы взаимодействовать) (наведите курсор мыши / щелкните, чтобы воспроизвести GIF) (нажмите и перетащите, чтобы настроить размер / положение / поворот прямоугольника; показано расстояние до круга)

Предположим, у вас есть повернутый прямоугольник и базовая форма, для которой вращение не имеет значения (например, точка, окружность или отрезок линии), и вы хотите проверить, пересекаются ли эти два элемента — будь то для обработки столкновений. , проверка нажатия или что-то еще.

На первый взгляд это может показаться проблемой, потому что с повернутыми прямоугольниками редко бывает слишком просто, но в данном случае это не так — потому что вы можете «повернуть» прямоугольник.

Этот небольшой пост об этом.

Предположим, у вас есть повернутый прямоугольник, определенный несколькими свойствами:

Размер (ширина и высота)
Смещение к центру вращения
(то есть, если установлено значение 0, h / 2, прямоугольник будет вращаться вокруг центра его левого края)
Положение (в котором центр вращения будет в любой момент времени)
Угол поворота

И у вас есть базовая форма, определяемая одним или двумя (если это линейный сегмент) позициями и, возможно, радиусом (если это круг).

Если вы должны вычесть положение прямоугольника из каждого положения формы и повернуть их на противоположное углу поворота прямоугольника, у вас будут локальные координаты для системы, в которой прямоугольник находится без вращения на 0,0, а форма плавает относительно него. На этом этапе вы можете использовать обычно тривиальные проверки пересечения для прямоугольников / ограничивающих рамок, выровненных по оси.

Приведенное выше описание переводится в код довольно простым способом,

rel_x = shape_x - rect_x;
rel_y = shape_y - rect_y;
angle = -rect_angle;
local_x = cos (угол) * rel_x + cos (угол - pi / 2) * rel_y;
local_y = sin (угол) * rel_x + sin (угол - pi / 2) * rel_y;

, конечно, согласно предыдущему посту, вы также можете вырезать второй вызов синуса / косинуса, если хотите,

rel_x = shape_x - rect_x;
rel_y = shape_y - rect_y;
angle = -rect_angle;
angle_cos = cos (угол);
angle_sin = грех (угол);
local_x = angle_cos * rel_x - angle_sin * rel_y;
local_y = angle_sin * rel_x + angle_cos * rel_y;

как только у вас есть local_x и local_y, вы можете проверить пересечение с такой точкой, как:

вернуть local_x> = -rect_offset_x && local_x <= -rect_offset_x + rect_width &&
       local_y> = -rect_offset_y && local_y <= -rect_offset_y + rect_height;

или для пересечения с кругом (связанная запись):

delta_x = max (-rect_offset_x, min (local_x, rect_width - rect_offset_x));
delta_y = max (-rect_offset_y, min (local_y, rect_height - rect_offset_y));
return delta_x * delta_x + delta_y * delta_y <радиус_круга * радиус_круга;

или любой другой алгоритм, включающий выровненный по оси прямоугольник, который простирается от (-rect_offset_x, -rect_offset_y) до (rect_width-rect_offset_x, rect_height-rect_offset_y).

Таким образом, полная функция может выглядеть следующим образом (в JS и обычном верблюжьем случае):

функция pointInRotatedRectangle (pointX, pointY,
    rectX, rectY, rectOffsetX, rectOffsetY, rectWidth, rectHeight, rectAngle
) {
    var relX = pointX - rectX;
    var relY = pointY - rectY;
    var angle = -rectAngle;
    var angleCos = Math.cos (угол);
    var angleSin = Math.sin (угол);
    var localX = angleCos * relX - angleSin * relY;
    var localY = angleSin * relX + angleCos * relY;
    вернуть localX> = -rectOffsetX && localX <= rectWidth - rectOffsetX &&
           localY> = -rectOffsetY && localY <= rectHeight - rectOffsetY;
}

И это все.

Повернуть фигуру с помощью отражения

Образование
Математика
Геометрия
Повернуть фигуру с помощью отражения

Марк Райан

A вращение - это то, что вы ожидаете это геометрическое преобразование, при котором фигура-прообраз поворачивается или вращается в положение фигуры-изображения.

При всех поворотах существует одна фиксированная точка - , центр вращения - вокруг которой вращается все остальное.Эта точка может быть внутри фигуры, и в этом случае фигура остается на месте и просто вращается. Или точка может находиться за пределами фигуры, и в этом случае фигура движется по дуге окружности (например, по орбите) вокруг центра вращения. Величина поворота называется углом поворота .

Можно добиться вращения с двумя отражениями. То, как это работает, немного сложно объяснить (и бессмысленность следующей теоремы может не сильно помочь), поэтому посмотрите рисунок, чтобы лучше понять эту идею.

Два отражения вращаются.

Вращение равняется двум отражениям: Вращение эквивалентно двум отражениям от линий, которые

пройти через центр вращения
Сформируйте угол, равный половине угла поворота

На рисунке вы можете видеть, что треугольник предварительного изображения RST был повернут против часовой стрелки на 70 градусов до треугольника изображения R’S’T ’. Это вращение можно произвести, сначала отразив треугольник RST по линии l ₁, а затем снова отразив его над l ₂.Угол, образованный l ₁ и l ₂, 35 градусов, составляет половину угла поворота.

Об авторе книги

Марк Райан - основатель и владелец Математического центра в районе Чикаго, где он проводит репетиторство по всем математическим предметам, а также готовит к экзаменам. Марк является автором «Исчисления для чайников », «Рабочей тетради по исчислению для чайников » и «Рабочей тетради по геометрии ».

Углы Эйлера — Euler angles

Эквивалентность цепных вращений

Правильные углы Эйлера

Геометрическое определение

Соглашения по внутреннему вращению

Соглашения по внешнему вращению

Знаки, диапазоны и условные обозначения

Прецессия, нутация и собственное вращение

Углы Тейта – Брайана

Определения

Конвенции

Знаки и диапазоны

Альтернативные названия

Углы данного кадра

Преобразование в другие представления ориентации

Матрица вращения

Матрица вращения — Rotation matrix

В двух измерениях

Направление

Нестандартная ориентация системы координат

Общие вращения

В трех измерениях

Основные вращения

Общие ротации

Преобразование из матрицы вращения в ось – угол

Определение оси

Зависимость угла вращения от условий измерения

Физико – химическое исследование оптически активных веществ

Факторы, влияющие на угол вращения

Угол — вращение — плоскость — поляризация

Угол — вращение — плоскость — поляризация

Угол — внутреннее вращение — Большая Энциклопедия Нефти и Газа, статья, страница 1

Угол — внутреннее вращение

Сферическое движение — Лекции и примеры решения задач технической механики

Преобразовать прямые углы в повороты

Повернуть изображения (правильно) с OpenCV и Python

Получите мгновенный доступ к коду для этого руководства и всех других 400+ руководств по PyImageSearch.

PyImageSearch Plus — Получите мгновенный доступ к коду для этого руководства и всех других 400 руководств по PyImageSearch!

Простая проверка пересечения повернутых прямоугольников и окружностей / точек

Похожие сообщения:

Повернуть фигуру с помощью отражения

Об авторе книги

Добавить комментарий Отменить ответ