Устройство планетарного механизма – коробка, механизм, шестерня, ряд и расчет
коробка, механизм, шестерня, ряд и расчет
Планетарная передача — вид зубчатой передачи, применяемой в механических и автоматических трансмиссиях. Помимо преобразования вращения «планетарка» способна суммировать и раскладывать мощности. Зная о планетарном механизме: что это такое, как работает, по каким критериям оценивают редуктор, станет понятно устройство и характеристики АКПП. В случае поломки расчёт передачи поможет выбрать надёжный и долговечный механизм.

Устройство и принцип работы
Планетарный механизм — это конструкция из зубчатых колёс, перемещающихся относительно центра. По центральной оси расположены колёса разного диаметра:
- малое солнечное с внешними зубцами;
- большое коронное или эпицикл с внутренними зубцами.

Между колёсами передвигаются сателлиты. Их вращение напоминает движение планет Солнечной системы. Оси сателлитов механические соединены на водиле, которое вращается относительно центральной оси.
Устройство простого планетарного блока:
- 1 эпицикл;
- 1 солнечное колесо;
- 1 водило.
Планетарный механизм собирают в каскады из двух и более звеньев на одном валу для получения широкого диапазона передач. Главной кинематической характеристикой зубчатой передачи является передаточное отношение.
Принцип работы планетарной коробки заключается в блокировке одного из основных элементов и передаче вращения через ведущее колесо. Для остановки элемента применяют тормозные ленты, блокировочные муфты, конические шестерни. Передаточное отношение меняется в зависимости от схемы закрепления. Описать принцип действия планетарного механизма удобнее на примере:
- Корона блокируется.
- Вал подаёт крутящий момент на солнце.
- Вращение солнца заставляет планеты обкатываться вместе с ним.
- Водило становится ведомым, сообщая пониженную передачу.
Управляя элементами простой «планетарки», получают разные характеристики:
Передача | Как работает планетарная коробка в АКПП |
1 | Солнце подаёт вращение на водило, корона двигается в противоположную сторону. |
2 | Корона подаёт вращение на водило, солнце зафиксировано. |
3 | Ведущее водило передаёт вращение солнцу. Корона заблокирована. |
4 | Водило двигает корону. Солнце зафиксировано. |
Задний ход | Водило заблокировано. Солнечное колесо вращается, планеты обкатывают и двигают корону в противоположную сторону. |
Кпд η простой передачи достигает 0,97.
Планетарный ряд с одной степенью свободы становится планетарной передачей. Две степени образуют дифференциал. Дифференциал складывает моменты на ведомом колесе, поступающие от основных ведущих звеньев.
Разновидности планетарных передач
По количеству ступеней планетарные механизмы разделяют на:
- однорядные;
- многорядные.

Планетарная передача из одной солнечной шестерни, одновенцовых сателлитов, водила и эпицикла будет однорядной. Замена сателлитов на двухвенцовые усложняет конструкцию, делая её двухрядной.
Многоступенчатая планетарная коробка передач — это последовательно установленные однорядные блоки. Такая схема позволяет суммировать передаточные числа и получать большие значения. 4-скоростные АКПП состоят из двухрядных планетарных конструкций, 8-скоростные — из четырёхрядных.

В АКПП применяют схемы, названные в честь изобретателей:
- Механизм Уилсона представляет собой трёхрядную конструкцию, в которой соединены корона первого, водило второго и корона третьего рядов. Количество передач — 5 прямых и 1 задняя.
- Механизм Лепелетье состоит из 3 соосно расположенных простых планетарных передач. Количество передач — 6 прямых и 1 задняя.
- Схема Симпсона — 2 редуктора с общей солнечной шестернёй. Водило второго ряда оборудовано тормозом. Корона первого ряда и солнце через две блокировочные муфты жёстко соединены с ведущим валом. Механизм реализует режимы: нейтраль; 1,2,3 передачи; задний ход.

По типу зубчатых конструкций планетарные редукторы делятся на:
- цилиндрические;
- конические;
- волновые;
- червячные.

Разные типы применяют для передачи момента между валами, расположенными параллельно или под углом. А также в механизмах, требующих низкой или высокой кинематической характеристики.
Характеристики основных разновидностей этого устройства
В конструкции планетарного ряда АКПП применяют различные типы зубчатых передач. Выделяют три основные наиболее распространенные: цилиндрические, конические и волновые.
Цилиндрические
Зубчатые механизмы передают момент между параллельными валами. В конструкцию цилиндрической передачи входит две и более пар колёс. Форма зубьев шестерней может быть прямой, косой или шевронной. Цилиндрическая схема простая в производстве и действии. Применяется в коробках передач, бортовых редукторах, приводах. Передаточное число ограничено размерами механизма: для одной колёсной пары достигает 12. КПД — 95%.

Конические
Колёса в конической схеме преобразуют и передают вращение между валами, расположенными под углом от 90 до 170 градусов. Зубья нагружены неравномерно, что снижает их предельный момент и прочность. Присутствие сил на осях усложняет конструкцию опор. Для плавности соединения и большей выносливости применяют круговую форму зубьев.
Производство конических передач требует высокой точности, поэтому обходится дорого. Угловые конструкции применяются в редукторах, затворах, фрезерных станках. Передаточное отношение конических механизмов для техники средней грузоподъёмности не превышает 7. КПД — 98%.
Волновые
Во волновой передаче отсутствуют солнечная и планетные шестерни. Внутри коронного колеса установлено гибкое зубчатое колесо в форме овала. Водило выступает в качестве генератора волн, и выглядит в виде овального кулачка на специальном подшипнике.
Гибкое стальное или пластмассовое колесо под действием водила деформируется. По большой геометрической оси зубья сцепляются с короной на всю рабочую высоту, по малой оси зацепление отсутствует. Движение передаётся волной, создаваемой гибким зубчатым колесом.
Во волновых механизмах КПД растёт вместе с передаточным числом, превышающим 300. Волновая передача не работает в схемах с кинематической характеристикой ниже 20. Редуктор выдает 85% КПД, мультипликатор — 65%. Конструкция применяется в промышленных роботах, манипуляторах, авиационной и космической технике.
Достоинства и недостатки планетарных передач
Планетарная передача выигрывает у простых зубчатых механизмов аналогичной мощности компактным размером и массой меньшей в 2 — 3 раза. Используя нескольких планетных шестерней, достигается зацепление зубьев на 80%. Нагрузочная способность механизма повышается, а давление на каждый зубец уменьшается.

Кинематическая характеристика планетарного механизма доходит до 1000 с малым числом зубчатых колёс без применения многорядных конструкций. Помимо передачи планетарная схема способна работать как дифференциал.
За счёт соосности валов планетарного механизма, компоновать машины проще, чем с другими редукторами.

Применение планетарного ряда в АКПП снижает уровень шума в салоне автомобиля. Сбалансированная система имеет высокую вибропрочность за счет демпфирования колебаний. Соответственно снижается вибрация кузова.
Недостатки планетарного механизма:
- сложное производство и высокая точность сборки;
- в сателлиты устанавливают подшипники, которые выходят из строят быстрее, чем шестерня;
- при повышении передаточных отношений КПД падает, поэтому приходится усложнять конструкцию.
Передаточное число планетарных передач
Передаточным называют отношение частоты ведущего вала планетарной передачи к частоте ведомого. Визуально определить его значение не получится. Механизм приводится в движение разными способами, а значит передаточное число в каждом случае различно.
Для расчёта передаточного числа планетарного редуктора учитывают число зубьев и систему закрепления. Допустим, у солнечной шестерни 24 зуба, у сателлита — 12, у короны — 48. Водило закреплено. Ведущим становится солнце.
Сателлиты начнут вращаться со скоростью, передаваемой солнечной шестернёй. Передаточное отношение равно: -24/12 или -2. Результат означает, что планеты вращаются в противоположном направлении от солнца с угловой скоростью 2 оборота. Сателлиты обкатывают корону и заставляют её обернуться на 12/48 или ¼ оборота. Колёса с внутренним закреплением вращаются в одном направлении, поэтому число положительное.
Общее передаточное число равно отношению числа зубьев ведущего колеса к количеству зубьев ведомого: -24/48 или -1/2 оборота делает корона относительно солнца при зафиксированном водиле.

Если водило станет ведомым при ведущем солнце, то передаточное отношение: (1+48/24) или 3. Это самое большое число, какое способна предложить система. Самое маленькое отношение получается при фиксировании короны и подачи момента на водило: (1+/(1+48/24)) или 1/3.
Передаточные числа простой планетарной схемы: 1,25 — 8, многоступенчатой: 30 — 1000. С ростом кинематической характеристики КПД снижается.
Подбор чисел зубьев планетарных передач
Число зубьев колёс подбирают на первом этапе расчёта планетарной схемы по заранее установленному передаточному отношению. Особенность проектирования планетарного ряда заключается в соблюдении требований правильной сборки, соосности и соседства механизма:
- зубья сателлитов должны совпадать с впадинами солнца и эпицикла;
- планеты не должны задевать друг друга зубьями. На практике более 6 сателлитов не используют из-за трудностей равномерного распределения нагрузки;
- оси водила, солнечного и коронного колёс должны совпадать.

Основное соотношение подбора зубьев передачи через передаточное число выглядит так:
i = 1+Zкорона/Zсолнце,
где i — передаточное число;
Zn — количество зубьев.
Условие соосности соблюдается при равных межосевых расстояниях солнечного колеса, короны и водила. Для простой планетарной зубчатой передачи проверяют межосевые расстояния между центральными колёсами и сателлитами. Равенство должно удовлетворять формуле:
Zкорона= Zсолнце+2×Zсателлит.
Чтобы между планетами оставался зазор, сумма радиусов соседних шестерней не должна превышать осевое расстояние между ними. Условие соседства с солнечным колесом проверяют по формуле:
sin (π/c)> (Zсателлит+2)/(Zсолнце+Zсателлит),
где с — количество сателлитов.

Планетные колёса размещаются равномерно, если соотношение зубьев короны и солнца к количеству сателлитов окажется целым:
Zсолнце/с = Z;
Zкорона/с = Z,
где Z — целое число.

Расчет на прочность планетарных передач
Прочностной расчёт планетарных передач проводят как для цилиндрических зубчатых передач. Вычисляют каждое зацепление:
- внешнее — между солнцем и планетными колёсами;
- внутреннее — между планетами и короной.
Если колёса изготовлены из одного материала, а силы в зацеплении равны, рассчитывают наименее прочное соединение — внешнее.
Алгоритм расчёта следующий:
- Выбирают схему редуктора.
- Определяют исходные данные: передаточное число i, крутящий момент Твых и частоту вращения выходного вала Uвых.
- Подбирают число зубьев с проверкой условий сборки и соседства планетных шестерней.
- Рассчитывают угловые скорости колёс.
- Вычисляют КПД и моменты выходных валов.
- Рассчитывают прочность зацепления.

В расчёте момента учитывают количество планетных колёс и неравномерное нагружение их зубьев. Вводят поправочный коэффициент η =1,5…2, если меры выравнивания отсутствуют:
- повышенная точность изготовления;
- радиальная подвижность солнца, короны или водила;
- применение упругих элементов.
Расчёт зубчатых передач выполняют по двум критериям:
- контактная прочность, т.е. выносливость рабочих поверхностей зубьев под нагрузкой;
- напряжение на изгиб, усталостный излом.

Расчёт контактной прочности сводится к проверке условия, что напряжение σн не превышает допустимого значения. Вычисления проводят по формуле Герца для цилиндрических поверхностей, добавляя уточняющие коэффициенты. В результате получают значение межосевого расстояния — главную геометрическую характеристику зубчатой передачи:
d=K×η×∛ (T×Kн(i±1))/(Ψ×i×[σн]^2),
где K — вспомогательный коэффициент для прямозубых колёс, МПа;
η — коэффициент неравномерности;
Т — вращающий момент, Н×мм;
Kн — коэффициент нагрузки;
Ψ — коэффициент ширины колеса равный 0,75;
i — передаточное число;
[σн] — допускаемое контактное напряжение, МПа. Определяется коэффициентом долговечности и пределом выносливости.
После определения геометрии передачи проверяют условие прочности:
σн= {310/(d×i)}×√ (T×Kн(i+1)^3)/(Ψ×d) ≤ [σн]

При расчёте на изгиб принимают условие, что вся нагрузка передаётся одной паре зубьев и приложена к его вершине. Расчётное напряжение не должно превышать допускаемое:
σf= (M/W) – (F/(b×s) ≤ [σf],
где М — изгибающий момент;
W — осевой момент сопротивления;
F — сила сжатия;
b, s — размеры зуба в сечении;
[σf] — допускаемое напряжение изгиба. Зависит от предела выносливости, шероховатости, погрешности изготовления зубьев.Советы по подбору планетарного редуктора
Перед выбором планетарного редуктора проводят точный расчёт нагружения и режимов работы механизма. Определяют тип передачи, осевые нагрузки, температурный диапазон и типоразмеры редуктора. Для тяжёлой спецтехники, где нужен большой крутящий момент при малых скоростях, выбирают редуктор с высоким передаточным отношением.
Чтобы сбавить угловую скорость, не снижая крутящего момента, применяют привод с электродвигателем и редуктором. При выборе мотор редуктора учитывают:
- эксплуатационную нагрузку;
- момент вала на выходе;
- частоту вращения входного и выходного валов;
- мощность электродвигателя;
- монтажное исполнение.
Область применения планетарных передач
Планетарная схема используется в:
- редукторах;
- автоматических и механических коробках передач;
- в приводах летательных аппаратов;
- дифференциалах машин, приборов;
- ведущих мостах тяжёлой техники;
- кинематических схемах металлорежущих станков.
Планетарную коробку передач применяют в агрегатах с переменным передаточным отношением, затормаживая водило. В гусеничной технике для сложения потоков мощности элементы в планетарном механизме не блокируют.
Заключение
Планетарные передачи в АКПП зарекомендовали себя десятилетиями эксплуатации со времён Ford T: компактными размерами, малым весом, высокими скоростями, надёжностью и выносливостью. Планетарная схема способна передавать вращение и управлять потоками мощности, поэтому нашла применение в авиации, машиностроении, промышленности.
Чтобы не ошибиться с выбором конструкции, проводят точный расчёт геометрии и прочности зубчатой передачи, сверяя с допустимыми значениями. Ошибки вычислений приводят к чрезмерной нагрузке зубчатых передач, поломке и истиранию зубьев.
akppoff.ru
Строим планетарную КПП, часть 1: планетарные ряды
В предыдущих статьях о трансмиссиях я касался только двухвальных, трёхвальных и безвальных коробок передач, а планетарные обходил стороной. На сей раз я решил подробно описать работу планетарных коробкок передач фирмы Pulsgetriebe для Тигра и прототипа Леопарда. Однако я не мог уместить в один пост и объяснение принципов работы планетарных редуторов, и рассмотрение простой планетарной коробки передач, и, наконец, описание реальных КПП Pulsgetriebe. Поэтому я написал три поста: в первых двух объясняется, как работают планетарные редукторы и коробки передач, а в третьем дано описание коробок передач PP33 и PP45.Если вы понимаете, как работают планетарные КПП, сразу переходите к третьему посту. Если нет, то прочтите этот пост и его вторую часть. В них я исхожу из того, что читатель знает, как работают двухвальные или трёхвальные коробки передач, но ничего не понимает в планетарных передачах.
ПРДПВ:
Устройство планетарной передачи
Для того, чтобы изучить, как работает простая коробка передач, нужно сперва понять, как работает простейший редуктор из пары шестерён, а затем из таких пар собрать коробку передач. Мы поступим аналогично: сперва разберёмся с планетарными редукторами, а затем посмотрим, как их можно применить. Скажу сразу: люди придумали очень много планетарных механизмов и очень много схем планетарных коробок передач, всё их многообразие мы, конечно, охватить не сможем.
Один из самых распространённых планетарных механизмов выглядит следующим образом:
Он состоит из трёх частей:
- Солнечная шестерня, выделена жёлтым
- Эпициклическая шестерня (или просто эпицикл) с внутренними зубьями, выделена красным
- Шестерни-Сателлиты, связывающие солнечную шестерню с эпициклом, выделены синим
- Зелёным цветом закрашено водило, которое связывает все сателлиты
У данной передачи есть три части: солнечная шестерня, эпицикл и водило. Если мы заблокируем одну из частей и начнём вращать другую, то начнёт вращаться третья. Её скорость вращения будет зависеть от чисел зубьев шестерён. Например, заблокируем серый эпицикл и начнём вращать красное водило, при этом будет вращаться и зелёный ведомый вал от солнечной шестерни:
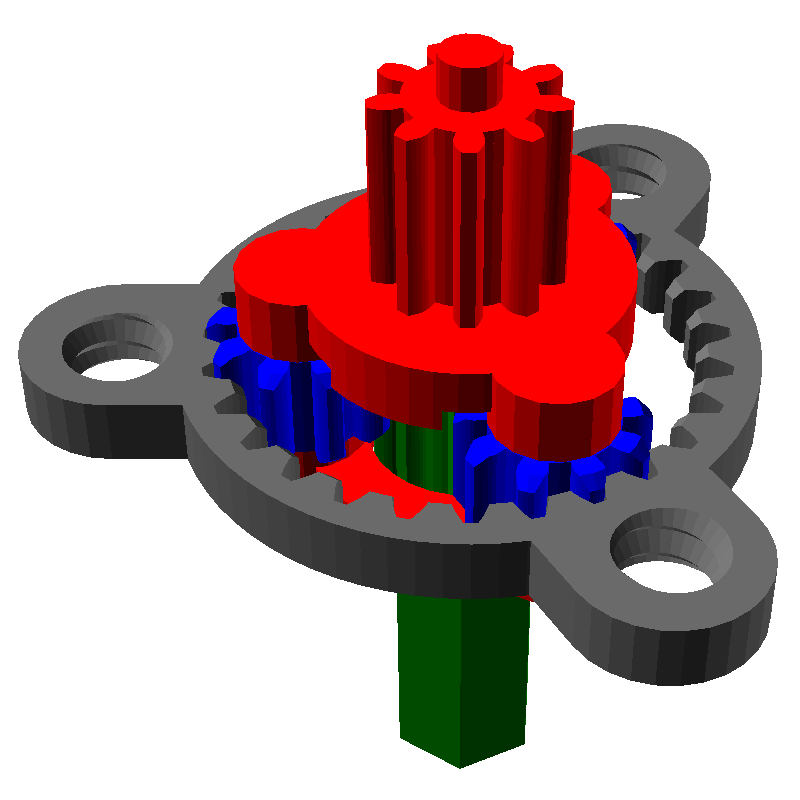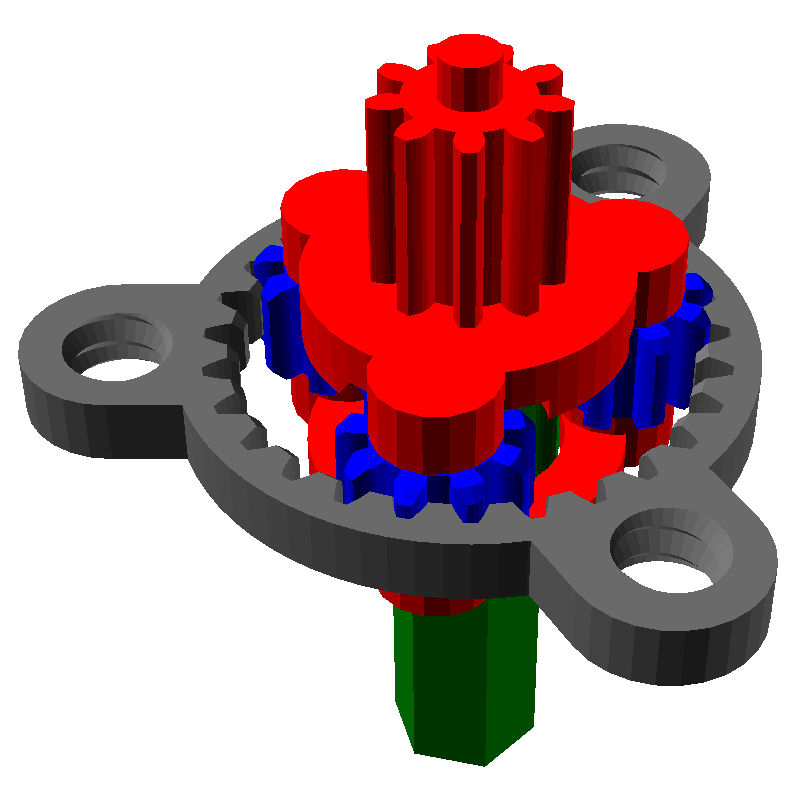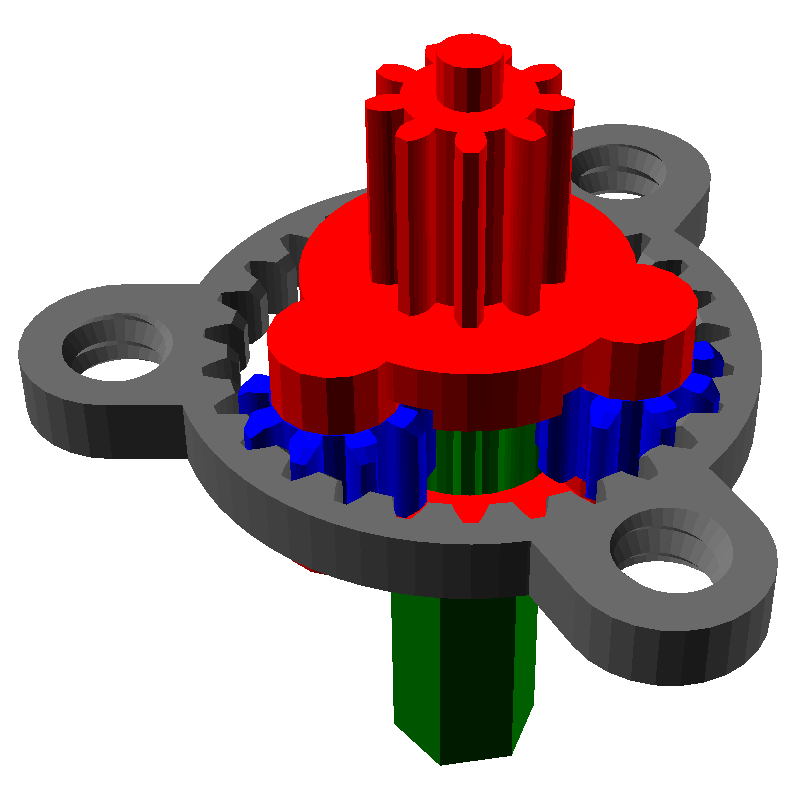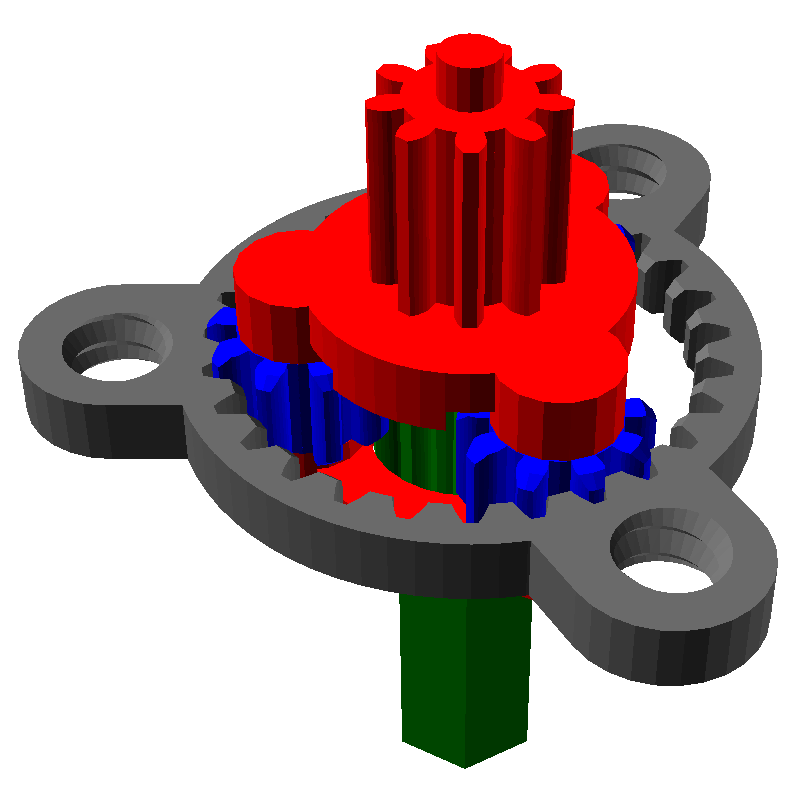
Рассмотрим все три случая. Для того, чтобы анимация не мешала читать, я не буду вставлять сами картинки, но дам ссылки на них:
Планетарные редукторы
Для того, чтобы использовать планетарную передачу как редуктор, нужно связать один элемент с ведущим валом, второй с ведомым, а третий заблокировать.
Вот схема редуктора с заблокированным эпициклом: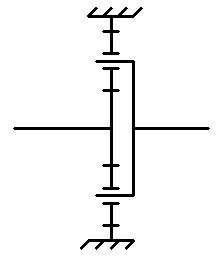
С заблокированной солнечной шестернёй: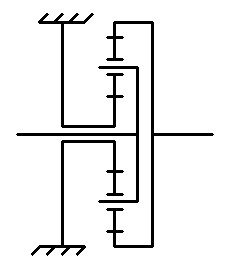
С заблокированным водилом: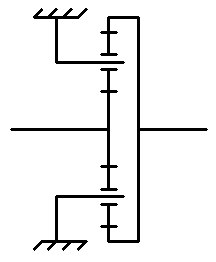
Планетарные редукторы имеют целый ряд достоинств перед обычными. Во-первых, мощность передаётся через несколько шестерён, как следствие, при прочих равных меньше нагрузка на зубья, выше надёжность и срок службы. Во-вторых, ведущий и ведомый валы соосны, часто это очень удобно с точки зрения компоновки. В-третьих, планетарная передача более компактна, чем простой редуктор с тем же передаточным числом:
Планетарный однопоточный механизм поворота
Планетарную передачу можно использовать не только как редуктор, но и в механизме поворота. На среднем танке Шерман, например, механизм поворота двойной дифференциал, а это тоже планетарный механизм. Но мы рассмотрим механизм поворота не дифференциального, а независимого типа.
На схемах выше мы жёстко блокировали один из элементов планетарного механизма, поэтому он всегда работал как редуктор, передавая мощность. Давайте уберём эту блокировку и добавим ленточный тормоз: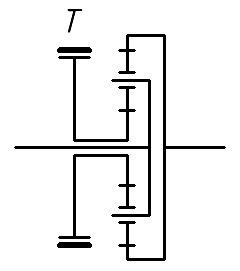
Представим, что двигатель связан с эпициклом, а водило с ведущими колёсами танка. Когда тормоз Т выключен происходит следующее. Двигатель вращает эпицикл, сателлиты и солнечную шестерню. Водило связано с ведущими колёсами, для того, чтобы оно вращалось нужно сдвинуть танк с места. Разумеется, намного проще вращать солнечную шестерню вхолостую, поэтому именно водило будет неподвижным. Для того, чтобы танк начал движение, нужно затянуть тормоз Т. Солнечная шестерня будет заблокирована и мощность пойдёт через водило к ведущим колёсам.
Осталось добавить остановочные тормоза и мы получим механизм поворота:
Тормоза Т2 и Т4 — остановочные, они тормозят ведущие колёса танка. Тормоза Т1 и Т3 называются опорными, они нужны для того, чтобы блокировать солнечные шестерни.
Для того, чтобы начать движение по прямой нам нужно выключить остановочные тормоза и затянуть опорные. Для поворота влево выключаем опорный тормоз Т1, а потом затягиваем остановочный тормоз Т2. Он тормозит левую гусеницу, мощность двигателя к ней не идёт. Для поворота вправо, соответственно, нужно выключить тормоз Т3 и занянуть Т4.
Планетарный механизм с внешним зацеплением
Выше мы рассмотрели планетарные механизмы с внутренним зацеплением, поскольку у их эпициклов внутренние зубья. Существуют аналогичные механизмы внешнего зацепления. В них используются эпициклы с внешними зубьями.
Всё познаётся в сравнении. Слева уже знакомый нам планетарный редуктор с заблокированным водилом и эпициклом внутреннего зацепления, а справа его аналог, тоже с заблокированным водилом, но с внешним зацеплением: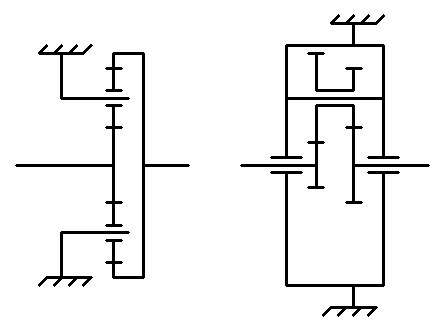
Давайте разберёмся, из каких частей он состоит и как работает.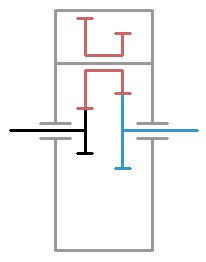
Чёрным цветом выделена солнечная шестерня, синим — эпицикл, красным — сдвоенный сателлит, а серым помечено водило.
Если заблокировать водило и начать вращать солнечную шестерню, то она станет вращать сателлит и через него эпицикл. Если заблокировать эпицикл и вращать солнечную шестерню, то будет вращаться водило. Одним словом, принцип работы точно такой же, просто другое исполнение.
На этом пока остановимся. В следующем посте на основе этих механизмов мы сделаем простейшие двухскоростные коробки передач и реверс, а затем соберём из них планетарную коробку передач и проанализируем её работу.
Читать дальше
kedoki.livejournal.com
Механизм планетарный: расчет, схема, синтез
Существуют всевозможные механические устройства. Одни из них знакомы нам с детства. Это, например, часы, велосипед, юла. О других мы узнаем, когда становимся старше. Это моторы машин, лебедки подъемных кранов и прочие. В каждом двигающемся механизме используется какая-либо система, заставляющая колесики крутиться, а машину работать. Одним из самых интересных и востребованных является планетарный механизм. Его суть состоит в том, что машину приводят в движение колесики или шестеренки, взаимодействующие между собой особым способом. Рассмотрим его подробнее.
Общие сведения
Планетарная передача и планетарный механизм так названы по аналогии с нашей Солнечной системой, которую условно можно представить так: в центре есть «солнце» (центральное колесо в механизме). Вокруг него движутся «планеты» (маленькие колесики или сателлиты). Все эти детали в планетарном механизме имеют наружные зубья. Условная солнечная система по ее диаметру имеет границу. Роль ее в планетарном механизме выполняет большое колесо или эпицикл. На нем тоже есть зубья, только внутренние. Большую работу в данной конструкции выполняет водило, представляющее собой рычажный механизм. Движение может осуществляться по-разному: либо солнце будет вращаться, либо эпицикл, но всегда совместно с сателлитами.
При работе планетарного механизма может использоваться и другая конструкция, например, два солнца, сателлиты и водило, но без эпицикла. Еще вариант — два эпицикла, но без солнца. Водило и сателлиты должны присутствовать всегда. В зависимости от количества колес и расположения осей их вращения в пространстве, конструкция может быть простой или сложной, плоской или пространственной.
Чтобы полностью понять, как работает такая система, необходимо разобраться в деталях.
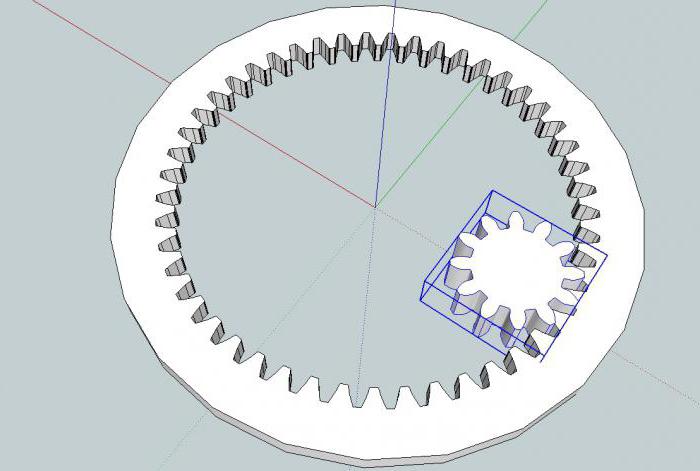
Расположение элементов
Самая простая форма планетарного механизма включает в себя три комплекта передач с разной степенью свободы. Указанные выше сателлиты вращаются вокруг своих осей и одновременно вокруг солнца, остающегося на месте. Эпицикл связывает планетарный механизм снаружи и тоже вращается посредством поочередного сцепления зубьев (его и сателлитов). Такая конструкция способна в одной плоскости изменять крутящий момент (угловые скорости).
В простом планетарном механизме может вращаться солнце и сателлиты, а эпицентр оставаться фиксированным. В любом случае, угловые скорости всех составляющих не хаотичны, а имеют линейную зависимость друг от друга. По мере поворота носителя, обеспечивается низкоскоростной выход с высоким крутящим моментом.
То есть суть планетарной передачи заключается в том, что такая конструкция способна изменять, раскладывать и складывать крутящий момент и проводимую угловую скорость. Вращательные движения при этом происходят в одной геометрической оси. Устанавливается необходимый элемент трансмиссии различных транспортных средств и механизмов.

Особенности структурных материалов и схем
Однако фиксированный компонент не всегда необходим. В дифференциальных системах каждый элемент вращается. Механизмы планетарные, подобные этому, включают в себя один выход, управляемый (управляющий) двумя входами. Например, дифференциал, который управляет осью в автомобиле, представляет собой подобную передачу.
Такие системы работают по тому же принципу, что и структуры с параллельным валом. Даже простая планетарная передача имеет два входа, закрепленная кольцевая шестерня представляет собой постоянный вход нулевой угловой скорости.
Детальное описание устройств
Смешанные планетарные конструкции могут иметь разное количество колес, а также различные передачи, посредством которых они соединяются. Наличие таких деталей значительно расширяет возможности механизма. Составные планетарные конструкции могут быть собраны так, чтобы вал несущей платформы двигался с высокой скоростью. В результате некоторые проблемы с редукцией, солнечной шестерней и прочими могут быть устранены в процессе усовершенствования устройства.
Таким образом, как видно из приведенной информации, планетарный механизм работает по принципу передачи вращения между звеньями, являющимися центральными и подвижными. При этом сложные системы более востребованы, чем простые.
Варианты конфигурации
В планетарном механизме можно использовать колеса (шестерни) различной конфигурации. Подходят стандартные с прямыми зубьями, косозубые, червячные, шевронные. Тип зацепления на общий принцип работы планетарного механизма не будет влиять. Главное, чтобы совпадали оси вращения водила и центральных колес. А вот оси сателлитов могут располагаться в других плоскостях (скрещивающихся, параллельных, пересекающихся). Пример скрещивающихся — дифференциал межколесный, у которого зубчатые колеса имеют коническую форму. Пример скрещивающихся — дифференциал самоблокирующийся, у которого зацепление червячное (Torsen).
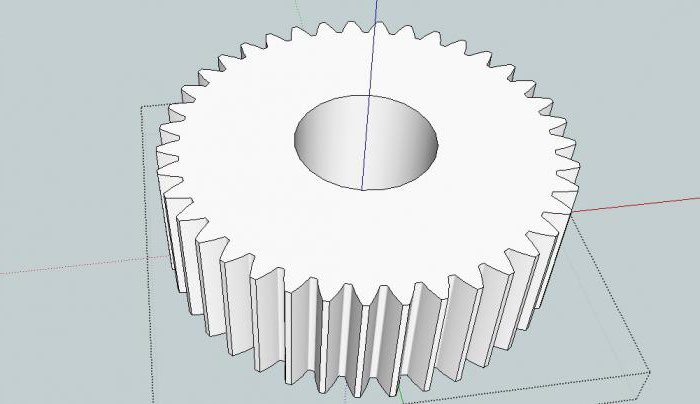
Простые и сложные устройства
Как уже отмечалось выше, схема планетарного механизма всегда включает водило и два центральных колеса. Сателлитов может быть сколько угодно. Это, так называемое, простое или элементарное устройство. В таких механизмах конструкции могут быть такими : «СВС», «СВЭ», «ЭВЭ», где:
- С — солнце.
- В — водило.
- Э — эпицентр.
Каждый такой набор колес + сателлиты называется планетарным рядом. При этом все колеса должны вращаться в одной плоскости. Простые механизмы бывают одно- и двухрядными. В различных технических приборах и машинах они используются редко. Примером может послужить планетарный механизм велосипеда. По такому принципу работает втулка, благодаря которой осуществляется движение. Ее конструкция создана по схеме «СВЭ». Сателлитов в не 4 штуки. При этом солнце жестко крепится к оси заднего колеса, а эпицентр является подвижным. Вращаться его вынуждает велосипедист, нажимающий на педали. При этом скорость передачи, следовательно, и скорость вращения могут меняться.
Гораздо чаще можно встретить сложные зубчатые планетарные механизмы. Их схемы могут быть самыми разными, что зависит от того, для чего предназначается та или иная конструкция. Как правило, сложные механизмы состоят из нескольких простых, созданных по общему правилу для планетарной передачи. Такие сложные системы бывают двух-, трех- или четырехрядные. Теоретически можно создавать конструкции и с большим числом рядов, но на практике такое не встречается.
Плоские и пространственные устройства
Некоторые думают, что простой планетарный механизм обязательно должен быть плоским. Это верно лишь отчасти. Сложные устройства тоже могут быть плоскими. Это значит, что планетарные ряды, сколько бы их ни использовалось в устройстве, находятся в одной либо в параллельных плоскостях. Пространственные механизмы имеют планетарные ряды в двух и более плоскостях. При этом самих колес может быть меньше, чем в первом варианте. Заметим, что плоский планетарный механизм такой же, как и пространственный. Разница состоит только в занимаемой устройством площади, то есть в компактности.
Степени свободы
Так называется совокупность координат вращения, позволяющая определить положение системы в пространстве в данный момент времени. Фактически каждый планетарный механизм имеет степеней свободы не менее двух. То есть угловые скорости вращения любого звена в таких устройствах не связаны линейно, как в других зубчатых передачах. Это позволяет получать на выходе угловые скорости не такие, какие есть на входе. Объяснить это можно тем, что в дифференциальной связи в планетарном механизме находятся три элемента в любом ряду, а остальные будут связаны с ним линейно, посредством какого-либо одного элемента ряда. Теоретически можно создать планетарные системы с тремя и более степенями свободы. Но на практике они оказываются неработоспособными.

Передаточное отношение планетарного механизма
Это важнейшая характеристика вращательного движения. Она позволяет определить, во сколько раз увеличился момент силы на валу ведомом по отношению к моменту вала ведущего. Определить передаточное отношение можно по формулам:
i = d2/d1 =Z2/Z1 = M2/M1 = W1/W2 = n1/n2, где:
- 1 — звено ведущее.
- 2 — звено ведомое.
- d1, d2 — диаметры первого и второго звеньев.
- Z1, Z2 — число зубьев.
- M1, M2 — крутящие моменты.
- W1 W2 — угловые скорости.
- n1 n2 — частота вращения.
Таким образом, при передаточном отношении выше единицы на ведомом валу увеличивается момент силы, а частота и угловая скорость уменьшаются. Это всегда нужно учитывать при создании конструкции, потому что передаточное отношение в планетарных механизмах зависит от того, сколько зубьев имеют колеса, и какой именно элемент ряда является ведущим.
Область применения
В современном мире существует множество различных машин. Многие из них работают с помощью планетарных механизмов.
Они используются в автомобильных дифференциалах, планетарных редукторах, в кинематических схемах сложных станков, в редукторах воздушных двигателей самолетов, в велосипедах, в комбайнах и тракторах, в танках и другой военной технике. По принципам планетарной передачи работают многие коробки передач, в приводах электрогенераторов. Рассмотрим еще одну такую систему.
Планетарный механизм поворота
Данная конструкция находит применение в некоторых тракторах, машинах на гусеничном ходу и танках. Простая схема устройства показана на рисунке ниже.
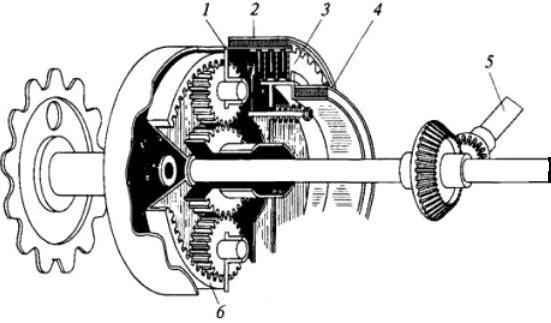 Принцип работы планетарного механизма поворота такой: водило (позиция 1) связано с барабаном тормоза (2) и ведущим колесом, расположенным в гусенице. Эпицикл (6) связан с валом передачи (позиция 5). Солнце (8) связано с диском фрикциона (3) и барабаном тормоза поворота (4). При включении блокировочного фрикциона и выключении ленточных тормозов сателлиты вращаться не будут. Они станут подобны рычагам, так как посредством зубьев связаны с солнцем (8) и эпициклом (6). Поэтому вынуждают их и водило одновременно вращаться вокруг общей оси. При этом угловая скорость одинаковая.
Принцип работы планетарного механизма поворота такой: водило (позиция 1) связано с барабаном тормоза (2) и ведущим колесом, расположенным в гусенице. Эпицикл (6) связан с валом передачи (позиция 5). Солнце (8) связано с диском фрикциона (3) и барабаном тормоза поворота (4). При включении блокировочного фрикциона и выключении ленточных тормозов сателлиты вращаться не будут. Они станут подобны рычагам, так как посредством зубьев связаны с солнцем (8) и эпициклом (6). Поэтому вынуждают их и водило одновременно вращаться вокруг общей оси. При этом угловая скорость одинаковая.При выключении блокировочного фрикциона и включении тормоза поворота солнце начнет останавливаться, а сателлиты начнут двигаться вокруг своих осей. Тем самым они создают момент на водиле и вращают ведущее колесо гусеницы.
Износ
Что касается срока службы и амортизации, то в линейных механизмах планетарных систем распределение нагрузки заметно среди основных компонентов.
Термическая и циклическая усталость могут повышаться в них за счет ограниченного распределения нагрузки и того факта, что планетарные передачи могут вращаться довольно быстро по их осям. Более того, при высоких скоростях и передаточных отношениях планетарного механизма, центробежные силы могут значительно увеличить величину движения. Также следует заметить, что по мере снижения точности производства и увеличения количества сателлитов тенденция к дисбалансу возрастает.
Эти устройства и их системы могут даже подвергнуться износу или амортизации. Некоторые конструкции будут чувствительны даже к небольшим дисбалансам и способны потребовать качественные и дорогие компоненты сборки. Точным расположением планетных штифтов вокруг оси солнечной шестерни может быть ключ.
Другие схемы планетарных механизмов, которые помогают балансировать нагрузки, включают использование плавающих подузлов или «мягких» креплений, чтобы обеспечить максимально долговечное движение солнца или эпицентра.

Основы синтеза планетарных устройств
Эти знания нужны при проектировании и создании узлов машин. Понятие «синтез планетарных механизмов» заключается в расчете числа зубьев в солнце, эпицентре и сателлитах. При этом необходимо соблюсти ряд условий:
- Передаточное отношение должно равняться заданному значению.
- Зацепление зубьев колес должно быть правильным.
- Необходимо обеспечить соосность входного вала и выходного.
- Требуется обеспечить соседство (сателлиты не должны мешать друг другу).
Также при проектировании нужно учитывать габариты будущей конструкции, ее массу и КПД.
Если задано передаточное число (n), то число зубьев на солнце (S) и на планетарных шестернях (P) должно удовлетворять равенству:
n = S/P
Если допустить, что число зубьев на эпицентре рано (А), то при заблокированном водиле должно быть соблюдено равенство:
n = -S/A
Если закреплен эпицентр, то будет верным следующее равенство:
n = 1+ A/S
Так производится расчет планетарного механизма.

Преимущества и недостатки
Существует несколько видов передачи, которые благополучно используются в различных устройствах. Планетарная среди них выделяется следующими достоинствами:
- Обеспечивается меньшая нагрузка на каждый зубец колес (и солнца, и эпицентра, и сателлитов) за счет того что нагрузка на них распределяется более равномерно. Это положительно влияет на срок службы конструкции.
- При той же мощности планетарный механизм имеет меньшие габариты и массу, чем при использовании других видов передачи.
- Возможность достигать большего передаточного числа с меньшим количеством колес.
- Обеспечение меньшего уровня шума.
Недостатки планетарных механизмов:
- Нужна повышенная точность при их изготовлении.
- Малый КПД при сравнительно большом передаточном отношении.
fb.ru
Планетарный механизм — это… Что такое Планетарный механизм?
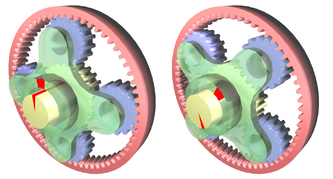
Планетарная передача в режиме повышения скорости. Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.
Планетарная передача — механическая система, состоящая из нескольких планетарных зубчатых колёс (шестерён), вращающихся вокруг центральной, солнечной, шестерни. Обычно, планетарные шестерни фиксируются вместе с помощью водила. Планетарная передача может также включать дополнительную внешнюю кольцевую шестерню, имеющую внутреннее зацепление с планетарными шестернями.
Передаточное отношение
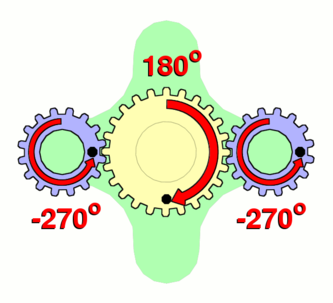
Водило (зелёное) закреплено неподвижно, в то время как солнечная шестерня (жёлтая) вращается внешним источником. В данном случае передаточное отношение равно -24/16, или -3/2; каждая планетарная шестерня поворачивается на 3/2 оборота относительно солнечной шестерни, в противоположном направлении.
Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение несколькими разными способами. Основными элементами планетарной передачи можно считать следующие:
- Солнечная шестерня: находится в центре;
- Водило: жёстко фиксирует друг относительно друга оси нескольких планетарных шестерён (сателлитов) одинакового размера, находящихся в зацеплении с солнечной шестерней;
- Кольцевая шестерня (эпицикл): внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями.
При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, другой элемент используется как ведущий, а третий – в качестве ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также того, какой элемент закреплён.
Часто планетарные передачи используются для суммирования двух потоков мощности (например, планетарные ряды двухпоточных трансмиссий некоторых танков и др. гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила.
Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как S, а для планетарных шестерён примем это число как P, то передаточное отношение будет определяться формулой —S/P, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет -24/16, или -3/2, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.
Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет A зубьев, то оно будет вращаться с соотношением P/A относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 16/64, или 1/4. Таким образом, объединив оба примера, мы получим следующее:
- Один оборот солнечной шестерни даёт —S/P оборотов планетарных шестерён;
- Один оборот планетарной шестерни даёт P/A оборотов кольцевой.
В итоге, если водило заблокировано, общее передаточное отношение системы будет равно —S/A.
В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет больше единицы и составит 1+A/S.
Всё вышесказанное можно описать следующим выражением:
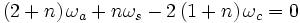 ,
,
где n – это параметр передачи, равный 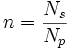 , то есть отношению числа зубьев солнечной и планетарных шестерён.
, то есть отношению числа зубьев солнечной и планетарных шестерён.
Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно 1/(1+A/S). Это самое маленькое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.
Применение

Наиболее широкое применение принцип нашёл в автомобильных дифференциалах, кроме того используется в суммирующих звеньях кинематических схем металлорежущих станков.
В современных устройствах могут использоваться каскады из нескольких планетарных передач для получения большого диапазона передаточных чисел. На этом принципе работают многие автоматические коробки передач.
Во время Второй мировой войны была разработана особая конструкция планетарной передачи, которая использовалась для привода небольших радаров. Кольцевая шестерня изготавливалась из двух частей, каждая толщиной в половину толщины других компонентов. Одна из этих половинок фиксировалась неподвижно и имела на 1 зуб меньше, чем вторая. В такой конструкции при полном обороте планетарных шестерён и нескольких оборотах солнечной шестерни, подвижное кольцо поворачивалось всего на 1 зуб. Таким образом, получалось очень высокое передаточное отношение при небольших габаритах.
Cм. также
Wikimedia Foundation. 2010.
dic.academic.ru
4.2.2. Планетарные механизмы
Механизмы, включающие неподвижные колёса, называются планетарными (рис. 4.12). Они состоят из центральных колёс 1 и 3, оси которых совпадают, водила Н и сателлита 2 (их может быть несколько). Сателлит вращается относительно своей оси и одновременно обкатывается вокруг колеса 1. Зубья колеса 1 нажимают на зубья колеса 2 и поворачивают его относительно неподвижного (опорного) колеса 3. При этом сателлит нажимает на свою ось и заставляет водило Н вращаться.
План механизма

План линейных скоростей
Рис. 4.12. Планетарный механизм
Кинематический анализ планетарных механизмов
Кинематический анализ планетарных механизмов выполняется по методу Виллиса, основанному на остановке водила. Для этого всей планетарной передаче (рис. 4.12) мысленно сообщается вращение с угловой скоростью водила, но направленной в обратную сторону, т.е. – ωН. Таким образом, получается обращенное движение, при котором водило мысленно останавливается, а другие колёса освобождаются. Преобразованный механизм представляет собой рядовой зубчатый механизм, скорость звеньев в котором составляет ωН = 0; ω1(н)=ω1(3) – ωН(3); колесо 3 было неподвижно, а в преобразованном механизме его угловая скорость равна ωН(3).
Верхний индекс показывает неподвижное звено. Мысленная остановка водила равноценна вычитанию его угловой скорости из угловых скоростей подвижных колёс. Передаточное отношение в преобразованном механизме в итоге представляется как
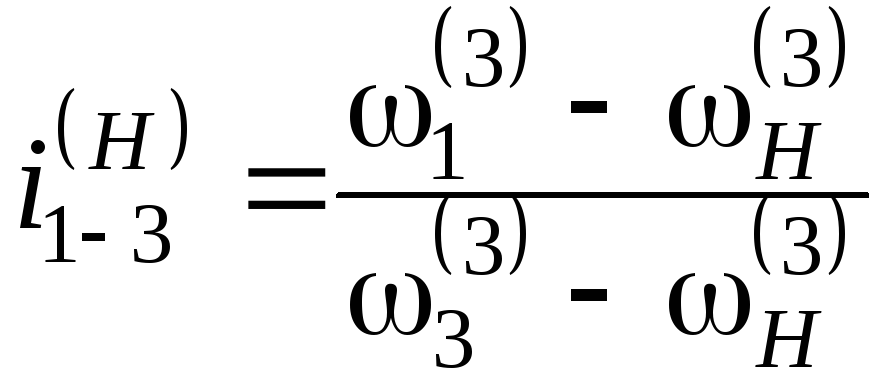 .
Но поскольку
ω3(3) = 0, то получается
.
Но поскольку
ω3(3) = 0, то получается
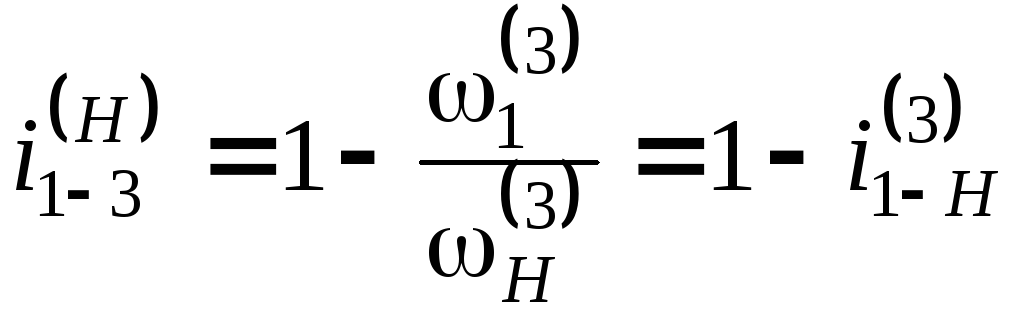 ,
откуда
передаточное отношение планетарного
механизма
будет
,
откуда
передаточное отношение планетарного
механизма
будет 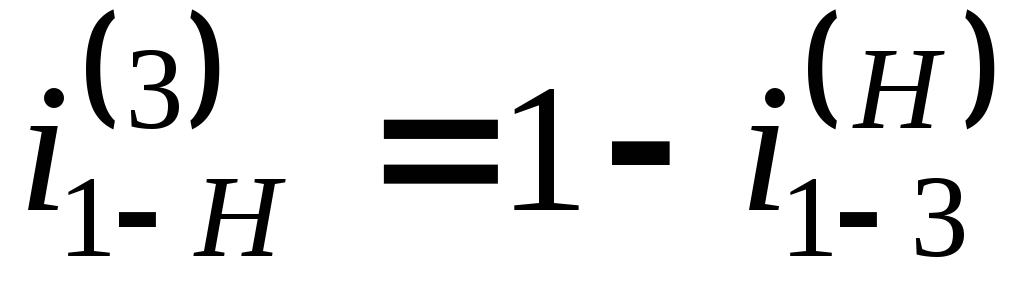 .
При этом
.
При этом 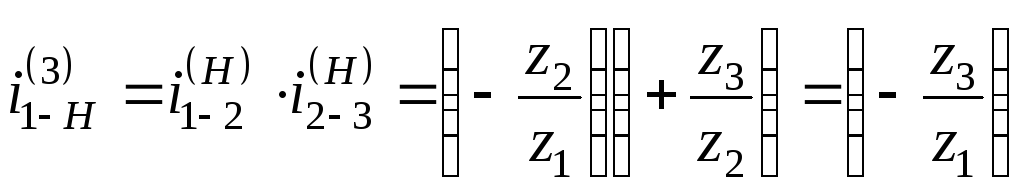 .
.
В обращенном механизме сателлит 2 является «паразитным» колесом и лишь изменяет направление вращения ведомого колеса. Окончательно будем иметь:
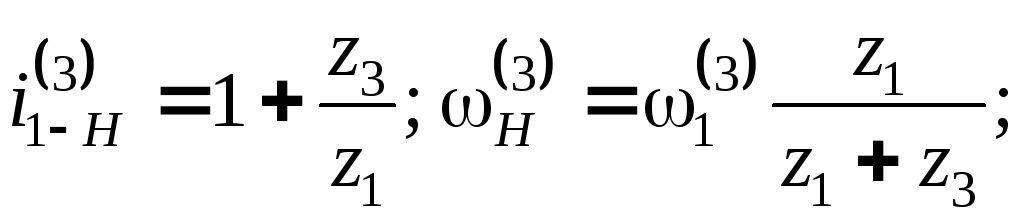
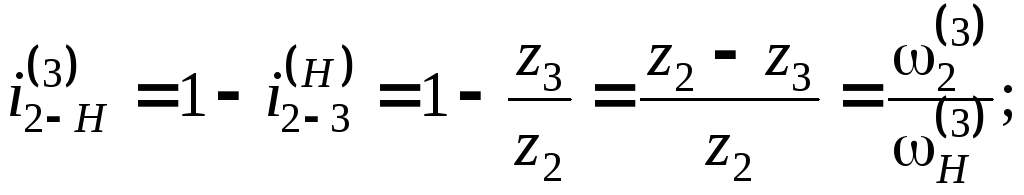
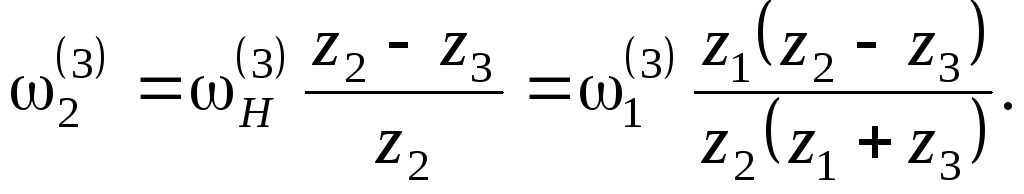
В общем виде формула Виллиса представляется как
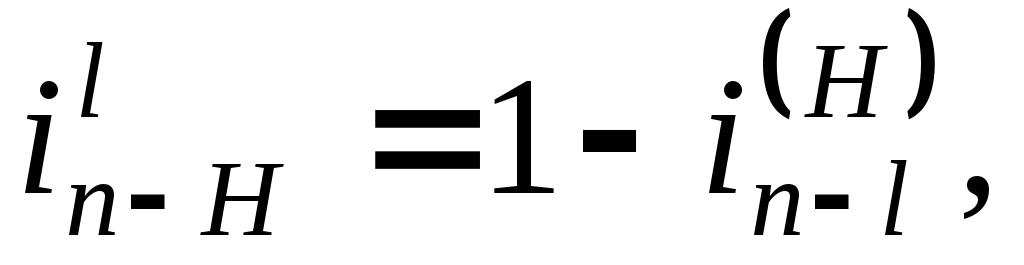
где n и l – центральные колёса. При этом
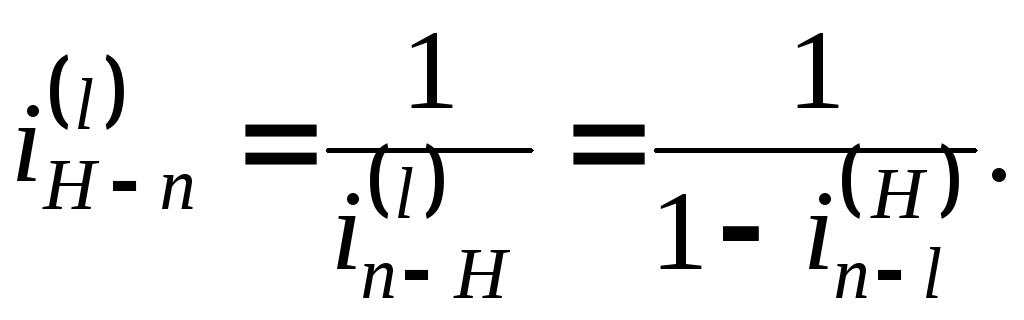
При графическом методе определения передаточных отношений в планетарном механизме строятся планы линейных и угловых скоростей (рис. 4.12). Тогда
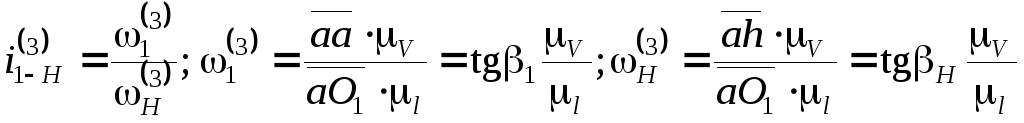 .
.
Из плана угловых скоростей:
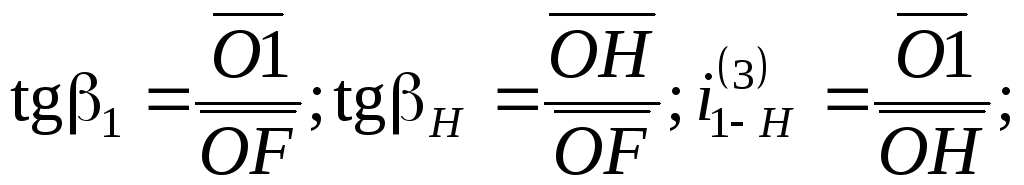
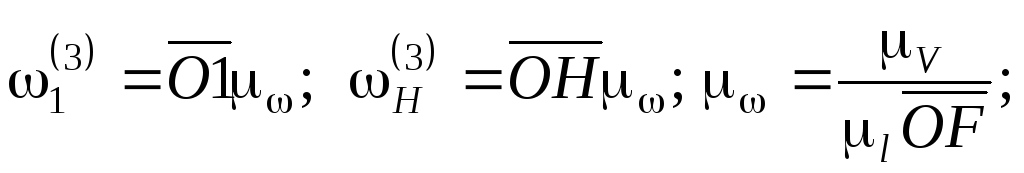
где μω – масштабный коэффициент плана угловых скоростей.
Передаточное
отношение i1-н(3) оказывается
положительным, так как отрезки 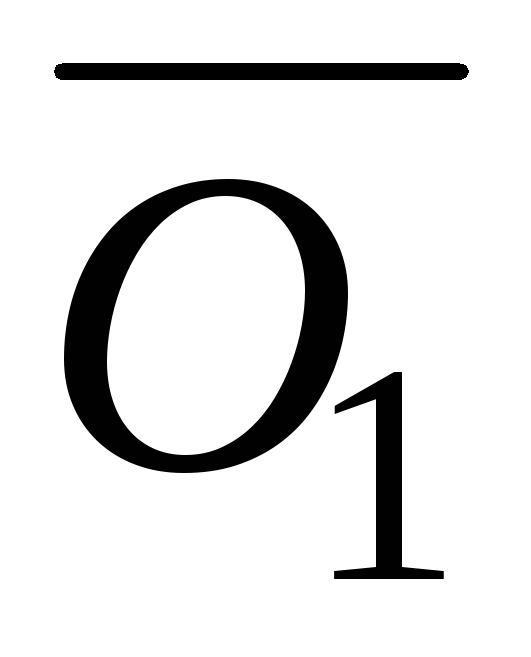 и
и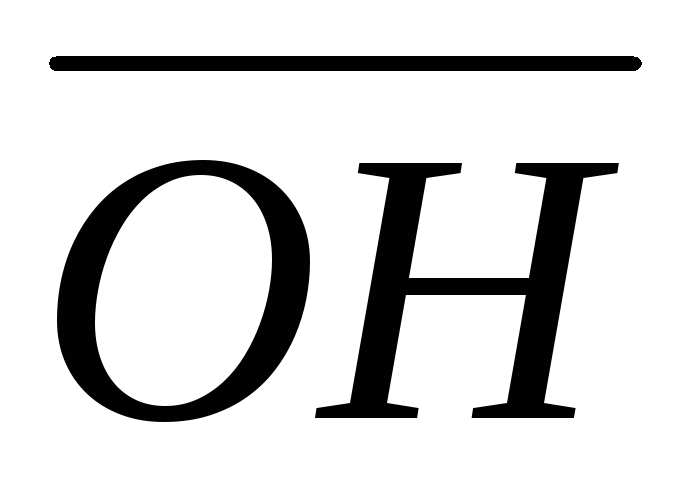 располагаются по одну и ту же сторону
от вертикалиOF.
располагаются по одну и ту же сторону
от вертикалиOF.
Наиболее распространённые схемы планетарных механизмов
Основные схемы планетарных механизмов представлены на рис. 4.13. В этих схемах неподвижным колесом может быть колесо 3 либо колесо 1.
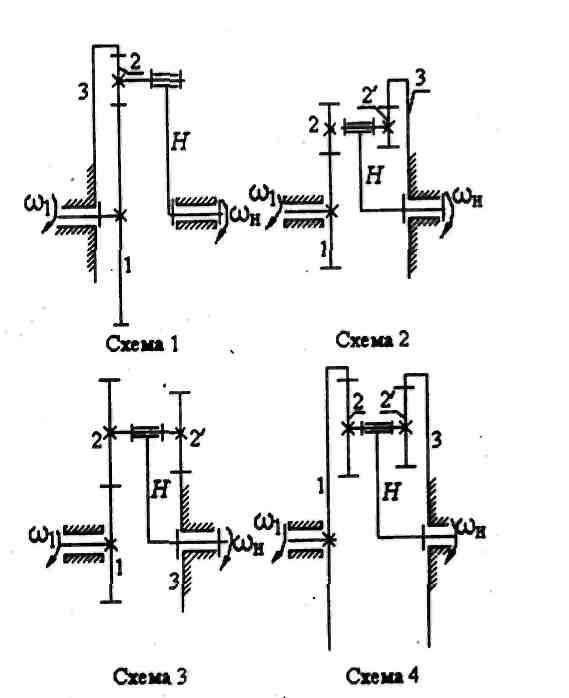
Рис. 4.13. Основные схемы планетарных механизмов
Схема
1. Планетарная
передача (Джемса) работает как силовой
редуктор, т.е. уменьшает угловую скорость
входного звена, если водило является
выходным. Передаточное отношение 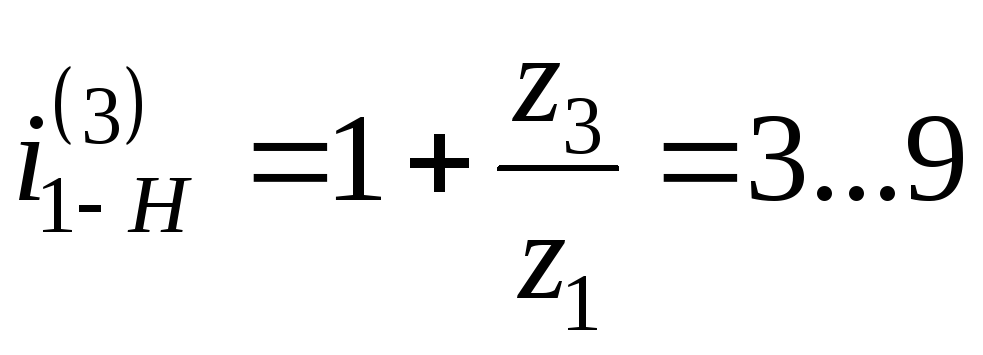 .
.
Наименьшие габариты механизм имеет при i1-H(3) = 4. Максимальное передаточное отношение можно получить в случае, когда неподвижным звеном является большое центральное колесо.
Эта передача работает как мультипликатор, т.е. увеличивает угловую скорость, когда входным звеном является водило. Направление угловой скорости входного звена в механизме не изменяется.
Схема
2. Редуктор
со сдвоенными сателлитами по габаритам
мало отличается от редуктора Джемса
при i1-H(3) = 7.
Передаточное отношение передачи 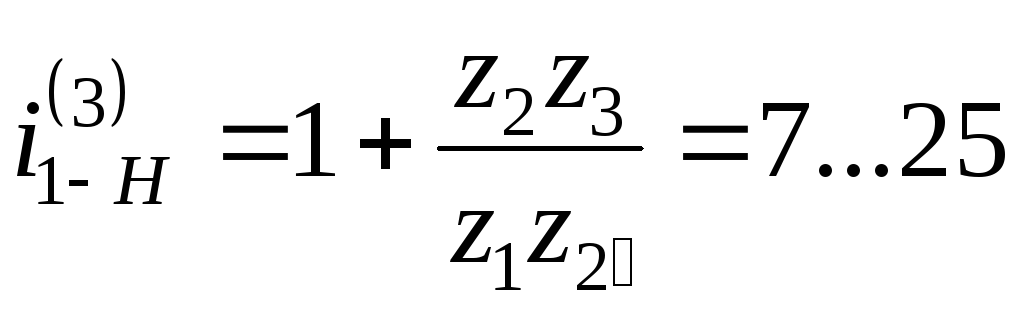 .
.
Направление вращения выходного звена совпадает с направлением угловой скорости входного колеса.
Схема 3. Редуктор Давида применяется в несиловых передачах, в основном в приборостроении. Передаточное отношение равно
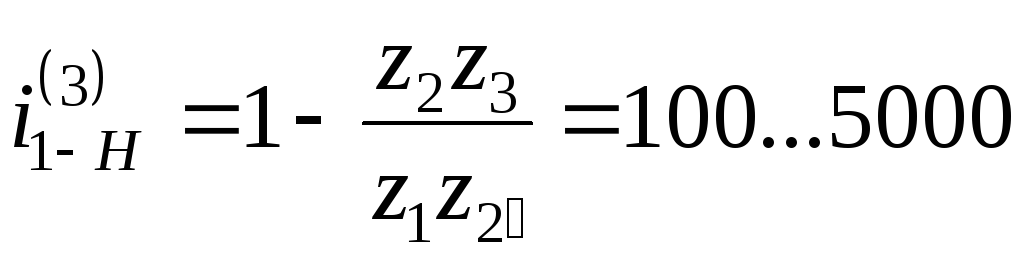 .
.
Схема 4. Редуктор Давида понижает скорость только при передаче от водила Н к колесу 1. Он имеет меньшие габариты по сравнению со схемой 3, но изготовление колёс с внутренним зацеплением более затруднительно. Передаточное отношение равно
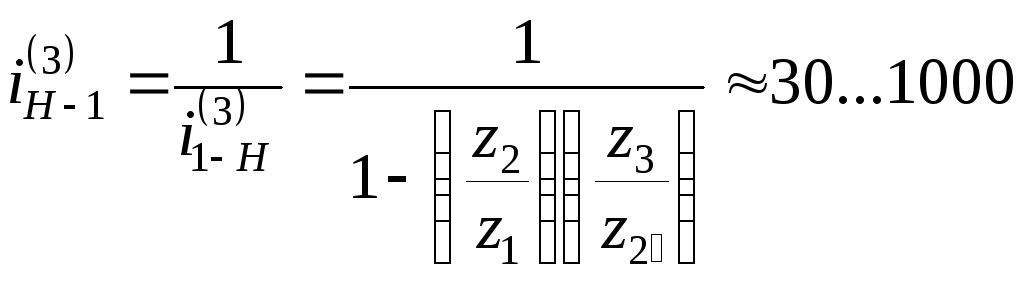 .
.
В редукторах Давида (схемы 3 и 4) знак передаточного отношения всегда отрицательный, т.е. входное и выходное звенья вращаются в разные стороны.
studfile.net
Планетарные зубчатые передачи.
Планетарные зубчатые передачи
Общие сведения о планетарных передачах
Планетарными называют передачи, имеющие зубчатые колеса с подвижными осями. Отличительной особенностью механизмов, включающих планетарную передачу (или передачи), является наличие двух или более степеней свободы. При этом угловая скорость любого звена передачи определяется угловыми скоростями остальных звеньев.
Наибольшее распространение получила простая одинарная планетарная передача (рис. 1), которая состоит из центрального колеса 1 с наружными зубьями, неподвижного центрального колеса 3 с внутренними зубьями; сателлитов 2 – колес с наружными зубьями, зацепляющихся одновременно с колесами 1 и 3 (на рис. 1 число сателлитов с = 3), и водила Н, на котором закреплены оси сателлитов. Водило соединено с тихоходным валом. В планетарной передаче одно колесо неподвижно (соединено с корпусом). Обычно внешнее центральное колесо с внутренними зубьями называют коронным (коронная шестерня или эпицикл), а внутреннее колесо с внешними зубьями – солнечным колесом (солнечная шестерня или солнце).
При неподвижном колесе 3 вращение колеса 1 вызывает вращение сателлитов 2 относительно собственных осей, а обкатывание сателлитов по колесу 3 перемещает их оси и вращает водило Н. Сателлиты таким образом совершают вращение относительно водила и вместе с водилом вокруг центральной оси, с. е. совершают движение, подобное движению планет. Поэтому такие передачи и называют планетарными.
При неподвижном колесе 3 движение передают чаще всего от колеса 1 к водилу Н, можно передавать движение от водила Н к колесу 1.
В планетарных передачах применяют не только цилиндрические, но и конические колеса с прямым или косым зубом.
Если в планетарной передаче сделать подвижными все звенья, т. е. оба колеса и водило, то такую передачу называют дифференциальной.
С помощью дифференциального механизма можно суммировать движение двух звеньев на одном или раскладывать движение одного звена на два других. Например, в дифференциале заднего моста автомобиля движение от водила Н передают одновременно колесам 1 и 3, что позволяет при повороте одному колесу вращаться быстрее другого.
***
Разновидности планетарных передач
Существует много различных типов и конструкций планетарных передач. Наиболее широко в машиностроении применяют однорядную планетарную передачу, схема которой показана на рисунке 1. Эта передача конструктивно проста, имеет малые габариты. Находит применение в силовых и вспомогательных приводах. КПД планетарной передачи η = 0,96…0,98 при передаточных числах u = 3…8.
Планетарные механизмы, в составе которых присутствуют одна или несколько планетарных передач подразделяются на однорядные, двухрядные и многорядные. Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой планетарный механизм с набором одновенцовых сателлитов является однорядным. Простые планетарные механизмы с двухвенцовыми сателлитами являются двухрядными. Сложные планетарные механизмы могут быть двух, трёх, четырёх и даже пятирядными.
Для получения больших передаточных чисел в силовых приводах применяют многоступенчатые планетарные передачи. На рис. 2,а планетарная передача составлена из двух последовательно соединенных однорядных планетарных передач. В этом случае суммарное передаточное число u = u1×u2 ≤ 64, а КПД равен η = η1×η2 = 0,92…0,96.
На рисунке 2, б показана схема планетарной передачи с двухрядным (двухвенцовым) сателлитом, для которой при передаче движения от колеса 1 к водилу Н при n4 = 0 передаточное число определяется из зависимостей:
u = n1/nН = 1 + z2z4/(z1z3).
В этой передаче u = 3…19 при КПД η = 0,95…0,97.
Как упоминалось выше, планетарные передачи, у которых все звенья подвижны, называют дифференциальными или просто дифференциалами.
Неизбежные погрешности изготовления приводят к неравномерному распределению нагрузки между сателлитами. Для выравнивания нагрузки в передачах с тремя сателлитами одно из центральных колес выполняют самоустанавливающимся в радиальном направлении (не имеющим радиальных опор). Для самоустановки сателлитов по неподвижному центральному колесу применяют сферические подшипники качения.
Высокие требования предъявляются к прочности и жесткости водила, при этом его масса должна быть минимальной. Обычно водила выполняют литыми или сварными.
***
Достоинства и недостатки планетарных передач
Основными достоинствами планетарных передач являются:
- малые габариты и масса вследствие передачи мощности по нескольким потокам, численно равным количеству сателлитов. При этом нагрузка в каждом зацеплении уменьшается в несколько раз;
- удобство компоновки в машинах благодаря соосности ведущего и ведомого валов;
- работа с меньшим шумом, чем в обычных зубчатых передачах, что обусловлено меньшими размерами колес и замыканием сил в механизме. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются;
- малые нагрузки на валы и опоры, что упрощает конструкцию опор и снижает потери в них;
- возможность получения больших передаточных чисел при небольшом числе зубчатых колес и малых габаритах передачи.
Не лишены планетарные передачи и недостатков:
- повышенные требования к точности изготовления и монтажа передачи;
- большее количество деталей, в т. ч. подшипников, и более сложная сборка.
***
Область применения планетарных передач
Планетарные передачи применяют как редукторы в силовых передачах и приборах, в коробках передач автомобилей и другой самоходной техники, при этом передаточное число такой КПП может изменяться путем поочередного торможения различных звеньев (например, водила или одного из колес), в дифференциалах автомобилей, тракторов и т. п.
Широкое применение планетарные передачи нашли в автоматических коробках передач автомобилей благодаря удобству управления передаточными числами (переключением передач) и компактности. Можно встретить планетарные передачи и в механизмах привода ведущих колес современных велосипедов. Часто применяют планетарную передачу, совмещенную с электродвигателем (мотор-редуктор, мотор-колесо).
***
Передаточное число планетарных передач
При определение передаточного числа планетарной передачи используют метод остановки водила (метод Виллиса).
По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с частотой вращения водила nН, но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами, т. е. колесами, не влияющими на передаточное число всего механизма.
Передаточное число в обращенном механизме определяется как в духступенчатой передаче с одним внешним и вторым внутренним зацеплением.
Здесь существенное значение имеет знак передаточного числа. Передаточное число считают положительным, если в обращенном механизме ведущее и ведомое звенья вращаются в одну сторону, и отрицательным, если в разные стороны. Так, для обращенного механизма передачи по рис. 1 имеем:
u = u1×u2 = (-n1/n2)×(-n2/-n3) = (-z2/z1)×(z3/z2) = — z3/z1,
где z – числа зубьев колес.
В рассматриваемом обращенном механизме знак минус показывает, что колеса 2 и 3 вращаются в обратную сторону по отношению к колесу 1.
В качестве примера определим передаточное число для планетарной передачи, изображенной на рис. 1, при передаче движения от колеса 1 к водилу Н. Мысленная остановка водила в этой передаче равноценна вычитанию его частоты nН из частоты вращения колес.
Тогда для обращенного механизма этой передачи имеем:
u’ = (n1 – n2)/(n3 – nН) = — z3/z1,
где (n1 – nН) и (n3 – nН) – частоты вращения колес 1 и 3 относительно водила Н;
z1 и z3 – числа зубьев колес 1 и 3.
Для планетарной передачи, у которой колесо 3 закреплено в корпусе неподвижно (n3 = 0), колесо 1 является ведущим, а водило Н – ведомым.
Тогда получим передаточное число такой передачи:
(n1 – nН)/(- nН) = — z3/z1;
— n1/nН+ 1 = -z3/z1
или
u = n1/nН= 1 + z3/z1.
***
Подбор чисел зубьев планетарных передач
В отличие от обычных зубчатых передач расчет планетарных начинают с подбора чисел зубьев на колесах и сателлитах. Рассмотрим последовательность подбора чисел зубьев на примере планетарной передачи, изображенной на рис. 1.
Число зубьев z1 центральной шестерни 1 задают из условия неподрезания ножки зуба: z1 ≥ 17. Принимают z1 = 24 при Н ≤ 350 НВ; z1 = 21 при Н ≤ 52 HRC и z1 = 17 при Н > 52 HRC.
Число зубьев неподвижного центрального колеса 3 определяют по заданному передаточному числу u:
z3 = z1(u – 1).
Число зубьев z2 сателлита 2 вычисляют из условия соосности, в соответствии которым межосевые расстояния aw зубчатых пар с внешним и внутренним зацеплением должны быть равны.
Из рис. 1 для немодифицированной прямозубой передачи:
aw = 0,5(d1 + d2) = 0,5(d3 – d2), (1)
где d = mz — делительные диаметры колес.
Так как модули зацеплений планетарной передачи одинаковые, то формула (1) принимает вид:
z2 = 0,5(z3 – z1).
Полученные числа зубьев z1, z2, и z3 проверяют по условиям сборки и соседства.
Условие сборки требует, чтобы во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу будет невозможно. Установлено, что при симметричном расположении сателлитов условие сборки удовлетворяется, когда сумма зубьев центральных колес (z1 + z3) кратна числу сателлитов с = 2…6 (обычно с = 3), т. е. должно соблюдаться условие:
(z1 + z3)/c = целое число.
Условие соседства требует, чтобы сателлиты не задевали зубьями друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов, равная da2 = m(z2 + 2) , была меньше расстояния l между их осями (рис. 1), т. е.:
da2 < l = 2aw sin (180˚/c), (2)
где aw = 0,5m(z1 + z2) – межосевое расстояние.
Из формулы (2) следует, что условие соседства удовлетворяется, когда
z2 + 2 (z1 + z2) sin (180˚/c). (3)
***
Расчет на прочность планетарных передач
Расчет на прочность зубчатых передач планетарного типа ведут по методике, применяемой для обычных зубчатых передач. Основными критериями работоспособности для большинства планетарных передач (как и для всех зубчатых передач), является усталостная контактная прочность рабочих поверхностей зубьев и прочность зубьев при изгибе. При этом под контактной прочностью понимают способность контактирующих поверхностей зубьев обеспечить требуемую безопасность против прогрессирующего усталостного выкрашивания, а прочностью при изгибе – способность зубьев обеспечить требуемую безопасность против усталостного излома зуба.
Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на рис. 1, необходимо рассчитать внешнее зацепление колес 1 и 2 и внутреннее – колес 2 и 3. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.
Расчет начинают с подбора чисел зубьев колес, как было показано выше.
При определении допускаемых напряжений коэффициенты долговечности находят по эквивалентных числам циклов нагружения. При этом число циклов перемены напряжений зубьев за весь срок службы вычисляют при вращении колес только относительно друг друга.
При определении допускаемых напряжений изгиба для зубьев сателлита вводят коэффициент YA, учитывающий двустороннее приложение нагрузки (симметричный цикл нагружения).
Межосевое расстояние планетарной прямозубой передачи для пары колес внешнего зацепления (центральной шестерни с сателлитом) определяют по формуле:
aw = 450(u’ + 1)× 3√{(КНТ1Кc)/(ψbau'[σ]Н2с)},
где u’ = z2/z1 – передаточное число рассчитываемой пары колес;
Кc = 1,05…1,15 – коэффициент неравномерности распределения нагрузки между сателлитами;
Т1 – вращающий момент на валу центральной шестерни, Нм;
с – число сателлитов;
ψba — коэффициент ширины венца колеса:
ψba = 0,4 для Н ≤ 350 НВ;
ψba = 0,315 при 350 НВ < Н ≤ 50 HRC,
ψba = 0,25 для Н > 50 HRC.
Ширина b3 центрального колеса 3 определяется по формуле b3 = ψbaaw.
Ширину b2 венца сателлита принимают на 2…4 мм больше значения b3; ширина центральной шестерни b1 = 1,1b2.
Модуль зацепления определяют по формуле:
m = 2aw/(z2 + z1).
Получнный расчетом модуль округляют до ближайшего стандартного значения, а затем уточняют межосевое расстояние:
aw = m(z2 + z1)/2.
Окружную силу Ft в зацеплении вычисляют по формуле:
Ft = 2×103КcТ1/сd1.
Радиальную силу Fr определяют по формуле:
Fr = Ft tg αw,
где αw = 20˚ – угол зацепления.
***
Волновые передачи
k-a-t.ru
Механизм планетарной передачи и чертеж
Кроме обычных зубчатых передач, рассмотренных выше, на тракторах часто применяется планетарная передача, которая получила такое название потому, что ее детали перемещаются относительно друг друга аналогично движению планет вокруг солнца.
Устройство
Простейшая планетарная передача состоит из следующих главных частей:
- Центральную — солнечную шестерню
- Наружную — коронную шестерню
- Сателлиты — спутники, вращающиеся вокруг центральной солнечной шестерни
- Водило.
Коронная шестерня содержит внутренний зубчатый венец – корону и соединяется с валом, опирающимся на подшипники. Солнечная шестерня с наружными зубьями закреплена на целом или полом валу, также опирающемся на подшипники. На чертеже представлена такая передача.
1 – ведущий вал; 2 – коронная шестерня; 3 – сателлит; 4 – водило; 5 – солнечная шестерня; 6 – тормоз солнечной шестерни; 7 – ведомый вал; 8 – муфта сцепления.
Сателлиты входят одновременно в зацепление с коронной и солнечной шестернями и свободно вращаются в подшипниках на осях, закрепленных во фланце, который называется водилом. Водило планетарной передачи соединяется с ведомым валом. Такая планетарная передача работает разными способами.
Рабочий процесс
Если вращать коронную шестерню, соединенную с ведущим валом, при свободно вращающейся на подшипниках солнечной шестерне, то водило, соединенное с ведомым валом, не будет вращаться. В этом случае сателлиты будут передавать вращение солнечной шестерне в обратном направлении с передаточным числом, которое зависит от соотношения диаметров сцепленных шестерен.
В случае если солнечную шестерню затормозить, то при вращении коронной шестерни, сателлиты, обкатываясь по неподвижной солнечной шестерне, будут вести за собой водило, вращая ведомый вал с необходимым передаточным числом.
Если же жестко соединить между собой солнечную шестерню и водило, например, при помощи муфты сцепления, планетарный механизм будет замкнут — заблокирован и начнет вращаться, как одно целое. При этом число оборотов ведущего и ведомого валов будет одинаковым, передаточное число равно 1,0.
Включать и выключать такую передачу можно без прекращения вращения коронной шестерни и ведущего вала.
Возможны и другие случаи использования планетарной передачи, когда ведущая часть — солнечная шестерня, а ведомая — коронная.
Рассмотренная простейшая планетарная передача, у которой сателлиты одновременно входят в зацепление с солнечной и коронной шестернями, носит название передачи с внешним и внутренним зацеплением.
Механизм передачи с внешним зацеплением
Такая передача снабжается двойными сателлитами, которые входят в зацепление только с двумя солнечными шестернями, одна соединяется с ведущим валом, а вторая — с ведомым.
Главные достоинства:
- универсальность использования
- малые размеры и вес при получении больших передаточных чисел
- возможность изменения передаточных чисел без остановки ведущего и ведомого валов, на ходу трактора
- большой срок службы, так как все шестерни в постоянном зацеплении друг с другом и работают в масле.
Для остановки планетарной передачи используют ленточные тормоза, а для соединения частей друг с другом, блокирования — дисковые муфты сцепления.
Планетарные механизмы из-за преимуществ начинают шире применять на тракторах для изменения передаточных чисел силовой передачи на ходу при помощи увеличителя крутящего момента, для поворота гусеничного трактора и в механизме независимого привода вала отбора мощности.
tractor-server.ru
