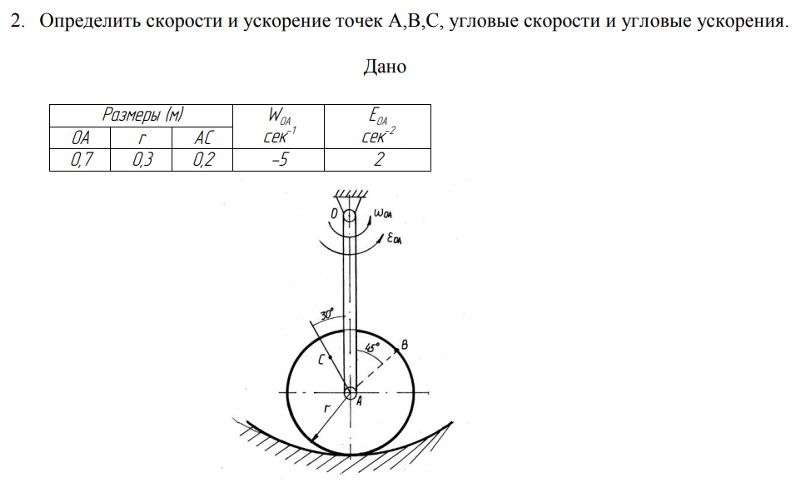
За какое время колесо имеющее угловую скорость: За какое время колесо, имеющее угловую скорость 6п рад/с, 45 оборотов
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ:Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов. Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы… Интересное: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ 36. 37. Вал вращается с частотой = 180об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением ε = 3рад/с2. Через какое время t вал остановится? Найдите число оборотов вала n до остановки. 38. Точка движется по окружности радиуса R = 20см с постоянным тангенциальным ускорением aτ = 5см/ с2. Через какое время t после начала движения нормальное ускорение an точки будет: а) равно тангенциальному; б) вдвое больше тангенциального? 39. В модели атома Бора электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найдите угловую скорость w вращения электрона вокруг ядра и его нормальное ускорение an. Считать радиус орбиты r = 0,5 10-10 м и линейную скорость на этой орбите v = 2,2 106м/с. 40. Колесо радиусом R = 10см вращается с угловым ускорением ε = 3,14 рад/ с2. Найдите для точек обода колеса к концу первой секунды: а) угловую скорость w; б) линейную скорость v; в) тангенциальное aτ и нормальное an ускорение; г) полное ускорение; д) угол, составляемый вектором полного ускорения с радиусом колеса, проведенным через соответствующую точку обода. 41. Точка движется по окружности радиусом R = 2см. Зависимость пути от времени дается уравнением s = ct3 , где c = 0,1см/с3. Найдите нормальное an и тангенциальное aτускорение точки в момент, когда линейная скорость точки v = 0,3м/с. 42. Колесо радиусом R = 10см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением , где a, b и c – константы, b = 2 рад/с2, c = 1 рад/с3. 43. Тело вращается вокруг неподвижной оси так, что , где — угол поворота тела относительно оси. В какой момент времени угловая скорость вращения будет равна 12с-1? Чему равно угловое ускорение в этот момент времени? 44. Колесо, имеющее частоту вращения 1500 мин-1, при торможении стало вращаться равномерно замедленно и остановилось через 30 с. Найдите угловое ускорение и число оборотов, которые сделает колесо с момента начала движения до полной остановки. 45. Материальная точка движется по окружности радиусом 10 м. Уравнение ее движения: . В какой момент времени тангенциальное ускорение материальной точки будет 44м/с2? Найдите нормальное ускорение в этот момент времени. 46. 47. Маховое колесо, спустя 1 минуту после начала вращения приобретает угловую скорость, равную 20с-1. Найдите угловое ускорение колеса и его число оборотов за эту минуту. Движение считать равноускоренным. Динамика Законы Ньютона 48. Тело массой 0,5кг движется прямолинейно, причем координата тела Х изменяется от времени как , где c = 5м/с2 и d = 1м/с3. Найдите силу F, действующую на тело с первой секунды движения. 49. Тело массой 1кг движется так, что его координаты x и y изменяются во времени следующим образом: , , где c = 1м/с2, d = 2м/с3. Определите ускорение тела и действующую на тело силу к концу 5-й секунды. 50. На горизонтальном столе лежат два тела массы M = 1кг каждое, связанные невесомой нерастяжимой нитью. а) ускорение движения тел; б) натяжение нитей; в) силу давления на ось блока. 51. На наклонной плоскости с углом к горизонту α = 30º движется тело массой m = 1кг, связанное невесомой нитью с телом 1 такой же массы. Найдите ускорение этих тел и силу натяжения нити. Трением в блоке можно пренебречь, также как и трением между телом 2 и наклонной плоскостью.
52. Решить предыдущую задачу при условии, что коэффициент трения тела 2 о наклонную плоскость k = 0,1. 53. Через время 0,1 с после выстрела в горизонтальном направлении пуля массой 7 г движется со скоростью 645м/с. Найдите величину средней силы сопротивления воздуха, если начальная скорость пули 650м/с. Действием на пулю силы тяжести пренебрегите. 54. Мячик массой 100 г упал с высоты 3,2 м и после удара об пол подпрыгнул на высоту 1,8 м. 55. Спускаемый аппарат массой 500кг приближается к Земле со скоростью 72км/ч. Найдите абсолютную величину импульса силы, сообщаемого аппарату двигателями мягкой посадки, для того, чтобы за две секунды скорость уменьшилась до 3,6км/ч. Определите силу, создаваемую двигателем. 56. Упругий шарик массой 50 г падает на упругую плиту под углом к нормали 60º и под таким же углом отскакивает от нее без потери скорости. Найдите импульс силы, действующей на шарик во время удара, если скорость шарика равна 20м/с. 57. Два тела движутся по взаимно перпендикулярным направлениям. Масса первого тела 3кг, а скорость 2м/с. Масса второго: 2кг и скорость 4м/с. Определите модуль суммарного импульса тел. 58. Камень массой 150 г брошен под углом 30º к горизонту со скоростью 20м/с. Найдите величину изменения импульса камня за время полета. Сопротивлением воздуха пренебрегите. 59. Из отверстия в боковой стенке бака с водой бьет струя. 60. Ракета массой 100 тонн начинает вертикальный подъем, выбрасывая 150кг продуктов сгорания топлива за 0,1с, со скоростью 2000м/с. Найдите величину ускорения ракеты в начале пути. 61. Стальной шарик падает на горизонтальную поверхность стола с высоты 25,6см и, отскочив, поднимается на высоту 19,6см. Масса шарика 10г. Какова средняя сила, с которой шарик действовал на стол при ударе, если соприкосновение шарика со столом длилось 10-4с? 62. Две гири массами m1 = 2кг и m2 = 1кг соединены нитью и перекинуты через невесомый блок. Найдите: ускорение, с которым движутся гири; натяжение нити. Трением в блоке пренебречь. 63. К нити подвешена гиря. Если поднимать эту гирю с ускорением a = 2м/с2, то натяжение T нити будет вдвое меньше того натяжения, при котором нить разрывается. С каким ускорением надо поднимать гирю, чтобы нить разорвалась? 64. ⇐ Предыдущая1234Следующая ⇒ Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
OpenStax College Physics Solution, глава 10, задача 15 (задачи и упражнения)
Chapter 10 question:
1PE2PE3PE4PE5PE6PE7PE8PE9PE10PE11PE12PE13PE14PE15PE16PE17PE18PE19PE20PE21PE22PE23PE24PE25PE26PE27PE28PE29PE30PE31PE32PE33PE34PE36PE37PE38PE39PE40PE41PE42PE43PE44PE45PE46PE47PE48PE
Изменить главуРасширенный поиск
Вопрос
Рассмотрим колесо мотоцикла массой 12,0 кг, показанное на рис. 10.38. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подножке, так что колесо может свободно вращаться. а) Если приводная цепь действует с силой 2200 Н на радиусе 5,00 см, чему равно угловое ускорение колеса? б) Каково тангенциальное ускорение точки на внешней кромке шины? в) Через какое время, начиная с состояния покоя, достигается угловая скорость 80,0 рад/с? 92$
10.38. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0,280 м и внешним радиусом 0,330 м. Мотоцикл стоит на центральной подножке, так что колесо может свободно вращаться. а) Если приводная цепь действует с силой 2200 Н на радиусе 5,00 см, чему равно угловое ускорение колеса? б) Каково тангенциальное ускорение точки на внешней кромке шины? в) Через какое время, начиная с состояния покоя, достигается угловая скорость 80,0 рад/с? 92$
c) 0,817$ \textrm{ s}$
Видеорешение
Зарегистрируйтесь для просмотра этого видеорешения!
Начать бесплатную неделю
Trustpilot
Рейтинг
ПлохоНе так уж плохоСреднеХорошоОчень хорошо
Голоса еще не отправлены.
Скриншоты калькулятора
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. У нас есть мотоциклетное колесо, которое мы собираемся смоделировать в виде кольцевого кольца. Кольцевое кольцо представляет собой кольцо, имеющее значительную толщину. Итак, внутренний радиус равен 9.0047 r один и внешний радиус r два , и нам дано, каковы эти радиусы здесь. Масса 12 килограммов. Цепь прикладывает силу, 2200 ньютонов, и она действует на расстоянии 5 сантиметров от оси, что составляет пять раз по десять с точностью до минус двух метров. В части А нас просят выяснить, каково угловое ускорение колеса? Итак, мы знаем, что крутящий момент, приложенный этой цепной силой, равен моменту инерции колеса, умноженному на его угловое ускорение. Момент инерции, когда мы смотрим в учебнике для кольцевого кольца, это масса кольца, деленная на удвоенную сумму квадратов внутреннего и внешнего радиусов. Таким образом, мы можем заменить это на и , а затем также скажем, что этот крутящий момент представляет собой силу, умноженную на радиус, и мы предполагаем, что они перпендикулярны, и поэтому мы можем найти альфа , разделив на это вещество, а затем умножив на два. Итак, мы собираемся пройти два по м раз r один в квадрате плюс r два в квадрате.
Итак, внутренний радиус равен 9.0047 r один и внешний радиус r два , и нам дано, каковы эти радиусы здесь. Масса 12 килограммов. Цепь прикладывает силу, 2200 ньютонов, и она действует на расстоянии 5 сантиметров от оси, что составляет пять раз по десять с точностью до минус двух метров. В части А нас просят выяснить, каково угловое ускорение колеса? Итак, мы знаем, что крутящий момент, приложенный этой цепной силой, равен моменту инерции колеса, умноженному на его угловое ускорение. Момент инерции, когда мы смотрим в учебнике для кольцевого кольца, это масса кольца, деленная на удвоенную сумму квадратов внутреннего и внешнего радиусов. Таким образом, мы можем заменить это на и , а затем также скажем, что этот крутящий момент представляет собой силу, умноженную на радиус, и мы предполагаем, что они перпендикулярны, и поэтому мы можем найти альфа , разделив на это вещество, а затем умножив на два. Итак, мы собираемся пройти два по м раз r один в квадрате плюс r два в квадрате. Мы делаем это с обеих сторон этого уравнения. Итак, у нас осталось альфа , равная удвоенной приложенной силе, умноженной на радиус цепи, деленной на общую массу колеса, умноженной на 9.0047 р один в квадрате плюс р два в квадрате. Итак, у нас есть два раза по 2200 ньютонов, умноженные на пять раз по десять, минус два метра, деленные на 12 килограммов, умноженные на 0,28 метра в квадрате, плюс внешний радиус 0,33 метра в квадрате. Это дает 97,9 радиана в секунду в квадрате. Тогда тангенциальное ускорение точки снаружи колеса будет равно внешнему радиусу, умноженному на угловое ускорение, которое составляет альфа , а не омега , там. Итак, это 0,33 метра, умноженное на ответ из части А, который равен 9.7,882 радиана на секунду в квадрате, и это дает 32,3 метра на секунду в квадрате. Затем в части C нас просят выяснить, сколько времени понадобится колесу, чтобы достичь угловой скорости 80 радиан в секунду? Итак, у нас есть конечная угловая скорость, равная начальной угловой скорости плюс угловое ускорение, умноженное на время.
Мы делаем это с обеих сторон этого уравнения. Итак, у нас осталось альфа , равная удвоенной приложенной силе, умноженной на радиус цепи, деленной на общую массу колеса, умноженной на 9.0047 р один в квадрате плюс р два в квадрате. Итак, у нас есть два раза по 2200 ньютонов, умноженные на пять раз по десять, минус два метра, деленные на 12 килограммов, умноженные на 0,28 метра в квадрате, плюс внешний радиус 0,33 метра в квадрате. Это дает 97,9 радиана в секунду в квадрате. Тогда тангенциальное ускорение точки снаружи колеса будет равно внешнему радиусу, умноженному на угловое ускорение, которое составляет альфа , а не омега , там. Итак, это 0,33 метра, умноженное на ответ из части А, который равен 9.7,882 радиана на секунду в квадрате, и это дает 32,3 метра на секунду в квадрате. Затем в части C нас просят выяснить, сколько времени понадобится колесу, чтобы достичь угловой скорости 80 радиан в секунду? Итак, у нас есть конечная угловая скорость, равная начальной угловой скорости плюс угловое ускорение, умноженное на время. Мы можем найти t , вычитая омега-ноль с обеих сторон, а затем разделив обе стороны на альфа . Итак, у нас есть т это омега финал минус омега ноль разделить на альфа и, таким образом, 80 радиан в секунду минус начальная угловая скорость, равная нулю, разделить на угловое ускорение, которое мы рассчитали в части А, равное 97,882 радиана в секунду в квадрате. Для достижения 80 радиан в секунду потребуется время 0,817 секунды.
Мы можем найти t , вычитая омега-ноль с обеих сторон, а затем разделив обе стороны на альфа . Итак, у нас есть т это омега финал минус омега ноль разделить на альфа и, таким образом, 80 радиан в секунду минус начальная угловая скорость, равная нулю, разделить на угловое ускорение, которое мы рассчитали в части А, равное 97,882 радиана в секунду в квадрате. Для достижения 80 радиан в секунду потребуется время 0,817 секунды.
Решения проблем, описанных в главе 10PE30PE31PE32PE33PE34PE36PE37PE38PE39PE40PE41PE42PE43PE44PE45PE46PE47PE48PE
5.3 Угловое ускорение – биомеханика движений человека
Угловое ускорение обозначается греческой буквой альфа (α). Угловое ускорение представляет собой скорость изменения угловой скорости во времени. Другой способ подумать об этом — как быстро что-то ускоряется или замедляется.
ускорение (α) = Δω/Δt
Единицы измерения: рад/с 2 или градусов/с 2 . Когда скорость увеличивается, ускорение происходит в том же направлении вращения, чтобы увеличить скорость. Когда скорость уменьшается, должно быть ускорение в направлении, противоположном движению, действующее как тормоз, чтобы уменьшить скорость.
Когда скорость увеличивается, ускорение происходит в том же направлении вращения, чтобы увеличить скорость. Когда скорость уменьшается, должно быть ускорение в направлении, противоположном движению, действующее как тормоз, чтобы уменьшить скорость.
У ускорения есть направление. Если объект движется в направлении против часовой стрелки (+) и набирает скорость, ускорение положительное. Если скорость уменьшается, ускорение отрицательно. Если объект движется по часовой стрелке (-) и набирает скорость, ускорение отрицательно. Если скорость уменьшается, ускорение положительно.
Пример 1: Расчет углового ускорения и замедления велосипедного колеса
Предположим, подросток кладет велосипед на спину и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об/мин за 5,00 с. (a) Рассчитайте угловое ускорение в рад/с 2 . (b) Если теперь она ударит по тормозам, вызывая угловое ускорение -87,3 рад/с 2 , сколько времени понадобится колесу, чтобы остановиться?
Стратегия для (a)
Угловое ускорение можно найти непосредственно из его определения в [latex]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}[/latex] потому что конечная угловая скорость и время заданы. Мы видим, что Δω равно 250 об/мин, а Δ t равно 5,00 с.
Мы видим, что Δω равно 250 об/мин, а Δ t равно 5,00 с.
Решение задачи (a)
Введя известную информацию в определение углового ускорения, получим
[латекс]\begin{array}{lcl} \boldsymbol{\alpha} & \boldsymbol{=} & \ boldsymbol{\frac{\Delta\omega}{\Delta{t}}} \\ {} & \boldsymbol{=} & \boldsymbol{\frac{250\textbf{об/мин}}{5,00\textbf{с.} }} \end{массив}[/latex]
Поскольку Δω выражается в оборотах в минуту (об/мин), а нам нужны стандартные единицы измерения рад/с 2 для углового ускорения, нам нужно преобразовать Δω из об/мин в рад/с:
[ латекс]\begin{массив}{lcl} \boldsymbol{\Delta\omega} & \boldsymbol{=} & \boldsymbol{250\frac{\textbf{rev}}{\textbf{min}}\cdotp\frac{ 2\pi\textbf{ рад}}{\textbf{об}}\cdotp\frac{1\textbf{ мин}}{60\textbf{ сек}}} \\ {} & \boldsymbol{=} & \boldsymbol {26,2\textbf{ рад.}} \end{массив}[/latex] 92} \end{array}[/latex]
Стратегия для (b)
В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решив для Δ t , получив
Мы можем найти время остановки, используя определение углового ускорения и решив для Δ t , получив
[латекс]\boldsymbol{\Delta{t}\:=}\boldsymbol{\frac{\Delta\ omega}{\alpha}}.[/latex]
Решение для (b)
Здесь угловая скорость уменьшается с 26,2 рад/с 92}} \\ {} & \boldsymbol{=} & \boldsymbol{0.300\textbf{ с.}} \end{array}[/latex]
Обсуждение
Обратите внимание, что угловое ускорение при вращении девушки колесо маленькое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.
Если бы велосипед в предыдущем примере стоял на колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение равно касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением а т .
Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение равно касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением а т .
Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Мы знаем , что при круговом движении центростремительное ускорение a c относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3. Таким образом, a t и a c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t напрямую связано с угловым ускорением [латекс]\жирныйсимвол{\альфа}[/латекс] и связано с увеличением или уменьшением скорости, но не с ее направлением.
Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3. Таким образом, a t и a c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t напрямую связано с угловым ускорением [латекс]\жирныйсимвол{\альфа}[/латекс] и связано с увеличением или уменьшением скорости, но не с ее направлением.
Теперь мы можем найти точное соотношение между линейным ускорением a t и угловым ускорением [латекс]\boldsymbol{\alpha}[/латекс]. Поскольку линейное ускорение пропорционально изменению величины скорости, оно определено как
Поскольку линейное ускорение пропорционально изменению величины скорости, оно определено как
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta{v}}{\Delta{t}}.}[/latex]
Для кругового движения обратите внимание, что v = r ω , так что
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}.}[/latex]
Радиус r является постоянным для кругового движения, поэтому Δ( r ω)= r (Δω) . Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r}\boldsymbol{\frac{\Delta\omega}{\Delta{t}}.}[/latex]
По определению [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}.[/latex] Таким образом,
[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha},[/латекс]
или
[латекс] \boldsymbol{\alpha\:=}\boldsymbol{\frac{a_{\textbf{t}}}{r}.}[/latex]
Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес велосипеда, тем больше ускорение велосипеда. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении [латекс]\boldsymbol{\alpha}[/латекс].
Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес велосипеда, тем больше ускорение велосипеда. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении [латекс]\boldsymbol{\alpha}[/латекс].
До сих пор мы определили три величины вращения — θ , ω и [латекс]\жирныйсимвол{\альфа}[/латекс]. Эти величины аналогичны поступательным величинам x , v и a . В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Ротационный | Трансляционное | Отношения |
|---|---|---|
| [латекс]\boldsymbol{\theta}[/латекс] | [латекс]\boldsymbol{x}[/латекс] | [латекс] \boldsymbol{\theta=\frac{x}{r}}[/латекс] |
| [латекс]\boldsymbol{\omega}[/латекс] | [латекс]\boldsymbol{v}[/латекс] | [латекс]\boldsymbol{\omega=\frac{v}{r}}[/латекс] |
| [латекс]\boldsymbol{\alpha}[/латекс] | [латекс]\boldsymbol{a}[/латекс] | [латекс] \boldsymbol{\alpha=\frac{a_{\textbf{t}}}{r}}[/latex] |
Таблица 1. Вращательные и поступательные величины. Вращательные и поступательные величины. | ||
- Равномерное круговое движение — это движение с постоянной угловой скоростью [латекс]\жирныйсимвол{\омега=\фракция{\Delta\theta}{\Delta{t}}}.[/latex]
- При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t} }}.[/латекс]
- Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]\жирныйсимвол{а_{\textbf{t}}=\frac{\Delta{v}}{\Delta{t} }}.[/латекс]
- Для кругового движения обратите внимание, что v = r ω , так что
[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}}.[/latex]
- Радиус r постоянен для кругового движения, поэтому Δ( r ω)= р Δω .


 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия
 ..
..
 Колесо, вращаясь равноускоренного, достигло угловой скорости w = 20рад/с через n = 10 оборотов после начала вращения. Найдите угловое ускорение колеса ε.
Колесо, вращаясь равноускоренного, достигло угловой скорости w = 20рад/с через n = 10 оборотов после начала вращения. Найдите угловое ускорение колеса ε.
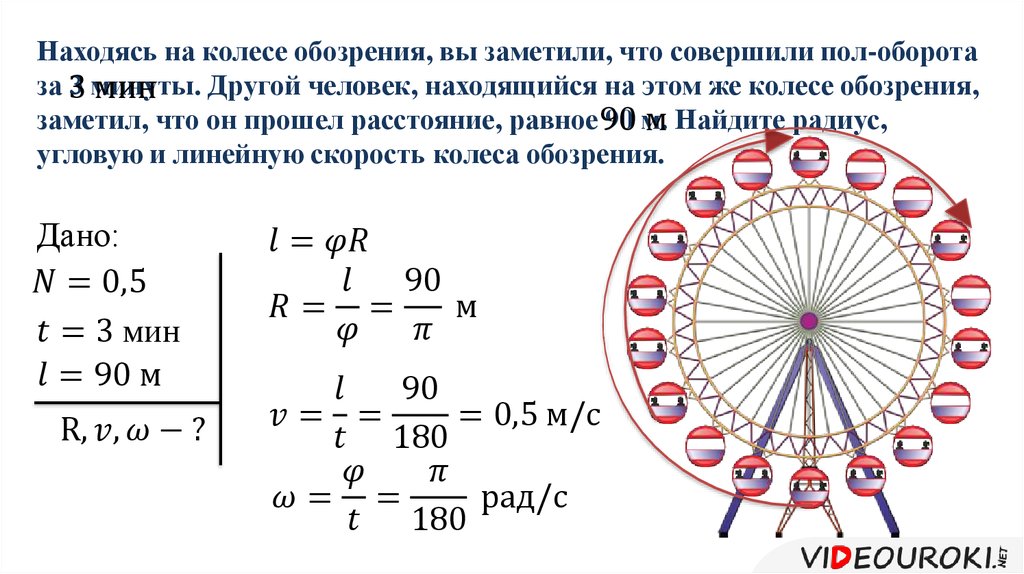 Для точек, лежащих на ободе колеса, найдите через время t = 2 с после начала движения: а) угловую w и линейную v скорости; б) нормальное an и тангенциальное aτ ускорения; в) угловое ускорение ε.
Для точек, лежащих на ободе колеса, найдите через время t = 2 с после начала движения: а) угловую w и линейную v скорости; б) нормальное an и тангенциальное aτ ускорения; в) угловое ускорение ε. Поезд движется по закруглению радиусом 400 м, причем его тангенциальное ускорение равно 0,2м/с2. Определите его нормальное и полное ускорения в тот момент, когда его скорость равна 10м/с.
Поезд движется по закруглению радиусом 400 м, причем его тангенциальное ускорение равно 0,2м/с2. Определите его нормальное и полное ускорения в тот момент, когда его скорость равна 10м/с. Тело 2 связано такой же нитью с грузом m = 0,5кг. Блок невесомый, трением в блоке можно пренебречь. Коэффициент трения первого тела со столом k
Тело 2 связано такой же нитью с грузом m = 0,5кг. Блок невесомый, трением в блоке можно пренебречь. Коэффициент трения первого тела со столом k Найдите изменение импульса мячика при ударе.
Найдите изменение импульса мячика при ударе. Найдите величину реактивной силы, если расход воды составляет 2кг/с, а ее скорость равна 10м/с.
Найдите величину реактивной силы, если расход воды составляет 2кг/с, а ее скорость равна 10м/с.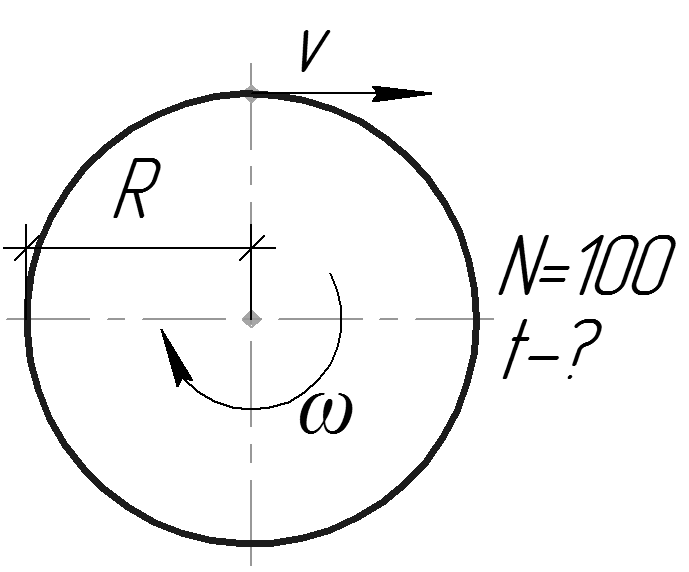 С каким ускорением будут двигаться по горизонтальному пути сани массой 200кг под действием силы 600Н, приложенной под углом 30º к направлению перемещения если а) сани толкают; б) тянут за веревку? Коэффициент трения равен 0,2.
С каким ускорением будут двигаться по горизонтальному пути сани массой 200кг под действием силы 600Н, приложенной под углом 30º к направлению перемещения если а) сани толкают; б) тянут за веревку? Коэффициент трения равен 0,2.