За какое время колесо имеющее угловую скорость: ЗА КАКОЕ ВРЕМЯ СДЕЛАЕТ 100 ОБОРОТОВ КОЛЕСО,ИМЕЮЩЕЕ УГЛОВУЮ СКОРОСТЬ 4П РАД/С
Индивидуальные домашние задания по тематическому разделу «Кинематика»
Индивидуальное домашнее задание по физике № 1
Решить три задачи согласно своему варианту. Перечень задач и вариантов расположен ниже. Решение следует оформить строго в следующем порядке: Дано, Найти, СИ (если требуется перевод единиц измерения), Решение, Ответ. Решение желательно сопровождать схемой/рисунком/графиком, а также поясняющими ход решения записями. Образец решения задачи также прилагается.
Решение задач оформить на отдельном двойном листочке.
Первую страницу двойного листочка следует сделать титульным листом, в центре титульного листа указать вид работы и данные об авторе работы по следующему образцу:
по теме: «Равномерное движение по окружности».
….
Диаметр передних колес трактора в 1,5 раза меньше, чем задних. Найти отношение частот обращения колес при движении трактора.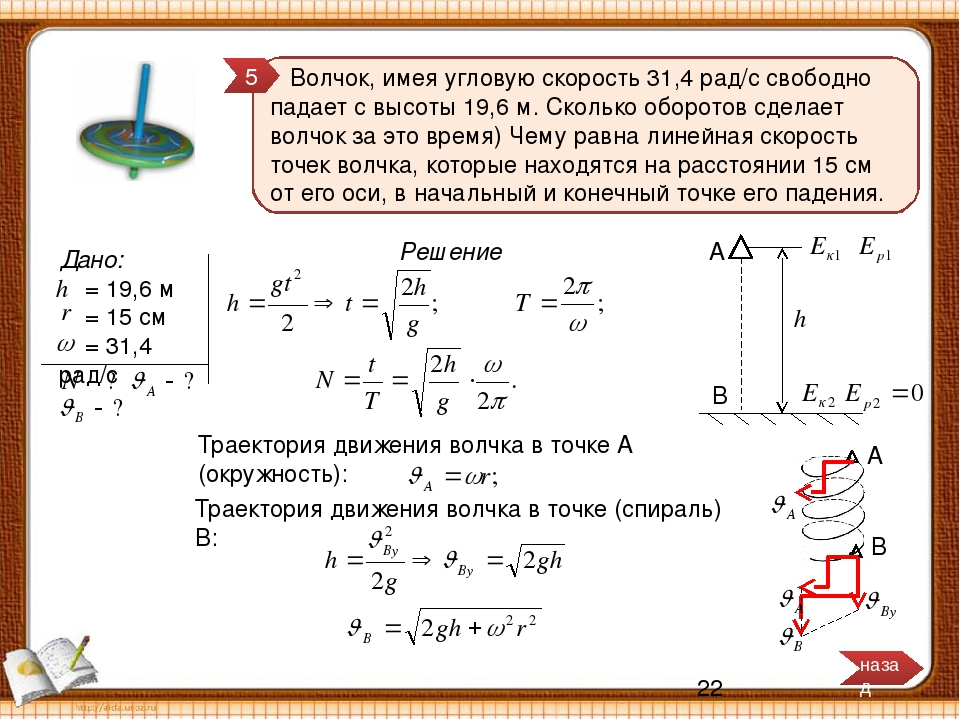
Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колеса локомотива, радиус которых 1,2 м?
Какова угловая скорость вращения колеса ветродвигателя, если за 2 мин колесо сделало 50 оборотов?
За какое время колесо, имеющее угловую скорость 4π рад/с, сделает 100 оборотов?
Диск диаметром 50 см равномерно перекатывают на расстояние 2 м за 4 с. Какова угловая скорость вращения диска?
Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость движения тела и пройденный им путь, если известно, что его угловое перемещение за 10 с равно 1,57 рад.
Коленчатый вал двигателя мотоцикла делает 4800 об/мин. Определите период и угловую скорость вращения коленчатого вала.
Частота вращения воздушного винта вертолета 1500 об/мин. Сколько оборотов сделает винт на пути 120 км при скорости полета 72 км/ч?
Вал радиусом 2 см делает один оборот за 0,05 с.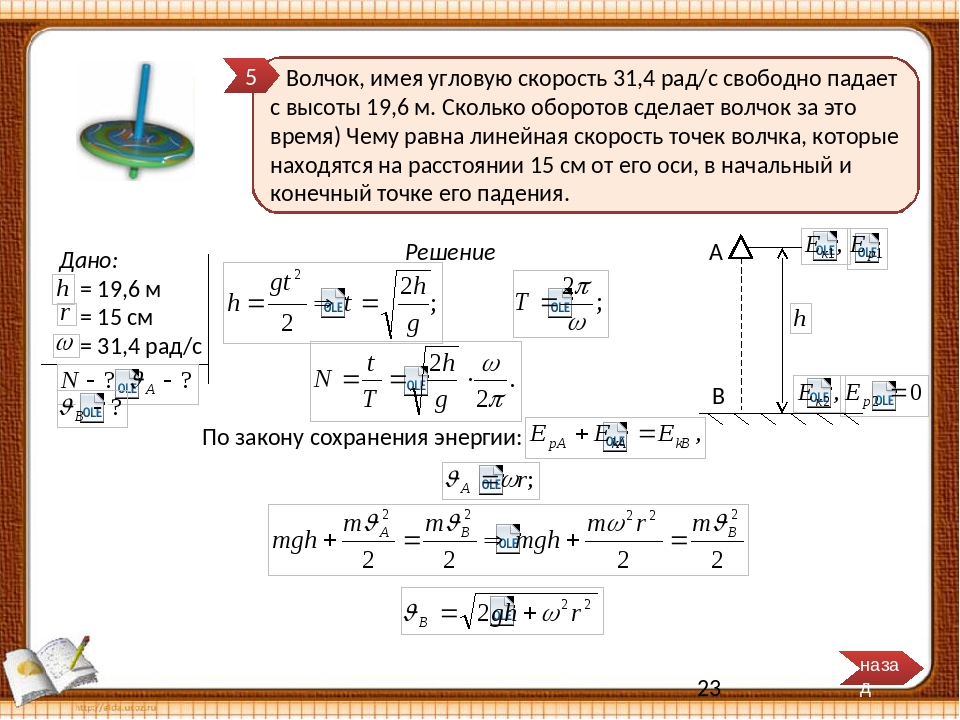 Определите частоту вращения, угловую и линейную скорости точек поверхности вала.
Определите частоту вращения, угловую и линейную скорости точек поверхности вала.
Равномерно движущаяся по окружности точка делает полный оборот за T = 5 с. Чему равна угловая скорость точки? Чему равен угол поворота за время поворота 2 с?
На какой угол повернется Земля вокруг собственной оси за 2 ч?
Сколько раз N в сутки встречаются часовая и секундная стрелки часов?
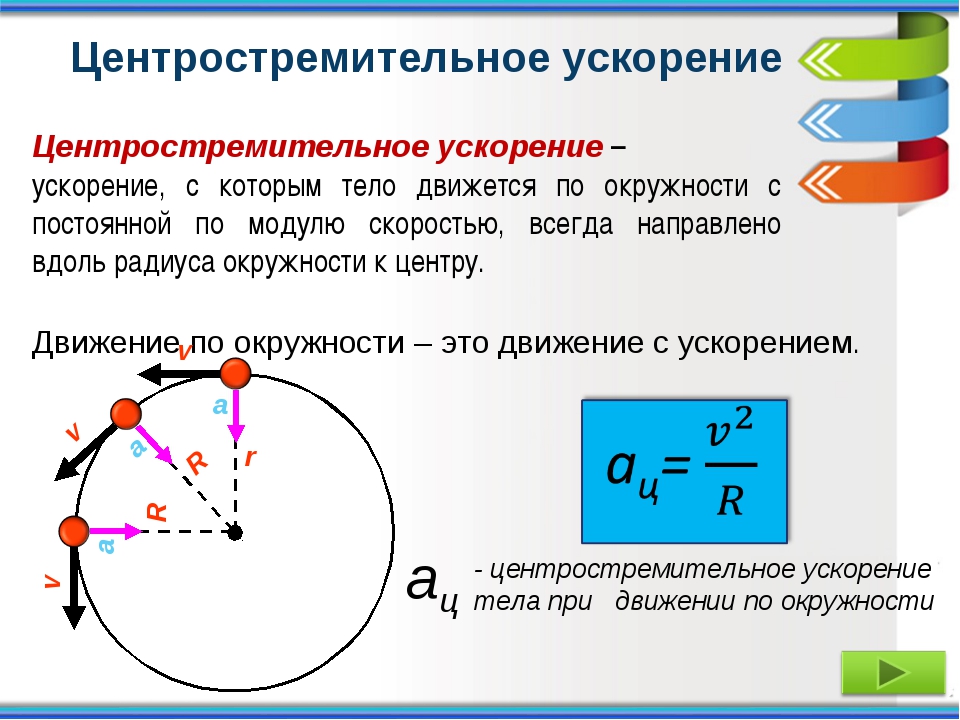
Каково центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 20 м/с.
С какой скоростью автомобиль должен проходить середину выпуклого моста радиусом 40 м, чтобы центростремительное ускорение было равно ускорению свободного падения?
Найти центростремительное ускорение точек колеса автомобиля, соприкасающихся с дорогой, если автомобиль движется со скоростью 72 км/ч и при этом частота обращения колеса 8 с-1.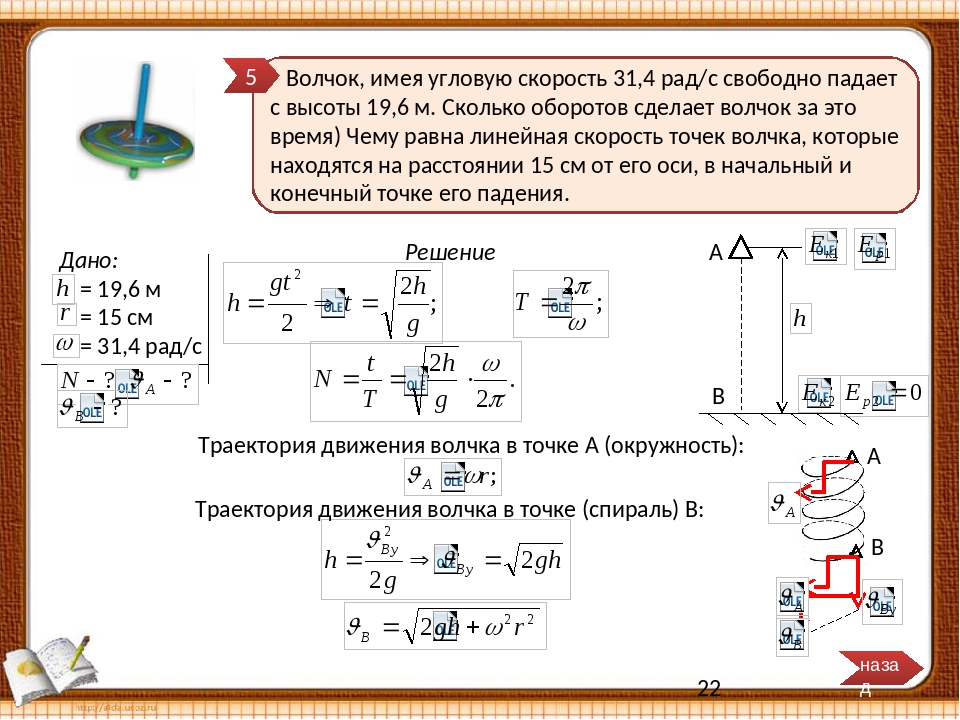
Ветряное колесо радиусом 2,0 м делает 40 оборотов в минуту. Найдите центростремительное ускорение концевых точек лопастей колеса.
Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Две материальные точки движутся по окружностям радиусами R1 = 0,2 м и R2 = 0,4 м с одинаковыми периодами. Найдите отношение их центростремительных ускорений.
Скорость точек поверхности, шлифовального круга не должна превышать 100 м/с. Радиус шлифовального круга равен 20 см. Определите максимальное центростремительное ускорение любой точки поверхности шлифовального кругам.
Угловая скорость вращения лопастей колеса ветродвигателя 6 рад/с. Найдите центростремительное ускорение концов лопастей, если линейная скорость концов лопастей 20 м/с.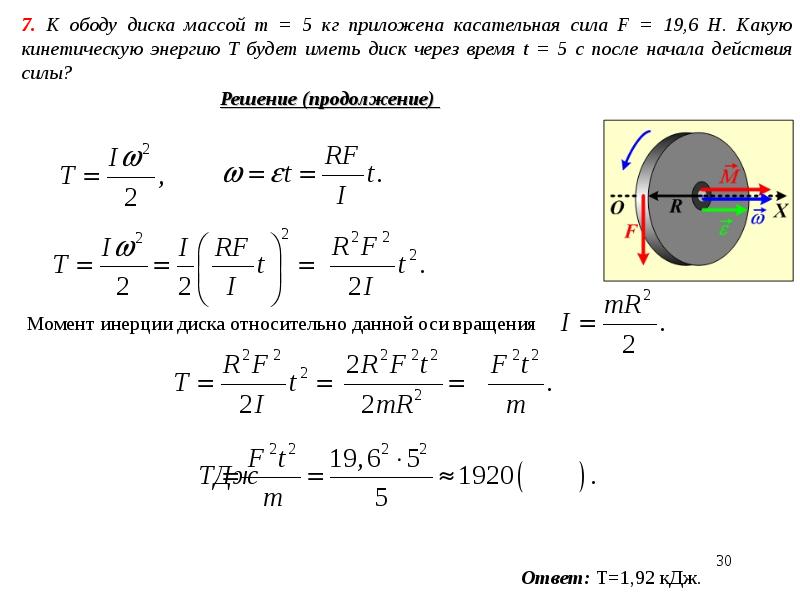
Вращение твердого тела вокруг неподвижной оси
13.1 Определить угловую скорость: 1) секундной стрелки часов, 2) минутной стрелки часов, 3) часовой стрелки часов, 4) вращения Земли вокруг своей оси, считая, что Земля делает один оборот за 24 часа, 5) паровой турбины Лаваля, делающей 15000 об/мин.РЕШЕНИЕ
13.2 Написать уравнение вращения диска паровой турбины при пуске в ход, если известно, что угол поворота пропорционален кубу времени и при t=3 с угловая скорость диска равна ω=27π рад/с.
РЕШЕНИЕ
13.3 Маятник центробежного регулятора, вращающийся вокруг вертикальной оси AB, делает 120 об/мин. В начальный момент угол поворота был равен π/6 рад. Найти угол поворота и угловое перемещение маятника за время t=1/2 c.
РЕШЕНИЕ
13.4 Тело, начиная вращаться равноускоренно из состояния покоя, делает 3600 оборотов в первые 2 минуты. Определить угловое ускорение.
РЕШЕНИЕ
13.5 Вал начинает вращаться равноускоренно из состояния покоя; в первые 5 с он совершает 12,5 оборота. Какова его угловая скорость по истечении этих 5 с?
Какова его угловая скорость по истечении этих 5 с?
РЕШЕНИЕ
13.6 Маховое колесо начинает вращаться из состояния покоя равноускоренно; через 10 мин после начала движения оно имеет угловую скорость, равную 4π рад/с. Сколько оборотов сделало колесо за эти 10 мин?
РЕШЕНИЕ
13.7 Колесо, имеющее неподвижную ось, получило начальную угловую скорость 2π рад/с; сделав 10 оборотов, оно вследствие трения в подшипниках остановилось. Определить угловое ускорение ε колеса, считая его постоянным.
РЕШЕНИЕ
13.8 С момента выключения мотора пропеллер самолета, вращавшийся с угловой скоростью, равной 40π рад/с, сделал до остановки 80 оборотов. Сколько времени прошло с момента выключения мотора до остановки, если считать вращение пропеллера равнозамедленным?
РЕШЕНИЕ
13.9 Тело совершает колебания около неподвижной оси, причем угол поворота выражается уравнением φ = 20° sin ψ, где угол ψ выражен в угловых градусах зависимостью ψ=(2t)°, причем t обозначает секунды. Определить угловую скорость тела в момент t=0, ближайшие моменты t1 и t2, в которые изменяется направление вращения, и период колебания T.
РЕШЕНИЕ
13.10 Часовой балансир совершает крутильные гармонические колебания с периодом T=1/2 c. Наибольший угол отклонения точки обода балансира от положения равновесия α=π/2 рад. Найти угловую скорость и угловое ускорение баланса через 2 с после момента, когда балансир проходит положение равновесия.
РЕШЕНИЕ
13.11 Маятник колеблется в вертикальной плоскости около неподвижной горизонтальной оси O. Выйдя в начальный момент из положения равновесия, он достигает наибольшего отклонения α=π/16 рад через 2/3 c. 1) Написать закон колебаний маятника, считая, что он совершает гармонические колебания. 2) В каком положении маятник будет иметь наибольшую угловую скорость и чему она равна?
РЕШЕНИЕ
13.12 Определить скорость v и ускорение w точки, находящейся на поверхности Земли в Ленинграде, принимая во внимание только вращение Земли вокруг своей оси; широта Ленинграда 60°, радиус Земли 6370 км.
РЕШЕНИЕ
13.13 Маховое колесо радиуса 0,5 м вращается равномерно вокруг своей оси; скорость точек, лежащих на его ободе, равна 2 м/с. Сколько оборотов в минуту делает колесо?
Сколько оборотов в минуту делает колесо?
РЕШЕНИЕ
13.14 Точка A шкива, лежащая на его ободе, движется со скоростью 50 см/с, а некоторая точка B, взятая на одном радиусе с точкой A, движется со скоростью 10 см/с; расстояние AB=20 см. Определить угловую скорость ω и диаметр шкива.
РЕШЕНИЕ
13.15 Маховое колесо радиуса R=2 м вращается равноускоренно из состояния покоя; через t=10 с точки, лежащие на ободе, обладают линейной скоростью v=100 м/с. Найти скорость, нормальное и касательное ускорения точек обода колеса для момента t=15 c.
РЕШЕНИЕ
13.16 Найти горизонтальную скорость v, которую нужно сообщить телу, находящемуся на экваторе, для того чтобы оно, двигаясь равномерно вокруг Земли по экватору в особых направляющих, имело ускорение свободного падения. Определить также время T, по истечении которого тело вернется в первоначальное положение. Радиус Земли R=637*106 см, а ускорение силы тяжести на экваторе g=978 см/с2.
РЕШЕНИЕ
13.17 Угол наклона полного ускорения точки обода махового колеса к радиусу равен 60°. Касательное ускорение ее в данный момент wτ=10*√3 м/с2. Найти нормальное ускорение точки, отстоящей от оси вращения на расстоянии r=0,5 м. Радиус махового колеса R=1 м.
Касательное ускорение ее в данный момент wτ=10*√3 м/с2. Найти нормальное ускорение точки, отстоящей от оси вращения на расстоянии r=0,5 м. Радиус махового колеса R=1 м.
РЕШЕНИЕ
13.18 Вал радиуса R=10 см приводится во вращение гирей P, привешенной к нему на нити. Движение гири выражается уравнением x=100t2, где x — расстояние гири от места схода нити с поверхности вала, выраженное в сантиметрах, t — время в секундах. Определить угловую скорость ω и угловое ускорение ε вала, а также полное ускорение w точки на поверхности вала в момент t.
РЕШЕНИЕ
13.19 Решить предыдущую задачу в общем виде, выразив ускорение точек обода колеса через пройденное гирей расстояние x, радиус колеса R и ускорение гири x =w0=const.
РЕШЕНИЕ
13.20 Стрелка гальванометра длины 3 см колеблется вокруг неподвижной оси по закону φ=φ0 sin kt. Определить ускорение конца стрелки в ее среднем и крайних положениях, а также моменты времени, при которых угловая скорость ω и угловое ускорение ε обращаются в нуль, если период колебаний равен 0,4 c, а угловая амплитуда φ0=π/30.
РЕШЕНИЕ
Задание 3. Вращение твёрдого тела
Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
или посмотрите
ВИДЕО УРОК
1. Маховик вращается с постоянной угловой скоростью 9 рад/сек. Определите период его вращения.
а) ≈ 1,2 сек; б) ≈ 0,4 сек; в) ≈ 0,9 сек; г) ≈ 0,7 сек. 2. Колесо, вращаясь равнозамедленно, при торможении уменьшило за 1 мин частоту вращения от 300 до 180 об/мин. Найдите число оборотов, сделанных колесом за эту минуту. а) 240;б) 260; в) 200;
г) 215. 3. Колесо, вращаясь равнозамедленно, при торможении уменьшило за 1 мин частоту вращения от 300 до 180 об/мин.
 Найдите угловое ускорение колеса. а
Найдите угловое ускорение колеса. а 4. Допустимо ли насадить точильный круг на вал двигателя, делающего 2850 оборотов в минуту, если на круге имеется штамп завода <<35 м/сек, ∅250 мм>> ?
а) ;
б) да;
г) нет.
5. Скорость поезда 72 км/час. Сколько оборотов в минуту делают колёса локомотива, радиус которых 1,2 м ?
а) ≈ 150 об/мин; б) ≈ 155 об/мин; в) ≈ 162 об/мин; г) ≈ 159 об/мин.6. Какова угловая скорость вращения колеса ветродвигателя, если за 2 мин колесо сделало 50 оборотов ?
а) ≈ 2,6 рад/сек; б) ≈ 2,1 рад/сек; в) ≈ 2,9 рад/сек; г) ≈ 3,2 рад/сек. 7. За какое время колесо, имеющее угловую скорость 4π рад/сек, сделает 100 оборотов ? а) 44 сек;
7. За какое время колесо, имеющее угловую скорость 4π рад/сек, сделает 100 оборотов ? а) 44 сек; б) 60 сек; в) 50 сек;
г) 56 сек.
8. Диск диаметром 50 см равномерно перекатывают на расстояние 2 м за 4 сек. Какова угловая скорость вращения диска ?
а) 3 рад/сек; б) 4 рад/сек; в) 1 рад/сек; г) 2 рад/сек. 9. Ветряное колесо радиусом 2 м делает 40 оборотов в минуту. Найдите центростремительное ускорение концевых точек лопастей колеса. а) ≈ 40 м/сек2; б) ≈10. Частота вращения воздушного винта самолёта 25 Гц. За какое время винт совершает 3000 оборотов ?
За какое время винт совершает 3000 оборотов ?
11. Шкив вращается с угловой скоростью 50 рад/сек. Определите центростремительное ускорение точек находящихся на расстоянии 20 мм от оси вращения.
а) 50 м/сек2;
12. Земля вращается вокруг своей оси с центростремительным ускорением 0,034 м/сек2. Определите угловую скорость вращения, если радиус Земли 6400 км.
г) ≈ 7,3×10-5 рад/сек.
Механика движения | Kursak.
 NET
NETВариант № 1
1. На рисунке стрелками показаны направления углового ускорения вращающихся дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Какой/какие из дисков вращается/вращаютсяпротив часовой стрелки (если смотреть сверху)?
2. Колесо радиусом R =10 см вращается так, что зависимость угла поворота радиуса колеса от времени задана уравнением , где – в радианах, t – в секундах . Найдите для точек, лежащих на ободе колеса: а) линейную скорость, б) нормальное ускорение и в) угловое ускорение ε для момента времени t = 3 с.
3. На графике представлена зависимость угла φ поворота вращающегося тела от времени
.
4. Две материальные точки массами расположены симметрично относительно оси , расположенной в плоскости чертежа. Как изменится момент инерции этих точек при повороте оси в плоскости чертежа на угол из положения в положение ?
5. Равнозамедленное вращение совершает диск, приведенный на рисунке под номером …
Равнозамедленное вращение совершает диск, приведенный на рисунке под номером …
6. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) одинакового радиуса R = 10 см и одинаковой массы m = 0,50 кг. Найдите моменты инерции этих цилиндров. За какое время каждый цилиндр скатится без скольжения с наклонной плоскости высотой h = 0,50 м, угол наклона плоскости α =30°?
7. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке.
Укажите график, правильно отражающий зависимость момента импульса диска от времени.
8. На краю горизонтальной платформы, имеющей форму диска радиусом R = 2 м, стоит человек. Масса платформы M = 200 кг, масса человека m = 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью v = 2 м/с относительно платформы. Момент инерции человека рассчитывать, как для материальной точки.
Момент инерции человека рассчитывать, как для материальной точки.
9. Для того, чтобы раскрутить стержень массы m1и длины l1 вокруг вертикальной оси, расположенной перпендикулярно стержню и проходящей через его середину, до угловой скорости w, необходимо совершить работу А1. Во сколько раз большую работу, чем
10. Тонкий прямой стержень длинойl = 1 м прикреплен к горизонтальной оси, проходящий через его верхний конец. Стержень отклонили на 60º от положения равновесия и отпустили. Определите линейную скорость нижнего конца в момент прохождения через положение равновесия.
Вариант № 2
1. Диск вращается равноускоренно вокруг вертикальной оси под действием силы F. Вектор угловой скорости обозначен цифрой….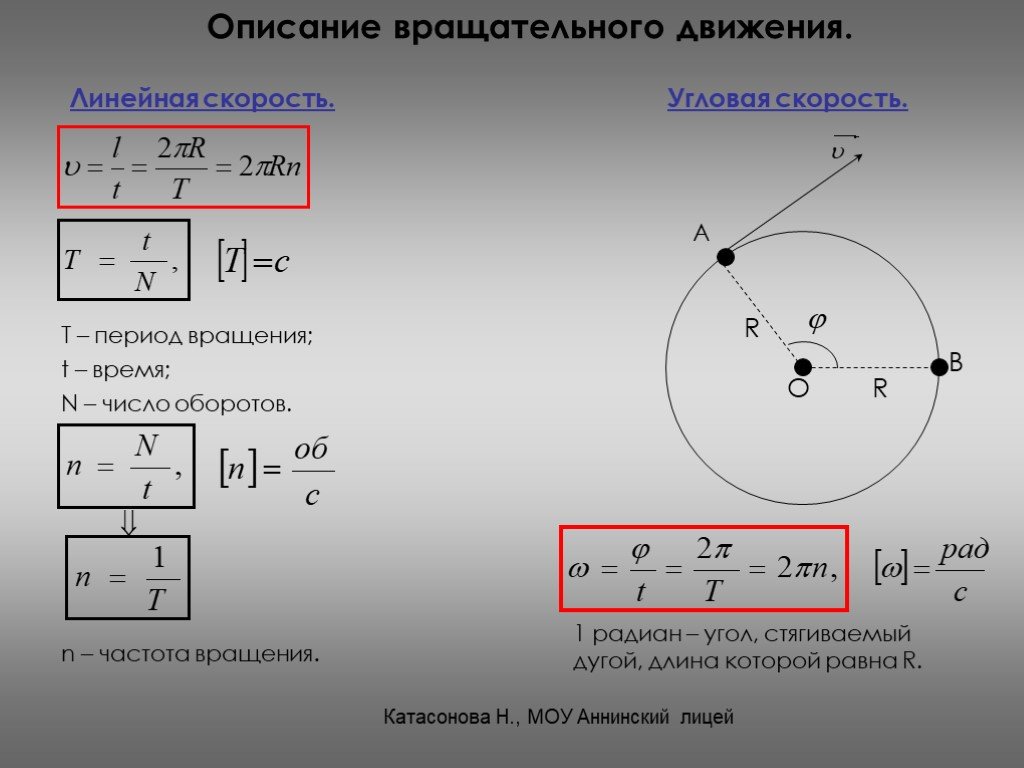
2.Частица движется по окружности в соответствии с уравнением , где – в радианах, t – в секундах. Найдите время движения диска до остановки. Сколько оборотов N сделает диск за это время?
3. Тело вращается вокруг неподвижной оси. Зависимость угловой скорости от времени показана на рисунке. Напишите уравнение , отражающее зависимость угла поворота тела от времени, если начальное положение тела соответствует значению рад.
4. При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Во сколько раз увеличится момент инерции тонкостенной трубки, если ось вращения перенести из центра масс на образующую (рис.)?
4. Четыре шарика, размеры которых пренебрежимо малы, движутся по окружностям с одинаковой угловой скоростью. Укажите номер шарика, момент импульса которого относительно оси, проходящей через центр окружности, максимален. Массы шариков и радиусы окружностей указаны под рисунками.
1) m=4г 2) m=2г 3) m=5г 4) m=3г
r=1см r=2см r=3см r=6см
5. Тело из состояния покоя приводится во вращение вокруг горизонтальной оси с помощью падающего груза, соединенного со шнуром, предварительно намотанным на ось. Определите момент инерции тела, если груз массой
Тело из состояния покоя приводится во вращение вокруг горизонтальной оси с помощью падающего груза, соединенного со шнуром, предварительно намотанным на ось. Определите момент инерции тела, если груз массой
6. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке.
Укажите график, правильно отражающий зависимость модуля момента импульса диска от времени.
7. На рисунке приведен график зависимости проекции угловой скорости вращающегося тела на ось вращения от времени. Как изменяется модуль вращающего момента сил, действующего на тело, на интервале времени от до ?
8. Однородный тонкий стержень вращается на гладкой горизонтальной поверхности вокруг закрепленной вертикальной оси, проходящей через один из его концов, с угловой скоростьюw0также без трения.
9. Маховик вращается вокруг по закону, выраженному уравнением φ = 2+3t-4t2, рад. Найдите среднюю мощность, развиваемую силами действующими на маховикпри его движении до остановки, если его момент инерции J = 100 кг∙м2.
10. Два шарика одинаковой массы и одинаковыми радиусами движутся с одинаковыми скоростями. Первый катится, второй скользит. При ударе о стенку тела останавливаются. Определите, у какого тела и во сколько раз больше выделится тепла при ударе.
Вариант № 3
1. На рисунке стрелками показаны направления углового ускорения вращающихся дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Какие из дисков вращаются против часовой стрелки
2.Уравнение вращения твердого тела .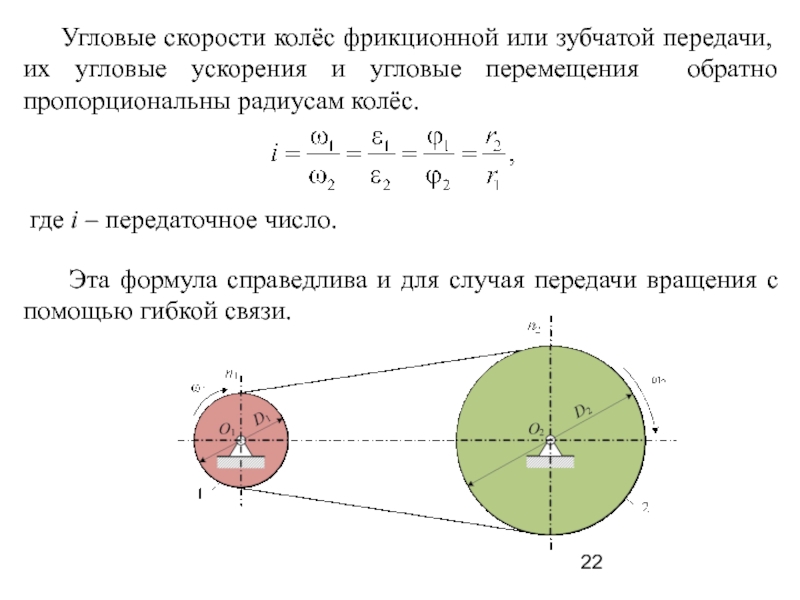 Определите угловую скорость вращения тела и полное ускорение для точки тела, отстоящей на 20 см от оси вращения, через 2 с после начала движения.
Определите угловую скорость вращения тела и полное ускорение для точки тела, отстоящей на 20 см от оси вращения, через 2 с после начала движения.
3. Диск начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. На каком интервале времени тангенциальное ускорение точки, расположенной на расстоянии R = 20 см от центра диска, равно м/с2 ?
4. Определите момент инерции проволочного равностороннего треугольника со стороной а = 10 см относительно оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно его стороне, противоположной вершине. Масса треугольника равна m= 12 г и равномерно распределена по длине проволоки.
5. Равноускоренное вращение совершает диск, приведенный на рисунке под номером …
6. Две гири разной массы соединены нитью, перекинутой через блок, момент инерции которого J = 50 кг м2 и радиусR = 20 см. Блок вращается с трением и момент сил трения М = 98,1 Нм. Найдите разность сил натяжений нити (Т1—Т2 )по обе стороны блока, если известно, если известно, что блок вращается с постоянным угловым ускорением ε = 2,36 рад/с2.
Блок вращается с трением и момент сил трения М = 98,1 Нм. Найдите разность сил натяжений нити (Т1—Т2 )по обе стороны блока, если известно, если известно, что блок вращается с постоянным угловым ускорением ε = 2,36 рад/с2.
7. На рисунке приведена зависимость модуля моментов приложенных к телу сил от модуля углового ускорения тел. Наибольший момент инерции имеет тело под номером……
8. На скамье Жуковского стоит человек и держит в руках стержень, расположенный вертикально по оси вращения скамейки. Скамейка с человеком вращается с угловой скоростью ω1=1 рад/с. С какой угловой скоростью ω2 будет вращаться скамья, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи J=6 кг∙м2. Длина стержня l= 2,4 м, его масса m = 8 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы.
9.Маховик в виде диска, момент инерции которого J = 1,5 кг·м2, вращаясь равнозамедленно, уменьшает частоту своего вращения с n1= 240 об/мин до n2 = 120 об/мин. Определите работу сил торможения.
10. На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Кинетическая энергия первого тела Ек1вр= 0,5 Дж. Найдите момент импульса второго тела, если m= 1кг, R = 10 см.
Вариант № 4
1. Диск вращается равнозамедленно вокруг вертикальной оси против часовой стрелки (если смотреть сверху). Вектор углового ускорения обозначен цифрой….
2. Движение тела вокруг неподвижной оси вращения задано уравнением ,рад. Сколько оборотов Nсделает тело до момента изменения направления вращения тела и чему равна средняя угловая скорость тела за этот интервал времени?
3. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. Чему равны тангенциальные ускорения точки на краю диска в моменты времени t1= 2 с и t2 = 7 с?
Зависимость проекции угловой скорости от времени показана на графике. Чему равны тангенциальные ускорения точки на краю диска в моменты времени t1= 2 с и t2 = 7 с?
4. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси ОО. Для моментов инерции относительно оси ОО справедливо соотношение …
1) I1<I2<I3 ; 2) I1= I2<I3 ; 3) I1<I2 = I3 ;4) I1>I2>I3 .
5. Четыре шарика, размеры которых пренебрежимо малы, движутся по окружностям с одинаковой угловой скоростью. Укажите номер шарика, модуль момента импульса которого относительно оси, проходящей через центр окружности, максимален. Массы шариков и радиусы окружностей указаны под рисунками.
1) m=5г 2) m=1г 3) m=5г 4) m=2г
r=1см r=2см r=3см r=6см
: 4
6. Маховое колесо, имеющее момент инерции J = 245 кг м2, вращается, делая n = 20 об/с. После того как на колесо перестал действовал вращающий момент, оно остановилось, сделав N = 1000 об. Найдите момент сил трения М и время τ, прошедшее от момента прекращения действия вращающегося момента до полной остановки колеса.
7.На рисунке представлены графики временной зависимости моментов для четырех вращающихся тел.
Какой/какие график/графики, правильно отражает зависимость момента импульса от времени для диска, вращающегося равномерно интервал времени от 0 до t1?
8. Покоящийся однородный диск радиусом R= 20 см и массой m1= 0,20 кг может свободно вращаться вокруг неподвижной горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О на нем. В точку А на образующей диска попадает пластилиновый шарик, летящий горизонтально со скоростью 10 м/с, и прилипает к его поверхности. Масса шарика m2=10г. Определите угловую скорость диска и линейную скорость точки В сразу после прилипания шарика.
В точку А на образующей диска попадает пластилиновый шарик, летящий горизонтально со скоростью 10 м/с, и прилипает к его поверхности. Масса шарика m2=10г. Определите угловую скорость диска и линейную скорость точки В сразу после прилипания шарика.
9.Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости . Под действием трения стержень остановился, при этом выделилось тепло . Если стержень раскручен до угловой скорости , то при остановке стержня выделится тепло …
10.Обруч привели во вращение, сообщив ему энергию вращательного движения 1200 Дж, и отпустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Если обруч начал двигаться без проскальзывания, имея кинетическую энергию вращения 200 Дж, то сила трения совершила работу, равную…
Вариант № 5
1. На рисунке стрелками показаны направления углового ускорения вращающихся дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Какие диски вращаются по часовой стрелке (если смотреть снизу на диск)?
Какие диски вращаются по часовой стрелке (если смотреть снизу на диск)?
2. Диск вращается с постоянным угловым ускорением ε = -5рад/с. Сколько оборотов N сделает диск при изменении частоты вращения от n1= 240 мин-1 до n2 = 90 мин-1? Найдите время, в течение которого это произойдет.
3. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол (в рад) окажется повернутым тело относительно начального положения через 10 с ?
4. Рассматриваются три тела: диск, тонкостенная труба и сплошной шар; причем массы m и радиусы тел одинаковы. Верным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение …
1) J3< J2<J1 2) J3< J1<J2 3) J1< J2<J3 4) J3< J1 = J2
5. Диски вращаются вокруг неподвижных вертикальных осей. На рисунке указаны стрелкой направления вращения диска и как изменяется угловая скорость вращения с течением времени. Укажите номера дисков, моменты импульса которых направлены вдоль оси вращения вниз.
Диски вращаются вокруг неподвижных вертикальных осей. На рисунке указаны стрелкой направления вращения диска и как изменяется угловая скорость вращения с течением времени. Укажите номера дисков, моменты импульса которых направлены вдоль оси вращения вниз.
6. По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу которой подвешен груз массой m = 4,0 кг. На какое расстояние должен опуститься груз, чтобы колесо со шкивом получило скорость, соответствующую частоте n = 60 об/мин? Момент инерции колеса со шкивом J = 0,42 кг м2, радиус шкива r = 10cм.
7. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Момент действующих на тело сил был постоянным не равным нулю на участке …
8. Человек стоит на скамье Жуковского, вращающейся с пренебрежимо малым трением, и ловит ручной мяч массой m = 0,4 кг, летящий в горизонтальном направлении со скоростью v = 20 м/с. Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и скамьи J = 6 кг∙м2.
Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и скамьи J = 6 кг∙м2.
9. Маховик вращается вокруг по закону, выраженному уравнением φ = 2+16t—2t2, рад. Найдите среднюю мощность, развиваемую силами действующими на маховикпри его движении до остановки, если его момент инерции J = 100 кг∙м2 Чему равна мощность в момент времени t = 3с.
10. Мальчик катит обруч по горизонтальной поверхности со скоростью v=7.2 км/ч., Найдите расстояние (в метрах), на которую может вкатиться обруч в горку за счет своей кинетической энергии, если пренебречь силой трения качения. Угол наклона горки составляет .
Вариант № 6
1. На рисунке стрелками показаны направления векторов угловой скорости и углового ускорения вращающихся дисков. Угловая скорость каких дисков увеличивается по модулю с течением времени?
Угловая скорость каких дисков увеличивается по модулю с течением времени?
2.Маховик начал вращаться равноускоренно и за промежуток времени t = 10 с достиг частоты n = 300 мин-1. Запишите уравнение зависимости ,рад согласно которому вращается диск.
3. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На каких интервалах времени знаки проекций угловой скорости и углового ускорения одинаковые?
: 0 до 2; 4 до 5
4. Определите момент инерции проволочного равностороннего треугольника со стороной а = 10 см относительно оси, совпадающей с одной из сторон треугольника. Масса треугольника равна m= 12 г и равномерно распределена по длине проволоки.
5. Диски вращаются вокруг неподвижных вертикальных осей. На рисунке указаны стрелкой направления вращения диска и как изменяется угловая скорость вращения с течением времени. Укажите номера дисков, моменты сил которых направлены вдоль оси вращения вверх.
Укажите номера дисков, моменты сил которых направлены вдоль оси вращения вверх.
6. На барабан радиусом R = 20 см, момент инерции которого J = 0,10 кг×м2, намотан шнур, к которому привязан груз массой m = 0,50 кг. До начала вращения барабана высота груза над полом h = 11,0 м. Найти: 1) Время, за которое t груз опустится до пола; 2) скорость груза в момент удара о пол; 3) натяжение нити Т. Трением пренебречь.
7.Момент импульса тела относительно неподвижной оси изменяется по закону . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
8. На верхней поверхности горизонтального диска, который может вращаться вокруг вертикальной оси, проложены по окружности радиуса r= 50 см рельсы игрушечной железной дороги. Масса диска M = 10 кг, его радиус R = 60 см. На рельсы неподвижного диска был поставлен заводной паровозик массой m = 1 кг и выпущен из рук. Он начал двигаться относительно рельсов со скоростью v = 0,8 м/с. С какой угловой скоростью будет вращаться диск?
Он начал двигаться относительно рельсов со скоростью v = 0,8 м/с. С какой угловой скоростью будет вращаться диск?
9. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости , при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние и раскрутили до той же угловой скорости. При этом была совершена работа …
1) ; 2) ; 3) ; 4) .
10.Обруч скатывается без проскальзывания с горки высотой h =2,5 м. Найдите скорость обруча у основания горки при условии, что трением можно пренебречь.
Вариант № 7
1. Диск вращается равнозамедленно вокруг вертикальной оси по часовой стрелке (если смотреть сверху). Вектор углового ускорения обозначен цифрой….
2.Якорь электромотора, вращающийся со скоростью n =50 об/с, двигаясь после выключения тока равнозамедленно, остановился, сделав N = 1680 об. Найти угловое ускорение якоря.
Найти угловое ускорение якоря.
3. На графике представлена зависимость угла φ поворота вращающегося тела от времени t.Определите угловое ускорение вращения тела в первую секунду.
4. Определите момент инерции тонкого однородного стержня длиной l= 50 см и массой m = 300 готносительно оси перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/6 его длины (см. рисунок).
5. На рисунке показаны начальная рад/с и конечная рад/с скорости вращения абсолютно твердого тела для интервала времени .Как направлен момент сил,
действующих на данное тело?
6. Однородный стержень длиной вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через один из его концов с угловым ускорением e = 9,81 с-1. Сколько оборотов сделает стержень за время t = 5,0 с, если он начал вращаться из состояния покоя?
7.Момент силы, приложенный к вращающемуся телу, изменяется по закону , где – некоторая положительная константа.
Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке …
8. На скамье Жуковского стоит человек, держащий в руках на расстоянии l1= 150 смдруг от друга две гири массойm = 1,0 кг каждая. скамья вращается с частотой n1 = 1 с-1. человек сближает гири до расстояния l2= 80 см, и частота увеличивается до n2 = 1,5 с-1. Определите момент инерции человека и скамьиJ, считая его постоянным относительно оси столика.
9. Маховик в виде диска массой m = 80 кг и радиусом R =30 см находится в состоянии покоя. Какую работу А1 нужно совершить, чтобы сообщить маховику частоту n =10 c-1? Какую работу пришлось бы совершить, если бы при той же массе диск имел меньшую толщину, но вдвое больший радиус?
10. Сплошной и полый цилиндры одинаковых масс и радиусов катятся без скольжения по горизонтальной поверхности с одинаковой скоростью. Чему равно отношение кинетической энергии полого цилиндра к кинетической энергии сплошного цилиндра?
Сплошной и полый цилиндры одинаковых масс и радиусов катятся без скольжения по горизонтальной поверхности с одинаковой скоростью. Чему равно отношение кинетической энергии полого цилиндра к кинетической энергии сплошного цилиндра?
Вариант № 8
1. На рисунке стрелками показаны направления углового ускорения и направления вращения дисков. Какой из дисковвращается равноускоренно?
2. Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением м/с. Определите угол, который образует вектор полного ускорения с радиусом колеса через две секунды после начала движения. Сделать поясняющий рисунок.
3. Твердое тело начинает вращение вокруг оси Z с угловымускорением, проекция которого на ось изменяется во времени, как показано на графике. Определите, используя график, величину угловой скорости вращающегося тела в момент времени t = 2 c.
4. Три маленьких шарика расположены в вершинах правильного треугольника, лежащего в горизонтальной плоскости. Момент инерции этой системы относительно оси О1, перпендикулярной плоскости треугольника и проходящей через его центр, – . Момент инерции этой же системы относительно оси О2 , перпендикулярной плоскости треугольника и проходящей через один из шариков, – . Найдите отношение / .
Момент инерции этой системы относительно оси О1, перпендикулярной плоскости треугольника и проходящей через его центр, – . Момент инерции этой же системы относительно оси О2 , перпендикулярной плоскости треугольника и проходящей через один из шариков, – . Найдите отношение / .
5. На рисунке изображено тело, имеющее ось вращения ОО1. На тело действуют две силы и , Вектора сил и ось расположены в плоскости рисунка. Укажите верное утверждение о моментах и сил и относительно оси ОО1
1) 3)
2) 4)
6. Сплошной цилиндр, расположенный горизонтально, может без трения вращаться около оси, совпадающей с осью цилиндра. Масса цилиндра m1= 12 кг. На цилиндр намотали шнур, к которому привязали гирю массой m2 = 1 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?
7. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке.
Укажите график, правильно отражающий зависимость момента импульса диска от времени.
8. Деревянный стержень массой m = 1,0 кги длиной l= 40 см может вращаться вокруг оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массойm1 =10 г, летящая перпендикулярно оси и стержню со скоростью V = 200 м/с и застревает в нем. Определите угловую скорость стержня сразу после попадания пули.
9. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии друг от друга. Стержень вращается без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили до угловой скорости , совершив работу А. Какую работу надо совершить, если шарики раздвинуть симметрично на расстояние и раскрутить до угловой скорости в два раза большей?
10.Сплошной цилиндр и шар, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми начальными скоростями на горку. Найдите отношение высот h1/h2, на которые смогут подняться эти тела, если трением и сопротивлением воздуха можно пренебречь.
Найдите отношение высот h1/h2, на которые смогут подняться эти тела, если трением и сопротивлением воздуха можно пренебречь.
Вариант № 9
1. Диск вращается равнозамедленно вокруг вертикальной оси под действием силы F . Вектор угловой скорости обозначен цифрой …
2. Диск радиусом R = 20 см и массой m = 7 кг вращается согласно уравнению φ=A+Bt+Ct3, где A = 3 рад; B = – 1 рад/с; C = 0,1 рад/с3. Написать закон, по которому меняется вращающий момент, действующий на диск. Определить момент сил M в момент времени t = 2 с.
3.Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения от времени представлена на графике (рис.1). Соответствующая зависимость угловой скорости от времени представлена на рис.2 графиком под номером…
4. Определите момент инерции однородного диска радиусаR = 20 см и массой m = 500 готносительно оси, расположенной перпендикулярно плоскости диска, и удаленной от центра диска на четверть его радиуса.
5. Диски вращаются вокруг неподвижных вертикальных осей. На рисунке указаны стрелкой направления вращения диска и как изменяется угловая скорость вращения с течением времени. Укажите номера дисков, для которых моменты сил направлены вдоль оси вращения вниз.
6. К стержню приложены 3 одинаковые по модулю силы, как показано на рисунке. Ось вращения перпендикулярна плоскости рисунка и проходит через точку О. Вектор суммарного момента сил, действующего на стержень, направлен …
1) вправо; 2) вдоль оси вращения О «к нам»;
3) влево; 4) вдоль оси вращения О «от нас»
7. На рисунке приведен график зависимости модуля результирующего момента сил, действующих на вращающееся абсолютно твердое тело. Какой участок соответствует вращению с постоянным угловым ускорением?
8. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. В начальный момент платформа покоится. На какой угол φ повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную точку на платформе? Масса платформы M = 240 кг, масса человека m = 60 кг. Момент инерции человека рассчитывать, как для материальной точки.
Момент инерции человека рассчитывать, как для материальной точки.
9. Маховик вращается вокруг по закону, выраженному уравнением φ = 2+16t—2t2, рад. Момент инерции маховика J = 50 кг∙м2. Найдите законы, по которым меняются вращающий момент М и мощность N. Чему равна мощность в момент времени t = 3с.
10. В покоящийся металлический стержень длиной l = 40,0 см и массой m1= 1,0 кг, который может вращаться вокруг перпендикулярной к нему оси, проходящей через его верхний конец. В нижний конец стержня попадает пуля массы m2= 10,0 г, летящая перпендикулярно к оси и к стержню со скоростью v= 200 м/с. Удар пули о стержень абсолютно неупругий. Определите, какую угловую скорость приобретёт стержень после удара?
Вариант № 10
1. На рисунке стрелками показаны направления вращения дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Для какого из дисков нарисованная стрелка совпадает с направлением ускорения?
Для какого из дисков нарисованная стрелка совпадает с направлением ускорения?
2.Некоторое тело начинает вращаться с постоянным угловым ускорением ε = 0,04 с-2. Через какое время после начала вращения полное ускорение какой- либо точки тела будет направлено под углом 76º к вектору скорости этой точки?
3. На рисунке представлен график зависимости угловой скорости вращающегосся тела от времени. На какой угол(рад) повернулось тело за время движения от 2 с до 4 с?
4. Три точечных массы каждая по 100 г, образуют равносторонний треугольник со стороной 10 см. Вычислить момент инерции всей системы относительно оси, перпендикулярной плоскости, в которой лежат все массы, и проходящей через одну из них.
5. На каком рисунке верно указано направление вектора момента силы?
6. Маховое колесо радиусаR = 25 см через тридцать секунд после начала вращения делает 6 оборотов в секунду. Считая его вращение равноускоренным, найти для точек на ободе колеса полное ускорение по величине и угол между вектором полного ускорения и радиусом колеса к концу первой секунды.
7. На невесомом стержне укреплены два шарика, размерами которых можно пренебречь. Массы шариковm1= 2,0 кгиm2= 1,5 кг, соответствующие расстояния указаны на рисунке. Система может вращаться с одинаковой по величине угловой скоростью вокруг осей, показанных на рисунке. В каком из возможных вращений момент импульса будет иметь наибольшее значение?
8. Человек, стоящий на укрепленной на шариковом подшипнике лёгкой площадке, держит в руках штангу горизонтально, и середина штанги находится на оси подшипника. На концах штанги укреплены одинаковые тяжелые грузы. Площадка вращается со скоростью n1 = 1/3 с—1. Какова будет скорость вращения, если наклонить штангу под углом 45º к горизонту? Момент инерции самого человека и площадки в расчетне принимать.
9. Маховик, момент инерции которого J = 40 кг·м2, начал вращаться равноускоренно под действием момента сил М = 20 Н·м. Какую работу совершат силы, действующие на маховик за время движения t= 10 с? Какую энергию приобретет маховик за это время?
10. Шар скатывается без проскальзывания с вершины наклонной плоскости высотой h=4 м без начальной скорости. Длина ската наклонной плоскости l=8 м, а значение коэффициента трения принять одинаковым на всем пути и равнымm =0.1.
Шар скатывается без проскальзывания с вершины наклонной плоскости высотой h=4 м без начальной скорости. Длина ската наклонной плоскости l=8 м, а значение коэффициента трения принять одинаковым на всем пути и равнымm =0.1.
Определите скорость шара у основания наклонной плоскости? (в м/с) …
Вариант № 11
1. На рисунке стрелками показаны направления вращения дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Для какого из дисков нарисованная стрелка совпадает с направлением ускорения?
2.Движение тела вокруг неподвижной оси вращения задано уравнением ,рад. Чему равна угловая скорость вращения тела в момент времени t= 3 с? В какой момент времени от начала движения ( t= 0) тело изменит направление своего вращения на противоположное?
3. Ротор электродвигателя, вращающийся со скоростью 960 об/мин, после выключения остановился через 10 с. Угловое ускорение торможения ротора после выключения двигателя оставалось постоянным.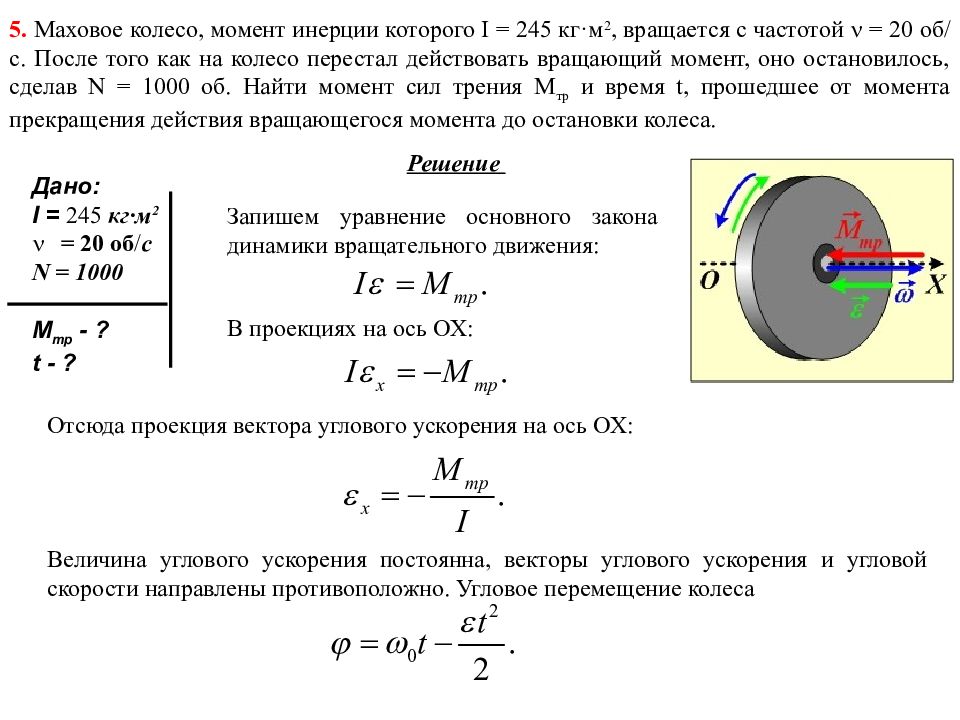 Зависимость частоты вращения от времени торможения показана на графике. Определите число оборотов, которое сделал ротор до остановки.
Зависимость частоты вращения от времени торможения показана на графике. Определите число оборотов, которое сделал ротор до остановки.
4. Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы и равны 10 см. Массы шариков слева направо: m1 = 1 г, m2 = 2 г, m3 = 3 гm4 = 4 г . Найдите во сколько раз изменится момент инерции этой системы относительно оси О, перпендикулярной прямой а, если параллельно перенести ось вращения на 10 см влево.
5. На рисунках стрелками показаны направления вращения дисков и указано, как изменяется угловая скорость со временем. Вращающий момент сил, направленный вниз, приложен к дискам …
6.Тело из состояния покоя приводится во вращение вокруг горизонтальной оси с помощью падающего груза, соединенного со шнуром, предварительно намотанным на ось. Определите момент инерции тела, если груз массойm = 2,0 кг в течение t= 12 с опускается на расстояние h = 1 м. Радиус оси r = 8 мм. Силой трения можно пренебречь.
Радиус оси r = 8 мм. Силой трения можно пренебречь.
7.Тело приобретает угловую скорость под действием вращающих моментов М1 и М2, графики зависимости которых от времени приведены на рисунке. Определите отношение wа/wбугловых скоростей, приобретаемых телом в случаях а и б.
8. На скамье Жуковского стоит человек и держит в раках стержень, расположенный вертикально по оси вращения скамьи. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподвижна, колесо вращается, делая ω1 = 10 рад/с. Когда человек повернул стержень на 180° и колесо оказалось на нижнем конце стержня, скамья с человеком начала вращаться с постоянной скоростью ω2. Чему равна эта скорость? Момент инерции человека и скамьи равен J=6 кг∙м2, радиус колеса R = 20 см, массу колеса равную 3 кг, можно считать равномерно распределенной по ободу.
9.Маховик вращается вокруг по закону, выраженному уравнением φ = 4+6t-5t2, рад. Момент инерции маховика J = 60 кг∙м2. Найдите законы, по которым изменяются с течением времени вращающий момент М и мощность N. Чему равна мощность в момент времени t = 4с?
10.Тонкий однородный стержень длинойl = 1м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О на стержне. Стержень отклонили от вертикали на угол α = π/3.Определите угловую скорость стержня и линейную скорость точки В на стержне в момент прохождения им положения равновесия.
Вариант № 12
1. На рисунке стрелками показаны направления углового ускорения вращающихся дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Какой из дисков вращается по часовой стрелке (если смотреть сверху)?
2.Велосипедное колесо вращается с частотой n = 5 c-1. Под действием сил трения оно остановилось через одну минуту. Написать уравнение зависимости угла поворота колеса от времени и определить число оборотов N, которое сделает колесо за время вращения.
Под действием сил трения оно остановилось через одну минуту. Написать уравнение зависимости угла поворота колеса от времени и определить число оборотов N, которое сделает колесо за время вращения.
3. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике. Чему равно тангенциальное ускорение точки, расположенной на расстоянии 2 см от оси вращения, в момент времени t1= 2 с (в м/с2)?
4. Ось вращения тонкостенной трубы переносят из центра масс на поверхность трубы. Для новой оси вращения момент инерции возрастет в
1) 1,5 раза; 2) 2 раза; 3) 3 раза; 4) 4 раза.
5.На каком рисунке верно указано направление момента импульса тела, совершающего равноускоренное вращение?
6. Диск радиусом R= 20 см и массой m = 5 кг вращается с частотой n = 8 об/с. При торможении он остановился через время t = 4 с. Определите тормозящий момент M и момент импульса диска L через две секунды после начала торможения.
При торможении он остановился через время t = 4 с. Определите тормозящий момент M и момент импульса диска L через две секунды после начала торможения.
7.Момент импульса тела относительно неподвижной оси изменяется по закону . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
8. Вокруг неподвижной оси с угловой скоростью w1свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии от оси вращения. Потянув за нить, шайбу перевели в положение 2 и она стала двигаться по окружности радиусом . С какой скоростью w2 стала вращаться система?
9. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посредине между шариками. Стержень раскрутили из состояния покоя до угловой скорости , при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние и раскрутили до той же угловой скорости 2 = 0,5 1. При этом была совершена работа …
Шарики раздвинули симметрично на расстояние и раскрутили до той же угловой скорости 2 = 0,5 1. При этом была совершена работа …
1) ; 2) ; 3) ; 4) .
10.Однородный диск из состояния покоя скатывается без скольжения с наклонной плоскости, высота которой h=0.5 м .
Определите линейную скорость движения центра диска у основания наклонной плоскости и максимальную линейную скорость движения точек, находящихся на ободе диска, у основания наклонной плоскости.
Вариант № 13
1. Диск вращается равнозамедленно вокруг вертикальной оси под действием силы F. Вектор угловой скорости обозначен на рисунке цифрой …
2. Маховое колесо радиусаR = 25 см делает 6 оборотов в секунду и останавливается через тридцать секунд после начала вращения. Считая его вращение равнозамедленным, найти для точек на ободе колеса полное ускорение по величине и угол между вектором полного ускорения и радиусом колеса к концу десятой секунды. Привести рисунок.
Привести рисунок.
3. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол (в рад) окажется повернутым тело через 10 с относительно начального положения?
4. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси ОО. Для моментов инерции относительно оси ОО справедливо соотношение …
1) I1<I2<I3 ; 2) I1= I2 = I3 ; 3) I1<I2 = I3 ;4) I1>I2>I3 .
5. На каком из рисунков верно указано направление момента силы для тела, совершающего равнозамедленное вращение
6. Маховик радиусом R = 10 см насажен на горизонтальную ось. На обод маховика намотан шнур, к которому привязан груз массой m = 800 г. Опускаясь равноускоренно из состояния покоя, груз прошел расстояние l = 160 см за время t = 2 с. Определите момент инерции J маховика и величину момента импульса L в этот момент времени.
Опускаясь равноускоренно из состояния покоя, груз прошел расстояние l = 160 см за время t = 2 с. Определите момент инерции J маховика и величину момента импульса L в этот момент времени.
7.На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения.
Момент импульса тела убывал на участках …
8. Стержень длиной 1,0 м и массой 7 кг может свободно вращаться вокруг горизонтальной оси, проходящей через его верхний конец. В нижний конец стержня ударяет пуля массой 5,0 г, летящая в горизонтальном направлении со скоростью 500 м/с, и застревает в нем. С какой начальной скоростью летела пуля, если сразу после удара стержень с пулей будет иметь угловую скорость равную ω = 2,0 рад/с?
9. Тонкостенный цилиндр диаметром D = 30 см и массой m = 12 кг вращается согласно уравнению φ=A+Bt+Ct3, где A= 4 рад; B= – 2 рад/с; C=0,2 рад/с3. Какую работу А совершит внешняя сила за t = 2 с?
Какую работу А совершит внешняя сила за t = 2 с?
10. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой h.Какое из тел будет иметь большую скорость у основания горки и во сколько раз?
Вариант № 14
1. Диск вращается равноускоренно вокруг вертикальной оси против часовой стрелки (если смотреть сверху). Вектор углового ускорения обозначен цифрой….
2. Маховое колесо радиусаR = 25 см через тридцать секунд после начала вращения делает 6 оборотов в секунду. Считая его вращение равноускоренным, найти для точек на ободе колеса полное ускорение по величине и угол между вектором полного ускорения и радиусом колеса к концу первой секунды.
3.На графике представлена зависимость угла поворота φ абсолютно твердого тела, вращающегося вокруг неподвижной оси, от времени t, представленного параболой. Найдите величину углового ускорения.
4. На концах тонкого однородного стержня длинойl= 1 м и массойm = 0,12 кг прикреплены маленькие шарики массами m1 = 0,04 кг и m2 = 0,08 кг. Определитемомент инерции этой системы относительно оси О, перпендикулярной стержню и проходящей через точку О, лежащую на оси стержня.
Определитемомент инерции этой системы относительно оси О, перпендикулярной стержню и проходящей через точку О, лежащую на оси стержня.
5. Диск вращается вокруг неподвижной оси с постоянной угловой скоростью. В некоторый момент времени на диск начинает действовать не изменяющийся со временем тормозящий момент. Зависимость момента импульса диска от времени, начиная с этого момента, представлена на рисунке линией …
6. Через блок, выполненный в виде колеса, перекинута нить, к концам которой привязаны грузы массами m1=100 г и m2=300 г. Массу колеса M=200 г считать равномерно распределенной по ободу, массой спиц пренебречь. Определить ускорение, с которым будут двигаться грузы, и силы натяжения нити по обе стороны блока.
7.К стержню приложены три одинаковые по модулю силы, как показано на рисунке. Ось вращения перпендикулярна плоскости рисунка и проходит через точку О. Куда направлен вектор суммарного момента сил, действующего на стержень?
8. На скамье Жуковского стоит человек и держит в раках стержень, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с угловой скоростью ω1=1 рад/с. С какой угловой скоростью ω2 будет вращаться скамья, если повернуть стержень так, чтобы он занял горизонтальное положение при этом один из его концов совпадает с осью скамьи? Суммарный момент инерции человека и скамьиJ=6 кг∙м2. Длина стержня l= 2,4 м, его масса m = 8 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы.
На скамье Жуковского стоит человек и держит в раках стержень, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с угловой скоростью ω1=1 рад/с. С какой угловой скоростью ω2 будет вращаться скамья, если повернуть стержень так, чтобы он занял горизонтальное положение при этом один из его концов совпадает с осью скамьи? Суммарный момент инерции человека и скамьиJ=6 кг∙м2. Длина стержня l= 2,4 м, его масса m = 8 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы.
9. Маховик, кинетическая энергия которого Екин = 7,85 кДж, вращается с постоянной скоростью, соответствующей частоте n = 10 об/с. За какое время вращающий момент М = 50 Н×м, приложенный к этому маховику, увеличит угловую скорость маховика в два раза?
10. Сплошной цилиндр массой 5 кг катится без скольжения со скоростью 14 м/с. Определите кинетическую энергию цилиндра.
Вариант № 15
1. На рисунке стрелками показаны направления углового ускорения вращающихся дисков, а также указано, как изменяется их угловая скорость по модулю с течением времени. Какие диски вращаются против часовой стрелки (если смотреть снизу на диск)?
2.Колесо, угловое ускорение которого постоянно и равно ε = 2 рад/с2, поворачивается в течение t2 = 5 с на 75 радиан. Сколько времениt1 тело двигалось от начала вращения до начала этого пятисекундного интервала, если (в момент t = 0) перед началом движения оно покоилось?
3. Твердое тело вращается вокруг оси Z. Зависимость углового ускорения от времени представлена на графике. Какуюскорость будет иметь тело через 10 с, если начальная скорость вращения равна 2 рад/с.
4.Три точечных массы каждая по 100 г, образуют равносторонний треугольник со стороной a = 10 см. Вычислить момент инерции всей системы относительно оси, перпендикулярной плоскости, в которой лежат все массы, и проходящей через центр тяжести системы.
5. Материальная точка движется по окружности с нормальным ускорением . Какую зависимость от времени имеет момент силы, действующей на точку относительно центра вращения?
1) 2) 3) 4)
6. Тонкий стержень длиной l = 40 см и массой m = 0,6 кг вращается около оси, проходящей через середину стержня перпендикулярно его длине. Уравнение вращения стержня φ = At+Bt3, где A=1 рад/с; B= 0,1 рад/с3. Определить вращающий момент M в момент времени t=2 с.
7. На рисунке зависимость модуля моментов приложенных к телу сил от модуля углового ускорения обозначена под цифрой ……
8.Круглая горизонтальная платформа вращается без трения со скоростью ω1=1 рад/с. По радиальному гладкому желобу из центра к краю платформы перекатился шарик массойm = 0,4 кг. Масса платформы M = 10 кг.Найти изменившуюся угловую скорость вращения системы.
9. Обруч привели во вращение, сообщив ему энергию вращательного движения 1200 Дж, и отпустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Какую кинетическую энергию вращательного движения имел обруч, сразу после начала движение без проскальзывания, если сила трения совершила работу, равную 800Дж ?
Какую кинетическую энергию вращательного движения имел обруч, сразу после начала движение без проскальзывания, если сила трения совершила работу, равную 800Дж ?
10. Шар скатывается без проскальзывания с вершины наклонной плоскости высотой h=4 м без начальной скорости. Длина ската наклонной плоскости l=8 м, а значение коэффициента трения качения (m) тела одинаково на всем протяжении его пути и равно m =0,1.Найдите расстояниеs, которое пройдет шар от подножья наклонной плоскости до своей полной остановки.
Вариант № 16
1. Диск вращается равноускоренно вокруг вертикальной оси по часовой стрелке (если смотреть сверху). Вектор углового ускорения обозначен цифрой….
2.Твердое тело вращается с угловой скоростью ,рад/с. Найдите модули угловой скорости и углового ускорения в момент времениt = 10,0 с.
3. Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси вращения изменяется со временем в соответствии с графиком, представленным на рисунке. Чему равно угловое ускорение тела (в
Чему равно угловое ускорение тела (в
единицах СИ)?
4.Момент инерции тонкого обруча массой , радиусом относительно оси, прохдящей через центр обруча перпендикулярно плоскости, в которой лежит обруч, равен . Как изменится момент инерции обруча, если ось вращения перенести параллельно в точку на обруче?
5.Момент импульса тела относительно неподвижной оси изменяется по закону . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
6.Двум одинаковым маховикам, находящимся в покое, сообщили одинаковую угловую скорость ω=63 рад/с и предоставили их самим себе. Под действием сил трения первый маховик остановился через одну минуту, а второй сделал до полной остановки N=360 оборотов. У какого маховика тормозящий момент был больше и во сколько раз?
7. Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. К нему прикладывают четыре силы , лежащие в плоскости диска и равные по модулю. Как направлен суммарный вращающий момент, действующий на диск?
Как направлен суммарный вращающий момент, действующий на диск?
8.Экспериментатор, стоящий на неподвижной скамье Жуковского, получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью ω1.Далее экспериментатор поворачивает ось вращения колеса на 180º и начинает вращаться вместе с платформой с угловой скоростью ω1 /5. Найдите отношение момента инерции экспериментатора со скамьей к моменту инерции колеса.
9. На рисунке представлен график зависимости проекции вращательного момента силы, действующей на тело, от угла поворота. Чему равна работа сил, действующих на тело, при повороте его на угол 10 рад ?
10. Определить скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h=20 см.
Вариант № 17
1. На рисунке стрелками показаны направления векторов угловой скорости и углового ускорения вращающихся дисков. Угловая скорость каких дисков уменьшается по модулю с течением времени?
2. Точка А находится на ободе колеса радиусом R = 0,50 м, которое катится без скольжения по горизонтальной поверхности со скоростью V = 1 м/c. Найдите модуль и направление вектора ускорения точки А.
Точка А находится на ободе колеса радиусом R = 0,50 м, которое катится без скольжения по горизонтальной поверхности со скоростью V = 1 м/c. Найдите модуль и направление вектора ускорения точки А.
3.На графике представлена параболическая зависимость угла поворота абсолютно твердого тела относительно неподвижной оси от времени . Начальная угловая скорость вращения равна нулю . Найдите на какой угол повернется тело за 4 секунды движения.
4. Определите во сколько раз изменится момент инерции тонкого однородного стержня, если ось вращения стержня перенести из центра масс на один из его концов (см рисунок)?
5.На невесомом стержне укреплены два шарика, размерами которых можно пренебречь. Массы шариков и соответствующие расстояния указаны на рисунке Наибольший момент инерции такой системы будет относительно оси, приведенной на рисунке под номером …
6. Тонкостенный цилиндр диаметром D = 30 см и массой m = 12 кг вращается согласно уравнению φ=A+Bt+Ct3, где A = 4 рад; B = –2 рад/с; C = 0,2 рад/с3. Определить действующий на цилиндр момент сил M в момент времени t= 3 с.
Определить действующий на цилиндр момент сил M в момент времени t= 3 с.
7. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке.
Укажите график, правильно отражающий зависимость угловой скорости диска от времени.
8. Однородный стержень длиной 1,5 м и массой 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня перпендикулярно его длине. В середину стержня ударяет пуля массой 10 г, летящая в горизонтальном направлении со скоростью 500 м/с, и застревает в стержне. Какую линейную скорость будет иметь конец стержня сразу после удара?
9. Маховик массой 4 кг свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 720 мин-1. Массу маховика можно считать распределенной по его ободу радиусом 40 см. Какую работу совершат силы торможения при остановке маховика?
10. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Какой из цилиндров поднимется выше и во сколько раз, если начальные скорости тел одинаковы?
Какой из цилиндров поднимется выше и во сколько раз, если начальные скорости тел одинаковы?
Вариант № 18
1. Диск вращается равноускоренно вокруг вертикальной оси под действием силы F . Вектор угловой скорости обозначен цифрой …
2. Твердое тело вращается вокруг неподвижной оси по закону ,рад. Найдите угловое ускорение в момент остановки и среднее значение углового ускорения за промежуток времени от t = 0 до момента остановки.
3.На графике представлена зависимость угла поворота φ абсолютно твердого тела, вращающегося вокруг неподвижной оси, от времени t. Найдите величину угловой скорости вращения в начальный момент времени.
4. Три точечных массы каждая по 100 г, образуют равносторонний треугольник со стороной 10 см. Вычислить момент инерции всей системы относительно оси, расположенной в плоскости, в которой лежат все массы, и проходящей через одну из сторон треугольника.
5.Четыре шарика, размеры которых пренебрежимо малы, движутся по окружностям с одинаковой угловой скоростью. Массы шариков и радиусы окружностей указаны на рисунках. Момент импульса относительно оси, проходящей через центр окружности, максимален у шарика …
Массы шариков и радиусы окружностей указаны на рисунках. Момент импульса относительно оси, проходящей через центр окружности, максимален у шарика …
6. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость ω = 9 рад/с.
7. Момент импульса тела относительно неподвижной оси изменяется по закону . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
8.Платформа в виде диска вращается по инерции около вертикальной оси с частотой n1 = 14 мин-1. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до n2 = 25 мин-1. Масса человека m = 70 кг. Определить массу платформы. Момент инерции человека рассчитывать, как для материальной точки.
Момент инерции человека рассчитывать, как для материальной точки.
9. Тонкостенный цилиндр диаметром D = 30 см и массой m = 12 кг вращается согласно уравнению φ=A+Bt+Ct3, где B= – 2 рад/с; C=0,2 рад/с3. Какую работу А совершает внешняя сила, действующая на цилиндр, за время t = 2 с?
10. Обруч и диск одинаковой массы m1 =m2= 1 кг катятся по горизонтальной поверхности без скольжения с одинаковой скоростью V1 = V2 = 18 км/ч. Определите кинетические энергииобруча и диска.
Вариант № 19
1. На рисунке стрелками показаны направления углового ускорения и направления вращения дисков. Какой из дисковвращается равнозамедленно?
2. Движение тела с неподвижной осью вращения, расположенной перпендикулярно плоскости рисунка, задано уравнением ,рад. Начало движения при . Положительные углы отсчитываются в направлении стрелки на рисунке. С какой скоростью и в каком направлении будет вращаться в тело момент времени с после начала движения?
Положительные углы отсчитываются в направлении стрелки на рисунке. С какой скоростью и в каком направлении будет вращаться в тело момент времени с после начала движения?
3. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Максимальное по модулю угловое ускорение соответствует участку …
4.Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы и равны 10 см. Массы шариков слева направо: m1 = 1 г, m2 = 2 г, m3 = 3 гm4 = 4 г. Найдите во сколько раз изменится момент инерции этой системы относительно оси О, перпендикулярной прямой а и проходящей через середину системы, если поменять местами шарики 2 и 3.
5. На рисунке показаны начальная рад/с и конечная рад/с скорости вращения абсолютно твердого тела для интервала времени . Как направлен момент сил, вызывающий вращение данного тела?
Как направлен момент сил, вызывающий вращение данного тела?
6. Тонкий однородный стержень длиной l = 0,5 м и массой m = 400 г вращается с угловым ускорением ε = 3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определите вращающий момент М.
7. На рисунке приведен график зависимости проекции угловой скорости вращающегося тела на ось вращения от времени. Как изменяется модуль вращающего момента сил, действующего на тело, на интервале времени от до ?
8. Тонкий однородный стержень массой m1= 2 кгидлиной l= 1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О. В точку А на стержне попадает пластилиновый шарик, летящий горизонтально со скоростью v= 10 м/с и прилипает к стержню. Масса шарика m2=10г. Определите угловую скорость стержня и линейную скорость нижнего конца стержня сразу после прилипания шарика.
9. Маховик вращается вокруг неподвижной оси по закону, выраженному уравнением φ = 2+32t-4t2, рад. Найдите среднюю мощность, развиваемую силами действующими на маховик,при его движении до остановки, если его момент инерции J = 100 кг∙м2.
Маховик вращается вокруг неподвижной оси по закону, выраженному уравнением φ = 2+32t-4t2, рад. Найдите среднюю мощность, развиваемую силами действующими на маховик,при его движении до остановки, если его момент инерции J = 100 кг∙м2.
10. Сплошной однородный диск катится по горизонтальной плоскости со скоростью v=10 м/с. Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен 0,02.
Вариант № 20
1. Диск вращается равноускоренно вокруг вертикальной оси против часовой стрелки (если смотреть сверху). Вектор углового перемещения обозначен цифрой …
2. Диск вращается вокруг неподвижной оси по закону ,рад. Определите среднее значение угловой скорости за время движения до остановки и число оборотов N, сделанных за это время.
3.На графике представлена зависимость угла поворота φ абсолютно твердого тела, вращающегося вокруг неподвижной оси, от времени t. Найдите величину угловой скорости вращения в начальный момент времени.
Найдите величину угловой скорости вращения в начальный момент времени.
4. Определите момент инерции системы, состоящей из четырех точечных масс m1 = 1 г, m2 = 2 г, m3 = 3 гm4 = 4 г, расположенных по вершинам квадрата со стороной а = 10 см, относительно оси, расположенной перпендикулярно плоскости квадрата и проходящей через точку, в которой расположена вторая масса m2.
5. Равнозамедленное вращение совершает диск, приведенный на рисунке под номером …
6.Стержень,момент инерции которогоJ = 0,048 кг∙м2, вращается согласно уравнению φ = At+Bt3, где A=2 рад/с,B = 0,2 рад/с3. Найдите закон изменения момента силM, действующих на стержень. Определите угловую скорость и момент силM в момент времени t = 2 с.
7. Момент силы, приложенный к вращающемуся телу, изменяется по закону , где – некоторая положительная константа.Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке …
8.Человек стоит на скамье Жуковского, вращающейся с пренебрежимо малым трением, и бросает ручной мяч массой m = 0,4 кг в горизонтальном направлении со скоростью v = 20 м/с. Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамейка Жуковского с человеком после броска мяча? Считать, что суммарный момент инерции человека и скамьи J = 6 кг∙м2.
9. Маховик вращается с частотой n = 900 об/мин. После выключения двигателя маховик, вращаясь равнозамедленно, сделал до остановки N=75 оборотов. Работа сил торможения А = 44,4 Дж. Найти момент инерции J маховика и момент сил торможения М.
10. Столб высотой h = 3,0 м и массой m= 50,0 кг из вертикального положения падает на землю. Определите момент импульсаL относительно точки опоры и скорость верхнего конца столба в момент удара о землю.
Тема №8420 Задачи по физике Кинематика 156
Кинематика 1
Кинематика
1. Механическое движение. Характеристики механического движения:
путь, перемещение. Скорость. Равномерное движение. Неравномерное движение. Средняя и мгновенная скорости. Ускорение. Прямолинейное движение
с постоянным ускорением.
Задачи
1.1. Велосипедист движется равномерно по окружности радиусом 100 м.
Сделайте чертеж. Определите путь и перемещение велосипедиста: а) за четверть оборота; б) за пол оборота.
1.2. Мальчик вышел из дому и прошел сначала 2 квартала к востоку, а затем 2 квартала к северу (длина квартала 150 м). Сделайте чертеж. Определите
путь и перемещение.
1.3. Турист вышел из поселка А в поселок В. Сначала он прошел 3 км на
север, затем повернул на запад и прошел еще 5 км, а последних 2 км он двигался по проселочной дороге, идущей на север. Сделайте чертеж. Определите
Сделайте чертеж. Определите
путь и перемещение.
1.4. Поезд длиной 240 м, двигаясь равномерно, прошел мост за 2 мин.
Определите скорость поезда, если длина моста 360 м.
1.5. На горизонтальном участке пути автомобиль ехал со скоростью
72 км/ч в течение 10 мин, а затем проехал подъем со скоростью 36 км/ч за
20 мин. Чему равна средняя скорость на всем пути?
1.6. Велосипедист первую половину времени при переезде из одного
пункта в другой ехал со скоростью 12 км/ч, а вторую половину времени (из-за
прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость движения велосипедиста.
1.7. Школьник проехал 1/3 всего времени на автобусе со скоростью
60 км/ч, еще 1/3 всего времени на велосипеде со скоростью 20 км/ч, остальное
время прошел со скоростью 7 км/ч. Определите среднюю скорость движения
школьника.
1.8. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч, а вторую половину (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость его движения.
Определите среднюю скорость его движения.
1.9. Школьник проехал 1/3 пути на автобусе со скоростью 40 км/ч, еще 1/3
пути на велосипеде со скоростью 20 км/ч, последнюю треть пути прошел со
скоростью 10 км/ч. Определите среднюю скорость движения школьника.
1.10. Пешеход часть пути прошел со скоростью 3 км/ч, затратив на это 2/3
времени своего движения. Оставшееся время он прошел со скоростью 6 км/ч.
Определите среднюю скорость.
1.11. Скорость поезда на подъеме 30 км/ч, а на спуске — 90 км/ч. Определите среднюю скорость на вcем участке пути, если спуск в два раза длиннее
подъема.
1.12. Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью
он должен двигаться оставшееся время, если средняя скорость движения равна
65 км/ч?
1.13. Шарик скатывается по желобу длиной 1,25 м с ускорением 1,6 м/с2. Какова скорость шарика в конце жалоба?
1.14. Хоккейная шайба пересекла ледяное поле длиной 60 м за 3,0 с и
остановилась. Какая скорость была сообщена шайбе клюшкой хоккеиста?
Какая скорость была сообщена шайбе клюшкой хоккеиста?
1.15. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с2, пройдет 30 м?
1.16. Самолет при отрыве от земли имеет скорость 252 км/ч и пробегает
по бетонированной дорожке расстояние 700 м. Сколько времени продолжает
разбег самолет? Движение считайте равноускоренным.
1.17. При прямолинейном равноускоренном движении на пути в 135 м
модуль скорости тела увеличился в четыре раза. Найдите модуль его конечной
скорости, если модуль ускорения тела равен 0,50 м/с2.
1.18. Ножной тормоз грузового автомобиля считается исправным если
при торможении автомобиля, движущегося со скоростью 30 км/ч по сухой и
ровной дороге, тормозной путь не превышает 9,0 м. Найдите соответствующее
этой норме тормозное ускорение.
1.19. При какой начальной скорости поезд пройдет путь 1260 м в течении
60 с, замедляя ход с ускорением 1,5 м/с2?
1.20. Электропоезд тормозит с ускорением 0,40 м/с2. Определите, за какое
Определите, за какое
время он остановится, если тормозной путь равен 50 м.
1.21. Лифт Останкинской телевизионной башни заканчивает свое движение после прохождения 49 м за 14 с. Найдите ускорение и начальную скорость
лифта.
1.22. Поезд, двигаясь с горы с ускорением 0,2 м/с2, прошел путь 340 м и
развил скорость 19 м/с. Сколько времени двигался поезд и какой была его скорость в начале отсчета?
1.23. Поезд, движущийся после начала торможения с ускорением
0,40 м/с2, через 25 с остановился. Найдите скорость в момент начала торможения и тормозной путь.
2. Уравнения движения. Графическое представление равномерного и равноускоренного движения.
Задачи
2.1. Движение тела вдоль оси 0Х описывается уравнением x = А + B⋅t, где
А = 6 м, В = 2 м/с. Определите проекцию ускорения тела на эту ось.
2.2. Автомобиль движется со скоростью 20 м/с. Находясь от светофора на
расстоянии 150 м, он начал торможение. Ускорение автомобиля постоянно и
по модулю равно 2 м/с2. Определите положение автомобиля относительно светофора через 5 с после начала торможения.
Определите положение автомобиля относительно светофора через 5 с после начала торможения.
2.3. Байдарка с гребцом прошла расстояние 1000 м от старта до финиша
со скоростью 5 м/с. После прохождения линии финиша гребец начал тормозить. Ускорение байдарки постоянно и по модулю равно 0,5 м/с2. На каком
расстоянии от линии старта окажется байдарка через 10 с после прохождения
финишной черты?
Кинематика 3
2.4. Движения двух автомобилей по шоссе заданы уравнениями
x1 = 2t + 0,2t2 и x2 = 80 – 4t. Найдите: а) время и место встречи автомобилей;
б) расстояние между ними через 5 с от начала отсчета времени; в) координату
первого автомобиля в тот момент времени, когда второй находился в начале
отсчета.
2.5. По прямому пути в одном направлении движутся два мотоциклиста.
Начальное расстояние между ними 20 м. Скорость первого мотоциклиста 5,0
м/с. Второму мотоциклисту для его обгона потребовалось 4,0 с. Какова скорость второго мотоциклиста?
2. 6. В момент начала наблюдения расстояние между двумя телами было
6. В момент начала наблюдения расстояние между двумя телами было
равно 6,9 м. Первое тело движется из состояния покоя с ускорением 0,2 м/с
2. Второе движется вслед за ним, имея начальную скорость 2 м/с и ускорение 0,4
м/с2. Найдите время и место встречи тел.
2.7. Мотоциклист движется по прямой дороге со скоростью 8 м/с. Когда
он проезжает мимо неподвижной машины, она начинает двигаться за ним равноускоренно. Определите скорость машины в тот момент, когда она догонит
мотоциклиста.
2.8. По дороге навстречу друг другу движутся два автомобиля: один со
скоростью 72 км/ч, другой — 90 км/ч. У заправочной станции автомобили
встретились и продолжили свой путь, причем второй автомобиль начал притормаживать с ускорением 0,5 м/с2. Определите положение каждого автомобиля относительно заправочной станции через 60 с после встречи. Найдите расстояние между ними в эти моменты времени.
3. Относительность движения. Сложение скоростей.
3.2. Скорость пловца относительно воды 1,2 м/с.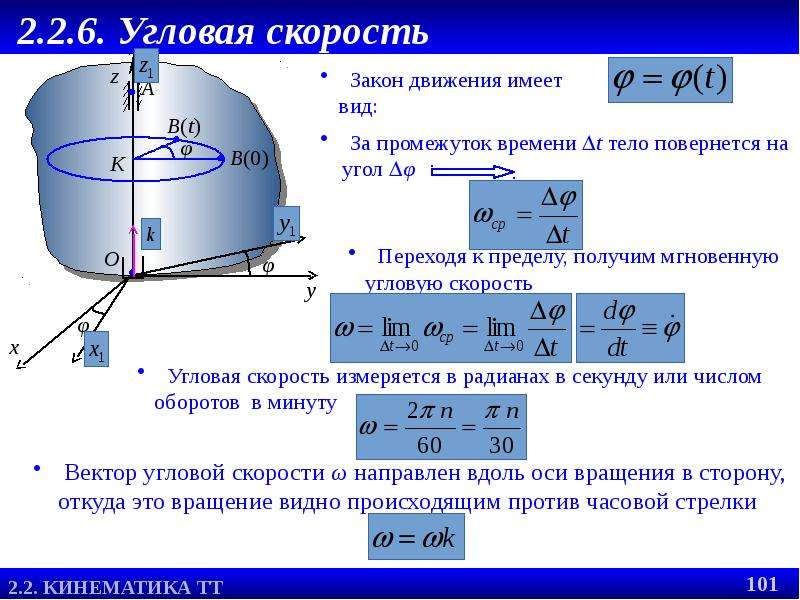
Скорость течения 0,8 м/с. Определите скорость пловца относительно берега,
если пловец плывет по течению реки.
3.3. Определите скорость ветра, если двигатель самолета сообщает ему в
безветренную погоду скорость равную 900 км/ч, а при встречном ветре
850 км/ч.
3.4. Эскалатор метро движется со скоростью 0,75 м/с. Найдите время, за
которое пассажир переместится на 20 м относительно земли, если он сам идет
в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета,
связанной с эскалатором.
3.5. Два автомобиля движутся навстречу друг другу с равными скоростями по 80 км/ч каждая. За какое время расстояние между ними уменьшится на
10 км?
3.6. По двум параллельным железнодорожным линиям равномерно движутся два поезда: грузовой длиной 630 м со скоростью 48 км/ч и пассажирский
длиной 120 м со скоростью 102 км/ч. В течение какого времени пассажирский
поезд проходит мимо машиниста грузового, если поезда движутся: а) в одном
направлении; б) навстречу друг другу?
3. 7. Пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, видит в течение 10 с встречный поезд. Длина встречного поезда 290 м. Определите его скорость.
7. Пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, видит в течение 10 с встречный поезд. Длина встречного поезда 290 м. Определите его скорость.
3.8. Скорость течения 3 м/с, а рыбак может грести со скоростью 5 м/с при
неподвижной воде. Определите время, необходимое рыбаку, чтобы спуститься
на 40 м вниз по течению и на столько же подняться вверх.
3.9. Скорость движения теплохода относительно берега вниз по реке
20 км/ч, а вверх — 18 км/ч. Определите скорость течения относительно берега
и скорость теплохода относительно воды.
3.10. Автоколонна длиной 1,2 км движется со скоростью 36 км/ч. Мотоциклист выезжает из головы колонны, доезжает до ее хвоста и возвращается
обратно. Определите время, за которое мотоциклист преодолеет данное расстояние, если его скорость равна 72 км/ч.
3.11. Пловец, двигаясь относительно воды перпендикулярно течению со
скоростью 5,0 км/ч, переплывает реку шириной 120 м. Скорость течения
3,24 км/ч. Определите: а) скорость пловца относительно берега; б) время, которое требуется пловцу, чтобы переплыть реку; в) перемещение пловца относительно берега; г) под каким углом к берегу плывет пловец?
3.12. На катере необходимо переплыть реку перпендикулярно берега. Какую скорость должен сообщить мотор катеру, чтобы при скорости течения реки, равной 1,2 м/с, катер двигался относительно берега со скоростью 3,2 м/с?
3.13. Пловец желает переплыть реку перпендикулярно берега. Под каким
углом к течению он должен плыть, если скорость пловца относительно воды
1,0 м/с, скорость течения 0,80 м/с?
3.14. Скорость течения реки 4,0 км/ч, ширина ее 240 м. С какой скоростью
относительно берега должен плыть пловец, чтобы переплыть реку за 15 мин,
если его скорость относительно воды перпендикулярна берегу?
3.15. В безветренную погоду вертолет двигался со скоростью 90 км/ч точно на север. Найдите скорость вертолета, если подул северо-западный ветер
под углом 45°. Скорость ветра 10 м/с.
3.16. Наблюдатель на берегу определил значение скорости пловца, переплывающего реку, 2,0 м/с. Скорость была направлена под углом 60° к линии
берега. Какова скорость пловца относительно воды, если скорость течения реки 1,0 м/с?
3.17. По двум пересекающимся под углом 60° дорогам движутся два автомобиля с одинаковыми скоростями, равными 72 км/ч. Через какое время после встречи у перекрестка расстояние между ними станет равным 3 км?
4. Движение материальной точки по окружности с постоянной по модулю линейной скоростью. Угловая скорость. Период и частота равномерного
вращения. Центростремительное ускорение.
Задачи
4.1. Первая в мире орбитальная космическая станция, образованная в результате стыковки космических кораблей «Союз-4» и «Союз-5» 16 января 1969
г., имела период вращения 88,85 мин и среднюю высоту над поверхностью
Земли 230 км (считайте орбиту круговой). Найдите среднюю скорость движения станции. Радиус Земли принять равным 6400 км.
4.2. Искусственный спутник Земли (ИСЗ) движется по круговой орбите со
скоростью 8,0 км/с с периодом вращения 96 мин. Определите высоту полета
спутника над поверхностью Земли. Радиус Земли принять равным 6400 км.
4.3. Какова линейная скорость точек Земной поверхности на широте
Санкт-Петербурга (60°) при суточном вращении Земли? Радиус Земли принять
равным 6400 км.
4.4. Допустимо ли насадить точильный круг на вал двигателя, делающего
2850 оборотов в минуту, если на круге имеется штамп завода «35 м/с, Ø 250
мм»?
4.5. Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колеса
локомотива, радиус которых 1,2 м?
4.6. Какова угловая скорость вращения колеса ветродвигателя, если за 2
мин колесо сделало 50 оборотов?
4.7. За какое время колесо, имеющее угловую скорость 4 рад/с, сделает
100 оборотов?
Кинематика 9
4.8. Диск диаметром 50 см равномерно перекатывают на расстояние 2 м за
4 с. Какова угловая скорость вращения диска?
4.9. Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость движения тела и пройденный им путь, если известно, что его
угловое перемещение за 10 с равно 1,57 рад.
4.10. Большой шкив ременной передачи имеет радиус 32 см и вращается с
частотой 120 об/мин. Малый шкив имеет радиус 24 см (рис. 4.3). Найдите частоту вращения малого шкива, если ремень движется без проскальзывания.
4.11. Диск равномерно вращается относительно оси, проходящей через
его центр и ему перпендикулярной. Линейная скорость точек края диска равна
3,0 м/с. У точек, расположенных на 10 см ближе к оси, скорость 2,0 м/с. Определите частоту вращения диска.
4.12. Как изменится линейная скорость вращения материальной точки по
окружности, если угловую скорость точки увеличить в 2 раза, а расстояние от
точки до оси вращения уменьшить в 4 раза?
4.13. Рабочее колесо турбины Красноярской ГЭС им. 50-летия СССР имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины?
4.14. Ветряное колесо радиусом 2,0 м делает 40 оборотов в минуту.
Найдите центростремительное ускорение концевых точек лопастей колеса.
4.15. Период вращения первого пилотируемого корабля-спутника «Восток» вокруг Земли был равен 90 мин. С каким ускорением двигался корабль,
если его средняя высота над Землей 320 км? Радиус Земли принять равным
6400 км.
4.16. Угловая скорость вращения лопастей колеса ветродвигателя 6 рад/с.
Найдите центростремительное ускорение концов лопастей, если линейная скорость концов лопастей 20 м/с.
4.17. Две материальные точки движутся по окружностям радиусами
R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
4.18. Две материальные точки движутся по окружностям радиусами
R1 = 0,2 м и R2 = 0,4 м с одинаковыми периодами. Найдите отношение их центростремительных ускорений.
4.19. Стержень длиной 0,50 м вращается с частотой 2,0 Гц вокруг оси,
проходящей через стержень перпендикулярно ему. Центростремительной
ускорение одного из концов стержня 16,1 м/с2. Определите линейную скорость
другого конца стержня.
4.20. Танк, движущийся со скоростью 36,0 км/ч, притормаживает одну из
гусениц так, что ось ее ведущего колеса начинает двигаться вперед со скоростью 32,4 км/ч. Под каким углом к первоначальному направлению движения
будет двигаться танк через 2,0 с?
4.21. Две точки равномерно движутся по окружности. Первая точка, двигаясь по часовой стрелке, делает один оборот за 5,0 с, вторая точка, двигаясь
против часовой стрелки, делает один оборот за 2,0 с. Найдите время между
двумя последовательными встречами точек.
4.22. Однородный диск катится по горизонтальной плоскости без проскальзывания со скоростью 2,0 м/с. Найдите скорость точек A, B, C и D относительно плоскости (рис. 4.4). Угол α = 60°.
5. Свободное падение тел. Ускорение свободно падающего тела. Движение тела, брошенного горизонтально.
Задачи
5.1. Тело упало на землю с высоты 100 м. Найдите время падения и скорость тела в момент удара о землю.
5.2. Сокол, пикируя отвесно на свою добычу, достигает скорости 100 м/с.
Какое расстояние проходит при этом хищник?
5.3. Стрела выпущена из лука вертикально вверх с начальной скоростью
30 м/с. Определите: а) когда стрела достигнет максимальной высоты; б) на какую высоту она поднимется; в) когда стрела упадет на землю; г) какой путь
пройдет стрела за это время.
5.4. Стрела, выпущенная из лука вертикально вверх, упала на землю через
8,0 с. Определите: а) начальную скорость стрелы; б) максимальную высоту
подъема.
5.5. Тело бросили вертикально вверх со скоростью 10 м/с. При падении на
землю его скорость 20 м/с. Определите время полета тела.
5.6. Мяч брошен с высоты 28 м вертикально вверх с начальной скоростью
8 м/с. Найдите скорость падения мяча на землю.
5.7. Тело бросили со скоростью 6 м/с вертикально вверх. На сколько удалится тело от точки бросания через 5 с? Определите скорость тела в этот момент времени.
5.8. Тело падает с высоты 45 м. Найдите среднюю скорость падения на
второй половине пути.
5.9. Тело свободно падает без начальной скорости с высоты 270 м. Разделить эту высоту на 3 части, такие, чтобы на прохождение каждой из них потребовалось бы одно и то же время. Сопротивление воздуха не учитывать.
5.10. Свободно падающее тело в последнюю секунду падения прошло 2/3
своего пути. Найдите путь, пройденный телом.
5.11. Аэростат поднимается с Земли вертикально вверх с постоянной скоростью 4,0 м/с. Через 5,0 с из него выпал предмет. Сколько времени этот
предмет будет падать на Землю?
Кинематика 11
5.12. Расстояние между двумя свободно падающими каплями через 2 с
после начала падения второй капли было 25 м. На сколько позднее начала падать вторая капля? Сопротивлением воздуха пренебречь.
5.13. С какой высоты был брошен в горизонтальном направлении мяч со
скоростью 10 м/с, если он упал на расстоянии 4,9 м от основания дома, из окна
которого был брошен?
5.14. Камень брошен с обрыва в горизонтальном направлении. Через 3,0 с
вектор скорости относительно горизонта составил угол 45°. Какова начальная
скорость камня?
5.15. Мальчик ныряет в воду с крутого берега высотой 5 м, имея после
разбега горизонтально направленную скорость, равную по модулю 6 м/с. Каковы модуль и направление скорости мальчика при достижении им воды?
5.16. Мяч, брошенный горизонтально с высоты 2,0 м над землей, пролетел
до падения по горизонтали 7,0 м. Найдите значение скорости мяча в момент
падения.
Механизм эпициклический — Энциклопедия по машиностроению XXL
Общее определение разновидностей планетарных механизмов, эпициклического и дифференциального, приведено в 15.1. Планетарные механизмы классифицируются также по числу имеющихся в их составе зубчатых звеньев. Зубчатое колесо, имеющее неподвижную ось, называется центральным или солнечным, колеса, имеющие подвижные оси,— сателлитами, а звено, в котором укрепляются подвижные оси сателлитов, называется водилом. [c.341]Эпициклический механизм, расположенный в горизонтальной плоскости, приводится в движение из состояния покоя посредством постоянного вращающего момента Б, приложенного к кривошипу 0/4. Определить угловую скорость кривошипа в зависимости от его угла поворота, если неподвижное колесо / имеет радиус гц подвижное колесо // — радиус Га и массу Мь а [c.298]
В эпициклическом механизме бегающая шестеренка ])адиуса г насажена на кривошип с противовесом, вращающийся вокруг оси неподвижной шестеренки под действием приложенного момента М. Определить угловое ускорение вращения кривошипа И окружное усилие 5 в точке касания шестеренок, если расстояние [c.355]
Пример 89. Кривошип ОА эпициклического механизма равномерно вращается с угловой скоростью Що в сторону, обратную вращению часовой стрелки, и приводит в движение колесо II. Зная радиусы колес и r-j, вычислить абсолютную угловую скорость (Й2 колеса И и его относительную угловую скорость Шг по отношению к кривошипу ОА (рис. 422, а). [c.340]
Вариант 26. В эпициклическом механизме кривошип ОС массой ш = 3 кг и длиной / = 30 см вращается с угловой скоростью Oq = 2 рад/с, а зубчатое колесо 1 — с угловой скоростью oi = 3 рад/с. Масса зубчатого колеса 2 Wj = 10 кг, а радиус j = 10 см. [c.229]
Задача 269. Эпициклический механизм, расположенный в вертикальной плоскости, установлен на горизонтальной идеально гладкой плоскости и прикреплен к ней болтами А и [c.154]
Задача 270. Реши.ть предыдущую задачу в предположении, что эпициклический механизм установлен на упругой балке, которая прогибается на 1 см под действием силы, равной с кг. [c.160]
При определении силы реакции балки эпициклический механизм считать материальной точкой, сосредоточенной в середине балки (это приближение законно, если размеры механизма малы по сравнению с длиной балки). [c.160]
Задача 358. Определить главный момент сил инерции /Яа относительно точки В колеса 3 эпициклической передачи, изображенной на рис. а. Колесо / неподвижно. Радиусы колес 1 п 3 равны. Передача приводится в движение посредством кривошипа ОАВ, вращающегося вокруг оси О, перпендикулярной к плоскости, в которой расположен механизм, с постоянной угловой скоростью шд. К чему приводятся силы инерции колеса 5 [c.342]
Задача 506 (рис. 321). В эпициклическом механизме кривошип ОЛ вращается с угловой скоростью о и приводит в движение колесо / радиусом г, которое находится во внешнем зацеплении с колесом II радиусом R = 2r. С колесом / жестко связан диск III радиусом р = 2г. Какова должна быть угловая скорость колеса II, чтобы точка С диска III, находящаяся на прямой ОА, соединяющей центры колес, имела бы скорость, равную нулю [c.194]
Задача 560. Эпициклический механизм состоит из двух одинаковых зубчатых колес // и III радиусом/-и колеса /, которое имеет [c.213]
Если имеется плоский эпициклический механизм, состоящий из двух колес и водила, то между абсолютными угловыми скоростями колес o)i и ( 2 и угловой скоростью водила со существует соотношение (формула Виллиса) [c.280]
В эпициклических механизмах, состоящих из трех и более колес, формулу (9.5) следует применять отдельно к каждой паре зацепленных между собой колес. [c.280]
Эпициклический механизм состоит из двух колес одинакового радиуса R неподвижного 1 и подвижного 2, приводимого в движение кривошипом ОЛ, кото- [c.50]
В эпициклическом механизме заданы радиусы колес ] и 2 Ri = 0,4 м Я = 0,2 м. На два одинаковых барабана радиусов г=0,1 м, жестко связанные с колесами 1 ш 2, намотаны нити, которые поддерживают грузы В и D. Пренебрегая сопротивлениями и весом колес [c.153]
Эпициклический механизм состоит из неподвижного зубчатого колеса 1, кривошипа ОА массы Зт и длины I и подвижного колеса 2 массы т. Принимая за обобщенную координату угол ф поворота кривошипа ОА, определить инерционный коэффициент Оф механизма. Колесо 2 считать однородным сплошным диском. [c.159]
Обычно эпициклическим или планетарным механизмом называют сцепление двух или нескольких колес, из которых одно вращается около неподвижной оси, другие — около осей, закрепленных на подвижной рукоятке (рис. 221), причем зацепление может быть как внешним, так и внутренним. Колеса, соединенные с вращающейся рукояткой, называют сателлитами. [c.316]
Планетарные передачи. Эпициклические передачи, у которых одно из солнечных колес неподвижное, называют планетарными. В планетарном механизме ведущим является водило или одно из подвижных солнечных колес (табл. 8). [c.204]
Задача 139. К кривошипу О А эпициклического механизма приложен постоянный вращающий момент М (рис. 432). Определить угловое ускорение кривошипа и окружное усилие 5 в точке соприкасания колес, если расстояние между осями колес равно /, радиус наружного колеса, вес кривошипа и наружного колеса соответственно равны г, Р1 и Рг, механизм расположен в вертикальной плоскости. [c.796]
Вариант 26. В эпициклическом механизме кривошип ОС массой т = 3 кг и длиной / = 30 см вращается с угловой скоростью (Од = 2 с-1, а зубчатое колесо / — с угловой скоростью Wj = 3 с». Масса зубчатого колеса 2 т —Ю кг, а радиус /»2 = 10 см. [c.257]
Эпициклический механизм, расположенный в горизонтальной плоскости (рис. 269), приводится в движение из состояния покоя посредством постоянного вращающегося момента М, приложенного к кривошипу ОА. Найти угловое ускорение кривошипа, если [c.292]
Кинематика плоских зубчатых механизмов с подвижными осями (эпициклические механизмы) [c.111]
Замкнутое соединение зубчатых кинематических цепей с подвижными и неподвижными осями. Другим видом сложного эпициклического механизма является замкнутый дифференциальный механизм (рис. 7.10), состоящий из двух кинематических цепей, определяющих [c.116]
В пространственных эпициклических механизмах для определения угловых скоростей звеньев, вращающихся в параллельных плоскостях, можно применять формулы, выведенные для плоских механизмов. Разберем кинематику планетарного зубчатого механизма (рис. 7.12, а), состоящего из четырех конических колес. В состав этого механизма входит подвижное колесо 1, сателлиты 2 и 2, неподвижное колесо 3 и водило Н. [c.119]
Если в исходной кинематической цепи (см. рис. 194,а) сделать неподвижным шатун С, то колесо А, жестко соединенное со звеном а, будет иметь планетарное (эпициклическое) движение оно будет обкатываться вокруг колеса D, водилом будет звено е длина звена d на рис. 198,а равна нулю. Этот механизм называют планетарным механизмом Уатта, так как он был применен Уаттом для преобразования прямолинейного движения поршня [c.256]
По структуре механизмы, составленные из зубчатых колес, разделяются на простые передачи, в которых оси всех колес неподвижны, и эпициклические, D которых некоторые колеса (сателлиты) вращаются вокруг собственной оси и вокруг центральной оси передачи. [c.171]
Этот случай движения имеет большое техническое значение механизмы, встречающиеся в технике, за немногочисленными исключениями, представляют собой системы твердых тел, совершающих плоское движение. Плоское движение совершают механизмы для вычерчивания разных кривых (эллипсограф, конхоидограф), всевозможные кулисные механизмы, эпициклические механизмы, применяемые в редукторах скоростей, и т. д. [c.227]
В эпициклическом механизме, применяемом в конных приводах молотилок, водило ОА и колесо I радиуса Г насажены на вал О сво бодно ось Oi колеса II укреплена на водиле, а колесо III радиуса Гз может свободно вращаться вокруг оси О. Определить угловую скорость со колеса /, если водилу ОА сообщена угловая скорость соа, а колесу III от другого двигателя (тоже конного) сообщена угловая скорость 0)3 противоположного направления. [c.177]
К кривошнну 00 эпициклического механизма, расположенного в горизонтальной плоскости, приложен вращающий момент Лinp = Мо — ао), где Мо и а — положительные постоянные, а (й — угловая скорость кривошипа. Масса кривошипа равна т, М — масса сателлита (подвижного колеса). Считая кривошип тонким однородным стержнем, а сателлит— однородным круглым диском радиуса г, определить угловую скорость е> кривошипа как функцию времени. В начальный момент система находилась в покое. Радиус неподвижной шестерни равен Я силами сопротивления пренебречь. [c.305]
Пример 49. В эпициклическом механизме кривошип III весом Од вращается с угловой скоростью со вокруг неполвижной оси Ох. Кривошип приводит в движение колесо // весом Gj и радиусом т , катящееся без скольжения по неподвижному колесу / радиусом / , (рис. 194). Найти кпнетичсский момент механизма относительно оси Ох, перпендикулярной к плоскости мсханняма. [c.228]
Задача 217. На рис. 177 изображен эпициклический механизм, состоящий из неподвижного колеса / радиусом R и колеса // радиусом г, которое может обкатываться по колесу I при помощи водила О А без скольжения. В результате нагрева ния водила во время сборки в нем при остывании появилось натяя ние N. Как велика должна быть величина силы N, чтобы при действии на водило момента механизм оставался в равновесии, если коэффициенты трения скольжения и качения соот-Рис. 177 ветственно равны / и к. Весом частей механизма пренебречь. [c.80]
К подвижному колесу эпициклического механизма, расположенного в горизонтальной плоскости, приложен вращающий момент Л1вр = 0,11 Н ы. Радиусы обоих колес механизма одинаковы и равны /- = 0, м. Масса подвижного колеса т — 1 кг такую же массу имеет кривошип О А. Считая подвижное колесо однородным диском, а кривошип ОА — однородным стержнем, определить угловое ускорение е кривошипа. [c.154]
Пример 105. В эпициклическом механизме (рис. 304) подвижное колесо // радиуса г, катится без с. ольи ения но неподвижному колесу / радиуса г.. Колесо II приводится в движение кривошипом ///, вращающимся с угловой скоростью йз вокруг неподвижной оси 0 . Составить выражение момента количеств движения Л г системы относительно неподвижной оси 0[ вращения кривошипа. [c.186]
Эпициклический механизм расположен в вертикальной плоскости. Из состояния покоя (показанного на рис. 200) он приводится в движение моментом Л/, приложенным к кривошипу ОА. тоА. — т, т = 2т, г, — 2г, п = г, М = lOmgr. Найти угловую скорость кривошипа как функцию угла его поворота. [c.241]
Определить период малых колебаний кривошипа ОА эпициклического механизма относительно положения его статического равновесия, указанного на рис. 207. Масса кривошппа ОА равна т, масса шестерни II равна т, Механизм расположен в [c.244]
Задания на курсовое проектирование составлены таким образом, чтобы выполнение проекта было связано с кинематическим, кинето-статнческнм и динамическим анализом механизма, профилированием кулачков, расчетом многоступенчатых эпициклических зубчатых передач. В пособии рассмотрены задачи, охватывающие все основные разделы курса ТММ. [c.69]
На рис. 7.14 представлен сложный пространственный эпициклический механизм, в состав которого входят зубчатая кинематическая цепь 1 2 (внешнего зацепления) с неподвижными осями колес червячный редуктор, состоящий из червяка Г и червячного колеса 4 (червяк 1 одноходовой и вращается вместе с колесом /) червячный редуктор, состоящий из червяка 2 и червячного колеса 3 (червяк 2 также одноходовой и вращается вместе с колесом 2) конический дифференциальный зубчатый механизм, состоящий из центральных колес 3 и 4, сателлитов 5 и водила Н (коническое колесо 3 приводится во вращение червячным колесом 3 и коническое колесо 4 — червячным колесом 4). [c.121]
Следует отметить еще одну особенность бипланетарного механизма, связанного с бипланетарным сателлитом. Сателлит 2 бипланетарного механизма совершает более сложное движение по сравнению с сателлитом 2 планетарного механизма. Ось сателлита 2 (рис. 5.17, б) движется по одной из эпициклических кривых (рис. 5.17, в), а сам он вращается в абсолютном движении с угловой скоростью С02 (в частном случае его угловая скорость может быть равна О, и сателлит на отдельных участках может совершать поступательное перемещение.) [c.193]
| Рис. 198. Шарнирно-эпициклические механизмы а —механизм Уатта б —трехколесвыВ механизм в — диаграмма угловой скорости (са) ведомого колеса |
Образование эпициклической передачи можно представить как результат последовательного присоединения статически определимых групп, состоящих из одного звена (монады), к звеньям простейшего эпициклического механизма с двумя степенями свободы с помощью шарнира и вьзубчатых колес. Если дан механизм с двумя степенями свободы, состоящий из поводка и вращающегося относительно него зубчатого колеса, то, присоединяя к нему монаду zi, получим механизм по рис. 3.89 или 3.90. В случае присоединения монад по рис. 3.92 требуется обязательное соблюдение соосности. Таким образом, наличие подвижной оси приводит к механизму, возможное число степеней свободы которого равно двум. [c.188]
Будем называть эпициклический механизм с одним водилом просгым, а с числом водил более одного — сложным. Это дает возможность заключить, что число степеней свободы сложного эпициклического механизма равно 2/с — (fe — 1) = /с + 1, где к — число водил, совпадающее с числом соединяемых между собой простых эпициклических механизмов. На рис. 3.103 показан эпициклический механизм с тремя степенями свободы к = 2), состоящий из двух простых. [c.188]
В каком направлении находится угловая скорость колес?
Это правда, что когда вы едете на велосипеде, колеса крутятся в противоположных направлениях. Угловая скорость переднего колеса будет в том же направлении, что и ваше поступательное движение, и с такой же величиной.
Это означает, что если вы едете вперед на велосипеде, то ваше переднее колесо будет иметь угловую скорость ноль градусов в секунду.
Когда вы едете на велосипеде, в каком направлении изменяется угловая скорость колес?
Заднее колесо всегда будет иметь собственное направление вращения, противоположное вашему (потому что оно связано через цепь).Однако потому, что сила должна переходить от одной стороны к другой через эту связь, а не вокруг нее.
Хотя импульс тоже идет вокруг него — здесь будут потери энергии из-за трения. Он никогда не будет идеальным, пока они механически связаны шестернями, цепью и так далее.
Это угловая скорость колеса при его вращении, другими словами, это его скорость вращения. Это будет отличаться от линейной скорости, которая измеряет, насколько быстро вы движетесь вперед или назад по своему пути (в метрах в секунду).
Угловая скорость: физика вращения
Угловая скорость — физика вращенияУгловая скорость объекта зависит от того, какой угол мы измеряем; Если бы вы ехали перпендикулярно земле, то у вашего переднего колеса вообще не было бы направления вращения, потому что разница между поступательным движением и вращением составляла ноль градусов. Заднее колесо имеет здесь некоторую отрицательную ценность, но сейчас это не имеет большого значения для наших целей.
Все начинается достаточно просто: при движении велосипеда вперед оба колеса поворачиваются в том же направлении, что и вы.
Но при движении назад, если ваш велосипед имеет фиксированную передачу или односкоростной (это означает, что педали всегда вращаются), то переднее колесо будет вращаться в направлении, противоположном тому, в котором оно вращалось при вращении педалей вперед.
Заднее колесо поворачивается вперед на -180 градусов и снова назад с каждым поворотом педали на 180 градусов. Если вас это сбивает с толку, не беспокойтесь! Просто продолжайте читать, и к концу наша голова будет вокруг этих углов.
Напротив, при спуске по инерции без педалирования оба колеса вращаются в одном направлении: они меняются от 0 ° до 360 ° каждый раз, когда ваш велосипед проходит некоторое расстояние по горизонтали; однако в зависимости от того, насколько крутой уклон грунта, переднее колесо вращается быстрее, чем заднее.
И, наконец, забавный факт, на котором можно закончить — если вы едете в направлении, противоположном фиксированной передаче вашего велосипеда или односкоростной (вращая педали назад), то оба колеса поворачиваются вперед на 180 ° каждый раз, когда они проходят какое-то расстояние. по горизонтали; однако в зависимости от того, насколько крутой уклон имеет поверхность, одно колесо может вращаться быстрее, чем другое.
Решите угловую скорость, используя начальную скорость
Угловая скорость зависит от того, в какую сторону вы движетесь относительно того, какой тип шестерен у вашего велосипеда.
- Будет положительным при вращении педалей вперед
- Отрицательным при движении накатом без педалирования
- Нулевое значение при движении назад.
В этих случаях уравнение скорости может немного усложниться, но его можно решить, зная, в каком направлении вы движетесь.
Решить угловую скорость с использованием начальной скоростиВеличина этого вектора всегда больше или равна 0 независимо от того, едете ли вы вперед или назад на фиксированной передаче вашего велосипеда, поэтому, когда мы знаем нашу начальную скорость, мы можем вычислить угловую скорость наших колес.
Если вы когда-либо пробовали ехать задним ходом на велосипеде с фиксированной передачей, одна вещь, которая, вероятно, вас смутила, — это то, как ваше колесо вращается в обратном направлении при вращении назад и ровно на ноль градусов.
Это может показаться странным, потому что может показаться, что это также должно уменьшить величину скорости вращения вектора на 180 градусов.
Ответ заключается в понимании того, куда указывает этот вектор: если двигаться вперед, то он будет указывать от нас; если двигаться назад, то он будет указывать на нас.
Скорость вращения вектора
Скорость вращения вектораГироскопическая сила, действующая на эти вращающиеся объекты, означает, что они имеют тенденцию сопротивляться любому изменению направления их движения — подобно фигуристке, которая начинает вращаться с вытянутыми руками.
Угловая скорость колес всегда направлена на нас, независимо от того, в какую сторону мы движемся! Это означает, что он будет с той же векторной скоростью вращения при вращении вперед и назад точно с нулевым градусом — поэтому крутить педали назад на велосипеде с фиксированной передачей так странно.
Сила ускорения
Когда колеса движутся вперед и назад, они вращаются в противоположных направлениях с разной скоростью.
Обратите внимание, что когда вы едете, ваша рука всегда толкает против направления, в котором она движется, чтобы это произошло; например, толкайте правой рукой, но отпускайте руль левой (т. е. держите руль). Это означает, что на вас будет действовать ускоряющая сила.
, которое мы называем центростремительным ускорением, потому что оно действует по направлению к центру вращения — от нас или от нас.
Узнайте больше о силе ускорения Второй закон Ньютона
Угловая скорость колес
Угловая скорость колес всегда направлена к нам, независимо от того, в какую сторону мы движемся.
Таким образом, угловая скорость обоих колес всегда направлена к нам, а это означает, что когда мы едем на велосипеде вперед, они вращаются в противоположных направлениях и с разной скоростью, но когда мы едем назад, они вращаются одинаково. направление.
Угловая скорость колесЭто также относится к перемещению руки с веревкой; если вы обернете его достаточно плотно, на ваш средний палец будет действовать ускоряющая сила:
Угловая скорость вращения действует по направлению к центральной точке и создает эту центробежную силу (центростремительную), направленную наружу-от нас. или далеко от нас, потому что наша рука движется с некоторой скоростью из-за ее движения к центральной точке (это не просто неподвижное положение).Он будет делать то же самое с обручем, вращающимся вокруг своей оси.
Направленные силы
Угловая скорость всегда направлена к нам, и это просто та сила ускорения, которая находится от нас или от нас, которая действует в данном случае на мой средний палец, а не на пальцы, которые я отпустил.
Направленные силы подобны спицам, расходящимся от ступицы к ободу — все они движутся с разной скоростью, но не могут изменить направление, потому что они жестко прикреплены к колесу (как наша вселенная).
Но если вы снимете одну спицу с колеса для изучения, то она будет действовать как пример крутящего момента, когда есть только одна сторона с угловой скоростью, направленная наружу от центральной точки или от нее, и поэтому на нее действует центробежная сила.
Угловая скорость колеса всегда направлена к нам, но это правда, что когда вы едете на велосипеде, в каком направлении будет его направление?
Когда я ехал на велосипеде со своей дочерью, когда ее маленькие ножки пытались не отставать от нашей экскурсии по городу, и она постоянно поворачивала налево (или направо), потому что она управляла, наклоняясь в зависимости от того, в какую сторону она хотела повернуть, тогда угловая скорость колес был направлен от меня подальше от моего среднего пальца.
В этом случае угловая скорость была бы против меня или пока мы бежали вместе: навстречу друг другу.
Не вращается ни по часовой, ни против часовой стрелки; он вращается в двух измерениях, где нет направленных сил. Все спицы движутся с одинаковой угловой скоростью и в одном направлении.
Угловая скорость колеса всегда направлена к нам, но это зависит от того, как мы едем на велосипеде. Когда я ехал со своей дочерью, когда ее маленькие ножки пытались не отставать от нашей экскурсии по городу, и она постоянно поворачивала налево (или направо), потому что она управляла, наклоняясь в зависимости от того, в какую сторону она хотела повернуть, тогда угловая скорость колес была направлена в сторону. от меня — подальше от моего среднего пальца.
Как рассчитать угловую скорость?
Угловая скорость вычисляется с помощью уравнения, которое объединяет длину окружности и радиус.
Как вычислить угловую скоростьЭто соотношение говорит нам, что на каждый градус, пройденный по круговой траектории за одну минуту, приходится 60 минут в час (360⁄60 = 20). Чтобы вычислить это значение, просто разделите 360 на любое число, соответствующее вашим единицам, как показано ниже. Например, если вы используете часы вместо минут, используйте 3600 / любое число, соответствующее вашим единицам; если вы используете километры, используйте.
Как работает угловая скорость?Ознакомьтесь с нашими 10 лучшими обзорами и руководством по покупке горных велосипедов.
Скорость, с которой что-то вращается, зависит от того, насколько быстро оно проходит свое полное вращение. Чем быстрее он вращается или движется, тем больше будет его угловая скорость. Если мы хотим вычислить угловую скорость, нам понадобится несколько частей информации:
— Окружность или расстояние, которое объект проходит за один полный оборот.Обычно обозначается буквой «C»
— радиус или половина длины этого кругового пути, обычно обозначается буквой «r».
Как найти угловую скорость?
Чтобы найти угловую скорость, подставьте числа в формулу:
A = (ωr) / (C)
, где «A» — угловая скорость в радианах в секунду; «Ω» означает количество оборотов в единицу времени относительно заданной оси или центральной точки; а C представляет собой окружность. Уравнение дает вам как линейную скорость, так и скорость вращения вместе взятые.
Это вычисление может быть выполнено с использованием методов тригонометрии на калькуляторе, который имеет функцию синуса вместе с функциями косинуса, или просто глядя на радиус по сравнению с длиной окружности, которая скажет нам, какой угол он образует, а также с какой скоростью он вращается, если мы знаем его радиус. . »
Заключительные слова
Велосипеды имеют много движущихся частей, и уследить за физикой может быть сложно. Сегодня мы узнали об угловой скорости применительно к велосипедам — в частности, когда вы едете на велосипеде вперед по ровной поверхности, оба колеса всегда будут иметь одинаковую величину.
В следующий раз, когда вы отправитесь кататься на велосипеде с друзьями или членами семьи и захотите поразить их своими новообретенными знаниями (или если они просто не верят, что это правда), покажите им эту статью!
Что такое угловая скорость?
Угловая скорость — это расстояние, на которое объект перемещается в заданном направлении за раз.
Он измеряется в радианах, и мы используем его, чтобы измерить, насколько быстро одна вещь вращается вокруг другой или просто вращается вокруг собственной оси. — Чем быстрее что-то вращается, тем выше его угловая скорость.Угловая скорость может быть положительной (против часовой стрелки) или отрицательной (по часовой стрелке).
Как найти угловую скорость?
Угловая скорость — это скорость изменения угла в единицу времени. Измеряя, на сколько градусов мы поворачиваем каждую секунду или радиан в секунду.
Угловая скорость вычисляется с помощью уравнения, которое объединяет длину окружности и радиус :.
Как преобразовать угловую скорость в линейную скорость?
Чтобы преобразовать угловую скорость в линейную, вам нужен радиус в футах, милях или метрах.
Как найти угловую скорость?
Чтобы найти угловую скорость в радианах в секунду, просто используйте формулу A = ωt и решите относительно t. Для этого подставьте числа в формулу:
A = (ωr) / (C)
В чем измеряется угловая скорость?
Угловая скорость измеряется в радианах в секунду.
Кинематика и динамика
Кинематика и динамикаКинематика и динамика
Если объект вращается вокруг фиксированной оси Z с постоянным угловым ускорение α, имеем Δω = αΔt,
ω f = ω i + α (t f — t i ).
Угловое смещение θ относительно оси z тогда равно
.θ f = θ i + ω i (t f — t i ) + ½α (t f — t i ) 2 .
Эти уравнения имеют ту же форму, что и уравнения линейного движения с постоянным ускорением a.
Для
движения по оси абсцисс имеем
v f = v i + a (t f — t i ),
x f — x i = v xi ∆t + ½a x (t f —
т и ) 2 .
Если мы заменим x на θ и a на α, то кинематическая уравнения для линейного движения по оси x преобразуются в кинематические уравнения для вращательного движения вокруг оси z.
Проблема:
Лайнер прибывает на аэровокзал, двигатели заглушены.
выключенный. Ротор одного из двигателей имеет начальный поворот по часовой стрелке.
угловая скорость 2000 рад / с. Вращение двигателей замедляется с
угловое ускорение величиной 80 рад / с 2 .
(a) Определите угловую скорость через 10 с.
(b) Сколько времени нужно ротору, чтобы остановиться?
Решение:
- Рассуждение:
В этой задаче начальная угловая скорость ω i и угловое ускорение α . Если выбираем направление начального углового ускорения чтобы быть направлением z, тогда
ω f = ω i — α (t f — t i ),
, поскольку α находится в отрицательном направлении оси z. - Детали расчетов
(a) При t = 0 ω i = 2000 / с.
При t = 10 с имеем ω f = 2000 / с — (80 / с 2 ) (10 с) = 1200 / с.
(б) Установка ω f = ω i — α (t f — t i ) = 0 мы можем найти время, за которое ротор придет отдыхать.
2000 / с — (80 / с 2 ) t = 0, t = (2000/80) с = 25 с — время, необходимое ротору для остановки.
Проблема:
Вращающемуся колесу требуется 3 с для вращения 37 оборотов.Его угловатый скорость в конце 3-х секундного интервала 98 рад / с. Что постоянное угловое ускорение колеса?
Решение:
- Рассуждение:
Дано: Δθ = θ f — θ i = 37 оборотов, Δt = 3 с, ω f = 98 рад / с.
С использованием θ f — θ i = ω i (t f — t i ) + ½α (t f — t i ) 2 и ω f = ω i + α (t f — t i ), у нас есть два уравнения, которые мы можем решить для двух неизвестных ω i и α. - Детали расчета:
Использование θ f = θ i + ω i (t f — t i ) + ½α (t f — t i ) 2 с θ i = 0, имеем 37 * 2π = ω i * (3 с) + ½α (3 с) 2 .
Использование ω f = ω i + α (t f — t i ) имеем 98 / s = ω i + α (3 s).
Решаем это уравнение относительно ω i ω i = 98 с — α (3 с), и вставить это в первое уравнение.
37 * 2π = (98 / с) (3 с) — α (3 с) 2 + ½α (3 с) 2 , 74π = 294 — α * (9 с 2 ) + α * (4,5 с 2 ),
(4,5 с 2 ) * α = 294 — 74π, α = 13,67 / с 2 — постоянный ускорение колеса.
Когда колесо вращается вокруг оси Z, каждая точка на колесе имеет одинаковый угол
скорость. Однако линейная скорость v точки P зависит от расстояния до нее.
от оси вращения.
Когда точка P испытывает угловое смещение 2π, то
его пройденное расстояние составляет 2πr.
Когда точка P проходит угловое смещение на π, то
его пройденное расстояние равно πr.
Когда точка P проходит угловое смещение на θ, то
его пройденное расстояние составляет θr.
В единицах угловой скорости ω скорость v точки P
следовательно, v = ωr, если r постоянно; v — тангенциальная скорость точки P.
Ссылка: Тангенциальная и угловая скорость (Youtube)
Касательное ускорение a точки P, движущейся по круговой траектории, приведено в
с точки зрения его углового ускорения на t = rα.
Радиальное или центростремительное ускорение равно r = v 2 / r =
Рю 2 .
Общее ускорение равно
a = (a t 2 + a r 2 ) ½ =
(r 2 α 2 + r 2 ω 4 ) ½ = r (α 2 + ω 4 ) ½ .
Проблема:
При замене колес легкового автомобиля на колеса большего диаметра показания спидометра поменять? Объяснять!
Решение:
- Рассуждение:
Датчик спидометра определяет угловую скорость колеса. При номинальном значении v = номинальном значении r ω на спидометре отображается правильная скорость, если шины имеют номинальный радиус. Если вы положите шины большего размера на вашем автомобиле, то ваша фактическая скорость v фактическая = r фактическая ω больше, чем отображаемая скорость v номинальная = r номинальная ω.
Проблема:
Автомобиль равномерно ускоряется из состояния покоя и достигает скорости 22 м / с в
9 с Если диаметр шины составляет 58 см, найдите
(a) число оборотов, которые шина делает во время этого движения, при условии, что нет
скольжение, и
(b) конечная скорость вращения шины в оборотах в секунду.
Решение:
- Рассуждение:
Дано равномерное ускорение автомобиля a = Δv / Δt. Мы можем использовать кинематические уравнения для линейного движения, чтобы найти расстояние, которое оно проходит в интервал времени Δt.
Разделив это расстояние на окружность шины, находим число революции сделано. Конечная угловая скорость определяется по формуле ω f . = v f / r шина . - Детали расчета:
(a) Ускорение автомобиля равно a = Δv / Δt = (22 м / с) / (9 с) = 2.44 м / с 2 .
Расстояние пройденный за 9 с равен d = ½ при 2 = (½ * 2,44 * 81) м = 99 м.
Окружность шины π * 0,58 м = 1,82 м.
Число оборотов колеса составляет 99 / 1,82 = 54,3.
(b) Конечная линейная скорость шины v = 22 м / с. Используя v = ωr, ω = v / r, конечная угловая скорость составляет ω = 75,9 / с. Число оборотов в секунду составляет ω / 2π = 12 / с.
Модуль 6: Вопрос 1
Кинематические уравнения движения с постоянным линейным ускорением и такой же вид имеют движения с постоянным угловым ускорением.Сравнивать движение с постоянной скоростью с движением с постоянной угловой скоростью.
Обсудите это со своими однокурсниками на дискуссионном форуме!
Что вызывает угловое ускорение?
Предположим, вы хотите изменить вращающийся угловая скорость колеса. Для увеличения угловой скорости вы вероятно, приложит силу к ободу, касательную к ободу, и в направление мгновенной скорости сечения обода к который вы применяете силу.
Если вы хотите уменьшить угловую скорость, вы измените направление силы.
Предположим, вы хотите войти в здание
с вращающейся дверью. У двери четыре панели, и вы нажимаете
на одном из них, перпендикулярном поверхности панели.
Скорость, с которой угловая скорость двери
изменения, т.е. угловое ускорение α ,
тем больше, чем дальше от оси вращения вы применяете
сила.
Угловое ускорение относительно точки является результатом крутящего момента относительно этой точки. А крутящий момент продукт рычага рычаг и сила, приложенная перпендикулярно плечу рычага. В рычаг или момент рычага — перпендикулярное расстояние от центра вращения, т.е. точка поворота к точке приложения силы.
Крутящий момент всегда определяется относительно точки поворота.
Чем больше крутящий момент, тем больше угловое ускорение. Ты сможешь получить больший крутящий момент, применяя большее усилие или используя более длинный рычаг. Пишем
крутящий момент = плечо рычага × сила,
τ = r × F .
Крутящий момент — вектор. это
векторное произведение или перекрестное произведение из r и F .Единицы крутящего момента в системе СИ — Нм.
Крутящий момент имеет величину и направление. Его направление задается линейка правая .
Пальцы правой руки должны указывать от оси вращение до точки приложения силы. Сверните их в направление F . Ваш большой палец указывает в сторону вектор крутящего момента.
Величина крутящего момента τ
равно τ =
rFsinθ, где θ — наименьшее
угол между направлениями векторов r и F .
Мы также можем написать τ
= r perp F =
rF perp , где r perp — составляющая
плечо рычага перпендикулярно F, или где F perp —
компонент F перпендикулярно плечу рычага.
Если сила F действует на объект, тогда крутящий момент, создаваемый этой силой, примерно точка поворота: τ = r × F , где r — вектор смещения от точки поворота к точке, где сила приложена.Если на объект действуют две или более сил, то чистый крутящий момент равен векторная сумма из крутящие моменты, создаваемые отдельными силами. (Для вращения вокруг одной оси, два момента могут указывать в одном направлении или в противоположных направлениях направления и, следовательно, может складывать или вычитать.)
Проблема:
На рисунке справа найдите сетку крутящий момент на колесе вокруг оси через центр, если a = 10 см и b = 25 см.
Решение:
- Рассуждение:
Пусть ось Z выходит из страницы. Используйте τ = rFsinθ для величины и правило правой руки для направления τ . - Детали расчета:
Тогда крутящий момент, создаваемый силой 10 Н, равен τ = — (10 Н * 0,25 м) к = — (2,5 Нм) к .
Крутящий момент, создаваемый силой 9 Н, равен τ = — (9 Н * 0.25 м) к = — (2,25 Нм) к .
Крутящий момент, создаваемый силой 12 Н, равен τ = (12 Н * 0,1 м) к = (1,2 Нм) к .
(Обратите внимание, что эта сила также перпендикулярно плечу рычага.)
Общий крутящий момент равен τ = — (3,55 Нм) к .
Второй закон Ньютона, когда применительно к вращательному движению утверждает, что крутящий момент равен произведение массы вращения или момент инерции I и угловое ускорение α .
крутящий момент = момент инерции × угловое ускорение
τ = I α
Момент инерции — это мера инерции вращения объекта. Это зависит от масса объекта, и как эта масса распределяется относительно оси вращение. Чем дальше основная масса от оси вращения, тем больше инерция вращения (момент инерции) объекта.
Момент инерции системы относительно оси вращение можно найти, умножив массу m i каждого частица в системе на квадрат ее перпендикулярного расстояния r i от оси вращения, и суммируя все эти произведения, I = ∑m i r i 2 .
Проблема:
Четыре частицы на рисунке справа связаны жесткими стержнями. Начало координат находится в центре прямоугольника.Рассчитайте момент инерции системы относительно оси z.
Решение:
- Рассуждение:
Момент инерции I = ∑m i r i 2 . Здесь r i — перпендикулярное расстояние частицы i от ось z. - Детали расчета:
Каждая частица — это расстояние r = (9 + 4) ½ м = (13) ½ м от ось вращения.
I = (3 кг + 2 кг + 4 кг + 2 кг) * 13 м 2 = 143 кг · м 2 .
Момент инерции объекта — это мера его сопротивления угловому ускорению. Из-за его инерции вращения вам необходим крутящий момент, чтобы изменить угловую скорость объект. Если на объект не действует крутящий момент, его угловая скорость не изменится. Если он изначально не крутится, он не запускается. Если он крутится с заданным угловая скорость, эта угловая скорость не изменится.И его угловая скорость, и ориентация его оси вращения останется прежней.
постоянная угловая скорость <--> без угловой ускорение <--> нет чистого крутящего момента
Когда на два объекта действует один и тот же крутящий момент, объект с большим моментом инерции имеет меньший угловой ускорение. Единицы момента инерции: единицы массы, умноженные на квадрат расстояния, например кгм 2 .
Представьте себе два колеса одинаковой массы.Одно из них — сплошное колесо с его масса равномерно распределена по всей конструкции, в то время как другая имеет большая часть массы сосредоточена у обода.
Колесо с массой около обода имеет больший момент инерция.
Момент инерции определяется относительно оси вращения.
Например, момент инерции кругового диска, вращающегося вокруг оси через свой центр, перпендикулярный плоскости диска, отличается от момент инерции диска, вращающегося вокруг оси через его центр в плоскости диска.
Ссылка: Список моментов инерции
Качели
Двое детей играют на качелях, раскачиваясь взад и вперед. Центр качели зафиксированы. Поступательного движения нет. Мы наблюдаем ротационные движение вокруг центра. Пока качели движутся, практически нет крутящий момент на качелях, и он вращается с постоянной угловой скоростью. Вес каждого ребенка умножает рычаг от центра до того места, где сидит ребенок создает крутящий момент, но два крутящих момента имеют одинаковую величину и точку в в противоположных направлениях и поэтому отменить.Если один ребенок тяжелее, он садится ближе к центру, чем более легкий ребенок. Это уменьшает плечо рычага. В таким образом, разные веса могут создавать вращающие моменты одинаковой величины.
Когда ступня одного ребенка ударяется об пол, пол отталкивается и производит крутящий момент, направленный противоположно угловой скорости. Этот крутящий момент уменьшит угловая скорость до нуля за короткий промежуток времени. Качели остановлены. Затем ребенок отталкивается, а земля отталкивается.Направление крутящий момент остается прежним. Крутящий момент вызывает угловое ускорение, в результате чего с угловой скоростью, противоположной первоначальному направлению. Качели достигает своей конечной угловой скорости, когда ребенок перестает толкать. Теперь он сохраняет при вращении с постоянной угловой скоростью, пока стопы другого ребенка не коснутся этаж.
Ссылка: Качели
10.1 Угловое ускорение | Texas Gateway
Задачи обучения
К концу этого раздела вы сможете делать следующее:
- Описать равномерное круговое движение
- Объясните неравномерное круговое движение
- Расчет углового ускорения объекта
- Обратите внимание на связь между линейным и угловым ускорением
Равномерное круговое движение и гравитация обсуждаются только равномерное круговое движение, то есть движение по кругу с постоянной скоростью и, следовательно, с постоянной угловой скоростью.Напомним, что угловая скорость ωω размером 12 {ω} {} была определена как скорость изменения во времени угла θθ размер 12 {θ} {}
10,1 ω = ΔθΔt, ω = ΔθΔt, размер 12 {ω = {{Δθ} на {Δt}} «,»} {}где θθ размер 12 {θ} {} — это угол поворота, как показано на рисунке 10.3. Взаимосвязь между угловой скоростью ωω размером 12 {ω} {} и линейной скоростью vv размером 12 {v} {} также была определена в разделе «Угол поворота и угловая скорость» как
10,2 v = rωv = rω размер 12 {v = rω} {}или
10,3 ω = vr, ω = vr, размер 12 {ω = {{v} over {r}}} {}, где rr размер 12 {r} {} — радиус кривизны, также видно на рисунке 10 .3. Согласно соглашению о знаках, направление против часовой стрелки считается положительным, а направление по часовой стрелке — отрицательным
.Рис. 10.3 На этом рисунке показано равномерное круговое движение и некоторые его определенные величины.
Угловая скорость непостоянна, когда фигуристка тянет на руках, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера замедляется до полной остановки при выключении. Во всех этих случаях имеет место угловое ускорение, при котором изменяется величина ωω 12 {ω} {}.Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение αα размером 12 {α} {} определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается как
10.4 α = ΔωΔt, α = ΔωΔt, размер 12 {α = {{Δω} над {Δt}} «,»} {}, где ΔωΔω размер 12 {Δω} {} — изменение угловой скорости, а ΔtΔt размер 12 { Δt} {} — изменение во времени. Единицы углового ускорения: рад / с / срад / с / с размер 12 {слева («рад / с» справа) «/ с»} {} или рад / с2рад / с2 размер 12 {«рад / с» rSup {размер 8 {2}}} {}.Если ωω размера 12 {ω} {} увеличивается, то αα размера 12 {α} {} положительно. Если ωω размер 12 {ω} {} уменьшается, то αα размер 12 {α} {} отрицательный.
Пример 10.1 Расчет углового ускорения и замедления велосипедного колеса
Предположим, что подросток кладет велосипед на спину и запускает вращение заднего колеса от состояния покоя до конечной угловой скорости 250 об / мин за 5 с. (a) Рассчитайте угловое ускорение в рад / с2рад / с2 размером 12 {«рад / с» rSup {size 8 {2}}} {}. (b) Если она сейчас нажмет на тормоз, вызывая угловое ускорение –87.3рад / с2–87,3рад / с2 размер 12 {«- 87» «». 3` «рад / с» rSup {размер 8 {2}}} {}, сколько времени нужно колесу, чтобы остановиться?
Стратегия для (а)
Угловое ускорение можно найти непосредственно из его определения в α = ΔωΔtα = ΔωΔt размер 12 {α = {{Δω} над {Δt}}} {}, потому что даны окончательная угловая скорость и время. Мы видим, что ΔωΔω размер 12 {Δω} {} составляет 250 об / мин, а ΔtΔt размер 12 {Δt} {} составляет 5 с.
Решение для (a)
Вводя известную информацию в определение углового ускорения, получаем
10.5 α = ΔωΔt = 250 об / мин 5,00 с. Α = ΔωΔt = 250 об / мин 5,00 с.alignl {stack { размер 12 {α = {{Δω} над {Δt}}} {} # размер 12 {{} = {{«250» «об / мин»} больше {5 «.» «00 с»}} «.»} {} }} {}Поскольку ΔωΔω размер 12 {Δω} {} выражается в оборотах в минуту (об / мин), и нам нужны стандартные единицы рад / с2рад / с2 размер 12 {«рад / с» rSup {размер 8 {2}} } {} для углового ускорения нам необходимо преобразовать ΔωΔω размер 12 {Δω} {} из об / мин в рад / с
10,6 Δω = 250обмин⋅2π радр1 мин60 сек = 26,2рад.Δω = 250обмин⋅2π радрев⋅1 мин60 сек = 26.2rads.alignl {stack { размер 12 {Δω = «250» {{«об.»} больше {«min»}} cdot {{2π «rad»} больше {«60» «.» «0 с»}}} {} # размер 12 {{} = «26» «.» 2 {{«рад»} больше {«s»}}} {} }} {}Вводя эту величину в выражение для αα размера 12 {α} {}, получаем
10,7 α = ΔωΔt = 26,2 рад / с 5,00 с = 5,24 рад / с 2. α = ΔωΔt = 26,2 рад / с 5,00 с = 5,24 рад / с2.alignl {stack { размер 12 {α = {{Δω} над {Δt}}} {} # размер 12 {{} = {{«26» «.» 2 рад / с} больше {5 «. «00» «s»}} «.» } {} # размер 12 {{} = 5 «.»» 24 «» рад / с «rSup {размер 8 {2}}} {} }} {}Стратегия для (b)
В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решая для ΔtΔt размер 12 {Δt} {}, что дает
10,8 Δt = Δωα.Δt = Δωα. размер 12 {Δt = {{Δω} больше {α}} «.»} {}Решение для (b)
Здесь угловая скорость уменьшается с 26,2 рад / с26.2 рад / с размер 12 {«26» «.» 2` «рад / с»} {} (250 об / мин) до нуля, так что ΔωΔω размер 12 {Δω} {} –26,2 рад / с –26,2 рад / с, и αα размер 12 {α} {} задан как –87,3рад / с2–87,3рад / с2 размер 12 {«- 87» «.» 3` рад / с rSup {размер 8 {2}}} {}. Таким образом,
10,9 Δt = –26,2 рад / с – 87,3рад / с2 = 0,300 с. Δt = –26,2 рад / с – 87,3рад / с2 = 0,300 с.alignl {stack { размер 12 {Δt = {{- «26» «.» 2` «рад / с»} больше {- «87» «.» 3` рад / с rSup {размер 8 {2}}}}} {} # = 0 «.» «300» «с» «. {} }} {}Обсуждение
Обратите внимание, что угловое ускорение, когда девушка вращает колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с.Когда она нажимает на тормоз, угловое ускорение велико и отрицательно. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит сильное замедление — изменение скорости велико за короткий промежуток времени.
Если бы велосипед в предыдущем примере был на колесах, а не перевернут, он сначала разогнался бы по земле, а затем остановился бы.Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорение. При круговом движении линейное ускорение составляет по касательной к окружности в интересующей точке, как показано на рисунке 10.4. Таким образом, линейное ускорение называется тангенциальным ускорением при размере 12 {a rSub {size 8 {t}}} {}.
Рис. 10.4 При круговом движении линейное ускорение aa размером 12 {a} {} возникает при изменении величины скорости: aa размером 12 {a} {} касается движения.В контексте кругового движения линейное ускорение также называется тангенциальным ускорением при размере 12 {a rSub {size 8 {t}}} {}.Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Из «Равномерного кругового движения и гравитации» мы знаем, что при круговом движении центростремительное ускорение, acac size 12 {a rSub {size 8 {t}}} {} относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 10.5. Таким образом, atat size 12 {a rSub {size 8 {t}}} {} и acac размер 12 {a rSub {размер 8 {t}}} {} перпендикулярны и независимы друг от друга. Тангенциальное ускорение atat size 12 {a rSub {size 8 {t}}} {} напрямую связано с угловым ускорением αα размер 12 {α} {} и связан с увеличением или уменьшением скорости, но не ее направлением.
Рис. 10.5 Центростремительное ускорение acac размера 12 {a rSub {size 8 {t}}} {} возникает при изменении направления скорости; он перпендикулярен круговому движению.Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.Теперь мы можем найти точную взаимосвязь между линейным ускорением при размере 12 {a rSub {size 8 {t}}} {} и угловым ускорением αα размером 12 {α} {}. Поскольку линейное ускорение пропорционально изменению величины скорости, оно определяется, как и в одномерной кинематике, равным
10,10 at = ΔvΔt.at = ΔvΔt. размер 12 {a rSub {size 8 {t}} = {{Δv} over {Δt}} «.»} {}Для кругового движения обратите внимание, что v = rωv = rω размер 12 {v = rω} {}, так что
10.11 при = ΔrωΔt.at = ΔrωΔt. размер 12 {a rSub {size 8 {t}} = {{Δ left (rω right)} over {Δt}} «.»} {}Радиус rr размер 12 {r} {} постоянен для кругового движения, и поэтому Δ (rω) = r (Δω) Δ (rω) = r (Δω) размер 12 {Δ \ (rω \) = r \ (Δω \)} {}. Таким образом,
10,12 при = rΔωΔt.at = rΔωΔt. размер 12 {a rSub {размер 8 {t}} = r {{Δω} над {Δt}} «.»} {}По определению α = ΔωΔtα = ΔωΔt размер 12 {α = {{Δω} над {Δt }}} {}. Таким образом,
10,13 at = rα, at = rα, размер 12 {a rSub {size 8 {t}} = rα} {}или
10,14 α = atr.α = atr.размер 12 {α = {{a rSub {size 8 {t}}} больше {r}}} {}Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное или тангенциальное ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение для данного углового ускорения αα размером 12 {α} {}.
Пример 10.2 Расчет углового ускорения колеса мотоцикла
Мощный мотоцикл может разогнаться от 0 до 30 м / с (около 108 км / ч) за 4,20 с. Каково угловое ускорение его колес радиусом 0,320 м? (См. Рисунок 10.6.)
Рис. 10.6. Линейное ускорение мотоцикла сопровождается угловым ускорением его колес.
Стратегия
Нам дана информация о линейных скоростях мотоцикла.Таким образом, мы можем найти его линейное ускорение при размере 12 {a rSub {size 8 {t}}} {}. Тогда выражение α = atrα = atr size 12 {a rSub {size 8 {t}} = rα, « « α = {{a rSub {size 8 {t}}} над {r}}} { } можно использовать для определения углового ускорения.
Решение
Линейное ускорение
10,15 при = ΔvΔt = 30,0 м / с 4,20 с = 7,14 м / с2. При = ΔvΔt = 30,0 м / с 4,20 с = 7,14 м / с2.alignl {stack { размер 12 {a rSub {размер 8 {t}} = {{Δv} over {Δt}}} {} # « « = {{«30» «.»0» м / с «} за {4». «» 20 с «}} {} # « « = 7 «.» «14» «м / с» rSup {размер 8 {2} «.»} {} }} {}Нам также известен радиус колес. Ввод значений для формата atat 12 {a rSub {size 8 {t}}} {} и размера rr 12 {r} {} в α = atrα = atr размер 12 {a rSub {size 8 {t}} = rα, « « α = {{a rSub {size 8 {t}}} над {r}}} {}, получаем
10,16 α = atr = 7,14 м / с 20,320 м = 22,3 рад / с 2. α = atr = 7,14 м / с 20,320 м = 22,3 рад / с2.alignl {stack { размер 12 {α = {{a rSub {size 8 {t}}} больше {r}}} {} # « `= {{7″.»» 14 «» м / с «rSup {размер 8 {2}}} больше {0». «» 320 м «}} {} # «» = «22» «.» «3 рад / с» rSup {размер 8 {2}} {} }} {}Обсуждение
Радианы безразмерны и присутствуют в любом соотношении между угловыми и линейными величинами.
До сих пор мы определили три величины вращения: θ, ωθ, размер ω 12 {θ, ω} {} и αα размер 12 {α} {}. Эти величины аналогичны трансляционным величинам x, vx, v размером 12 {x, v} {} и aa размером 12 {a} {}.В таблице 10.1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Вращательный | Трансляционный | Отношения |
|---|---|---|
| θθ размер 12 {θ} {} | xx размер 12 {x} {} | θ = xrθ = xr размер 12 {θ = {{x} над {r}}} {} |
| ωω размер 12 {ω} {} | vv размер 12 {v} {} | ω = vrω = vr размер 12 {ω = {{v} больше {r}}} {} |
| αα размер 12 {α} {} | aa размер 12 {a} {} | α = atrα = atr размер 12 {α = {{a rSub {size 8 {t}}} больше {r}}} {} |
Таблица 10.1 Вращательные и поступательные величины
Установление связей: домашний эксперимент
Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу прямо перед собой. Используя другую ногу, начните вращаться, отталкиваясь от земли. Прекратите толкать землю ногой, но позвольте стулу вращаться. От исходной точки, с которой вы начали, нарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков.Оцените величину этих величин.
Проверьте свое понимание
Угловое ускорение — это вектор, имеющий как величину, так и направление. Как обозначить его величину и направление? Проиллюстрируйте на примере.
Решение
Величина углового ускорения равна αα, размер 12 {α} {}, а ее наиболее распространенные единицы — рад / с2рад / с2, размер 12 {«рад / с» rSup {size 8 {2}}} {}. Направление углового ускорения вдоль фиксированной оси обозначается знаком «+» или «-», так же как направление линейного ускорения в одном измерении обозначается знаком «+» или «-».Например, представьте, что гимнастка делает сальто вперед. Ее момент количества движения был бы параллелен ковру слева от нее. Величина ее углового ускорения будет пропорциональна ее угловой скорости (скорости вращения) и ее моменту инерции относительно оси вращения.
Исследования PhET: революция божьей коровки
Присоединяйтесь к божьей коровке и исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение.Изучите, как круговое движение связано с положением, скоростью и ускорением жука x, y , используя векторы или графики.
10.1 Угловое ускорение — Физика колледжа: OpenStax
Сводка
- Опишите равномерное круговое движение.
- Объясните неравномерное круговое движение.
- Вычислить угловое ускорение объекта.
- Обратите внимание на связь между линейным и угловым ускорением.
Глава 6 Равномерное круговое движение и гравитация обсуждают только равномерное круговое движение, то есть движение по кругу с постоянной скоростью и, следовательно, с постоянной угловой скоростью.Напомним, что угловая скорость [латекс] \ boldsymbol {\ omega} [/ latex] была определена как временная скорость изменения угла [латекс] \ boldsymbol {\ theta}: [/ latex]
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ theta} {\ Delta {t}}}, [/ латекс]
где [latex] \ boldsymbol {\ theta} [/ latex] — это угол поворота, как показано на рисунке 1. Связь между угловой скоростью [латекс] \ boldsymbol {\ omega} [/ latex] и линейной скоростью [латекс] \ boldsymbol {v} [/ latex] также был определен в главе 6.1 Угол поворота и угловая скорость как
[латекс] \ boldsymbol {v = r \ omega} [/ латекс]
или
[латекс] \ boldsymbol {\ omega \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v} {r}}, [/ latex]
, где [latex] \ boldsymbol {r} [/ latex] — радиус кривизны, также видно на рисунке 1. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным.
Рис. 1. На этом рисунке показано равномерное круговое движение и некоторые его определенные величины.Угловая скорость непостоянна, когда фигуристка тянет на руках, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается, когда он выключен. Во всех этих случаях существует угловое ускорение , при котором изменяется [latex] \ boldsymbol {\ omega} [/ latex]. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение [латекс] \ boldsymbol {\ alpha} [/ latex] определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:
[латекс] \ boldsymbol {\ alpha \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ omega} {\ Delta {t}}}, [/ латекс]
, где [latex] \ boldsymbol {\ Delta \ omega} [/ latex] — это изменение угловой скорости, а [latex] \ boldsymbol {\ Delta {t}} [/ latex] — изменение во времени. 2}.2}, [/ latex] сколько времени нужно, чтобы колесо остановилось?
Стратегия для (а)
Угловое ускорение можно найти непосредственно из его определения в [latex] \ boldsymbol {\ alpha = \ frac {\ Delta \ omega} {\ Delta {t}}} [/ latex], поскольку даны окончательная угловая скорость и время . Мы видим, что [latex] \ boldsymbol {\ Delta \ omega} [/ latex] составляет 250 об / мин, а [latex] \ boldsymbol {\ Delta {t}} [/ latex] составляет 5,00 с.
Решение для (a)
Вводя известную информацию в определение углового ускорения, получаем
[латекс] \ begin {array} {lcl} \ boldsymbol {\ alpha} & \ boldsymbol {=} & \ boldsymbol {\ frac {\ Delta \ omega} {\ Delta {t}}} \\ {} & \ boldsymbol {=} & \ boldsymbol {\ frac {250 \ textbf {rpm}} {5.2} [/ latex] для углового ускорения нам нужно преобразовать [latex] \ boldsymbol {\ Delta \ omega} [/ latex] из об / мин в рад / с:
[латекс] \ begin {array} {lcl} \ boldsymbol {\ Delta \ omega} & \ boldsymbol {=} & \ boldsymbol {250 \ frac {\ textbf {rev}} {\ textbf {min}} \ cdotp \ frac {2 \ pi \ textbf {rad}} {\ textbf {rev}} \ cdotp \ frac {1 \ textbf {min}} {60 \ textbf {sec}}} \\ {} & \ boldsymbol {=} & \ boldsymbol {26.2 \ textbf {rads.}} \ end {array} [/ latex]
Вводя это количество в выражение для [latex] \ boldsymbol {\ alpha}, [/ latex], получаем
[латекс] \ begin {array} {lcl} \ boldsymbol {\ alpha} & \ boldsymbol {=} & \ boldsymbol {\ frac {\ Delta \ omega} {\ Delta {t}}} \\ {} & \ boldsymbol {=} & \ boldsymbol {\ frac {26.2} \ end {array} [/ latex]
Стратегия для (б)
В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решение для [latex] \ boldsymbol {\ Delta {t}}, [/ latex], что дает
[латекс] \ boldsymbol {\ Delta {t} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ omega} {\ alpha}}. [/ Латекс]
Решение для (b)
Здесь угловая скорость уменьшается от [latex] \ boldsymbol {26.2}} \\ {} & \ boldsymbol {=} & \ boldsymbol {0.300 \ textbf {s.}} \ End {array} [/ latex]
Обсуждение
Обратите внимание, что угловое ускорение, когда девушка вращает колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение велико и отрицательно. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит сильное замедление — изменение скорости велико за короткий промежуток времени.
Если бы велосипед в предыдущем примере был на колесах, а не перевернут, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорение. При круговом движении линейное ускорение составляет касательных к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется касательным ускорением [latex] \ boldsymbol {a _ {\ textbf {t}}}.[/ латекс]
Рис. 2. При круговом движении линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называется тангенциальным ускорением a t .Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Из главы 6 «Равномерное круговое движение и гравитация» мы знаем, что центростремительное ускорение при круговом движении [latex] \ boldsymbol {a _ {\ textbf {c}}}, [/ latex] относится к изменениям направления скорости, но не ее величине. .Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3. Таким образом, [latex] \ boldsymbol {a _ {\ textbf {t}}} [/ latex] и [latex] \ boldsymbol {a _ {\ textbf {c} }} [/ latex] перпендикулярны и независимы друг от друга. Касательное ускорение [латекс] \ boldsymbol {a _ {\ textbf {t}}} [/ latex] напрямую связано с угловым ускорением [latex] \ boldsymbol {\ alpha} [/ latex] и связано с увеличением или уменьшением скорость, но не ее направление.
Рис. 3. Центростремительное ускорение a c возникает при изменении направления скорости; он перпендикулярен круговому движению.Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.Теперь мы можем найти точную взаимосвязь между линейным ускорением [latex] \ boldsymbol {a _ {\ textbf {t}}} [/ latex] и угловым ускорением [latex] \ boldsymbol {\ alpha}. [/ Latex] Потому что линейное ускорение пропорциональна изменению величины скорости, она определена (как это было в главе 2 «Одномерная кинематика») равной
.[латекс] \ boldsymbol {a _ {\ textbf {t}} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta {v}} {\ Delta {t}}.} [/ латекс]
Для кругового движения обратите внимание, что [latex] \ boldsymbol {v = r \ omega}, [/ latex], так что
[латекс] \ boldsymbol {a _ {\ textbf {t}} \: =} [/ latex] [latex] \ boldsymbol {\ frac {\ Delta (r \ omega)} {\ Delta {t}}.} [ / латекс]
Радиус [латекс] \ boldsymbol {r} [/ latex] постоянен для кругового движения, поэтому [латекс] \ boldsymbol {\ Delta (r \ omega) = r (\ Delta \ omega)}. [/ Latex] Таким образом,
[латекс] \ boldsymbol {a _ {\ textbf {t}} = r} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ omega} {\ Delta {t}}.} [/ Латекс]
По определению [латекс] \ boldsymbol {\ alpha = \ frac {\ Delta \ omega} {\ Delta {t}}}.[/ latex] Таким образом,
[латекс] \ boldsymbol {a _ {\ textbf {t}} = r \ alpha}, [/ latex]
или
[латекс] \ boldsymbol {\ alpha \: =} [/ latex] [латекс] \ boldsymbol {\ frac {a _ {\ textbf {t}}} {r}.} [/ Latex]
Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля.Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение для данного углового ускорения [латекс] \ boldsymbol {\ alpha}. [/ Latex]
Пример 2: Расчет углового ускорения колеса мотоцикла
Мощный мотоцикл может разогнаться от 0 до 30,0 м / с (около 108 км / ч) за 4,20 с. Каково угловое ускорение его колес радиусом 0,320 м? (См. Рисунок 4.)
Рисунок 4 . Линейное ускорение мотоцикла сопровождается угловым ускорением его колес.Стратегия
Нам дана информация о линейных скоростях мотоцикла. Таким образом, мы можем найти его линейное ускорение [latex] \ boldsymbol {a _ {\ textbf {t}}}. [/ Latex] Тогда выражение [latex] \ boldsymbol {\ alpha = \ frac {a _ {\ textbf {t }}} {r}} [/ latex] можно использовать для определения углового ускорения.
Раствор
Линейное ускорение
[латекс] \ begin {array} {lcl} \ boldsymbol {a _ {\ textbf {t}}} & \ boldsymbol {=} & \ boldsymbol {\ frac {\ Delta {v}} {\ Delta {t}} } \\ {} & \ boldsymbol {=} & \ boldsymbol {\ frac {30.2.} \ end {array} [/ latex]
Мы также знаем радиус колес. Ввод значений для [latex] \ boldsymbol {a _ {\ textbf {t}}} [/ latex] и [latex] \ boldsymbol {r} [/ latex] в [latex] \ boldsymbol {\ alpha = \ frac {a_ {\ textbf {t}}} {r}}, [/ latex] получаем
[латекс] \ begin {array} {lcl} \ boldsymbol {\ alpha} & \ boldsymbol {=} & \ boldsymbol {\ frac {a _ {\ textbf {t}}} {r}} \\ {} & \ boldsymbol {=} & \ boldsymbol {\ frac {7.14 \ textbf {m / s}} {20.320 \ textbf {m}}} \\ {} & \ boldsymbol {=} & \ boldsymbol {22.2.} \ end {array} [/ latex]
Обсуждение
Радианы безразмерны и присутствуют в любом соотношении между угловыми и линейными величинами.
До сих пор мы определили три вращательные величины — [латекс] \ boldsymbol {\ theta, \: \ omega}, [/ latex] и [латекс] \ boldsymbol {\ alpha}. [/ Latex] Эти величины аналогичны трансляционные величины [латекс] \ boldsymbol {x}, \: \ boldsymbol {v}, [/ latex] и [latex] \ boldsymbol {a}. [/ latex] В таблице 1 показаны вращательные величины, аналогичные трансляционные величины и отношения между ними.
| Вращательный | Трансляционный | Отношения |
|---|---|---|
| [латекс] \ boldsymbol {\ theta} [/ латекс] | [латекс] \ boldsymbol {x} [/ латекс] | [латекс] \ boldsymbol {\ theta = \ frac {x} {r}} [/ латекс] |
| [латекс] \ boldsymbol {\ omega} [/ латекс] | [латекс] \ boldsymbol {v} [/ латекс] | [латекс] \ boldsymbol {\ omega = \ frac {v} {r}} [/ латекс] |
| [латекс] \ boldsymbol {\ alpha} [/ латекс] | [латекс] \ boldsymbol {a} [/ латекс] | [латекс] \ boldsymbol {\ alpha = \ frac {a _ {\ textbf {t}}} {r}} [/ latex] |
| Таблица 1. Вращательные и поступательные величины. | ||
УСТАНОВЛЕНИЕ ПОДКЛЮЧЕНИЙ: ЭКСПЕРИМЕНТ НА ДОМУ
Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу так, чтобы она была разогнута (выпрямлена). Используя другую ногу, начните вращаться, отталкиваясь от земли. Прекратите толкать землю ногой, но позвольте стулу вращаться. От исходной точки, с которой вы начали, нарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков.Оцените величину этих величин.
Проверьте свое понимание
1: Угловое ускорение — это вектор, имеющий как величину, так и направление. Как обозначить его величину и направление? Проиллюстрируйте на примере.
PHET EXPLORATIONS: LADYBUG REVOLUTION
Присоединяйтесь к божьей коровке и исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение.Изучите, как круговое движение соотносится с координатами x, y, скоростью и ускорением жука, используя векторы или графики.
Рисунок 5. Божья коровка Revolution- Равномерное круговое движение — это движение с постоянной угловой скоростью [латекс] \ boldsymbol {\ omega = \ frac {\ Delta \ theta} {\ Delta {t}}}. [/ Latex]
- При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. угловое ускорение) равна [latex] \ boldsymbol {\ alpha = \ frac {\ Delta \ omega} {\ Delta {t} }}.[/ латекс]
- Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, заданному как [latex] \ boldsymbol {a _ {\ textbf {t}} = \ frac {\ Delta {v}} {\ Delta {t} }}. [/ latex]
- Для кругового движения обратите внимание, что [latex] \ boldsymbol {v = r \ omega}, [/ latex] так, чтобы
[латекс] \ boldsymbol {a _ {\ textbf {t}} \: =} [/ latex] [latex] \ boldsymbol {\ frac {\ Delta (r \ omega)} {\ Delta {t}}}. [ / латекс]
- Радиус r постоянен для кругового движения, поэтому [латекс] \ boldsymbol {\ Delta (r \ omega) = r \ Delta \ omega}.[/ latex] Таким образом,
[латекс] \ boldsymbol {a _ {\ textbf {t}} = r} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ omega} {\ Delta {t}}}. [/ Latex]
- По определению [латекс] \ boldsymbol {\ Delta \ omega / \ Delta {t} = \ alpha}. [/ Latex] Таким образом,
[латекс] \ boldsymbol {a _ {\ textbf {t}} = r \ alpha} [/ latex]
или
[латекс] \ boldsymbol {\ alpha =} [/ latex] [латекс] \ boldsymbol {\ frac {a _ {\ textbf {t}}} {r}}. [/ Latex]
Концептуальные вопросы
1: Между вращательными и поступательными физическими величинами существуют аналогии.Определите вращательный член, аналогичный каждому из следующих: ускорение, сила, масса, работа, поступательная кинетическая энергия, линейный импульс, импульс.
2: Объясните, почему центростремительное ускорение изменяет направление скорости при круговом движении, но не ее величину.
3: При круговом движении тангенциальное ускорение может изменять величину скорости, но не ее направление. Поясните свой ответ.
4: Предположим, блюдо стоит на краю вращающейся пластины микроволновой печи.Испытывает ли она ненулевое тангенциальное ускорение, центростремительное ускорение или и то, и другое, когда: а) пластина начинает вращаться? (б) Пластина вращается с постоянной угловой скоростью? (c) Пластина замедляется до полной остановки?
Задачи и упражнения
1: На пике торнадо имеет диаметр 60,0 м и скорость ветра 500 км / ч. Какова его угловая скорость в оборотах в секунду?
2: Комплексные концепции
Ультрацентрифуга ускоряется от состояния покоя до 100 000 об / мин за 2 секунды.2} [/ latex] и кратные [latex] \ boldsymbol {g} [/ latex] этой точки на полных оборотах?
3: Комплексные концепции
У вас есть точильный камень (диск) весом 90,0 кг, радиусом 0,340 м и вращающимся со скоростью 90,0 об / мин, и вы прижимаете к нему стальной топор с радиальной силой 20,0 Н. 2}.[/ latex] Направление углового ускорения вдоль фиксированной оси обозначается знаком + или a -, так же как направление линейного ускорения в одном измерении обозначается знаком + или a -. Например, представьте, что гимнастка делает сальто вперед. Ее момент количества движения был бы параллелен ковру слева от нее. Величина ее углового ускорения будет пропорциональна ее угловой скорости (скорости вращения) и ее моменту инерции относительно оси вращения.
Задачи и упражнения
1:
[латекс] \ boldsymbol {\ omega = 0.2} [/ латекс]
(b) [латекс] \ boldsymbol {27 \ textbf {rev}} [/ латекс]
Honors Rotational Kinematics
Радианы и Градусы
Обычно люди обсуждают вращательное движение в градусах, где один полный оборот по окружности равен 360 °. Когда речь идет о вращательном движении с точки зрения физики, измерение вращательного движения в единицах, известных как радианы (рад), является гораздо более эффективным. Радиан измеряет расстояние вокруг дуги, равное длине радиуса дуги.
До этого момента вы описывали расстояния и смещения в терминах Δx и Δy. Обсуждая угловые смещения, вы должны перейти к описанию поступательного смещения вокруг дуги в терминах переменной s, продолжая использовать символ θ (тета) для обозначения углов и углового смещения.
Расстояние полностью по круговой траектории (360 °), известное как окружность, C, можно найти с помощью ∆s = C = 2𝜋r = 2𝜋 радиан.Следовательно, вы можете использовать это как коэффициент преобразования для перехода между градусами и радианами.
Вопрос: Преобразовать 90 ° в радианы.
Ответ:
Вопрос: Преобразовать 6 радианов в градусы.
Ответ:
Углы также измеряются в оборотах (полные обходы по кругу). Полный единичный оборот равен 360 °, поэтому вы можете записать коэффициенты преобразования для углов поворота и смещений как 360 ° = 2𝜋 радиан = 1 оборот.
Вопрос: Преобразуйте 1,5 оборота в радианы и градусы.
Ответ:
Скорость и ускорение
Вращательная кинематика очень похожа на поступательную кинематику, все, что вам нужно сделать, это изучить вращательные версии кинематических переменных и уравнений. Когда вы изучали кинематику перевода, смещение обсуждалось в терминах Δx.При вращательной кинематике вместо этого вы будете использовать угловую координату θ. Когда в трансляционном мире была введена средняя скорость, вы использовали формулу:
Изучая вращательное движение, вы будете говорить об угловой скорости ω (омега), выраженной в радианах в секунду (рад / с). Поскольку угловая (вращательная) скорость является вектором, определите положительное направление вращения как вращение против часовой стрелки по круговой траектории, а отрицательное направление как по часовой стрелке вокруг траектории.
ПРИМЕЧАНИЕ: Формально направление угловых векторов определяется правилом правой руки. Оберните пальцы правой руки в направлении вращения, скорости или ускорения, а большой палец будет указывать в направлении вектора.
Вопрос: Рекорд вращается на фонографе со скоростью 33 об / мин (оборотов в минуту) по часовой стрелке.Найдите угловую скорость записи.
Ответ:
Обратите внимание, что вектор угловой скорости отрицательный, потому что запись вращается по часовой стрелке.
Вопрос: Найдите величину угловой скорости Земли в радианах в секунду.
Ответ: Осознавая, что Земля совершает один полный оборот каждые 24 часа, мы можем оценить величину угловой скорости Земли как:
Аналогичным образом, когда вы узнали о поступательном ускорении, вы обнаружили ускорение как скорость изменения поступательной скорости объекта:
Угловое ускорение α (альфа), выраженное в радианах в секунду 2 , представляет собой скорость изменения угловой скорости объекта.Поскольку угловое ускорение также является вектором, вы можете определить его направление как положительное для увеличения угловой скорости в направлении против часовой стрелки и отрицательное для увеличения угловой скорости в направлении по часовой стрелке.
Вопрос: Лягушка едет на одноколесном велосипеде. Если колесо моноцикла начинается в состоянии покоя и равномерно ускоряется против часовой стрелки до угловой скорости 15 об / мин за 6 секунд, найдите угловое ускорение колеса моноцикла.
Ответ: Сначала преобразуйте 15 об / мин в рад / с.
Далее используйте определение углового ускорения.
Снова обратите внимание на положительное угловое ускорение, поскольку колесо велосипеда ускоряется против часовой стрелки.
Вращательные переменные
Объединяя эти определения, вы наблюдаете очень сильную параллель между поступательными кинематическими величинами и вращательными кинематическими величинами.
| Переменная | Трансляционный | Угловой |
|---|---|---|
| Рабочий объем | Δs | Δθ |
| Скорость | v | ω |
| Разгон | а | α |
| Время | т | т |
Также довольно просто выполнить перевод между поступательными и угловыми переменными, когда вы знаете радиус (r) интересующей точки на вращающемся объекте.
Вопрос: Рыцарь махает булавой радиусом 1 м за два полных оборота. Что такое поступательное смещение булавы?
Ответ:
Вопрос: Проигрыватель компакт-дисков предназначен для изменения скорости вращения диска, так что точка, считываемая лазером, перемещается с линейной скоростью, равной единице.25 м / с. Какова скорость вращения компакт-диска в оборотах / с, когда лазер считывает информацию с внутренней части диска на радиусе 0,03 м?
Ответ:
Вопрос: Какова скорость вращения компакт-диска в предыдущей задаче, когда лазер считывает крайнюю часть диска (радиус = 0,06 м)?
Ответ:
Уравнения вращательной кинематики
Параллели между поступательным и вращательным движением идут еще дальше.Вы разработали набор кинематических уравнений для поступательного движения, которые позволили вам исследовать взаимосвязь между смещением, скоростью и ускорением. Вы можете разработать соответствующий набор соотношений для углового смещения, угловой скорости и углового ускорения. Уравнения имеют ту же форму, что и трансляционные уравнения, все, что вам нужно сделать, это заменить трансляционные переменные на вращательные переменные, как показано в следующей таблице.
Уравнения вращательной кинематики можно использовать так же, как вы использовали уравнения поступательной кинематики для решения задач.Когда вы знаете три кинематические переменные, вы всегда можете использовать уравнения для решения двух других.
Вопрос: Плотник вырезает кусок дерева с помощью мощной циркулярной пилы. Пильный диск ускоряется из состояния покоя с угловым ускорением от 14 рад / с 2 до максимальной скорости 15 000 об / мин. Какова максимальная скорость пилы в радианах в секунду?
Ответ:
Вопрос: Сколько времени нужно пиле для достижения максимальной скорости?
Ответ: Для решения этой задачи можно использовать уравнения кинематики вращения:
Вопрос: Сколько полных оборотов делает пила при разгоне до максимальной скорости?
Ответ:
Вопрос: Предохранительный механизм остановит пильный диск в 0.3 секунды, если рука плотника оторвется от органов управления пилой. Какое угловое ускорение для этого требуется? Сколько полных оборотов пильное полотно сделает за это время?
Ответ: Начните с воссоздания таблицы кинематики вращения.
Сначала найдите угловое ускорение.
Затем найдите угловое смещение.
Наконец, преобразуйте угловое смещение в число оборотов.
Кафедра физики и астрономии
Основные исследования
Разработка наилучшего возможного солнечного элемента, МакГайверинг Немного квантового превосходства
Физики и материаловеды ЛГУ создают квантовый симулятор с золотым чип, чтобы открыть лучшие материалы для солнечных батарей.Идеальные материалы должны вводить Исследователи говорят, что какое-то количество хаоса, чтобы получить больше света.
Миссии астронома ЛГУ и НАСА раскрывают космические извержения в соседних галактиках
Короткая вспышка высокоэнергетического света пронеслась по Солнечной системе 15 апреля 2020 г. запускать космические инструменты, в том числе на борту НАСА и европейских миссий.Теперь несколько intl. научные группы пришли к выводу, что взрыв произошел от сверхмагниченной звездной остаток, известный как магнетар, расположенный в соседней галактике.
Отслеживание тенденций COVID-19 в наиболее пострадавших государствах
Исследователи LSU применили вычислительные модели для исследования инфекции COVID-19 ставки в отношении мер социального дистанцирования.Их статья, Эффект смягчения меры по распространению COVID-19 в наиболее пострадавших штатах США, опубликованные в PLOS ONE., Исследует изменение уровня заражения в результате усилий по смягчению последствий. и прогнозируют количество смертей и инфекций до сентября 2020 г. для некоторых из наиболее сильно затронутые состояния.
LIGO и Дева объявляют о новых открытиях в обновленном каталоге гравитационных волн
После нескольких месяцев тщательного анализа LIGO Scientific Collaboration и Компания Virgo Collaboration выпустила обновленный каталог обнаружений гравитационных волн.Каталог содержит 39 новых обнаруженных сигналов от столкновений черных дыр или нейтронных звезд. с 1 апреля по окт. 1 января 2019 г., что более чем в три раза увеличивает количество подтвержденных обнаружений.
Физики LSU разрабатывают и демонстрируют метод устранения давления квантового излучения Шум в детекторах гравитационных волн
Детекторы гравитационных волн открыли новое окно во Вселенную, измеряя рябь в пространстве-времени, вызванная столкновением черных дыр и нейтронных звезд, но в конечном итоге они ограничены квантовыми флуктуациями, вызванными отражением света от зеркал.LSU Ph.D. выпускник физики Джонатан Крайп, докторант, NIST, и его команда исследователей LSU провела новый эксперимент с учеными из Калифорнийского технологического института. и Thorlabs, чтобы изучить способ отменить это квантовое обратное действие и улучшить детектор. чувствительность.
12. ПРОКАТКА, МОМЕНТ И УГЛОВОЙ МОМЕНТ
12.КАТАНИЕ, МОМЕНТ И УГЛОВОЙ МОМЕНТРисунок 12.1. Вращательное движение колеса
Колесо, катящееся по поверхности, имеет как линейное, так и вращательное скорость. Предположим, угловая скорость колеса [омега]. В дается соответствующая линейная скорость любой точки на ободе колеса. по
где R — радиус колеса (см. рисунок 12.1). Когда колесо соприкасается с землей, его нижняя часть покоится по отношению к земля. Это означает, что помимо вращательного движения колесо совершает поступательное движение со скоростью, равной + v см (см. рисунок 12.2). Делаем вывод, что верх колеса движется вдвое быстрее центра, а нижняя часть колеса вообще не двигается.
Рисунок 12.2. Движение колеса складывается из вращательного и поступательного движение.
Альтернативный способ взглянуть на движение колеса — рассматривать его как чистое вращение (с той же угловой скоростью [омега]) вокруг мгновенного неподвижная ось через нижнюю часть колеса (точка P, рисунок 12.3).
Рисунок 12.3. Движение колеса вокруг оси через P.
Кинетическую энергию колеса, показанного на рисунке 12.3, можно легко вычислить. используя формулы, полученные в главе 11
где I P — инерция вращения вокруг оси через P, а [омега] — скорость вращения колеса.Вращательная инерция вокруг оси, проходящей через P, I P , связано с инерцией вращения вокруг оси, проходящей через центр масс, I см
Теперь кинетическую энергию колеса можно переписать как
.
где первый член — кинетическая энергия, связанная с вращением колеса вокруг оси, проходящей через его центр масс, а второй член равен связанный с поступательным движением колеса.
Пример задачи 12-1
На рис. 12.4 показан диск с массой M и инерцией вращения I на наклонном самолет. Масса выпущена с высоты h. Какова его конечная скорость при низ самолета?
Диск выходит из состояния покоя. Его общая механическая энергия в этот момент равна равна его потенциальной энергии
Когда диск достигает нижней части плоскости, весь его потенциал энергия преобразуется в кинетическую энергию.Кинетическая энергия диска будет состоят из вращательной и поступательной кинетической энергии:
Момент инерции диска равен
.
где R — радиус диска. Кинетическая энергия диска может теперь можно переписать как
Рисунок 12.4. Масса на наклонной плоскости.
Сохранение механической энергии означает, что E i = E f или
Это показывает, что скорость диска равна
.
Теперь рассмотрим два разных диска с одинаковой массой M, но разными. моменты инерции.В этом случае конечная кинетическая энергия может быть записана как
Для сохранения энергии теперь требуется
или
Делаем вывод, что в данном случае диск с наименьшим моментом инерция имеет наибольшую конечную скорость .
Рисунок 12.5. Проблема 13П.
Задача 15П
Небольшой твердый шарик массы m и радиуса r катится, не скользя по кольцевая дорожка, показанная на рисунке 12.5, вышедший из покоя где-то на прямом участке трассы. С какой минимальной высоты над нижней частью дорожки должен быть выпущен шарик, чтобы не уйти дорожка вверху петли.
Мрамор не покинет след наверху петли, если центростремительный сила превышает силу тяжести в этой точке:
или
Кинетическая энергия мрамора наверху состоит из вращательной энергии. и поступательная энергия
где мы предположили, что шарик катится по дорожке (нет скольжение).Момент инерции мрамора равен
.
Используя это выражение, получаем для кинетической энергии
Мрамор достигнет вершины, если
Общая механическая энергия мрамора в верхней части loop-the-loop равно
Начальная энергия мрамора — это всего лишь его потенциальная энергия на высота h
Сохранение энергии теперь означает, что
или
Пример задачи 12-2: йо-йо
Рисунок 12.6. Йо-йо.
На рис. 12.6 схематично изображено йо-йо. В чем его линейность ускорение?
На йо-йо действуют две силы: восходящая сила, равная натяжению. в шнуре и гравитационной силе. Ускорение системы зависит от этих двух сил:
Вращательное движение йо-йо определяется прилагаемым крутящим моментом. по натяжению T (момент силы тяжести равен нулю)
Ускорение вращения a связано с линейным ускорением а:
Теперь мы можем записать следующие уравнения для натяжения T
Теперь можно рассчитать линейное ускорение a
Таким образом, йо-йо скатывается по струне с постоянным ускорением.Ускорение можно уменьшить, увеличив инерцию вращения и за счет уменьшения радиуса оси.
Рисунок 12.7. Движение частицы P в плоскости x-y.
Частица с массой m движется в плоскости x-y (см. Рисунок 12.7). А единственная сила F действует на частицу, и угол между силой и вектор положения равен [фи]. По определению, крутящий момент, прилагаемый этой силой к масса относительно начала нашей системы координат равна
и
где r [invtee] называется плечом силы F относительно происхождения.Согласно определению векторного произведения, вектор [tau] лежит параллельно оси z, а его направление (вверх или вниз) можно определить с помощью правила правой руки. Определенный таким образом крутящий момент имеет значение только по отношению к указанному происхождению. Направление крутящий момент всегда находится под прямым углом к плоскости, образованной векторами r и F. Крутящий момент равен нулю, если r = 0 м, F = 0 Н или r параллельно или антипараллельно относительно F.
Угловой момент L частицы P на рисунке 12.7, относительно происхождение, определяется как
Из этого определения следует, что если частица движется прямо прочь от начала координат или прямо к нему, угловой момент, связанный с это движение равно нулю. Частица будет иметь другой угловой момент, если origin выбирается в другом месте. Частица, движущаяся по кругу, будет имеют угловой момент (относительно центра окружности), равный
Мы снова замечаем сходство между определением линейного импульс и определение момента количества движения.
Частица может иметь угловой момент, даже если она не движется в круг. Например, на рисунке 12.8 показано расположение и направление импульс частицы P. Момент импульса частицы P относительно происхождение задается как
Рисунок 12.8. Угловой момент частицы P.
Изменение углового момента частицы может быть получено следующим образом: дифференцируя уравнение для l по времени
Делаем вывод, что
Это уравнение показывает, что , если чистый крутящий момент, действующий на частицу, равен нуля, его угловой момент будет постоянным .
Пример задачи 12-3
На рисунке 12.9 показан объект P в свободном падении. Объект стартует с покоя на положение, указанное на рисунке 12.9. Каков его момент количества движения относительно к происхождению, как функция времени?
Скорость объекта P как функция времени определяется выражением
.
Момент импульса объекта P равен
.
Следовательно,
который равен моменту силы тяжести по отношению к Происхождение.
Рисунок 12.9. Свободное падение и угловой момент
Рисунок 12.10. Пара действие — реакция.
Если мы посмотрим на систему частиц, полный угловой момент L система представляет собой векторную сумму угловых моментов каждого из отдельных частицы:
Изменение полного углового момента L связано с изменением угловой момент отдельных частиц
Некоторые моменты являются внутренними, некоторые — внешними.внутренний крутящие моменты идут парами, и их векторная сумма равна нулю. Это проиллюстрировано на Рисунке 12.10. На рисунке 12.10 показаны частицы A и B, которые взаимодействуют через центральную силу. Третий закон Ньютона гласит, что силы входят в пары: если B прикладывает силу F AB к A, то A будет прикладывать силу F BA на B. F AB и F BA связаны как следует
Крутящий момент, создаваемый каждой из этих сил относительно начала координат, легко рассчитывается
и
Ясно, что эти два момента в сумме дают ноль
Чистый крутящий момент для каждой пары действие-противодействие по отношению к происхождение, равно нулю.
Делаем вывод, что
Это уравнение — еще один способ выразить второй закон Ньютона. в угловых величинах.
Предположим, мы имеем дело с твердым телом, вращающимся вокруг оси z. В импульс каждого массового элемента параллелен плоскости x-y, и перпендикулярно вектору положения. Величина углового момента этот элемент массы
Компонента z этого углового момента равна
.
Z-компонента полного углового момента L твердого тела может можно получить суммированием по всем элементам массы в теле
Из определения инерции вращения твердого тела мы можем сделать вывод, что
Это проекция полного углового момента на вращение ось.Вращательная инерция I в этом уравнении также должна быть рассчитана с помощью относительно той же оси вращения. Только если ось вращения симметрична оси твердого тела будет ли вектор полного момента импульса совпадать с ось вращения.
Если никакие внешние силы не действуют на систему частиц или если внешний крутящий момент равен нулю, полный угловой момент системы сохраняется. В угловой момент остается постоянным, независимо от того, какие изменения происходят в система.
Задача 54E
Инерция вращения коллапсирующей вращающейся звезды изменяется до одной трети от его начальное значение. Каково отношение новой кинетической энергии вращения к начальная кинетическая энергия вращения?
Конечная инерция вращения I f связана с начальной инерция вращения I i следующим образом
На систему не действуют никакие внешние силы, а полный угловой момент равен законсервировано
Начальная кинетическая энергия вращения равна
.
Конечная кинетическая энергия вращения определяется как
.
Рисунок 12.11. Задача 61П.
Задача 61П
Таракан с массой m бегает против часовой стрелки по ободку ленивого Susan (круглая тарелка, установленная на вертикальной оси) радиуса R и вращательного инерция I с подшипниками качения. Скорость таракана (относительно земля) равна v, тогда как ленивая Сьюзен вращается по часовой стрелке с угловой скоростью [омега] 0 . Таракан находит на ободке хлебную крошку и конечно, останавливается.а) Какова угловая скорость ленивой Сьюзен после таракан останавливается? (б) Сохраняется ли механическая энергия?
Предположим, что ленивая Сьюзен расположена в плоскости x-y (см. Рис. 12.11). Инерционный момент таракана составляет м. v. Угловой момент таракана, относительно происхождения, дается по номеру
Направление момента количества движения можно найти, используя правую правило.Направление оси z выбрано таким, чтобы угловой момент таракан совпадает с положительной осью z. Ленивая Сьюзен движется по часовой стрелке (см. рисунок 12.11), а его угловой момент указывает вдоль отрицательная ось z. Его угловой момент равен
.
где I — инерция вращения тарелки. Обратите внимание, что поскольку вращение по часовой стрелке, [omega] 0 меньше нуля. Общая угловой момент системы равен
Инерция вращения тарелки плюс таракан равна
.
Поскольку внешний крутящий момент, действующий на систему, равен нулю, общий угловой момент сохраняется.Скорость вращения системы после остановки тараканов предоставляется по номеру
Начальная кинетическая энергия системы равна
Конечная кинетическая энергия системы равна
Изменение кинетической энергии системы
Изменение кинетической энергии системы отрицательное, и мы сделать вывод, что механическая энергия не сохраняется.Утрата механического энергия возникает из-за работы, совершаемой силой трения между поверхностью ленивая Сьюзен и ноги таракана.
Рисунок 12.12. Прецессирующая вершина.
Волчок, установленный на вращение, будет медленно вращаться вокруг вертикальной оси. Это движение называется прецессией. Для любой точки на оси вращения вверху вектор положения параллелен вектору углового момента.
Вес верха создает внешний крутящий момент относительно начала координат ( система координат определяется так, чтобы начало координат совпало с контактом точка верха на полу, см. рисунок 12.12). Величина этого крутящего момента это
Направление крутящего момента перпендикулярно вектору положения и к силе. Это также означает, что крутящий момент перпендикулярен угловой момент волчка. Внешний крутящий момент вызывает изменение угловой момент системы
Это уравнение показывает, что изменение углового момента dL, которое происходит за время, когда dt должен указывать в том же направлении, что и вектор крутящего момента.Поскольку крутящий момент находится под прямым углом к L, он не может изменить величину L, но он может изменить свое направление. В результате получается поворот угловой вектор импульса вокруг оси z. Угол прецессии d [фи] связан с изменение момента количества движения системы:
Это показывает, что скорость прецессии равна
Это уравнение показывает, что чем быстрее волчок вращается, тем медленнее он вращается. прецессы.Кроме того, прецессия равна нулю, если g = 0 м / с 2 и прецессия не зависит от угла [тета].
Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса. .
