Закон изменения угловой скорости – —
Вращательное движение тела. Закон вращательного движения :: SYL.ru
В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».
Основные понятия кинематики вращательного движения
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.
Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.
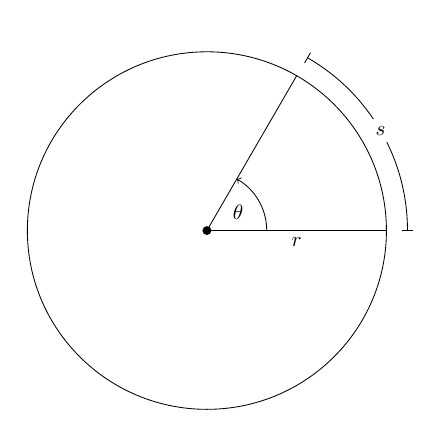
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.
За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:
φ = φ(t).
Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:
ΔS = Δφr.
Основные элементы кинематики равномерного вращательного движения
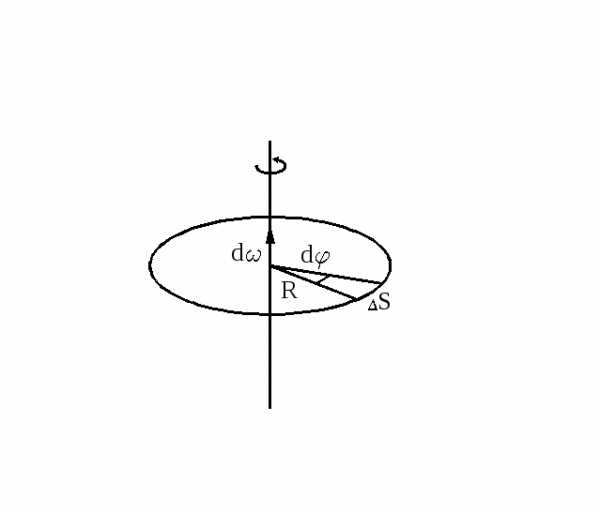
Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.
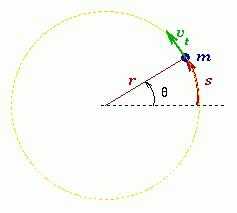
Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:
ω = dφ/dt.
Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле
ω = φ/t.
Согласно предварительной формуле размерность угловой скорости
[ω] = 1 рад/с.
Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то
ω = 2π/T,
поэтому период вращения определим следующим образом:
T = 2π/ω.
Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:
ν = 1/T.
Единицы измерения частоты: [ν]= 1/c = 1 c-1 = 1 Гц.
Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:
ω = 2πν.
Основные элементы кинематики неравномерного вращательного движения
Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.
Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:
ε = dω/dt.
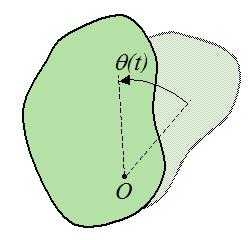
Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.
Если вращательное движение замедлено — dω/dt < 0, то векторы ε и ω противоположно направлены.
Замечание. Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).
Связь величин, характеризующих поступательное и вращательное движение
Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением
ΔS = Δφ r.
Тогда линейная скорость материальной точки, выполняющей вращательное движение
υ = ΔS/Δt = Δφr/Δt = ωr.
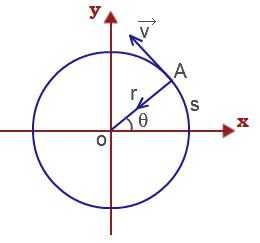
Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:
a = υ2/r = ω2r2/r.
Итак, в скалярном виде
a = ω2r.
Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение
a = ε r.
Момент импульса материальной точки
Векторное произведение радиуса-вектора траектории материальной точки массой mi на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.
Момент импульса материальной точки (Li) направлен перпендикулярно плоскости, проведенной через ri и υi, и образует с ними правую тройку векторов (то есть при движении с конца вектора riк υi правый винт покажет направление вектора Li).
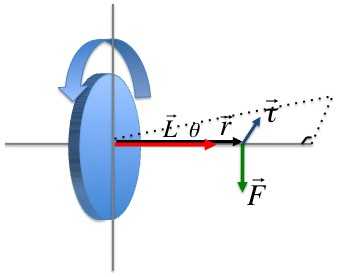
В скалярной форме
L = miυirisin(υi,ri).
Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,
sin(υi,ri) = 1.
Так что момент импульса материальной точки для вращательного движения примет вид
L = miυiri.
Момент силы, которая действует на i-ю материальную точку
Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.
В скалярной форме
Mi = riFisin(ri, Fi).
Считая, что risinα = li, Mi = liFi.
Величина li, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы Fi.
Динамика вращательного движения
Уравнение динамики вращательного движения записывается так:
M = dL/dt.
Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.
Момент импульса и момент инерции
Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой
Li = miυiri.
Если вместо линейной скорости подставить ее выражение через угловую:
υi = ωri,
то выражение для момента импульса примет вид
Li = miri2ω.
Величина Ii = miri2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:
Li = Iiω.
Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:
L = Iω.
Момент силы и момент инерции
Закон вращательного движения гласит:
M = dL/dt.
Известно, что представить момент импульса тела можно через момент инерции:
L = Iω.
Тогда
M = Idω/dt.
Учитывая, что угловое ускорение определяется выражением
ε = dω/dt,
получим формулу для момента силы, представленного через момент инерции:
M = Iε.
Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.
Теорема Штейнера. Закон сложения моментов инерции
Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I0 + ma2,
где I0 — начальный момент инерции тела; m — масса тела; a — расстояние между осями.
Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).
www.syl.ru
Определение закона изменения угловой скорости платформы
Задание для контрольной работы по теоретической механике (динамика Д3) | |
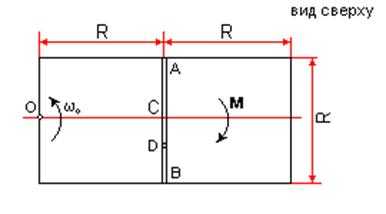
| a. Однородная горизонтальная платформа (прямоугольная плита со сторонами 2R и R, R=0.5м) имеющая массу m1=16 кг, жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угловой скоростью w0=2 с-1. В момент времени t0=0 на вал начинает действовать вращающий момент М=6t, направленный противоположно w0; одновременно груз D массой m2=10 кг, находящийся в желобе AB в точке С, начинает двигаться по желобу под действием внутренних сил по закону s=CD=0.4t2. Определить закон изменения угловой скорости платформы w=f(t). |
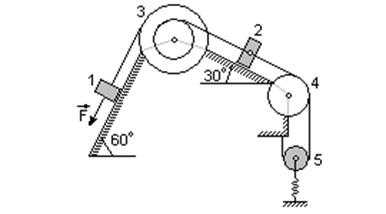
| b. Механическая система состоит из грузов 1 и 2 (m1=0кг, m2=6кг), ступенчатого шкива 3 (m3=4кг) с радиусами ступеней R3=03.м и r3=0.1м и радиусом инерции относительно оси вращения r3=0.2м, блока 4 (m4=0) радиуса R4, подвижного блока 5 (m5=5кг). Тело 5 считать сплошным однородным цилиндром. Коэффициент трения грузов о плоскость f=0.1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. К одному из тел прикреплена пружина с коэффициентом жесткости c=200 Н/м, ее начальная деформация равна нулю. Система приводится в движение из состояния покоя под действием силы F=80(4+5s) Н, зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М=1.2 Н*м сил сопротивления. Определить w 3 в тот момент времени, когда s=0.2 м. |
Решение задачи a
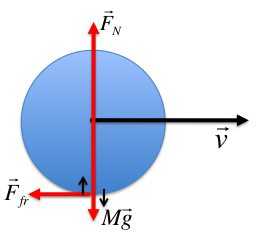
Рассмотрим механическую систему, состоящую из платформы и груза D. Для определения w применим теорему об изменении кинетического момента системы относительтно оси z :
| На систему действуют внешние силы Р1, Р2 (вес платформы и груза), реакции в оси и момент М. Все силы параллельны или пересекают ось z, поэтому в сумму моментов в правой части теоремы они не войдут, так как их моменты относительно оси z равны нулю. Тогда, считая положительным направление w0 против хода часовой стрелки, запишем теорему в виде: |
Разделяя переменные и интегрируя это уравнение, получим
(*)
Для рассматриваемой механической системы
(**)
где Lzпл и LzD – кинетические моменты платформы и груза относительно оси z соответственно
Так как платформа вращается вокруг оси z, то . Значение найдем по теореме Гюйгенса:
где — момент инерции относительно оси z:’, параллельной оси z и проходящей через центр С платформы.
Но, как известно, . Тогда и, следовательно,
.
Для определения обратимся к рисунку и рассмотрим движение груза D как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси z переносным движением. Тогда абсолютна скорость груза . Так как груз D движется по закону s=CD=0.4t 2, то . Изображаем вектор с учетом знака ds/dt (при ds/dt<0 направление этого вектора было бы противоположным). Затем, учитывая направление w, изображаем вектор , численно vпер=w OD. Тогда, по теореме Вариньона
.
Но из рисунка видно, что OD2=R2+s2=R2+0.16t4. Подставляя эту величину в выражение для кинетического момента груза D, а затем значения кинетических моментов груза и платформы в равенство (**), получим с учетом данных задачи
Тогда уравнение (*) примет вид
(***)
Постоянную интегрирования С1 определяем по начальным условиям: при t=0 w=w0. Получим С1=8.17w0=16.34. При этом значении С1 из уравнения (***) находим искомую зависимость w от t:
, где t — в секундах, w — в с-1.
Решение задачи
Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 2,3,5 и невесомых тел 1,4, соединенных нитями.
| 1. Изобразим действующие на систему силы: активные F, Fупр, Р3, Р2, Р5, реакции N2, N3, натяжение нити S5, силу трения F2тр и момент М. Для определения угловой скорости вращения шкива 3 воспользуемся теоремой об изменении кинетической энергии: 2. Определяем кинетическую энергию системы Т0 и Т. Так как в начальный момент система находилась в покое, то Т0=0. |
Величина Т равна сумме энергий всех тел системы, имеющих массу:
Т=Т3+ Т2+ Т5
Учитывая, что тело 3 вращается вокруг неподвижной оси, тело 2 движется поступательно, а подвижный блок 5 – плоскопараллельно, получим:
(*)
Все входящие сюда скорости нужно выразить через искомую w3. Для этого предварительно заметим, что v5 (скорость центра подвижного блока 5) и w5 (угловая скорость вращения блока 5) связаны соотношением w5r5=v5, где r5— радиус блока 5. Из кинематики также знаем, что v5=v2 / 2 и v2=w3r3. Кроме того, входящие в (*) моменты инерции имеют значения
Подставляя все выражения для скоростей и моментов инерции в (*) получим окончательно выражение для кинетической энергии системы
3. Теперь найдем сумму работ всех действующих внешних сил
при перемещении, которое будет иметь система, когда точка приложения силы
; ; ;
; ;
Работы остальных сил равны нулю, так как сила Р3 и реакция N3 приложены к неподвижной оси шкива 3, реация N2 перпендикулярна перемещению груза 2, а сила натяжения нити S5 – приложена к мгновенному центру скоростей подвижного блока 5.
По условию задачи l0=0 (начальная деформация пружины равна нулю), тогда l1=s5 (удлинение пружины равно перемещению центра подвижного блока 5). Кроме того, перемещение s точки приложения силы F связано с углом поворота шкива 3 соотношением j3R3=s (то есть j 3=s/R3). Величины s2 и s5 нужно также выразить через заданное перемещение s. При этом учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Так как, например, v2=w3r3, то и s2=j3r3; v5=v2 / 2, то и s5=s2 / 2. Тогда для перемещений s2 и s5 будем иметь: s2=(r3/R3)s, s5=(r3/2R3)s. При найденных значениях j3, s2 и s5 для суммы вычисленных работ получим
Подставляя полученные выражения для работы и кинетической энергии системы в теорему об изменении кинетической энергии будем иметь:
и, подставляя в это равенство численные значения заданных величин, найдем искомую угловую скорость:
vunivere.ru
Вопрос 2. Кинематика вращательного движения. Угловая скорость, угловое ускорение. Связь линейных и угловых величин. Псевдовекторы.
Вопрос 1. Механическое движение. Система отсчёта. Путь, перемещение, траектория. Расчёт пути при равноускоренном движении. Кинематика поступательного движения. Скорость мгновенная, средняя. Модуль скорости. Ускорение и его составляющие.
Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.
Механика Галилея-Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения тел со скоростями, сравнимыми со скоростью света, изучаются релятивистской механикой.
Движение тел происходит в пространстве и во времени. Положение материальной точки определяется по отношению к какому-либо другому телу, называемому телом отсчёта. С ним связана система отсчета – совокупность системы координат и часов, связанных с телом отсчета.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Длина участка АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути и является скалярной функцией времени: . Вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени называется перемещением.
Равноускоренное движение – движение точки с постоянным ускорением. Ускорение – величина, характеризующая быстроту изменения скорости. В равноускоренном движении . Формула расчета скорости при равноускоренном движении в момент времени:
Проинтегрируем эту формулу: — путь при равноускоренном движении.
Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. При поступательном движении все точки тела движутся одинаково, поэтому достаточно изучить движение одной какой-то произвольной точки тела (например, движение центра масс тела). Так же при поступательном движении тело не изменяет ни своего вида, ни строения, одновременные скорости всех точек равны и сонаправлены.
Мгновенная скорость (скорость) — предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при стремлении длительности промежутка времени к нулю. Модуль мгновенной скорости равен первой производной пути по времени.
Средняя скорость (средняя путевая скорость) – отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной. Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.
В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.
Ускорение – величина, характеризующая быстроту изменения скорости по величине и направлению. Ускорение – векторная величина, состоит из двух составляющих – тангенциальной составляющей и нормальной.
Тангенциальная составляющая характеризует изменение скорости по величине и направлена по направлению вектора скорости (если движение равноускоренное) или противоположно вектору скорости (равнозамедленное движение), равна:
Вторая составляющая ускорения называется нормальной и направлена по нормали к траектории к центру ее кривизны (центростремительное ускорение):
При вращательном движении точки тела описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением.
Если точка движется по окружности радиусом R, то через её положение можно задать углом поворота — элементарный угол поворота. Угол поворота – координата точки при вращательном движении; векторная величина, модуль которой равен углу поворота, а направление этого вектора связано с направлением вращения (по правилу правого винта). Сам вектор находится на оси вращения.
Угловая скорость — векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первой производной от угла поворота по времени. Направлен так же, как и вектор.
Если угловая скорость остается постоянной, то вращение будет равномерное, и оно характеризуется периодом вращения (время полного оборота на угол ).
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени.
Векторы, направления которых связаны с направлением вращения, называются псевдовекторами.
Связь линейных и угловых величин:
Вопрос3. Масса, свойство массы. Сила. Инерция. Первый закон Ньютона.
Динамика изучает движение тел, вскрывая причины, придающие движению тел тот или иной характер. Основы динамики составляют 3 закона Ньютона, которые представляют собой обобщение большого числа экспериментальных фактов.
Сила — векторная величина, которая является мерой механического воздействия одного тела на другое.
Вектор силы полностью задаётся точкой приложения, направлением, модулем (величиной).
Направление вектора силы совпадает с направлением ускорения сообщаемого телу данным воздействием. Под действием силы тела либо деформируются, либо изменяют скорость.
Инерция – свойство тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.
Из этого закона следует:
— Тела обладают свойствами инертности (свойство состоит в стремлении тел сохранить состояние покоя или равномерного прямолинейного движение).
— Система отсчета, в которой материальная точка, свободная от внешних воздействий либо покоится, либо движется равномерно и прямолинейно, называется инерциальной системой отсчета.
Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.
□ Если рассматривать действие различных сил на одно и то же тело, то оказывается, что ускорение прямо пропорционально равнодействующей приложенных сил: и . Можем записать, что. Это соотношение выражает второй закон Ньютона. ■
Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В СИ коэффициент k=1.
Векторная величина, равная произведению массы тела на его скорость и имеющая направление скорости, называется импульсом:
Выражение — второй закон Ньютона в общем виде: скорость изменения импульса материальной точки равна действующей на неё силе.
Принцип независимости сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, как если бы других сил не было вообще.
Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют тела друг на друга, всегда равны по модулю и противоположно направлены, действуют вдоль прямой, соединяющей эти точки.
В любой системе тел, силы действуют попарно и являются силами одной природы.
Таким образом, –закон сохранения импульса: импульс замкнутой системы сохраняется, то есть не изменяется с течением времени. Закон сохранения импульса выполняется не только в классической физике. Закон носит универсальный характер и является фундаментальным законом природы.
В классической механике из-за независимости массы от скорости импульс системы может быть выражен через скорость её центра масс. Центром масс системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Её радиус-вектор равен:
Если мы найдём производную от радиус-вектора, то мы найдём скорость, с которой движется центр масс. .
Центр масс системы движется так, как двигалась бы материальная точка с массой равной сумме масс системы тел под действием результирующей внешних сил. Для замкнутой системы сумма внешних сил равна 0, поэтому центр масс замкнутой системы движется равномерно и прямолинейно.
Вопрос 4. Динамика вращательного движения. Момент силы, момент импульса точки, твердого тела относительно оси вращения. Основной закон динамики вращательного движения. Понятие момента инерции точки, тв.тела относительно оси вращ-я.
Основное уравнение динамики вращательного движения:
Производная по времени от момента количества движения механической системы относительно неподвижной точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе: dL/dt=M.
Пример: Вращение системы вокруг неподвижной оси Oz: LX=LY=0, LZ=JZ, где –угловая скорость, JZ -момент инерции системы относительно оси Oz. Уравнение движения: (d/dt)(JZ)=MZ. Если система является абсолютно твёрдым телом, то JZ (d/dt)=MZ.
Момент импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
Модуль вектора момента импульса:
Моментом импульса материальной точки относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса , не зависит от положения точки О на осиz.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точки тела движется по окружности постоянного радиуса с некоторой скоростью . Скоростьи импульсперпендикулярны этому радиусу, то есть радиус является плечом вектора. Поэтому можем записать, что момент импульса отдельной частицы равени направлен по оси в сторону, определяемую правильном правого винта.
Момент инерции является мерой инертности при вращательном движении. Момент инерции материальной точки относительно оси – это произведение массы этой точки на квадрат расстояния до оси Z.
Моментом инерции тела относительно оси, проходящей через центр масс, называется сумма произведений масс материальных точек на квадрат расстояния их до оси вращения.
Если масса распределена неправильным образом, то тогда определить момент инерции в этом случае можно переходя к интегрированию.
Момент инерции — это величина аддитивная. Момент инерции системы материальных точек равен сумме моментов инерций этих точек, рассчитанных относительно одной и той же оси.
Момент инерции зависит от формы и размеров тела, от материалов, из которых сделано тело, а также от расположения тела относительно оси.
studfiles.net
Угловое ускорение тела
Пусть теперь известен закон изменения угловой скорости
и в момент времени  угловая скорость тела равна
угловая скорость тела равна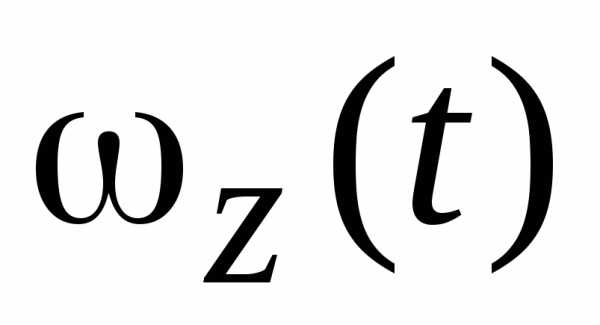 ,
а в момент времени
,
а в момент времени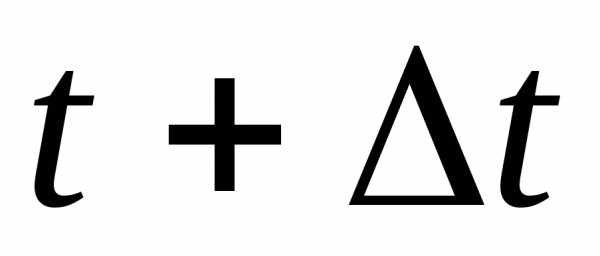 — .
— .
Тогда
— приращение угловой
скорости за время .
.
Средним угловым
ускорением тела за промежуток времени  называется отношение приращения угловой
скорости к промежутку времени, за который
это изменение произошло, т.е.
называется отношение приращения угловой
скорости к промежутку времени, за который
это изменение произошло, т.е.
 .
.
Алгебраическим угловым ускорением тела в данный момент времени называется предел отношения приращения угловой скорости к промежутку времени, за которое это приращение произошло, при стремлении последнего к нулю.
. (7.3)
Таким образом, алгебраическое угловое ускорение тела в данный момент времени равно первой производной по времени от алгебраической угловой скорости или второй производной от угла поворота
 .
(7.4)
.
(7.4)
Угловое ускорение тела характеризует быстроту изменения угловой скорости тела с течением времени.
Если знаки 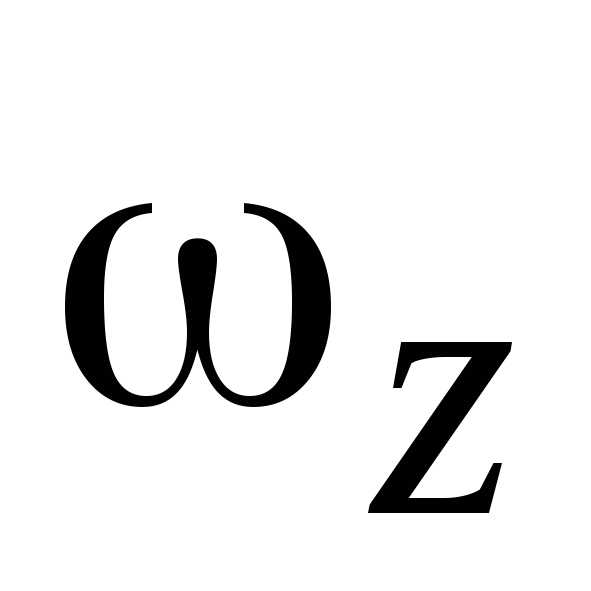 и
и 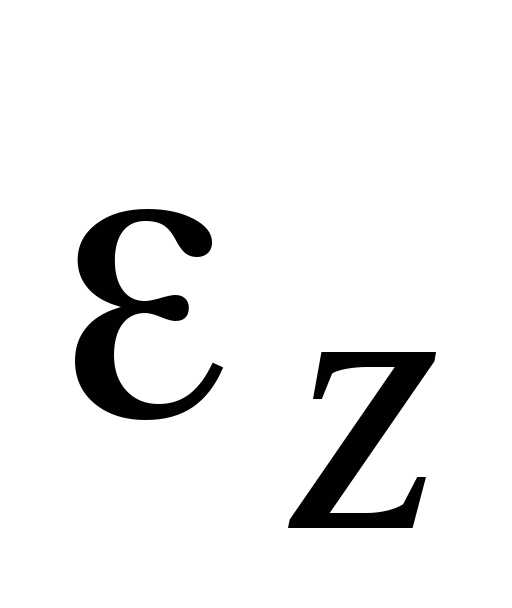 совпадают, т.е.,
то вращение тела называется ускоренным.
совпадают, т.е.,
то вращение тела называется ускоренным.
Если знаки 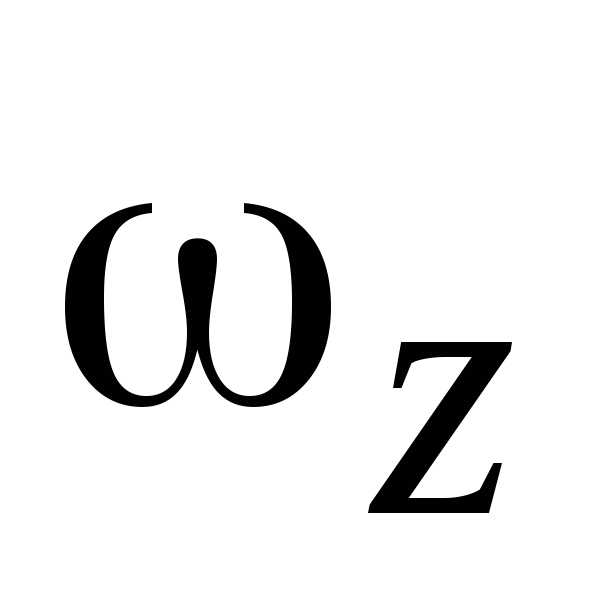 и
и 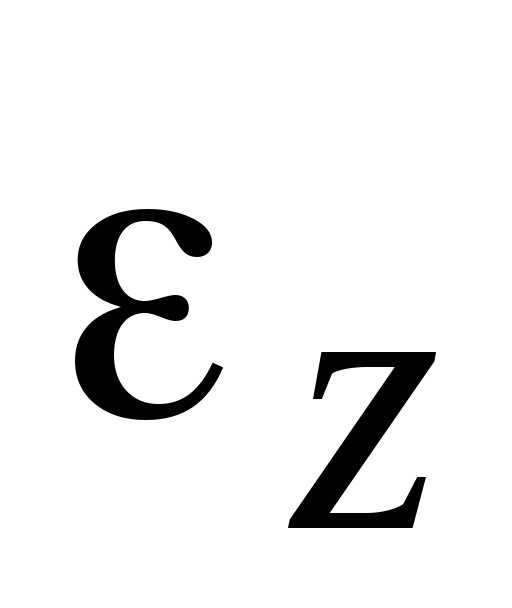 не совпадают, т.е.,
то вращение тела называется замедленным.
не совпадают, т.е.,
то вращение тела называется замедленным.
Абсолютное значение
углового ускорения будем обозначать  :
:
.
Единица измерения углового ускорения тела в системе СИ – рад/с2.
Частные случаи
Равномерное вращение
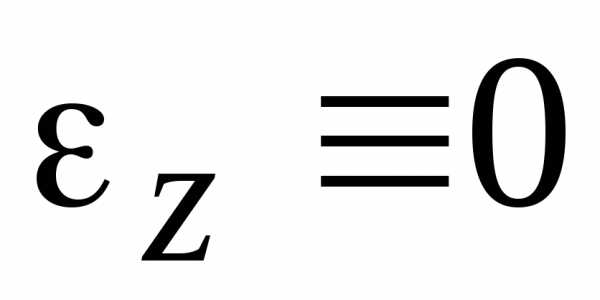 — условие равномерного
вращения.
— условие равномерного
вращения.
Определим закон движения.
Пусть при  :
: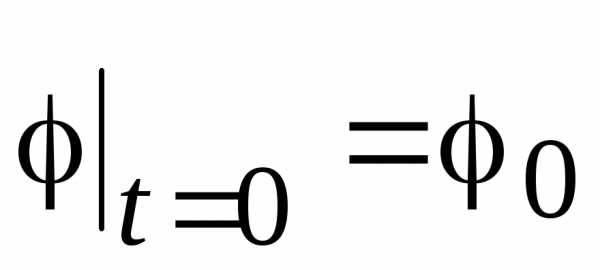 ,
, .
.
Из условия равномерного вращения следует
.
Откуда 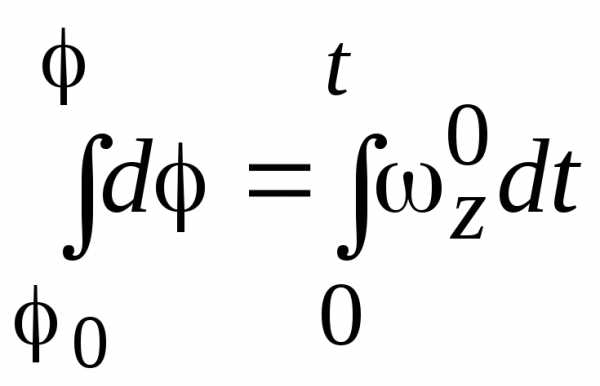 и, следовательно, закон равномерного
вращения тела
и, следовательно, закон равномерного
вращения тела
2. Равнопеременное вращение твердого тела
— условие равнопеременного вращения.
Из этого условия следует
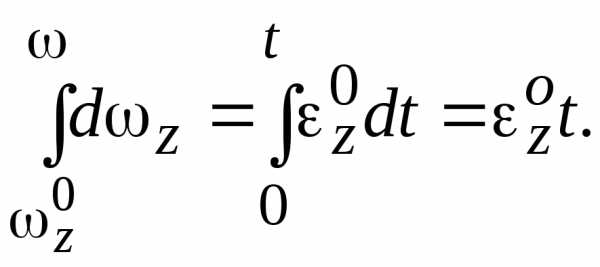
Откуда .
Из последнего следует
И, следовательно,
закон равнопеременного вращения тела
имеет вид  .
.
При этом, если
знаки 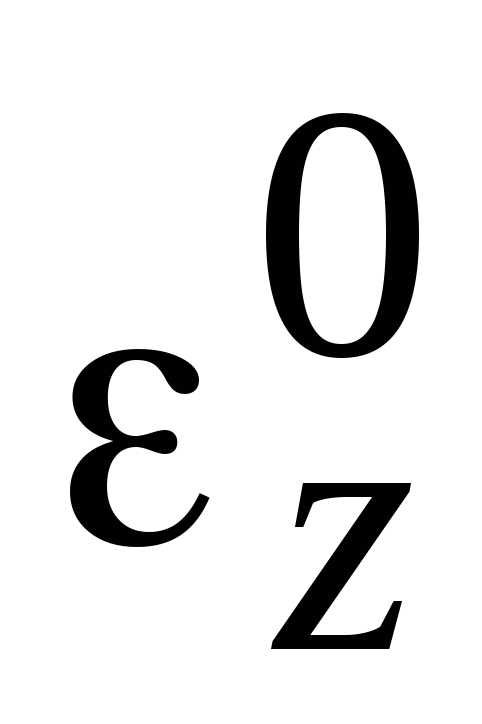 и
и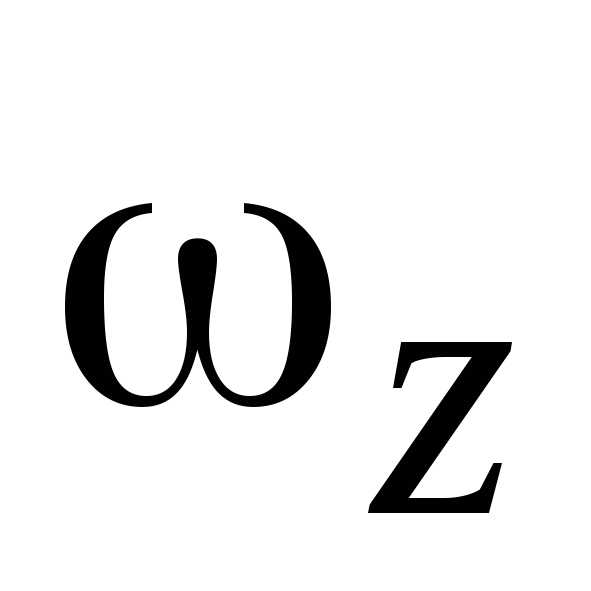 совпадают, то вращение называется
равноускоренным, если знаки
совпадают, то вращение называется
равноускоренным, если знаки  и
и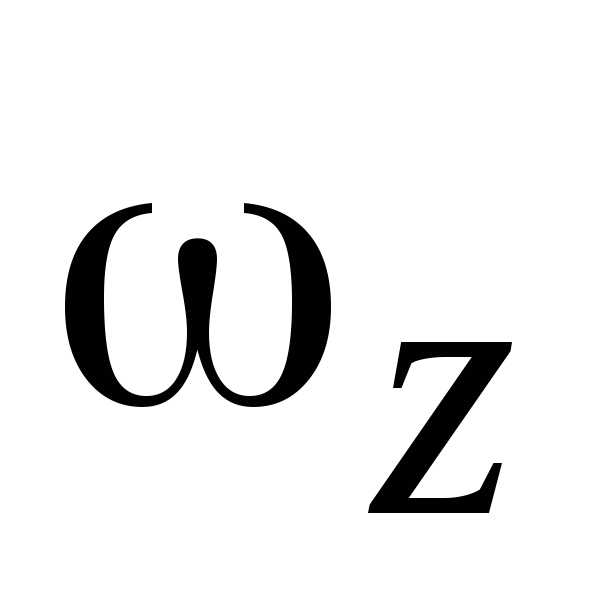 различны, то вращение называется
равнозамедленным.
различны, то вращение называется
равнозамедленным.
Замечание. Угловая скорость и угловое ускорение могут быть только у тела. Нельзя говорить угловая скорость или угловое ускорение точки. На первой лекции мы определили, что под материальной точкой понимают простейшую модель материального тела любой формы, размерами и вращением которого можно пренебречь. У точки есть только скорость и ускорение.
Таким образом, угловая скорость и угловое ускорение являются кинематическими характеристиками твердого тела. Определение этих характеристик, как известно из прошлой лекции, является второй основного задачей кинематики твердого тела. Перейдем к третьей задаче кинематики вращательного движения твердого тела.
Распределение скоростей и ускорений в теле при вращательном движении
Выберем в теле
произвольную точку М.
Обозначим ее начальное положение М0.
Проведем через нее и ось вращения
неподвижную плоскость отсчета По.
Свяжем также точку М с подвижной плоскостью П. Если закон
вращательного движения задан  ,
то положение точкиМ в момент времени t будет определяться углом
,
то положение точкиМ в момент времени t будет определяться углом  .
Траекторией точкиМ будет окружность, лежащая в плоскости
перпендикулярной оси вращения. На рис.
7.1 изображено это сечение.
.
Траекторией точкиМ будет окружность, лежащая в плоскости
перпендикулярной оси вращения. На рис.
7.1 изображено это сечение.
Пусть задано
положительное направление отсчета угла  против хода часовой стрелки в сторону
движения. П0,
П – прямые пересечения соответствующие
плоскостей с плоскостью сечения. Тогда
зависимость дуги от угла запишется для
движения точки М следующим образом
против хода часовой стрелки в сторону
движения. П0,
П – прямые пересечения соответствующие
плоскостей с плоскостью сечения. Тогда
зависимость дуги от угла запишется для
движения точки М следующим образом
, (7.5)
где  — радиус окружности, по которой движется
точка.
— радиус окружности, по которой движется
точка.
Так как 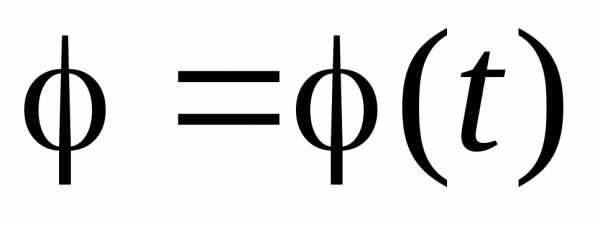 задано, то таким образом движения точкиМ будет задано естественным способом.
При этом проекция вектора скорости
точки на касательную равна
задано, то таким образом движения точкиМ будет задано естественным способом.
При этом проекция вектора скорости
точки на касательную равна
. (7.6)
Направление вектора скорости точки определяется направлением вращения тела:
. (7.7)
Таким образом,
величина скорости 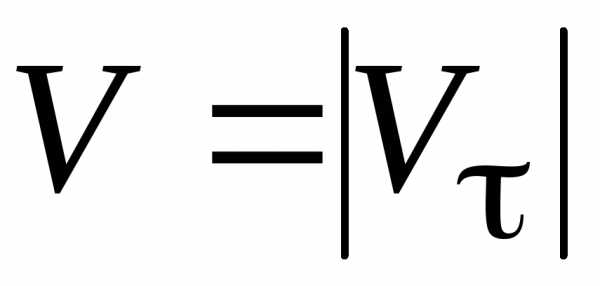 равна:
равна:
. (7.8)
Скорости точек тела при его вращении вокруг неподвижной оси пропорциональны их кратчайшим расстояниям до этой оси. Скорости точек тела направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.
Определим ускорение произвольной точки М при естественном способе задания ее движения (7.5). Раскладывая ускорение точки на касательную и нормальную составляющие , получим
,
.
Величина полного ускорения равна .
Таким образом, ускорение произвольной точки тела при вращательном движении вокруг неподвижной оси определяется по формулам:
, 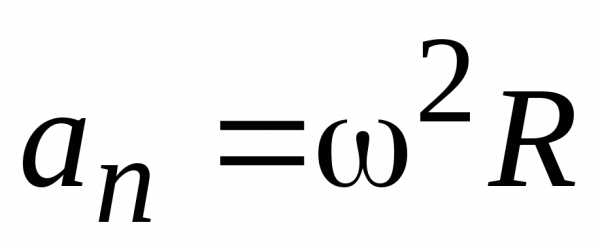 ,.
(7.9)
,.
(7.9)
Как видно из формул (7.9) касательное, нормальное и полное ускорения точек, как и скорости, распределены по линейному закону. Они линейно зависят от расстояний до оси вращения. Вектор нормального ускорения направлен по радиусу окружности к оси вращения (рис.7.2).
Направление вектора
касательного ускорения зависит от знака
алгебраического углового ускорения.
Если знаки  и
и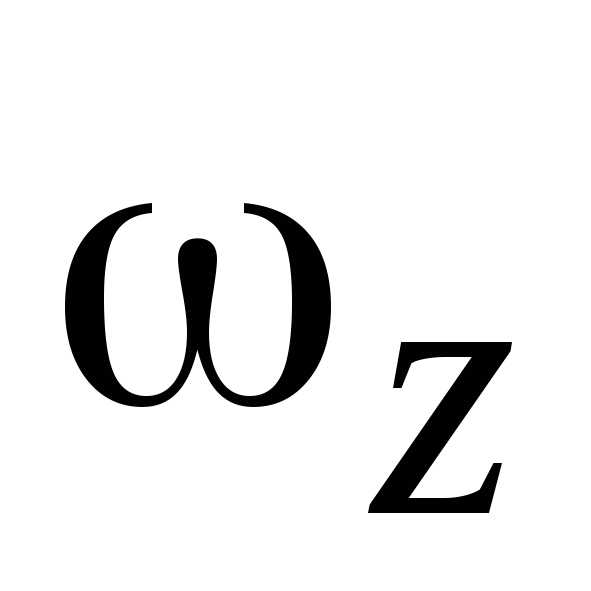 совпадают, т.е. ,то направления
векторов
совпадают, т.е. ,то направления
векторов  и
и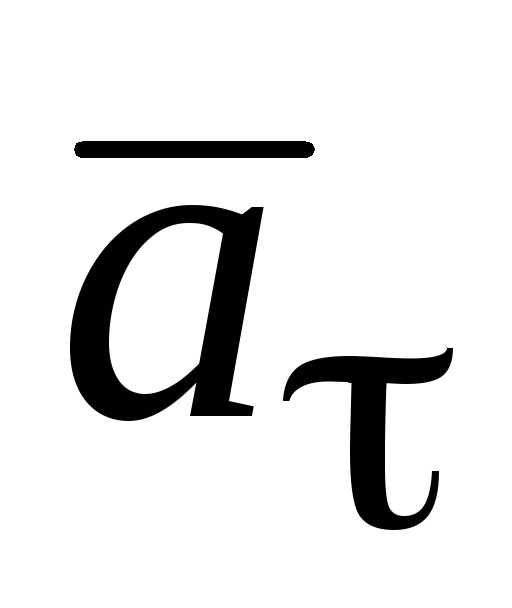 совпадают, если,
то векторы
совпадают, если,
то векторы  и
и направлены противоположно друг другу.
направлены противоположно друг другу.
Обозначим угол α
между полным ускорением  и радиусом вращения. Имеем
и радиусом вращения. Имеем
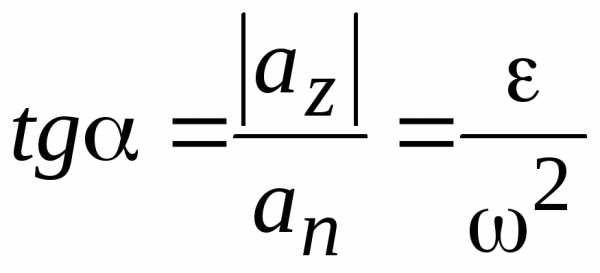 ,
(7.10)
,
(7.10)
т.е. угол α для всех точек тела один и тот же и от расстояния до оси вращения не зависит. Откладывать его следует от вектора ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения, независимо от направления вращения тела.
studfiles.net
Ускорение
Ускорение характеризует быстроту изменения скорости.
При векторномспособе описания среднее ускорение равно отношению изменения скорости к тому промежутку времени, за который это произошло это изменение:
При координатномспособе описаниясредниезначенияпроекций ускоренияопределяются следующими выражениями:
,.
Чтобы перейти к мгновеннымзначениям ускорения, следует устремитьt 0.
,
т.е. ускорение равно производной вектора скорости по времени. Аналогичными выражениями определяются проекции вектора ускорения:
,.
Модульвектора мгновенного ускорения легко находится по теореме Пифагора. При двумерном движении.
Перейдем к естественномуспособу описания движения. Поскольку скорость может изменяться как по величине, так и по направлению, с каждым из этих изменений связана составляющая вектора полного ускорения.
Составляющая ускорения, характеризующая быстроту изменения скорости по величине, называетсятангенциальным ускорением. Она связана с приращением вектора скорости, направленным по касательной к траектории, как и сама скорость. При ускоренном движении тангенциальная составляющая совпадает с вектором скорости, при замедленном — противоположна. Величина тангенциального ускорения равна производной от модуля вектора скорости по времени:
 .
.
Составляющая ускорения, характеризующая быстроту изменения скорости по направлению, называетсянормальным ускорением. Она связана с приращением вектора скорости, направленным перпендикулярно касательной к траектории и равна
 ,
,
где R— радиус кривизны траектории. Нормальное ускорение всегда направлено к центру кривизны траектории:
Вектор полного ускорения
Его модуль легко найти по теореме Пифагора:
.
1.3. Кинематика вращательного движения Положение точки при ее движении по окружности
При вращательном движении по окружности радиусаRее положение можно задатьугловой координатой(t), а ее перемещение — изменением угловой координаты=(t+t)— (t).
Бесконечно малый угол поворота dможно рассматривать какпсевдовектор, направление которого связано с направлением вращения правилом правого винта (или правилом буравчика). При движении по часовой стрелкеdнаправлен перпендикулярно плоскости рисунка “от нас”, при движении против часовой стрелки — “к нам”.
Число оборотовпри вращательном движении связано с углом поворота соотношением: .
Угловая скорость
Угловая скорость характеризует быстроту вращения. Средняя угловая скоростьравна отношению угла поворота к тому промежутку времени, за который произошел этот поворот:
.
Мгновенная угловая скоростьравна производной угловой координаты по времени:
.
Это псевдовектор, его направление связано с направлением вращения правилом буравчика.
Нередко вместо угловой скорости вводится частота вращения n, т.е. число оборотов за единицу времени, а также (в случае равномерного вращения) периодT, т.е. время одного оборота.
.
Угловое ускорение
Угловое ускорение характеризует быстроту изменения угловой скорости. Среднее угловое ускорениеравно отношению изменения угловой скорости к тому промежутку времени, за который произошло это изменение:
.
Мгновенное угловое ускорениеравно производной от угловой скорости по времени:
.
Угловое ускорение — тоже псевдовектор; его направление совпадает с вектором угловой скорости при ускоренном вращении и противоположно ему — при замедленном вращении.
Связи между линейными и угловыми величинами
Движение по окружности — частный случай движения по криволинейной траектории. Поэтому оно характеризуется не только угловыми величинами — углом поворота, угловой скоростью и угловым ускорением, но и теми величинами, которые были введены при естественном способе описания, — криволинейной координатой s, скоростью, нормальным и тангенциальным ускорениями. Линейные и угловые величины связаны соотношениями:
; ;
;
; .
2. Законы динамики
2.1. Основные определения
Физические величины, характеризующие модели объектов
Масса m — мера инертности материальной точки или твердого тела при его поступательном движении.Инертностьюназывается свойство тел оказывать сопротивление при попытках привести его в движение или изменить величину или направление его скорости.
Момент инерции J — мера инертности при вращательном движении. Момент инерции материальной точки, находящейся на расстоянииrот оси вращенияz, определяется формулой. Момент инерции твердого тела как системы материальных точек равен. Выражения для моментов инерции некоторых однородных твердых тел приведены в таблице 3:
Моменты инерции твердых тел Таблица 3
Твердое тело | Ось вращения | Момент инерции |
Шар радиуса R | Проходит через центр шара | 2/5 |
Сплошной цилиндр радиуса R | Совпадает с осью цилиндра | 1/2 |
Полый тонкостенный цилиндр радиуса R | Совпадает с осью цилиндра | |
Тонкое кольцо радиуса R | Совпадает с осью кольца | |
Совпадает с осью диска | 1/2 | |
Тонкий диск радиуса R | Совпадает с диаметром диска | 1/4 |
Продолжение таблицы 3
Твердое тело | Ось вращения | Момент инерции |
Тонкий стержень длины l | Перпендикулярна стержню и проходит через его центр | 1/12 |
Перпендикулярна стержню и проходит через его конец | 1/3 |
Момент инерции относительно произвольной оси в ряде случаев можно рассчитать по теореме Штейнера: , т.е.момент инерции J относительно произвольной оси z равен моменту инерции относительно оси, параллельной данной и проходящей через центр масс С тела, плюс произведение массы m тела на квадрат расстояния d между осями.
studfiles.net
5. Вращательное движение. Угловая скорость и угловое ускорение.
Рассмотрим движение материальной точки
по окружности радиуса  .
За время
.
За время ее положение изменится на угол
ее положение изменится на угол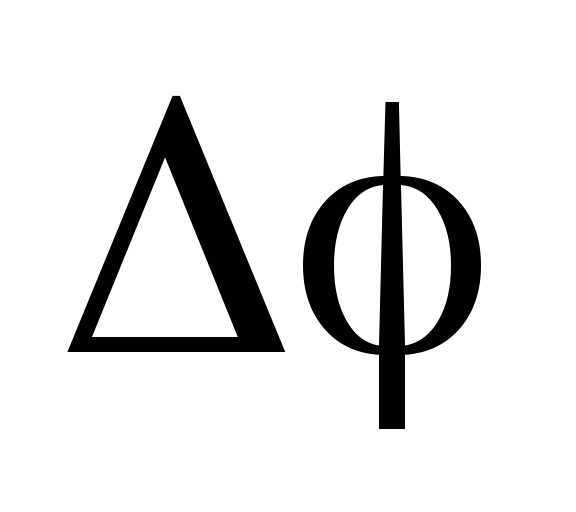 .
Углы поворота рассматриваются как
векторы. Модуль вектора
.
Углы поворота рассматриваются как
векторы. Модуль вектора равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, то есть подчиняется
правилу правого винта.
равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, то есть подчиняется
правилу правого винта.
Угловой скоростью называется векторная величина, равная первой производной угла поворота по времени
,
| Она направлена по оси вращения по правилу правого винта. Ее размерность [w]= с-1., а единица – рад/сек. Линейная скорость точки равна
|
Рис.5. |
Число полных оборотов за единицу времени
называется частотой, 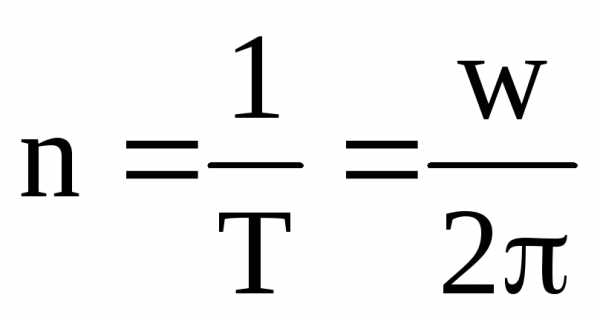 .
Откуда.
.
Откуда.
Угловым ускорением называется первая
производная угловой скорости по времени, 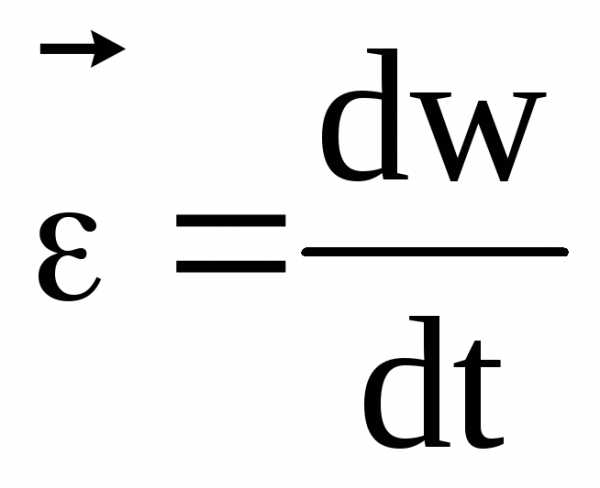 .
.
|
|
Рис.7. | Рис.8. |
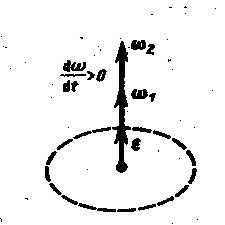
При ускоренном движении  сонапрвлено с
сонапрвлено с ,
при замедленном – противоположно
направлению
,
при замедленном – противоположно
направлению .
.
Тангенциальная составляющая ускорения
равна  ,
а так как
,
а так как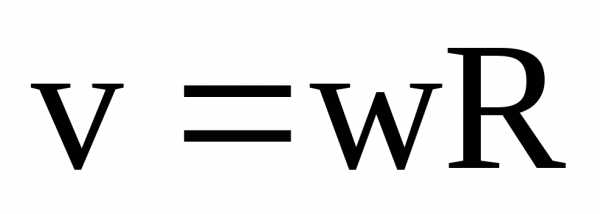 ,
то.
Для нормальной составляющей имеем.
В случае равнопеременного движения по
окружности ()
,
то.
Для нормальной составляющей имеем.
В случае равнопеременного движения по
окружности ()
,.
Связь между линейными и угловыми величинами:
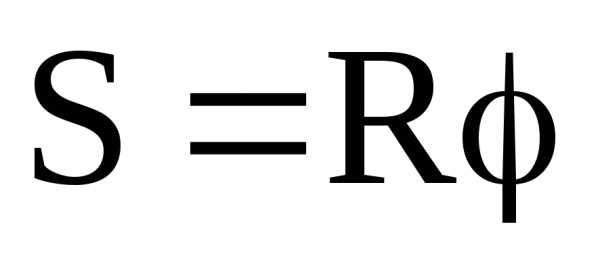 ,
, ,
, ,
,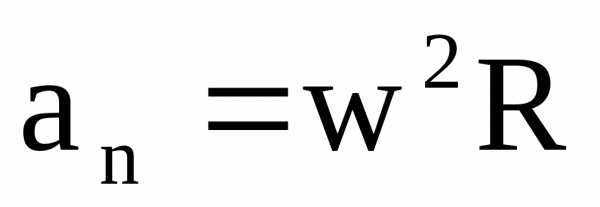 .
.
6. Качение тела.
Цилиндрическое тело равномерно катится по горизонтальной плоскости без проскальзывания. Все точки тела одновременно участвуют в двух движениях – поступательном и вращательном. Найдем скорость любой точки тела.
| В этом
случае скорость любой точки тела
складывается из скорости поступательного
и вращательного движения. Пусть за
время |
Рис.9. |
на 
 ,
,
При этом тело поворачивается на угол  ,
а угловая скорость равна
,
а угловая скорость равна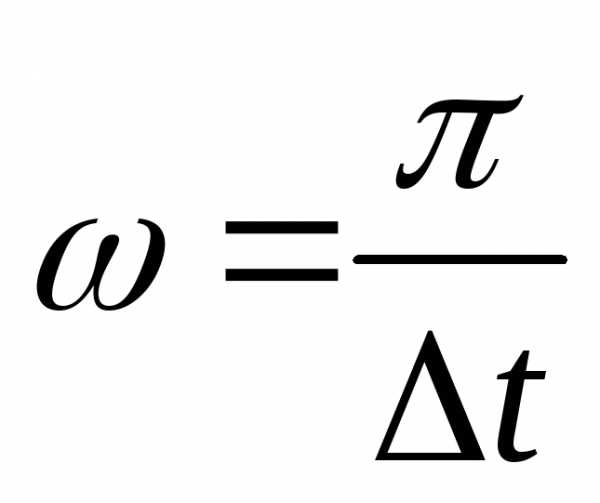 .
Если угловая скорость известна, то по
формулеможно найти линейную скорость точки за
счет вращения,
.
Если угловая скорость известна, то по
формулеможно найти линейную скорость точки за
счет вращения,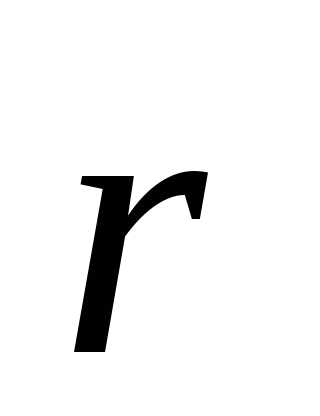 —
расстояние от точки до центра О.
—
расстояние от точки до центра О.
Для точки на ободе тела
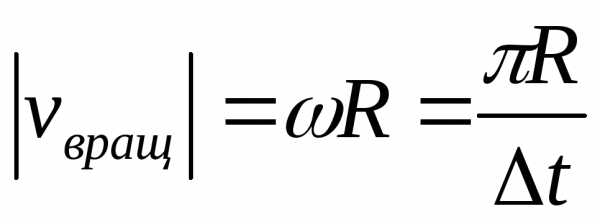 .
.
Полная скорость точки будет определяться из равенства
= /
Определим скорости точек 1, 2, 3, 4. (рис.10)
| 1: 2: 3:
, 4: |
Рис.10. |
Лекция 2. Динамика материальной точки.
Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение. Динамика изучает связь между взаимодействиями тел и изменениями в их движении.
В основе динамики лежат три закона Ньютона. Эти законы – результат обобщения опытных данных и теоретических сведений в области механики, которые были получены до Ньютона и самим Ньютоном.
1. Первый закон Ньютона.
Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор пока воздействие со стороны других тел не заставят его изменить это состояние.
Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инертностью.I- закон обычно называют законом инерции, а движение тела, свободного от внешних воздействий – движением по инерции.
I- закон выполняется не во всякой системе отсчета координат. Например, тела лежащие на гладком полу поезда, идущего с постоянной скоростью по прямолинейному участку пути, начинают двигаться, если поезд тормозит или ускоряется или выходит на криволинейный участок.
Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета.
Системы отсчета, движущиеся с ускорением относительно инерциальных систем, называются неинерциальными.
С большой степенью точности инерциальной можно считать гелиоцентрическую систему. Начало системы связано с Солнцем, а оси проведены в направлении трех удаленных звезд. Любая другая система, движущаяся относительно гелиоцентрической без ускорения будет также инерциальной. Так как Земля вращается вокруг собственной оси, система отсчета жестко связанная с Землей не будет инерциальной. Однако вращение Земли происходит медленно, поэтому в большинстве задач неинерциальностью этой системы можно пренебречь.
Важной особенностью инерциальных систем отсчета является, то что в них время однородно, а пространство однородно и изотропно. Однородность времени означает, что протекание физических процессов в разное время одинаково (в одних и тех же условиях). Однородность пространства – физические процессы протекают одинаково во всех его точках. Изотропность – во всех направлениях физические явления протекают одинаково.
В неинерциальных системах отсчета пространство неоднородно и неизотропно, а время неоднородно.
studfiles.net
Движение материальной точки по окружности. Угловая скорость и угловое ускорение и их связь с линейными характеристиками движения
Движение по окружности – частный случай
криволинейного движения. Скорость  тела в любой точке криволинейной
траектории направлена по касательной
к ней (рис.2.1). Скорость как вектор при
этом может изменяться и по модулю
(величине) и по направлению. Если модуль
скорости
тела в любой точке криволинейной
траектории направлена по касательной
к ней (рис.2.1). Скорость как вектор при
этом может изменяться и по модулю
(величине) и по направлению. Если модуль
скорости остается неизменным, то говорят оравномерном криволинейном движении.
остается неизменным, то говорят оравномерном криволинейном движении.
Пусть тело движется по окружности с постоянной по величине скоростью из точки 1 в точку 2.
Рис.2.1
При этом тело пройдет путь, равный длине дуги ℓ12между точками 1 и 2 за времяt. За это же времяtрадиус- векторR, проведенный из центра окружности 0 к точке, повернется на угол Δφ.
Вектор скорости в точке 2 отличается от вектора скорости в точке 1 по направлениюна величину ΔV:
;
Для характеристики изменения вектора скорости на величину δv введем ускорение :
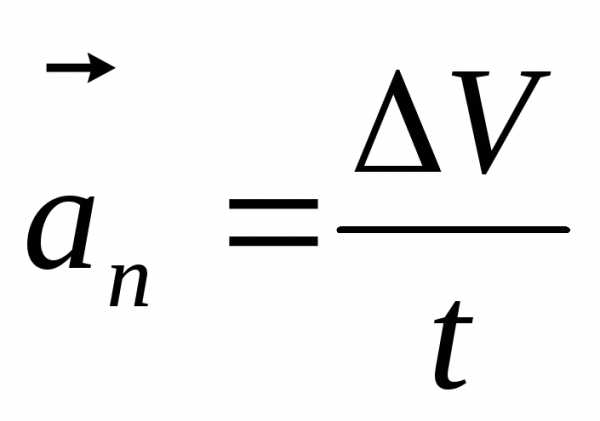 (2.4)
(2.4)
Вектор 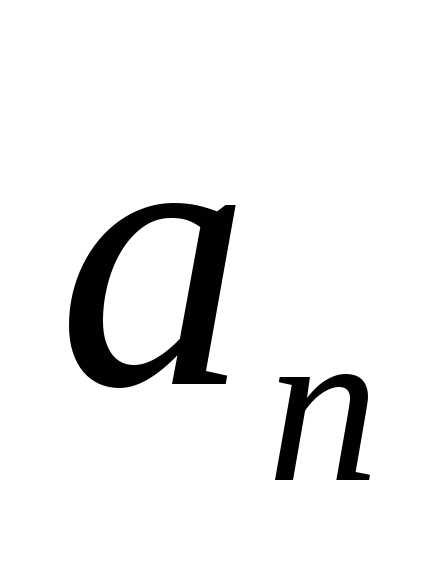 в любой точке траектории направлен по
радиусуRкцентруокружности перпендикулярно к вектору
скоростиV2. Поэтому
ускорение
в любой точке траектории направлен по
радиусуRкцентруокружности перпендикулярно к вектору
скоростиV2. Поэтому
ускорение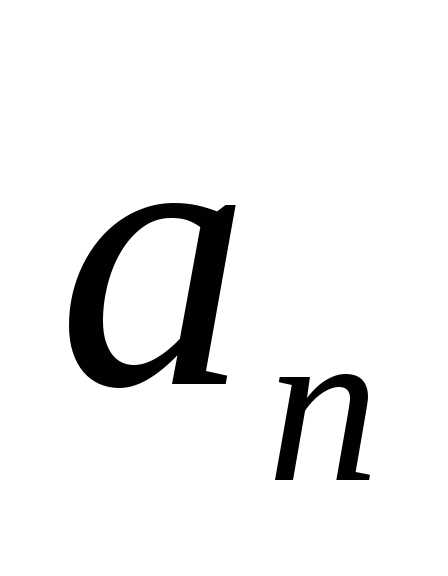 ,
характеризующее при криволинейном
движении изменение скорости
,
характеризующее при криволинейном
движении изменение скорости по направлению, называютцентростремительным
или нормальным. Таким образом, движение
точки по окружности с постоянной по
модулю скоростью являетсяускоренным.
по направлению, называютцентростремительным
или нормальным. Таким образом, движение
точки по окружности с постоянной по
модулю скоростью являетсяускоренным.
Если скорость  изменяется
не только по направлению, но и по модулю
(величине), то кроме нормального ускорения
изменяется
не только по направлению, но и по модулю
(величине), то кроме нормального ускорения вводят еще икасательное (тангенциальное) ускорение
вводят еще икасательное (тангенциальное) ускорение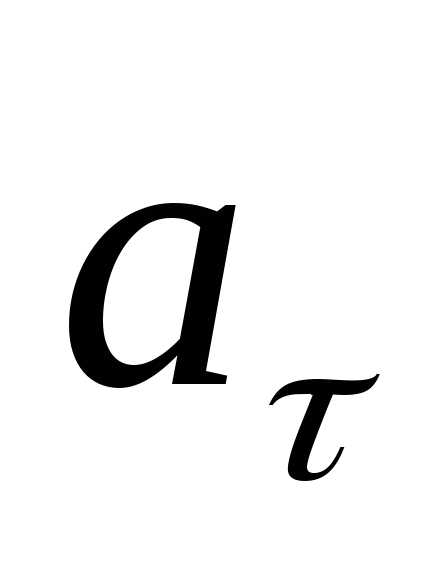 ,
которое характеризует изменение скорости
по величине:
,
которое характеризует изменение скорости
по величине:
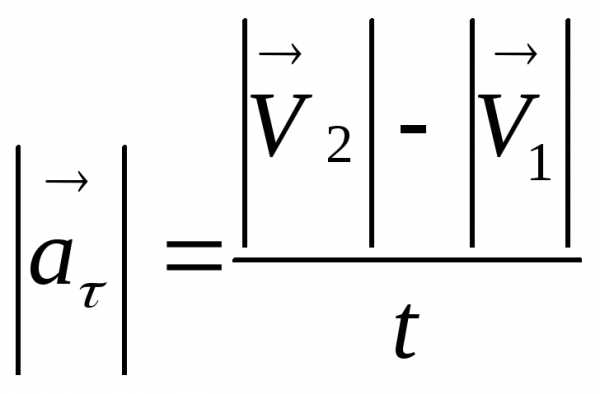 или
или
Направлен вектор 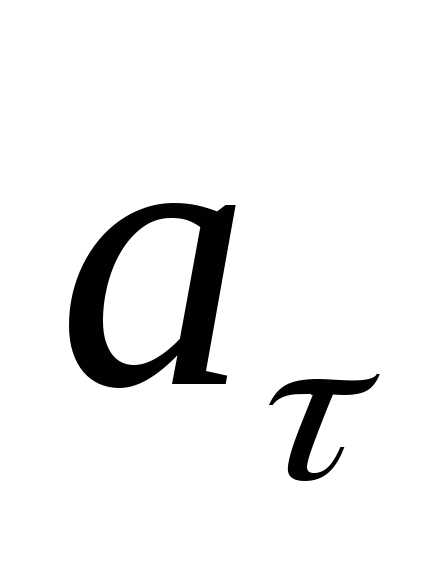 по
касательной в любой точке траектории
(т.е. совпадает с направлением вектора
по
касательной в любой точке траектории
(т.е. совпадает с направлением вектора ).
Угол между векторами
).
Угол между векторами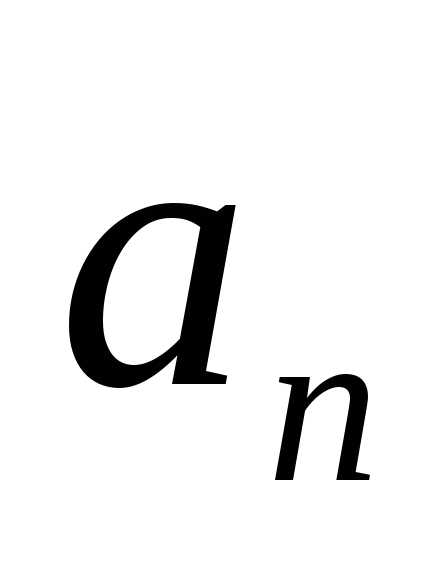 и
и равен
900.
равен
900.
Полное ускорение точки, движущейся по криволинейной траектории, определяется как векторная сумма (рис.2.1.).
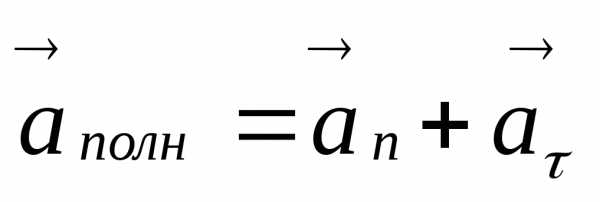 .
.
Модуль вектора .
Угловая скорость и угловое ускорение
При движении материальной точки по окружностирадиус-векторR, проведенный из центра окружности О к точке, поворачивается на угол Δφ (рис.2.1). Для характеристики вращения вводятся понятия угловой скорости ω и углового ускорения ε.
Угол φ можно измерять в радианах. 1 радравен углу, который опирается на дугу ℓ, равную радиусуRокружности, т.е.
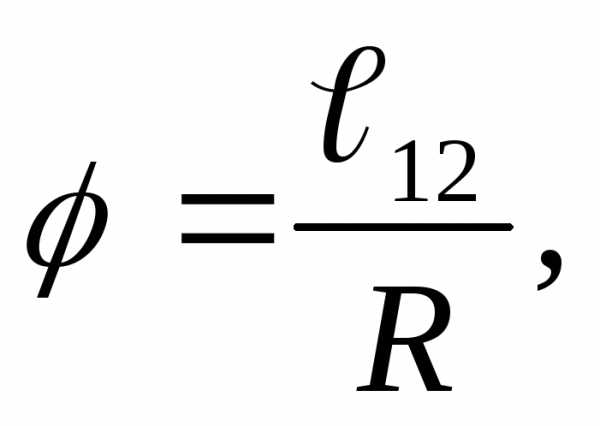 илиℓ12 = Rφ(2.5.)
илиℓ12 = Rφ(2.5.)
Продифференцируем уравнение (2.5.)
 (2.6.)
(2.6.)
Величина dℓ/dt=Vмгн. Величину ω =dφ/dtназываютугловой скоростью(измеряется в рад/с). Получим связь между линейной и угловой скоростями:
V = ωR, (2.7)
Величина
ω векторная. Направление вектора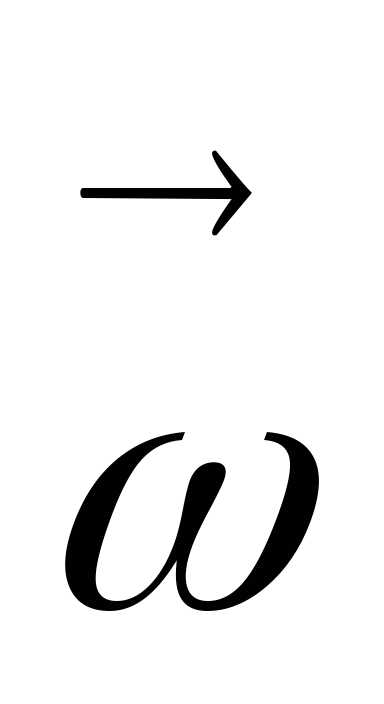 определяетсяправилом винта (буравчика):
оно совпадает с направлением перемещения
винта, ориентированного вдоль оси
вращения точки или тела и вращаемого в
направлении поворота тела (рис.2.2), т.е.
определяетсяправилом винта (буравчика):
оно совпадает с направлением перемещения
винта, ориентированного вдоль оси
вращения точки или тела и вращаемого в
направлении поворота тела (рис.2.2), т.е.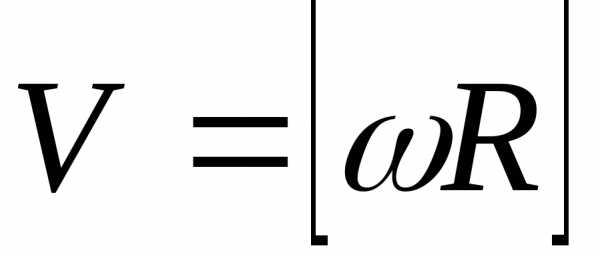 .
.
Рис.2.2
Угловым ускорением называется векторная величина производная
от угловой скорости (мгновенное угловое
ускорение)
называется векторная величина производная
от угловой скорости (мгновенное угловое
ускорение)
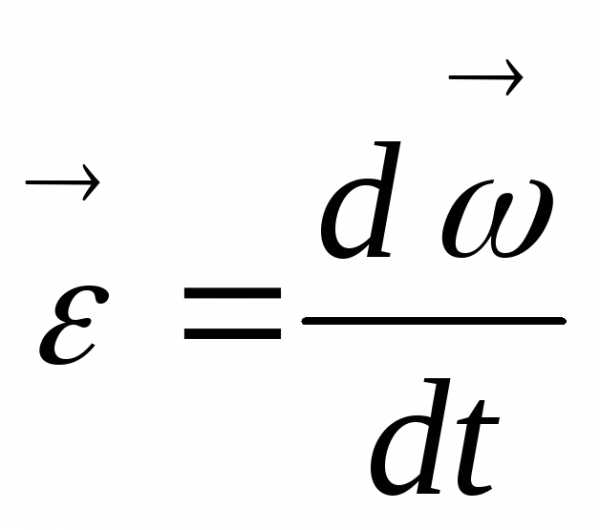 ,
(2.8.)
,
(2.8.)
Вектор 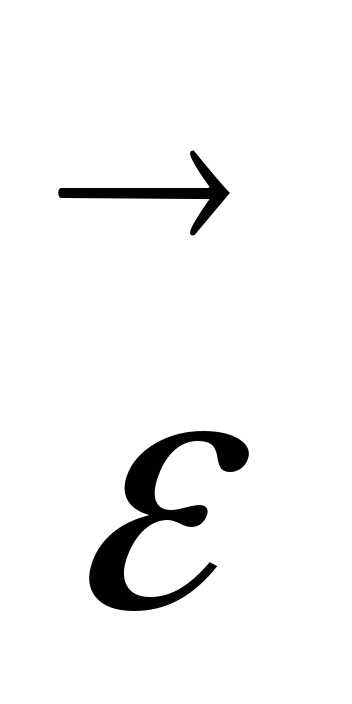 совпадает
с осью вращения и направлен в туже
сторону, что и вектор
совпадает
с осью вращения и направлен в туже
сторону, что и вектор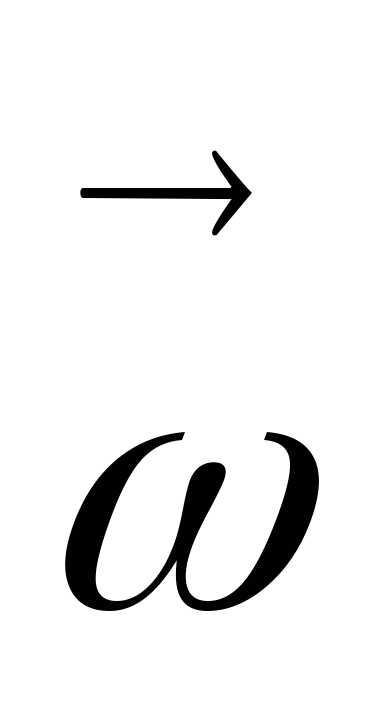 ,
если вращение ускоренное, и в
противоположную, если вращение
замедленное.
,
если вращение ускоренное, и в
противоположную, если вращение
замедленное.
Число оборотов n тела в единицу времени называют частотой вращения.
Время Т одного полного оборота тела называют периодом вращения. При этом R опишет угол Δφ=2π радиан
n=1/T
С учетом сказанного
, (2.9)
Уравнение (2.8) можно записать следующим образом:
(2.10)
Тогда тангенциальная составляющая ускорения
а=R(2.11)
Нормальное ускорение аnможно выразить следующим образом:
с учетом (2.7) и (2.9)
(2.12)
Тогда полное ускорение .
Для вращательного движения с постоянным угловым ускорением можно записать уравнение кинематики по аналогии с уравнением (2.1) – (2.3) для поступательного движения:
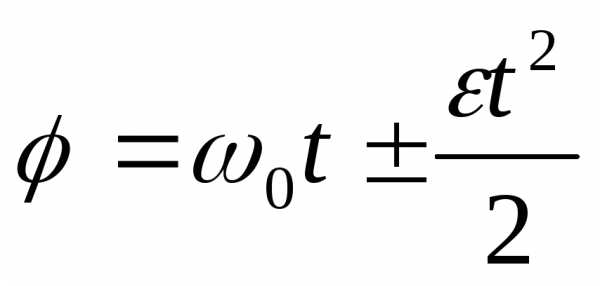 ,
,
.
studfiles.net



 =
=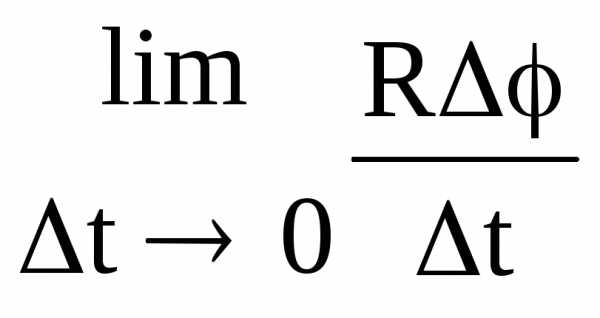 =
=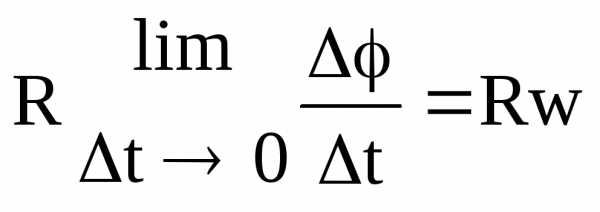

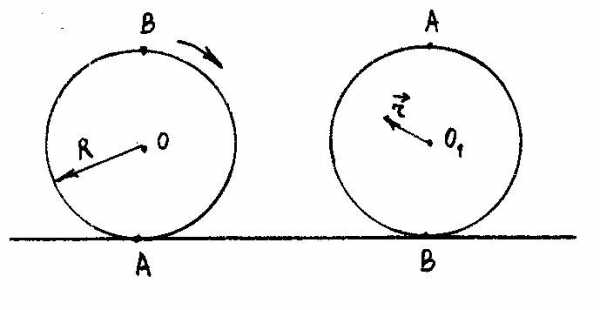
 ц.т. переместился на расстояние АВ (из
О в О1). Точка О, через которую
проходит ось вращения участвует только
в поступательном движении. Модуль
этой скорости равен длине дуги АВ,
деленной
ц.т. переместился на расстояние АВ (из
О в О1). Точка О, через которую
проходит ось вращения участвует только
в поступательном движении. Модуль
этой скорости равен длине дуги АВ,
деленной
 ,
, ,
,