Формула связи периода и частоты: Период и частота колебаний – формула зависимости

3. Длина волны. Связь длины волны со скоростью её распространения и периодом (частотой)

Каждая волна имеет свои параметры движения.

Скорость волны — скорость распространения возмущения.

Пример:

воздействуя на стальной стержень с одного конца, можно вызвать волны сжатия и разрежения со скоростью \(5000 \frac{м}{с}\).

Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.

Помимо скорости, важной характеристикой волны является длина волны.

Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.

Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. \(1\)).

Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.

 

 

Рис. \(1\). Модель упругой среды для демонстрации колебаний

 

Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.

Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. \(2\)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на \(1/4\) колебания.

 

 

Рис. \(2\). Изображение максимального смещения от положения равновесия первого шарика

 

В момент времени, когда смещение четвертого шарика будет наибольшим  (рис. \(3\)), седьмой шарик будет отставать от него на \(1/4\) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет \(1/2\) колебания.   

 

 

Рис. \(3\). Изображение максимального смещения от положения равновесия четвёртого шарика

 

Между седьмым и четвёртым шариком, а также седьмым и десятым \(1/4\) часть колебания (рис. \(4\)).

 

 

Рис. \(4\). Изображение максимального смещения от положения равновесия седьмого шарика

 

Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. \(5\)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.

 

 

Рис. \(5\). Изображение максимального смещения от положения равновесия десятого шарика

 

Начиная с тринадцатого шарика, мы можем отсчитывать новую волну (рис. \(6\)).

 

 

Рис. \(6\). Изображение модели новой волны

 

Длину волны измеряют расстоянием, на которое перемещается волновая поверхность за один период колебания источника волн;

Длиной волны является расстояние между двумя ближайшими точками бегущей волны на одном луче, который колеблется в одинаковой фазе:

λ=υT, где \(λ\) («лямбда») — длина волны, \(\upsilon\) — скорость волны, \(T\) — период колебания.

Период колебаний можно выразить как величину, обратную частоте колебаний: T=1ν.
Тогда выразим длину волны как отношение скорости и частоты: λ=υν.
Длина волны прямо пропорциональна скорости волны и обратно пропорциональна частоте колебаний (прямо пропорциональна периоду колебаний).

Поперечные и продольные волны описываются одними и теми же законами.

Выразим скорость волны:

как отношение длины волны к периоду колебаний: υ=λT;

как произведение длины волны на частоту колебаний: υ=λν.

 

За длину волны \(λ\) примем расстояние между шариками, колеблющимися в одинаковых фазах. Например (см. рис. \(6\)), между четвёртым и шестнадцатым, третьим и пятнадцатым.

 

Колебания проходят шарики, начиная с первого и заканчивая двенадцатым, проходят все фазы колебания. Новая волна начинается с тринадцатого шарика. Каждый шарик совершает одно полное колебание за время, которое называют периодом колебаний \(T\). За это время колебательный процесс проходит расстояние, называемое длиной волны \(λ. \)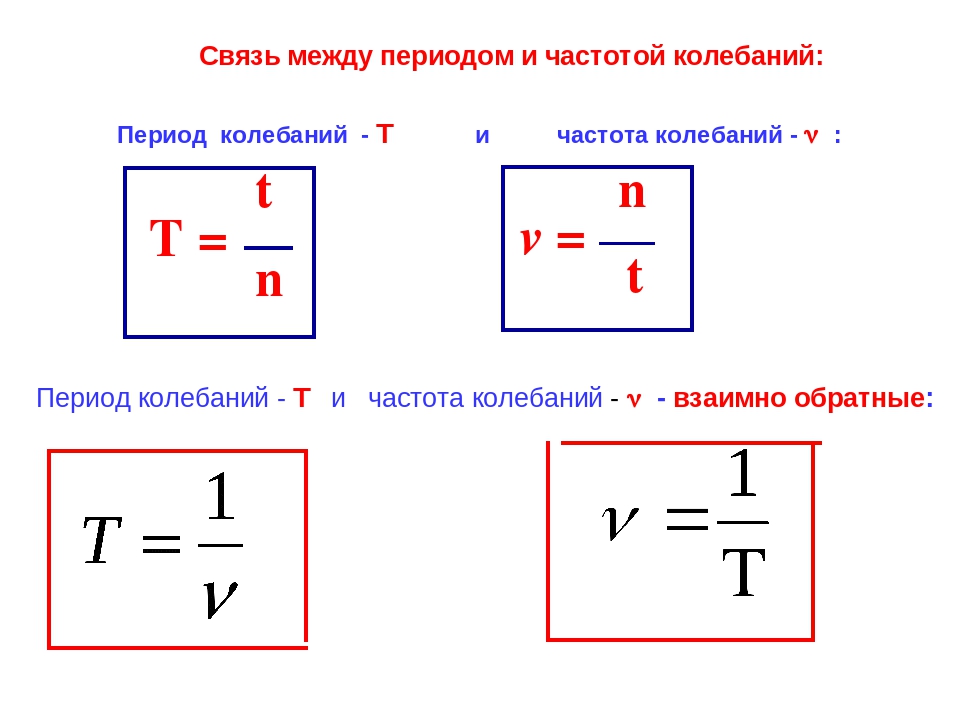

 

Модель распространения продольных волн представлена на рисунке \(7\).

Длиной волны будет расстояние между соседними центрами сжатия пружины.

 

 

Рис. \(7\). Распространение продольных волн в упругой пружине

 

Источником колебаний генерируется волна той же частоты, поэтому вынужденные колебания совпадают по частоте с осциллятором и не зависит от плотности среды, в которой движется волна.

Если в ходе движения волна переходит в среду другой плотности, то скорость движения волны изменяется, а частота колебаний остаётся прежней.

Источники:

Рис. 1. Модель упругой среды для демонстрации колебаний. © ЯКласс.
Рис. 2. Изображение максимального смещения от положения равновесия первого шарика. © ЯКласс.

Рис. 3. Изображение максимального смещения от положения равновесия четвёртого шарика. © ЯКласс.

Рис. 4. Изображение максимального смещения от положения равновесия седьмого шарика. © ЯКласс.

Рис. 5. Изображение максимального смещения от положения равновесия десятого шарика. © ЯКласс.

Рис. 6. Изображение модели новой волны. © ЯКласс.

Рис. 7. Распространение продольных волн в упругой пружине. © ЯКласс.

Рабочая программа по физике

11	Законы взаимодействия и движения тел	Контрольная работа №1 по теме «Основы кинематики»	Самостоятельное выполнение работы по вариантам	Формулы скорости, ускорения, перемещения при прямолинейном равноускоренном движения; скорости, перемещения и координаты при прямолинейном равномерном движении Понятия: перемещение тела, материальная точка	Рассчитывать характеристики прямолинейного равноускоренного, равномерного  движений Читать графики скорости
12		Относительность движения	Анализ контрольной работы Самостоятельное изучение п. 9 Решение задач из упр. 9	Сущность относительности движения	Решать задачи на расчет относительной скорости	П. 9 Упр. 9 (1,4) * Упр. 9(5)
13		Инерциальные системы отсчета Первый закон Ньютона	Объяснение учителя п. 10 Решение задач №112, 113, 115 – Р   Доклад «И. Ньютон»	Понятия: ИСО Первый закон Ньютона	Применять первый закон Ньютона для объяснения физических явлений	П. 10 Упр. 10
14	Законы взаимодействия и движения тел	Второй закон Ньютона	Объяснение учителя п. 11 Решение задач упр. 11 (1), №143 – Р   *№146 – Р	Второй закон Ньютона Формула  второго закона Ньютона, Факты: физический смысл 1 Н	Решать задачи на применение второго закона Ньютона	П. 11 Упр. 11 (2,4)
15		Третий закон Ньютона	Объяснение учителя п. 12 Демонстрация «Третий закон Ньютона» Решение задач №151 – Р,  упр. 12 Самостоятельная работа «I и II законы Ньютона»	Третий закон Ньютона	Применять третий закон Ньютона для объяснения физических явлений	П. 12 Упр. 12 (2,3)
16		Свободное падение тел	Объяснение учителя п. 13 Демонстрация «Свободное падение тел» Решение задач упр. 13 (2),	Понятие6 свободное падение тел Факты: особенности свободного падения тел Формулы скорости и перемещения  при свободном падении тел	Решать задачи на расчет характеристик свободного падения тел	П. 13 Упр. 13 (1,3) * №205- Р
17		Движение тела, брошенного вертикально вверх	Объяснение учителя п. 14 Решение задач на расчет времени, высоты подъема тела	Формулы скорости и перемещения тела, брошенного вертикально вверх	Решать задачи на расчет характеристик тела, брошенного вертикально вверх	П. 14 Упр. 14 * №210 – Р
18		Лабораторная работа №2 «Исследование свободного падения»	Инструктаж по ТБ Выполнение работы по инструкции с. 231 под руководством учителя	Понятие свободное падение Формулы скорости и перемещения при свободном падении тел	Экспериментально рассчитывать ускорение тела при равноускоренном движении	П. 14
19	Законы взаимодействия и движения тел	Закон всемирного тяготения	Объяснение учителя п. 15 Решение задач № 170, 171 – Р Упр. 15	Понятия: всемирное тяготение, гравитационная сила Закон всемирного тяготения Факты: значение и физический смысл гравитационной постоянной	Решать задачи на применение закона всемирного тяготения	П. 15 Упр. 15 (1,3) * № 172 – Р
20		Ускорение свободного падения на Земле и других небесных телах	Объяснение учителя п. 16 Решение задач п. 16	Формула ускорения свободного падения Факты: зависимость ускорения свободного падения от радиуса Земли	Решать задачи на расчет ускорения свободного падения	П. 16 Упр. 16 (1,2) * Упр. 16 (6)
21		Урок-игра «Звездный час»	Повторение теоретического материала по темам «Основы кинематики», «Основы динамики» Решение качественных задач
22		Прямолинейное и криволинейное движение. Движение тела по окружности с постоянной по модулю скоростью	Объяснение учителя п. 18, 19 Решение задач упр. 18 (20, №103, 104 – Р	Понятия: криволинейное движение, период, частота обращения, Факты: направления перемещения, скорости и ускорения при криволинейном движении Формула центростремительного ускорения	Решать задачи на расчет центростремитель- ного ускорения	П. 18, 19 Упр. 18 (1) *Упр. 18 (4)
23	Законы взаимодействия и движения тел	Искусственные спутники Земли	Объяснение учителя п. 20 Решение задач упр. 19 (2), №236-Р	Понятия: ИСЗ, первая космическая скорость Формулы первой космической скорости	Решать задачи на расчет скорости ИСЗ	П. 20 Упр. 19 (1) *№238-Р
24		Импульс тела. Закон сохранения импульса.	Объяснение учителя п. 21, 22 Решение задач упр. 20 (1), упр. 21 (2), №314-Р   Самостоятельная работа «Криволинейное движение, ИСЗ»	Понятия: импульс тела Формула и единицы импульса тела Закон сохранения импульса	Решать задачи на расчет импульса тела, на применение закона сохранения импульса тела	П. 21, 22 Упр. 20 (2) Упр. 21 (1)
25		Реактивное движение. Ракеты	Самостоятельное изучение п. 23 Решение задач упр. 22 (2)   Доклады «К. Э. Циолковский», «Полет фантазии»	Понятия: реактивное движение Факты: устройство, принцип движения ракет		П. 23 * №316-Р Повт. п. 9-23
26		Решение задач по теме «Основы динамики»	Физический диктант Решение типовых задач (подготовка к контрольной работе)	1,2,3 законы Ньютона, закон всемирного тяготения, закон сохранения импульса Формулы: импульса тела, первой космической скорости, центростремитель-ного ускорения, скорости и перемещения при свободном падении	Объяснять физические явления на основе знаний законов Ньютона Решать задачи на расчет импульса, центростремительного ускорения, характеристик свободного падения тел; на применение закона сохранения импульса Читать графики скорости тел	Повт. п. 10-23 Зад  в тетр
27		Контрольная работа №2 по теме «Основы динамики»	Самостоятельное выполнение работы по вариантам

Основные формулы по физике — колебания и волны. Связь между периодом и круговой частотой

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Таблица формул: колебания и волны

Физические законы, формулы, переменные	Формулы колебания и волны
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; α — начальная фаза; (ωt+α) — фаза.
Связь между периодом и круговой частотой:
Частота:
Связь круговой частоты с частотой:
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора.
Частота собственных колебаний:
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А 1 и А 2 — амплитуды составляющих колебаний, α 1 и α 2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания
Уравнение затухающих колебаний: е = 2,71. .. — основание натуральных логарифмов.
Амплитуда затухающих колебаний: где А 0 — амплитуда в начальный момент времени; β — коэффициент затухания;
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура.
Частота затухающих колебаний ω:
Период затухающих колебаний Т:
Логарифмический декремент затухания:

(лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша-рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах , санти-метрах и т. д. На графике колебаний амплитуда определяется как макси-мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша-ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т ) — это время, за которое совершается одно полное ко-лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы-рем амплитудам. Период колебаний измеряется в единицах времени — секундах , минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей-ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес-ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю-щихся величин, например, для затухающих колебаний .

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с .

Единица частоты в СИ названа герцем (Гц ) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v ) равна 1 Гц , то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической , или круговой частоты ω . Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Сила Кориолиса равна:

где — точечнаямасса ,-вектор угловой скорости вращающейся системы отсчёта,- вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операциявекторного произведения .

Величина называется кориолисовым ускорением.

По физической природе

Механические (звук ,вибрация )

Электромагнитные (свет ,радиоволны , тепловые)

Смешанного типа — комбинации вышеперечисленных

По характеру взаимодействия с окружающей средой

Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явлениерезонанса : резкое возрастание амплитуды колебаний при совпадениисобственной частоты осциллятора и частоты внешнего воздействия.

Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегдазатухающие ). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Автоколебания — колебания, при которых система имеет запаспотенциальной энергии , расходующейся на совершение колебаний (пример такой системы —механические часы ). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.

Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.

Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.

Гармонические колебания

где х А ω

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное

Скорость и ускорение при гармонических колебаниях.

Согласно определению скорости, скорость – это производная от координаты по времени

Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.

Величина — максимальная скорость колебательного движения (амплитуда колебаний скорости).

Следовательно, для скорости при гармоническом колебании имеем: ,

а для случая нулевой начальной фазы (см. график).

Согласно определению ускорения, ускорение – это производная от скорости по времени:

—

вторая производная от координаты по времени. Тогда: .

Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения наp(говорят, что колебания происходятв противофазе) .

Величина

Максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: ,

а для случая нулевой начальной фазы: (см. график).

Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).

Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t;А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия;ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;- полная фаза колебаний,- начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой)

До сих пор мы рассматривали собственные колебания, т. е. колебания, происходящие в отсутствие внешних воздействий. Внешнее воздействие было нужно лишь для того, чтобы вывести систему из состояния равновесия, после чего она предоставлялась самой себе. Дифференциальное уравнение собственных колебаний вообще не содержит следов внешнего воздействия на систему: это воздействие отражается лишь в начальных условиях.

Установление колебаний. Но очень часто приходится сталкиваться с колебаниями, которые происходят при постоянно присутствующем внешнем воздействии. Особенно важен и в то же время достаточно прост для изучения случай, когда внешняя сила имеет периодический характер. Общей чертой вынужденных колебаний, происходящих под действием периодической внешней силы, является то, что спустя некоторое время после начала действия внешней силы система полностью «забывает» свое начальное состояние, колебания приобретают стационарный характер и не зависят от начальных условий. Начальные условия проявляются только в период установления колебаний, который обычно называют переходным процессом.

Синусоидальное воздействие. Рассмотрим вначале наиболее простой случай вынужденных колебаний осциллятора под действием внешней силы, изменяющейся по синусоидальному закону:

Рис. 178. Возбуждение вынужденных колебаний маятника

Такое внешнее воздействие на систему можно осуществить различными способами. Например, можно взять маятник в виде шарика на длинном стержне и длинную пружину с малой жесткостью и прикрепить ее к стержню маятника недалеко от точки подвеса, как показано на рис. 178. Другой конец горизонтально расположенной пружины следует заставить двигаться по закону ? с помощью кривошипно-шатунного механизма, приводимого в движение электромотором. Действующая

на маятник со стороны пружины вынуждающая сила будет практически синусоидальна, если размах движения левого конца пружины В будет много больше амплитуды колебаний стержня маятника в точке закрепления пружины С.

Уравнение движения. Уравнение движения для этой и других подобных систем, в которых наряду с возвращающей силой и силой сопротивления на осциллятор действует вынуждающая внешняя сила, синусоидально изменяющаяся со временем, можно записать в виде

Здесь левая часть в соответствии со вторым законом Ньютона, является произведением массы на ускорение. Первый член в правой части представляет собой возвращающую силу, пропорциональную смещению из положения равновесия. Для подвешенного на пружине груза это упругая сила, а во всех других случаях, когда ее физическая природа иная, эту силу называют квазиупругой. Второе слагаемое есть сила трения, пропорциональная скорости, например сила сопротивления воздуха или сила трения в оси. Амплитуду и частоту со раскачивающей систему вынуждающей силы будем считать постоянными.

Разделим обе части уравнения (2) на массу и введем обозначения

Теперь уравнение (2) принимает вид

В отсутствие вынуждающей силы правая часть уравнения (4) обращается в нуль и оно, как и следовало ожидать, сводится к уравнению собственных затухающих колебаний.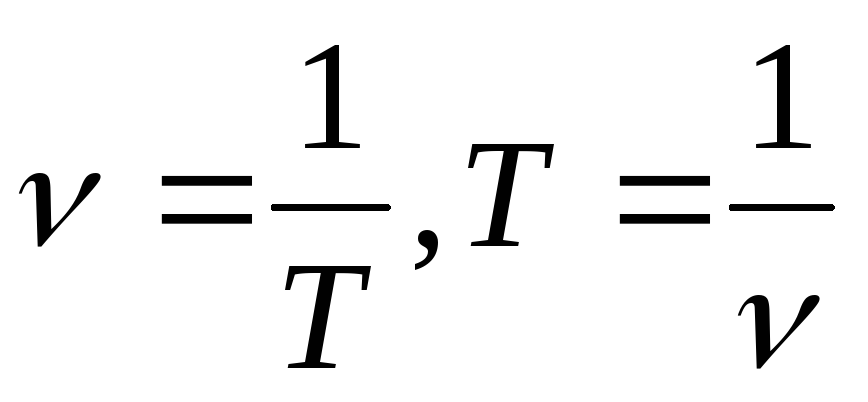

Опыт показывает, что во всех системах под действием синусоидальной внешней силы в конце концов устанавливаются колебания, которые также происходят по синусоидальному закону с частотой вынуждающей силы со и с постоянной амплитудой а, но с некоторым сдвигом по фазе относительно вынуждающей силы. Такие колебания называются установившимися вынужденными колебаниями.

Установившиеся колебания. Рассмотрим вначале именно установившиеся вынужденные колебания, причем для простоты пренебрежем трением. В этом случае в уравнении (4) не будет члена, содержащего скорость:

Попробуем искать решение соответствующее установившимся вынужденным колебаниям, в виде

Вычислим вторую производную и подставим ее вместе с в уравнение (5):

Чтобы это равенство было справедливо в любой момент времени, коэффициенты при слева и справа должны быть одинаковы. Из этого условия находим амплитуду колебаний а:

Исследуем зависимость амплитуды а от частоты вынуждающей силы. График этой зависимости показан на рис. 179. При формула (8) дает Подставив сюда значения видим, что постоянная во времени сила просто смещает осциллятор в новое положение равновесия, сдвинутое от старого на Из (6) следует, что при смещение

как, очевидно, и должно быть.

Рис. 179. График зависимости

Фазовые соотношения. По мере роста частоты вынуждающей силы от 0 до установившиеся колебания происходят в фазе с вынуждающей силой а их амплитуда постоянно увеличивается, сначала медленно, а по мере приближения со к — все быстрее и быстрее: при амплитуда колебаний неограниченно возрастает

При значениях со, превосходящих частоту собственных колебаний формула (8) дает для а отрицательное значение (рис. 179). Из формулы (6) ясно, что при колебания происходят в противофазе с вынуждающей силой: когда сила действует в одну сторону, осциллятор смещен в противоположную. При неограниченном увеличении частоты вынуждающей силы амплитуда колебаний стремится к нулю.

Амплитуду колебаний во всех случаях удобно считать положительной, чего легко добиться, вводя сдвиг фаз между вынуждающей

силой и смещением:

Здесь а по-прежнему дается формулой (8), а сдвиг фазы равен нулю при и равен при Графики зависимости от частоты вынуждающей силы показаны на рис. 180.

Рис. 180. Амплитуда и фаза вынужденных колебаний

Резонанс. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы имеет немонотонный характер. Резкое увеличение амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте осциллятора называется резонансом.

Формула (8) дает выражение для амплитуды вынужденных колебаний в пренебрежении трением. Именно с этим пренебрежением связано обращение амплитуды колебаний в бесконечность при точном совпадении частот Реально амплитуда колебаний в бесконечность, конечно же, обращаться не может.

Это означает, что при описании вынужденных колебаний вблизи резонанса учет трения принципиально необходим. При учете трения амплитуда вынужденных колебаний при резонансе получается конечной. Она будет тем меньше, чем больше трение в системе. Вдали от резонанса формулой (8) можно пользоваться для нахождения амплитуды колебаний и при наличии трения, если оно не слишком сильное, т. е. Более того, эта формула, полученная без учета трения, имеет физический смысл только тогда, когда трение все же есть. Дело в том, что само понятие установившихся вынужденных колебаний применимо только к системам, в которых есть трение.

Если бы трения совсем не было, то процесс установления колебаний продолжался бы бесконечно долго. Реально это означает, что полученное без учета трения выражение (8) для амплитуды вынужденных колебаний будет правильно описывать колебания в системе только спустя достаточно большой промежуток времени после начала действия вынуждающей силы. Слова «достаточно большой промежуток времени» означают здесь, что уже закончился переходный процесс, длительность которого совпадает с характерным временем затухания собственных колебаний в системе.

При малом трении установившиеся вынужденные колебания происходят в фазе с вынуждающей силой при и в противофазе при как и в отсутствие трения. Однако вблизи резонанса фаза меняется не скачком, а непрерывно, причем при точном совпадении частот смещение отстает по фазе от вынуждающей силы на (на четверть периода). Скорость изменяется при этом в фазе с вынуждающей силой, что обеспечивает наиболее благоприятные условия для передачи энергии от источника внешней вынуждающей силы к осциллятору.

Какой физический смысл имеет каждый из членов в уравнении (4), описывающем вынужденные колебания осциллятора?

Что такое установившиеся вынужденные колебания?

При каких условиях можно использовать формулу (8) для амплитуды установившихся вынужденных колебаний, полученную без учета трения?

Что такое резонанс? Приведите известные вам примеры проявления и использования явления резонанса.

Опишите сдвиг по фазе между вынуждающей силой и смещением при разных соотношениях между частотой со в вынуждающей силы и собственной частотой осциллятора.

Чем определяется длительность процесса установления вынужденных колебаний? Дайте обоснование ответа.

Векторные диаграммы. Убедиться в справедливости приведенных выше утверждений можно, если получить решение уравнения (4), описывающее установившиеся вынужденные колебания при наличии трения. Поскольку установившиеся колебания происходят с частотой вынуждающей силы со и некоторым сдвигом по фазе то решение уравнения (4), соответствующее таким колебаниям, следует искать в виде

При этом скорость и ускорение, очевидно, тоже будут изменяться со временем по гармоническому закону:

Амплитуду а установившихся вынужденных колебаний и сдвиг фазы удобно определять с помощью векторных диаграмм. Воспользуемся тем обстоятельством, что мгновенное значение любой изменяющейся по гармоническому закону величины можно представить как проекцию вектора на некоторое заранее выбранное направление, причем сам вектор равномерно вращается в плоскости с частотой со, а его неизменная длина равна

амплитудному значению этой осциллирующей величины. В соответствии с этим сопоставим каждому члену уравнения (4) вращающийся с угловой скоростью вектор, длина которого равна амплитудному значению этого члена.

Поскольку проекция суммы нескольких векторов равна сумме проекций этих векторов, то уравнение (4) означает, что сумма векторов, сопоставляемых членам, стоящим в левой части, равна вектору, сопоставляемому величине стоящей в правой части. Чтобы построить эти векторы, выпишем мгновенные значения всех членов левой части уравнения (4), учитывая соотношения

Из формул (13) видно, что вектор длины сопоставляемый величине опережает на угол вектор сопоставляемый величине Вектор длины сопоставляемый члену х, опережает на вектор длины т. е. эти векторы направлены в противоположные стороны.

Взаимное расположение этих векторов для произвольного момента времени показано на рис. 181. Вся система векторов вращается как целое с угловой скоростью со против часовой стрелки вокруг точки О.

Рис. 181. Векторная диаграмма вынужденных колебаний

Рис. 182. Вектор сопоставляемый внешней силе

Мгновенные значения всех величин получаются проецированием соответствующих векторов на заранее выбранное направление Вектор, сопоставляемый правой части уравнения (4), равен сумме векторов, изображенных на рис. 181. Это сложение показано на рис. 182. Применяя теорему Пифагора, получаем

откуда находим амплитуду установившихся вынужденных колебаний а:

Сдвиг фазы между вынуждающей силой и смещением как видно из векторной диаграммы на рис. 182, отрицателен, так как вектор длины отстает от вектора Поэтому

Итак, установившиеся вынужденные колебания происходят по гармоническому закону (10), где а и определяются формулами (14) и (15).

Рис. 183. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы

Резонансные кривые. Амплитуда установившихся вынужденных колебаний пропорциональна амплитуде вынуждающей силы Исследуем зависимость амплитуды колебаний от частоты вынуждающей силы. При малом затухании у эта зависимость имеет очень резкий характер. Если то при стремлении со к частоте свободных колебаний амплитуда вынужденных колебаний а стремится к бесконечности, что совпадает с полученным ранее результатом (8). При наличии затухания амплитуда колебаний в резонансе уже не обращается в бесконечность, хотя и значительно превышает амплитуду колебаний под действием внешней силы той же величины, но имеющей частоту, далекую от резонансной. Резонансные кривые при разных значениях постоянной затухания у приведены на рис. 183. Для нахождения частоты резонанса сорез, нужно найти, при каком со подкоренное выражение в формуле (14) имеет минимум. Приравнивая производную этого выражения по со нулю (или дополняя его до полного квадрата), убеждаемся, что максимум амплитуды вынужденных колебаний имеет место при

Резонансная частота оказывается меньше частоты свободных колебаний системы. При малых 7 резонансная частота практически совпадает с При стремлении частоты вынуждающей силы к бесконечности, т. е. при амплитуда а, как видно из (14), стремится к нулю. При т. е. при действии постоянной внешней силы, амплитуда Если подставить сюда и получим Это есть статическое смещение осциллятора из положения равновесия под действием постоянной силы и смещение осциллятора происходит в противофазе с вынуждающей силой. В резонансе, как видно из (15), смещение отстает по фазе от внешней силы на Вторая из формул (13) показывает, что при этом внешняя сила изменяется в фазе со скоростью т. е. все время действует в направлении движения. Что именно так и должно быть, ясно из интуитивных соображений.

Резонанс скорости. Из формулы (13) видно, что амплитуда колебаний скорости при установившихся вынужденных колебаниях равна . С помощью (14) получаем

Рис. 184. Амплитуда скорости при установившихся вынужденных колебаниях

Зависимость амплитуды скорости от частоты внешней силы показана на рис. 184. Резонансная кривая для скорости хотя и похожа на резонансную кривую для смещения, но отличается от нее в некоторых отношениях. Так, при т. е. при действии постоянной силы, осциллятор испытывает статическое смещение из положения равновесия и скорость его после того, как закончится переходный процесс, равна нулю. Из формулы (19) видно, что амплитуда скорости при обращается в нуль. Резонанс скорости имеет место при точном совпадении частоты внешней силы с частотой свободных колебаний

Как строятся векторные диаграммы для установившихся вынужденных колебаний при синусоидальном внешнем воздействии?

Чем определяется частота, амплитуда и фаза установившихся вынужденных гармонических колебаний?

Опишите различия резонансных кривых для амплитуды смещения и амплитуды скорости. Какими характеристиками колебательной системы определяется острота резонансных кривых?

Как связан характер резонансной кривой с параметрами системы, определяющими затухание ее собственных колебаний?

13.2 Свойства волн: скорость, амплитуда, частота и период — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Определение амплитуды, частоты, периода, длины волны и скорости волны
• Связь частоты волны, периода, длины волны и скорости
• Решение задач, связанных со свойствами волн

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим ученикам освоить следующие стандарты:

• (7) Научные концепции. Учащийся знает характеристики и поведение волн. Ожидается, что студент:
  • (В) исследовать и анализировать характеристики волн, включая скорость, частоту, амплитуду и длину волны, и рассчитывать, используя взаимосвязь между скоростью волны, частотой и длиной волны;
  • (D) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.

Ключевые термины раздела

Служба поддержки учителей

Служба поддержки учителей

[BL][OL][AL] Проверьте амплитуду, период и частоту простого гармонического движения.

Волновые переменные

В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:

• Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
• Частота — количество событий в единицу времени
• Период — время, необходимое для совершения одного колебания

Для волн эти переменные имеют одинаковое основное значение. Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:

• Амплитуда — расстояние между положением покоя и максимальным смещением волны
• Частота — количество волн, проходящих через определенную точку в секунду
• Период — время, необходимое для завершения одного цикла волны

Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны.Длина волны λλ — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения. Скорость волны vwvw — это скорость, с которой движется возмущение.

Советы для достижения успеха

Скорость волны иногда также называют скоростью распространения или скоростью распространения , потому что возмущение распространяется из одного места в другое.

Рассмотрим периодическую волну воды на рис. 13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины.Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо с волновой скоростью v _w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны. Важно отметить, что это движение волны на самом деле является возмущением , движущимся вправо, а не самой водой; в противном случае птица двигалась бы вправо.Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 X за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.

Рисунок 13.7 Волна имеет длину волны λ , что является расстоянием между соседними идентичными частями волны. Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v _w .

Смотреть физику

Амплитуда, период, частота и длина волны периодических волн

Это видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.

советов для достижения успеха

Гребень волны иногда также называют пиком .

Проверка захвата

Смотреть Физика: амплитуда, период, частота и длина волны периодических волн.В этом видео представлены несколько концепций звука; амплитуда, период, частота и длина волны периодических волн.

Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1\,\text{м}, какова высота волны с вашего местоположения?

1. 1\,\текст{м}
2. 2\,\текст{м}
3. 4\,\текст{м}
4. 8\,\текст{м}

Связь между частотой волны, периодом, длиной волны и скоростью

Поскольку частота волны — это количество волн в секунду, а период — это, по сути, количество секунд на волну, связь между частотой и периодом равна

или

так же, как и в случае гармонического движения объекта.Из этого соотношения видно, что более высокая частота означает более короткий период. Напомним, что единицей измерения частоты является герц (Гц), а 1 Гц — это один цикл — или одна волна — в секунду.

Скорость распространения v _w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как

или

Из этого соотношения мы видим, что в среде, где v _w постоянно, чем выше частота, тем меньше длина волны.См. рисунок 13.8.

Рисунок 13.8. Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.

Поддержка учителя

Поддержка учителя

[BL] Для звука более высокая частота соответствует более высокому тону, а более низкая частота соответствует более низкому тону.Амплитуда соответствует громкости звука.

[BL][OL] Поскольку звук на всех частотах имеет одинаковую скорость в воздухе, изменение частоты означает изменение длины волны.

[Поддержка рисунка] Один и тот же динамик способен воспроизводить как высокочастотные, так и низкочастотные звуки. Однако высокие частоты имеют более короткую длину волны и, следовательно, лучше всего воспроизводятся динамиком с маленьким, твердым и плотным диффузором (твитер), тогда как более низкие частоты лучше всего воспроизводятся с большим и мягким диффузором (вуфер).

Эти фундаментальные соотношения справедливы для всех типов волн. Например, для волн на воде v _w — это скорость поверхностной волны; для звука v _w — скорость звука; а для видимого света v _w — это скорость света. Амплитуда X совершенно не зависит от скорости распространения v _w и зависит только от количества энергии в волне.

Snap Lab

Волны в чаше

В этой лаборатории вы проведете измерения, чтобы определить, как на амплитуду и период волн влияет передача энергии от пробки, брошенной в воду. Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.

• Большая чаша или таз
• Вода
• Пробка (или мячик для пинг-понга)
• Секундомер
• Рулетка

Инструкции

Процедура

1. Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
2. Аккуратно бросьте пробку в середину чаши.
3. Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, посчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
4. Выньте пробку из миски и подождите, пока вода снова не осядет.
5. Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
6. Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, сбрасывая пробку с разной высоты и записывая полученные длины волн и периоды.
7. Интерпретируйте свои результаты.

Проверка захвата

Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?

1. Нет, влияет только на амплитуду.
2. Да, длина волны затронута.

Поддержка учителя

Поддержка учителя

Учащиеся могут заранее измерить чашу, чтобы лучше оценить длину волны.

Ссылки на физику

Геология: физика сейсмических волн

Рис. 13.9 Разрушительный эффект землетрясения является ощутимым свидетельством энергии, переносимой волнами землетрясения. Оценка землетрясений по шкале Рихтера связана как с их амплитудой, так и с энергией, которую они несут.(старшина 2-го класса Кэндис Вильярреал, ВМС США)

Геологи в значительной степени полагаются на физику при изучении землетрясений, поскольку землетрясения связаны с несколькими типами волновых возмущений, включая возмущение поверхности Земли и возмущения давления под поверхностью. Поверхностные волны землетрясения подобны поверхностным волнам на воде. Волны под поверхностью Земли имеют как продольную, так и поперечную составляющие. Продольные волны при землетрясении называются волнами давления (P-волнами), а поперечные волны называются поперечными волнами (S-волнами).Эти два типа волн распространяются с разными скоростями, и скорость, с которой они распространяются, зависит от жесткости среды, в которой они распространяются. Во время землетрясений скорость Р-волн в граните значительно превышает скорость S-волн. Оба компонента землетрясений распространяются медленнее в менее жестких материалах, таких как отложения. P-волны имеют скорость от 4 до 7 км/с, а S-волны — от 2 до 5 км/с, но обе они быстрее в более жестких материалах. P-волна постепенно опережает S-волну по мере того, как они проходят через земную кору.По этой причине разница во времени между продольными и поперечными волнами используется для определения расстояния до их источника — эпицентра землетрясения.

Из сейсмических волн, создаваемых землетрясениями, мы знаем, что части недр Земли жидкие. Сдвиговые или поперечные волны не могут проходить через жидкость и не передаются через ядро ​​Земли. Напротив, волны сжатия или продольные волны могут проходить через жидкость и проходят через ядро.

Все волны несут энергию, и энергию волн землетрясений легко наблюдать, основываясь на количестве повреждений, оставшихся после того, как земля перестала двигаться.Землетрясения могут сровнять с землей целые города, выполняя работу тысяч шаров-разрушителей. Количество энергии в волне связано с ее амплитудой. Землетрясения большой амплитуды вызывают большие смещения грунта и больший ущерб. По мере распространения волн землетрясения их амплитуда уменьшается, поэтому чем дальше они удаляются от источника, тем меньше повреждений.

Проверка захвата

Какая связь между скоростью распространения, частотой и длиной волны S-волн при землетрясении?

1. Соотношение между скоростью распространения, частотой и длиной волны vw=fλ.vw=fλ.
2. Соотношение между скоростью распространения, частотой и длиной волны vw=fλ.vw=fλ.
3. Соотношение между скоростью распространения, частотой и длиной волны vw=λf.vw=λf.
4. Соотношение между скоростью распространения, частотой и длиной волны vw=fλ.vw=fλ.

Виртуальная физика

Волна на струне

В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение».Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.

Проверка захвата

Какая из настроек — амплитуда, частота, затухание или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?

1. Частота; он уменьшает амплитуду волны по мере ее распространения.
2. Частота; он увеличивает амплитуду волны по мере ее распространения.
3. Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
4. Демпфирование; он увеличивает амплитуду волны по мере ее распространения.

Решение волновых задач

Рабочий пример

Расчет скорости распространения волн: чайка в океане

Рассчитайте скорость морской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10. 0 м, а время покачивания чайки вверх и вниз составляет 5,00 с.

Стратегия

Даны значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем использовать vw=λTvw =λT, чтобы найти скорость волны.

Решение

Введите известные значения в vw=λTvw=λT

vw=10,0 м5,00 с=2,00 м/с. vw=10,0 м5,00 с=2,00 м/с.

13,5

Обсуждение

Такая низкая скорость кажется приемлемой для океанской волны.Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.

Рабочий пример

Расчет периода и скорости волны игрушечной пружины

Женщина на рис. 13.3 создает две волны каждую секунду, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (b) Если каждая волна проходит 0,9 метра после одного полного волнового цикла, какова скорость распространения волны?

Стратегия ДЛЯ (А)

Чтобы найти период, мы решаем T=1fT=1f, учитывая значение частоты (f=2s−1). (f=2с−1).

Раствор для (а)

Введите известное значение в T=1fT=1f

T=12 с-1=0,5 с. T=12 с-1=0,5 с.

13,6

Стратегия ДЛЯ (Б)

Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, приводятся значения длины волны (λ = 0,9 м) (λ = 0,9 м), а также частоты. Следовательно, мы можем использовать vw=fλvw=fλ, чтобы найти скорость волны.

Решение для (б)

Введите известные значения в vw=fλvw=fλ

vw=fλ=(2 s−1)(0.9 м) = 1,8 м/с. vw=fλ=(2 с−1)(0,9 м) = 1,8 м/с.

Обсуждение

Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части (a), и мы пришли бы к тому же ответу.

Практические задачи

7.

Частота волны 10 Гц. Каков его период?

1. Период волны 100 с.
2. Период волны 10 с.
3. Период волны 0,01 с.
4. Период волны 0,1 с.

8.

Какова скорость волны с длиной волны 2 м и частотой 5 Гц?

1. 20 м/с
2. 2,5 м/с
3. 0,4 м/с
4. 10 м/с

Проверьте свое понимание

Поддержка учителей

Поддержка учителей

Используйте эти вопросы, чтобы оценить достижения учащихся в соответствии с целями обучения раздела.Если учащиеся борются с определенной целью, эти вопросы помогут определить такую ​​цель и направить их к соответствующему содержанию.

9.

Какова амплитуда волны?

1. Четверть общей высоты волны
2. Половина общей высоты волны
3. Удвоенная общая высота волны
4. Четырехкратная общая высота волны

10.

Что понимают под длиной волны?

1. Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.
2. Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
3. Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
4. Длина волны — это расстояние между гребнем и прилегающей впадиной волны, перпендикулярное направлению распространения.

11.2

12.

Когда длина волны прямо пропорциональна периоду волны?

1. Когда скорость волны уменьшается вдвое
2. Когда скорость волны постоянна
3. Когда скорость волны удваивается
4. Когда скорость волны утроится

Объясните связь между частотой и периодом времени

Мы знаем, что число полных колебаний колеблющейся частицы за одну секунду называется ее частотой.Частота обозначается f. Опять же, период времени — это время одной полной вибрации. Частота и период являются обратно пропорциональными величинами. Частота (f) волны — это количество полных сигналов, генерируемых в секунду. Это то же самое, что количество повторений в секунду или количество колебаний в секунду.

Период времени (T) — количество секунд на сигнал или количество секунд на колебание. Ясно, что частота и период времени обратны.

Если период времени T, то за T секунд количество вибраций равно 1

Следовательно, количество вибраций в одну секунду = 1/T

Количество вибраций в 1 секунду – это частота.Итак, частота f = 1/T

Частота означает, как часто что-то происходит; тогда как период относится ко времени, которое требуется для того, чтобы что-то произошло. Частота означает, сколько раз периодическое событие происходит в секунду.
Период — это время между любыми двумя событиями. Как правило, период должен быть обратен частоте, отсюда и уравнение: Период = 1/Частота.

Частота, f, представляет собой количество циклов колебаний в секунду и измеряется в циклах в секунду или герцах (Гц). Период волны Т — это время, за которое волна совершает один полный цикл колебаний. Эти два члена обратно пропорциональны друг другу: f = 1/T и T = 1/f.

Например, если волне требуется 1 секунда, чтобы колебаться вверх и вниз, период волны равен 1 секунде. Частота обратно пропорциональна 1 циклу в секунду, потому что в секунду происходит только один цикл.

Математический пример: Длина волны звука, производимого объектом в воздухе, составляет 20 см.Если скорость звука в воздухе 340 мс ^-1 , найдите частоту и период объекта.

Здесь, Длина волны, γ = 20 см = 0,2 м

Скорость звука = 340 мс ^-1

Частота, f =?

Период (время), T = ?

Мы знаем, Скорость = fγ

Итак, f = v/γ = 340 мс ^-1 / 0,20 м = 1700 Гц

И T = 1/f = 1 / 1700 с ^-1 = 0,00 = 5,88 x 10 ^-4 с

Частота 1700 Гц; Период (время) 5.88 x 10 ^-4 с (Обратное, потому что если частота высока, то период времени низок).

Частота — это величина скорости. Период – это величина времени. Частота — это количество циклов в секунду, обозначаемое как Герц (Гц). Период — секунды/цикл. Период – во времени – измеряется в секундах, часах, днях или годах.

Частота — Период — Видео физики от Brightstorm

Хорошо. Поговорим о частоте и периоде волны. Частота и период — это свойства периодических волн, поэтому они и называются периодическими волнами, поэтому частота — это количество волн, которые проходят данную точку за определенный промежуток времени.Как вы помните, периодическая волна — это волна, которая ударяет снова и снова и снова, и поэтому частота характеризует, сколько раз она атакует среду за заданный промежуток времени.

Точка в каком-то смысле противоположна этому. Это то, сколько времени требуется одной волне, чтобы атаковать среду. Хорошо. Итак, у нас есть очень простой способ думать о периоде. Итак, представьте, что вы находитесь в океане. Итак, вы в лодке в океане и подошли к гребню волны. Период — это то, сколько времени вам потребуется, чтобы спуститься и вернуться к следующему гребню. Так что это действительно простой способ понять, что означает период.

Хорошо. Итак, давайте продолжим и просто сделаем пример с частотой. Предположим, что частота составляет 3 волны в секунду. И, конечно, это имеет смысл, если частота показывает, сколько волн приходит за заданный промежуток времени, тогда 3 волны в секунду означают, что за одну секунду приходят 3 волны. Хорошо. Обычно мы не используем волны в секунду в качестве единицы измерения, вместо этого мы используем единицу измерения герц, названную в честь нашего физика, который фактически первым представил электромагнитные волны в 1887 году.Хорошо.

Таким образом, мы могли бы сказать, что частота составляет 3 герца. Так какой период? Ну что ж, посмотрим. Если каждую секунду приходят 3 волны, то сколько времени длится каждая волна? Ну, 3 волны в секунду, каждая займет треть секунды. Так что это дает нам на самом деле очень-очень общее соотношение между частотой и периодом. Частота равна единице за период. Это всегда так. Это следует непосредственно из определений этих величин, и это всегда приятно, потому что это означает, что я всегда могу записать это, и оно никогда не будет неправильным.Хорошо.

Итак, давайте продолжим и посмотрим на некоторые свойства, связанные с этой реальностью. Частота умноженная на период равна единице. Это означает, что если я увеличу частоту, ну, господи, это число станет больше, но результат останется прежним, поэтому период должен уменьшиться. Таким образом, большая частота, меньший период. И наоборот, чем меньше частота, тем больше период. Хорошо? Еще одна вещь, которую я видел во многих тестах, спрашивают, если я удвою частоту, что произойдет с периодом? Что ж, это очень просто, потому что у меня здесь 2, удваивая частоту, но мне нужно, чтобы продукт оставался прежним.Так что я должен положить одну половину там. Поэтому, если я удвою частоту, я уменьшу период вдвое. И наоборот, если я урежу частоту вдвое, я удвою период. Очень, очень, очень просто, но иногда ученики не замечают, как это происходит и насколько это просто, пока не увидят пример.

Хорошо. Еще одно важное свойство частоты и периода, которое появится намного позже в более поздних исследованиях периодических волн, заключается в том, что период и частота не могут измениться. И это на самом деле замечательная вещь о периоде и частоте.Потому что другие свойства волны изменятся. Если я поступлю так, как если бы ко мне проник свет и он попал на кусок стекла, многие его свойства изменились бы, но его частота и период не изменились бы. Почему? Ну, это очень просто. Если у вас есть 3 волны, приходящие в секунду, у вас должно быть 3 волны, уходящие в секунду. Потому что иначе волны соберутся на границе, а граница этого не выдержит. Таким образом, частоту и период можно использовать для характеристики волны, когда она проходит через то, через что она собирается пройти.Что бы с ним ни случилось, частота и период остаются неизменными. И это частота и период.

Разница между периодом и частотой

Основное различие между периодом и частотой заключается в их определении. Оба они являются вибрационными характеристиками. Колебания и вибрации механических систем являются важными областями изучения в физике. Почти все системы свободно колеблются или вибрируют по-разному.

Колебание — это повторяющееся движение инструмента, обычно во времени, вокруг центрального состояния или между двумя или более отдельными точками.Именно термин «вибрация» описывает механические колебания. Чтобы узнать больше о разнице между колебаниями и вибрацией, вы можете посетить эту ссылку. Типичными примерами колебаний являются качающийся маятник, гитарные струны, биение сердца и переменный ток. Даже атомы нашего тела вибрируют.

Каждая колебательная система имеет нечто общее, включая силу и энергию. Раскачивая ребенка на качелях, начинается движение. Также при использовании тепла увеличивается энергия атомов, и они вибрируют. Таким образом, колебания порождают волны.

Характерной чертой всех волн является периодичность. Ясно, что несколько фундаментальных принципов описывают все явления, которые доказывают, что они более распространены, чем вы думали. В каждом явлении вы видите определенную модель движения, которая повторяется снова и снова. Периодические движения, такие как движение струны гитары или движение ребенка вперед и назад на качелях, повторяются через равные промежутки времени. Время, необходимое для завершения цикла вибрации или колебаний, называется периодом волны.Частота – это параметр, равный количеству циклов колебаний в секунду.

Основы периода и частоты

Принципиальное различие между периодом и частотой восходит к их определению.

Период

Период определяется как время, необходимое для одного полного цикла вибрации или колебаний. Это относится ко времени периодического возникновения, измеряемому в секундах за цикл. Период обычно обозначается буквой «Т».

Частота

Частота волны относится к числу полных циклов вибрации или колебаний, происходящих в одну секунду. Единицей измерения частоты являются циклы в секунду или герц (Гц). Частота обычно обозначается буквой «f».

Оба значения периода времени и частоты обратно пропорциональны друг другу. На математическом языке период и частота связаны следующим уравнением:

Т=\фракция{1}{е}

или

f=\frac{1}{T}

Характеристика периода и частоты

Определения периода и частоты показывают, что природа этих двух параметров различна.

Период

Исходя из определения периода как продолжительности завершения волнового цикла в его единице, т. е. времени, природа периода — время.

Частота

Частота как количество полных циклов, происходящих в единицу времени, является величиной скорости.

Схемы периода и частоты

В этом разделе мы хотим проиллюстрировать понятия периода и частоты волны на диаграммах.

Период 

Если мы посмотрим на диаграмму распространения повторяющихся волн с точки зрения времени, мы можем представить период как расстояние между двумя последовательными гребнями волны (или идентичными последовательными точками) на временной оси.

Волна как функция времени, чтобы показать период

Рассмотрим волну, которая совершает два полных цикла в секунду (как показано ниже). Следовательно, частота этой волны равна 2 Гц.

Волна как функция времени для отображения периода (Ссылка: Circuitglobe.com )

Отношение периода и частоты к длине волны

Рассмотрим распространение волны со скоростью v в м/с. Расстояние между двумя последовательными идентичными точками (например, двумя гребнями или впадинами) на волновой диаграмме как функция расстояния называется длиной волны. Обозначается греческой буквой «λ» и измеряется в метрах.

Волна как функция расстояния для отображения длины волны (ссылка: afsharphysics.wordpress.com )

Период 

Период и длина волны связаны следующим уравнением:

Т = \ гидроразрыва {\ лямбда} {v}

Частота

Связь между частотой и длиной волны определяется следующим уравнением:

f=\frac{v}{\lambda}

Это может быть очевидно, так как период и частота обратно пропорциональны друг другу.

Пример периода и частоты

Для лучшего понимания частоты и периода посмотрите на этот пример. Рассмотрим человеческое сердце, бьющееся 75 раз в минуту. Если рассматривать каждый раз полный цикл, то придется вычислять период и частоту:

Период

Использование математического определения периода приводит к:

T=\frac{Общее\время}{Количество\ циклов}=\frac{60}{75}=0,8\ (с)

Частота

Для расчета частоты имеем:

f=\frac{Количество\циклов}{Общее\время}=\frac{1}{T}=\frac{75}{60}=1. 25\ (Гц)

Период и частота в физике

Понятия периода и частоты широко используются в физике, особенно в области энергетики.

Период 

Хорошо известным примером применения периода является движение маятника. Период этого движения – это время, затрачиваемое на перемещение из одной стороны в другую и обратно.

Другим физическим примером является электрон, движущийся по винтовой орбите. Он имеет период, заданный:

T=\frac{2\pi·m}{qB}

, где m , q и B — масса электрона, заряд электрона и магнитное поле в области.

Частота

Частота является важным параметром в инженерных и научных приложениях. Он определяет скорость колебательных и вибрационных событий, таких как механические вибрации, звуковые сигналы, радиоволны и свет.

Частота волны совпадает с частотой вибрации, создающей волну. Чтобы создать волну с более высокой частотой в веревке, вы должны перемещать веревку вверх и вниз с большей скоростью. При этом потребляется больше энергии, и эта энергия передается волне.Следовательно, высокочастотные волны обладают большей энергией, чем низкочастотные волны той же амплитуды.

Частота обычно представлена ​​в двух формах:

Угловая частота

Угловая частота определяет количество оборотов за фиксированный интервал времени. Единицей угловой частоты является Герц. Следующее уравнение выражает отношение между частотой и угловой частотой:

\омега=2\пи f

Где ω — угловая частота.

Пространственная частота

Пространственная частота зависит от пространственной координаты и обратно пропорциональна длине волны. Пространственная частота содержит характеристику системы, периодически работающей в пространстве.

Низкие и высокие пространственные частоты (Ссылка: cns.nyu.edu )

Разница между периодом и частотой

Колебания и колебания механических систем остаются одной из важнейших областей изучения физики. Практически каждая система свободно колеблется или вибрирует самыми разнообразными способами.

Что общего у океанского буя, гитары, ребенка на качелях или биения сердца? Все они колеблются, то есть двигаются вперед и назад между двумя точками. Человеческое тело само по себе является сокровищницей вибрационных явлений. Даже атомы в нашем теле вибрируют. Каждая система, которая колеблется, имеет что-то общее. Он включает в себя силу и энергию. Вы начинаете движение, раскачивая ребенка на качелях, или можете увеличить энергию атомов, вибрирующих в кристалле с помощью тепла.Таким образом, колебания создают волны.

Что общего между колебаниями и волнами? Признак, роднящий такие явления, – периодичность. Понятно, что небольшое количество основополагающих принципов описывает все явления, что доказывает, что они распространены больше, чем вы могли себе представить. Вы заметите определенную закономерность или движение в каждом явлении, которое повторяется снова и снова. Периодическое движение — это движение, которое повторяется снова и снова через равные промежутки времени, например движение гитарной струны или движение вперед и назад ребенка на качелях. Время, за которое совершается один колебательный цикл или колебание, называется периодом волны. Частота просто относится к числу циклов колебаний, происходящих в секунду.

Что такое частота?

Частота волны просто относится к числу полных циклов или колебаний, которые происходят в одну секунду. Измеряется в циклах в секунду или герцах (Гц). Цикл — это одно полное колебание, а колебание может быть единичным или множественным событием, тогда как колебания в основном повторяются в течение нескольких циклов.Обычно он обозначается буквой «f» и выражается как:

f = 1/T, где «T» представляет период времени, а «f» — частоту.

Что такое период?

Период обратно пропорционален частоте и определяется как время, необходимое для одного полного прохождения вибрации или колебаний туда и обратно. Это просто относится ко времени, когда что-то происходит периодически, и измеряется в секундах за цикл. Период времени обратно пропорционален частоте, что означает, что обе величины обратно пропорциональны друг другу. В форме уравнения период выражается как:

T = 1/f, где f — частота, а T — период времени.

Разница между периодом и частотой

1. Определение периода и частоты

Термины «период» и «частота» связаны между собой, поскольку демонстрируют определенную модель движения, однако они совершенно разные. Оба относятся к периодическим явлениям и часто путаются друг с другом. Период относится к количеству времени, которое требуется волне для завершения одного полного цикла колебаний или вибрации.Частота, напротив, относится к числу полных циклов или колебаний, происходящих в секунду. Период — это величина, связанная со временем, тогда как частота связана со скоростью. Период просто означает время, в течение которого что-то происходит периодически, тогда как частота означает, как часто это происходит.

2. Связь периода и частоты

Обе величины обратно пропорциональны друг другу. Частота выражается в циклах в секунду, колебаниях в секунду, колебаниях в секунду и т. д.и обычно обозначается буквой «ф». Период выражается в секундах за цикл. Единицей частоты является герц (Гц), а «Т» представляет период времени одного полного колебания. С математической точки зрения обе величины обратны друг другу. В форме уравнения частота и период выражаются как:

f = 1/T, где f — частота, а T — период.

Можно также выразить как:

Т = 1/ф

3. Пример периода и частоты

Допустим, волне требуется одна секунда, чтобы колебаться вверх и вниз, что означает, что период времени волны равен 1 секунде.Частота и период обратно пропорциональны друг другу. Поскольку в секунду происходит только один цикл, частота волны будет равна 1 циклу в секунду. И если волне потребовалось полсекунды, чтобы совершить полный цикл, период этой волны был бы 0,5 секунды, а частота была бы 1/0,5 = 2, то есть 2 цикла в секунду. Таким образом, чем дольше период времени, тем ниже частота и наоборот.

Период и частота: сравнительная таблица

Резюме периода против.

Частота

И частота, и период времени являются фундаментальными параметрами волн, связанными друг с другом, но они явно различаются с точки зрения количества. Частота волны связана с величиной скорости, тогда как период волны связан с величиной времени. Период времени относится к времени, которое требуется волне для завершения одного полного цикла колебаний или вибрации, что обратно пропорционально частоте. Частота относится к количеству вибраций, которые происходят в одну секунду, что является обратным периодом времени.Частота обычно измеряется в герцах (Гц), а период измеряется в секундах. Оба обратно пропорциональны друг другу, что означает, что чем выше частота, тем ниже период, и наоборот. Частота обозначается буквой «f», а период обозначается буквой «T».

Сагар Хиллар — плодовитый автор контента / статей / блогов, работающий старшим разработчиком / писателем контента в известной фирме по обслуживанию клиентов, базирующейся в Индии. У него есть желание исследовать разноплановые темы и разрабатывать высококачественный контент, чтобы его можно было лучше всего читать. Благодаря его страсти к писательству, он имеет более 7 лет профессионального опыта в написании и редактировании услуг на самых разных печатных и электронных платформах.

Вне своей профессиональной деятельности Сагар любит общаться с людьми из разных культур и происхождения. Можно сказать, что он любопытен по натуре. Он считает, что каждый — это опыт обучения, и это приносит определенное волнение, своего рода любопытство, позволяющее продолжать работу. Поначалу это может показаться глупым, но через некоторое время это расслабит вас и вам будет легче начать разговор с совершенно незнакомыми людьми — вот что он сказал.»

Последние сообщения Сагар Хиллар (посмотреть все)

: Если вам понравилась эта статья или наш сайт. Пожалуйста, расскажите об этом. Поделитесь им с друзьями/семьей.

См.
APA 7
Хиллар, С. (2018, 21 августа). Разница между периодом и частотой. Разница между похожими терминами и объектами. http://www.differencebetween. net/science/mathematics-statistics/difference-between-period-and-frequency/.
MLA 8
Хиллар, Сагар.«Разница между периодом и частотой». Разница между похожими терминами и объектами, , 21 августа 2018 г., http://www.differencebetween.net/science/mathematics-statistics/difference-between-period-and-frequency/.

Частота и период — AP Physics 1

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105

Или заполните форму ниже:

Параметры волны

: длина волны, амплитуда, период, частота и скорость — видео и стенограмма урока

Период и частота

Период — это время, которое требуется волне для завершения одного цикла. Мы измеряем период в секундах и обозначаем его заглавной буквой T . Вы можете думать о периоде как о времени, которое требуется одной частице в среде, чтобы двигаться вперед и назад. Если бы это была водная волна, все частицы в воде двигались бы вверх и вниз по мере прохождения волны. Время, за которое одна молекула воды движется вверх, опускается вниз и затем возвращается в исходное положение, называется периодом.

Хорошо знать период волны, но нам часто нужно говорить о волнах с точки зрения того, как часто приходят волновые циклы.Другими словами, мы хотим знать частоту волны. Частота волны — это количество циклов, которые совершаются за определенный промежуток времени. Частота обозначается строчными буквами f , и мы измеряем ее в циклах в секунду, что соответствует единице измерения в герцах. Волна с частотой 20 Гц каждую секунду совершает 20 волновых циклов.

Будьте осторожны, не путайте частоту с периодом. Это распространенная ошибка. Частота и период имеют обратную зависимость. В то время как период измеряется в секундах за цикл, частота измеряется в циклах в секунду. Рассмотрим нашу волну с периодом 2 секунды. Так как волна совершает один цикл каждые две секунды, то ее частота равна половине или 0,5 Гц. Итак, вы видите — период и частота обратны друг другу. Мы можем представить их отношение простым уравнением:

Это уравнение представляет соотношение между частотой и периодом.

Чем больше период волны, тем меньше волновых циклов может уместиться в секунду, и тем ниже становится частота.Точно так же волна с большей частотой должна была бы умещать больше волновых циклов в каждую секунду, а это означает, что период каждого цикла должен быть меньше. Независимо от того, на какую волну вы смотрите, период и частота всегда будут обратно пропорциональны друг другу.

Амплитуда и энергия

Итак, теперь мы знаем, как измерить волну на основе циклов и времени, но как насчет высоты волны? Можем ли мы измерить, как высоко достигает гребень волны или как низко опускается впадина? Мы уже упоминали амплитуду в нашем предыдущем уроке. Это расстояние между средней линией волны и ее гребнем или впадиной. Амплитуда измеряет, сколько энергии переносится волной. Чем больше амплитуда, тем больше энергии имеет волна.

Амплитуда обозначается заглавной буквой A . Будьте осторожны, чтобы не ошибиться, думая, что амплитуда — это расстояние от гребня до впадины. Это только расстояние от точки покоя. Возьмем в качестве примера гигантскую водную волну.

Амплитуда этой волны равна 0.5 метров.

Мы видим, что гребни достигают полуметра выше точки покоя, а впадины достигают полуметра ниже точки покоя. Неважно, смотрим ли мы на гребень или корыто. Амплитуда этой волны составляет 0,5 метра.

Скорость и длина волны

Если волны несут энергию, а энергия волны иллюстрируется ее амплитудой, значит ли это, что волны с большой амплитудой движутся быстрее, чем волны с малой амплитудой? У вас может возникнуть соблазн так подумать. Но скорость волны не имеет ничего общего с амплитудой ее гребней и впадин. Скорость измеряется расстоянием, которое волна проходит за определенное время. В частности, она измеряется в метрах в секунду. У нас уже есть часть «в секунду». Помните, частота говорит нам, сколько циклов совершается в секунду. Но откуда мы знаем, каково расстояние для каждого полного цикла?

Расстояние за цикл волны называется длиной волны .Легче всего найти длину волны, измерив пространственное расстояние между двумя гребнями волн. Ранее мы измеряли время, необходимое для завершения одного цикла. Но сейчас мы измеряем длину одного полного цикла волны. Длина волны длинных волн может быть измерена в метрах, но мы используем нанометры для измерения длины более коротких волн. Символом, обозначающим длину волны, является греческая буква лямбда.

Это символ длины волны.

Итак, теперь мы можем узнать скорость волны? Конечно! У нас есть мера расстояния по длине волны, и у нас есть мера времени по частоте. Длина волны в метрах на цикл. Частота циклов в секунду. Итак, умножение двух дает нам метры в секунду. В науке мы используем строчные буквы и для обозначения скорости, потому что это также называется скоростью. Итак, теперь мы можем суммировать наши выводы с помощью уравнения: скорость равна длине волны, умноженной на частоту.

Уравнение для расчета скорости волны

Ну, это было не так уж и плохо, не так ли? Вы узнали пять способов описания волны, используя ваши параметры волны .Период, частота, амплитуда, скорость и длина волны используются для различения и разделения волн на группы. Позже мы узнаем о множестве различных типов волн и о том, как использовать эти параметры, чтобы понять их все.

Краткий обзор урока

Волна — это возмущение, которое периодически проходит через среду, перенося энергию без переноса материи. Волны описываются и измеряются пятью волновыми параметрами: периодом, частотой, амплитудой, длиной волны и скоростью.