Формула связывающая линейную и угловую скорости: Линейная и угловая скорость, теория и онлайн калькуляторы
Кинематика вращательного движения
Если все точки тела совершают движения по окружностям, при этом все центры данных окружностей находятся на одной прямой, тогда такое движение тела (системы) называют вращением. При этом ось, на которой находятся центры окружностей, получила название оси вращения:
- ее положение может быть внутри тела (системы) или вне его;
- она может двигаться или быть неподвижной;
- плоскости траекторий движения точек тела перпендикулярны оси вращения;
- в трехмерном пространстве каждое вращение обладает осью вращения (теорема Эйлера).
Угловая скорость
Допустим, что некоторое твердое тело совершает вращения вокруг неподвижной оси. В таком движении точки данного тела описывают окружности. Центы этих окружностей принадлежат оси вращения, радиусы их различны.
Рассмотрим одну точку нашего тела. Пусть она перемещается по окружности, радиус которой равен $R$ (рис.1).
Рисунок 1.
Положение, рассматриваемой точки будем задавать при помощи угла поворота $\Delta \varphi$.
Элементарно малые углы поворота можно рассматривать как векторы. При этом величина вектора $d\vec \varphi$ равна величине угла поворота $\Delta \varphi$ (рис.1).
Направление $d\vec \varphi$ подчинено правилу правого буравчика, то есть направлено вдоль направления поступательного перемещения острия винта, при вращении его головки, совпадающем с направлением вращения точки по ее окружности.
$d\vec \varphi$ называют аксиальным вектором (псевдовектором). Псевдо векторы не имеют точки приложения, их изображают в любой точке на оси вращения.
Определение 1
$\vec \omega =\frac {d\vec \varphi}{dt} (1)$,
$\vec \omega$ — угловая скорость.
Вектор $\omega$ направлен по оси вращения (правило правого винта), и совпадает по направлению с элементарным углом поворота $d\vec \varphi$ (рис.1).
Единица $\omega$ — это радиан, деленный на секунду (рад/с).
Линейную скорость нашей материальной точки можно связать с угловой скоростью, эту связь легко установить, рассматривая рис.1.
$v=\lim {_{\Delta t \to 0}}( \frac {\Delta s}{\Delta t})=R \lim {_{\Delta t \to 0}}(\frac{\Delta \varphi}{\Delta t})=R\omega.$
Мы получили, линейная скорость по величине равна:
$v=\omega R (2).$
Определение 2
В виде вектора линейная скорость материальной точки, определяется так:
$\vec v = \vec \omega \times \vec R (3),$
где $R$ — радиус окружности.
Из формулы (3) следует, что величина линейной скорости равна:
$v=\omega \times R sin (\alpha )(4),$
где $\alpha$ — угол между векторами $\vec \omega$ и $\vec R$.
Направление результата векторного произведения в (4) определяет правило правого винта. Головку винта вращают от $\vec \omega$ к $\vec R$, поступательное перемещение острия указывает направление $\vec v$.
При постоянной угловой скорости вращение называют равномерным. 2}.$
2}.$
При движении по окружности вектор $\omega$ изменяется только по величине, не изменяя своего направления. В этом случае полное ускорение материальной точки можно найти, применяя выражение (3) и (8) как:
$\vec \varepsilon= \frac {d\vec \omega}{dt}=\frac {d\vec \omega}{dt} \times \vec R+\vec \omega \times \frac{d\vec R}{dt}=\frac {d\vec \omega}{dt} \times \vec R+ \vec \omega \times \vec v $.
Если тело совершает вращения около неподвижной оси, то $\vec \varepsilon$ имеет направление вдоль оси вращения тела.
Если угловая скорость вращения тела увеличивается (вращение ускоренное), то вектор углового ускорения и вектор угловой скорости сонаправлены.
При замедленном вращении векторы углового ускорения и угловой скорости имеют противоположные направления.
Тангенциальная и нормальная компоненты линейного ускорения
По определению, составляющая линейного ускорения ($a_{\tau}$), которая отвечает за изменение величины скорости движения тела (тангенциальное ускорение) равна:
$a_{\tau}=\frac{dv}{dt}(9).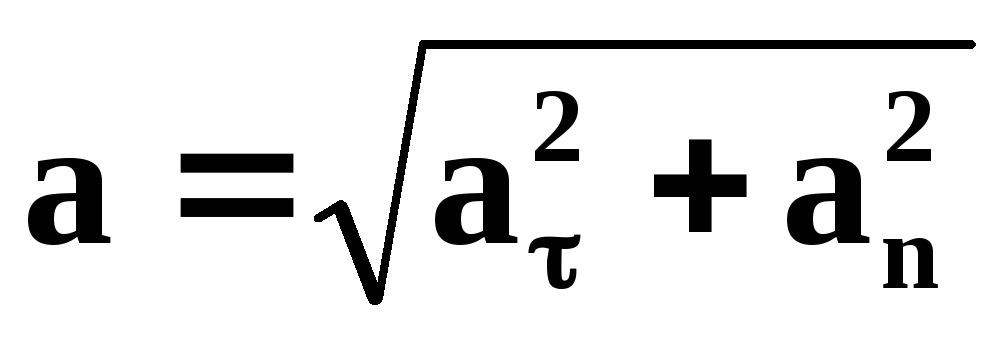 2}{2} (16)$
2}{2} (16)$
при равнозамедленном движении. В уравнениях (15) и (16) $\varphi_0 $ — начальный угол поворота.
|
ЗНАЕТЕ ЛИ ВЫ? |
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒ Угловой скоростьюназывается векторная величина, равная первой производной угла поворота тела по времени: .Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dф. Размерность угловой скорости dim = , а ее единица — радиан в секунду (рад/с). 7.Задачи динамики. Инерциальные системы отсчета. Первый закон Ньютона. Преобразования Галилея. Принцип относительности. Первый закон Ньютона: существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций(тело,которое при воздействии на него меняет свою форму или объём). Ма́сса — скалярная физическая величина, одна из важнейших величин в физике. Первый закон Ньютона: существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Второй закон Ньютона: в инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. F=ma; F –сила, приложенная к материальной точке; m –масса материальной точки; a –ускорение материальной точки; Третий закон Ньютона: материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F= -F. ?????9.Силы трения. Трение покоя и трение скольжения. Зависимость сил трения от скорости. Трение– один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел. 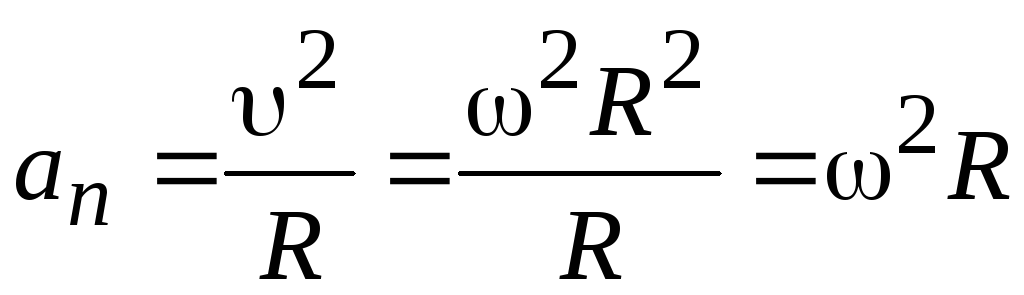 Внутренним трениемназывается трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Тело придет в движение лишь тогда, когда приложенная сила F будет больше силы трения FTр. Французские физики Г. Амонтон(1663—1705) и Ш. Кулон(1736—1806) опытным Путем установили следующий закон:сила трения скольжения FTp пропорциональна силе N нормального давления, с которой одно тело действует на другое: Fтр = ƒN, где ƒ — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей. Дерягиным был предложен закон трения скольжения:Fтр = ƒист (N + Sp0), где р0 – добавочное давление обусловленное силами межмолекулярного притяжения, оно быстро уменьшается с ростом расстояния, S – площадь контакта, ƒист – истинный коэффициент трения скольжения. Внутренним трениемназывается трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Тело придет в движение лишь тогда, когда приложенная сила F будет больше силы трения FTр. Французские физики Г. Амонтон(1663—1705) и Ш. Кулон(1736—1806) опытным Путем установили следующий закон:сила трения скольжения FTp пропорциональна силе N нормального давления, с которой одно тело действует на другое: Fтр = ƒN, где ƒ — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей. Дерягиным был предложен закон трения скольжения:Fтр = ƒист (N + Sp0), где р0 – добавочное давление обусловленное силами межмолекулярного притяжения, оно быстро уменьшается с ростом расстояния, S – площадь контакта, ƒист – истинный коэффициент трения скольжения.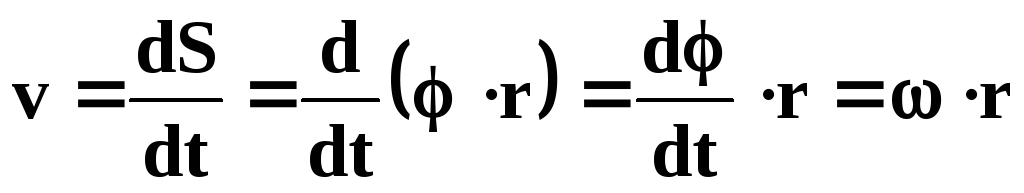 Как же зависят силы трения от скорости. 1) внешнее (сухое) не зависит от скорости; 2) внутреннее (вязкое) зависит от скорости Как же зависят силы трения от скорости. 1) внешнее (сухое) не зависит от скорости; 2) внутреннее (вязкое) зависит от скорости
Читайте также: |
Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7. |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7. |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.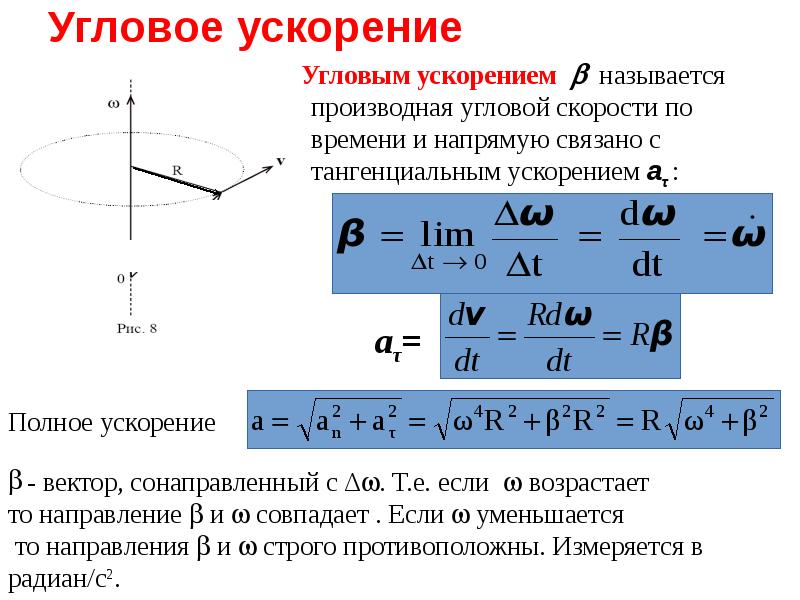 1.5), из формулы (7.5) находим квадрат угловой скорости диска
1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна .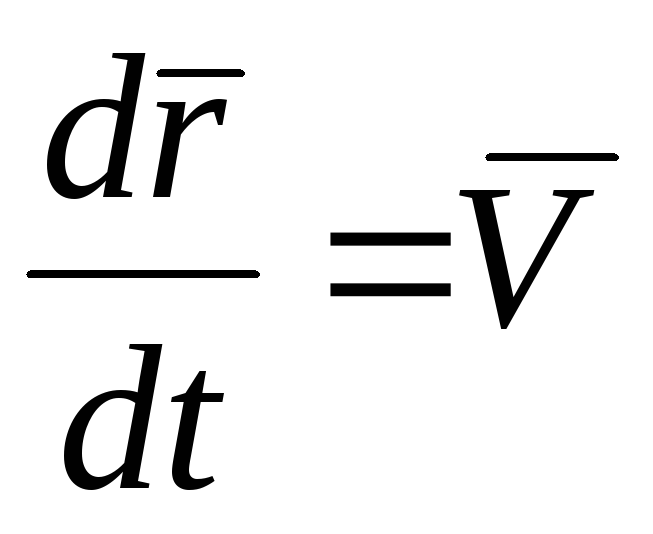 Поэтому центростремительное ускорение мальчика будет равно
Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7.2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
Угловая скорость, угловое ускорение, частота и период вращения. Связь между линейной скоростью и угловой, линейным ускорением и угловым.
Физические основы кассической механики
1). Основные понятия и формулы кинематики?
Основные понятия кинематики
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
Система отсчёта — сопоставленная с континуумом реальных или воображаемых тел отсчёта система координат и прибор(ы) для измерения времени (часы). Используется для описания движения.
Координаты — способ определять положение точки или тела с помощью чисел или других символов.
Траектория — непрерывная линия, которую описывает точка при своём движении.
Скорость — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. где — единичные векторы, направленные вдоль соответствующих координат.
Ускорение — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.
Материа́льная то́чка (частица) — простейшая физическая модель в механике — тело, размеры которого допустимо считать бесконечно малыми в пределах допущений исследуемой задачи. v=v’+u,
2) основные законы динамики. понятие силы и массы. виды сил в механике.
Классическая динамика основана на трёх основных законах Ньютона:
1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.
2-й: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).
В наиболее общем случае, который описывает также движение тела с изменяющейся массой (например, реактивное движение), 2-й закон Ньютона принято записывать следующим образом: где — импульс тела. Таким образом, сила характеризует быстроту изменения импульса.
3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению
Силой называют векторную величину, характеризующую такое действие на данное тело других тел (или полей), которое может вызвать ускорение и деформацию тела (здесь мы имеем в виду произвольное твердое тело, а не материальную точку).
Масса тела, являющаяся характеристикой его инерционных и гравитационных свойств, представляет собой величину, зависящую только от самого тела и не зависящую от того, в каких именно взаимодействиях с другими телами это тело участвует. Однако масса зависит от скорости движения тела. Эта зависимость обнаруживается только при движениях со скоростями, сравнимыми со скоростью света. Поэтому в физике различают два качественно различных случая движения.
Однородная сила тяжести
Упругая силапропорциональна смещению материальной точки из положения равновесия и направлена к положению равновесия: где -радиус-вектор, характеризующий смещение частицы из положения равновесия
Сила трения скольжения, возникающая при скольжении данного тела по поверхности другого тела,
Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости, называемая также силой вязкого трения. где — положительный коэффициент, характерный для данного тела и данной среды. Этот коэффициент зависит, вообще говоря, от скорости , однако при малых скоростях во многих случаях его можно практически считать постоянным.
Кулоновская сила, где: r- расстояние между зарядами, k — коэффициент пропорциональности, зависящий от выбора системы единиц. В отличие от гравитационной силы кулоновская сила может быть как силой притяжения, так и силой отталкивания.
Сила гравитационного притяжения, действующая между двумя материальными точками, в соответствии с законом всемирного тяготения пропорциональна произведению масс точек и обратно пропорциональна квадрату расстояния r между ними и направлена вдоль прямой, соединяющей эти точки, от одного тела к другому где G-гравитационная постоянная.
3) импульс. закон сохранения импульса
Импульс тела — это физическая векторная величина, равная произведению массы тела на его скорость.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
4) механическая работа и мощность. Механическая энергия. Закон сохранения энергии в механики
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы
Мощность ( N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа.
Мощность показывает, какая работа совершается за единицу времени.
В Международной системе (СИ) единица мощности называется Ватт (Вт) в честь английскогоизобретателя Джеймса Ватта ( Уатта ), построившего первую паровую машину.
[ N ] = Вт = Дж / c
1 Вт = 1 Дж / 1с
1 Ватт равен мощности силы, совершающей работу в 1 Дж за 1 секунду
или,
когда груз массой 100г поднимают на высоту 1м за 1 секунду
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Закон сохранения энергии — в замкнутой системе с одними только консервативными гироскопическими силами полная механическая энергия остается неизменной с течением времени.
E=Ek+U=const
Закон сохранения механической энергии является следствием однородности времени. Однородность времени означает, что если в любые два момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то начиная с этих моментов все явления в ней будут протекать одинакого.
Угловая скорость, угловое ускорение, частота и период вращения. Связь между линейной скоростью и угловой, линейным ускорением и угловым.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени
Угловое ускорение — производная по времени от вектора угловой скорости ω (соответственно вторая производная по времени от угла поворота)
циклическая частота вращения. ν =1/T
Линейная скорость точки
Связь
Линейная скорость показывает какой путь проходится за единицу времени при движении по окружности, линейное ускорение показывает на сколько изменяется линейная скорость в единицу времени. Угловая скорость показывает на какой угол перемещается тело при движении по окружности, угловое ускорение показывает на сколько изменяется угловая скорость в единицу времени. Vл = R*w; a = R*(бета)
угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением
Вращательным называют такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной кривой, называемой осью вращения (рис.1.9).Ось вращения может находиться как внутри (рис.1.9.а), так и вне тела (рис.1.9.б).
Поворот тела на некоторый угол можно задать в виде отрезка, длина которого, а направление совпадает с осью вращения. Для того, чтобы указать, в какую сторону совершается поворот вокруг данной оси, связывают направление поворота и изображающего его отрезка правилом правого винта: направление отрезка должно быть таким, чтобы, глядя вдоль него, мы видели поворот совершающимся по часовой стрелке (рис.1.10). Вектор поворотаявляется не истинным вектором, а псевдовектором.
Векторная величина ,
где –время, за которое совершается поворот, называется угловой скоростью тела. Она направлена по оси вращения в сторону, определяемую правилом правого винта, и представляет собой псевдовектор. Модуль угловой скорости равен.
Вращение с постоянной угловой скоростью называют равномерным. Такое движение характеризуют периодом , под которым понимают время полного оборота. При этом, тогда, и. Число оборотов в единицу времени ( частота обращения) равно.
Подставив, получаем:.
Вектор может изменяться как при изменении скорости вращения тела вокруг оси ( по величине), так и при повороте оси вращения в пространстве ( в этом случаеменяется по направлению). Изменение вектора угловой скорости со временем характеризуется угловым ускорением. Угловое ускорение, также как и угловая скорость, является псевдовектором.
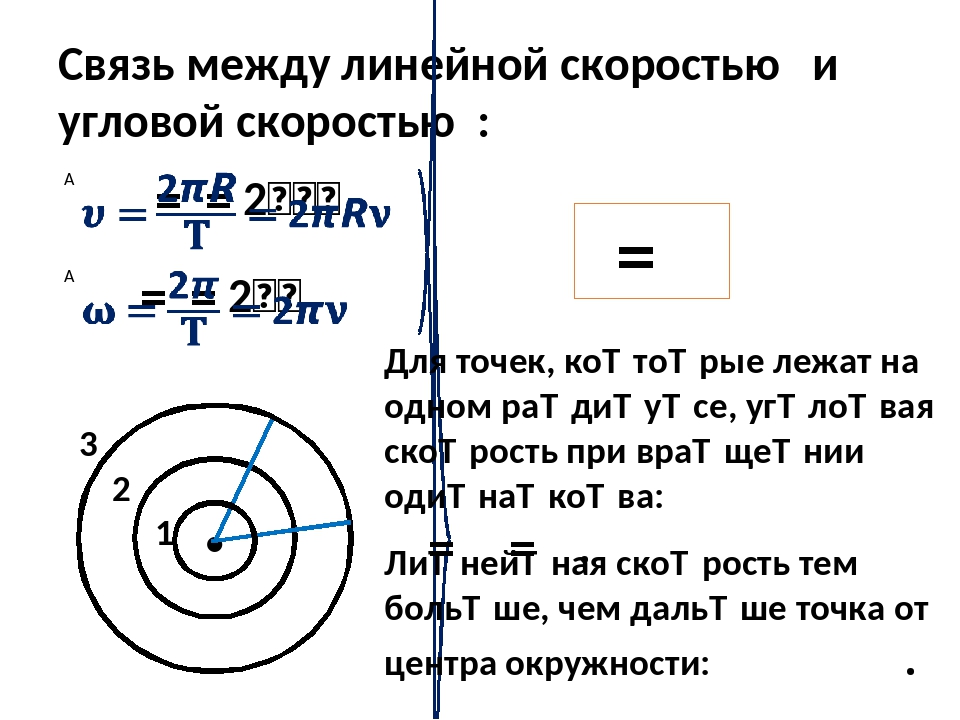
Отдельные точки вращающегося тела имеют различные линейные скорости . Скорость каждой из точек непрерывно изменяет свое направление. Величина скоростиопределяется угловой скоростью вращения телаи расстояниемрассматриваемой точки от оси вращения. Пусть за малый промежуток времени тело повернулось на угол(рис.1.11). Точка, находящаяся на расстоянииот оси, проходит при этом путь. Линейная скорость точки равна. (1.9)
Эта формула связывает модули линейной и угловой скоростей. Найдем выражение, связывающее векторы и. Положение рассматриваемой точки тела будем определять радиус-вектором, проведенным из лежащего на оси вращения начала координатО ( рис.1.12). Из рисунка видно, что векторное произведение совпадает по направлению с вектороми имеет модуль, равный. Следовательно,.
Нормальное ускорение точек вращающегося тела равно .
Если ввести перпендикулярный к оси вращения вектор , проведенный в данную точку тела (рис.1.12), это выражение можно записать в векторной форме . Знак минус поставлен, так как векторы и направлены противоположно.
Будем считать, что ось вращения не поворачивается в пространстве. В этом случае расстояние рассматриваемой точки до оси вращения не меняется, , и, взяв производную от выражения (1.9), получаем
Таким образом, нормальное и тангенциальное ускорения растут линейно с увеличением расстояния точки от оси вращения.
В случае сложного вращения, когда тело движется одновременно относительно нескольких осей, необходимо производить сложения угловых скоростей. Рассмотрим движение твердого тела, вращающегося одновременно вокруг двух пересекающихся осей. Сообщим некоторому телу вращение с угловой скоростью вокруг осиОА (рис. 1.13) и затем эту ось приведем во вращение с угловой скоростью вокруг осиOB, неподвижной в К-системе отсчета. Найдем результирующее движение тела в К-системе.
Введем вспомогательную K‘-систему отсчета, жестко связанную с осями ОА и ОВ. Ясно, что эта система вращается с угловой скоростью , и тело вращается относительно нее с угловой скоростью.
За промежуток времени тело совершит поворотвокругоси АО в K‘— системе и одновременно поворот вокруг оси ОВ вместе с K‘- системой. Суммарный поворот есть = + . Разделив обе части этого равенства на получим
.
Таким образом, результирующее движение твердого тела в K— системе представляет собой чистое вращение с угловой скоростью вокруг оси, совпадающей в каждый момент с вектором и проходящей через точкуO (рис. 1.13). Эта ось перемещается относительно K— системы — она поворачивается с угловой скоростью вместе с осью ОА вокруг оси ОВ.
Нетрудно сообразить, что даже в том случае, когда угловые скорости и не меняются по модулю, тело будет обладать в K— системе угловым ускорением , направленным, согласно, за плоскость (рис. 1.13).
И последнее замечание. Поскольку вектор угловой скорости удовлетворяет основному свойству векторов — векторному сложению, можно представить как векторную сумму составляющих на определенные направления, т. е. =++…, где все векторы относятся к одной и той же системе отсчета. Этим удобным и полезным приемом часто пользуются при анализе сложного движения твердого тела.
1.34. Векторная связь линейной и угловой скоростей
Пусть абсолютно твердое тело вращается вокруг неподвижной оси с угловой скоростьюВыберем на оси за начало отсчета т. 0 (рис. 21).
Рис. 21
Положение точки М характеризуется в данный момент времени радиус-вектором . Разложим радиус-векторна составляющие:Тогда, согласно рис.1.21, имеем. Эти векторы расположены во взаимно перпендикулярных плоскостях (рис. 22). Действительно, согласно (22) и рис. 21, имеемv = R или v = r, (64)
где R = r, а угол между вектором угловой скорости и векторомравен 90о. Согласно рис. 21 имеем r= r sin . С учетом этого формула (64) примет вид v = r sin , т. е. имеем дело с векторным произведением
Рис. 1.22
. (65)Так как
,
то формула (1.65) принимает вид
.
Учитывая, что векторное произведение двух коллинеарных векторов равно нулю (, рис. 21), получим
. (66)
Векторное произведение всегда связано с правилом правого винта.
Поэтому, вращая головку винта по направлению от вектора , стоящего на первом месте в (65), к вектору, стоящему на втором месте, определяем по поступательному движению винта направление третьего вектора, равного векторному произведению (рис. 22).
Вектор линейной скорости равен векторному произведению вектора угловой скорости и радиус-вектора.
Абсолютная величина этого векторного произведения
(67)
или v = r sin90O= r , так как r sin = r.
1.35. Связь векторов тангенциального ускорения
и углового ускорения
Проведя аналогичные рассуждения, можно показать, что
. (68)
Вектор касательного ускорения равен векторному произведению вектора углового ускорения и радиус-вектора.
По модулю а = r sin . Вектор нормального ускорения
, (). (69)
Рис. 23
Рис. 24
В заключение определим положение аксиальных векторов:
и полярных векторов: в случае равноускоренного > 0 (рис. 23) и равнозамедленного < 0 (рис. 24) вращения м. т. вокруг неподвижной оси.
Формулы движения — линейное и круговое
Формулы линейного движения
Средняя скорость / скорость движущегося объекта может быть рассчитана как
v = s / t (1a)
где
v = скорость или скорость (м / с, фут / с)
с = пройденное линейное расстояние (м, фут)
t = время (с)
- расстояние — длина пути тело следует при перемещении из одной точки в другую — смещение — это расстояние по прямой линии между начальным и конечным положениями тела
- мы используем взаимозаменяемые скорость и скорость — но имейте в виду, что скорость — это мера того, насколько быстро или медленно проходит расстояние пройдено, скорость, с которой пройдено расстояние — скорость — это вектор, определяющий, насколько быстро или медленно пройдено расстояние, и направление
Если ускорение постоянное, то скорость c an можно выразить как:
v = v 0 + a t (1b)
где
v 0 = начальная линейная скорость (м / с, фут / с)
a = ускорение (м / с 2 , фут / с 2 )
Линейное расстояние можно выразить как (если ускорение постоянное):
с = v 0 t + 1/2 a t 2 (1c)
Объединение 1b и 1c для выражения конечной скорости
v = (v 0 2 + 2 as) 1 / 2 (1d)
Скорость может быть выражена как (скорость переменная)
v = ds / dt (1f)
где
ds = изменение di стойка (м, фут)
dt = изменение во времени (с)
Ускорение может быть выражено как
a = dv / dt (1g)
где
dv = изменение скорости (м / с, фут / с)
Пример — марафон
Если марафон — 42195 м — выполняется за 2:03:23 (7403 секунды) (Уилсон Кипсанг , Кения — 29 сентября 2013 г. Берлинский марафон) — можно рассчитать среднюю скорость
v = (42195 м) / (7403 с)
= 5.7 м / с
= 20,5 км / ч
Пример — ускорение автомобиля
Автомобиль ускоряется с 0 км / ч до 100 км / ч за 10 секунд . Ускорение можно рассчитать, преобразовав (1b) в
a = (v — v 0 ) / t
= ((100 км / ч) (1000 м / км) / (3600 с / ч) — (0 км / ч) ( 1000 м / км) / (3600 с / ч)) / (10 с)
= 2.78 (м / с 2 )
Калькуляторы линейных перемещений
Средняя скорость
с — расстояние (м, км, футы, мили)
т — использованное время (с, ч)
Расстояние
v 0 — начальная скорость (м / с, фут / с)
a — ускорение (м / с 2 , фут / с 2 )
т — затраченное время (с, ч)
Конечная скорость
v 0 — начальная скорость (м / с, фут / с)
a — ускорение (м / с 2 , фут / с 2 )
с — расстояние (м, фут)
Ускорение
v — конечная скорость (м / с, фут / с)
v 0 — начальная скорость (м / с, фут / с)
t — используемое время (с)
Круговое движение — вращение
Угловая скорость
Угловая скорость может быть выражена как (угловая скорость = постоянная):
ω = θ / t (2)
где
ω = угловая скорость (рад / с)
θ = угловое расстояние (рад)
t = время (с)
Угловая скорость и частота вращения:
ω = 2 π n / 60 (2a)
где
n = оборотов в минуту (об / мин)
π = 3.14 …
Тангенциальная скорость точки в угловой скорости — в метрических или британских единицах, таких как м / с или фут / с — может быть рассчитана как
v = ω r (2b )
где
v = тангенциальная скорость (м / с, фут / с, дюйм / с)
r = расстояние от центра до точки (м, фут, дюйм)
Пример — тангенциальная скорость велосипедной шины
A 26 дюймов велосипедное колесо вращается с угловой скоростью π радиан / с (0.5 оборотов в секунду) . Тангенциальная скорость шины может быть рассчитана как
v = ( π радиан / с ) ((26 дюймов) / 2)
= 40,8 дюйма / с
Угловая скорость и ускорение
Угловая скорость также может быть выражена как (угловое ускорение = константа):
ω = ω o + α t (2c)
где
ω o = угловая скорость в нулевой момент времени (рад / с)
α = угловое ускорение или замедление (рад / с 2 )
Угловое смещение
Угловое расстояние может быть выражено как (угловое ускорение постоянно):
θ = ω o t + 1/2 α t 2 (2d)
Объединение 2a и 2c:
ω = (ω 900 41 o 2 + 2 α θ) 1/2
Угловое ускорение
Угловое ускорение можно выразить как:
α = dω / dt = d 2 θ / dt 2 (2e)
, где
dθ = изменение углового расстояния (рад)
dt = изменение во времени (с)
Пример — замедление маховика
Автор Geni (Фото автора Пользователь: geni) [GFDL или CC-BY-SA-3.0-2,5-2,0-1,0], через Wikimedia Commons
Маховик замедляется с 2000 об / мин ( оборотов, об / мин) до 1800 об / мин за 10 с . Замедление маховика можно рассчитать как
α = ((2000 об / мин ) — (1800 об / мин )) (0,01667 мин / с) (2 π рад / об. ) / (10 с)
= 2,1 рад / с 2
= (2.1 рад / с 2 ) (360 / (2 π) градусов / рад)
= 120 градусов / с 2
Угловой момент — или крутящий момент
Угловой момент или крутящий момент можно выразить как:
T = α I (2f)
где
T = угловой момент или крутящий момент (Н · м)
I = момент инерции (фунт м фут 2 , кг м 2 )
Связь линейного и углового движения
- Образование
- Наука
- Физика
- Связь линейного и углового движения
Стивен Хольцнер
В физике, как и вы используйте формулы для вычисления линейной скорости, ускорения, смещения и движения, вы также можете использовать эквивалентные формулы для углового (вращательного) движения.
Вы можете думать об угле, тета, во вращательном движении так же, как вы думаете о смещении, s , в линейном движении. Это здорово, потому что это означает, что у вас есть угловой аналог для многих уравнений линейного движения. Вот подстановки переменных, которые вы производите, чтобы получить формулы углового движения:
Рабочий объем. Вместо s , который вы используете при линейном перемещении, используйте
угловое перемещение;
измеряется в радианах.
Скорость. Вместо скорости v используйте угловую скорость
.угловая скорость — это количество радианов, пройденных за секунду.
Разгон. Вместо ускорения a используйте угловое ускорение
единица измерения углового ускорения — радианы в секунду 2 .
В таблице сравниваются формулы для линейного и углового перемещения.
Скажем, например, у вас есть мяч, привязанный к веревке. Какова угловая скорость мяча, если его повернуть? Делает полный круг,
за 0,5 секунды, поэтому его угловая скорость равна
Еще одна демонстрация полезности радианов при измерении углов заключается в том, что линейную скорость можно легко связать с угловой скоростью. Если взять уравнение
И умножаем обе стороны на радиус, r , получаем
Срок
— это просто расстояние, которое проходит объект, движущийся по кругу с радиусом r , поэтому это уравнение принимает вид
Вы можете узнать правую часть этого уравнения как уравнение скорости.Итак, вы можете видеть, что линейная скорость и угловая скорость связаны соотношением
.2 секунды, каким будет его среднее угловое ускорение? Разберитесь, подключив числа:
Об авторе книги
Стивен Хольцнер, доктор философии, работал редактором журнала PC Magazine и работал на факультете Массачусетского технологического института и Корнельского университета. Он написал Physics II for Dummies , Physics Essentials for Dummies , and Quantum Physics for Dummies .
Физика колледжа: угол вращения и угловая скорость
В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии.В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Когда объекты вращаются вокруг некоторой оси, например, когда CD (компакт-диск) в [link] вращается вокруг своего центра, каждая точка объекта следует по дуге окружности. Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время.Угол поворота — это величина поворота, аналогичная линейному расстоянию. Угол поворота Δθ размера 12 {Δθ} {} определяется как отношение длины дуги к радиусу кривизны:
Δθ = Δsr. размер 12 {Δθ = {{Δs} больше {r}} «.»} {}Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ размер 12 {Δθ} {} за время Δt размер 12 {Δt} {}.
Радиус круга повернут на угол Δθ размера 12 {Δθ} {}.Длина дуги Δs размером 12 {Δs} {} указана на окружности.Длина дуги Δs размер 12 {Δs} {} — это расстояние, пройденное по круговой траектории, как показано в [ссылка]. Обратите внимание, что размер r 12 {r} {} — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r размером 12 {r} {}. Окружность круга равна 2πr размера 12 {2πr} {}. Таким образом, за один полный оборот угол поворота составляет
°. Δθ = 2πrr = 2π.размер 12 {Δθ = {{2πr} over {r}} = 2π «.»} {}Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δθ размер 12 {Δθ} {} в радианах ( рад), определенная так, что
2πрад = 1 оборот. size 12 {2π «rad» = «1 оборот»} {}Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в [ссылка].
| Градусы | Радианная мера |
| 30 ° размер 12 {«30» °} {} | π6 размер 12 {{{π} больше {6}}} {} |
| 60º размер 12 {«60» °} {} | π3 размер 12 {{{π} больше {3}}} {} |
| 90 ° размер 12 {«90» °} {} | π2 размер 12 {{{π} больше {2}}} {} |
| 120º размер 12 {«120» °} {} | 2π3 размер 12 {{{2π} больше {3}}} {} |
| 135º размер 12 {«135» °} {} | 3π4 размер 12 {{{3π} больше {4}}} {} |
| 180 ° размер 12 {«180» °} {} | π размер 12 {π} {} |
Если Δθ = 2π размер 12 {Δθ = 2π} {} рад, то КД сделал один полный оборот, и каждая точка на КД вернулась в исходное положение. Так как круг или один оборот составляют 360º размером 12 {«360» °} {}, соотношение между радианами и градусами составляет
2πrad = 360º, размер 12 {2π «rad» = «360» rSup {size 8 {circ }}} {}, так что
1рад = 360º2π≈57,3º. размер 12 {1 «rad» = {{«360» rSup {size 8 {circ}}} больше {2π}} = «57» «.» 3 rSup {размер 8 {circ}} «.»} {}Насколько быстро вращается объект? Определим угловую скорость ω величиной 12 {ω} {} как скорость изменения угла.В символах это
ω = ΔθΔt, размер 12 {ω = {{Δθ} над {Δt}} «,»} {}, где угловой поворот Δθ размер 12 {Δθ} {} происходит за время Δt размер 12 {Δt} {} . Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω размером 12 {ω} {} аналогична линейной скорости v размером 12 {v} {}. Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD.Эта яма перемещает дугу длиной Δs размером 12 {Δs} {} за время Δt размер 12 {Δt} {}, и поэтому имеет линейную скорость
v = ΔsΔt. размер 12 {v = {{Δs} на {Δt}} «.»} {}Из Δθ = Δsr размер 12 {Δθ = {{Δs} на {r}}} {} мы видим, что Δs = rΔθ размер 12 {Δs = rΔθ} {}. Подставляя это в выражение для размера v 12 {v} {}, получаем
v = rΔθΔt = rω. размер 12 {v = {{rΔθ} over {Δt}} = rω «.»} {}Мы записываем это соотношение двумя разными способами и получаем два разных вывода:
v = rω или ω = vr.размер 12 {v = rω« «или» ω = {{v} over {r}} «.»} {}Первое соотношение в v = rω или ω = vr размер 12 {v = rω« «или «ω = {{v} over {r}}} {} утверждает, что линейная скорость v размером 12 {v} {} пропорциональна расстоянию от центра вращения, таким образом, она является наибольшей для точки на ободе. (самый большой размер r 12 {r} {}), как и следовало ожидать. Мы также можем назвать эту линейную скорость v размером 12 {v} {} точки на ободе тангенциальной скоростью . Второе соотношение в v = rω или ω = vr размера 12 {v = rω« «или» ω = {{v} over {r}}} {} можно проиллюстрировать, рассматривая шину движущегося автомобиля.Обратите внимание, что скорость точки на ободе шины такая же, как скорость v размера 12 {v} {} автомобиля. См. [Ссылка]. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой размер v 12 {v} {} означает большой размер ω 12 {ω} {}, потому что v = rω размер 12 {v = rω} {}. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (размер ω 12 {ω} {}), будет создавать для автомобиля большую линейную скорость (размер v 12 {v} {}).
Автомобиль, движущийся вправо со скоростью v размером 12 {v} {}, имеет шину, вращающуюся с угловой скоростью ω размером 12 {ω} {}.Скорость протектора шины относительно оси составляет v размер 12 {v} {}, такая же, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = rω, размер 12 {v = rω} {}, где r, размер 12 {r} {} — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м / с размером 12 {«15» «». 0` «м / с»} {} (около 54 км / ч размер 12 {«54″ `» км / ч «} {}).См. [Ссылка].
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем v = 15,0 м / с. размер 12 {v} {} Радиус шины принимается равным r = 0,300 м. размер 12 {r} {} Зная v размер 12 {v} {} и размер r 12 {r} {}, мы можем использовать второе соотношение в v = rω, ω = vr size 12 {v = rω, « ω = {{v} over {r }}} {} для вычисления угловой скорости.
Решение
Для вычисления угловой скорости воспользуемся следующим соотношением:
ω = vr.размер 12 {ω = {{v} over {r}} «.»} {}Подставляя известные,
ω = 15,0 м / с 0,300 м = 50,0рад / с. размер 12 {ω = {{«15» «.» 0 «м / с»} больше {0 «.» «300» «m»}} = «50» «.» 0 рад / с.} {}Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости.Также обратите внимание, что если бы землерой с гораздо большими шинами, скажем, радиусом 1,20 м, двигался с той же скоростью 15,0 м / с, его шины вращались бы медленнее. У них будет угловая скорость
ω = (15,0 м / с) / (1,20 м) = 12,5 рад / с. размер 12 {ω = \ («15» «.» 0` «м / с» \) / \ (1 «.» «20» `m \) =» 12 «». » 5` «рад / с.»} {}И размер ω 12 {ω} {}, и размер v 12 {v} {} имеют направления (следовательно, это угловая и линейная скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки.Линейная скорость касается пути, как показано в [ссылка].
Take-Home Experiment
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Когда объект движется по кругу, например муха на краю старомодной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.Исследования PhET: революция божьей коровки
Ladybug RevolutionПрисоединяйтесь к божьей коровке и исследуйте вращательное движение. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение.Изучите, как круговое движение связано с координатами x, y, скоростью и ускорением жука, используя векторы или графики.
- Равномерное круговое движение — это движение по окружности с постоянной скоростью. Угол поворота Δθ размера 12 {Δθ} {} определяется как отношение длины дуги к радиусу кривизны:
Δθ = Δsr, размер 12 {Δθ = {{Δs} over {r}} «,»} {}
, где длина дуги Δs размер 12 {Δs} {} — это расстояние, пройденное по круговой траектории, и размер r 12 {r} {} — радиус кривизны круговой траектории.Величина Δθ размера 12 {Δθ} {} измеряется в радианах (рад), для которых
2πrad = 360º = 1 оборот. размер 12 {2π` «rad» = `» 360 «» ° = «` 1` «оборот.»} {} - Преобразование между радианами и градусами: 1рад = 57,3 ° размер 12 {1 «рад» = «57» «.» 3 °} {}.
- Угловая скорость ω размер 12 {ω} {} — скорость изменения угла,
ω = ΔθΔt, размер 12 {ω = {{Δθ} над {Δt}} «,»} {}
, где поворот Δθ размером 12 {Δθ} {} происходит за время Δt размер 12 {Δt} {}. Единицы угловой скорости — радианы в секунду (рад / с).Линейная скорость v размером 12 {v} {} и угловая скорость ω размером 12 {ω} {} связаны соотношением
v = rω или ω = vr. размер 12 {v = rω« «или» ω = {{v} over {r}} «.»} {}
Есть аналогия между вращательными и линейными физическими величинами. Какие вращательные величины аналогичны расстоянию и скорости?
Грузовики с полуприцепом имеют одометр на одной ступице колеса прицепа. Ступица утяжеляется так, что она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние.Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
Микроволновые печи вращаются со скоростью около 6 об / мин. Что это в оборотах в секунду? Какова угловая скорость в радианах в секунду?
Автомобиль с шинами радиусом 0,260 м проезжает 80 000 км, прежде чем износится. Сколько оборотов делают шины без учета поддержки и любого изменения радиуса из-за износа?
5 × 107 оборотов, размер 12 {9 «.»» 79 «умножить на» 10 «rSup {размер 8 {8}}» «вращений»} {}
(а) Каков период вращения Земли в секундах? б) Какова угловая скорость Земли? (c) Учитывая, что Земля имеет радиус 6,4 × 106 м и размер 12 {6 дюймов «. 4 умножить на 10 rSup {size 8 {6}}} {} на его экваторе, какова линейная скорость у поверхности Земли?
Бейсбольный питчер выносит руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера 35.0 м / с и мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
В лакроссе мяч выбрасывается из сетки на конец клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча относительно локтевого сустава составляет 30,0 рад / с, а мяч находится на 1,30 м от локтевого сустава, какова скорость мяча?
Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
Integrated Concepts При ударе по футбольному мячу игрок, выполняющий удар, поворачивает ногу вокруг тазобедренного сустава.
(a) Если скорость кончика ботинка кикера составляет 35,0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика ботинка, какова угловая скорость кончика ботинка?
(b) Башмак находится в контакте с первоначально почти неподвижным футбольным мячом весом 0,500 кг в течение 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с?
(c) Найдите максимальную дальность действия футбольного мяча, не обращая внимания на сопротивление воздуха.
(а) 33,3 рад / с
(б) 500 Н
(в) 40,8 м
Создайте свою проблему
Рассмотрим аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками.

 е. поворачивается на угол 2 . Так как промежутку времени соответствует , то откуда Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называет- называется частотой вращения: ,откуда . Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: .Связь линейных и угловых кинематических величин:связь между линейными (длина пути s, пройденного точкой дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение , нор-нормальное ускорение ) и угловыми величинами (угол поворота , угловая скорость , угловое ускорение выражается следующими формулами: , и , , , и .
е. поворачивается на угол 2 . Так как промежутку времени соответствует , то откуда Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называет- называется частотой вращения: ,откуда . Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: .Связь линейных и угловых кинематических величин:связь между линейными (длина пути s, пройденного точкой дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение , нор-нормальное ускорение ) и угловыми величинами (угол поворота , угловая скорость , угловое ускорение выражается следующими формулами: , и , , , и . Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.
Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.  Обратная задача динамики: по заданным силам определить характер движения тела. Преобразова́ния Галиле́я — в классической механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета к другой. Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея ). При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения- это принцип относительности Эйнштейна и есть принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.
Обратная задача динамики: по заданным силам определить характер движения тела. Преобразова́ния Галиле́я — в классической механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета к другой. Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея ). При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения- это принцип относительности Эйнштейна и есть принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.


 3)
3) 5)
5)