Формулы углового движения: Вращательное движение тела | Формулы и расчеты онлайн
Тангенциальное ускорение — определение, формула и измерение
Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией.
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
- Тангенциальное — направленное вдоль касательного пути точки в определённый момент. Из-за происхождения слова его часто называют касательным.
- Нормальное — совпадающее с нормалью траектории изменения положения.
- Полное — определяющееся суммой тангенциального и нормального ускорений.
Но также используется понятие «вектор среднего ускорения тела».
Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
- Через промежуток времени Δt скорость изменяется как по направлению, так и по модулю: Δt = t — t0.
- Вектор изменения скорости, определяемый по правилу треугольника, будет равняться разности существующей скорости на данный момент и начальной: Δv = v — v0.
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
- at — тангенциальной составляющей, совпадающей с отрезком V;
- an — перпендикулярным по отношению расположения V вектором.

Используя теорему Пифагора, можно сказать, что модуль полного ускорения равняется корню квадратному из суммы квадратов тангенциального и нормального ускорения: a = √at 2 + an 2.
Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
- Вычислить все ускорения точки, лежащей на окружности, через десять секунд после воздействия на диск вращателя. При этом учесть, что радиус окружности составит 20 см, а угол между валом и радиус вектором тела соответствует закону: j =3-t+0.2t3. Для решения примера необходимо использовать формулы для нахождения угловой скорости и ускорения.

- Материальное тело перемещается по окружности, имеющей радиус 20 см. При этом тангенциальное ускорение равняется 5 см на секунду в квадрате. Определить, сколько понадобится времени, чтобы ускорения сравнялись и нормальное стало больше тангенциального в два раза. Исходя из условия, можно утверждать, что движение является равноускоренным. Поэтому можно применить формулы: an = V2 / t; at = V / t. Отсюда: t = V / at, а V = √an * R. Подставив второе выражение в первое, получится: t = (√an * R) / at.
 При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Сложная задача
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Нормальное ускорение можно выразить через скорость и радиус: an = V2 / R. Затем необходимо записать формулу для тангенциального ускорения: at = dV / dt. Так как они равны, то справедливым будет равенство: V2 / R = dV / dt. Анализируя уравнение, можно сделать вывод, что так как скорость и радиус положительный, то слева будет стоять величина со знаком плюс. Но, с другой стороны, со временем скорость убывает, поэтому с правой стороны нужно поставить знак минус: V2 / R = — dV / dt.
Полученное уравнение является дифференциальным и показывает зависимость скорости от времени. Равенство можно преобразовать, умножив на отношение dt / V2. В итоге должно получиться выражение: dV / V2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.
Равенство можно преобразовать, умножив на отношение dt / V2. В итоге должно получиться выражение: dV / V2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Теперь можно найти тангенциальное убыстрение, так как оно представляет производную от скорости. После взятия производной получится: at = dV / dt = — V02 / R (1 + V0 * t / R)2 = — V2 / R. Отсюда можно написать, что модуль полного ускорения будет равняться: a = √2 *|ar| = (√2 * V2) / R. Осталось найти путь. Он совпадает с длиной дуг и равняется интегралу модуля скорости от времени. После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.
После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.
Вращательное движение | РАЗМЫШЛЯЕМ
Лекция № 3 Виды движения: равномерное и равноускоренное.
Вращательное движение.
Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения. Произведя в последних уравнениях следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость V — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
Вращательное движение Угловая скорость Угловое ускорение
Равномерное Постоянная Равно нулю
Равномерно ускоренное Изменяется равномерно Постоянно
Неравномерно ускоренное Изменяется неравномерно Переменное
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Рис.1 Угол поворота — вращательное движение
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
1.φ=s/r
Соотношение между единицами угла
2.φрад/φ°=π/180°
1 рад= 57.3°
1°= 17.45 мрад
1´= 291 мкрад
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). график угловой скорости — вращательное движение Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Рис.2 Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
3. [n]=[f]=Обороты/Секунда = (об)/с =1/c = Герц
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
4. T=1/f=1/n
f — (частота, Гц) или n — (число оборотов в секунду)
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
5. φ= 2 π N
φ= 2 π N
N — (полное число оборотов)
Угловая скорость
Из формулы для одного оборота следует:
6. ω= 2 π f=2π/T
T — (Период вращательного движения, секунд)
f — (частота вращательного движения, Герц)
Обратите внимание:
- формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
- вопреки своему названию число оборотов n — это не число, а физическая величина.
- следует различать число оборотов n и полное число оборотов N.
Равномерное круговое движение
l = R * φ
l — длина дуги окружности
R — радиус
φ — угол
Равномерное круговое движение: линейная скорость
v = R * ω
v — линейная скорость
R — радиус
ω — угловая скорость
Период вращения
T = t / N
T — период
t — время
N — число вращений
Период вращения
T = 2 π R / v
T — период
R — радиус
v — линейная скорость
Период вращения
T = 2 π / ω
T — период
ω — угловая скорость
Центростремительное ускорение
a = 4 π^2*R / T^2
a — центростремительное ускорение
R — радиус
T — период вращения
Центростремительное ускорение
a = 4 π^2*R * n^2
a — центростремительное ускорение
R — радиус
n — частота вращения
Центростремительное ускорение
a = ω^2 * R
a — центростремительное ускорение
ω — угловая скорость
R — радиус
Движение тела в условиях земного тяготения
Дальность броска тела, брошенного под углом к горизонту
x = v0 * t *cos(α)
x — координата (дальность)
v0 — начальная скорость
t — время
α — угол
Высота подъема тела, брошенного под углом к горизонту
y = v0* t * sin(α) — gt^2/2
y — координата (высота подъема )
v0 — начальная скорость
t — время
g — ускорение свободного падения
α — угол
Вертикальная скорость тела, брошенного под углом к горизонту
vy = v0 * sin(α) — gt
vy — вертикальная скорость
v0 — начальная скорость
α — угол
g — ускорение свободного падения
t — время
Максимальная высота подъема тела, брошенного под углом к горизонту
hmax = v0^2 sin(α)^2/ (2g)
hmax — максимальная высота
v0 — начальная скорость
α — угол
g — ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t = 2 v0 * sin(α)/g
t — время
v0 — начальная скорость
α — угол
g — ускорение свободного падения
Максимальная дальность броска тела, брошенного под углом к горизонту
smax = v0^2/g
smax — максимальная дальность
v0 — начальная скорость
g — ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x = x0 + v*t
x — координата (дальность)
x0 — начальная координата
v — скорость
t — время
Высота подъема тела, брошенного горизонтально
y = y0 — g*t^2/2
y — координата (высота подъема)
y0 — начальная координата (высота)
g — ускорение свободного падения
t — время
Общее время движения тела, брошенного горизонтально
t max = √(2*h/g)
t max — максимальное время
h — высота
g — ускорение свободного падения
Kvant. Кинематика вращательного движения — PhysBook
Кинематика вращательного движения — PhysBook
Чивилёв В.И. Кинематика вращательного движения //Квант. — 1986. — № 11. — С. 17-18.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Медленно проехав перекресток, троллейбус стал удаляться по улице, плавно увеличивая свою скорость…
Движение колеса троллейбуса — лишь один из многих примеров сложного механического движения в окружающем нас мире. Оказывается, любое сложное движение можно представить как сумму двух простых движений — поступательного и вращательного. Понимать это следует так: всегда можно подобрать такую поступательно движущуюся систему отсчета, относительно которой движение выглядит только как вращение вокруг некоторой неподвижной оси.
Какую же в нашем случае надо выбрать систему отсчета, чтобы в ней колесо троллейбуса совершало чистое вращение? Какими физическими величинами описывается это вращение, как эти величины связаны друг с другом и как зависят от времени? Такие вопросы могут возникнуть не только на пешеходном переходе, но и на уроке, экзамене, при решении конкретной задачи.
На первый вопрос ответить легко, догадавшись, что поступательно движущуюся систему отсчета можно связать с самим троллейбусом (его корпусом). Перед тем как ответить на остальные вопросы, заметим, что в нашем примере колесо вращается неравномерно — модуль скорости любой точки колеса меняется со временем.
Рассмотрим некоторую точку М колеса, находящуюся на расстоянии r от оси вращения и имеющую в некоторый момент времени скорость \(~\vec \upsilon\) и ускорение \(~\vec a\) (рис. 1). Из физических соображений разумно ускорение \(~\vec a\) представить как сумму двух составляющих: одна из них \(~\vec a_c\) направлена по радиусу к центру окружности — центростремительное ускорение, вторая \(~\vec a_k\) направлена по касательной к окружности — касательное ускорение. Оба эти ускорения имеют определенный физический смысл — касательное ускорение характеризует быстроту изменения модуля скорости, а центростремительное характеризует быстроту изменения направления скорости. 2}{r}\) («Физика 8», §16), а модуль касательного ускорения \(~a_k = \frac{\Delta \upsilon}{\Delta t}\), где Δυ — изменение модуля υ скорости точки за сколь угодно малое время Δt.
2}{r}\) («Физика 8», §16), а модуль касательного ускорения \(~a_k = \frac{\Delta \upsilon}{\Delta t}\), где Δυ — изменение модуля υ скорости точки за сколь угодно малое время Δt.
Рис. 1
Линейные и угловые величины
Как уже говорилось, нам надо ввести такие физические величины, которые характеризовали бы неравномерное вращение колеса (в системе отсчета, связанной с троллейбусом). Попробуем это сделать по аналогии с прямолинейным неравномерным движением.
Проследим за точкой М колеса в течение малого промежутка времени Δt. За это время точка пройдет по дуге окружности путь s и будет иметь скорость υ и касательное ускорение ak (рис. 2). Три величины s, υ и ak, называемые линейными величинами, характеризуют движение точки М, но не могут служить для описания вращения всего колеса, так как в один и тот же момент времени другие точки, расположенные на других расстояниях от оси вращения, имеют другие линейные скорости, и касательные ускорения и пройденные ими пути тоже не одинаковы. Поэтому кроме линейных вводятся так называемые угловые величины, которые одинаковы для всех точек вращающегося колеса: угол поворота φ радиуса, соединяющего точку М с центром окружности, угловая скорость \(~\omega = \frac{\Delta \varphi}{\Delta t}\) (Δφ — изменение угла поворота за время Δt) и угловое ускорение \(~\varepsilon = \frac{\Delta \omega}{\Delta t}\) (Δω — изменение угловой скорости).
Поэтому кроме линейных вводятся так называемые угловые величины, которые одинаковы для всех точек вращающегося колеса: угол поворота φ радиуса, соединяющего точку М с центром окружности, угловая скорость \(~\omega = \frac{\Delta \varphi}{\Delta t}\) (Δφ — изменение угла поворота за время Δt) и угловое ускорение \(~\varepsilon = \frac{\Delta \omega}{\Delta t}\) (Δω — изменение угловой скорости).
Рис. 2
Очевидно, что введенными здесь угловыми величинами можно описывать вращение не только троллейбусного колеса, но и любого другого тела. При этом с течением времени может изменяться не только угол поворота φ, но и угловая скорость ω и угловое ускорение ε. В частности, если угловое ускорение не зависит от времени, то угловая скорость изменяется равномерно и в таком случае говорят, что имеет место равноускоренное вращение. Когда же угловая скорость остается постоянной, то угловое ускорение оказывается равным нулю и говорят о равномерном вращении тела.
Связь линейных и угловых величин
Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.
При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь
\(~s = r \varphi\) . (1)За малое время Δt точка проходит расстояние \(~\Delta s = r \varphi_2 — r \varphi_1\) , где φ2 и φ1 — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что \(~\frac{\Delta s}{\Delta t} = \upsilon\) и \(~\frac{\varphi_2 — \varphi_1}{\Delta t} = \frac{\Delta \varphi}{\Delta t} = \omega\), получим
\(~\upsilon = r \omega\) . (2)Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть \(~\Delta \upsilon = r \omega_2 — r \omega_1\) , где ω2 и ω1 — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что \(~\frac{\Delta \upsilon}{\Delta t} = a_k\) и \(~\frac{\omega_2 — \omega_1}{\Delta t} = \frac{\Delta \omega}{\Delta t} = \varepsilon\), тогда касательное ускорение
Разделим последнее равенство на Δt и учтем, что \(~\frac{\Delta \upsilon}{\Delta t} = a_k\) и \(~\frac{\omega_2 — \omega_1}{\Delta t} = \frac{\Delta \omega}{\Delta t} = \varepsilon\), тогда касательное ускорение
Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.
Формулы кинематики для равноускоренного вращательного движения
Найдем зависимость угловой скорости ω и угла поворота φ колеса троллейбуса от времени t для случая вращения колеса с постоянным угловым ускорением ε.
Пусть начальная угловая скорость равна ω0. Тогда точка М, имея начальную скорость υ0 = rω0, будет двигаться с постоянным по модулю касательным ускорением ak = rε.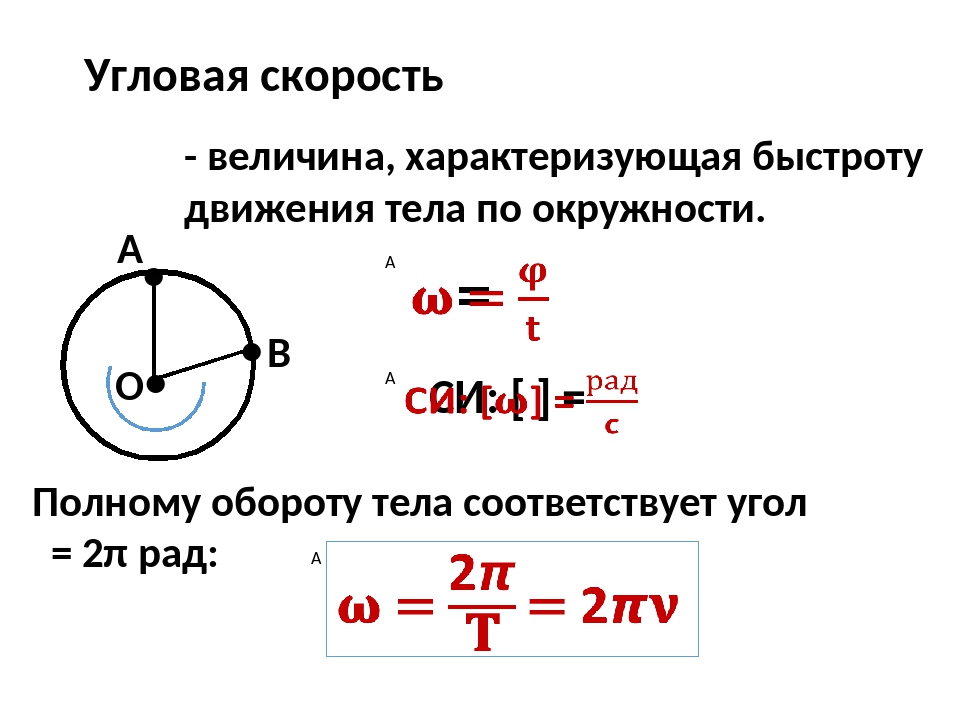 2_0 = 2 \varepsilon \varphi \end{matrix}\) .
2_0 = 2 \varepsilon \varphi \end{matrix}\) .
Это и есть формулы кинематики для. вращательного движения любого тела (а не только колеса троллейбуса) с постоянным угловым ускорением.
Глава 10. Вращаем объекты: момент силы – FIZI4KA
В этой главе…
- Переходим от поступательного движения к вращательному движению
- Вычисляем тангенциальную скорость и тангенциальное ускорение
- Выясняем связь между угловым ускорением и угловой скоростью
- Разбираемся с моментом силы
- Поддерживаем вращательное движение
Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости.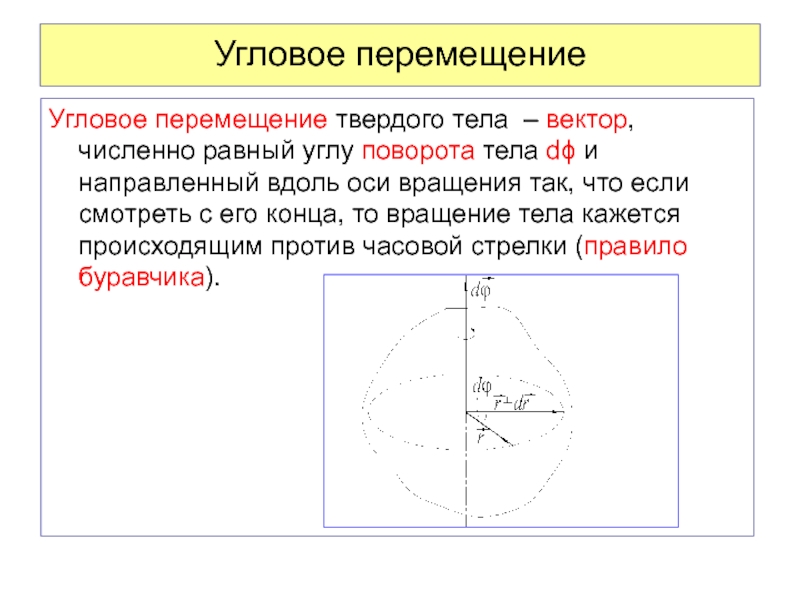 2_0=2as \), где \( \omega_1 \) — это конечная скорость.
2_0=2as \), где \( \omega_1 \) — это конечная скорость.
Разбираемся с параметрами вращательного движения
В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.
Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:
Допустим, колеса мотоцикла вращаются с угловой скоростью \( \omega \), равной 21,5\( 21,5\pi \) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.
Вычисляем линейную скорость вращательного движения
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом \( \mathbf{r} \) и линейной скоростью \( \mathbf{v} \). Скорость \( \mathbf{v} \) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору \( \mathbf{r} \).
Угловая скорость связана с линейной скоростью соотношением \( v=r\omega \), которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.
Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости \( v=r\omega \). Длина окружности \( L \) радиуса \( r \) выражается известной формулой \( L=2\pi r \), а полный угол, который охватывает окружность, равен \( 2\pi \) радиан. Соответственно, длина дуги окружности длиной \( \Delta s \), охватывающая угол \( \Delta\theta \), равна:
Соответственно, длина дуги окружности длиной \( \Delta s \), охватывающая угол \( \Delta\theta \), равна:
Из формулы прямолинейного движения
путем подстановки выражения для \( \Delta s \) получим:
Поскольку:
где \( \omega \) — угловая скорость, \( \Delta{\theta} \)— угол поворота, \( \Delta{t} \) — время поворота на угол \( \Delta{\theta} \), то:
Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью \( \omega \), равной 21,5\( \pi \) радиан в секунду. Пусть радиус колеса \( r \) равен 40 см, тогда достаточно использовать следующую формулу:
Подставляя в нее значения, получим:
Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.
Вычисляем тангенциальное ускорение
Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение
Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение
где \( a \) — это ускорение, \( \Delta v \) — изменение скорости, a \( \Delta t \) — время изменения скорости, с угловым ускорением
где \( \Delta\omega \) — изменение угловой скорости, \( \Delta t \) — время изменения угловой скорости?
Как мы уже знаем, линейная и угловая скорости связаны равенством
Подставим это выражение в предыдущую формулу линейного ускорения:
Поскольку радиус остается постоянным, то его можно вынести за скобки:
Поскольку угловое ускорение \( \alpha=\Delta\omega/\Delta t \), то:
Итак, получаем следующую формулу связи между линейным и угловым ускорением:
Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.
Вычисляем центростремительное ускорение
Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):
Теперь, используя известную формулу связи линейной и угловой скорости \( v=r\omega \), получим:
По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.
Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит \( 2\pi \) радиан. Отсюда получаем угловую скорость Луны:
Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:
После подстановки этого значения в предыдущую формулу получим:
Средний радиус орбиты Луны равен 3,85·108 м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:
Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:
Зная это ускорение и массу Луны, которая равна 7,35·1022 кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость \( \omega \), оказывается, направлена вдоль оси вращающегося колеса (рис.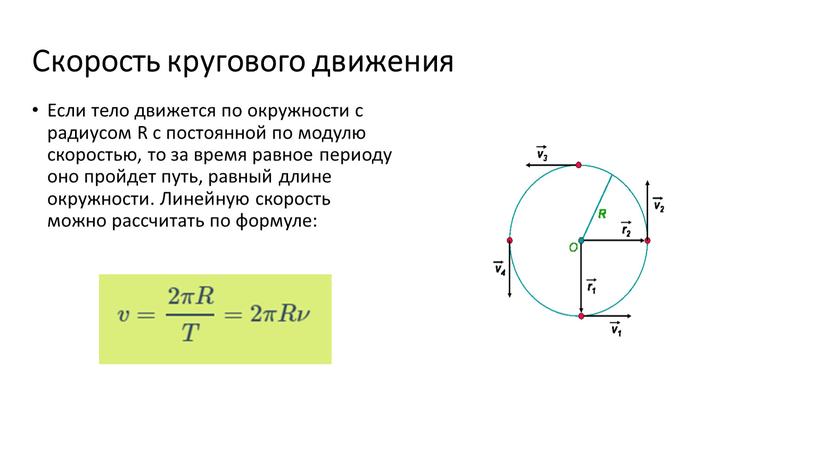 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
Для определения направления вектора угловой скорости \( \omega \) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости \( \omega \).
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
предыдущие разделы), угловое ускорение определяется формулой:
где \( \alpha \) — угловое ускорение, \( \Delta\omega \) — изменение угловой скорости, \( \Delta t \)— время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
где \( \mathbf{\alpha} \) — вектор углового ускорения, а \( \Delta\mathbf{\omega} \) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.
А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис.
10.4.
Поднимаем грузы: момент силы
В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.
Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).
В верхней части рис. 10.5 показаны весы-качели с грузом массы \( m_1 \) на одном конце и грузом большей массы \( m_2=2m_1 \) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой \( m_2 \) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой \( m_2=2m_1 \) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой \( m_1 \).
Чтобы уравновесить весы, нужно сдвинуть груз с большей массой \( m_2=2m_1 \) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой \( m_1 \).
Знакомимся с формулой момента силы
Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).
На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы \( F \) на плечо силы \( l \):
Моментом силы называется произведение прилагаемой силы \( F \) на плечо силы \( l \):
Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).
Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы \( l \) равно 0,5 м и момент силы будет равен:
В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы \( l \) равно 1 м и момент силы будет равен:
Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?
Разбираемся с направлением приложенной силы и плечом силы
Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.
10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.
Размышляем над тем, как создается момент силы
Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.
Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом \( \theta \). Как в таком случае определить плечо силы? Если бы угол \( \theta \) был прямым, то мы могли бы воспользоваться уже известно нам формулой:
Однако в данном случае угол \( \theta \) не является прямым.
В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.
Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:
Если угол \( \theta \) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).
Итак, получаем для момента силы для схемы Б на рис. 10.7:
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом \( \theta \) = 45°, то создаваемый момент этой силы будет равен:
Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.
Определяем направление момента силы
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.
Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.
На рис. 10.8 показан пример силы \( \mathbf{F} \) с плечом \( \mathbf{l} \) и соответствующего вектора момента сил \( \mathbf{M} \).
Уравновешиваем моменты сил
В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).
Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:
Иначе говоря, результирующая действующая сила равна нулю.
Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.
е. с постоянной угловой скоростью.
Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:
Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.
Простой пример: вешаем рекламный плакат
Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.
Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.
Болт находится в 10 см от точки опоры шеста.
Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:
Иначе говоря:
где \( \mathbf{M_п} \) — это момент силы со стороны плаката, а \( \mathbf{M_б} \) — это момент силы со стороны болта.
Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:
где \( m \) = 50 кг — это масса плаката, \( \mathbf{g} \) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), \( m\mathbf{g} \) — сила тяжести плаката, а \( l_п \) = 3 м — это плечо силы тяжести плаката.
Подставляя значения, получим:
Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.
Момент силы со стороны болта определяется формулой:
где \( \mathbf{F_б} \) — это искомая сила, с которой болт должен удерживать всю конструкцию, а \( l_б \) = 0,1 м — это ее плечо.
Подставляя полученные выражения для моментов сил в формулу:
получим, что:
Отсюда с помощью простых алгебраических преобразований получим искомую силу:
Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.
Подставляя значения, получим искомый ответ:
Более сложный пример: учитываем силу трения при расчете равновесия
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.
Пусть лестница длиной \( l_л \) = 4 м стоит под углом \( \theta \) = 45° к поверхности тротуара, работник имеет массу \( m_р \) = 45 кг и находится на ней на расстоянии \( l_р \) = 3 м от нижнего конца лестницы, лестница имеет массу \(m_л \) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен \( \mu_п \) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?
Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?
Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:
- \( \mathbf{F_с} \) — нормальная сила со стороны стены;
- \( \mathbf{F_р} \) — вес рабочего;
- \( \mathbf{F_л} \) — вес лестницы;
- \( \mathbf{F_{тр}} \) — сила трения между поверхностью тротуара и концами лестницы;
- \( \mathbf{F_т} \) — нормальная сила со стороны тротуара.
Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:
Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены \( \mathbf{F_с} \) и силы трения между поверхностью тротуара и концами лестницы \( \mathbf{F_{тр}} \), должна быть равна нулю, то есть:
или
Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие
Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего \( \mathbf{F_р} \), веса лестницы \( \mathbf{F_л} \) и нормальной силы со стороны тротуара \( \mathbf{F_т} \), должна быть равна нулю, то есть:
или
Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:
Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего \( \mathbf{M_р=[L_р\!\times\! F_р]} \), весом лестницы \( \mathbf{M_л=[L_л\!\times\!F_л]} \) и нормальной силой со стороны стены \( \mathbf{M_с=[L_с\!\times\! F_с]} \):
или
или
Поскольку \( L_р=l_р \), \( L_л=l_л/2 \) (центр тяжести лестницы находится посередине лестницы), \( L_с=l_л \), \( \alpha=360^{\circ}-\theta \), \( \beta=360^{\circ}-\theta \) и \( \gamma=\theta \), то получим:
или
Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил \( \mathbf{F_с} \) и \( \mathbf{F_т} \):
Зададимся вопросом: соблюдается ли условие
Из системы двух уравнений получим:
Итак, остается выяснить, соблюдается ли условие:
После подстановки значений получим:
Поскольку \( \mu_т \) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.
Глава 10. Вращаем объекты: момент силы
3.5 (69.23%) 13 votesГлава 11. Раскручиваем объекты: момент инерции – FIZI4KA
В этой главе…
- Переходим от динамики поступательного движения к динамике вращательного движения
- Вычисляем момент инерции
- Определяем работу вращательного движения
- Находим связь между работой и изменением кинетической энергии
- Изучаем закон сохранения момента импульса
Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.
главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.
Применяем второй закон Ньютона для вращательного движения
Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:
где \( \mathbf{a} \) — это вектор ускорения, \( \mathbf{F} \) — вектор силы, а \( m \) — масса объекта. Подробнее о векторах рассказывается в главе 4. Соблюдается ли этот закон для вращательного движения?
В главе 10 мы уже познакомились характеристиками вращательного движения, которые являются эквивалентами (аналогами) некоторых характеристик поступательного движения. А как будет выглядеть аналог у второго закона Ньютона? Похоже, что во вращательном движении роль ускорения \( \mathbf{a} \) играет угловое ускорение \( \alpha \), а роль силы \( \mathbf{F} \) — момент силы \( \mathbf{M} \)? Не вдаваясь в подробности, скажем лишь, что это действительно так. А что же с массой? Оказывается, что для этого используется новое понятие — момент инерции \( l \). Известно, что второй закон Ньютона для вращательного движения принимает следующий вид:
А что же с массой? Оказывается, что для этого используется новое понятие — момент инерции \( l \). Известно, что второй закон Ньютона для вращательного движения принимает следующий вид:
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)
Поскольку:
то, умножая обе части этой формулы на радиус окружности \( r \), получим:
Поскольку \( r\mathbf{F}=\mathbf{M} \) то
или
Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. 2 \), называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.
2 \), называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.
Пример: вычисляем момент силы для обеспечения углового ускорения
Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:
где \( \mathbf{\sum\!F} \) обозначает векторную сумму всех сил, действующих на объект.
Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:
где \( \mathbf{\sum\! M} \) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м2.
Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула \( \mathbf{\sum\! M}=l\alpha \), т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.
{-2} \)? Подставляя значения в уже известную нам формулу
получим:
Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.
Вычисляем момент инерции протяженного объекта
Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения \( r \). В таком случае момент инерции имеет знакомый вид:
где \( r \) — это расстояние, на котором сосредоточена вся масса мячика \( m \).
Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине.
2 \):
А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.
Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.
Пример: замедление вращения компакт-диска
Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:
Момент инерции диска с радиусом \( r \), вращающегося относительно своего центра в плоскости диска, выражается формулой:
Подставляя значения, получим:
Теперь нужно определить угловое ускорение, которое определяется следующей формулой:
Изменение угловой скорости \( \Delta\omega \) произошло за промежуток времени:
В данном примере изменение угловой скорости:
где \( \omega_1 \) — конечная, а \( \omega_0 \) — начальная угловая скорость компакт-диска.
Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит \( 2\pi \) радиан:
Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит \( 2\pi \) радиан:
Подставляя значения в формулу углового ускорения, получим:
Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:
Итак, средний момент равен 10-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:
Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.
Еще один пример: поднимаем груз
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис.
11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.
В данном примере нужно вычислить сумму всех моментов сил \( \mathbf{\sum\! M} \), которые действуют на веревку:
В данном примере на веревку действует два момента сил: один \( M_1 \) со стороны груза весом \( mg \), а другой \( M_2 \) — со стороны горизонтальной силы \( F \):
Отсюда получаем формулу для углового ускорения:
Эти моменты \( M_1 \) и \( M_2 \) имеют одинаковое плечо, равное радиусу блока \( r \), поэтому:
Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:
Подставляя выражения для \( l \), \( M_1 \) и \( M_2 \) в формулу для углового ускорения, получим:
Подставляя значения, получим:
Вычисляем энергию и работу при вращательном движении
При изучении поступательного движения в главе 8 мы познакомились с понятием работа.
Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.
Работа при вращательном движении
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.
Пусть шина имеет радиус \( r \) и для ее вращения используется сила \( F \), как показано на рис. 11.3.
Чему равна работа этой силы? Применим знакомую нам формулу:
где \( s \) — это перемещение веревки под действием этой силы. В данном примере перемещение \( s \) равно произведению радиуса \( r \) на угол поворота шины \( \theta \):
Подставляя это выражение в формулу работы, получим:
Поскольку момент \( M \), создаваемой этой силой, равен:
то получаем для работы:
Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.
Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.
Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м.
Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:
Полный оборот соответствует повороту на угол \( 2\pi \). Подставляя значения в формулу, получим:
Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.
Изучаем кинетическую энергию вращательного движения
Из главы 8 нам уже известно, что объект массы \( m \), движущийся поступательно со скоростью \( v \), обладает кинетической энергией:
А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.
При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.
Как известно (см. главу 10), тангенциальная скорость \( v \) и угловая скорость \( \omega \) связаны соотношением:
где \( r \) — это радиус окружности вращения.
Подставляя это соотношение в предыдущую формулу, получим:
Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:
Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:
Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:
Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:
Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду.
Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.
Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.
На рис. 11.4 показан случай, когда с наклонной плоскости высотой \( h \) скатываются сплошной и полый цилиндры с одинаковой массой \( m \).2 \).
Итак, для полого цилиндра получим:
а для сплошного цилиндра:
А их отношение равно:
Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.
Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.
Не можем остановиться: момент импульса
Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.
В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:
где \( m \) — это масса, a \( v \) — скорость материальной точки.
По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):
где \( l \) — это момент инерции, а \( \omega \) — угловая скорость материальной точки.
Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.
Момент импульса в системе СИ измеряется в кг·м2·с-1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.
Сохраняем момент импульса
Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста \( \omega_0 \) и его моменты инерции в позе с разведенными руками \( I_0 \) и в позе с сомкнутыми руками \( I_1 \), легко найти конечную угловую скорость \( \omega_1 \) по формуле:
Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.
Пример закона сохранения момента импульса: вычисляем скорость спутника
Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·106 м от центра Плутона и имеет скорость 9·103 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·107 м от центра Плутона?
Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.
Итак, рассмотрим формулу закона сохранения момента импульса:
где \( I_{бл} \) — это момент инерции спутника в самой близкой точке, \( I_{дал} \) — это момент инерции спутника в самой далекой точке, \( \omega_{бл} \) — угловая скорость спутника в самой близкой точке, а \( \omega_{дал} \) — угловая скорость спутника в самой далекой точке.
Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:
и
где \( r_{бл} \) — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а \( r_{дал} \) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.
Кроме того:
и
Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса
получим:
Отсюда путем несложных алгебраических преобразований, получим:
Подставляя значения, получим:
Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.
Глава 11. Раскручиваем объекты: момент инерции
3 (60%) 7 votesРавномерное вращательное движение
⇐ ПредыдущаяСтр 6 из 15Следующая ⇒Если угловая скорость ω=const, то вращательное движение называется равномерным.
При равномерном вращении его быстроту также описывают частотой оборотов n и периодом вращения T.
Частота оборотов n равна числу оборотов, сделанных за единицу времени,
где N – число оборотов за время t. Т.к. за один оборот тело поворачивается на угол, равный 2p, то j = 2pN и w = 2pn.
Период вращения T– это время, за которое тело совершает один оборот.
Т.к.
, то
, .
[ω] = [ рад/с] , [n] =[об/с] , [T] = [c]
Уравнение равномерного вращения имеет вид
φ = φ0 + ωt.В частном случае, когда начальный угол поворота φ0 = 0,
φ = ωt.Угловую скорость равномерно вращающегося тела
ω = φ/tможно выразить и так: ω = 2π/T, где T – период вращения тела;
φ = 2π – угол поворота за один период.
Неравномерное вращение
Неравномерное вращение (угловая скорость изменяется со временем) характеризуется угловым ускорением e.
Угловое ускорение e — вектор, равный производной от угловой скорости w по времени t,
.
dw — изменение угловой скорости за время dt.
[e] = [ рад/с2].
Векторы и направлены по оси вращения тела. При ускоренном вращении тела направления векторов и совпадают, при замедленном – противоположны (рис. 2).
Рис. 2
Равнопеременное вращение
Если угловое ускорение ε = const, то вращательное движение называется равнопеременным. Равнопеременное вращение характеризуется следующими уравнениями:
и ,
w0 и j0 – угловая скорость и угол поворота тела в начальный момент t0=0,
w и j – в момент времени t. При ускоренном вращении в этих уравнениях выбирается знак «+», а при замедленном – знак «–».
Связь линейных и угловых характеристик
Если точка тела отстоит от оси вращения на расстоянии r, то за время dt она проходит путь
dS = dj × r
Скорость точки
, или v = w×r.
При вращении тела тангенциальное ускорение его точки
, или at = e×r
Нормальное ускорение точки тела
, или
.an = w2×r
Полное ускорение, как указывалось ранее, определяют по формуле
Момент инерции
Момент инерции — скалярная величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Единица измерения СИ: кг·м². Обозначение: I или J.
Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы относительно этой оси. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело.
Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен:
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
· mi — масса i-й точки,
· ri — расстояние от i-й точки до оси.
,
где:
· — масса малого элемента объёма тела ,
· — плотность,
· — расстояние от элемента до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния а между осями:
J = Jc+ ma2.
Рис. 3
где m — полная масса тела (рис. 3).
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
.
Момент силы
Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают Момент силы относительно центра (точки) и относительно оси.
Если имеется материальная точка О, к которой приложена сила , то момент силы относительно этой точки равен векторному произведению радиус-вектора , соединяющего точку О и точку приложения силы, на вектор силы :
., (Н•м).
Момент силы — аксиальный вектор1. Он направлен вдоль оси вращения.
Направление вектора момента силы определяется правилом буравчика, а величина его равна M (рис.2).
Рис. 2
Модуль момента силы:
M =F·l =F·r·sin α,
где: M – момент силы (Ньютон · метр), F – приложенная сила (Ньютон),
r – расстояние от центра вращения до места приложения силы (метр),
l = r•sin α – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр), α – угол, между вектором силы F и вектором положения r.Момент силы относительно оси величина алгебраическая, равная проекции на эту ось вектора Ммомента силы относительно любой точки О оси.
Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:
если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:
М1 + М2 + … + Мn = 0.
Считают момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.3, силам F1 и F2 следует приписать положительный момент, а силе F3— отрицательный.
Рис. 3.
Моменты сил F1 и F2 положительны, момент силы F3 отрицателен.
Момент импульса
Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Моментом импульса L материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r этой материальной точки, проведенного из точки О, на величину ее импульса p (рис. 6):
L= rx p (Дж×с),
где r – радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, p – импульс частицы.
Рис.6.
Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела Lz относительно этой оси (Lz – скалярная величина).
Суммирование производим по всем элементарным массам mi (имеющим линейную скорость vi и радиус вращения ri), на которые разбивается тело. Так как vi=ωri, где ω — угловая скорость вращения тела, а I=∑miri2 — момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен:
Lz=∑miviri=∑ωmiri2=ω∑miri2=Izω .
В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:
L= I ω.(1)
Продифференцируем выражение (1) по времени:
dLz/dt = Izdω/dt = Ize = Mz,
В итоге:
Lz / dt = dMz (2)
Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси:
dL/dt = M (3)
Из уравнения (3) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.
Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)
Выражение (4) представляет собой закон сохранения момента импульса:
момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.
Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.
Читайте также:
Формулы движения снаряда
Снаряд — это объект, которому задана начальная скорость, и на который действует сила тяжести. Путь, по которому следует объект, определяется этими эффектами (без учета сопротивления воздуха). Этот путь и есть траектория объекта. Траектория имеет горизонтальную (x) и вертикальную (y) компоненты. Скорость — это вектор (у него есть величина и направление), поэтому общую скорость объекта можно найти с помощью векторного сложения компонентов x и y: v 2 = v x 2 + v y 2 .Единицы измерения горизонтального и вертикального расстояний — метры (м). Горизонтальная и вертикальная скорости выражаются в метрах в секунду (м / с).
Расстояние по горизонтали
горизонтальное расстояние = (начальная горизонтальная скорость) (время)
x = v xo т
Вертикальное расстояние
Горизонтальная скорость
горизонтальная скорость = начальная горизонтальная скорость
v x = v xo
Вертикальная скорость
вертикальная скорость = начальная вертикальная скорость — (ускорение свободного падения) (время)
v y = v лет — gt
x = горизонтальное расстояние (м)
y = вертикальное расстояние (м)
v = скорость (комбинированные компоненты, м / с)
v x = горизонтальная скорость (м / с)
v y = вертикальная скорость (м / с)
v xo = начальная горизонтальная скорость (м / с)
v yo = начальная вертикальная скорость (м / с)
т = время (с)
г = ускорение свободного падения (9.80 м / с 2 )
Формулы движения снаряда Вопросы:
1) Ребенок сбивает футбольный мяч с вершины холма. Начальная скорость мяча 15,0 м / с по горизонтали. Какова величина скорости мяча через 5,00 с?
Ответ: Скорость мяча через 5,00 с имеет две составляющие. Как только эти два компонента найдены, их необходимо объединить с помощью векторного сложения, чтобы найти конечную скорость. Мяч был нанесен горизонтально, поэтому v xo = 15.0 м / с, и v yo = 0,0 м / с. Компонент x скорости после 5,00 с:
v x = v xo
, а компонент y:
v y = v лет — gt
v y = (0,0 м / с) — (9,80 м / с 2 ) (5,00 с)
v y = -49,0 м / с
В задачах о движении снаряда вверх определяется как положительное направление, поэтому компонент y имеет величину 49.0 м / с по направлению вниз.
Чтобы найти величину скорости, необходимо сложить компоненты x и y с векторным сложением:
v 2 = v x 2 + v y 2
v 2 = (15,0 м / с) 2 + (-49,0 м / с) 2
v 2 = 2626 (м / с) 2
∴ v = 51.24 м / с
Величина скорости 51,24 м / с.
Хотя в вопросе этого не спрашивали, можно также найти направление скорости в виде угла. Если горизонтальное направление равно 0,0 радиана, угол можно найти с помощью уравнения:
tanθ = -3,267
∴
θ = -1,274 радиана
θ = -72,98 °
Следовательно, скорость (величина и направление) мяча после 5.00 с было 51,24 м / с, -72,98 ° вниз от горизонтали.
2) Игрушечная ракета запускается в плоском поле под углом 60,0 ° вверх от горизонтальной оси (x). Его начальная скорость составляет 20,0 м / с. Сколько времени игрушечная ракета проводит в воздухе и как далеко от точки запуска приземляется в поле?
Ответ: Первое, что необходимо найти для решения этой проблемы, — это начальная скорость в направлениях x и y. Приведенная скорость имеет компоненты x и y, потому что она имеет направление 60.0 ° вверх от горизонтального (x) направления. Начальная скорость может быть разбита с помощью уравнения, связывающего синус и косинус:
1 = cos 2 θ + sin 2 θ
Умножаем обе части на квадрат начальной скорости v o 2 :
( v o 2 ) (1) = ( v o 2 ) ( cos 2 θ ) + ( v o 2 ) ( sin 2 θ )
v o 2 = ( v o cosθ ) 2 + ( v o sinθ ) 2
Уравнение векторного сложения начальных составляющих скорости:
v o 2 = v xo 2 + v лет 2
Итак, компоненты скорости могут быть установлены равными частям приведенного выше уравнения:
v xo 2 = ( v o cosθ ) 2
∴ v xo = v o cosθ
и v лет 2 = ( v o sinθ ) 2
∴ v лет = v o sinθ
Итак, начальная скорость в направлении x v xo составляет:
v xo = v o cosθ
v xo = (20.0 м / с) (cos60 °)
v xo = 10,0 м / с
, а начальная скорость в направлении y:
v лет = v o sinθ
v лет = (20,0 м / с) (sin60 °)
v лет = 17,32 м / с
Чтобы определить, как долго игрушечная ракета находилась в воздухе, используйте уравнение для вертикального расстояния для ракеты:
Поле ровное, поэтому ракета снова ударится о землю при y = 0.00 мин. Итак, установите левую часть уравнения равной этой высоте:
(-4,90 м / с 2 ) t 2 + (17,32 м / с) t + 0,00 м = 0
Это имеет форму квадратного уравнения с t в качестве переменной:
Если на 2 + bt + c = 0,.
Существует два решения для t, в зависимости от того, выбрано положительное или отрицательное значение в символе ±. Решаем для каждого:
т + = 0.00 с
и
т — = 3,53 с
Первое решение — это время запуска, а второе — время, когда игрушечная ракета снова достигает земли. Таким образом, игрушечная ракета провела в воздухе 3,53 секунды.
Чтобы найти расстояние от исходного положения до положения приземления, используйте уравнение для горизонтального расстояния:
x = v xo т
Время, которое игрушечная ракета летела по воздуху, оказалось равным 3.53 с . Используя это число, горизонтальное расстояние составляет:
x = v xo т
x = (10,0 м / с) (3,53 с)
x = 35,3 м
Игрушечная ракета приземляется на расстоянии 35,3 м от стартовой позиции.
Формула простого гармонического движения
Простое гармоническое движение (SHM) — это особый тип периодического движения, которое следует определенной схеме. Положение объекта в простом гармоническом движении описывается синусоидальной функцией, которая зависит от амплитуды движения A, угловой частоты, времени t и начального условия, называемого фазовым сдвигом.Единицы измерения положения и амплитуды — метры (м), единицы измерения угловой частоты — радианы / с, единицы времени — секунды (с) и единица измерения фазового сдвига — радианы.
x = положение (м)
A = амплитуда (м)
угловая частота (радиан / с)
t = время (с)
фазовый сдвиг (радианы)
Формула простого гармонического движения Вопросы:
1) Шарик на пружине вытягивается и отпускается, что приводит его в простое гармоническое движение.Амплитуда движения мяча 0,080 м, фазовый сдвиг. Если угловая частота движения мяча равна, каково будет положение мяча в момент времени t = 2,00 с?
Ответ: Амплитуда движения мяча A = 0,080 м. Положение мяча относительно положения равновесия равно x, и его можно найти по формуле:
x = 0,080 м
В момент времени t = 2,00 с мяч будет в положении x = 0,080 м относительно положения равновесия.
2) Пчела летает взад и вперед над цветком, двигаясь по схеме, которую можно описать простым гармоническим движением. Положение равновесия — центр цветка. В момент времени t = 0,00 с пчела находится в позиции x = -0,020 м. Амплитуда движения пчелы A = 0,020 м, угловая скорость. Каким будет положение пчелы в момент времени t = 4,00 с?
Ответ: Первым шагом к решению этой проблемы является расчет фазового сдвига. Вместо того чтобы указывать значение фазового сдвига, были заданы начальные условия.Начальные условия можно использовать с простой формулой гармонического движения для вычисления фазового сдвига:
Следующим шагом к определению положения пчелы в момент времени t = 4,00 с является замена известных значений, включая значение фазового сдвига, в формулу простого гармонического движения:
х = 0.020 кв.м
Положение пчелы при t = 4,00 с составляет 0,020 м.
Формулы движения снаряда | Концепции и примеры
×
Извините !, эта страница сейчас недоступна для добавления в закладки.
Формулы движения снаряда — концепции и решенные примеры
Вокруг нас много типов движения.Движение снаряда — это форма движения, испытываемого объектом или частицей, которые брошены около поверхности Земли и движутся по кривой траектории только под действием силы тяжести (в частности, предполагается, что влияние сопротивления воздуха незначительно). Такой объект называется снарядом, а криволинейная траектория, по которой движется снаряд, называется траекторией.
СМОТРЕТЬ БОЛЬШЕ
Формулы, относящиеся к снаряду, который запускается под наклонным углом по отношению к горизонтали и движение которого относится к горизонтали, следующие:
(v0 — скорость выброса,
θ
Вопрос: Если горизонтальная дальность полета снаряда в 4 раза превышает максимальную высоту, достигаемую им, то угол проекции равен:
Варианты:
(a) 45 °
(b) 30 °
(в) 60 °
(г) 15 °
Ответ: (а)
Вращательное движение жесткого тела
Дверь легче открыть, нажав на край, наиболее удаленный от петель, чем посередине.Интуитивно понятно, что величина приложенной силы и расстояние от точки приложения до петли влияют на склонность двери к повороту. Эта физическая величина, крутящий момент , — это t = r × F sin θ, где F — приложенная сила, r — это расстояние от точки приложения до центра вращения, а θ — угол от r до F .
Подставьте второй закон Ньютона в определение крутящего момента с θ 90 градусов (прямой угол между F и r ) и используйте соотношение между линейным ускорением и тангенциальным угловым ускорением, чтобы получить t = r F. = rma = mr 2 ( a / r ) = mr 2 α.Величина mr 2 определяется как момент инерции точечной массы относительно центра вращения.
Представьте два объекта одинаковой массы с различным распределением этой массы. Первым объектом может быть тяжелое кольцо, поддерживаемое стойками на оси, подобной маховику. Второй объект мог иметь массу, близкую к центральной оси. Несмотря на то, что массы двух объектов равны, интуитивно понятно, что маховик будет труднее нажимать на большое число оборотов в секунду, потому что не только количество массы, но и ее распределение влияет на легкость запуска. вращение для твердого тела.Общее определение момента инерции, также называемого инерцией вращения , для твердого тела составляет I = ∑ м i r i 2 и измеряется в единицах СИ в килограмм-метрах. 2 .
Моменты инерции для различных правильных форм показаны на рисунке 2.
Рисунок 2
Моменты инерции для различных правильных форм.
Проблемы механики часто включают как линейные, так и вращательные движения.
Пример 1: Рассмотрим рисунок 3, где груз свисает на веревке, обернутой вокруг шкива. Падающая масса (м) заставляет шкив вращаться, и больше нет необходимости требовать, чтобы шкив был безмассовым. Присвойте шкиву массу ( M ) и рассматривайте его как вращающийся диск с радиусом (R) . Какое ускорение падающей массы и каково натяжение веревки?
Рисунок 3
Висящая масса вращает шкив.
Уравнение силы для падающей массы: T — мг = — мА . Натяжение каната — это сила, приложенная к краю шкива, заставляющая его вращаться. Таким образом, t = I α, или TR = (1/2) MR 2 ( a / R), что сокращается до T = (1/2) млн лет , где угловое ускорение заменено на на / R, потому что шнур не проскальзывает, а линейное ускорение блока равно линейному ускорению обода диска.Объединение первого и последнего уравнения в этом примере приводит к
Решение:
Угловой момент — это вращательный момент, который сохраняется так же, как и линейный момент. Для твердого тела угловой момент (L) является произведением момента инерции и угловой скорости: L = I ω. Для точки массы угловой момент может быть выражен как произведение количества движения и радиуса ( r ): L = mvr . L измеряется в килограммах-метрах 2 в секунду или, как правило, в джоуль-секундах. Закон сохранения углового момента может быть заявлен, что угловой момент системы объектов сохраняется, если на систему не действует внешний чистый крутящий момент.
Аналогично закону Ньютона (F = Δ ( mv ) / Δ t ) существует вращательный эквивалент для вращательного движения: t = Δ L / Δ t , или крутящий момент — скорость изменения углового момента.
Рассмотрим пример ребенка, который бежит по касательной к краю карусели на игровой площадке со скоростью v o и прыгает дальше, пока карусель находится в состоянии покоя. Единственными внешними силами являются сила тяжести и контактные силы, создаваемые опорными подшипниками, ни одна из которых не вызывает крутящего момента, потому что они не прикладываются, чтобы вызвать горизонтальное вращение. Рассматривайте массу ребенка как точку массы, а карусель — как диск с радиусом R и массой M .Согласно закону сохранения, полный угловой момент ребенка до взаимодействия равен полному угловому моменту ребенка и карусели после столкновения: mrv o = mrv ′ + I ω, где r — радиальное расстояние от центра карусели до места удара ребенка. Если ребенок прыгает на край, (r = R) и угловая скорость для ребенка после столкновения может быть заменена на линейную скорость, mRv o = mR ( R ω ) + (1/2) MR 2 .Если даны значения масс и начальной скорости ребенка, можно рассчитать конечную скорость ребенка и карусели.
У одиночного объекта может измениться угловая скорость из-за сохранения углового момента, если изменяется распределение массы твердого тела. Например, когда фигуристка тянет вытянутые руки, ее момент инерции уменьшается, вызывая увеличение угловой скорости. Согласно сохранению углового момента, I o (ω o ) = I f (ω f ), где I o — момент инерции фигуристки с вытянутыми руками, I f — ее момент инерции с руками, близко расположенными к ее телу, ω o — ее исходная угловая скорость, а ω f — ее конечная угловая скорость.
Кинетическая энергия вращения, работа и мощность. Кинетическая энергия, работа и мощность определены во вращении как K . E = (1/2) I ω 2 , W = t θ, P = t ω.
Сравнение уравнений динамики линейного и вращательного движения. Динамические соотношения приведены для сравнения уравнений линейного и вращательного движения (см. Таблицу).
Урок двенадцатого класса «Введение в угловое движение»
Класс начинается с задания, в ходе которого учащихся просят использовать транспортир для измерения диапазона движений их колен.У меня активность отображается на передней доске, когда студенты входят в комнату, и они также могут схватить транспортир, чтобы сесть. Отображаемый вопрос и транспортир — единственные материалы, которые нужны учащимся для начала работы, но чтобы официально начать занятие, я зачитываю вопрос вслух.
Учащиеся выполняют это задание в парах, хотя при желании они могут работать индивидуально. Цель состоит в том, чтобы заставить учащихся задуматься о том, как измерить что-то вращающееся.На сегодняшний день наш курс AP Physics 1 сосредоточен на линейном движении, и я хочу вывести студентов из зоны комфорта, попросив их измерить что-то, что может вращаться. Я намеренно не привел процедуру для этого упражнения, так как я также использую ее как метод, чтобы оценить, насколько студенты имеют предварительные знания об угловом смещении.
Пока студенты обсуждают вопросы и измеряют диапазоны движения, я хожу вокруг, чтобы неформально наблюдать за методами измерения и беседами студентов.Пока я хожу по кругу, студенты могут попросить совета о том, как измерить диапазон их движений, но я стараюсь оставаться пассивным, потому что хочу, чтобы это было настоящим исследовательским заданием. Я не ищу конкретного ответа; вместо этого я хочу, чтобы ученики заново познакомились с транспортирами и измерениями углов.
Примерно через десять минут я беру транспортиры и прошу студентов устно поделиться своими ответами. Обмен ответами носит довольно неформальный характер, так как разные ученики поднимают руки, и каждому, кто хочет поделиться, предоставляется такая возможность.Некоторые студенты могут прокомментировать то, что разделяют другие, и я могу попросить разъяснений по некоторым утверждениям. Цель нашего обсуждения — заставить студентов задуматься об углах, но я также оцениваю предыдущие знания студентов с помощью той информации, которой они делятся. Хотя мои ученики имеют отличный математический фон и много знают об углах, если они не справляются с этим заданием, я предлагаю дополнительный пакет онлайн-обзора или обзорную сессию перед школой. Когда студентов, желающих поделиться, больше нет, мы переходим к следующей части урока, в которой определяется угловое смещение (а также угловая скорость и ускорение).
Список формул момента инерции для различных форм
формулы момента инерцииВ этом посте вы узнаете список формул момента инерции для различных форм с примерами.
Состав:
- Моменты инерции Определение
- Формула момента инерции
- Уравнение
- Блок
- Намного больше
Продолжайте читать…
Что такое момент инерции?
Момент инерции ( I ) определяется как сумма произведений массы каждой частицы тела и квадрата ее перпендикулярного расстояния от оси.Это также известно как инерция вращения. Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но не зависит от сил, участвующих в движении.
Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но не зависит от сил, участвующих в движении.
Момент инерции играет роль, аналогичную роли инерционной массы в случае прямолинейного и равномерного движения. Это скалярное значение продольного углового момента твердого тела.I = mr²
Для твердого тела, движущегося вокруг фиксированной оси, законы движения имеют ту же форму, что и законы прямолинейного движения, с моментом инерции вместо массы, угловой вместо линейной скорости, угловым моментом вместо количества движения и т. Д. Следовательно, кинетическая энергия тела, вращающегося вокруг фиксированной оси с угловой скоростью ω, составляет ½ω², что соответствует ½mv² для кинетической энергии тела массы m, перемещаемой со скоростью v.См. Также правило Рауса; Теорема о параллельных осях.
Уравнение момента инерции
Рассмотрим массу m, прикрепленную к концу безмассового стержня. Предположим, что подшипник в точке поворота O не имеет трения. Пусть система находится в горизонтальной плоскости. Сила F действует на массу, перпендикулярную стержню, и, следовательно, это ускоряет массу в соответствии с:
F = ma
При этом сила заставит массу вращаться вокруг оси O. Так как тангенциальное ускорение связано с угловым ускорением
α уравнением.угловое ускорение = rα
Поскольку вращающий эффект создается крутящим моментом τ, поэтому было бы лучше записать уравнение для вращения в терминах крутящего момента. Это можно сделать, умножив обе части приведенного выше уравнения на r. Таким образом,
rF = τ = крутящий момент = mr²α
Какой вращательный аналог второго закона движения Ньютона?
Здесь F заменяется на τ, a на α и m на mr². Величина mr² известна как момент инерции и обозначается I.Важность момента инерции
Момент инерции играет в угловом движении ту же роль, что и масса при линейном движении. Можно отметить, что момент инерции зависит не только от массы m, но и от r².
Момент инерции Формулы
Вот список формул момента инерции различной формы:
момент инерции гильзы цилиндра
Момент инерции обруча
Момент инерции диска
Момент инерции диска
момент инерции сплошного цилиндра
Момент инерции твердого шара
момент инерции полого цилиндра
Момент инерции полого цилиндра
момент инерции длинного тонкого стержня
Момент инерции тонкого стержня
момент инерции прямоугольника
Момент инерции прямоугольника
момент инерции тонкого стержня
Момент инерции длинного тонкого стержня
Момент инерции тонкой сферической оболочки
Момент инерции сферической оболочки
Момент инерции (видео)

 Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.


 При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c. Кинематика вращательного движения — PhysBook
Кинематика вращательного движения — PhysBook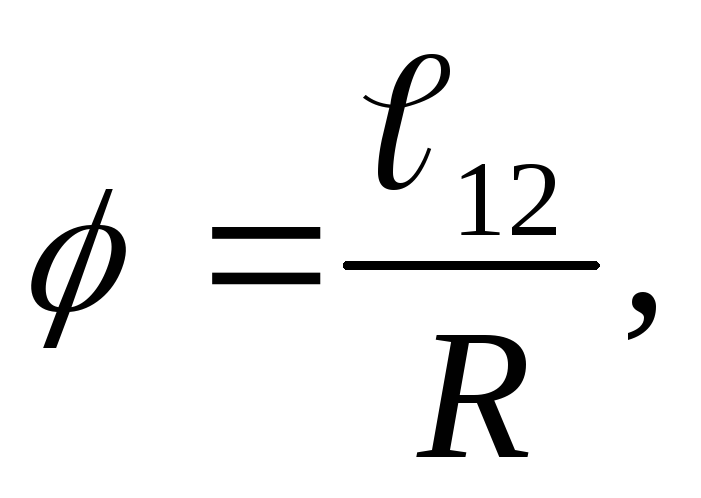 10.4.
10.4. е. с постоянной угловой скоростью.
е. с постоянной угловой скоростью. {-2} \)? Подставляя значения в уже известную нам формулу
{-2} \)? Подставляя значения в уже известную нам формулу 2 \):
2 \):
 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.
11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.
Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.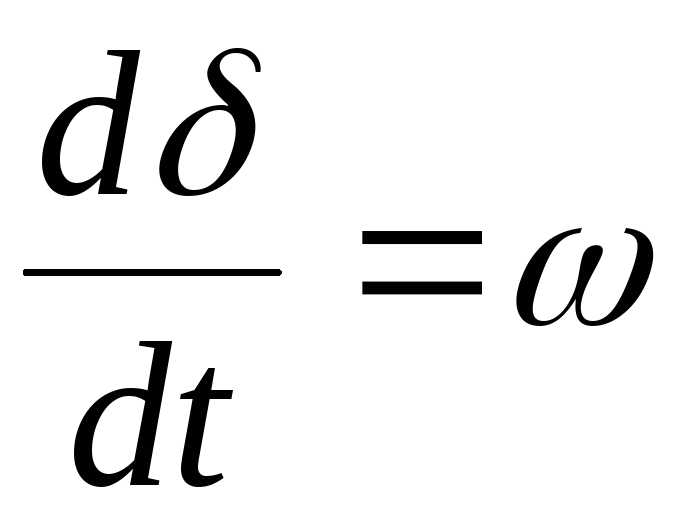
 Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:
Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы: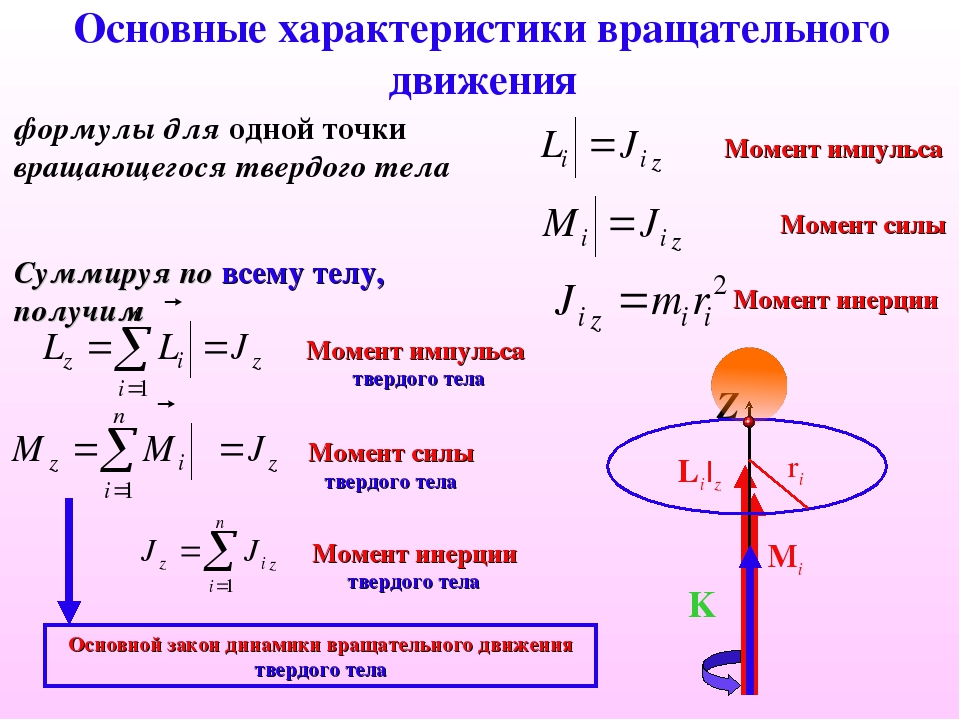
 Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.
Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.