Расстояние до объекта: Купите дорожный знак 8.1.1 Расстояние до объекта

Содержание

Как определить расстояние без специальных приспособлений

Человеку, находящемуся в какой-либо местности может понадобится возможность измерения расстояний до определенных объектов, а также определение ширины и высоты этих обьектов. Такие измерения лучше и точнее можно провести с иcпользованием специальных средств (лазерных дальномеров, дальномерных шкал оптический приборов и.т.д.), но таковые не всегда могут оказаться под рукой. Поэтому в данной ситуации на выручку придет знание «дедовских», проверенных временем, способов. К таковым относятся:

  • определение расстояний на глаз
  • по угловой величине
  • определение расстояний при помощи линейки и сподручных предметов
  • по звуку

Определение расстояний на глаз

Данный способ является наиболее простым и быстрым. Определяющим здесь является умение мысленно откладывать на местности равные отрезки в 50, 100, 500 и 1000 м. Данные отрезки расстояний необходимо изучить и хорошо закрепить в зрительной памяти. При этом необходимо принимать во внимание следующие особенности:

  • на ровной местности и водном пространстве расстояния кажутся меньше, чем они есть на самом деле,
  • лощины и овраги уменьшают видимое расстояние,
  • более крупные предметы кажутся ближе мелких, находящимися на одной с ними линией,
  • все предметы кажутся ближе во время тумана, дождя, во время пасмурных дней,
  • предметы с яркой окраской кажутся ближе,
  • при наблюдении снизу вверх, расстояния кажутся ближе, а при наблюдении сверху вниз больше,
  • ночью светящиеся предметы кажутся ближе.

Дистанции более 1 км определяются с большей погрешностью, достигающей 50%. У опытных людей, собенно на малых дистанциях погрешность составляет менее 10%. Глазомер необходимо постоянно тренировать в различных условиях видимости, на различной местности. При этом огромную положительную роль вносит занятие туризмом, альпинизмом, охотой. [nextpage title=»Определение расстояний по угловой величине»] Этот способ основывается на понятии тысячной. Тысячная — это единица измерения расстояний по горизонту, и составляет 1/6000 горизонта. Понятие тысячной принято во всех странах мира, и применяется для введения горизонтальных поправок ведения огня стрелкового оружия и артиллерийских систем, а также определение расстояний и дистанций. Тысячные записываются и читаются след. образом:

  • 1 тысячная 0-01, читается как ноль, ноль один,
  • 5 тысячных 0-05, читается как ноль, ноль пять,
  • 10 тысячных 0-10, читается как ноль, десять,
  • 150 тысячных 1-50, читается как один, пятьдесят,
  • 1500 тысячных 15-00, читается как пятнадцать, ноль ноль.

Применение этого способа возможно, если известна одна из линейных величин предмета — ширина или высота. Дальность до предмета определяется по след. формуле: Д = (Bx1000) / Y , где Д — дальность до цели B — ширина или высота объекта в метрах Y — угловая величина в тысячных. Для того, чтобы определить угловую величину, необходимо знать, что отрезок в 1 мм, удаленному на 50 см от глаза соответствует углу в 2 тысячные (0-02). На основании этого существует метод определения расстояний при помощи линейки:

  • линейку с миллиметровыми делениями вытянуть на расстояние 50 см,
  • засечь, во сколько делений на линейке укладывается ширина или высота объекта,
  • полученное кол-во миллиметров умножить на 2, и подставить в выше приведенную формулу.

Еще удобней для этих целей использовать штангенциркуль, который для компактности можно укоротить.

Пример: Высота телеграфоного столба равна 6 м при измерения на линейке займет 8 мм (16 тысячных ,т.е. 0-16),следовательно расстояние до столба будет (6×1000)/16 = 375 м

Также существует более простая формула определения дистанции при помощи линейки:
Д = (высота или ширина объекта в см / кол-во миллиметров на линейке) x 5

Пример: ростовая фигура имеет высоту 170 см и на линейке закрывает 2 мм, следовательно дистанция до нее будет:(170см / 2мм) x 5 = 425 м

Определение расстояний при помощи линейки и сподручных предметов

Линейные размеры распространенных объектов

ОбъектВысота, мДлина, м
Телеграфный столб деревянный6—-
Телеграфный столб бетонный8—-
Расстояние между столбами ЛЭП 6м—-50
Расстояние между столбами высковольт. линий—-100
Товарный вагон, 4-х осный414-15
Пассажирский вагон цельнометаллический424
Цистерны, 2-х осные36,75
Цистерны, 4-х осные39
Один этаж панельного дома3—-
Дом сельского типа6-7—-
Высота железнодорожной будки4—-
Ростовая фигура (средн.)1,7—-
Голова без каски0,250,20
Голова в каске0,300,30
Танк2,5-3—-
Грузовой автомобиль2-2,5—-

При отсутствии линейки угловые величины можно измерять помощи подручных предметов, зная их линейные размеры. Это может быть, например спичечный коробок, спичка, карандаш, монета, патроны, пальцы рук и. т.д Например, спичечный коробок имеет длину — 45 мм, ширину 30 мм, высоты 15 мм, следовательно если его вытянуть на расстояние 50 см, его длина будет соответствовать 0-90, ширина 0-60, высота 0-30.

Определение расстояний по звуку

Человек обладает способностью улавливать и различать звуки различной природы, как в горизонтальной плоскости, так и в вертикальной, что позволяет весьма успешно навскидку определять расстояния до источников звука. Слух, как и глазомер необходимо постоянно тренировать.

  • Слух работает с полной отдачей только при полном спокойствии психики.
  • Лежа на спине, слуховая ориентация ухудшается, а лежа на животе улучшается
  • Зеленый цвет улучщает слух
  • Кусочек сахара, положенный под язык, заметно улучшает ночное зрение и слух, поскольку глюкоза необходима для работы сердца, мозга, нервной системы, а следовательно и органов чувств.
  • Звуки хорошо слышны на открытой местности, особенно водной, в спокойную погоду
  • Слышимость ухудшается в жаркую погоду, против ветра, в лесу, в камышах, на рыхлой траве.

Средняя дальность слышимости различных источников

ОбъектРасстояние, км
Выстрел их охотничьего ружья3,5
Шум поезда10
Паровозный гудок7-10
Сигнал автомобиля2-3
Рокот работающего трактора3-4
Топот лошадей1-1,5
Крики человека1-1,5
Лай собак2-3
Негромкая речь, шум шагов0,3-0,5
Всплески от весел0,25-0,5
Кашель0,05
Движение автомобиля (ровный шум мотора)1

Можно ли измерить расстояние до объекта с помощью камеры? Oh! Android

Можно ли измерить расстояние до объекта с помощью камеры телефона. Я имею в виду, что в своем приложении я запускаю камеру, обращаясь к камере к объекту (скажем, дом), а затем нажимаю кнопку, и он вычисляет расстояние и показывает мне на экране.

Если возможно, где я могу найти учебник или информацию об этом?

Ну, вы должны прочитать, как ithinkdiff.com «измеряет» расстояние:

Использует угол iPhone для оценки расстояния до точки на земле. Держите iPhone перед собой, выровняйте точку в камере и получите прямое считывание расстояния. Затем расстояние можно использовать в инструменте скорости.

Таким образом, в основном это занимает высоту, где вы держите телефон (уровень глаз), тогда вы должны указывать камеру на точку, где объект касается земли. Затем телефон измеряет наклон и с простой тригонометрией вычисляет расстояние.

Это, конечно, не очень точно. Он становится менее точным, чем дальше объект. Также он предполагает, что земля является уровнем.

Я согласен, что на вопрос ответили адекватно (с очевидными предостережениями о необходимости определения уровня и возможных проблем с точностью), но для тех, кто не считает, что это может быть сделано или что ему нужна видеокамера, позвольте мне объяснить математику низкого уровня Нужно было это сделать ….

На рисунке выше показано, что я стоял вне дома. Горизонталь (d) – это расстояние, которое я хочу измерить, а вертикаль (h) – высота над землей, на которой я держу камеру. В этом случае «h» является известным значением, когда я держу камеру андроида на уровне глаз (около 67 дюймов или 1,7 метра). Когда я наклоняю камеру, чтобы прицелиться прямо в точку, где мой дом встречает землю, все программное обеспечение, которое нужно сделать, это выработать угол (а) относительно вертикали, и он может вычислять «d», используя …

d = h * tan a

Неа. Камера может предоставить только данные изображения, и только изображение не дает вам достаточной информации, чтобы предоставить вам информацию о глубине. Если у вас было несколько изображений, в которых у вас была информация о местоположении для или даже видео, вы могли обработать его для триангуляции расстояния, но одного изображения было бы недостаточно, чтобы дать вам дистанцию.

У вас есть угол в акселерометре телефона. Если вы вычислите касательную этого угла и умножьте ее на высоту объектива камеры, вы получите расстояние.

Вы можете использовать ту же технику, что и наш глаз, чтобы получить представление о глубине и расстоянии. Получите 2 изображения одного и того же объекта с двух разных позиций камеры. Дисталь или пиксели между объектами в двух изображениях обратно пропорциональны расстоянию между камерой и объектом. Реализация доступна на странице https://github.com/agnelvishal/Distance-between-camera-and-object. Вот исследовательский документ http://dsc.ijs.si/files/papers/S101%20Mrovlje.pdf

Нет. Только с двумя камерами в стерео режиме, например, с кинетом xbox 360. Требуется не менее 3 точек для триангуляции расстояния.

Я думаю, что это приложение использует подход MisterSquonk (его бесплатный). Посмотрите на технику «Тригонометрия».

Я думаю, используя FastCV, вы можете рассчитать расстояние между камерой и объектом. В этом вам не нужно знать угол или положение камеры, которые вы держите над уровнем земли. Взгляните на этот вопрос здесь

Один из способов добиться этого – использовать DPI на вашем устройстве. Вы можете сделать снимок и рассчитать высоту. Но вам понадобится другой объект в качестве ссылки, и тогда вы сможете узнать, что проблема с этим методом может быть перспективой между объектами

Как инструменты близости вычисляют расстояние—ArcGIS Pro

Как определяется расстояние

Расстояние между любыми двумя объектами вычисляется как минимальный интервал между ними, т.е., там, где два объекта расположены ближе всего друг к другу. Эта логика действует во всех инструментах геообработки, которые вычисляют расстояние, включая такие инструменты, как Ближайший объект, Построить таблицу ближайших объектов и Пространственное соединение (с опцией ближайших совпадений).

Измерения расстояний имеют наибольшую точность, если входные данные используют систему координат равнопромежуточной проекции. Хотя вычисление расстояния может быть выполнено независимо от системы координат, результат может оказаться не точным или даже бессмысленным, если данные используют географическую систему координат или система координат задана неправильно.

Более подробно о картографических проекциях и системах координат

Для дальнейшего обсуждения, расстоянием всегда будет считаться минимальный интервал между двумя объектами.

Особые соображения

  • Несколько объектов могут оказаться на одинаковом удалении от другого объекта. В таком случае один из равноудаленных объектов будет выбираться в качестве ближайшего случайным образом.
  • Если один из объектов содержит другой или находится внутри другого объекта, расстояние между ними равно 0.
    • Это означает, что если объект находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
  • Расстояние между двумя объектами равняется нулю всякий раз, когда у них имеется хотя бы одна общая координата x,y.
    • Это означает, что при пересечении, перекрытии или касании двух объектов, расстояние между ними равняется 0.
  • Расстояние всегда вычисляется до границы полигонального объекта, не до центра или центроида полигона.
    • Как отмечено выше, если объект полностью находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
  • Расстояние между двумя объектами (любого типа) не меняется в зависимости от направления измерения.

Основные операции для определения расстояния

Вычисление расстояния зависит от типа геометрии объектов, а также от других факторов, таких как система координат. Однако есть три основных правила, подробнее описанные ниже, которые определяют способ вычисления расстояния.

  1. Расстояние между двумя точками является прямой линией, соединяющей их.
  2. Расстояние от точки до линии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины.
  3. Расстояние между полилиниями определяется вершинами сегментов.

Правило 1: расстояние между двумя точками является прямой линией, соединяющей их

На рисунке ниже показано расстояние между двумя точками, вместе с несколькими ключевыми словами и объектами, использующимися инструментами близости.

Ключевые слова в вышеуказанных выносках (IN_FID, NEAR_DIST, NEAR_FID, NEAR_X, NEAR_Y и NEAR_ANGLE) являются полями, добавляемыми к выходным данным инструментами Построить таблицу ближайших объектов и , а также к входному классу объектов при использовании инструмента Ближайший объект.

Расстояние между мультиточками

Для особого случая, когда определяется расстояние между мультиточками, вычисляются расстояния от каждой точки входного мультиточечного объекта до каждой точки ближайшего мультиточечного объекта с помощью Правила 1, минимальное из этих трех расстояний станет расстоянием между мультиточечными объектами.

Кроме того, когда одна из точек мультиточечного объекта находится поверх одной из точек другого мультиточечного объекта, расстояние между ними равняется 0. Это справедливо для всех составных объектов.

Правило 2: расстояние от точки до полилинии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины

В ArcGIS линейные объекты называются полилиниями. Эти два термина, линия и полилиния, взаимозаменяемы. Полилиния является упорядоченным набором точек, эти точки называются вершинами. An individual vertice is a vertex. Полилиния может иметь любое количество вершин. Линия, заданная двумя вершинами, называется сегментом. Две вершины, которые задают сегмент линии, называются конечными вершинами.

Сходным образом, полигон является замкнутой областью, заданной одной или несколькими полилиниями.

Кратчайшим расстоянием от точки до сегмента линии является перпендикуляр к ней. Если в пределах конечных вершин сегмента перпендикуляр провести не удается, кратчайшим расстоянием будет расстояние до ближайшей конечной вершины.

Расстояние от точки до полилинии

Если полилиния содержит только один сегмент, для вычисления расстояния применяется Правило 2.

Если полилиния состоит из нескольких сегментов (чаще всего), сначала определяется ближайший к точке сегмент линии, затем для вычисления расстояния применяется Правило 2.

Расстояние от точки до полигона

Поскольку полигон является замкнутой областью, образованной набором сегментов линий, вычисление расстояния от точки до полигона включает определение ближайшего к точке сегмента, затем применяется Правило 2.

Расстояние будет определяться, только если точка находится вне полигона; иначе, расстояние равно 0.

На рисунке выше, для точек 2 и 3 расстояние равно 0, для точек 1 и 4 – расстояние положительно.

Правило 3: расстояние между полилиниями определяется вершинами сегментов линии

Для двух объектов, не являющихся точками, таких как два сегмента линий:

  1. Расстояние вычисляется от каждой из конечных вершин входного сегмента до ближайшего сегмента с использованием Правила 2.
  2. Расстояние вычисляется от каждой из конечных вершин ближайшего сегмента до входного сегмента.
Минимальное из этих двух значений принимается за расстояние между двумя сегментами.

Расстояние от полилинии до полилинии

В простейшем случае, предположим, что оба полилинейных объекта состоят из одного сегмента. На рисунке ниже показан перпендикуляр CX от вершины C до сегмента, заданного вершинами AB. Перпендикуляр от вершины D также вычисляется, но это расстояние больше, чем расстояние CX. Поэтому CX является кратчайшим расстоянием от сегмента CD до сегмента AB.

Обратите внимание, что перпендикуляр от вершины A или B до сегмента CD провести нельзя, поэтому, кратчайшее расстояние вычисляется от вершин A и B до вершины C. В результате, именно AC является кратчайшим расстоянием между сегментами AB и CD.

Из двух вычисленных расстояний (AC и CX), CX является кратчайшим между двумя сегментами, поскольку это минимальное расстояние из всех расстояний между вершинами и сегментом.

Когда обе полилинии состоят из нескольких сегментов, определяются два наиболее близкорасположенных друг к другу сегмента, затем вычисляется расстояние, согласно Правилу 3.

Расстояние от полилинии до полигона

При вычислении расстояния между полилинией и полигоном определяются два наиболее близкорасположенных сегмента: один сегмент полилинии и один сегмент из образующих границу полигона. Расстояние между этими двумя сегментами определяется так же, как описано в Правиле 3.

Краткая информация

На следующем рисунке показано, как измеряется расстояние между объектами различных типов и определяется положение ближайших объектов. Показаны не все возможные комбинации.

Связанные разделы

Отзыв по этому разделу?

Как вычислить расстояние до объекта по фотографии

В связи с известным событием по всему интернету развернулись бурные дискуссии, участники которых обвиняют своих оппонентов то в незнании программы средней школы, то в непонимании того очевидного факта, что в военное время косинус угла может достигать четырёх.

Не желая в эти дискуссии ввязываться, я лучше на наглядном примере покажу вам, как, имея на руках фотографию какого-либо известного объекта и немного вспомогательной информации, можно с большой точностью по совсем не сложным формулам рассчитать, на каком расстоянии этот объект находился от фотографа в момент съёмки.  По возможности я постараюсь каждый шаг сопровождать иллюстрацией, расчётом или ссылкой на источник. Итак, приступим.

Как известно, простейший объектив для фотоаппарата можно сделать из одной двояковыпуклой линзы. Конечно, существуют фотоаппараты вообще без объектива (так называемые пинхол-камеры, предок которых — камера-обскура), но в данном случае они нам не слишком интересны. Для начала мы рассмотрим, как строится изображение в простейшем однолинзовом объективе, а затем я покажу, что те же методы хорошо подходят и для сложных объективов, сочетающих в себе более десятка последовательно расположенных линз.

Напомню вам схему хода лучей в тонкой линзе из школьного курса геометрической оптики:

На этой схеме d — расстояние от линзы до объекта, D — расстояние от линзы до изображения объекта (на матрице или плёнке), а f — фокусное расстояние линзы.

Формула тонкой линзы из того же курса связывает эти три расстояния:

Теперь ещё раз посмотрим на оптическую схему: h — это линейный размер объекта съёмки, а H — размер его уменьшенного изображения. Нетрудно заметить, что h = d tan α, а H = D tan α (это следует из свойств прямоугольного треугольника). Подставив эти величины в формулу тонкой линзы, увидим, что tan α сокращается, и в результате получим следующее уравнение:

«Неудобная» величина D ушла, а остальные мы знаем или можем легко вычислить. На основе этого уравнения получаем вот такую формулу расстояния до объекта:

Ну а теперь давайте проверим её на практике.

Вот фотография, которую я сделал из своего окна:

На ней запечатлён дом 1 по 3-му Дорожному проезду, что в Москве. Это 22-этажная башня серии И-700А.

Какую полезную информацию можно извлечь из данной фотографии? Напомню, для расчёта нам нужны неизвестные пока величины h, H и f. h — это реальная высота дома (в метрах). Сходу я её не нагуглил, зато выяснил вот что: высота потолков в этом доме — 2,64 м, а толщина перекрытий — 0,22 м. Наверняка при измерении высоты потолков не учитывалась толщина напольного покрытия. Точно она мне не известна, так что, немного округлив, примем высоту одного этажа равной 2,9 м. Хорошо видны 23 панели, таким образом, высота видимого участка составляет примерно 66,7 м. Запомним эту величину и приступим к анализу фотографии.

H — это размер изображения дома на матрице фотоаппарата. По фотографии мы можем подсчитать его в пикселях, но, как известно, размер пикселя — это всё равно что размер ангела: точных данных ни у кого нет. Но здесь нужно вспомнить, что конкретные физические размеры имеет матрица фотоаппарата. Лезем в поисковик и узнаём, что для камеры Nikon D90 размер матрицы составляет 2,36 × 1,58 см, а разрешение — 4288 × 2848 пикс. Наша фотография не была кадрирована или повёрнута, поэтому мы можем узнать точный линейный размер изображения дома на матрице, составив пропорцию. Но чтобы делать это не вручную, воспользуемся программой Adobe Photoshop, где есть масса полезных инструментов.

По умолчанию Photoshop, конечно, не знает, какого размера должна быть наша фотография, и указывает ей разрешение 300 пикс. /дюйм, или 118,11 пикс./см:

Но мы, зная физический размер матрицы и количество пикселей по длинной стороне снимка, делаем такой расчёт: 4288 / 2,36 (размер матрицы в сантиметрах), и получаем правильное разрешение — 1817 пикс./см. Вписываем его в соответствующее окошко и, чтобы не изменились реальные размеры фотографии, а лишь были пересчитаны её длина и ширина в см, указываем в верхних полях «100 проц»:

Как видите, при этом в поле «Размер печатного оттиска» появились уже известные нам размеры матрицы: 2,36 × 1,57 см. Точнее, в спецификации было указано 1,58 см, но это несущественная погрешность.

Теперь при помощи инструмента «Линейка» измерим высоту видимого участка дома (23 панели) на фотографии (смотрите в правый верхний угол):

Получается, что высота изображения дома на матрице составляет 1,92 см, или 0,0192 м.

Осталось только выяснить фокусное расстояние, но для этого, к счастью, ничего считать не нужно: оно сразу прописывается при съёмке в метаданных фотографии (EXIF). Открываем их в фоторедакторе и видим:

Фокусное расстояние при съёмке составляло 105 мм, или 0,105 м, то есть я снимал дом с максимально возможным для этого объектива приближением.

Ну что ж, теперь у нас есть все данные для расчёта. Подставляем их в формулу

и получаем: d = (0,105(0,0192 + 66,7)) / 0,0192 = 364,9 м. Внимательный читатель наверняка заметил, сколь ничтожно мала величина H в сравнении с h, поэтому нашу формулу смело можно упростить до вида

Для любых фотографий относительно крупных объектов, сделанных с расстояния больше 10 м, она будет давать практически тот же результат.

Ну а теперь самое интересное — нужно проверить, верна ли была использованная нами формула? Ведь в начале я говорил, что мы рассматриваем упрощённую конструкцию объектива, а не реальную. Может быть, наши расчёты не имеют ничего общего с действительностью? К счастью, это легко выяснить. Заходим на Яндекс.Карты и переходим в точку с координатами 55. 604364, 37.611455. Затем активируем инструмент «Линейка» и ставим на карте две точки: одну — возле окна, из которого было сделано фото, а другую — возле стены дома, на которой мы считали панели:

Получаем 365 м. Ну не красота, а? Величины совпали с точностью до 0,1 м! Конечно, такая точность в известной мере является результатом везения, потому что и при измерении размеров изображения, и при подсчёте высоты этажей, и при расстановке точек на карте я вполне мог допускать погрешности в 1–3%. Но, как бы то ни было, в конечном итоге расчётная и измеренная величины сошлись.

Скептически настроенный читатель может подумать, что я подгонял цифры, и что для другой фотографии всё будет по-другому. Что ж, у меня есть ещё одно фото того же дома, сделанное с аналогичной точки, но совсем с другим фокусным расстоянием:

Проделаем для него те же измерения и расчёты. У меня получилось, что размер изображения дома составляет 0,39 см, а фокусное расстояние — 21 мм. Подставляем эти числа в упрощённую формулу и получаем d = (0,021 × 66,7) / 0,0039 = 359,2 м. Результат немного отличается, но всё равно в рамках погрешности совпадает с измеренным по карте. Расхождение несложно объяснить: камера указывает фокусное расстояние как целое число, то есть и 20,51, и 21,49 мм она покажет как 21 мм. А это уже даёт погрешность 2,4%.

Впрочем, самых въедливых скептиков наверняка не убедил и этот пример. Ведь в обоих случаях я использовал один и тот же объектив — а что, если формула работает для него чисто по совпадению? Справедливое замечание. Чтобы проверить, так ли это, я возьму кадр, сделанный не только другим объективом, но и другим фотоаппаратом, причём не цифровым, а плёночным.

Вот фотография, которую мы будем анализировать:

Её много лет назад сделал мой отец на свой «Зенит-Е» с объективом Гелиос-44-2. Фокусное расстояние этого объектива составляет 58 мм. Определить физический размер изображения дома очень просто: у меня есть слайд, который я оцифровал с определённым разрешением, и сканер прописал его в свойствах файла. Тут даже пересчитывать ничего не нужно, достаточно воспользоваться линейкой.

Участок из тех же 23-х панелей имеет на слайде высоту 1,06 см. Подставляем значения в формулу: d = (0,058 × 66,7) / 0,0106 = 365 м. Полное совпадение!

Что ж, мы получили интересные результаты: выходит, простая формула для тонкой линзы позволяет получать весьма точные (и легко проверяемые) результаты при анализе реальных фотографий, а не «сферических коней в вакууме». Почему же так происходит, если реальный объектив представляет собой не одну линзу, а целый бутерброд из линз? Ответ на этот вопрос поможет дать статья Википедии. Для сложного объектива при расчёте вводят не одну, а две главные плоскости. Фактически, расстояния d и D, которые вы видели на схеме в самом начале этого поста, в этом случае отсчитываются от разных (хотя и не слишком удалённых друг от друга) точек. Но расстояние D, даже небольшое изменение которого могло бы существенно повлиять на результат просто в силу небольших размеров этого плеча оптической системы, нам, к счастью, знать не нужно, потому что производитель объектива уже рассчитал и нанёс на его корпус фокусное расстояние, через которое величину D, как было показано выше, легко выразить. А что касается изменения расстояния от передней главной плоскости до объекта, то какими бы толстыми ни были линзы и каким бы длинным ни был объектив (мы, конечно, говорим о реальных конструкциях, а не воображаемых объективах размером с дом), при расстоянии до объекта съёмки в несколько сотен метров, как в нашем случае, величиной в десяток-другой сантиметров можно смело пренебречь.

На основании вышеизложенного легко вывести формулу для соотношения расстояний до объектов, запечатлённых на одной и той же фотографии. Причём знать фокусное расстояние объектива и размер матрицы в этом случае уже будет не нужно, поскольку они сократятся при составлении пропорции.

Как видите, даже знаний из программы средней школы достаточно, чтобы убедиться в полной некомпетентности отдельных «экспертов». Любите математику и не давайте себя обмануть!

Датчики

| Бесплатный полнотекстовый | Оценка расстояния до объекта с использованием одного изображения, сделанного с камеры с подвижным затвором

1.

Введение В настоящее время большинство камер, используемых широкой публикой, установлены, например, на смартфоны, цифровые однообъективные зеркальные (DSLR) камеры, и беззеркальные фотоаппараты с рольставнями. Роликовый затвор относится к методу, при котором весь пиксель датчика не получает значения сразу, а последовательно получает значения. Причины использования этого типа затвора включают снижение стоимости производства датчика, энергопотребления и затрат на обработку данных [1].Обладая многочисленными преимуществами, камеры с роликовым затвором используются в различных технологиях, таких как роботы, дроны, портативные камеры и смартфоны. Благодаря характеристикам датчика, который получает значения пикселей последовательно, начиная с верхнего ряда датчика, особый Явление, называемое эффектом скользящего затвора (RSE) или эффектом желе, появляется на изображении, снятом камерой с роликовым затвором. В изображении, выраженном в RSE, объект наклонен, длина изменена или форма деформирована. Датчик типа рольставни — незнакомая концепция, но в настоящее время проводятся некоторые исследования. Форссен и Рингаби [1] математически смоделировали движение портативной видеокамеры для выполнения коррекции RSE. Их работа показала, что движение камеры может быть наиболее эффективно скорректировано при моделировании с использованием модели только вращения. Meingast et al. [2] изучали геометрическую модель камеры со скользящим затвором. Авторы не только создали геометрическую модель в соответствии с движением камеры, но и изучили калибровку камеры со скользящим затвором.Они подчеркнули, что необходимо учитывать моделирование камеры со скользящим затвором, поскольку эти типы камер широко используются в динамических системах, таких как беспилотные летательные аппараты (БПЛА) и наземные роботы. Юн и др. [3] провели исследование для идентификации структурной системы с использованием рольставни, установленной в БПЛА, и предложили методику коррекции эффекта рольставни в этом процессе. В литературе [4,5] траектория движения камеры интерполировалась используя шлиц. На основе предложенной математической модели рольставни Ait-Aider et al.[6] оценили позу и скорость движущегося объекта по одной фотографии. В их исследовании был предложен метод одновременного расчета позы и мгновенной скорости объекта. Другое исследование включает точное получение трехмерных положений объектов с использованием нескольких изображений с камеры с роликовым затвором [7,8,9,10,11]. Эйт-Айдер и Берри изучали использование модели проекции камеры с роликовым затвором для пространственно-временной триангуляции стереоизображений с роликовым затвором [7].Регулировка связки производилась с помощью смартфона со шторным затвором и компактной камеры [8,9]. Kim et al. [10] применили концепцию рольставни к фотограмметрии с одновременной локализацией и картированием (SLAM), а Vautherin et al. [11] к фотограмметрии БПЛА для повышения точности трехмерного позиционирования. Чжоу и др. [12] выполнили математическое моделирование времени считывания показаний датчика для устранения искажений, вызванных рольставнями, и выполнили регулировку блока пучка. Обсуждались вопросы относительной оценки позы [13] и абсолютной оценки позы [14,15] камер со скользящим затвором.Schubert et al. [16] разработали систему визуально-инерционной одометрии, которая объединяет измерения инерциального измерительного блока (IMU) с оценками позы и скорости с использованием геометрии рольставни. Taketomi et al. [17] подчеркнули важность применения модели рольставни в визуальном SLAM. Калибровка датчиков рольставен также рассматривается как важная тема исследования [2,18,19,20]. Ли и др. [21] пытались объединить датчики недорогого IMU и камеры с роликовым затвором.Для этого авторы представили методику оценки калибровочных и шумовых параметров недорогого IMU и камеры с роликовым затвором. Таким образом, необходимо применять конкретную математическую модель для камер со скользящим затвором по мере того, как объект или камера движется во время фотосъемки, и многие исследования могут быть проведены с использованием искажения, вызванного характеристиками скользящего затвора. Однако большинство исследований в основном сосредоточено на оценке параметров внешнего ориентирования (EOP) и получении точной геометрической модели камер со скользящим затвором.

Хотя многие работы сосредоточены на исправлении RSE или моделировании EOP, мало исследований по получению геоинформации от появления RSE. Основываясь на наших наблюдениях на изображениях, полученных с камеры с роликовым затвором, степень RSE варьируется в зависимости от скорости камеры или объекта и расстояния между камерой и объектом. У нас возникла идея раскрыть взаимосвязь расстояния между камерой и объектом, используя одно изображение, полученное с помощью камеры со скользящим затвором.

Было предпринято несколько попыток получить трехмерную информацию из одного изображения. Chen et al. [22] реконструировали трехмерную модель, объединив когнитивные способности людей с вычислительной точностью компьютеров с использованием одного изображения. Авторы предоставили инструмент моделирования на основе жестов, так называемую развертку по трем, поскольку общие объекты можно разделить на цилиндры, кубы и т. Д. В этом исследовании авторы предложили метод восстановления трехмерной формы путем объединения человеческих фигур. когнитивные способности и вычислительная точность компьютера.Этот метод имеет хорошие характеристики при воссоздании трехмерной формы, но он не дает решения для определения трехмерного положения точного объекта, и существует ограничение на воспроизведение формы, подобной естественному объекту, а не искусственному. один. В других исследованиях [23,24] трехмерные формы воспроизводились с использованием обработки изображений и структурных характеристик объектов. Поскольку эти исследования извлекают трехмерные формы из одного изображения с использованием существующих трехмерных моделей, они показывают хорошие результаты для объектов с трехмерными моделями, но не показывают хороших результатов для объектов, которые этого не делают.Кроме того, есть недостаток в том, что параметр масштаба не может быть задан. Эти методы не могут извлекать трехмерную информацию, поскольку геометрическое расположение камер и объектов не было математически определено.

При проведении экспериментов, изучая литературу о камере с роликовым затвором, мы обнаружили, что расстояние между камерой и объектом увеличилось, а размер RSE изменился. Во многих документах показано, что размер RSE зависит от выдержки камеры или скорости движения камеры или объекта, но не сообщается, что это связано с расстоянием между камерой и объектом.Основываясь на интенсивных обзорах камер со скользящим затвором, цель этого исследования — измерить расстояние до объекта с помощью камеры со скользящим затвором, прикрепленной к робототехнике в помещении, мобильной картографической системе (MMS) и других наземных подвижных платформах. Отношения между камерой и объектом были геометрически смоделированы с учетом трех сценариев; движение параллельно плоскости изображения, движение перпендикулярно плоскости изображения и движение под определенным углом к ​​плоскости изображения. В этой статье перечислены и математически организованы переменные, влияющие на RSE.Степень RSE была математически смоделирована с использованием этих переменных, а расстояние по вертикали между объектом и камерой было получено с помощью RSE. Наконец, фактическое расстояние между объектом и камерой было получено с использованием геометрии сенсора камеры. Этот процесс был выполнен с использованием геометрического расположения объекта, камеры и сенсора камеры. В рамках этого исследования мы стремились разработать уравнения для оценки расстояния с использованием недорогого оптического оборудования. Кроме того, это исследование было проведено для изучения возможности получения простой трехмерной информации без использования дорогостоящего оборудования, такого как световое обнаружение и определение дальности (LiDAR) или радарные устройства.

Документ оформлен следующим образом: в следующем разделе дается обзор рольставни и краткое объяснение RSE, а расстояние между камерой и объектом определяется с использованием степени RSE. Впоследствии подробно описывается эксперимент по проверке уравнений, представленных в этой статье, с использованием тестовых данных. Наконец, представлены выводы этого исследования.

Как расстояние до объекта и фокусное расстояние влияют на глубину резкости? «Physics Soup

»

Примечание. Это вторая часть серии статей о глубине резкости.Щелкните здесь, чтобы перейти к части 1, в которой объясняется взаимосвязь между размером диафрагмы и глубиной резкости.)

Помимо размера диафрагмы, фотографы могут также управлять глубиной резкости, изменяя расстояние от камеры до объекта или фокусное расстояние объектива. В частности:

  • При фиксированном фокусном расстоянии и размере диафрагмы увеличение расстояния до объекта увеличивает глубину резкости.
  • Для фиксированного расстояния до объекта и размера диафрагмы увеличение фокусного расстояния приведет к уменьшению глубины резкости.

Эти два эффекта тесно связаны, и стремление понять их предлагает отличный пример того, как мы можем использовать уравнения для усиления нашей интуиции при решении относительно сложных задач. Продолжайте читать, если хотите узнать больше!

Прежде чем мы перейдем к сути этого поста, нам нужно вкратце рассмотреть факторы, определяющие глубину резкости. В моем предыдущем посте о размере диафрагмы и глубине резкости мы видели, что точечный объект создает круг (кружок нерезкости ) на датчике камеры, когда датчик не совсем точно расположен в положении изображения.Когда кружок нерезкости «достаточно мал», мы говорим, что объект находится в приблизительном фокусе . Существует ряд положений изображения вокруг датчика, при которых все образуются круги, достаточно маленькие, чтобы быть в фокусе. Мы можем обозначить ширину этого диапазона как Δd

i, приемлемо . Точно так же существует соответствующий диапазон положений объекта, которые создают изображения в этом диапазоне. Ширина диапазона положений объекта называется глубиной резкости (DOF).Эти идеи показаны на рисунке ниже:

Давайте сначала рассмотрим взаимосвязь между глубиной резкости и расстоянием до объекта. Для начала давайте взглянем на некоторые лучевые диаграммы, которые иллюстрируют, что происходит, когда мы увеличиваем расстояние между объектом и линзой для фиксированного фокусного расстояния. Мы сдвинем объект дважды (каждый раз на одну и ту же величину) и посмотрим, как изменится изображение:

На основании этих диаграмм мы можем сделать два важных наблюдения:

  1. По мере удаления объекта от линзы изображение приближается к линзе и уменьшается в размере.В результате увеличивается угловой размер изогнутого светового конуса. В моем предыдущем посте мы видели, что более широкий изогнутый световой конус уменьшает Δd i, приемлемо . Назовем это угловым эффектом .
  2. Даже несмотря на то, что первый и второй сдвиги объекта имеют одинаковый размер, сдвиг второго изображения меньше, чем сдвиг первого изображения. Другими словами, положение изображения менее чувствительно к положению объекта, когда объект находится дальше от линзы. В этом случае конкретный Δd i, допустимый должен соответствовать большему диапазону положений объекта.Назовем это эффектом чувствительности .

Так что это значит для глубины резкости? Ответ на этот вопрос не очень однозначный, потому что у нас есть две конкурирующие силы.

По мере удаления объекта от линзы угловой эффект уменьшается Δd i, допустимый , до меньшего значения. Однако эффект чувствительности означает, что это меньшее Δd i, приемлемое значение соответствует большей глубине резкости, чем было бы в исходном положении объекта. В зависимости от относительной силы углового эффекта и эффекта чувствительности, глубина резкости может уменьшаться или увеличиваться!

Чтобы продолжить, нам нужно будет количественно определить глубину резкости для различных расстояний до объекта.Для объектива с заданным фокусным расстоянием общая процедура будет следующей:

  1. Выберите центральное положение объекта.
  2. Определите соответствующее положение изображения.
  3. Предположим, что датчик камеры находится в этом положении.
  4. Выберите другое положение объекта, найдите соответствующее изображение и определите размер кружка нерезкости, который он создает.
  5. Повторите шаг 4 много раз, чтобы найти положение объекта на крайних краях приблизительного диапазона фокусировки. Это определит глубину резкости в этом центральном положении объекта.
  6. Повторите шаги 2–5 много раз для различных положений центрального объекта.

Это можно сделать графически, нарисовав базиллионы лучевых диаграмм. Однако гораздо проще рассчитать глубину резкости численно, используя уравнения, описывающие простую модель объектива. Давай сделаем это вместо этого!

Уравнение для тонкой линзы является ключом к численному определению глубины резкости.Если вы раньше посещали уроки физики, вы, вероятно, хорошо с ним знакомы. Для точечного объекта, который излучает свет в сторону линзы, уравнение связывает расстояние от объекта до линзы (d

o ), расстояние от изображения до линзы (называемое d i ) и фокусное расстояние линзы. длина (обозначается f ) следующим образом:

.

Строго говоря, это уравнение применимо только к идеализированным линзам с нулевой толщиной. Конечно, в реальной жизни таких линз не существует.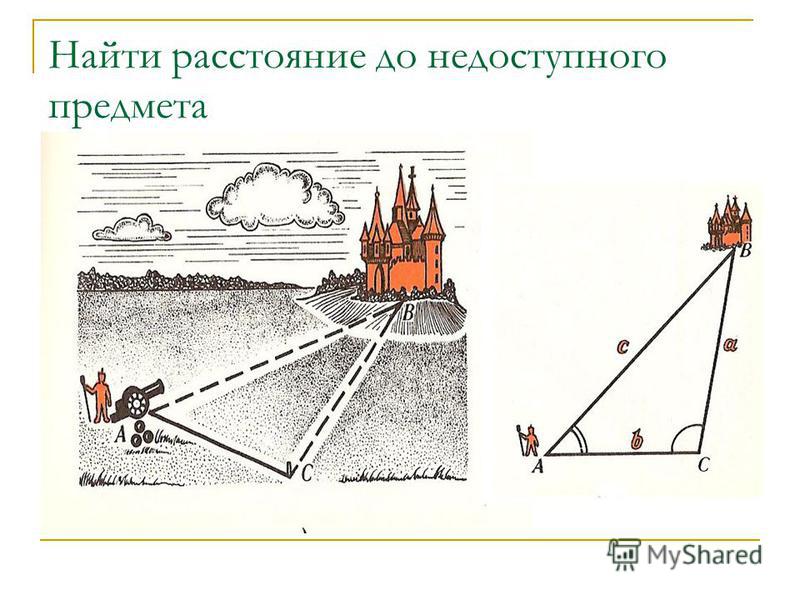 Однако линзы фотоаппаратов тщательно спроектированы так, чтобы работать почти так же, как идеальные тонкие линзы. Мы не сможем полностью доверять точным значениям чисел, которые мы получаем из этого уравнения, но мы должны иметь возможность поверить в общие тенденции, которые мы обнаруживаем.

Обратите внимание, что уравнение тонкой линзы содержит всю информацию, которую мы узнали из лучевых диаграмм, которые я нарисовал выше. В частности, мы можем использовать уравнение тонкой линзы, чтобы обнаружить угловые эффекты и эффекты чувствительности. Для этого мы можем решить уравнение для расстояния до изображения, а затем построить график зависимости d

i от d o для конкретного фокусного расстояния, скажем, 50 мм:

Мы легко можем видеть, что по мере увеличения положения объекта положение изображения уменьшается по направлению к фокусной точке.Отсюда мы можем сделать вывод об угловом эффекте. Кроме того, мы можем видеть, что кривая становится более пологой при увеличении положения объекта. Отсюда мы можем сделать вывод об эффекте чувствительности. Я подробно проиллюстрировал это, показав, как тот же Δd i, приемлемый может привести к большей глубине резкости при больших расстояниях до объекта (меньших расстояниях между изображениями).

Прежде чем мы сможем численно рассчитать глубину резкости, нам нужно будет определить диаметр кружка нерезкости (C) как функцию положения объекта, фокусного расстояния, радиуса апертуры (A) и положения датчика (S).Следующая диаграмма показывает, как эти величины связаны между собой, а также включает высоту объекта (h o ) и высоту изображения (h i ):

Прежде всего, мы можем найти диаметр кружка нерезкости, используя θ 1 , θ 2 , d i и S:

.

Затем мы можем найти углы, используя A и h i :


Когда мы объединяем эти три уравнения, высота изображения фактически сокращается:

.

В качестве последнего алгебраического шага мы можем найти расстояние до изображения, используя уравнение тонкой линзы. Когда мы объединяем все вместе, мы можем получить большое уродливое уравнение для C. Не волнуйтесь, я только хотел дать набросок того, как это сделать — я не буду утомлять вас деталями алгебры!

Теперь, когда мы знаем, как найти C, мы можем выбрать S, A и f и вычислить C для различных положений объекта. Например, мы можем представить себе использование объектива 55 мм, чтобы сфотографировать объект, расположенный в 10 футах от объектива камеры.Типичный радиус апертуры составляет около 1 дюйма. На следующем графике показан диаметр кружка нерезкости для различных положений соседних объектов:

Я использую камеру Pentax K10D. Его сенсор имеет 10,75 миллиона пикселей, которые расположены в прямоугольнике размером 23,5 x 15,7 мм. Таким образом, мы можем оценить, что каждый пиксель составляет около 5,9 мкм в поперечнике. Если мы выберем 6 мкм в качестве порогового значения для максимального диаметра круга, мы сможем найти глубину резкости около 1,7 дюйма в поперечнике.

Наконец, мы можем повторить этот процесс много раз для разных расстояний до объекта, чтобы увидеть, как изменяется глубина резкости:

В конечном итоге мы видим, что глубина резкости увеличивается при увеличении расстояния до объекта.Но на самом деле, если мы подумаем о нашем предыдущем анализе, мы узнали кое-что еще: это означает, что эффект чувствительности более важен, чем угловой эффект, для определения глубины резкости на разных расстояниях до объекта.

Мы можем повторно использовать некоторые из тех же идей, чтобы понять, как фокусное расстояние влияет на глубину резкости. В частности, давайте воспользуемся уравнением тонкой линзы для построения графика зависимости d i от d o для разных фокусных расстояний:

Из этого графика мы можем видеть, что для больших фокусных расстояний расстояние до изображения изменяется быстрее с расстоянием до объекта.Другими словами, положение изображения более чувствительно к положению объекта при увеличении фокусного расстояния. Из нашего предыдущего анализа мы знаем, что эффект чувствительности определяет глубину резкости, и что увеличение чувствительности должно приводить к уменьшению глубины резкости. Мы можем проверить этот прогноз, используя нашу простую модель для расчета глубины резкости для разных фокусных расстояний. Опять же, давайте представим, что вы используете камеру, чтобы сфотографировать объект на расстоянии 10 футов. Предположим, что радиус апертуры составляет 1 дюйм, а порог фокусировки — 6 мкм.

Наш первоначальный вывод был правильным — с увеличением фокусного расстояния глубина резкости уменьшается!

Повторяю то, что мы сделали:

  • Мы начали с рисования нескольких диаграмм лучей для объектов на разных расстояниях. Это позволило нам выделить два конкурирующих эффекта: угловой эффект и эффект чувствительности.
  • Затем мы использовали уравнение тонкой линзы для создания числовой модели, которая позволила нам рассчитать глубину резкости для любой комбинации положения объекта и фокусного расстояния.
  • Сравнивая эти численные результаты с интуицией, которую мы получили из лучевых диаграмм, мы обнаружили, что эффект чувствительности определяет общее поведение глубины резкости при изменении расстояния до объекта и фокусного расстояния.

Обратите внимание: если бы мы сразу перешли к численной модели, мы бы не поняли, что эффект чувствительности является основной причиной поведения! Этот пример демонстрирует важность сочетания интуиции с расчетами при попытке понять сложные проблемы.

Итак, теперь мы определили три правила для управления глубиной резкости:

  • Для фиксированного фокусного расстояния и положения объекта увеличение размера диафрагмы приведет к уменьшению глубины резкости.
  • При фиксированном фокусном расстоянии и размере диафрагмы увеличение расстояния до объекта увеличивает глубину резкости.
  • Для фиксированного расстояния до объекта и размера диафрагмы увеличение фокусного расстояния приведет к уменьшению глубины резкости.

Конечно, трудно предсказать, как изменится глубина резкости при одновременном изменении фокусного расстояния, положения объекта и размера диафрагмы.Тем не менее, об этих отношениях полезно знать. Надеюсь, вы сможете использовать их в своих фотографиях!

Нравится:

Нравится Загрузка …

Связанные

DRIVE Labs: определение расстояния

Примечание редактора: это последняя публикация из серии NVIDIA DRIVE Labs , в которой с инженерной точки зрения рассматриваются отдельные проблемы автономных транспортных средств и способы их решения с помощью NVIDIA DRIVE.Читайте наши предыдущие посты, здесь .

Простое правило: если вы не умеете судить о расстоянии, не садитесь за руль. Проблема: судить о расстоянии совсем не просто.

У людей, конечно же, есть два высокосинхронизированных визуальных датчика с высоким разрешением — наши глаза — которые позволяют нам измерять расстояния с помощью обработки стереозрения в нашем мозгу.

Однако сопоставимая стереосистема с двумя камерами в беспилотном автомобиле была бы очень чувствительной.Если камеры даже немного рассинхронизированы, это приводит к так называемому «рассогласованию по времени», что приводит к неточным оценкам расстояния.

Вот почему мы выполняем определение расстояния до объекта, используя данные с одной камеры. Однако использование только одной камеры сопряжено с определенными трудностями.

До появления глубоких нейронных сетей обычным способом вычисления расстояния до объектов по изображениям с одной камеры было предположение, что земля плоская. Исходя из этого предположения, трехмерный мир моделировался с использованием двумерной информации с изображения камеры. Геометрия оптики будет использоваться для оценки расстояния от объекта до эталонного транспортного средства.

Однако в реальном мире это не всегда работает. Подъем или спуск с холма могут привести к неточным результатам, потому что земля неровная.

Такие неверные оценки могут иметь негативные последствия. Автоматический круиз-контроль, проверка безопасности при смене полосы движения и выполнение смены полосы движения — все это зависит от правильной оценки расстояния.

Завышение расстояния — определение того, что объект находится дальше, чем он есть — может привести к невозможности включения автоматического круиз-контроля.Или, что еще более важно, невозможность задействовать функции автоматического экстренного торможения.

Неправильное определение препятствия ближе, чем оно может привести к другим сбоям, таким как включение круиз-контроля или экстренное торможение, когда они не нужны.

На расстоянии с помощью глубокого обучения

Чтобы понять это правильно, мы используем сверточные нейронные сети и данные с одной фронтальной камеры. DNN обучена предсказывать расстояние до объектов, используя данные радаров и лидарных датчиков в качестве достоверной информации.Инженеры знают, что эта информация точна, потому что прямые отражения передаваемых сигналов радара и лидара предоставляют точную информацию о расстоянии до объекта, независимо от топологии дороги.

Обучая нейронные сети на данных радара и лидара вместо того, чтобы полагаться на предположение о плоской поверхности, мы позволяем DNN оценивать расстояние до объектов с одной камеры, даже когда транспортное средство движется вверх или вниз по склону.

Камера DNN обнаруживает расстояние до объекта в туннеле автомагистрали.Зеленые ограничивающие рамки обозначают обнаружение объектов. Число в верхней части каждого поля — это радиальное расстояние в метрах между центром задней оси эго-автомобиля и обнаруженным объектом.

В нашей обучающей реализации конвейер создания и кодирования наземных данных автоматизирован. Таким образом, DNN можно обучить с помощью такого количества данных, которое может быть собрано датчиками, при этом ручная маркировка ресурсов не станет узким местом.

Мы используем оценку расстояния до объекта на основе DNN в сочетании с обнаружением объекта и отслеживанием с помощью камеры как для продольного управления (ускорение и замедление), так и для бокового управления (рулевое управление).Чтобы узнать больше о вычислении расстояния до объекта с использованием DNN, посетите нашу страницу DRIVE Networks.

Как рассчитать ближайшее расстояние до пятен в Имарис | Имарис

Июнь 2014 г.

Этот учебник знакомит с Xtension of Spots to Spots Closest Distance. XTension вычисляет и отображает расстояние до ближайшего соседа объектов Spots. Результат этого XTension может быть особенно полезен для исследований стволовых клеток и тканей, морфогенеза, прогрессирования рака или развития биопленок, в которых количественная оценка расстояния может выявить некоторые уникальные пространственные отношения.

Мы начнем с того места, где был завершен мастер создания пятен и созданы объекты пятен.

Все доступные XTensions для пятен перечислены на вкладке «Инструмент».

Как только вы щелкнете по кнопке Spots Closest Distance, откроется окно MATLAB. Есть три различных варианта отображения результатов:

  • Новые статистические значения
  • Объект новые пятна
  • Новый канал

Статистика точек

Если вы выберете опцию «Статистика пятен», то на вкладке «Статистика» будет добавлен набор новых статистических переменных.Создается новый объект «Пятна», и на вкладке «Статистика», на вкладке «Подробные» в разделе «Определенные значения» доступны три новых типа измерения расстояния: максимальное, среднее и минимальное расстояние.

Щелкните непосредственно на интересующем объекте, и соответствующая строка таблицы будет выделена. Чтобы найти все статистические значения только для выбранного объекта или группы объектов, выберите вкладку «Выбор».

Радиус пятна

Если вы выберете параметр «Радиус пятен» и начнете со всех пятен того же размера, что и в этом руководстве, после запуска этого расширения будет создан новый объект пятен, а значение расстояния будет закодировано в радиусе пятен.

Поскольку расстояние до следующей точки представлено в виде радиуса, вы можете быстро визуально определить, где точки расположены близко друг к другу, а где дальше друг от друга. Чем больше радиус, тем больше расстояние от другого места.

Также на вкладке «Статистика» вы можете найти значение радиуса для каждого вновь созданного пятна. Эти значения представляют собой расстояние до следующего точечного объекта. Для дальнейшего улучшения визуализации вы можете кодировать пятна цветом в зависимости от диаметра.

И теперь изображение показывает то же значение, представленное как в цвете, так и в размере

Канал набора данных

Наконец, если вы выбираете опцию DataSet Channel, значения расстояния кодируются во вновь созданных интенсивностях каналов. В окно настройки дисплея добавлен новый канал.

Для всех объектов интенсивности за пределами пятен устанавливается нулевое значение, а для интенсивности внутри пятен задается значение расстояния до следующего пятна. Этот новый канал также можно использовать в визуализации, если его диапазон увеличен, а цвет и значение гаммы отрегулированы.

На вкладке «Статистика» новая статистическая переменная показывает центр интенсивности вновь созданного канала, указывающий расстояние до следующей точки.

Возможность получения нескольких результатов доступна при нажатии кнопки «Выбрать все».

Следующий шаг — решить, как будет выполняться расчет расстояния.

Режим расчета расстояния

Расстояние можно рассчитать либо от центра точечного объекта, либо от границы.

Опция расчета расстояния от границы полезна, если вы уже создали несколько пятен разного размера. Затем этот XTension вычислит расстояние между краями объектов. В других случаях могут быть более подходящими измерения между центрами объектов. Все ранее показанные примеры основаны на измерениях между центрами объектов.

Если у вас есть вопросы об этих или любых других функциях Imaris, пожалуйста, свяжитесь с нашей командой продаж или поддержки.

Видео с вопросом: Расчет расстояния, пройденного объектом с учетом его скорости и времени перемещения

Стенограмма видеозаписи

На какое расстояние перемещается объект со скоростью 15 метров в секунду за четыре секунды?

Хорошо, в этом вопросе у нас есть некий объект, и нам сообщают скорость этого объекта и время, в течение которого он путешествует.Затем нас просят рассчитать расстояние, которое он проходит за это время. Чтобы рассчитать это расстояние с учетом скорости и времени, за которое он проходит, мы можем вспомнить, что существует формула, связывающая скорость, расстояние и время.

У нас есть, что скорость равна расстоянию, разделенному на время. Если мы обозначим скорость как 𝑠, расстояние как 𝑑 и время как 𝑡, то мы можем записать это как равно 𝑑, деленному на 𝑡. Вопрос в том, на какое расстояние путешествует наш объект. Итак, в этой формуле мы пытаемся найти расстояние 𝑑. Итак, давайте изменим формулу, чтобы стать объектом 𝑑.

Если мы возьмем наше уравнение, равное 𝑑, разделенному на, и умножим обе части этого уравнения на, то в правой части уравнения будут сокращены в числителе и знаменателе. Таким образом, 𝑡, умноженное на 𝑠, равно. Затем, поменяв местами левую и правую части этого уравнения, мы можем записать это как 𝑑 равно 𝑡, умноженному на. Таким образом, это уравнение говорит нам, что расстояние 𝑑, пройденное объектом, равно времени, которое он проходит, умноженному на скорость 𝑠, с которой он движется.

Теперь нам просто нужно подставить в наши значения 𝑡 и 𝑠. Вопрос говорит нам, что объект перемещается за четыре секунды. Итак, мы знаем, что 𝑡 равно четырем секундам. Нам говорят, что скорость объекта составляет 15 метров в секунду. Итак, мы знаем, что 𝑠 равно 15 метрам в секунду.

Итак, если мы подставим, равное четырем секундам, и 𝑠, равное 15 метрам в секунду, в это уравнение для 𝑑, мы получим, что 𝑑 равно четырем секундам, умноженным на 15 метров в секунду. Если мы сделаем это умножение, мы обнаружим, что 𝑑 равно 60 метрам. Итак, наш ответ на вопрос: объект проходит расстояние 60 метров.

% PDF-1.6 % 328 0 объект> эндобдж xref 328 74 0000000016 00000 н. 0000002880 00000 н. 0000003057 00000 н. 0000003185 00000 н. 0000003242 00000 н. 0000003689 00000 н. 0000003849 00000 н. 0000003976 00000 н. 0000005017 00000 н. 0000006193 00000 п. 0000007368 00000 н. 0000007561 00000 п. 0000008580 00000 н. 0000009599 00000 н. 0000010342 00000 п. 0000010522 00000 п. 0000010577 00000 п. 0000010881 00000 п. 0000010984 00000 п. 0000011181 00000 п. 0000018486 00000 п. 0000018679 00000 п. 0000019088 00000 п. 0000019458 00000 п. 0000026884 00000 п. 0000027075 00000 п. 0000027457 00000 п. 0000027791 00000 п. 0000027858 00000 п. 0000028042 00000 п. 0000028906 00000 п. 0000029746 00000 п. 0000030609 00000 п. 0000031427 00000 п. 0000032259 00000 п. 0000033156 00000 п. 0000033794 00000 п. Re: C \ NTfQs ~; ˱Aa / C.hgZBi.P82RR | $ dq% ‘My ߨ zn6Sk ڮ + rwӼ% uor9Vsr = wk $ 9s ִ! sL6 \ = EK $ 򣟞T : lDҹE + z / & M \% W r Ճ f9N97-duīUKB, .aQX8If ګ jLz

B) KeB63xɅ.R ֽ f iiPH񒖖

Как рассчитать расстояние между объектами на изображении с помощью Python

Сегодня я хочу показать вам, как рассчитать расстояние между объектами на изображении. Мы напишем отличный алгоритм, который вы сможете изменить и расширить в соответствии с вашими потребностями.

Это наш тестовый образ:

Давайте перейдем к коду!

Сначала нам нужно импортировать необходимые пакеты: 

  из scipy.пространственное импортное расстояние как расстояние
с точки зрения импорта imutils
из imutils импортировать контуры
импортировать numpy как np
import argparse
импорт imutils
импорт cv2
Войти в полноэкранный режимВыйти из полноэкранного режима

Затем мы создаем синтаксический анализ аргументов и анализируем аргументы 

  средняя точка по умолчанию (ptA, ptB):
    return ((ptA [0] + ptB [0]) * 0,5, (ptA [1] + ptB [1]) * 0,5)
Войти в полноэкранный режимВыйти из полноэкранного режима

после этого загружаем изображение, конвертируем его в оттенки серого: 

  изображение = cv2. imread ('images / test.jpg')
серый = cv2.cvtColor (изображение, cv2.COLOR_BGR2GRAY)
серый = cv2.GaussianBlur (серый, (7, 7), 0)
Войти в полноэкранный режимВыйти из полноэкранного режима

, затем мы выполняем обнаружение краев и закрываем промежутки между краями объекта: 

  edged = cv2.Canny (серый, 50, 100)
edged = cv2.dilate (обрезной, Нет, итераций = 1)
edged = cv2.erode (обрезной, Нет, итерации = 1)
Войти в полноэкранный режимВыйти из полноэкранного режима

найти контуры на карте краев 

  центов = cv2.findContours (edged.copy (), cv2.RETR_EXTERNAL,
                        cv2.CHAIN_APPROX_SIMPLE)
cnts = imutils.grab_contours (cnts)
Войти в полноэкранный режимВыйти из полноэкранного режима

, затем инициализируйте цвета расстояния и опорный объект: 

  (cnts, _) = contours.sort_contours (cnts)
цвета = ((0, 0, 255), (240, 0, 159), (0, 165, 255), (255, 255, 0),
          (255, 0, 255))
refObj = Нет
Войти в полноэкранный режимВыйти из полноэкранного режима

затем обводим контуры по отдельности: 

  для ц в центрах:
    если cv2. contourArea (c) <100:
        Продолжать
    box = cv2.minAreaRect (c)
    box = cv2.cv.BoxPoints (поле) если imutils.is_cv2 () иначе cv2.boxPoints (поле)
    box = np.array (box, dtype = "int")
    box = перспектива.order_points (поле)
    cX = np.average (поле [:, 0])
    cY = np.average (поле [:, 1])
    если refObj равно None:
        (tl, tr, br, bl) = коробка
        (tlblX, tlblY) = средняя точка (tl, bl)
        (trbrX, trbrY) = средняя точка (tr, br)
        D = dist.euclidean ((tlblX, tlblY), (trbrX, trbrY))
        refObj = (коробка, (cX, cY), D / 70)
        Продолжать
    ориг = изображение.копия ()
    cv2.drawContours (orig, [box.astype ("int")], -1, (0, 255, 0), 2)
    cv2.drawContours (orig, [refObj [0] .astype ("int")], -1, (0, 255, 0), 2)
    refCoords = np.vstack ([refObj [0], refObj [1]])
    objCoords = np.vstack ([box, (cX, cY)])
Войти в полноэкранный режимВыйти из полноэкранного режима

, затем мы перебираем исходные точки: 

  для ((xA, yA), (xB, yB), color) в zip (refCoords, objCoords, colors):
        cv2. circle (orig, (int (xA), int (yA)), 5, цвет, -1)
        cv2.круг (ориг, (int (xB), int (yB)), 5, цвет, -1)
        cv2.line (ориг, (int (xA), int (yA)), (int (xB), int (yB)),
                 цвет, 2)
        D = dist.euclidean ((xA, yA), (xB, yB)) / refObj [2]
        (mX, mY) = средняя точка ((xA, yA), (xB, yB))
        cv2.putText (orig, "{: .1f} in" .format (D), (int (mX), int (mY - 10)),
                    cv2.FONT_HERSHEY_SIMPLEX, 0.55, цвет, 2)
        cv2.imshow ("Изображение", ориг)
        cv2.waitKey (0)
cv2.destroyAllWindows ()
Войти в полноэкранный режимВыйти из полноэкранного режима

Это наш окончательный результат:

Всем спасибо.

.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *