Разметка 1 4: Разметка 1.4 — горизонтальная разметка пдд
Разметка 1.4 — горизонтальная разметка пдд
Горизонтальная разметка (линии, стрелы, надписи и другие обозначения на проезжей части) устанавливает определенные режимы и порядок движения либо содержит иную информацию для участников дорожного движения.
Горизонтальная разметка может быть постоянной или временной. Постоянная разметка имеет белый цвет, кроме линий 1.4, 1.10, 1.17 и 1.26 желтого цвета, временная — оранжевый цвет.
Горизонтальная разметка:
- 1.1 Разметка 1.1
Горизонтальная разметка 1.1 разделяет транспортные потоки противоположных направлений и обозначает границы полос движения в опасных местах на дорогах; обозначает границы проезжей части, на которые въезд запрещен; обозначает границы стояночных мест транспортных средств.
Линию 1.1 пересекать запрещается.
- 1.
2 Разметка 1.2Горизонтальная разметка 1.2 — обозначает край проезжей части.
Линию 1.2. допускается пересекать для остановки транспортного средства на обочине и при выезде с нее в местах, где разрешена остановка или стоянка.
- 1.3 Разметка 1.3
Горизонтальная разметка 1.3 разделяет транспортные потоки противоположных направлений на дорогах с четырьмя и более полосами для движения в обоих направлениях, с двумя или тремя полосами — при ширине полос более 3,75 м.
Линию 1.3 пересекать запрещается.
- 1.4 Разметка 1. 4
Горизонтальная разметка 1.4 (цвет — желтый) — обозначает места, где запрещена остановка транспортных средств.
- 1.5 Разметка 1.5
Горизонтальная разметка 1.5 разделяет транспортные потоки противоположных направлений на дорогах, имеющих две или три полосы; обозначает границы полос движения при наличии двух и более полос, предназначенных для движения в одном направлении. Линию 1.5 разрешается пересекать с любой стороны.
- 1.6 Разметка 1.6
Горизонтальная разметка 1.6 предупреждает о приближении к разметке 1.1 или 1.
11, которая разделяет транспортные потоки противоположных или попутных направлений. Линию 1.6 разрешается пересекать с любой стороны. - 1.7 Разметка 1.7
Горизонтальная разметка 1.7 обозначает полосы движения в пределах перекрестка. Линию 1.7 разрешается пересекать с любой стороны.
- 1.8 Разметка 1.8
Горизонтальная разметка 1.8 обозначает границу между полосой разгона или торможения и основной полосой проезжей части. Линию 1.8 разрешается пересекать с любой стороны.
- 1. 9 Разметка 1.9
Горизонтальная разметка 1.9 обозначает границы полос движения, на которых осуществляется реверсивное регулирование; разделяет транспортные потоки противоположных направлений (при выключенных реверсивных светофорах) на дорогах, где осуществляется реверсивное регулирование. Линию 1.9 при отсутствии реверсивных светофоров или когда они отключены разрешается пересекать, если она расположена справа от водителя; при включенных реверсивных светофорах — с любой стороны, если она разделяет полосы, по которым движение разрешено в одном направлении. При отключении реверсивных светофоров водитель должен немедленно перестроиться вправо за линию разметки 1.9. Линию 1.9, разделяющую транспортные потоки противоположных направлений, при выключенных реверсивных светофорах пересекать запрещается.
- 1. 10 Разметка 1.10
Горизонтальная разметка 1.10 (цвет — желтый) — обозначает места, где запрещена стоянка транспортных средств.
- 1.11 Разметка 1.11
Горизонтальная разметка 1.11 разделяет транспортные потоки противоположных или попутных направлений на участках дорог, где перестроение разрешено только из одной полосы; обозначает места, где необходимо разрешить движение только со стороны прерывистой линии (в местах разворота, въезда и выезда с прилегающей территории). Линию 1.11 разрешается пересекать со стороны прерывистой, а также со стороны сплошной, но только при завершении обгона или объезда.
- 1.12 Разметка 1.12
Горизонтальная разметка 1.12 указывает место, где водитель должен остановиться при наличии знака 2.5 или при запрещающем сигнале светофора (регулировщика).
- 1.13 Разметка 1.13
Горизонтальная разметка 1.13 указывает место, где водитель должен при необходимости остановиться, уступая дорогу транспортным средствам, движущимся по пересекаемой дороге.
- 1.14.1
1.14.2
Разметка 1.14 Горизонтальная разметка 1.14.1 и 1. 14.2 обозначает пешеходный переход. Стрелы разметки 1.14.2 указывают направление движения пешеходов. - 1.15 Разметка 1.15
Горизонтальная разметка 1.15 обозначает место, где велосипедная дорожка пересекает проезжую часть.
- Разметка 1.16
Горизонтальная разметка 1.16.1 обозначает островки, разделяющие транспортные потоки противоположных направлений, места для стоянки транспортных средств (парковки) и велосипедные полосы. Горизонтальная разметка 1.16.2 обозначает островки, разделяющие транспортные потоки одного направления. Горизонтальная разметка 1.16.3 обозначает островки в местах слияния транспортных потоков.
- 1.17 Разметка 1.17
Горизонтальная разметка 1.17 обозначает места остановок маршрутных транспортных средств и стоянки такси.
- 1.18 Разметка 1.18
Горизонтальная разметка 1.18 указывает разрешенные на перекрестке направления движения по полосам. Разметка с изображением тупика наносится для указания того, что поворот на ближайшую проезжую часть запрещен; разметка, разрешающая поворот налево из крайней левой полосы, разрешает и разворот.
- 1. 19 Разметка 1.19
Горизонтальная разметка 1.19 предупреждает о приближении к сужению проезжей части (участку, где уменьшается число полос движения в данном направлении) или к линиям разметки 1.1 или 1.11, разделяющим транспортные потоки противоположных направлений.
- 1.20 Разметка 1.20
- 1.21 Разметка 1.21
Горизонтальная разметка 1.21 (надпись «СТОП») — предупреждает о приближении к разметке 1.12, когда она применяется в сочетании со знаком 2.
5 . - 1.22 Разметка 1.22
Горизонтальная разметка 1.22 ообозначает номер дороги.
- 1.23.1 Разметка 1.23.1
Горизонтальная разметка 1.23.1 — обозначает специальную полосу для маршрутных транспортных средств.
- 1.23.2 Разметка 1.23.2
Горизонтальная разметка 1.23.2 обозначает пешеходную дорожку или пешеходную часть дорожки, предназначенную для совместного движения пешеходов и велосипедов.
- 1.23.3 Разметка 1.23.3
Горизонтальная разметка 1.23.3 обозначает велосипедную дорожку (часть дорожки) или полосы.
- 1.24.1 Разметка 1.24.1
Горизонтальная разметка 1.24.1 — дублирует предупреждающие дорожные знаки.
- 1.24.2 Разметка 1.24.2
1.24.2 — дублирует запрещающие дорожные знаки.
- 1. 24.3 Разметка 1.24.3
1.24.3 — дублирует дорожный знак «Инвалиды».
- 1.24.4 Разметка 1.24.4
1.24.4 — дублирование дорожного знака «Фотовидеофиксация» и (или) обозначение участков дороги, на которых может осуществляться фотовидеофиксация, разметка 1.24.4 может применяться самостоятельно.
- 1.24.5 Разметка 1.24.5
1.24.5 — дублирование таблички 8.4.3.1 , разметка 1.24.5 может применяться самостоятельно.
- 1. 24.6 Разметка 1.24.6
1.24.6 — дублирование знака 5.33.1 «Велосипедная зона», разметка 1.24.6 может применяться самостоятельно.
- 1.24.7 Разметка 1.24.7
1.24.7 — дублирование таблички 8.9.2 «Стоянка только транспортных средств дипломатического корпуса», разметка 1.24.7 может применяться самостоятельно.
- 1.25 Разметка 1.25
Горизонтальная разметка 1.25 обозначает искусственную неровность по ГОСТу Р 52605-2006.
- 1. 26 Разметка 1.26
Горизонтальная разметка 1.26 (цвет — желтый) — обозначает участок перекрестка, на который запрещается выезжать, если впереди по пути следования образовался затор, который вынудит водителя остановиться, создав препятствие для движения транспортных средств в поперечном направлении, за исключением поворота направо или налево в случаях, установленных настоящими Правилами. Разметка может применяться самостоятельно либо совместно с дорожным знаком 1.35 .
2 Разметка 1.2
11, которая разделяет транспортные потоки противоположных или попутных направлений. Линию 1.6 разрешается пересекать с любой стороны.
9 Разметка 1.9
10 Разметка 1.10
14.2 обозначает пешеходный переход. Стрелы разметки 1.14.2 указывают направление движения пешеходов.
19 Разметка 1.19
5 .
24.3 Разметка 1.24.3
24.6 Разметка 1.24.6
26 Разметка 1.26В случаях если значения дорожных знаков, в том числе временных, и линий горизонтальной разметки противоречат друг другу либо разметка недостаточно различима, водители должны руководствоваться дорожными знаками. В случаях если линии временной разметки и линии постоянной разметки противоречат друг другу, водители должны руководствоваться линиями временной разметки.
Правила дорожного движения
Дорожные знаки
Дорожная разметка
Основные положения и неисправности
1/4″ — Головки и трещотки — Продукция
1/4″ — Головки и трещотки — Продукция | Bahco Russia The store will not work correctly in the case when cookies are disabled.
JavaScript seems to be disabled in your browser. For the best experience on our site, be sure to turn on Javascript in your browser.
Мы используем файлы cookie, чтобы Вам было удобнее использовать сайт
В соответствии с Общим регламентом по защите данных нам необходимо Ваше согласие на хранение этих файлов. Узнать больше.
Разрешить файлы cookie
Please indicate which country or region you are in to view specific content: /
ЗакрытьМагазин по
Применить фильтр к товарам
Крестовой шлиц Pozidriv
Шестигранная головка TORX®
Ширина рукоятки
Шестигранная головка с отверстием TORX®
Число деталей
Четырехгранная головка
Крестовой шлиц Phillips
«Байер» победил «Рейнджерс» и вышел в 1/4 финала Лиги Европы
https://rsport.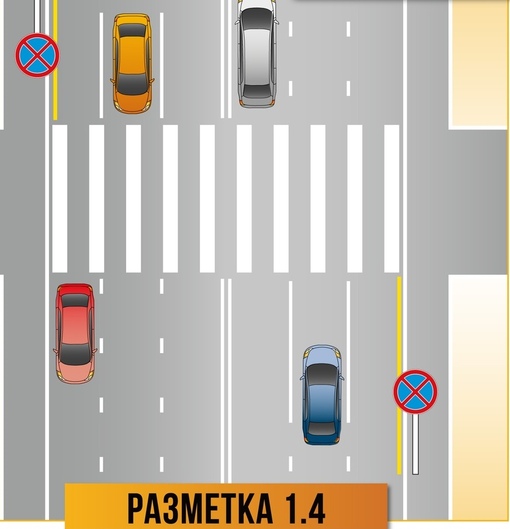
ria.ru/20200806/1575467341.html
«Байер» победил «Рейнджерс» и вышел в 1/4 финала Лиги Европы
«Байер» победил «Рейнджерс» и вышел в 1/4 финала Лиги Европы — РИА Новости Спорт, 06.08.2020
«Байер» победил «Рейнджерс» и вышел в 1/4 финала Лиги Европы
Леверкузенский «Байер» одержал победу над шотландским «Рейнджерс» и пробился в четвертьфинал футбольной Лиги Европы. РИА Новости Спорт, 06.08.2020
2020-08-06T21:57
2020-08-06T21:57
2020-08-06T21:57
футбол
лига европы уефа
рейнджерс
байер 04
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/rsport/113963/55/1139635501_0:198:2727:1732_1920x0_80_0_0_1ea49afbb135d65f69902b1d56799abd.jpg
МОСКВА, 6 авг — РИА Новости. Леверкузенский «Байер» одержал победу над шотландским «Рейнджерс» и пробился в четвертьфинал футбольной Лиги Европы.Ответная встреча 1/8 финала, прошедшая в Леверкузене, завершилась со счетом 1:0, единственный гол на 51-й минуте забил Мусса Диаби.
В первой игре, состоявшейся в марте в Глазго, немецкий клуб также одержал победу — 3:1.Все матчи еврокубков, которые возобновились на этой неделе после паузы, вызванной пандемией коронавируса, начинаются с минуты молчания в память о жертвах COVID-19. Также, согласно распоряжению УЕФА, команды вышли на игру в футболках, на которых было написано «спасибо» в знак благодарности всем, «кто трудится на передовой битвы с пандемией».Соперником «Байера» в четвертьфинале Лиги Европы будет миланский «Интер».Ранее УЕФА объявил, что финальная стадия Лиги Европы (начиная с 1/4 финала) пройдет в Германии в августе, все противостояния будут состоять из одного матча.
РИА Новости Спорт
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2020
РИА Новости Спорт
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://rsport.
ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости Спорт
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/rsport/113963/55/1139635501_78:0:2651:1930_1920x0_80_0_0_ada6c67e5725225764571083724b4dd5.jpgРИА Новости Спорт
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
РИА Новости Спорт
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
лига европы уефа, рейнджерс, байер 04
МОСКВА, 6 авг — РИА Новости. Леверкузенский «Байер» одержал победу над шотландским «Рейнджерс» и пробился в четвертьфинал футбольной Лиги Европы.
Ответная встреча 1/8 финала, прошедшая в Леверкузене, завершилась со счетом 1:0, единственный гол на 51-й минуте забил Мусса Диаби.
В первой игре, состоявшейся в марте в Глазго, немецкий клуб также одержал победу — 3:1.
Все матчи еврокубков, которые возобновились на этой неделе после паузы, вызванной пандемией коронавируса, начинаются с минуты молчания в память о жертвах COVID-19. Также, согласно распоряжению УЕФА, команды вышли на игру в футболках, на которых было написано «спасибо» в знак благодарности всем, «кто трудится на передовой битвы с пандемией».
Соперником «Байера» в четвертьфинале Лиги Европы будет миланский «Интер».
Ранее УЕФА объявил, что финальная стадия Лиги Европы (начиная с 1/4 финала) пройдет в Германии в августе, все противостояния будут состоять из одного матча.
Россиянка сыграет со второй ракеткой мира в 1/4 финала Кубка Кремля :: Теннис :: РБК Спорт
Во втором круге Екатерина Александрова победила украинку Ангелину Калинину.
Встреча завершилась со счетом 6:4, 6:1
Читайте нас в
Новости НовостиЕкатерина Александрова (Фото: Global Look Press)
Россиянка Екатерина Александрова обыграла украинку Ангелину Калинину в матче второго круга московского турнира WTA «ВТБ Кубок Кремля».
Встреча завершилась со счетом 6:4, 6:1 в пользу 26-летней россиянки. Ее следующей соперницей станет вторая ракетка мира и лидер посева Кубка Кремля белоруска Арина Соболенко.
Соболенко ранее во втором круге обыграла Айлу Томлянович из Австралии со счетом 7:6 (7:2), 4:6, 6:1.
Россиянка проиграла бывшей первой ракетке мира на Кубке КремляАлександрова занимает 37-е место в рейтинге WTA, на ее счету один титул ассоциации. На турнирах «Большого шлема» спортсменка не проходила дальше третьего круга. 24-летняя Калинина занимает 57-е место в мировом рейтинге.
Кубок Кремля завершится 24 октября. Призовой фонд турнира составляет $1,345 млн.
Автор
Иван Витченко
«Процент» словесных проблем: разметка и уценка
«Проценты
из» Word задач:
Примеры разметки и уценки (страница
2 из 3)
Секции: Основные процентные упражнения, Наценка/уценка, Общие увеличение/уменьшение
Важная категория
процентные упражнения — это проблемы с разметкой и уценкой.
Для них вы вычисляете
наценка или уценка в абсолютном выражении (вы находите, на сколько количество
изменено), а затем вы вычисляете процентное изменение относительно исходного
ценность. Так что на самом деле это просто еще одна форма «увеличения-уменьшения».
упражнения.
- Программное обеспечение для ЭВМ ритейлер использовал ставку наценки в размере 40%. Найти продажи цена компьютерной игры, которая стоила розничному продавцу 25 долларов.
Наценка составляет 40% от стоимости в 25 долларов, поэтому наценка составляет:
Тогда цена продажи, стоимость плюс наценка:
25 + 10 = 35
Товар продан за 35 долларов.
- Магазин гольфа платит
его оптовый торговец 40 долларов за определенный клуб, а затем продает его игроку в гольф за 75 долларов. Какова ставка наценки?
Какова ставка наценки? Сначала посчитаю наценка в абсолютном выражении:
Тогда я найду родственника наценка сверх первоначальной цены или ставка наценки: (35 долларов) составляет (несколько процентов) от (40 долларов), или: авторское право © Элизабет Стапель 1999-2011 Все права защищены
… поэтому относительная разметка выше первоначальной цены:
Поскольку x означает процент, мне нужно не забыть преобразовать это десятичное число. значение на соответствующий процент.
- Обувной магазин использует наценка 40% от себестоимости. Найдите стоимость пары обуви, которая продается за 63 доллара.
Эта проблема несколько
назад.Они назвали мне продажную цену, которая представляет собой себестоимость плюс наценка.
и мне дали наценку, но не сказали фактическую
стоимость или наценка. Так что я должен быть умным, чтобы решить это.
я позволю « x » быть стоимость. Тогда наценка, составляющая 40% от стоимости, составляет 0,40 х . А цена продажи 63 доллара — это сумма себестоимости и наценки, значит:
63 = х + 0.40 х
63
= 1 х + 0,40 х
63
= 1,40 х
63
÷ 1,40 = х = 45
Обувь стоит хранить 45 долларов.
- Товар изначально по цене $55 отмечена скидка 25%. Какова цена продажи?
Сначала я найду уценка.Уценка составляет 25% от первоначальной цены в 55 долларов США, так:
Вычитая эту уценку от первоначальной цены я могу найти цену продажи:
- Предмет, который регулярно
продается за 425 долларов, снижен до 318,75 долларов. Какова ставка дисконтирования?
Какова ставка дисконтирования? Сначала я найду сумма уценки:
Тогда я посчитаю » уценка сверх первоначальной цены», или ставка уценки: ($106.25) составляет (несколько процентов) от (425 долларов США), так:
…и относительная уценка выше первоначальной цены:
Начиная с « х » обозначает процент, мне нужно помнить, чтобы преобразовать это десятичное число в процентную форму.
- Пункт отмечен вниз на 15%; цена продажи составляет 127,46 долларов США. Какая была первоначальная цена?
Эта проблема обратная.Они назвали цену продажи (127,46 долларов США) и ставку уценки (15%).
но ни суммы уценки, ни исходной цены. Я позволю « x »
стоять за первоначальную цену. Тогда уценка, составляющая 15% от этой цены, составила 0,15 x .
И цена продажи — это первоначальная цена за вычетом уценки, поэтому я получаю:
Эта проблема не указана как округлить окончательный ответ, но всегда пишут доллары и центы с двумя десятичными знаками, поэтому:
Обратите внимание на последнюю задачу что в третьей строке вычислений я пришел к уравнению, которое сказал: «Восемьдесят пять процентов от первоначальной цены составляют 127 долларов.46″. Вы можете сэкономить время, если будете думать о скидках таким образом: если цена снижена на 15%, то на самом деле вы платите только 85%. Точно так же, если цена снижена на 25%, вы платите 75%; если цена снижена на 30%, то вы платите 70%; и так далее.
<< Предыдущая Верх | 1 | 2 | 3 | Возвращение к индексу Далее >>
Процитировать эту статью как: | Стапель, Элизабет. |
«Процент проблем со словами: разметка и уценка». Пурпурная математика . Доступно от Язык математической разметки (глава 1)
Язык математической разметки (глава 1)1.1 Математика и ее обозначения
Отличительной особенностью математики является использование сложного и весьма
развитая система двумерных символьных обозначений.Как сказал Дж. Р. Пирс
написано в его книге по теории коммуникации, математике и ее обозначениям
не следует рассматривать как одно и то же
[Пирс
1961]. Математические идеи существуют независимо от обозначений, которые
представлять их. Однако связь между значением и обозначением тонкая,
и часть способности математики описывать и анализировать проистекает из
его способность представлять и манипулировать идеями в символической форме. Соревнование
размещать математику в Сети — значит фиксировать как нотацию, так и содержание в таком
способ, которым документы могут использовать высокоразвитые методы записи
печатных изданий, а также потенциал взаимосвязи электронных средств массовой информации.
Математические обозначения постоянно развиваются по мере того, как люди продолжают
открыть для себя инновационные способы подхода и выражения идей. Четное
обычные арифметические обозначения претерпели удивительные изменения.
разнообразие стилей, в том числе многие несуществующие, за которые выступали ведущие
математические фигуры своего времени [Cajori 1928/1929]. Современный
математическая нотация является продуктом многовекового совершенствования, и
условные обозначения для высококачественного набора довольно
сложный. Например, переменные или буквы, обозначающие
цифры, обычно сегодня набираются специальным курсивным шрифтом тонко
отличается от текста курсивом.Расстояние вокруг символов для операций
такие как +, -, x и / немного отличается от текста, чтобы
отражают соглашения о приоритете операторов. Целые книги были
посвященный условностям математического набора, от
выравнивание надстрочных и подстрочных индексов с правилами выбора
размеры круглых скобок, специализированные методы записи для подполей
математики [например, Чаудри,
Баррет и Бейти, 1954, Суонсон.
1979, Хайэм 1993,
или в литературе TeX
Кнут, 1986, и Спивак, 1986].
Условные обозначения в математике и печатном тексте в целом, направляют взгляд и делают печатные выражения более легкими для чтения и понимать. Хотя мы обычно принимаем их как должное, мы полагаемся на сотни условных обозначений, таких как абзацы, заглавные буквы, шрифт семей и дел, и даже прием десятичной нумерации разделы, такие как мы используем в этом документе (изобретение благодаря Г. Пеано, который, вероятно, более известен своими аксиомами естественного числа). Такие условные обозначения еще более важны для электронных СМИ, где приходится бороться с трудностями чтение с экрана.
Тем не менее, размещение математики в Интернете — это нечто большее, чем
просто найти способы отображения традиционных математических
обозначения в веб-браузере. Сеть представляет собой фундаментальный
изменение лежащей в основе метафоры хранения знаний,
изменение, в котором взаимосвязь играет центральную роль
роль.
Все более важным становится поиск путей
передача математики, которые облегчают автоматический
обработка, поиск и индексирование, а также повторное использование в других
математические приложения и контексты.С этим продвижением в
технологии связи, есть возможность расширить
наша способность представлять, кодировать и, в конечном счете,
передавать наши математические идеи и понимание с
друг с другом. Мы считаем, что MathML — это важный шаг в
развитие математики в Интернете.
1.2 Истоки и цели
1.2.1 История MathML
Проблема кодирования математики для компьютерной обработки или электронное общение намного старше, чем Интернет. То обычной практикой среди ученых до Интернета было писать документы в какой-либо закодированной форме на основе набора символов ASCII, и отправить их друг другу по электронной почте.Несколько методов разметки для математика, в частности TeX [Knuth 1986], уже были в широкое распространение в 1992 году, как раз перед тем, как Всемирная паутина приобрела известность [Poppelier, van Herwijnen and Роули, 1992].
С момента своего создания Интернет показал себя очень эффективный способ донесения информации до широко обособленные группы людей. Однако, хотя Всемирная паутина изначально была задумана и реализована ученые для ученых, возможность включать математические выражения в HTML очень ограничены.В настоящий момент, большая часть математики в Интернете состоит из текста с изображениями в формате GIF. научных обозначений, которые трудно читать и автор.
Консорциум World Wide Web (W3C) признал, что отсутствие
серьезной проблемой была поддержка научной коммуникации.
Дэйв Рэггетт включил предложение по HTML Math в HTML 3.0.
рабочий проект в 1994 году. Круглый стол по математической разметке был
состоявшейся на конференции WWW в Дармштадте в апреле 1995 г. В
Ноябрь 1995 г., представители Wolfram Research представили
предложение по математике в HTML команде W3C.В мае
1996 г., встреча Инициативы цифровой библиотеки в
Шампейн-Урбана сыграла важную роль в объединении
много заинтересованных сторон.
После встречи HTML Math
Сформирован редакционный совет. В прошедшие годы,
эта группа выросла и была официально воссоздана как
Рабочая группа W3C Math, март 1997 г.
Предложение MathML отражает интересы и опыт очень
разнообразная группа. Многие вклады в развитие MathML заслуживают
особого упоминания, некоторые из которых мы коснемся здесь.Один такой вклад
касается вопроса доступности, особенно для визуально
инвалид. Особенно примечателен в этом отношении Т. В. Раман. Нил
Сойффер и Брюс Смит из Wolfram Research поделились своим
опыт работы с проблемами представления математики в связи
с дизайном Mathematica 3.0, который оказал большое влияние на
оформление элементов презентации. Пол Топпинг из Design Science
также внес свой вклад в математическое форматирование и редактирование.MathML выиграл от участия ряда рабочих
члены группы, участвующие в других усилиях по математическому кодированию в
SGML и
Нико Поппелье из Elsevier Science, Стефан Далмас из INRIA,
София Антиполис,
Стэн Девитт из Waterloo Maple, Анхель Диаз и Роберт С.
Сутор из
IBM и Стивен М. Ватт из Университета Западного Онтарио. В
в частности, на MathML повлиял проект OpenMath,
работа рабочей группы ISO 12083 и работа Stilo Technologies над
Фрагмент «семантического» математического DTD.Американское математическое общество
сыграл ключевую роль в развитии MathML. Среди прочего, это
предоставил двух председателей рабочих групп: Рон Уитни возглавлял группу из
С мая 1996 г. по март 1997 г. и Патрик Ион, который был сопредседателем группы.
с Робертом Майнером из Центра геометрии с марта 1997 г.
настоящее время.
Рабочая группа получила помощь от многих людей. Мы особо хотелось бы назвать Барбару Битон, Криса Хэмлина, Джона Дженкинс, Айра Поланс, Артур Смит, Робби Вильегас и Джо Юрвати за помощь и информация по сборке таблиц символов в Главе 6, а также Питер Флинн, Рассел С.С. О’Коннор, Андреас Стротманн и другим участникам списка рассылки www-math за их внимательное вычитка и конструктивная критика.
1.2.2 Ограничения HTML
Спрос на эффективные средства электронной научной
общение на высоте.
Все чаще исследователи, ученые,
инженеры, преподаватели, студенты и техники оказываются
работать удаленно и полагаться на электронную связь. В
в то же время методы на основе изображений, которые в настоящее время являются
преобладающее средство передачи научных обозначений над
Сеть примитивна и неадекватна.Качество документа низкое,
авторская работа сложна, а математическая информация содержалась
в изображениях недоступен для поиска, индексации или повторного использования
в других приложениях.
Наиболее очевидные проблемы с HTML для математической коммуникации: двух типов:
Проблемы с дисплеем. Рассмотрим уравнение . Это уравнение рассчитано на
совпадать с окружающей линией шрифтом 14pt в той системе, где она
был автором. Конечно, на других системах или для другого шрифта
размеры, уравнение слишком маленькое или слишком большое.Второй момент
заметить, что изображение уравнения было создано против
белый фон. Таким образом, если читатель или браузер сбрасывает страницу
фон на другой цвет, сглаживание на изображении
приводит к появлению белых «ореолов».
Далее рассмотрим уравнение . Это уравнение имеет нисходящий элемент, который
помещает базовую линию уравнения в точку примерно на треть
пути от нижней части изображения. Можно дополнить изображение
нравится: ,
таким образом, чтобы центральная линия изображения и базовая линия
уравнения совпадают, но это вызывает проблемы с
межстрочный интервал, что также затрудняет вычисление уравнения
читать.Кроме того, выравнивание изображений по центру выполняется в
немного по-разному в разных браузерах, что делает его
невозможно гарантировать правильное выравнивание для различных
клиенты.
Уравнения на основе изображений, как правило, труднее увидеть, прочитать и понять чем окружающий текст в окне браузера. Более того, эти проблемы ухудшаются при печати документа. Решение уравнений будет около 70 точек на дюйм, а окружающий текст обычно быть 300 или более точек на дюйм.Различие в качестве оценивается как неприемлемо для большинства людей.
Проблемы с кодировкой. Рассмотрите возможность поиска на этой странице части
уравнения, например, «=10» из первого уравнения выше.
В
в том же духе, подумайте о том, чтобы попытаться вырезать и вставить уравнение в другое
применение; еще более требовательным является вырезание и вставка подвыражения.
Используя методы, основанные на образах, ни одна из этих общих потребностей не может быть решена.
быть адекватно рассмотрены. Хотя использование текста ALT в исходном документе
может помочь, ясно, что интерактивные веб-документы должны обеспечивать
более сложный интерфейс между браузерами и математическими обозначениями.Другая проблема с кодированием математики в виде изображений заключается в том, что для этого требуется
больше пропускной способности. Используя кодирование на основе разметки, процесс рендеринга
перемещается на клиентскую машину. Разметка, описывающая уравнение, обычно
меньше и более сжимаемо, чем образ уравнения.
1.2.3 Требования к математической разметке
Некоторые проблемы с отображением, связанные с включением математических обозначений в
HTML-документы как изображения можно было бы решить, улучшив изображение в браузере.
умение обращаться. Однако, даже если бы обработка изображений была улучшена, проблема
сделать информацию, содержащуюся в математических выражениях,
доступным для других приложений, останутся.Поэтому при планировании
в будущем недостаточно просто обновить
методы. Чтобы полностью интегрировать математический материал в веб-документы,
основанное на разметке кодирование математической записи и содержимого
обязательный.
При разработке любого языка разметки важно тщательно учитывать потребности своих потенциальных пользователей. В случае MathML, потребности потенциальных пользователей охватывают широкий спектр, от образования до исследований и в коммерцию:
Образовательное сообщество — большая и важная группа, которую необходимо
иметь возможность размещать научные учебные материалы в Интернете.В то же
время, педагоги часто имеют ограниченные ресурсы времени и оборудования,
и им серьезно мешает сложность создания технических веб-сайтов.
документы. Учащиеся и учителя должны уметь создавать
математическое содержание быстро и легко, используя интуитивно понятный,
простые в освоении и недорогие инструменты.
Электронные учебники — это еще один способ использования Интернета, который потенциально быть очень важным в воспитании. Консультант по вопросам управления Питер Друкер недавно пророчил конец высшему образованию в больших кампусах и его распространение в Интернете [Drucker 1997].Электронные учебники должны быть активными, позволяя взаимосвязь между текстом и научным программным обеспечением и графикой.
Академическое исследовательское сообщество создает большие объемы плотных
научный материал. Все чаще публикуются научные публикации.
хранятся в базах данных, таких как очень успешный препринт по физике
сервер в Лос-Аламосской национальной лаборатории. Это особенно верно в
некоторые области физики и математики, где цены на академические журналы
росли неустойчивыми темпами.В математике есть
большие коллекции в Герцог ,
ИИГС
и
СИССА и на
Электронная математика AMS
сервер. Кроме того, базы данных по математическим
исследований, таких как Mathematical Reviews и Zentralblatt für
Mathematik, предлагайте в Интернете миллионы записей, содержащих математику.
В интересах исследовательского сообщества дизайн математической разметки должны облегчать обслуживание и работу с большими документами коллекции, где автоматический поиск и индексация важный.Из-за большого количества устаревших данных, особенно документы TeX, возможность преобразования между существующими форматами и новыми форматы также очень важны для исследовательского сообщества. Ну наконец то, способность хранить информацию для архивных целей жизненно важна для академическое исследование.
Корпоративные и академические ученые и инженеры также используют технические документы в своей работе сотрудничать, фиксировать результаты опытов и компьютерных моделирования и проверки расчетов. Для таких целей математика в Интернете должен обеспечивать стандартный способ обмена информацией, которая может быть легко прочитана, обрабатываются и генерируются с помощью общедоступных инструментов.
Другим требованием к дизайну является возможность воспроизведения математического материала
в других средствах массовой информации, таких как речь или шрифт Брайля, что чрезвычайно важно
для слабовидящих.
Коммерческие издатели также вообще занимаются математикой в Интернете. уровни от электронных версий печатных книг до интерактивных учебников в академические журналы. Издателям требуется метод включения математики в Сеть, способная выводить высококачественный продукт, достаточно надежная для крупномасштабных коммерческое использование и, желательно, совместимые с их текущими, обычно на основе SGML, производственные системы.
1.2.4 Цели проектирования MathML
Чтобы удовлетворить разнообразные потребности научного сообщества, MathML был разработан с учетом следующих конечных целей.
MathML должен:
- закодировать математический материал, пригодный для обучения и научная коммуникация на всех уровнях.
- кодируют как математическую запись, так и математический смысл.
- облегчить преобразование в другую математику и обратно
форматы, как презентационные, так и семантические.Выходные форматы должны включать:
- графические дисплеи
- синтезаторы речи
- ввод систем компьютерной алгебры
- другие языки математической компоновки, такие как TeX
- текстовые дисплеи, напр. Эмуляторы VT100
- печатные носители, включая шрифт Брайля
- разрешить передачу информации, предназначенной для конкретные рендереры и приложения.
- поддерживают эффективный просмотр длинных выражений.
- обеспечивают расширяемость.
- хорошо подходит для редактирования шаблонов и других математических операций. методы.
- быть удобочитаемым для человека и простым для создания и обработки программным обеспечением.
Эмуляторы VT100- Уравнения MathML на HTML-страницах должны правильно отображаться в популярных веб-браузерах. в соответствии с предпочтениями читателя и автора при просмотре, а также на самом высоком уровне возможное качество с учетом возможностей платформы.
- HTML-документы, содержащие уравнения MathML, должны печататься правильно и быстро. высокое разрешение принтера.
- Уравнения MathML на веб-страницах должны реагировать на жесты мыши, и координировать связь с другими приложениями через браузер.
- Редакторы уравнений и преобразователи должны быть разработаны для облегчения создания веб-страниц, содержащих уравнения MathML.
Рабочая группа W3C по математике
продолжит работу с рабочей группой Document Object Model и
предлагаемая рабочая группа Extensible Style Language, чтобы гарантировать, что
потребности научного сообщества будут удовлетворены в будущем.1.3 Роль MathML в Интернете
1.3.1 Многоуровневый дизайн математической сети Услуги
Цели дизайна MathML требуют системы для кодирования математический материал для Интернета, который является гибким и расширяемым, подходит для взаимодействия с внешним программным обеспечением и способен производство высококачественного рендеринга на нескольких носителях. Любая разметка язык, который кодирует достаточно информации, чтобы хорошо выполнять все эти задачи будет неизбежно включать некоторую сложность.
В то же время это важно для многих групп, таких как
студентов, чтобы иметь простые способы включения математики в веб-страницы путем
рука.Точно так же другие группы, такие как сообщество TeX, будут
лучше всего обслуживается системой, допускающей прямой ввод наценки
языки, такие как TeX, на веб-страницах.
В общем, конкретный пользователь
группы лучше обслуживаются более специализированными видами ввода и вывода
с учетом их потребностей. Поэтому идеальная система для
общение по математике в Интернете должно предоставлять как специализированные
услуги для ввода и вывода, а также общие услуги для обмена
информации и рендеринга на несколько носителей.
С практической точки зрения наблюдение, что математика в Интернете должна удовлетворения как специализированных, так и общих потребностей, естественно, приводит к идея многоуровневой архитектуры.Один слой состоит из мощных, общие программные средства обмена, обработки и рендеринга соответствующим образом закодированные математические данные. Второй слой состоит из специализированные программные средства, ориентированные на определенные группы пользователей и способны легко генерировать закодированные математические данные, которые могут затем поделиться с широкой аудиторией.
MathML предназначен для обеспечения кодирования математических данных для
нижний, более общий уровень в двухуровневой архитектуре.
это
предназначен для кодирования сложной нотации и семантической структуры в
явный, регулярный и простой в обработке способ для рендереров, поиск
программное обеспечение для индексирования и другие математические приложения.
Как следствие, MathML , а не в первую очередь предназначен для прямого использования авторами. Хотя MathML удобочитаем для человека, во всем, кроме простейших случаях это слишком многословно и подвержено ошибкам для ручной генерации. Вместо этого ожидается, что авторы будут использовать уравнение редакторы, программы преобразования и другие специализированные программные инструменты для генерировать MathML. Кроме того, некоторые рендереры могут преобразовывать другие виды ввода, непосредственно включенные в веб-страницы в MathML на лету, например, в ответ на операцию вырезания и вставки.
В некотором смысле MathML аналогичен другим низкоуровневым коммуникационным
форматы, такие как язык Adobe PostScript. Вы можете создать
PostScript различными способами, в зависимости от ваших потребностей; эксперты
писать и изменять их вручную, авторы создают их с помощью слова
процессоры, художники-графики с программами для иллюстраций и так далее.
Однажды ты
иметь файл PostScript, однако вы можете поделиться им с очень большим
аудитории, так как устройства, отображающие PostScript, такие как принтеры и
средства предварительного просмотра экрана широко доступны.
Одна из причин разработки MathML в качестве языка разметки для низкоуровневый, общий, коммуникационный уровень должен стимулировать математические Разработка веб-приложений на более высоких уровнях. MathML предоставляет способ координации разработка модульных инструментов авторинга и программного обеспечения для рендеринга. От упрощение разработки функциональной части более крупной системы, MathML может стимулировать «критическую массу» разработки программного обеспечения, в значительной степени на благо потенциальных пользователей математики в Интернете.
Аналогичную ситуацию можно представить и для математических данных.Авторы могут свободно создавать документы MathML, используя наиболее подходящие инструменты.
к их потребностям. Например, студент может предпочесть использовать
редактор формул на основе меню, который может записывать MathML в HTML
файл.
Исследователь может использовать пакет компьютерной алгебры, который
автоматически кодирует математическое содержание выражения, поэтому
что его можно вырезать из веб-страницы и оценить коллега. Ан
издатель академического журнала может использовать программу, которая конвертирует TeX
разметка для HTML и MathML. Независимо от способа создания
Веб-страница MathML, как только она существует, все преимущества мощного и
общий коммуникационный уровень становится доступным.Разновидности MathML
программное обеспечение может быть использовано с одним и тем же документом для его отображения в
речь или печать, чтобы отправить ее в систему компьютерной алгебры или управлять
как часть большой коллекции веб-документов. Можно ожидать, что
в конечном итоге MathML может быть интегрирован в другие области, где
встречаются математические формулы, такие как электронные таблицы, статистические
пакеты и инженерные инструменты.
Рабочая группа W3C Math работает с поставщиками, чтобы гарантировать, что
скоро будет доступен широкий спектр программного обеспечения MathML, в том числе
инструменты для рендеринга и разработки.
Текущий список программного обеспечения MathML:
поддерживается Консорциумом World Wide Web.
1.3.2 Связь с другим Интернетом Технология
Первоначальная концепция HTML Math была простой и понятной. расширение для HTML, которое будет изначально реализовано в браузерах. Однако уже на раннем этапе взрывной рост Интернета показал, что что необходим общий механизм расширения, и что математика только один из многих видов структурированных данных, которые должны быть интегрированы в Сеть с помощью такого механизма.
Учитывая, что MathML должен интегрироваться в Интернет как расширение,
чрезвычайно важно, чтобы MathML и программное обеспечение MathML могли взаимодействовать
хорошо с существующей веб-средой. В частности, MathML имеет
был разработан с учетом трех видов взаимодействия. Первый в
Для создания математического веб-контента важно, чтобы
существующие языки математической разметки могут быть преобразованы в MathML, и
что существующие инструменты разработки могут быть изменены для создания MathML.
Во-вторых, должна быть возможность беспрепятственно встраивать разметку MathML в HTML.
разметка таким образом, чтобы она была доступна для будущих браузеров,
поисковые системы и всевозможные веб-приложения, которые теперь манипулируют
HTML.Наконец, должна быть возможность отображать MathML, встроенный в HTML, в
сегодняшние веб-браузеры некоторым образом, даже если это далеко не идеально.
Существующие языки математической разметки
Возможно, наиболее важное влияние на языки математической разметки за последние два десятилетия — система набора текста TeX, разработанная Дональд Кнут [Кнут 1986]. TeX является стандартом де-факто в математических исследованиях. сообщества, и она широко распространена в научном сообществе в большой. TeX устанавливает стандарт качества визуального рендеринга, а много усилий было потрачено на то, чтобы MathML мог обеспечить одинаковое качество визуального рендеринга.Более того, из-за множества унаследованные документы в TeX, а также благодаря большому авторскому сообществу разбираясь в TeX, приоритетом при разработке MathML была возможность конвертировать математический ввод TeX в формат MathML.
Осуществимость такого
преобразование было продемонстрировано прототипом программного обеспечения.Обширная работа по кодированию математики также была проделана в Сообщество SGML и схемы кодирования на основе SGML широко используются коммерческие издательства. ISO 12083 — важный язык разметки, который содержит математический фрагмент DTD, предназначенный в первую очередь для описания визуального представление математических обозначений.Поскольку математика ISO 12083 и ее производные имеют много общих аспектов представления с TeX, и поскольку SGML обеспечивает структуру и регулярность больше, чем TeX, большая часть работы в обеспечении совместимости MathML с TeX также хорошо подходит для ИСО12083.
MathML также уделяет особое внимание совместимости с другими
математическое обеспечение, и в частности, с компьютерной алгеброй
системы. Многие из элементов представления MathML получены в
часть от механизма наборных ящиков.Содержимое MathML
элементы в значительной степени обязаны проекту OpenMath и Semantic
Математическое DTD.
Проект OpenMath тесно связан как с SGML, так и с
сообщества компьютерной алгебры и заложил основу для
Средства связи между математическим программным обеспечением на основе SGML
пакеты между прочим. Возможность как создания, так и
была продемонстрирована интерпретация MathML в системах компьютерной алгебры
с помощью программного обеспечения-прототипа.
Механизмы расширения HTML
Как отмечалось выше, успех HTML привел к огромному давлению со стороны
включать широкий спектр типов данных и программных приложений
в Сети.Каждый новый формат или приложение потенциально создает новые
Требования к HTML и к поставщикам браузеров. Некоторое время было
ясно, что общий механизм расширения необходим для размещения
новые расширения HTML. Мы начали нашу работу, думая о простом расширении
в HTML в духе первой математической поддержки, предложенной для HTML 3.2.
Но по разным причинам, как только мы углубились в детали, оказалось, что
не очень хорошая идея. С тех пор как работа над MathML началась, XML
стал ведущим кандидатом на такой общий механизм расширения.
XML означает расширяемый язык разметки. Он разработан как упрощенная версия SGML, метаязыка, используемого для определения грамматика и синтаксис HTML. Одна из целей XML — быть подходящим для использования в Интернете, и в контексте этого обсуждения это может быть рассматривается как общий механизм расширения HTML. Как следует из названия, расширяемость — ключевая особенность XML; авторы могут свободно заявлять и использовать новые теги и атрибуты. В то же время грамматика и синтаксис XML правила тщательно следят за структурой документа, чтобы облегчить автоматическую обработка и ведение больших коллекций документов.
Хотя подробности о том, как XML-разметка в конечном итоге будет встроена в
HTML еще предстоит решить, XML получил широкую поддержку в отрасли
включая основных поставщиков браузеров. Разработка стандартного способа встраивания
XML в HTML также важен для W3C. Кроме того, другие
применения XML для всех видов публикации документов и
обработка обещает стать все более важной.
Следовательно,
как с теоретической, так и с практической точки зрения,
смысла указывать MathML как XML-приложение, и мы это сделали.
Механизмы расширения браузера
Хотя детали общей модели для рендеринга и обработки XML расширения для HTML все еще решаются, широкие возможности модель уже достаточно ясна. Разработаны свойства форматирования Рабочей группой по каскадным таблицам стилей и свойствам форматирования для CSS и сделал доступный через объектную модель документа (DOM), будет применяться к MathML элементы, чтобы получить некоторый стилистический контроль над презентацией MathML. Дальнейшее развитие этих свойств форматирования падает в рамках устава рабочих групп CSS&FP и XSL.Таким образом, это скоро можно будет написать таблицу стилей, которая будет в значительной степени описать правильное отображение MathML.
MathML был разработан с целью рендеринга на основе таблиц стилей в
разум. Рабочая группа W3C по математике намерена работать
тесно связан с действиями с таблицами стилей W3C, чтобы обеспечить адекватное
поддержка MathML включена в будущие механизмы таблиц стилей,
и что разработаны таблицы стилей MathML.
В частности, предоставление
для адекватных последующих действий, выходящих за рамки W3C Math
устав рабочей группы является приоритетной задачей.
До тех пор, пока механизмы таблицы стилей не смогут предоставлять собственный браузер
рендеринг MathML, однако необходимо расширить браузер
возможности с помощью встроенных элементов для рендеринга MathML. Это может
скоро можно будет указать браузеру использовать конкретный встроенный
визуализатор для обработки встроенной XML-разметки, такой как MathML, и координации
результирующий вывод с окружающей веб-страницей. Действительно, для
специализированная обработка, такая как подключение к компьютерной алгебре
системы, эта возможность, вероятно, останется весьма желательной.Однако для того, чтобы этот вид взаимодействия был действительно удовлетворительным,
потребуется для определения достаточно богатой объектной модели документа, чтобы
упростить сложное взаимодействие между браузерами и встроенными
элементы. По этой причине рабочая группа W3C по математике координирует
его усилия тесно связаны с рабочей группой Document Object Model.
Для обработки закладными элементами и для связи между ними между научным программным обеспечением, как правило, макет на основе таблиц стилей модель не идеальна в некоторых отношениях.Он может налагать доп. бремя реализации в условиях, когда это может дать мало преимуществ, и налагает требования реализации для координации между браузеры и встроенные средства визуализации, которые, вероятно, будут недоступны в ближайшее будущее.
По этим причинам спецификация MathML определяет
модель компоновки на основе атрибутов, которая оказалась очень эффективной для
качественная отрисовка сложных математических выражений в
несколько независимых реализаций. Атрибуты представления MathML
использовать форматирование W3C
Свойства, где это возможно.Кроме того, элементы MathML принимают класс,
атрибуты style и id для облегчения их использования с таблицами стилей CSS.
Однако в настоящее время существует несколько настроек, в которых используется механизм CSS.
в настоящее время доступно для визуализаторов MathML.
Когда механизмы таблиц стилей станут доступны для MathML, ожидается, что их использование станет доминирующий метод стилистического контроля представления MathML означал для использования в средах рендеринга, которые поддерживают эти механизмы.
Далее: Основы MathML
Уровень выше: Содержание
: Элемент упорядоченного списка — HTML: язык гипертекстовой разметки
HTML-элемент
| Категории контента | Содержимое потока, и если дочерние элементы |
|---|---|
| Разрешенный контент | Ноль или более <скрипт> и элементов. |
| Отсутствие тега | Нет, начальный и конечный теги обязательны. |
| Разрешенные родители | Любой элемент, принимающий потоковое содержание. |
| Неявная роль ARIA | список |
| Разрешенные роли ARIA | каталог , группа , список , меню , панель меню , нет , презентация , радиогруппа , таблист , панель инструментов , дерево |
| Интерфейс DOM | HTMLOListElement |
Этот элемент также принимает глобальные атрибуты.
-
реверс Этот логический атрибут указывает, что элементы списка расположены в обратном порядке.
Элементы будут пронумерованы от большего к меньшему.-
начало Целое число, с которого начинается отсчет элементов списка. Всегда арабская цифра (1, 2, 3 и т. д.), даже если нумерация
типапредставляет собой буквы или римские цифры. Например, чтобы начать нумерацию элементов с буквы «d» или римской цифры «iv», используйтеstart="4".-
тип Устанавливает тип нумерации:
-
aдля строчных букв -
Aдля прописных букв -
iдля строчных римских цифр -
Iдля прописных римских цифр -
1для номеров (по умолчанию)
Указанный тип используется для всего списка, если для заключенного элемента
типа.Примечание: Если тип номера списка не имеет значения (например, юридические или технические документы, в которых элементы указаны по номеру/букве), вместо этого используйте свойство CSS
list-style-type.-
Элементы будут пронумерованы от большего к меньшему.
Обычно элементы упорядоченного списка отображаются с предшествующим маркером, например цифрой или буквой.
Элементы
Элементы
- Шаги в рецепте
- Пошаговые инструкции
- Список ингредиентов в убывающей пропорции на этикетках с информацией о пищевой ценности
Чтобы определить, какой список использовать, попробуйте изменить порядок элементов списка; если смысл меняется, используйте элемент
Простой пример
- Плата
- Fi
- Фо
- Фум
Приведенный выше HTML выведет:
Использование типа римских цифр
- Введение
- Список жалоб
- Заключение
Приведенный выше HTML-код выведет:
Используя атрибут start
Финишные места участников, не входящих в круг победителей:
<старт = "4">
Спидуок Стью
Сэм Сонтерин
Трудолюбивый Родригес
Приведенный выше HTML выведет:
Вложенные списки
- первый элемент
- второй элемент
<ол>
- второй элемент первый подэлемент
- второй элемент второй подэлемент
- второй элемент третий подэлемент
третий элемент
Приведенный выше HTML выведет:
Неупорядоченный список внутри упорядоченного списка
- первый элемент
- второй элемент
<ул>
- второй элемент первый подэлемент
- второй элемент второй подэлемент
- второй элемент третий подэлемент
- третий элемент
Приведенный выше HTML выведет:
Таблицы BCD загружаются только в браузере
- Другие HTML-элементы, связанные со списками:
- свойства CSS, которые могут быть особенно полезны для стилизации элемента
- свойство в стиле списка , чтобы выбрать способ отображения порядкового номера
- Счетчики CSS для обработки сложных вложенных списков
- свойство
line-heightдля имитации устаревшего атрибутаcompact. - свойство
marginдля управления отступом списка
Популярное приложение для семейной безопасности Life360 продает точные данные о местонахождении десятков миллионов пользователей — разметка
Life360, популярное приложение для семейной безопасности, которым пользуются 33 миллиона человек по всему миру, позиционируется как отличный способ для родителей отслеживать перемещения своих детей с помощью мобильных телефонов.Однако The Markup узнал, что приложение продает данные о местонахождении детей и семей примерно дюжине брокеров данных, которые продали данные практически всем, кто хочет их купить.
Из интервью с двумя бывшими сотрудниками компании, а также с двумя людьми, которые ранее работали в брокерах данных о местоположении Cuebiq и X-Mode, The Markup обнаружил, что приложение действует как поток данных для противоречивой отрасли, которая работала в тени. с небольшими гарантиями для предотвращения неправомерного использования этой конфиденциальной информации.
Бывшие сотрудники поговорили с The Markup при условии, что мы не будем использовать их имена, поскольку все они все еще работают в индустрии данных. Они сказали, что согласились поговорить из-за опасений по поводу безопасности и конфиденциальности индустрии данных о местоположении и желания пролить больше света на непрозрачную экономику данных о местоположении. Все они описали Life360 как один из крупнейших источников данных для отрасли.
«У нас нет возможности подтвердить или опровергнуть точность» того, является ли Life360 одним из крупнейших источников данных для отрасли, заявил основатель и генеральный директор Life360 Крис Халлс в ответе по электронной почте на вопросы The Markup.«Мы рассматриваем данные как важную часть нашей бизнес-модели, которая позволяет нам предоставлять основные услуги Life360 бесплатно для большинства наших пользователей, включая функции, которые повысили безопасность водителей и спасли множество жизней».
Бывший инженер X-Mode сказал, что необработанные данные о местоположении, полученные компанией от Life360, были одними из самых ценных предложений X-Mode из-за огромного объема и точности данных.
Бывший сотрудник Cuebiq пошутил, что компания не сможет проводить свои маркетинговые кампании без постоянного потока данных о местоположении Life360.
Конфиденциальность
Существует многомиллиардный рынок данных о местоположении вашего телефона
Огромная, но малоизвестная индустрия возникла вокруг монетизации движений людей
Разметка смогла подтвердить с бывшим сотрудником Life360 и бывшим сотрудником X-Mode, что X-Mode — в дополнение к Cuebiq и Arity Allstate, которые компания раскрывает в своей политике конфиденциальности — входит в число компаний, которым Life360 продает данные к.Бывший сотрудник Life360 также сообщил нам, что Safegraph был среди покупателей, что подтверждается электронным письмом от руководителя Life360, которое было просмотрено The Markup. Потенциально есть больше компаний, которые извлекают выгоду из данных Life360 на основе клиентов этих партнеров.
Hulls отказался раскрыть полный список клиентов данных Life360 и отказался подтвердить, что Safegraph входит в их число, сославшись на положения о конфиденциальности, которые, по его словам, содержатся в большинстве его деловых контрактов. Партнеры по данным публично раскрываются только тогда, когда партнеры запрашивают прозрачность или для этого есть «особая причина», сказал Халлс.Он подтвердил, что X-Mode покупает данные у Life360 и что он является одним из «примерно дюжины партнеров по данным». Халлс добавил, что компания поддержит законодательство, требующее публичного раскрытия информации о таких партнерах.
X-Mode, SafeGraph и Cuebiq — известные компании, занимающиеся данными о местоположении, которые предоставляют данные и идеи, полученные из этих данных, другим игрокам отрасли, а также клиентам, таким как хедж-фонды или фирмы, занимающиеся целевой рекламой.
Представитель Cuebiq Билл Дадди сообщил в электронном письме, что компания не продает необработанные данные о местоположении, а предоставляет доступ к агрегированному набору данных через свой инструмент Workbench клиентам, включая Центры по контролю и профилактике заболеваний.
Компания Cuebiq, которая получает необработанные данные о местоположении от Life360, публично сообщила о своем партнерстве с CDC для отслеживания «тенденций мобильности», связанных с пандемией COVID-19.
«CDC экспортирует только сводные, безопасные для конфиденциальности аналитические данные для исследовательских целей, которые полностью анонимизируют любые данные отдельных пользователей», — сказал Дадди. «Cuebiq не продает данные правоохранительным органам и не предоставляет необработанные данные государственным партнерам (в отличие от других, таких как X-Mode и SafeGraph)».
X-Mode продал данные о местоположении США.Согласно публичным записям, Министерство обороны США и SafeGraph продали данные о местоположении CDC.
X-Mode и SafeGraph не ответили на запросы о комментариях.
Генеральный директор Life360 заявил, что компания внедрила политику, запрещающую продажу или маркетинг данных Life360 любым государственным учреждениям для использования в правоохранительных целях в 2020 году, хотя компания продает данные как минимум с 2016 года.
«С философской точки зрения мы не считаем уместным, чтобы государственные органы пытались получить данные на коммерческом рынке, чтобы обойти право человека на надлежащую правовую процедуру», — сказал Халлс.
Семьям, вероятно, не понравится слоган «Вы можете следить за тем, где находятся ваши дети, как и любой, кто покупает эту информацию»,
Джастин Шерман, научный сотрудник лаборатории технической политики Дьюка По его словам, клиенты Life360 обмениваются данными. Халлс сказал, что компания поддерживает «открытый и постоянный диалог» со своими клиентами, чтобы убедиться, что они соблюдают политику, хотя он признал, что контролировать деятельность партнеров было непросто.Life360 мелким шрифтом сообщает в своей политике конфиденциальности, что продает данные, полученные от пользователей приложений, но Джастин Шерман, научный сотрудник по киберполитике в лаборатории технической политики Duke, сказал, что люди, вероятно, не знают, как далеко могут распространяться их данные.
Политика конфиденциальности компании отмечает, что Life360 «может также делиться вашей информацией с третьими лицами в форме, которая не идентифицирует вас напрямую. Эти третьи стороны могут использовать деидентифицированную информацию для любых целей.
«Вероятно, семьям не понравится лозунг «Вы можете следить за тем, где находятся ваши дети, как и любой, кто покупает эту информацию», — сказал Шерман.
Два бывших сотрудника Life360 также сообщили The Markup, что компания, хотя и заявляет, что анонимизирует продаваемые данные, не принимает необходимых мер предосторожности, чтобы гарантировать, что история местоположений не может быть отслежена до отдельных лиц. Они сказали, что, хотя компания удалила наиболее очевидную идентифицирующую информацию о пользователе, она не предприняла усилий для «размытия», «хеширования», агрегирования или снижения точности данных о местоположении для сохранения конфиденциальности.
Hulls заявил, что все контракты Life360 запрещают его клиентам повторно идентифицировать отдельных пользователей, наряду с другими методами защиты конфиденциальности и безопасности.
«Некоторые из наших партнеров по обработке данных получают хешированные данные, а некоторые не зависят от того, как эти данные будут использоваться», — сказал основатель Life360.
Между тем, продажа данных о местоположении становится все более важной для здоровья компании, поскольку она изо всех сил пытается достичь прибыльности. В 2016 году компания заработала 693 000 долларов на продаже собранных ею данных. В 2020 году компания заработала 16 миллионов долларов — почти 20 процентов ее выручки за тот год — от продажи данных о местоположении, а также еще 6 миллионов долларов от партнерства с Arity.
Несмотря на то, что в прошлом году компания по-прежнему сообщала об убытках в размере 16,3 млн долларов, компания расширяет свой бизнес, включив в него другие продукты «цифровой безопасности», внедряя оповещения об утечке данных, кредитный мониторинг и функции защиты от кражи личных данных. Компания Life360, публично торгуемая на Австралийской фондовой бирже и планирующая стать публичной в США, также приобрела компании, которые расширяют возможности отслеживания и, возможно, сбора данных. В 2019 году компания приобрела ZenScreen, семейное приложение для мониторинга экранного времени.А в апреле она приобрела компанию Jiobit, производящую носимые устройства для определения местоположения, предназначенную для отслеживания детей младшего возраста, домашних животных и пожилых людей, за 37 миллионов долларов. Халлс сказал, что Life360 не планирует продавать данные с устройств Jiobit или свои службы цифровой безопасности.
22 ноября Life360 также объявила о планах купить Tile, производителя устройств слежения, которое помогает находить потерянные вещи.
«Я уверен, что есть много семей, которые действительно находят настоящее утешение в подобном приложении, и это действительно так», — сказал Шерман.«Это не означает, что эти данные не могут причинить вред другим людям. Это также не означает, что семья не может быть повреждена данными способами, о которых они не знают, например, что данные о местоположении используются для таргетированной рекламы [или] используются страховыми компаниями, чтобы выяснить, где они находятся. путешествуют и повышают их ставки».
Hulls заявил, что Life360 не передает личную информацию пользователей страховщикам таким образом, чтобы это могло повлиять на страховые тарифы.
ПриложениеLife360 позволяет пользователю видеть точное местонахождение друзей или членов семьи в режиме реального времени, включая скорость, с которой они едут, и уровень заряда батареи на их устройствах.
Приложение Life360, позиционируемое как приложение для обеспечения безопасности, популярно среди родителей, которые хотят отслеживать и контролировать своих детей на расстоянии.
Но функции Life360, основанные на местоположении, также являются источником точек данных для растущей многомиллиардной индустрии, которая торгует данными о местоположении, собранными с мобильных телефонов.Рекламодатели, государственные учреждения и инвесторы готовы тратить сотни тысяч долларов на данные о местоположении и информацию, которую можно из них извлечь.
Хотя дети могут использовать приложение (с согласия родителей), политика Life360 гласит, что компания не продает данные пользователей младше 13 лет. Правило защиты конфиденциальности детей в Интернете (более известное как «COPPA») устанавливает ограничения на используемые цифровые услуги. детьми младше 13 лет, и у Life360 есть методы обнаружения, такие как требование сканирования удостоверения личности родителя для несовершеннолетних пользователей.
Маркетологи используют данные о местоположении, чтобы нацеливать рекламу на людей, находящихся рядом с предприятиями, а инвесторы покупают данные, чтобы определять популярность на основе посещаемости. Правительственные агентства купили данные о местоположении, чтобы отслеживать схемы передвижения и, в одном случае, для поддержки «требований миссии сил специальных операций за границей».
«Похоже, компания указывает на пару случаев, когда они, конечно, кому-то помогли, они смогли сделать что-то хорошее», — сказал Шерман. «Но тогда они не будут говорить обо всех других случаях, когда покупка и продажа этих данных потенциально очень вредна».
В июле высокопоставленный католический священник подал в отставку после того, как католическое новостное агентство разоблачило его, используя данные о местоположении из приложения для гей-знакомств Grindr, связанного с его устройством. Данные были получены неизвестным продавцом, и в отчете утверждалось, что священник часто посещал гей-бары.Нет никаких указаний на то, что Life360 был причастен к этому инциденту.
Grindr, как и другие приложения, передающие данные в эту отрасль, должен запрашивать разрешения на определение местоположения, когда пользователь впервые открывает приложение.
«Нам неизвестно ни об одном случае, когда наши данные были отслежены до отдельных лиц через наших партнеров по данным», — сказал Халлс. «Кроме того, наши контракты содержат формулировку, прямо запрещающую любую повторную идентификацию, и мы будем активно принимать меры против любого нарушения этого условия.
В случае с Life360, из-за того, как работает приложение, оно запрашивает самые широкие права доступа к местоположению, возможные для функциональных целей.
В нижней части экрана разрешений мелким шрифтом появляется заявление об отказе от ответственности: «Данные о вашем местоположении могут быть переданы Партнерам в целях обнаружения сбоев, исследований, аналитики, атрибуции и индивидуальной рекламы.«Пользователи могут отключить продажу данных о своем местоположении в настройках конфиденциальности, хотя этот параметр не раскрывается в подсказке или ее части.
Халлс из Life360 заявил, что миллионы его пользователей использовали эту функцию, чтобы отказаться от продажи своих данных.
Для тех, кто не отказался, их данные Life360 могут быть переданы партнерам компании в течение 20 минут после записи, сказал бывший сотрудник Life360.
Халлс сказал, что это описание является «точно направленным», заявив, что оно применимо только к определенным партнерам и вариантам использования.
«Например, для некоторых вариантов использования, таких как зондирование дорожного движения, которое используется для оценки времени в пути в автомобильных навигационных системах и приложениях GPS, требуются очень свежие данные», — сказал он.
Исследователи конфиденциальности и операторы магазинов приложений часто ищут в приложениях код брокеров данных на предмет признаков того, что приложение отправляет данные третьим лицам. Но Life360 собирает свои данные непосредственно из приложения и предоставляет их брокерам данных через свои собственные серверы.
Магазины приложений Apple и Google не могут обнаружить эту передачу данных о местоположении третьей стороне.«Имеет смысл отправлять эти данные напрямую со стороны сервера от поставщика приложения, чтобы их никто никогда не мог отследить или просмотреть», — сказал Вольфи Кристл, исследователь, занимающийся цифровым отслеживанием.
Халлс сказал, что метод предоставления данных Life360 через собственные серверы не был преднамеренной попыткой избежать обнаружения исследователями и магазинами приложений.
«Это совершенно не связано. У нас есть собственная запатентованная сенсорная технология, которую мы начали разрабатывать в 2008 году, задолго до появления индустрии данных, и мы избегаем использования SDK, которые могут отрицательно сказаться на батарее или иным образом взаимодействовать с нашей собственной сенсорной технологией», — сказал он.
Google не прокомментировал, почему Life360 смогла продавать данные таким образом, несмотря на свою политику против продажи данных о местоположении. Представитель Apple Адам Дема ответил ссылкой на политику конфиденциальности Life360, но не прокомментировал продажу данных компанией таким компаниям, как SafeGraph и X-Mode.
Спросите разметку
Когда анонимность на самом деле не анонимна?
Анонимизации данных недостаточно для обеспечения конфиденциальности
Hulls заявил, что Life360 деидентифицирует продаваемые данные, которые могут включать в себя мобильный рекламный идентификатор устройства, IP-адрес, а также координаты широты и долготы, собранные приложением Life360.
Hulls пояснил, что «деидентификация» включает удаление имен пользователей, адресов электронной почты, номеров телефонов и других типов идентифицируемой информации о пользователе до того, как данные будут переданы клиентам Life360. Продаваемые данные по-прежнему включают мобильный рекламный идентификатор устройства, а также координаты широты и долготы.
Даже без имен и номеров телефонов исследователи неоднократно демонстрировали, как «анонимные» данные о местоположении можно легко связать с людьми, от которых они поступили.
А эксперты по конфиденциальности отмечают, что мобильные рекламные идентификаторы более ценны, чем такие идентификаторы, как имена.
«Этот код можно использовать для отслеживания и отслеживания вас во многих жизненных ситуациях», — сказал Кристл.
Индустрия данных о местоположении работает в основном вне поля зрения общественности и практически без надзора или регулирования. Некоторые из партнеров Life360 в прошлом сталкивались со спорами по поводу того, как они обрабатывают данные и конфиденциальность.
Запущенный в 2013 году как Drunk Mode, новое приложение, которое «предотвращает звонки пользователей в состоянии алкогольного опьянения», X-Mode, как сообщается, был запрещен в крупных магазинах приложений после того, как Vice’s Motherboard сообщила, что компания продавала данные о местоположении из мусульманских молитвенных приложений, таких как Muslim Pro, в У.S. правительственные подрядчики, связанные с национальной безопасностью, вызывают обеспокоенность по поводу неконституционного государственного надзора.
Общедоступные записи показывают, что X-Mode получила не менее 423 000 долларов от ВВС США и Разведывательного управления Министерства обороны США за данные о местоположении в период с 2019 по 2020 год.
В августе компания X-Mode была куплена компанией Digital Envoy, занимающейся разведкой интеллектуальной собственности, и переименована в Outlogic.
В ответ на негативную реакцию X-Mode на продажу данных о местоположении оборонным подрядчикам его новые владельцы заявили, что компания прекратит продажу данных о местоположении в США таким компаниям.
«Мы не можем комментировать методы другой компании или то, что эта компания делает с данными, которые она получает из других источников», — сказал Халлс. «Однако Life360 тесно сотрудничает с X-Mode, чтобы гарантировать, что X-Mode и все его клиенты данных не продают данные, исходящие от Life360, правоохранительным органам или любому государственному учреждению для использования в правоохранительных целях.
SafeGraph — одна из крупнейших фирм в сфере данных о местоположении, среди ее инвесторов — венчурный капиталист Питер Тиль; принц Турки аль-Фейсал аль-Сауд, бывший глава саудовской разведки; и главный бизнес-директор Life360 Итамар Новик.
Компания специализируется на данных, которые связывают достопримечательности с необработанными координатами, добавляя слой смысла к необработанным данным о местоположении, которые получает компания. SafeGraph был указан не только как клиент данных Life360, но и как крупный партнер в электронном письме от руководителя Life360, которое было просмотрено The Markup.
В апреле, как впервые сообщило Motherboard, компания SafeGraph получила контракт на 420 000 долларов США на продажу данных Центрам по контролю за заболеваниями, описанный как «Сбор данных и отчетность». The Washington Post также сообщила, что SafeGraph поделился миллиардами записей о местоположении телефонов с Министерством здравоохранения округа Колумбия через свою дочернюю компанию Veraset.
Компания открыто продает данные о местоположении на рынке данных Amazon, включая годовую подписку на 240 000 долларов США на данные о людях в США.S. Veraset хвастается продажей данных о местоположении для таких целей, как маркетинг, недвижимость, инвестиции и городское планирование.
Сенатор Рон Уайден отметил SafeGraph как «брокера данных, вызывающего обеспокоенность» Google, сообщил в электронном письме директор по связям с общественностью Уайдена Кит Чу. По словам Чу, демократ из Орегона неоднократно пытался поговорить с SafeGraph, чтобы узнать больше о том, как компания получает, продает и делится данными о местоположении американцев, но компания так и не ответила.
Согласно публичным записям,Cuebiq также работал с Центрами по контролю за заболеваниями, заключив в июне контракт на 208 000 долларов США за агрегированные данные о местоположении.
CDC не ответил на запросы о комментариях.
В начале пандемии коронавируса Cuebiq стал основным источником данных о местоположении для новостных агентств, желающих сообщать о передвижениях людей после того, как города и штаты издали приказы оставаться дома. Журналы, в том числе The New York Times и NBC News, получили данные о местоположении от Cuebiq для анализа.
Было высказано предположение, что брокеры данных о местоположении, такие как Cuebiq, используют пандемию для улучшения своей общественной репутации, представляя себя инструментами общественного здравоохранения, а не механизмами наблюдения.
Дадди изCuebiq сказал, что данные компании помогли в ликвидации последствий стихийных бедствий и кризисов в области общественного здравоохранения.
Life360 позиционирует себя как «ведущий бренд цифровой безопасности для семей». Но эксперты говорят, что семьи, которые его используют, не обязательно думают о своей цифровой безопасности.
«Приложение, которое утверждает, что является службой семейной безопасности, продающее точные данные о местоположении нескольким другим компаниям, — это настоящая катастрофа», — сказал Кристл. «Была бы проблема, если бы это было любое другое приложение, и еще большая проблема, когда это приложение претендует на роль службы семейной безопасности.
Приложение, которое утверждает, что является службой безопасности семьи, продающее точные данные о местоположении нескольким другим компаниям, это полная катастрофа.
Вольфи Кристл, исследовательВ прошлом Life360 сталкивалась с проблемами конфиденциальности.
В ответHulls добавил функцию «пузырей», которая показывает родителям более расплывчатое местоположение их ребенка (но все же позволяет родителям видеть точное местоположение с помощью дополнительного шага). Он также нанял и заплатил подросткам, чтобы они распространяли приложение на TikTok, что, по данным компании, привело к «вирусному всплеску загрузок».
Эти подростки, однако, вероятно, не знали, что их родители были далеко не единственными, кто имел доступ к данным об их передвижениях.
Самира Мади, 18-летняя студентка из Техаса, начала пользоваться Life360, когда ей было 15 лет.
Узнав о том, кому Life360 продавала данные и в каких масштабах они продавались, Мади почувствовал, что компания перешла черту.
«Я понятия не имел, что это будет распространяться таким образом», — написал Мади в электронном письме. «Это беспокоит меня, потому что я не хотел бы, чтобы данные о моем местоположении могли быть проданы людям с недобрыми намерениями».
Брокерские наценки | ООО «Интерактив Брокерс»
Абсолютная надбавка
Брокеры могут взимать абсолютную надбавку за сделку.Абсолютная надбавка — это определенная сумма, добавляемая к комиссии Interactive Brokers. Брокеры вводят абсолютную надбавку в валюте или обмене класса активов. На странице Client Fees в Account Management единицы, перечисленные в столбце Валюта/обмен/продукт Единица , указывают, применяется ли абсолютная надбавка к акциям, контрактам или % от номинальной стоимости.
Пример
Например, брокер вводит 1 в качестве абсолютной наценки для опционов на акции и индексы в долларах США.Позже исполняется один смарт-опционный контракт IBKR. С клиента будет взиматься плата в размере 2 долларов США (1 доллар комиссии IBKR + 1 доллар абсолютной надбавки).
Многоуровневая абсолютная сумма
Брокеры могут взимать Абсолютную сумму, из которой вычитается комиссия Interactive Brokers. Вы можете установить до трех уровней абсолютной суммы на основе разрывов объема. Брокеры должны следить за комиссиями своих клиентов, поскольку Interactive Brokers может взимать больше, чем клиентская комиссия.
Чтобы установить Абсолютную сумму, введите от одной до трех комиссий (Комиссия № 1, Комиссия № 2, Комиссия № 3) и введите разрывы объема (Том № 1, Том № 2) для каждой сделки для Клиентские сборы на странице «Управление счетом».
Пример
Например, брокер хочет взимать 0.0,05 долларов США за акции до 500, 0,03 долларов США за акции до 1000 и 0,002 долларов США за акции свыше 1000, а также сбор за билет в размере 1 доллар США.
Абсолютные многоуровневые комиссии клиента являются взаимоисключающими многоуровневыми комиссиями Interactive Brokers. Их можно комбинировать с многоуровневыми комиссиями IBKR, или можно использовать одну абсолютную ставку клиента с многоуровневыми комиссиями IBKR.
Разметка и уценка: расчеты и примеры — видео и расшифровка урока
Наценка
Чтобы рассчитать свою наценку, Шейлон должна принять во внимание такие вещи, как стоимость ее времени, потраченного на разработку рубашки, стоимость изготовления рубашки и стоимость содержания магазина в рабочем состоянии.
Скажем, например, после рассмотрения всех факторов, которые мы упомянули, что общая стоимость изготовления каждой рубашки для Шалон составляет 10 долларов. Конечно, Шейлон хочет получить прибыль от продажи каждой рубашки, поэтому она увеличивает цену своей рубашки до 30 долларов. Насколько это наценка? Давайте посчитаем. 30 долларов на 20 долларов больше, чем 10 долларов. Итак, разделив 20 долларов на 10 долларов, мы получим 20/10 = 2.Преобразовав это в проценты, мы увидим, что у Шалона наценка 200%.
Шейлон хочет убедиться, что она конкурентоспособна с другими производителями футболок в городе, поэтому она проводит собственное расследование. Она посещает другой магазин и обнаруживает, что в этом магазине наценка составляет 100%. Если себестоимость продукта составляет 10 долларов, по какой цене этот магазин продает рубашки?
Мы можем рассчитать это, умножив 10 долларов на 100%, чтобы узнать, насколько увеличилась наша сумма.
Хм, Шэлон думает, что ее цены могут быть немного завышены для покупателей по соседству, основываясь на ее расследованиях.
Уценка
Теперь она думает, на сколько снизить цены. Ее стартовая цена составляет 30 долларов. Если она хочет снизить цены до 20 долларов, какая скидка ей нужна? Чтобы рассчитать это, мы сначала посмотрим, какая у нас разница.У нас разница 30$ — 20$ = 10$. Таким образом, уценка составляет 10/30 долларов США = 0,3333 или примерно 33%.
Шалон может сделать это двумя способами. Она может либо предложить купон на скидку 33% всем своим клиентам, либо снизить цены, не предлагая купоны. Даже если она продает рубашку за 20 долларов, она все равно получает прибыль.
Что, если Шейлон захочет рассчитать цену рубашки на основе процентной скидки? Что, если она захочет снизить цены всего на 20%? Сколько тогда будут стоить ее рубашки? Посмотрим.
Цены на специальное мероприятие
Шалон только что сообщили, что через несколько недель состоится особое мероприятие, торжественное открытие скейт-парка. Чтобы помочь с празднованием, Шалон создал специальную лимитированную серию футболок специально для этого события. Ее стоимость производства каждой рубашки составляет 12 долларов.У нее наценка 150%, и она предлагает купоны со скидкой 40%. По какой цене продается каждая рубашка?
При наценке 150% дополнительная стоимость рубашки составляет 12 долл. США * 1,5 = 18 долл. США. Таким образом, стоимость рубашки после наценки составляет 12 долларов + 18 долларов = 30 долларов. Уценка в размере 40% снижает цену рубашки на 30 * 0,4 = 12 долларов. Таким образом, окончательная стоимость рубашки составляет 30 — 12 = 18 долларов США.
Резюме урока
Давайте повторим, что мы узнали:
Надбавка — насколько увеличить цены и уценка — насколько снизить цены.Чтобы рассчитать наценку, нам нужно выяснить, насколько наши цены превышают затраты на производство товара. Затем мы находим процент наценки, разделив разницу на стоимость их производства. Если нам дают процент наценки, мы умножаем процент на стоимость производства товара. Затем мы добавляем это увеличение к стоимости производства предмета, чтобы найти окончательную стоимость.
Для расчета уценки находим разницу между начальной ценой и сниженной ценой, затем находим процент путем деления разницы на начальную цену.Если нам дан процент уценки, мы умножаем процент на первоначальную цену, чтобы узнать, какое снижение мы получаем, затем мы вычитаем эту разницу из исходной цены, чтобы найти уцененную цену.
Результаты обучения
Этот видеоурок призван подготовить вас к следующим действиям:
- Понимание концепций наценок и уценок в продажах
- Расчет наценки, суммы уценки или процента
Использовать разметку—Полевые карты ArcGIS | Документация
Используйте разметку для создания зарисовок и заметок на карте.
Внимание:
Разметка не связана с картой, которую вы просматривали при ее создании.
При удалении приложения удаляются все слои разметки. Перед удалением убедитесь, что вы предоставили общий доступ ко всем слоям разметки, которые хотите сохранить, например, отправив их себе по электронной почте.
Добавить разметку
Используйте ArcGIS Field Maps для создания разметки, включая маркеры и стрелки, линии и формы. Добавляйте примечания и метки в разметку для передачи дополнительной информации. При просмотре карты коснитесь «Переполнение» , затем коснитесь «Разметка», чтобы добавить или изменить слой разметки.
Панель инструментов меняется, и вы видите, что появляются инструменты разметки.
Совет:
Вы можете увеличивать и уменьшать масштаб и вращать карту, а также перемещать карту двумя пальцами при использовании инструментов разметки.
- Слои разметки — управляйте слоями разметки.
- Готово — прекратить изменение разметки.
- Очистить все — удаление всех пометок на слое пометок.
- Добавить маркер — поместите маркер в центр экстента карты.
- Общий доступ — общий доступ к вашему слою разметки.
Попробуйте разметку
Чтобы попробовать разметку и научиться создавать разные типы, выполните следующие действия:
- Коснитесь «Переполнение» , затем коснитесь «Разметка», чтобы начать редактирование разметки.
Если вы использовали разметку раньше и у вас есть несколько слоев разметки, коснитесь «Разметка», чтобы выбрать, с каким слоем вы хотите работать.
- Добавить маркер на карту.
- В определенном месте — долгое нажатие на карте.
- В центре экстента карты — коснитесь «Добавить маркер» .
На панели отображаются сведения о маркере и инструменты для работы с выбранной разметкой. Вы можете удалить маркер, добавить стрелку или изменить цвет маркера. Проведите вверх по панели, чтобы предоставить метку или примечания.
- Нажмите и удерживайте маркер и перетащите его, чтобы переместить в новое место на карте.
Совет:
При нажатии на разметку на карте отображаются ее детали. В деталях вы можете просмотреть и отредактировать метку и примечания.
- Предоставьте этикетку для маркера.
Метка — это фрагмент короткого текста, идентифицирующего маркер, в сочетании с цветом маркера.
Например, если вы используете разметку для планирования строительной площадки, вы можете использовать маркеры для обозначения вашего оборудования.Если у вас есть вспомогательные прицепы и краны, используйте метки «Прицеп» и «Кран» для каждого маркера, который вы размещаете на карте, в идеале с разными цветами, чтобы увидеть их размещение, не просматривая детали каждого маркера.
Метки не предназначены для текста, уникального для каждого маркера — используйте для этого примечания. Вместо этого каждая добавленная вами метка становится выбором в списке доступных меток со следующим добавляемым вами маркером. Если вы выберете существующую метку, к выбранной вами разметке будут применены и метка, и связанный с ней цвет.
Символ маркера на карте отображает первую букву метки. Если вы предоставляете примечания, на символе маркера отображаются три точки.
- Коснитесь стрелки на панели, чтобы добавить стрелку к маркеру.
Вы можете долго нажимать на стрелку и перетаскивать ее, чтобы изменить ее длину и направление. Если вы перемещаете маркер, положение кончика стрелки остается фиксированным, а длина и направление стрелки изменяются.
- Нарисуйте линию или фигуру на карте пальцем.
Как и в случае с маркером, вы можете добавлять метки и примечания к линиям и фигурам.
Если вы нарисовали линию, инструменты на панели сведений позволяют удалить линию, добавить к ее концу стрелку или изменить ее цвет.
Если вы нарисовали фигуру, инструменты на панели сведений позволяют удалить фигуру, заполнить ее или изменить цвет. Цвет заливки такой же, как у контура фигуры, но он имеет некоторую прозрачность.
Совет:
Если вы нарисовали линию, которая была почти прямой, или фигуру, которая была почти прямоугольником или кругом, рядом с фигурой появится всплывающая подсказка, показывающая фигуру, обнаруженную приложением, которую вы, возможно, пытаетесь нарисовать.
- Нажмите и удерживайте линию или фигуру и перетащите ее, чтобы переместить на карту.
- Нажмите «Готово», чтобы прекратить разметку карты после добавления маркеров, линий и фигур.
Отображается карта вместе со стандартной панелью инструментов. Теперь вы можете перемещаться одним пальцем, отбрасывать булавки и просматривать сведения о булавках и функциях.
Совет:
Если вы больше не видите разметку, убедитесь, что ваш слой разметки отображается на карте.Как и для любого слоя, его видимость можно включать и выключать в списке Слои.
Управление слоями разметки
Чтобы упорядочить свои наброски и заметки, будь то для ваших собственных целей или для обмена ими с другой аудиторией, вы можете создать несколько слоев разметки в ArcGIS Field Maps. Один с именем Markup создается при установке приложения.
Слои разметки можно создавать, переименовывать и удалять в разделе Слои разметки, который доступен при работе с разметкой. Используйте «Добавить», чтобы создать новый слой разметки, или «Переполнение», чтобы переименовать или удалить существующий слой.
Совет:
Слой разметки можно удалить только в том случае, если остался хотя бы один другой слой разметки.
Поскольку разметка хранится на вашем устройстве, она удаляется при удалении приложения.
Если вы не хотите видеть свою разметку, но не хотите, чтобы она удалялась с вашего устройства, отключите ее видимость в списке Слои на карте.
Совместное использование разметки
Совместное использование разметки делает его полезным инструментом для общения с другими.
При совместном использовании разметки вы предоставляете общий доступ к копии.Изменения, внесенные в оригинал, не отражаются в общей разметке, а изменения, внесенные в общую разметку, не влияют на исходный слой.
Разметка доступна, пока вы редактируете ее слой. Если вы еще не редактируете разметку, которой хотите поделиться, коснитесь «Переполнение» , затем коснитесь «Разметка», чтобы начать редактирование.
Публикация разметки в виде изображения. Вы можете создать снимок экрана с разметкой и поделиться ею, как любым изображением. На снимке экрана учитывается текущий экстент карты.
Чтобы создать снимок экрана и поделиться своей разметкой в виде изображения, нажмите «Поделиться» , коснитесь «Поделиться снимком экрана» и выберите, как вы хотите поделиться изображением.
Поделитесь необработанной разметкой непосредственно с другим устройством или пользователем — вы можете поделиться разметкой, предоставив слой получателю. Он включает в себя всю разметку слоя, который вы редактируете в данный момент, включая геометрию, символы, метки и любые примечания для каждого объекта в вашей разметке, содержащиеся в файле .файл разметки, который можно импортировать в Field Maps.
Чтобы поделиться разметкой с другим устройством или пользователем, коснитесь «Поделиться» , коснитесь «Поделиться разметкой» и выберите, как вы хотите поделиться разметкой. Например, вы можете поделиться им по электронной почте, в сообщении или через AirDrop.
Получатель вашей разметки может использовать Field Maps для просмотра, добавления и редактирования разметки, поскольку она хранится на их устройстве. Таким образом, наценка может распределяться между мобильными работниками.
Информация о карте, которую вы просматриваете, когда делитесь разметкой, не включена.
Чтобы открыть разметку, у получателя должны быть установлены ArcGIS Field Maps.
Опубликовать как элемент пометки в вашей организации — если ваш тип пользователя — Creator или GIS Professional, вы можете опубликовать пометку как элемент в своей организации либо в ArcGIS Online, либо в ArcGIS Enterprise. Элемент разметки, созданный в вашей организации, содержит всю разметку слоя, который вы редактируете в данный момент, включая геометрию, символы, метки и любые примечания для каждого объекта в вашей разметке.
Коснитесь «Поделиться» , коснитесь «Поделиться разметкой» и коснитесь ArcGIS Online или ArcGIS Enterprise (доступный вариант зависит от вашей учетной записи). Укажите, с кем поделиться элементом разметки (если есть), и нажмите «Сохранить».
Элементы разметки совместно используются в вашей организации так же, как и любой другой элемент — см.
Информация о карте, которую вы просматриваете, когда делитесь разметкой, не включена.
При совместном использовании вашей разметки в вашей организации создается копия вашей разметки в элементе разметки, хранящемся в вашей организации. Будущие обновления разметки на вашем устройстве не отражаются в элементе разметки в вашей организации. Чтобы внести изменения в вашу организацию, вам нужно снова опубликовать слой, создав новый слой разметки в вашей организации.
ArcGIS Enterprise 10.5 и Portal for ArcGIS 10.3.1 и 10.4.1 имеют ограниченную поддержку разметки.
Использование разметки
Совместное использование вашей разметки позволяет другим использовать ее. Мобильные работники в полевых условиях и пользователи ArcGIS в офисе могут видеть то, что вы нашли, и действовать в соответствии с ними. То, как получатели могут использовать разметку, которой вы делитесь, зависит от того, как вы ею делитесь. Если вы поделитесь им непосредственно с другим мобильным работником в виде файла .markup, они смогут открыть и работать с разметкой в ArcGIS Field Maps.Если вы поделитесь им со своей организацией в качестве слоя разметки, те, с кем вы поделитесь им, смогут использовать его через вашу организацию как в поле, так и в офисе.
Использование разметки, опубликованной в виде файла .markup напрямую от другого пользователя или устройства, аналогично использованию созданной вами разметки. Вы можете открыть его в Field Maps и добавить разметку, управлять слоями разметки и делиться разметкой.
При использовании разметки, совместно используемой в качестве слоя разметки с вашей организацией, вы можете работать с разметкой вне Field Maps.
Совет:
Вы можете преобразовать разметку в KML в ArcGIS Pro.
Разметка используется как копия. Изменения, внесенные в оригинал, не отражаются в общей разметке, а изменения, внесенные в общую разметку, не влияют на исходный слой.
Ограничения
Ниже приведены ограничения и известные проблемы с использованием разметки:
- Редактирование разметки вне ArcGIS Field Maps (например, в ArcGIS Online) не поддерживается.
- ArcGIS Enterprise 10.5 и Portal for ArcGIS 10.3.1 и 10.4.1 имеют ограниченную поддержку разметки.
.
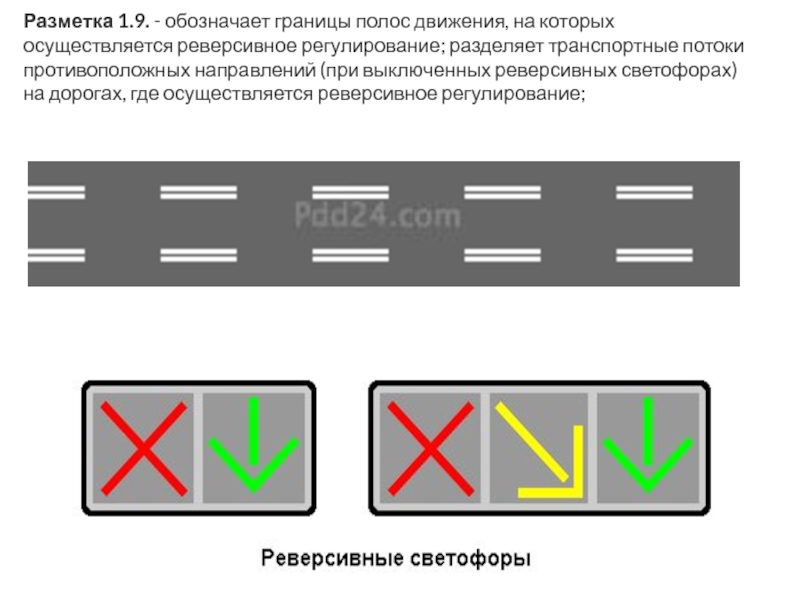
Он сказал, что Life360 следует «передовым отраслевым практикам» в отношении конфиденциальности и что только определенные клиенты, такие как Cuebiq, получают необработанные данные о местоположении. Бывший инженер X-Mode сказал, что компания также получила необработанные данные от Life360. Халлс добавил, что компания полагается на то, что ее клиенты будут запутывать эти данные в зависимости от их конкретных приложений.
Халлс сказал, что компания не планирует продавать данные с устройств Tile.
Приложение предлагает большую часть функций встроенных функций Apple для обмена данными о местоположении, но оно включает в себя функции аварийной безопасности, такие как кнопка SOS и обнаружение аварии автомобиля. Компания заявляет, что эти функции спасли жизни.
Life360 «раскрывает» информацию о детях младшего возраста третьим лицам «по мере необходимости для анализа и обнаружения данных о поведении за рулем, выполнения аналитики или иным образом, [sic] для поддержки функций и функций нашего Сервиса» в соответствии со своей политикой конфиденциальности, но не «для маркетинговых или рекламных целях».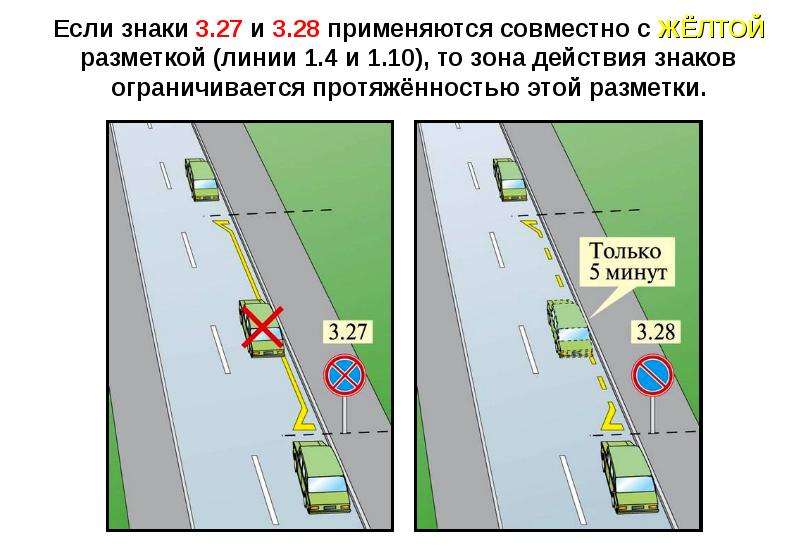
Многие приложения, использующие данные о местоположении, позволяют пользователям предоставлять доступ только во время их использования. Поскольку Life360 предназначен для отслеживания местонахождения в режиме реального времени, приложение постоянно запрашивает данные о местоположении и не работает, если это разрешение не включено.
«Таким образом, это гораздо лучший идентификатор, чем имя».
Компания также продавала данные об американцах в профилированных наборах, таких как люди, которые были водителями или могли делать покупки. в универмагах, согласно Motherboard.
В середине 2020 года подростки, недовольные вторжением в частную жизнь приложения, которое позволяло их родителям подробно отслеживать их передвижения, обратились к TikTok, чтобы побудить своих сверстников бомбить приложение негативными отзывами. В течение месяца приложение получило более миллиона отзывов с одной звездой, в результате чего средний рейтинг снизился с 4.от 6 до 2,7 звезд.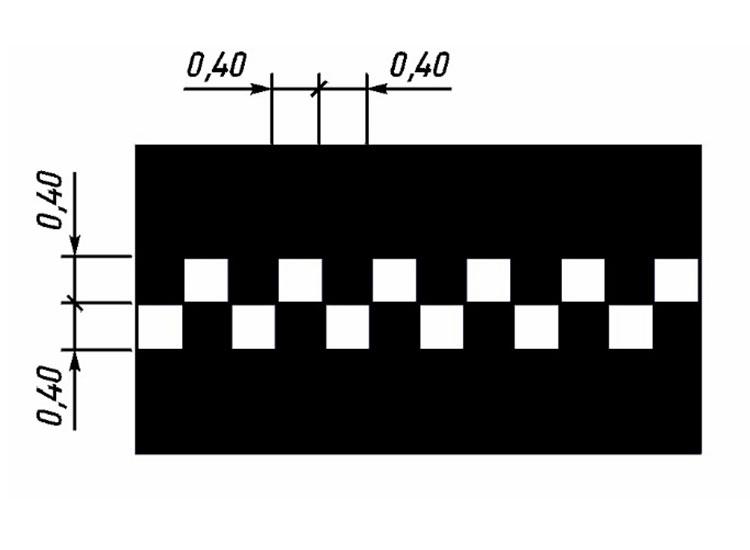
У нее не было проблем с тем, что компания предоставила данные о ее местоположении в маркетинговых и рекламных целях, которые компания с готовностью раскрыла.
Абсолютная сумма наценки может включать до трех знаков после запятой.
Единицы, перечисленные в столбце Единица валюты/обмена/продукта , указывают, применяется ли абсолютная надбавка к акциям, контрактам или процентам. Абсолютные суммы могут включать до трех знаков после запятой.
После того, как все эти расходы подсчитаны, ей нужно выяснить, сколько еще ей нужно добавить, чтобы она могла хорошо зарабатывать на своем бизнесе по производству футболок.
Мы умножаем ее начальную цену в 30 долларов на 20% или 0,2, чтобы узнать, насколько уменьшилась наша цена. Получаем 30$ * 0,2 = 6$. Таким образом, цена футболки с уценкой 20% будет составлять 30 — 6 = 24 доллара.
Шейлон устраивает эта цена, поэтому она начинает раздавать купоны на скидку 40% на мероприятие.
Разметка сохраняется в виде слоя на вашем устройстве. Вы можете использовать его с любой картой, и обновления, внесенные в карты, не повлияют на него. Вы можете использовать разметку для собственной информации, аналогично рисованию на бумажной карте, или поделиться ею для общения с другими, включая сотрудников в офисе и коллег на местах.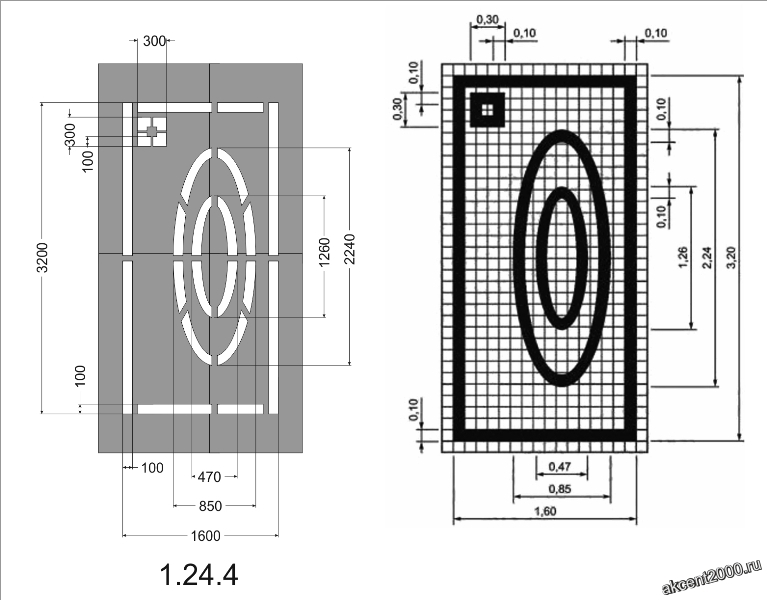
Поведение карты меняется для поддержки разметки. Поскольку жесты используются для поведения, зависящего от разметки, вы больше не можете перетаскивать булавки или просматривать сведения о булавках или функциях.Если вы уронили булавку, она очищается.
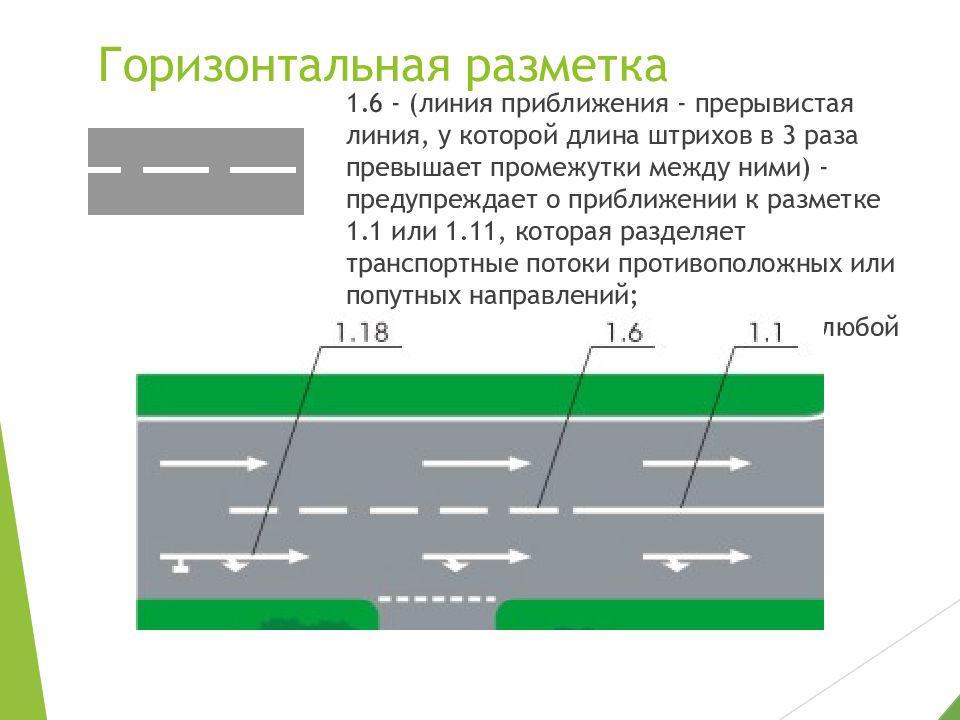
Нажатие на всплывающую подсказку превращает фигуру в прямую линию, идеальный круг или идеальный прямоугольник.
По умолчанию это слой, к которому вы добавляете разметку. Как и в случае любого другого слоя разметки, который вы создаете, вы можете переименовать этот слой. Field Maps требует, чтобы у вас был хотя бы один слой разметки.Однако если у вас есть несколько слоев разметки, вы можете удалить их.
Даже если он предназначен для вашего собственного использования, вы можете захотеть использовать его в другой части системы ArcGIS. Разметку можно опубликовать в виде изображения или необработанной разметки с помощью функции «Поделиться» во время редактирования разметки.
Например, вы можете поделиться им по электронной почте, в сообщении, AirDrop или на принтере.
Совместное использование элементов в ArcGIS Online или Совместное использование элементов в ArcGIS Enterprise. Как только элемент разметки станет частью вашей организации, вы сможете использовать его во всей системе ArcGIS. Таким образом, разметка может передаваться от мобильного работника к офисным работникам.Дополнительные сведения об использовании разметки, предоставленной вашей организации, см. в разделе Использование разметки.
Вы можете использовать его в ArcGIS Pro 2.0 или более поздней версии, ArcGIS Online и ArcGIS Enterprise. В ArcGIS Pro откройте панель Каталог, выберите категорию Портал, перейдите к элементу разметки в вашей организации и перетащите его на карту. В ArcGIS Online или ArcGIS Enterprise вы можете добавить разметку к новой карте, сохранить и использовать эту карту, как и любую другую карту.