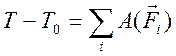Закон изменения угловой скорости – —
Вращательное движение тела. Закон вращательного движения :: SYL.ru
В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».
Основные понятия кинематики вращательного движения
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.
Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.
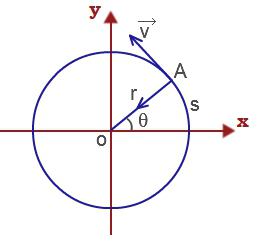
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.
За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:
φ = φ(t).
Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:
ΔS = Δφr.
Основные элементы кинематики равномерного вращательного движения
Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.
Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:
ω = dφ/dt.
Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле
ω = φ/t.
Согласно предварительной формуле размерность угловой скорости
[ω] = 1 рад/с.
Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то
ω = 2π/T,
поэтому период вращения определим следующим образом:
T = 2π/ω.
Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:
ν = 1/T.
Единицы измерения частоты: [ν]= 1/c = 1 c-1 = 1 Гц.
Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:
ω = 2πν.
Основные элементы кинематики неравномерного вращательного движения
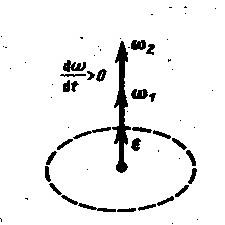
Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.
Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:
ε = dω/dt.
Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.
Если вращательное движение замедлено — dω/dt < 0, то векторы ε и ω противоположно направлены.
Замечание. Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).
Связь величин, характеризующих поступательное и вращательное движение
Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением
ΔS = Δφ r.
Тогда линейная скорость материальной точки, выполняющей вращательное движение
υ = ΔS/Δt = Δφr/Δt = ωr.
Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:
a = υ2/r = ω2r2/r.
Итак, в скалярном виде
a = ω2r.
Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение
a = ε r.
Момент импульса материальной точки
Векторное произведение радиуса-вектора траектории материальной точки массой mi на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.
Момент импульса материальной точки (Li) направлен перпендикулярно плоскости, проведенной через ri и υi, и образует с ними правую тройку векторов (то есть при движении с конца вектора riк υi правый винт покажет направление вектора Li).
В скалярной форме
L = miυirisin(υi,ri).
Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,
sin(υi,ri) = 1.
Так что момент импульса материальной точки для вращательного движения примет вид
L = miυiri.
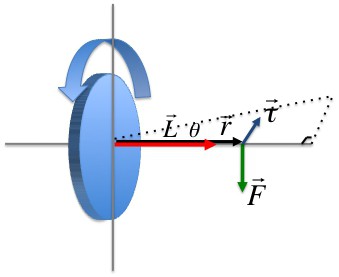
Момент силы, которая действует на i-ю материальную точку
Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.
В скалярной форме
Mi = riFisin(ri, Fi).
Считая, что risinα = li, Mi = liFi.
Величина li, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы Fi.
Динамика вращательного движения
Уравнение динамики вращательного движения записывается так:
M = dL/dt.
Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.
Момент импульса и момент инерции
Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой
Li = miυiri.
Если вместо линейной скорости подставить ее выражение через угловую:
υi = ωri,
то выражение для момента импульса примет вид
Li = miri2ω.
Величина Ii = miri2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:
Li = Iiω.
Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:
L = Iω.
Момент силы и момент инерции
Закон вращательного движения гласит:
M = dL/dt.
Известно, что представить момент импульса тела можно через момент инерции:
L = Iω.
Тогда
M = Idω/dt.
Учитывая, что угловое ускорение определяется выражением
ε = dω/dt,
получим формулу для момента силы, представленного через момент инерции:
M = Iε.
Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.
Теорема Штейнера. Закон сложения моментов инерции
Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I0 + ma2,
где I0 — начальный момент инерции тела; m — масса тела; a — расстояние между осями.
Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).
www.syl.ru
5. Вращательное движение. Угловая скорость и угловое ускорение.
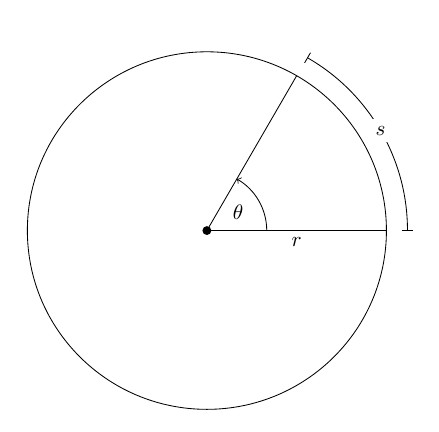
Рассмотрим движение материальной точки
по окружности радиуса  .
За время
.
За время ее положение изменится на угол
ее положение изменится на угол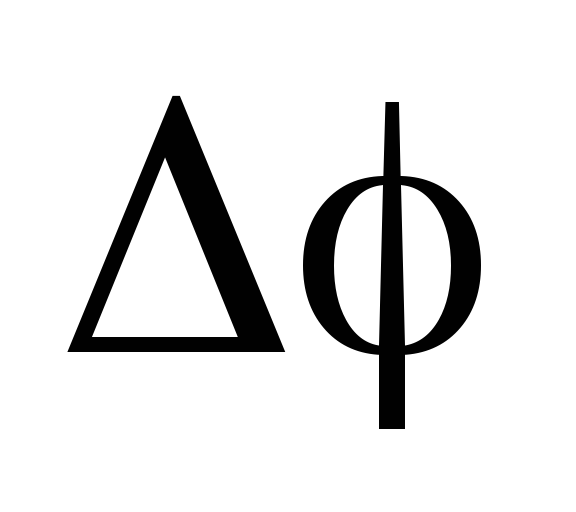 .
Углы поворота рассматриваются как
векторы. Модуль вектора
.
Углы поворота рассматриваются как
векторы. Модуль вектора равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, то есть подчиняется
правилу правого винта.
равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, то есть подчиняется
правилу правого винта.
Угловой скоростью называется векторная величина, равная первой производной угла поворота по времени
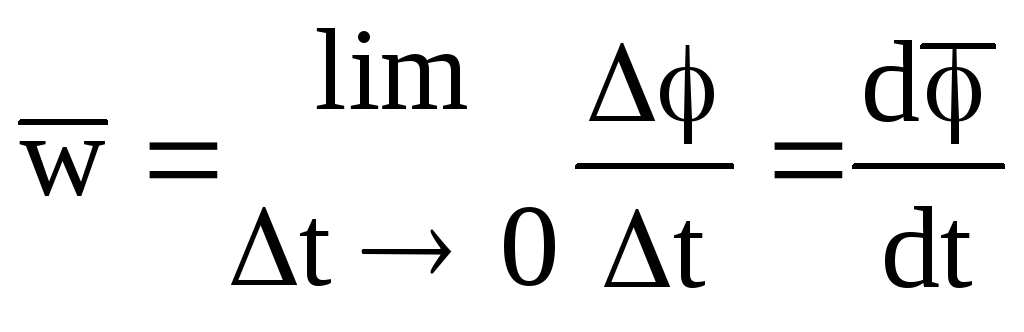 ,
,
| Она направлена по оси вращения по правилу правого винта. Ее размерность [w]= с-1., а единица – рад/сек. Линейная скорость точки равна
|
Рис.5. |
Число полных оборотов за единицу времени
называется частотой, 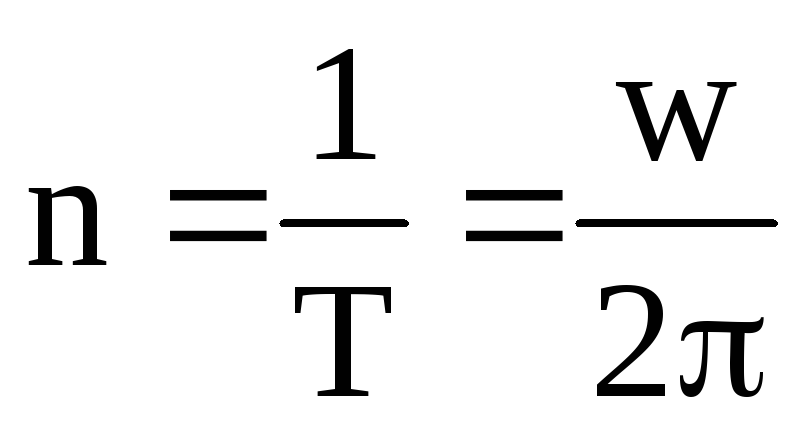
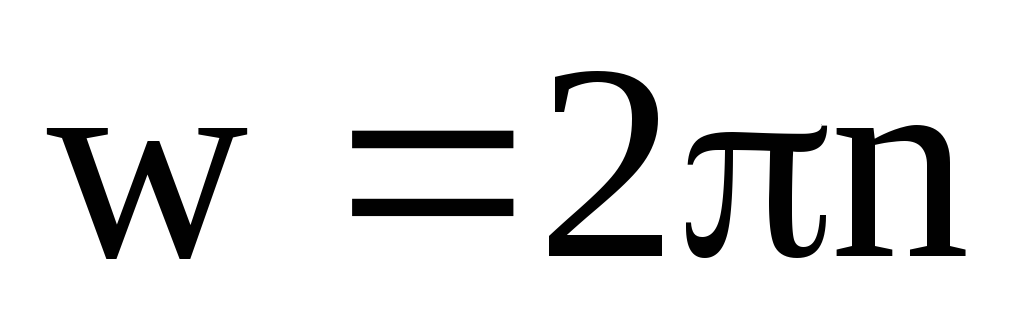 .
. Угловым ускорением называется первая
производная угловой скорости по времени, 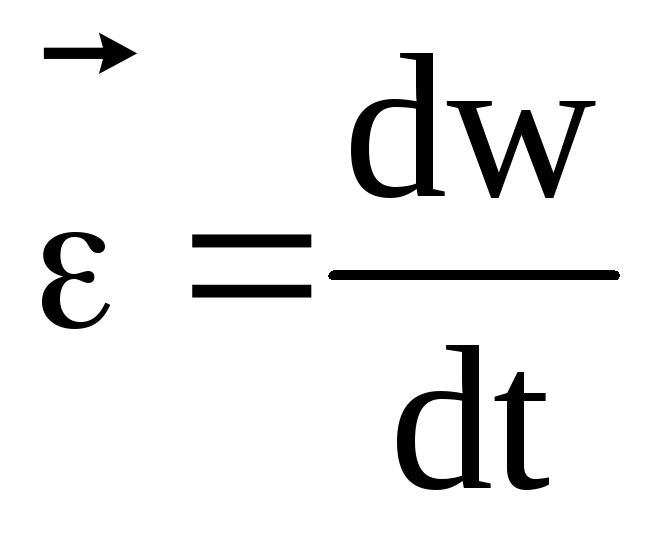 .
.
|
|
Рис.7. | Рис.8. |
При ускоренном движении  сонапрвлено с
сонапрвлено с
 .
. Тангенциальная составляющая ускорения
равна 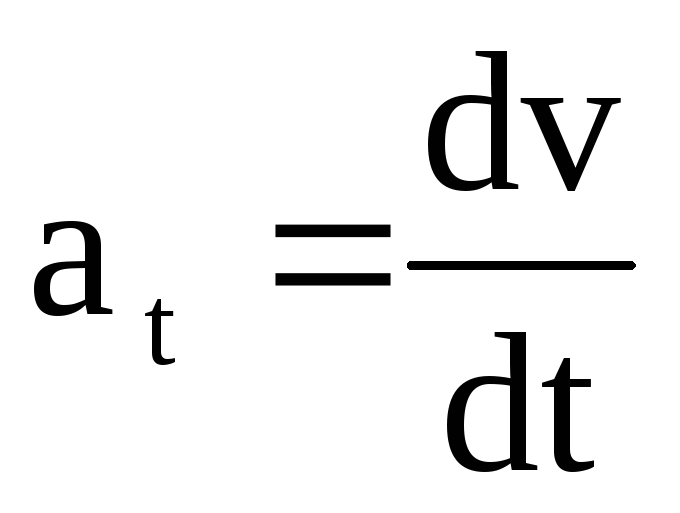 ,
а так как
,
а так как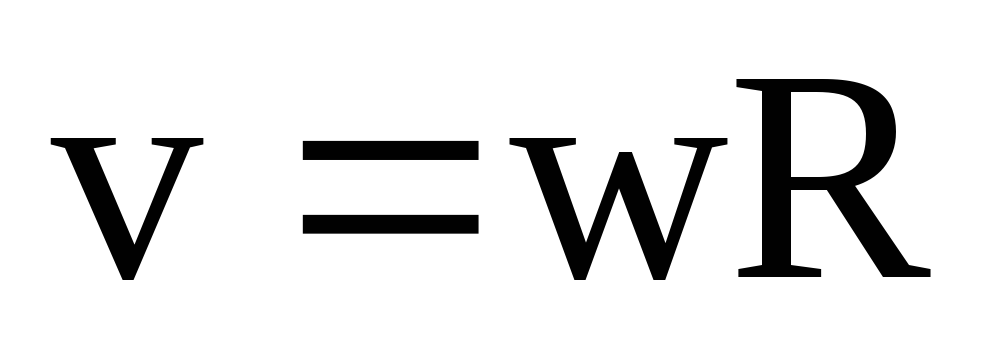 ,
то
,
то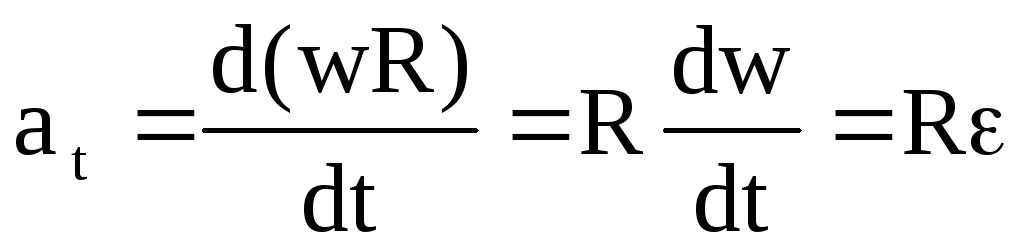 .
Для нормальной составляющей имеем
.
Для нормальной составляющей имеем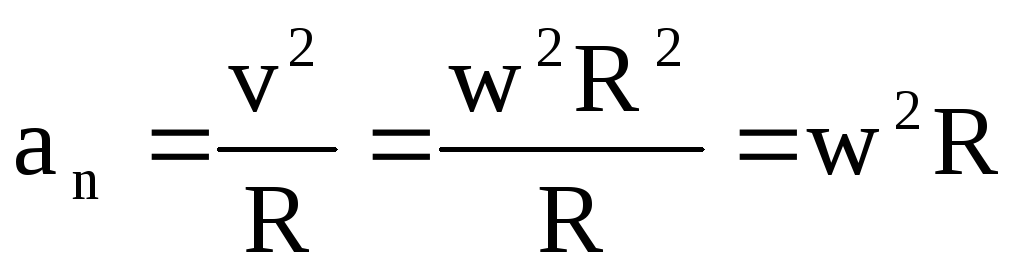 .
В случае равнопеременного движения по
окружности (
.
В случае равнопеременного движения по
окружности (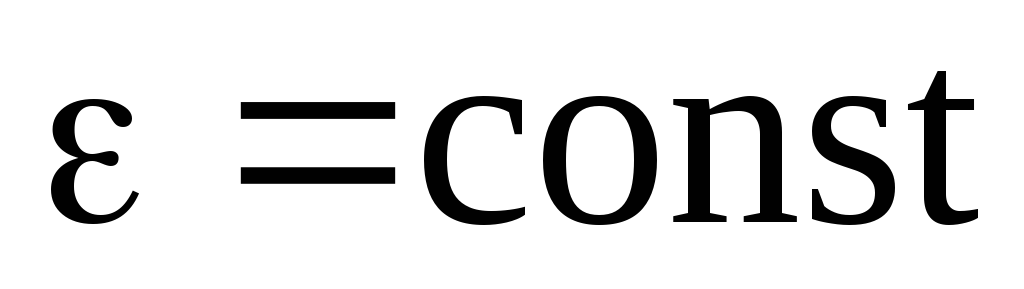 )
)
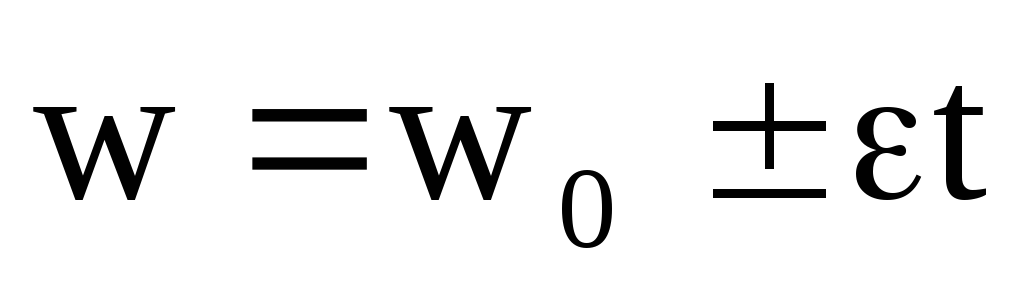 ,
,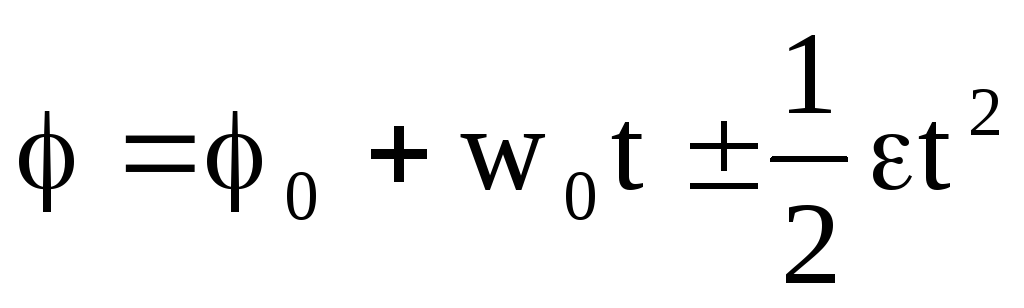
Связь между линейными и угловыми величинами:
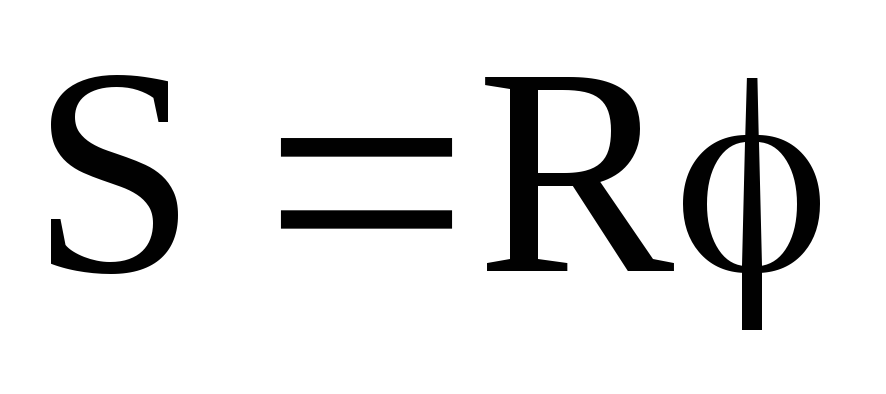 ,
,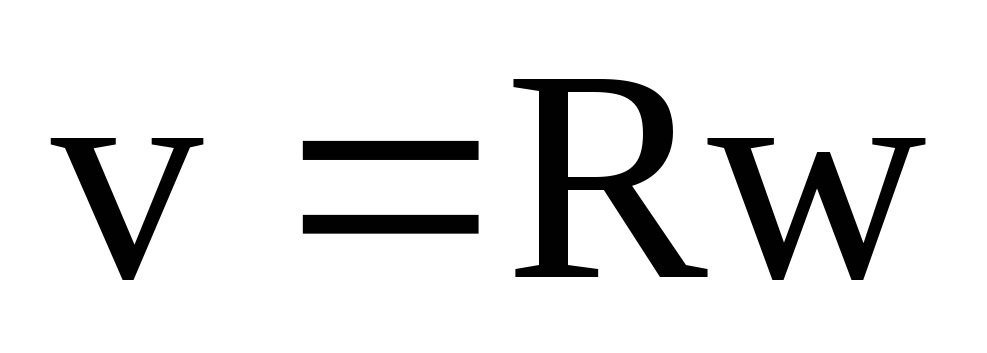 ,
,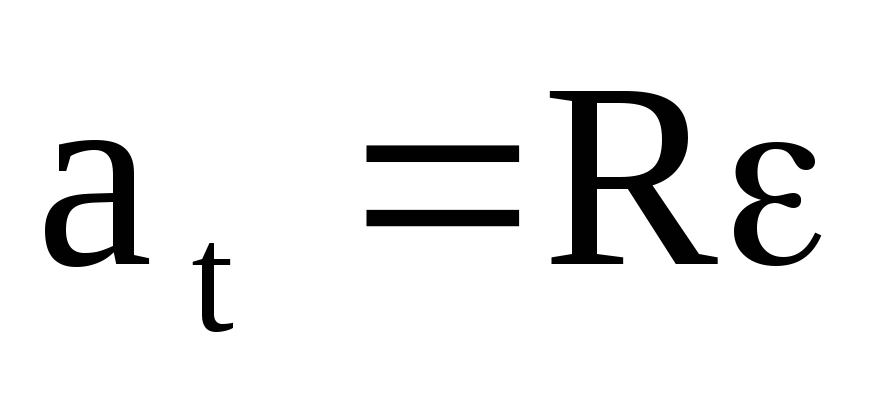 ,
,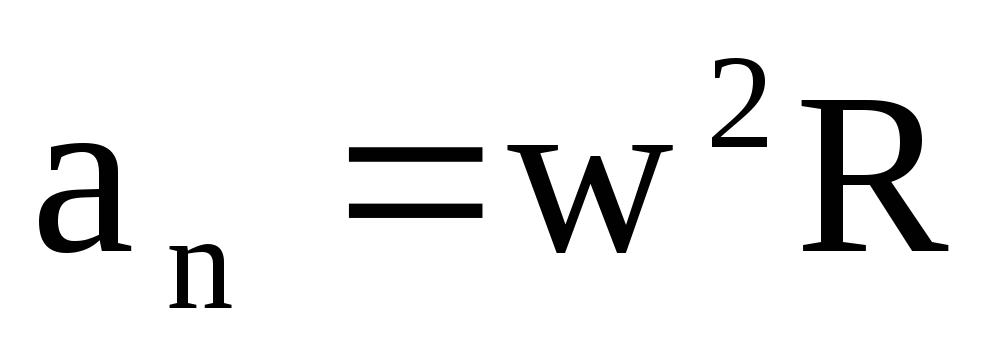 .
.
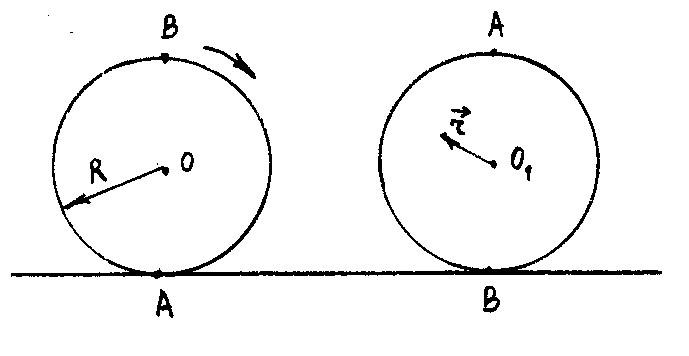
6. Качение тела.
Цилиндрическое тело равномерно катится по горизонтальной плоскости без проскальзывания. Все точки тела одновременно участвуют в двух движениях – поступательном и вращательном. Найдем скорость любой точки тела.
| В этом
случае скорость любой точки тела
складывается из скорости поступательного
и вращательного движения. Пусть за
время |
Рис.9. |
на 
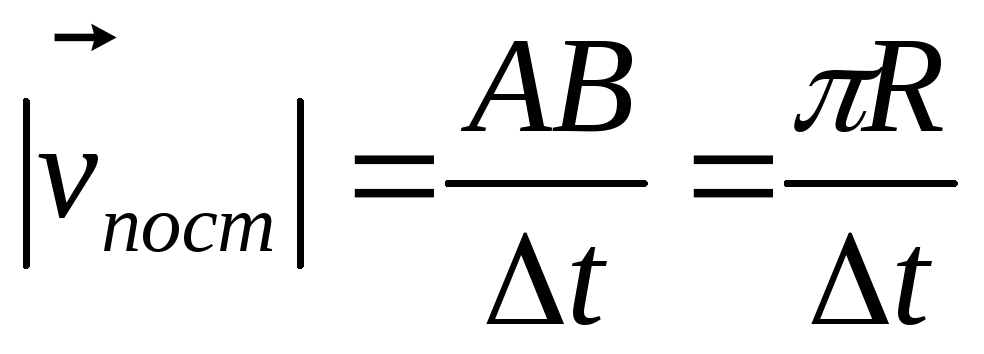 ,
,
При этом тело поворачивается на угол  ,
а угловая скорость равна
,
а угловая скорость равна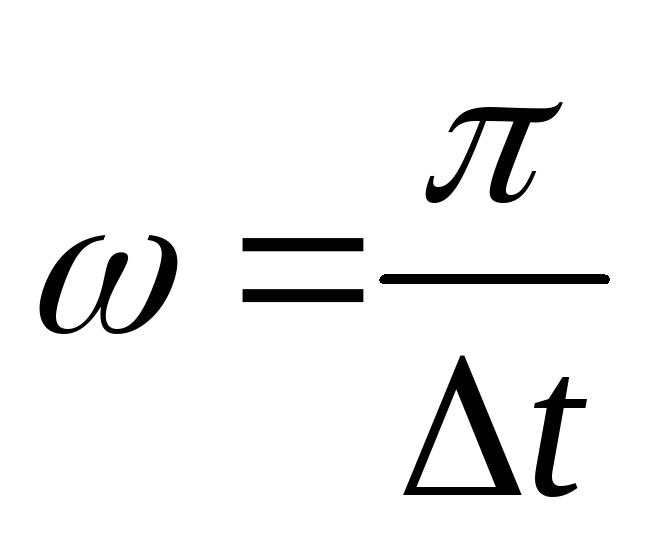
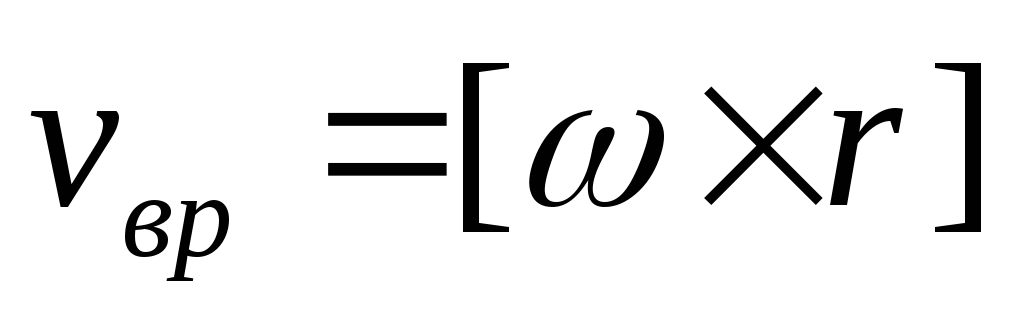 можно найти линейную скорость точки за
счет вращения,
можно найти линейную скорость точки за
счет вращения,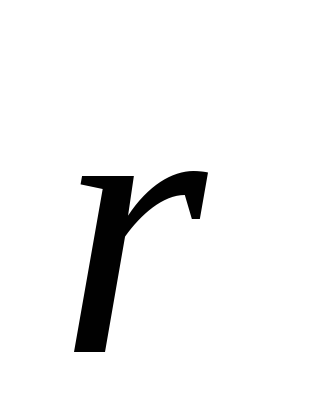 —
расстояние от точки до центра О.
—
расстояние от точки до центра О.Для точки на ободе тела
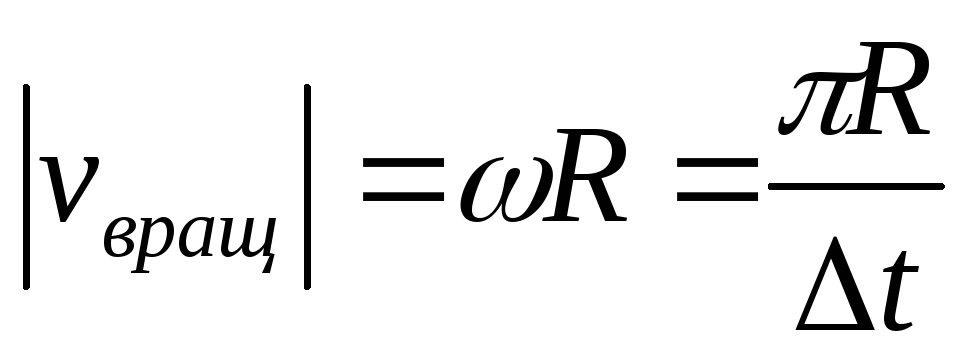 .
.
Полная скорость точки будет определяться из равенства
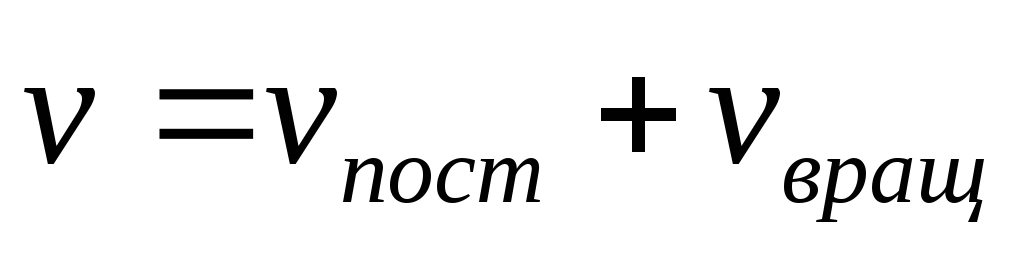 =
= 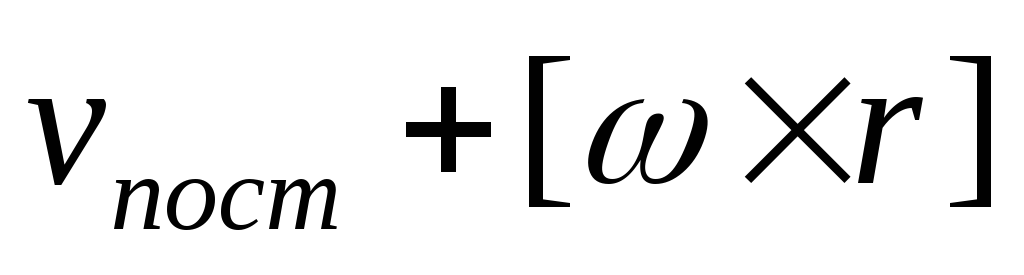 /
/
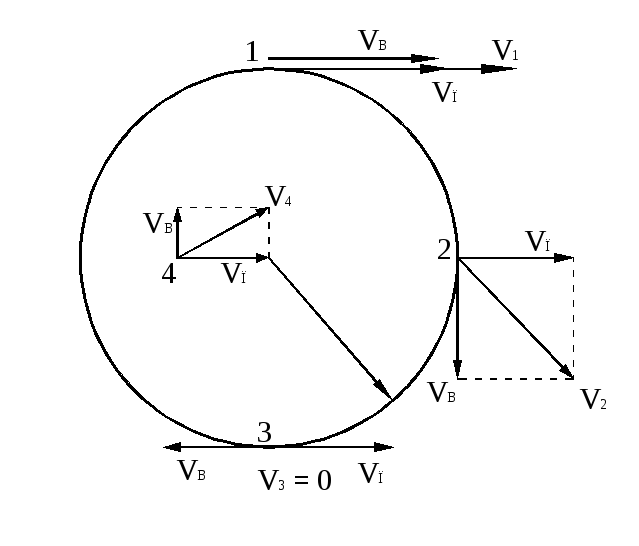
Определим скорости точек 1, 2, 3, 4. (рис.10)
| 1: 2: 3: 4: |
Рис.10. |
Лекция 2. Динамика материальной точки.
Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение. Динамика изучает связь между взаимодействиями тел и изменениями в их движении.
В основе динамики лежат три закона Ньютона. Эти законы – результат обобщения опытных данных и теоретических сведений в области механики, которые были получены до Ньютона и самим Ньютоном.
1. Первый закон Ньютона.
Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор пока воздействие со стороны других тел не заставят его изменить это состояние.
Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инертностью.I- закон обычно называют законом инерции, а движение тела, свободного от внешних воздействий – движением по инерции.
I- закон выполняется не во всякой системе отсчета координат. Например, тела лежащие на гладком полу поезда, идущего с постоянной скоростью по прямолинейному участку пути, начинают двигаться, если поезд тормозит или ускоряется или выходит на криволинейный участок.
Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета.
Системы отсчета, движущиеся с ускорением относительно инерциальных систем, называются неинерциальными.
С большой степенью точности инерциальной можно считать гелиоцентрическую систему. Начало системы связано с Солнцем, а оси проведены в направлении трех удаленных звезд. Любая другая система, движущаяся относительно гелиоцентрической без ускорения будет также инерциальной. Так как Земля вращается вокруг собственной оси, система отсчета жестко связанная с Землей не будет инерциальной. Однако вращение Земли происходит медленно, поэтому в большинстве задач неинерциальностью этой системы можно пренебречь.
Важной особенностью инерциальных систем отсчета является, то что в них время однородно, а пространство однородно и изотропно. Однородность времени означает, что протекание физических процессов в разное время одинаково (в одних и тех же условиях). Однородность пространства – физические процессы протекают одинаково во всех его точках. Изотропность – во всех направлениях физические явления протекают одинаково.
В неинерциальных системах отсчета пространство неоднородно и неизотропно, а время неоднородно.
studfile.net
Угловая скорость. Угловое ускорение
При вращательном движении твердого тела его точки, находящиеся на разных расстояниях r от оси вращения, за равные промежутки времени проходят разные пути; следовательно, они имеют разные скорости и ускорения. Пусть радиус окружности, описываемой некоторой точкой, равен r, а ее линейное перемещение — ds. Тогда угловое перемещение
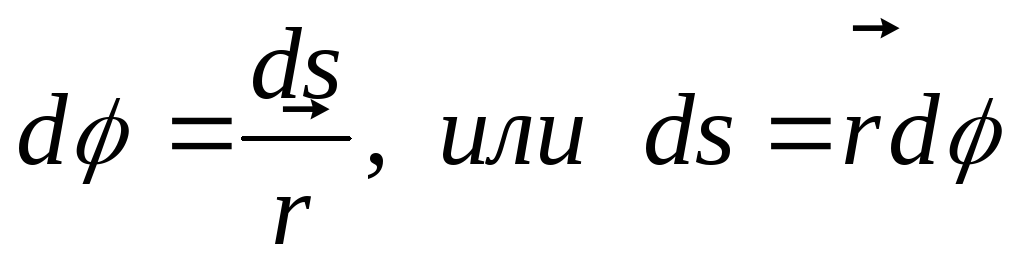
Кинематическими характеристиками вращательного движения так же являются угловая скорость w и угловое ускорение ε.
Если за промежуток времени Dt тело поворачивается на угол jD, то быстрота его вращения характеризуется угловой скоростью
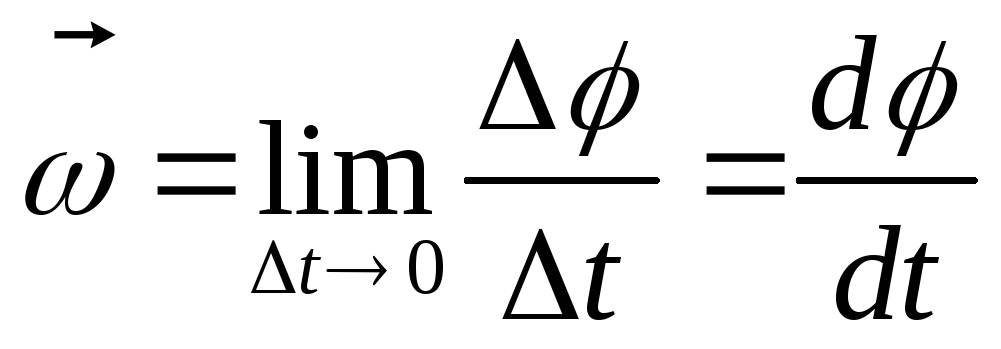
Угловая скорость равна первой производной от угла поворота радиуса-вектора по времени.
Направление вектора w вдоль оси вращения, можно определить, пользуясь правилом правого винта: если направление вращения винта совпадает с вращением тела, то конец винта укажет направление вектора w.
Если w=const, то вращательное движение называют равномерным.
Время одного полного поворота тела вокруг оси вращения называют периодом обращения Т, а величину n, обратную периоду — частотой:
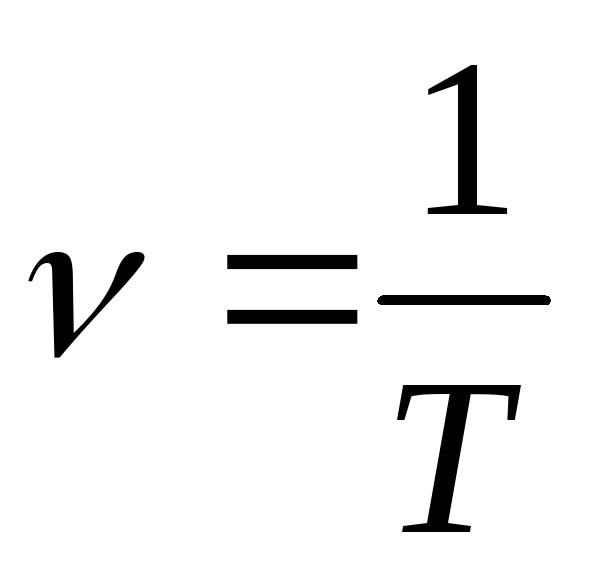
Связь между линейными и угловыми характеристиками движущейся точки
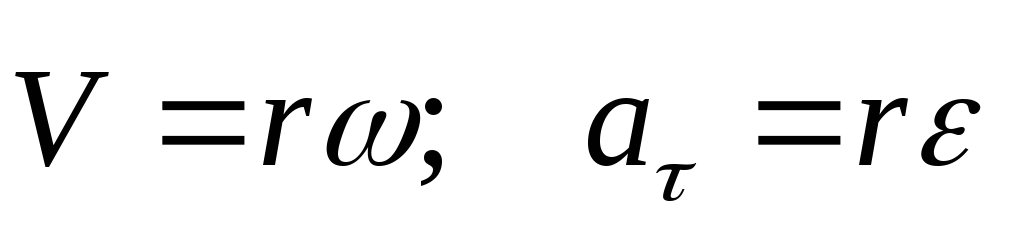
За один период угол поворота радиуса-вектора точки равен 2p рад, поэтому 2p =wТ, или
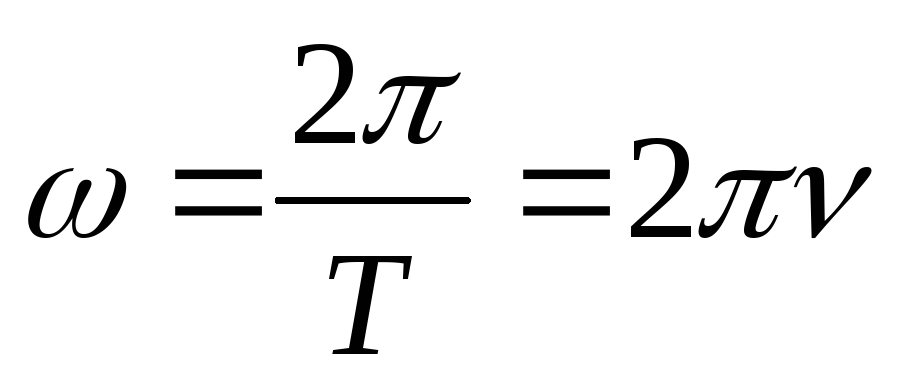
Угловая скорость выражается в радианах в секунду (рад/с).
Быстрота изменения угловой скорости характеризуется угловым ускорением.
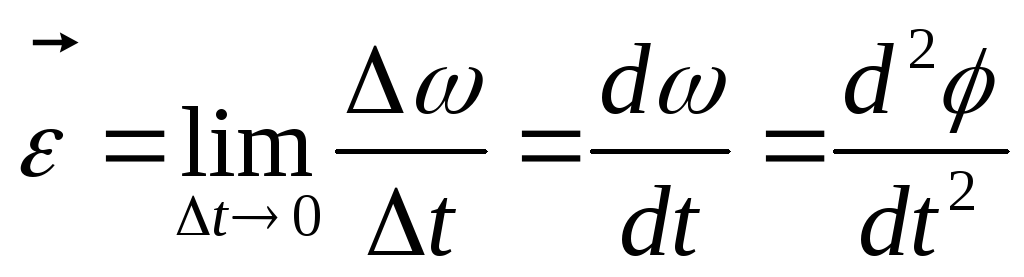
Угловое ускорение равно первой производной от угловой скорости по времени или второй производной от угла поворота радиуса-вектора по времени.
Единица углового ускорения —радиан на секунду в квадрате (рад/с2).
Формулы поступательного и вращательного движения
Равномерное движение
1. Поступательное:
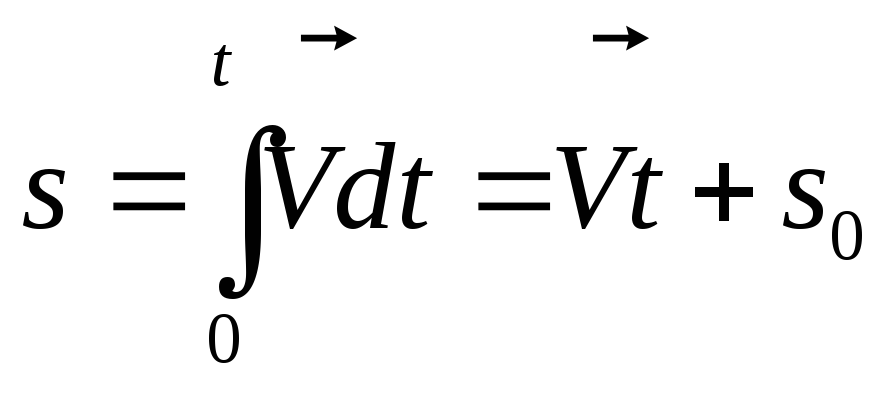
2. Вращательное:
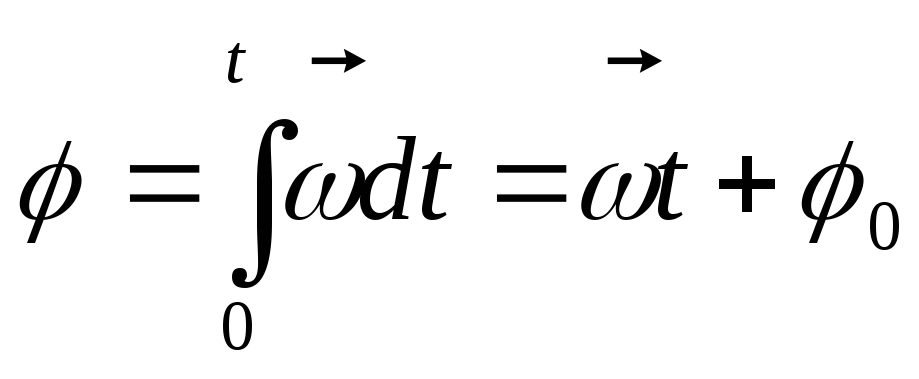
Равнопеременное движение
1. Поступательное:
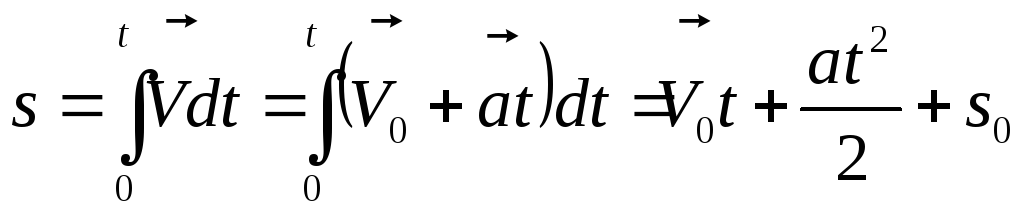
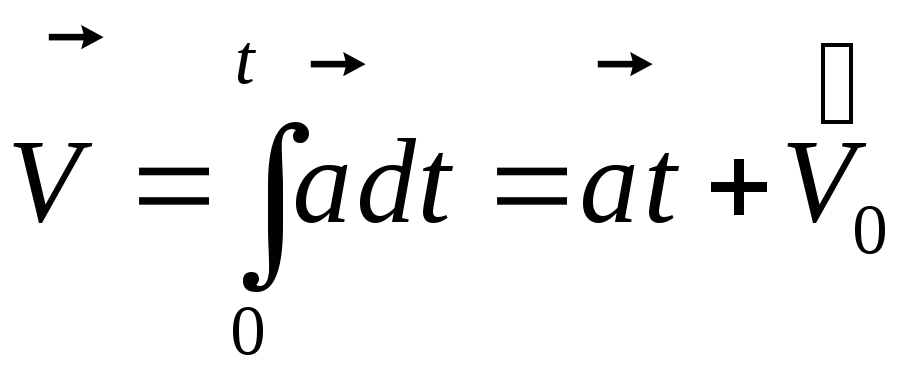
2. Вращательное:
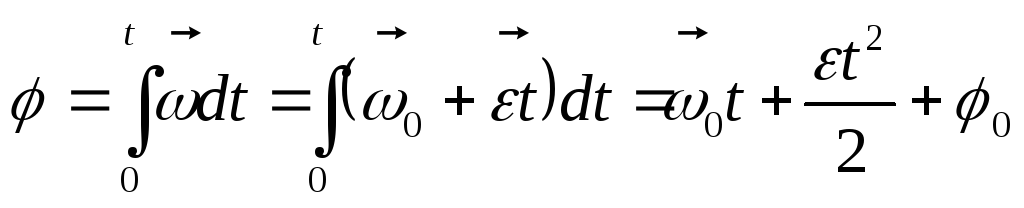
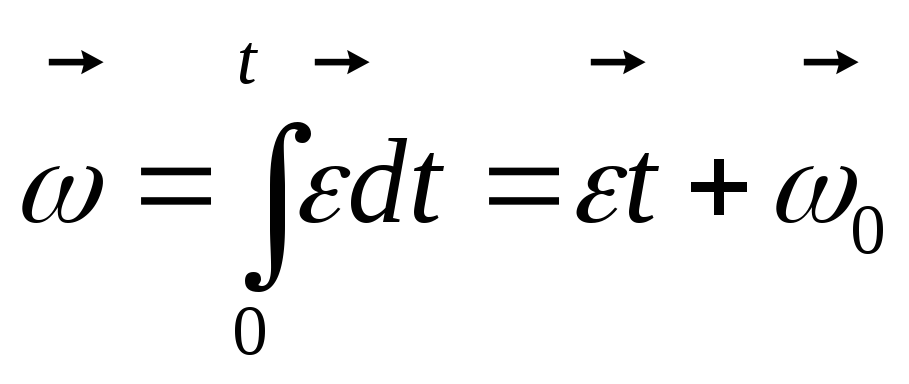
Лекция №2 динамика материальной точки и поступательного движения твердого тела
Динамика – раздел механики, который рассматривает законы движения тел и те причины, которые его вызывают или изменяют.
В основе так называемой классической или ньютоновской механики лежат три закона динамики, сформулированные Ньютоном в 1687 году.
Законы Ньютона возникли в результате обобщения большого количества опытных фактов. Правильность их подтверждается согласием с опытом тех следствий, которые из них вытекают.
Первый закон Ньютона (закон инерции)
Существуют такие системы отсчета где, всякое тело сохраняет состояние относительного покоя или равномерного прямолинейного движения до тех пор, пока внешние воздействия не изменят этого состояния.
При отсутствии внешних воздействий тело, находившееся в движении, продолжает равномерно двигаться по прямой без изменения скорости.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии воздействия на него других тел называется инерцией.
Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными.
Например:
Гелиоцентрическая система отсчета, в которой за начало координат принимают Солнце, а оси проводят в направлении звезд, которые считаются неподвижными.
Система, которая движется относительно выбранной инерциальной системы равномерно и прямолинейно-поступательно.
Если система отсчета движется по отношению к инерциальной системе с ускорением, то она относится к неинерциальным системам отсчета.
В неинерциальных системах отсчёта первый закон Ньютона не выполняется.
Масса тела. Центр масс
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения называют инертностью.
Физическая величина, являющаяся мерой инертности тела при поступательном движении, называется массой.
В классической механике масса тела считается постоянной и равной массе покоя:
т = т0
Масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит.
Сила
Векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел, называется силой.
Это воздействие проявляется в изменении скорости движущегося тела или изменении формы и размеров тела.
Сила, как и любая векторная величина, считается заданной, если известны её числовое значение, направление и точка приложения.
Центром масс системы материальных точек называют точку, координаты которой определяются следующими соотношениями:
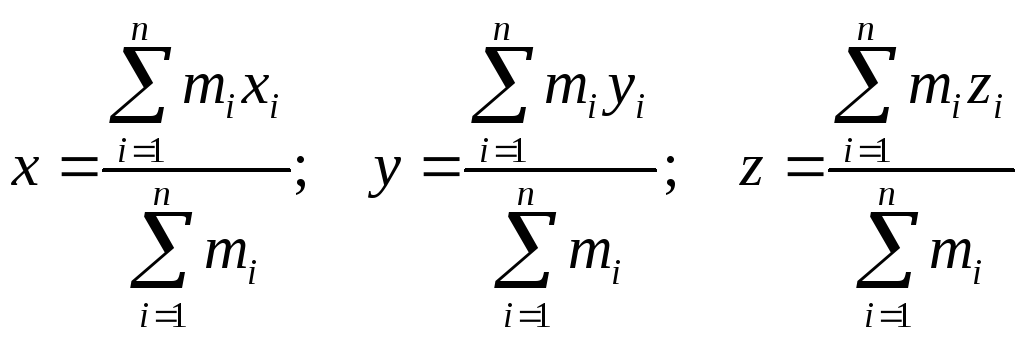
где n — число материальных точек; mi — масса i-й материальной точки системы; хi,yi,zi — координаты i-й материальной точки.
Второй закон Ньютона
Ускорение, приобретаемое материальной точкой (телом) в инерциальной системе отсчета, пропорционально действующей на точку силе, обратно пропорционально массе материальной точки и по направлению совпадает с силой:
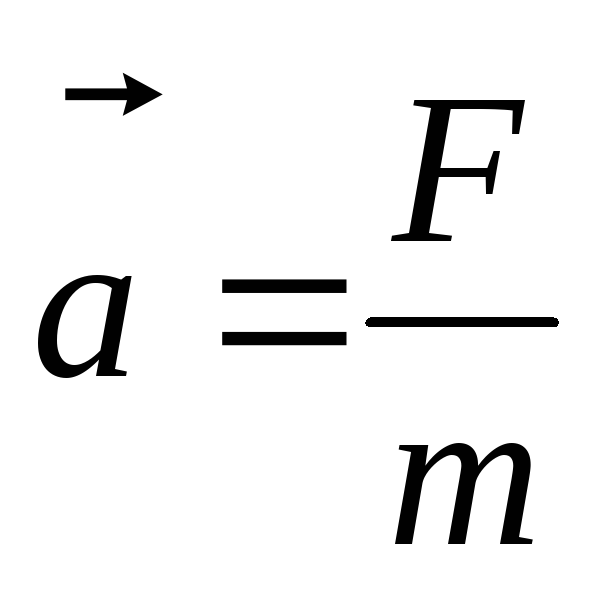
Если на материальную точку (тело) одновременно действует несколько сил, то каждая из этих сил действует независимо от других сил и сообщает точке ускорение, определяемое вторым законом Ньютона.
Ускорение центра масс системы определяется результирующей силой:
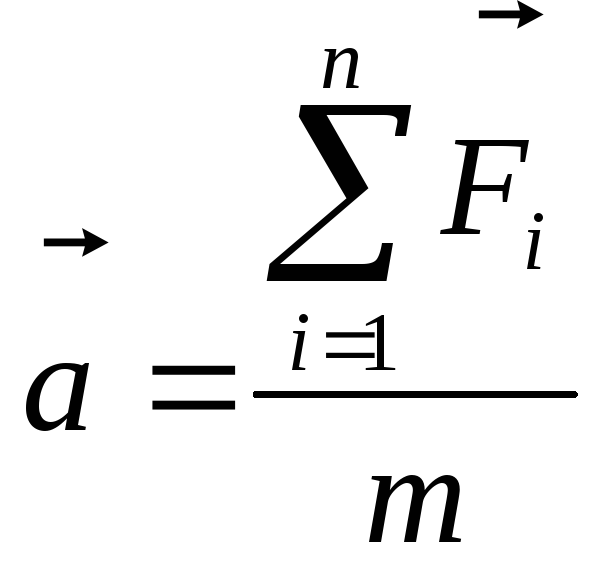
где т — суммарная масса всех точек системы.
Импульсом тела называют векторную величину, равную произведению массы тела на скорость его движения.
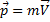
Запишем первый закон Ньютона используя импульс
Единица силы в СИ — ньютон (Н).
1 Н — сила, которая телу массой 1 кг сообщает ускорение 1 м/с2 в направлении действия силы.
Так как 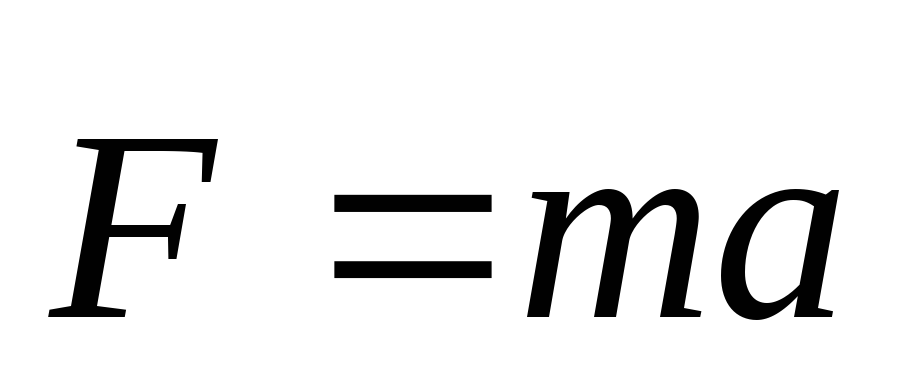 и
и 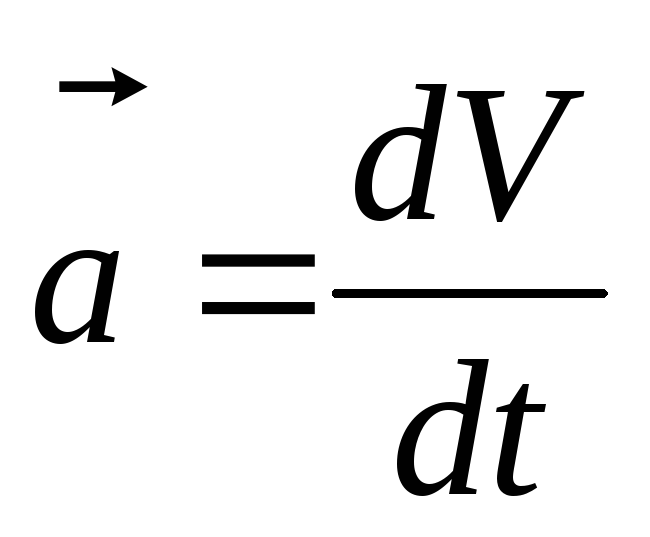 .
Представив ускорение как первую
производную от скорости по времени
имеем:
.
Представив ускорение как первую
производную от скорости по времени
имеем:
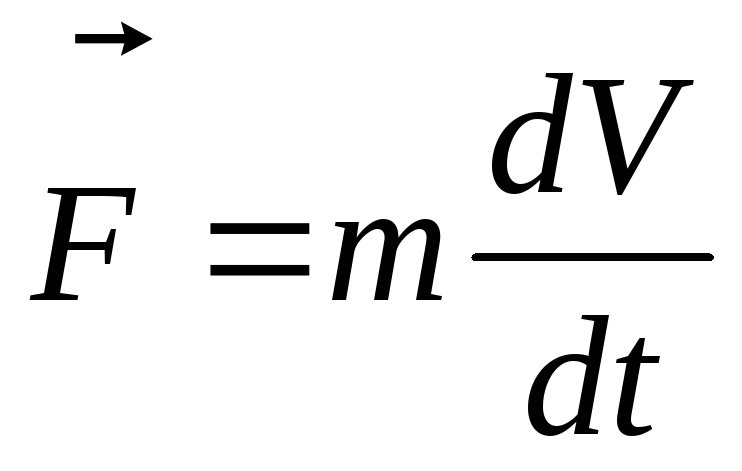
С учетом 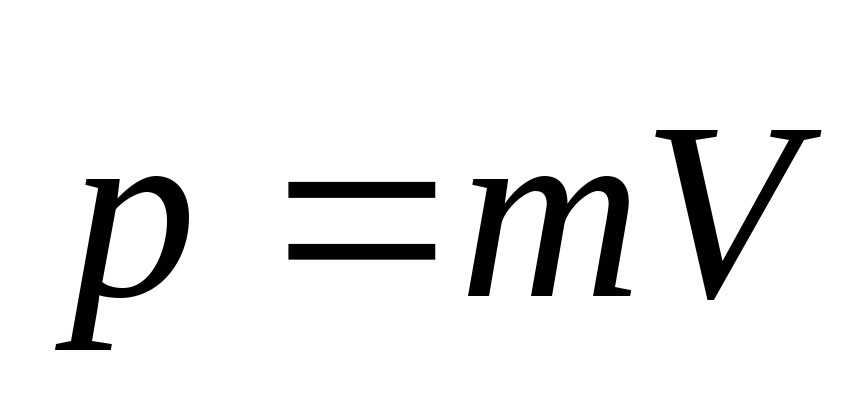 ,
окончательно второй закон Ньютона
запишем в виде:
,
окончательно второй закон Ньютона
запишем в виде:
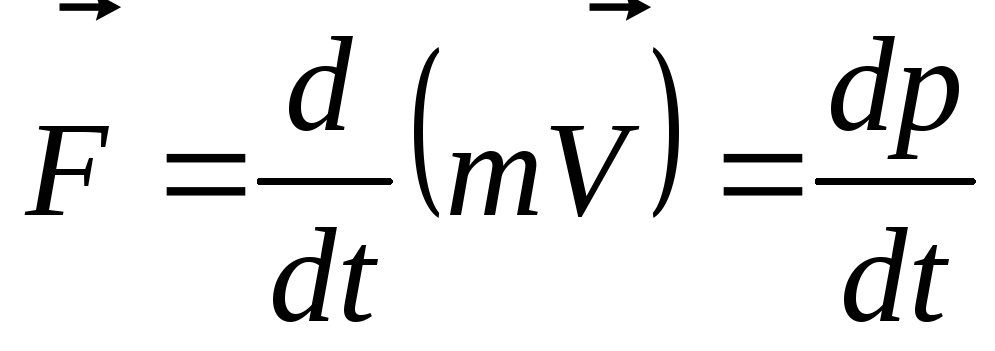
Третий закон Ньютона
Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти тела
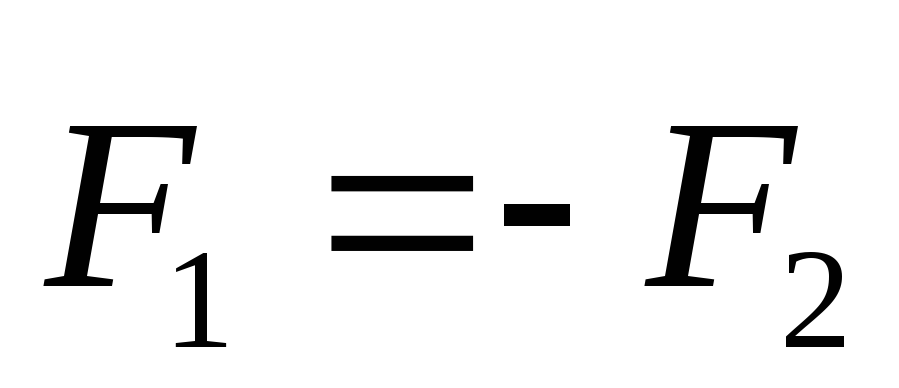
сила F1 — это сила, с которой второе тело действует на первое, и приложена она к первому телу, F2 — сила, с которой первое тело действует на второе, и приложена она ко второму телу, поэтому эти силы не уравновешивают друг друга.
Закон сохранения импульса
Силы взаимодействия между частицами (частями) некоторой рассматриваемой системы тел называют внутренними.
Силы, действующие на тела данной системы со стороны тел, не включенных в эту систему, называют внешними.
Если система состоит из n материальных точек, то
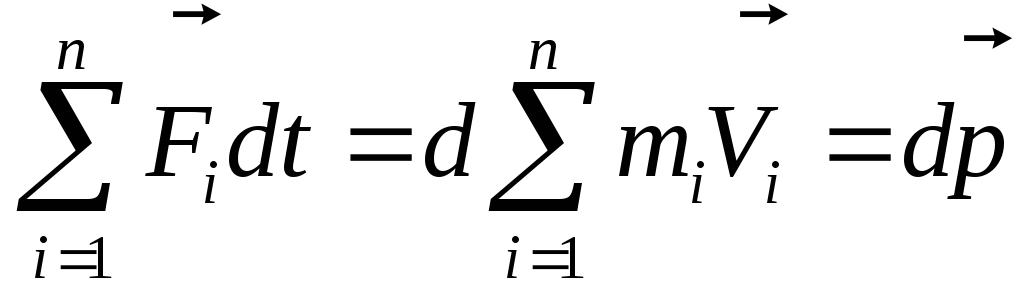
где 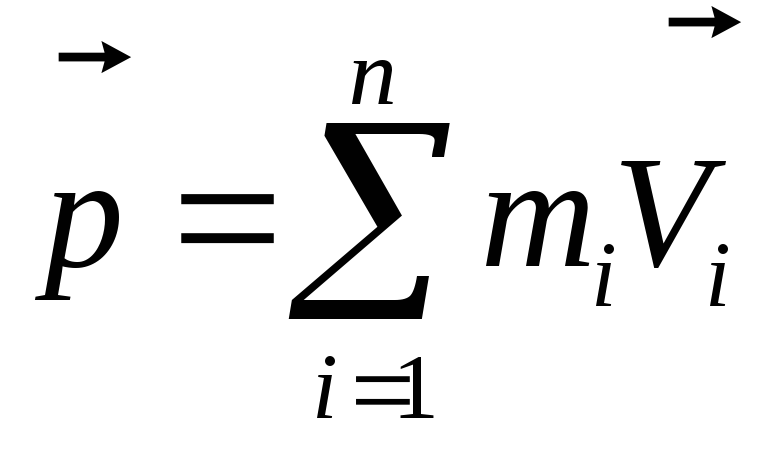 — импульс всей системы.
— импульс всей системы.
Перепишем это равенство в виде 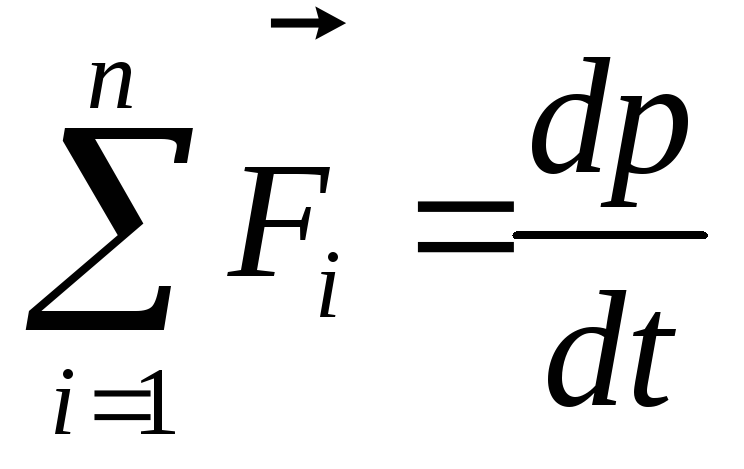
В замкнутой системе внешние силы
отсутствуют, т.е. 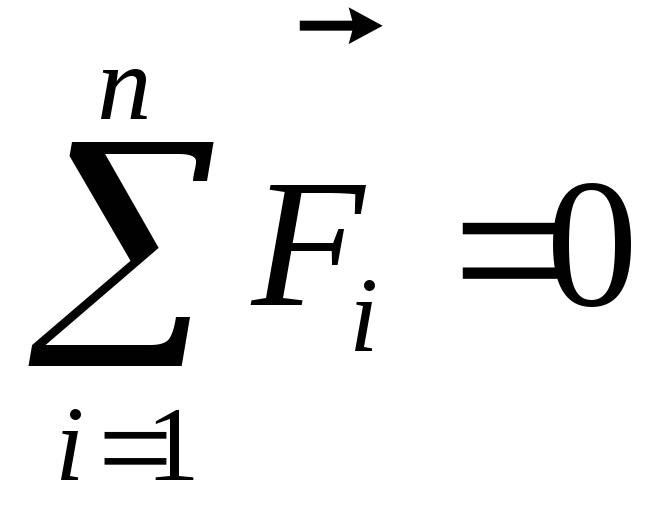
следовательно, 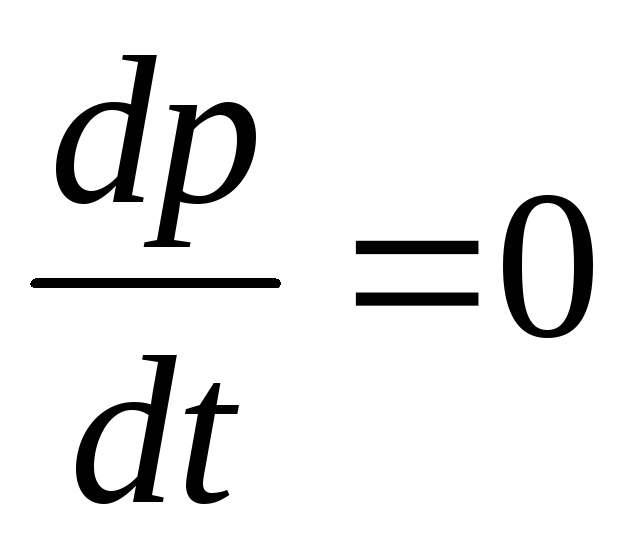 или
или
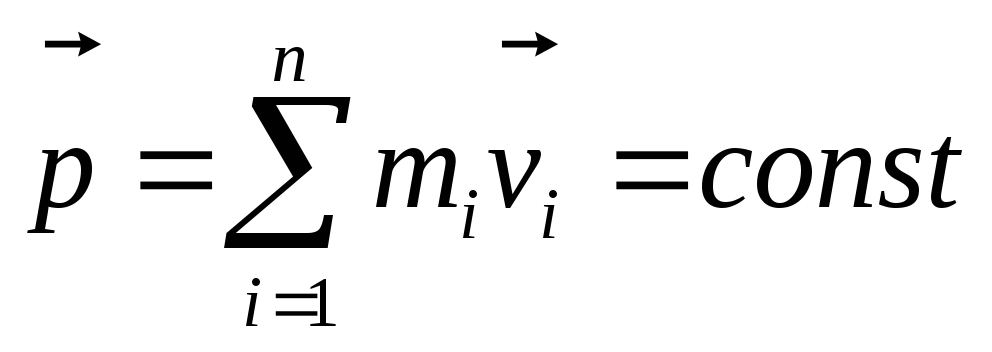
Это равенство выражает закон сохранения импульса: вектор полного импульса замкнутой системы тел с течением времени не изменяется.
В неинерциальных системах отсчета закон сохранения импульса не выполняется, так как силы инерции являются внешними некомпенсированными силами по отношению к неинерциальной системе. Однако второй закон Ньютона остается справедливым в данной системе, если в сумму внешних сил включить и силы инерции:
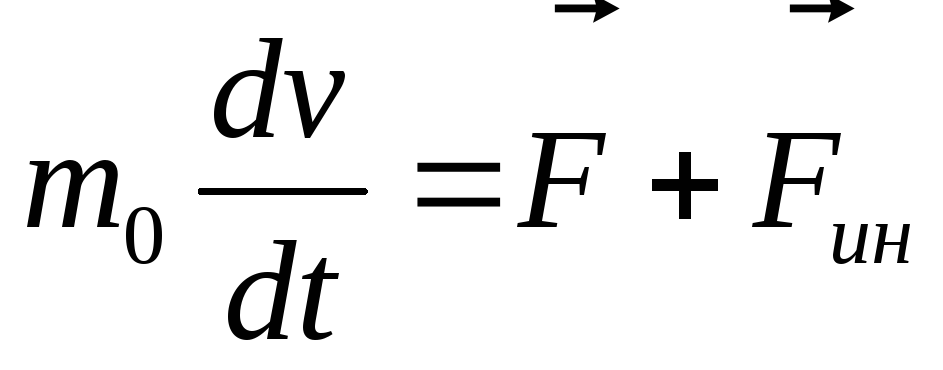
где F — сумма внешних сил, Fин — сила инерции.
Силы в механике
Силы тяготения (гравитационные силы) — это силы притяжения, которые подчиняются закону всемирного тяготения.
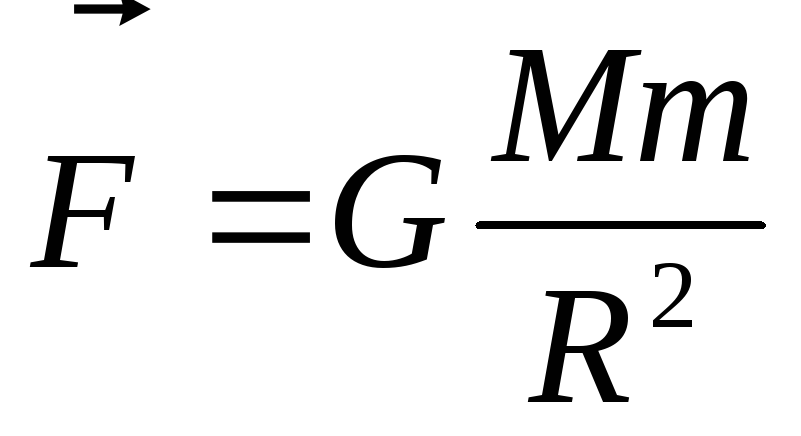
Сила тяжести — сила, с которой тело притягивается Землей.
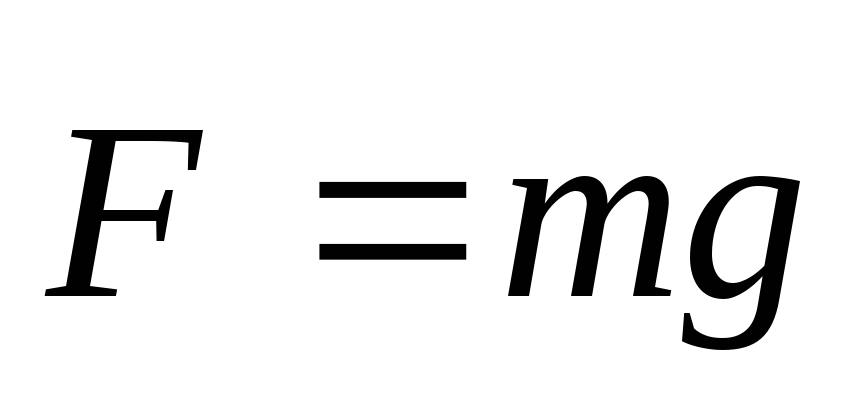
Под действием силы притяжения к Земле все тела падают в данном месте земного шара с одинаковым ускорением g=9,8 м/с2, называемым ускорением свободного падения.
Тогда на основании второго закона Ньютона можно утверждать, что это ускорение вызывается силой тяжести:
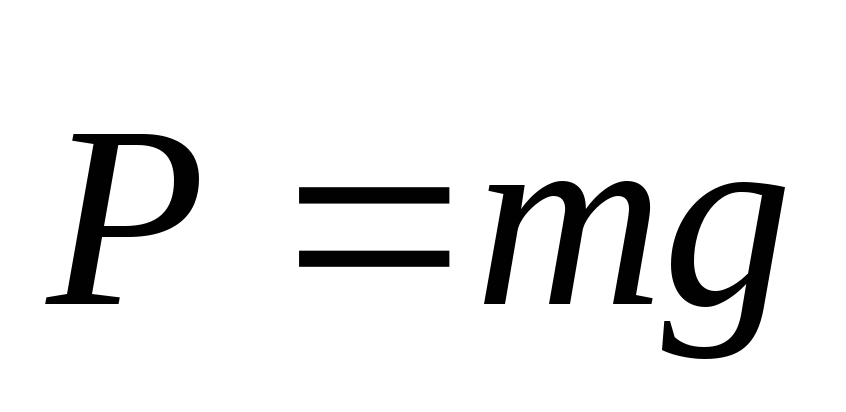
Вес — сила, с которой тело, притягиваясь к Земле, действует на опору или натягивает нить подвеса.
Сила тяжести равна весу только в том случае, когда ускорение тела вместе с опорой (подвесом) относительно Земли равно нулю, т. е. когда тело относительно Земли неподвижно или движется с постоянной скоростью. В противном случае
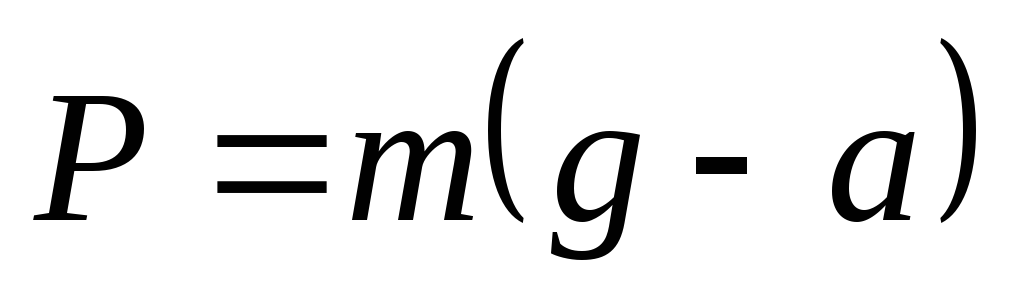
где а — ускорение тела с опорой относительно Земли.
При свободном падении тела вес этого тела равен нулю, т.е. оно находится в состоянии невесомости.
Силы упругости возникают в результате взаимодействия тел, сопровождающегося их деформацией.
Упругая (квазиупругая) сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия:
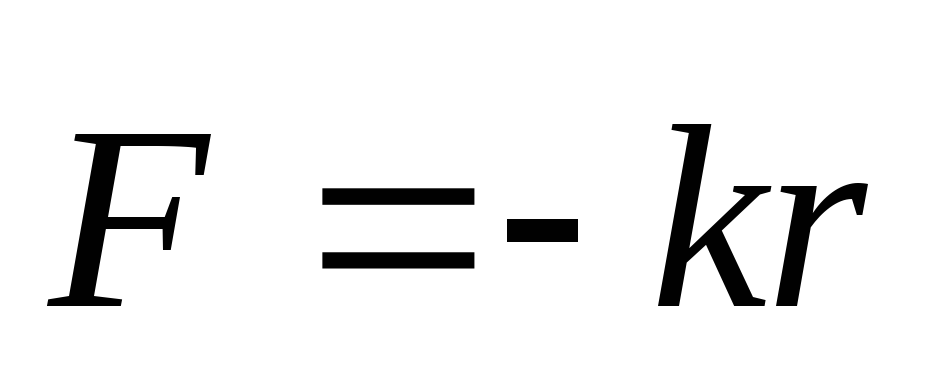
где r — радиус-вектор, характеризующий смещение частицы из положения равновесия, k — коэффициент упругости.
Сила трения скольжения возникает при скольжении данного тела по поверхности другого:
где k — коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей; N — сила нормального давления, прижимающая трущиеся поверхности друг к другу.
Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого.
Лекция 3.
МЕХАНИКА ТВЕРДОГО ТЕЛА
Момент силы. Момент инерции
Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси 00′. Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы (рис. 3).
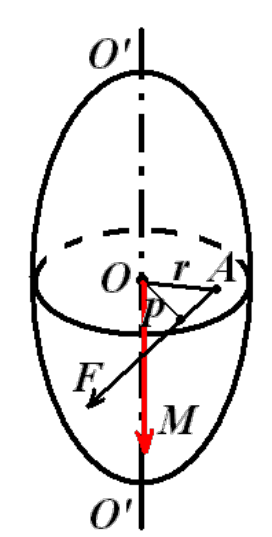
Рисунок 3. Твердое тело, вращающееся под действием силы F
Произведение силы на плечо определяет модуль момента силы относительно точки О: M=Fp=Fr sin (rF).
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:
M=[rF].
Направление М можно найти с помощью правила правого винта
Мерой инертности при вращательном движении служит величина, называемая моментом инерции тела относительно оси вращения.
Моментом инерции материальной точки относительно оси вращения называют произведение массы этой точки на квадрат расстояния от оси:
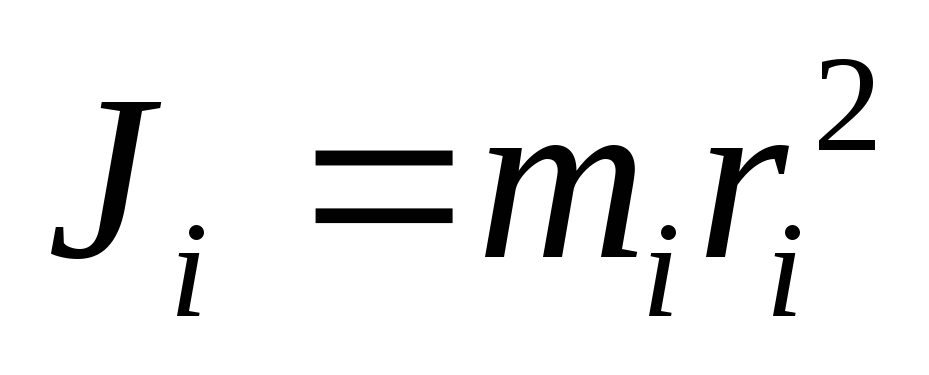
Моментом инерции тела относительно оси вращения называют сумму моментов инерции материальных точек, из которых состоит это тело:
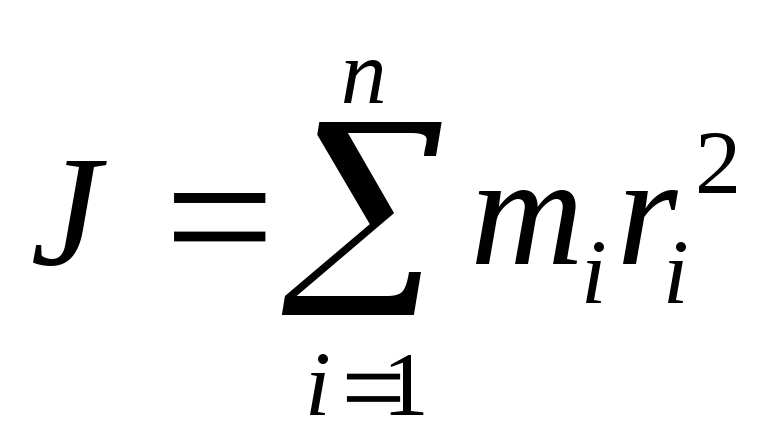
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Если тело сплошное и представляет собой совокупность точек с малыми массами dm, то момент инерции равен:
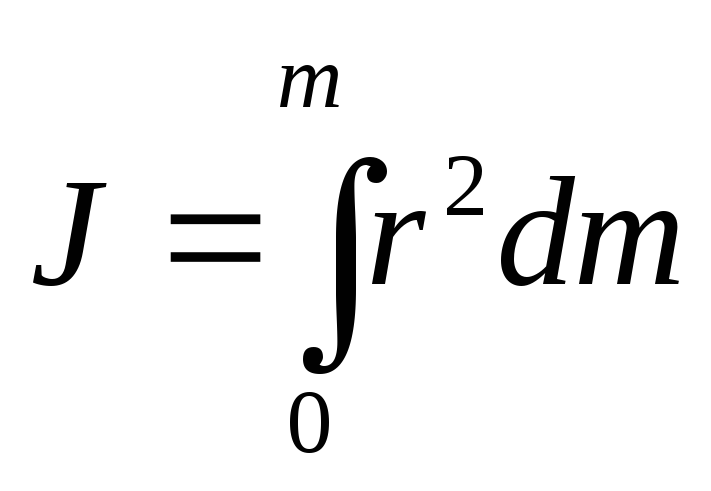
где r — расстояние от оси вращения до элемента массой dm.
Если тело однородно и его плотность r=m/V, то момент инерции тела
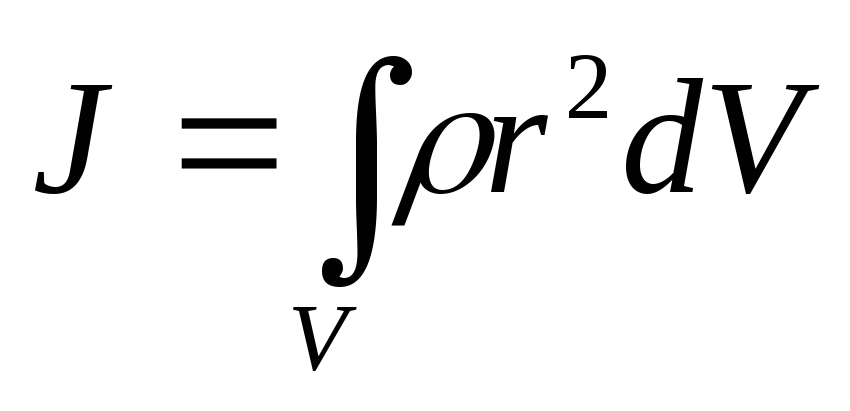
Теорема Штейнера
Момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и величины md2:
J=J0+md2
где m — масса тела, d— расстояние от центра масс до выбранной оси вращения.
Основной закон динамики
Рассмотрим материальную точку А массой т, движущуюся по окружности радиусом r.
Пусть на нее действует постоянная сила F, направленная по касательной к окружности. Эта сила вызывает тангенциальное ускорение F=aτ m.
Если 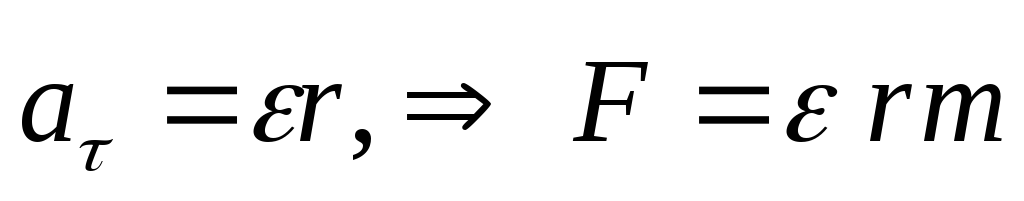 .
Умножим обе части на r.
.
Умножим обе части на r.
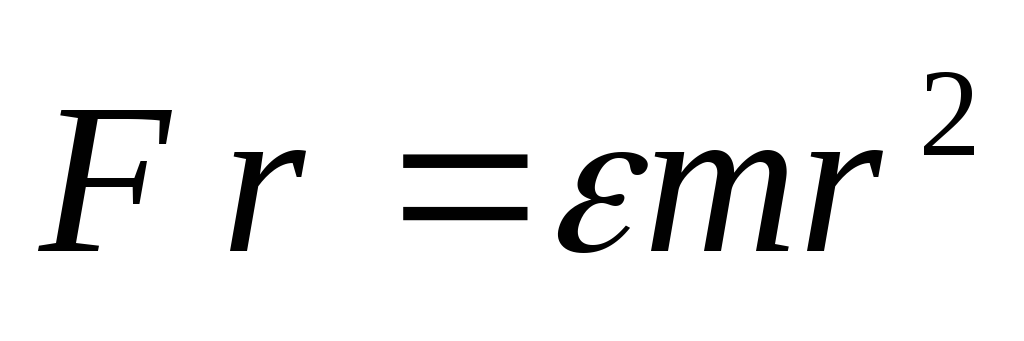
Тогда М=εJ или ε=M/J – основное уравнение динамики вращательного движение м.т..
Угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
Для твердого тела:
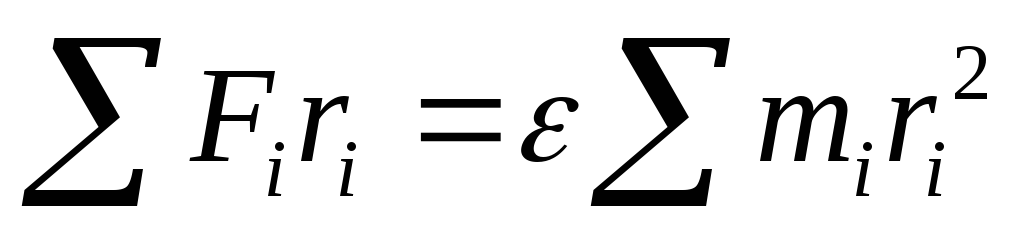 или
или
ε=M/J
Основное уравнение динамики вращательного движения твердого тела
При постоянном моменте вращающей силы угловое ускорение будет величиной постоянной и его можно выразить через разность угловых скоростей:
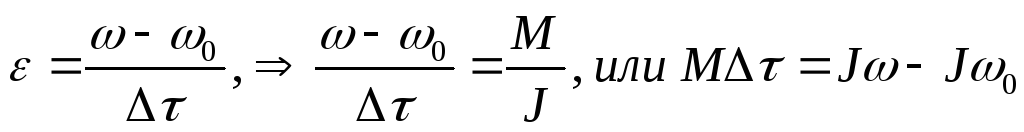
где Jω — момент импульса (или момент количества движения), МΔτ — импульс момента сил (или импульс вращающего момента).
Эти величины векторные и совпадают по направлению с векторами ω и М.
Кинетическая энергия вращающегося тела
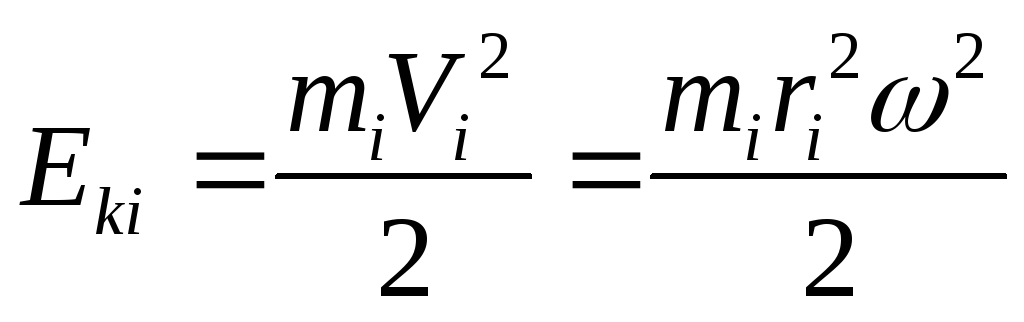
Разобьем тело на n материальных точек. Каждая точка движется с линейной cкоростью Vi=ωri, тогда кинетическая энергия точки
Полная кинетическая энергия вращающегося твердого тела относительно данной неподвижной оси вращения:
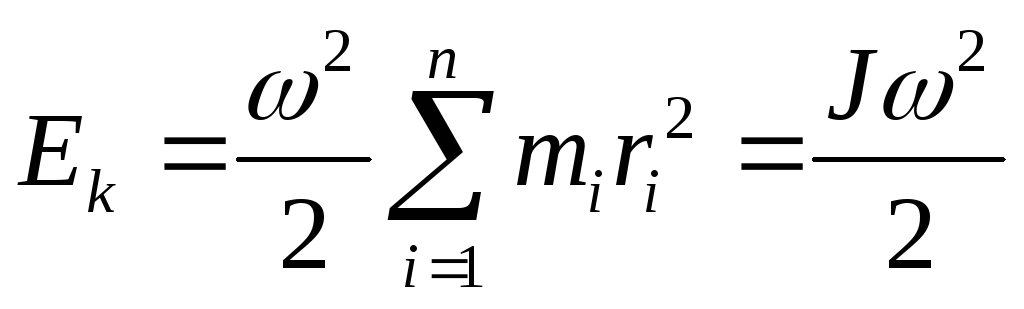
Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна
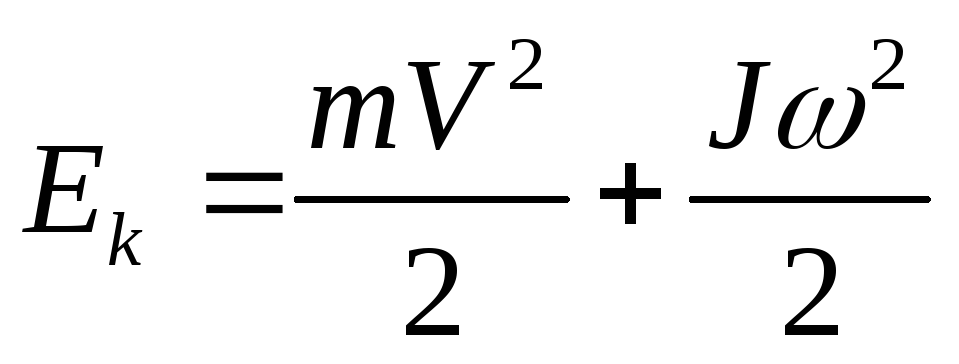
Работа внешних сил при вращении твердого тела
При вращении твердого тела его потенциальная энергия не изменяется, поэтому элементарная работа внешних сил равна приращению кинетической энергии тела:
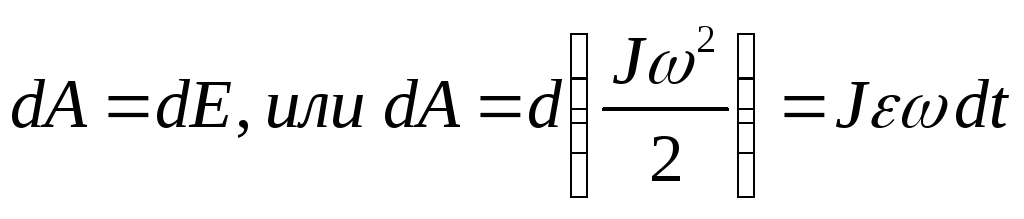
Учитывая, что Jε=M, ωdt=dφ, имеем dA=Mdφ. Окончательно работа выражется через уравнение:
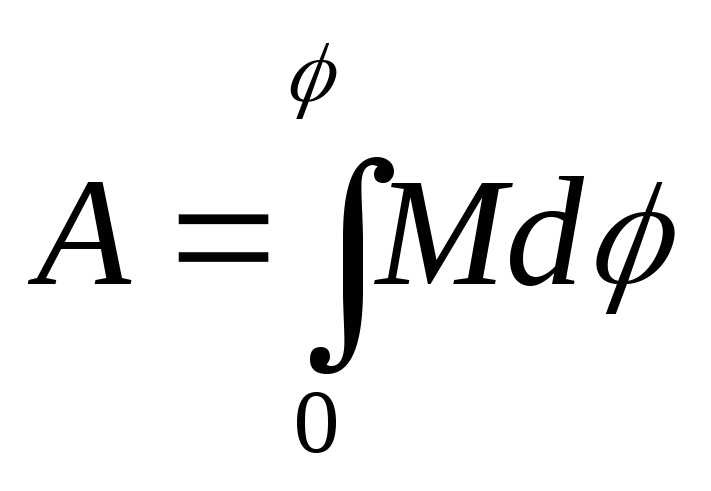
При вращении твердого тела вокруг неподвижной оси работа внешних сил определяется действием момента этих сил относительно данной оси.
Если момент сил относительно оси равен нулю, то эти силы работы не производят.
Закон сохранения момента импульса
Момент импульса вращающегося тела равен сумме моментов импульсов отдельных его частиц:
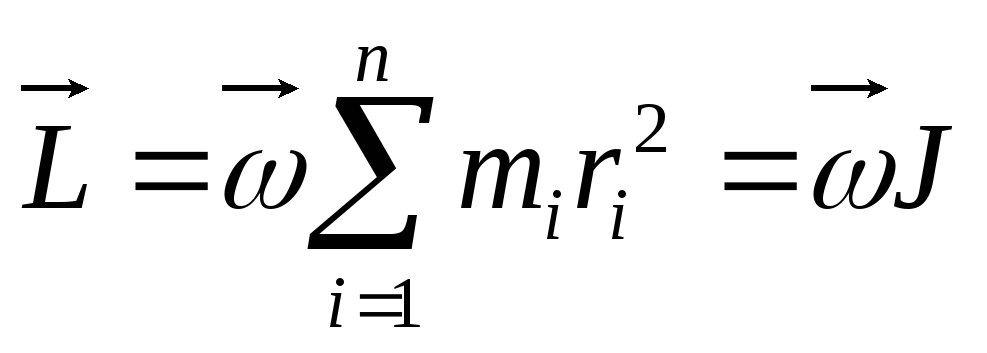
Момент импульса — это вектор, совпадающий по направлению с вектором угловой скорости. Изменение момента импульса равно импульсу момента сил:
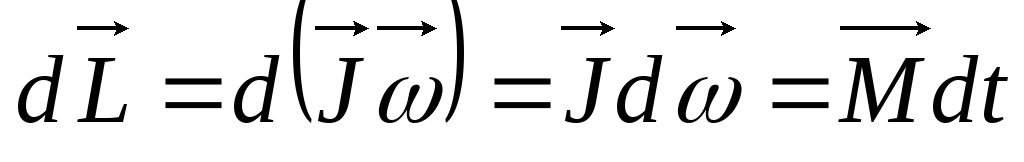
Если суммарный момент всех внешних сил, действующих на систему тела относительно произвольной неподвижной оси, равен нулю, т. е. М=0, то dL=0 и векторная сумма моментов импульсов тел системы не изменяется с течением времени:
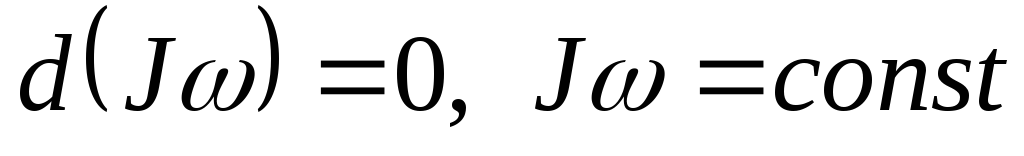
Сумма моментов импульсов всех тел изолированной системы остается неизменной
Закон сохранения момента импульса связан с однородностью и изотропностью пространства.
Под однородностью пространства понимают равноправность всех точек пространства.
Под изотропностью пространства понимают равноправность всех направлений в пространстве.
studfile.net
пр1ст
1. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
1. Кинематика поступательного движения (A)
1. Знать определения: мгновенная скорость материальной точки , перемещение, ускорение, длина пути (векторная величина или скалярная, первая производная или вторая, от какой величины)
2. Куда направлен вектор мгновенной скорости, вектор тангенциального ускорения, вектор нормального ускорения?
3. Что характеризует нормальное ускорение, тангенциальное ускорение?
4. Скорость движения тела меняется с течением времени t по закону v=(3t3-t+5) (м/с). Записать закон изменения ускорения тела со временем (в м/с2). Чему равно ускорения тела в момент времени t=0 ?
2. Кинематика вращательного движения (А)
5. Знать определения: угловая скорость, угловое ускорение, угловое перемещение (векторная величина или скалярная, первая производная или вторая, от какой величины)?
6. Куда направлен вектор углового ускорения (при ускоренном вращении, при замедленном вращении), вектор угловой скорости , вектор углового перемещения?
7. Знать правило, по которому определяется направление углового перемещения
8. Знать правило, по которому определяется направление угловой скорости
9. Угловое перемещение тела меняется с течением времени t по закону
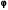 =(3t2-2t+5)
(рад). Записать
закон изменения угловой скорости тела
со временем, углового ускорения тела
со временем. Чему равны угловые скорость
и ускорение при t=0 ?
=(3t2-2t+5)
(рад). Записать
закон изменения угловой скорости тела
со временем, углового ускорения тела
со временем. Чему равны угловые скорость
и ускорение при t=0 ?
10. При движении автомобиля его колеса радиусом 0,5 м вращаются с угловой скоростью 6 рад/с. Какова при этом линейная скорость автомобиля ?
3. Кинематика поступательного и вращательного движения (B)
11. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. Как при этом изменяется величина нормального ускорения (увеличивается, уменьшается, остается неизменной, невозможно определить)?
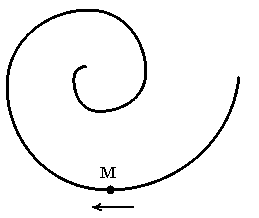
12. Точка М движется по спирали с постоянной по величине угловой скоростью в направлении, указанном стрелкой (смотри рис. Задачи 11). Как при этом изменяется величина линейной скорости?
13. Точка М движется по спирали в направлении, указанном стрелкой (смотри рис. Задачи 11) . Угловое ускорение по величине не меняется. Как при этом изменяется величина тангенциального ускорения?
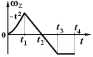
14. Зависимость угловой скорости тела от времени показана на рисунке. 1) Какие уравнения характеризуют движение тела в интервалах 0-3 с, 3-9 с, 9-12 с? 2) Определите угловое перемещение тела за промежуток времени от 0 до 6 с, от 3 до 9 с, от 6 до 12 с.
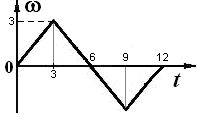
15.
Твердое тело начинает вращаться вокруг
оси z.
Зависимость проекции углового ускорения  на
ось z меняется
от времени t согласно графику
на
ось z меняется
от времени t согласно графику
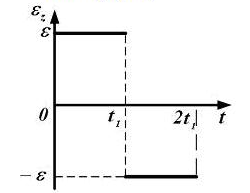
Такому
движению соответствует график зависимости
проекции угловой скорости  от
времени t …
от
времени t …
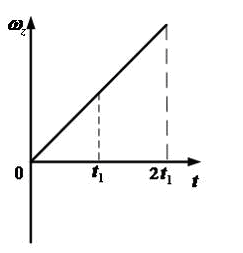
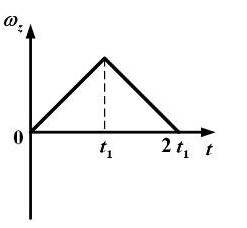
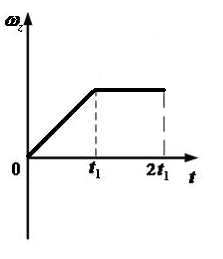
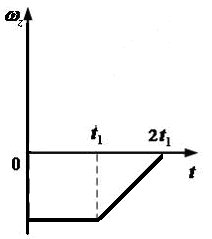
16. Зависимость проекции угловой скорости на ось z от времени показана на рисунке. В какие интервалы времени вектор угловой скорости и вектор углового ускорения направлены в одну сторону?
studfile.net
Определение закона изменения угловой скорости платформы
Задание для контрольной работы по теоретической механике (динамика Д3) | |
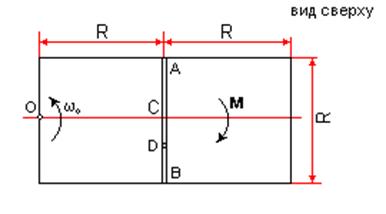
| a. Однородная горизонтальная платформа (прямоугольная плита со сторонами 2R и R, R=0.5м) имеющая массу m1=16 кг, жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угловой скоростью w0=2 с-1. В момент времени t0=0 на вал начинает действовать вращающий момент М=6t, направленный противоположно w0; одновременно груз D массой m2=10 кг, находящийся в желобе AB в точке С, начинает двигаться по желобу под действием внутренних сил по закону s=CD=0.4t2. Определить закон изменения угловой скорости платформы w=f(t). |
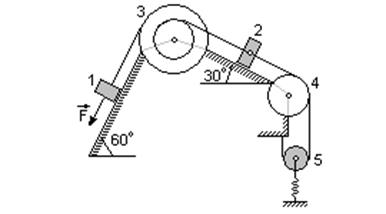
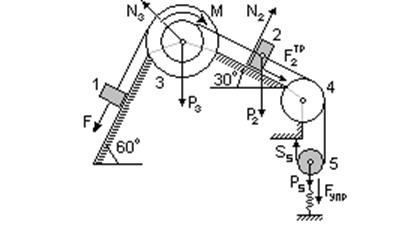
| b. Механическая система состоит из грузов 1 и 2 (m1=0кг, m2=6кг), ступенчатого шкива 3 (m3=4кг) с радиусами ступеней R3=03.м и r3=0.1м и радиусом инерции относительно оси вращения r3=0.2м, блока 4 (m4=0) радиуса R4, подвижного блока 5 (m5=5кг). Тело 5 считать сплошным однородным цилиндром. Коэффициент трения грузов о плоскость f=0.1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3. К одному из тел прикреплена пружина с коэффициентом жесткости c=200 Н/м, ее начальная деформация равна нулю. Система приводится в движение из состояния покоя под действием силы F=80(4+5s) Н, зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М=1.2 Н*м сил сопротивления. Определить w3 в тот момент времени, когда s=0.2 м. |
Решение задачи a
Рассмотрим механическую систему, состоящую из платформы и груза D. Для определения w применим теорему об изменении кинетического момента системы относительтно оси z :
|
На систему действуют внешние силы Р1, Р2 (вес платформы и груза), реакции в оси и момент М. Все силы параллельны или пересекают ось z, поэтому в сумму моментов в правой части теоремы они не войдут, так как их моменты относительно оси z равны нулю. Тогда, считая положительным направление w0 против хода часовой стрелки, запишем теорему в виде: |
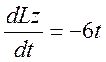
Разделяя переменные и интегрируя это уравнение, получим
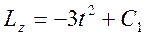 (*)
(*)
Для рассматриваемой механической системы
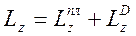 (**)
(**)
где Lzпл и LzD – кинетические моменты платформы и груза относительно оси z соответственно
Так как платформа вращается вокруг оси z,
то 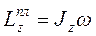 . Значение
. Значение 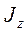 найдем
по теореме Гюйгенса:
найдем
по теореме Гюйгенса:
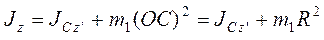
где 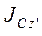 — момент
инерции относительно оси z:’, параллельной оси z и проходящей через центр С платформы.
— момент
инерции относительно оси z:’, параллельной оси z и проходящей через центр С платформы.
Но, как известно, 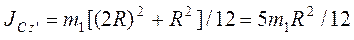 . Тогда
. Тогда 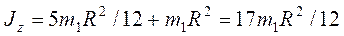 и,
следовательно,
и,
следовательно,
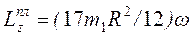 .
.
Для
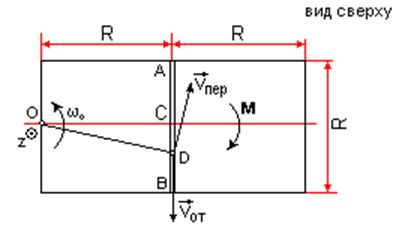
определения 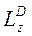 обратимся к рисунку и рассмотрим движение
груза D как сложное, считая его движение по платформе
относительным, а вращение самой платформы вокруг оси z
переносным движением. Тогда абсолютна скорость груза
обратимся к рисунку и рассмотрим движение
груза D как сложное, считая его движение по платформе
относительным, а вращение самой платформы вокруг оси z
переносным движением. Тогда абсолютна скорость груза 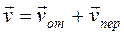 .
Так как груз D движется по закону s=CD=0.4t2, то
.
Так как груз D движется по закону s=CD=0.4t2, то 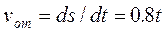 . Изображаем вектор
. Изображаем вектор 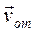 с
учетом знака ds/dt (при ds/dt<0 направление этого вектора
было бы противоположным). Затем, учитывая направление w, изображаем вектор
с
учетом знака ds/dt (при ds/dt<0 направление этого вектора
было бы противоположным). Затем, учитывая направление w, изображаем вектор 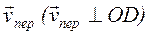 , численно vпер=w OD. Тогда, по теореме Вариньона
, численно vпер=w OD. Тогда, по теореме Вариньона
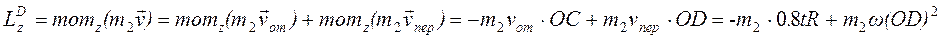 .
.
Но из рисунка видно, что OD2=R2+s2=R2+0.16t4. Подставляя эту величину в выражение для кинетического момента груза D, а затем значения кинетических моментов груза и платформы в равенство (**), получим с учетом данных задачи
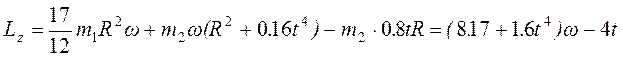
Тогда уравнение (*) примет вид
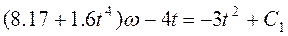 (***)
(***)
Постоянную интегрирования С1 определяем по начальным условиям: при t=0 w=w0. Получим С1=8.17w0=16.34. При этом значении С1 из уравнения (***) находим искомую зависимость w от t:
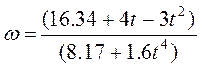 , где t — в
секундах, w — в с-1.
, где t — в
секундах, w — в с-1.
Решение задачи b
Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 2,3,5 и невесомых тел 1,4, соединенных нитями.
| 1. Изобразим действующие на систему силы: активные F, Fупр, Р3, Р2, Р5, реакции N2, N3, натяжение нити S5, силу трения F2тр и момент М. Для определения угловой
скорости вращения шкива 3
2. Определяем кинетическую энергию системы Т0 и Т. Так как в начальный момент система находилась в покое, то Т0=0. |
Величина Т равна сумме энергий всех тел системы, имеющих массу:
Т=Т3+ Т2+ Т5
Учитывая, что тело 3 вращается вокруг неподвижной оси, тело 2 движется поступательно, а подвижный блок 5 – плоскопараллельно, получим:
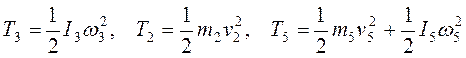 (*)
(*)
Все входящие сюда скорости нужно выразить через искомую w3. Для этого предварительно заметим, что v5 (скорость центра подвижного блока 5) и w5 (угловая скорость вращения блока 5) связаны соотношением w5r5=v5, где r5— радиус блока 5. Из кинематики также знаем, что v5=v2 / 2 и v2=w3r3. Кроме того, входящие в (*) моменты инерции имеют значения
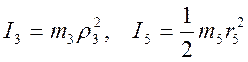
Подставляя все выражения для скоростей и моментов инерции в (*) получим окончательно выражение для кинетической энергии системы
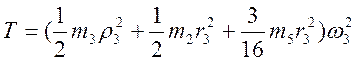
3. Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда точка приложения силы F пройдет путь s=0.2 м. Введя обозначения s2 – перемещение груза 2, s5 – перемещение центра подвижного блока 5, j3 – угол поворота шкива 3, l0 и l1 – начальное и конечное удлинение пружины, получим
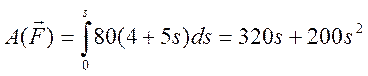 ;
; 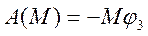 ;
; 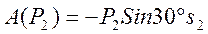 ;
;
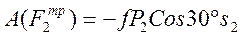 ;
; 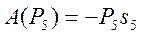 ;
; 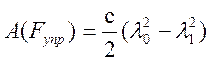
Работы остальных сил равны нулю, так как сила Р3 и реакция N3 приложены к неподвижной оси шкива 3, реация N2 перпендикулярна перемещению груза 2, а сила натяжения нити S5 – приложена к мгновенному центру скоростей подвижного блока 5.
По условию задачи l0=0 (начальная деформация пружины равна нулю), тогда l1=s5 (удлинение пружины равно перемещению центра подвижного блока 5). Кроме того, перемещение s точки приложения силы F связано с углом поворота шкива 3 соотношением j3R3=s (то есть j3=s/R3). Величины s2 и s5 нужно также выразить через заданное перемещение s. При этом учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Так как, например, v2=w3r3, то и s2=j3r3; v5=v2 / 2, то и s5=s2 / 2. Тогда для перемещений s2 и s5 будем иметь: s2=(r3/R3)s, s5=(r3/2R3)s. При найденных значениях j3, s2 и s5 для суммы вычисленных работ получим
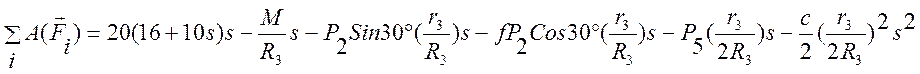
Подставляя полученные выражения для работы и кинетической энергии системы в теорему об изменении кинетической энергии будем иметь:
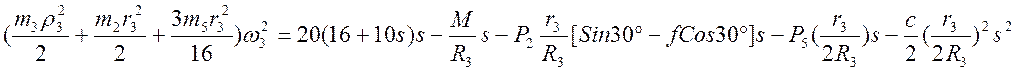
и, подставляя в это равенство численные значения заданных величин, найдем искомую угловую скорость:
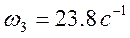
vunivere.ru

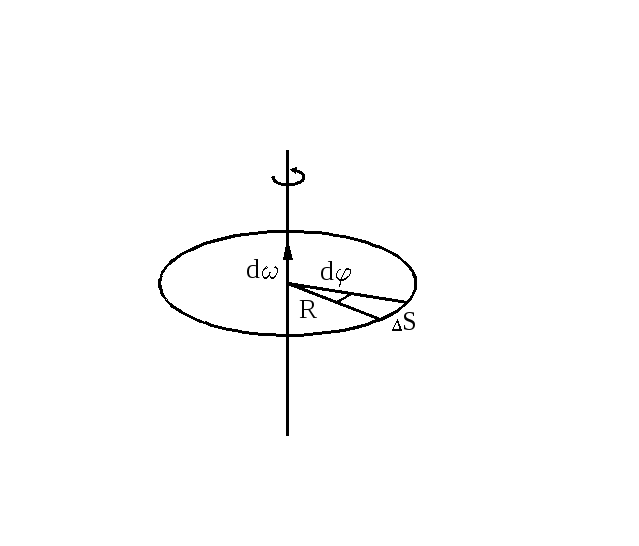
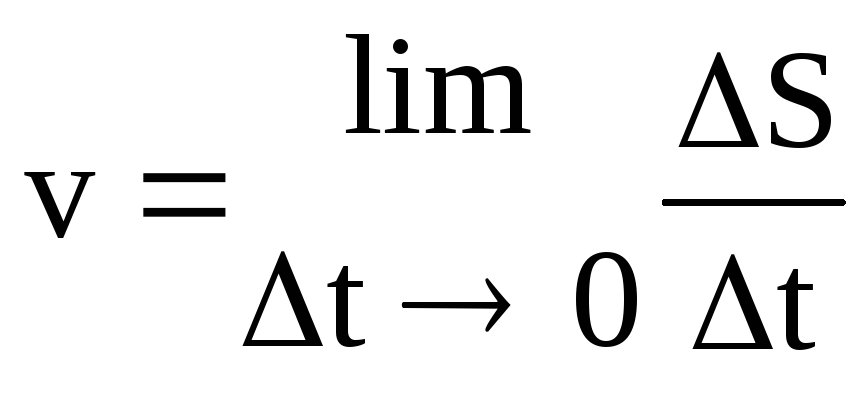 =
=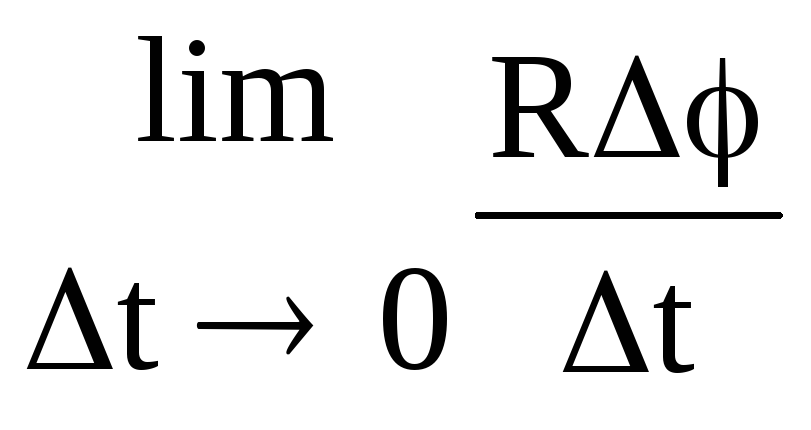 =
=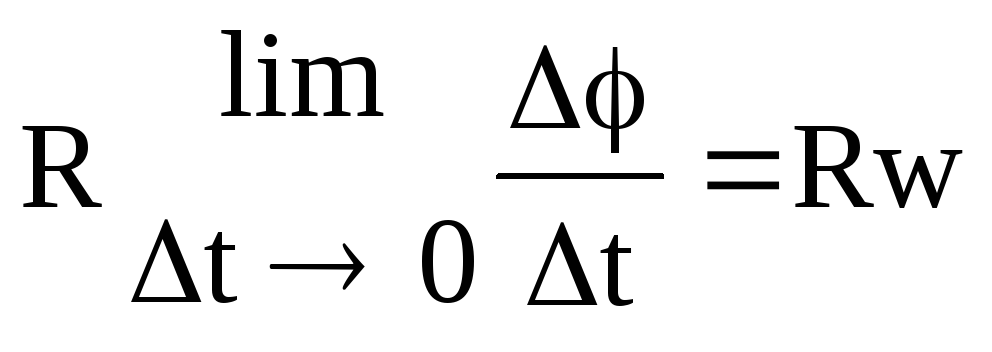


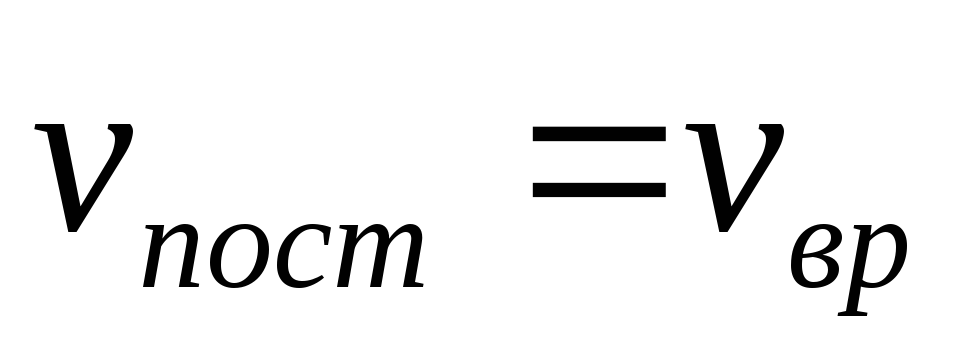 ,
,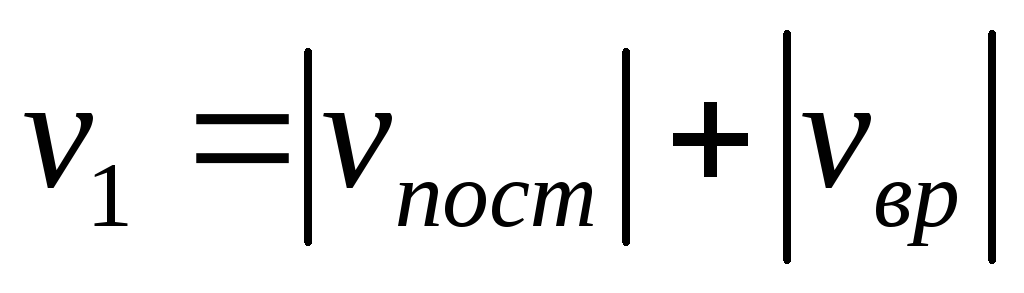
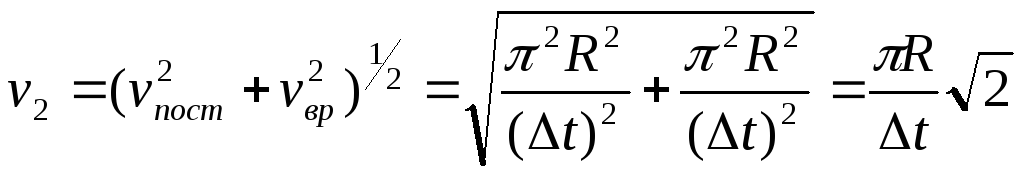
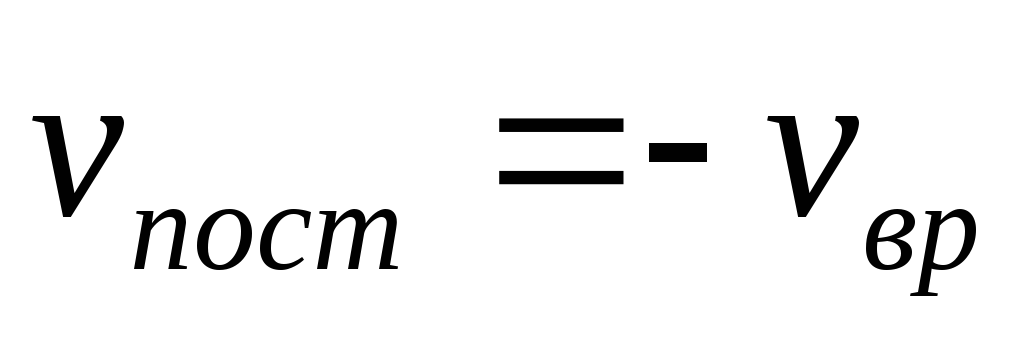 ,
,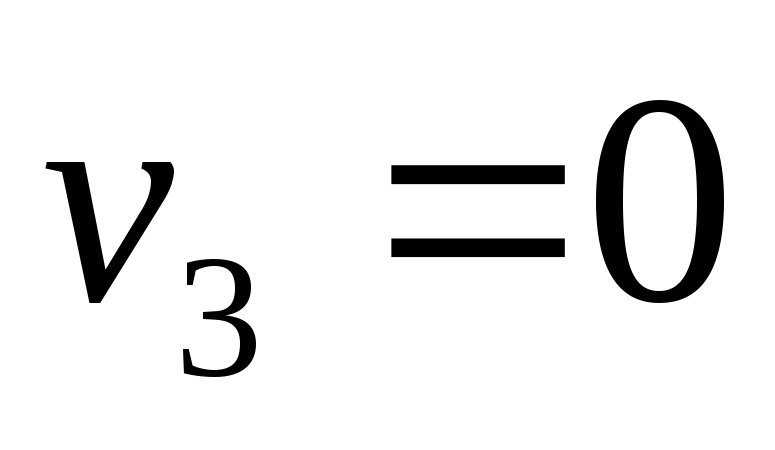 ,
,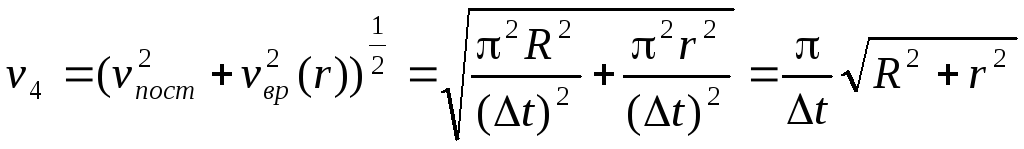
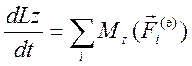
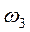 воспользуемся
теоремой об изменении кинетической энергии:
воспользуемся
теоремой об изменении кинетической энергии: